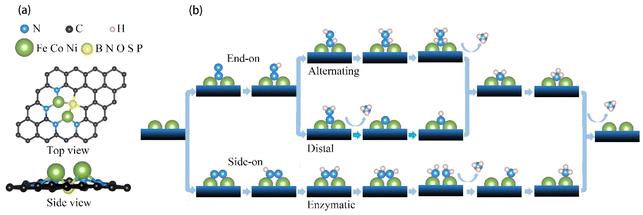
Synergetic effect between non-metals and dual metal catalysts for nitrogen reduction reaction†
Ji
Zhang
a,
Weisong
Yang
b and
Chenghua
Sun
 *c
*c
aDepartment of Electronical Engineering, Tongling University, Tongling, 244061, China
bDepartment of Communication and Electronics, Jiangxi Science and Technology Normal University, Nanchang, 330013, China
cDepartment of Chemistry and Biotechnology, Swinburne University of Technology, Hawthorn, VIC 3122, Australia. E-mail: chenghuasun@swin.edu.au
First published on 14th June 2023
Abstract
Nitrogen reduction reaction (NRR) is an essential process for ammonia synthesis. Currently, such process is overwhelmingly catalyzed with iron-based metal catalysts and still confronts the big challenge of high overpotential when room-temperature electrosynthesis is targeted due to the intrinsic inertness of N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond in N2. In this study, dual metal catalysts have been computationally designed and modulated by different non-metals dispersed in a graphene frame. As scanned by density functional theory (DFT) calculations, five candidates, namely Fe2@SN4, Fe2@BN4, Co2@BN4, Co2@PN4 and Ni2@PN4 catalysts, have been identified as promising catalysts with a calculated onset potential of −0.20, −0.27, −0.36, −0.34, and −0.33 V, respectively; more importantly, the competitive hydrogen evolution reaction (HER) can be well suppressed during the NRR. Such excellent catalytic performance origins from two synergetic effects, including the metal–metal and metal–ligands (non-metals) interactions, both of which can promote the electron transfer from d-orbitals of metal atom pair to the anti-bonding orbitals of adsorbed N2 molecules. This can effectively activate the N
N bond in N2. In this study, dual metal catalysts have been computationally designed and modulated by different non-metals dispersed in a graphene frame. As scanned by density functional theory (DFT) calculations, five candidates, namely Fe2@SN4, Fe2@BN4, Co2@BN4, Co2@PN4 and Ni2@PN4 catalysts, have been identified as promising catalysts with a calculated onset potential of −0.20, −0.27, −0.36, −0.34, and −0.33 V, respectively; more importantly, the competitive hydrogen evolution reaction (HER) can be well suppressed during the NRR. Such excellent catalytic performance origins from two synergetic effects, including the metal–metal and metal–ligands (non-metals) interactions, both of which can promote the electron transfer from d-orbitals of metal atom pair to the anti-bonding orbitals of adsorbed N2 molecules. This can effectively activate the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, resulting in low NRR onset potential and high NH3 selectivity. The presented theoretical effort advances the theoretical understanding and provides guidance for the rational design of advanced non-precious NRR catalysts with high efficiency and selectivity.
N bond, resulting in low NRR onset potential and high NH3 selectivity. The presented theoretical effort advances the theoretical understanding and provides guidance for the rational design of advanced non-precious NRR catalysts with high efficiency and selectivity.
Introduction
NH3 plays an important role in numerous industrial production processes and human life owing to it being the main component of nitrogen fertilizers,1 basic raw material for most industrial chemicals,2 and an excellent green energy carrier.3 The Haber–Bosch process (HBP), established more than 100 years ago, is still the dominating technology for large-scale ammonia production. However, this process requires high temperature (350–550 °C) and pressure (15–25 MPa)4 to break the inert N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, under which condition a large amount of fossil energy is consumed along with severe emission of greenhouse gases. In this situation, extensive efforts have been made to search for environmentally friendly and resource-sustainable NH3 synthesis methods.
N bond, under which condition a large amount of fossil energy is consumed along with severe emission of greenhouse gases. In this situation, extensive efforts have been made to search for environmentally friendly and resource-sustainable NH3 synthesis methods.
Inspired by legumes effectively capturing N2 from the atmosphere under ambient conditions, researchers have explored many strategies for the artificial fixation of N2 to NH3, including heterogeneous, photo, and electrical catalysis.5–8 In particular, electrochemical nitrogen reduction reaction (NRR) is a promising alternative owing to its low cost, greenness, and easy accessibility.9–11 Although numerous NRR catalysts have been reported, various open challenges, such as high overpotentials, poor selectivity, the consumption of precious metals, and low efficiency, make it far from achieving the performance of HBP,12 which subsequently put forward a challenge to develop advanced electrocatalysts.
Single-atom catalysts (SACs) have been widely used in catalytic reactions owing to their unique electronic properties, ultrahigh utilization, and high catalytic activity and selectivity.13–17 For the fabrication of SACs, two-dimensional materials have been widely used as the substrate to fix single metals, such as metal anchored in N-doped graphene to form M@Nx catalysts (M, N, and x represent the metal atom, nitrogen atom, and the number of N atoms, respectively), as demonstrated in various electrocatalytic reactions.18–20 However, these catalysts feature a single active site, which often cannot meet the demand of these reactions with multiple elementary steps because the ideal reactivity requested by the early stage is often different or even opposite of the late stage. For instance, strong N–metal interaction is helpful to activate N2, which is critical for its initial reduction, but such strong bonding often leads to difficult desorption of ammonia products at the late stage.21–25
As inspired by molecular catalysts,26–28 several transition metals, such as Fe, Co, and Ni, are often active for NRR, whose empty d-orbitals can accept lone-pair electrons of N2 to enhance the binding strength and donate the partially filled d-electrons back to the anti-bonding orbital of the molecular N2 adsorbed on it to weaken the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond.29 As determined by this mechanism, transition metals need to be partially oxidized rather than pure metals or highly oxidized, as well demonstrated by Li et al.30 This underlines the significant roles of surrounding ligands, which should offer a strong capacity to fix SACs, but cannot be too strong to fully oxidize active metals. Another key factor is conductivity, which is critically important for electron transport during electrocatalysis processes but hardly available when transition metals are fully oxidized. Therefore, a delicate balance has to be satisfied between strong fixation and proper metal–ligands interaction, which is an open challenge for the rational design of SACs. To overcome this issue, dual-metal catalysts, which feature metal–metal and multiple metal–ligands interactions, have been developed and demonstrated for NRR. Different from SACs, dual-metals offer the flexibility to choose large sets of metal combinations and work together, under which single metal–N interaction does not have to be strong;31 more importantly, metal–metal bonding can offer excellent conductivity, as requested by NRR electrocatalysis. It is particularly worth noting that non-metals themselves can also serve as active center to catalyze NRR.32 Such a strategy has been successfully demonstrated by dual-atom catalysts (DACs)33,34 and even triple-atom catalysts.35,36 Not surprisingly, the central question is what metal combinations are ideal.
N triple bond.29 As determined by this mechanism, transition metals need to be partially oxidized rather than pure metals or highly oxidized, as well demonstrated by Li et al.30 This underlines the significant roles of surrounding ligands, which should offer a strong capacity to fix SACs, but cannot be too strong to fully oxidize active metals. Another key factor is conductivity, which is critically important for electron transport during electrocatalysis processes but hardly available when transition metals are fully oxidized. Therefore, a delicate balance has to be satisfied between strong fixation and proper metal–ligands interaction, which is an open challenge for the rational design of SACs. To overcome this issue, dual-metal catalysts, which feature metal–metal and multiple metal–ligands interactions, have been developed and demonstrated for NRR. Different from SACs, dual-metals offer the flexibility to choose large sets of metal combinations and work together, under which single metal–N interaction does not have to be strong;31 more importantly, metal–metal bonding can offer excellent conductivity, as requested by NRR electrocatalysis. It is particularly worth noting that non-metals themselves can also serve as active center to catalyze NRR.32 Such a strategy has been successfully demonstrated by dual-atom catalysts (DACs)33,34 and even triple-atom catalysts.35,36 Not surprisingly, the central question is what metal combinations are ideal.
In the present work, a computational effort has been made towards a systematic investigation of various combinations of dual metals using nonmetal-doped graphene as the substrate. Our design starts from low-cost elements for both transition metals and ligands, focusing on Fe, Co, and Ni as identified from early SACs studies.37 Five nonmetals, including B, N, O, S, and P, have been scanned with N as the major one because N-doped graphene has been successfully synthesized and widely used to load SACs and DACs. Following these rules, dual metals are generated using five ligands, including 15 combinations with a formula M2@XN4 (M = Fe, Co, Ni; X = B, O, S, P, N). As demonstrated below, candidates have been identified as promising catalysts, namely, Fe2@SN4 (0.20 V), Fe2@BN4 (0.27 V), Co2@BN4 (0.36 V), Co2@PN4 (0.34 V), and Ni2@PN4 (0.33 V), with NRR onset potentials presented in the brackets, which outperform most of the current NRR catalysts.
Computational details
All the geometric optimization and energetic calculations were performed within the density functional theory (DFT) framework by employing the Vienna ab initio simulation package (VASP).38 The exchange–correlation interactions were treated by the spin-polarized general gradient approximation (GGA) using the Perdew–Burke–Emzerhof functional.39 The projector augmented wave (PAW) was used to describe the electron-ion interactions.40 The plane wave energy cutoff of 400 eV and the Monkhorst–Pack grid of 2 × 2 × 1 k-point were set for structure relaxation, while the density of states (DOS) calculation was carried out by using a 4 × 4 × 1 Monkhorst–Pack grid. The energy convergence criterion of 1 × 10−5 eV and maximum force of 0.02 eV Å−1 were adopted to allow for full structural optimization. Bader charge analysis was applied to analyze the atomic charge and charge transfer.41 To describe the van der Waals (vdW) interactions, the DFT-D3 (the semi-empirical dispersion-corrected density functional theory with the zero-damping method of Grimme) approach was used in the calculation.42 The projected crystal orbital Hamilton population (pCOHP) was employed to analyze the intermediate orbitals and bond structure by using lobster code.43,44 All structures obtained by DFT were visualized using the VESTA program.45To evaluate the electrode potentials of the NRR process, the Gibbs free energies of intermediates were calculated using the computational hydrogen electrode (CHE) model introduced by Nørskov and co-workers.46 In this study, the standard hydrogen electrode (SHE) was used as the reference electrode: H+ + e− → ½H2 in equilibrium at 298.15 K and at 1 bar.
Thus, the free energy of proton/electron (H+ and e−) was set to the chemical potential of ½H2 under potential, U = 0, and pH = 0. In addition, all reactions were performed at 1 bar and 298.15 K.
The Gibbs free energy change for each reaction step is defined by the expression:
| ΔG = ΔE + ΔZPE − TΔS + ΔGu + ΔGpH | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × pH, where kB is the Boltzmann constant and pH = 0 for the acid medium.
10 × pH, where kB is the Boltzmann constant and pH = 0 for the acid medium.
In the present study, transition metal pairs were anchored into a 5 × 5 supercell graphene containing three vacancies surrounded by five pyridinic N sites to form M2@NN4 (M = Fe, Co, Ni) structures, as shown in Fig. 1. If one N atom was substituted by another non-metal atom, such as B, O, S and P atoms, the M2@BN4, M2@ON4, M2@SN4, M2@PN4 structures were formed, respectively. These structures can be expressed uniformly by the formula M2@XN4 (M = Fe, Co, Ni; X = B, N, O, S, P). The vacuum layer was set to 20 Å to avoid interaction with the mirror image of slab. To evaluate the stability of paired metal atom catalysts, the average binding energy (Eb) was calculated as follows:
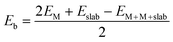 | (2) |
The intrinsic activity of an electrocatalyst is determined by the potential determination step (PDS), which has the most positive Gibbs free energy change (Gmax). Based on the PDS, the onset potential Uonset (Uonset = −ΔGmax/e) is computed to evaluate the catalytic performance, which is defined as the reducing potential with all steps in the pathway being thermodynamically downhill.
Results and discussion
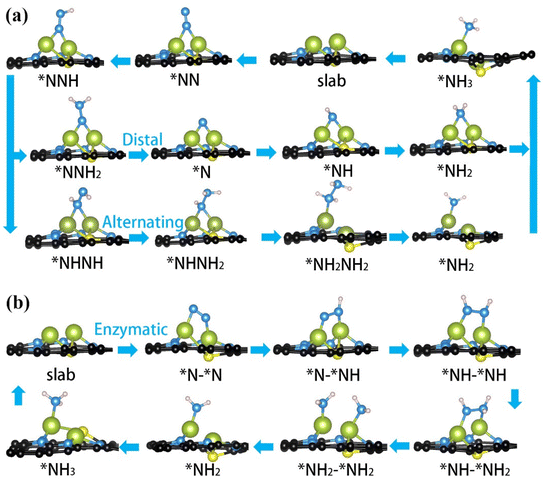
To investigate the electrocatalytic properties of these DACs, we fully considered the possible mechanisms, which have been well-established and widely used over time as presented in Fig. 1b. As the first step of NRR, the molecular N2 is adsorbed on the active sites to form an *N2 intermediate through two configurations: end-on or side-on configuration, which then lead to three different hydrogenation pathways, including the distal or alternating reaction pathway for end-on configuration and enzymatic pathway for side-on configuration. Taking Fe2@SN4 as an example, we demonstrate the optimized structures of every intermediate for NRR along the three reaction pathways with both configurations, as shown in Fig. 2.Two end-on geometries have been considered for initial N2 adsorption, with N2 adsorbed on the bridge site of Fe dimer and on the top site on one of the Fe atoms, with the former being energetically favorable, as shown in Fig. 2(a). With respect to free gas, following N2 adsorption, the N–N distance increases from 1.09 Å to 1.17 Å due to the activation. The first proton–electron pair attacks the distal N to form *NNH intermediate, which is the first step of six elementary reduction steps. Starting from the second hydrogenation, the reaction takes two different pathways, namely distal and alternating mechanisms. The *NNH2 intermediates in the distal pathway still maintain adsorption on the bridge-site, but the *NHNH intermediates in the alternating pathway transform into adsorption on the top-site, as fully demonstrated in Fig. 2(a). Different from distal/alternating paths, the enzymatic process starts from side-on adsorption, as shown in Fig. 2(b), with N2 being fixed over two metals. With respect to end-on adsorption, the N–N distance is enlarged to 1.22 Å, indicating stronger activation of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, as shown in Fig. S1.† Following this adsorption, the full enzymatic pathway has been presented in Fig. 2(b), whose energy profiles will be further calculated.
N bond, as shown in Fig. S1.† Following this adsorption, the full enzymatic pathway has been presented in Fig. 2(b), whose energy profiles will be further calculated.
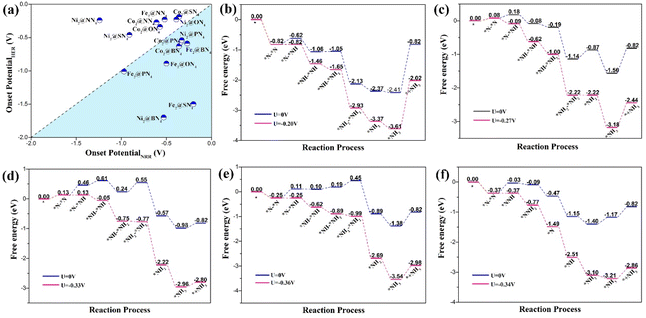
To screen the optimal reaction pathway and catalysts, we calculated the free energy changes ΔG of PDS of each catalytic mechanism and then obtained the maximum change (ΔGmax) and the onset potential (Uonset), which can help us to compare the performance of different catalysts. The maximum change in free energy of 15 dual-atom catalysts for NRR via alternating, distal, and enzymatic pathways is summarized in Fig. 3. Except for Fe2@PN4, Co2@PN4, Ni2@NN4 and Ni2@SN4, the minimum ΔGmax appears at enzymatic pathways of all the DACs, indicating that the NRR on DACs prefers to take the enzymatic mechanism. This catalytic property may be ascribed to the synergetic effect of two transition metal atoms as active sites, which also occur in the natural N2 fixation through the enzyme nitrogenase in diazotrophic micro-organisms47 and other dual-site catalysts.48,49 Furthermore, it should be noted that seven out of fifteen DACs exhibit excellent catalytic activity possessing very low values of ΔGmax < 0.40 eV, including Fe2@BN4 (0.27 eV), Fe2@SN4 (0.20 eV), Co2@BN4 (0.36 eV), Co2@SN4 (0.30 eV), Co2@PN4 (0.34 eV), Ni2@ON4 (0.39 eV), and Ni2@PN4 (0.33 eV) catalysts, with ΔGmax being presented in the brackets.
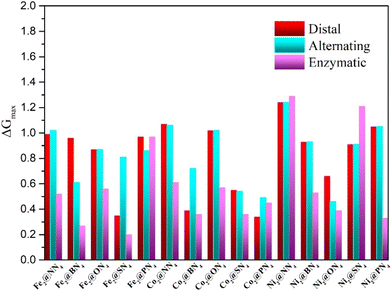 | ||
| Fig. 3 Summary of the maximum change in free energy of 15 Dual-atom catalysts for NRR via alternating, distal, and enzymatic pathways. | ||
For further performance evaluation of catalyst candidates, it is necessary to consider the competition between NRR and HER (hydrogen evolution reaction) that consumes protons and electrons. We investigated the HER process by calculating free energy change for the formation of *H, as shown in Fig. S2,† and then obtained the onset potentials for HER, which are compared with the corresponding onset potential for NRR, as illustrated in Fig. 4(a). As we can see that NRR is dominant in the bottom right region, while HER is dominant in the top left region. Five candidates, Fe2@BN4, Fe2@SN4, Co2@BN4, Co2@PN4, and Ni2@PN4, demonstrate both high catalytic selectivity and low onset potential for NRR, making them very promising candidates for the reduction of N2.
The energetic details for NRR on five candidates are illustrated in free energy diagrams, as shown in Fig. 4(b)–(f). Accordingly, the adsorption free energy changes of N2 molecule on Fe2@SN4, Co2@BN4, and Co2@PN4 catalysts are negative with values of −0.82 eV, −0.25 eV, and −0.37 eV, respectively, indicating that N2 adsorption can occur spontaneously. Therefore, these catalysts are superior for the adsorption of N2 to Fe2@BN4 and Ni2@PN4, which undergo 0.08 and 0.13 eV uphill, respectively. Additionally, for Fe2@SN4, Ni2@PN4, Co2@BN4, and Fe2@BN4, the PDS appears at the first proton–electron transfer step, while for Fe2@BN4, the PDS is found at the fifth step but not the first hydrogenation step. For the other DACs, the PDS is found almost at the first hydrogenation step, as seen in Table S2.† The PDS is directly related to the onset potentials, under which all the reaction steps are downhill. Especially, the Fe2@SN4 exhibits excellent catalytic activity with ultralow onset potential −0.20 V, which is less than that for the other Fe-based catalysts, such as FeN4@Gra SAC (−1.66 V),50 Fe2N6@Gra (−0.46 V) DAC,49 and Fe(0001) flat surface (about −1.23 V).51 It is worth mentioning that we also calculated the catalytic properties of the corresponding Fe@SN4 SAC, which consists of a unitary single Fe atom as an active site, as shown in Fig. S1 and S3.† By contrast, the onset potential of Fe@SN4 increases to −1.01 and −0.91 V through distal and enzymatic processes, respectively. Therefore, the improvement of catalytic performance may be attributed to both the synergistic effect of dual-metal active sites and significant boosting from proper ligands.
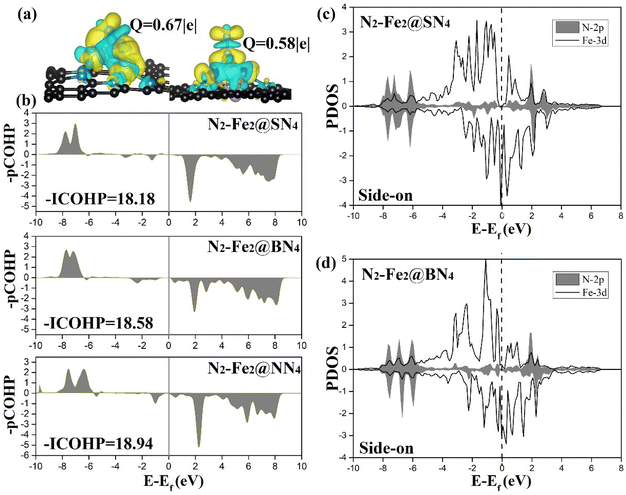
The origin of the high catalytic performance of DACs was further investigated by studying their electronic properties. First, the adsorption of N2 molecules on the active site plays an important role, which is mainly related to orbital hybridization and electron transfer. As shown in Fig. 5(a), charge density differences for end-on and side-on adsorptions have been presented, in which significant electron transfer has been observed from two metal centers. Given that bonding orbitals have been fully occupied in free N2 gas, newly injected electrons from the catalysts will inevitably fill into the anti-bonding states; as a result, N2 has been activated. To better understand the orbital interaction associated with N2 activation, projected crystal orbital Hamilton populations (pCOHP) and its integration (ICOHP) have been obtained for N–N adsorbed over Fe2@SN4, Fe2@BN4, and Fe2@NN4 with side-on configuration, as shown in Fig. 5(b). Interestingly, –ICOHP decreases slightly from 18.94 for Fe2@NN4 to 18.58 for Fe2@BN4 and 18.12 for Fe2@SN4. Such a result is essentially determined by the electronegativity; as a result, B and S, with Pauli electronegativity χ = 2.06 and 2.58,52 present lower capacity to oxidize Fe dimer than that by N-ligands (χ = 3.04), which is helpful to keep the metal nature of Fe–Fe dimer. Such features can be better illustrated by calculated DOS profiles in Fig. 5(c) and (d). As demonstrated by calculated projected DOS of N-2p and Fe-3d orbitals after N2 adsorption on Fe2@SN4, and Fe2@BN4 surfaces, two features can be summarized: (i) clear overlap area between the Fe-3d and N-2p has been observed, suggesting substantial orbital hybridization, which contributes to the electron transfer between N2 adsorbate and DACs and is beneficial for N2 activation; and (ii) stronger peaks at Fermi energy have been observed, as determined by lowly oxidized Fe2. Towards efficient NRR, lone-pair electrons from N2 fill into empty d-orbitals of partially oxidized transition metals, driving initial N2 adsorption, following which metals further back donate electrons to the anti-bonding state of N2 and result in effective activation. As illustrated in Fig. 5(a), the electron density accumulation areas are mainly observed between the Fe atom and N2, indicating the enhancement of the N–Fe bond as a result of the electron transfer. In comparison, electron density depletion is mainly concentrated on the areas between adsorbed N atoms, which will activate the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond. Such analysis has been supported by Bader charge analysis, which shows an electron transfer of 0.67e from Fe2 to N2 adsorbed via side-on configuration. In contrast, the transferred electron to N2 adsorbed via end-on configuration is only 0.58e, indicating that the adsorption of N2 with side-on configuration is more conducive to the activation of N2. As a reference, the transferred electrons to N2 bound to single Fe@SN4 is only 0.33e, as illustrated in Table S3,† indicating that the dual-metal atom site can significantly strengthen the electron donation to absorbed N2 and subsequently enhance the catalytic activity. It is also worth noting that the transferred electrons are different from Fe dimer to N2 adsorbed on the catalyst with different no-metal ligands, as illustrated in Table S3.† In particular, 0.57e transfer from Fe dimer to N2 adsorbed on Fe2@NN4 catalyst. But the transferred electrons increase when another no-metal atom is introduced in ligands, which are related to the Pauli electronegativity of different no-metal elements.
N bond. Such analysis has been supported by Bader charge analysis, which shows an electron transfer of 0.67e from Fe2 to N2 adsorbed via side-on configuration. In contrast, the transferred electron to N2 adsorbed via end-on configuration is only 0.58e, indicating that the adsorption of N2 with side-on configuration is more conducive to the activation of N2. As a reference, the transferred electrons to N2 bound to single Fe@SN4 is only 0.33e, as illustrated in Table S3,† indicating that the dual-metal atom site can significantly strengthen the electron donation to absorbed N2 and subsequently enhance the catalytic activity. It is also worth noting that the transferred electrons are different from Fe dimer to N2 adsorbed on the catalyst with different no-metal ligands, as illustrated in Table S3.† In particular, 0.57e transfer from Fe dimer to N2 adsorbed on Fe2@NN4 catalyst. But the transferred electrons increase when another no-metal atom is introduced in ligands, which are related to the Pauli electronegativity of different no-metal elements.
Finally, the average binding energy Eb of the TM pairs was calculated to evaluate the stability of the M2@XN4 catalysts, which are listed in Table S3.† The binding energies for Fe2@SN4, Fe2@BN4, Co2@BN4, Co2@PN4, and Ni2@PN4 are calculated and compared with the cohesive energy associated with bulk metals in vacuum (bulk metal), 3.03(1.94), 5.46(4.36), 5.76(3.09), 5.36(2.69) and 5.51(1.39) eV, respectively. The binding energies are all positive, indicating the metal pairs are thermodynamically stable in the non-metal doped graphene. It is worth mentioning that dual-metal catalysts have been synthesized readily in experiments, such as isolated diatomic metal–nitrogen catalyst NiFe–N–C by a metal–organic framework (MOF) assisted method,53 CoFe–N–C catalyst by a two-step pyrolysis process,54 and ZnCo bimetallic sites supported on N doped carbon through a competitive complexation strategy.55 The strategy to combine metal and non-metal ligands has been experimentally demonstrated by Zhao et al. with Fe–S–C linkage, showing impressive NRR performance.56 Following these lab-based achievements, it is believed that the M2@XN4 catalysts proposed in this work are approachable experimentally.
Conclusions
In summary, we proposed the concept of dual-atom catalysts M2@XN4 for NRR, specifically using low-cost transition metals (Fe, Co, Ni) and non-metal ligands (O, S, P, B, N). High performance catalysts have been identified from computational scanning, with five outstanding candidates, Fe2@SN4, Fe2@BN4, Co2@BN4, Co2@PN4, and Ni2@PN4 catalysts, offering an onset potential as low as −0.20, −0.27, −0.36, −0.34, and −0.33 V. This is not only remarkably better than corresponding SACs, but also superior to expensive noble metals (such as single Ru57). These promising candidates also present excellent NRR selectivity over HER and catalyst stability. The electronic structure analysis displayed that the chemical environment around the metal atom-pair seriously impacts the electron transfer between adsorbed N2 and catalysts, which plays an important role in the catalytic activity for NRR. We believe that our theoretical study on transition metal atom-pair catalysts provides guidance for the rational design of non-precious NRR catalysts with high efficiency and selectivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Natural Science Foundation of the Anhui Province (No. KJ2021A1171).References
- Q. Wang, G. Zheng, S. Hao, X. Liu, J. Zheng, Y. Wang, Z. Su, N. Xu, Y. He, L. Lei and X. Zhang, Au1Co1 Alloy supported on graphene oxide with enhanced performance for ambient electrolysis of nitrogen to ammonia computational detail, ACS Sustainable Chem. Eng., 2020, 8, 44–49 CrossRef CAS.
- V. Rosca, M. Duca, M. T. de Groot and M. T. M. Koper, Nitrogen cycle electrocatalysis, Chem. Rev., 2009, 109, 2209–2244 CrossRef CAS PubMed.
- M. Aziz, T. Oda, A. Morihara and T. Kashiwagi, Combined nitrogen production, ammonia synthesis, and power generation for efficient hydrogen storage, Energy Procedia, 2017, 143, 674–479 CrossRef CAS.
- M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. W. Kim, M. Hara and H. Hosono, Ammonia synthesis using a stable electride as an electron donor and reversible hydrogen store, Nat. Chem., 2012, 4, 934–940 CrossRef CAS PubMed.
- Y. Kobayashi, Y. Tang, T. Kageyama, H. Yamashita, N. Masuda, S. Hosokawa and H. Kageyama, Titanium-based hydrides as heterogeneous catalysts for ammonia synthesis, J. Am. Chem. Soc., 2017, 139, 18240–18246 CrossRef CAS PubMed.
- Z. Wang, W. Tian, Z. Dai, T. Zhou, Q. Mao, Y. Xu, X. Li, L. Wang and H. Wang, Bimetallic mesoporous RhRu film for electrocatalytic nitrogen reduction to ammonia, Inorg. Chem. Front., 2021, 8, 4276–4281 RSC.
- X. Lu, M. Li, H. Wang and C. Wang, Advanced electrospun nanomaterials for highly efficient electrocatalysis, Inorg. Chem. Front., 2019, 6, 3012–3040 RSC.
- X. Y. Cui, C. Tang and Q. Zhang, A review of electrocatalytic reduction of dinitrogen to ammonia under ambient conditions, Adv. Energy Mater., 2018, 8, 1800369 CrossRef.
- J. Deng, J. A. Iñiguez and C. Liu, Electrocatalytic nitrogen reduction at low temperature, Joule, 2018, 2, 846–856 CrossRef CAS.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Catalysts for nitrogen reduction to ammonia, Nat. Catal., 2018, 1, 490–500 CrossRef.
- G. Soloveichik, Electrochemical synthesis of ammonia as a potential alternative to the Haber-Bosch process, Nat. Catal., 2019, 2, 377–380 CrossRef CAS.
- A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, Electrochemical ammonia synthesis-the selectivity challenge, ACS Catal., 2017, 7, 706–709 CrossRef CAS.
- Y. J. Chen, S. F. Ji, C. Chen, Q. Peng, D. S. Wang and Y. D. Li, Single-atom catalysts: Synthetic strategies and electrochemical applications, Joule, 2018, 2, 1242–1264 CrossRef CAS.
- Y. Pan, C. Zhang, Z. Liu, C. Chen and Y. D. Li, Structural regulation with atomic-level precision: From single-atomic site to diatomic and atomic interface catalysis, Matter, 2020, 2, 78–110 CrossRef.
- A. Q. Wang, J. Li and T. Zhang, Heterogeneous single-atom catalysis, Nat. Rev. Chem., 2018, 2, 65–81 CrossRef CAS.
- S. Sultan, J. N. Tiwari, A. N. Singh, S. Zhumagali, M. Ha, C. W. Myung, P. Thangavel and K. S. Kim, Single atoms and clusters based nanomaterials for hydrogen evolution, oxygen evolution reactions, and full water splitting, Adv. Energy Mater., 2019, 9, 1900624 CrossRef.
- M. Ha, D. Y. Kim, M. Umer, V. Gladkikh, C. W. Myung and K. S. Kim, Tuning metal single atoms embedded in N x C y moieties toward high-performance electrocatalysis, Energy Environ. Sci., 2021, 14, 3455–3468 RSC.
- H. Fei, J. Dong, D. Chen, T. Hu, X. Duan, I. Shakir, Y. Huang and X. Duan, Single atom electrocatalysts supported on graphene or graphene-like carbons, Chem. Soc. Rev., 2019, 48, 5207–5241 RSC.
- X. Wan, X. Liu, Y. Li, R. Yu, L. Zheng, W. Yan, H. Wang, M. Xu and J. Shui, Fe–N–C electrocatalyst with dense active sites and efficient mass transport for high performance proton exchange membrane fuel cells, Nat. Catal., 2019, 2, 259–268 CrossRef CAS.
- H. T. Chung, D. A. Cullen, D. Higgins, B. T. Sneed, E. F. Holby, K. L. More and P. Zelenay, Direct atomic-level insight into the active sites of a high-performance PGMfree ORR catalyst, Science, 2017, 357, 479–484 CrossRef CAS PubMed.
- C. He, Z. Y. Wu, L. Zhao, M. Ming, Y. Zhang, Y. Yi and J. S. Hu, Identification of FeN4 as an efficient active site for electrochemical N2 reduction, ACS Catal., 2019, 9, 7311–7317 CrossRef CAS.
- F. Lü, S. Zhao, R. Guo, J. He, X. Peng, H. Bao, J. Fu, L. Han, G. Qi and J. Luo, Nitrogencoordinated single Fe sites for efficient electrocatalytic N2 fixation in neutral media, Nano Energy, 2019, 61, 420–427 CrossRef.
- M. Zafari, M. Umer, A. S. Nissimagoudar, R. Anand, M. Ha, S. Umer, G. Lee and K. S. Kim, Unveiling the role of charge transfer in enhanced electrochemical nitrogen fixation at single-atom catalysts on BX sheets (X = As, P, Sb), J. Phys. Chem. Lett., 2022, 13, 4530–4537 CrossRef CAS PubMed.
- Y. Wan, H. Zhou, M. Zheng, Z. H. Huang, F. Kang, J. Li and R. Lv, Oxidation state modulation of bismuth for efficient electrocatalytic nitrogen reduction to ammonia, Adv. Funct. Mater., 2021, 31, 2100300 CrossRef CAS.
- M. Zafari, A. S. Nissimagoudar, M. Umer, G. Lee and K. S. Kim, First principles and machine learning based superior catalytic activities and selectivities for N 2 reduction in MBenes, defective 2D materials and 2D π-conjugated polymer-supported single atom catalysts, J. Mater. Chem. A, 2021, 9, 9203–9213 RSC.
- S. Shaw, D. Lukoyanov, K. Danyal, D. R. Dean, B. M. Hoffman and L. C. Seefeldt, Nitrite and hydroxylamine as nitrogenase substrates: mechanistic implications for the pathway of N2 reduction, J. Am. Chem. Soc., 2014, 136, 12776–12783 CrossRef CAS PubMed.
- Y. Liu, S. Zhang, W. Li, H. Zhou, G. Wang and H. Zhang, Metal (Co/Mo)–N bond anchor-doped N in porous carbon for electrochemical nitrogen reduction, Inorg. Chem. Front., 2021, 8, 1476–1481 RSC.
- T. J. Del Castillo, N. B. Thompson and J. C. Peters, A synthetic single-site Fe nitrogenase: high turnover, freeze-quench 57Fe Mössbauer data, and a hydride resting state, J. Am. Chem. Soc., 2016, 138, 5341–5350 CrossRef CAS PubMed.
- M. A. Légaré, G. Bélanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Nitrogen fixation and reduction at boron, Science, 2018, 359, 896–900 CrossRef PubMed.
- Q. Li, S. Qiu, C. Liu, M. Liu, L. He, X. Zhang and C. Sun, Computational design of single-molybdenum catalysts for the nitrogen reduction reaction, J. Phys. Chem. C, 2019, 123, 2347–2352 CrossRef CAS.
- S. Gao, X. Liu, Z. Wang, Y. Lu, R. Sa, Q. Li, C. Sun, X. Chen and Z. Ma, Spin regulation for efficient electrocatalytic N2 reduction over diatomic Fe-Mo catalyst, J. Colloid Interface Sci., 2023, 630, 215–223 CrossRef CAS PubMed.
- C. Liu, A. Tian, Q. Li, T. Wang, G. Qin, S. Li and C. Sun, Metal-Free Electrocatalysts for the Nitrogen Reduction Reaction, EnergyChem, 2023, 33, 2210759 CAS.
- L. J. Arachchige, Y. Xu, Z. Dai, X. Zhang, F. Wang and C. Sun, Theoretical investigation of single and double transition metals anchored on graphyne monolayer for nitrogen reduction reaction, Phys. Chem. C, 2020, 124, 15295–15301 CrossRef.
- L. J. Arachchige, Y. Xu, Z. Dai, X. Zhang, F. Wang and C. Sun, Double transition metal atoms anchored on Graphdiyne as promising catalyst for electrochemical nitrogen reduction reaction, J. Mater. Sci. Technol., 2021, 77, 244–251 CrossRef CAS.
- X. Wang, S. Qiu, J. Feng, Y. Tong, F. Zhou, Q. Li, L. Song, S. Chen, K. Wu, P. Su, S. Ye, F. Hou, S. Dou, H. Liu, G. Lu, C. Sun, J. Liu and J. Liang, Confined Fe-Cu clusters as sub-nanometer reactors for efficiently regulating the electrochemical nitrogen reduction reaction, Adv. Mater., 2020, 32, 2004382 CrossRef CAS PubMed.
- S. Gao, Z. Ma, C. Xiao, Z. Cui, W. Du, X. Sun, Q. Li, R. Sa and C. Sun, TM3 (TM = V, Fe, Mo, W) single-cluster catalyst confined on porous BN for electrocatalytic nitrogen reduction, J. Mater. Sci. Technol., 2022, 108, 46–53 CrossRef CAS.
- T. Wang, Z. Guo, X. Zhang, Q. Li, A. Yu, C. Wu and C. Sun, Recent progress of iron-based electrocatalysts for nitrogen reduction reaction, J. Mater. Sci. Technol., 2023, 140, 121–134 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Y. Rohling, I. C. Tranca, E. J. M. Hensen and E. A. Pidko, Correlations between density-based bond orders and orbital-based bond energies for chemical bonding analysis, J. Phys. Chem. C, 2019, 123, 2843–2854 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, Origin of the overpotential for oxygen reduction at a fuel-cell cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- V. K. Shah and W. J. Brill, Isolation of an iron-molybdenum cofactor from nitrogenase, Proc. Natl. Acad. Sci. U. S. A., 1977, 74, 3249–3253 CrossRef CAS PubMed.
- T. He, A. R. P. Santiago and A. Du, Atomically embedded asymmetrical dual-metal dimers on N-doped graphene for ultra-efficient nitrogen reduction reaction, J. Catal., 2020, 388, 77–83 CrossRef CAS.
- T. Deng, C. Cen, H. Shen, S. Wang, J. Guo, S. Cai and M. Deng, Atom-Pair Catalysts Supported by N-Doped Graphene for the Nitrogen Reduction Reaction: d-Band Center-Based Descriptor, J. Phys. Chem. Lett., 2020, 11, 6320–6329 CrossRef CAS PubMed.
- J. Xie, H. Dong, X. Cao and Y. Li, Computational insights into nitrogen reduction reaction catalyzed by transition metal doped graphene: Comparative investigations, Mater. Chem. Phys., 2020, 243, 122622 CrossRef CAS.
- E. Skulason, T. Bligaard, S. Gudmundsdottir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jonsson and J. K. Norskov, A Theoretical Evaluation of Possible Transition Metal Electrocatalysts for N2 Reduction, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 RSC.
- J. Emsley, The Elements, Oxford University Press, 3rd edn, 1998 Search PubMed.
- W. Ren, X. Tan, W. Yang, C. Jia, S. Xu, K. Wang, S. C. Smith and C. Zhao, Isolated diatomic Ni-Fe metal-nitrogen sites for synergistic electroreduction of CO2, Angew. Chem., Int. Ed., 2019, 58, 6972–6976 CrossRef CAS PubMed.
- X. Zhou, J. Gao, Y. Hu, Z. Jin, K. Hu and K. M. Reddy, Theoretically Revealed and Experimentally Demonstrated Synergistic Electronic Interaction of CoFe Dual-Metal Sites on N-doped Carbon for Boosting Both Oxygen Reduction and Evolution Reactions, Nano Lett., 2022, 22, 3392–3399 CrossRef CAS PubMed.
- Z. Lu, B. Wang, Y. Hu, W. Liu, Y. Zhao, R. Yang, Z. Li, J. Luo, B. Chi and Z. Jiang, An isolated zinc-cobalt atomic pair for highly active and durable oxygen reduction, Angew. Chem., 2019, 131, 2648–2652 CrossRef.
- A. M. I. Ahmed, L. J. Arachchige, Z. Su, D. B. Hibbert, C. Sun and C. Zhao, Nitrogenase-Inspired Atomically Dispersed Fe–S–C Linkages for Improved Electrochemical Reduction of Dinitrogen to Ammonia, ACS Catal., 2022, 12, 1443–1451 CrossRef.
- C. Liu, Q. Li, J. Zhang, Y. Jin, D. R. MacFarlanea and C. Sun, Conversion of dinitrogen to ammonia on Ru atoms supported on boron sheets: a DFT study, J. Mater. Chem. A, 2019, 7, 4771–4776 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3qi00517h |
| This journal is © the Partner Organisations 2023 |