Interplay between chalcogen bonds and dynamic covalent bonds

Abstract

Chalcogen bonds as a type of supramolecular interactions have been attracting increasing attention, and studies on their regulating mechanisms are of importance. Herein, we demonstrate the interplay between chalcogen bonds and dynamic covalent chemistry (DCC) toward the investigation of chalcogen bonding and control over imine systems. The intramolecular Chal⋯O/N chalcogen bonding was revealed to modulate the conformational preference of ortho-chalcogen benzaldehydes and associated imines. The role of chalcogen bond in shifting dynamic imine exchange was systematically studied, with chalcogen bonding significantly decelerating the kinetics, while thermodynamically stabilizing the imines. Computational studies further unraveled mechanistic insights for chalcogen bonding, with orbital and electrostatic interactions accounting for the major contribution. Moreover, orbital interaction mainly makes up the difference from S to Te, and tellurium enables the strongest interaction, in line with the largest effect of Te on the movement of the imine exchange equilibrium. By utilizing the effects of chalcogen bonds on imine DCC, the reversal of the thermodynamic and kinetic selectivity of dynamic covalent systems was controlled. The results should open up opportunities for molecular recognition, dynamic assemblies, catalysis, and associated endeavors.

---

Introduction

Chalcogen–chalcogen contacts are widespread in chemistry, and as one class of emerging non-covalent bonding forces, chalcogen-bonding interactions have been creating intensive interest in recognition, assembly, catalysis, and drug design.^1–7 Considered as a sister interaction of halogen bonding, chalcogen bonding is generally viewed as one type of “σ-hole interaction”.^8–11 In addition to electrostatic interactions, n → σ* orbital delocalization contributes greatly to chalcogen bonding, as revealed by extensive experimental and theoretical studies.^4,12–15 As a building motif for molecular recognition, novel chalcogen bond-based hosts have been developed for anion binding and transport.^1,16–19 Moreover, chalcogen bonds have been employed for driving supramolecular assemblies, including those in solution, solid-state, and interfaces.^20–24 Analogous to hydrogen bonding, chalcogen bonding catalysis is capturing attention in organocatalysis, such as in carbonyl activation.^25–28 In addition, by taking advantage of its directional effect, chalcogen bonding offers a handle for regulating the conformation of drug molecules, reactive intermediates, as well as organic optoelectronic materials.^7,29–32 Therefore, the development of new structures, regulating mechanisms, and applications of chalcogen bonding is of great significance.

Through reversible formation, breakage, and exchange of covalent bonds, research on dynamic covalent chemistry (DCC) has extended the realm of supramolecular chemistry and found broad utility in the construction of molecular assemblies and functional materials.^33–40 The interplay between dynamic covalent and non-covalent interactions has become a powerful tool for modulating DCC and concomitantly provides a versatile platform for probing and regulating weak bonding forces.^41–48 However, the use of chalcogen bonding in DCC has virtually escaped attention.⁴⁹ Recently, we demonstrated the capability of n → π* orbital interactions for controlling the formation and exchange of imines, one of the most employed dynamic covalent bonds.^50,51 Inspired by these studies, we were further interested in exploring the influence of chalcogen bonding and DCC on each other. With aldehyde as the central functional group in DCC, the manipulation of non-covalent chalcogen⋯O interactions would offer new possibilities for DCC endeavors.

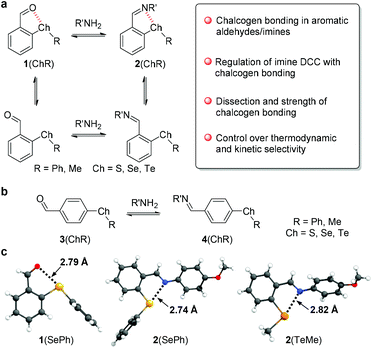
Instead of using heterocycles, we focused on aromatic thioether/selenoether/telluroether as chalcogen bond donors in light of their structural variability and facile accessibility. Considering the amphoteric behavior of chalcogens, the ether analogs have been commonly employed as Lewis bases and metal ligands,^2,52 and their associated chalcogen bonding as electron acceptors is relatively underexplored. We have postulated that the incorporation of sulfur, selenium, or tellurium on the ortho position of aromatic aldehydes (1, Fig. 1a) could give rise to intramolecular chalcogen⋯O contacts. Moreover, such chalcogen bonding interactions could be regulated through intermolecular dynamic covalent reactions (DCRs) with amines to afford imines (2) due to varying electron-donating ability between the aldehyde oxygen and imine nitrogen. In the current work, the chalcogen bond and its interrelation with the imine bond were explored through the strategy of DCC. The modulation of chalcogen bonds within aldehyde/imine structures, as well as underlying contributing factors and interacting strengths, was elucidated. The impact of chalcogen bonding on the kinetics and thermodynamics of imine exchange was systematically examined. The unique reactivity also allowed the reversal of the thermodynamic and kinetic selectivity of dynamic covalent systems. The mechanistic insights revealed lay the foundation for molecular assemblies and related functionalization studies.

Fig. 1 (a) Illustration of the interplay between the chalcogen bond and dynamic imine chemistry. (b) Structures of control compounds and their imines. (c) Crystal structures of 1(SePh), 2(SePh), and 2(TeMe). The distances of chalcogen bonds are listed.

Results and discussion

Synthesis and structural analysis

With the concept in place, a suite of ortho-chalcogen benzaldehydes (1, Fig. 1a and Scheme S1†) were prepared through nucleophilic aromatic substitution reactions, with para-chalcogen benzaldehydes (3) and their imines (4) as controls (Fig. 1b). Crystal analysis was employed to identify potential weak interactions within aldehydes and their imines. Taking 1(SePh) as an example, the selenium atom and aldehyde unit adopt a planar configuration relative to the benzene ring, with a distance of 2.79 Å for Se⋯O (Fig. 1c). These results are indicative of a chalcogen bonding interaction between the aldehyde oxygen and selenoether. Furthermore, the oxygen atom resides along the axis of the C–Se bond, supporting the directionality of the interaction. Intermolecular C–Se/π and π stacking interactions could also have a stabilizing effect on crystal packing (Fig. S21†).^53,54 Similar solid-state structures were obtained with 1(SPh) (S⋯O 2.81 Å) and 1(TePh) (Te⋯O 2.78 Å) (Fig. S21†). The presence of the Chal⋯N chalcogen bond was confirmed with p-anisidine-derived imines 2(SePh) (Se⋯N 2.74 Å) and 2(TeMe) (Te⋯N 2.82 Å) (Fig. 1c).

To explore the conformational effect of the chalcogen bond in solution, DFT calculations were conducted for aldehyde 1 and imine 2 with M06-2X-D3/def2-TZVP/IEF-PCM(acetonitrile). Both open and closed conformations were considered, with closed conformer 1 exhibiting chalcogen bonding (Fig. 2a). Taking 1(SePh) as an example, the major conformer 1 was identified from the torsion scan (Fig. 2a and S22†), and closed conformer 4 is neglectable (∼4 kcal mol⁻¹ higher), likely due to electronic repulsion between phenyl and oxygen lone pairs. The distribution of 1(SePh) is shown in Fig. 2b, with 88%, 6%, and 5% for the populations of conformers 1, 2, and 3, respectively. There is an increasing trend in the amount of conformer 1 for S, Se, and Te, with conformer 1 (>99%) being dominant for 1(TePh) and 2(TePh). Moreover, a similar sequence was unraveled for 1(ChalMe) and 2(ChalMe), and 1(TeMe) and 2(TeMe) exist as conformer 1 (>99%) (Fig. S23†). The dependence of the conformational distribution on the type of chalcogen atom indicates the stabilizing role of chalcogen bonding, for which Te would afford the strongest interaction.^{1–9,21–26}

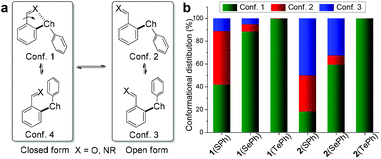Fig. 2 (a) The open and closed conformations of 1(ChalPh) and 2(ChalPh). (b) Comparison of conformer distribution of 1(ChalPh) and 2(ChalPh) obtained by DFT calculations.

The effect of chalcogen bonding on imine exchange

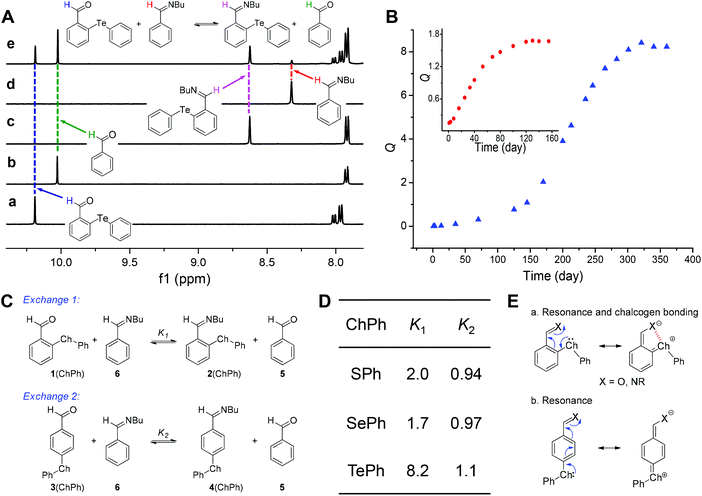
In the next step, we investigated the impact of chalcogen bonds on the formation and exchange of imines. DCRs of aldehydes (1) with 1-butylamine were run in CD₃CN with molecular sieves present, and the quantitative formation of imines (2) was detected (Fig. 3A and S24–S50†). Moreover, the rate for imine formation had the following order for 1(ChalPh): Te < Se < S (Fig. S25, S28, and S31†). In order to quantify the role of chalcogen bonding on imine DCC, a series of aldehyde competition experiments between 1 and benzaldehyde (5) for reactions with 1-butylamine were conducted with 5 and its imine (6) as the reference (exchange 1, Fig. 7A and C). As recently shown by us with π stacking⁵⁵ and n → π* interactions,^50,51 the shift in the dynamic covalent exchange equilibrium would serve as a barometer for probing chalcogen bonds.

Fig. 3 (A) ¹H NMR spectra of 1(TePh) (a), 5 (b), 2(TePh) (c), 6 (d), and imine exchange (e) in CD₃CN. (B) Kinetic profile of the one-pot reaction of 1(TePh), 5 (1.0 equiv.), and 1-butylamine (1.0 equiv.) in CD₃CN. The y-axis Q is referred to as the reaction quotient. The corresponding plot of 1(SePh) is shown in the inset. (C) Comparison of imine exchange reactions 1 and 2. (D) Summary of equilibrium constants of imine exchange reactions 1 and 2. (E) Illustration of the resonance effect and chalcogen bonding.

Imine 6 was created predominately at the early stage followed by a slow exchange with aldehyde 1 to afford imine 2. It took approximately 55, 140, and 340 days for the exchange of 1(SPh), 1(SePh), and 1(TePh) to equilibrate, respectively (Fig. 3B and S54–S59†). The sluggish aldehyde exchange is likely due to the lack of water in the reaction media since the hydrolysis of imine created initially to recover the original aldehyde and amine is required for its reaction with the second aldehyde.⁵⁶ The trend of the rate for imine formation and exchange (Te < Se < S) can be interpreted with resonance-assisted chalcogen bonding, which imparts aldehyde/imine partial single bond character and thereby their deactivation (Fig. 3E). Such a regulating mechanism is different from chalcogen bonding catalysis, which could activate the carbonyl group.^25–28

The exchange between 1(SPh) and 6 afforded an equilibrium constant (K) of 2.0, in favor of 2(SPh) and 5. A similar trend was observed for 1(SePh), with a K value of 1.7. The largest K value was obtained with 2(TePh) (8.2, Fig. 3A and D). The sequence of calculated K values (Te ≫ S > Se) further confirmed the experimental data (Table S3†). We rationalized these results as follows. Intramolecular chalcogen bonds play a stabilizing role in aldehyde 1/imine 2, and with imine nitrogen being a better electron donor than the aldehyde oxygen, imine 2 would accumulate. The sequence of equilibrium constants is largely in line with the capability to form chalcogen bonds (Te > Se ∼ S). The anomaly of sulfur could be attributed to the lack of conformer 1 (18%) in 2(SPh) and thus decreased contribution of the chalcogen bond.

In order to discriminate chalcogen bonding from the pure resonance effect, analogous aldehyde exchange reactions were performed with 3 as a control (exchange 2, Fig. 3C and S60–S62†). As in the case of the ortho-substituted aldehyde and imine (1 and 2), the resonance between the para-chalcogen and the aldehyde/imine (3 and 4) is plausible, but not chalcogen bonding (Fig. 3E). An equilibrium constant near unity was afforded for 3(SPh), 3(SePh), and 3(TePh), significantly smaller than the data for the corresponding 1(ChalPh) (Fig. 3D). These results strongly corroborate the importance of chalcogen bonding in shifting the equilibrium of imine exchange for aldehyde 1/imine 2.

The origin of chalcogen bonding

Energy decomposition analysis (EDA) has been gaining increasing popularity in exploring the nature of non-covalent interactions.^57–64 To probe intramolecular contact, generalized Kohn–Sham energy decomposition analysis (GKS-EDA)^65–67 was used to calculate the total interaction energy of 1/2 and dissect the contributing factors to chalcogen bonding by the modified GAMESS package.⁶⁸ GKS-EDA divides the total interaction energy (ΔE^TOT) into electrostatic (ΔE^ele), exchange-repulsion (ΔE^ex-rep), polarization (ΔE^pol), correlation (ΔE^corr), and dispersion (ΔE^disp) terms as follows in eqn (1).

ΔE^TOT = ΔE^ele + ΔE^ex-rep + ΔE^pol + ΔE^corr + ΔE^disp (1)

The exchange-repulsion term (ΔE^ex-rep) is associated with Pauli repulsion representing an unfavorable repulsive component as a result of the overlapping electron densities of the interacting groups and is also reflective of steric interaction. The polarization term (ΔE^pol) is associated with orbital interaction. The correlation term (ΔE^corr) is the contribution of the correlation energy.^65–67

The same level of M06-2X-D3/def2-TZVP was also employed for GKS-EDA calculation (Tables S4 and S5†). Both closed conformer 1 and open conformer 2, for which the difference lies in chalcogen bonding or not, were considered for EDA analysi`s (Fig. 4). The values of ΔE^TOT of conformer 1 of 1(ChalPh) and 1(ChalMe) were found to have a decreasing trend (i.e., more favorable) from S to Te, suggesting the strongest chalcogen bonding with Te (Fig. 4a). It is notable that polarization and electrostatic terms (negative), as well as exchange-repulsion energies (positive), increase from S to Te with significant values. In contrast, only small dispersion and correlation terms were found. Analogous results were obtained with conformer 1 of 2(ChalPh) and 2(ChalMe) (Table S4†).

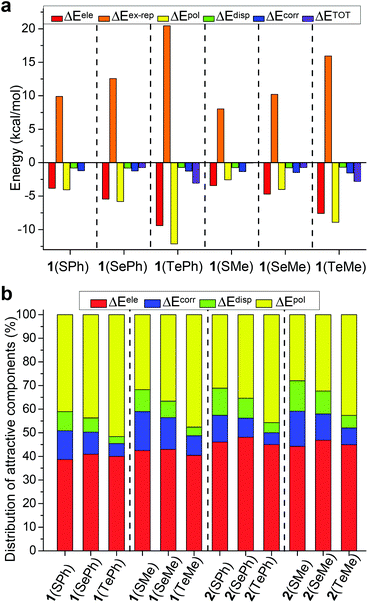Fig. 4 (a) Total and dissected interaction energies for conformer 1 of aldehyde 1. (b) Percentage contributions of attractive components to the total attraction for 1/2.

The percentage contributions of attractive components, including electrostatics, polarization, dispersion, and correlation, are chalcogen and substituent dependent (Fig. 4b). Both electrostatic and polarization terms play a significant role (around 80%) in chalcogen bonding with similar percentages, while the contribution of the dispersion term is minor (less than 10%). More importantly, the percentage of ΔE^pol increases from S to Te within each compound series (i.e., 1(ChalPh), 1(ChalMe), 2(ChalPh), and 2(ChalMe)), and the percentage of ΔE^ele remains consistent for S, Se, and Te (change within 5%). For example, polarization and electrostatics amount to 51% and 40% for 1(TePh). These results demonstrate the significance of orbital interaction in dictating the variation of chalcogen bonding from S to Te. Furthermore, the difference (ΔΔE^TOT) between interaction energies of closed and open conformers is listed (Table S6†), and an excellent linear correlation was obtained between ΔΔE^TOT and calculated conformational energy difference (R² = 0.979, Table S6†).

The strength of chalcogen bonding

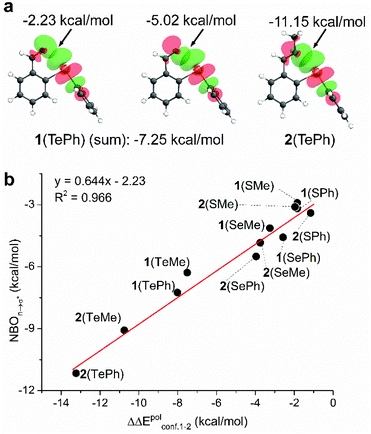
As another useful tool for probing supramolecular interactions, natural bond orbital (NBO) analysis was performed for conformer 1.^69,70 Taking 1(TePh) as an example, the alignment and overlap of the σ* orbital of the C(Ph)–Te bond and two oxygen lone pairs of the aldehyde confirmed n → σ* orbital interactions for C=O⋯Te chalcogen bonding (Fig. 5a). The stabilization energy, calculated based on the second-order perturbation theory (ΔE²), provides an estimation of interacting strength and is −7.25 kcal mol⁻¹ for 1(TePh) (sum of −2.23 and −5.02 kcal mol⁻¹). In addition, n → σ* orbital delocalization in 1(SPh) and 1(SePh) afforded the interaction energy of −3.19 and −4.58 kcal mol⁻¹, respectively (Fig. 5b and S23†). Such an order (Te > Se > S) parallels the conformational distribution and EDA analysis described above.

Fig. 5 (a) NBO orbitals and stabilization energies of n → σ* interactions in 1(TePh) and 2(TePh). (b) Correlation of n → σ* NBO values for 1/2 with the differences (ΔΔE^pol) in dissected energies of the polarization part of conformers 1 and 2 of 1/2.

There is an enhancement in NBO values for imines as compared to associated aldehydes, with n → σ* NBO stabilization energies of −3.40, −5.51, and −11.15 kcal mol⁻¹ for 2(SPh), 2(SePh), and 2(TePh), respectively (Fig. 5b). The higher NBO energy of the chalcogen bonding of imines (2) than their aldehydes (1) falls in line with the stronger electron-donating ability of imine nitrogen. A similar sequence on NBO values of chalcogen bonding was found for 1(ChalMe) and 2(ChalMe), albeit with a decreased strength as compared to their phenyl analogs (Fig. S65 and S66†). With sulfur or selenium, the trend of the n → σ* NBO energy of aldehyde 1 and associated imine 2 is different from conformational distribution. In order to align with each other for chalcogen bonding, close contact between the chalcogen atom and aldehyde oxygen/imine nitrogen would lead to electronic and steric repulsion. The strong chalcogen bonding of Te containing aldehyde/imine renders the closed conformer 1 overwhelming. For S and Se, two opposite effects could rival each other, thus leading to the rising of other conformers, especially 2(SPh) and 2(SePh) due to the greater bulkiness of the imines. Such a rationalization is in agreement with EDA results. Furthermore, the n → σ* NBO values correlated well with the change (ΔΔE^pol) in dissected energies of the polarization term upon flipping from open to closed conformation (R² = 0.966, Fig. 5b).

NCI (non-covalent interaction) analysis supported the Chal⋯O/N chalcogen bond within conformer 1 (Fig. S67 and S68†), which was further validated by the existence of a bond critical point (BCP) (3, −1) in the topological analysis^71,72 of the electron density distribution (Fig. S69 and S70†). More properties of these BCPs calculated by Multiwfn⁷³ revealed a low magnitude of electron density (ρ_BCP 0.018–0.026), positive Laplacian values (∇²ρ(r) 0.060–0.070), and approximately zero energy density (H(r)), which were typical for non-covalent interactions (Table S7†). A correlation between the strength of non-covalent interactions and the charge density at the corresponding bond critical point (ρ_BCP) was attempted.^74–76 Gratifyingly, a plot of n → σ* NBO energies of chalcogen bonding against ρ_BCP afforded a linear relationship for 1 and 2 (R² = 0.992, Table S7†), indicating that an increase in concentrated charge density strengthens chalcogen bonds.

Resonance-assisted chalcogen bonding

The resonance donation from the chalcogen atom toward aldehyde/imine and its relationship with the chalcogen bond was further explored (Fig. 6a).^77,78 The concept of resonance-assisted hydrogen bonding is well-documented and substantially contributes to the stability of salicylaldehyde-derived imines (Fig. 6a) and nucleic acid–base pairs.^79–81 However, resonance-assisted chalcogen bonding (Fig. 6a) is under-investigated although theoretical studies did reveal its viability.^77,78 Since the interrelation between chalcogen bonding and resonance effect would be reflected in the decrease or increase of bond lengths, the calculated structures of conformers 1 and 2 were therefore scrutinized. The lengthening of the accepting Te–Ph bond (Te5–C6) in closed conformer 1 relative to the open conformer 2 of 1(TePh) supports the existence of the Te⋯O chalcogen bond (Fig. 6b). Moreover, the bond lengthening of O1–C2 (formyl double bond) and C3–C4 (phenyl double bond), accompanied by the bond shortening of C2–C3 and C4–Te5, is indicative of an enhanced resonance effect in conformer 1 as compared to conformer 2. These results were corroborated by the change in the Wiberg bond index (Tables S9 and S10†) and NPA charge (Tables S11 and S12†). Similar findings were revealed for 1(SPh), 2(SPh), 1(SePh), 2(SePh), and 2(TePh). In addition, the smaller wavenumber of the carbonyl frequency of 1 as compared to the para analog 3 in the IR spectra matches its lengthening in 1 (Fig. S51–S53†).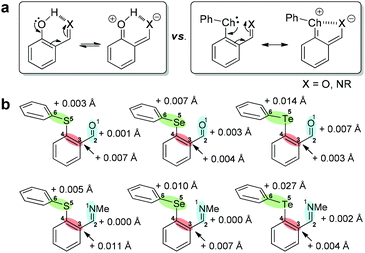

Fig. 6 (a) Resonance-assisted hydrogen/chalcogen bonding. (b) Calculated changes in bond length in closed versus open conformer for 1(ChalPh) and 2(ChalPh).

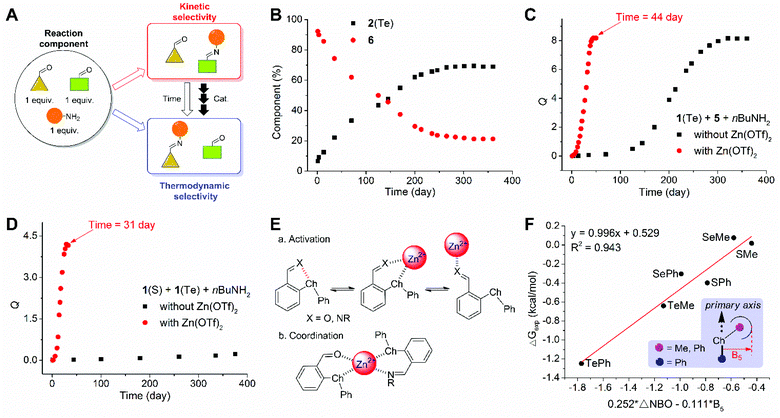
Thermodynamic and kinetic selectivity of imine systems

Finally, to take advantage of the unique effects of chalcogen bonding on imine DCC, the thermodynamic and kinetic selectivities were manipulated (Fig. 7A). With a mixture of 1(TePh), 5, and 1-butylamine (1 : 1 : 1, exchange 1) the component distribution at the early stage and after equilibration preferred imines 6 and 2(TePh), respectively (Fig. 7B). The kinetic and thermodynamic selectivity for imine distribution was thus reversed. The reversal of kinetic and thermodynamic selectivity was also observed for a library of 1(SPh), 5, and 1-butylamine (1 : 1 : 1), albeit with significantly less time (Fig. S71†). An analogous trend was obtained with the competition between 1(SePh) and 5 (Fig. S75†). A mixture of 1(SPh), 1(TePh), and 1-butylamine predominantly gave 2(SPh) initially. 2(TePh) was slowly built up, and the equilibrium was not reached after one year (reaction quotient around 0.2, Fig. 7D). A K value was predicted to be around 4.1 according to the data of 1(SPh) and 1(TePh) in exchange 1, preferring 2(TePh). In other words, the kinetic and thermodynamic selectivity would be reversed.

Fig. 7 (A) The control of the thermodynamic and kinetic selectivity of imine DCC. (B) Kinetic profile of the one-pot reaction of 1(TePh), 5 (1.0 equiv.), and 1-butylamine (1.0 equiv.) to track the formation of imines 2(TePh) and 6 in CD₃CN. (C) The effects of Zn(OTf)₂ (0.1 equiv.) on the kinetics of the reaction of 1(TePh), 5 (1.0 equiv.), and 1-butylamine (1.0 equiv.). (D) The effects of Zn(OTf)₂ (0.1 equiv.) on the kinetics of the reaction of 1(SPh), 1(TePh) (1.0 equiv.), and 1-butylamine (1.0 equiv.). (E) Rationalization of the activation (a) and coordination (b) effects of Zn²⁺ on aldehyde/imine. (F) The correlation of ΔG values of imine exchange 1 with ΔNBO of conformers 1 of 1/2 and Sterimol parameters (B₅).

As a means of speeding up the scrambling of imines, a series of acids were screened. Interestingly, Zn(OTf)₂ (0.1 equiv.) allowed the remarkable acceleration of exchange 1, equilibrating after 2, 8, and 44 days for 1(SPh), 1(SePh), and 1(TePh) (Fig. 7C), respectively (Fig. S71–S80†). The equilibrium of 1(SPh), 1(TePh), and amine was attained after 31 days with Zn(OTf)₂ present, in favor of 2(TePh) (K ∼ 4.2, Fig. 7D and S79†), consistent with the prediction above. Zn(OTf)₂ as a Lewis acid catalyst can facilitate the decomposition of imines and also the activation of aldehydes, accounting for accelerating the imine exchange (Fig. 7E(a)).^82–84 Although methanesulfonic acid (MA) induced the decomposition of imine 2, its kinetic effect on imine exchange was modest relative to Zn(OTf)₂ (Fig. S96 and S97†). Other metal ions, including Cd²⁺, Fe³⁺, and In³⁺, could also speed up aldehyde exchange (Fig. S98–S103†). One rationalization comes from the coordination effect of metal ions, bringing together the imine and aldehyde engaging in the exchange and essentially enhancing the local concentration of the transferred amine (Fig. 7E(b)).^85–87

Zinc ions also accelerated the reaction of 1(ChalMe), 5, and 1-butylamine, and tellurium (1(TeMe)) afforded the largest K value (2.9), as compared to 1(SMe) (0.97) and 1(SeMe) (0.98) (Table S13†). The K values for imine exchange reactions of 1(SMe), 1(SeMe), and 1(TeMe) are again larger than the values from their respective para analogs 2(SMe) (0.57), 2(SeMe) (0.66), and 2(TeMe) (0.87). On correlating the experimental results of the imine exchange reactions with the theoretical data from NBO analysis, a modest linear relationship between ΔG values of imine exchange 1 and the difference between NBO strength of conformer 1 of aldehyde 1 and imine 2 (ΔNBO) was obtained (R² = 0.798), with SPh and SMe deviating from the line (Fig. S104†). To further consider steric effects, Sterimol parameters were employed.⁸⁸ B₅ represents the longest distance perpendicular to the primary axis of attachment⁸⁹ and is reflective of the steric interaction between the phenyl ring and the substituent on the chalcogen atom (i.e., ChalR). A multivariate linear correlation of ΔG values of imine exchange 1 with ΔNBO and B₅ of ChalR was apparent (R² = 0.943, Fig. 7F). These findings support the critical role of orbital interaction in chalogen bonding and its impact on imine DCC.

Conclusions

In summary, we report the interrelation between chalcogen bonds and dynamic imine bonds through the strategy of dynamic covalent chemistry. First, a suite of ortho-chalcogen benzaldehydes were synthesized, and the impact of intramolecular Chal⋯O/N chalcogen bonding on modulating the conformational preference of aldehyde/imine structures was elucidated. The effects of the chalcogen bond on imine exchange were further investigated in detail, with chalcogen bonding decelerating the kinetics and yet thermodynamically stabilizing the imines. Electrostatic and orbital interactions represent the dominant attractive forces in chalcogen bonding, as supported by energy decomposition analysis. The strength of chalcogen bonding (Te > Se > S) was quantified and falls in line with the largest effect of tellurium on shifting the imine exchange equilibrium. Finally, the thermodynamic and kinetic selectivity of dynamic covalent systems was facilely controlled by utilizing features of chalcogen bonding on modulating imine DCC. In order to amplify the effect of chalcogen bonding on imine DCC, the synergy of non-covalent interactions within molecular assemblies, as well as the potential for guest recognition, will be pursued in the future. The strategies and results described herein should also find utility in many areas, such as molecular recognition, biological labelling, and asymmetric catalysis.

Author contributions

S. J. carried out the synthetic work and dynamic covalent reactions. H. Y. carried out the theoretical calculation. L. Y. designed the project and wrote the manuscript. All authors discussed the results and have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank National Natural Science Foundation of China (22071247, 22101283, 22101284, and 92156010), the Strategic Priority Research Program (XDB20000000) and the Key Research Program of Frontier Sciences (QYZDB-SSW-SLH030) of the Chinese Academy of Sciences, Natural Science Foundation of Fujian Province (2020J06035), and Fujian Science & Technology Innovation Laboratory for Optoelectronic Information of China (2021ZR112) for funding. We thank Prof. Peifeng Su (Xiamen University) and the XMVB team for the great help of the software. The computation was carried out at Shanxi Supercomputing Center of China, and the calculations were performed on TianHe-2.

Notes and references

1. N. Biot and D. Bonifazi, Chalcogen-bond driven molecular recognition at work, Coord. Chem. Rev., 2020, 413, 213243.
2. A. J. Mukherjee, S. S. Zade, H. B. Singh and R. B. Sunoj, Organoselenium chemistry: Role of intramolecular interactions, Chem. Rev., 2010, 110, 4357–4416.
3. R. Gleiter, G. Haberhauer, D. B. Werz, F. Rominger and C. Bleiholder, From noncovalent chalcogen-chalcogen interactions to supramolecular aggregates: Experiments and calculations, Chem. Rev., 2018, 118, 2010–2041.
4. L. Vogel, P. Wonner and S. M. Huber, Chalcogen bonding: An overview, Angew. Chem., Int. Ed., 2019, 58, 1880–1891.
5. S. Kolb, G. A. Oliver and D. B. Werz, Chemistry evolves, terms evolve, but phenomena do not evolve: From chalcogen-chalcogen interactions to chalcogen bonding, Angew. Chem., Int. Ed., 2020, 59, 2–7.
6. K. Selvakumar and H. B. Singh, Adaptive responses of sterically confined intramolecular chalcogen bonds, Chem. Sci., 2018, 9, 7027–7042.
7. B. R. Beno, K. S. Yeung, M. D. Bartberger, L. D. Pennington and N. A. A. Meanwell, Survey of the role of noncovalent sulfur interactions in drug design, J. Med. Chem., 2015, 58, 4383–4438.
8. C. B. Aakeroy, D. L. Bryce, G. R. Desiraju, A. Frontera, A. C. Legon, F. Nicotra, K. Rissanen, S. Scheiner, G. Terraneo, P. Metrangolo and G. Resnati, Definition of the chalcogen bond, Pure Appl. Chem., 2019, 91, 1889–1892.
9. M. H. Kolář and P. Hobza, Computer modeling of Halogen Bonds and Other σ-Hole Interactions, Chem. Rev., 2016, 116, 5155–5187.
10. P. Politzer, J. S. Murray and T. Clark, Halogen bonding and other sigma-hole interactions: a perspective, Phys. Chem. Chem. Phys., 2013, 15, 11178–11789.
11. W. Wang, B. Ji and Y. Zhang, Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond, J. Phys. Chem. A, 2009, 113, 8132–8135.
12. D. J. Pascoe, K. B. Ling and S. L. Cockroft, The origin of chalcogen-bonding interactions, J. Am. Chem. Soc., 2017, 139, 15160–15167.
13. G. Haberhauer and R. Gleiter, The nature of strong chalcogen bonds involving chalcogen-containing heterocycles, Angew. Chem., Int. Ed., 2020, 59, 21236–21243.
14. L. de Azevedo Santos, S. C. C. van Der Lubbe, T. A. Hamlin, T. C. Ramalho and F. Matthias Bickelhaupt, A Quantitative Molecular Orbital Perspective of the Chalcogen Bond, ChemistryOpen, 2021, 10, 391–401.
15. P. L. Bora, M. Novák, J. Novotný, C. Foroutan-Nejad and R. Marek, Supramolecular covalence in bifurcated chalcogen bonding, Chem. – Eur. J., 2017, 23, 7315–7323.
16. S. Benz, J. López-Andarias, J. Mareda, N. Sakai and S. Matile, Catalysis with chalcogen bonds, Angew. Chem., Int. Ed., 2017, 56, 812–815.
17. J. Y. C. Lim and P. D. Beer, Sigma-hole interactions in anion recognition, Chem, 2018, 4, 731–783.
18. A. Borissov, I. Marques, J. Y. C. Lim, V. Félix, M. D. Smith and P. D. Beer, Anion recognition in water by charge-neutral halogen and chalcogen bonding foldamer receptors, J. Am. Chem. Soc., 2019, 141, 4119–4129.
19. G. Park and F. P. Gabbaï, Redox-controlled chalcogen and pnictogen bonding: The case of a sulfonium/stibonium dication as a preanionophore for chloride anion transport, Chem. Sci., 2020, 11, 10107–10112.
20. J. Fanfrlík, A. Přáda, Z. Padělková, A. Pecina, J. Macháček, M. Lepšík, J. Holub, A. Růžička, D. Hnyk and P. Hobza, The dominant role of chalcogen bonding in the crystal packing of 2D/3D aromatics, Angew. Chem., Int. Ed., 2014, 53, 10139–10142.
21. B. J. Eckstein, L. C. Brown, B. C. Noll, M. P. Moghadasnia, G. J. Balaich and C. M. McGuirk, A Porous Chalcogen-Bonded Organic Framework, J. Am. Chem. Soc., 2021, 143, 20207–20215.
22. A. Dhaka, O. Jeannin, I. R. Jeon, E. Aubert, E. Espinosa and M. Fourmigue, Activating chalcogen bonding (ChB) in alkylseleno/alkyltelluroacetylenes toward chalcogen bonding directionality control, Angew. Chem., Int. Ed., 2020, 59, 23583–23587.
23. S. Mehrparvar, C. Wölper, R. Gleiter and G. Haberhauer, The carbonyl⋯tellurazole chalcogen bond as a molecular recognition unit: From model studies to supramolecular organic frameworks, Angew. Chem., Int. Ed., 2020, 59, 17154–17161.
24. P. Scilabra, G. Terraneo and G. Resnati, The chalcogen bond in crystalline solids: A world parallel to halogen bond, Acc. Chem. Res., 2019, 52, 1313–1324.
25. B. Zhou and F. P. Gabbai, Anion Chelation via Double Chalcogen Bonding: The Case of a Bis-telluronium Dication and Its Application in Electrophilic Catalysis via Metal-Chloride Bond Activation, J. Am. Chem. Soc., 2021, 143, 8625–8630.
26. P. Wonner, A. Dreger, L. Vogel, E. Engelage and S. M. Huber, Chalcogen bonding catalysis of a nitro–Michael reaction, Angew. Chem., Int. Ed., 2019, 58, 16923–16927.
27. R. Weiss, E. Aubert, P. Pale and V. Mamane, Chalcogen-Bonding Catalysis with Telluronium Cations, Angew. Chem., 2021, 133, 19430–19435.
28. W. Wang, H. Zhu, L. Feng, Q. Yu, J. Hao, R. Zhu and Y. Wang, Dual chalcogen-chalcogen bonding catalysis, J. Am. Chem. Soc., 2020, 142, 3117–3124.
29. C. A. Leverett, V. C. Purohit and D. Romo, Enantioselective, Organocatalyzed, Intramolecular aldol lactonizations with keto acids leading to bi- and tricyclic β-lactones and topology-morphing transformations, Angew. Chem., Int. Ed., 2010, 49, 9479–9483.
30. C. Shu, H. Liu, A. M. Z. Slawin, C. Carpenter-Warren and A. D. Smith, Isothiourea-catalysed enantioselective michael addition of N-heterocyclic pronucleophiles to α,β-unsaturated aryl esters, Chem. Sci., 2020, 11, 241–247.
31. F. Di Maria, M. Zangoli, M. Gazzano, E. Fabiano, D. Gentili, A. Zanelli, A. Fermi, G. Bergamini, D. Bonifazi, A. Perinot, M. Caironi, R. Mazzaro, V. Morandi, G. Gigli, A. Liscio and G. Barbarella, Controlling the functional properties of oligothiophene crystalline nano/microfibers via tailoring of the self-assembling molecular precursors, Adv. Funct. Mater., 2018, 28, 1801946.
32. M. Fourmigué and A. Dhaka, Chalcogen bonding in crystalline diselenides and selenocyanates: From molecules of pharmaceutical interest to conducting materials, Coord. Chem. Rev., 2020, 403, 213084.
33. S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Dynamic covalent chemistry, Angew. Chem., Int. Ed., 2002, 41, 898–952.
34. J. M. Lehn, From supramolecular chemistry towards constitutional dynamic chemistry and adaptive chemistry, Chem. Soc. Rev., 2007, 36, 151–160.
35. Y. Jin, C. Yu, R. J. Denman and W. Zhang, Recent advances in dynamic covalent chemistry, Chem. Soc. Rev., 2013, 42, 6634–6654.
36. Q. Ji, R. C. Lirag and O. Š. Miljanić, Kinetically controlled phenomena in dynamic combinatorial libraries, Chem. Soc. Rev., 2014, 43, 1873–1884.
37. G. Zhang and M. Mastalerz, Organic cage compounds -, from shape-persistency to function, Chem. Soc. Rev., 2014, 43, 1934–1947.
38. X. Feng, X. Ding and D. Jiang, Covalent organic frameworks, Chem. Soc. Rev., 2012, 41, 6010–6022.
39. M. Mondal and A. K. Hirsch, Dynamic combinatorial chemistry: A tool to facilitate the identification of inhibitors for protein targets, Chem. Soc. Rev., 2015, 44, 2455–2488.
40. E. Moulin, G. Cormos and N. Giuseppone, Dynamic combinatorial chemistry as a tool for the design of functional materials and devices, Chem. Soc. Rev., 2012, 41, 1031–1049.
41. A. Wilson, G. Gasparini and S. Matile, Functional systems with orthogonal dynamic covalent bonds, Chem. Soc. Rev., 2014, 43, 1948–1962.
42. J. Li, P. Nowak and S. Otto, Dynamic combinatorial libraries: From exploring molecular recognition to systems chemistry, J. Am. Chem. Soc., 2013, 135, 9222–9239.
43. D. A. Roberts, B. S. Pilgrim and J. R. Nitschke, Covalent post-assembly modification in metallosupramolecular chemistry, Chem. Soc. Rev., 2018, 47, 626–644.
44. J. F. Reuther, S. D. Dahlhauser and E. V. Anslyn, Tunable orthogonal reversible covalent (TORC) bonds: Dynamic chemical control over molecular assembly, Angew. Chem., Int. Ed., 2019, 58, 74–85.
45. F. Van Lijsebetten, J. O. Holloway, J. M. Winne and F. E. Du Prez, Internal catalysis for dynamic covalent chemistry applications and polymer science, Chem. Soc. Rev., 2020, 49, 8425–8438.
46. C. H. Fox, G. M. ter Hurrne, R. J. Wojtecki, G. O. Jones, H. W. Horn, E. W. Meijer, C. W. Frank, J. L. Hedrick and J. M. García, Supramolecular motifs in dynamic covalent PEG-hemiaminal organogels, Nat. Commun., 2015, 6, 7417.
47. M. He and J. M. Lehn, Time-dependent switching of constitutional dynamic libraries and networks from kinetic to thermodynamic distributions, J. Am. Chem. Soc., 2019, 141, 18560–18569.
48. X. Lin, J. Wang, B. Ding, X. Ma and H. Tian, Emission-tunable amorphous room-temperature phosphorescent polymers based on thermoreversible dynamic covalent bond, Angew. Chem., Int. Ed., 2021, 60, 3459–3463.
49. J. García-Calvo, J. Maillard, I. Fureraj, K. Strakova, A. Colom, V. Mercier, A. Roux, E. Vauthey, N. Sakai, A. Fürstenberg and S. Matile, Fluorescent membrane tension probes for super-resolution microscopy: Combining mechanosensitive cascade switching with dynamic covalent ketone chemistry, J. Am. Chem. Soc., 2020, 142, 12034–12038.
50. H. Zheng, H. Ye, X. Yu and L. You, Interplay between n→π* interactions and dynamic covalent bonds: Quantification and modulation by solvent effects, J. Am. Chem. Soc., 2019, 141, 8825–8833.
51. H. Chen, H. Ye, Y. Hai, L. Zhang and L. You, n→π* interactions as a versatile tool for controlling dynamic imine chemistry in both organic and aqueous media, Chem. Sci., 2020, 11, 2707–2715.
52. Z. Tao, K. A. Robb, K. Zhao and S. E. Denmark, Enantioselective, Lewis Base-Catalyzed Sulfenocyclization of Polyenes, J. Am. Chem. Soc., 2018, 140, 3569–3573.
53. T. Glodde, Y. V. Vishnevskiy, L. Zimmermann, H. G. Stammler, B. Neumann and N. W. Mitzel, The nature of chalcogen-bonding-type tellurium–nitrogen interactions: A first experimental structure from the gas phase, Angew. Chem., Int. Ed., 2021, 60, 1519–1523.
54. C. R. Forbes, S. K. Sinha, H. K. Ganguly, S. Bai, G. P. A. Yap, S. Patel and N. J. Zondlo, Insights into thiol-aromatic interactions: A stereoelectronic basis for S-H/π interactions, J. Am. Chem. Soc., 2017, 139, 1842–1855.
55. H. Ye, Y. Hai, Y. Ren and L. You, Versatile dynamic covalent assemblies for probing π-stacking and chirality induction from homotopic faces, Chem. – Eur. J., 2017, 23, 3804–3809.
56. M. Ciaccia and S. Di Stefano, Mechanisms of imine exchange reactions in organic solvents, Org. Biomol. Chem., 2015, 13, 646–654.
57. M. V. Hopffgarten and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62.
58. M. J. Phipps, T. Fox, C. S. Tautermann and C. K. Skylaris, Energy decomposition analysis approaches and their evaluation on prototypical protein-drug interaction patterns, Chem. Soc. Rev., 2015, 44, 3177–3211.
59. T. Clark, J. S. Murray and P. Politzer, A perspective on quantum mechanics and chemical concepts in describing noncovalent interactions, Phys. Chem. Chem. Phys., 2018, 20, 30076–30082.
60. P. R. Horn, Y. Mao and M. Head-Gordon, Probing non-covalent interactions with a second generation energy decomposition analysis using absolutely localized molecular orbitals, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
61. P. Su and H. Li, Energy decomposition analysis of covalent bonds and intermolecular interactions, J. Chem. Phys., 2009, 131, 014102.
62. D. J. Duarte, G. L. Sosa and N. M. Peruchena, Nature of halogen bonding. A study based on the topological analysis of the Laplacian of the electron charge density and an energy decomposition analysis, J. Mol. Model., 2013, 19, 2035–2041.
63. S. Mehrparvar, Z. N. Scheller, C. Wölper and G. Haberhauer, Design of Azobenzene beyond Simple On-Off Behavior, J. Am. Chem. Soc., 2021, 143, 19856–19864.
64. E. C. Vik, P. Li, D. O. Madukwe, I. Karki, G. S. Tibbetts and K. D. Shimizu, Analysis of the Orbital and Electrostatic Contributions to the Lone Pair-Aromatic Interaction Using Molecular Rotors, Org. Lett., 2021, 23, 8179–8182.
65. P. Su, Z. Jiang, Z. Chen and W. Wu, Energy decomposition scheme based on the generalized Kohn-Sham scheme, J. Phys. Chem. A, 2014, 118, 2531–2542.
66. P. Su, Z. Tang and W. Wu, Generalized Kohn-Sham energy decomposition analysis and its applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1460.
67. Z. Tang, Y. Song, S. Zhang, W. Wang, Y. Xu, D. Wu and P. Su, XEDA, a fast and multipurpose energy decomposition analysis program, J. Comput. Chem., 2021, 42, 2341–2351.
68. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen and S. Su, et al., General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363.
69. E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
70. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926.
71. R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928.
72. R. F. W. Bader, A bond path: a universal indicator of bonded interactions, J. Phys. Chem. A, 1998, 102, 7314–7323.
73. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
74. P. Sanz, O. Mó and M. Yáñez, Characterization of intramolecular hydrogen bonds and competitive chalcogen-chalcogen interactions on the basis of the topology of the charge density, Phys. Chem. Chem. Phys., 2003, 5, 2942–2947.
75. C. A. Deakyne, A. K. Ludden, M. V. Roux, R. Notario, A. V. Demchenko, J. S. Chickos and J. F. Liebman, Energetics of the lighter chalcogen analogues of carboxylic acid esters, J. Phys. Chem. B, 2010, 114(49), 16253–16262.
76. M. E. Brezgunova, J. Lieffrig, E. Aubert, S. Dahaoui, P. Fertey, S. Lebègue, J. G. Ángyán, M. Fourmigué and E. Espinosa, Chalcogen bonding: experimental and theoretical determinations from electron density analysis. Geometrical preferences driven by electrophilic-nucleophilic interactions, Cryst. Growth Des., 2013, 13, 3283–3289.
77. P. Sanz, M. Yáñez and O. Mó, Resonance-assisted intramolecular chalcogen-chalcogen interactions?, Chem. – Eur. J., 2003, 9, 4548–4555.
78. A. V. Gurbanov, M. L. Kuznetsov, K. T. Mahmudov, A. J. L. Pombeiro and G. Resnati, Resonance assisted chalcogen bonding as a new synthon in the design of dyes, Chem. – Eur. J., 2020, 26, 14833–14837.
79. G. Gilli and P. Gilli, The nature of the hydrogen bond: Outline of a comprehensive hydrogen bond theory, Oxford University Press., 2009.
80. S. H. Mehr, B. O. Patrick and M. J. MacLachlan, Stabilization of a strained heteroradialene by peripheral electron delocalization, Org. Lett., 2016, 18, 1840–1843.
81. C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, Hydrogen bonding in DNA base pairs: Reconciliation of theory and experiment, J. Am. Chem. Soc., 2000, 122, 4117–4128.
82. N. Giuseppone, J. L. Schmitt, E. Schwartz and J. M. Lehn, Scandium(III) catalysis of transimination reactions. Independent and constitutionally coupled reversible processes, J. Am. Chem. Soc., 2005, 127, 5528–5539.
83. S. France, M. H. Shah, A. Weatherwax, H. Wack, J. P. Roth and T. Lectka, Bifunctional lewis acid-nucleophile-based asymmetric catalysis: Mechanistic evidence for imine activation working in tandem with chiral enolate formation in the synthesis of β-lactams, J. Am. Chem. Soc., 2005, 127, 1206–1215.
84. K. N. Lee, Z. Lei and M. Y. Ngai, β-selective reductive coupling of alkenylpyridines with aldehydes and imines via synergistic lewis acid/photoredox catalysis, J. Am. Chem. Soc., 2017, 139, 5003–5006.
85. G. K. Cantrell and T. Y. Meyer, Catalytic C=N bond formation by metal-imide-mediated imine metathesis, J. Am. Chem. Soc., 1998, 120, 8035–8042.
86. Y. Reddi and R. B. Sunoj, Origin of stereoselectivity in cooperative asymmetric catalysis involving N-heterocyclic carbenes and lewis acids toward the synthesis of spirooxindole lactone, ACS Catal., 2017, 7, 530–537.
87. R. Tomifuji, K. Maeda, T. Takahashi, T. Kurahashi and S. Matsubara, FeCl₃ as an ion-pairing lewis acid catalyst. formation of highly lewis acidic FeCl₂⁺ and thermodynamically stable FeCl₄⁻ to catalyze the aza-Diels-Alder reaction with high turnover frequency, Org. Lett., 2018, 20, 7474–7477.
88. L. Pauling and R. Corey, Atomic Coordinates and Structure Factorsfor Two Helical Configurations of Polypeptide Chains, Proc. Natl. Acad. Sci. U. S. A., 1951, 37, 235–240.
89. A. V. Brethome, S. P. Fletcher and R. S. Paton, Conformational Effects on Physical-Organic Descriptors: The Case of Sterimol Steric Parameters, ACS Catal., 2019, 9, 2313–2323.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, X-ray data, NMR and mass spectra, and DFT calculations. CCDC 2089490–20894932116922. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qo00684g

---