Chemical tuning of molecular quantum materials κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃: from the Mott-insulating quantum spin liquid to metallic Fermi liquid

Abstract

The electronic properties of molecular conductors can be readily varied via physical or chemical pressure as it enlarges the bandwidth W. This enables them to cross the Mott insulator-to-metal phase transition by reducing electronic correlations U/W. Here we introduce an alternative path by spatially expanding the molecular orbitals when partially replacing sulfur by selenium in the constituting bis-(ethylenedithio)-tetrathiafulvalene (BEDT-TTF) molecules of the title compound. We characterize how the insulating quantum-spin-liquid state is tuned via a Mott transition to the metallic Fermi-liquid state crossing a narrow region of superconductivity. The transport, dielectric, and optical measurements reveal that at this first-order phase transition, metallic regions coexist in the insulating matrix leading to pronounced percolative effects, which are most obvious in the strong enhancement of the dielectric constant at low temperatures.

---

1 Introduction

Materials with novel and exciting properties rarely emerge by chance; commonly it takes a long struggle and joint effort of a dedicated group, such as the Molecular Nanoscience and Organic Materials Research Unit (NANOMOL) at the Institut de Ciència de Materials de Barcelona (ICMAB-CSIC), led by Jaume Veciana and Concepció Rovira. Their focus is on molecule-based compounds because these materials are particularly versatile and specific at the same time; their methods of production are well understood and scalable, except when single crystals are required; where available, organic materials outscore inorganic compounds quickly. The research tasks are distributed among the team of synthetic chemists responsible for the creation of novel products and materials, experimental and theoretical solid-state physicists necessary for exploration and understanding the behavior, and materials scientists for optimizing the properties in the view of possible applications. This concept worked successfully for half a century, but can it be prolonged as molecular quantum materials shift into the focus of future research and applications?

About five years ago, the notion of “Quantum Materials” became popular, evidenced, for example, by editorials and special issues of Nature Physics and Nature Materials.^1–7 These compounds exhibit either strong electronic interactions where often some type of electronic order occurs, such as superconductivity, magnetism, density waves, or their electronic properties are determined by non-generic quantum effects, such as topological insulators and Dirac and Weyl electron systems. In prototypical strongly correlated materials, such as heavy fermions or transition metal compounds, f- and d-electrons with their rather narrow bands govern the electronic properties. Often the Fermi surface is very complex and multiple bands compete. Materials composed of organic molecules, on the other side, are characterized by delocalized π-electrons that are distributed over the extended molecule. In most cases, only one electronic band cuts the Fermi energy, leading to rather simple Fermi surfaces. By now, organic conductors are recognized as versatile molecular quantum materials, which exhibit numerous exciting and unprecedented features.⁸ In comparison to inorganic compounds, it is cleaner and easier to tune molecular conductors by chemical and physical means, hence they are well established as model compounds for the investigation of several fundamental problems. Eventually, these molecular compounds might bring quantum materials and their emergent phenomena to our daily life.

In the following, we will present an outstanding example of tuning a molecular quantum material. By chemical substitution in the organic molecule, the molecular transfer integrals are extended resulting in larger wave function overlap (sketched at top of Fig. 1). This is the most direct way to vary the electronic bandwidth and, hence, to diminish the effect of electronic correlations; the Mott insulator eventually becomes a Fermi liquid. Along this avenue, we can elucidate the fundamental nature of the Mott insulator-metal transition (IMT) that has remained the subject of controversy and debate for decades. Early theories^9–11 favored a robust first-order scenario but apart from hysteresis effects, it has been proven difficult to identify conclusive experimental evidence for the expected phase-coexistence region.^12–17 Alternative viewpoints envision a more continuous crossover at finite temperatures featuring aspects of quantum criticality.^18–21 Recently, quantum-spin-liquid candidates have been recognized as the best suited materials for studying the pristine Mott state in the absence of a magnetic order,²² and its low-temperature transition to a Fermi liquid.²¹

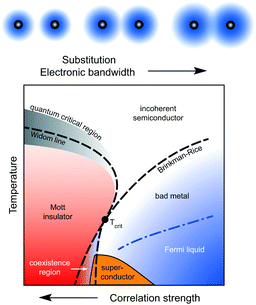Fig. 1 Upon increasing the molecular orbitals via chemical substitution (upper sketches) the electronic wavefunction overlap t ∝ W increases. The enlarged bandwidth W reduces the effect of electronic correlations U/W (U is the on-site Coulomb interaction). For a fully frustrated system with no magnetic order, dynamical mean-field theory predicts a first-order transition from a paramagnetic Mott insulator to a correlated metal up to a critical endpoint T_crit (main frame).¹⁰ The range, where metallic and insulating phases coexist, gives rise to unprecedented phenomena that have shifted into the focus only very recently. Above that, a fan-shaped quantum-critical regime associated with the quantum Widom line is expected at higher temperatures.^19,23 The metallic state is confined by the Brinkman–Rice temperature,^24,25 identified by a maximum in ρ(T); the coherent Fermi-liquid regime occurs at lower temperatures. When thermal fluctuations exceed the bandwidth W and interaction strength U, semiconducting behavior prevails; neither a gap nor a quasiparticle peak is stabilized. A series of studies on the quantum-spin-liquid candidate κ-(BEDT-TTF)₂Cu₂(CN)₃ provided experimental and theoretical confirmation of this scenario.^{21,22,26–29}

Since most molecular solids are rather soft, their electronic properties can readily be tuned by a relatively low hydrostatic pressure.^30–34 Nevertheless, many experiments become cumbersome, inaccurate or even impossible when confined to pressure cells, hence alternative methods are desirable. In the case of charge-transfer salts, reducing the size of anions acts like chemical pressure that brings the organic donor molecules closer together. This approach is frequently applied to quasi-one-dimensional TMTTF or quasi-two-dimensional BEDT-TTF salts.^30–33,35 Already in the 1970s it has been realized by Bechgaard and others that replacing sulfur by selenium in the fulvalene-type central unit TTF increases the orbital overlap of adjacent molecules and thus the bandwidth, eventually leading to superconductivity in (TMTSF)₂PF₆.³⁶Fig. 1 displays a generic phase diagram of an electron system with a half-filled conduction band subjected to strong electron–electron interactions. When the effect of electronic correlations increases, the metal turns into a Mott insulator. A superconducting phase is often observed around metal–insulator transitions and quantum critical points. This may be related to the fact that quasiparticles constituting a Fermi liquid are on the verge of destruction.

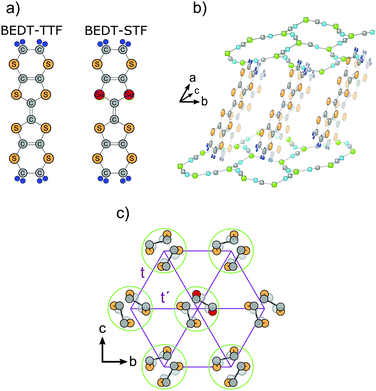
Here, we apply this approach to quasi-two-dimensional BEDT-TTF salts, where we replace two out of the four inner sulfur atoms by selenium as depicted in Fig. 2(a), resulting in BEDT-STF, in contrast to the so-called BETS molecule (BEDT-TSF, bis-ethylene-dithio-tetraselenafulvalene) which contains four selenium atoms in the fulvalene unit.³⁹ While κ-(BEDT-TTF)₂Cu₂(CN)₃ is a Mott insulator, considered as the most promising realization of a quantum spin liquid,¹⁷ κ-(BEDT-STF)₂Cu₂(CN)₃ is a good conductor in the entire temperature regime. Performing the substitution on the donor molecules ensures that the polymeric anion network and the crystal symmetry remain unaffected, which is crucial for highly frustrated compounds. By this way, we can cross the Mott transition from a paramagnetic insulator – potentially a quantum spin liquid – to a paramagnetic metal, without any indications of a magnetic order down to lowest temperatures. Despite the similarities, this approach is distinct from the incremental substitution previously used in the case of κ-(BEDT-TTF)₂Cu[N(CN)₂]Br_xCl_1−x, where the antiferromagnetic Mott insulator κ-(BEDT-TTF)₂Cu[N(CN)₂]Cl is turned into the metallic superconductor κ-(BEDT-TTF)₂Cu[N(CN)₂]Br by chemical pressure.^40–42

Fig. 2 (a) Organic donor molecules bis-(ethylenedithio)-tetrathiafulvalene, called BEDT-TTF and bis-(ethylenedithio)-diseleniumdithiafulvalene, abbreviated BEDT-STF. In the latter case, two sulfur atoms of the inner rings are replaced by selenium. (b) The crystal structure contains dimers of the donor molecules forming layers in the bc-plane which are separated by the Cu₂(CN)₃ anion sheets. (c) The dimers are arranged in a triangular pattern with transfer integrals t′/t = 0.83 close to complete frustration. The STF-substitution, which is randomly distributed in space, leads to a local extension of the transfer integrals due to the larger molecular orbitals.

In the present study, we focus on the electronic properties and investigate the coexistence regime at the first-order phase transition by transport, optical and dielectric methods. We observe a divergency in the permittivity as the hallmark of a percolative transition; in other words, we prove the insulator–metal phase coexistence below the critical endpoint T_crit ≈15–20 K.

2 Experimental details

Single crystals of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ with various stoichiometry (x = 0, 0.04, 0.1, 0.12, 0.16, 0.19, 0.21, 0.25, 0.28, 0.44, 0.78 and 1) were prepared at Hokkaido University in Sapporo following the standard procedure of electrochemical oxidation.⁴³ The size of the single crystals rarely exceeds 2 mm, and typical samples used for the present study range from 250 to 500 μm in lateral dimensions and 20 to 100 μm in thickness. For the alloying series, the number of donor molecules, BEDT-TTF and BEDT-STF, was preselected. For each batch the actual substitution value x was determined a posteriori by energy-dispersive X-ray spectroscopy and using κ-(BEDT-TTF)₂Cu₂(CN)₃ as a reference we compared the intensity of S atoms to that of Se atoms.⁴⁴

The structure consists of bc layers of strongly dimerized BEDT-TTF or BEDT-STF molecules, with each dimer oriented approximately perpendicular to its nearest neighbors (Fig. 2). Overall, it is assumed that the compounds crystallize in the monoclinic and centrosymmetric P2₁/c space group. Based on an X-ray study of the parent compound, Foury-Leylekian et al. recently suggested a triclinic symmetry P1̄ with two non-equivalent dimers in the unit cell;³⁸ however, the charge imbalance among the sites is minuscule. Upon sulfur substitution, the unit-cell volume slightly increases (less than 2%) in a linear fashion without any change in symmetry. In Table 1 we list the unit cell parameters for the limiting cases, assuming both, P2₁/c and P1̄ space group symmetry.

Table 1 Room-temperature values of the unit cell parameters of κ-(BEDT-TTF)₂Cu₂(CN)₃ and κ-(BEDT-STF)₂Cu₂(CN)₃ assuming space groups P2₁/c and P1̄ for the analysis of the X-ray scattering results. Data for the former compound are taken from studies by Pinterić et al.³⁷ and Foury-Leylekian et al.³⁸

	κ-(BEDT-TTF)2Cu2(CN)3		κ-(BEDT-STF)2Cu2(CN)3
	P21/c	P1̄	P21/c	P1̄
a	16.0920(4) Å	16.1221(10) Å	16.2965(8) Å	16.5625(8) Å
b	8.5813(2) Å	8.591(6) Å	8.6082(5) Å	8.6292(3) Å
c	13.3904(4) Å	13.412(8) Å	13.3985(6) Å	13.4025(5) Å
α	90°	89.99(2)°	90°	90.00°
β	113.381(3)°	113.43(2)°	113.1300(16)°	115.0115(14)°
γ	90°	90.01(2)°	90°	90.00°
V	1697.25 Å^3	1704.46 Å^3	1728.5 Å^3	1735.87 Å^3
Z	2	2	2	2

---

Electrical transport was measured parallel to the crystallographic c-axis using a standard four-probe technique, cooling from room temperature down to T = 1.8 K. The contacts were made from thin gold wires attached using carbon paste. Furthermore, we measured the complex electrical impedance as a function of temperature and frequency in order to obtain the dielectric permittivity [small epsilon, Greek, circumflex] = ε₁ + iε₂. Here, gold wires were attached to opposite crystal surfaces and the data were recorded using an impedance analyzer in the frequency range from f = 40 Hz to 10 MHz covering temperatures down to T = 5 K. The applied ac voltage was set to 0.5 V, making sure that we operate in the Ohmic regime.²⁷

The optical properties of several single crystals have been studied by reflectivity measurements using standard Fourier-transform spectroscopy from the far-infrared up to the near-infrared and visible range.⁴⁵ The light was polarized along the two principal optical axes, i.e. E‖b and E‖c, on the as-grown surfaces. Besides regular in-plane experiments, we also probed the polarization perpendicular to the conducting planes, a direction which couples to the most charge-sensitive infrared-active intramolecular vibrational mode ν₂₇(b_1u). The sample was cooled down to T = 10 K by using a helium-cooled optical cryostat. In addition, the high-frequency properties (up to 35 000 cm⁻¹) were determined by spectroscopic ellipsometry under ambient conditions. The optical conductivity was calculated via Kramers–Kronig analysis using a constant reflectivity extrapolation at low frequencies and temperatures for the Mott insulators, while a Hagen-Rubens behavior was assumed for elevated temperatures and substitution values of x > 0.12 where metallic properties prevail.^46,47

3 DC transport

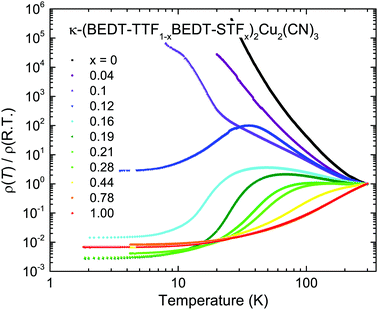
Fig. 3 displays the c-axis dc resistivity ρ(T) as a function of temperature for all samples in our substitution series from x = 0 to 1. The room-temperature values increase from approximately 0.03 Ω cm for x = 1 to around 1 Ω cm for x = 0. For x = 0.12 and higher the systems turn metallic at low temperatures; the temperature range of metallic conductivity increases for larger substitution and exceeds T = 300 K for x ≥ 0.44. No hysteresis is observed in ρ(T) confirming previous reports. The quantum Widom line indicates the crossover from the more-metallic to the more-insulating regime and is defined as the inflection point of log{ρ} as a function of substitution or pressure.²² The maximum in ρ(T) defines the Brinkman–Rice temperature T_BR that increases upon alloying.^24,25,27,29 For very low temperatures, the metallic properties are clearly characterized by a ρ(T) ∝ T² behavior, which is the hallmark of electron–electron interaction. A detailed analysis of the Fermi-liquid properties and the crossover to the bad metallic regime is provided elsewhere.²⁹ Also the superconducting state that can be identified for x = 0.10 and 0.12 will be the subject of a separate publication⁴⁸ where we compare it to similar observations of the pristine κ-(BEDT-TTF)₂Cu₂(CN)₃ under pressure.^17,21,43

Fig. 3 DC resistivity of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ for various substitution values x measured as a function of temperature along the highly conducting c-axis and normalized to the room-temperature values. The substitution spans the full range from the insulating x = 0 to the metallic side.

4 Optical properties

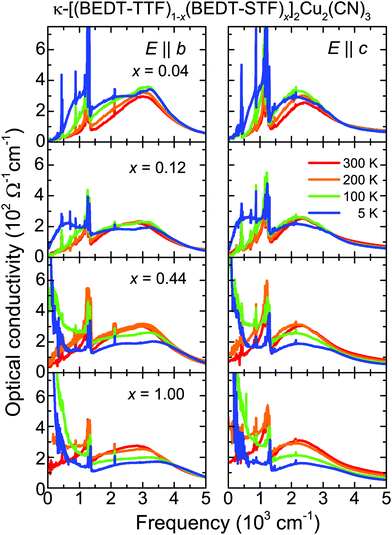
The in-plane optical conductivity σ₁(ω) of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ is shown in Fig. 4 for crystals of varying substitution values 0 ≤ x ≤ 1. The data are measured for the in-plane directions E‖b and E‖c from room temperature down to T = 5 K. The properties are rather similar for both polarizations indicating electronically isotropic behavior within the bc-plane.

Fig. 4 Frequency dependent conductivity of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ for several substitution values x = 0.04, 0.12, 0.44, and x = 1 recorded for the two polarizations within the plane (left column E‖b; right column E‖c) at different temperatures as indicated in the legend.

For BEDT-STF substitutions, x < 0.1, the compounds remain insulating at all temperatures; but no Mott gap develops upon cooling. In contrast, similar to the pristine crystals,^22,46,49 a pronounced in-gap absorption is present that becomes enhanced as T is reduced or x increases. In these cases we enter the coexistence regime of metallic and insulating regions expected for first-order phase transitions; the increasing metallic fraction increasingly contributes to the optical properties. Eventually, the alloys exhibit a Drude-like contribution to the optical conductivity, indicating the metallic properties in accordance with the dc results presented in Fig. 3. An extended Drude analysis of the optical conductivity and an in-detail discussion of the temperature and frequency dependence of the scattering rate are presented elsewhere.²⁹

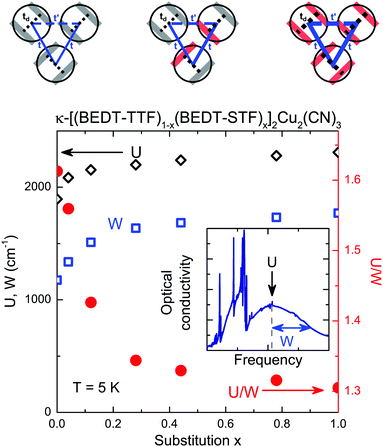
In Fig. 4 we also see that the mid-infrared peak consists of two contributions: intra-dimer excitations and transitions between the lower and the upper Hubbard bands, which almost coincide when probed along the c-axis. This has been observed in most κ-phase BEDT-TTF compounds and confirmed by ab initio calculations.^{40,41,46,50–52} We focus on the low-temperature spectra (T = 5 K, E‖c) where we assign the maximum of the mid-infrared peak to the transitions between the lower and the upper Hubbard bands separated by U. The half-width of the conductivity band in σ₁(ω) corresponds to the electronic bandwidth W, as illustrated in the inset of Fig. 5.⁵³

Fig. 5 Dependence of the electronic repulsion U (open diamonds), the bandwidth W (open squares), and the effective Coulomb interaction U/W (red solid dots, right axis) on the substitution x in κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ as determined from low-temperature optical conductivity. The inset explains the estimation of U from the mid-infrared maximum in σ₁(ω) and W from the half-width at half maximum. The three sketches above illustrate how the substitution x gradually tunes κ-(BEDT-TTF)₂Cu₂(CN)₃ to κ-(BEDT-STF)₂Cu₂(CN)₃; the lines of increasing thickness indicate the enhancement of transfer integrals t (solid blue), t′ (dashed blue) and t_d (dotted black).

The electronic repulsion U slightly increases as a function of STF-substitution x due to the larger intra-dimer overlap t_d as the orbitals extend further. From Fig. 5 we see that the increase of the bandwidth W is even more pronounced, resulting from the increase of the transfer integrals t and t′ between adjacent dimers. Most importantly, however, the ratio U/W – as it measures the effect of correlations – decreases with increasing x, providing evidence that the metallic compound κ-(BEDT-STF)₂Cu₂(CN)₃ is much less correlated compared to the Mott insulator κ-(BEDT-TTF)₂Cu₂(CN)₃. Fig. 5 shows that the variation is far from linear; a dramatic decrease of U/W is found for x < 0.2, while for larger x, the ratio saturates around U/W ≈ 1.3. Overall, from these optical experiments, the Mott insulator-to-metal transition can be located around x ≈ 0.1 in agreement with the dc resistivity.

5 Vibrational spectroscopy

By now, it is well established that most of the dimerized BEDT-TTF salts, such as κ-(BEDT-TTF)₂Cu[N(CN)₂]Cl, κ-(BEDT-TTF)₂Cu₂(CN)₃, or κ-(BEDT-TTF)₂Ag₂(CN)₃ do not possess sizeable charge disproportionation within the dimers,^47,54,55 with a few exceptions, like κ-(BEDT-TTF)₂Hg(SCN)₂Cl.^56–58 Raman and infrared spectroscopies are the best suited tools to locally probe the charge per molecule by inspecting the intramolecular vibrations that are known to be extremely sensitive to the amount of charge residing on the molecule.^45,59–61 Here we addressed the question of whether charge imbalance occurs when sulfur is replaced by selenium in the alloys κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃.

To this end, we recorded the optical properties perpendicular to the planes. In Fig. 6 the out-of-plane conductivity of κ-(BEDT-TTF)₂Cu₂(CN)₃ is compared to that of κ-(BEDT-STF)₂Cu₂(CN)₃ in the finger-print spectral region where the most charge-sensitive molecular vibrations of the central C=C occur.

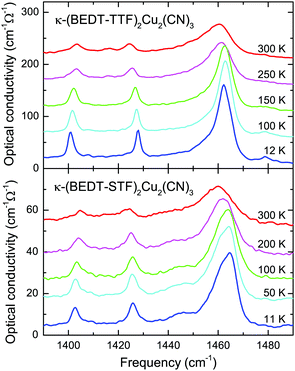Fig. 6 Optical conductivity of κ-(BEDT-TTF)₂Cu₂(CN)₃ and κ-(BEDT-STF)₂Cu₂(CN)₃ recorded for the out-of-plane polarization E‖a. The curves for the different temperatures are displaced for clarity reasons. The strong C=C vibrational mode ν₂₇(B_1u) around 1460 cm⁻¹ sharpens upon cooling but does not exhibit any severe modifications or splitting, as expected if strong charge disproportionation would occur. The data for κ-(BEDT-TTF)₂Cu₂(CN)₃ were discussed previously.⁴⁷

The dominant mode ν₂₇(B_1u) alters only slightly upon STF-substitution. If we focus on the limiting cases x = 0 and x = 1, we see that both compounds exhibit basically the same temperature dependence; a typical sharpening and slight hardening upon cooling. This behavior is explained by the fact that the sulfur/selenium atoms in the pentagonal inner ring are basically not involved in these modes. It can best be seen from the vibrational analysis and animations⁶² that these vibrations are well confined to the C=C bonds. Most importantly, since we do not observe any pronounced mode splitting in the κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ series, we conclude the absence of any significant charge imbalance among the donor molecules.

6 Dielectric properties

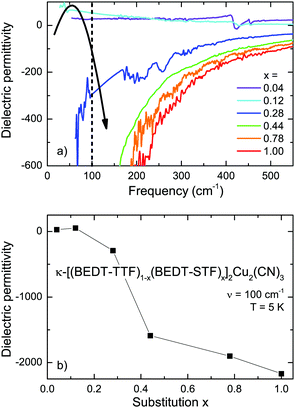
The metal–insulator transition is commonly defined by the change in conductivity, which can be probed by dc transport, dielectric or optical measurements. Equally, in some cases even more sensitive, however, are the dielectric properties, i.e. the dielectric constant. The low-frequency ε₁ is positive for an insulator and negative values indicate a metallic response. Along this line, we have analyzed the measured reflectivity spectra and obtained the complex dielectric permittivity [small epsilon, Greek, circumflex](ω, T, x) as a function of frequency, temperature and substitution by using the Kramers–Kronig transformation.⁶³Fig. 7 shows the real part ε₁(ω) for the different κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ crystals recorded at the lowest temperature T = 5 K. In the Mott-insulating state (x ≤ 0.1), the dielectric constant is basically frequency-independent and acquires a small, positive value. With increasing values of substitution, x, the quasi-static permittivity ε₁(ω → 0) first increases before it rapidly reduces to large negative values. After crossing the Mott insulator-to-metal transition, the system becomes conductive; the strong screening of the coherent quasiparticles drives ε₁ negative. A similar observation was reported for the Mott transition of VO₂, where the low-frequency permittivity diverges as a function of temperature. Near-field optical microscopy revealed that this behavior stems from the phase coexistence of metallic puddles in an insulating matrix.⁶⁴

Fig. 7 Despite continuously increasing conductivity, in the low-frequency limit, the dielectric permittivity ε₁(x) exhibits a peak around the Mott transition, reminiscent of a percolative-type coexistence of metallic and insulating regions. Panel (a) displays the real part of the dielectric permittivity ε₁(x) as obtained from far-infrared reflectivity measurements for E‖c at T = 5 K for κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ with various substitutions, x, as indicated. To better follow the substitutional dependence, panel (b) displays the dielectric permittivity taken at ν = ω/2πc = 100 cm⁻¹ indicated by the dashed line in panel (a).

In general, the divergency of the dielectric permittivity ε₁(x) is a hallmark of percolative phase transitions in microemulsions,^65–69 composites^70–72 or and percolating metal films.^73–77

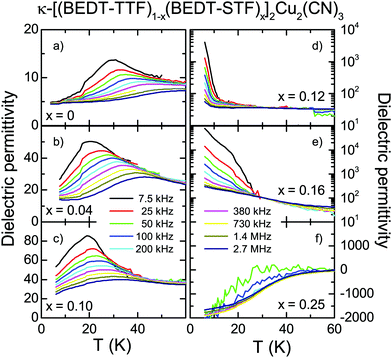
Since audio- and radio-frequency experiments are more suitable for exploring the dielectric behavior at the insulator–metal transition, we have conducted dielectric experiments down to 7.5 kHz. Fig. 8 summarizes the dielectric response of κ-(BEDT-TTF)₂Cu₂(CN)₃ and how it is affected by moving across the Mott IMT via STF-substitution. We plot the real part of the permittivity ε₁ as a function of temperature T for selected frequencies f and substitution values, x, as indicated. The pronounced peak dominating the temperature dependence of ε₁(T) in the insulating state (x ≤ 0.1) was discovered by Abdel-Jawad et al.⁷⁸ and subsequently confirmed by other groups.^{28,37,55,79,80} When probed at f = 7.5 kHz, the maximum is observed around T = 30 K in the case of κ-(BEDT-TTF)₂Cu₂(CN)₃ [Fig. 8(a)], with a slight sample-to-sample dependence, in agreement with previous reports. The peak shifts to higher temperatures as the frequency increases and at the same time, however, it gets less pronounced. This behavior resembles the well-known phenomenology of relaxor ferroelectrics.⁸¹

Fig. 8 The dielectric permittivity of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ is shown for substitutions x = 0, 0.04, 0.10, 0.12, 0.16 and 0.25 as a function of temperature for different frequencies. (a–c) A relaxor–ferroelectric response is observed for the insulating compounds (x ≤ 0.10) below T = 50 K. Upon reducing the measurement frequency, the feature becomes more pronounced and shifts to lower temperatures. On approaching x = 0.10, ε₁(T) is strongly enhanced up to 10⁵ and the peak moves to lower temperatures. (d and e) As a result of coexistence of spatially separated metallic and insulating regions at the IMT, ε₁ reaches values of 10⁵, with a pronounced frequency dependence. (f) Well above the percolation threshold, from x > 0.2 up to x = 1, the dielectric constant acquires negative values for x > 0.2 as the sample turns metallic. Note the different ordinates of the various panels.

Already the minimal substitutions of x = 0.04 and 0.1 have enhanced the dielectric permittivity significantly with the maximum ε₁(f = 7.5 kHz) ≈ 50 and 80. This strong increase of ε₁(T) and the concomitant shift of the peak to lower temperatures when we approach the IMT are in full accordance with our pressure-dependent dielectric studies,²⁸ where an extensive and detailed analysis is given. As we approach the phase transition further (x = 0.12 and 0.16), the dielectric constant drastically diverges, reaching values up to 10⁵ in the static low-temperature limit. A divergency in ε₁(x) is the fingerprint of a percolative phase transition where metallic regions form in an insulating matrix.^9,82,83 When crossing the percolation threshold, the system acts like a metal, characterized by a negative dielectric permittivity, ε₁ < 0. With an increase in x the sign change of the dielectric constant traces the Brinkman–Rice temperature, as it was identified by the maximum in ρ(T) (Fig. 1 and 3).²⁷ These results confirm the observations we extracted from the optical response in Fig. 7.

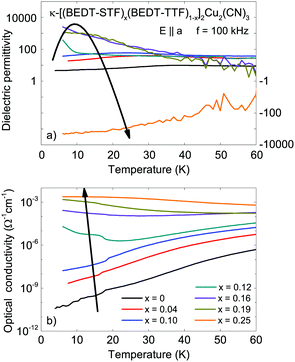
In order to illustrate the evolution of the low-frequency (f = 100 kHz) dielectric properties with increasing substitution x, in Fig. 9 we plot the permittivity ε₁(T) and conductivity σ₁(T) of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ as a function of temperature for the example of E‖a. While the optical conductivity monotonously increases with substitution, the low-temperature dielectric constant ε₁(x) first increases up to x = 0.16 before it decreases to a negative value when the metallic regions percolate. The use of a logarithmic scale underlines that the behavior is much stronger compared to the optical response plotted in Fig. 7. The comparison of the dielectric permittivity in the optical and radio-frequency regimes (Fig. 7 and 9) makes unambiguously clear that closing of the Mott gap has a minor effect on the dielectric properties while the effects of phase coexistence and percolation dominate.

Fig. 9 Temperature dependence of the dielectric properties of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ probed at f = 100 kHz and for various substitution levels x as indicated. (a) Upon increasing x, a strong enhancement in ε₁(T) is observed below 30 K, shifting to higher temperatures as x increases. (b) Simultaneously, the conductivity σ₁(T) increases by several orders of magnitude. At x = 0.25 a decrease in ε₁(T) to negative values indicates a purely metallic behavior. Note the logarithmic scale.

Fig. 10 Dielectric properties of κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ in dependence of the substitution level x, recorded perpendicular to the bc-plane at a fixed frequency f = 100 kHz at different temperatures as indicated. Note the logarithmic scales. (a) The permittivity ε₁(x) forms a pronounced maximum followed by a rapid decrease to negative values, corresponding to the right scale. (b) The conductivity σ₁(x) exhibits a step-like increase at x = 0.12, indicating the Mott transition. The observed behavior matches the signature of a percolating system. At the IMT, the nucleation and growth of metallic puddles sets in, which are spatially separated in an insulating matrix. Upon increasing x, the metallic filling fraction grows until the metallic state is completely established at x = 0.25. With an increasing temperature, the features diminish in amplitude and step size, respectively, consistent with the change from the first-order IMT to the crossover region at elevated temperatures.

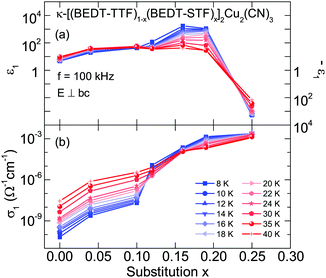
For better comparison, we plot ε₁(x) and σ₁(x) for the complete series κ-[(BEDT-TTF)_1−x(BEDT-STF)_x]₂Cu₂(CN)₃ in Fig. 10 measured at various temperatures T. Increasing the STF-content results in a strong enhancement of the dielectric constant up to 10³, whereas for x = 0.25 a decrease to large negative values of the order of ε₁(x) ≈ −10³ is observed. Concurrently, σ₁(x) increases by several orders of magnitude: the rapid decrease at x ≈ 0.12 indicates the crossing of the phase boundary into the metallic regime.

7 Discussion and conclusions

In a complementary study²⁸ the dielectric properties of κ-(BEDT-TTF)₂Cu₂(CN)₃ have been measured as a function of hydrostatic pressure. This is an alternative way to shift the Mott insulator through the first-order phase transition until the Fermi-liquid state is reached above p≈1 kbar. The behavior observed by the pressure-dependent investigations is in full accordance with the dielectric response observed here in the substitutional series; both can be well described using dynamical mean-field theory on the single-band Hubbard model when combined with percolation theory.²⁷

The fact that both approaches reach very much the same results provides firm evidence for a percolative Mott transition. Substituting BEDT-STF molecules increases the intra- and inter-dimer transfer integrals on a local scale, but this effect is smeared out. Local strain does not alter the crystal symmetry; the substitution results in a slightly larger unit cell as seen from Table 1. Since the organic molecules are rather large, diffusion within the crystal is prohibited, ruling out the formation of BEDT-STF clusters or domains of extended size beyond the stochastic occurrence. As depicted in Fig. 5, STF-substitution results in a gradual decrease of effective correlation strength U/W.

Our findings are summarized in Fig. 11 where the dielectric permittivity ε₁ is plotted as a function of temperature and STF-substitution x producing a contour plot that constitutes the corresponding phase diagram. We conclude that the discovery of the enormous divergency in the low-temperature quasi-static dielectric permittivity ε₁(x) indicates that metallic regions coexist with the insulating matrix. The reduction of electronic interactions U/W due to increasing x leads to a spatial phase separation that is confined to temperatures below the critical endpoint T_crit ≈ 15–20 K. With an increasing metallic fraction, the resistivity decreases, as can be well understood by effective medium models.⁸⁴ At large substitutions, metallic fluctuations dominate the electronic response. This range is well distinct by the negative and very large permittivity; its boundary trails the Brinkman–Rice temperature for the onset of metallic conductivity. The complete electrodynamical properties of this correlated electron system including the percolative aspect of the first-order Mott transition can be reproduced by the hybrid approach of dynamical mean-field theory amended with percolation theory.²⁷ Finally, we would like to point out that the novel path of tuning the effective correlations by increasing the molecular orbitals when partially replacing BEDT-TTF by the selenium-containing BEDT-STF molecules can be applied to other charge-transfer salts as well, providing an interesting alternative to physical pressure and chemical modification of the anions.

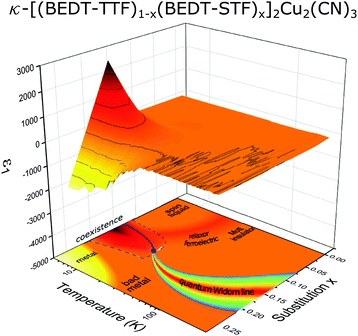Fig. 11 Contour plot of the dielectric permittivity ε₁ recorded at f = 380 kHz as a function of temperature and STF-substitution, x. We observe a strong increase of ε₁ up to 2500, centered around x = 0.15–0.2 and below T ≈ 15–20 K, close to the first-order Mott transition. We ascribe this to the phase coexistence around the first-order Mott transition hosting spatially separated metallic and insulating regions, in agreement with state-of-the-art dynamical-mean-field-theory.^19,27 See text for more details.

Author contributions

M. D. and A. P. guided and conceived the experimental work. Crystals were grown and characterized by Y. S. and A. K. Dc transport measurements were performed by A. L. and Y. S. Dielectric spectroscopy was carried out by M. W. and R. R. Optical experiments were conducted by M. S. A. and A. P., and supported by Y. S.; M. D., A. P. and R. R. analyzed the results and wrote the paper with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) and the Alexander von Humboldt Foundation.

References

1. Editorial, Nat. Phys., 2016, 12, 105.
2. B. Keimer and J. E. More, Nat. Phys., 2017, 13, 1045–1055.
3. N. Samarth, Nat. Mater., 2017, 16, 1068–1076.
4. D. N. Basov, R. D. Averitt and D. Hsieh, Nat. Mater., 2017, 16, 1077–1088.
5. Y. Tokura, M. Kawasaki and N. Nagaosa, Nat. Phys., 2017, 13, 1056–1068.
6. K. A. Moler, Nat. Mater., 2017, 16, 1049–1052.
7. N. Gedik and I. Vishik, Nat. Phys., 2017, 13, 1029–1033.
8. M. Dressel and S. Tomić, Adv. Phys., 2020, 69, 1–120.
9. N. Mott, Metal–Insulator Transitions, 2nd edn, Taylor & Francis, 1990.
10. A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Rev. Mod. Phys., 1996, 68, 13–125.
11. D. Vollhardt, Ann. Phys., 2012, 524, 1–19.
12. M. Imada, A. Fujimori and Y. Tokura, Rev. Mod. Phys., 1998, 70, 1039–1263.
13. S. Lefebvre, P. Wzietek, S. Brown, C. Bourbonnais, D. Jérome, C. Mézière, M. Fourmigué and P. Batail, Phys. Rev. Lett., 2000, 85, 5420–5423.
14. P. Limelette, P. Wzietek, S. Florens, A. Georges, T. A. Costi, C. Pasquier, D. Jérome, C. Mézière and P. Batail, Phys. Rev. Lett., 2003, 91, 016401.
15. P. Limelette, A. Georges, D. Jérome, P. Wzietek, P. Metcalf and J. M. Honig, Science, 2003, 302, 89–92.
16. F. Kagawa, T. Itou, K. Miyagawa and K. Kanoda, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 64511.
17. Y. Kurosaki, Y. Shimizu, K. Miyagawa, K. Kanoda and G. Saito, Phys. Rev. Lett., 2005, 95, 177001.
18. T. Senthil, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045109.
19. J. Vučičević, H. Terletska, D. Tanasković and V. Dobrosavljević, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 75143.
20. T. Furukawa, K. Miyagawa, H. Tanigchi, R. Kato and K. Kanoda, Nat. Phys., 2015, 11, 221–224.
21. T. Furukawa, K. Kobashi, Y. Kurosaki, K. Miyagawa and K. Kanoda, Nat. Commun., 2018, 9, 307.
22. A. Pustogow, M. Bories, A. Löhle, R. Rösslhuber, E. Zhukova, B. Gorshunov, S. Tomić, J. A. Schlueter, R. Hübner, T. Hiramatsu, Y. Yoshida, G. Saito, R. Kato, T.-H. Lee, V. Dobrosavljević, S. Fratini and M. Dressel, Nat. Mater., 2018, 17, 773–777.
23. H. Terletska, J. Vučičević, D. Tanasković and V. Dobrosavljević, Phys. Rev. Lett., 2011, 107, 026401.
24. M. M. Radonjić, D. Tanasković, V. Dobrosavljević, K. Haule and G. Kotliar, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 85133.
25. X. Deng, J. Mravlje, R. Žitko, M. Ferrero, G. Kotliar and A. Georges, Phys. Rev. Lett., 2013, 110, 086401.
26. A. Pustogow, Y. Saito, E. Zhukova, B. Gorshunov, R. Kato, T.-H. Lee, S. Fratini, V. Dobrosavljević and M. Dressel, Phys. Rev. Lett., 2018, 121, 056402.
27. A. Pustogow, R. Rösslhuber, Y. Tan, E. Uykur, A. Böhme, M. Wenzel, Y. Saito, A. Löhle, R. Hübner, A. Kawamoto, J. A. Schlueter, V. Dobrosavljević and M. Dressel, npj Quantum Mater., 2021, 6, 9.
28. R. Rösslhuber, A. Pustogow, E. Uykur, A. Böhme, A. Löhle, R. Hübner, J. Schlueter, Y. Tan, V. Dobrosavljević and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 125111.
29. A. Pustogow, Y. Saito, A. Löhle, M. S. Alonso, A. Kawamoto, V. Dobrosavljević, M. Dressel and S. Fratini, Nat. Commun., 2021, 12, 1571.
30. T. Ishiguro, K. Yamaji and G. Saito, Organic superconductors, 2nd edn, Springer-Verlag, Berlin, 1998.
31. N. Toyota, M. Lang and J. Müller, Low-Dimensional Molecular Metals, Springer-Verlag, Berlin, 2007.
32. The physics of organic superconductors and conductors, ed. A. Lebed, Springer-Verlag, Berlin, 2008.
33. T. Mori, Electronic Properties of Organic Conductors, Springer, Tokyo, 2016.
34. S. Yasuzuka and K. Murata, Sci. Techn. Adv. Mater., 2009, 10, 024307.
35. TTF Chemistry, ed. J. Yamada and T. Sugimoto, Springer-Verlag, Berlin, 2004.
36. D. Jérome, A. Mazaud, M. Ribault and K. Bechgaard, J. Phys. (Paris) Lett., 1980, 41, L95–L98.
37. M. Pinterić, M. Čulo, O. Milat, M. Basletić, B. Korin-Hamzić, E. Tafra, A. Hamzić, T. Ivek, T. Peterseim, K. Miyagawa, K. Kanoda, J. A. Schlueter, M. Dressel and S. Tomić, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195139.
38. P. Foury-Leylekian, V. Ilakovac, V. Balédent, P. Fertey, A. Arakcheeva, O. Milat, D. Petermann, G. Guillier, K. Miyagawa, K. Kanoda, P. Alemany, E. Canadell, S. Tomić and J.-P. Pouget, Crystals, 2018, 8, 158.
39. H. Kobayashi, H. Cui and A. Kobayashi, Chem. Rev., 2004, 104, 5265–5288.
40. D. Faltermeier, J. Barz, M. Dumm, M. Dressel, N. Drichko, B. Petrov, V. Semkin, R. Vlasova, C. Meźière and P. Batail, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165113.
41. M. Dumm, D. Faltermeier, N. Drichko, M. Dressel, C. Mézière and P. Batail, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195106.
42. S. Yasin, M. Dumm, B. Salameh, P. Batail, C. Meźière and M. Dressel, Eur. Phys. J. B, 2011, 79, 383–390.
43. U. Geiser, H. H. Wang, K. D. Carlson, J. M. Williams, H. A. Charlier, J. E. Heindl, G. A. Yaconi, B. J. Love, M. W. Lathrop, J. E. Schirber, D. Overmyer, J. Ren and M.-H. Whangbo, Inorg. Chem., 1991, 30, 2586–2588.
44. Y. Saito, T. Minamidate, A. Kawamoto, N. Matsunaga and K. Nomura, Phys. Rev. B, 2018, 98, 205141.
45. M. Dressel and N. Drichko, Chem. Rev., 2004, 104, 5689.
46. S. Elsässer, D. Wu, M. Dressel and J. A. Schlueter, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155150.
47. K. Sedlmeier, S. Elsässer, D. Neubauer, R. Beyer, D. Wu, T. Ivek, S. Tomić, J. A. Schlueter and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245103.
48. Y. Saito, A. Löhle, A. Kawamoto, A. Pustogow and M. Dressel, will be published in Crystals.
49. I. Kézsmárki, Y. Shimizu, G. Mihály, Y. Tokura, K. Kanoda and G. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 201101.
50. J. Merino, M. Dumm, N. Drichko, M. Dressel and R. H. McKenzie, Phys. Rev. Lett., 2008, 100, 086404.
51. M. Dressel, D. Faltermeier, M. Dumm, N. Drichko, B. Petrov, V. Semkin, R. Vlasova, C. Méziere and P. Batail, Phys. B, 2009, 404, 541–544.
52. J. Ferber, K. Foyevtsova, H. O. Jeschke and R. Valentí, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205106.
53. Due to the metallic contribution at low frequencies, we determined the bandwidth W from the high-frequency half-width at half maximum of the Hubbard bands as sketched in the inset of Fig. 5. As a matter of course, the resulting Mott–Hubbard band parameters of κ-(BEDT-TTF)₂Cu₂(CN)₃ are slightly different than those obtained previously.²² The qualitative behavior, however, is unaffected by the particular procedure.
54. M. Pinterić, P. Lazić, A. Pustogow, T. Ivek, M. Kuveždić, O. Milat, B. Gumhalter, M. Basletić, M. Čulo, B. Korin-Hamzić, A. Löhle, R. Hübner, M. Sanz Alonso, T. Hiramatsu, Y. Yoshida, G. Saito, M. Dressel and S. Tomić, Phys. Rev. B, 2016, 94, 161105.
55. S. Tomić and M. Dressel, Rep. Prog. Phys., 2015, 78, 096501.
56. N. Drichko, R. Beyer, E. Rose, M. Dressel, J. A. Schlueter, S. A. Turunova, E. I. Zhilyaeva and R. N. Lyubovskaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 075133.
57. A. Löhle, E. Rose, S. Singh, R. Beyer, E. Tafra, T. Ivek, E. I. Zhilyaeva, R. N. Lyubovskaya and M. Dressel, J. Phys.: Condens. Matter, 2016, 29, 055601.
58. T. Ivek, R. Beyer, S. Badalov, M. C. Čulo, S. Tomić, J. A. Schlueter, E. I. Zhilyaeva, R. N. Lyubovskaya and M. Dressel, Phys. Rev. B, 2017, 96, 085116.
59. T. Yamamoto, M. Uruichi, K. Yamamoto, K. Yakushi, A. Kawamoto and H. Taniguchi, J. Phys. Chem. B, 2005, 109, 15226–15235.
60. A. Girlando, J. Phys. Chem. C, 2011, 115, 19371–19378.
61. A. Girlando, M. Masino, S. Kaiser, Y. Sun, N. Drichko, M. Dressel and H. Mori, Phys. Status Solidi B, 2012, 249, 953–956.
62. M. Dressel, P. Lazić, A. Pustogow, E. Zhukova, B. Gorshunov, J. A. Schlueter, O. Milat, B. Gumhalter and S. Tomić, Phys. Rev. B, 2016, 93, 081201.
63. M. Dressel and G. Grüner, Electrodynamics of solids, Cambridge University Press, Cambridge, 2002.
64. M. M. Qazilbash, M. Brehm, B.-G. Chae, P.-C. Ho, G. O. Andreev, B.-J. Kim, S. J. Yun, A. V. Balatsky, M. B. Maple, F. Keilmann, H.-T. Kim and D. N. Basov, Science, 2007, 318, 1750–1753.
65. D. M. Grannan, J. C. Garland and D. B. Tanner, Phys. Rev. Lett., 1981, 46, 375–378.
66. M. A. van Dijk, G. Casteleijn, J. G. H. Joosten and Y. K. Levine, J. Chem. Phys., 1986, 85, 626–631.
67. M. T. Clarkson and S. I. Smedley, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 2070–2078.
68. M. T. Clarkson, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 37, 2079–2090.
69. Y. Alexandrov, N. Kozlovich, Y. Feldman and J. Texter, J. Chem. Phys., 1999, 111, 7023–7028.
70. C. Pecharromán and J. S. Moya, Adv. Mater., 2000, 12, 294–297.
71. C. Pecharromán, F. Esteban-Betegón, J. F. Bartolomé, S. López-Esteban and J. S. Moya, Adv. Mater., 2001, 13, 1541–1544.
72. C.-W. Nan, Y. Shen and J. Ma, Annu. Rev. Mater. Res., 2010, 40, 131–151.
73. S. Berthier, J. Peiro, S. Fagnent and P. Gadenne, Phys. A, 1997, 241, 1–5.
74. M. Hövel, B. Gompf and M. Dressel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035402.
75. M. Hövel, B. Gompf and M. Dressel, Thin Solid Films, 2011, 519, 2955–2958.
76. S. De Zuani, T. Peterseim, A. Berrier, B. Gompf and M. Dressel, Appl. Phys. Lett., 2014, 104, 241109.
77. S. De Zuani, M. Rommel, B. Gompf, A. Berrier, J. Weis and M. Dressel, ACS Photonics, 2016, 3, 1109–1115.
78. M. Abdel-Jawad, I. Terasaki, T. Sasaki, N. Yoneyama, N. Kobayashi, Y. Uesu and C. Hotta, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125119.
79. M. Pinterić, T. Ivek, M. Čulo, O. Milat, M. Basletić, B. Korin-Hamzić, E. Tafra, A. Hamzić, M. Dressel and S. Tomić, Phys. B, 2015, 460, 202–207.
80. S. Sasaki, S. Iguchi, N. Yoneyama and T. Sasaki, J. Phys. Soc. Jpn., 2015, 84, 074709.
81. L. E. Cross, Relaxor Ferroelectrics, Springer-Verlag, Berlin, Heidelberg, 2008, pp. 131–155.
82. S. Kirkpatrick, Rev. Mod. Phys., 1973, 45, 574–588.
83. A. L. Efros and B. I. Shklovskii, Phys. Status Solidi B, 1976, 76, 475–485.
84. T. C. Choy, Effective Medium Theory: Principles and Applications, 2nd edn, Oxford University Press, Oxford, 2015.

---