Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding and solving disorder in the substitution pattern of amino functionalized MIL-47(V)†
Jurn
Heinen
* and
David
Dubbeldam
Van't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: J.Heinen@uva.nl
First published on 30th November 2015
Abstract
Electronic energies and elastic constants of four amino functionalized MIL-47(V) supercells were computed using plane wave density functional theory to determine the influence of the substituent positions on the organic linker. An inverse relationship between the ab initio energies and the elastic constants was found, indicating that the high electronic stability correlates with high mechanical stability. Torsion in all supercells was induced upon substitution, which caused strain in the NH2-MIL-47(V) supercell. The combined effect of the substituent bulkiness and the induced torsion reduced the pore volume of the NH2-MIL-47(V) structures by >7% and the surface area by >14% with respect to MIL-47(V). This reduction was confirmed by lower saturation capacities of methane, CO2 and benzene. When unfavourable substituent positions are chosen, large torsions caused a further reduction of the saturation capacity. Differences in surface area, pore volume and saturation capacity illustrate the importance of choosing the correct NH2-MIL-47(V) supercell.
Introduction
Metal–organic frameworks (MOFs), also known as coordination polymers, are a class of nanoporous materials consisting of metal clusters interconnected with organic linkers. Due to their large surface area, high porosity and enormous number of synthesizable topologies, MOFs have promising applications in hydrogen,1,2 CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and methane4 storage, adsorptive separation5–7 and catalysis.8,9 In contrast to other porous materials, such as zeolites, the pore characteristics of MOFs can be easily functionalized by substituting one or more hydrogens of the organic linker for various functional groups.10–12 This can be achieved by prefunctionalizing the organic linkers or by post-synthetic modification. Functionalization of MOFs can, for example, heavily affect the breathing properties as was shown by Devic et al.10 for the narrow pore–large pore transition of functionalized MIL-53(Fe).
3 and methane4 storage, adsorptive separation5–7 and catalysis.8,9 In contrast to other porous materials, such as zeolites, the pore characteristics of MOFs can be easily functionalized by substituting one or more hydrogens of the organic linker for various functional groups.10–12 This can be achieved by prefunctionalizing the organic linkers or by post-synthetic modification. Functionalization of MOFs can, for example, heavily affect the breathing properties as was shown by Devic et al.10 for the narrow pore–large pore transition of functionalized MIL-53(Fe).
An excellent example of a functionalized MOF was recently shown by Hu et al.13 They constructed UTSA-100, an amino derivative of tetrazol-1,3-benzenedicarboxylic acid, that efficiently removes acetylene at room temperature from ethylene/acetylene mixtures containing only 1% acetylene. Another interesting example is NH2-MIL-88B(Fe) which improved the performance of multiple applications with respect to MIL-88B(Fe), such as acting as a better photocatalyst for the reduction of Cr(VI)14 and having a higher saturation capacity for ethanol, without losing the flexibility.15 For NH2-MIL-53(Fe) it was found to be an excellent solid base catalyst for the transesterification of triglycerides with methanol16 and Serra-Crespo et al.17 showed that it can be used in a vacuum pressure swing adsorption process for natural gas upgrading.
As described above, amino functionalized MOFs can provide improved performance for various applications. From single X-ray structures it is possible to determine the appropriate unit cell of the functionalized MOF; the question remains however, how these substituted linkers are distributed with respect to each other? This is important for modeling these materials, since it is expected that different substitution patterns, resulting in linker-pair combinations, might lead to different adsorptive properties. For mono-substituted linkers there are numerous degrees of freedom with respect to the substituent positions, which are discussed below.
In this study, we address the substitution pattern of mono-amino functionalized MIL-47(V). MIL-47(V)18 is a vanadium-based metallic cluster connected to BDC (= 1,4-benzenedicarboxylate) linkers and MIL-47(V) has the formula [VIV(O)BDC]. In contrast to the MIL-53 family, MIL-47(V) is missing the μ2-OH group due to thermal activation and does not show significant breathing.19,20 The unit cell of MIL-47(V) is displayed in Fig. 1a.
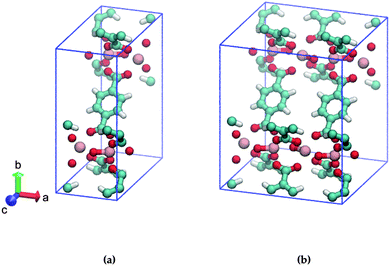 | ||
| Fig. 1 Ball and stick model of (a) one, (b) two MIL-47(V) unit cells. The BDC-linkers of interest are displayed face-up. Cyan: C, red: O, pink: V, white: H. | ||
Consider two MIL-47(V) unit cells along the a-axis that form a supercell; this results in adjacent BDC linkers, as shown in Fig. 1b. Only the left/right ortho/meta positions of the aromatic ring of the BDC-linker are available for mono-substitution since the ipso and para positions are connected to the carboxylate. To our knowledge, it is currently unclear if the substituent positions on both BDC-linkers are identical or that they differ. We expect that the most stable structures are those with low energetics and high mechanical stability.
By comparing the ab initio energies and the elastic constants of the different linker-pair combinations, we can determine the effect that linker substitution has on the overall supercell. Furthermore, we computed single component adsorption isotherms (methane, CO2 and benzene) and the corresponding heat of adsorptions for the various isomeric supercells to illustrate the difference in adsorption properties (surface area and saturation capacity) due to these different linker-pair combinations.
Methodology
Approach
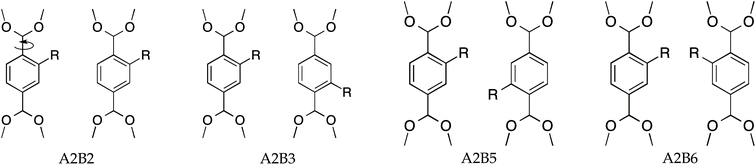
Two MIL-47(V) unit cells, see Fig. 1b, each containing four BDC-linkers, were considered as a supercell to resemble two independent adjacent BDC-linkers. If only two adjacent BDC-linkers are substituted, this is called partial substitution which shows the local effect of two adjacent linkers upon substitution. Full substitution implies that all BDC-linkers are substituted and will reflect the overall effect on the supercell. The proposed substitution patterns are shown in Fig. 2. A and B refer to the first and second BDC-linker, numbers indicate the positions of the aromatic ring with 1 = top ipso position and going clockwise until 6 = left ortho position.Calculation of relative ab initio energies
To calculate the relative ab initio energies of the isomeric supercells, the geometry and lattice parameters of the structures were optimized using the Vienna Ab Initio Software Package21,22 (VASP) with the Grimme dispersion corrected23 PBE24 exchange–correlation functional. A plane wave basis was employed with an energy density cut-off of 600 eV in order to achieve high accuracy, needed for the computation of the stress tensor. Core-electrons were described by the projected augmented wave method25,26 and integration in k-space was performed over the Γ-point using the Monkhorst–Pack sampling scheme.27 A Gaussian electron smearing of 0.05 eV was applied to converge the electronic structure. The geometric convergence criteria of the ionic forces were set to 10−3 eV Å−1.Calculation of elastic constants
The mechanical and elastic properties of various MOFs have been studied intensively28–30 and are essential to determine the stability of the supercells. A MOF subjected to a certain strain ε can be described by Hooke's law (within the elastic limit) as31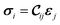 | (1) |
 being the 6 × 6 elastic constant matrix in Voigt notation.‡ For a low symmetry orthorhombic unit cell, such as MIL-47(V), the elastic constant matrix has the form
being the 6 × 6 elastic constant matrix in Voigt notation.‡ For a low symmetry orthorhombic unit cell, such as MIL-47(V), the elastic constant matrix has the form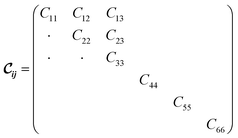 | (2) |
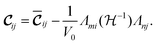 | (3) |
The first term of the r.h.s. of eqn (3), known as the clamped ion term (or the Born term) is calculated by the stress–strain relationship33 for which six finite distortions (3 normal, 3 shear) of the lattice are applied, resulting in strained supercells. For each strain E, E + e1,…, E + e6, the corresponding stresses are computed ab initio. The clamped ionic elastic constants are then obtained by the least squares fitting procedure as described by Le Page and Saxe.33
The Born expression is generalized by including the relaxation effects which are taken into account in the second term. The contributions due to relaxation of the elastic constants are calculated by multiplying the internal strain tensor Λmj with the inverted Hessian matrix 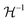 . Here, Λmj is the internal strain tensor34 given by
. Here, Λmj is the internal strain tensor34 given by
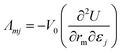 | (4) |
It should be noted that by substituting the BDC-linkers, the symmetry of the supercell is destroyed reducing the space group to P1. Therefore, calculation of the elastic constants is subjected to numerical inaccuracies. For this reason, we also computed the elastic constants for MIL-47(V) in the P1 space group to assess trends in the elastic constants.
Calculation of structural and adsorption properties
For the optimized structures we computed the pore volume, accessible surface area and single component adsorption isotherms using the molecular software package RASPA-2.0.35 The void fraction is computed using the Widom particle insertion method36 with helium as a probe at room temperature. Multiplying the helium void fraction by the total volume gives the pore volume.The accessible surface area is calculated by the Shrake and Rupley method37 in which a probe atom is used to ‘roll’ over the surface. It has been shown that the accessible surface area is a valid characteristic for describing the actual surface area of a MOF.38 Values are close to surface areas obtained by the frequently used BET method.38–40
Single component adsorption isotherms for methane, CO2 and benzene were computed using Grand Canonical Monte Carlo41 simulations. Here, the temperature (T), chemical potential (μ) and volume (V) are fixed whereas the number of molecules are allowed to fluctuate.42,43 We adopted the Configurational Bias Monte Carlo (CBMC) approach44–46 where growth of the adsorbate molecules is biased towards favourable configurations. The amount of initialization cycles was set to 1000 and number of production cycles to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Fugacity coefficients and excess loadings were computed using the Peng–Robinson equation47 of state. For statistical purposes, the simulation is divided into five intervals. For each interval the standard deviation within a 95% confidence interval was determined. The adsorbent interactions were described using the generic DREIDING48 force field and adsorbates were described by the TraPPE force field.49–51 Here, CO2 is modelled as a tri-atomic molecule with partial atomic charges of 0.70e and −0.35e for C and O respectively to represent the quadrupole moment.52 Framework charges53 were computed using the REPEAT/ChelpG method54,55 by fitting atomic charges on the ab initio electrostatic potential. The charge–charge interactions were computed using the Ewald summation56 with a precision of 10−6 and the van der Waals cut-off radius was set to 12.0 Å. Since MIL-47(V) does not show significant breathing upon adsorption, the framework atoms were kept rigid.
000. Fugacity coefficients and excess loadings were computed using the Peng–Robinson equation47 of state. For statistical purposes, the simulation is divided into five intervals. For each interval the standard deviation within a 95% confidence interval was determined. The adsorbent interactions were described using the generic DREIDING48 force field and adsorbates were described by the TraPPE force field.49–51 Here, CO2 is modelled as a tri-atomic molecule with partial atomic charges of 0.70e and −0.35e for C and O respectively to represent the quadrupole moment.52 Framework charges53 were computed using the REPEAT/ChelpG method54,55 by fitting atomic charges on the ab initio electrostatic potential. The charge–charge interactions were computed using the Ewald summation56 with a precision of 10−6 and the van der Waals cut-off radius was set to 12.0 Å. Since MIL-47(V) does not show significant breathing upon adsorption, the framework atoms were kept rigid.
The heat of adsorption is computed using two methods: (i) the Widom insertion method36,43 and (ii) the fluctuation theorem.57,58 The heat of adsorption obtained from the Widom insertion method36,59 is computed according to
| ΔH = 〈Uhg〉 − 〈Ug〉 − 〈Uh〉 − RT | (5) |
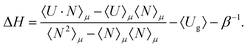 | (6) |
Results and discussion
Lattice parameters and physical properties
The optimized lattice parameters (Table 1) show that the amino functionalized MIL-47(V) supercells have angles that are not exactly 90°. The MIL-47 family members have orthorhombic space groups with angles of 90 degrees.11,61 This implies that various orientations of the unit cells and various linker-pair combinations give on average, in the long range, cell parameters of α = β = γ = 90°.| a | b | c | α | β | γ | V pore | S ASA | |
|---|---|---|---|---|---|---|---|---|
| MIL-47(V) | 13.588 | 16.262 | 13.783 | 90.00 | 90.00 | 90.00 | 1823.40 | 1839.15 |
| A2B2 | 13.578 | 16.386 | 13.653 | 90.05 | 90.17 | 90.37 | 1687.94 | 1589.82 |
| A2B3 | 13.606 | 16.369 | 13.571 | 90.00 | 90.20 | 89.99 | 1685.58 | 1583.83 |
| A2B5 | 13.584 | 16.569 | 13.433 | 90.06 | 90.27 | 90.27 | 1663.29 | 1560.84 |
| A2B6 | 13.573 | 16.652 | 13.292 | 90.00 | 89.99 | 90.05 | 1536.21 | 1479.45 |
The lattice axis a and lattice angle α are similar in their structures which can be attributed to the rigid metal–oxide bonds along the a-axis. Functionalizing MIL-47(V) reduces the pore volume and the effective surface area by >150 A3 and 200 m2 g−1 respectively. Two effects can be attributed to the pore volume and surface area reduction: the finite size of the substituent and the induced torsion due to the rotation of the BDC-linker described by the dihedral angles ϕA and ϕB (Table 2). Although A2B3 has the smallest torsions, the cell parameters deviate more than those of A2B6 which has significantly larger dihedral angles (−14.20° and −10.88° vs. −2.21° and 2.5°).
| Partial | Full | |||
|---|---|---|---|---|
| ϕ A | ϕ B | ϕ A | ϕ B | |
| A2B2 | 8.32 | 8.52 | 7.71 | 7.71 |
| A2B3 | −1.56 | −5.05 | −2.21 | 2.52 |
| A2B5 | 7.45 | 9.76 | 6.14 | 6.35 |
| A2B6 | 11.34 | 13.11 | −14.20 | −10.88 |
Upon full substitution, configurations A2B2 and A2B5 show a decrease in the dihedral angles with respect to the partial substitution. This might imply that the full substitution reduces strain from the supercell for these configurations. Large dihedral angles of A2B6 are due to repulsive steric interactions caused by the amino groups and therefore result in significantly lower pore volume and effective surface area. For A2B3, the sign of the dihedral angles differ, indicating that the BDC-linkers are twisted in opposite directions. Fig. S1-A2B3† shows indeed that the geometry between V atoms is convex.
Relative ab initio energies and elastic constants
Given the small energy difference (≤2.00 kJ mol−1) at 0 K, A2B2 and A2B5 are the most stable amino functionalized MIL-47(V) supercells for both partial and full substitution. At finite temperature, it is expected that from an energetic point of view, supercells A2B2 and A2B5 are equally likely. Despite the small dihedral angle of A2B3, the high relative ab initio energy indicates that this structure is energetically unfavourable. It is expected that this structure is strained due to the opposite positioning of the BDC-linkers. For A2B6 there is an unfavourable cooperative interaction upon substitution, since there is a factor 4.4 gain in ab initio energy going from partial to full substitution (Table 3).| A2B2 | A2B3 | A2B5 | A2B6 | |
|---|---|---|---|---|
| ΔEpartial | 0.00 | 12.94 | 0.55 | 13.68 |
| ΔEfull | 0.00 | 25.59 | 2.00 | 60.30 |
Fig. 3 visualizes the nine independent elastic constants for the various NH2-MIL-47(V) and MIL-47(V) supercells. Overall, the elastic constants for MIL-47(V) are higher than for any of the NH2-MIL-47(V) supercells. Among the amino functionalized MIL-47(V) supercells, A2B2 and A2B5 have the highest elastic constants with the largest, absolute, difference for 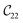 with
with 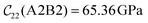 and
and 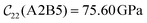 . The clamped ionic term
. The clamped ionic term  for A2B2 is 117.74 GPa and 123.54 GPa for A2B5 and the contributions due to relaxation for A2B2 and A2B5 are −52.38 GPa and −47.94 GPa respectively.
for A2B2 is 117.74 GPa and 123.54 GPa for A2B5 and the contributions due to relaxation for A2B2 and A2B5 are −52.38 GPa and −47.94 GPa respectively.
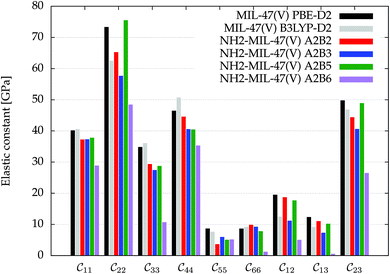 | ||
Fig. 3 The nine independent elastic constants  in Voigt notation of MIL-47(V) and the four isomeric NH2-MIL-47(V) supercells. MIL-47(V) has been computed by Ortiz et al.62,63 at the B3LYP-D2 level. in Voigt notation of MIL-47(V) and the four isomeric NH2-MIL-47(V) supercells. MIL-47(V) has been computed by Ortiz et al.62,63 at the B3LYP-D2 level. | ||
The amino groups of the adjacent linkers are in proximity to each other for A2B5, see Fig. 2 and S3.† Note that the linkers have a torsion and thus the nitrogens have different positions along the b-axis. Straining along the b-axis reduces the nitrogen–nitrogen distance resulting in a repelling interaction which gives a more rigid structure. This repelling nitrogen–nitrogen behaviour is not present in A2B2.
An inverse trend between the relative ab initio energies and the elastic constants can be observed. NH2-MIL-47(V) supercells that have high ab initio energies (A2B3 and A2B6) have lower elastic constants, whereas supercells that have low ab initio energies (A2B2 and A2B5) have high elastic constants. It is not clear if this relationship holds for other functionalized MIL-47(V) structures.
Single component adsorption isotherm
The amino functionalized MIL-47(V) structures have lower surface areas than MIL-47(V) (Table 1) and this can also be observed from the saturation capacity for methane and CO2 as shown in Fig. 4 and for benzene in Fig. S2.† In particular for A2B6 this effect is more profound.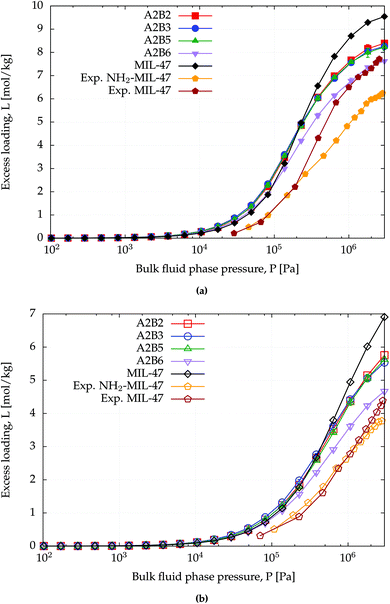 | ||
| Fig. 4 CB-GCMC adsorption isotherms of (a) CO2 and (b) methane for MIL-47(V) and NH2-MIL-47(V) at T = 303 K. Standard deviations of methane and CO2 isotherms are smaller than symbol sizes. Experimental saturation capacities for CO2 and methane uptake in NH2-MIL-47(V) are and 6.2 and 3.6 mol kg−1.61 | ||
At lower pressures the CO2 isotherms differ, whereas for methane the isotherms are identical. For CO2 this difference is expected due to the dominating sorbent–adsorbate interaction between the quadrupole moment of CO2 and the amino group. Comparing heat of adsorptions at infinite dilution Table 4 shows that the simulated trend agrees with the experimental trend: larger heat of adsorption for the amino functionalized MIL-47(V). A similar behaviour has been observed between MIL-53(Al) and NH2-MIL-53(Al).64 At finite loading, it is also observed, see Fig. S4,† that the heat of adsorption is more favourable for NH2-MIL-47(V) than for MIL-47(V) for methane and CO2 adsorption. At higher loadings, the heat of adsorption changes due to adsorbate–adsorbate interactions (Fig. S5†). The heat of adsorption for CO2 is higher than for methane as expected, although there is a slight difference between experimental and computational results. This difference is attributed to the rigidity of the force field framework; upon CO2 adsorption, the amino group is no longer in the same plane as the BDC-linker. Optimized VASP structures from Leus et al.61 show a dihedral angle of −15.20° with the hydrogens pointing away. The heat of adsorption difference among the various supercells is negligible and is not surprising since CO2 will adsorb most-likely on the nitrogen of the amino group which is irrelevant of the substitution pattern of the linkers. The combined effect of the substituted linker can alter the adsorption positions at higher loadings.
At saturation loadings the isotherms change for both adsorbates. Leus et al.61 measured experimentally the single component isotherms of methane and CO2 at T = 303 K for MIL-47(V) and NH2-MIL-47(V) with a saturation capacity for CO2 and CH4 in MIL-47(V) of 7.7 and 4.1 mol kg−1 respectively. The simulated saturation capacities are higher than the experimental ones, which is a general feature since for simulated isotherms, defects and impurities are not taken into account.
For larger adsorbates, the influence of the substitution patterns is more significant. Fig. S2† shows the computed single component adsorption isotherms for benzene at 328 K. Steeper uptake of the benzene adsorption isotherms for NH2-MIL-47(V) is observed and indicates that benzene adsorbs stronger in NH2-MIL-47(V) than in MIL-47(V). This is not a confinement effect, which has been observed for benzene adsorption in zeolite MFI,65 since benzene is approximately 5.5 Å in size and the pore diameter of MIL-47(V) is 10.5 and 11.0 Å.66 However, at high pressures, the saturation capacity of MIL-47(V) for benzene is higher than that for NH2-MIL-47(V) due to the better packing of the benzene adsorbates.
Conclusions
We demonstrated that various linker-pair combinations of amino functionalized MIL-47(V) affect structural and adsorption properties of the sorbent. Functionalizing MIL-47(V) with amino groups reduces the accessible surface area, pore volume and the saturation capacities for methane, CO2 and benzene. Heat of adsorption at infinite dilution of various linker-pair combinations is equal, indicating that different substitution patterns do not affect adsorption in the Henry regime. As a result of linker substitution, torsions of the BDC-linker induce strain in the material leading to both energetically and mechanically unstable structures. An inverse relationship between the relative ab initio energy and elastic constants was observed. It is therefore crucial to consider an appropriate unit cell in simulation studies. For amino functionalized MIL-47(V), A2B2 and A2B5 are the most stable structures.Conflict of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the Netherlands Research Council for Chemical Sciences (NWO/CW) through a VIDI grant (David Dubbeldam). We thank Sofia Calero and Ariana Torres-Knoop for fruitful discussions and SURFsara (http://www.surfsara.nl) for the support in using the Lisa Compute Cluster.References
- L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314 RSC.
- S. S. Han, J. L. Mendoza-Cortes and W. A. Goddard III, Chem. Soc. Rev., 2009, 38, 1460–1476 RSC.
- Z. Zhang, Z.-Z. Yao, S. Xiang and B. Chen, Energy Environ. Sci., 2014, 7, 2868–2899 CAS.
- Y. He, W. Zhou, G. Qian and B. Chen, Chem. Soc. Rev., 2014, 43, 5657–5678 RSC.
- B. Van de Voorde, B. Bueken, J. Denayer and D. De Vos, Chem. Soc. Rev., 2014, 43, 5766–5788 RSC.
- J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869–932 CrossRef CAS PubMed.
- A. Torres-Knoop and D. Dubbeldam, ChemPhysChem, 2015, 2046–2067 CrossRef CAS PubMed.
- A. H. Chughtai, N. Ahmad, H. A. Younus, A. Laypkov and F. Verpoort, Chem. Soc. Rev., 2015, 44, 6804–6849 RSC.
- J. Liu, L. Chen, H. Cui, J. Zhang, L. Zhang and C.-Y. Su, Chem. Soc. Rev., 2014, 43, 6011–6061 RSC.
- T. Devic, et al. , J. Am. Chem. Soc., 2010, 132, 1127–1136 CrossRef CAS PubMed.
- S. Biswas, D. E. P. Vanpoucke, T. Verstraelen, M. Vandichel, S. Couck, K. Leus, Y.-Y. Liu, M. Waroquier, V. V. Speybroeck, J. F. M. Denayer and P. V. D. Voort, J. Phys. Chem. C, 2013, 117, 22784–22796 CAS.
- W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle III, M. Bosch and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593 RSC.
- T.-L. Hu, H. Wang, B. Li, R. Krishna, H. Wu, W. Zhou, Y. Zhao, Y. Han, X. Wang, W. Zhu, Z. Yao, S. Xiang and B. Chen, Nat. Commun., 2015, 6, 7328 CrossRef CAS PubMed.
- L. Shi, T. Wang, H. Zhang, K. Chang, X. Meng, H. Liu and J. Ye, Adv. Sci., 2015, 2, 3 Search PubMed.
- C. Scherb, J. J. Williams, F. Hinterholzinger, S. Bauer, N. Stock and T. Bein, J. Mater. Chem., 2011, 21, 14849–14856 RSC.
- J. Chen, R. Liu, H. Gao, L. Chen and D. Ye, J. Mater. Chem. A, 2014, 2, 7205–7213 CAS.
- P. Serra-Crespo, T. A. Wezendonk, C. Bach-Samario, N. Sundar, K. Verouden, M. Zweemer, J. Gascon, H. v. d. Berg and F. Kapteijn, Chem. Eng. Technol., 2015, 38, 1183–1194 CrossRef CAS.
- K. Barthelet, J. Marrot, D. Riou and G. Ferey, Angew. Chem., Int. Ed., 2002, 41, 281–284 CrossRef CAS.
- F. Salles, H. Jobic, T. Devic, P. L. Llewellyn, C. Serre, G. Férey and G. Maurin, ACS Nano, 2010, 4, 143–152 CrossRef CAS PubMed.
- N. Rosenbach, H. Jobic, A. Ghoufi, F. Salles, G. Maurin, S. Bourrelly, P. Llewellyn, T. Devic, C. Serre and G. Férey, Angew. Chem., Int. Ed., 2008, 47, 6611–6615 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- J.-C. Tan, B. Civalleri, C.-C. Lin, L. Valenzano, R. Galvelis, P.-F. Chen, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502 CrossRef PubMed.
- W. Li, S. Henke and A. K. Cheetham, APL Mater., 2014, 2, 1–9 CrossRef CAS PubMed.
- J. F. Nye, Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford Science Publications, 1984 Search PubMed.
- VASP Manual, http://cms.mpi.univie.ac.at/VASP Search PubMed.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter, 2002, 65, 104104 CrossRef.
- X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B: Condens. Matter, 2005, 72, 035105 CrossRef.
- D. Dubbeldam, S. Calero, D. Ellis and R. Snurr, RASPA 2.0: Molecular Software Package for Adsorption and Diffusion in (Flexible) Nanoporous Materials, 2015, DOI:10.1080/08927022.2015.1010082.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- A. Shrake and J. Rupley, J. Mol. Biol., 1973, 79, 351–371 CrossRef CAS PubMed.
- T. Düren, F. Millange, G. Férey, K. S. Walton and R. Q. Snurr, J. Phys. Chem. C, 2007, 111, 15350–15356 Search PubMed.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- K. S. Walton and R. Q. Snurr, J. Am. Chem. Soc., 2007, 129, 8552–8556 CrossRef CAS PubMed.
- D. Nicholson and N. G. Parsonage, Computer simulation and the statistical mechanics of adsorption, Academic Press, New York, 1988 Search PubMed.
- D. Dubbeldam, A. Torres-Knoop and K. S. Walton, Mol. Simul., 2013, 39, 1253–1292 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, 2nd edn, 2002 Search PubMed.
- J. I. Siepmann, Mol. Phys., 1990, 70, 1145–1158 CrossRef CAS.
- J. I. Siepmann and D. Frenkel, Mol. Phys., 1992, 75, 59–70 CrossRef CAS.
- D. Frenkel, G. C. A. M. Mooij and B. Smit, J. Phys.: Condens. Matter, 1992, 4, 3053 CrossRef.
- D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam., 1976, 15, 59–64 CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682 CrossRef CAS.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- N. Rai and J. I. Siepmann, J. Phys. Chem. B, 2007, 111, 10790–10799 CrossRef CAS PubMed.
- J. G. Harris and K. H. Yung, J. Phys. Chem., 1995, 99, 12021–12024 CrossRef CAS.
- S. Hamad, S. R. Balestra, R. Bueno-Perez, S. Calero and A. R. Ruiz-Salvador, J. Solid State Chem., 2015, 223, 144–151 CrossRef CAS.
- C. Campañá, B. Mussard and T. K. Woo, J. Chem. Theory Comput., 2009, 5, 2866–2878 CrossRef.
- T. Watanabe, T. A. Manz and D. S. Sholl, J. Phys. Chem. C, 2011, 115, 4824–4836 CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- D. Nicholson and N. G. Parsonage, Computer simulation and the statistical mechanics of adsorption, Academic Press, New York, USA, 1982 Search PubMed.
- T. J. H. Vlugt, E. Garcia-Perez, D. Dubbeldam, S. Ban and S. Calero, J. Chem. Theory Comput., 2008, 4, 1107–1118 CrossRef CAS.
- T. J. H. Vlugt, Mol. Simul., 1999, 23, 63 CrossRef CAS.
- F. Karavias and A. L. Myers, Langmuir, 1991, 7, 3118 CrossRef CAS.
- K. Leus, S. Couck, M. Vandichel, G. Vanhaelewyn, Y.-Y. Liu, G. B. Marin, I. V. Driessche, D. Depla, M. Waroquier, V. V. Speybroeck, J. F. M. Denayer and P. V. D. Voort, Phys. Chem. Chem. Phys., 2012, 14, 15562–15570 RSC.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, Phys. Rev. Lett., 2012, 109, 195502 CrossRef PubMed.
- A. U. Ortiz, A. Boutin, A. H. Fuchs and F.-X. Coudert, J. Chem. Phys., 2013, 138, 174703 CrossRef PubMed.
- A. Torrisi, R. G. Bell and C. Mellot-Draznieks, Microporous Mesoporous Mater., 2013, 168, 225–238 CrossRef CAS.
- L. A. Clark and R. Q. Snurr, Chem. Phys. Lett., 1999, 308, 155–159 CrossRef CAS.
- D. Tanaka, K. Nakagawa, M. Higuchi, S. Horike, Y. Kubota, T. Kobayashi, M. Takata and S. Kitagawa, Angew. Chem., Int. Ed., 2008, 47, 3914–3918 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Figures of the four amino functionalized MIL-47(V), viewed along the a-axis. Benzene adsorption isotherms at T = 328 K. Heat of adsorption as finite loading. See DOI: 10.1039/c5dt03399c |
| ‡ σi = (σ1 = σxx, σ2 = σyy, σ3 = σzz, σ4 = σyz, σ5 = σxz, σ6 = σxy). |
| This journal is © The Royal Society of Chemistry 2016 |