Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: concepts, methods and challenges
Alejandro A.
Franco
*ab
aLaboratoire de Réactivité et de Chimie des Solides (L.R.C.S.), Université de Picardie Jules Verne, CNRS UMR 7314–33 rue Saint Leu, Amiens, France. E-mail: a.a.franco.electrochemistry@gmail.com; alejandro.franco@u-picardie.fr; Tel: +33 3 22 82 75 86
bRéseau sur le Stockage Electrochimique de l’Energie (RS2E), FR CNRS 3459, France
First published on 3rd April 2013
Abstract
This review focuses on the role of physical theory and computational electrochemistry for fundamental understanding, diagnostics and design of new electrochemical materials and operation conditions for energy storage through rechargeable Li ion batteries (LIBs). More particularly, deep insight based on multiscale physical modelling techniques, spanning scales from few atoms to the device level, can advise about the materials behaviour and aging and how components with optimal specifications could be made and how they can be integrated into operating devices. Concepts and different existing multiscale modelling methodologies are presented and some of the ongoing efforts within the community to understand from physical multiscale modelling and numerical simulation electrochemical mechanisms and degradation processes in LIBs are discussed. Finally, major challenges and perspectives in multiscale modelling for battery applications are highlighted.
 Alejandro A. Franco | Alejandro A. Franco is senior scientist at LRCS-CNRS/UPJV in Amiens, France. He led for 11 years the electrochemistry modelling activities at CEA-Grenoble until 2013. He is the inventor of pioneering multiscale models scaling up ab initio and microstructural data at the device level, for the performance and durability prediction of fuel cells, electrolyzers and batteries. He delivered invited talks (including keynotes) in several international conferences and workshops, as well as in USA, Canada and Europe institutes and universities. He is organizer of international symposia on electrochemistry modelling, three of them within the Annual Meetings of the International Society of Electrochemistry. |
1 Introduction
1.1 Rechargeable lithium ion batteries: context
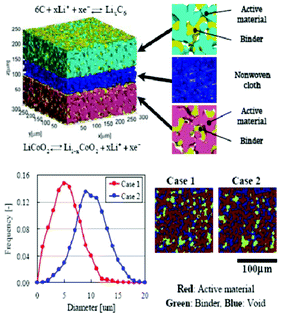
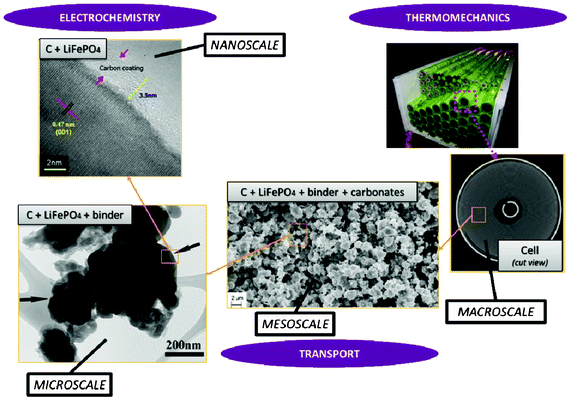
Modern electronic equipment and electric vehicle applications have been rapidly developing, resulting in a growing demand for high energy density power sources such as rechargeable lithium ion batteries (LIBs). There is nowadays in R&D laboratories a strong interest on designing the new generation of LIBs with enhanced efficiency of storage, charging speed and safety.1,2 The inherent difficulty is that LIBs are multiscale and multiphysics systems, as illustrated in Fig. 1 for a positive electrode made of LiFePO4, one of the most popular electrode materials because of its high power density and safety among a large variety of compounds developed since the 1970s.3,4 In this case, non-porous LiFePO4 crystals represent the smallest scale observed, whereas the porous agglomerates represent the second size scale. The third size scale is the positive electrode itself, which consists of carbon black, binder and the porous agglomerates of the LiFePO4 particles.5 Carbon black is usually added to reduce the formation of agglomerates during the synthesis process and to enhance the electronic conductivity properties.6 The binder is usually made of Polyvinylidine difluoride (PVDF) polymer, which provides to the electrode an aspect of “polymer composite”. The binder spatial distribution depends on the electrode preparation method, coating and drying process, and surface properties of each compound, such as the active material. In early work without careful morphology control, considerable crystal agglomeration occurred.7 This is also true for more recent materials, where agglomerated particles are often present.8–10 Negative electrodes are typically made of carbonaceous materials and also present a complex multiscale structure as illustrated in Fig. 2. The application of carbonaceous materials instead of Li-metal has several advantages such as better cycle-life and reliability preventing severe degradation problems such as Li dendrites formation during cycling. Carbon has in fact the ability to reversibly absorb and release large quantities of lithium (Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C = 1
C = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6) without altering the mechanical and electrical properties of the material. On the first charge of the battery a polymeric layer, the so-called solid electrolyte interphase (SEI), forms from the electrolyte decomposition. This “passivation” or “protective” layer is of crucial importance for the battery operation in terms of safety as it prevents the carbon from reacting with the electrolyte and helps on avoiding graphite exfoliation.11
6) without altering the mechanical and electrical properties of the material. On the first charge of the battery a polymeric layer, the so-called solid electrolyte interphase (SEI), forms from the electrolyte decomposition. This “passivation” or “protective” layer is of crucial importance for the battery operation in terms of safety as it prevents the carbon from reacting with the electrolyte and helps on avoiding graphite exfoliation.11
 | ||
| Fig. 1 Schematics of the multiscale character of a LiFePO4 electrode in a LIB and physicochemical mechanisms.24 Schematics made with TEM and SEM pictures reported in ref. 25 (courtesy of X. Sun, University of Waterloo, Canada) and from the spiral battery tomography picture in ref. 26 (reprinted with permission of Elsevier). | ||
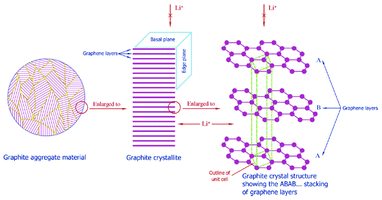 | ||
| Fig. 2 Multiscale structure of a graphite electrode in a LIB. Reprinted from ref. 27 with permission of Elsevier. | ||
Moreover, several materials have also been proposed as alternatives to replace graphite in the negative electrode, also showing more or less a multiscale structure.12
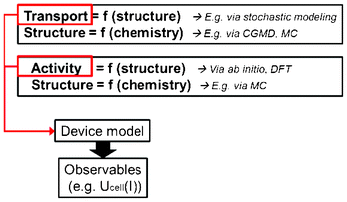
As the electrodes structure of rechargeable LIBs can be seen as a complex set of lithium sources and sinks embedded in an electrolyte medium, the rate-determining processes during charge and discharge will depend on the Li+ concentration on the (e.g. intercalation, conversion) electrode active material surface, Li+ concentration in the electrolyte, the potential drop between the active material and the electrolyte and the lithium concentration inside the active material.13–15 The LIB operation may thus be limited by Li+ transport in the electrolyte, lithium transport in the electrode material or by the ionic or electronic conductivity of the electrolyte or electrodes.
Electrochemical reaction of lithium intercalation and/or conversion takes place on a nanometer scale and strongly depends on the chemistry and on the nano- and microstructural properties of the intercalation/conversion material. Charge transport, heat transport and mechanical stresses take place from the material level up to the cell level and also depend on the materials and components structural properties. Typical time scales vary from sub-nanoseconds (electrochemical reactions) over seconds (transport) up to days or even months (structural and chemical degradation). All the mechanisms are strongly and nonlinearly coupled over the various scales, and thus processes at the nano and microscale can therefore dominantly influence the LIB macroscopic behaviour. A detailed understanding of the relevant processes on all these materials and components scales is required for a physical-based optimization of the LIB design regarding its efficiency, durability and safety.
Parallel to various experimental research programs, mathematical models that describe the behaviour of LIBs and their interaction with other devices (e.g. vehicle electric engines) have received more and more attention for almost 30 years. These models range from those that are fitted to experimental data under various conditions (e.g. equivalent circuit16 and neural network models17) to the ones that describe the various physical mechanisms in the cell.18 For instance, only very few reviews on LIB modelling have been reported in the last 10 years.19–21 The majority of the published reviews provide a state of the art of LIBs modelling from a top-down engineering viewpoint, covering key issues such as the reusability of the governing equations for different battery systems, the aspects related to the coupling between mathematical descriptions of the electrochemical and thermal mechanisms in the cells, and the modelling at three different scales, namely stack-level, cell-level and electrode-level.
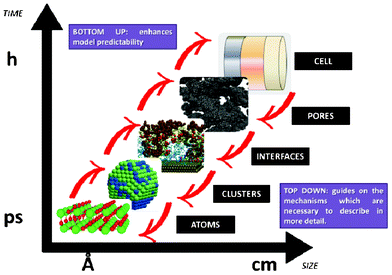
This paper reviews key efforts on developing bottom-up multiscale models for LIBs, i.e. spanning scales from atomistic mechanisms to the single cell level. Such types of models are also important for the prediction of the impact of the chemical and structural properties of the materials onto the overall LIB response. This paper does not intend to be exhaustive, but instead, it brings together general concepts and approaches (both methodological and numerical) as well as examples of applications. First, general aspects on physical modelling are revisited and some approaches for multiscale modelling are presented. Then, a critical review on ongoing efforts within the community is discussed. Finally, general conclusions, indications of the remaining challenges and suggested directions of further research are provided.
1.2 From philosophy to physical modelling
Modern physics teaches us that one cannot “see directly” the “reality”, but just perform abstraction of it to develop some understanding. The following quotation attributed to W. Heinsenberg, summarizes well this idea: "I think that modern physics has definitely decided in favour of Plato. The smallest units of matter are not physical objects in the ordinary sense; they are forms, ideas which can be expressed unambiguously only in mathematical language."22 Models are abstractions of reality, they are mathematical, logical or some other structured representation of the reality. Models allow to provide insights about the mechanisms and operation of the physical system being studied, and often deliberately emphasize one part of reality at the expense of other parts.Numerical simulation is the specific application of mathematical models to predict the behaviour of the physical system under “controlled” conditions, in the way of a “virtual experiment”. It is then possible, if applied to technological devices, to use numerical simulation to optimize designs and operation conditions vs. desired goals of device efficiency, for example. Through mathematical modelling one could thus simulate observables as function of the materials chemical and structural properties in order to reduce the number of trial-error experiments. In particular, the interest in mathematical modelling for optimizing real electrochemical power generators starts now to be largely recognized.23
Assumption of determinism is a current feature of mathematical models. For a physical system, determinism is the view that each event and behaviour is causally determined by an unbroken “chain” of prior events. In particular, the Laplacian determinism assumes that the system is fully governed by causal laws resulting in only one possible state at any time: such determinism supposes that if one knows the precise location and momentum (states) of “all the elements” constituting a physical system, then it is possible to reconstruct all the past physical and future events.28 Laplacian determinism assumes that such a complete level of understanding would always be beyond the practical capabilities of human knowledge, as an infinite calculating power would be needed to take into account every precondition in a given instant. Within this viewpoint, it arises that perfect predictability of the behaviour of a physical system would imply strict determinism, but lack of perfect predictability does not mean lack of determinism: limitations on predictability can in fact be caused by factors such as a lack of information or excessive complexity.
It should be noticed that the Laplacian determinism is strongly connected with the idea of reversibility in classical thermodynamics. However, with the developments since the early 19th century of the concepts of irreversible thermodynamics and, later in the 1960s, of the Lorenzian chaos theory,29,30 Laplace's determinism lost sense.31,32 In fact, it appears to be impossible to reconstruct all past and future events from the exhaustive knowledge of a single state. The so-called deterministic chaos theory, describing the dynamical behaviour of physical systems without random events involved, implies that small differences in initial conditions yield widely diverging outcomes making long-term prediction impossible in general. Thus the deterministic nature of these physical systems does not make them predictable.
Based on these concepts, one could ask up to which extent one can “perfectly” predict, based on mathematical modelling, a real LIB operation: actually, having an exhaustive knowledge of all the characteristics and properties of the LIB materials, such as their microstructure and defaults locations at multiple spatial scales (e.g. generated during the fabrication or assembling process) is beyond the human capabilities. An “idealization” or “model” of each material and/or each mechanism at each relevant scale is unavoidable and necessarily introduce deviations (or “errors”) from the real system in terms of its structural properties but also in terms of its dynamic behaviour.
However “imperfect” models first focalizing in the mechanisms believed to be relevant at each single scale, and then in the interplaying between the scales, can still prove to be very helpful for understanding LIB response and for the materials design and operation conditions optimization. Depending on the development context of these models (engineer or physicist based), they would be built following top-down or bottom-up viewpoints. Top-down models connect detailed macroscopic descriptions of mechanisms with global parameters representing microscopic mechanisms. On the other hand, bottom-up cell models scale up detailed descriptions of microscopic mechanisms onto global parameters to be used in macroscopic models. As it is illustrated in Section 2 of this paper, it is important to develop approaches which synergistically combine these two complementary views, as the former provides “a closer” comparison with macroscopic experiments, and the latter predictability towards the materials chemical and structural properties (Fig. 3).
 | ||
| Fig. 3 Schematics of top-down and bottom-up models of electrochemical power generators. | ||
In the following subsection, some general terminologies, currently used in modelling literature, are briefly discussed.
1.3 Multiphysics, multiscale and multiparadigm models
The word “multiphysics” usually characterizes, in published literature, models that mathematically describe the interplaying of mechanisms belonging to different physical domains. Multiphysics models include models describing these multiple mechanisms within a single and unique spatial scale (e.g. a model describing the impact of heating on the mechanical stress of a material).33 Multiphysics models can be by construction “multiscale” on time, as they can be built on the basis of mathematical descriptions of multiple mechanisms with different characteristic times (e.g. when the heat dissipation time constant is different to the material deformation time constant). The majority of models developed to describe the operation of LIBs fall within this category as they have to consider as least two different physical domains: the electrochemistry and the charge transport. Several groups have developed various rigorous LIB models based on the porous electrode theory, coupled with concentration solution theory and modified Ohm's law, which allow treating thermal, mechanical and capacity fade mechanism aspects, as discussed in Section 2 of this paper.“Multiscale models” typically refer to models accounting for mathematical descriptions of mechanisms taking place at different spatial scales.34 Multiscale models aim, by construction, to considerably reduce empirical assumptions than can be done in simple multiphysics models. This is because they explicitly describe mechanisms in scales neglected in the simple multiphysics model. Actually, multiscale models have a hierarchical structure: that means that solution variables defined in a lower hierarchy domain have finer spatial resolution than those solved in a higher hierarchy domain. Consequently, physical and chemical quantities of smaller length-scale physics are evaluated with a finer spatial resolution to resolve the impact of the corresponding small-scale geometry. Larger-scale quantities are in turn calculated with coarser spatial resolution, homogenising the (possibly complex) smaller-scale geometric features.
A large diversity of multiscale models exists in numerous domains, such as climate science, geology, nuclear energy and physical chemistry.35–37 In the case of LIBs, model geometry decoupling and domain separation for the physicochemical process interplay are valid where the characteristic time or length scale is “segregated”. Assuming statistical homogeneity for repeated architectures typical of LIB devices is often adequate and effective for modelling submodel geometries and physics in each domain. For example, the so called multiple-scale technique38–40 provides a systematic way for accounting for the LIB mechanisms which occur within a microscopic quasi-periodic microstructure in terms of a macroscopic system of equations, as used in.41–45 Such method allows deriving the macroscopic equations and determining the corresponding parameters from a local problem for the microscopic behaviour. Model coefficients are calibrated in terms of the microstructure, and thereby provide a tool for improving LIB particles design. This approach can be contrasted with averaging methods as for example in46 where spatial averages are taken of the microscopic equations resulting in equations on a macroscopic scale for the microscopically averaged variables: these macroscopic equations are closed by making ad hoc assumptions about the mathematical closure conditions and fitting these to empirical data.
Finally, the mathematical descriptions in a multiscale model can be part of a single simulation paradigm (e.g. only continuum) or of a combination of different simulation paradigms (e.g. stochastic model describing a surface reaction coupled with a continuum description of reactants transport phenomena). In the latter, one speaks about “multiparadigm” models. Multiparadigm models can be classified in two classes: “direct” or “indirect”.
Direct multiparadigm models are multiparadigm models which include “on-the-fly” mathematical couplings between descriptions of mechanisms realized with different paradigms: for example, coupling continuum equations describing transport phenomena of multiple reactants in a porous electrode with Kinetic Monte Carlo (KMC) simulations describing electrochemical reactions among these reactants. Several numerical techniques are well established to develop such a type of models applied in the simulation of physicochemical processes e.g. catalytic and electro-deposition processes.47,48 In the field of catalysis, KMC simulations have been used to calculate instantaneous kinetic reaction rates on a catalyst calculated iteratively from concentrations which are in turn calculated from Computational Fluid Dynamics (CFD)-like continuum transport models:49 the calculated reaction rates are in fact sink/source terms for the transport models.
Even if very precise, these methods can reveal themselves to be computationally expensive. For this reason, indirect multiparadigm models consisting in injecting data extracted from a single scale model into upper scale models via their parameters, can constitute an elegant alternative. For example, in the field of catalysis, one can use Nudged Elastic Band (NEB) calculations50 to estimate the values of the activation energies Eact of single elementary reaction kinetic steps, and then inject them into Eyring's expressions to estimate the kinetic parameters k
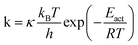 | (1) |
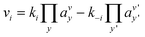 | (2) |
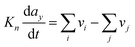 | (3) |
More precisely, NEB method aims in fact to find reaction pathways when both the initial and final states are known. The pathway corresponding to the minimal energy for any given chemical process may be calculated, but however, both the initial and final states must be known. NEB method consists in linearly interpolating a set of images between the known initial and final states, and then minimizing the energy of this string of images. Each "image" corresponds to a specific geometry of the atoms on their way from the initial to the final state, a snapshot along the reaction path. Thus, once the energy of this string of images has been minimized, the pathway corresponding to the minimal energy is found.
Another example of multiparadigm model results from the use of Coarse Grain Molecular Dynamics (CGMD) for the calculation of the materials structural properties (e.g. tortuosity and porosity) as function of the materials chemistry, which are used in turn for the estimation of the effective diffusion parameters used in continuum reactants transport models:52
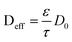 | (4) |
One could then imagine building up in this way an electrochemical power generator model with macroscopic equations based on materials parameters extracted from atomistic and molecular level calculations (Fig. 4). This approach gives a method for systematically investigating the effect of different materials designs on the LIB efficiency and durability.
 | ||
| Fig. 4 Schematics of an indirect multiparadigm approach for the simulation of an electrochemical power generator. | ||
Fig. 5 summarizes the logical independencies of the three concepts revisited in this section.
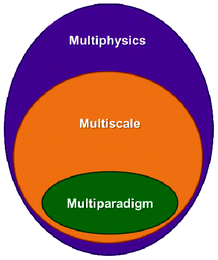 | ||
| Fig. 5 Schematics of the logical interdependencies between the multiphysics, multiscale and multiparadigm terminologies: a multiphysics model is not necessary “multiscale” either “multiparadigm”; a “multiscale” model is necessarily “multiphysics” but not necessarily “multiparadigm”. | ||
1.4 Managing multiscale models complexity
Application of multiscale modelling to LIBs is quite recent. This is also true for the modelling of other electrochemical power generators such as fuel cells.53,54 As it is computationally expensive to perform a predictive numerical simulation of a LIB operation response while capturing all the possible couplings among the different physicochemical processes in varied characteristic length and time scales in complex geometries using a single computational domain, the majority of the ongoing research efforts concentrate on developing indirect multiparadigm models as discussed in Section 2 of this paper.Globally speaking, governing equations in indirect multiparadigm model include numerous nonlinear, coupled and multidimensional partial differential equations (PDEs) that are needed to be solved simultaneously in time along with some highly nonlinear algebraic expressions for transport and kinetic parameters. Rigorous LIBs models need from several seconds to a few minutes to simulate a discharge curve depending on the computer, solver, etc.
From a programming point of view, different languages, in-house or commercial software have been used to solve such model equations, e.g. Matlab, Simulink, C, Fluent, Comsol,55 or even combinations of those software and languages. Each class of software presents advantages and disadvantages depending on the desired application of the model developed. For example, Simulink is more adapted for system level simulation and Comsol is more dedicated to multiphysics models with detailed spatial resolution at the single cell level.
The numerical solver is also a critical aspect for robust simulations. As commercial software such as Simulink and Comsol propose a limited number of numerical solvers, or limited spatial meshing capabilities, numerous groups develop their own numerical solvers of Ordinary Differential Equations (ODEs) and PDEs, such as PETSc,56 LIMEX57 or FiPy.58 In-house codes are usually more flexible and can be integrated within High Performance Computing (HPC) frameworks for sequential or parallel calculations.59
The generation of parameters for such indirect multiparadigm models can be done with any kind of software available for ab initio calculations (e.g. VASP,60 CRYSTAL,61 ADF,62 Gaussian,63 BigDFT64–66) or for molecular dynamics calculations (e.g. GROMACS,67 LAMMPS,68 AMBER,69 CHARMM70), the choice depending on the particularities of the material being studied and the kind of information one wants to extract with. A complete introduction to ab initio and MD methods including fundamental concepts and detailed algorithms is beyond the goal of this paper and cab be easily found in text books.71–74
Multiscale simulation of device materials exhibits extreme complexity due to the variation of a huge number of possible compounds, device morphology and external parameters. Such simulation requires new hierarchical concepts to connect simulation protocols with the computing infrastructure, particularly with HPC architectures, on which the simulations can be executed (e.g. in the case of ab initio codes). Automatization of the generation of database libraries and their integration in indirect multiparadigm models is also an important aspect to be considered as highlighted by Bozic and Kondov.75 Some software platforms allowing to create data flows (or pipelines), to selectively execute some computational steps and to automatically inspect the results, are already available, such as KNIME and the platform UNICORE.76,77 Particularly for LIBs, an in-house flexible and scalable computational framework for integrated indirect multiparadigm modelling is reported by Elwasif et al.78 The framework includes routines for the codes execution coordination, computational resources management, data management, and inter-codes communication. The framework is interfaced with sensitivity analysis and optimization software to enable automatic LIB design.
Further than the choice of the programming language and the software characteristics, there are also other key issues related to the mathematical formulation of the models, such as their modularity and their parameters identifiability.
Numerous models in process engineering are based on a structured approach using sets of balance equations, constitutive equations and constraints.79 Mangold et al.80 proposed a block-diagram approach which also applies to distributed parameter systems. This block-diagram is constituted of the components elements (representing the storage of conserved quantities) and the coupling elements (defining the fluxes between components) related by bidirectional signal flows (composed of potentials and fluxes). In this approach causality is thus assigned once for all which harms the reusability of the submodels, the submodels have to be re-defined for each new set of boundary conditions (i.e. for each new configuration of the interconnection with the environment). Maschke et al. proposed a port-based model using a novel extension of the bond graph language to multiscale and non-uniform models (also known as infinite-dimensional bond graphs).34 Their work extends previous work on structured modelling for chemical engineering using bond graph for finite dimensional systems.81–87 This approach leads to a simple and easily re-usable graphical description of the system which is an interesting modelling alternative to sets of PDEs and boundary conditions. The infinite dimensional bond graph models represent the basic thermodynamic properties, conservation laws at each scale and the multiscale coupling in terms of a network of multiport elements acausally related by edges (bonds) indicating the identity of pairs of power conjugated variables (intensive and variations of extensive variables). This network includes energy dissipative elements (“R” elements) and energy cumulative elements (“C” elements). Cumulative elements concern the balance equations such as
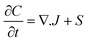 | (5) |
| S = γ × J∂V | (6) |
Dissipative elements concern the constitutive equations such as,
| J = −Γ(C) × ∇μ | (7) |
Because of the multidisciplinary property and the “universal” formulation inherent to the bond graph approach, it provides a framework which facilitates the collaboration between experts working on different physical domains.
The modularity of infinite dimensional bond graphs provides to the multiscale models a hierarchical, flexible and expandable mathematical architecture.
An example of infinite dimensional bond graph representation is provided in Fig. 6 for the case of the modelling of a chemical reactor.34 Because of the reusability of the approach, the same representation will be valid, for example, for the modelling of lithium ion transport across the LIB porous electrodes.
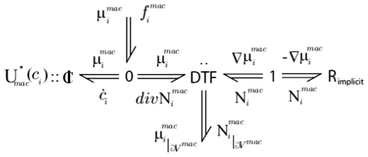 | ||
| Fig. 6 Example of an infinite dimensional bond graph model, representing the transport of a reactant across a porous media with a sink/source term connected to a microscale model (not shown here). Source: 82. | ||
Specific software can be used to build up these types of models and to calculate the propagation of the causality, e.g. 20-Sim88 or using similar concepts, AMESim,89 Dymola90 and OpenModelica.91
Only very few efforts have been reported on modelling batteries paying particular attention on their a-causality, modularity and reusability by using the bond graph approach.92,93
For other electrochemical power generators, such as in PEM Fuel Cells, considerable progress within this sense has been achieved.94–96 The multiscale model MEMEPhys, developed by Franco since 2002 and described in detail at the end of this manuscript, is fully based on the use of infinite dimensional bond graphs. The model represents explicitly the different physical phenomena as nonlinear sub-models in interaction. Such developed model is a multi-level one in the sense that it is made of a set of interconnected sub-models describing the phenomena occurring at different levels in the PEMFC. However, this description remains macroscopic (suitable for engineering applications) in the sense that it is based on irreversible thermodynamic concepts as they are extensively used in chemical engineering: use of conservation laws coupled to closure equations. Such an approach allows to easily modify the sub-models and to test new assumptions keeping the mathematical structure of the model and the couplings. The infinite dimensional bond graph structure of a generic multiscale model for the numerical simulation of electrochemical devices for energy conversion and storage is presented in97 where several application examples are discussed, including fuel cells, electrolyzers and batteries.
By construction, bottom-up multiparadigm and multiscale models are not designed for fitting, especially if they contain parameter values estimated by atomistic or molecular level calculations. Predicting observable trends with these models with good order of magnitude in a large diversity of conditions and materials properties can be sufficient enough to consider them as “validated”. But estimation of all the parameters of such a type of models from atomistic or molecular calculations is impossible and experimental fitting of some empirical parameters, inherent to the non-ideality of the real system being simulated (cf. Section 1), is always necessary.
For this, identifiability is a crucial aspect to be treated when developing multiscale models. When these models are used for LIB optimization, the estimation of accurate physical parameters is important in particular when the underlying dynamical model is nonlinear. Identifiability concerns the question of whether the parameters in a model mathematical structure can be uniquely retrieved from input-output data. Literature on identifiability and techniques to check identifiability is extensive.98–101 Being able to first assess the identifiability of a model without going through the estimation work (e.g. by using iterative methods such as Gauss–Newton or Steepest-Descent, or the Bayesian method) allows gaining time in the model development. Identifiability analysis can result in structurally non-identifiable model parameters. Furthermore, practical non-identifiability can arise from limited amount and quality of experimental data. In the challenge of growing model complexity on one side, and experimental limitations on the other side, both types of non-identifiability arise frequently, often prohibiting reliable prediction of system dynamics. Once non-identifiability is detected, it can be resolved either by experimental design, measuring additional data under suitable conditions, or by model reduction, linearization,102 tailoring the size of the model to the information content provided by the experimental data, or by more model refinement based on lower scale calculations. In the latter, for the domain of catalysis, Reuter et al. proposes a systematic methodology for the development of error-controlled ab initio based kinetic models (Fig. 7).103–105 The methodology consists on refining iteratively the kinetic rates by starting from coarse models. The parameter sensitivity analysis guides the further efforts still necessary from ab initio calculations. The same thing could be also applied to the structural parameters. The extension of this methodology for the simulation of electrochemical power generators, and in particular LIBs, could be very helpful.
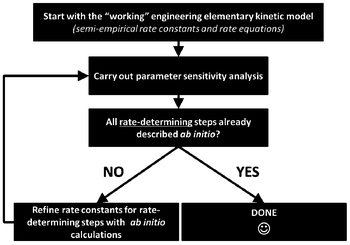 | ||
| Fig. 7 Methodology for the development of error-controlled ab initio based kinetic models (schematics adapted from ref. 106). | ||
LIB multiscale models usually present a large number of equations that result from finite difference reformulation of the mathematical expressions. Until recently,107–116 there were no significant efforts in developing efficient techniques for estimating parameters in multiscale LIB models because of computational constraints. In particular, Boovaragavan et al. reports a numerical approach for a real-time parameter estimation using a reformulated LIB model.117 It is to be noted in this work that the estimation of parameters using LIB models are performed only for up to 2C rate of discharge. Further reformulation of the authors' multiscale LIB model is required to enable estimation of parameters at higher rates of discharge.
2 Ongoing efforts: a review
2.1 General context
LIBs are frequently modelled based on or using variants of the one-dimensional multiphysics model initially developed by Newman et al.42–45,119,118 and Botte et al.41 These models capture lithium diffusion dynamics and charge transfer kinetics, predict current–voltage response of a LIB, and provide powerful design guide for thermodynamics, kinetics and transport across the electrodes.120–123 These models are however difficult to apply in large-format batteries where local heat and electron current transport heterogeneities critically affect the battery response. A key aspect of such a Newman-like approach is the assumptions about the electrode microstructure: this approach replaces the effect of the microstructure by a few phenomenological parameters, and quantitative predictions depend upon empirical parameters such as effective conductivities and diffusion coefficients.Despite their dependence on empirical parameters, these models have already shown large capabilities for performance prediction, and have been also nicely extended to describe degradation phenomena, e.g. providing new insights on the effects of the electronic conductivity loss onto the electrodes capacity.124–126
Given the modern growing interest in designing nano/microstructured materials for LIBs, a modelling approach that is able to directly relate the microstructural and chemical properties of the materials to the coefficients in a macroscopic model of LIB behaviour would provide a valuable tool towards their design and optimization. Furthermore, scaling down LIB dimensions, for example for microelectronics or MEMS applications, also leads to complex capacity/volume optimization problems that can only be solved if both nanosciences and classical physics are simultaneously considered.127,128
For these reasons, there is now a significant theoretical effort in developing multiscale models of LIBs.129–132 The following subsections exclusively review the ongoing efforts onto the development of such multiscale models connecting two or more length scales.
2.2 Modelling intercalation and conversion electrochemistry
Phase formation during intercalation or conversion reactions at the active material scale, is a crucial process to be modelled for understanding, designing, and controlling LIBs more effectively. It is in particular difficult to model real material behaviour in which the electrodes experience a series of successive incomplete charges and discharges: some electrode materials exhibit a hysteresis effect such that if the LIB is charged and discharged in incomplete cycles, the relationship between current and voltage is path dependent. For example, for intercalation electrode materials such as LiFePO4, the pioneering work by Srinivasan and Newman demonstrated this path dependence phenomenon by combining modelling with experiments.131 They suggested a phenomenological model consisting on a “shrinking core” to show that new shells of the lithium-deficient phase would form upon charging from a partially discharged state. Then they postulated that since the activation energy for lithium hopping in the lithium deficient phase is smaller than in the lithium rich phase, there should be a smaller ohmic drop associated with moving through the new shell region.To tackle these questions in detail, atomistic quantum mechanical and molecular dynamics simulations are already extensively employed and allow studying elementary ion and electron transport in bulk and nanostructured energy storage materials.133,134
Asari et al. report an ab initio DFT investigation of the lithium-rich/lithium-poor interface region in LiFePO4 compounds.135,136 The crystal and the electronic structures are determined by using spin-polarized generalized gradient approximation with short range Coulomb interactions (GGA + U). On the assumption of the quasi two-dimensional interface region parallel to the bc plane, the authors constructed an interface model composed of three regions (Fig. 8): fully lithiated, fully delithiated, and interface region. The authors calculated formation energies of solid-solution structures in each region by considering possible configurations of lithium ions and localized electrons.
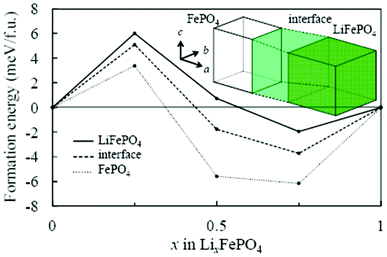 | ||
| Fig. 8 Calculated formation energy of solid-solution phase of olivine-type LixFePO4 by Asari et al. Solid, broken and dotted lines indicate lithiated, interface, and delithiated regions respectively. Reprinted with permission from ref. 135. Copyright 2012, The Electrochemical Society. | ||
Malik et al. used DFT + U calculations to show the advantages towards Li diffusion by nano-sizing LiFePO4 materials.137 Moreover, Yang and Tse report a direct multiparadigm modelling study on the mechanisms for thermal (self) diffusion of Li+ in fully lithiated LiFePO4.138 The authors use spin polarized ab initio molecular dynamics (AIMD) calculations. The effect of electron correlation is taken into account with the GGA + U formalism. The authors found that Li+ diffusion is not a continuous process but proceeds through a series of jumps from one site to another. A dominant process is the hopping between neighbouring Li sites around the PO4 groups, which results in a “zigzag” pathway along the crystallographic b-axis (Fig. 9). According to the authors, a second process involves the collaborative movements of the Fe ions leading to the formation of defects which promote Li+ diffusion across the Li+ channels. The authors explain that the simultaneous occurrence of these two different Li+ transport processes suggests that Li+ diffusion is not a simple linear process but may exhibit features of a “two-dimensional” diffusion pattern.
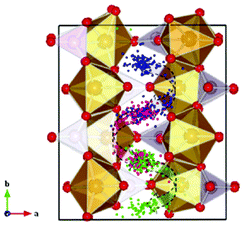 | ||
| Fig. 9 Trajectories of the three Li atoms originally situated in the crystalline LiFePO4 structure along the b-axis obtained from the AIMD at 2000 K by Yang and Tse. The three specific Li atoms are highlighted with different colors, and all other Li atoms are omitted for clarity. A zigzag diffusion pathway can be clearly identified (shown with the curved arrows) along the b-direction and confined in the ab plane. Reprinted with permission from ref. 138. Copyright, 2011, American Chemical Society. | ||
It has to be noticed that the study of diffusion mechanisms by AIMD is still a challenging problem owing to the limited accessible time scale. The preliminary results presented by the authors however demonstrate the strength of this approach in providing deeper insight into the atomistic processes for the diffusion mechanisms. The authors indicate that further investigations are necessary to explore Li transport in partially lithiated LixFePO4 (x < 1) systems with and without the presence of an electric field gradient (also still challenging to be implemented, despite tremendous progress in the last few years).139
Regarding indirect multiparadigm models, Filhol et al. presents a method to calculate phase diagrams using first-principles methods and statistical physics.140 The method is applied to lithium intercalated graphite (Fig. 10). The method has led to a determination of the LixC6 phase diagram (depending on the composition), and revealed unknown phase transitions and at least two new phases.
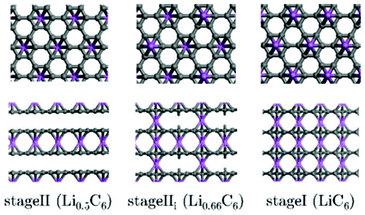 | ||
| Fig. 10 Projection views of stage II and stage I crystal structures into the grapheme planes (upper view and along the interlayer direction (lower view). Lithium atoms are given by large circles on the top of the grapheme layers. Reprinted with permission from ref. 140. Copyright 2008, American Chemical Society. | ||
Doublet et al. presents a methodology based on a multi-interface superlattice approach to investigate interface electrochemistry in conversion reactions, through first-principles Density Functional Theory (DFT) or DFT + U calculations, combined with classical thermodynamics (ab initio-based thermodynamics approach).141 This method is applied to a CoO electrode and describes the main interface effects by means of three interdependent descriptors: the chemical (interface bonding), the mechanical (stress) and the electrical/electrochemical (electric bias) descriptors. Based on this decomposition, the most probable CoO/Li2O/Co° interfaces during the CoO conversion have been determined, and possible electrode morphologies at the microscopic level have been proposed (Fig. 11). Moreover, the addition of an external redox potential to the multi-interface superlattice has revealed asymmetric electrochemical interface phenomena in charge and discharge, providing some insights into the voltage hysteresis experimentally observed for the CoO-based positive electrodes upon the conversion/reconversion cycles. The authors recently extended their approach for the study of CoP electrodes.142
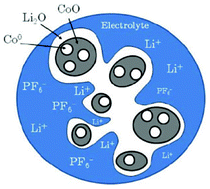 | ||
| Fig. 11 schematic representation of the most probable electrode morphology, as deduced from the computation of interface energies and energy stress.141 | ||
Zhu et al. use DFT calculations to investigate the average voltage of lithiation/delithiation for LIB materials including LiMO2, LiMn2O4, LiMPO4, Li2MSiO4 and graphite.143 The average voltage of lithiation/delithiation was obtained from classical thermodynamics and by comparing the total-energy difference, before and after an electrochemical reaction, with results in good agreement with experimental data. A similar DFT approach, combined with experiments, has been used by Chevrier and Dahn to study lithiation/delithiation in Si electrodes with the induced volume changes.144
Suhko et al. report a direct multiparadigm model coupling ion and electron transport in nanostructured energy storage materials.145,146 In their approach, instead of formal consecutive upscaling, the authors introduce collective long-range interactions along with short-range effects of the finer-scale models. The fine scale-model uses the results of quantum mechanical simulations of elementary charge transport. The collective long-range electrostatic and excluded volume interactions are introduced at the mesoscale (10–300 nm) via DFT coupled with the Poisson–Nernst–Planck (PNP) formalism for dynamic effects.147 In their model the authors provide a charge-transport model in three-dimensions for the prediction of both ion and electron conductivities in nanoparticles or nanofilms and also apply the model to gain fundamental understanding of temperature-dependent conductivity in solid electrolyte materials, such as lithium phosphorus oxynitride.
Ceder et al. massively use ab initio-based thermodynamics to compute the reactivity properties trends of a huge number of materials: the discovery of new materials is then possible (this approach is also known as the data mining approach).148,149 This methodology works like a “virtual LIB materials explorer” for given criteria such as voltage, capacity, stability and energy density. The goal behind this effort is that experimental research can be targeted to the most promising compounds from computational data sets accelerating innovation in materials research.
Statistical mechanics and thermodynamics efforts have been also carried out to describe intercalation electrochemistry. A general lattice–gas model of an intercalation material is proposed by Kalikmanov et al.150 The material is described as an effective one-component medium of equally charged intercalated ions forming a lattice of interstitial sites with short-range nearest-neighbour repulsive interactions. For sufficiently strong interactions a second order phase transition has been found accompanied by the formation of a fine structure of intercalated ions at certain critical concentrations. The phase diagram and the electrode open circuit voltage (OCV) are studied theoretically, within the framework of the mean field theory and by means of MC simulations.
The so-called phase-field modelling approach is now receiving growing attention to understand phase separation, until now mainly on LiFeO4 materials. Phase field models allow moving beyond traditional Fick's law in describing lithium diffusion in LIB electrodes. Phase field models are potentially more accurate and allow simpler tracking of phase boundaries than Fick's equation.
The phase field modelling approach, initially developed for describing phase separation and coarsening phenomena in a solid151 and later for electrochemistry applications,152,153 first consists in considering the total free energy of the intercalation (or conversion material), as follows:154
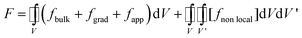 | (8) |
 | ||
| Fig. 12 Example of free energy density functional used in the phase field modelling of LiFePO4 electrodes. Reprinted with permission from ref. 159 with permission of Elsevier. | ||
The chemical potential of each phase is given by
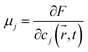 | (9) |
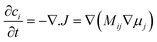 | (10) |
Han et al. reported one of the pioneering works on the application of a phase field model to describe phase separation in LiFePO4 electrodes.159 Using the phase field model the authors investigate to what extent non-Fickian behaviour can affect results from experimental techniques for measuring diffusion coefficients, such as Galvanostatic Intermittent Titration Technique (GITT) and Potentiostatic Intermittent Titration Technique (PITT).
Kao et al. compared phase field modelling results on LiFePO4 to X-ray diffraction data and proposed the idea of overpotential-dependent phase transformation pathways.160 From then, models developed account more and more for the strongly anisotropic transport in crystalline LiFePO4161–163 as well as surface reaction kinetics.164,165 Within this sense, Bazant et al. introduced significant contributions on the application of anisotropic phase field modelling coupled with faradaic reactions to describe the intercalation kinetics in LiFePO4 (Fig. 13).166–168 For small currents, spinodal decomposition or nucleation leads to moving phase boundaries (Fig. 14). Above a critical current density, the spinodal decomposition is found to disappear, and the particles start to fill homogeneously. This effect increases the active area for intercalation, and likely contributes to the high-rate capabilities and favourable cycle life of LiFePO4.168,169 According to Bazant et al., this may explain the superior rate capability and long cycle life of nano-LiFePO4 cathodes.
 | ||
| Fig. 13 Schematic model of a LixFePO4 nanoparticle at low overpotential (a) lithium ions are inserted into the particle from the active (010) facet with fast diffusion and no phase separation in the depth (y) direction, forming a phase boundary of thickness lambda between full and empty channels (b) the resulting 1D concentration profile (local filling fraction) transverse to the FePO4 planes for a particle of size L. Reprinted with permission from ref. 167. Copyright 2011, American Chemical Society. | ||
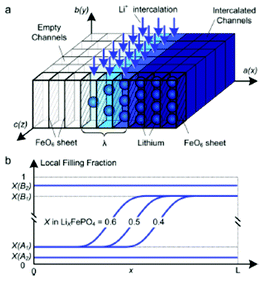
 | ||
| Fig. 14 Top) calculated phase separation in a particle which has been allowed to relax from a homogeneous state at zero current with stress-free boundaries. White regions are lithium-rich. Down) Calculated LIB voltage at different applied currents. Reprinted with permission from ref. 169. Copyright 2011, The Electrochemical Society. | ||
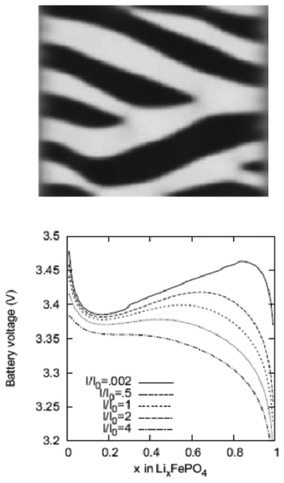
Lai and Ciucci170 propose a lattice-gas model which, compared to phase field models, has the technical advantage of mathematical simplicity because no fourth-order PDEs have to be solved. Their approach leads to a simple dimensionless diffusion equation with concentration dependent diffusivity. This equation served to the authors as a model to understand the effect of phase transformation on different electrochemical processes, in particular in relation with the intercalation particle morphology (planar, cylindrical or spherical) (Fig. 15). The authors couple this equation with a model based on generalized PNP equations which allows tackling the relationship between the voltage and the applied current.
 | ||
| Fig. 15 Calculated concentration profiles for the dimensionless diffusion equation with phase transformation of the (a) planar, (b) cylindrical, and (c) spherical symmetry. The selected dimensionless times are labelled on the curves. (d) Time dependence of the moving phase boundary. Reprinted from ref. 170 with permission of Elsevier. | ||
Lai also used this approach to model a single intercalation battery particle for four different electrical signals, such as the current step, voltage step, linear sweep voltage, and the sinusoidal voltage in relation to Electrochemical Impedance Spectroscopy (EIS).171 The impact of the assumed thermodynamic and kinetic properties of the materials (solid solution with constant diffusivity, solid solution with variable diffusivity, and a phase transformation material) on the overall electrode response is studied. Some interesting phenomena were observed from the simulation of the phase transformation material. Typical progression for the current/voltage response in the phase transformation exhibited a single-phase diffusion, the initiation of phase separation, movement of the phase boundary, and another single-phase diffusion. This has important implications in the interpretation of experimental data involving phase transformation LIB materials.
Other indirect multiparadigm approaches, similar to the one by Lai, have been recently reported:172 Landstorfer et al. raised the issue of the applicability of the classical Butler–Volmer equation by showing that it could overestimate the anode reaction rate while underestimating the cathode rate of an electrochemical reaction between two solids. The authors use modified PNP equations to resolve the interfacial processes between the electrode surface and electrolyte, with a mathematical formulation based on physical properties that in principle, as claimed by the authors, can be obtained by quantum chemistry simulations of the intercalation processes. The idea of using quantum chemistry data to parametrize detailed mean field elementary kinetic models not based in Butler–Volmer equations has been introduced by Franco et al. for PEMFCs (see discussion in Section 1, MEMEPhys model).51,53,54 The goal of Landstorfer et al. is to calculate the exchange current density value, in contrast to classical LIB models where the exchange current density is an empirical parameter. Using their approach the authors report numerical simulations of single crystal and bi-crystal-based electrodes, in particular of EIS, for several model parameters, including energy barriers for the intercalation reaction, diffusion coefficients in the electrodes and the electrolyte, and permittivity.
Other recent approaches have been proposed to explore the effect of the anisotropy of LiFePO4 particles onto the cell charge/discharge rates. For example, Hin uses a KMC model for this purpose.173 The author's KMC model treats the kinetics of Li-insertion and the structure and morphological evolution of the Li-rich/Li-poor phase boundary in the electrode particles. This KMC model is coupled “on-the-fly” to a finite difference model describing the Li-ion diffusion into the surrounding electrolyte (thus resulting into a direct multiparadigm approach). This diffusion simulation couples the far-field ion flux (imposed by galvanostatic boundary conditions) to the concentration fields in the vicinity of the electrode particles. These local concentration fields are coupled to particle adsorption model with Butler–Volmer interfacial kinetics. The interfacial reaction depends on local concentration and the potential drop at the interface via the Butler–Volmer relation. The kinetic anisotropy of lithium ion adsorption and lithium absorption for LixFePO4 is found to depend on the orientation of the electrolyte/LixFePO4 interface with respect to the far-field ionic flux. As a consequence of this kinetics and a Li miscibility gap in LixFePO4, the particle geometry and orientation also have an effect on the morphology of the two-phase evolution.
The atomic potentials for the KMC simulation are derived from empirical solubility limits (as determined by OCV measurements). The main results show that the galvanostatic lithium-uptake/cell voltage has three regimes: 1) a decreasing cell potential for Li-insertion into a Li-poor phase; 2) a nearly constant potential after the nucleation of a Li-rich phase; 3) a decreasing cell potential after the Li-poor phase has been evolved into a Li-rich phase. Hin found that the behaviour in the second regime is sensitive to the crystallographic orientation.
2.3 Electrolyte and active material/electrolyte interfacial phenomena
Moreover solid-state electrolytes and ionic liquids start to be simulated and studied to provide potentially high energy density LIB cells and to overcome safety issues (e.g. explosions, fire) of LIB using liquid electrolytes. For example, diffusion behaviour of Li+ ions in LISICON-based ionic conductors was studied by AIMD simulations175 and Borodin et al. reported MD simulations of Li-ions diffusion in some ionic liquids.176,177
Ikeda et al. reported AIMD simulations for Li+ diffusion in Li3PO4 and Li3PS4 electrolytes.178,179 The authors study Li+ diffusion in Li3PO4 by changing the temperature and the Li+ concentration of the systems. By analysing the trajectories of Li+ atoms in the super cell, the authors estimate the activation energies of Li+ in Li3PO4 at 0.42 and 0.59 eV for the Li-rich and the Li-poor electrolytes, respectively. The authors also study Li3PS4 (Fig. 16, each P atom is surrounded by four nearest neighbour S atoms forming a tetrahedron).
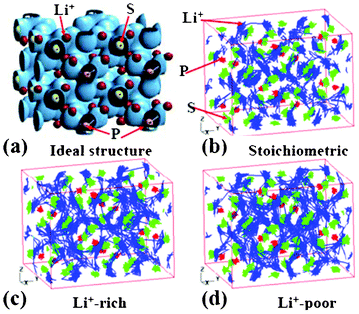 | ||
| Fig. 16 (a) the charge density of super cell structure of Li3PS4. The trajectories of Li+ ions at 600 K during 36 ps and 90 ps are shown in (b), and (c) to (d), where the concentration of Li is stoichiometric, Li+−rich, and Li+−poor, respectively. Reprinted with permission from ref. 178. Copyright 2012, The Electrochemical Society. | ||
Moreover, the chemical instability of commonly employed electrolytes results in the formation of the SEI. Although the SEI layer would be in some extent necessary, as it passivates the electrode/electrolyte interface from further solvent decomposition, SEI formation consumes lithium and thus contributes to irreversible capacity loss or capacity fade. In normal operation, a LIB undergoes many charging and discharging cycles, with a SEI layer forming mainly in the first cycle of charging. The SEI layer provides a barrier between the electrolyte and electrode while allowing lithium ions to permeate through the SEI layer in order to intercalate into and out of the bulk solid to store and release energy. This is expected to increase the resistance and reduces the efficiency of the LIB. This phenomenon produces high temperature and can result in a thermal runaway within the LIB.
The properties and chemical composition of the SEI is a subject of intense modelling research due to their importance in the safety, capacity fade, and cycle life of LIBs. Thermodynamics models describing the SEI formation have been proposed27, and a phenomenological model describing the SEI growth has been reported by Yana et al.180 The formation and evolution of the SEI film during the first electrochemical intercalation of lithium into graphite is modelled by Yana et al. as a special precipitation process including a nucleation phase of the SEI film solid deposition, and followed by a growth phase involving the precipitation of new solids on previously formed solid nuclei. It is shown by the authors that the solid species can nucleate in the electrolyte solution, directly on the graphite surface, or adjacent to an already present particle on the graphite surface when precipitating from the electrolyte solution. Within the framework of classical nucleation theory, the authors can qualitatively explain the origin of the two-layer structure of SEI films, which consists of a thin, compact polycrystalline or heteromicrophase layer rich in inorganic species (e.g., LiF, Li2O) close to the electrode, and a thicker porous and amorphous layer composed mainly of organic compounds (e.g., ROLi, ROCO2Li) that is farther from the graphite. However any impact of the formation of the SEI on the capacity is provided: the electrical conductivity and the lithium ion diffusivity within the SEI are relevant to the rate performance of the graphite electrode. Following this work, by using DFT, Chen et al. calculate the electronic structures of Li2CO3, Li2O, and LiF and simulate the lithium migration dynamics using NEB method.181 Results show that all three components have insulating electronic structures, while lithium vacancies create some strongly localized holes that do not contribute much to the electronic conduction. According to the authors, lithium diffusion across Li2CO3 and Li2O can be very fast when lithium vacancies are available. The calculated energy barriers of lithium migration in Li2CO3 (ranging, according to the authors, from 0.227 to 0.491 eV) and in Li2O (0.152 eV) appear to be comparable to the one in graphite with vacancies. However, lithium migration in LiF (calculated energy barrier 0.729 eV) appears to be much slower even with lithium vacancies in the lattice.
Other important modelling works have been reported calculating temperature dependent Li+ diffusion coefficients, conductivities and transport mechanism in key SEI components such as Li2CO3, Li2MeCO3 and dilithium ethylene dicarbonate (LiEDC).182,183
The decomposition of ethylene carbonate (EC) in liquid EC, at the interface between the liquid EC and lithium-intercalated graphite and at the EC/lithium metal interface, during the initial growth (and post-film-cracking regeneration) of the SEI films, is studied by Leung by employing AIMD simulations (Fig. 17, on top).184,185 In liquid EC, the author found that an excess electron can cause EC ring opening reactions in picosecond timescales, and that carbon edge terminations at LiC6-EC interfaces have large effects at this stage of SEI growth. With C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O decorated edges, Leung observes electron transfer to the solvent and EC ring-opening reactions to form multiple products including OC2H4O2−, which are either found in SEI or are chemical precursors to SEI components. Similar, but even faster, reactions are observed at the lithium metal-EC interface (Fig. 17, down). Leung concludes that achievable experimental conditions can lead to EC decomposition via multiple pathways.
O decorated edges, Leung observes electron transfer to the solvent and EC ring-opening reactions to form multiple products including OC2H4O2−, which are either found in SEI or are chemical precursors to SEI components. Similar, but even faster, reactions are observed at the lithium metal-EC interface (Fig. 17, down). Leung concludes that achievable experimental conditions can lead to EC decomposition via multiple pathways.
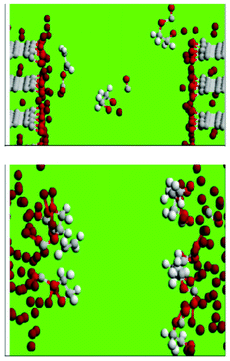 | ||
| Fig. 17 C, O, H, and Li atoms are coloured grey, red, white, and brown, respectively (see explanation within the text). Source: 183. | ||
In a comprehensive review paper, Leung has recently indicated a “crisis” in DFT SEI studies as DFT studies of the single reduction reactions fail to explain formation of LiEDC (instead, the formation of dilithium butylene dicarbonate is found to be favored due to lower reaction barrier).186 Leung used DFT calculations to suggest an alternative double reduction pathway that will lead to formation of the LiEDC.
Borodin et al. use a multiparadigm modelling approach, combining DFT calculations in the gas-phase with a polarized continuum model (PCM) to predict electrolyte oxidation stability and decomposition pathways that are expected to occur at non-active electrodes.187,188 DFT studies of representative electrolyte clusters revealed a spontaneous oxidation-induced H- and F- abstraction reactions from carbonates and sulfone-based solvents with the halogen containing anions. This reaction mechanism is observed to significantly reduce the electrolyte oxidation stability and influences the decomposition reaction pathways.
Furthermore, MD simulations demonstrated that the state of the electrode charge influenced the double layer composition leading to preferential adsorption of EC and desorption of DMC from the electrode in contact with EC: DMC/LiPF6 electrolyte and changes in the Li+ desolvation free energy.189 The same study also revealed that the composition of the Li+ solvation shell in the double layer is dependent on the electrode charge and different from that found in bulk mixed electrolytes.190 The Li+ solvation shell was correlated with the SEI composition in a joint DFT/MD/experiment work.191
Methekar et al. apply KMC simulations to explore the formation of the passive SEI layer on the surface of a graphite intercalation material (Fig. 18).192 The simulation results are found to be consistent with some experimental observations reporting that the active surface coverage decreases with time slowly in the initial LIB charging cycles, and then decreases monotonically with the number of charging cycles (Fig. 19). The effects of operating parameters such as the exchange current density, charging voltage, and temperature on the formation of the passive SEI layer are investigated by the authors. The active surface coverage at the end of each charging cycle remained constant for more cycles at higher temperature, but was lower at later cycles. The interest of coupling this KMC model with porous electrode theory-continuum models is discussed by the authors, in particular for understanding, analysing, and minimizing capacity fade. Furthermore, it would be interesting to estimate the parameters used in the KMC model from ab initio calculations (Methekar et al. used empirically estimated parameters).
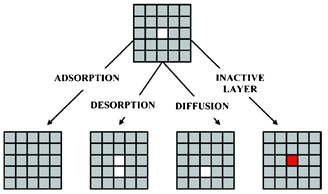 | ||
| Fig. 18 Schematic representation of the phenomena in the KMC model of Methekar et al. Source: 191. | ||
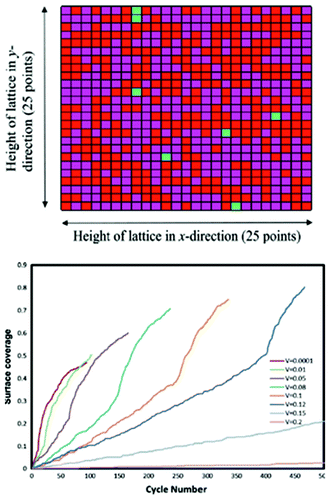 | ||
| Fig. 19 top) Final lattice configuration of the last cycle. Magenta represents virgin sites, red represents sites with passive SEI layer, and green represents absorbed lithium sites; bottom) end of cycle passive surface coverage for various charging potentials. Reprinted with permission from ref. 192. Copyright 2011, The Electrochemical Society. | ||
More recently, Northrop et al. reported ongoing efforts onto the development of a direct multiparadigm model coupling their KMC code with a continuum porous electrode model to study the effect of SEI growth and the resulting capacity fade (Fig. 20).193 The idea behind is similar to the indirect multiparadigm model proposed by Franco et al. coupling a MC-generated database with continuum multiscale simulations to describe the feedback between catalyst PtxCoy nanoparticles dissolution and PEMFC instantaneous performance.194–197
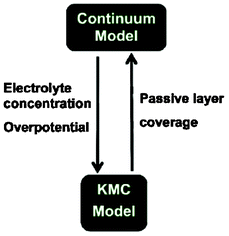 | ||
| Fig. 20 Schematics of the coupling of a KMC model with a continuum porous electrode modelling efforts ongoing by Northrop et al. Reproduced with permission from ref. 193. Copyright 2012, The Electrochemical Society. | ||
Northrop et al. goal is to calculate the passive layer formation from the SEI layer, and to be incorporated in the porous electrode model. Conversely, the porous electrode model aims to calculate the liquid-phase concentrations and the overpotential at all points and times so that the probability of each event can be calculated for use in the KMC simulations.
More recently and alternatively to the discrete models by Methekar et al. and Northrop et al. described here-above, Pinson and Bazant proposed two mathematical continuum models to describe capacity fade in LIBs with graphite negative electrodes: a single-particle one and a porous electrode one.198 The models focus on SEI growth and predict fade based on initial fitting with experimental data. Particularly, the authors found that the SEI growth is essentially homogeneous throughout the electrode.
Overcharging of LIBs is also a problem under a large diversity of operating scenarios, not limited to fast charging and operation at low temperatures. Various failure modes have been experimentally identified to occur when a cell is overcharged, such as the decomposition of the electrolyte due to the extreme voltages at either electrode, the instability of the cathode at higher states of charge, and short-circuit due to the plating of metallic lithium at the anode surface. Design changes in the electrode formulation, the use of electrolytes that are stable over a 5 V range and additives (including a few redox shuttles) to prevent overcharge are increasingly popular.
Many modelling studies address electrodes degradation on the basis of simple mathematical relations with empirically fitted parameters with experimental data, e.g. at different temperatures.201,202
However, for predicting LIB lifetime in a reliable way, deep understanding of the mechanisms responsible for the irreversible electrodes degradation becomes crucial. Some pioneering work in that sense has been reported by Arora et al., by using continuum modelling.203 Ecker et al. present a continuum LIB model that is able to describe the electrical and thermal behaviour of the LIB based on physicochemical processes in spatial resolution.204 The model enables to study lithium plating under different LIB conditions. The Li+ concentrations are calculated based on the porous electrode model developed by Newman et al.42,43 Herein the active material is described by spherical particles of a certain radius surrounded by electrolyte, filler and binder. The main processes governing the concentration gradient of Li+ during charging and discharging are charge transfer and diffusion, whereas diffusion in the active material particles and in the electrolyte is considered separately. To obtain the spatial resolution, the system is divided by the authors into volume elements of porous media. A simple thermal part for the calculation of the temperature in the cell is also incorporated in the model. Lithium plating is accounted for in the model and occurs at local potentials close to the potential of metallic lithium. This can be the case during overcharge, at high rate charging or at low temperature charging. With the model the authors calculate the Li+ concentration in the outer shell of the active mass particles and therewith the local potential determining the plating reaction.
Newman et al. recently proposed a continuum model implemented, through a finite-element approach, in Comsol Multiphysics software. Their model addresses large-scale shape change of the lithium/separator interface.205 It solves for the solid-phase concentration in the porous cathode, concentration distributions in the liquid electrolyte, kinetics at both the positive and negative electrodes, as well as the net movement of the lithium electrode interface during cycling using a moving boundary at the negative electrode/separator interface. From previous research it has been seen that during cycling the region of the cell nearest the negative tab is used far more than the rest of the cell and after the completion of a full cycle, the lithium in the negative electrode has shifted toward the negative tab. This movement, or shape change, has been shown to be highly dependent on the rate of discharge and charge of the cell. This non-uniform utilization, as well as the migration of the lithium toward the negative tab was predicted to cause the failure of a cell, devoid of dendrites, after only a few hundred cycles. The authors studied the effect of the movement of the lithium in the negative electrode after multiple cycles. Results show that while much of the movement occurs after the full cycle, subsequent cycles, cause incremental increases in the amount of movement of the lithium towards the negative tab, which suggests, that the migration of the lithium may reach a steady state, but leading to the failure of the cell.
Dissolution of active material is one of the primary reasons for capacity fade in lithium-ion batteries, particularly at elevated temperatures. The effects of the volume fraction changes due to dissolution in both the active and inert material phases in composite Li-ion electrodes are investigated by a thermal–electrochemical coupled model developed by Park et al.206 The study reveals that the changes in effective transport properties result in a reduction in the electrochemical reaction rate and an increase in the cell resistance, reducing capacity (Fig. 21). The simulation results are also used to map the nature of the effects of dissolution of the active particles on the capacity decrease during cycling with different conditions, including temperature and voltage range. However, no explicit description of the dissolution kinetics is accounted for in the model. The dissolution process is modelled via a noncatalytic reaction of particles with a surrounding medium.207
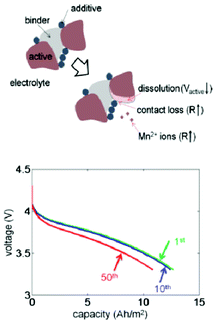 | ||
| Fig. 21 top) Schematic diagram of the dissolution process: two Mn3+ cations convert into one Mn4+ and one Mn2+, then Mn2+ ions leave the solid phase; down) calculated effect of dissolution and discharge voltage profiles for different numbers of cycles. Reprinted with permission from ref. 206. Copyright 2011, The Electrochemical Society. | ||
Several continuum models treating overcharge are reported in literature.208,209 Pesaran et al., propose a continuum model which consider the influence of the local geometry, and changes to the physical properties of the material close to the interface, on the current and overpotential distribution during overcharge.210 The steep concentration gradients at the interface also contribute to significant differences in the physical properties of the interface. The influence of electrode properties and the interfacial composition on the shape and size of lithium dendrites is simulated using a force-balance at the interface. Incorporating these effects enables the authors to relate design parameters such as the pore-size and tortuosity of the electrode to the performance of the cell under overcharge conditions and the mechanism of mitigating the risk under such instances using various additives.
In relation with graphite exfoliation, Kubota reports DFT calculations to investigate the potential energy surface (PES) for lithium diffusion into an edged double-layer graphene.211 The supercell used in the slab model contains two graphene layers, which are shifted relative to each other. The bottom layer is composed of a graphene extended infinitely over the two-dimensional plane, and is assumed to have no defects. The top layer with edge structure is prepared by removing a few tens from an infinite graphene. For lithium atom inside two graphene sheets, the diffusion barriers are found to be much lower than in the case of lithium on a graphene. Compared to lithium atom on a graphene sheet, lithium atom can easily diffuse inside the graphene sheets without traversal of carbon–carbon bond. The PES found two lithium intercalation paths. One is via the protruded edge, and another is via the concave edge. A lithium atom can easily migrate into the double-layer graphene along two paths. The comparison of energy barriers along two paths implies that delithiation likely occurs along the concave edge. For lithium atom sandwiched by two graphene sheets, the calculated charge transfers are ca. 0.85 e per lithium-atom at the stable states, and slightly lower than in the case of lithium on a graphene sheet. The comparison of vertical distances from two graphene sheets shows that the lithium atom is closer to the center of the carbon atom hexagon in one graphene than the carbon atom in another graphene at the stable states. The distances between the lithium atom and the center of the carbon hexagon are found to be longer than in the case of lithium on a graphene. The stability and vertical distance from the carbon atom hexagon for lithium atom inside double-layer graphene have been explained using the electrostatic model for a point charge and two charged wires.
Regarding the decomposition of the most popular electrolytes, the ethylene carbonate (EC)- and propylene carbonate (PC)-based electrolytes, numerous modelling works have been reported on the reduction reactions of the two solvents.212,213 Mostly, the calculations were performed in the gas phase or in solution and provided very few convincing results to explain the sharp contrast in cycling behaviours between the EC- and PC-based electrolytes.
More recently, Tasaki et al. performed DFT calculations to understand these mechanisms in relation with graphite exfoliation.214 Their results indicated that the Li+(EC)iC72 complex shown in Fig. 22 was more stable than Li+(PC)iC72. In addition, the interlayer distances of Li+(PC)iC72 were more than 0.1 nm longer than those of Li+(EC)iC72 indicating a significant expansion of graphite upon PC intercalation compared to EC intercalation. MD simulations that were also performed in this manuscript suggested that using high salt concentration might reduce graphite exfoliation when PC-based electrolytes are used.
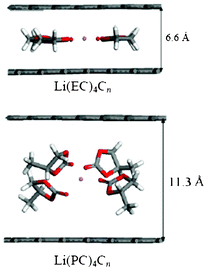 | ||
| Fig. 22 the side views of optimized grapheme structures with intercalated solvated lithium, calculated by Tasaki et al. Reproduced with permission from ref. 215. Copyright 2012, The Electrochemical Society. | ||
2.4 Electrode mesostructure and transport phenomena
Several models have been developed attempting to capture the influence of the electrodes structural properties (at the micro and mesoscales) onto the cell capacity response. For instance, the anisotropic nature of ion diffusivity in LiFePO4 has motivated synthesis approaches that facilitate control of size and shape of LiFePO4 agglomerates to maximize Li+ transport. In general, it is important to develop modelling tools that can evaluate the relative impact of each single scale onto the overall efficiency of the LIB. A major problem in most modelling approaches is the reliable determination of model parameters. Especially for homogenized models, the microstructural parameters have a strong influence on the simulation results. A lack of knowledge of several parameters leads to a reduction of the models prediction capabilities.To provide a detailed description of the mechanisms, a 3D representation is required for the morphology of composite materials used in LIBs.216 Nowadays, two ways of accounting for the detailed structure of the electrodes have been developed: one consisting in building up artificial structures capturing the main features of the real electrodes (e.g. length scales, particles shapes.), and another one based on computer-aided reconstruction of the real electrode structure.
 | ||
| Fig. 23 Schematic of the three size scales in the model of Dargaville and Farrell: a) crystal, b) particle, c) positive electrode. Reprinted with permission from ref. 130. Copyright 2010, The Electrochemical Society. | ||
A stochastic model consisting on energy-based structural optimization, has been developed by Smith et al.217,218 and allows the calculation of re-arranged equilibrium particle positions and orientations are calculated at given density (Fig. 24). Resultant grain morphologies and assessment of the efficacy of each microstructure to enhance Li ion transport is quantified by the authors, who also report optimized grain morphologies for Li transport.
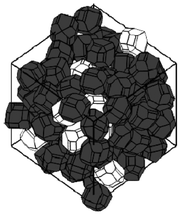 | ||
| Fig. 24 example of stochastically simulated LiFePO4 agglomerate morphology. Reprinted with permission from ref. 217. Copyright 2011, The Electrochemical Society. | ||
Du et al. recently reported a similar study in which a fixed number of monodisperse ellipsoidal particles are randomly packed based on a MD algorithm and then meshed using Cartesian voxels.219 The authors carried out 3-D finite element simulations on representative elementary volumes (REV) to estimate the parameters values in a cell model that vary with electrode microstructure, including the effective diffusivity, effective conductivity, and volumetric reaction rate. Results show lower effective diffusivity and conductivity in the electrode than predicted by the Bruggeman relation used in their cell model (cf.eqn (4)), and a significant sensitivity in cell performance to this difference at high discharge rates.
Goldin et al. present a three-dimensional model that can resolve electrode structure at the submicron scale.220 Although the three-dimensional model is capable of representing arbitrary electrode microstructure, the authors consider regular arrays of spherical particles. The model is applied to evaluate approximations in one-dimensional models and to assist in establishing empirical relationships that can be used in reduced-dimension models. General relationships for effective particle radius in one-dimensional models are derived from the three-dimensional simulations. The results also provide a basis for estimating the empirical Bruggeman exponents that affect Li-ion transport within electrolyte solutions (Fig. 25). Three dimensional simulations of a dual-insertion Li-ion cell during galvanostatic discharge are compared with an equivalent one-dimensional model. The three-dimensional model fully resolves the electrode particles, which are assumed to be spherical but are packed into alternative lattice arrangements. The three dimensional model also fully resolves the porous electrolyte volume between the electrode particles. Under all conditions studied, intercalation diffusion appears to be the rate-limiting process that controls discharge characteristics.
 | ||
| Fig. 25 Calculated Li concentration within the electrode particles during a 5C discharge. Reprinted from ref. 220 with permission of Elsevier. | ||
Wang and Sastry develop and analyse finite element models of a three-dimensional porous positive electrode by using commercial software.221 The authors model different types of active material particles, arranged in both regular and random arrays, and simulations results are compared with experimental data, including Li ion diffusivity into the intercalation particles and contact resistance at the interface between the cathode particles and the current collector. The authors found that regular arrays are shown to increase achievable capacity from 5 to 50% of the theoretical capacity, compared with random arrays (calculations done at C/10 and at 500 °C). Smaller particle sizes of active material are also found to be beneficial for high power density applications and for low diffusivity active materials.
Dreyer et al. report a modelling study of a rechargeable LIB that uses a many-particle FePO4 electrode to reversibly store lithium atoms.222 This process is assumed to be accompanied by a phase transition and charging/discharging run along different paths, so that hysteretic behaviour is observed. Although there are experimental studies suggesting that the overall behaviour of the LIB is a many particle effect, most authors exclusively describe the phase transition within a single particle model of the electrode. In this work, the authors study in detail a many-particle model for the electrode. The model is capable of describing a kind of phase transition where each individual particle of the electrode is homogeneous. It is shown by the authors that the particles are either in the first phase or in the second phase. This phenomenon is due to the non-monotone relation between the chemical potential and the lithium mole fraction of a single particle. A nice analogy is proposed by the authors with the pressure–radius relation of a spherical elastic rubber balloon which also exhibits non-monotone behaviour. In fact, a system of many interconnected balloons behaves correspondingly to an electrode consisting of many storage particles (Fig. 26).
 | ||
| Fig. 26 States of interconnected rubber balloons during loading and unloading with air via a pressure vessel. Reprinted from ref. 222 with permission of Elsevier. | ||
More recently Song and Bazant proposed a simple but interesting model for the simulation of EIS as function of the morphology of the active particles (Fig. 27).223 The model allows accounting for curved diffusion geometries as well as the diffusion length distribution. Using this model, the authors have investigated the ways these configurational aspects affect interpretation of diffusion impedance spectra. The model has been also applied to experimental impedance data of a Si nanowire electrode. Comparing the regression results of the different versions, we are able to show that including each of the cylindrical diffusion geometry and the heterogeneous radius distribution of the nanowires greatly improves the fit and leads to rather different, and presumably more accurate, values of the electrochemical parameters.
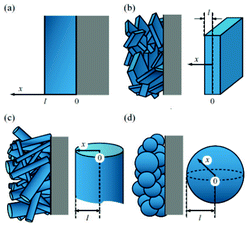 | ||
| Fig. 27 Song and Bazant's model electrode configurations, particle geometries, and corresponding coordinate systems, where the blue region and the gray region represent the active material and the current collector, respectively: (a) thin film electrode, (b) electrode with planar particles, (c) electrode with cylindrical particles, and (d) electrode with sphere particles. Reprinted with permission from ref. 223. Copyright 2013, The Electrochemical Society. | ||
An alternative route to transform the microscopic equations to equations with only macroscopic features is to use volume averaging.226 Volume averaging consists of the integration of the partial differential equations describing transport over a representative volume element (RVE). The RVE is sufficiently “large” so that it is an accurate description of macroscale, but “small” enough to be only a small portion of the full system. In the RVE one defines an average and a fluctuation of a given quantity. If the fluctuation is “small”, then the average value can be used in order to describe the macroscopic behaviour of the system. Differential mathematical manipulations and integrations, including effective parameters, give the final form of the transport equations described ultimately as a function of the averaged quantities. RVE approach has been used in the modelling of other electrochemical devices such as fuel cells.
Ciucci et al.228 have derived Newman's LIB model using mathematical tools from homogenization theory.227 The physical-chemical starting points of this work are the PNP equations and basic electrochemical principles. The strengths of the approach are that parameters like the porosity and tortuosity can be estimated by solving a set of partial differential equations, which has as input the detailed geometric description of the microstructure; a hierarchy of equations can be determined, each of which is endowed with a certain error.
The end result is that Newman's LIB model is recovered. According to the authors, in principle, all fitting parameters that pertain to geometry such as tortuosity, porosity, effective volumetric area available for reactions can be determined by knowing the detailed nature of the microstructure.
Thiedmann et al. develop an impressive stochastic simulation model in 3D to reconstruct real and generate virtual electrode microstructures.229 For this purpose, a statistical technique to fit the model to 3D image data gained by X-ray tomography is developed. The detailed knowledge of the spatial distribution of the components of composite electrodes (e.g. LiFePO4 electrodes with carbon additive) allows the authors to calculate macroscopic model parameters such as the active surface areas and the tortuosity, not directly accessible by other measurements, as well as physical parameters (e.g. diffusion constants, exchange parameters, conductivities.). These spatially-resolved numerical representations are used by the authors to simulate the local and macroscopic electrochemical response of a LIB graphite electrode as a function of galvanostatic cycling (Fig. 28).230 Through this analysis, the C-rate dependence on the dendrite formation and salt precipitation, a comparison against classical models based on artificial structures, and the well-known Newman models is determined. For high C-rates, the effect of tortuosity on salt precipitation, lithium accumulation and depletion is quantified.
 | ||
| Fig. 28 Calculated discharge sequence of a reconstructed graphite electrode. Reprinted with permission from ref. 230. Copyright 2012, The Electrochemical Society. | ||
Similarly, Ender et al. report 3D FIB tomography results of a complete LIB, including a positive LiFePO4-based electrode, a negative graphite-based electrode and a glass fiber separator (Fig. 29).231–233 Macroscopic model parameters are also determined and their influence on the simulate overall LIB response is analysed.
 | ||
| Fig. 29 3D reconstructions obtained by FIB tomography of (a) a LiFePO4 composite positive electrode, (b) a glass fiber separator and (c) a graphite negative electrode. Reprinted with permission from ref. 231. Copyright 2012, The Electrochemical Society. | ||
Bazant et al. report a very interesting microstructurally-resolved model of Li electrochemical intercalation and deintercalation processes (discharge and charge, respectively) in experimentally obtained 3D microstructures.234 In their approach, an experimentally obtained voxelated 3D microstructure array is converted to an input geometry described by a phase-field-like domain parameter. With such a parameter to distinguish the electrolyte, electrode and additive particles, the authors are able to solve the transport equations of Li+ in the electrolyte coupled with the transport equations in the active material, without using complex structural meshing technique. The authors investigate several conditions of intercalation kinetics such as the effect of different voltage or current loadings on the electrode behaviour as well as the role of the microstructure. In addition, different transport dynamics in the electrode, such as solid solution behaviour (as observed in a portion of concentration range in LiCoO2, Fig. 30) or phase-separation behaviour (as observed in LiFePO4), were studied.
 | ||
| Fig. 30 Li concentration (mol cm−3) evolution during the discharge of a LixCoO2 microstructure at a constant voltage loading. Through electrochemical reaction, Li ions are injected into cathode particles: (a)–(d) corresponding to time of 4.04, 20.1, 133.3 and 1226.5 s (assuming the value of the diffusion coefficient of 10−10 cm2 s−1). Reprinted with permission from ref. 234. Copyright 2012, The Electrochemical Society. | ||
Other papers focalize more on the specificity of the binder. For example, Liu et al. investigate positive electrodes as polymer composites to explain their performance variation due to changes in formulation.235 A physical model is introduced by the authors in which the carbon black and the active particles compete for polymer binder, which forms fixed layers of polymer on their surfaces (Fig. 31). This competition leads to the observed variations in electrode morphology and performance for different electrode formulations. The electronic conductivities of the electrodes were measured and compared to an effective conductivity calculation based on the physical model to probe the interaction among the three components and reveal the critical factors controlling electrode conductivity and electrochemical performance.
 | ||
| Fig. 31 Schematic of the formation of fixed polymer layers ba and bc on active particles and carbon black, respectively, and the polymer binder redistribution when combining active particles particles with the carbon black (AB in the figure)/PVDF composite. (A) active particle. (B) carbon black/PVDF matrix. (C) Mixed active particles/carbon black/PVDF. (D) There is enough polymer binder to form fixed layers on both active particles and carbon black. (E) There is a deficiency of polymer binder to form the fixed layer on active particles and carbon black. Reprinted with permission from ref. 235. Copyright 2012, The Electrochemical Society. | ||
Marimoto et al. recently report efforts on developing a three dimensional electrochemical and transport model, based on Newman et al. approach, and allowing to calculate local potential, lithium concentration and utilization distribution across the electrodes (positive and negative), with particular focus on the effect of the binder distribution on the effective reaction local effectiveness and cell performance.236–239 Sphere particle of LixCoO2 and LiyC6 were assumed as positive and negative active material, respectively, and the binder was filled as micro sphere in void space. The authors report a study for two binder distributions shown in Fig. 32: the binder filling small (case 1) and large pores (case 2). In their simulations, carbon black is not taken into account. Local effective transfer coefficient, such as Li+ diffusion coefficient, electrical conductivity, was estimated by local pore size, permeability and porosity. The authors found that the LIB response strongly depends on the binder distribution: case 1 provides a less effective scenario for Li+ transport across the electrodes favouring non uniform concentration in the electrode volume. The authors concluded that, to stabilize the electrode reaction and to relax stress resulted from charge-discharge cycles, the reaction distribution has to be uniform.
2.5 Mechanical and thermal stresses
Zang and Zhao investigate, by using a coupled continuum diffusion-mechanical model, the impact of the surface tension, surface curvature and ions diffusion on the elastic properties of lithium ion intercalation nanostructures.240 In the electro-chemical diffusion process, the surface tension, ions diffusion and stress distribution are considered to be strongly dependent with each other. In their model, the coupling between the stress and ions diffusion is revealed through the chemical potential variation. As an application example of the model, the authors analyse the stress distributions in the silicon anode of a LIB, where huge volume changes of silicon in charging and discharging process hinders its application. Their results show that hollow silicon nanosphere will be a more suitable structure for electrode.
A continuum LIB model, including mathematical descriptions of the charge transfer in the electrodes (both positive and negative), separator and current collector has been recently proposed by Purkayastha and McMeeking.241 The positive electrode submodel distinguishes the storage particles and the electrolyte and binder regions. The transport of each of the species, lithium ions and electrons are modelled individually in the different regions. The transport in electrolyte is modelled using the transport theory in concentrated solutions, while electrons are modelled using Ohm's law. For the storage particles, a coupled stress-diffusion model is used. The particles are assumed to be cylindrical in shape. Extraction of lithium from the storage particles is carried out using a scheme of galvanostatic charging followed by potentiostatic charging, in order to deplete the particles completely. According to the authors, stress arises due to the development of large concentration gradients within the particle. The uneven rates of extraction from the particles lead to variations in the concentration gradient within the particles, which subsequently lead to different values of stress. The uneven rate of extraction is caused due to the transport properties, with ionic diffusion within the electrolyte being much slower than electronic conduction in the binder. Simulations with three particles showed an even larger variation in stress between the particles, with the particle closer to the separator experiencing higher stresses. The particle distance from the separator, combined with the material properties of the particle, is critical in predicting the stress generated within the storage particles.
Garcia et al. propose a model including mechanical effects and study the performance of various nano-structured electrode layouts using dilute solution theory.242,243 Golmon et al. presents a multi-scale finite element approach for LIBs to study electrochemical–mechanical interaction phenomena at macro- and micro-scales.244 Their LIB model consists of a lithium foil anode, a separator, and a porous cathode that includes solid active materials and a liquid electrolyte (Fig. 33). The authors use the model to analyse the surface kinetics and electrochemical–mechanical phenomena within a single spherical particle of the active material. Homogenization techniques relate parameters in the micro-scale particle model to those in the macro-scale model describing the lithium ion transport, electric potentials and mechanical response based on porous electrode theory. In this way, the authors calculate the macro- and micro-scale response of the LIB model for several mechanical boundary conditions. In particular, Golmon et al. study the case where the LIB is clamped at both ends, and the case where an external pressure (e.g. 10 MPa, 100 MPa) is applied at the anode–separator interface, and the cathode–current collector interface is clamped. In the case of spherical particles, their model predicts that there is no influence of the interlaminate stress on the electrochemical performance of the LIB. A micro-scale diffusion equation is introduced which depends on the gradient of the hydrostatic stress. The predicted insensitivity of the electrochemical performance with respect to external mechanical loading conditions is in qualitative agreement with experimental work. However, according to the authors the dependency of macro- and micro-scale stresses across the battery on the mechanical boundary conditions cannot be ignored, as they can contribute to failure mechanisms in the LIB. Furthermore, the authors found that greater interlaminate stress correlates to higher strains and stresses across the LIB.
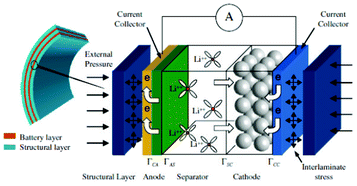 | ||
| Fig. 33 Schematics of the mechanical model by Golmon et al. Reprinted from ref. 244 with permission of Elsevier. | ||
Greve and Fehrenbanch recently reported a comprehensive combined experimental-3D finite element modelling study of fracture formation and initiation of internal short circuit in cylindrical LIBs.245 The study reveals correlations between the fracture locations, local heating and short circuit phenomena, certainly of interest for the LIBs optimization in terms of performance and safety. Similar interesting work has been reported by Sahraei et al.246,247
Of particular interest is the uniformity of the temperature distribution in and across the battery as this strongly affects the lifetime. The problem of determining temperature distributions in battery packs has long been of interest.
The spirally-wound design of LIBs is the most commercially important but also the most complex to analyse. The complexity results not only from the spiral geometry but also from considering the myriad tabbing and electrode possibilities.261 Electrodes can have a large diversity of coatings such as single sided, double sided, asymmetric, or patched, and tabs can extend the height of the electrode or extend just from the edge, and the number of tabs can vary from one to continuous.
Pioneering LIB thermal models have been presented by Sunu and Burrows,248,249 Song and Evans,250 Pesaran,251 Wang and Srinivasan,252 Verbrugge,253 Gomadam et al.254 and Kim et al.255 Currently almost all the studies in the literature correspond to thermal analyses only with ad hoc assumed and prescribed heat generation rate. However on-the-fly coupling between mathematical descriptions of electrochemistry and thermal management is mandatory.
Hellwig et al. propose a 1D + 1D + 1D multi-scale electrochemical and thermal model of a LIB with LiFePO4 positive electrode material.256 The model uses a hierarchical representation of spatial scales. At the nanoscopic level, diffusive lithium transport is assumed to take place in the active material particles. At the microscopic level, multi-component mass and charge transport as well as heat production is described in a single repeat unit (anode, separator, cathode, current collectors). At the macroscopic scale, the model describes heat transport in the radial direction of a cylindrical cell. Molar enthalpies and entropies are incorporated as function of state of charge (SOC) for the simulation of heat production. The model is validated using experimentally-determined discharge curves over a wide range of discharge currents.
Kim et al. present a general LIB model introducing multiple coupled computational domains to resolve the interplay of physicochemical mechanisms in several length scales.257 The model accounts for electrochemical-, electrical-, and thermal-coupled physics in large-format stacked prismatic cell designs. Each domain uses its own independent coordinate system for spatial discretization of the variables solved in that domain (Fig. 34). Separation of the model domain and adoption of the statistical homogeneity assumption are enabled based on the intrinsic nature of typical LIB systems where physics with significant time-scale differences interplay.
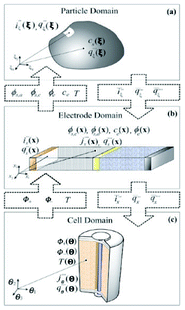 | ||
| Fig. 34 Model solution variables in each computational domain and the coupling variables exchanged between the adjacent length scales domains. Reprinted with permission from ref. 257. Copyright 2011, The Electrochemical Society. | ||
An approach is proposed by Spotnitz et al.258 consisting on the inclusion of LIB models in a computer-aided engineering (CAE) package (STAR-CCM+259). The approach followed is to use battery models for the calculation of the heat generation and the CAE package for solving the overall thermal problem. The CAE package accounts for the detailed geometry of the battery including means for thermal management such as cooling plates. The LIB model accounts for the heat due to current distribution in the current collectors and heat due to electrochemical processes. The current distribution problem is solved using Poisson's equation.
Baba et al. proposed an electrochemical-thermal on-the-fly coupled simulation method for LIBs (Fig. 35):260 a 3D thermal conduction analysis solver is coupled with a 2D electrochemical analysis solver. The 2D electrochemical analysis solver implements a new lumped model of LIBs. The new lumped model is capable for estimating the local heat generation rate accurately. Hence, the 2D distribution data of the heat generation rate are produced, which are mapped to the real cell geometry by the coordinate transformation. The 3D thermal conduction analysis solver simulates the 3D temperature distribution by taking into account for the mapped heat generation rates. Again, the 3D temperature distribution data are mapped on the 2D expansion plane of spirally wound electrodes by the reverse coordinate transformation. This data exchange process between two solvers is reported by the authors to be performed every computational time-step, as a result both thermal and electrochemical behaviours can be reproduced simultaneously.
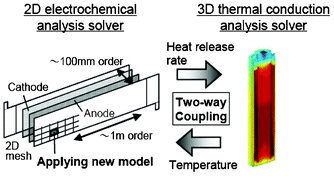 | ||
| Fig. 35 Schematics of the electrochemical-thermal on-the-fly coupled simulation method of LIBs. Reproduced with permission from ref. 260. Copyright 2012, The Electrochemical Society. | ||
Other models of spirally-wound cells have been proposed to calculate the ohmic drop in the current collectors as well as the electrochemical processes taking place between the current collectors.261
Prismatic wound cells are considered to have advantages over cylindrical cells in thermal management and packaging efficiency due to its larger surface to volume form factor, and in manufacturing cost over stacked prismatic cells thanks to its higher yields. Lee et al. report a cell domain model for prismatic wound cells.262 The authors found that corner parts are cooled down more than the other parts of the cell because the corner parts have large surface area per volume (Fig. 36).
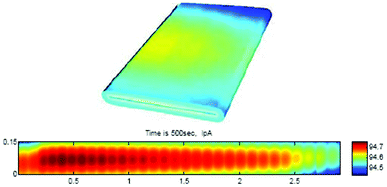 | ||
| Fig. 36 Reaction current density distribution after 500 s at 4C discharge of 20 Ah cell with continuous tabs at (a) surface and (b) unrolled jelly roll. Reproduced with permission from ref. 262. Copyright 2012, The Electrochemical Society. | ||
Moreover, internal short-circuit in LIBs may be caused by metal particle contamination during the manufacturing process. The metal particle creates short circuit between the two electrodes. Large amount of current passes through the cells and short-circuit area, producing a significant amount of heat generation, which can trigger exothermic reactions and eventually leads to thermal runaway. An electrochemical-thermal coupled model is proposed by Zhao et al. to analyse nail penetration process in LIBs (Fig. 37).263 The authors report interesting results on the internal short circuit of a large-format LIB by a metal particle embedded in the cell structure upon the impact of the short-circuit location, metal particle resistance, cell geometry, etc.
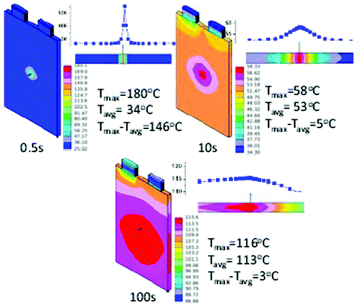 | ||
| Fig. 37 Temperature distributions at different times during nail penetration process. Reproduced with permission from ref. 263. Copyright 2012, The Electrochemical Society. | ||
Based on the porous electrode and concentrated solution theory, a thermal model of a LIB pack has been recently proposed by Zhu et al.264 highlighting once again the impressive progress of the discipline in the last years.
2.6 Spanning multiple scales from atomistic to macroscopic
Mathematical order reduction of complex models is also an important task towards the integration of the prediction capabilities of sophisticated multiphysics models into macroscopic ones describing LIB stacks or dedicated to control-command at the system level in automotive applications.265 Reduced-order models approximate in fact more complex physics-based models which are not suitable for real time applications as it usually takes a long time (e.g. hours) to spatially discretize the system via a finite difference method and solve the system numerically as a collective of differential equations in terms of the state variables. Therefore, a fast and robust approximate model is required. A simplified LIB model for automotive applications has to be carried out at a good accuracy while ensuring the maximum computational cost reduction to achieve an efficient system management.An important aspect within this control-command issue for optimal operation strategies is the battery degradation. LIB cell life critically depends on how the cell is used. Thus, LIB chargers and LIB management systems must be designed to control cell usage carefully. In order to design optimal LIB controls that effect the cell performance and lifetime, a simple model describing the cell degradation is necessary. Randalla et al.266 reported a controls-oriented cell degradation model by deriving a reduced-order model of a single mechanism: the growth process of the SEI layer, along with the resulting resistance rise and capacity loss.
Dao et al. propose effective and systematic steps in the mathematical simplification and reduction of multiphysics LIB models to improve computational efficiency.267 The LIB model used for simulations is an isothermal model which incorporates the concentrated solution theory, the porous electrode theory, and the variations in electronic/ionic conductivities and diffusivities. The simplified model is formulated by exploiting the mathematical structure of the governing equations and by using a combination of several techniques such as volume-averaging, Galerkin's numerical method, and curve-fitting. The authors show that the approximate model can simulate in milliseconds without a significant loss in accuracy compared to the full-order rigorous model.
In regard with the goal of developing LIB models which can predict the impact of the chemical and structural properties of the materials on the efficiency and durability of the LIB, significant progress has been achieved on the modelling of other electrochemical power generators. In 2002, Franco invented the multiscale simulation package called “MEMEPhys”, from the French spelling Modèle Multi-Echelle Physique. This package was first dedicated to the simulation of PEM Fuel Cells (PEMFCs) but, later, was extended for the simulation of other electrochemical systems, such as PEM Water Electrolyzers (PEMWEs)268,269 and Lithium Air Batteries (LABs).270
The model is an indirect multiparadigm approach: a continuum model describing electrochemical and transport mechanisms with parameters extracted from ab initio databases (for the reactions kinetic parameters as function of the catalyst chemistry and morphology) and CGMD calculations (for the materials structural properties as function of their chemistry) (cf.Fig. 4).
Franco has designed this model to connect within a non- equilibrium thermodynamics framework atomistic phenomena (elementary kinetic processes) with macroscopic electrochemical observables (e.g. i-V curves, EIS, Ucell(t).) with reasonable computational efforts. MEMEPhys is a transient, multi-scale and multiphysics single electrochemical cell model accounting for the coupling between physical mechanistic descriptions of the phenomena taking place in the different components and materials scales. In the case of PEMFCs, it accounts for detailed descriptions of the electrochemical and transport mechanisms in the electrodes, the membrane, the gas diffusion layers and the channels:23,51–54,94,271–273 H2, O2, N2 and vapour H2O transport 1-D macroscale description along the channels, H2, O2, N2 and biphasic H2O transport 1-D mesoscale description across the gas diffusion layers and the electrodes (including H2O condensation between the carbon agglomerates), protons transport 1-D mesoscale description across the MEA, electrons transport 1-D mesoscale description across the electrodes and gas diffusion layers, H2 and O2 diffusion 1-D microscale description across the on-catalyst ionomer film inside the electrodes, and the interfacial nanoscale mechanisms at the vicinity of the catalyst nanoparticles including both elementary kinetics and electrochemical double layer effects. The model includes novel descriptions of coupled electrochemical aging processes (e.g. Pt and PtxCoy oxidation/dissolution/ripening, carbon catalyst support corrosion, polymer electrolyte membrane degradation.).274–283
The model is isothermal and neglects mechanical issues, but on a physical basis, the model already describes the feedback between the instantaneous performance and the intrinsic material aging processes, thus the individual components and cell durability can be predicted. The approach provides new insights on the interplaying between the different aging phenomena and analyses the cell response sensitivity to operating conditions, initial catalyst/C/ionomer loadings and temporal evolution of the electro-catalytic activity (Fig. 38 and 39). This model is pioneering the field of PEMFC durability prediction at the laboratory scale (e.g. impact of simple on/off cycles on the durability). For instance, within this context, the tool has provided very interesting information on the competition of aging phenomena. Some experimental data suggests that external anode and cathode contaminants (e.g. CO in the anode, SO2 in the cathode) can enhance the damage of the PEMFC materials. Even the injection of these contaminants can mitigate, under appropriate current-cycled conditions, the intrinsic materials aging mechanisms.23 MEMEPhys helped to clearly illustrate the interest of treating the complex mechanisms interacting between them towards engineering optimization of the PEMFC operation. Generally speaking, there is still a lack of understanding on the interplaying between all the relevant transport processes, detailed electrochemistry and thermo-mechanical stresses and on their relative impact on the global cell performance loss.
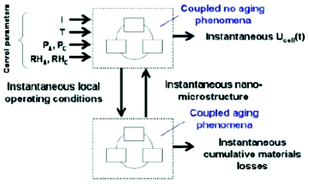 | ||
| Fig. 38 Schematics of the algorithm developed by Franco et al.53 | ||
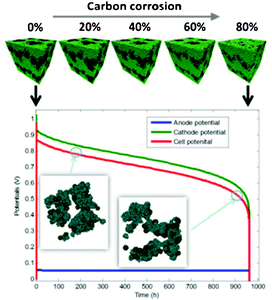 | ||
| Fig. 39 Multiscale simulation of the PEMFC carbon corrosion by combining a continuum model with a CGMD structural data.53 | ||
An analogy can be made between the multiscale character of PEMFCs and LIBs, and thus it appears to be interesting transferring Franco's approach for the modelling of LIBs (Fig. 40). On the one hand, the adaptation of such an approach to LIBs could seem not to be as difficult as in PEMFCs where the description of coexisting liquid and vapour phases is needed for the accurate simulation of water transport in the porous electrodes. But in the other hand the description of the PEMFC surface (two-dimensional) electrochemistry (still difficult, for example because of the numerous elementary reaction steps involved in the oxygen reduction reaction) is replaced in LIBs by the necessity of describing electrochemical reactions occurring in the “volume” of the active material (three-dimensional problem). These reactions are inherently coupled to non-linear phenomena such as the formation and morphological evolution of solid phases. Estimating transition states and activation energy barriers for the elementary intercalation or conversion processes which can occur in such “three dimensional” systems present obvious methodological difficulties: for example, for conversion reactions, in order to have a complete overview of the elementary kinetic steps, the energetics of all the possible (solid phase/solid phase, solid phase/liquid electrolyte) inter-phases which could be formed should be explored by ab initio calculations.141,142
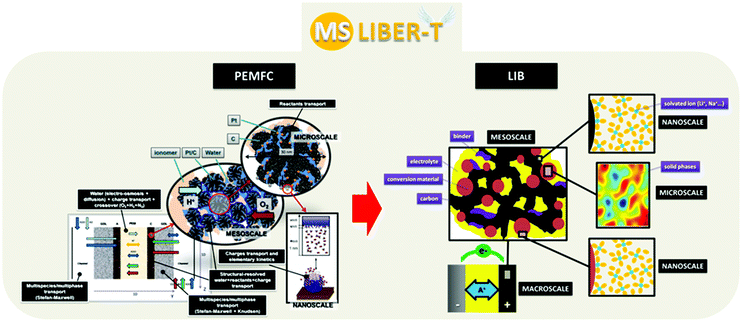 | ||
| Fig. 40 Moving from the multiscale modelling of PEMFC to the multiscale modelling of LIBs (case of conversion materials) within the framework of the computational software MS LIBER-T developed by Franco et al. | ||
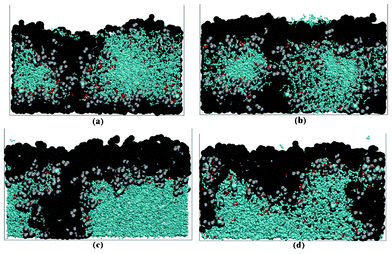 | ||
| Fig. 41 CGMD simulations of the self-organization of the proton conducting polymer in PEMFCs at the vicinity of substrates with different hydrophobicity properties (water contact angle equal to (a) ∼ 150°, (b) ∼ 100°, (c) ∼ 70° and (d) ∼ 30°). Black spheres represent polymer backbone monomers CF2 and CF3; the side-chains monomers are gray spheres; the water molecules are represented by light blue dots, and the hydronium by red dots. Source: 284. | ||
3 Conclusions and challenges
Numerical simulation and computer-aided engineering emerge nowadays as important tools to speed up the LIBs research and development particularly for their use in automotive applications. Numerous theoretical efforts to mathematically describe the LIB operation have been reported worldwide since around 30 years. Physical models became more and more accurate and predictive, for example thanks to the widespread development of quantum mechanics and molecular dynamics approaches allowing capturing the impact of the materials chemistry onto some effective properties essentially related to the electrochemical reactions and lithium ion transport. Non-equilibrium thermodynamics phase field modelling approach appears to be a powerful modelling technique to understand solid phase formation and separation in LIB intercalation materials at the nano/microscale. Moreover, impressive electrode 3D reconstruction techniques have been developed allowing to capture for the first time the impact of the “real” mesostructure (e.g. binder distribution) onto the local lithium reactivity and transport properties and the global cell efficiency. In particular, integrative multiphysics, multiscale and multiparadigm models spanning multiple scales and aiming to simulate competitions and synergies between electrochemical, transport, mechanical and thermal mechanisms become now available. One of the major interests of such a class of models is its capability to analyse the impact of the materials and components structural properties on the global cell performance.Some of the reported models have been already used to understand materials degradation phenomena and their impact on the LIB efficiency and capacity fade: metallic dissolution, lithium plating, SEI formation and graphite exfoliation are some of the mechanisms largely studied.
Despite the tremendous progress achieved on developing LIB models with predictive capabilities, there are still major challenges to be overcome.
First of all it should be noticed that the majority of the reported multiscale models focus on the understanding of the operation and the impact of the structural properties of LiFePO4 or graphite electrodes onto the global cell efficiency. And on the other hand, quantum mechanics and molecular dynamics models focalize on the understanding of the impact of the materials chemistry onto their storage or lithium transport properties at the nanoscale. It is now crucial to develop multiscale models that are able to incorporate both structure and chemical databases, in other words, that they are able to mimic the materials behaviour in realistic electrochemical environments (Fig. 42). Within this sense, other intercalation and conversion materials have to be also modelled. The development of such a model tackles the issues related to how to couple discrete with continuum models and will need to set up rigorous methods to integrate ab initio data into elementary kinetics models of the lithiation/delithiation reactions.
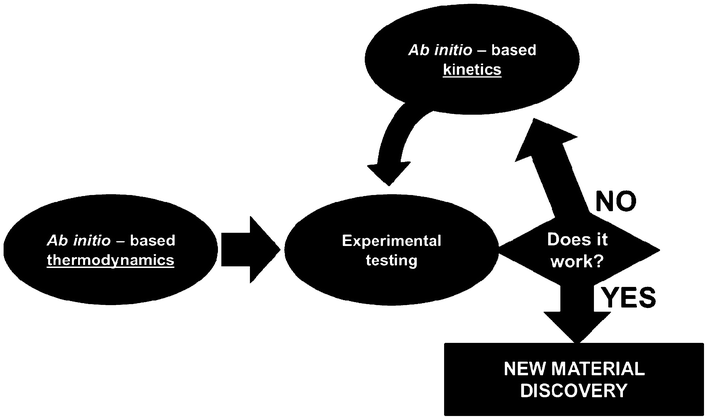 | ||
| Fig. 42 Complementarity between ab initio thermodynamics and ab initio kinetics models. | ||
Moreover, accurate modelling of the interfacial electrochemical reactions that combine chemistry with diffusion of radicals and formation of the heterogeneous crystalline or glassy SEI layer of anode or a passivation layer on the cathode is an intrinsically multiscale problem, which is largely unaddressed but of great technological relevance.
Probably a combination of the properties behind models like MEMEPhys, previously developed for PEMFCs, with phase field models describing the lithium kinetics on the basis of parameters which can in principle be estimated from quantum mechanics calculations, would be the key to achieve these goals. The new simulation package MS LIBER-T (Multiscale Simulator of Lithium Ion Batteries and Electrochemical Reactor Technologies), being developed by Franco et al. at LRCS is aiming to respond to this need because it is designed to support on-the-fly coupling between phase-field simulations of the electrochemistry and materials degradation phenomena, as it will be reported elsewhere.284 Such a class of model should be seen as complementary to ab initio thermodynamics approaches already used for data mining: actually if a material candidate detected by using ab initio thermodynamics fails at the experimental level, that could mean that the kinetics and the physicochemical environment of the material should play a role, and thus a multiscale kinetic model could be used to virtually test the material in realistic electrochemical conditions to detect, if possible, operation conditions favoring its operation.
Furthermore, the generation and the integration of those chemical and structural databases in the phase field and cell models should be carried out in a fully integrated way by exploiting the recent progresses in data flows management.
Secondly, computational tools for the analysis of performance and safety of LIBs are currently fragmented and developed independently at different groups. Ideally, a multiscale LIB model useful in engineering practice should have the following characteristics: it should be flexible, i.e. it should allow the developers to switch between different LIB designs to decide which LIB provides their technical needs, as well as quickly testing new LIB designs; it should be portable, i.e. the model should be a hardware (or computing platform) independent code; it should be scalable, i.e. the model code should allow developers to run it on single computers and multicore processors up to supercomputers; it should be easy to use (including for experimentalists), i.e. the model implementation details should be abstracted in a way that the developer interacts with a user-friendly interface; it should allow cloud computing and network development, i.e. simultaneous development by multiple researchers should be permitted as well as a performing exchange of information to benchmark different model versions. web platforms should be developed aiming to share physics and mathematical modules to facilitate models calibration and benchmarking. This would go towards the development of general-purpose design tools available worldwide enhancing communication and exchanges between scientists and engineers.
Methodological approaches synergetically combing both top down and bottom up modelling viewpoints should be further developed. Macroscopic equations in top-down models should be written in terms of parameters with values calculated from lower scale simulations. Implementation of such parameters into the macroscopic model should be done including empirical errors. Methodological evaluation of these parameters should be done systematically: for instance, coarse models should be developed first, with parameters sensitivity studies guiding further calculations at lower scales.
Morphogenesis of the electrodes as function of the ink properties and manufacture process (e.g. solvent used, deposition time, etc.), as well as the composition and structure of the SEI and its impact on the LIB capacity, should be further studied, e.g. by importing CGMD models already successfully applied for the simulation of complex materials mixtures in other systems such as PEMFCs (Fig. 41).285 These models can predict the materials chemistry impact on their structure, and thus generate important parameters for continuum models.
Numerical simulation of competitive degradation phenomena on the basis of a bottom-up framework should also be achieved, in order to determine the most important mechanisms as function of the applied external operation conditions and to quantitatively predict LIB durability.
More generally, combining multiscale modelling with the use of virtual reality could provide significant progress on providing virtual experimentation of LIBs.286
Finally, to get progress on the development of multiscale models, it is crucial to develop multidisciplinarity between application domains. For example, computational scientists working in cosmology, geology and climate science could bring interesting methodological concepts for the widespread use of multiscale modelling in electrochemistry.
It should be noticed that the analysis and discussions here above also applies for other electrochemical systems for energy storage, such as lithium air and lithium sulphur batteries, supercapacitors and devices for energy conversion such as fuel cells and electrolyzers.23,53,287–289
Acknowledgements
The author gratefully acknowledges Dr Marie-Liesse Doublet (Institut Charles Gehradt, Montpellier, France) for the ongoing scientific collaborations as well as very helpful discussions. Prof. Jean-Marie Tarascon, Dr Mathieu Morcrette and Dr Charles Delacourt (Laboratoire de Réactivité et de Chimie de Solides, Amiens, France) are also gratefully acknowledged for inviting the author doing a highly motivating scientific visit in their laboratory since February 2013. Prof. Martin Z. Bazant is also acknowledged for very interesting discussions during the author's MIT visit in September 2012. Comments from the referees are also highly appreciated.References
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451(7179), 652 CrossRef CAS.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271 CrossRef CAS.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144(4), 1188 CAS.
- M. Maccario, L. Croguennec, F. Weill, F. Le Cras and C. Delmas, Solid State Ionics, 2008, 179, 2383 Search PubMed.
- D. Choi and P. N. Kumta, J. Power Sources, 2007, 163, 1064 CrossRef CAS.
- H. Huang, S.-C. Yin and L. F. Nazar, Electrochem. Solid-State Lett., 2001, 4, A170 CrossRef CAS.
- S.-T. Myung, S. Komaba, N. Hirosaki, H. Yashiro and N. Kumagai, Electrochim. Acta, 2004, 49, 4213 CrossRef CAS.
- A. Aimable, D. Aymes, F. Bernard and F. Le Cras, Solid State Ionics, 2009, 180, 861 Search PubMed.
- T. Takeuchi, M. Tabuchi, A. Nakashima, T. Nakamura, Y. Miwa, H. Kageyama and K. Tatsumi, J. Power Sources, 2005, 146, 575 CrossRef CAS.
- K. Xu, U. Lee, S. S. Zhang, M. Wood and T. R. Jow, Electrochem. Solid-State Lett., 2003, 6, A144 CrossRef CAS.
- J. Cabana, Z. Stoeva, J. J. Titman, D. H. Gregory and M. R. Palacín, Chem. Mater., 2008, 20, 1676 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 982 CrossRef CAS.
- M. D. Levi, G. Salitra, B. Markovsky, H. Teller, D. Aurbach, U. Heider and L. Heider, J. Electrochem. Soc., 1999, 146, 1279 CrossRef CAS.
- S. Kobayashi and Y. Uchimoto, J. Phys. Chem., 2005, 109, 13322 Search PubMed.
- V. Johnson, A. Pesaran and T. Sack in: Proceedings of the 17th Electric Vehicle Symposium, Montreal, Canada, 2000 Search PubMed.
- C. O'Gorman, D. Ingersoll, R. Jungst and T. Paez in: Selected Battery Topics, ed. W. R. Cieslak, et al., Vol. PV 98-15, The Electrochemical Society Proceedings Series, Pennington, NJ, 1998, p. 248 Search PubMed.
- J. Newman, Electrochemical Systems, 2nd edition, Prentice-Hall, Englewood Cliffs, NJ, 1973 Search PubMed.
- R. Spotnitz, Interface, 2005, Winter, 39 Search PubMed.
- C. Y. Wang and V. Srinivasan, J. Power Sources, 2002, 110, 364 Search PubMed.
- V. Ramadesigan, P. W. C. Northrop, S. De, S. Santhanagopalan, R. D. Braatz and V. R. Subramanian, J. Electrochem. Soc., 2012, 159(3), R31 Search PubMed.
- The MacTutor History of Mathematics Achive, http://www-history.mcs.st-and.ac.uk/site consulted on December, 2012 Search PubMed.
- A. A. Franco, PEMFC degradation modelling and analysis, book chapter in: Polymer electrolyte membrane and direct methanol fuel cell technology (PEMFCs and DMFCs)-Volume 1: Fundamentals and performance, ed. C. Hartnig and C. Roth, Woodhead, Cambridge, UK, 2012 Search PubMed.
- A. A. Franco, seminar given at Argonne National Laboratory, May 11th, 2011 (http://www.msd.anl.gov/seminars/allred-042512) Search PubMed.
- X. Sun, K. Sun, C. Chen, H. Sun and B. Cui, International Journal of Materials and Chemistry, 2012, 2(5), 218 Search PubMed.
- E. Sahraei, R. Hill and T. Wierzbicki, J. Power Sources, 2012, 201, 307 Search PubMed.
- J. Yan, J. Zhang, Y.-C. Su, X.-G. Zhang and B.-J. Xia, Electrochim. Acta, 2010, 55, 1785 Search PubMed.
- S. Laplace, A Philosophical Essay of Probabilities, translated from the 6th French Edition by F. W. Truscott and F. L. Emory, John Wiley & Sons, New York, 1902 Search PubMed.
- E. N. Lorenz, J. Atmos. Sci., 1963, 20(2), 130 CrossRef.
- V. G. Ivancevic and I. T. Tijana, Complex nonlinearity: chaos, phase transitions, topology change, and path integrals, Springer, 2008 Search PubMed.
- D. Kondepudi and I. Prigogine, Modern Thermodynamics: From Heat Engines to Dissipative Structures, Wiley, 1998 Search PubMed.
- I. Prigogine, Introduction to Thermodynamics of Irreversible Processes, (2nd ed.), New York, Interscience, 1961 Search PubMed.
- G. A. Holzapfel and T. C. Gasser, Comput. Methods Appl. Mech. Eng., 2001, 190, 4379 Search PubMed.
- F. Couenne, D. Eberard, C. Jallut, L. Lefèvre and B. Maschke, Multiscale distributed parameter model of an adsorption column using a port-based geometric approach, European Symposium on Computer Aided Process Engineering, ESCAPE 15, 29 May-1 June 2005, Barcelona, Spain Search PubMed.
- R. Marchand and T. Ackerman, J. Geophys. Res., 2010, 115, D16207 Search PubMed.
- M. Stan, Nucl. Eng. Technol., 2009, 41(1) Search PubMed.
- A. A. Baklanov, B. Grisogono, R. Bornstein, L. Mahrt, S. S. Zilitinkevich, P. Taylor, S. E. Larsen, M. W. Rotach and H. J. S. Fernando, Bull. Am. Meteorol. Soc., 2011, 92, 123 Search PubMed.
- J. D. Cole, SIAM J. Appl. Math., 1995, 55, 410 Search PubMed.
- M. Ptashnyk and T. Roose, SIAM J. Appl. Math., 2010, 70, 2097 Search PubMed.
- M. Ptashnyk, T. Roose and G. Kirk, Eur. J. Soil Sci., 2010, 61, 108 Search PubMed.
- G. Botte, V. R. Subramanian and R. E. White, Electrochim. Acta, 2000, 45, 2595 Search PubMed.
- M. Doyle and J. Newman, J. Appl. Electrochem., 1996, 27, 846 Search PubMed.
- M. Doyle and J. Newman, J. Electrochem. Soc., 1996, 143, 1890.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 982 CrossRef CAS.
- C. Y. Wang, W. B. Gu and B. Y. Liaw, J. Electrochem. Soc., 1998, 145, 3407 Search PubMed.
- L. Madec, L. Falk and E. Plasari, Chem. Eng. Sci., 2001, 56, 1731 Search PubMed.
- P. Mandin, J. M. Cense, F. Cesimiro, C. Gbado and D. Lincot, Comput. Chem. Eng., 2007, 31(8), 980 Search PubMed.
- K. Reuter, in Modelling Heterogeneous Catalytic Reactions: From the Molecular Process to the Technical System, ed. O. Deutschmann, Wiley-VCH, Weinheim, 2011 Search PubMed.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 CrossRef.
- R. Ferreira de Morais, D. Loffreda, P. Sautet and A. A. Franco, Electrochim. Acta, 2011, 56(28), 10842 CrossRef.
- K. Malek and A. A. Franco, J. Phys. Chem. B, 2011, 115(25), 8088 CrossRef.
- A. A. Franco, Towards a bottom-up multiscale modelling framework for the transient analysis of PEM Fuel Cells operation, book chapter in: Polymer Electrolyte Fuel Cells: Science, Applications and Challenges, ed. A. A. Franco (publisher: Pan Stanford, distributor: Francis & Taylor), 2013 Search PubMed.
- A. A. Franco, A multiscale modelling framework for the transient analysis of electrochemical power generators-From theory to the engineering practice; Habilitation to become Research Director (H.D.R.) manuscript, Université Claude Bernard Lyon-1 (France), 2010 (available online) Search PubMed.
- L. Cai and R. E. White, J. Power Sources, 2011, 196, 5985 Search PubMed.
- http://www.mcs.anl.gov/petsc/ .
- http://www.zib.de/ehrig/software.html .
- http://www.ctcms.nist.gov/fipy/ .
- G. Hager, Introduction to High Performance Computing for Scientists and Engineers, Chapman & Hall/CRC, Computational Science, 2010 Search PubMed.
- https://www.vasp.at/ .
- http://www.crystal.unito.it/ .
- http://www.scm.com/ .
- http://www.gaussian.com/ .
- http://bigdft.org/Wiki/index.php?title=BigDFT_website .
- M. A. Gabriel, T. Deustch, L. Genovese, G. Krosnicki, O. Lemaire and A. A. Franco, Phys. Chem. Chem. Phys., 2010, 12, 9406 RSC.
- M. A. Gabriel, T. Deustch and A. A. Franco, ECS Trans., 2010, 25(22), 1 Search PubMed.
- http://www.gromacs.org/ .
- http://lammps.sandia.gov/ .
- http://ambermd.org/ .
- http://www.charmm.org/ .
- D. Frenkel and B. Smit, Understanding Molecular Simulation: from algorithms to applications, Academic Press, 2002 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- D. C. Rapaport, The art of molecular dynamics simulation, Cambridge University Press, 2009 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Clarendon Press, 1989 Search PubMed.
- S. Bozic and I. Kondov, eChallenges e-2012 Conference Proceedings ed. P. Cunningham and M. Cunningham, IIMC International Information Management Corporation, 2012 Search PubMed.
- http://www.knime.org/ .
- http://www.unicore.eu/index.php .
- W. R. Elwasif, D. E. Bernholdt, S. Pannala, S. Allu and S. S. Foley, cse, pp.102–110, 2012IEEE 15th International Conference on Computational Science and Engineering, 2012 Search PubMed.
- M. C. Georgiadis, S. Myrian, N. Efstratios and R. Gani, Comput. Chem. Eng., 2002, 26, 735 Search PubMed.
- M. Mangold, S. Motz and E. D. Gilles, Chem. Eng. Sci., 2002, 57, 4099 Search PubMed.
- P. Breedveld, F. Couenne, C. Jallut, B. Maschke and M. Tayakout–Fayolle, Proc. 4th European Congress on Chemical Engineering, Grenada, Spain, 2003 Search PubMed.
- F. Couenne, C. Jallut, B. Maschke, P. Breedveld and M. Tayakout, Math. Comput. Modell. Dyn. Syst., 2006, 12(2–3), 159 Search PubMed.
- P. C. Breedveld, Physical systems theory in terms of bond graphs, PhD thesis, University of Twente, Enschede, Netherlands, 1984 Search PubMed.
- P. C. Breedveld and G. Dauphin-Tanguy (ed.), Current topics in bond graph related research, Journal of The Franklin Institute, Special issue on bond–graph modelling, 3285–6, Pergamon Press, 1991 Search PubMed.
- H. M. Paynter, Analysis and design of engineering systems, MIT Press, Cambridge, MA, 1961 Search PubMed.
- J. U. Thoma, Introduction to bond graphs and their applications, Pergamon Press, Oxford, 1975 Search PubMed.
- J. U. Thoma, Simulation by bond graphs-Introduction to a graphical method, Springer Verlag, 1989 Search PubMed.
- http://www.20sim.com/ .
- http://www.lmsintl.com/amesim-platform .
- http://www.3ds.com/products/catia/portfolio/dymola .
- https://www.openmodelica.org/ .
- L. Menard, G. Fontes and S. Astier, Math. Comput. Simul., 2010, 81(2), 327 Search PubMed.
- J. J. Esperilla, J. Felez, G. Romero and A. Carretero, Simulation Modelling Practice and Theory, 2007, 15(1), 82 Search PubMed.
- A. A. Franco, PhD thesis, Université Claude Bernard Lyon 1, 2005 (available online) Search PubMed.
- A. A. Franco, C. Jallut and B. Maschke, Multi-scale Bond Graph Model of the Electrochemical Dynamics in a Fuel Cell, in Proc. 5th MATHMOD Conference, ed. I Troch and F. Breitenecker, Vienna, Austria, 2006, P103 Search PubMed.
- A. A. Franco, M. Tembely, C. Jallut and B. Maschke, in Proc. World Hydrogen Conference (WHEC) 16, Lyon, France, 2006, 572 Search PubMed.
- A. A. Franco, C. Jallut and B. Maschke, in preparation, 2013.
- L. Ljung, System Identification-Theory for the User, Prentice-Hall, Upper Saddle River, New Jersey, 2nd edition, 1999 Search PubMed.
- L. Ljung and T. Glad, Automatica, 1994, 30(2), 265 Search PubMed.
- E. Walter, Identification of State Space Models, Springer Verlag, Berlin, 1982 Search PubMed.
- Identifiability of Parametric Models, ed. E. Walter, Pergamon Press, Oxford, 1987 Search PubMed.
- P. M. J. Van den Hof, J. F. M. Van Doren and S. G. Douma, Indetification of parameters in large-scale physical model structures, for the purpose of model-based operations, In: Model-Based Control: Bridging Rigorous Theory and Advanced Technology, ed. P. M. J. Van den Hofet al., Springer-Verlag, New York, USA, 2009 Search PubMed.
- B. Temel, et al. , J. Chem. Phys., 2007, 126, 204711 CrossRef.
- M. Maestri and K. Reuter, Angew. Chem., 2011, 123, 1226 Search PubMed.
- M. K. Sabbe, M.-F. Reyniers and K. Reuter, Catal. Sci. Technol., 2012, 2, 2010 RSC.
- http://th.fhi-berlin.mpg.de/th/Meetings/DFT-workshop-Berlin2011/presentations/2011-07-21_Reuter_Karsten.pdf .
- S. Santhanagopalan, Q. Guo and R. E. White, J. Electrochem. Soc., 2007, 154, A198 Search PubMed.
- V. R. Subramanian, S. Devan and R. E. White, J. Power Sources, 2004, 135, 361 Search PubMed.
- V. R. Subramanian and R. E. White, Comput. Chem. Eng., 2000, 24, 2405 Search PubMed.
- V. R. Subramanian, D. Tapriyal and R. E. White, Electrochem. Solid-State Lett., 2004, 7, A259 Search PubMed.
- V. Boovaragavan and C. A. Basha, J. Appl. Electrochem., 2006, 36, 745 Search PubMed.
- V. Boovaragavan and C. A. Basha, J. Power Sources, 2006, 158, 710 Search PubMed.
- Q. Guo, V. R. Subramanian, J. W. Weidner and R. E. White, J. Electrochem. Soc., 2002, 149, A307 Search PubMed.
- V. R. Subramanian, V. Boovaragavan, K. Potukuchi, V. D. Diwakar and A. Guduru, Electrochem. Solid-State Lett., 2007, 10, A25 Search PubMed.
- V. R. Subramanian, V. Boovaragavan and V. D. Diwakar, Electrochem. Solid-State Lett., 2007, 10, A225 CrossRef CAS.
- V. R. Subramanian, V. D. Diwakar and D. Tapriyal, J. Electrochem. Soc., 2005, 152, A2002 Search PubMed.
- V. Boovaragavan, S. Harinipriya and V. R. Subramanian, Journal of Power Sources, 2008, 183, 361 Search PubMed.
- W. Lai and F. Cucci, Electrochim. Acta, 2011, 56, 4369 Search PubMed.
- K.-H. Xue and G. L. Plett, Electrochim. Acta, 2013, 87, 575 Search PubMed.
- M. Safari and C. Delacourt, J. Electrochem. Soc., 2011, 158(2), A63 CrossRef CAS.
- M. Safari and C. Delacourt, J. Electrochem. Soc., 2011, 158(5), A562 Search PubMed.
- D. Fabre, D. Guy-Bouyssou, P. Bouillon, F. Le Cras and C. Delacourt, J. Electrochem. Soc., 2012, 159(2), A104 Search PubMed.
- M. Farkhondeh and C. Delacourt, J. Electrochem. Soc., 2012, 159(2), A177 Search PubMed.
- C. Delacourt and M. Safari, J. Electrochem. Soc., 2012, 159(8), A1283 Search PubMed.
- M. Safari and C. Delacourt, J. Electrochem. Soc., 2011, 158(12), A1436 Search PubMed.
- M. Safari and C. Delacourt, J. Electrochem. Soc., 2011, 158(10), A1123 Search PubMed.
- J. W. Long, B. Dunn, D. R. Rolison and H. S. White, Chem. Rev., 2004, 104, 4463 CrossRef CAS.
- B. Dunn, J. Long and D. Rolison, ECS Interface, Fall, 2008 Search PubMed.
- A. Awarke, S. Lauer, M. Wittler and S. Pischinger, Comput. Mater. Sci., 2011, 50, 871 Search PubMed.
- S. Dargaville and T. W. Farrell, J. Electrochem. Soc., 2010, 157, A830 CrossRef CAS.
- J. Newman and V. Srinivasan, J. Electrochem. Soc., 2004, 151, A1517 CrossRef CAS.
- E. Weinan, B. Engquist and Z. Y. Huang, Phys. Rev. B, 2003, 67, 092101 Search PubMed.
- C. R. A. Catlow, Z. X. Guo, M. Miskufova, S. A. Shevlin, A. G. H. Smith, A. Walsh, D. J. Wilson and S. M. Woodley, Philos. Trans. R. Soc. London, Ser. A, 2010, 368, 3379 CrossRef CAS.
- G. Ceder, Y. M. Chiang, D. R. Sadoway, M. K. Aydinol, Y. I. Jang and B. Huang, Nature, 1998, 392, 694 CrossRef CAS.
- Y. Asari, Y. Suwa, T. Hamada, V. A. Dinh, J. Nara and T. Ohno, Abstract #631, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- Y. Asari, Y. Suwa and T. Hamada, Physical Review B, 2011, 84, 134113 Search PubMed.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano Lett., 2010, 10(10), 4123 CrossRef CAS.
- J. Yang and J. S. Tse, J. Phys. Chem. A, 2011, 115, 13045 Search PubMed.
- S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402 CrossRef CAS.
- J.-S. Filhol, C. Combelles, R. Yazami and M.-L. Doublet, J. Phys. Chem. C, 2008, 112, 3982 CrossRef CAS.
- A.-L. Dalverny, J.-S. Filhol and M.-L. Doublet, J. Mater. Chem., 2011, 21, 10134 RSC.
- R. Khatib, A. L. Dalverny, M. Saubanère, M. Gaberscek and M. L. Doublet, J. Phys. Chem. C, 2013, 117, 837 Search PubMed.
- X. H. Zhu, N. Chen and F. Lian, et al. , Chin. Sci. Bull., 2011, 56, 3229 Search PubMed.
- V. L. Chevrier and R. Dahn, J. Electrochem. Soc., 2009, 156, A454 CrossRef CAS.
- M. L. Suhko, K. M. Rosso and J. Liu, J. Phys. Chem. Lett., 2010, 1, 1967 Search PubMed.
- M. L. Suhko, K. M. Rosso and J. Liu, J. Phys. Chem. C, 2010, 114, 20277 CrossRef CAS.
- M. L. Sushko, K. M. Rosso, J.-G. Zhang and J. Liu, J. Phys. Chem. Lett., 2011, 2, 2352 Search PubMed.
- S. P. Ong, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, D. Bailey, D. Skinner, K. Persson and G. Ceder, The Materials Project, http://materialsproject.org/ Search PubMed.
- A. Jain, G. Hautier, C. Moore, S. P. Ong, C. Fischer, T. Mueller, K. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50(8), 2295 CrossRef CAS.
- V. I. Kalikmanov, M. V. Koudriachova and S. W. de Leeuw, Solid State Ionics, 2000, 136–137, 1373 CrossRef CAS.
- J. Cahn and J. Hilliard, J. Chem. Phys., 1958, 28(2), 258 CrossRef CAS.
- J. E. Guyer, W. J. Boettinger, J. A. Warren and G. B. McFadden, Phys. Rev. E, 2004, 69, 021603 Search PubMed.
- J. E. Guyer, W. J. Boettinger, J. A. Warren and G. B. McFadden, Phys. Rev. E, 2004, 69, 021604 Search PubMed.
- L. Q. Chen, in Multiscale materials modelling: fundamentals and applications, ed. Z. X. Guo, Woodhead, Cambridge, 2007 Search PubMed.
- A. J. Bray, Adv. Phys., 1994, 43, 357.
- J. Kim, Commun. Nonlinear Sci. Numer. Simul., 2007, 12, 1560 Search PubMed.
- S. M. Choo, S. K. Chung and K. I. Kim, Comput. Math. Appl., 2000, 39, 229 Search PubMed.
- M. Copetti and C. M. Elliott, Mater. Sci. Technol., 1990, 6, 273 Search PubMed.
- B. C. Han, A. Van der Ven, D. Morgan and G. Ceder, Electrochim. Acta, 2004, 49, 4691 Search PubMed.
- Y. H. Kao, M. Tang, N. Meethong, J. M. Bai, W. C. Carter and Y. M. Chiang, Chem. Mater., 2010, 22(21), 5845 CrossRef CAS.
- B. Kang and G. Ceder, Nature, 2009, 458(7235), 190 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7(2), A30 CrossRef CAS.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17(20), 5085–5092 CrossRef CAS.
- N. Dupre, J. Oliveri, J. Degryse, J. F. Martin and D. Guyomard, Ionics, 2008, 14(3), 203 Search PubMed.
- H. J. Tan, J. L. Dodd and B. Fultz, J. Phys. Chem. C, 2009, 113(48), 20527 Search PubMed.
- G. K. Singh, G. Ceder and M. Z. Bazant, Electrochim. Acta, 2008, 53(26), 7599 CrossRef CAS.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 4890 CrossRef.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6(3), 2215 CrossRef CAS.
- D. A. Cogswell and M. Z. Bazant, Abstract #734, 220th ECS Meeting, 2011 Search PubMed.
- W. Lai and F. Ciucci, Electrochim. Acta, 2010, 56, 531 Search PubMed.
- W. Lai, J. Power Sources, 2011, 196, 6534 CrossRef CAS.
- M. Landstorfer, S. Funken and T. Jacob, Phys. Chem. Chem. Phys., 2011, 13, 12817 RSC.
- C. Hin, Adv. Funct. Mater., 2011, 21, 2477 Search PubMed.
- J. O. Besenhard and H. P. Fritz, J. Electrochem. Soc., 1974, 3, 329 Search PubMed.
- K. Fujimura, A. Kuwabara, H. Moriwake, A. Seko, Y. Koyama and I. Tanaka, Abstract #1195, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- O. Borodin, G. D. Smith and W. Henderson, J. Phys. Chem. B, 2006, 110, 16879 CrossRef CAS.
- O. Borodin, G. D. Smith, O. Geiculescu, S. E. Creager, B. Hallac and D. DesMarteau, J. Phys. Chem. B, 2006, 110, 24266 CrossRef CAS.
- M. Ikeda, T. Yamasaki, C. Kaneta, K. Homma, T. Yamamoto and T. Tanaka, Abstract #1194, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- M. Ikeda, T. Yamasaki, C. Kaneta, K. Homma, T. Yamamoto and T. Tanaka, the 52nd Battery symposium in Japan, 4C05, 2011, 240, October 17–20, Tokyo Search PubMed.
- J. Yana, B.-J. Xiaa, Y.-C. Sub, X.-Z. Zhoub, J. Zhanga and X.-G. Zhang, Electrochim. Acta, 2008, 53, 7069 CrossRef CAS.
- Y. C. Chen, C. Y. Ouyang, L. J. Song and Z. L. Sun, J. Phys. Chem. C, 2011, 115, 7044 Search PubMed.
- S. Q. Shi, P. Lu, Z. Y. Liu, Y. Qi, L. G. Hector, H. Li and S. J. Harris, J. Am. Chem. Soc., 2012, 134, 15476 Search PubMed.
- O. Borodin, G. D. Smith and P. Fan, J. Phys. Chem. B, 2006, 110, 22773 CrossRef CAS.
- K. Leung, 217th ECS Meeting, Abstract #212 Search PubMed.
- K. Leung and J. L. Budzien, Phys. Chem. Chem. Phys., 2010, 12, 6583 RSC.
- K. Leung, Chem. Phys. Lett., 2013 Search PubMed (http://dx.doi.org/10.1016/j.cplett.2012.08.022).
- O. Borodin and T. R. Jow, ECS Trans., 2011, 33, 77 Search PubMed.
- L. Xing and O. Borodin, Phys. Chem. Chem. Phys., 2012, 14, 12838 RSC.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Phys. Chem. C, 2012, 116, 1114 CrossRef CAS.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2009, 113, 1763 CrossRef CAS.
- A. von Wald Cresce, O. Borodin and K. Xu, J. Phys. Chem. C, 2012, 116, 26111 Search PubMed.
- R. N. Methekar, P. W. C. Northrop, K. Chen, R. D. Braatz and V. R. Subramanian, J. Electrochem. Soc., 2011, 158(4), A363 Search PubMed.
- P. W. C. Northrop, R. D. Braatz and V. R. Subramanian, Abstract #730, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- A. A. Franco, S. Passot, P. Fugier, E. Billy, N. Guillet, L. Guetaz, E. De Vito and S. Mailley, ECS Trans., 2008, 13(17), 29 Search PubMed.
- A. A. Franco, S. Passot, P. Fugier, E. Billy, N. Guillet, L. Guetaz, E. De Vito and S. Mailley, J. Electrochem. Soc., 2009, 156, B410 CrossRef CAS.
- S.-K. Cheah, O. Lemaire, P. Gélin and A. A. Franco, ECS Trans., 2010, 25(35), 275 Search PubMed.
- S. K. Cheah, O. Sycardi, L. Guetaz, O. Lemaire, P. Gelin and A. A. Franco, J. Electrochem. Soc., 2011, 158(11), B1358 Search PubMed.
- M. B. Pinson and M. Z. Bazant, J. Electrochem. Soc., 2013, 160(2), A243 Search PubMed.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K.-C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269 CrossRef CAS.
- P. Arora and R. White, J. Electrochem. Soc., 1998, 145, 3647 CAS.
- R. Deshpande, M. Verbrugge, Y.-T. Cheng, J. Wang and P. Liu, J. Electrochem. Soc., 2012, 159(10), A1730 Search PubMed.
- Y. Ye, Y. Shi and A. A. O. Tay, J. Power Sources, 2012, 217, 509 Search PubMed.
- P. Arora, M. Doyle and R. White, J. Electrochem. Soc., 1999, 146, 3543 Search PubMed.
- M. Ecker, S. Käbitz, J. Gerschler and D. U. Sauer, Abstract #201, 218th ECS Meeting, 2010 Search PubMed.
- A. Ferrese, P. Albertus, J. Christensen and J. Newman, J. Electrochem. Soc., 2012, 159(10), A1615 Search PubMed.
- J. Park, J. H. Seo, G. Plett, W. Lu and A. M. Sastry, Electrochem. Solid-State Lett., 2011, 14(2), A14 Search PubMed.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, New York, 1972 Search PubMed.
- K. E. Thomas-Alyea, J. Newman, G. Chen and T. J. Richardson, J. Electrochem. Soc., 2004, 151(4), A509 Search PubMed.
- M. Tang and J. Newman, J. Electrochem. Soc., 2011, 158(5), A530 Search PubMed.
- S. Santhanagopalan, G.-H. Kim, K.-J. Lee, K. Smith and A. Pesaran, Abstract #420, 220th ECS Meeting, 2011 Search PubMed.
- Y. Kubota, Abstract #944, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- Y. Wang and P. B. Balbuena, J. Phys. Chem. B, 2002, 106, 4486 CrossRef CAS.
- K. Tasaki, J. Phys. Chem. B, 2005, 109, 2920 CrossRef CAS.
- K. Tasaki, A. Goldberg and M. Winter, Electrochim. Acta, 2011, 56, 10424 Search PubMed.
- K. Tasaki and A. Goldberg, Abstract #1259, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- G. B. Less, J. H. Seo, S. Han, A. M. Sastry, J. Zausch, A. Latz, S. Schmidt, C. Wieser, D. Kehrwald and S. Fell, J. Electrochem. Soc., 2012, 159(6), A697 Search PubMed.
- K. C. Smith, P. P. Mukherjee and T. S. Fisher, Abstract #748, 220th ECS Meeting, 2011 Search PubMed.
- K. C. Smith, P. P. Mukherjee and T. S. Fisher, Phys. Chem. Chem. Phys., 2012, 14, 7040 RSC.
- W. Du, N. Xue, A. M. Sastry, J. R. R. A. Martins and W. Shyy, Abstract #883, Honolulu, ECS Meting PRiME, 2012 Search PubMed.
- G. M. Goldin, A. M. Colclasure, A. H. Wiedemann and R. J. Kee, Electrochim. Acta, 2012, 64, 118 Search PubMed.
- C.-W. Wang and A. M. Sastry, J. Electrochem. Soc., 2007, 154(11), A1035 Search PubMed.
- W. Dreyer, C. Guhlke and R. Huth, Phys. D, 2011, 240, 1008 Search PubMed.
- J. Song and M. Z. Bazant, J. Electrochem. Soc., 2013, 160(1), A15 Search PubMed.
- J. H. Cushman, L. S. Bennethum and B. X. Hu, Adv. Water Resour., 2002, 25(8–12), 1043 Search PubMed.
- G. Richardson, G. Denuault and C. P. Please, J. Eng. Math., 2012, 72, 41 Search PubMed.
- S. Whitacker, The Method of Volume Averaging, Kluwer Academic Publishers, The Netherlands, 1998 Search PubMed.
- A. Bensoussan, J. L. Lion and G. Papanicolaou, Asymptotic Analysis for Periodic Structures, Studies in Mathematics and its Applications, North Holland, Amsterdam, 1978 Search PubMed.
- F. Ciucci and W. Lai, Transp. Porous Media, 2011, 88, 249 Search PubMed.
- R. Thiedmann, O. Stenzel, A. Spettl, P. R. Shearing, S. J. Harris, N. P. Brandon and V. Schmidt, Comput. Mater. Sci., 2011, 50, 3365 Search PubMed.
- B. Vijaraghavan, D.-W. Chung, P. Shearingz, N. Brandon, S. Harris and R. E. García, Abstract #347, 221st ECS Meeting, 2012 Search PubMed.
- M. Ender, J. Illig and E. Ivers-Tiffée, Abstract #1069, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- M. Ender, J. Joos, T. Carraro and E. Ivers-Tiffée, J. Electrochem. Soc., in press, 2012 Search PubMed.
- M. Ender, J. Joos, T. Carraro and E. Ivers-Tiffée, Electrochem. Commun., 2011, 13(2), 166 CrossRef CAS.
- B. Orvananos, H.-C. Yu, M. Bazant and K. Thornton, Abstract #750, 220th ECS Meeting, 2011 Search PubMed.
- G. Liu, H. Zheng, X. Song and V. Battaglia, J. Electrochem. Soc., 2012, 159(3), A214 Search PubMed.
- G. Inoue, T. Matsuoka, Y. Matsukuma and M. Minemoto, Abstract #803, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- G. Inoue, et al. , J. Power Sources, 2008, 175, 145 CrossRef CAS.
- G. Inoue, et al. , ECS Trans., 2008, 16(2), 1661 Search PubMed.
- G. Inoue, et al. , ECS Trans., 2009, 25(1), 1519 Search PubMed.
- J.-L. Zang and Y.-P. Zhao, International Journal of Engineering Science, 2012, http://dx.doi.org/10.1016/j.ijengsci.2012.06.018 Search PubMed.
- R. Purkayastha and R. M. McMeeking, Comput. Mech., 2012, 50, 209 Search PubMed.
- R. E. Garcia, J. Electrochem. Soc., 2005, 152, 255 Search PubMed.
- R. E. Garcia and Y. Chiang, J. Electrochem. Soc., 2007, 154(9), 856 Search PubMed.
- S. Golmon, K. Maute and M. L. Dunn, Comput. Struct., 2009, 87, 1567 CrossRef.
- L. Greve and C. Fehrenbach, J. Power Sources, 2012, 214, 377 Search PubMed.
- E. Sahraei, J. Campbell and T. Wierzbicki, J. Power Sources, 2012, 220, 360 Search PubMed.
- E. Sahraei, R. Hill and T. Wierzbicki, J. Power Sources, 2012, 201, 307 Search PubMed.
- W. G. Sunu and B. W. Burrows, J. Electrochem. Soc., 1982, 129(4), 688 Search PubMed.
- W. G. Sunu and B. W. Burrows, J. Electrochem. Soc., 1984, 129(4), 1 Search PubMed.
- S. Li and J. W. Evans, J. Electrochem. Soc., 2000, 147(6), 2086 Search PubMed.
- A. Pesaran, J. Power Sources, 2002, 110(2), 377 Search PubMed.
- C. Y. Wang and V. Srinivasan, J. Power Sources, 2002, 110(2), 364 Search PubMed.
- M. Verbrugge, AIChE J., 2004, 41(6), 1550 Search PubMed.
- P. Gomadam, R. E. White and J. W. Weidner, J. Electrochem. Soc., 2003, 150, A1339 Search PubMed.
- U. S. Kim, C. B. Shin and C.-S. Kim, J. Power Sources, 2009, 189(1), 841–846 Search PubMed.
- C. Hellwig, S. Sorgela and W. G. Bessler, ECS Trans., 2011, 35(32), 215 Search PubMed.
- G.-H. Kim, K. Smith, K.-J. Lee, S. Santhanagopalan and A. Pesaran, J. Electrochem. Soc., 2011, 158(8), A955 Search PubMed.
- R. Spotnitz, G. Yeduvaka, S. Hartridge, R. J. D. Schad and W. Smith, Abstract #836, The 15th International Meeting on Lithium Batteries–IMLB, 2010 Search PubMed.
- http://www.cd-adapco.com/products/star_ccm_plus/ .
- N. Baba, H. Yoshida, M. Nagaoka, C. Okuda and S. Kawauchi, Abstract #477, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- R. Spotnitz and G. Yeduvaka, Abstract #1070, Honolulu, ECS Meeting PRiME, 2012 Search PubMed.
- K.-J. Lee, K. Smith and G.-H. Kim, Abstract #535, 221st ECS Meeting, 2012 Search PubMed.
- W. Zhou and C.-Y. Wang, Abstract #536, 221st ECS Meeting, 2012 Search PubMed.
- C. Zhu, X. Li, L. Song and L. Xiang, J. Power Sources, 2013, 223, 155 Search PubMed.
- H. Sun, X. Wang, B. Tossan and R. Dixon, J. Power Sources, 2012, 206, 349 Search PubMed.
- A. V. Randalla, R. D. Perkinsa, X. Zhangb and G. L. Plett, J. Power Sources, 2012, 209, 282 Search PubMed.
- T.-S. Dao, C. P. Vyasarayani and J. McPhee, J. Power Sources, 2012, 198, 329 Search PubMed.
- L. F. Lopes Oliveira, S. Laref, E. Mayousse, C. Jallut and A. A. Franco, Phys. Chem. Chem. Phys., 2012, 14, 10215 RSC.
- L. F. Lopes Oliveira, C. Jallut and A. A. Franco, Electrochimica Acta, submitted, 2012 Search PubMed.
- A. A. Franco, ECS Trans., 2013, 45(27), 11 Search PubMed.
- R. Ferreira de Morais, D. Loffreda, P. Sautet and A. A. Franco, ECS Trans., 2010, 25(24), 167 Search PubMed.
- A. A. Franco, P. Schott, C. Jallut and B. Maschke, Fuel Cells, 2007, 7, 99 CrossRef CAS.
- A. A. Franco, P. Schott, C. Jallut and B. Maschke, J. Electrochem. Soc., 2006, 153(6), A1053 CrossRef CAS.
- A. A. Franco and K. Malek, in preparation, 2013.
- R. Coulon, D. Ichinose, W. Bessler and A. A. Franco, in preparation, 2013.
- S. K. Cheah, O. Sycardi, L. Guetaz, O. Lemaire, P. Gelin and A. A. Franco, J. Electrochem. Soc., 2011, 158(11), B1358 Search PubMed.
- R. Coulon, W. Bessler and A. A. Franco, ECS Trans., 2010, 25(35), 259 Search PubMed.
- S.-K. Cheah, O. Lemaire, P. Gélin and A. A. Franco, ECS Trans., 2010, 25(35), 275 Search PubMed.
- A. A. Franco, S. Passot, P. Fugier, E. Billy, N. Guillet, L. Guetaz, E. De Vito and S. Mailley, J. Electrochem. Soc., 2009, 156, B410 CrossRef CAS.
- A. A. Franco, R. Coulon, R. Ferreira de Morais, S.-K. Cheah, A. Kachmar and M. A. Gabriel, ECS Trans., 2009, 25(1), 65 Search PubMed.
- A. A. Franco, M. Guinard, B. Barthe and O. Lemaire, Electrochim. Acta, 2009, 54(22), 5267 CrossRef CAS.
- A. A. Franco and M. Gerard, J. Electrochem. Soc., 2008, 155(4), B367 CrossRef CAS.
- A. A. Franco and M. Tembely, J. Electrochem. Soc., 2007, 154(7), B712 CrossRef CAS.
- A. A. Franco, in Encyclopedia of Applied Electrochemistry: SpringerReference, ed. R. Savinell, K. Ota and G. Kreysa, Springer-Verlag, Berlin Heidelberg, 2013, DOI:10.1007/SpringerReference_303780.
- D. Damasceno Borges, K. Malek, S. Mossa, G. Gebel and A. A. Franco, ECS Trans., 2013, 45(23), 101 Search PubMed.
- M. Combes, B. Buin, M. Parenthoên and J. Tisseau, Proc. Comput. Sci., 2012, 1, 761 Search PubMed.
- A. A. Franco, W. G. Bessler and M. L. Doublet, ed., Multiscale modelling and numerical simulation of electrochemical devices for energy conversion and storage, Springer, 2013, in preparation Search PubMed.
- A. A. Franco Ed., Rechargeable lithium batteries: from fundamentals to applications, Woodhead (UK), 2013, in preparation Search PubMed.
- A. A. Franco, modelling of Direct Alcohol Fuel Cells, book chapter in: Direct Alcohol Fuel Cells Technologies: research and development, ed. E. Gonzalez and H. Corti, Springer, in press, 2013 Search PubMed.
| This journal is © The Royal Society of Chemistry 2013 |