Doping and thermoelectric properties of the zero-dimensional inorganic halide perovskite derivative, Cs₃Cu₂I₅

Abstract

Halide perovskites have been considered as promising thermoelectric materials due to their unusual combination of good charge mobility and ultralow thermal conductivity. Low dimensional halide perovskite derivatives (0D, 1D and 2D) have been predicted to have high thermoelectric figure of merit due to quantum confinement effects, but this class of metal halides has been under-explored experimentally. Here, we investigate the thermoelectric properties of the all-inorganic 0D halide perovskite, Cs₃Cu₂I₅, doped with barium. Ba-doped pellets were fabricated by solid state synthesis. An enhancement of electrical conductivity by >3 orders of magnitude was achieved upon doping and extended X-ray absorption fine structure measurements indicate that Ba substituted Cs on the smaller of the two A-sites. We show that thermal conductivity is in the ultralow regime and decreases with doping, consistent with increased scattering from defects. The positive Seebeck coefficient of +2400 ± 60 μV K⁻¹ for Cs₃Cu_2(1−x)Ba_xI₅ (x = 0.1) confirmed p-type doping. To our knowledge, this is the first study on substitutional doping of a 0D halide perovskite to improve the thermoelectric figure of merit.

---

Introduction

Halide perovskites are well established theoretically and experimentally for optoelectronic applications, memristors, radiation detectors and scintillators. They have gained increasing attention as thermoelectric materials owing to a unique combination of high charge carrier mobility and diffusion length, high Seebeck coefficient and ultralow thermal conductivities.^1–3 The principal reasons for ultralow thermal conductivity are generally cited as the scattering of the phonons by rotational modes of the A-site cation, cluster rattling mechanisms, low elastic stiffness and strong anharmonicity.^4–7 However, their relatively low electrical conductivities compared to conventional thermoelectric materials have highlighted the need to develop new doping strategies such as chemical doping, photo-induced doping and self-doping. Chemical doping of CH₃NH₃PbI₃ and photo-induced doping of CH₃NH₃SnI₃ have been shown to improve the thermoelectric figure of merit, zT, by more than two orders of magnitude.³ Substitutional doping of CH₃NH₃PbBr₃ with Bi was shown to increase electrical conductivity by more than three orders of magnitude.⁸ CH₃NH₃SnI₃ perovskites with high conductivity resulting from the self-doping process of Sn²⁺ to Sn⁴⁺ in were reported by Takahashi et al.,⁹ and a similar effect in CsSnI₃ films resulted in electrical conductivity >100 S cm⁻¹ and zT = 0.14 ± 0.01.¹⁰ Stoichiometry adjustment in the copper based perovskite C₆H₄NH₂CuBr₂I enabled carrier concentrations of ∼10²⁰ cm⁻³, extremely high power factor up to 1.9 mV m⁻² K⁻¹, electrical conductivity ∼3.6 × 10³ S cm⁻¹ and zT value of 0.14 (at RT).¹¹ The highest reported zT in this class of materials is 0.19 (at room temperature), achieved with charge transfer doping of (NH₂CHNH₂)SnI₃ films using the molecular dopant 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ).¹²

Compared to organic–inorganic perovskites, fully inorganic halide perovskites are expected to have higher stability due to the lack of volatile and weakly bonded organic molecules as well as a lack of near room temperature phase transitions.^13–15 Another consideration is the toxicity of lead,¹⁶ which is widely used in halide perovskites for optoelectronic applications,¹⁷ but would need to be replaced in halide perovskite thermoelectric devices for them to be viable. Sn²⁺ and Ge²⁺ are alternatives to Pb²⁺ cations in halide perovskites as they have similar ionic radii. However, the oxidation of Sn²⁺ and Ge²⁺ to Sn⁴⁺ and Ge⁴⁺ causes instability, limiting the use of these materials in optoelectronic devices such as solar cells.¹⁸ On the other hand, oxidative instability can generate free charge carriers and increase electrical conductivity and has been exploited to optimise the thermoelectric properties of these materials.⁴

Low dimensional halide perovskite derivatives are sub-classes of halide perovskites which exhibit a confinement on the crystal lattice level which breaks the 3D metal halide lattice into 2D sheets, 1D wires or 0D clusters.¹⁹ Low dimensional halide perovskites derivatives have shown excellent electronic and optical properties due to quantum confinement effects and anisotropic properties.²⁰ They exhibit good charge transport as well as lower thermal conductivity and better chemical and thermal stabilities than 3D analogues making them interesting for thermoelectrics.²¹ In hybrid halide perovskites, 0D [Mn(C₂H₆OS)₆]I₄ and (CH₃NH₃)₃Bi₂I₉ have been reported to have ultralow thermal conductivities of 0.15 W m⁻¹ K⁻¹ (ref. 22) and 0.23 ± 0.02 W m⁻¹ K⁻¹,²³ respectively. A large high Seebeck coefficient of +2.6 mV K⁻¹ was reported for 0D (CH₃NH₃)₃Bi₂I₉ (ref. 24) as well as exceptionally high non-Seebeck thermal voltages of >40 mV K⁻¹.²⁵ The thermal conductivity of the OD all inorganic halide perovskite derivative, Cs₄PbCl₆,²⁶ was shown to be lower (0.30 W m⁻¹ K⁻¹) than derivatives with higher dimensionalities (3D Cs₄PbCl₆ and 2D CsPb₂Cl₅).²⁶

Cs₃Cu₂X₅ (X: I, Cl, Br) 0D halide perovskite derivatives, the subject of this work, are well established theoretically and experimentally for optoelectronic applications such as light-emitting diodes (LEDs),^13,27–32 photodetectors,³³ memristors,³⁴ radiation detectors³⁵ and scintillators³⁶ as well as nuclear batteries³⁷ consisting of a scintillator and a photovoltaic device. A computational study on thermoelectric properties of Cs₃Cu₂I₅ predicted ultralow thermal conductivity, high power factor and a remarkably high zT value of 2.6.³⁸ This is in line with the state-of-the-art exhibited by SnSe³⁹ and PbTe⁴⁰ based materials, but without the toxicity concerns of Pb and, to a lesser extent, Se, and the heavy regulation of Pb-usage.

Cs₃Cu₂I₅ has an orthorhombic crystal structure in the Pnma space group with two distinct Cu⁺ cations where Cu1 resides in a cluster with trigonal planar geometry, ([CuI₃]²⁻), whilst Cu2 binds to four I⁻ in distorted tetrahedral geometry ([CuI₄]³⁻), as shown in Fig. 1.^28,42–44 In general, low dimensionality features of copper-based metal halides come from the smaller dispersion of the valence band maximum (VBM) of CuX that consists of Cu 3d and halogen p orbitals.³⁸ The upper valence band of Cs₃Cu₂I₅ consists of Cu 3d and I 5p orbitals, whilst Cu 4s and I 5s orbitals dominate the lower conduction band. In this structure, Cs⁺ neither contributes directly to the VBM nor to the CBM, acting instead to separate the copper iodide clusters and maintain charge balance.²⁸ Room temperature electron mobility in Cs₃Cu₂I₅ has been calculated previously as 18.2 cm² V⁻¹ s⁻¹,³⁸ whilst hole mobility has been measured to be a bit lower than the electron mobility.⁴⁵ The lower hole mobility is most likely because the valence band maximum is highly localised on the Cu sites, whereas the conduction band maximum is spread over Cu and I sites.⁴⁶

Fig. 1 Crystal structure of Cs₃Cu₂I₅. Reprinted with permission.⁴¹ ©2022 American Chemical Society.

Here, we report the thermoelectric properties of 0D Ba-doped Cs₃Cu₂I₅ pellets that are synthesized via a room temperature mechanical grinding method.⁴⁷ Ba is incorporated into the crystal lattice without any significant distortions. The substitution of Cs with Ba with an increasing feed ratio (%) enhanced the electrical conductivity by ∼3 orders of magnitude, and the location of Ba substitution on the lattice is established by extended X-ray absorption fine structure studies. Thermal conductivity was in the ultralow regime and decreased further with an increasing doping concentration. The positive Seebeck coefficient of Cs₃Cu_2(1−x)Ba_xI₅ (x = 0.1) confirmed p-type doping with a value of 2.40 ± 0.06 mV K⁻¹ at room temperature.

Experimental

Materials

Cesium iodide (≥99.9%) and barium iodide (≥99.9%) were purchased from Alfa Aesar™ and cuprous iodide (≥99.9%) was purchased from ACROS Organics™. All precursor materials were opened in a nitrogen glovebox and stored there. All precursors were used as received without any further purification.

Fabrication of pellets

Cs₃Cu_2(1−x)Ba_xI₅ was prepared by a solid state reaction according to previous work⁴⁷ with some modifications. For the synthesis of undoped Cs₃Cu₂I₅, 3 mmol CsI and 2 mmol CuI were mixed and ground for 45 min in an agate mortar. For doped Cs₃Cu_2(1−x)Ba_xI₅, CsI (3 mmol), CuI and BaI₂ were mixed in the desired stoichiometric ratio and ground for a longer time (60 min) to prevent any by-products such as CsCu₂I₃ forming.⁴⁷ Subsequently, materials were cold pressed with an Atlas™ Series Autotouch Automatic Hydraulic Press (Specac Ltd) at 4 tonnes or 5 minutes. All synthetic procedures were carried out in an N₂ environment, and the pellets were pressed in a 13 mm diameter evacuable pellet die that had been loaded in an N₂ environment. Fabricated pellets were 13 mm in diameter and had suitable thicknesses (1.43–1.99 mm) for measuring thermoelectric properties. Our labelling is the nominal degree of doping based on the amount of Ba used in the synthesis place of Cu. Fabricated pellets were stored and transported in inert atmosphere before being exposed to air during electrical and thermal measurements. No degradation in properties was observed over the timescale of the measurement.

X-ray diffraction (XRD)

XRD patterns of powders were recorded on a D5000 X-ray powder diffractometer (Siemens) using Cu-K_α radiation and a Ni-filter. The diffraction patterns were collected at room temperature over a 2θ range of 5–70°.

X-ray photoelectron spectroscopy (XPS)

XPS measurements were performed on freshly synthesized powders with a Thermo Scientific™ Nexsa™ Surface Analysis System. Thermo Avantage software was used for the recording and analysis of all XPS spectra.

DFT calculations

Periodic ab initio quantum mechanical calculations were carried out with density functional theory (DFT) using the PWscf package in the Quantum Espresso 6.7 suite.^48–50 Ready-to-use PBEsol pseudopotentials were selected from the standard solid-state pseudopotentials (SSSP) library.^51,52 Energy cutoffs of 55 Ry and 440 Ry were used for wavefunctions and charge density, respectively. A fully relaxed 1 × 2 × 1 Cs₃Cu₂I₅ supercell was used as starting point for defective systems comparison. Structure relaxations and single-point calculations were carried out on G-centered Monkhorst–Pack (MP) grids with a k-point distance of 0.3 and 0.2 Å, respectively. The convergence threshold criteria are as follows: 10⁻⁶ atomic units (a.u.) for electronic structure, 10⁻⁴ a.u. for total energy, 10⁻³ a.u. for forces, and 0.5 kbar for pressure. To evaluate the defect formation energy in the doped structure, full relaxation and single point energy calculations of bulk Cs, Cu, Ba, CsI, CuI and BaI₂ were first carried out at the same level of theory of Cs₃Cu₂I₅. Then, the appropriate chemical potential of each element was chosen as to ensure the stability of Ba doped-Cs₃Cu₂I₅ against precipitation of elemental phases (i.e., Cs, Cu, Ba and I₂) and secondary phases (i.e., BaI₂, CsI and CuI).

Extended X-ray absorption fine structure (EXAFS)

X-ray absorption spectroscopy experiments were performed at the BM8 beamline of the European Synchrotron Radiation Facility on Cs₃Cu_2(1−x)Ba_xI₅ samples with different doping concentrations (x = 0.05 and 0.1) at the Ba K-edge. BaI₂ was also measured as a reference. The samples were prepared as pellets. Powders (9–15 mg) were mixed with cellulose binder (<100 mg) in air, and then cold pressed in an Atlas™ Series Manual Hydraulic Press under 5 T for 10 minutes. Ba K-edge spectra were acquired in fluorescence mode using a multielement energy-resolving detector. Samples were kept at 80 K using a liquid nitrogen cryostat. All data reduction and analysis was performed with Viper⁵³ using theoretical amplitudes and phase shifts generated with the FEFF9 code.⁵⁴ Even if special precautions were taken for EXAFS (i.e. the pellet was kept in the liquid nitrogen cryostat at 80 K under vacuum before the measurements), sample degradation as a result of X-ray irradiation, combined with air exposure during, may explain the presence of non-negligible Ba–O contributions in all samples. This was visible in all samples as a Ba–O signal at 2.75 Å but was easily distinguished from Ba–I signals that occur at distances >3.5 Å. Nonetheless, Cs₃Cu_2(1−x)Ba_xI₅ samples showed Ba–I distances (3.56 Å and 4.10 Å when x = 0.1) that were distinct from Ba–I distances in BaI₂ (3.5–3.67 Å). The footprint of the beam was also evident in the pellet after the measurements, hinting to a beam-induced surface degradation. For this reason, shorter measurements were acquired on 16 different points on the pellet, and eventually averaged. No further improvements on the data quality are arguably achievable on this system since: (a) both higher photon flux or longer measurements are bound to result in higher beam damage; (b) fluorescence counts on the detector are saturated by iodine fluorescence lines, which are much more intense than barium ones because of stoichiometry. For these reasons, while the evidence presented in this manuscript on Ba²⁺ chemical environment is limited, it is arguably the best that can be achieved using X-ray absorption spectroscopy.

Electrical conductivity measurement

Two-point electrical resistance measurements were performed using a C-Series Analytical Probe Station (Lambda Photometrics Ltd) with a Keithley 2636B Source Measure Unit. A two-point method was used instead of a 4-point method because of the high resistance of the samples. Contacts were formed by applying 5 mm × 5 mm of silver paste on the two opposite surfaces of the pellet. The contact configuration and experimental apparatus are depicted in Fig. S2 (ESI†). The electrical conductance was obtained by fitting the linear region of a current–voltage (I–V) curve. During the measurement, the sample was kept in ambient atmosphere at room temperature and in a dark environment. The error bars denote standard errors of three data points for each doping concentrations.

Thermal conductivity

The thermal conductivities (κ) of the pellets were calculated from κ = DC_pρ, where D is the thermal diffusivity, C_p is the specific heat capacity and ρ is the density. For D measurement (Fig. S4†), Cs₃Cu_2(1−x)Ba_xI₅ pellets were coated with graphite on both sides for prevention of any reflection and transmission of the incident laser pulse to the detector. Thermal diffusivity was measured (Netzsch 453 LFA) along the short (∼1 mm) pellet dimension with a 13 × 13 mm holder using a laser voltage of 1730 V. The raw data were analysed using a Cowan model with pulse correction. The specific heat capacities of the pellets were measured using differential scanning calorimetry (DSC 25, TA Instruments) between 20 °C and 80 °C and the density of pellets were determined using Archimedes' principle (Fig. S1 and Table S1†).

Seebeck coefficient

The Seebeck coefficient was measured using SB1000 Seebeck Measurement System with integrated K20 Programmable Temperature Controller (MMR Technologies Inc.), in the temperature range 293 K to 353 K under a vacuum of 10⁻⁵ mbar in complete darkness. Ba-doped Cs₃Cu₂I₅ pellets were cut into smaller pieces (∼1 mm width). The reference sample and pellet were mounted onto the sample holder using silver paste, as shown in Fig. S3.†

Photoelectron yield spectroscopy in air (PYSA)

The ionization potential of the pristine Cs₃Cu₂I₅ pellet was determined by photoelectron yield spectroscopy in air using (PYSA) using a Riken Keiki spectrophotometer (Japan) model AC-2. The conditions employed during the measurements were a scanning energy range from 4.30 to 6.20 eV with a measurement interval of 0.05 eV, an integration time of 10 s and an ultraviolet spot intensity of 50 nW. The resolution of the instrument is 10 meV and the incident ultraviolet spectrum is calibrated against a standard photodiode.

Results and discussion

Solid state reactions such as mechanochemical synthesis are induced by mechanical energy from grinding or milling of solid reactants and eliminate the need for solvents, which have economic and environmental benefits.^55,56 Cation doping in halide perovskite derivatives can be challenging when low chemical activity of the dopant ions during synthesis results in low incorporation into the structure as compared to the feed ratio.^47,57–59 On the other hand, the driving force of solid-state reactions is more significant than driving forces in solution synthesis due to the higher chemical potential¹⁹ and might be advantageous for cation doping. Recently, Mn was successfully doped into Cs₃Cu₂I₅ by a solid-state grinding method, with undoped Cs₃Cu₂I₅ and Mn-doped Cs₃Cu₂I₅ showing similar lattice structure.⁴⁷

The XRD spectra (Fig. 2) of doped and pristine Cs₃Cu_2(1−x)Ba_xI₅ show consistency with standard data (JCPDS: 45-0077). Peaks of CuI, that might be present either due to incomplete incorporation of precursors during synthesis or precipitation due Ba incorporation, were not observed in the spectra. Rietveld refinement (Fig. S6–S10 and Table S2†) confirms this, but detects CsI contributions that increase with Ba-doping. This would point to a precipitation of CsI to maintain charge balance upon doping with BaI₂. We explore this possibility with EXAFS measurements and DFT calculations, vide infra. 1D CsCu₂I₃ was also identified in all samples by the Rietveld refinement, but only in small quantities (<3 w/w%). A small shift of the XRD peaks towards higher 2θ angles, as shown in Fig. 2(b), was detected upon doping. A lattice contraction might be due to the change in the lattice parameters by the introduction of vacancies on anion site.³⁷ Alternatively, ionic radius differences between Ba²⁺ (135 pm) and Cs⁺ (178 pm) could explain the contraction if the Ba²⁺ dopes onto a Cs⁺ site rather than a Cu⁺ (radius 74 pm) site.^37,59,60 However, Rietveld refinement (see ESI†) indicates that peak shifts upon doping are mostly due to sample displacement in the vertical axis during measurement and not significant changes in lattice parameter.

Fig. 2 (a) Powder XRD patterns of pristine and Ba doped Cs₃Cu₂I₅. Diffraction peaks located at 13.1°, 15.2°, 24.1°, 25.6°, 26.4°, 27.1°, 28.2°, 30.7° and 47.8° correspond to the (111), (002), (122), (312), (222), (130), (131), (313) and (152) planes, respectively. (b) Is shows the principal peaks in the 25–27.5° region in more detail.

X-ray photoelectron spectroscopy (XPS) survey spectra confirm the presence of Cs, Cu, I and Ba in the pellets (Fig. 3(a)). There is an oxygen signal at ∼535.3 eV and a carbon signal at ∼288.7 eV. These binding energies point to adventitious hydrocarbons being present (including C–O; O–C=O etc. groups) i.e. the Ar⁺ clean didn't remove all of the adventitious hydrocarbons. High-resolution XPS spectra of the Cu 2p peak with various Ba feed ratios are shown in Fig. 3(b). We assign the peaks at ∼931.5 eV for 2p_3/2 and ∼951.5 eV for 2p_1/2 to Cu⁺.⁶¹ No peaks were observed at 932 eV or 952 eV, the linewidth is narrow, and there are no significant satellites, which confirms that Cu⁺ is not oxidized to Cu²⁺. Fig. 3(c) shows high resolution XPS spectra of the I 3d peaks at different doping concentrations. Peaks at ∼619 eV and ∼630 eV are assigned to I 3d_5/2 and I 3d_3/2, respectively, and there is a small shift towards higher binding energy with an increasing Ba concentration. If Cu is substituted by Ba, the shift of I might be due to the higher bond dissociation energy of Ba–I (>431 kJ mol⁻¹) than Cu–I bonds (197 kJ mol⁻¹).⁶² The slightly positive charge on Cu leads to higher binding energy in XPS. On the other hand, unlike Cu–I chemical bonding, Cs–I bonds are weak physical bonds which are likely van der Waals type bonds which are typical for interactions between atoms 3 to 6 Å apart.⁶³ In Cs₃Cu₂I₅, the two distinct Cs⁺ ions bond with I⁻ in different coordination geometries; in the first site Cs⁺ is bonded to eight I⁻ and the bond distance is between 3.78 and 4.03 Å, whereas, in the second site, Cs⁺ is bonded to nine I⁻ and the bond distance is in the range of 3.91–4.37 Å.^43,44 Thus, it is difficult to know if the I 3d shift would be due to Ba on a Cs⁺ or Cu⁺ site because of the large number of bonds involved. The Ba 3d binding energies (Fig. 3) are consistent with previous work on Ba incorporated in CsPbI₃.⁶⁴ However, no further insights are gained on the structure. We therefore need to use other techniques to explore the local structure of barium in Cs₃Cu_(2−x)Ba_xI₅.

Fig. 3 Structural characterization of Cs₃Cu_2(1−x)Ba_xI₅ via XPS. (a) XPS survey spectra of a 10% Ba doped pellet, (b) Cu 2p and (c) I 3d spectra in pellets with different dopant concentrations.

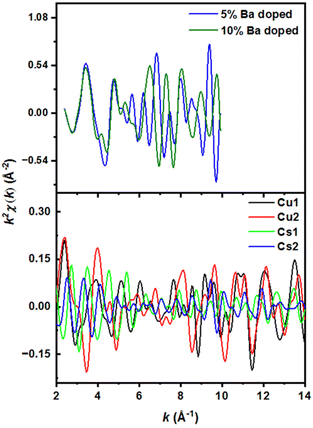
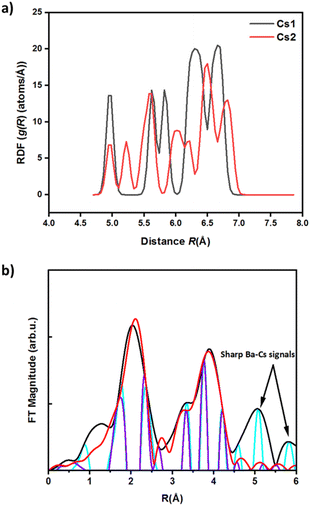
Although XPS has revealed binding energy differences between the undoped and doped material, the nonequivalent crystallographic positions of the dopant atoms and their distribution among these positions cannot be determined directly by XRD or XPS alone. The local structure and coordination of barium in Cs₃Cu_2(1−x)Ba_xI₅ pellets was therefore studied by extended X-ray absorption fine structure (EXAFS) using signal from the barium K-edge. Smoothed EXAFS spectra of 5% and 10% Ba-doped Cs₃Cu_2(1−x)Ba_xI₅ samples are shown in Fig. 4 (upper panel). The lower panel of Fig. 4 shows the simulated EXAFS spectra at the Ba K-edge for a barium atom placed in different Cu and Cs sites. Theoretically, the substitution of Cu⁺ with Ba²⁺ would imply Ba–I distances between 2.5 Å and 2.8 Å, yet there is no reported Ba–I bond distance below 3.3 Å in the literature.^65,66 Our DFT calculations show that the Cs₃Cu₂I₅ crystal structure contains two different crystallographic sites for cesium where the Cs1 site has a much smaller polyhedral volume (100.7089 ų) than Cs2 (133.2977 ų) (Fig. 6). Such a difference in volume is due to the lower average Cs–I bond length of Cs1 site (3.84 Å vs. 4.08 Å for Cs2), and the lower effective coordination number of Cs1 (7.87 vs. 8.54 for Cs2).

Fig. 4 (Top panel) Smoothed EXAFS experimental spectra at the Ba K-edge of 5% and 10% doped samples analysis of Cs₃Cu_2(1−x)Ba_xI₅. (Bottom panel) Simulated EXAFS data of first-shell signals for a Ba atom placed in different cations sites of the Cs₃Cu₂I₅ structure.

The distribution of selected atomic distances around the Cs sites is shown in Fig. 5(a). By comparing the Cs–X distances (with X being a heavy atom) around the two different Cs sites, it is evident that the smaller Cs site (Cs1) shows sharper Cs–X distance distribution in the range between 4 and 7 Å, which is more consistent with the recorded spectra.

Fig. 5 (a) Radial distribution function (RDF) of Cs–Cs and Cs–I interatomic distances around the Cs1 and Cs2 sites, between 4.5 and 7 Å. Cs–Cu distances are not included for clarity. (b) Fourier-transformed (FT) EXAFS data of 10% Ba-doped Cs₃Cu₂I₅ (black) and a calculated first shell fit (red).

Fig. 6 DFT simulations of Ba doped Cs₃Cu₂I₅ on different Cs sites. (a) DFT simulation of Ba doped Cs₃Cu₂I₅ The Cs–I polyhedra around the Cs1 site have been shaded green. (b) DFT simulation of Ba doped Cs₃Cu₂I₅. The Cs–I polyhedral around the Cs2 site have been shaded green.

To further corroborate such a dopant localization, DFT simulated Ba-doped Cs₃Cu₂I₅ structures were computed by substituting Ba²⁺ at each of the two possible Cs⁺ sites (i.e. in Kroger–Vink notation, creating 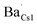and 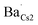defects), respectively. The total energy is lower (∼0.22 eV) when Ba²⁺ is placed in the smaller site (Cs1). To sum up, the bond lengths of the shells in the EXAFS data are more consistent with Ba sitting on one of the Cs sites, with both the EXAFS data and the DFT simulations indicating that the smaller Cs1 site is preferred, consistent with a previous computational study³⁸

If Ba²⁺ resides in the Cs1 site, there are three possible ionic compensation mechanisms (not involving valence changes, excluded by all experimental evidence):

(3) can be ruled out due to steric hindrance considerations. The formation energies for the systems described in (1) and (2) are very similar: 1.33 eV and 1.17 eV respectively. is slightly preferred, though it cannot be excluded that mechanism (1) also occurs. Our Rietveld refinement of the XRD data (Table S2†) shows no precipitation of CuI, which rules out compensation mechanism of (2) by itself. However, CsI precipitation in quantities less than the feed ratio of BaI₂ was observed. This indicates that mechanism (1) could be occurring, but not in isolation as this would result in CsI precipitation in quantities greater than the Ba incorporation. Our experimental evidence, therefore points to (1) and (2) both occurring. For example, if (2) occurred with double the frequency of (1), the precipitated CuI from (2) could react with the precipitated CsI from (1) and (2) to form Cs₃Cu₂I₅. This would leave residual CsI at about a third of the concentration of incorporated Ba – not far off what we observe.

We note that substitution on the Cs sites might point to Cs_3(1−x)Ba_xCu₂I₅ being a more logical stoichiometry. However, we found that Cs_3(1−x)Ba_xCu₂I₅ showed similar electrical properties to Cs₃Cu_2(1−x)Ba_xI₅ so we didn't pursue the Cs_3(1−x)Ba_xCu₂I₅ stoichiometry further.

The ionisation energy obtained from PYSA on the undoped pellet was 5.31 ± 0.02 eV. This value is comparable, albeit slightly lower than the previously reported valence band maximum of 5.65 eV,³³ though that was recorded by ultraviolet photoelectron spectroscopy (UPS) in high vacuum on thin films. Adsorbates from the atmosphere tend to reduce work functions in air through the push-back effect on electrons near the surface of the material under study.

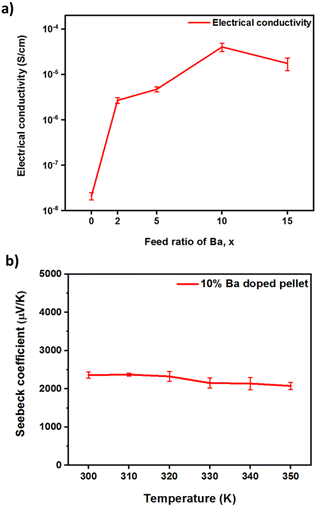
The thermal diffusivity (D, Fig. S4(a)†) of Ba-doped pellets is between 0.19 and 0.40 mm² s⁻¹ at room temperature and decreases with both increasing temperature and increasing doping. With increasing temperature, the internal energy also rises (due to the vibrational and rotational energies) and, therefore, so does the heat capacity (C_p, Fig. S4(b)†). However, doping doesn't have a large effect on C_p or ρ (Fig. S4 and Table S1†), noting that our values for ρ are comparable with the values obtained for Cs₃Cu₂I₅ nanocrystals⁶⁷ and single crystals³⁵ indicating a high density of our pellets. Doping decreases the thermal conductivity substantially (Fig. 7), which might be due to phonon scattering off the Ba point defects, small lattice distortions to incorporate Ba, or other defects introduced by the doping process such as copper vacancies. Overall, the thermal conductivities of pristine and Ba-doped pellets are in the ultralow regime, between 0.19 and 0.40 W m⁻¹ K⁻¹. The ultralow thermal conductivities might be due to the ultralow group velocities,²³ weak bonds and soft phonon dispersions,²⁴ which are typical for halide perovskites and their derivatives. At high doping concentrations the thermal conductivity is <0.2 W m⁻¹ K⁻¹ at room temperature, a reduction of ∼50% from the pristine value. This is also lower than doped 3D halide perovskites (e.g. ∼0.33 W m⁻¹ K⁻¹ for Bi-doped MAPbBr₃ single crystals⁸), but not as low as predicted for Cs₃Cu₂I₅ (<0.1 W m⁻¹ K⁻¹) by a computational study.³⁸

Fig. 7 Temperature-dependent thermal conductivity (κ) of pristine and Ba-doped Cs₃Cu₂I₅ pellets.

Electrical conductivity, σ, increases from 2.1 × 10⁻⁸ S cm⁻¹ for non-doped pellets to 4.1 × 10⁻⁵ S cm⁻¹ for 10% Ba-doped Cs₃Cu_2(1−x)Ba_xI₅, a difference of >3 orders of magnitude (Fig. 8(a)). The positive sign of the Seebeck coefficient in 10% Ba-doped Cs₃Cu_2(1−x)Ba_xI₅ (Fig. 8(b)) confirms that holes are the majority charge carriers. This is contrary to predictions of a shallow donor level supporting n-type doping for Ba_Cs⁺ defects.³⁸ This is probably a further indication that doping substitutes Ba atoms onto Cs sites as well as generating other defects such as the copper vacancies predicted by our DFT calculations, which are known to be a source of positive charge carriers in cuprous iodide.⁶⁸ From the low electrical conductivity it is likely that only a low density of free charges are created, perhaps due to ionic compensation of Ba_Cs⁺ defects.⁶⁹ Indeed, the charge mobility is expected to be up to 18 cm² V⁻¹ s⁻¹ for electrons, though slightly lower for holes due to the valence band maximum being highly localized on the Cu sites, whereas the conduction band minimum is spread across Cu and I sites.^38,46 The large S value (2400 ± 60 μV K⁻¹ at 293 K) arises in part due to the low carrier density but can also come from the large band gap and low dimensional character. The Goldschmidt relation E_g > 2e|S_max|T_max links the Seebeck coefficient to the bandgap. The direct bandgap of Cs₃Cu₂I₅ (3.82 eV,³⁸ and 3.98 eV for pristine pellet from our measurement) is large and the Goldschmidt relation predicts |S_max| ≈ 6 mV K⁻¹ in this material. The reduced dimensionality in Cs₃Cu₂I₅ is known to result in wave function localization of electrons and holes, larger bandgap, more discrete states, and could increase the sharpness of the density of states (dg(E)/dE) at the Fermi Level (E_F) which results in enhanced Seebeck coefficient according to the Cutler and Mott equation.⁷⁰ The obtained S value is comparable to the value obtained with 0D (CH₃NH₃)₃Bi₂I₉ (2600 ± 200 μV K⁻¹).²⁴ However, it is much larger than reported in 3D halide perovskites such as MAPbI₃ (∼920 μV K⁻¹, at room temperature [RT]),⁷¹ MAPb_0.85Bi_0.15Br₃ (378 μV K⁻¹ at RT),⁸ and CsSnBr₃ (325 μV K⁻¹ at RT).⁷²

Fig. 8 Electrical conductivity and Seebeck coefficient of pristine and Ba-doped Cs₃Cu₂I₅ pellets. (a) Electrical conductivity. (b) Temperature-dependent Seebeck coefficient of 10% Ba-doped Cs₃Cu₂I₅ pellets.

Conclusions

In summary, the substitutional doping of Cs₃Cu₂I₅ with barium and its effect on thermoelectric properties was studied. Structural analysis showed that introduction of barium leads to a lattice distortion, whilst XAFS data combined with ab initio calculations indicates that Ba²⁺ resides preferentially in the smaller Cs⁺ site (Cs1). Ba improved the electrical conductivity of the 0D perovskite derivative by >3 orders of magnitude and a large positive Seebeck coefficient was observed (+2400 ± 60 μV K⁻¹ at RT and 10% Ba), indicating p-type doping. The thermal conductivities of pristine and Ba-doped pellets are ultralow between 0.19 and 0.40 W m⁻¹ K⁻¹ and decrease with increasing dopant concentrations. zT, however, remains low (2.2 ± 0.3 × 10⁻⁵ at RT) despite a computational study on Cs₃Cu₂I₅ (ref. 38) predicting a maximum zT for Cs₃Cu₂I₅ of 2.57 at 600 K. This was in part because κ in our doped pellets was larger than the computational work predicted (<0.1 W m⁻¹ K⁻¹). However, the main difference is due to larger predicted electrical conductivities of 3.5–2.3 × 10⁴ S m⁻¹ enabled by carrier concentrations of 10¹⁶ to 10²⁰ cm⁻³ and a high dispersion of the conduction band. In our work, we found experimentally that the substitution of Ba²⁺ onto the Cs1 site is favourable, but actually delivers Cu vacancies and weak p-type doping. Therefore, a lower dispersion of the valence band may be reducing charge mobility, whilst ionic compensation of defects is likely to be suppressing free charge carrier density, the combination of which reduces the electrical conductivity drastically. However, this is nonetheless the first study where full zT measurements have been reported for a low dimensional halide perovskite. The substitution of Ba²⁺ onto the Cs1 site has been well established in our work, and the high Seebeck coefficient in combination with ultralow thermal conductivity of this material gives hope for high zT in the future if the electrical conductivity can be improved through an increase in doping efficiency.

Data availability

Data are available upon request from the authors.

Author contributions

The manuscript was written through contributions of all authors. The synthesis and structural characterization (except EXAFS) was performed by CA. Thermoelectric property measurement was performed by CA, ESSG, SL, MR and KC. PESA measurement was performed by GR and PS. The DFT simulations were done by CP and AM. The EXAFS analysis of Cs₃Cu_2(1−x)Ba_xI₅ was done by FG and CP. The project was supervised by OF.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was primarily financed under OF's Royal Society University Research Fellowship (UF140372 and URF/R/201013) and by the EPSRC (project EP/Y008405/1). The authors acknowledge the CERIC-ERIC Consortium for the access to experimental facilities and financial support and thank the staff of beamline BM8 at the ESRF for technical support.

Notes and references

1. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
2. Y. He and G. Galli, Chem. Mater., 2014, 26, 5394–5400.
3. X. Mettan, R. Pisoni, P. Matus, A. Pisoni, J. Jaćimović, B. Náfrádi, M. Spina, D. Pavuna, L. Forró and E. Horváth, J. Phys. Chem. C, 2015, 119, 11506–11510.
4. W. Lee, H. Li, A. B. Wong, D. Zhang, M. Lai, Y. Yu, Q. Kong, E. Lin, J. J. Urban, J. C. Grossman and P. Yang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8693–8697.
5. T. Liu, S.-Y. Yue, S. Ratnasingham, T. Degousée, P. Varsini, J. Briscoe, M. A. McLachlan, M. Hu and O. Fenwick, ACS Appl. Mater. Interfaces, 2019, 11, 47507–47515.
6. X. Wang, Y. Zhao, S. Zeng, Z. Wang, Y. Chen and J. Ni, Phys. Rev. B, 2022, 105, 014310.
7. X. Qian, X. Gu and R. Yang, Appl. Phys. Lett., 2016, 108, 063902.
8. W. Tang, J. Zhang, S. Ratnasingham, F. Liscio, K. Chen, T. Liu, K. Wan, E. S. Galindez, E. Bilotti, M. Reece, M. Baxendale, S. Milita, M. A. McLachlan, L. Su and O. Fenwick, J. Mater. Chem. A, 2020, 8, 13594–13599.
9. Y. Takahashi, H. Hasegawa, Y. Takahashi and T. Inabe, J. Solid State Chem., 2013, 205, 39–43.
10. T. Liu, X. Zhao, J. Li, Z. Liu, F. Liscio, S. Milita, B. C. Schroeder and O. Fenwick, Nat. Commun., 2019, 10, 5750.
11. Y. Liu, X. Li, J. Wang, L. Xu and B. Hu, J. Mater. Chem. A, 2017, 5, 13834–13841.
12. L. Zheng, T. Zhu, Y. Li, H. Wu, C. Yi, J. Zhu and X. Gong, J. Mater. Chem. A, 2020, 8, 25431–25442.
13. R. Roccanova, A. Yangui, H. Nhalil, H. Shi, M.-H. Du and B. Saparov, ACS Appl. Electron. Mater., 2019, 1, 269–274.
14. Y. Zhou and Y. Zhao, Energy Environ. Sci., 2019, 12, 1495–1511.
15. D. Li, P. Liao, X. Shai, W. Huang, S. Liu, H. Li, Y. Shen and M. Wang, RSC Adv., 2016, 6, 89356–89366.
16. J. Li, J. Duan, X. Yang, Y. Duan, P. Yang and Q. Tang, Nano Energy, 2021, 80, 105526.
17. R. Kour, S. Arya, S. Verma, J. Gupta, P. Bandhoria, V. Bharti, R. Datt and V. Gupta, Global Challenges, 2019, 3, 1900050.
18. I. López-Fernández, D. Valli, C.-Y. Wang, S. Samanta, T. Okamoto, Y.-T. Huang, K. Sun, Y. Liu, V. S. Chirvony, A. Patra, J. Zito, L. De Trizio, D. Gaur, H.-T. Sun, Z. Xia, X. Li, H. Zeng, I. Mora-Seró, N. Pradhan, J. P. Martínez-Pastor, P. Müller-Buschbaum, V. Biju, T. Debnath, M. Saliba, E. Debroye, R. L. Z. Hoye, I. Infante, L. Manna and L. Polavarapu, Adv. Funct. Mater., 2024, 34, 2307896.
19. V. Trifiletti, C. Asker, G. Tseberlidis, S. Riva, K. Zhao, W. Tang, S. Binetti and O. Fenwick, Frontiers in Electronics, 2021, 2, 758603.
20. L. Mino, G. Agostini, E. Borfecchia, D. Gianolio, A. Piovano, E. Gallo and C. Lamberti, J. Phys. D: Appl. Phys., 2013, 46, 423001.
21. C. Pipitone, S. Boldrini, A. Ferrario, G. Garcìa-Espejo, A. Guagliardi, N. Masciocchi, A. Martorana and F. Giannici, Appl. Phys. Lett., 2021, 119, 101104.
22. M. A. Haque, A. N. Gandi, R. Mohanraman, Y. Weng, B. Davaasuren, A.-H. Emwas, C. Combe, D. Baran, A. Rothenberger, U. Schwingenschlögl, H. N. Alshareef, S. Dong and T. Wu, Adv. Funct. Mater., 2019, 29, 1809166.
23. H. Ma, C. Li, Y. Ma, H. Wang, Z. W. Rouse, Z. Zhang, C. Slebodnick, A. Alatas, S. P. Baker, J. J. Urban and Z. Tian, Phys. Rev. Lett., 2019, 123, 155901.
24. X. Long, Z. Pan, Z. Zhang, J. J. Urban and H. Wang, Appl. Phys. Lett., 2019, 115, 072104.
25. V. Trifiletti, M. Massetti, A. Calloni, S. Luong, A. Pianetti, S. Milita, B. C. Schroeder, G. Bussetti, S. Binetti, S. Fabiano and O. Fenwick, J. Phys. Chem. C, 2024, 128, 5408–5417.
26. T. Haeger, R. Heiderhoff and T. Riedl, J. Mater. Chem. C, 2020, 8, 14289–14311.
27. F. Zhang, Z. Zhao, B. Chen, H. Zheng, L. Huang, Y. Liu, Y. Wang and A. L. Rogach, Adv. Opt. Mater., 2020, 8, 1901723.
28. T. Jun, K. Sim, S. Iimura, M. Sasase, H. Kamioka, J. Kim and H. Hosono, Adv. Mater., 2018, 30, e1804547.
29. H. Chen, J. M. Pina, F. Yuan, A. Johnston, D. Ma, B. Chen, Z. Li, A. Dumont, X. Li, Y. Liu, S. Hoogland, Z. Zajacz, Z. Lu and E. H. Sargent, J. Phys. Chem. Lett., 2020, 11, 4326–4330.
30. X. Huang, Q. Sun and B. Devakumar, Mater. Today Chem., 2020, 17, 100288.
31. L. Xie, B. Chen, F. Zhang, Z. Zhao, X. Wang, L. Shi, Y. Liu, L. Huang, R. Liu, B. Zou and Y. Wang, Photonics Res., 2020, 8, 768–775.
32. Y. Li, P. Vashishtha, Z. Zhou, Z. Li, S. B. Shivarudraiah, C. Ma, J. Liu, K. S. Wong, H. Su and J. E. Halpert, Chem. Mater., 2020, 32, 5515–5524.
33. Y. Li, Z. Shi, W. Liang, L. Wang, S. Li, F. Zhang, Z. Ma, Y. Wang, Y. Tian, D. Wu, X. Li, Y. Zhang, C. Shan and X. Fang, Mater. Horiz., 2020, 7, 530–540.
34. F. Zeng, Y. Guo, W. Hu, Y. Tan, X. Zhang, J. Feng and X. Tang, ACS Appl. Mater. Interfaces, 2020, 12, 23094–23101.
35. Q. Xu, J. Wang, Q. Zhang, X. Ouyang, M. Ye, W. Xie, X. Yan, D. Li, X. Ouyang, X. Tang and X. Zhang, Photonics Res., 2021, 9, 351–356.
36. D. Yuan, ACS Appl. Mater. Interfaces, 2020, 12, 38333–38340.
37. X. Li, J. Chen, D. Yang, X. Chen, D. Geng, L. Jiang, Y. Wu, C. Meng and H. Zeng, Nat. Commun., 2021, 12, 3879.
38. Y.-K. Jung, I. T. Han, Y. C. Kim and A. Walsh, npj Comput. Mater., 2021, 7, 51.
39. L.-D. Zhao, C. Chang, G. Tan and M. G. Kanatzidis, Energy Environ. Sci., 2016, 9, 3044–3060.
40. Y. Xiao and L.-D. Zhao, npj Quantum Mater., 2018, 3, 55.
41. Y. Yin, Y. Wang, Q. Sun, Y. Yang, Y. Wang, Z. Yang and W.-J. Yin, J. Phys. Chem. Lett., 2022, 13, 4177–4183.
42. Z. Guo, J. Li, R. Pan, J. Cheng, R. Chen and T. He, Nanoscale, 2020, 12, 15560–15576.
43. K. P. Bigalke, A. Hans and H. Hartl, Z. Anorg. Allg. Chem., 1988, 563, 96–104.
44. S. Hull and P. Berastegui, J. Solid State Chem., 2004, 177, 3156–3173.
45. X. Wang, Y. Zhang, J. Zou, Z. Han, R. Chen, J. Li and Y. Zou, Opt. Mater., 2023, 143, 114168.
46. R. Zhang, X. Mao, D. Zheng, Y. Yang, S. Yang and K. Han, Laser Photonics Rev., 2020, 14, 2000027.
47. J. Qu, S. Xu, F. Liu, Z. Wang, H. Shao, Y. Cui and C. Wang, J. Mater. Sci., 2021, 56, 1–10.
48. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.:Condens. Matter, 2009, 21, 395502.
49. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio Jr, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.:Condens. Matter, 2017, 29, 465901.
50. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
51. G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, npj Comput. Mater., 2018, 4, 72.
52. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. Probert, K. Refson, M. Richter, G. M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G. X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
53. K. V. Klementev, J. Phys. D: Appl. Phys., 2001, 34, 209.
54. J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513.
55. S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447.
56. F. Palazon, Y. El Ajjouri and H. J. Bolink, Adv. Energy Mater., 2020, 10, 1902499.
57. W. Xiang, Z. Wang, D. J. Kubicki, X. Wang, W. Tress, J. Luo, J. Zhang, A. Hofstetter, L. Zhang, L. Emsley, M. Grätzel and A. Hagfeldt, Nat. Commun., 2019, 10, 4686.
58. S. Das Adhikari, A. K. Guria and N. Pradhan, J. Phys. Chem. Lett., 2019, 10, 2250–2257.
59. H. Liu, Z. Wu, J. Shao, D. Yao, H. Gao, Y. Liu, W. Yu, H. Zhang and B. Yang, ACS Nano, 2017, 11, 2239–2247.
60. R. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
61. L. Thirumalaisamy, R. Raliya, S. Kavadiya, S. Palanivel, K. Sethuraman and P. Biswas, CrystEngComm, 2017, 19, 6602–6611.
62. T. L. Cottrell, The Strengths of Chemical Bonds, Butterworths, London, 2d edn, 1958.
63. P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 10th edn, 2014.
64. S. Kajal, G.-H. Kim, C. W. Myung, Y. S. Shin, J. Kim, J. Jeong, A. Jana, J. Y. Kim and K. S. Kim, J. Mater. Chem. A, 2019, 7, 21740–21746.
65. K. F. Tesh, D. J. Burkey and T. P. Hanusa, J. Am. Chem. Soc., 1994, 116, 2409–2417.
66. S. Mishra, L. G. H. Pfalzgraf and E. Jeanneau, Polyhedron, 2007, 26, 66–72.
67. L. Lian, M. Zheng, W. Zhang, L. Yin, X. Du, P. Zhang, X. Zhang, J. Gao, D. Zhang, L. Gao, G. Niu, H. Song, R. Chen, X. Lan, J. Tang and J. Zhang, Adv. Sci., 2020, 7, 2000195.
68. P. Darnige, Y. Thimont, L. Presmanes and A. Barnabé, J. Mater. Chem. C, 2023, 11, 630–644.
69. A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S.-H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794.
70. M. Cutler and N. F. Mott, Phys. Rev., 1969, 181, 1336–1340.
71. T. Ye, X. Wang, X. Li, A. Q. Yan, S. Ramakrishna and J. Xu, J. Mater. Chem. C, 2017, 5, 1255–1260.
72. H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, J. Am. Chem. Soc., 2020, 142, 9553–9563.

---

Footnote

† Electronic supplementary information (ESI) available: Density of pristine and doped materials; bulk electrical resistivity measurements; a description of the Seebeck measurement process; uncertainty calculation for thermal conductivity; Ba 3d XPS spectra; XPS atomic ratio determination of a 5% Ba doped pellet; heat diffusivity and heat capacity measurements; and Rietveld refinement of XRD spectra. See DOI: https://doi.org/10.1039/d5ta02695d

---