Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The interaction of Pu(IV) with low index ferrihydrite surfaces: a periodic boundary condition DFT study†
Ryan L.
Dempsey
 and
Nikolas
Kaltsoyannis
and
Nikolas
Kaltsoyannis
 *
*
Department of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: nikolas.kaltsoyannis@manchester.ac.uk
First published on 14th July 2025
Abstract
Nanoparticulate ferrihydrite (Fh) has a strong affinity towards environmental contaminants, particularly radionuclides. Recently, Pu(IV) was found experimentally to form a tetradentate inner-sphere surface complex with Fh, motivating the present study of the interaction of Pu(IV) with Fh(100), Fh(110) and Fh(120) surfaces using DFT+Ueff. Prior to introduction of Pu(IV), we first discuss the effects of spin arrangement and the choice of Ueff on bulk Fh. The relaxed lattice parameters agree well with previous experiments and simulations, and band gaps (direct/indirect) are determined. The work function, bare and hydrated surface energies of the three terminations are in agreement with previous studies, though we highlight the need for further experimental work in this area. Multidentate binding to the Fh surfaces is highly favorable, with Pu(IV) surface complexation energies significantly exothermic (−3.01 to −6.24 eV). Average Pu–O and Pu–Fe distances are within 0.31 Å of EXAFS measurements, for the lowest energy complexes. Pu(IV) binding is tetradentate on Fh(110) and Fh(120) and tridentate on Fh(100). Surface complex stability depends on the charge of the Pu, indicating primarily ionic Pu–O bonds, though Pu(f) and O(p) states hybridise in the bonding region of the valence band. The Pu–O interactions are determined as partially covalent using the quantum theory of atoms in molecules, consistent with our previous findings for Pu(IV) bound to the Fe13 Keggin cluster. Our work supports recent experimental evidence that Pu(IV) uptake begins via the Keggin and remains bound through transformation to Fh.
Environmental significanceIron (oxyhyr)oxide minerals play a critical role in the transport and long-term fate of both natural and anthropogenic contaminants. During operation of the Enhanced Actinide Removal Plant (EARP) at Sellafield in the UK, which significantly diminishes the discharge of radioactive actinide elements into the Irish Sea, the separation of these radionuclides from the waste stream is achieved via surface complexation to ferrihydrite. This process is not well characterised, and understanding the nature of radionuclide-surface complexation is important for present and future EARP operations. We here provide a detailed study of ferrihydrite bulk and surface properties, and the interaction of the latter with the key α emitting actinide Pu(IV). |
Introduction
Ferrihydrite (Fh, Fe5O7(OH))1 is a ubiquitous nanocrystalline iron (oxyhydr)oxide mineral that is of great importance in many natural2,3 and industrial processes.3,4 It plays a role in the geochemical cycling of iron, contaminant transport, and as the source of iron within the ferritin protein in biological systems.2,3 It is the first phase that forms from ferric hydrolysis,5 and its high specific surface area makes its formation thermodynamically competitive with other iron (oxyhydr)oxides, although it is metastable with respect to transformation to hematite (α-Fe2O3) and goethite (α-FeOOH) under ambient conditions.5,6 The formation of Fh from ferric solutions has been studied extensively, and it was recently found to proceed via a pathway involving the Fe13 Keggin cluster in nuclear waste clean-up operations.7,8 The exact composition and structure of Fh remains ambiguous, as for a nanocrystalline material lacking long-range order crystal structure determination is difficult. Depending on conditions, varying levels of crystallisation in Fh lead to two varieties, the so-called “two-line” and “six-line” Fh, hereafter 2LFh and 6LFh, named after the number of broad features in the powder X-ray diffraction PXRD pattern.In the UK, the reprocessing of spent nuclear fuel ceased in 2018 with the closure of the Thermal Oxide Reprocessing Plant (THORP) after 24 years of operation. This was followed by the final round of Magnox fuel reprocessing in 2022 and the closure of the Magnox reprocessing plant. These two plants, both located at Sellafield, form the main feed for the Enhanced Actinide Removal Plant (EARP) which separates radioactive isotopes from the waste stream via a base-induced flocculation process.4,8 The EARP substantially reduces the discharge of alpha emitters into the Irish Sea and has been very successful in this task since 1994. At the EARP the pH of the acidic aqueous waste stream is raised by the addition of NaOH, resulting in 2LFh nanoparticle formation which has a large surface area and affinity towards actinides.8–11 The mechanism of Fh formation and the exact processes by which actinides and Fh coprecipitate are unknown and of great interest. As THORP and Magnox enter post-operational clean-out (POCO) the EARP feed will diversify in ways that could impact Fh formation and efficiency of the actinide removal process, and hence it is important to understand the mechanisms in operation during the EARP process.
During controlled experiments under EARP conditions it was shown that in the case of U(VI) and Np(V) the majority of Fe(III) precipitates out of solution, consistent with 2LFh formation, and then the actinide precipitates indicating that surface complexation to the Fh has occurred.9,10 In the case of Pu(IV) it was observed that the actinide coprecipitates with Fe(III) between pH 1.5 and 3.11 After precipitation the Fh was measured using Pu L3-edge EXAFS, which showed that a tetradentate inner-sphere surface complex had formed with a coordination environment of eight oxygens and four irons at 2.29 Å and 3.34 Å from Pu, respectively. Upon aging the Pu@Fh sample recrystallised into Pu@hematite without affecting the coordination of Pu. In our recent work,12 we explored this chemistry computationally for a series of tetravalent actinides Th(IV)–Pu(IV) and found increasing stability for the An-bound Fe13 complex across the series, which we attributed to increasingly strong ionic interaction between An and O as well as minor Np/Pu(5f)–O(2p) covalent contributions not present in the earlier actinides. The Pu(IV) binds to the Fe13 cluster in a tetradentate fashion with two Pu–O and two Pu–OH bonds at distances consistent with that of Pu bound to the Fh surface observed experimentally, supporting the Keggin cluster pathway.
In this work, we turn our focus to later in the process, i.e. after the Fe13 clusters aggregate into Fh nanoparticles. We begin by discussing the complexities of Fh bulk composition and proceed to generate the Fh(100), Fh(110), and Fh(120) surface slabs and then study the surface binding of Pu(IV). We show that our models reproduce experimental Pu–O and Pu–Fe distances reasonably well and that Pu(IV) is strongly sorbed to the surfaces via mainly ionic interactions. Analysis of bonding properties from the Quantum Theory of Atoms in Molecules (QTAIM) shows that there is partial covalency similar to that found in the Pu–Fe13 Keggin cluster, supporting the suggestion that Pu(IV) is sequestered via interaction with the Keggin and remains bound during the transformation to Fh.11 We also find that Pu(IV) is significantly more stable when bound to the surfaces compared to in aqueous solution, in line with expectation given the success of the EARP process.
Computational details
General considerations
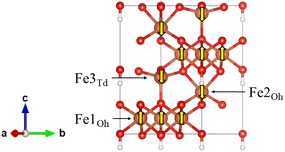
All Density Functional Theory (DFT) calculations were conducted using the Vienna ab initio Simulation Package (VASP) versions 6.1.2, 6.3.0 and 6.4.1.13–15 The generalised gradient approximation (GGA) functional PBE16 was used in conjunction with Grimme's D3 dispersion correction.17 It is well known that GGA functionals produce over-delocalised 3d states in iron (oxyhydr)oxide materials, resulting in significantly underestimated magnetic moments and band gaps.18 Therefore, it is common to apply a Hubbard correction to the Fe 3d states; Ueff = 3–5 eV is typically used for Fh and other similar iron (oxyhydr)oxide materials.18–26 A comparison between lattice parameters and band gaps in Fh while varying Ueff = 0–5 eV can be found in the supplementary information Fig. S1 and Table S1.† As Ueff is increased the a and b lattice parameters increase and c decreases, and good agreement with experiment is found for Ueff ≥ 3 eV. In this work Ueff = 4 eV was applied according to the Dudarev formulism,27 as determined by comparison of Fh bulk lattice parameters compared to experiment1 and previous literature calculation of iron (oxyhyr)oxides.22–25 Plane wave basis sets were employed with core electrons modelled using Projector Augmented Wave (PAW) pseudopotentials.28,29 All calculations are spin-polarised with initial magnetic moment of ±5 μB applied to the Fe(III) sites. Multiple spin arrangements were tested (Fig. S2 and Table S2†) and it was found that the ferrimagnetic (FM) arrangement determined by Pinney et al. was the lowest energy (Fig. 1).22 Convergence testing was completed to determine that a plane wave cutoff of 600 eV is sufficient (Fig. S3†). The total energy and forces were converged <10−6 eV and <10−3 eV Å−1 respectively.Bulk
Convergence with respect to the Γ-centred k-point mesh was carried out (Fig. S3, Tables S3 and S4†), and the data presented in the results and discussion section correspond to geometric optimisation using a 7 × 7 × 3 mesh with Gaussian smearing, whereas results presented for density of states use a larger 11 × 11 × 5 mesh with the tetrahedron method with Blöchl corrections.30 The electronic band structure was calculated in line-mode with k-points defined to represent high symmetry points in the Brillouin zone and the results were analysed using sumo, a python toolkit for plotting ab initio solid-state data.31 The phonon band structure was calculated using phonopy32 with a 3 × 3 × 1 supercell expansion. The phonon density of states was computed by interpolating the phonon frequencies onto a 16 × 16 × 16 q-point grid. The bulk structure is a stable minimum as indicated by all phonon frequencies being real (Fig. S4†).Surfaces
METADISE33 was employed to rotate and cut the relaxed Fh bulk to form dipole free terminations; this method has previously been used successfully on iron minerals.23,34,35 A dipole correction was applied in the c direction to minimise the effects of surface dipole formation upon relaxation.36 A vacuum region of 20 Å ensures that the slab does not interact with the periodic image of itself, even after molecular adsorption. Convergence with respect to the Γ-centred k-point mesh was carried out (Fig. S5 and Tables S5–S7†), and results presented for geometric optimisation use a 5 × 5 × 1 mesh with Gaussian smearing, whereas results presented for density of states use a larger 11 × 11 × 1 mesh with the tetrahedron method with Blöchl corrections. The surface models were then relaxed layer by layer, where layers were determined using VASPKIT,37 until the energy is converged to <1 meV per atom (Tables S8–S10†).In this model, one side of the slab is relaxed while the other is kept fixed. The surface energy γ represents the energy required to cut the bulk to generate the surface, or in the case of a slab model, the two surfaces at the top and bottom of the slab.38 The equations below represent energetic differences between relaxed and unrelaxed stochiometric slabs with respect to the relaxed bulk and account for asymmetric slab relaxation. The unrelaxed surface energy is obtained by performing a single point calculation on the unrelaxed slab and is calculated according to eqn (1)
 | (1) |
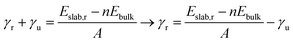 | (2) |
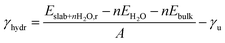 | (3) |
After determining stable hydrated Fh surfaces, a hydrated Pu(IV) species with the formula [Pu(H2O)5]4+ was placed in multiple initial configurations above the surfaces and the geometries were optimised. A Hubbard correction of Ueff = 4 eV was applied to the Pu 5f states for the same reasons as given for Fe 3d. In the absence of Pu-complexed iron (oxyhydr)oxide surface studies for comparison, we note that Ueff = 4 eV has been previously applied successfully in predicting structural and magnetic properties of bulk and surface Pu oxides, and should perform reasonably here.40–44 Substitution reaction energies are calculated according to the following equations
| Fh + [Pu(H2O)9]4+ → Pu@Fh + 4H2O | (4) |
 | (5) |
Analysis of the charge density was carried out using charge density difference and the Quantum Theory of Atoms in Molecules (QTAIM). The charge density difference is calculated according to
| Δρ = ρ(Pu@Fh) − [ρ(Fh) + ρ(Pu(H2O)5)] | (6) |
Results and discussion
Choice of ferrihydrite bulk model
As a nanocrystalline material lacking long-range order, the exact composition and structure of Fh is not known, yet it is of significant interest primarily due to the presence and role of Fh in environmental systems. The amount of OH/H2O relative to Fe is known to vary, and separation of structural OH and sorbed OH/H2O further complicates structural determination. There are many models of Fh as a complex multiphase system consisting of varying amounts of nanocrystalline hematite, magnetite, and other defective materials.20 There are also models suggested with varying OH/H2O content and varying depletion of Fe polyhedra at the surfaces.49 Today, two models remain at the forefront of Fh research; the Drits–Manceau model50 (FeOOH), and the Michel model (Fe5O8H).1 The main difference between these models is that while the Drits–Manceau model is comprised of a mixture of three phases with entirely octahedrally coordinated Fe(III) and an anti-ferromagnetic (AFM) spin arrangement, the Michel model is single phase and contains 20% tetrahedrally coordinated Fe(III) and overall ferrimagnetic (FM) spin arrangement.This highly variable Fh composition poses a significant problem for modelling Pu@Fh surface adsorption, one which becomes tractable by first establishing a single phase, defect free, bulk structure. We here choose to focus on the Michel model for the following reasons. Firstly, the Fe13 Keggin cluster contains a central FeTd moiety, which has been observed in Fh experimentally,51 and Michel's model is isostructural with Akdalaite, an Al(III) bearing mineral which contains the Al13 Keggin as a structural unit with AlTd coordination. Secondly, the Drits–Manceau model is AFM yet the ground state magnetic ordering of bulk Fh has been measured to be ferrimagnetic (FM), and has been modelled accurately by Pinney et al.22,52 It has been proposed that FeTd may form as a defect generated to relax magnetic stress between the Fe atoms arising from rapid growth.19 To complicate things further, the magnetism in Fh varies as a function of particle size52 with both FM and AFM behaviour observed; particles smaller than ∼4 nm are determined to have a FM core whereas larger particles are predicted to be AFM.49 Thirdly, direct comparison between experimental neutron scattering pair distribution functions (PDFs) and those generated using the two models shows that Michel's single phase provides a better fit than the three component model, and further analysis showed that the structural OH/Fe content of the Michel model (0.18) matches experiment (0.20) far better than the Drits–Manceau (1.00).53,54 Finally, Sassi and Rosso recently evaluated over 5000 unique structures, the largest theoretical structure investigation ever performed on Fh, to explore the role of hydration and magnetism on Fh structure.19 During this search the Michel model was “discovered” and comparison of PDFs and XRD showed that among the 50 lowest energy structures Michel's model was the only one which matches experiment. We note, however, that this work found lower energy structures when increasing the water content and in a non-magnetic search, indicating that Michel's model may not always represent Fh found in nature. Michel himself is not unaware of this, and reminds us that “the structural model is just that, a model”.53 In real nanoparticles structural deviations are more apparent than in crystalline materials, but on the whole his model remains impressively accurate.
At the EARP, 2LFh forms with particle sizes of ∼2–5 nm,8 and it is generally accepted that 2LFh contains OH content consistent with Michel's model.19,54 The magnetic properties of EARP-derived Fh have not been measured, but we would expect small nanoparticles to show FM behaviour. Therefore, in this work, we begin with Michel's single phase 2LFh structure with an FM spin arrangement and proceed to generate hydrated Fh(100), Fh(110), and Fh(120) surface slabs and then study Pu(IV) complexation on those surfaces.
Bulk magnetism, structural parameters and electronic structure
The magnetic arrangement of the d5 Fe(III) centres is important for the calculation of many properties, and the consensus is that Pinney et al.'s collinear ferrimagnetic arrangement best describes bulk Fh.19,22–25 This arrangement consists of Fe spins alternating in layers along the c axis in the unit cell as shown in Fig. 1.Other magnetic arrangements were tested, involving flipping symmetrically equivalent Fe sites as well as without spin polarisation. The latter yields optimised lattice parameters which are significantly too small (Table S2†), whereas the specific choice of spin arrangement including spin polarisation did not impact the lattice parameters much, but Pinney's FM arrangement (Fig. S2 and Table S2†) was the lowest energy in agreement with previous studies. This magnetic arrangement consists of alternating antiferromagnetically coupled layers along the [001] direction with ferromagnetic coupling between neighbouring Fe1Oh within that layer. The net magnetisation of the unit cell was calculated as 10 μB which is to be expected as there is an excess of two spin-up Fe1 each with a high-spin d5 configuration. Given the complexities of Fh structural determination discussed earlier, this value is generally considered to be consistent with Michel's experimentally measured 9 μB.22,52 The calculated magnetic moments on the Fe atoms are presented in Table 1 and show good agreement with previously reported values.22–24
| Parameter | Theoretical | Experimental | ||||
|---|---|---|---|---|---|---|
| This work | Ref. 22 | Ref. 23 | Ref. 24 | Ref. 25 | Ref. 1 | |
| a = b/Å | 5.93 (−0.5%) | 5.97 (+0.2%) | 5.96 (0%) | 5.99 (+0.5%) | 5.84 (−2.0%) | 5.96 |
| c/Å | 9.29 (+3.6%) | 9.37 (+4.5%) | 9.22 (+2.8%) | 9.22 (+2.8%) | 9.15 (+2.0%) | 8.97 |
| c/a | 1.57 | 1.57 | 1.55 | 1.54 | 1.55 | 1.50 |
| Volume/Å3 | 283.1 (+2.7%) | 289.6 (+5.1%) | 283.6 (+2.9%) | 286.5 (+4.0%) | 270.7 (−1.8%) | 275.6 |
| Fe1Oh↑/μB | 4.16 | 4.00 | 4.20 | 3.72 | — | — |
| Fe2Oh↓/μB | −4.13 | 4.00 | −4.17 | −3.72 | — | |
| Fe3Td↓/μB | −4.06 | 4.00 | −4.13 | −3.65 | — | |
For Ueff = 4 eV the calculated lattice parameters are a = b = 5.93 Å and c = 9.29 Å (Table 1) which is in good agreement with the experimental values for Michel's Fh model a = b = 5.96 Å and c = 8.97 Å.1 The significant overestimation of c is not a problem specific to this study, but rather a limitation of periodic boundary condition DFT for simulating bulk Fh. Table 1 compares our lattice parameters and other DFT+Ueff works showing consistent overestimation of c, which is attributed to the infinite axis in simulation compared to limited nanocrystalline size in reality.24 A theoretical c lattice parameter, extrapolated for a 1000 nm particle, was determined to be 9.36 Å and it was suggested that nanoparticles suffer from significant strain possibly related to Fe vacancies and increased surface-to-bulk ratio.52
Experimental measurements of Fh electronic properties, such as the band gap and work function, are rare, and those which are reported often disagree. Fh has been described as a charge-transfer insulator,24 with various reported band gaps: ∼1.5 eV and ∼2.7 eV sic,55 1.60 eV and 1.70 eV,56 2.02 eV,57 and 2.14 eV.58 These values are similar to those obtained for other iron(oxyhydr)oxide materials such as hematite, goethite, and lepidocrocite which have band gaps ∼2 eV,59 although the range is quite large and appears to depend on the size of the Fh nanoparticle measured. In one study, quantum confinement effects were observed resulting in smaller band gaps being measured for larger nanoparticles, with a band gap of 1.92 eV being reported for a particle with 1200 Fe atoms.58 Under the periodic boundary condition, we could consider that the Fh bulk is infinitely large making band gap comparison to the largest nanoparticle most reasonable. The calculated electronic band structure of our pristine, defect free, Fh bulk system is presented in Fig. 2. The direct band gap is measured to be 1.39 eV occurring at the Γ-point and an indirect band gap of 1.93 eV occurs in the spin-down states from M → Γ which is remarkably close to the 1.92 eV reported. The projected density of states (pDOS) show that the valence band maximum and conduction band minimum are comprised of occupied O(2p) and unoccupied Fe(3d) states respectively, with significant overlap in the valence band. The real space wavefunction involved in these transitions is presented in Fig. S9.†
Surface modelling
The magnetic moments of the surface layer Fe atoms are reduced (∼3.6 μB) compared to the bulk (∼4.1 μB, Table 1) attributed to the change in coordination upon cleavage of the Fe–O bonds.60 The magnetic moments are restored upon hydrating the surface. There is good agreement between our calculated hydrated surface energy for Fh(100) and Fh(110) with previous calculations (Table 2). To our knowledge, this is the first effort to simulate the Fh(120) termination and so no comparison can be made. The hydrated surface energies are highly dependent on the optimised geometry; only the lowest energy structures are presented in Table 2 and Fig. 3 but we present other higher energy structures in Fig. S6–S8 and Table S11,† showing γhydr ranging from around 0.50 to 1.08 J m−2. A comparison between these structures suggests that, in general, dissociative adsorption of H2O is favourable, resulting in lower surface energy, and that structures with shorter Fe–Osurf bonds are more stable. Extensive hydrogen bonding networks form on the surface as denoted by dashed lines between H and O in Fig. 3.
| Surface termination | γ hydr/J m−2 | Fe–Osurf/Å | Φ/eV | ||||
|---|---|---|---|---|---|---|---|
| This work | Lit. calc | This work | Lit. calc | This work | Lit. calc | Lit. exp | |
| Fh(100) | 0.50 | 0.56 (ref. 20) | 2.05, 2.05, 2.06, 2.06, 2.10, 2.10 | — | 5.61 | — | 4.45 (ref. 57), 4.86 (ref. 61) |
| Fh(110) | 0.70 | 0.81 (ref. 20), 0.67 (ref. 23) | 1.86, 1.87, 2.08, 2.16 | 1.86, 1.88, 2.06, 2.14 (ref. 23) | 4.96 | 5.11 (ref. 57) | |
| Fh(120) | 0.67 | — | 2.00, 2.08, 2.09, 2.10, 2.19, 2.19, 2.34 | — | 5.12 | — | |
On all three surfaces spontaneous H2O dissociation occurs preferentially on the FeTd sites; this has been noted once before.23 Fe(110) has no sites which correspond with Fe3Td in the bulk, thus the surface Fe atoms are all spin-up, as observed in the spin density in Fig. S10.† These spin densities show that the terminal Fe atoms in Fh(100) and Fh(120) are mixed spin-up and spin-down. Hiemstra proposed a modified Michel model for Fh with a defect-free core and defective hydrous surface layer, specifically, Fe2Oh and Fe3Td sites are depleted at the surface.62 It has also been suggested that tetrahedral Fe sites in ferrihydrite may exist as metastable structural defects to accommodate magnetic stress,19 where particle size and surface composition affect magnetic behaviour.49,63 Specifically, it was shown that ferrimagnetic surface contributions are found to decrease with increasing nanoparticle size.49 At the EARP, ∼2–5 nm Fh nanoparticles form and so ferrimagnetic surface contributions would be expected. The cleavage generating the (110) plane results in under-coordinated Fe1Oh sites which adopt tetrahedral symmetry upon hydration. We observed that relaxation of the Fh(100) surface shows significant reconstruction - the cleaved bulk results in Fe2Oh sites terminating with 3-fold coordination, which would result in tetrahedral symmetry after hydration as observed in Fh(110), but instead these Fe sites optimise by moving between rows of Fe1Oh with 5-fold coordination and eventually regaining octahedral symmetry after hydration (Fig. S11†).
The pDOS for the surfaces are shown in Fig. S12–S14† and are similar to that of the bulk, although we find states appearing in the band gap that are not present in the bulk material, which are associated with the fixed surface at the bottom of the slab. These states disappear when assessing the pDOS of the relaxed atoms and are non-physical. All three surfaces can be described as charge-transfer insulators much like the bulk. The band gaps for the Fh(100) and Fh(110) surfaces are bulk-like but that for the Fh(120) surface is decreased by ∼0.40 eV as the conduction band edge shifts closer to the valence band; this has been observed in adsorption studies on the hematite surface and can result in easier electron transfer across the gap.60
The work function Φ was also calculated for the different terminations (Table 2) as the difference between the vacuum electrostatic potential and the Fermi level, as implemented in VASPKIT.37 Experimentally determined values are limited and are not specific to the terminations due to the reasons previously stated regarding Fh nanoparticle structure determination. To our knowledge, the only other calculation of the Fh work function employed GGA level DFT and yielded 5.11 eV, similar to our value of 4.96 eV and experiment (Table 2). Φ for Fh(120) (5.12 eV) is similar to Fh(110), but that for Fh(100) is rather higher at 5.61 eV, although within the range expected for iron(oxyhydr)oxide surfaces.26 The two experimental work function measurements differ by 0.41 eV and were determined using different methods; we note this to draw attention to the lack of experimentally determined electronic properties for Fh which limits our comparison. Nevertheless, the agreement between our results and previous studies of Fh surface energies and work function lends confidence that our surface model is reasonable, and we now proceed to study the surface complexation of Pu(IV).
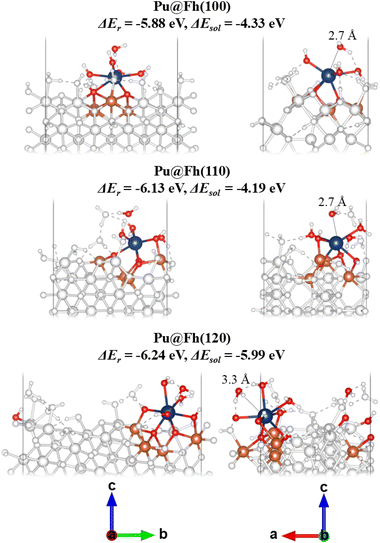
The lowest energy, most stable, Pu@Fh complexes are presented in Fig. 4 with accompanying data in Table 3. On the Fh(100) surface the lowest energy structure forms a tridentate complex with three Pu–Osurf bonds. The longest Pu–Owater included in the average of eight is from a water molecule 2.75 Å away from Pu. Two explicit waters bound to Pu dissociate into Pu–OH. On the Fh(110) surface the lowest energy structure forms a tetradentate complex with four Pu–Osurf bonds. Again, the eighth O is slightly further away as a free water molecule at 2.74 Å. None of complexed waters dissociates. Finally, the Pu(IV) forms a tetradentate surface complex to the Fh(120) surface, much like Fh(110).
| Pu@Fh(100) | Pu@Fh(110) | Pu@Fh(120) | |
|---|---|---|---|
| ΔEr/eV | −5.88 | −6.13 | −6.24 |
| ΔEsol/eV | −4.33 | −4.19 | −5.99 |
| q(Pu) | 2.13 | 2.13 | 2.15 |
| Average of closest 8Pu–O/Å | 2.53 | 2.54 | 2.58 |
| Average of closest 4Pu–Fe/Å | 3.65 | 3.55 | 3.61 |
| ρ BCP | 0.05 | 0.05 | 0.06 |
| H BCP | −0.01 | −0.01 | −0.01 |
| –(G/V)BCP | 0.90 | 0.93 | 0.88 |
The average Pu–O distance in the lowest energy structure of Pu@Fh(120) is larger than for the other terminations, and yet ΔEr is the most negative. A close inspection of the geometries shows that the furthest water molecule included in the averages are in different environments; this water is shown with a dotted black line in the right-hand panel of Fig. 4. In Pu@Fh(100) and Pu@Fh(110) this water molecule is positioned above Pu and forms a single hydrogen bond with a nearby water molecule. In Pu@Fh(120) the furthest water molecule is not directly above Pu, but lies between two other coordinated oxygens forming a hydrogen bond to each. This results in a larger distance to Pu, increasing the average (ca. 2.7 Å vs. 3.3 Å) while still resulting in a stable structure overall. This highlights the complexity of the coordination environment surrounding Pu@Fh, with extensive hydrogen bonding networks clearly impacting the stability. Further explicit water coordination and structure searching would be prohibitively expensive, and so we re-calculated the single point energies of our lowest energy structures using continuum solvation in VASPsol.46,47 The solvated reaction free energies ΔEsol are reduced compared to the electronic energy ΔEr, as would be expected given that the Pu fragment will now interact with the continuum solvent as well as with the explicit surface groups.
We do not see any trend that shorter Pu–Osurf bonding results in increased stability. In fact we notice that across our range of structures the average Pu–O distance of the closest six oxygens, mostly comprised of Osurf and a few Owater, has a small range (2.43–2.49 Å) whereas the average over eight oxygens, which include more Owater, has a much larger range of 2.53–2.76 Å (Table S12†). Given this increase in range of average distance, we note that generally the Pu@Fh surface complex is more stable (more negative ΔEr) in coordination environments with a smaller average of eight oxygens which suggests that stability is dictated by how many Owater can pack closely around the Pu rather than how close Pu can get to the surface.
The average distances in the lowest energy complexes are all larger than those determined experimentally, with a largest deviation of 0.31 Å in the Pu@Fh(100) Pu–Fe distance; 3.65 Å compared to the experimental value 3.34 Å.11 We note that the authors of the experimental work state that the EXAFS fitting has a large Debye–Waller factor of σ2 = 0.018 Å2 when, for distances this short, we would expect σ2 ≤ 0.01 Å2. This indicates that Pu–O and Pu–Fe distances are disordered, which may reflect the range of distances in the averages of our optimised complexes.11 Overall, we consider our Pu–O and Pu–Fe distances to be in good agreement with the experiment, and are pleased that our Fh surface model provides an accurate representation of the Pu@Fh measured experimentally.
There is a general trend that as the Bader charge of Pu increases the structures' stability increases, as indicated by a more negative ΔEr (Table S12†). This is expected when the binding mode is primarily ionic, and is in line with our previous work on actinide interaction with the α-Fe13 Keggin cluster, in which we showed that increasing the positive charge on the actinide results in more stable actinide–Fe13 binding.12 A closer packing of O atoms surrounding Pu is conducive to metal to oxygen charge transfer, which is observed in the calculated Bader charge q(Pu). The Bader charge on Pu in molecular [Pu(H2O)9]4+ was calculated as +1.65 which is significantly less cationic than Pu in the surface complexes. This increase in charge is also observed in the charge density difference (Fig. S18†) which shows significant depletion of electron density surrounding Pu and accumulation on the surface oxygen atoms.
Fig. S18† also shows the QTAIM molecular graphs for the lowest energy Pu@Fh complexes. Properties relating to covalency at the Pu–O bond critical points (BCPs) are listed in Table 3 for the lowest energy complexes, and all complexes studied are summarised in Table S13.† The properties listed at the BCPs are the electron density ρBCP, the total energy density HBCP, and the ratio of the kinetic to potential energy densities –(G/V)BCP. These data suggest partial covalency in the Pu–O bonds with the Pu–Osurf interactions being more covalent than the Pu–Owater as indicated by larger ρBCP, more negative HBCP, and –(G/V)BCP being closer to 0.50. These data also indicate that the Pu–O bonding here is similar to that found in the Pu–Fe13 Keggin cluster.12 For example, the value of ρBCP(Pu–OH) and –(G/V)BCP(Pu–OH) in the Pu–Fe13 Keggin are 0.06 and 0.89 respectively, cf. the values found in this work in the lowest energy structures: 0.07 and 0.82–0.85.
Finding BCPs between the adsorbing Pu(IV) and surface oxygen atoms does not necessarily indicate strong bonding, particularly in polar-covalent bonds such as observed here. Therefore, we present the projected density of states (pDOS) for the lowest energy complexes in Fig. 5. The pDOS for each surface is much like that of the bulk (Fig. 2) and that of the hydrated surfaces discussed previously (Fig. S14†). After complexation Pu (f) and O (p) hybridisation is observed in the valence region spin-up states up to 2 eV below the Fermi level. It is in this region where the strength of the bonding interactions is determined.64 Therefore, the pDOS in conjunction with the QTAIM BCP data provides clear evidence that strong Pu–O form between Pu and O on all three terminations, which is in agreement with experimental observations.11
Conclusions
The complexation of Pu(IV) to three low index ferrihydrite (Fh) surfaces was studied using periodic boundary condition DFT+Ueff. Starting from Michel's single phase, defect free, Fh bulk model we explored various Ueff and magnetic spin arrangements, finding results consistent with previous work. For the first time the work function is presented for three terminations, including Fh(120) which has never been studied before. The bulk band gap, surface energies and surface work functions are in good agreement with the admittedly limited experimental data available; we highlight the need for further experimental work in this area.The interaction of hydrated Pu(IV) with the surfaces was also studied. Pu(IV) was found to have strong affinity for the Fh surfaces, as evidenced by significantly negative reaction energies for the sorption of hydrated Pu(IV) to the hydrated Fh surfaces, both in vacuum and aqueous solution. The Pu–O and Pu–Fe distances in our lowest energy complexes show good agreement with previously determined EXAFS data. The binding mode observed in the lowest energy complexes for Pu@Fh(110) and Pu@Fh(120) are found to be tetradentate while that for Pu@Fh(100) is tridentate. Complexes displaying bidentate binding are significantly less stable, though still show negative reaction energies.
Analysis of the electron density reveals that the Pu–O bonds are partially covalent, in agreement with our previous work on Pu bound to the Fe13 Keggin cluster, thereby providing a link between the coordination environment observed in the Fe13 cluster and on the surface of Fh. The Pu–O bonding interactions are observed in the valence region of the DOS up to 2 eV below the Fermi level, and charge density difference calculations indicate significant charge transfer occurs between the Pu and surface O atoms.
This study supports the idea that under EARP conditions, Pu(IV) can bind to an Fe13 Keggin cluster with subsequent transformation to Fh in which the Pu(IV) has a similar coordination environment. In the experimental work that motivated this study, it was also shown that aged Pu@Fh adducts recrystallised into Pu@hematite with the binding mode remaining intact, and we are currently modelling Pu(IV) binding on hematite surfaces, work which will be presented in a future publication.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for an EPSRC funded PhD studentship to R. L. D. We also thank the University of Manchester for its Computational Shared Facility (CSF3 and CSF4) and associated support services. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/X035859), this work used the ARCHER2 UK National Supercomputing Service (http://www.archer2.ac.uk/). We also extend our thanks to Dr Joseph Flitcroft at the University of Manchester for support with the Phonopy calculations.References
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, The Structure of Ferrihydrite, a Nanocrystalline Material, Science, 2007, 316, 1726–1729 CrossRef CAS PubMed.
- N. D. Chasteen and P. M. Harrison, Mineralization in Ferritin: An Efficient Means of Iron Storage, J. Struct. Biol., 1999, 126, 182–194 CrossRef CAS PubMed.
- J. L. Jambor and J. E. Dutrizac, Occurrence and Constitution of Natural and Synthetic Ferrihydrite, a Widespread Iron Oxyhydroxide, Chem. Rev., 1998, 98, 2549–2586 CrossRef CAS PubMed.
- K. L. Hildred, P. S. Townson, G. V. Hutson and R. A. Williams, Characterisation of particulates in the BNFL Enhanced Actinide Removal Plant, Powder Technol., 2000, 108, 164–172 CrossRef CAS.
- U. Schwertmann and R. M. Cornell, Iron Oxides in the Laboratory: Preparation and Characterization, Wiley-VCH, Weinheim; New York, 2nd completely rev. and extended edn, 2000 Search PubMed.
- A. Navrotsky, L. Mazeina and J. Majzlan, Size-Driven Structural and Thermodynamic Complexity in Iron Oxides, Science, 2008, 319, 1635–1638 CrossRef CAS PubMed.
- O. Sadeghi, L. N. Zakharov and M. Nyman, Aqueous formation and manipulation of the iron-oxo Keggin ion, Science, 2015, 347, 1359–1362 CrossRef CAS PubMed.
- J. S. Weatherill, K. Morris, P. Bots, T. M. Stawski, A. Janssen, L. Abrahamsen, R. Blackham and S. Shaw, Ferrihydrite Formation: The Role of Fe13 Keggin Clusters, Environ. Sci. Technol., 2016, 50, 9333–9342 CrossRef CAS PubMed.
- L. T. Townsend, K. F. Smith, E. H. Winstanley, K. Morris, O. Stagg, J. F. W. Mosselmans, F. R. Livens, L. Abrahamsen-Mills, R. Blackham and S. Shaw, Neptunium and Uranium Interactions with Environmentally and Industrially Relevant Iron Minerals, Minerals, 2022, 12, 165 CrossRef CAS.
- E. H. Winstanley, K. Morris, L. G. Abrahamsen-Mills, R. Blackham and S. Shaw, U(VI) sorption during ferrihydrite formation: Underpinning radioactive effluent treatment, J. Hazard. Mater., 2019, 366, 98–104 CrossRef CAS PubMed.
- K. F. Smith, K. Morris, G. T. W. Law, E. H. Winstanley, F. R. Livens, J. S. Weatherill, L. G. Abrahamsen-Mills, N. D. Bryan, J. F. W. Mosselmans, G. Cibin, S. Parry, R. Blackham, K. A. Law and S. Shaw, Plutonium(IV) Sorption during Ferrihydrite Nanoparticle Formation, ACS Earth Space Chem., 2019, 3, 2437–2442 CrossRef CAS PubMed.
- R. L. Dempsey and N. Kaltsoyannis, Computational study of the interactions of tetravalent actinides (An = Th–Pu) with the α-Fe13 Keggin cluster, Dalton Trans., 2024, 53, 5947–5956 RSC.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. Meng, X.-W. Liu, C.-F. Huo, W.-P. Guo, D.-B. Cao, Q. Peng, A. Dearden, X. Gonze, Y. Yang, J. Wang, H. Jiao, Y. Li and X.-D. Wen, When Density Functional Approximations Meet Iron Oxides, J. Chem. Theory Comput., 2016, 12, 5132–5144 CrossRef CAS PubMed.
- M. Sassi and K. M. Rosso, Roles of Hydration and Magnetism on the Structure of Ferrihydrite from First Principles, ACS Earth Space Chem., 2019, 3, 70–78 CrossRef CAS.
- M. Sassi, A. M. Chaka and K. M. Rosso, Ab initio thermodynamics reveals the nanocomposite structure of ferrihydrite, Commun. Chem., 2021, 4, 134 CrossRef CAS PubMed.
- M. Sassi and K. M. Rosso, Ab Initio Evaluation of Solid-State Transformation Pathways from Ferrihydrite to Goethite, ACS Earth Space Chem., 2022, 6, 800–809 CrossRef CAS.
- N. Pinney, J. D. Kubicki, D. S. Middlemiss, C. P. Grey and D. Morgan, Density Functional Theory Study of Ferrihydrite and Related Fe-Oxyhydroxides, Chem. Mater., 2009, 21, 5727–5742 CrossRef CAS.
- N. Y. Dzade and N. H. De Leeuw, Density functional theory characterization of the structures of H3AsO3 and H3AsO4 adsorption complexes on ferrihydrite, Environ. Sci.:Processes Impacts, 2018, 20, 977–987 RSC.
- W. G. Guimarães, G. Ferreira De Lima and H. A. Duarte, Probing the Local Environment of Al-Substitution into Ferrihydrite Using DFT+U Calculations, J. Phys. Chem. C, 2023, 127, 3285–3294 CrossRef.
- H. F. Chappell, W. Thom, D. T. Bowron, N. Faria, P. J. Hasnip and J. J. Powell, Structure of naturally hydrated ferrihydrite revealed through neutron diffraction and first-principles modeling, Phys. Rev. Mater., 2017, 1, 036002 CrossRef.
- F. Kraushofer, Z. Jakub, M. Bichler, J. Hulva, P. Drmota, M. Weinold, M. Schmid, M. Setvin, U. Diebold, P. Blaha and G. S. Parkinson, Atomic-Scale Structure of the Hematite α-Fe2O3(1
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 02) “R-Cut” Surface, J. Phys. Chem. C, 2018, 122, 1657–1669 CrossRef CAS PubMed.
02) “R-Cut” Surface, J. Phys. Chem. C, 2018, 122, 1657–1669 CrossRef CAS PubMed. - S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved tetrahedron method for Brillouin-zone integrations, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, sumo: command-line tools for plotting and analysis of periodic ab initio calculations, J. Open Source Softw., 2018, 3, 717 CrossRef.
- A. Togo, First-principles Phonon Calculations with Phonopy and Phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001 CrossRef.
- G. W. Watson, E. T. Kelsey, N. H. De Leeuw, D. J. Harris and S. C. Parker, Atomistic simulation of dislocations, surfaces and interfaces in MgO, Faraday Trans., 1996, 92, 433 RSC.
- N. Y. Dzade, A. Roldan and N. H. De Leeuw, Structures and Properties of As(OH)3 Adsorption Complexes on Hydrated Mackinawite (FeS) Surfaces: A DFT-D2 Study, Environ. Sci. Technol., 2017, 51, 3461–3470 CrossRef CAS PubMed.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. De Leeuw, A DFT study of the structures, stabilities and redox behaviour of the major surfaces of magnetite Fe3O4, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 RSC.
- G. Makov and M. C. Payne, Periodic boundary conditions in ab initio calculations, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code, Comput. Phys. Commun., 2021, 267, 108033 CrossRef CAS.
- D. S. Sholl and J. A. Steckel, DFT Calculations for Surfaces of Solids, John Wiley & Sons, Ltd, 2009 Search PubMed.
- S. S. Tafreshi, A. Roldan, N. Y. Dzade and N. H. De Leeuw, Adsorption of hydrazine on the perfect and defective copper (111) surface: a dispersion-corrected DFT study, Surf. Sci., 2014, 622, 1–8 CrossRef CAS.
- B. E. Tegner, M. Molinari, A. Kerridge, S. C. Parker and N. Kaltsoyannis, Water Adsorption on AnO2 {111}, {110}, and {100} Surfaces (An = U and Pu): A Density Functional Theory + U Study, J. Phys. Chem. C, 2017, 121, 1675–1682 CrossRef CAS.
- J.-L. Chen and N. Kaltsoyannis, Computational Study of the Bulk and Surface Properties of Minor Actinide Dioxides MAnO2 (MAn = Np, Am, and Cm); Water Adsorption on Stoichiometric and Reduced {111}, {110}, and {100} Surfaces, J. Phys. Chem. C, 2019, 123, 15540–15550 CrossRef CAS.
- J.-L. Chen and N. Kaltsoyannis, DFT+U Study of Uranium Dioxide and Plutonium Dioxide with Occupation Matrix Control, J. Phys. Chem. C, 2022, 126, 11426–11435 CrossRef CAS PubMed.
- W. M. Bender and U. Becker, Quantum-Mechanical Investigation of the Structures and Energetics of Uranium and Plutonium Incorporated into the Magnetite (Fe3O4) Lattice, ACS Earth Space Chem., 2019, 3, 637–651 CrossRef CAS.
- M. S. Talla Noutack, G. Geneste, G. Jomard and M. Freyss, Investigation of the bulk and point defect properties in uranium–plutonium mixed oxides (U,Pu)O2 using DFT+U: effect of a low americium content, J. Appl. Phys., 2022, 131, 225106 CrossRef CAS.
- N. L. Banik, V. Vallet, F. Réal, R. M. Belmecheri, B. Schimmelpfennig, J. Rothe, R. Marsac, P. Lindqvist-Reis, C. Walther, M. A. Denecke and C. M. Marquardt, First structural characterization of Pa(IV) in aqueous solution and quantum chemical investigations of the tetravalent actinides up to Bk(IV): the evidence of a curium break, Dalton Trans., 2016, 45, 453–457 RSC.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- K. Mathew, V. S. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, Implicit self-consistent electrolyte model in plane-wave density-functional theory, J. Chem. Phys., 2019, 151, 234101 CrossRef PubMed.
- A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Critic2: a program for real-space analysis of quantum chemical interactions in solids, Comput. Phys. Commun., 2014, 185, 1007–1018 CrossRef CAS.
- T. Hiemstra, Surface structure controlling nanoparticle behavior: magnetism of ferrihydrite, magnetite, and maghemite, Environ. Sci.: Nano, 2018, 5, 752–764 RSC.
- V. A. Drits, B. A. Sakharov, A. L. Salyn and A. Manceau, Structural Model for Ferrihydrite, Clay Miner., 1993, 28, 185–207 CrossRef CAS.
- D. Peak and T. Regier, Direct Observation of Tetrahedrally Coordinated Fe(III) in Ferrihydrite, Environ. Sci. Technol., 2012, 46, 3163–3168 CrossRef CAS PubMed.
- F. M. Michel, V. Barrón, J. Torrent, M. P. Morales, C. J. Serna, J.-F. Boily, Q. Liu, A. Ambrosini, A. C. Cismasu and G. E. Brown, Ordered ferrimagnetic form of ferrihydrite reveals links among structure, composition, and magnetism, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- R. Harrington, D. B. Hausner, W. Xu, N. Bhandari, F. M. Michel, G. E. Brown, D. R. Strongin and J. B. Parise, Neutron Pair Distribution Function Study of Two-Line Ferrihydrite, Environ. Sci. Technol., 2011, 45, 9883–9890 CrossRef CAS PubMed.
- W. Xu, D. B. Hausner, R. Harrington, P. L. Lee, D. R. Strongin and J. B. Parise, Structural water in ferrihydrite and constraints this provides on possible structure models, Am. Mineral., 2011, 96, 513–520 CrossRef CAS.
- G. Liu, S. Debnath, K. W. Paul, W. Han, D. B. Hausner, H.-A. Hosein, F. M. Michel, J. B. Parise, D. L. Sparks and D. R. Strongin, Characterization and Surface Reactivity of Ferrihydrite Nanoparticles Assembled in Ferritin, Langmuir, 2006, 22, 9313–9321 CrossRef CAS PubMed.
- Y. Wang, J. Wang, Z. Ding, W. Wang, J. Song, P. Li, J. Liang and Q. Fan, Light Promotes the Immobilization of U(VI) by Ferrihydrite, Molecules, 2022, 27, 1859 CrossRef CAS PubMed.
- W. Bai, Y. Zhou, G. Peng, J. Wang, A. Li and P. F.-X. Corvini, Engineering efficient hole transport layer Ferrihydrite-MXene on BiVO4 photoanodes for photoelectrochemical water splitting: Work function and conductivity regulated, Appl. Catal., B, 2022, 315, 121606 CrossRef CAS.
- J. S. Colton, S. D. Erickson, T. J. Smith and R. K. Watt, Sensitive detection of surface- and size-dependent direct and indirect band gap transitions in ferritin, Nanotechnol, 2014, 25, 135703 CrossRef CAS PubMed.
- J. M. Gardner, S. Kim, P. C. Searson and G. J. Meyer, Electrodeposition of Nanometer-Sized Ferric Oxide Materials in Colloidal Templates for Conversion of Light to Chemical Energy, J. Nanomater., 2011, 2011, 1–8 CrossRef.
- N. Y. Dzade, A. Roldan and N. H. De Leeuw, A Density Functional Theory Study of the Adsorption of Benzene on Hematite (α-Fe2O3) Surfaces, Minerals, 2014, 4, 89–115 CrossRef.
- Q. Bu, S. Li, Q. Wu, L. Bi, Y. Lin, D. Wang, X. Zou and T. Xie, Ferrihydrite-Modified Ti–Fe2O3 as an Effective Photoanode: The Role of Interface Interactions in Enhancing the Photocatalytic Activity of Water Oxidation, ChemSusChem, 2018, 11, 3486–3494 CrossRef CAS PubMed.
- T. Hiemstra, Surface and mineral structure of ferrihydrite, Geochim. Cosmochim. Acta, 2013, 105, 316–325 CrossRef CAS.
- X. Wang, M. Zhu, L. K. Koopal, W. Li, W. Xu, F. Liu, J. Zhang, Q. Liu, X. Feng and D. L. Sparks, Effects of crystallite size on the structure and magnetism of ferrihydrite, Environ. Sci.: Nano, 2016, 3, 190–202 RSC.
- P. Grover, L. S. Ferch and G. Schreckenbach, Adsorption of Actinide (U–Pu) Complexes on the Silicene and Germanene Surface: A Theoretical Study, J. Phys. Chem. A, 2020, 124, 1522–1534 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information, data and figures, on the convergence testing with respect to k-points and cutoff energy as well as the effect of spin polarisation and Ueff. Figures and structural information for higher energy hydrated and Pu-complexed surfaces. Coordinates for the lowest energy structures are provided in the VASP POSCAR format. See DOI: https://doi.org/10.1039/d5em00076a |
| This journal is © The Royal Society of Chemistry 2025 |