High-pressure study of barium metavanadate monohydrate

Abstract

This study presents a single-crystal X-ray diffraction investigation of the high-pressure behavior of barium metavanadate monohydrate, BaV₂O₆·H₂O, up to 7.1 GPa. These measurements were combined with high-pressure optical absorption measurements performed up to 10.1 GPa and with density-functional theory calculations. The X-ray diffraction analysis indicates that BaV₂O₆·H₂O adopts an orthorhombic structure described by the space group P2₁2₁2₁ at ambient pressure. This structure maintains stability up to 8 GPa, in contrast to anhydrous BaV₂O₆ which undergoes a phase transition at 4 GPa. Throughout the pressure range examined, the compression of the crystal is highly anisotropic with the b-axis exhibiting nearly zero linear compressibility. Additionally, our optical absorption measurements reveal that BaV₂O₆·H₂O exhibits an indirect band gap that decreases from 4.62(5) eV at 0.03 GPa to 4.48(5) eV at 10.1 GPa. Density-functional theory calculations give similar results to the experiments and support that the decrease of the band-gap energy with pressure is caused by the enhancement of the hybridization between O 2p and V 3d states. We have also calculated the elastic constant. According to experiments and calculations BaV₂O₆·H₂O is one of the most compressible vanadates with a bulk modulus of 33.0(5) GPa.

---

I. Introduction

Aqueous zinc-ion batteries featuring nonflammable electrolytes provide enhanced safety, rapid charge and discharge capabilities, long-term cycling stability, and cost-effectiveness, while achieving an energy density comparable to that of lithium-ion batteries.¹ Hydrated vanadates present a promising option as layered cathodes for aqueous zinc-ion batteries. This is because of their impressive specific capacity of up to 400 mA h g⁻¹. Nevertheless, their structural instability leads to significant degradation during cycling, primarily due to the repeated intercalation and deintercalation processes.² Among hydrated vanadates, a compound with promising properties is barium metavanadate monohydrate BaV₂O₆·H₂O.³ This material was synthesized and its crystal structure was solved in 1968.⁴ It has also attracted attention because it is a non-linear optical material with a large band-gap energy of 4.6 eV.⁵ BaV₂O₆·H₂O exhibits a second-harmonic generation (SHG) efficiency of approximately 50% of that of KH₂PO₄, the most common material utilized in optical modulators and in nonlinear optics.⁵

For the different applications of BaV₂O₆·H₂O it is important to know how this material is affected by external perturbations, including stresses and hydrostatic compression.⁶ Pressure, as an external parameter, plays a crucial role in influencing the structural and physical properties of materials. It can induce phase transitions, lead to disordering, and result in amorphization, among various other structural alterations.⁷ Metavanadates,⁸ pyrovanadates,⁹ and orthovanadates¹⁰ have been extensively studied under high-pressure conditions. All of them exhibit a significant degree of polymorphism when subjected to compression. Anhydrous barium vanadate, BaV₂O₆, was studied up to 12 GPa, utilizing powder X-ray diffraction and density-functional theory (DFT).¹¹ The findings reveal a phase transition from the orthorhombic phase at ambient pressure (space group C222) to a monoclinic phase (space group C2) occurring at 4 GPa, likely influenced by the distortion of the vanadium oxide polyhedron. At pressures exceeding 10 GPa, BaV₂O₆ experiences amorphization, which is attributed to the disintegration of the continuous [VO₄] chains into [VO₃⁻] units.

Based on the behavior of other hydrated oxides,¹² it could be expected that compression could induce phase transitions in BaV₂O₆·H₂O at pressures as low as a few gigapascals. In contrast to the substantial body of literature concerning the behavior of vanadates under high pressure,^8–11 there is a lack of knowledge regarding the behavior of hydrated vanadates when subjected to compression. To contribute to the understanding of the behavior of hydrated vanadates upon compression, a comprehensive investigation of the high-pressure behavior of BaV₂O₆·H₂O has been conducted up to 10 GPa. The influence of pressure on the crystal structure and the band-gap energy has been analyzed through the combination of single-crystal X-ray diffraction (SC-XRD), optical-absorption measurements (OA), and DFT calculations. The elastic constants and moduli have also been determined. We found that in contrast to what happens in BaV₂O₆, there are no phase transitions taking place in BaV₂O₆·H₂O up to 10 GPa. We also determined that BaV₂O₆·H₂O is highly compressible with a bulk modulus of 33.0(5) GPa and that the response to pressure is highly anisotropic, with one axis showing near-zero linear compressibility. Finally, we also found that the band gap decreases under pressure from 4.62(5) eV at 0.03(3) GPa to 4.48(5) eV at 10.12(5) GPa.

II. Methods and calculations

a. Sample preparation

The starting materials for the synthesis were VO(OH)₂ and Ba(NO₃)₂. VO(OH)₂ was obtained by a precipitation process in the ambient environment, as reported by Guo et al.¹³ Ba(NO₃)₂ (99.999% purity) was obtained from Merck. For the synthesis of BaV₂O₆·H₂O, we adapted the synthesis reported by Yao et al.¹⁴ In particular, the aqueous solution of the reagents [VO(OH)₂ and Ba(NO₃)₂] was heated at 210 °C in an autoclave for 72 h. The obtained colorless crystals were washed with distilled water and dried at 70 °C for 1 h. We confirmed by SC-XRD that the crystals correspond to the orthorhombic structure of BaV₂O₆·H₂O (space group P2₁2₁2₁)¹⁵ without detecting any impurities or minority phases.

b. Single-crystal high-pressure XRD

SC-XRD was performed at room temperature using a Rigaku SuperNOVA diffractometer equipped with an EOS CCD detector and a Mo radiation micro-source (λ = 0.71073 Å). All measurements were processed with CrysAlis software version 1.171.43.143a.¹⁶ Numerical absorption correction based on Gaussian integration over a multifaceted crystal model was applied using the ABSORB-7 program.¹⁷

For HP measurements, we used a Mini-Bragg diamond-anvil cell (DAC) from Almax-EasyLab, with an opening angle of 85° and anvil culets of 500 μm diameter, fit with a stainless-steel gasket containing a hole of 200 μm diameter and 75 μm depth. The thickness of the crystals loaded in the DAC was 50 μm. The pressure transmission medium used in all experiments was a 4 : 1 methanol–ethanol (ME) mixture that gave us a quasi-hydrostatic condition in the range of pressures used in this experiment.¹⁸ The pressure was estimated using the shift of the R1 peak of ruby fluorescence.¹⁹ Three experiments were performed, named HP1, HP2, and HP3, in this study. Pictures of the samples loaded in the DAC are shown in Fig. 1. During experiments we verified that the crystals were not bridged between the diamonds due to the decrease in the thickness of the gasket under compression.

Fig. 1 Images of the samples loaded for experiments HP1 (a), HP2 (b), and HP3 (c). A scale is included in the figure.

The crystal structure was refined, for each pressure, using previous results as a starting point, on F² by full-matrix least-squares refinement using the SHELXL program.²⁰ Due to the limitations of the opening angle of our DAC, it is only possible to collect about 35–40% of the reflections present in a full dataset for the orthorhombic space group under ambient conditions.

c. High-pressure optical absorption

For the optical-absorption measurements, a single crystal measuring 80 μm × 80 μm with a thickness of 10 μm was cleaved along the (010) plane. The crystals were placed in a 200 μm hole of an Inconel gasket that had been pre-indented to 50 μm, within a membrane DAC. The culet size of the IIA-type diamond anvils was 500 μm. Small ruby balls were included with the sample to facilitate pressure determination.¹⁹ The pressure medium used was the same as in the XRD experiments. OA measurements were performed in the ultraviolet (UV)–visible (VIS) range using an optical setup that included a deuterium lamp, fused silica lenses, reflective optics objectives, and a UV-VIS spectrometer.²¹ This configuration enables transmission measurements up to 5.5 eV. The OA spectra were derived from the transmittance spectra of the sample, measured using the sample-in, sample-out method.²²

d. Density-functional theory calculations

We conducted DFT simulations to investigate the HP properties of BaV₂O₆·H₂O. The Vienna ab initio simulation package (VASP)²³ was utilized, employing the projector-augmented wave pseudopotential alongside the plane-wave method.²⁴ The exchange–correlation energy was characterized using the generalized-gradient approximation, specifically the Perdew–Burke–Ernzerhof (PBE) formulation.²⁵ We applied a plane-wave kinetic energy cutoff of 500 eV and utilized dense meshes of 5 × 4 × 3 special k-points generated via the Monkhorst–Pack scheme.²⁶ Full optimization of all structural parameters was carried out for the crystal structure at selected volumes. In the final optimized configurations, the atomic forces acting on the atoms were below 0.005 eV Å⁻¹, and the discrepancies between the diagonal components of the stress tensor were less than 0.1 GPa. The equation of state was derived from the energy–pressure–volume (E, V, P) data collected at each selected volume. The band structure and electronic density of states were calculated using the Heyd–Scuseria–Ernzerhof (HSE06)²⁷ hybrid functional which usually gives more accurate values of the band-gap energy than PBE. The mechanical properties were assessed by calculating the elastic constants. These constants were derived from the stress tensor, which was computed by applying strain to the relaxed structure through modifications of its lattice vectors, including both magnitude and angle, utilizing the stress–strain methodology implemented in VASP.²⁸ From the elastic constants, we subsequently extracted various elastic moduli.

III. Results and discussion

a. Single-crystal XRD

In the three experiments we performed, we confirmed that the samples studied have the orthorhombic crystal structure (space group P2₁2₁2₁) reported by Ulicka et al.¹⁵ Information on the structural determination at ambient pressure in experiment HP1 is given in Table 1. The other two experiments gave consistent information, which is not shown in the table to avoid redundancy. The obtained unit-cell parameters agree with previous studies^5,15 as shown in Table 2. The crystal structure is presented in Fig. 2(a). It is composed of VO₄ tetrahedra and BaO₁₀ irregular polyhedra. The V atoms are placed at two positions with different symmetries, with the atoms being identified as V1 and V2. Each type of VO₄ tetrahedron is connected to two adjacent VO₄ tetrahedra of the other type by sharing corners with them. The Ba atom is coordinated by nine oxygen atoms from adjacent VO₄ tetrahedra and one from a water molecule. The sequence of consecutive VO₄ units forms an infinite twisted spiral [V₂O₆]_∞ which runs along the a-axis as shown in Fig. 2(b) and (c). These metavanadate chains are intercalated by BaO₁₀ polyhedra forming pseudo-two-dimensional layers running perpendicular to the c-axis. This is shown in Fig. 2(d) and (e).

Fig. 2 (a) Crystal structure of BaV₂O₆·H₂O. Ba atoms are large green spheres, V and O atoms are the large and small red spheres, respectively, and H atoms are the pink spheres. BaO₁₀ and VO₄ polyhedra are shown as well as the H₂O molecules. (b) Projection of the structure showing only interconnected VO₄ tetrahedra. (c) Infinite twisted spiral [V₂O₆]_∞ chains of corner-sharing VO₄ tetrahedra. (d) and (e) are projections of the structure showing only VO₄ and BaO₁₀ polyhedra.

Table 1 Crystal data and structure refinement for BaV₂O₆·H₂O under ambient conditions. We present the data of experiment HP1. These data are consistent with data from experiments HP2 and HP3

Empirical formula	H2O7V2Ba
Formula weight	353.22
Temperature [K]	298(2)
Wavelength [Å]	0.71073
Crystal system orthorhombic	P21 21 21
a [Å]	7.3993(1)
b [Å]	8.9942(1)
c [Å]	9.7220(2)
Volume [Å^3]	647.007(17)
Z	4
Calculated density [Mg m^−3]	3.626
Absorption coefficient [mm^−1]	8.827
F(000)	642.5
Crystal size [μm^3]	0.170 × 0.110 × 0.050
Theta range for data collection [°]	3.09 to 28.68
Limiting indices	−9 ≤ h ≤ 4, −12 ≤ k ≤ 12, −13 ≤ l ≤ 7
Reflections collected/unique	2932/1660 [R(int) = 0.0177]
Completeness to theta = 27.54 [%]	99.9%
Refinement method	Full-matrix least-squares on Fo^2
Data/restraints/parameters	1660/0/93
Goodness-of-fit on Fo^2	1.026
Final R indices [Fo^2 > 2σ(Fo^2)]	R 1 = 0.0167, wR2 = 0.0387
R indices (all data)	R 1 = 0.0171, wR2 = 0.0389
Absolute structure parameter	−0.026(17)
Extinction coefficient	0.0076(3)
Largest diff. peak and hole [e Å^−3]	0.64 and −0.45

---

Table 2 Unit-cell parameters determined from experiments HP1, HP2, and HP3 compared with the literature^5,15 and the results of the present DFT calculations

Study	a (Å)	b (Å)	c (Å)	V (Å^3)
Experiment HP1	7.3993(1)	8.9942(1)	9.7220(2)	647.007(17) Å^3
Experiment HP2	7.40211(11)	8.99924(15)	9.72468(15)	647.794(17) Å^3
Experiment HP3	7.4017(1)	8.9957(2)	9.7218(2)	647.31(2) Å^3
Chen et al.^5	7.3993(6) Å	8.9934(7) Å	9.7206(8) Å	646.85(2) Å^3
Ulicka et al.^15	7.409(1) Å	8.997(2) Å	9.728(1) Å	648.5(2) Å^3
DFT	7.4496 Å	9.06958 Å	9.7955 Å	661.83 Å^3

---

Inspection of the XRD patterns as a function of pressure reveals that the orthorhombic crystal structure is retained up to the highest pressure covered in this study. We obtained the pressure dependence of the unit-cell parameters. The results are shown in Table 3 and Fig. 3(a). In Fig. 3(b), we present the results normalized using the unit-cell parameters at ambient pressure (i.e. a₀, b₀ and c₀). This figure shows that compression is highly anisotropic. The c-axis is the most compressible of the crystallographic axes and the b-axis is nearly incompressible. The b-axis is reduced by less than 0.5% from 0 GPa to 7.1 GPa and most of the change in this lattice parameter takes place below 2 GPa. From our results, a linear compressibility of 0.8 × 10⁻³ GPa⁻¹ is determined. This indicates that BaV₂O₆·H₂O has near-zero linear compressibility along the b-axis, resembling PbVO₆.²⁹ This fact makes it suitable for a wide range of potential applications in complex extreme environments.³⁰

Fig. 3 (a) Pressure dependence of unit-cell parameters. (b) Relative change of unit cell parameters versus pressure. In (a) and (b), squares represent data from experiment HP1, circles from HP2, and diamonds from HP3, and the lines represent the results of DFT calculations.

Table 3 Unit-cell parameters determined from experiments HP1, HP2, and HP3 at different pressures

P (GPa)	a (Å)	b (Å)	c (Å)	Experiment
0	7.3993(2)	8.9942(1)	9.7220(2)	HP1
0.47(4)	7.3645(3)	8.9747(4)	9.645(6)	HP1
0.80(4)	7.3557(3)	8.9771(4)	9.579(7)	HP1
1.26(4)	7.2997(2)	8.9413(3)	9.582(6)	HP1
1.62(4)	7.2711(3)	8.9335(4)	9.540(6)	HP1
2.03(4)	7.2596(3)	8.9436(3)	9.454(6)	HP1
2.52(4)	7.2339(2)	8.9403(3)	9.386(6)	HP1
3.20(4)	7.1946(3)	8.9330(4)	9.321(6)	HP1
0	7.40211(11)	8.99924(15)	9.72468(15)	HP2
0.77(6)	7.3484(3)	8.9762(4)	9.593(6)	HP2
1.45(4)	7.3056(3)	8.9632(4)	9.513(6)	HP2
2.24(4)	7.2539(4)	8.9475(5)	9.411(8)	HP2
2.97(4)	7.2115(4)	8.9426(5)	9.323(8)	HP2
3.77(4)	7.1752(3)	8.9447(4)	9.211(6)	HP2
4.25(4)	7.1542(4)	8.9356(5)	9.178(9)	HP2
4.92(4)	7.1359(4)	8.9492(7)	9.073(9)	HP2
0	7.4017(1)	8.9957(2)	9.7218(2)	HP3
1.03(4)	7.3282(3)	8.977(4)	9.5427(4)	HP3
4.60(4)	7.1365(4)	8.938(5)	9.1313(4)	HP3
5.44(4)	7.1041(3)	8.941(6)	9.0395(4)	HP3
5.93(4)	7.0816(4)	8.951(6)	8.9868(4)	HP3
6.61(4)	7.0672(4)	8.937(6)	8.9271(4)	HP3
7.10(4)	7.0483(3)	8.944(5)	8.8711(4)	HP3

---

The anisotropic deformation of the crystal structure under compression is a direct consequence of the two-dimensional layered crystal structure of BaV₂O₆·H₂O. As we described above, the structure is formed by layers running perpendicular to the c-axis. The interlayer distance is determined by BaO₁₀ polyhedra, which are much more compressible than the VO₄ tetrahedra, and therefore it is more compressible than layers that have a compressibility determined by VO₄ tetrahedra. Consequently, the c-axis is more compressible than the other two axes. Within the layers, the different responses to pressure of the a-axis and b-axis are related to the deformation induced in the infinite [V₂O₆]_∞ chains. This can be understood by analyzing how the volume of the VO₄ tetrahedra and the V–O–V angles change with pressure. This information is shown in Fig. 4. The infinite twisted spiral [V₂O₆]_∞ chains run along the a-axis. Therefore, the change in the a-axis is in the first approximation determined by the change in the volume of the VO₄ tetrahedra. The volume of the tetrahedra decreases by 4% from 0 to 7.1 GPa. This change is of the same magnitude as the change in the a-axis in the same pressure range, which is consistent with our hypothesis. The incompressibility of the b-axis could be related to changes in V–O–V angles.³⁰ These angles show opposite behavior. On the one hand, the V₁–O₃–V₂ angle increases under compression, becoming nearly 180°. On the other hand, the V₁–O₄–V₂ angle decreases under compression. The first phenomenon will cause an expansion of the b-axis, and the second one a compression of the a-axis. Then, both the change in the V₁–O₄–V₂ angle and the contraction of the VO₄ tetrahedra favor the compression of the a-axis. In contrast, the change in the V₁–O₃–V₂ angle favors the expansion of the b-axis, which compensates for the decrease in the volume of the VO₄ tetrahedra making the b-axis nearly incompressible. In other words, pressure causes rearrangement of the [V₂O₆]_∞ chains in a way that if the volume of the VO₄ polyhedra would not be modified, the a-axis would contract and the b-axis would expand. The reduction in the volume of VO₄ tetrahedra under compression favors the decrease in the a-axis and compensates for the increase in the b-axis, making this axis incompressible. We would like to add here that after the maximum value of the V₁–O₃–V₂ angle is reached at 6 GPa, this angle remains nearly constant. The understanding of this phenomenon remains an open issue for future studies.

Fig. 4 (a) Pressure dependence of the volume of the VO₄ tetrahedron. Black (red) color represents the tetrahedron of the V1 (V2) atom. (b) Pressure dependence of the V–O–V angles. The V₁–O₃–V₂ (V₁–O₄–V2) angle is represented in black (red). Different symbols correspond to different experiments which are identified within the plots. In (c), we show a network of VO₄ tetrahedra for the identification of V–O–V angles.

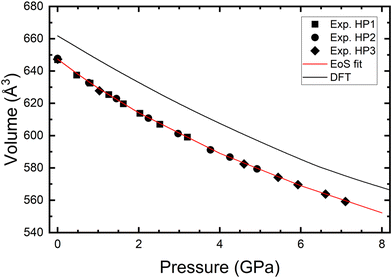
We have also analyzed the pressure dependence of the unit-cell volume. The results are shown in Fig. 5. We have analyzed them, including the three sets of data, using a third-order Birch–Murnaghan equation of state (EoS).³¹ The analysis was carried out using the EosFit7-GUI package.³² From this fit, we obtained the unit-cell volume at zero pressure, V₀ = 647.4(5) ų, the bulk modulus at zero pressure, B₀ = 33.0(5) GPa, and its pressure derivative, . The obtained bulk modulus is smaller than the same parameter in anhydrous BaV₂O₆, B₀ = 50.4(8) GPa, and the rest of metavanadates.¹¹ This makes BaV₂O₆·H₂O the most compressible vanadate among those studied so far. Indeed, the reported value for the bulk modulus is comparable to that of compounds with halogen bonds³³ which is not very common for a compound with a framework formed by covalent bonds like BaV₂O₆·H₂O. To conclude this part of the discussion, we would like to comment on how H₂O affects compression behavior. The bulk modulus of BaV₂O₆·H₂O, B₀ = 33 GPa, is 66% smaller than the bulk modulus of anhydrous BaV₂O₆, B₀ = 50 GPa.¹¹ This result is consistent with the well-established fact that hydrated oxides exhibit greater compressibility than their dehydrated forms.³⁴ Specifically, the presence of water (H₂O) can significantly affect the characteristics of oxides.³⁵ For instance, gypsum (CaSO₄·2H₂O, B₀ = 44 GPa)³⁶ has a bulk modulus that is approximately 70% of that of the anhydride (CaSO₄, B₀ = 64 GPa).³⁷ Similarly, hydrated MgSO₄ (B₀ = 50 GPa)³⁸ has a bulk modulus that is roughly 80% of the bulk modulus of MgSO₄ (B₀ = 62 GPa).³⁹ Based on these observations, we would expect that other vanadate monohydrates, like K₃VO₄·H₂O, MnV₂O₆·H₂O, SrV₂O₆·H₂O, and Na₄V₂O₇·H₂O, would be more compressible than the related dehydrated vanadates. Future studies on hydrated vanadates are needed to confirm this hypothesis.

Fig. 5 Unit-cell volume versus pressure as obtained from experiments and DFT calculations. Symbols represent data from three experiments; the black line shows the DFT results and the red line represents the fitted EoS.

b. Optical absorption

In Fig. 6, we present the optical-absorption spectra of BaV₂O₆·H₂O measured at selected pressures. The absorption coefficient shows that the studied compound has a large gap that linearly decreases under compression. The absorption around 4.6 eV does not have any excitonic contribution. In a previous study,⁵ as well as in our calculations, it was found that BaV₂O₆·H₂O is an indirect-gap material. Knowing this and that excitons are not relevant, we have determined the band-gap energy (E_g) using a Tauc plot analysis.⁴⁰ The linear fit used to determine the band-gap energy at 0.03 GPa, the lowest pressure we measured, is shown in the inset of Fig. 6. We determined a band-gap energy of 4.62(5) eV, which agrees with the value measured by Chen et al.⁵ The smooth evolution of the absorption spectrum with pressure indicates that there are no structural phase transitions up to 10.12(5) GPa.

Fig. 6 Optical-absorption coefficient (α) versus energy at different pressures. The inset shows the Tauc plot used to determine the band-gap energy.

We have also determined the influence of pressure on the band-gap energy. The results are shown in Fig. 7. The band gap closes with pressure following a linear behavior, and the pressure coefficient given by dE_g/dP = −14(1) meV GPa⁻¹. This value resembles the pressure coefficient of anhydrous BaV₂O₆, dE_g/dP = −16 meV GPa⁻¹.¹¹ The band-gap energy of BaV₂O₆·H₂O reaches a value of 4.48(5) eV at 10.1 GPa. This phenomenon is a consequence of the increased hybridization between the 2p orbitals of oxygen and the 3d orbitals of vanadium as we will show when discussing the results of DFT calculations.

Fig. 7 Band-gap energy (E_g) at different pressures. We show results from the experiment and DFT calculations.

c. Density-functional theory

In Fig. 3, we show that DFT gives a good description of the crystal structure at ambient pressure and high pressure. The unit-cell parameters at ambient pressure agree within 1% with experimental data. The unit-cell volume at ambient pressure is overestimated by 2% by DFT as shown in Fig. 5. Such a small discrepancy is typical of DFT calculations. DFT gives a good description of the pressure dependence of the unit-cell parameters and volume; see Fig. 3 and 5. According to DFT, the parameters of the third-order EoS describing the pressure dependence of the volume are as follows: V₀ = 662.6(5) ų, the bulk modulus at zero pressure, B₀ = 39(1) GPa, and its pressure derivative, . They show good agreement with experimental data.

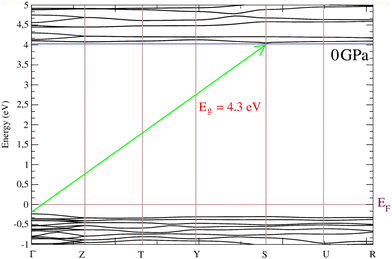
Given the good description of the effect of pressure on the crystal structure provided by DFT, we used this method to calculate the electronic properties of BaV₂O₆·H₂O. The calculated band structure and electronic density of states at 0 GPa are presented in Fig. 8 and 9, respectively. The band structure shows that the material is an indirect-gap wide-gap semiconductor with the top of the valence band at the Γ point of the Brillouin zone and the bottom of the conduction band at the S point. The band gap connecting both points is shown with a green arrow in Fig. 8. The bands are flat near the valence-band maximum and the conduction-band minimum. Notice that calculations performed using the PBE functional⁵ give a similar topology for the band structure as our calculations performed with the HSE06 functional. The emergence of these low-dispersion bands is an indication that they are formed from states that have weak orbital overlap between the lattice sites. In our calculations, we obtained a band-gap energy of 4.3 eV which aligns much better with the experimental value than previous calculations⁵ which gave E_g = 3.23 eV. In Fig. 9, it is evident that our calculations yield a comparable pressure dependence of E_g. In our calculations, dE_g/dP = −13 meV GPa⁻¹, which within one standard deviation agrees with experimental results.

Fig. 8 Calculated band structure of BaV₂O₆·H₂O. The green arrow connects the maximum of the valence band at G with the minimum of the conduction band at S. The Fermi energy (E_F) is at 0 eV. The horizontal blue line is drawn to show that the minimum of the conduction band is at S.

Fig. 9 Calculated total and partial electronic density of states of BaV₂O₆·H₂O at 0 GPa.

According to the calculated electronic density of states reported in Fig. 9, the states near the Fermi level are contributed basically by the 2p orbitals of oxygen and the 3d orbitals of vanadium. O 2p states are particularly prominent in the upper region of the valence band, while V 3d states, which are hybridized with O 2p states, are predominant in the lower region of the conduction band. As pressure increases the strength of hybridization is increased due to changes induced in the crystal field.⁴¹ This phenomenon can be seen in Fig. 10, where we show the electronic density of states at 0 GPa. Notice that the contribution of V 3d states and O 2p states to the bottom of the conduction band is enhanced at 8 GPa. Such a phenomenon causes a decrease in the gap between bonding and anti-bonding states, making the band-gap energy decrease as observed in our calculations and experiments. Thus, DFT provides a rationale for the reduction of the band gap measured in our study under compression.

Fig. 10 Calculated total and partial electronic density of states of BaV₂O₆·H₂O at 10 GPa.

To further characterize BaV₂O₆·H₂O, we calculated the elastic constants. There are nine independent constants. Their values are summarized in Table 4. We found that C₂₂ > C₁₁ > C₃₃ which is consistent with the fact that the compressibility of the axes decreases in the sequence b < a < c. The calculated elastic constants meet the Born criteria of stability.⁴² From these constants, we obtained the elastic moduli using the Hill approximation.⁴³ The bulk modulus extracted from elastic components, 31.1 GPa, agrees very well with the value obtained from the EoS (calculated from SC-XRD experiments). Regarding the other moduli, the value of the Young's modulus, 40.1 GPa, indicates that tensile/compressive stiffness is larger than volumetric compression. On the other hand, the shear modulus of 15.6 GPa reveals that shear deformation is favored over volume contraction. The value of the B/G ratio is 1.99 which implies that BaV₂O₆·H₂O is a brittle material.⁴⁴ Finally, the calculated Poisson's ratio is ν = 0.285, a value comparable with those of minerals with a similar density like amphibolite, peridotite, and eclogite.⁴⁵

Table 4 Calculated elastic constants (C_ij in GPa), and derived bulk modulus (B in GPa), Young's modulus (E in GPa), shear modulus (G in GPa), and Poisson's ratio (ν, dimensionless)

C 11 = 53.4	C 22 = 70.6	C 44 = 15.9	B = 31.1
C 12 = 26.4	C 23 = 23.1	C 55 = 18.5	E = 40.1
C 13 = 24.7	C 33 = 29.9	C 66 = 25.1	G = 15.6
			ν = 0.285

---

IV. Conclusions

We present a comprehensive experimental and theoretical investigation of the synthesized BaV₂O₆·H₂O. The crystal structure and band-gap energy have been meticulously characterized through both experimental and computational methods at ambient pressure and under compression up to 10 GPa, revealing a strong correlation between the two approaches. Our findings indicate that the orthorhombic crystal structure of BaV₂O₆·H₂O at ambient pressure is retained up to 10 GPa. Our findings indicate a significant anisotropic characteristic in the linear compressibility of the crystallographic axes. Interestingly, the b-axis was determined to have near zero axial compressibility. The bulk modulus of BaV₂O₆·H₂O was determined to be 33.0(5) GPa. At ambient pressure, BaV₂O₆·H₂O exhibits an indirect band gap of 4.62(5) eV, which decreases at a rate of −14 meV GPa⁻¹. According to our calculations, the closing of the band gap is caused by the enhancement of hybridization of O 2p and V 3d orbitals. Finally, the elastic constants and moduli were also reported.

Author contributions

Javier Gonzalez-Platas: investigation, formal analysis, and writing – review & editing. Tarik Ouahrani, Fabio Piccinelli, and Marco Bettinelli: investigation, and writing – review & editing. Daniel Errandonea: conceptualization, investigation, formal analysis, and writing – original draft and review & editing.

Data availability

All relevant data are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

D. E. acknowledges the financial assistance received from the Spanish Research Agency (AEI) and the Spanish Ministry of Science and Investigation (MCIN) under Projects PID2022-138076NB-C41 and RED2022-134388-T (10.13039/501100011033). Additionally, D. E. is thankful for the support provided by Generalitat Valenciana through grants PROMETEO CIPROM/2021/075 (GREENMAT) and MFA/2022/007. This study is part of the Advanced Materials program and is funded by MCIN with contributions from the European Union Next Generation EU (PRTR-C17.I1) as well as by Generalitat Valenciana. F. P. and M. B. thank Erica Viviani (Univ. Verona) for expert technical assistance. J. G. P. thanks the SCXRD laboratory of the Interdepartmental Research Service and Servicios Generales de Apoyo a la Investigación (SEGAI) at La Laguna University. This work has been supported by ProID 2024010034 Gobierno Autónomo de Canarias.

References

1. M. Li, J. Lu, Z. Chen and K. Amine, 30 Years of Lithium-Ion Batteries, Adv. Mater., 2018, 30, 1800561,  DOI:10.1002/adma.201800561.
2. C. Liu, Z. Neale, J. Zheng, X. Jia, J. Huang, M. Yan, M. Tian, M. Wang, J. Yang and G. Cao, Expanded hydrated vanadate for high-performance aqueous zinc-ion batteries, Energy Environ. Sci., 2019, 12, 2273–2285,  10.1039/C9EE00956F.
3. S. Luo, X. Cao, Q. Su, Y. Zhang, S. Liu, X. Xie, S. Liang and A. Pan, Layered Barium Vanadate Cathodes for Aqueous Zinc Batteries: Enhancing Cycling Stability through Inhibition of Vanadium Dissolution, ACS Appl. Energy Mater., 2021, 4, 6197–6204,  DOI:10.1021/acsaem.1c00979.
4. L. Žurková, J. Čorba and V. Suchá, Preparation of crystalline barium metavanadate and some of its physicochemical properties, Chem. Pap., 1968, 22, 73–76.
5. W. Chen, W. Zhang, M.-H. Lee, Q. Jing, X. Lu and Z. Chen, BaV₂O₆·H₂O: A nonlinear optical crystal with a large bandgap, Opt. Mater., 2019, 88, 642–647,  DOI:10.1016/j.optmat.2018.12.043.
6. Z. Liu, B. Wang and C. Cazorla, Mechanical and electronic properties of CeO₂ under uniaxial tensile loading: A DFT study, Materialia, 2021, 15, 101050,  DOI:10.1016/j.mtla.2021.101050.
7. R. Turnbull, J. González-Platas, F. Rodríguez, A. Liang, C. Popescu, Z. He, D. Santamaría-Pérez, P. Rodríguez-Hernández, A. Muñoz and D. Errandonea, Pressure-Induced Phase Transition and Band Gap Decrease in Semiconducting β-Cu₂V₂O₇, Inorg. Chem., 2022, 61, 3697–3707,  DOI:10.1021/acs.inorgchem.1c03878.
8. D. Díaz-Anichtchenko, D. Santamaria-Perez, T. Marqueño, J. Pellicer-Porres, J. Ruiz-Fuertes, R. Ribes, J. Ibañez, S. N. Achary, C. Popescu and D. Errandonea, Comparative study of the high-pressure behavior of ZnV₂O₆, Zn₂V₂O₇, and Zn₃V₂O₈, J. Alloys Compd., 2020, 837, 155505,  DOI:10.1016/j.jallcom.2020.155505.
9. D. Diaz-Anichtchenko, E. Bandiello, J. Gonzáles-Platas, A. Liang, Z. He, A. Muñoz, P. Rodríguez-Hernández, D. Errandonea and C. Popescu, Physical Properties and Structural Stability of Cobalt Pyrovanadate Co₂V₂O₇ under High-Pressure Conditions, J. Phys. Chem. C, 2022, 126, 13416–13426,  DOI:10.1021/acs.jpcc.2c03101.
10. D. Errandonea and A. B. Garg, Recent progress on the characterization of the high-pressure behaviour of AVO₄ orthovanadates, Prog. Mater. Sci., 2018, 97, 123–169,  DOI:10.1016/j.pmatsci.2018.04.004.
11. P. Zhang, P. Botella, N. Bura, J.-L. Rodrigo, J. Sanchez-Martin, D. Vie, C. Popescu and D. Errandonea, High-pressure phase transition and amorphization of BaV₂O₆, Dalton Trans., 2025, 54, 2011–2017,  10.1039/D4DT03091E.
12. J. Gonzalez-Platas, P. Rodriguez-Hernandez, A. Muñoz, U. R. Rodríguez-Mendoza, G. Nénert and D. Errandonea, A High-Pressure Investigation of the Synthetic Analogue of Chalcomenite, CuSeO₃·2H₂O, Crystals, 2019, 9, 643,  DOI:10.3390/cryst9120643.
13. K. Guo, Y. Li, D. Luo, Y. Guo, S. Pan, S. Lin and N. Yu, Room-temperature synthesis of VO(OH)₂ as a high-capacity cathode material for aqueous zinc ion batteries, J. Alloys Compd., 2024, 1004, 175772,  DOI:10.1016/j.jallcom.2024.175772.
14. T. Yao, Y. Oka and N. Yamamoto, Structure refinement of barium metavanadate BaV₂O₆, Inorg. Chim. Acta, 1995, 238, 165–168,  DOI:10.1016/0020-1693(95)04654-R.
15. L. Ulicka, F. Pavelcik and K. Huml, Structure of barium metavanadate monohydrate, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 1987, 43, 2266–2268,  DOI:10.1107/S0108270187088127.
16. CrysAlisPro Software System, Rigaku Oxford Diffraction, 2022.
17. R. Angel and J. Gonzalez-Platas, ABSORB-7 and ABSORB-GUI for single-crystal absorption corrections, J. Appl. Crystallogr., 2013, 46, 252–254,  DOI:10.1107/S0021889812048431.
18. S. Klotz, J.-C. Chervin, P. Munsch and G. Le Marchand, Hydrostatic limits of 11 pressure transmitting media, J. Phys. D: Appl. Phys., 2009, 42, 075413,  DOI:10.1088/0022-3727/42/7/075413.
19. K.-K. Mao, P. M. Bell, J. W. Shaner and D. J. Steinberg, Specific volume measurements of Cu, Mo, Pd, and Ag and calibration of the ruby R1 fluorescence pressure gauge from 0.06 to 1 Mbar, J. Appl. Phys., 1978, 49, 3276–3283,  DOI:10.1063/1.325277.
20. G. M. Sheldrick, A short history of SHELX, Acta Crystallogr., Sect. A:Found. Crystallogr., 2008, A64, 112–122,  DOI:10.1107/S0108767307043930.
21. A. Segura, J. A. Sanz, D. Errandonea, D. Martinez-Garcia and V. Fages, High conductivity of Ga-doped rock-salt ZnO under pressure: Hint on deep-ultraviolet-transparent conducting oxides, Appl. Phys. Lett., 2006, 88, 011910,  DOI:10.1063/1.2161392.
22. D. Errandonea, E. Bandiello, A. Segura, J. J. Hamlin, M. B. Maple, P. Rodriguez-Hernandez and A. Muñoz, Tuning the band gap of PbCrO₄ through high-pressure: Evidence of wide-to-narrow semiconductor transitions, J. Alloys Compd., 2014, 587, 14–20,  DOI:10.1016/j.jallcom.2013.10.179.
23. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
24. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865,  DOI:10.1103/PhysRevLett.77.3865.
26. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13, 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
27. J. Heyd, G. Scuseria and M. Ernzerhof, Hybrid Functionals Based on a Screened Coulomb Potential, J. Chem. Phys., 2003, 118, 8207–8215,  DOI:10.1063/1.1564060.
28. O. H. Nielsen and R. M. Martin, Quantum-mechanical theory of stress and force, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 32, 3780–3791,  DOI:10.1103/PhysRevB.32.3780.
29. J. Sánchez Martín, J. Pellicer-Porres, R. Turnbull, D. Díaz-Anichtchenko, S. Anzellini, A. Liang, C. Popescu, M. Bettinelli, P. Rodríguez-Hernández, A. Muñoz and D. Errandonea, PbV₂O₆ under compression: near zero-linear compressibility and pressure-induced change in vanadium coordination, Dalton Trans., 2024, 53, 11490–11499,  10.1039/D4DT01321B.
30. D. Jiang, T. Wen, H. Song, Z. Jiang, C. Li, K. Liu, W. Yang, H. K. Mao and Y. Wang, Intrinsic Zero-Linear and Zero-Area Compressibilities over an Ultrawide Pressure Range within a Gear-Spring Structure, CCS Chem., 2022, 4, 3246,  DOI:10.31635/ccschem.022.202101739.
31. F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824,  DOI:10.1103/PhysRev.71.809.
32. J. Gonzalez-Platas, M. Alvaro, F. Nestola and R. Angel, EosFit7-GUI: a new graphical user interface for equation of state calculations, analyses and teaching, J. Appl. Crystallogr., 2016, 49, 1377–1382,  DOI:10.1107/S1600576716008050.
33. A. Liang, R. Turnbull and D. Errandonea, A review on the advancements in the characterization of the high-pressure properties of iodates, Prog. Mater. Sci., 2023, 136, 101092,  DOI:10.1016/j.pmatsci.2023.101092.
34. D. Errandonea, O. Gomis, D. Santamaría-Perez, B. García-Domene, A. Muñoz, P. Rodríguez-Hernández, S. N. Achary, A. K. Tyagi and C. Popescu, Exploring the high-pressure behavior of the three known polymorphs of BiPO₄: Discovery of a new polymorph, J. Appl. Phys., 2017, 117, 105902,  DOI:10.1063/1.4914407.
35. D. J. Frost, The stability of dense hydrous magnesium silicates in Earth’s transition zone and lower mantle, Mantle Petrology: Field Observations and High Pressure Experimentation, 1999, 6, 283–296.
36. J. Fu and W. Lin, Elastic constants and homogenized moduli of gypsum structure based on density functional theory, Adv. Eng. Res., 2018, 120, 390–395,  DOI:10.2991/ifeesm-17.2018.73.
37. L. Gracia, A. Beltrán, D. Errandonea and J. Andrés, CaSO₄ and its pressure-induced phase transitions: A density functional theory study, Inorg. Chem., 2012, 51, 1751–1759,  DOI:10.1021/ic202056b.
38. A. D. Fortes, K. S. Knight and I. G. Wood, Structure, thermal expansion and incompressibility of MgSO₄·9H₂O, its relationship to meridianiite (MgSO₄·11H₂O) and possible natural occurrences, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2017, 73, 47–64,  DOI:10.1107/S2052520616018266.
39. A. Benmakhlouf, D. Errandonea, M. Bouchenafa, S. Maabed, A. Bouhemadoud and A. Bentabete, New pressure-induced polymorphic transitions of anhydrous magnesium sulfate, Dalton Trans., 2017, 46, 5058–5068,  10.1039/c7dt00539c.
40. A. B. Garg, D. Vie, P. Rodriguez-Hernandez, A. Muñoz, A. Segura and D. Errandonea, Accurate Determination of the Bandgap Energy of the Rare-Earth Niobate Series, J. Phys. Chem. Lett., 2023, 14, 1762–1768,  DOI:10.1021/acs.jpclett.3c00020.
41. J. Laverock, L. F. J. Piper, A. R. H. Preston, B. Chen, J. McNulty, K. E. Smith, S. Kittiwatanakul, J. W. Lu, S. A. Wolf, P.-A. Glans and J.-H. Guo, Strain dependence of bonding and hybridization across the metal-insulator transition of VO₂, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 081104,  DOI:10.1103/PhysRevB.85.081104.
42. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford University Press, Oxford, U.K., 1954.
43. D. H. Chung and W. R. Buessem, The Voigt–Reuss–Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β–ZnS, ZnSe, and CdTe, J. Appl. Phys., 1967, 38, 2535–2540,  DOI:10.1063/1.1709944.
44. S. F. Pugh, Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45, 823–843,  DOI:10.1080/14786440808520496.
45. S. Ji, Q. Wang and M. H. Salisbury, Composition and tectonic evolution of the Chinese continental crust constrained by Poisson's ratio, Tectonophysics, 2009, 463, 15–30.

---