Biphenylene concentric nanorings as high-performance anode materials for lithium-ion batteries: a DFT-based study on lithium intercalation and capacity enhancement

Abstract

Biphenylene network (BPN), a newly discovered two-dimensional sp²-hybridized carbon allotrope composed of 4-6-8 carbon rings, shows great potential for energy storage applications. In this study, biphenylene concentric nanorings (BPNCRs), derived from hydrogen-terminated finite-sized BPN units, are explored as anode materials for lithium-ion batteries (LIBs) using density functional theory (DFT) based simulations. The lithium intercalation and adsorption on BPNCRs of varying sizes are investigated. BPNCR with an inner–outer ring diameter of 5–17 Å is found to exhibit an impressive specific capacity of 1509 mA h g⁻¹ and an energy density of ∼4500 mW h g⁻¹, with a low open-circuit voltage of 0.01 V (average voltage: 0.102 V). An increase in inter-ring spacing offers more lithium intercalation, which leads to further capacity enhancement and open-circuit voltage reduction. For example, BPCNR with an inner–outer ring diameter of 5–19 Å delivers a capacity of 1973 mA h g⁻¹ with an OCV of 0.001 V. Notably, for every 1 Å increase in inter-ring spacing, the capacity increases by ∼500 mA h g⁻¹. Finally, a three-dimensional assembly of lithiated BPNCR is modelled to evaluate its stability in the bulk form. Bulk-BPCNR is not only found to be stable but also provides experimental viability and promises the best features of both nano-particles and micro-particles at the same time. It is also noted that all intercalated lithium atoms are charged, thereby, ruling out lithium plating. These promising results suggest BPNCRs as high-performance anode materials for next-generation LIBs.

---

1 Introduction

Today, rechargeable Li-ion batteries (LIBs) are the leading energy storage technology for a wide range of applications, including grid storage, electric vehicles, and portable devices.^1–3 The performance of these batteries largely depends on the electrode materials,⁴ which play a crucial role in determining key factors such as capacity, charge/discharge rates, and cycle life. Over the past few decades, several intercalation-based, alloying, and conversion-alloying based materials have been extensively studied as potential candidates for energy storage, particularly as anodes in LIBs. However, finding a stable anode material that enhances the performance of LIBs in terms of capacity and voltage without compromising mechanical integrity remains a significant challenge. Commercially, graphite is the dominant anode material for LIBs, characterized by its layered structure composed of sp² hybridized carbon sheets with Li intercalated between the two graphene layers, forming a LiC₆ configuration.^5–10 Graphite indeed gives excellent cyclability along with good mechanical stability, electrical conductivity, and Li transport, but, its low gravimetric capacity (372 mA h g⁻¹) leads to its limited performance in LIBs.¹¹ Silicon, in contrast, offers a gravimetric capacity (4200 mA h g⁻¹)^12,13 ten times higher than that of graphite; however, the substantial volume expansion (∼400%) during lithium intercalation leads to issues such as electrode pulverization, capacity loss, and reduced cycle life.^14,15 Conversion-alloying based materials, such as Sn₂S₃ (1189 mA h g⁻¹),¹⁶ SnO₂ (1494 mA h g⁻¹),¹⁷ SnS (1022 mA h g⁻¹),¹⁸ Sb₂S₃ (946 mA h g⁻¹),¹⁹ and so on, exhibit high theoretical capacities due to their multi-electron transfer capabilities. Despite this, their practical application is limited primarily due to still a large volume expansion (100–300%), which leads to pulverization of the active material and rapid capacity degradation.

It is thus clear that the intercalation based anode materials offer less capacity but at the same time, they are much more robust in terms of mechanical integrity. For this reason, over the past several years, various carbon allotropes with different dimensionalities (0D, 1D, 2D and 3D), including C₆₀-fullerene (446 mA h g⁻¹),²⁰ phagraphene (487 mA h g⁻¹),²¹ graphene (744 mA h g⁻¹),^22–28 carbon nanotubes (600–1000 mA h g⁻¹),^29–31 graphdiyne (744 mA h g⁻¹),³² ψ-graphene (made of 5-6-7 carbon rings having a capacity of 372 mA h g⁻¹),³³etc., have been investigated to achieve a higher capacity in carbon based materials. While the capacity is slightly enhanced in fullerene and phagraphene, it gets doubled as compared to graphite in graphdiyne due to the formation of LiC₃ configuration. On the other hand, in sp²-bonding dominated structures such as graphene and carbon nanotubes, lithium is captured within the hexagonal lattice formed by six carbon atoms, similar to graphite, resulting in a LiC₆ configuration. However, capacity enhancement in these systems can be achieved by using thinner sheets or nanotubes with rough edges, as the adsorption of lithium on the surface and edges of these systems significantly contributes to the overall capacity increase.³⁴

In 2010, a novel two-dimensional (2D) planar non-benzenoid carbon allotrope, called biphenylene network (BPN), was predicted theoretically to be stable by Hudspeth et al.^35,36 and was later experimentally synthesized³⁷ in 2021. A BPN sheet consists of octagonal (8), hexagonal (6), and tetragonal (4) carbon rings bounded to sp² hybridization. It is metallic in nature in its pristine form³⁷ but it transitions to its semiconducting state when cut into nanoribbons³⁵ or functionalized.³⁸ Interestingly, biphenylene nanotubes, formed by rolling BPN sheets, are predicted to retain their metallic nature regardless of their chirality, distinguishing them from conventional carbon nanotubes.³⁵ The biphenylene network has also been investigated as an anode material for LIBs, with a theoretical capacity of 623.72 mA h g⁻¹.²¹ Recent theoretical studies suggest that a biphenylene monolayer can offer a maximum capacity of 1308 mA h g⁻¹ with a low open circuit voltage of 0.34 V.³⁹ Additionally, boron and nitrogen doped biphenylene networks (C₄BN and C₂B₂N₂) have been theoretically studied as promising anode materials for LIBs (940 mA h g⁻¹ and 768 mA h g⁻¹),⁴⁰ respectively. Furthermore, studies have proposed that BPN and its monolayer could serve as promising anode materials for sodium ion batteries, as well.^41,42 However, it is worth noting that BPN undergoes a significant volume expansion ranging between 20% and 30%,⁴³ which is approximately two to three times greater than that of graphite. Recently, a porous 3D-biphenylene-based carbon allotrope derived from combining biphenylene nanoribbons and single-walled carbon nanotubes (SWCNTs) has been both theoretically studied and experimentally synthesized. This structure was found to be stable and showed potential as an anode material for LIBs, with a capacity of 458 mA h g⁻¹ and a volume expansion of just 1.5%.⁴³

Motivated by the goal of increasing gravimetric capacity with minimal volume expansion, we investigated biphenylene network concentric nanorings (BPNCRs), as potential anode materials for lithium-ion batteries (LIBs). Initially, finite-sized, one-dimensional hydrogen-terminated biphenylene nanoribbons were considered and subsequently folded to form rings of varying diameters. These rings were then arranged concentrically, producing structures with different inter-ring spacings. The formation energy spectrum was utilised to understand the process of intercalation and adsorption of Li in BPNCRs. Our first-principles density functional theory-based results show that BPNCRs with inner–outer ring diameters of 5–17 Å exhibit a high capacity of 1509 mA h g⁻¹, which is almost five times greater than that of graphite, along with a remarkably low open-circuit voltage of 0.01 V. Furthermore, we observed a proportional increase in capacity with an increase in the inter-ring spacing in BPNCRs. A modelled three-dimensional bulk structure composed of lithiated BPNCRs is also explored. Overall, the study demonstrates that considering concentric BPN nanorings could be a promising strategy to enhance lithium intercalation/adsorption and thereby the gravimetric capacity by many folds with minimal volume expansion, leading to the realisation of high-performance anode materials for the purpose of energy storage.

2 Computational details

All the calculations were performed within the density functional theory (DFT) framework as implemented in the Vienna Ab initio Simulation Package (VASP).^44,45 Projector-augmented wave (PAW)⁴⁶ pseudopotentials with a plane wave cutoff energy of 520 eV were used to account for electron–ion interaction. The exchange–correlation effects between the electrons were described using generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE)⁴⁷ functional. To account for van der Waals (vdW) corrections, the DFT-D3 method, as proposed by Grimme,⁴⁸ was considered. The convergence criteria for the energy and Hellmann–Feynman forces were set to 10⁻⁴ eV and 0.01 eV, respectively. A vacuum of approximately ∼15 Å along the a, b, and c directions was considered, to prevent any interaction with the periodic images in any of the directions. A Γ-centered 1 × 1 × 1 k-point mesh was used for Brillouin zone integration for geometry optimization, while a high-density 3 × 3 × 3 k-point grid was employed for density of states (DOS) calculations. Bader charge analysis^49–52 and charge density difference analysis were performed to examine the charge transfer. To investigate the thermal stability of BPNCRs, ab initio molecular dynamics (AIMD) simulations were conducted under the canonical (NVT) ensemble at elevated temperatures. The simulations were run for 5 ps with a time step of 2 fs at these temperatures. The climbing-image nudged elastic band (CI-NEB)^53,54 method was employed to evaluate the diffusion energy barriers and minimum energy pathways of Li migration on biphenylene concentric nanorings (BPNCRs). For the CI-NEB calculations, the force convergence criterion was set to 0.01 eV Å⁻¹.

2.1 Structures, stability, and electronic properties

The 2D sheet of biphenylene, as shown in Fig. 1(a), consists of octagonal, hexagonal, and tetragonal carbon rings. A 1D nanoribbon can be achieved by bisecting the octagons along the b-direction. Fig. 1(b) illustrates the optimized structure of a one-dimensional (1D) hydrogen-terminated biphenylene nanoribbon comprising hexagonal and tetragonal carbon rings. The optimized lattice constant of a BPN nanoribbon is 3.78 Å. A nanoring can be formed by joining the ends of a finite-sized nanoribbon, which can be concentric in another nanoring. Though there can be unlimited combinations, here in this work, we consider a model system of two concentric rings with the inner ring being the smallest possible ring (made up of 4 units of the primitive cell) having a diameter of ∼5 Å, and the outer ring (made up of 14 units of the primitive cell) exhibiting a diameter of ∼17 Å (Fig. 1(c) and (d)), with an inter-ring spacing of ∼6 Å. A larger inter-ring space is chosen to facilitate the intercalation of more number of Li atoms. To examine the effect of inter-ring spacing on the number of intercalated Li ions, we also studied concentric BPN nanorings (BPNCRs) with varying inner–outer ring diameters of 6–17 Å (made up of 5 and 14 units of the primitive cell), 6–18 Å (made up of 5 and 15 units of the primitive cell), and 5–19 Å (made up of 4 and 16 units of the primitive cell) as shown in Fig. 1(e)–(g), respectively. Furthermore, such concentric nanorings also allow adsorption of Li on the surface of the outer ring, thereby increasing the capacity of the anode material. It should be noted that the width of these nanorings will play a role in defining the capacity; however, a larger capacity arises at the edge,³⁴ and therefore we have kept it to a minimum width of the nanorings.

Fig. 1 (a) Top view of a monolayer 2D BPN nanosheet and (b) top view of a hydrogen-terminated 1D BPN nanoribbon. The basic BPN nanoribbon unit cell is indicated by the red dashed square. For visualization purposes, a 5 × 1 × 1 supercell of the BPN nanoribbon unit is considered. (c) Top and (d) side views of 5–17 Å concentric BPN nanorings, with an inter-ring spacing of 6 Å. (e), (f) and (g) BPNCRs with inner–outer ring diameters of 6–17 Å, 6–18 Å, and 5–19 Å respectively. The C atoms are denoted by the black balls and the H atoms are denoted by the blue balls.

The thermal stability of the anode, a critical factor influencing battery safety and performance under varying thermal conditions, was systematically evaluated using ab initio molecular dynamics (AIMD) simulations. These simulations, conducted over a duration of 5 ps at three distinct temperatures (300 K, 500 K, and 1000 K), provide a comprehensive assessment of the material's thermal behavior, as illustrated in Fig. 2(a)–(c). While some structural distortions are observed, the structural skeleton remains largely intact and preserved, with the total potential energy exhibiting only minor fluctuations around a constant value. These findings underscore the anode's excellent thermal stability, ensuring safe battery operation even at elevated temperatures. Results for three additional configurations are provided in the ESI† (Fig. S2).

Fig. 2 (a)–(c) Variation of total potential energy as a function of simulation time for a BPNCR with inner–outer ring diameters of 5–17 Å at temperatures of 300 K, 500 K, and 1000 K, respectively. Insets display the equilibrium structures captured at the end of a 5 ps AIMD simulation. (d) Projected density of states (PDOS) of the 5–17 Å BPNCR, with the Fermi level set to zero. (e) and (f) Electron localization function (ELF) of the 5–17 Å BPNCR, with sliced sections showing the top and side views, respectively.

The electronic properties of BPNCRs were analyzed using projected density of states (PDOS) calculations. The PDOS results, as illustrated in Fig. 2(d) and Fig. S3 (in the ESI†), with the Fermi level set at 0 eV, reveal the presence of electronic states at the Fermi level, confirming the metallic behavior and excellent electrical conductivity of BPNCRs. Notably, the states near the Fermi level are dominated by the 2p_y orbitals, which impart the metallic character to BPNCRs. To further analyze the bonding nature and spatial distribution of electrons in BPNCRs, we calculated the electron localization function (ELF). The ELF values are normalized between 0 and 1, where a value of 1 (red) represents a perfectly localized state of electrons, 0.5 (green) corresponds to a fully delocalized electron state (like a homogeneous electron gas), and 0 (blue) indicates regions of very low charge density. As shown in Fig. 2(e) and (f), the ELF slices reveal that electrons are localized on the C–C bonds, indicating the presence of strong σ-bonding states between neighboring carbon atoms. Additionally, the diffused low electron density surrounding the carbon rings suggests the formation of π bonds within the BPNCR structure. Thus, the excellent thermal stability and electronic properties strongly highlight its potential for use as an electrode material in LIBs.

3 Results and discussion

With an idea of enhancing lithium intercalation in between the concentric rings, a model system with a small ring (with a diameter of 5 Å) concentric to a larger ring (with a diameter of 17 Å) is first realized and relaxed to embark on a study of Li insertion in BPNCRs. To begin with, a single Li atom is inserted at the center of the inner ring as shown in Fig. 3(a). Addition of more atoms within the center of the smallest possible BPN nanoring is not found to be favorable. Thus, later Li atoms are placed on the top of the four hexagonal sites at the outer side of the inner ring as shown in Fig. 3(b). Later, Li atoms are placed at the tetragonal sites of the outer-side of the inner ring as well, to examine the effect of a higher lithium concentration, as shown in Fig. 2(d). Furthermore, the concentration is gradually increased up to 23 Li atoms, by forming a second layer of Li such that additional Li atoms lie at the hexagonal sites of the inner-side of the outer ring (Fig. 3(e)). The lithium intercalated BPNCRs are allowed to relax in each configuration so that Li attains its favorable intercalated position in between the rings, as illustrated in Fig. 3.

Fig. 3 (a) The optimized structures of Li₁BPNCR. (b) and (c) The side view and top view, respectively, of Li₅BPNCR. (d) and (e) The top views of Li₉BPNCR and Li₁₉BPNCR, respectively. (f) and (g) The side and top views of Li₃₇BPNCR, respectively. (h) and (i) The top views of Li₅₃BPNCR and Li₇₅BPNCR, respectively. Here, the purple balls represent the intercalated Li atoms on top of hexagonal and tetragonal rings. The green balls represent Li atoms sitting on the edges of BPNCR.

To further explore the possibility of capacity enhancement, lithium atoms are introduced into the vacant positions, i.e., at the tetragonal sites of the inner-side of the outer ring. In particular, intriguing findings emerged, illustrating the pronounced edge effect.³⁴ It was observed that lithium atoms exhibit a tendency to migrate toward the unoccupied edge sites of the rings as illustrated in Fig. 3(f)–(i). A further increase in Li concentration results in the formation of a dual-layer configuration along the edge sites, consequently yielding a significant increase in the capacity.

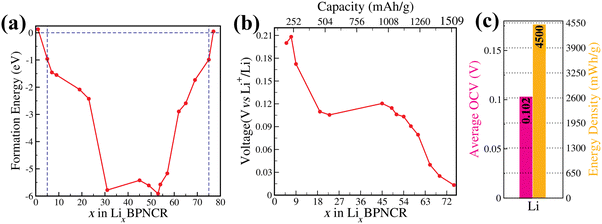
To evaluate the maximum possible Li storage in 5–17 Å BPNCRs, the thermodynamic stability of each lithiated configuration (Li_xBPNCR) is analyzed by calculating the formation energy (E_f)⁵⁵ as:

E_f = E_LixBPNCR − E_BPNCR − (x·E_Li) (1)

where E_LixBPNCR, E_LiBPNCR, and E_Li are the total energies of the Li_xBPNCR structure, pristine BPNCR, and single lithium atom in bulk lithium, respectively. Fig. 4(a) shows the variation of formation energy with respect to lithium concentration, x in Li_xBPNCR. With a single Li atom inserted at the center of the inner ring, the formation energy is calculated to be +0.13 eV revealing Li₁BPNCR to be unstable. This is due to the significant electrostatic repulsion between the Li atom and the surrounding carbon ring (see Fig. S1, ESI†). The increase in the lithium concentration leads to better charge redistribution over the carbon rings as shown in Fig. 5, forming the stable phases when 1 < x ≤ 75. It can be noted from Fig. 4(a) that the formation energy increases with an increase in Li concentration, and it becomes maximum when x = 53 in Li_xBPNCR (i.e., when 1 Li atom is at the center and 52 are in between the concentric rings), indicating the maximum stability of the system in this configuration, with a capacity of ∼1100 mA h g⁻¹. In addition, we investigated the thermal stability of the most stable lithiated configuration, Li₅₃BPNCR, and the fully lithiated configuration, Li₇₅BPNCR, by performing ab initio molecular dynamics (AIMD) simulations at 300 K and 500 K, as illustrated in Fig. S4 and S5 (ESI†). The results indicate that the total potential energy exhibits only minor fluctuations around a constant value, and the structures remain stable without any significant distortions, making it an excellent candidate for use as an electrode material for LIBs.

Fig. 4 (a) Variation of formation energy with respect to lithium concentration, x in Li_xBPNCR, (b) variation of the open circuit voltage (vs. Li/Li⁺) with Li-concentration (x) (and in terms of theoretical capacity), and (c) calculated average OCV and energy density of a 5–17 Å BPNCR.

Fig. 5 Charge density difference plots for (a) Li₇BPNCR, (b) Li₁₉BPNCR, (c) Li₂₃BPNCR, (d) Li₃₁BPNCR, (e) Li₄₅BPNCR, (f) Li₅₃BPNCR, (g) Li₆₂BPNCR, (h) Li₆₉BPNCR, and (i) Li₇₅BPNCR. The iso-surface level is set to 0.002 e Å⁻³. The yellow and blue colors indicate electron excess and deficiency, respectively. Here, the purple and red color balls represent Li atoms with negative and positive charges, respectively.

To evaluate the maximum capacity that the 5–17 Å BPNCR can behold, we increased the Li concentration in two ways: (i) by intercalating more Li atoms within the concentric rings and (ii) by adsorbing Li atoms on the outer surface of the outer ring. It is observed that in the first case when Li is intercalated between the concentric rings, a maximum of 75 Li atoms (i.e., when 1 Li atom is at the center and 74 are in between the concentric rings) can be intercalated. Beyond that the Coulomb repulsion between the Li atoms dominates, leading to the positive value of formation energy, making the structure unstable.

For the second scenario, we investigated the lithium adsorption on the outer ring of the BPNCR by placing Li atoms on the hexagonal and tetragonal sites of the most lithiated stable configuration, Li₅₃BPNCR, followed by optimization to ensure favorable adsorption configurations (see Fig. S6 and Table ST1, ESI†). The outer ring of BPNCR consists of 14 hexagonal and tetragonal rings. In the beginning, Li atoms are placed on alternate seven hexagonal rings (Fig. S6(a), ESI†) and, separately, on alternate seven tetragonal rings (Fig. S6(b), ESI†), forming the Li₆₀BPNCR configuration (see Fig. S6(a) and (b), ESI†). This leads to a decrease in formation energy by roughly 1 eV. It should be noted from Table ST1 (ESI†) that Li prefers to sit on the hexagonal site (E_f = −4.92 eV) as compared to the tetragonal site (E_f = −4.76 eV). Next, the Li concentration is further increased by placing Li atoms on the rest of the hexagonal and tetragonal rings in three different ways, probing the Li₆₇BPNCR configuration (see Fig. S6(c), (d) and (f), ESI†). In Fig. S6(c) (ESI†), 14 Li atoms are placed on the outer-side of each of the hexagonal rings, while in Fig. S6(d) (ESI†), 14 Li atoms are adsorbed at the centre of all the outer-side of the tetragonal rings. On the other-hand, in Fig. S6(f) (ESI†), we started with two layers of Li on the hexagonal sites with 7 atoms adsorbed on the alternate hexagonal rings in the first layer while the other 7 are adsorbed on the rest of the hexagonal rings at a larger height, forming a second layer of Li on the outer-side of the BPNCR. However, on relaxation, the Li atoms in the second layer come down to the first layer forming a configuration analogous to Fig. S6(c) (ESI†). This is further confirmed by the formation energy of both the systems which are similar (see Table ST1, ESI†). It can be noted again that the adsorption on hexagonal sites is more favourable than on tetragonal ones, consistent with previous studies.^21,39 To further increase the Li concentration, Li atoms on all hexagonal and tetragonal sites of the outer ring are placed, corresponding to Li₈₁BPNCR (Fig. S6(e), ESI†). The positive formation energy (1.5 eV) of this structure indicates its instability (see ST1, ESI†). This instability arises due to the decrease in the Li–Li distance (∼2.4 Å) compared to the Li–Li bond length (2.6 Å), causing a dominant repulsion between Li atoms and reduced attraction between Li and the BPNCR. Thus, in the case of Li intercalation along with adsorption, a maximum capacity of ∼1348 mA h g⁻¹ may be achieved in the 5–17 Å BPNCR. Placing a second layer of Li on the outer ring at alternate places over the first layer (Fig. S6(g), ESI†) also leads to positive formation energy. Furthermore, on adding an outer layer of Li on the maximum intercalated Li system, i.e., Li₇₅BPNCR (Fig. S6(h) and (i), ESI†), a positive formation energy is achieved citing its instability beyond a maximum capacity of 75 Li atoms in the 5–17 Å BPNCR. Overall, these results indicate that both intercalation and adsorption mechanisms could play a role in defining the capacity of such concentric rings; however, intercalation within the rings provides more capacity, making it a viable approach for maximising Li storage capacity. Therefore, for further discussion in this article, we consider only the intercalation of Li within BPNCRs.

To evaluate the volume expansion (ΔV) in lithiated BPNCRs (for the 5–17 Å BPNCR), we calculated the difference in volume of the most lithiated configuration, i.e., Li₇₅BPNCR and the unlithiated BPNCR using the formula: 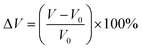, where V is the volume of the fully lithiated BPNCR and V₀ is the volume of the unlithiated BPNCR. Our results show that under full lithiation, BPNCR expands only by ∼3%, which is significantly lower as compared to graphite (10%)⁸ and biphenylene (20–30%),⁴³ indicating the excellent cyclability of the BPNCR.

3.1 Charge transfer

Lithium plating which is one of the most common phenomena in LIBs that occurs due to the deposition of Li on the anode surface in the metallic form instead of intercalating into the anode material leads to dendrite formation, and thus, capacity loss. In order to ensure that Li stored in the current system is not neutral, we conducted the Bader charge and charge density difference analyses. The average Bader charge values on C, H and Li atoms for each of the examined configurations are presented in Table ST2 of the ESI† while charge density difference plots are presented in Fig. 5. The charge density difference Δρ is calculated as:

Δρ = ρ_Li+BPNCR − (ρ_BPNCR + ρ_Li) (2)

where ρ_Li+BPNCR, ρ_BPNCR, and ρ_Li represent the charge density of the lithiated BPNCR (Li and BPNCR), unlithiated BPNCR (without Li), and isolated Li atom placed at the same location as in the total system, respectively. Fig. 5 reveals a substantial charge transfer from the Li atoms to carbon rings, as expected.

The higher the Li concentration, the more the charge transferred from Li to C. This occurs because the C concentration remains constant despite an increase in Li concentration. Consequently, this leads to an increase in the average charge on C to −0.27e (see Table ST2, ESI†). However, the system still retains an excess of charge contributed by Li atoms with the increase in Li concentration, creating a state of non-equilibrium. To maintain the equilibrium within the system (i.e., to ensure the overall charge neutrality), the charge from multiple Li atoms is redistributed, consequently making a few Li atoms negatively charged. This eventually reduces the average positive charge on Li atoms from x = 19 (Fig. 5 and Table ST2, ESI†). This is consistent with the analysis of Farjana et al.³⁴ This re-distribution of charges on Li atoms results in maintaining dense Li layers due to favourable Coloumbic interactions between the Li atoms. Additionally, it is important to clarify that all the Li atoms intercalated in the BPNCR possess a charge, either positive or negative with none being neutral. This process of Li intercalation in the BPNCR differs from lithium plating and thus promises an escape from battery degradation due to dendrite formation.

3.2 Theoretical capacity, voltage and lithium diffusion

An essential consideration in evaluating the performance of an anode material revolves around its storage capacity. This attribute directly impacts the quality of an anode, with a higher storage capacity indicating a better anode. The maximum theoretical capacity is given by:where z is the charge state of cation in the electrolyte, i.e., z = 1 for Li, x is the number of Li atoms inserted in the unit cell, F is the Faraday constant (26 801 mA h mol⁻¹), and M is the molar mass of the BPNCR unit cell. For the 5–17 Å BPNCR, a maximum of 75 lithium ions are intercalated corresponding to Li₇₅BPNCR, which gives a maximum theoretical capacity of 1509 mA h g⁻¹, as shown in Fig. 4(b). This can be further increased by increasing the inter-ring spacing, as discussed in the above sections. Remarkably, the maximum capacity obtained in this work is much higher than that of other carbon-based nano-materials explored, as shown in Table 1.

Table 1 Comparison of gravimetric capacity (mA h g⁻¹), average voltage and Li diffusion energy barrier of various carbon-based anode materials for Li-ion batteries

Materials	Capacity (mA h g^−1)	Average voltage (V)	Diffusion barrier (eV)	Ref.
BPNCR	1509	0.10	0.27–0.43	This work
Graphite	372	0.11	0.22–0.40	6
SWCNT	300–1000	—	—	56–61
MWCNT	800	—	—	62–64
3D-porous biphenylene	458	0.38	0.22	43
Biphenylene network	623	0.33	0.02–0.43	21
Phagraphene	488	—	0.08–0.42	21
Biphenylene monolayer	1302	0.34	0.24	39
Graphenylene	1116	0.46	0.25	65
ψ-Graphene	372	0.64	0.31	33
Graphdiyne	744	1.60	0.17–0.84	66
C60-fullerene	446	—	—	67
2D-C5678	697	0.33	0.37	68

---

Another important aspect of evaluating an anode material is its open-circuit voltage (OCV). The OCV is crucial in understanding how well the anode material performs and is a key measurement for assessing electrode materials. The OCV of an anode in lithium-ion batteries is calculated using the framework of DFT total energies^69,70 and is given by:

The voltage profile with respect to Li concentration in Li_xBPNCR is shown in Fig. 4(b). It can be seen from the figure that voltage varies in the range of 0.2 V to 0.01 V, when x varies from 5 to 75, respectively. In particular, the initial high value of 0.2 V OCV corresponds to the capacity of 100 mA h g⁻¹, which dropped to 0.109 V as the capacity goes to 382 mA h g⁻¹. Furthermore, with an increase in Li concentration, the OCV decreases to ∼0.1 V, passing through a plateau region between x = 19 and x = 45. A further increase in Li concentration leads to a decrease in OCV, which reaches up to a minimum value of 0.01 V on maximum Li storage (x = 75). Additionally, Fig. 4(c) shows the calculated average OCV for Li to be 0.102 V, which falls in the desirable range (0 – 1 V) of a suitable anode working potential and ensures the fabrication of high-voltage LIBs when the BPNCR is combined with an appropriate high-voltage cathode material. The average voltage is significantly lower than those of several other carbon-based anode materials as illustrated in Table 1.

For more practical applicability of a new anode material in industrial approaches, it is important to evaluate its energy density, as well. The energy density of an anode material according to the standard hydrogen electrode (SHE) method⁷¹ is determined by the product of the specific capacity and its relative potential against the SHE reference of the half-cell setup. As metallic Li has a redox potential of about −3.04 V versus SHE,⁷¹ the corresponding relative potential is calculated to be 2.94 V, based on the average value of the OCV. Therefore, in the maximum lithiated state of the 5–17 Å BPNCR, the energy density can reach up to 4500 mW h g⁻¹ (see Fig. 4(c)). The low average voltage and high energy density effectively avoid the formation of Li dendrites and significantly improve the stability and safety of LIBs. In conclusion, considering its impressive high theoretical capacity, low open-circuit voltage and high energy density, BPNCR is expected to be a competitive anode material for high-performance LIBs.

Furthermore, we investigated the diffusion of Li ions through the BPNCR, a process crucial for determining the charge/discharge rate of a battery. Using the climbing-image nudged elastic band (CI-NEB) method, we analysed the migration pathways of Li ions in both fully lithiated and delithiated systems as shown in Fig. S7 and S8 (ESI†). In the case of BPNCR, hexagonal rings are the most stable sites for Li adsorption. Therefore, we explore the migration of Li ions between hexagonal rings located on the inner and outer sides of the concentric nanoring structure. In path-I and path-II, lithium diffuses from the most stable hollow site of the hexagonal ring to another via the hollow site of the tetragonal ring, located on the inner side and outer side of the outer concentric ring, respectively (see Fig. S7(b) and S8(b), ESI†). Our observations reveal that the diffusion energy barriers for lithium in the delithiated state are 0.43 eV and 0.27 eV for path-I and path-II, respectively, while in the lithiated state, the barriers increase to 0.46 eV and 0.28 eV, respectively. Our analysis indicates that the computed lithium diffusion energy barriers in both the delithiated and lithiated states are comparable. This suggests that lithium diffusion kinetics can maintain a lower energy barrier during the charging and discharging processes, ultimately leading to higher lithium-ion mobility and enhanced charge/discharge rate performance. Furthermore, the computed energy barriers are similar to those of recently reported carbon allotropes, as summarized in Table 1.

3.3 Effect of ring diameter and inter-ring spacing

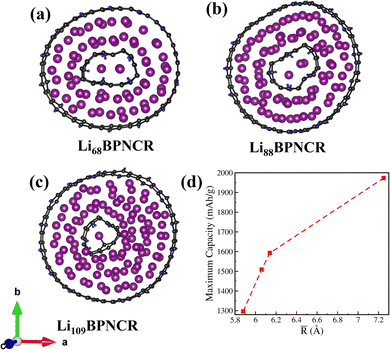
To explore the effect of the ring diameter and thereby inter-ring spacing on Li storage, we also investigate the BPN concentric nanorings with varying diameters. For this, other than the 5–17 Å BPNCR, we also studied 6–17 Å, 6–18 Å and 5–19 Å BPNCRs and calculated their stability (formation energy), maximum theoretical capacity, and corresponding voltage as illustrated in Table 2. Following the same lithiation procedure as considered for the 5–17 Å BPNCR, the maximum number of Li intercalated in the 6–17 Å, 6–18 Å and 5–19 Å BPNCRs is found to be 68 (Li₆₈BPNCR), 88 (Li₈₈BPNCR) and 109 (Li₁₀₉BPNCR) respectively, as shown in Fig. 5(a)–(c). Thus, with the change in inter-ring spacing, the lithium storage capacity can be modulated.

Table 2 Investigating lithium intercalation capabilities of various BPNCRs of different diameters: a comparative study

Inner–outer ring diameter (Å)	Inter-ring spacing R̄ (Å)	No. of Li intercalated	Maximum capacity (mA h g^−1)	Voltage (V)	Formation energy (eV)
6–17	5.88	68	1296	0.003	−0.2
5–7	6.06	75	1509	0.01	−0.1
6–18	6.14	88	1594	0.001	−0.1
5–19	7.25	109	1973	0.001	−0.06

---

Thus, it can be said that the diameter of the rings plays a measure role in deciding the capacity of BPNCRs as with a larger diameter of the inner ring and the same inter-ring spacing (e.g., 5–17 Å and 6–18 Å having an inter-ring spacing of 6 Å), more Li can be stored. This is because an inner-ring of 5 Å diameter can hold only 1 Li atom, and a ring of 6 Å can hold up to 3 Li atoms as shown in Fig. 6(a)–(c). It is also noted that the system in which the inner ring accommodates more than 1 Li atom gets little deformed from a circular symmetry. We, therefore, calculated the average inter-ring spacing (R̄) and plotted it against the maximum capacity in Fig. 6(d). It is quite evident from Fig. 6(d) and Table 2 that a small increase in inter-ring spacing (∼1 Å) can lead to a substantial increase in capacity (∼500 mA h g⁻¹). The 5–19 Å BPNCR, where the inter-ring separation is 7 Å, can stay stable till intercalation of up to 108 Li atoms within the inter-ring space, giving a maximum capacity of 1973 mA h g⁻¹ and a corresponding voltage of 0.001 V. It should be noted that all the Li atoms are found to be in their charged state in all of these examined BPNCRs. These results indicate a strong correlation between the ring diameter, inter-ring spacing and capacity, which can be exploited to realise a performance anode material for LIBs.

Fig. 6 (a)–(c) Fully lithiated configuration of 6–17 Å (Li₆₈BPNCR), 6–18 Å (Li₈₈BPNCR), and 5–19 Å (Li₁₀₉BPNCR) rings, respectively. (d) Variation of the maximum Li storage capacity, voltage, and formation energy of BPNCRs with varying inner–outer ring diameters and average inter-ring spacings (R̄).

Furthermore, we conducted a detailed analysis of the structural deformations occurring during lithium intercalation to understand the long-term stability of BPNCRs under high lithium loads. In the pristine structure, the C–C bond lengths are BL1 (d_AB = d_CD = d_ED = d_AE) = 1.39 Å, BL2 (d_BC = d_FE) = 1.45 Å, and BL3 (d_EH = d_CG) = 1.48 Å, as shown in Fig. 7(a). Upon full lithiation, we observed minimal structural deformations, indicating excellent structural integrity. Specifically, BL1 is found to increase by 2.8%, BL2 increases by 3.4%, and BL3 decreases by 1.35%. These changes are relatively small, demonstrating that the structure retains its integrity even under full lithium loading. Furthermore, the change in the annular area (A) = π(r₂² − r₁²), where r₁ and r₂ are the radii of the inner and outer rings, respectively) upon full lithiation relative to the pristine delithiated structure. For rings with inner and outer diameters of 5–17 Å, 6–17 Å, 6–18 Å, and 5–19 Å, the area increased by approximately 1.3%, 7.7%, 5%, and 5.2%, respectively. These minor area expansions further confirm that the structural framework of the material is well-preserved during lithium intercalation, ensuring the robust stability of the system under high lithium loading.

Fig. 7 (a) Side view of a BPNCR and (b) a BPNCR structure upon delithiation.

Finally, as shown in Fig. 7(b), the structure (5–17 Å BPNCR) regains its original configuration upon delithiation, underscoring its reversible nature. This behavior is indicative of the excellent mechanical resilience and minimal permanent deformation after repeated lithiation–delithiation cycles. This reversible behavior ensures that the material not only performs well under high lithium loads but also resists degradation over prolonged usage, making it a promising candidate for high-performance anode materials.

In addition, we investigated the total and projected density of states (TDOS and PDOS) to understand the electronic properties of the BPNCR at varying Li adsorption concentrations. Our results, presented in Fig. S9 (ESI†), indicate that the BPNCR consistently maintains metallic properties regardless of the Li concentration. From the PDOS analysis, we observed that the contribution of the Li s-orbital to the Fermi level increases with higher Li adsorption concentrations. This leads to a rise in the TDOS value at the Fermi level, indicating that Li adsorption enhances the electronic conductivity of the BPNCR monolayer. Furthermore, for larger nanorings with an interlayer spacing of 7 Å, the DOS, as shown in Fig. S10 (ESI†), increases with Li adsorption, suggesting improved Li storage capacity. This enhancement in electronic conductivity during the Li-ion intercalation process makes the BPNCR a promising material for electrode applications.

3.4 Modelled bulk structure

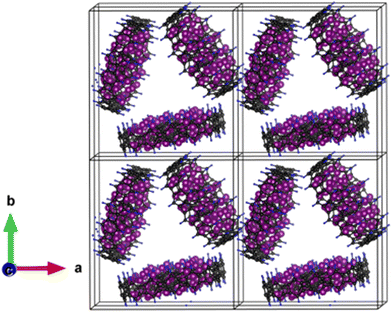
Nano-structured electrodes provide many advantages including high-rate capability, increased power density, greater lithium solubility and gravimetric capacity, reduced memory effect and outstanding fracture toughness with better mechanical stability. Despite advancements, the LIB industry has not yet adopted them as a direct replacement for microparticles because of limitations like low first-cycle efficiency, poor volumetric performance, and high complexity and production costs.⁷² Therefore, in future battery systems, combining the best features of both nanoparticles and microparticles into a single multi-scale particle will be key to achieving the best performance.

Considering this, we modelled a bulk structure, particularly a quasi-crystalline structure made up of zero-dimensional Li₅₃BPNCRs, which are arranged in an orderly manner. This model 3D-system (Fig. 8) consists of three units of the most stable lithiated configuration, i.e., Li₅₃BPNCR, having an inner–outer diameter of 5–17 Å. The optimised lattice parameters are calculated as follows: a = 26 Å, b = 27 Å, and c = 21 Å, with an optimized minimum distance of ∼2.7 Å between these BPNCRs. We understand that this modelled bulk structure is not the global minimum structure of the bulk BPNCR and using advanced computational techniques and powerful high-performance computers a more realistic structure could have been predicted; however, this is currently beyond our limitations. It should though be noted that the modelled bulk structure is found to be stable as indicated by the negative formation energy per atom (−0.04 eV per atom). Furthermore, this structure exhibits a highly encouraging theoretical capacity of 1065 mA h g⁻¹ and an OCV of 0.14 V, which is promising when compared with other bulk carbon based anode materials like bulk graphite (372 mA h g⁻¹), 3D-carbon foams (747 mA h g⁻¹),⁷³ and 3D-carbon aerogels (consisting of nanospheres) (904 mA h g⁻¹).⁷⁴ Considering experimental viability, utilizing bulk structures is a more convenient method than using individual zero-dimensional BPNCRs. Hence, these results suggest that they can be promising candidates for high-performance anode materials in LIBs.

Fig. 8 A 2 × 2 × 2 supercell of a bulk structure model using three units of Li₅₃BPNCR.

4 Conclusion

To summarise, we designed biphenylene concentric nanorings (BPNCRs) from one-dimensional, finite-sized, hydrogen-terminated nanoribbons of the biphenylene network (BPN) and investigated their potential as anode materials for lithium-ion batteries (LIBs). Using DFT based first-principles calculations, we extensively studied lithiation of BPNCRs to understand the mechanism that governs a high capacity in BPNCRs. Our initial studies show that a BPNCR is metallic in nature and using AIMD simulations, the thermal stabilities of pristine and lithiated BPNCR systems at room and higher temperatures were validated. It is observed that with a minimal volume expansion of ∼3%, a high capacity can be achieved just by intercalation of Li-ions in between the concentric thin rings. The role of inter-ring space and the diameter is also examined by considering BPNCRs of varying inner–outer ring diameters: 5–17 Å, 6–17 Å, 6–18 Å and 5–19 Å. It is found that with the change in inter-ring spacing, the capacity can be widely tuned such that a variation of 1 Å inter-ring spacing distance can lead to a change of ∼500 mA h g⁻¹. For example, in the case of 5–17 Å, a capacity of 1509 mA h g⁻¹ has been calculated which was enhanced to 1973 mA h g⁻¹ when the inter-ring spacing of 1 Å is increased by considering the 5–19 Å BPNCR. These systems are also found to exhibit ultra-low OCV (0.001–0.01 V), high energy density (4500 mW h g⁻¹) and a low Li diffusion energy barrier (0.27–0.43 eV). The charge analysis shows a significant amount of charge transfer from Li to carbon nanorings with most of the Li atoms exhibiting positive charge and a few negative charge, ruling out the possibility of lithium plating. Furthermore, it is also demonstrated that a bulk BPNCR with high capacity and low OCV could be realised, on the basis of its negative formation energy. We believe that this study will encourage the experimental synthesis of BPNCRs, unlocking their potential as high-performance anode materials for commercial LIB applications.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article. Raw data were generated at Shiv Nadar Institution of Eminence. Derived data supporting the findings of this study are available from the corresponding author Priya Johari, on request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Shiv Nadar Institution of Eminence, School of Natural Sciences for providing funds and high-performance computer facilities that were utilised for all of the computations. Z. N. G. would like to thank Suman Chowdhury for helping in writing code for constructing nanorings.

References

1. D. Larcher and J. M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29.
2. Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi and J. P. Lemmon, et al., Electrochemical Energy Storage for Green Grid, Chem. Rev., 2011, 111, 3577–3613 . PMID: 21375330.
3. B. Dunn, H. Kamath and J. M. Tarascon, Electrical Energy Storage for the Grid: A Battery of Choices, Science, 2011, 334, 928–935.
4. M. Armand and J. M. Tarascon, Building Better Batteries, Nature, 2008, 451, 652–657.
5. J. R. Dahn, T. Zheng, Y. Liu and J. S. Xue, Mechanisms for Lithium Insertion in Carbonaceous, Mater. Sci., 1995, 270, 590–593.
6. R. C. Boehm and A. Banerjee, Theoretical study of lithium intercalated graphite, J. Chem. Phys., 1992, 96, 1150–1157.
7. C. S. Wang, G. T. Wu and W. Z. Li, Lithium insertion in ball-milled graphite, J. Power Sources, 1998, 76, 1–10.
8. H. Shi, J. Barker, M. Y. Saïdi, R. Koksbang and L. Morris, Graphite structure and lithium intercalation, J. Power Sources, 1997, 68, 291–295 . Proceedings of the Eighth International Meeting on Lithium Batteries.
9. J. R. Dahn, Phase diagram of Li_x C₆, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170–9177.
10. J. R. Dahn, A. K. Sleigh, H. Shi, J. N. Reimers, Q. Zhong and B. M. Way, Dependence of the electrochemical intercalation of lithium in carbons on the crystal structure of the carbon, Electrochim. Acta, 1993, 38, 1179–1191.
11. J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414, 359–367.
12. B. Boukamp, G. Lesh and R. Huggins, All-solid lithium electrodes with mixed-conductor matrix, J. Electrochem. Soc., 1981, 128, 725.
13. B. Liang, Y. Liu and Y. Xu, Silicon-based materials as high capacity anodes for next generation lithium ion batteries, J. Power Sources, 2014, 267, 469–490.
14. J. H. Ryu, J. W. Kim, Y. E. Sung and S. M. Oh, Failure modes of silicon powder negative electrode in lithium secondary batteries, Electrochem. Solid-State Lett., 2004, 7, A306.
15. X. Su, Q. Wu, J. Li, X. Xiao, A. Lott and W. Lu, et al., Silicon-based nanomaterials for lithium-ion batteries: a review, Adv. Energy Mater., 2014, 4, 1300882.
16. D. Chakraborty, Z. N. Ganaie and P. Johari, High-performance Sn₂S₃ as a conversion-alloying anode material for lithium-ion batteries: insights from first-principles calculations, J. Mater. Chem. A, 2025, 13, 4650–4661.
17. Y. Cheng, A. Nie, L. Y. Gan, Q. Zhang and U. Schwingenschloogl, A global view of the phase transitions of SnO₂ in rechargeable batteries based on results of high throughput calculations, J. Mater. Chem. A, 2015, 3, 19483–19489.
18. L. Yao, M. Nie, C. Zhu, R. Cai, W. Xia and L. Sun, et al., Revealing a conversion-alloying reaction mechanism behind high capacity and rate capability of SnS/N-doped graphene anode by in situ TEM, Electrochim. Acta, 2019, 297, 46–54.
19. D. Y. W. Yu, H. E. Hoster and S. K. Batabyal, Bulk antimony sulfide with excellent cycle stability as next-generation anode for lithium-ion batteries, Sci. Rep., 2014, 4, 4562.
20. Y. Chabre, D. Djurado, M. Armand, W. R. Romanow, N. Coustel and J. P. McCauley Jr, et al., Electrochemical intercalation of lithium into solid fullerene C60, J. Am. Chem. Soc., 1992, 114, 764–766.
21. D. Ferguson, D. J. Searles and M. Hankel, Biphenylene and phagraphene as lithium ion battery anode materials, ACS Appl. Mater. Interfaces, 2017, 9, 20577–20584.
22. R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, The role of graphene for electrochemical energy storage, Nat. Mater., 2015, 14, 271–279.
23. D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Enhanced lithiation in defective graphene, Carbon, 2014, 80, 305–310.
24. D. Pan, S. Wang, B. Zhao, M. Wu, H. Zhang and Y. Wang, et al., Li Storage Properties of Disordered Graphene Nanosheets, Chem. Mater., 2009, 21, 3136–3142.
25. P. Lian, X. Zhu, S. Liang, Z. Li, W. Yang and H. Wang, Large reversible capacity of high quality graphene sheets as an anode material for lithium-ion batteries, Electrochim. Acta, 2010, 55, 3909–3914.
26. E. Yoo, J. Kim, E. Hosono, H.-s Zhou, T. Kudo and I. Honma, Large reversible Li storage of graphene nanosheet families for use in rechargeable lithium ion batteries, Nano Lett., 2008, 8, 2277–2282.
27. X. Fan, W. Zheng and J. L. Kuo, Adsorption and diffusion of Li on pristine and defective graphene, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438.
28. C. K. Yang, A metallic graphene layer adsorbed with lithium, Appl. Phys. Lett., 2009, 95, 049901.
29. H. Shimoda, B. Gao, X. Tang, A. Kleinhammes, L. Fleming and Y. Wu, et al., Lithium intercalation into opened single-wall carbon nanotubes: storage capacity and electronic properties, Phys. Rev. Lett., 2001, 88, 015502.
30. V. Meunier, J. Kephart, C. Roland and J. Bernholc, Ab initio investigations of lithium diffusion in carbon nanotube systems, Phys. Rev. Lett., 2002, 88, 075506.
31. B. Gao, A. Kleinhammes, X. Tang, C. Bower, L. Fleming and Y. Wu, et al., Electrochemical intercalation of single-walled carbon nanotubes with lithium, Chem. Phys. Lett., 1999, 307, 153–157.
32. C. Sun and D. J. Searles, Lithium storage on graphdiyne predicted by DFT calculations, J. Phys. Chem. C, 2012, 116, 26222–26226.
33. X. Li, Q. Wang and P. Jena, ψ-Graphene: a new metallic allotrope of planar carbon with potential applications as anode materials for lithium-ion batteries, J. Phys. Chem. Lett., 2017, 8, 3234–3241.
34. F. J. Sonia, M. K. Jangid, B. Ananthoju, M. Aslam, P. Johari and A. Mukhopadhyay, Understanding the Li-storage in few layers graphene with respect to bulk graphite: experimental, analytical and computational study, J. Phys. Chem. A, 2017, 5, 8662–8679.
35. M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, Electronic properties of the biphenylene sheet and its one-dimensional derivatives, ACS Nano, 2010, 4, 4565–4570.
36. A. Bafekry, M. Faraji, M. Fadlallah, H. Jappor, S. Karbasizadeh and M. Ghergherehchi, et al., Biphenylene monolayer as a two-dimensional nonbenzenoid carbon allotrope: a first-principles study, J. Phys.: Condens. Matter, 2021, 34, 015001.
37. Q. Fan, L. Yan, M. W. Tripp, O. Krejčí, S. Dimosthenous and S. R. Kachel, et al., Biphenylene network: A nonbenzenoid carbon allotrope, Science, 2021, 372, 852–856.
38. P. A. Denis, Stability and electronic properties of biphenylene based functionalized nanoribbons and sheets, J. Phys. Chem. C, 2014, 118, 24976–24982.
39. N. Duhan, B. Chakraborty and T. D. Kumar, 2-dimensional biphenylene monolayer as anode in Li ion secondary battery with high storage capacity: Acumen from density functional theory, Appl. Surf. Sci., 2023, 629, 157171.
40. A. H. Pasanaje and N. Singh, Evolutionary prediction of novel biphenylene networks as an anode material for lithium and potassium-ion batteries, Nano Mater. Sci., 2024 DOI:10.1016/j.nanoms.2024.02.008.
41. T. Han, Y. Liu, X. Lv and F. Li, Biphenylene monolayer: a novel nonbenzenoid carbon allotrope with potential application as an anode material for high-performance sodium-ion batteries, Phys. Chem. Chem. Phys., 2022, 24, 10712–10716.
42. X. W. Chen, Z. Z. Lin and X. M. Li, Biphenylene network as sodium ion battery anode material, Phys. Chem. Chem. Phys., 2023, 25, 4340–4348.
43. M. M. Obeid and Q. Sun, Assembling biphenylene into 3D porous metallic carbon allotrope for promising anode of lithium-ion batteries, Carbon, 2022, 188, 95–103.
44. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
45. G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
46. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
49. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
50. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908.
51. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
52. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134, 064111.
53. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
54. G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985.
55. A. J. Morris, C. Grey and C. J. Pickard, Thermodynamically stable lithium silicides and germanides from density functional theory calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054111.
56. B. Gao, A. Kleinhammes, X. Tang, C. Bower, L. Fleming and Y. Wu, et al., Electrochemical intercalation of single-walled carbon nanotubes with lithium, Chem. Phys. Lett., 1999, 307, 153–157.
57. S. Kawasaki, T. Hara, Y. Iwai and Y. Suzuki, Metallic and semiconducting single-walled carbon nanotubes as the anode material of Li ion secondary battery, Mater. Lett., 2008, 62, 2917–2920.
58. R. S. Morris, B. G. Dixon, T. Gennett, R. Raffaelle and M. J. Heben, High-energy, rechargeable Li-ion battery based on carbon nanotube technology, J. Power Sources, 2004, 138, 277–280.
59. V. Meunier, J. Kephart, C. Roland and J. Bernholc, Ab initio investigations of lithium diffusion in carbon nanotube systems, Phys. Rev. Lett., 2002, 88, 075506.
60. S. Yang, J. Huo, H. Song and X. Chen, A comparative study of electrochemical properties of two kinds of carbon nanotubes as anode materials for lithium ion batteries, Electrochim. Acta, 2008, 53, 2238–2244.
61. B. Gao, C. Bower, J. Lorentzen, L. Fleming, A. Kleinhammes and X. Tang, et al., Enhanced saturation lithium composition in ball-milled single-walled carbon nanotubes, Chem. Phys. Lett., 2000, 327, 69–75.
62. E. Franckowiak, S. Gautier and H. Gaucher, Electrochemical Storage of Lithium Multiwalled Carbon Nanotubes, Carbon, 1999, 37, 61–69.
63. G. Maurin, C. Bousquet, F. Henn, P. Bernier, R. Almairac and B. Simon, Electrochemical lithium intercalation into multiwall carbon nanotubes: a micro-Raman study, Solid State Ionics, 2000, 136, 1295–1299.
64. H. C. Shin, M. Liu, B. Sadanadan and A. M. Rao, Electrochemical insertion of lithium into multi-walled carbon nanotubes prepared by catalytic decomposition, J. Power Sources, 2002, 112, 216–221.
65. Y. X. Yu, Graphenylene: a promising anode material for lithium-ion batteries with high mobility and storage, J. Phys. Chem. A, 2013, 1, 13559–13566.
66. C. Sun and D. J. Searles, Lithium storage on graphdiyne predicted by DFT calculations, J. Phys. Chem. C, 2012, 116, 26222–26226.
67. C. Shan, H. J. Yen, K. Wu, Q. Lin, M. Zhou and X. Guo, et al., Functionalized fullerenes for highly efficient lithium ion storage: Structure-property-performance correlation with energy implications, Nano Energy, 2017, 40, 327–335.
68. D. Li, Two-dimensional c 5678: A promising carbon-based high-performance lithium-ion battery anode, Adv. Mater., 2021, 2, 398–402.
69. M. Aydinol, A. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Ab initio study of lithium intercalation in metal oxides and metal dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354.
70. I. A. Courtney, J. Tse, O. Mao, J. Hafner and J. R. Dahn, Ab initio calculation of the lithium-tin voltage profile, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 15583.
71. Y. Cao, M. Li, J. Lu, J. Liu and K. Amine, Bridging the academic and industrial metrics for next-generation practical batteries, Nat. Nanotechnol., 2019, 14, 200–207.
72. R. Jain, A. S. Lakhnot, K. Bhimani, S. Sharma, V. Mahajani and R. A. Panchal, et al., Nanostructuring versus microstructuring in battery electrodes, Nat. Rev. Mater., 2022, 7, 736–746.
73. L. Deng, T. Wei, J. Liu, L. Zhan, W. Chen and J. Cao, Recent developments of carbon-based anode materials for flexible lithium-ion batteries, Crystals, 2022, 12, 1279.
74. C. Wang, Y. Xiong, H. Wang, C. Jin and Q. Sun, Naturally three-dimensional laminated porous carbon network structured short nano-chains bridging nanospheres for energy storage, J. Mater. Chem. A, 2017, 5, 15759–15770.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04033c

---