Single-molecule fluorescence imaging of photocatalytic nanomaterials

Abstract

Photocatalytic nanomaterials can intensively interact with light to drive catalytic reactions and have emerged as a novel class of catalysts for sustainability applications and mitigating environmental crises. Understanding the fundamental processes of photocatalytic reactions, such as charge carrier generation, separation, and transport as well as reactivity site distribution, is key to the rational design of optimal catalysts. However, conventional ensemble measurements are unable to differentiate the heterogeneities intrinsic to individual nanocatalysts in size, facet, morphology, and crystal phase, imposing a grand challenge in explicitly uncovering the structure–property relationship. In this review, we highlight the versatility of an emerging operando imaging technique, namely single-molecule fluorescence microscopy (SMFM), in unravelling the puzzles in photocatalytic processes. In particular, the high spatiotemporal resolution of SMFM allows to study single- or even sub-particle catalysis, thus offering unprecedented insights into mechanistic understanding and catalyst design. We first discuss the fundamentals of SMFM and its use for investigating catalytic reactions based on plasmonic metals and semiconductors. We then highlight heterostructured photocatalysts with diverse combinations of plasmonic metals, non-plasmonic catalytic nanomaterials, and/or semiconductors. Recent advances in investigating bio-inorganic hybrids and non-fluorescent entities are also reviewed. Finally, we provide a discussion on the challenges and opportunities in this field, aiming to inspire novel ideas and promote the exploration of SMFM for new applications.

---

Ming Zhao

Dr Ming Zhao is currently an assistant professor in the Department of Materials Science and Engineering at National University of Singapore. He received his BS and ME degrees in Materials Physics and Chemistry from Nanjing University, China. In 2019, he obtained his PhD from the Georgia Institute of Technology. Before joining NUS, he worked as a postdoctoral associate at Cornell University. His current research interests include the rational design and chemical imaging of advanced nanocatalysts for sustainability applications.

---

1. Introduction

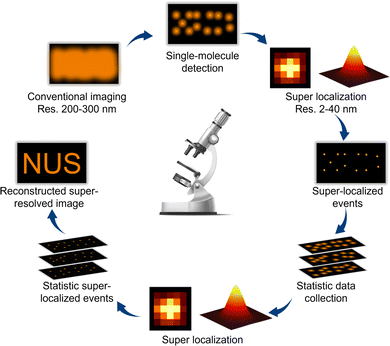
With the ever-increasing growth in the global energy demand and the pressing need for environmentally friendly technologies, photocatalysis has received considerable attention as an efficient, clean, and sustainable method for chemical transformation and energy conversion.^1–3 Photocatalysis harnesses light to activate chemical reactions on the surface of catalysts, facilitating a wide range of clean-energy reactions such as water splitting,^4,5 micropollutant degradation,^6,7 and CO₂ conversion,⁸ thus offering novel avenues for addressing global energy and environmental challenges. Despite these merits, the practical applications of photocatalysis are significantly hindered by the inexplicit understanding of reaction mechanisms and catalyst dynamics, which imposes a huge barrier to the development of high-efficiency photocatalysts.^9,10 To overcome this challenge, advanced characterization techniques are needed to study the molecular-level dynamics of photocatalytic reactions in real-time and under operando conditions. Recently, super-resolution fluorescence microscopy has emerged as a powerful analytical tool with unique advantages, including high spatial and temporal resolution and capabilities for quantitative analysis and non-invasive observation, providing new prospects for deciphering the microscopic mechanisms and dynamic processes of photocatalytic reactions.^11–13

Compared with conventional microscopy techniques featuring a spatial resolution of a few hundred nanometers, super-resolution microscopy is characterized by remarkably improved spatial resolution.^14,15 Among the various super-resolution microscopic techniques, single-molecule fluorescence microscopy (SMFM) has emerged as a novel and promising tool for studying heterogeneous catalysis. In principle, SMFM relies on detecting the fluorescence of individual molecules whose intensity distributions follow an Airy pattern and can be well depicted by an approximate Gaussian profile.¹⁶ Through mathematical fitting, SMFM can precisely localize molecules with precision of up to a few nanometers.^17,18 By collecting a sufficient number of single-molecule events, a super-resolution image is reconstructed by merging the positions of all the individually activated fluorophores (Fig. 1). Additionally, SMFM imaging technology holds advantages in temporal resolution, i.e., at the millisecond level, allowing the capture of rapid reaction dynamics throughout the photocatalytic reaction. By employing high-speed imaging and sophisticated data acquisition strategies, these techniques can achieve sub-millisecond or even sub-nanosecond temporal resolutions.^19,20 The high spatiotemporal resolution enables, in a quantitative manner, the visualization of molecular interactions and surface restructuring, monitoring of reaction kinetics, real-time tracking of reaction intermediates, and probing the electron transfer process at a single-molecule level, shedding light on the reaction mechanisms and catalyst design. Another strength of SMFM is its capability to study catalytic processes in situ and under operando reaction conditions, providing valuable insights into the properties of photocatalytic nanomaterials in realistic applications.²¹ Furthermore, SMFM offers non-invasive observation capability, minimizing perturbations to the system under study. Unlike invasive probes or labeling techniques that may alter the properties of photocatalysts or interfere with reaction kinetics, fluorescence imaging allows for the label-free visualization of molecules and nanostructures with high specificity and sensitivity.²² This non-destructive imaging feature preserves the integrity of the sample and enables longitudinal studies of photocatalytic processes over extended periods, promoting the exploration of long-term performance, degradation mechanisms, and catalyst evolution.^23,24

Fig. 1 Schematic illustrating the principles of single-molecule fluorescence imaging.

In essence, SMFM is based on the detection of fluorescence signals, which requires the involvement of fluorescent species in imaging systems. When applying SMFM to study photocatalysis, fluorogenic reactions that can be catalyzed by photocatalytic nanomaterials are usually employed. In a typical fluorogenic reaction, non-fluorescent or weakly fluorescent reactant molecules are activated by catalysts and then converted into highly fluorescent product molecules, as indicated by the emission of fluorescence signals.²⁵ Even reactions involving fluorescent reactants can still be studied as long as their fluorescence wavelengths differ from those of the intermediates and/or products. Fig. 2 summarizes the fluorogenic reactions commonly used in the SMFM imaging of photocatalytic nanomaterials.^26–34 In this Review, we discuss the studies of photocatalytic nanomaterials via SMFM imaging, including plasmonic metals, semiconductors, metal–metal heterostructures, metal–semiconductor junctions, and semiconductor–semiconductor junctions. Recent advances in imaging techniques and methodologies, together with their implementation into studying bio-inorganic hybrids and non-fluorescent reactions/molecules, are also evaluated. We then highlight the major challenges and an outlook in broadening the application of SMFM techniques for investigating photocatalytic nanomaterials and reactions. We anticipate that these discussions could inspire researchers to explore more opportunities in this field.

Fig. 2 List of fluorogenic reactions for single-molecule fluorescence imaging of photocatalytic catalysis. The colored shade illustrates the approximate color of the fluorescence signal. (LDH = layered double hydroxide and BTTAA = (4-{[bis-(1-tert-butyl-1H-[1,2,3]triazol-4-ylmethyl)-amino]-methyl}-[1,2,3]triazol-1-yl)-acetic acid).

2. Plasmonic metal nanomaterials

2.1. Gold

Gold (Au) nanoparticles have been extensively investigated for various types of catalysis including thermal catalysis and plasmon-involved photocatalysis.^35,36 Owing to the capability to catalyze the fluorogenic reduction of non-fluorescent resazurin (Rz) into highly fluorescent resorufin (Rf), Au nanoparticles have been extensively investigated by SMFM to unravel the catalytic kinetics and mechanisms. Moreover, there exist a number of well-established protocols for synthesizing Au nanocatalysts with controllable size, facet, shape, morphology, etc., making Au an effective platform for studying the structure–property relationship via SMFM imaging.^37–40 The gained knowledge from SMFM imaging provides unprecedented insights into the mechanistic understanding and rational design of optimal Au nanocatalysts.

2.1.1. Thermal catalysis. Although the unique plasmonic effects stemming from light–Au interactions make Au a promising photocatalytic nanocatalyst, Au-catalyzed thermal catalysis has also been extensively investigated by SMFM.^41,42 To build a solid foundation for understanding plasmonic catalysis (discussed later), here, we provide a brief overview of SMFM imaging studies on Au-catalyzed thermal catalysis. One very early study of Au nanoparticle catalysts using super-resolution imaging was reported by Xu and co-workers, where they utilized the fluorogenic Rz reduction reaction by hydroxylamine to produce Rf, a strongly fluorescent molecule.⁴³ A typical setup for super-resolution fluorescence imaging is depicted in Fig. 3a, which is based on a total internal reflection fluorescence (TIRF) microscopy configuration.⁴⁴ In this TIRF configuration, an evanescent wave is generated at the quartz–solution interface with a penetration depth of a few hundred nanometers, which can effectively excite the fluorescent molecules at the interface region while avoiding illuminating outside areas that may cause high background noise. Typically, a microfluidic cell is fabricated by double-sided tape sandwiched between a quartz slide and a coverslip, with a proper density of Au nanoparticles drop cast and immobilized on the quartz slide. As the solution containing Rz and hydroxylamine is introduced, Au nanoparticles serve as the catalysts to catalyze the reduction reaction to generate the strongly fluorescent Rf molecules. An incident 532 or 561 nm laser is introduced to excite the fluorescence of Rf molecules in single-molecule detection by an electron-multiplying charge-coupled device (EMCCD). Fig. 3b displays a typical fluorescence turnover trajectory on a single Au nanoparticle. The stochastic off–on fluorescence bursts and constant on-level height characterize the single-molecule fluorescence detection. The waiting times τ_off and τ_on in these single-turnover fluorescence trajectories represent the time period before each Rf product formation and the time for Rf dissociation after formation, respectively. The digital nature of these waiting times helps to examine the kinetic mechanism of catalysis. While τ_off and τ_on have stochastic individual values, their statistical properties, such as average values and distributions, are well defined by the underlying reaction kinetics. In the study by Xu and co-workers, the redox catalysis of individual colloidal Au nanoparticles in solution was investigated.⁴³ The reduction of Rz was examined, focusing on understanding the catalytic kinetics involved. A single-molecule analysis helps to link a stochastic single-molecule quantity with traditional kinetic parameters, predicting the saturation kinetics of the product formation rate. As shown in Fig. 3c, to explain the dependency of the product dissociation rate 〈τ_on〉⁻¹ on the concentration of resazurin [Rz], researchers investigated a substrate-assisted product dissociation pathway, including a fast substrate adsorption equilibrium (reactions (I)), a pre-substrate-binding step (reactions (II) and (III)), in addition to direct dissociation (reaction (IV)). Averaging the turnover trajectories from numerous Au nanoparticles revealed that both 〈τ_off〉⁻¹ and 〈τ_on〉⁻¹, which correspond to the generation rate and desorption rate of Rf, respectively, depend on [Rz] and exhibit saturation kinetics. Researchers employed a pseudo-first-order reaction kinetics as excess hydroxylamine was introduced into the reaction. Interestingly, the [Rz]-dependent 〈τ_off〉⁻¹ effectively follows a Langmuir–Hinshelwood mechanism for the Rz reduction reaction (Fig. 3d), implying that the Au nanoparticles could catalyze the substrate conversion to the product while maintaining a fast substrate adsorption equilibrium.

Fig. 3 Super-resolution fluorescence imaging of thermal catalysis on Au nanoparticles. (a) Experimental scheme using TIRF microscopy to image the fluorogenic deacetylation reaction of Rz to Rf on Au nanoparticles. (b) Fluorescence intensity versus time trajectory of a single Au nanoparticle. (Panels a and b) are reproduced with permission from ref. 44. Copyright 2016, American Chemical Society. (c) Schematic of the kinetic mechanism. Au_m: Au nanoparticle; S: resazurin; P: resorufin. Au_m–S_n represents an Au nanoparticle having n adsorbed substrate molecules. (d) [Rz] dependence of 〈τ_on〉⁻¹. (Panels c and d) are reproduced with permission from ref. 43. Copyright 2008, Nature Publishing Group. (e) Dependence of the activity fluctuation rate of the τ_on reaction on TORs. Panel e is reproduced with permission from ref. 45. Copyright 2009, American Chemical Society. (f) 2D reactivity pattern of the Au nanorod. The vertical lines separate the side and end segments. (g) Dependence of specific TOR on location along the length of the nanorod in (f). (Panels f and g) are reproduced with permission from ref. 31. Copyright 2012, Nature Publishing Group. (h) Size dependencies of the specific activities of different regions as well as the nanoplate as a whole particle. Each data point is an average of similar-sized nanoplates. (i) Spatially resolved activity quantitation on single Au@mSiO₂ nanoplates. (Panels h and i) are reproduced with permission from ref. 49. Copyright 2013, American Chemical Society. (j) Arrhenius plot for reactions catalyzed by single Au nanoparticles (dotted lines) and the average over many nanoparticles (full lines) for the product formation process. Inset: solid lines are Gaussian fits with the center at 35.7 ± 0.5 kJ mol⁻¹. (Panel j) is reproduced with permission from ref. 44. Copyright 2016, American Chemical Society. (k) Distributions of the microscopic reaction time τ from a single Au@mSiO₂ nanorod. The solid red line is an empirical fit, with y = A(e^−k₁τ − e^−k₂τ). (Panel k) is reproduced with permission from ref. 53. Copyright 2014, American Chemical Society. (l and m) Intraparticle catalytic communication within single Pd nanocatalysts: (l) the photoinduced Rz disproportionation: Pearson's cross-correlation coefficient versus the intraparticle distance separation △x_ij. (m) Dependencies of the intraparticle catalytic communication distance x^intra₀ on the orientation angle relative to the electric-field direction at various voltages. (Panels l and m) are reproduced with permission from ref. 57. Copyright 2018, Nature Publishing Group.

For spherical nanocatalysts, their surfaces are enclosed by diverse facets and the proportion of each facet varies significantly over size, resulting in a size-dependent catalytic performance.⁴⁵ To this end, Xu and co-workers employed SMFM to study the size-dependent catalytic activity and dynamics of Au nanoparticles.⁴⁵ When 6.0, 9.1, and 13.7 nm Au nanoparticles were used as catalysts, the fluctuation rate was enhanced with increasing turnover rates (TORs; the number of fluorescence off–on cycles per unit time) (Fig. 3e), showing a linear correlation. In conjunction with the activity, the surface restructuring of Au nanoparticles also suggests a size dependence. The faster activity fluctuation rates for the smaller particles indicate that the catalysis-induced dynamic surface restructuring occurs more rapidly with decreasing particle size. Additionally, the unique size-dependent catalytic activity of Au clusters was investigated at the single-molecule level.⁴⁶ In general, reactant adsorption on catalysts has two distinctive adsorption mechanisms: competitive adsorption and non-competitive adsorption.⁴⁷ In competitive adsorption, reactants compete for the same surface sites, leading to a decreased reaction rate at high concentrations. In non-competitive adsorption, the rate of product formation rises with the reactant concentration and reaches saturation at high concentrations. In particular, smaller Au clusters follow the competitive Langmuir–Hinshelwood mechanism with a stronger substrate-binding ability and weaker product-binding ability, whereas larger Au clusters follow the non-competitive mechanism with opposite abilities. Researchers attributed this phenomenon to the different adsorption behaviors of the substrate and product molecules on the clusters, leading to the distinctive catalytic properties between Au clusters and traditional nanoparticles. These findings collectively highlight the pivotal role of particle size and surface defects in catalysis through investigations using SMFM.

Expanding their study beyond spherical Au nanoparticles, Xu and co-workers delved into the facet-dependent catalytic activity of Au nanoparticles using Au nanorods as the catalysts. The side facets of these nanorods are enclosed by {110} planes, whereas their ends are enclosed by {111} planes.³¹ As shown in Fig. 3f, the activity map on a single Au nanorod suggests that the side surface shows the highest activity at the center and decreasing activity towards the two ends, which was attributed to their distinctive facets and thus different adsorbate–catalyst interactions during catalysis. Given that single-molecule fluorescence imaging has a nanometer-level spatial resolution (much smaller than the length of Au nanorods (150–700 nm)), it allows the researchers to further study the sub-particle catalytic property. Significantly, the TORs of a single Au nanorod show a peak value in the center and then gradually decrease along its length (Fig. 3g). This observation indicated that within the same surface facets on a single nanorod, reactivity displays a gradient from the center towards its two ends, which could be rationalized by the linear decay in defect density stemming from the gradually decreased growth rate during synthesis.⁴⁸ The site-specific activity and radial activity gradient on single two-dimensional (2D) Au nanoplates were further investigated. Utilizing super-resolution fluorescence microscopy coupled with electron microscopy, Andoy et al. mapped out catalytic event locations within individual triangular and hexagonal Au nanoplates and found clear site-dependent catalytic behavior.⁴⁹ Specifically, when the Au nanoplate surface is dissected into flat facets, edges, and corners, the catalytic activity follows the order of corners > edges > flat facets (Fig. 3h). This disparity in activity can be explained by the different atom coordination numbers (CNs) of the corner, edge, and flat facets (CN_corner < CN_edge < CN_{flat facet}), as low-coordinated sites are typically more catalytically active for catalysis.^50,51 Even within the same flat {111} surface, the catalytic activity also exhibits a 2D radial gradient from the center toward the edges (Fig. 3i). Similar to the case of activity gradient in the nanorod side,³¹ the 2D radial activity gradient was also associated with the linear decay in growth rate when the nanoplate grew from a seed during synthesis.

By resolving the catalysis of individual nanoparticles at a single-turnover level, single-molecule fluorescence imaging also provides unprecedented insights into the mechanistic understanding of catalytic reactions.⁵² By introducing temperature as a new variant, Chen and co-workers successfully extracted, in a quantitative manner, the activation energy (E_a) for a classic fluorogenic reduction reaction between non-fluorescent Rz and hydroxylamine on single Au nanoparticles via single-molecule fluorescence imaging.⁴⁴ Specifically, E_a,on and E_a,off were derived for the product Rf formation and dissociation processes, respectively (Fig. 3j). The E_a,off (36.7 ± 1.1 kJ mol⁻¹) value obtained from the Au nanoparticles, with a wide range of activation energies (12–73 kJ mol⁻¹), suggests significant catalytic heterogeneity. In addition, the value of E_a,off is much larger than E_a,on (18.3 ± 1.3 kJ mol⁻¹), indicating that the product formation process is the rate-limiting step. Another capability of SMFM is to differentiate the reaction intermediates involved in a catalytic reaction, which is crucial for elucidating the reaction mechanisms but generally challenging due to their low populations in a reaction mixture. A compelling example can be found in the study of the oxidative deacetylation of Amplex Red (AR) by H₂O₂ catalyzed by mesoporous silica (mSiO₂)-coated Au nanorods, in which the mSiO₂ shell can effectively confine the generated fluorescent products for imaging.⁵³Fig. 3k illustrates the distributions of the microscopic reaction time τ from a single Au@mSiO₂ nanorod, which shows an initial rise and follows by the decay behavior with a delayed maximum at τ > 0. This rise-followed-by-decay behavior of τ distributions indicates that the catalytic kinetics in forming the product contains at least two sequential rate-determining steps, which suggests the existence of a hidden kinetic intermediate.^54–56 The distributions of τ could be fitted by an empirical equation: y = A(e^−k₁τ − e^−k₂τ), as indicated by the solid red lines shown in Fig. 3k, where k₁ and k₂ are the apparent rate constants for the two rate-determining steps straddling the kinetic intermediate, and A is a scaling factor. Interestingly, by investigating [AR]-dependent τ distribution, k₁ was found to be positively correlated with [AR] before reaching saturation, indicating that the associated rate-determining step involves AR. On the contrary, k₂ is independent of [AR]. Further experiments suggest that the hidden kinetic intermediate is probably a surface-adsorbed one-electron-oxidized AR radical.⁵⁴

In addition, spatiotemporally resolved single-molecule catalysis imaging can also unveil the interactions of reaction species. Recently, Zou and co-workers studied several fluorogenic reactions including the disproportionation of Rz, oxidative deacetylation of AR, and reductive deoxygenation of Rz on Pd nanorods, Au nanorods, and Au nanoplates, respectively.⁵⁷ Excitingly, they found that the catalytic reactions on a single Pd or Au nanocatalyst can communicate with each other. As shown in Fig. 3l, the cross-correlation coefficient ρ_τi,τj between τ_i (the microscopic reaction time of any catalytic event at a segment i) and τ_j (the time of the immediate subsequent event at another segment j) starts positive and decays exponentially with increasing intraparticle separation or time separation, indicative of effective spatial and temporal communication between reactions. Interparticle communication can occur over a distance of ∼10² nm and with a temporal memory of ∼10 to 10² s, giving rise to positive cooperativity among its surface active sites. Moreover, the intraparticle communication distance, x^intra₀, exhibits co-sinusoidal modulations versus the orientation angle to the electric-field direction, suggesting the involvement of positively charged messenger species in the communication (Fig. 3m). A similar communication behavior is also observed among different nanocatalysts, which operates via a molecular diffusion mechanism involving negatively charged species. As intraparticle and interparticle catalytic communications are quite common phenomena in catalysis, exploring their generality and utility via single-molecule catalysis imaging could contribute to the development of a novel conceptual framework for understanding nanoscale catalysis.

2.1.2. Plasmonic catalysis. Apart from thermal catalysis, plasmon-mediated photocatalysis, enabled by the localized surface plasmonic resonance (LSPR) of noble-metal nanoparticles, has offered a unique approach to enhance light-driven chemical conversions.^58,59 Unlike thermal catalysis involving solely chemical transformation, plasmonic photocatalysis entails the excitation of hot charge carriers and the transfer of these carriers from plasmonic nanostructures to the adsorbed reactants.⁶⁰ Understanding the crucial factors in this process, such as the rate-determining step and its E_a value, is vital for identifying the contribution of hot carriers.^61,62 SMFM has been proven to be a powerful tool in exploring the mechanism underlying plasmon-involved photocatalytic reactions.

Recently, Li and co-authors used SMFM to study an LSPR-enhanced photocatalytic reaction, i.e., the Au-catalyzed oxidation of non-fluorescent AR by H₂O₂ into fluorescent products Rf, with sub-turnover resolution (Fig. 4a).⁶³ Au nanorods with an aspect ratio of 3.6 and an LSPR excitation peak at 785 nm were investigated. Under laser illumination, Au nanorods displayed an average rate of product generation three-fold faster than that under dark conditions, indicating enhanced catalytic ability due to plasmon activation. The 〈τ_off〉 distribution for Rf formation exhibits a rapid increase followed by a gradual decrease as they identified earlier,⁵³ which could be attributed to the formation of an AR· radical. By adjusting the reaction temperature and analyzing the statistical results of individual turnovers, the activation energies E_a of tandem reaction steps, including intermediate generation, product generation, and product desorption, were distinctly identified. It was demonstrated that under dark conditions, E_a for AR· generation is significantly higher compared to that for Rf formation, suggesting that the intermediate AR· generation acts as the rate-limiting step. To validate the reduced E_a due to plasmon excitation, the isokinetic temperature (T_iso) was investigated. As shown in Fig. 4b and c, intersecting plots for reactions under both dark and light conditions indicate an isokinetic relationship in photocatalysis. Compared with the dark reaction, T_iso under laser illumination was decreased by 2 K, implying that the substrate might have a lower energy barrier to undergo structural transformation in the presence of light. It was, thus, speculated that the primary contribution to the decreased E_a value was due to plasmon enhancement, where plasmon-excited electrons can induce multiple vibrational transitions of the Au–O bond, thereby increasing the vibrational energy stored in the bond.⁵⁸

Fig. 4 Super-resolution fluorescence microscopy study of plasmonic reactions on Au. (a) Single-molecular catalysis identifying E_a of the intermediate product and rate-limiting step in plasmonic photocatalysis over Au nanorods. Inset: TEM image of Au nanorods. Isokinetic relationship of three groups of single Au nanorods with different average activation energies for the intermediate product formation process, plotted in the coordinates of 1000/T and the effective rate constants of intermediate product formation (ln γ_eff1) for (b) the dark reaction and (c) laser illumination. (Panels a–c) are reproduced with permission from ref. 63. Copyright 2020, American Chemical Society. (d) Calculated near-field intensity map of an Au nanorod that is 47 nm long and 25 nm wide. (e) Measured maximum fluorescence enhancement factors for 11 nanorods as functions of their SPR wavelengths under 594 nm (blue) and 633 nm (red) excitation. The theoretically estimated enhancement factors are shown as open circles. (Panels d and e) are reproduced with permission from ref. 65. Copyright 2014, American Chemical Society. (f) [AR] dependence of 〈τ_off〉 from AuCMs (green) and AuCDs (red). (g) Distributions of γ_app from about 50 trajectories of AuCMs (green) and AuCDs (red), and the solid lines are Gaussian fitting. (h and i) Schematics showing the conversion of pNTP catalyzed by (h) AuCMs and (i) AuCDs during SERS measurement. (j and k) FDTD simulations of the electric-field distribution of (j) the AuCM and (k) AuCD at 532 nm. (Panels f–k) are reproduced with permission from ref. 74. Copyright 2022, Chinese Chemical Society. (l) Illustration of the Au nanorods and potential enhancement mechanisms. (m) Average TORs against binned green irradiance with 200 nM Rz and 100 μM hydroxylamine. The inset shows the dark-field characterization. (n) TORs of the superficial and far events normalized by the unit area, including only particles with more than 50 events (upper panel). To visualize the different irradiance dependencies in both groups, the y axis is normalized to the activity in the lowest irradiance bin for the superficial and far categories (lower panel). (Panels l–n) are reproduced with permission from ref. 82. Copyright 2023, American Chemical Society.

In addition to promoting catalytic reactions, the LSPR effects of plasmonic nanoparticles could also effectively enhance the fluorescence of a weak emitter,⁶⁴ which is vital for broadening the applications of single-molecule fluorescence imaging to various unexplored systems. Thus, it is necessary to investigate the role of SPR in fluorescence enhancement to build a solid foundation for its further applications. To this end, Khatua et al. studied the fluorescence variation on individual Au nanorods and explored the role of SPR in performance enhancement.⁶⁵ They employed the discrete dipole approximation (DDA) method to assess the enhancement in excitation, radiative, and non-radiative rates of a crystal violet (CV) molecule near an Au nanorod. The nanorod was represented as an array of dipoles, with each dipole replacing cubic volume elements measuring 0.25 nm in size, and the SPR wavelengths could be adjusted by altering the nanorod length within the range of 39 to 60 nm while maintaining a constant width of 25 nm. The near-field intensity maps indicate that the maximum intensity enhancement occurs when the nanorod's SPR aligns with the wavelength of the excitation laser. Fig. 4d depicts the near-field intensity distribution of an Au nanorod with a width of 25 nm and a length of 47 nm (SPR at 629 nm) under 633 nm excitation, showcasing a maximum intensity enhancement of several hundred times when the nanorod's SPR aligns with the excitation wavelength. In addition, different spectral components of the CV emission spectrum will be enhanced by various degrees depending on their overlap with the SPR, corresponding to different radiative enhancement (E_rad) values. The fluorescence enhancement is greatly influenced by the nanorod SPR wavelength, reaching its peak when both the excitation laser and emission spectrum of the dye overlap with the SPR. At the optimal SPR wavelength, a remarkable fluorescence enhancement of 1100 times was observed, comprising a 130-fold increase in excitation rate and 9-fold improvement in effective emission. This notable enhancement encompasses an increase in the excitation rate as well as a substantial improvement in the decay rates of the emitter. Furthermore, researchers compared the experimental results with theoretical estimations, represented by open circles and dashed lines in Fig. 4e. One can easily conclude that the experimental findings closely align with the theoretical predictions in terms of both maximum enhancement factors and their dependence on the SPR wavelength.⁶⁶ Furthermore, Lu and co-workers demonstrated how single-molecule fluorescence can be significantly enhanced using a single Au nanorod. This enhancement enables the detection of molecules with extremely low quantum yields, such as 10⁻⁴, with a three-order-of-magnitude enhancement factor, whereas theoretical simulations suggest detection for molecules with quantum yields as low as 10⁻⁶.⁶⁷

Recently, researchers reported that the LSPR effects of plasmonic nanoparticles could be effectively regulated by controlling the size and morphology of nanocrystals as well as form dimers.^68–71 To further promote plasmon-driven catalytic reactions, it is crucial to design Au nanocatalysts with precise geometric structures and surfaces featuring low-coordination sites. Apart from Au nanorods, Au nanocubes have shown great promise due to their low-coordination corners and edges among various plasmonic metal nanostructures, resulting in significantly enhanced localized electromagnetic (EM) fields on individual nanoparticles or between coupled nanoparticles.^72,73 Using SMFM, Wang and co-workers observed a notable activity enhancement in the AR oxidation reaction on coupled Au nanocube dimers (AuCDs), compared with Au nanocube monomers (AuCMs).⁷⁴ They employed a substrate-supported assembly strategy to engineer this dimeric structure and utilized the non-fluorescent AR to fluorescent Rf as a model reaction. In contrast to AuCMs, the statistically analyzed TOR from individual AuCDs demonstrates a 3.2 times faster pace under saturating [AR] (Fig. 4f), which is attributed to enhanced spontaneous surface restructuring within the nanogap induced by the strong EM field. In addition, the distribution of the apparent rate constant γ_app for Rf generation on AuCDs (0.99 ± 0.16 s⁻¹ per particle) is broader compared to that of AuCMs (0.30 ± 0.12 s⁻¹ per particle) (Fig. 4g), signifying the increased reaction heterogeneity from the dimeric structure. The augmented hot carriers from AuCDs were confirmed through surface-enhanced Raman spectroscopy (SERS), in which p-nitrothiophenol (pNTP) was used as an electron acceptor to reveal hot carriers' involvement (Fig. 4h and i).^75,76 Briefly, pNTP, acting as a thiolated molecule, creates a tightly packed monolayer on Au surfaces. Under light illumination, the Au nanostructures produce hot electrons that transfer into pNTP on the surface, triggering a four-electron reduction process to produce p,p′-dimercaptoazobenzene (DMAB). Thus, the pNTP conversion efficiency represents the density of hot carriers. To provide further evidence of hot carriers promoting catalysis, they analyzed the catalytic products of AuCMs and AuCDs from pNTP using SERS, which shows the time-dependent SERS spectra. Interestingly, the results show little change in AuCMs, whereas characteristic DMAB peaks emerged on AuCDs with longer laser exposure. The efficiency was measured by comparing DMAB and pNTP peaks, revealing much higher efficiency for AuCDs relative to AuCMs, confirming their enhanced hot electron generation. In plasmonic nanoparticles, the transition of hot carriers from the ground state to a higher-energy state is primarily influenced by the EM field produced by plasmon resonance.^77,78 Therefore, the authors further used the finite-difference time-domain (FDTD) method to analyze the distribution of EM fields. As shown in Fig. 4j and k, the calculated EM-field enhancement factor of AuCDs is one-order-of-magnitude higher than that of AuCMs, leading to a higher density of hot electrons in both corners and within the nanogap. As a consequence, these hot electrons would facilitate spontaneous surface restructuring and ultimately lead to an improvement in catalytic activity at the single-particle level.

Although the plasmonic catalysts using LSPR have been widely studied to accelerate chemical reactions, the underlying mechanisms are difficult to decouple due to the involvement of multiple plasmon-derived phenomena, such as EM-field enhancement, thermal effect, and the generation of hot carriers. Untangling these effects exclusively presents a challenge but is essential for differentiating reaction pathways and increasing reaction rates.^79,80 To this end, Hamans and co-workers presented an in situ examination of a fluorogenic chemical reaction powered by plasmonic near-fields at the single-particle level.⁸¹ Employing SMFM, they established a direct link between the electric-field distribution surrounding individual nanoparticles and their finely resolved catalytic activity maps, which could be extended to systems with more complex electric-field distributions. Ezendam and co-workers attempted to address this challenge by employing ordered arrays of Au nanorods (length: 51 ± 7 nm; width: 28 ± 3 nm) coated with an ∼95 nm porous SiO₂ shell as nanocatalysts (AuNR@mSiO₂), which provide the advantage of simultaneously investigating numerous equivalent systems at once.⁸² The fluorogenic reaction used in this work was Rz reduction to Rf. The research delves into spatial reactivity distribution and correlations between turnover events, catalytic enhancements, temperature, and local-electric-field enhancement, aiming to uncover the simultaneous operation of multiple enhancement mechanisms (Fig. 4l). Although hot carriers are solely extracted from the plasmonic metal surface, temperature and field enhancements can spread to the surrounding area. Different decay behaviors of temperature and EM fields from the nanorod's surface could help discern the mechanism, and the spatial localization of single-molecule events may reveal the catalytically active region. Au nanorods exhibit two resonances, leading to different reactivity patterns: surface for hot carriers, near-surface for enhanced EM fields (transversal resonance excitation), and far surface for temperature (longitudinal resonance excitation). By investigating the correlations between the spatial distribution of turnover events, catalytic enhancements, temperature distributions, and local-electric-field enhancements over hundreds of nanoparticles, the mechanisms underlying plasmon-enhanced catalysis were uncovered. Specifically, the authors patterned individual AuNR@mSiO₂ nanoparticles on a cover slip using template dissolution interfacial patterning to create an array with controlled spacing (Fig. 4m, inset) and then assembled them under a microfluidic channel to maintain a continuous supply of reactants, enabling observations using a TIRF microscope. They first tracked the reduction of Rz to Rf, utilizing a 561 nm laser to excite the fluorescent Rf product and confirming the accessibility of the Au surface through hydroxylamine-induced TOR enhancement. To explore the impact of field enhancement, they further studied the impact of excitation power density on the reaction rate under illumination at 561 nm. As shown in Fig. 4m, the reaction rate initially increases and saturates at high power density, attributable to the saturation of catalytic sites on the Au surface. This saturation phenomenon is well described by a Langmuir–Hinshelwood mechanism for surface reactions, indicating a complex interplay between excitation power density and catalytic activity. Then, the spatial distribution of reactivity was examined for two distinct groups: those near the Au surface (<40 nm) and those far away (70–120 nm). Fig. 4n illustrates the relationship between the excitation power density and the activity of superficial and far events, showing that although superficial events exhibit higher activity, the proportion of far events increases with rising power density. These results indicate the presence of two reaction pathways: one catalyzed on the surface and another not involving the surface. Taken together, the reduction of Rz can take place through multiple reaction pathways, and the spatial distribution of enhancements was found to vary, depending on the underlying mechanism. All these collective findings significantly contribute to the fundamental understanding of plasmonic catalysis and the rational design of plasmonic nanocatalysts.

2.1.3. Modification of Au nanostructures. It is well documented that the catalytic property of nanomaterials can be well-tuned by alloying with a second metal, by which the catalyst surface–reactant interactions can be remarkably modulated.^83–85 However, owing to the lack of effective analytical tools that can spatially resolve catalytic reactions in situ, it remains a grand challenge to quantitatively understand the effects of these modifications on the catalyst–adsorbate interactions for mechanistic rationalization. To address this challenge, SMFM has demonstrated its capability to unveil the underlying mechanisms by quantitatively monitoring the kinetics of product formation and dissociation during catalysis.

In a recent study, using Ag and Au@AuAg nanoparticles as the catalysts, Qu and co-workers applied SMFM to investigate the alloying effect exerted by Au on the catalytic performance of Au nanoparticles using the fluorogenic AR oxidation by H₂O₂ as the probe reaction (Fig. 5a).⁸⁶ For this disproportionation reaction on Ag nanoparticles, the catalytic mechanism follows the non-competitive mechanism, where only AR molecules are adsorbed at the Ag sites by chemisorption. The results indicate that the presence of Au in Au@AuAg transforms the reaction pathway from a non-competitive to a competitive mechanism, where both H₂O₂ and AR prefer to adsorb on the Ag sites by chemisorption. In particular, the adsorption equilibrium constant of the competitive path is much higher than that of the non-competitive adsorption path. The synergistic effect between Au and Ag significantly enhances both reactant adsorption and product desorption, thereby boosting the catalytic activity. Density functional theory (DFT) calculations suggest that with an increase in the number of H₂O₂ molecules, the adsorption energy of AR on Au@AuAg nanoparticles increases from −2.36 to −3.08 eV (Fig. 5b). In contrast, the adsorption of AR on Ag nanoparticles remains unaffected by H₂O₂, indicating an adsorption-promoting effect through modification. To further substantiate the influence of H₂O₂ on adsorption, the difference between the adsorption energy of reactants and products (ΔE) was compared (Fig. 5c). Specifically, ΔE of Au@AuAg nanoparticles significantly exceeds those of Ag nanoparticles, and their difference is further amplified upon the addition of H₂O₂, indicating a strong electronic interaction between H₂O₂ and the Au@AuAg surface. Taken together, compared with Ag nanoparticles, Au@AuAg nanoparticles exhibit distinctive features, including a strengthened affinity for AR and H₂O₂, leading to increased reactant adsorption rates and creating a pathway for product formation. Furthermore, the introduction of Au suppresses spontaneous surface reconstruction and facilitates reaction-induced catalyst surface restructuring, thereby enhancing the catalytic efficiency and stability.

Fig. 5 Modification of nanocatalysts. (a) Schematics of the reaction pathway of AR oxidation on AuAg@Ag (left) and Ag particles (right). (b) DFT results showing the adsorption energy of a single AR molecule on Au@AuAg nanoparticles and Ag nanoparticles with different numbers of H₂O₂ molecules. (c) DFT results showing the adsorption energy difference (ΔE) between Rf and AR molecules on Au@AuAg nanoparticles and Ag nanoparticles. (Panels a–c) are reproduced with permission from ref. 86. Copyright 2022, American Chemical Society. (d) Schematic illustrating the role of plasmonic effects of Au nanoparticles in enhancing the photocatalytic HER ability of CoTPyP molecular catalysts. (e) HER rates of Ru(bpy)₂/CoTPyP and AuNP@CoTPyP in air and at 50 °C. (f) Scheme of the AuNP@CoTPyP-catalyzed Rz reduction in SMFM. (Panels d–f) are reproduced with permission from ref. 90. Copyright 2023, Nature Publishing Group.

In addition, the catalytic performance of molecular catalysts can also be modified by introducing plasmonic metal nanoparticles, in which the plasmonic effects of localized EM field, local heating, and enhanced hot-carrier excitation may play critical roles.^87–89 Recently, Sheng and co-workers developed a highly efficient and stable molecular catalyst by compositing a molecular catalyst of cobalt porphyrin with plasmonic Au nanoparticles.⁹⁰ Au nanoparticles with an average diameter of approximately 15 nm were used as the plasmonic nanostructures, whereas cobalt porphyrin (5,10,15,20-meso-tetrakis(4-pyridyl)porphyrin (CoTPyP)) molecules were used due to the strong coordination bonds between pyridine groups and heavy metals. As such, the CoTPyP molecules could be easily adsorbed onto the surface of Au nanoparticles, forming an organic–inorganic hybrid nanostructure (AuNP@CoTPyP) (Fig. 5d). Interestingly, the generation rate of fluorescent Rf products, formed by reducing Rz with H₂, which directly reflects the HER activity, using the AuNP@CoTPyP catalyst was 4.6 times greater than that of the Ru(bpy)₂/CoTPyP (Ru(bpy)₂ is a traditional photosensitizer) catalyst where plasmonic metals are absent (Fig. 5e). The HER rate and turn-over frequency (TOF) for AuNP@CoTPyP catalysts reach 3.21 mol g⁻¹ h⁻¹ and 4650 h⁻¹, respectively. But when CoTPyP molecules are used as catalysts in the absence of Au, a very low HER rate of ∼0.09 mol g⁻¹ h⁻¹ was observed. Furthermore, the catalytic performance of the AuNP@CoTPyP nanostructures remained stable after two weeks of exposure to light illumination, indicating the high stability of the hybrid photocatalyst. To probe the function of the plasmonic effect in boosting the catalytic performance of CoTPyP, SMFM imaging based on the Rz reduction reaction was conducted by studying the spatial heterogeneity of the reaction around AuNP@CoTPyP nanostructures (Fig. 5f). The results confirm the considerable contribution of LSPR excitation in HER enhancement, which was also confirmed by the FDTD simulation results. Moreover, the authors studied the role of interface charge transfer in enhancing the HER activity and found that the plasmon-generated hot electrons could transfer from AuNPs to CoTPyP molecules, leading to improved charge transfer and separation at the interface, ultimately enhancing the HER performance. DFT calculations further support these findings by showing that AuNPs favor the excitation of CoTPyP molecules and promote the HER reaction by altering the Gibbs free energies and electronic structure. In summary, the above studies affirm the versatility of SMFM in revealing the origin of catalytic activity in modified catalysts, shedding light on the understanding of reaction mechanisms.

2.1.4. Plasmonic cavity catalysis. In addition to tailoring the morphology and composition of catalysts described above, employing confined EM fields has emerged as a promising method for regulating the catalytic properties of plasmonic nanomaterials.^91–93 Plasmonic cavities, characterized as charge density waves simulated by EM waves, offer an alternative form of a confined EM field.⁹³ Acting as a unique mediator between light and free electrons, plasmonic cavities allow for focusing light into the nanoscale to excite polaritons, enhancing the local density of states (DOSs) confined in a microcavity that can form standing waves and create periodic plasmonic hotspots at the metal–dielectric interface.^94–98 Most significantly, this standing plasmonic wave allows further manipulation of the distributions of energy and hot carriers for tuning the catalytic properties of plasmonic metals. To probe the plasmonic cavity catalysis enabled by standing hot carrier waves, Lyu and co-workers employed a combination of experimental and simulated approaches to study the Au-plasmon-catalyzed AR oxidation reaction.^99,100 Owing to the nanometer-level spatial resolution, SMFM enables the study of the sub-particle catalysis of Au nanoplates with an edge length of ∼1–3 μm. In the plasmonic cavity, SPP refers to the plasmonic charge density wave that can be confined to a 2D Au nanoplate and form standing waves at the surface, which can also propagate along a planar metal surface as traveling waves. However, the excitation of the SPP mode requires momentum matching and thus typically requires total internal reflection illumination (Fig. 6a). However, for the cavity mode, it is achieved by vertical coherent excitation (Fig. 6c). Simply by illuminating Au nanoplates using light with different incident angles, the catalytic mode of Au nanoplates can be switched between the SPP and cavity modes. Fig. 6b and d shows the locations of product molecules on three Au nanoplates operated in the SPP and cavity modes, respectively. Clearly, in the SPP mode, a majority of the products are located at the corner areas and the number of products gradually decays away from the corner areas (Fig. 6b), which is also independent of the plate size. In sharp contrast, most of the products for the cavity mode are distributed at the center of the Au nanoplate, and the area of the product distribution pattern is enlarged along with the size of the Au nanoplate. The locations of detected fluorescent products under different excitation modes effectively reflect the distributions of EM waves in the SPP and cavity modes, offering an effective method for monitoring the diverse modes in the plasmonic cavity. Through an analysis of a large number of particles, the authors found that the catalytic activity in the cavity mode exceeds that in the SPP mode by more than two orders of magnitude (Fig. 6e). This is attributed to the highly concentrated energy and charge carriers in specific regions through the mode in the standing-wave resonator, which further amplifies the plasmonic resonance and the generation of more energetic hot carriers. In addition to the size effect, Au nanoplates also display distinctive shape dependence under different excitation modes. As shown in Fig. 6f, the shape evolution of Au nanoplates from triangle to hexagon leads to corresponding alterations in catalytic hotspots: transition from three spots near the corners to six spots forming a hexagon. Periodic catalytic hotspots could be effectively adjusted by manipulating the cavity geometry, charge density, and excitation angle. To rationalize the mechanisms of plasmonic cavity catalysis, researchers employed femtosecond interferometric scattering microscopy (Femto-iSCAT) to explore the distribution and dynamics of hot carriers in single Au nanoplates. Excitingly, the distributions of hot carriers on Au nanoplates effectively match the locations of catalytic hotspots, validating the critical role of hot carriers in plasmonic cavity catalysis. In brief, plasmonic cavity catalysis outperforms and surpasses the robustness of optical cavity catalysis, offering a versatile and broadly applicable approach to plasmon-driven chemical reactions.

Fig. 6 Plasmonic cavity catalysis by standing hot carrier waves. (a) Schematic of the SPP mode via total-internal-reflection excitation. k′, wavevector of SPP. (b) Locations of product molecules on three Au nanoplates in the SPP mode. (c) Schematic of the cavity mode via vertical excitation. k, wavevector; E, electric field. (d) Locations of product molecules on three Au nanoplates in cavity mode. (e) Normalized statistical catalytic activity of the SPP mode and cavity mode. (f) Locations of product molecules overlaid on the SEM images of the Au triangles varying in shape. All the scale bars in (panels b and d), and f are 1 μm. All the panels are reproduced with permission from ref. 99. Copyright 2023, American Chemical Society.

2.2. Other plasmonic metals

In addition to Au-based nanoparticles, researchers have also extended SMFM to study other plasmonic metals including silver (Ag) and copper (Cu). By exciting fluorophores remotely using plasmons propagating along Ag nanowires, Su and co-authors investigated the impact of the plasmonic effect on molecular fluorescence point spread functions (PSFs) using an improved single-molecule switching fluorescence microscopy technique (Fig. 7a).¹⁰¹ The authors chose Alexa 647 as the label for Ag nanowires and the distance between the dyes and the surface of nanowires is estimated to be 7–15 nm,^102,103 which is in the range where both enhancement and quenching of molecular fluorescence can occur by interaction with the metal.^104–107Fig. 7b illustrates a series of PSFs observed on a segment of an Ag nanowire under remote excitation, in which a 633 nm laser is focused at the end of the nanowire to launch SPPs that propagate >10 μm along the wire to excite Alexa molecules adsorbed within the SPP near-field. Fluorescence spots are generally observed at the edge of the nanowire, but with distinctive complexity in terms of the appearance location and number of PSFs, such as symmetric single-spot PSFs (Fig. 7b(i)), elongated single-spot PSFs (Fig. 7b(ii)), symmetric two-spot PSFs appearing at opposite sides of the wire (Fig. 7b(iii)), and four-spot PSFs with two spots on either side of the nanowire (Fig. 7b(iv)). However, after fitting each PSF via a 2D Gaussian function, the reconstructed image cannot precisely reproduce the nanowires (Fig. 7c), showing a clear overestimate (490 nm vs. 250 nm). A similar phenomenon of PSF distortion was also reported by Baiyasi and co-workers, in which they found that the presence of plasmonic effect could lead to an overestimate of >60 nm when measuring the exact width of nanoparticles using SMFM.¹⁰⁸ The combination of switching fluorescence microscopy and remote excitation unveiled a complex array of single-molecule fluorescence PSFs, influenced not only by the nanowire dimensions but also by the position and orientation of molecular transition dipoles. To further validate these observations, the authors employed a simulation method to generate a comprehensive set of PSFs for molecule positions and orientations on Ag nanowires with theoretical diameters of 110 and 250 nm. Subsequently, each simulated PSF was fitted to a single- or multicomponent 2D Gaussian function, and the simulated “molecule” positions were recorded at the centroid of each Gaussian peak. For simulated 250 nm-diameter nanowires, as shown in Fig. 7d, the histograms representing the cross-sections of these simulated localization maps closely matched those obtained experimentally (Fig. 7b). However, a line of molecular localization exactly along the nanowire is predicted by the simulations, but was not observed in wide-field or remote excitation switch fluorescence microscopy imaging, which was attributed to the potential photobleaching of dyes in direct contact with the glass substrate during the imaging process. Additionally, they proposed a method for rapidly classifying the size of metal nanoparticles using far-field optical imaging and a technique for determining the direction and position of molecules adsorbed on metal nanoparticles. Taking Ag nanowires as an example, this research holds implications for both single-molecule-regime sensing and super-resolution imaging involving metallic nanoparticles, opening up new possibilities for potential applications in improving photovoltaics, photocatalysts, and (bio)chemical sensors based on their sizes classification of metal nanoparticles.

Fig. 7 SMFM study of catalysis on Ag and Cu nanoparticles. (a) Schematic of the wide-field excitation of the Alexa 647-labeled silver nanowire. Legends on the right denote the components for labelling the Ag nanowire. (b) A series of PSFs of single-molecule fluorescence in the vicinity of a silver nanowire observed during RE-SFM measurement. (c) Cross-sectional histograms of “molecule” localizations perpendicular to the nanowire long axis for the simulated PSFs of the full range of molecular adsorption positions and orientations for nanowires of 250 nm. (d) Experimental scheme using TIRF and a microfluidic reactor to image the fluorogenic click reaction between phenylacetylene and CalFluor 647 azide catalyzed by individual copper nanowires. (Panels a–d) are reproduced with permission from ref. 101. Copyright 2015, Nature Publishing Group. (e) Experimental scheme using TIRF microscopy and a microfluidic reactor to image the fluorogenic click reaction of phenylacetylene to CalFluor 647 azide catalyzed by individual copper nanowires. (f) 2D kernel density plot of the measured emission positions for single CalFluor 647 triazole molecules. (g) Correlation between the ratio of turnover near the end vs. center segments of the nanowires as a function of nanowire lengths. Each open circle is one nanowire. The solid squares are binned and averaged results. (h) SEM image of a tapered copper nanowire of 11.7 μm in length. The surface defects can be found along the nanowire. The white arrow points to the start of nanowire growth. (i) The specific catalytic rate constant g of six segments of the nanowire. (j) Reactant adsorption equilibrium constant K of each segment from (i). (Panels e–j) are reproduced with permission from ref. 112. Copyright 2020, American Chemical Society.

In the context of click reactions, Cu nanoparticles have emerged as versatile catalysts to produce a triazole product via the reaction between an azide and a terminal alkyne owing to the high surface-to-volume ratio, outstanding activity and selectivity, and high stability.^109–111 It is well documented that click reactions are significantly dependent on the surface structures of nanocatalysts, making it necessary to understand the underlying structure–property relations.^31,49 Recently, Ow and co-workers employed SMFM to probe the nanoscale activity pattern of Cu nanowires toward a fluorogenic click reaction between CalFluor 647 azide and alkyne for the generation of CalFluor 647 triazole.¹¹² In a typical imaging experiment of Cu nanowires, researchers dispersed the nanocatalysts on the functionalized glass coverslip of a microfluidic cell and applied a continuous flow of the reactant solution containing CalFluor 647 azide, phenylacetylene, sodium ascorbate, and (4-{[bis-(1-tert-butyl-1H-[1,2,3]triazol-4-ylmethyl)-amino]-methyl}-[1,2,3]triazol-1-yl)-acetic acid (BTTAA) (Fig. 7e). Within a single Cu nanowire, site-specific activity exhibits variations across different regions (Fig. 7f), and the activity ratios between end regions and side facets are dependent on the nanowire's length. As shown in Fig. 7g, super-resolution imaging reveals a growing turnover density ratio between segments near the end and those at the center as the nanowire length increases. Recent investigations on Cu nanowires revealed that the growth rate of Cu nanowires is kinetically constrained by the diffusion rate of dihydroxy copper(I) to the end of the nanowire.^113,114 Therefore, as the growth rate decreases due to reactant depletion, a decreasing gradient of surface defects from the center segment to the two ends of the nanowire may account for the observed reactivity gradient. In a compelling example of Cu nanowire with a tapered structure (Fig. 7h), both end segments exhibit higher catalytic reactivity than their side segments, as indicated by the larger g values (g is the specific catalytic rate constant) (Fig. 7i). Surprisingly, the adsorption affinity K was found to show an opposite trend (Fig. 7j), with a larger g correlated with a smaller K. Building on the above information, the authors concluded a fundamental structure–property relation for the Cu-nanowire-catalyzed click reaction: the higher catalytic activity at the ends of Cu nanowires suggests that the two ends are less crystalline, structurally less coordinated, and functionally more reactive in click reactions; however, a reactivity gradient along the side indicates a decrease in similar physical and structural features along the length of the Cu nanowires.

Additionally, Decan and co-workers employed SMFM to unveil that copper-in-charcoal, a highly effective click catalyst, displays remarkably sparse catalytic sites, with only a tiny fraction of the surface being active.¹¹⁵ Leveraging the intermittent nature of these catalytic events, sub-diffraction resolution facilitates a precise mapping of these catalytic sites. Moreover, Zhang and co-workers proposed a fluorescence-free super-resolution imaging technique for Au and Ag nanoparticles, utilizing enhanced dark-field illumination and wavelength modulation.¹¹⁶ By resolving the coordinates of nanoparticles and their orientation angles, remarkable sub-diffraction limit images were obtained, showcasing potential applications in live-cell imaging.

3. Semiconductor nanomaterials

3.1. TiO₂

Fluorescence-responsive single-molecule microscopy has found widespread use in enzyme catalysis owing to its high spatiotemporal resolution, non-invasive analysis, and capability of studying single-enzyme kinetics.^117,118 Recently, building on the above merits, researchers extended SMFM to study heterogeneous catalysis involving semiconductor nanomaterials. In one of the earliest studies, Roeffaers and co-authors applied this technique to monitor the fluorogenic reaction of 5-carboxyfluorescein diacetate (C-FDA) and 1-butanol via counting single-turnover events for mapping the spatial distribution of catalytic activity on [Li⁺–Al³⁺] layered double hydroxide (LDH) (Fig. 8a).²⁶ They discovered that ester hydrolysis predominantly takes place on the lateral {1010} crystal faces, whereas transesterification occurs across the entire outer crystal surface. At almost the same time, Majima and co-workers examined the photocatalytic processes occurring on TiO₂ nanostructures using TIRF microscopy.¹¹⁹ They found that active oxygen (O_x) is probably the hydroxyl radical (·OH) generated after the decomposition of H₂O₂ by ultraviolet (UV) light. Subsequently, they attempted to selectively detect ROSs in air diffusing from the surface of pristine and N-doped TiO₂ nanoparticles at the single-molecule level.¹²⁰ Under UV excitation, both singlet oxygen (¹O₂) and hydroxyl radical (·OH) were detected on pristine and N-doped TiO₂. However, under visible-light excitation, ¹O₂ was only detected on N-doped TiO₂ (Fig. 8b and c). Moreover, further investigation on the spatiotemporal distribution of ·OH intermediates suggests that the ·OH molecules should be generated from the photolysis of H₂O₂ and not in air or on the glass surface but rather on the UV-irradiated TiO₂. These results, anticipated based on their formation mechanisms but unattainable through conventional measurements, affirm the validity of the methodology employed in the single-molecule detection of ROS in this study.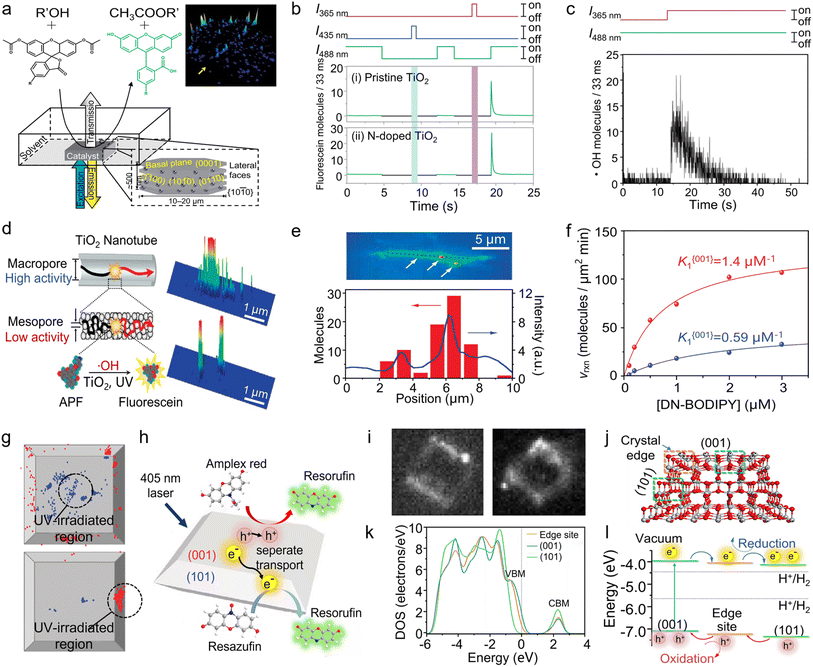

Fig. 8 (a) Schematic of the experimental setup for the single-molecule catalysis imaging of a single LDH particle. The inset at the lower right shows the different facets of a hexagonal LDH crystallite with indication of the Miller indices. The inset at the upper right shows the accumulated spot intensity on the same crystal over 256 consecutive images. (Panel a) is reproduced with permission from ref. 26. Copyright 2006, Nature Publishing Group. (b) The detected number of fluorescein molecules using pristine and N-doped TiO₂ under the alternative irradiation with UV or visible light. The initial value of the burst corresponds to the number of ·OH molecules diffused from the TiO₂. (c) Real-time single-molecule detection of the airborne ·OH diffused from the surface of pristine TiO₂ under the simultaneous 365 nm irradiation. (Panels b and c) are reproduced with permission from ref. 119. Copyright 2008, American Chemical Society. (d) Schematic of the photocatalytic reaction occurring on a single nanotube and the detection of fluorescent products. (e) Integrated fluorescence intensity of the TiO₂ nanotube over 120 s during the photocatalytic reaction. There are three highly active sites indicated by arrows. The line profile of the integrated fluorescence intensity along the long axis is shown by a dotted line (blue) and the histogram of the number of fluorescein molecules generated at the position, which is determined from the peak of the Gaussian distribution (red). (Panels d and e) are reproduced with permission from ref. 120. Copyright 2008, American Chemical Society. (f) Fluorescence image of a representative single-molecule event (i) and transmission image overlay with the distribution of fluorescent events (ii) of the same TiO₂ crystal in a DN-BODIPY solution under 488 nm laser irradiation. The scale bars are 4 μm. The inset in (i) shows the expanded image, as indicated by the arrow, and the cross mark in the inset shows the location of the reactive site. (iii) DN-BODIPY concentration dependence of the reduction reaction rates obtained for {001} (blue) and {101} (red) facets of a single TiO₂ crystal. (g) Location of fluorescence bursts on the {001} (blue) and {101} (red) facets. The UV-irradiated areas are inside the black circles (diameter, 2 μm). (Panels f and g) are reproduced with permission from ref. 129. Copyright 2011, American Chemical Society. (h) Schematic showing the photocatalytic AR oxidation and Rz reduction on a single TiO₂ particle. (i) Fluorescent images showing the formation of fluorescent products on a single TiO₂ particle via AR photooxidation (left) and Rz photoreduction (right). (j) Model of anatase TiO₂ with both (001) and (101) surfaces and their crystal edge. (k) DOSs of the edge site, (001) surface, and (101) surface of the cluster model without the scissor operator. (l) Relative energy levels of the bands for different photocatalytic sites from the positions of the valence band maximum and the conduction band minimum in DOSs and the flow route of photogenerated charge carriers. (Panels h–l) are reproduced with permission from ref. 130. Copyright 2019, National Academy of Sciences.

Recently, TiO₂ photocatalysts with a hollow structure, such as hollow spheres and nanotubes, have been explored owing to the high specific surface area, excellent molecular selectivity, and efficient light adsorption.^121–123 This unique hollow structure allows the exposure of more surface atoms for accessing reactant molecules, thereby enhancing the catalytic performance. However, the structural heterogeneities, such as disorder and agglomeration, present inside the bulk catalyst considerably impede the efficient transport of molecules, which cannot be explicitly differentiated by the conventional performance evaluation based on ensemble measurements.^124,125 To this end, Naito and co-workers investigated the photocatalytic activity of individual porous TiO₂ nanotubes via the single-molecule counting of hydroxyl radicals (·OH) using a fluorogenic reaction, i.e., the oxidation of weakly fluorescent probe, 3′-(p-aminophenyl) fluorescein (APF), into strongly fluorescent fluorescein¹²⁶ (Fig. 8d). Through the temporally and spatially resolved observations of emissive fluorescein molecules on single porous TiO₂ nanotubes, it was found that the fluorescein intensity from the mesopores is one-order-of-magnitude smaller than that from the macropores, despite the potential advantage of the mesopores' smaller volume facilitating the accumulation of ·OH. These findings suggest that the kinetics of reagent transport significantly affect the photocatalytic activity. Fig. 8e illustrates the distribution of catalytically active sites on the surface of TiO₂ nanotubes, corroborating the presence of spatial heterogeneity among the catalytically active sites within individual TiO₂ nanotubes.

Identifying active sites on semiconductor catalysts and elucidating the kinetics of photogenerated electron–hole pairs are imperative for designing optimal catalysts with improved photocatalytic efficiency.^127,128 Owing to the nanometer-level spatial resolution, SMFM has demonstrated its capability in probing the nature of charge carriers and their distributions. As depicted in Fig. 8f, TIRF microscopy was employed to examine the crystal-facet-dependent photocatalytic reduction of 3,4-dinitrophenyl-BODIPY (DN-BODIPY) on individual anatase TiO₂ bipyramidal nanoparticles.¹²⁹ Based on the distribution of detected single-molecule events and the [DN-BODIPY]-dependent reaction rate, the lateral {101} facets were found to be catalytically four times more active than the basal {001} facets. Meanwhile, DN-BODIPY adsorption on TiO₂ also shows facet dependence, with the adsorption equilibrium constant K of 0.59 and 1.4 μM⁻¹ on the {001} and {101} facets, respectively. Moreover, when UV light irradiated the (001) facet of TiO₂ through a 100 μm pinhole, fluorescent product molecules were also detected on the (101) facets without direct irradiation (Fig. 8g). In sharp contrast, when the (101) facet was selectively irradiated by UV light, the (001) facet exhibited significantly reduced the catalytic activity. These observations imply that the {101} facets may function as reservoirs for photogenerated electrons.

Later on, Wang et al. further investigated the charge carrier distributions on individual TiO₂ bipyramidal nanoparticles by using the electron (e⁻)-catalyzed Rz reduction to Rf and hole (h⁺)-catalyzed AR oxidation to Rf as the probe reactions via SMFM (Fig. 8h).¹³⁰Fig. 8i shows the representative TIRF images of TiO₂-catalyzed fluorogenic reactions under laser irradiation, with the bright spots indicating the occurrence of AR oxidation to Rf (left panel) and Rz reduction to Rf (right panel). Notably, the fluorescent product distribution suggests that the edges and corners of the crystals are catalytically more active than the basal {001} facets for both oxidation and reduction reactions. Analysis of the DOSs within the cluster model highlights that the energy band structure at the crystal edges is distinctive from those at the {001} and {101} surfaces (Fig. 8j), suggesting that the edges where the {001} and {101} surfaces converge serve as pivotal accumulation points for photogenerated electrons and holes, thereby acting as effective sites for redox reactions (Fig. 8k and l).

Photoelectrochemical water splitting represents a promising technology for green hydrogen production, which, however, is limited by the sluggish anodic water oxidation reaction, i.e., oxygen evolution reaction (OER).^131–133 To enhance the efficiency of photogenerated holes in oxidizing water, oxygen evolution catalysts (OECs) are typically used to increase the photocurrent and reduce the onset potential.¹³⁴ Nonetheless, the use of excess OECs would hinder light adsorption and deteriorate the performance of photoanode catalysts.^135,136 Thus, it is necessary to precisely localize the optimal deposition sites for OECs by differentiating the heterogeneous surfaces on photocatalysts. To overcome this challenge, Sambur and co-workers introduced an innovative approach via the integration of single-molecule fluorescence imaging, sub-particle photocurrent mapping, and site-selective co-catalyst deposition on individual photocatalysts for rationalizing and enhancing the performance of rutile TiO₂ photoanodes in water-splitting reactions.³³ In a typical apparatus, rutile TiO₂ nanorods with proper density were dispersed on transparent indium tin oxide (ITO), which was sandwiched with a coverslip to form a microfluidic photoelectrochemical cell and served as the working electrode (Fig. 9a). An Ag/AgCl electrode and Pt wires were placed at the outlet of the microfluidic cell, serving as the reference and counter electrode, respectively, for connecting to an electrochemical workstation. By mapping the distributions of charge carriers on individual TiO₂ nanorods using h⁺-induced AR oxidation and e⁻-induced Rz reduction reaction, respectively, the authors found that the most active sites for both h⁺-induced oxidation and e⁻-induced reduction reaction are identical, which are also the most important sites for hole–electron recombination (Fig. 9b). These sites form catalytic “hotspots” on TiO₂ nanorods and should originate from surface structural defects.

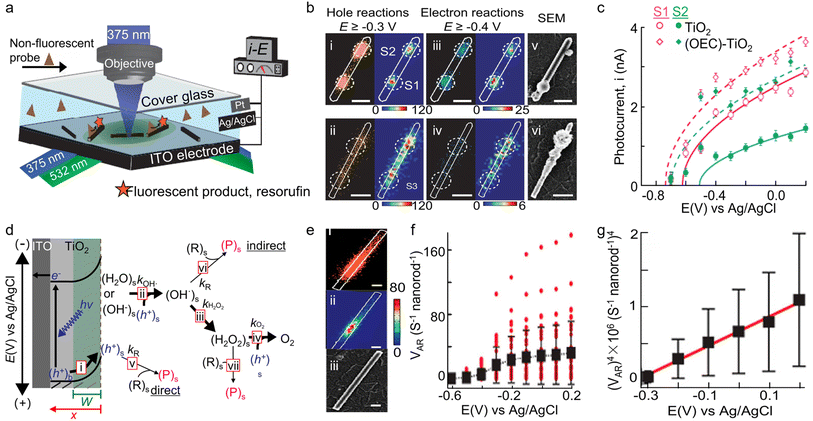Fig. 9 (a) Schematic of the experimental setup for wide-field charge carrier chemical imaging of photoelectrocatalysis via TIR excitation by 375 and 532 nm lasers or sub-particle photocurrent mapping by focused 375 nm laser excitation, in a three-electrode photoelectrochemical microfluidic device. (b) Super-resolution mapping of the electron- and hole-induced reactions on the surface of individual TiO₂ nanorods. (c) i–E curves from spots S1 and S2 before and after OECs deposition. (Panels a–c) are reproduced with permission from ref. 33. Copyright 2016, Nature Publishing Group. (d) Illustration of photoelectrooxidation of an organic substrate R to a product P and of H₂O/OH⁻ to O₂ on a TiO₂ photoanode. (e) Scatter plot (i) and 2D histograms in 40 × 40 nm² pixels (ii) of all the individual P molecules (orange dots) generated from h⁺-induced AR oxidation reactions. The white line is the nanorod structural contour from its SEM image (iii). The scale bars are 200 nm. (f) Single-molecule AR oxidation rate (v_AR) for 37 individual nanorods (red dots) and the average v_AR over 37 nanorods (black squares). Error bars represent SD. (g) Nanorod-averaged v_AR data from (G) plotted as v_AR⁴versus potential for E ≥ −0.3 V. Error bars represent error propagated SEM. (Panels d–g) are reproduced with permission from ref. 141. Copyright 2016, American Chemical Society.

To probe local water oxidation efficiencies, the authors focused a 375 nm laser on a nanorod spot and measured the potential-dependent photocurrents through the three-electrode microfluidic cell (Fig. 9a). Surprisingly, they found that spots with higher hole and electron activities also show larger photocurrents, indicating that higher surface activity is related to higher water oxidation efficiency. To further enhance the photoelectrocatalytic performance of TiO₂ nanorods, the authors proposed a sub-particle, site-selective deposition of OECs on the TiO₂ surface spots with high or low activity. Significantly, depositing OECs on both the high- and low-activity spots led to a remarkable enhancement in photocurrent (Fig. 9c). Moreover, it was discovered that the optimal catalyst deposition sites for photocurrent enhancement are the lower-activity sites, whereas for overpotential reduction, the optimal sites are these with more positive onset potentials (Fig. 9c). These findings provide an activity-based strategy for rationally engineering catalyst-improved photoelectrodes for photoelectrochemical water splitting.

Apart from water splitting, the generated holes in semiconductor photocatalysts can also be utilized to degrade micropollutants via oxidation reaction for water decontamination in either a direct or indirect manner.¹³⁷ For direct oxidation, holes are transported from the semiconductor interior to the semiconductor–electrolyte interface.^138,139 However, for indirect oxidation, holes are consumed by water oxidation and generate ROSs such as hydroxyl radical and superoxide anion, which further degrade the micropollutants (Fig. 9d).¹⁴⁰ However, the underlying mechanism for micropollutant degradation remains unclear owing to the lack of analytical tools. Recently, Sambur and co-workers employed quantitative single-molecule, single-particle fluorescence imaging to measure the photoelectrocatalytic oxidation rate of a model organic substrate, AR, on the surface of individual rutile TiO₂ nanorods.¹⁴¹ When the oxidation reaction occurs, AR molecules are oxidized into Rf molecules, which are strongly fluorescent and can be detected by microscopy imaging at the single-molecule level (Fig. 9e). Based on the calculation of reaction kinetics, the AR oxidation rate v_AR shows distinctive dependence on the light intensity I₀ and applied potential E. For the direct mechanism, v_AR should scale with I₀ and (E)^1/2, which is inconsistent with the measured results (Fig. 9f and g). For the indirect mechanism via reaction with surface-adsorbed H₂O₂, v_AR should be independent of both I₀ and E, again inconsistent with the data (Fig. 9f and g). Significantly, for the indirect mechanism via surface adsorbed ·OH, v_AR is predicted to scale with (I₀)^1/2 and potential (E)^1/4, in agreement with the experiment results (Fig. 9f and g). The light-intensity- and potential-dependent scaling relations demonstrate the indirect oxidation mechanism for AR degradation, offering new insights into the underlying mechanism of micropollutant removal.

3.2. Other semiconductor nanomaterials

Although TiO₂ has garnered extensive attention for its stability and photocatalytic efficiency, its wide bandgap requires the adsorption of UV light with sufficient photon energy for exciting charge carriers, thereby showing low adsorption of visible light that limits its applications in photocatalysis.^142–144 Recently, photocatalysts such as bismuth vanadate (BiVO₄) and indium selenide (InSe) have drawn significant attention owing to their superior capabilities in absorbing visible light and facilitating efficient charge transport.^133,145 In particular, when multiple facets are present on photocatalyst particles, inter-facet junctions may be formed at the edges of different crystal facets. Such inter-facet junctions present notable deviations from the conventional 2D heterostructures, with the band structure near the edges markedly diverging from that within the interior regions of the particle.^146–148 Additionally, the electric fields generated by the work-function differences between adjacent planes may alter unpredictably along the particle surface or internally. As such, it is necessary to probe the effects of these interfacial connections and the consequent variations in intraplanar functional properties, especially under practical conditions.

To this end, Mao et al. employed BiVO₄ truncated bipyramids with well-defined {010} and {110} planes to investigate the effects of inter-facet junction on the photoelectrocatalytic properties of anisotropically shaped BiVO₄ particles using subfacet-level multimodal functional imaging (Fig. 10a–g).¹⁴⁹ The O²⁻ (electron donor)-rich {010} facets feature a higher work function than the {110} facets that are Bi⁵⁺ rich (electron acceptor),¹⁵⁰ forming an inter-facet junction.¹⁵⁰ Consequently, the valence and conduction band levels at the surface (E^surf_V and E^surf_C, respectively) show intra-facet variation and a location-dependent band-bending degree (Δφ_SEI) when contacting electrolytes. By measuring the sub-particle photocurrent i_phvia an illuminated local structure across the inter-facet junction, they found that i_ph exhibited variations across different facets that span a few micrometers and even within the same facet near the edge regions, showing an s-like monotonic increase from the center of the {010} facet to the {110} facet (Fig. 10d). The authors attributed the striking subfacet-dependent photocurrent to the effects of inter-facet junctions, which lead to the variation in the local band structure and thus the photoelectrochemical properties.^151,152

Fig. 10 (a) SEM image of a representative BiVO₄ particle. (b and c) Super-resolution images of h⁺-induced oxidation (b) and e⁻ induced reduction reactions (c). (d and e) Subfacet-position dependences of i_ph (d), v_h and v_e (e) at selected potentials. (f) Subfacet-position dependencies of V_FB and η_sep. (g) Facet size L dependencies of whole-particle photoelectrochemical current densities (j_ph) at an overwhelmingly anodic potential of 1.13 V. Each circle represents an experimentally measured quantity from one catalyst particle. The shaded surface is based on theoretical prediction. Orange (green) lines: j_phvs. L_{010} at fixed L_{110}. (Panels a–g) are reproduced with permission from ref. 149. Copyright 2022, Nature Publishing Group. (h) Mapping of photocatalytic events on InSe flakes. The color bar denotes the number of detected fluorescent product molecules. (i) Histogram distribution of photocatalytic TORs at four kinds of typical subregions. (j) APF concentration dependence of APF reaction rate (v_APF) (top) and fluorescein dissociation rate (v_d) (bottom). (k) Single-molecular tracks over InSe during a short imaging period under 1 M APF in 1× phosphate-buffered saline (PBS) buffer. The interval between the two data points is 0.1 s. Inset: Apparent diffusion coefficients of fluorescein at different structural features. (Panels h–k) are reproduced with permission from ref. 159. Copyright 2021, AAAS.

To further explore the local photoelectrochemical properties with precision surpassing that of diffraction-limited photocurrent mapping, SMFM imaging experiments based on fluorogenic Rz reduction and AR oxidation suggest the charge carrier distribution, with {010} and {110} facets dominated by electrons and holes, respectively (Fig. 10b and c). Significantly, they unveiled spatial variations in surface hole activities within the same facet for the first time, with the specific reaction rate (v_h) exhibiting a micrometer-scale sigmoidal trend across the facet junction (Fig. 10e, red), paralleling the local anodic photoelectrochemical current trend from h⁺-induced water oxidation but with significantly finer spatial resolution (∼10 times). At less anodic potentials (e.g., <0.6 V), e⁻-induced reactions were observed, with the specific reaction rate (v_e) indicating an opposite sigmoidal spatial trend to that of v_h (Fig. 10e, blue), indicating intra-facet spatial variations. Additionally, the flat-band potential (V_FB) of this particle exhibits an s-like transition along the x direction across the {010}|{110} edge (Fig. 10f, red), providing a direct insight into inter-facet junction effects within an anisotropically shaped semiconductor particle. Similarly, the electron–hole separation efficiency (η_sep) displays an s-like transition along the x direction across the inter-facet edge over the same length scale (Fig. 10b, blue), but in the opposite direction to V_FB, as anticipated, given that steeper solid–electrolyte interface (SEI) band bending correlates with more efficient charge separation. Moreover, the facet-size scaling relationships (Fig. 10g) provide quantitative insights for optimizing shaped particulate photoelectrodes by adjusting the sizes of junction-forming facets. These results confirm the impact of inter-facet junction effects on the photoelectrocatalytic activity of anisotropically shaped semiconducting catalysts, paving the way for a novel understanding of the photoelectrocatalytic properties of faceted semiconducting materials.

In recent years, defect-rich 2D layered material catalysts have been extensively investigated and are anticipated to potentially replace noble metal catalysts for various catalytic reactions owing to abundant active sites, low cost, and tunability.^153,154 More attractively, it is well demonstrated that compared with other surface sites, the defect sites are catalytically more active.^155,156 To this end, enormous efforts have been devoted toward engineering the defect sites on nanocatalysts to enhance the catalytic performance of 2D material catalysts. In this case, acquiring a comprehensive understanding of the physicochemical properties and catalytic reaction kinetics of individual defects will offer necessary insights into defect engineering.¹⁵⁷ However, conventional analytic techniques, such as transmission electron microscopy¹⁵⁴ and tip-enhanced Raman spectroscopy,¹⁵⁸ are unable to investigate the catalytic properties of individual defects under operando conditions, thereby imposing an obstacle to the understanding of reaction mechanisms.

Recently, Fang and co-workers spatially deconvoluted the heterogeneous reaction dynamics of photocatalytic reactions at the individual defects of 2D layered InSe nanoflakes via single-molecule fluorescence imaging.¹⁵⁹ Utilizing an h⁺-induced APF oxidation to strongly fluorescent fluorescein, they spatially differentiated the photocatalytic activities at several different structural defects (i.e., basal plane, edge, wrinkle, and vacancy), as shown in Fig. 10h. By counting single-molecule turnover events at specific defect sites of a 2D InSe nanoflake, the photocatalytic activity was found to follow an increasing order of basal plane < edge < wrinkle < vacancy (Fig. 10i). By titrating the photocatalytic oxidation versus the APF concentration, a variety of quantitative parameters including adsorption equilibrium, reactant conversion, and product dissociation were derived at the single-turnover level. As illustrated in Fig. 10j (top), reaction kinetic data derived from distinct structural features of a single InSe flake reveal adherence to the Langmuir–Hinshelwood kinetic model,^160,161 showing a clear saturation behavior at high [APF]. Specifically, the as-derived chemical conversion rate constants k_eff at three defect types (edges, wrinkles, and vacancies) were found to be 2.2, 5.0, and 10.5 times higher than those on the basal plane, respectively. This superior performance was attributed to the different efficiencies in photogeneration and separation of electron–hole pairs, which are strongly structure dependent. Other factors such as different photon adsorption efficiencies¹⁶² and effective masses of the electrons and holes at different structural features¹⁶³ may also contribute to the variation in photocatalytic activities. In sharp contrast, the adsorption equilibrium constant K_APF demonstrates an opposite trend. Compared with the low-coordinated edges, wrinkles, and vacancies, the large flat surface allows the APF molecules to possess a lay-down configuration and thus gives the largest K_APF value.

To further elucidate the effects of various structural features on the surface diffusion behaviors of fluorescein, they tracked the lateral movements of single fluorescein molecules. Fig. 10k exhibits the trajectories of single molecules on InSe, where three types of molecular diffusion behaviors, i.e., mobile, immobile, and hybrid trajectories, were observed at all surface sites. Notably, the distribution of these diffusion behaviors varies across different structural features, with the basal plane and edge exhibiting considerable proportions of mobile trajectories, approximately 30%. Conversely, fluorescein molecules are more likely to be trapped at wrinkles and vacancies, leading to a reduced prevalence of mobile trajectories (12% and 5%, respectively), aligning with the observed trends in apparent diffusion coefficients (Fig. 10k, inset), indicating gradually strengthened interactions between fluorescein and these four structural features (basal plane, edge, wrinkle, and vacancy). These observations contribute to a deeper understanding of catalytic dynamics at specific defects, informing the strategic design of high-efficiency 2D material catalysts through targeted defect engineering.

4. Heterostructured nanomaterials

4.1. Metal–metal heterostructures

Bimetallic nanoparticles exhibit enhanced catalytic activity due to the geometric effect and/or the ligand effect as a result of metal–metal interactions compared with their monometallic counterparts.^164–166 Numerous experimental and computational endeavors have been dedicated to comprehending the catalytic enhancements stemming from bimetallic effects. In particular, bimetallic catalysts consisting of a plasmonic nanoparticle, such as Au and Ag, and a non- or weakly plasmonic catalyst nanoparticle like Pd, Pt, Ru, and Rh have garnered significant attention due to the widespread use of these transition metals for industrial applications.^167–169

By combining single-molecule super-resolution catalysis imaging with electron microscopy, Chen and co-workers reported the quantitative visualization of enhanced activity within bimetallic nanoparticles.²⁹ They focused on heterostructured bimetallic Pd–Au nanoparticles, which are composed of a penta-twinned Pd nanorod (length: ∼500–4000 nm; diameter: 25.5 ± 2.8 nm) with a pseudospherical Au nanoparticle (diameter: ∼60–140 nm) grown on one or both of its tips, encapsulated within a thin mesoporous silica shell. The Pd–Au nanoparticles presented a bimetallic interface for catalyzing a photo-driven fluorogenic Rz disproportionation to produce Rf, where the 532 nm light serves a dual role: driving the reaction and exciting the fluorescence of Rf. As shown in the 2D activity map (Fig. 11a), a large number of catalytic events were observed around the Pd–Au interfacial region, marking a direct visualization of the catalytic enhancement resulting from the bimetallic effect. By dissecting each Pd–Au heterostructure into different regions (Fig. 11b: Pd_Au region, a bimetallic component dominated by Pd with minor Au doping; the monometallic Pd component; Au_Pd region, the bimetallic component dominated by Au with minor Pd doping; and the monometallic Au component) and titrating the reaction rate as a function of reactant concentration [Rz] or light power density I, the authors derived the catalytic rate constant k and reactant adsorption equilibrium constant K for each region. As [Rz] increases, the TORs of Pd–Au nanoparticles follow the Langmuir saturation kinetics for heterogeneous catalysis (Fig. 11c). As I increases, the TORs of individual particles exhibit a linear increase (Fig. 11c), opposite to the quadratic power dependence of the uncatalyzed reaction, indicating that the rate-limiting step of the catalytic reaction involves only one photoexcited reactant molecule. Furthermore, the specific catalytic rates in four regions of each heteronuclear Pd–Au nanoparticle (Fig. 11b) display saturation kinetics with an increase in reactant concentration and a linear correlation with I (Fig. 11d and e). They observed that the as-derived k values for Pd_Au and Au_Pd regions are approximately 50% higher than those of the corresponding monometallic counterparts, whereas the K values for these regions are roughly 30% smaller. For each type of region, the individual k and K values for single Pd–Au nanoparticles are inversely correlated. The opposite trends indicate that the enhanced catalytic activity is associated with weakened reactant adsorption, as explained by the transition state theory, where less stable reactants have a lower activation barrier to reach the transition rate.¹⁷⁰ DFT calculations indicate that replacing Pd with Au on Pd(100) or replacing Au with Pd on Au(111) can elongate the N–O bond. This elongation arises from heightened forward- and back-donation interactions, thereby enhancing the activation of the N–O bond for cleavage on the bimetallic surfaces. Quantifying the activity at the sub-particle level not only provides a detailed understanding of catalytic enhancements at bimetallic interfaces but also identifies optimal locations for constructing bimetallic sites. Recently, using SMFM, Li and co-workers observed a significant increase in the catalytic efficiency of Pd nanoparticles near silver nanowires, which was attributed to LSPR excitation.¹⁷¹ Catalysis is further boosted near roughened Ag nanowires or nanogaps, shedding light on the plasmon excitation's role in enhancing catalysis and guiding the development of efficient plasmonic photocatalysts. By quantifying the enhancement of bimetallic activity on the nanoparticles and pinpointing favorable locations for bimetallic site formation, these studies demonstrate the effectiveness of super-resolution catalysis imaging in guiding the development of bimetallic catalysts.

Fig. 11 Super-resolution fluorescence imaging of metal–metal heterostructured nanomaterials. (a) 2D histogram of product positions on a Pd–Au heterostructured nanoparticle. Outer white line, structural contour; white circle, the contour of the Au particle. (b) Segmentation of a typical Pd–Au nanoparticle. (c) Reactant concentration [Rz] (black) and 532 nm laser power density I (red) dependencies of the TOR per Pd–Au nanoparticle. Solid symbols: the single particle in panel a. Open symbols: results averaged over 53 nanoparticles. Error bars: SEM for y and SD for x. (d) [Rz] and (e) I dependencies of specific TORs of the segments for the nanoparticle in (panels a). (Panels a–e) are reproduced with permission from ref. 29. Copyright 2017, American Chemical Society. (f) Plasmon-driven modulation of reaction pathways of individual Pt-modified Au nanorods. (Panels f) is reproduced with permission from ref. 175. Copyright 2020, American Chemical Society. (g) From left to right are the FDTD simulations of electric-field distribution from Au NBPs, aPt–Au NBPs, and ePt–Au NBPs. The red arrows indicate the orientation of the incident electric field. (h) Corresponding schematic of the catalytic mechanism of nanostructures in (g). Panels g and h are reproduced with permission from ref. 176. Copyright 2022, American Chemical Society. (i) Quantitative super-resolution mapping of catalytic products on a nanostructure. (j) FDTD simulation of electric-field enhancement pattern on the nanostructure in (i) at 532 nm with circularly polarized incident light. (k) Quantitative super-resolution mapping of catalytic products on the Au–Ag nanostructure. (l) Specific TORs of individual linked Au–Au nanorods at the gap and non-gap regions vs. their local incident light power density incident at 532 nm. Each open symbol represents a single nanostructure. The solid symbols are binned and averaged data to obtain general trends. Lines are quadratic fits. (Panels i–l) are reproduced with permission from ref. 182. Copyright 2018, American Chemical Society.

In addition, Au–Pt bimetallic nanostructures have also received tremendous attention owing to the versatility of Pt in various catalytic reactions.^172–174 However, understanding the underlying kinetic mechanisms of plasmon-enhanced catalysis remains ambiguous, which is key to designing optimal bimetallic nanocatalysts. To this end, Chen and co-authors characterized the product formation rate of a fluorogenic Rz reduction to Rf at both single-particle and ensemble levels on Pt-tipped Au nanorods (Au–Pt nanorods).¹⁷⁵ The difference in catalytic behaviors observed with and without illumination indicates that energetic charge carriers induce a transition from a competitive reactant adsorption type to a non-competitive adsorption type (Fig. 11f). A similar change in the reactant adsorption mechanism was observed for Au nanorods, whereas Pt nanoparticle catalysis consistently follows a competitive mechanism regardless of light illumination. The transition in the adsorption mechanism was attributed to the excitation of LSPR in the Au–Pt nanorods upon illumination. Moreover, the authors conducted FDTD calculations to compute the optical properties of Au–Pt nanorods and found that the charge generation rate in the Pt cap is enhanced by the presence of Au, even surpassing the charge generation rate in the Au core itself. In particular, the capping of Au nanorods with Pt also increased the absorption efficiency over the entire wavelength range of 400–1000 nm. Additionally, compared with pure Pt, Au–Pt nanorods exhibit volumetric absorptivity approximately four times greater for transversal surface plasmon resonance (LSPR_T) peaks and around 200 times greater for longitudinal surface plasmon resonance (LSPR_L) peaks, suggesting that high-energy charges probably originate from the optical excitation of intermediate plasmon modes in Pt. Taken together, the coupling between non-plasmonic and plasmonic metals can facilitate the formation of high-energy charge carriers and their transfer to catalytically active sites.

To gain deeper insights into the structure-dependent hot carrier transfer mechanism from bimetallic nanostructures, Chen and co-workers investigated Pt-modified Au nanobipyramids (Pt–Au NBPs) at the single-particle level using single-molecule fluorescence imaging, where AR N-deacetylation to fluorescent Rf served as a model reaction.¹⁷⁶ Specifically, they successfully synthesized Au nanobipyramids (NBPs) with Pt nanoparticles deposited on all the surfaces (aPt–Au NBPs) or selectively on the two ends (ePt–Au NBPs). When used as catalysts, the catalytic activity of ePt–Au NBPs was significantly improved compared with those of Au NBPs and aPt–Au NBPs. At saturated [AR], the TORs of ePt–Au NBPs (1.71 ± 0.09 s⁻¹) and aPt–Au NBPs (0.76 ± 0.04 s⁻¹) were approximately 2.67 and 1.19 times faster than that of Au NBPs (0.64 ± 0.03 s⁻¹). The superior performance of ePt–Au NBPs relative to aPt–Au NBPs and Au NBPs was explained by the fast spontaneous-surface-restructuring rate, which generates more active sites for catalytic reactions. Moreover, the hot electrons generated by the plasmonic effect of Au can transfer their energy to Pt nanoparticles during self-thermalization and relaxation, inducing boosted Pt lattice vibrations with a strong EM field that promotes substrate activation and photocatalytic reactions. To further probe the effect of EM, FDTD calculations were conducted to map the EM-field distribution. Fig. 11g displays the calculated localized electric-field mapping of Au NBPs, aPt–Au NBPs, and ePt–Au NBPs. In particular, Au NBPs generate EM-field enhancement with a maximum value |E_max|²/|E₀|² of 75.4 at two tips, where E_max represents the local maximum electric field and E₀ denotes the amplitude of the input electric field. The plasmon resonance undergoes significant damping after Pt nanoparticles are loaded around the surface of Au NBPs due to direct energy absorption by the deposited Pt nanoparticles. As a result, the EM-field enhancement decayed to 35.2, leading to rapid recombination of the generated hot carriers (Fig. 11h). For ePt–Au NBPs, the negligible surface coating allows for the retention of a noticeable LSPR, with a measured |E_max|²/|E₀|² up to 49.1. Compared with aPt–Au NBPs, the strong EM field at the tips endows additional hot electron generation capability from Pt nanoparticles, thereby leading to a superior catalytic activity of ePt–Au NBPs (Fig. 11h). Taken together, these two studies of Au–Pt nanocatalysts offer valuable insights and guidelines for the design of plasmon-based photocatalysts, particularly bimetallic nanostructures.

Apart from bimetallic catalysts consisting of plasmonic/non-plasmonic paired nanoparticles, there is considerable interest in plasmonic bimetallic nanostructures that consist of two plasmonic metals.^177–179 These structures exhibit localized surface plasmon (SP) resonance upon excitation with visible light, creating a strong oscillating electric field within nanometers of the nanoparticle surface. Despite that, ensemble-level measurements have been crucial in investigating the mechanisms of SP-enhanced catalysis,^180,181 they are unable to differentiate the intrinsic heterogeneities of plasmonic nanostructures. In particular, the electric-field enhancement on plasmonic particles varies depending on their shape and polarization of the excitation light, creating intense regions called “hotspots” notably found in nanoscale gaps between particles, which significantly impact the measured catalytic activity at the ensemble level. To address this challenge, Zou and colleagues reported a quantitative visualization of SP-enhanced catalytic activity on two nanostructures that present nanoscale plasmonic hotspots: linked Au–Au nanorods and linked Au–Ag nanorod/nanoparticles, both encapsulated by mSiO₂ to stabilize the linkage structures.¹⁸² Specifically, the two nanostructures exhibit nanoscale gaps of ∼8 nm between the linked nanorod/nanoparticles. The catalytic reaction used for single-molecule fluorescence imaging is the reductive deoxygenation of Rz by hydroxylamine to generate Rf. Higher reaction rates at these gaps, compared to non-gap regions, indicate SP-induced catalytic enhancements, which were directly correlated with nanostructure geometries and local-electric-field enhancements. Specifically, under 532 nm laser illumination with a power density of 1.27 kW cm⁻², the catalytic activity in gap regions of Au–Au nanorods surpasses that in non-gap regions by approximately 1.9 times on average, with a maximum enhancement of 3.1 times at the single-nanostructure level (Fig. 11i). FDTD calculations suggest a clear electric-field hotspot at the gap regions that effectively correlates with the activity distribution on the linked Au–Au nanorod (Pearson's correlation coefficient ρ = 0.76 ± 0.05), directly supporting the fact that the catalytic enhancement at the gap region arises from local-electric-field enhancement (Fig. 11j). Moreover, the authors discovered that the local-electric-field enhancement at the gap region sensitively depends on the size of the gap, with a large gap size leading to a decreased catalytic activity. In addition, Au–Ag nanostructures were also investigated in catalyzing the same Rz reduction reaction. Similar to the case of linked Au–Au nanorods, the catalytic activities in the gap regions of Au–Ag nanostructures were also boosted (Fig. 11k), approximately 2.1 times higher on average than those in the non-gap regions. In particular, for individual nanostructures, the activity in the gap regions can be enhanced up to ∼3.9 times—clear evidence for catalytic enhancements by the plasmonic hotspots. The role of plasmonic hotspots in promoting the catalytic activity was further confirmed by light-intensity-dependent activity measurements. As shown in Fig. 11l, the specific TORs in the gap regions exhibit a quadratic increase with rising local incident power density, which was due to the promoted plasmonic effect by the increased 532 nm laser intensity. When the light power density is below 1.5 kW cm⁻², the specific TOR shows a slight dependence on the light power density, consistent with the studies on individual Au nanoparticles mentioned above.⁴⁹ When the light power density is above 1.5 kW cm⁻², the TOR increases rapidly. This dependence suggests that the potential mechanisms for catalytic enhancement must involve two types of photoexcited species, such as SP-induced hot electrons or photoexcited Rz molecules.^81,183

4.2. Metal–semiconductor heterostructures

Metal–semiconductor heterostructures hold promise as effective photocatalysts for various catalytic reactions.^184–186 The incorporation of noble metals with a large work function onto metal oxide supports has been shown to significantly enhance the charge separation efficiency, thereby greatly enhancing the photocatalytic performance.¹⁸⁴ Understanding the interfacial electron transfer mechanism within metal–semiconductor nanostructures is crucial for optimizing their optoelectronic and catalytic properties. To this end, the single-molecule fluorescence imaging technique has been extensively employed to study the interfacial electron transfer dynamics in such nanocomposite systems.

Using super-resolution imaging, Majima and co-workers identified the photocatalytic reaction sites of individual TiO₂ particles loaded with Au nanoparticles (Au/TiO₂).^187,188 In 2011, they introduced a boron-dipyrromethene (BODIPY) derivative that can be reduced from non-fluorescent 3,4-dinitrophenyl-BODIPY (DN-BODIPY) to fluorescent 4-hydroxyamino-3-nitrophenyl-BODIPY (HN-BODIPY) to study the photocatalytic redox reaction of Au/TiO₂.¹⁸⁷ Compared with pristine TiO₂, the Au/TiO₂ metal–semiconductor junctions exhibited significantly superior photocatalytic activity, attributable to the enhanced charge separation within TiO₂ in the presence of Au co-catalyst. The photocatalytic activity, as indicated by the generation rate of fluorescent products, was found to be influenced by both substrate concentration and UV-light intensity, as well as the size of Au particles. Specifically, as the size of the Au nanoparticles decreases from 14 to 5 nm, the obtained apparent adsorption constant for substrate (K_ad) values on Au/TiO₂ nanoparticles increases from ∼0.8 to ∼1.1 mM⁻¹ (Fig. 12a and b), all of which are much greater than that of the TiO₂ system (∼0.5 mM⁻¹). These results indicate that DN-BODIPY tends to adsorb on the surface of Au in Au/TiO₂ and smaller Au nanoparticles show stronger substrate-binding affinity, primarily due to the existence of more low-coordination Au atoms. Combined with the fact that the fluorescence bursts are probably distributed across the loaded Au nanoparticles, it was speculated that the reduction of DN-BODIPY on Au/TiO₂ was primarily triggered by accepting electrons accumulated in the Au nanoparticles.

Fig. 12 Super-resolution fluorescence imaging of metal–semiconductor heterostructured nanomaterials. (a and b) DN-BODIPY concentration dependence of (a) 〈τ_off〉 and (b) 〈τ_on〉 obtained for TiO₂ (black), 5 nm Au/TiO₂ (blue), 8 nm Au/TiO₂ (green), and 14 nm Au/TiO₂ (red). The inset in panel a shows a typical TEM image of 8 nm Au/TiO₂ particles. (Panels a and b) are reproduced with permission from ref. 187. Copyright 2011, The Royal Society of Chemistry. (c) Excitation spectra of the TiO₂ (solid black line) and Au/TiO₂ (solid red line) samples measured at a fixed emission wavelength of 531 nm (width, 40 nm). The excitation spectrum of the bulk solution of the product DS-HN-BODIPY (solid blue line) and the absorption spectra (broken lines) of TiO₂ (gray), AuTiO₂ (pale red), and DS-DN-BODIPY (pale blue) are also shown. (d) Proposed mechanisms of plasmon-induced photochemical reactions on Au/TiO₂. S and P are the substrate and fluorescent products, respectively. E_F is the Fermi energy of the Au nanoparticles. (e) Overlay of the SEM image and spatial distributions of fluorescence spots (red dots, >50 spots) collected from TiO₂ and 14 nm Au/TiO₂ particles. Scale bar = 100 nm. The locations of the reactive sites and Au nanoparticle are surrounded with dashed lines in red and blue, respectively. (Panels c–e) are reproduced with permission from ref. 188. Copyright 2013, American Chemical Society. (f) Schematic illustrating two distinct photocatalysis mechanisms. (g) Super-resolution mapping of individual reactive sites on a high-metal-loading Au–CdS heterostructure at 532 nm. The circled blue crosses show a product molecule caused by the h⁺ reactive sites on Au, whereas the circled red minuses show a product molecule from the e⁻ reactive sites. Inset: TEM image of typical single high-metal-loading Au–CdS heterostructures. (Panels f and g) are reproduced with permission from ref. 189. Copyright 2014, American Chemical Society. (h) Single-particle fluorescence imaging elucidates semiconductor shell influence on Ag@TiO₂ photocatalysis. (i) TEM image of a representation Ag@TiO₂ nanoparticle with a TiO₂ shell thickness of 20 nm. (j) [AR] dependence of TOR with different nanoparticles as the catalyst. Error bars show the standard derivation. (k) γ_eff and K₁vs. Ag@TiO₂ with different shell thicknesses. Error bars show the standard deviations. (l and m) The E-field enhancement |E|² for (l) P5 and (m) P20 nanocatalysts. (Panels h–m) are reproduced with permission from ref. 194. Copyright 2021, American Chemical Society.

Later on, the research group further developed two novel water-soluble fluorogenic probes for investigating interfacial electron transfer processes on the same nanocatalysts.¹⁸⁸ The probes belong to the DN-BODIPY family and feature mono- and disulfonated groups on the BODIPY fluorophore, namely, MS-DN-BODIPY and DS-DN-BODIPY, respectively, which could facilitate the generation of fluorescent products through multiple interfacial electron transfer processes. Excitingly, the sulfonated probes showed a significant fluorescence intensity increase in an acidic solution, with the probe concentration reduced to 10 nM, more than two orders of magnitude lower than that of unmodified DN-BODIPY, highlighting their stronger adsorption on TiO₂ surfaces. Then, the authors showcased the use of DS-DN-BODIPY to explore visible-light-induced redox reactions on TiO₂ and Au/TiO₂ at the single-particle, single-molecule level (Fig. 12c). The emission spectra observed during photoirradiation confirm the generation of product molecules, with slight differences observed between TiO₂ and Au/TiO₂ samples, indicating possible fluorescence quenching and enhancement effects by the presence of Au nanoparticles. Moreover, the observed spectra closely resemble the absorption and excitation spectra of the product in the bulk solution, suggesting that the electrostatic interactions between the product molecules and TiO₂ minimally influence the spectral properties of the product molecules. The possible reaction mechanism on Au/TiO₂ is depicted in Fig. 12d. For pristine TiO₂ nanoparticles, UV light is required to activate the conduction band and initiate BODIPY photoreduction. In contrast, in the case of Au–TiO₂ nanoparticles, visible excitation induces plasmon-generated hot electrons in Au nanoparticles, which drive the photoreduction reaction. The plasmon-induced hot electrons are injected into the conduction band of TiO₂ across the Schottky barrier and then participate in reducing the probe molecules, whereas the remaining holes are scavenged by methanol. Interestingly, the distribution of detected fluorescence bursts on TiO₂ and Au/TiO₂ was distinct, showing a uniform distribution on TiO₂ nanoparticles but concentrated distribution at the Au nanoparticles of Au/TiO₂ (Fig. 12e) Moreover, the super-resolution mapping of visible-light-induced reduction reactions on Au/TiO₂ shows that the reactive sites were spatially distributed within a distance of a few tens of nanometers from the deposited Au nanoparticles. Both studies suggest that photocatalytic reduction and photocatalytic oxidation take place at or around the Au nanoparticles on the TiO₂ surface, implying the importance of controlling the short deposition distance of Au nanoparticles on TiO₂. The proposed single-particle, single-molecule methods with ultrasensitive and water-soluble fluorescent probes may be highly valuable for studying redox reactions in heterogeneous systems, including solid materials and enzyme catalysts.

Apart from Au–TiO₂ hybrid nanocatalysts, researchers have also extended the application of high-resolution super-localization imaging to investigate other hybrid metal–semiconductor nanocatalysts, including Au–CdS,¹⁸⁹ Sb–TiO₂,¹⁹⁰ and others.³³ Clarifying the fundamental mechanisms in these metal–semiconductor hybrid heterostructures is crucial for the rational design of novel nanocatalysts with enhanced activity, selectivity, and stability. Ha and co-workers synthesized CdS semiconductor nanorods decorated with Au nanoparticles (Au–CdS) and investigated their real-time redox photocatalysis at the single-particle level with millisecond time resolution.¹⁸⁹ The Au nanoparticles had diameters ranging from 2 to 7 nm, and the Au loading on the CdS nanorod (average length: 186 nm; diameter: 6.0 nm) was estimated to be approximately 10.8 wt%. Due to the separation of plasmonic and excitonic characteristics in Au–CdS heterostructures, it was speculated that two distinct photoinduced charge separation mechanisms should exist, depending on the incident excitation energy (Fig. 12f). Mechanism A begins with Au absorbing 532 nm light, leading to the formation of d-band electron–hole pairs above the Fermi level due to SP decay. Exciting plasmonic nanoparticles with dimensions much smaller than their plasmon resonance wavelength can efficiently generate hot electrons and holes. Mechanism B starts with the semiconductor absorbing 405 nm light, resulting in electron transfer to the metal. This process increases the electron density within the Au nanoparticles, shifting the Fermi level toward more negative potentials until it aligns with the semiconductor's conduction band edge. Unlike mechanism A, mechanism B charges Au negatively and the CdS semiconductor positively, leading to two different charge-separated Au–CdS species with opposite polarity. The researchers employed fluorogenic AR oxidation to produce highly fluorescent Rf to study the charge separation mechanisms. In particular, during AR oxidation to Rf by holes, fluorescence bursts were recorded at multiple spots. As shown in Fig. 12g, they mapped the individual reactive sites on a single high-metal-loading Au–CdS heterostructure under 532 nm laser excitation by localizing the position of every Rf molecule, in which the distribution of events correlates well with the 1D Au–CdS structure (Fig. 12g, inset). Plasmon-induced energetic electrons (red minuses), initially generated in metal particles, are injected into the conduction band of CdS, consistent with mechanism A involving photoinduced charge transfer from Au nanoparticles to the CdS semiconductor under 532 nm light illumination. The presence of mechanism B involving photogenerated electrons and holes in CdS nanorods was further confirmed at the ensemble level. In the presence of CdS nanorods, the absorption maximum of the Rf product at 573 nm was observed to increase every 30 s, whereas it remained constant without CdS nanorods, proving the oxidation of AR to Rf and thus the existence of mechanism B. Taken together, on one hand, the plasmon of Au metal can be selectively excited at 532 nm to generate hot electrons injecting into the conduction band of CdS for activating mechanism A (Fig. 12f, top); on the other hand, the CdS semiconductor nanorod can be selectively excited at 405 nm to generate charge carriers and the electrons flowing into Au can effectively activate mechanism B (Fig. 12f, bottom). The researchers also compared the product formation and dissociation rates of mechanisms A and B during the photocatalytic reaction. Significantly, they found that the average product formation rate 〈τ_off〉⁻¹ of mechanism B is approximately six times higher than that of mechanism A, suggesting that mechanism B generates Rf molecules faster. This could be attributed to the formation of more active and longer-lived photogenerated carriers primarily within the CdS nanorods under mechanism B.

Beyond investigating the photocatalytic electron transfer process, understanding the structure–property relationship of metal–semiconductor nanostructures plays a crucial role in the design of outstanding photocatalysts. Current research on this relationship is mainly limited to providing generalized information at the ensemble level, which smears the heterogeneous properties of individual nanocatalysts.^191–193 Therefore, it is necessary to study the catalytic process at the single-particle level. Recently, Liu et al. examined the effect of the semiconductor shell on photocatalytic AR oxidation over Ag@TiO₂ nanoparticles through single-molecule imaging (Fig. 12h).¹⁹⁴ By adjusting the amount of hydrolysis of titanium tetraisopropoxide (TTIP) on Ag nanoparticles, the authors prepared nanocatalysts with different thicknesses of TiO₂ shells (5, 10, 20, and 30 nm, denoted as P5, P10, P20 (Fig. 12i), and P30, respectively). Under 532 nm laser illumination for exciting the plasmon of Ag nanoparticles, the average TORs of photocatalytic AR were found to increase with increasing substrate concentration [AR] and then reach saturation but with different saturation levels and initial slopes for Ag@TiO₂ with various shell thicknesses, all of which can be effectively depicted by the Langmuir–Hinshelwood adsorption model (Fig. 12j). Fig. 12k shows the scatter plots of the specific rate constant γ_eff and adsorption equilibrium constant K₁ against the thickness of TiO₂, clearly illustrating the parabolic-like trends between shell thickness and γ_eff and K₁ values. Specifically, P20 exhibits the highest γ_eff and K₁, indicating superior activity relative to P5, P10, and P30. As the shell thickness was increased from 5 to 20 nm, γ_eff and K₁ show a clear increasing trend, attributable to the rise in the number of electron–hole pairs that lead to a higher likelihood of catalytic collisions. However, a further increase in shell thickness leads to a decrease in γ_eff and K₁. This is due to the increase in the diffusion length of energetic carriers along with the increased TiO₂ shell thickness, causing a reduction in plasma enhancement and thus reduced efficiency of catalytic reactions. To comprehend the maximum catalytic efficiency at P20, the authors further calculate the E-field distribution in the surrounding space of the Ag nanoparticle with varying TiO₂ shell thicknesses to quantitatively elucidate the mechanisms. As shown in Fig. 12l and m, the E-field intensity on the surface of the Ag core, which stems from the LSPR of Ag nanoparticles, exhibits an axisymmetric distribution along the axis of beam propagation. When the TiO₂ shell thickness of the Ag core was increased from 5 to 20 nm, the magnitude of the E field was remarkably enhanced, in agreement with the enhanced catalytic activity. Although increasing the TiO₂ shell thickness to 30 nm could further enhance the E field near the Ag core, the long diffusion length imposed by the shell to hot electrons compromises the E-field enhancement. These results indicate that both photogenerated electrons and hot electrons are simultaneously involved in the catalytic process, and their contributions to catalytic efficiency highly depend on the structure of the nanocatalysts, which should be properly evaluated in photocatalyst design. All these super-resolution measurements contribute to a more comprehensive understanding of the structure–performance relationship, as well as the charge transfer mechanism of metal–semiconductor hybrid nanocatalysts, which contribute to the development of efficient nanocatalysts.

4.3. Semiconductor–semiconductor heterostructures

Although metal–semiconductor heterojunctions offer advantages such as conductivity and stability, the mismatched band alignment between the metal and the semiconductor often imposes a barrier to charge injection and results in considerable surface recombination efficiency, significantly limiting their applications in photocatalysis. In contrast, semiconductor–semiconductor heterojunctions enable more effective control of the band structure and electron transport properties, facilitating enhanced charge separation and carrier transport efficiency, thereby demonstrating greater potential for a wide range of applications.^195,196 Nevertheless, the inherent complexity of these heterojunctions, including challenges associated with interface defects and charge recombination dynamics, demands the employment of advanced characterization techniques for comprehensive investigation. To this end, Wu and co-workers investigated the charge separation mechanisms of type II and Z-scheme CdS/g-C₃N₄ (g-C₃N₄ represents graphitic carbon nitride) nanocomposites toward H₂ production via photodeposition and super-resolution fluorescence microscopy.¹⁹⁷ To explore the charge separation in CdS/g-C₃N₄ composites, the authors mapped the distributions of the deposited co-catalysts via e⁻-induced photoreduction and h⁺-induced photooxidation reactions. As shown in Fig. 13a, Pt nanoparticles stemming from Pt⁴⁺ photoreduction were mainly formed on the CdS surface, suggesting the dominance of electrons. In comparison, PbO₂ clusters generated by the photooxidation of Pb²⁺ ions with NaIO₃ as the electron scavenger were preferentially deposited on the g-C₃N₄ nanosheets, especially at the edge positions (Fig. 13b). The selective deposition of PbO₂ suggests holes were concentrated more at the g-C₃N₄ edges than on the basal planes, leading to a higher reactivity at the edges. These observations confirm the spatial separation of photoinduced electrons and holes in the heterojunctions, with electrons migrating to the conduction band of CdS for photoreduction (Pt or H₂ generation) and holes to the valence band of g-C₃N₄ for photooxidation (oxidation of Pb²⁺). Moreover, to investigate the charge distribution and photocatalytic heterogeneity at single-turnover resolution, SMFM imaging was utilized for the precise visualization of photoreactions. The photoreduction of non-fluorescent Rz to fluorescent Rf localized electrons, whereas photogenerated h⁺ was detected via AR photooxidation to Rf by ·OH generated from h⁺-mediated water oxidation reaction. Fig. 13c and d reveals the fluorescent bursts from photoreduction products Rf, which were predominantly distributed at the CdS nanorods, indicating the diffusion and preferred sites of photoinduced electrons. Specifically, more electrons were found at the ends rather than at the centers of the CdS nanorod, in agreement with the photodeposition results (Fig. 13d). In sharp contrast, the fluorescent events of photooxidation events mainly occurred at the g-C₃N₄ edges, suggesting the accumulation of h⁺ in these areas owing to the higher local curvature of edges relative to the basal planes (Fig. 13e and f). This study not only offers profound insights into the structure–property relationships of semiconductor–semiconductor heterojunctions but also advances the design of outstanding heterogeneous catalysts via morphology regulation, interface engineering, band modulation, and control of charge and energy flow.

Fig. 13 (a and b) High-angle annular dark-field scanning transmission electron microscopy images of CdS/g-C₃N₄ with (a) 1 wt% Pt and (b) 3 wt% PbO₂ loaded. (c–f) Bright-field images (c and d) and single-molecule events density maps (e and f) of CdS/g-C₃N₄. Bin size is 10 nm × 10 nm for panel d and 25 nm × 25 nm for panel f. Scale bar = 1 μm. (Panels a–f) are reproduced with permission from ref. 197. Copyright 2022, The Royal Society of Chemistry. (g) Schematic of single-molecule fluorescence imaging of Rz photoreduction on the catalyst in a microflow cell. (h) Schematic of the kinetic process including Rz adsorption, conversion, and Rf dissociation. C, S, and P represent the composite, substrate, and product, respectively. (i) Bright-field image of the composite with the heterojunction and four labeled positions (P1, P2, P3, and P4). (j) Density maps of fluorescent Rf molecules on the heterostructure in (i) under 150 nM of Rz. Bin size: 25 nm × 25 nm. (Panels g–j) are reproduced with permission from ref. 202. Copyright 2023, Wiley-VCH GmbH. (k) Distribution of 〈τ_off〉⁻¹ among the 31 different sites in TiO₂-tipped CNT without MV²⁺ (red circle solid) and with MV²⁺ (blue box solid); the decreasing percentage of 〈τ_off〉⁻¹ values after the addition of MV²⁺ (purple solid star). (l) Fluorescence images obtained from the integration of all the frames over 60 s reaction without MV²⁺ (left) and with MV²⁺ (right) for TiO₂-tipped CNT. (m) Bright-field (left) and fluorescence (right) images of a representative TiO₂(S)-CNT. The scale bars in panels l and m are 2 μm. (Panels k–m) are reproduced with permission from ref. 203. Copyright 2021, American Chemical Society.

Recently, one-dimensional (1D) multiphase catalysts, such as nanotubes, nanowires, and nanorods, have garnered significant attention in the field of nanotechnology due to their unique structural characteristics and photophysical properties at the nanoscale.^198,199 Carbon nanotubes (CNTs), in particular, have received considerable attention in the field of photocatalysis owing to their exceptional electronic, physicochemical, and mechanical attributes.^200,201 When combined with semiconductors to create heterojunctions, CNTs can facilitate electron transfer from the semiconductor to the CNTs, serving as reservoirs to enhance charge carrier conductivity and mitigate charge recombination. Building upon this, Wu and co-workers fabricated 1D–1D CNT/CdS nanocomposites via electrostatic self-assembly and probed the site-specific catalytic activity and kinetics of this heterojunction structure via in situ SMFM (Fig. 13g).²⁰² Upon laser excitation at 488 nm, photoinduced e⁻ generated by CdS facilitated the reduction of Rz to Rf on both CdS and CNT surfaces. Subsequently, Rf molecules were excited by a 532 nm laser for single-molecule fluorescence imaging, by which the kinetic steps including Rz adsorption and conversion as well as Rf dissociation were successfully quantified at various structural features of CNT/CdS (Fig. 13h). As depicted in Fig. 13i, the lower section of the sample exhibits a straight and darker morphology, corresponding to CdS nanorods, whereas the upper bending part with lower contrast indicates the presence of CNTs, with the heterojunction formed in the middle. The corresponding reactivity map of fluorescent products Rf molecules is shown in Fig. 13j, illustrating the heterogeneous distribution of catalytically active sites on the 1D heterostructure. Specifically, the two ends P1 and P3 of CdS show higher activity than the CdS side surface and CNTs. Moreover, the end P1, which is in contact with a CNT, suggests superior activity to the pristine end P3, which was attributed to the promoted charge separation induced by CNTs and thus boosted the catalytic performance. Further study on reactant adsorption reveals that the CdS–CNT heterojunction area could bind Rz molecules more strongly compared with other regions, thereby contributing to the activity enhancement. Moreover, the dissociation behavior of product Rf on CdS and CNTs was found distinctive, with direct dissociation prevailing on CdS, whereas both direct dissociation and reactant-assisted indirect dissociation occurred on CNTs. These findings provide a deeper understanding of activity heterogeneity and site specificity in 1D heterostructures, thereby facilitating the optimization of 1D photocatalysts.

In addition, An and co-workers investigated real-time photoinduced electron transfer dynamics in TiO₂-tipped CNTs using redox-responsive AR fluorescent probes.²⁰³ They identified 31 distinct sites continuously from left to right along the TiO₂-tipped CNTs under 365 nm laser irradiation, in which charge carriers are generated in TiO₂ nanoparticles. As illustrated in Fig. 13k, they found that 〈τ_off〉⁻¹, which reflects the product generation frequency and thus the catalytic activity, shows a decrease from the two tips of the TiO₂ nanoparticles towards the center. In particular, a sharp decrease in 〈τ_off〉⁻¹ from 7.81 s⁻¹ at site 31 to 2.15 s⁻¹ at site 12 was observed. This trend suggests that the photogenerated electrons originally generated at the TiO₂ tips were transferred to CNTs for the reduction of O₂ to generate O₂˙⁻, which further oxidizes AR to generate fluorescent products. Moreover, when an electron acceptor methyl viologen (MV²⁺) was introduced, 〈τ_off〉⁻¹ was found to show a decrease in values at the 31 sites, indicating that MV²⁺ consumes photogenerated electrons competitively and thus suppresses the O₂˙⁻ formation. Meanwhile, fluorescence imaging over a 60 s reaction revealed a significant decrease in the fluorescence intensity of TiO₂-tipped CNTs after MV²⁺ addition (Fig. 13l), confirming the role of MV²⁺ in photogenerated electron capture. To further determine the transfer distance of photoelectrons from TiO₂ to CNT, an individual photocatalyst TiO₂(s)–CNT, consisting of a CNT with a single TiO₂ nanoparticle cluster at one tip, was investigated. Remarkably, the TiO₂(s)–CNT exhibited electron transfer distances surprisingly up to 16.82 μm (Fig. 13m).

5. Bio-inorganic hybrid system

Harnessing solar energy to drive the synthesis of high-value chemicals from naturally abundant small molecules, such as CO₂, remains a grand challenge. Microbial–semiconductor biohybrids, combining the versatility and outstanding selectivity of microbes in conducting complex chemical transformations with the high light-harvesting capabilities of inorganic semiconductors, have been recognized as a promising solar-to-chemical conversion system to address this challenge.^204–206 The key to maximize the efficiency of such biohybrid systems lies in optimizing the nanobio interface and extra-/intracellular electron transfer. However, the investigation of the underlying mechanisms through bulk measurements is rendered challenging owing to the pervasive heterogeneities in gene expression among microbial cells and in photocatalytic activity across semiconductor particles.^207,208 Such heterogeneities necessitate the implementation of quantitative measurements at both the single-cell/particle and sub-cellular/particle levels.

Recently, Fu and co-workers developed a new imaging platform combining multichannel optical imaging with the electrochemical mapping of light-induced currents to probe energy conversion pathways and the players in such biohybrids for electron transfer down to single- to sub-cell/particle levels (Fig. 14a and b).²⁰⁹ The study concentrated on the lithoautotrophic Gram-negative bacterium Ralstonia eutropha (R. eutropha), previously employed in decoupled biohybrid systems utilizing H₂ generated from electrolyzed water as the exclusive energy source for CO₂ fixation into the biopolymer polyhydroxybutyrate (PHB).^210,211 In integrated biohybrids, the microbes are directly interfaced with semiconductor photoelectrodes or photocatalysts and take up photogenerated electrons to drive the downstream reactions (Fig. 14a, bottom). The authors first probed the role of two types of hydrogenases, i.e., membrane-bound hydrogenase (MBH) and cytosolic soluble hydrogenase (SH), used by R. eutropha in bioplastic production. By tagging the respective subunit of MBH and SH for fluorescence imaging, they found that MBH is membrane localized, as expected, whereas SH surprisingly exhibits localization not only in the cytoplasm but also in the cell envelope, which was ascribed to the interaction of SH with proteins bound to the inner membrane or the membrane itself, or to its partial secretion into the periplasm (Fig. 14c and d). Moreover, upon adaptation, the cellular concentrations of both MBH and SH are elevated by over 20-fold, substantiating their critical roles in H₂ metabolism (Fig. 14e).²¹² Specifically, the elimination of MBH does not alter the PhaP1^mV level, whereas the deletion of SH results in approximately a 100-fold decrease in the PhaP1^mV level (Fig. 14f, columns 2 vs. 1; 3 vs. 1, respectively). Thus, SH plays an indispensable role in the oxidation of H₂ to generate reducing equivalents for PHB production from CO₂ fixation (Fig. 14k, steps (i) and (v)), whereas MBH, though not essential, is shown to facilitate this process. These findings indicate that MBH and SH serve distinct functions in relation to PHB synthesis when metabolizing H₂.

Fig. 14 (a) Decoupled and integrated biohybrids for energy conversion. [H]: H⁺/H₂ as the redox mediator, where H₂ can be generated by electrocatalysts or photocatalysts; [M]: other redox mediators. (b) Single-cell and sub-particle photocurrent imaging using focused laser illumination to probe single-spot photoelectrochemical currents on single cells in contact with a semiconductor film (i) or with single semiconductor particles (ii and iii). i_ph, photocurrent. (c and d) Wide-field fluorescence images of adapted MBH^PAmC1_HoxG (c) and SH^mV_HoxY (d) cells. Insets: false-coloured confocal fluorescence images. The scale bars are 1 μm. (e) Cellular concentrations of MBH^PAmC1_HoxG and SH^mV_HoxY in non-adapted (columns 1 and 3) and adapted (columns 2 and 4) cells. Two-sided t-test, ****p < 0.0001. (f) Cellular PhaP1^mV concentrations in different adapted strains. Column 1: PhaP1^mV; column 2: PhaP1^mV, ΔMBH (ΔHoxG); column 3: PhaP1^mV, ΔSH (ΔHoxY); column 4: MBH^PAmC1_HoxG, PhaP1^mV; column 5: SH^PAmC1_HoxY, PhaP1^mV; column 6: MBH^mC_HoxG, SH^PAmC1_HoxY, PhaP1^mV. NS, not significant. Two-sided t-test, ****p  <  0.0001. In (e) and (f), the white circles denote the median; horizontal black lines, the mean; vertical black lines, 25% to 75% quantile. (g) Photoelectrochemical current densities at 0.2  V vs. Ag/AgCl electrode of a bulk Cu₂WS₄ thin-film electrode with and without deposited multilayer adapted R. eutropha cells in a minimal medium under different gas environments. (h) Transmission image of adapted R. eutropha cells encoding MBH^mV_HoxG on a Cu₂WS₄ film. Single-spot photocurrents were measured with a focused 405 nm laser illuminating at on-cell (red crosses) and nearby off-cell (green crosses) locations. (i) Histograms of single-cell Δi_ph (blue) obtained on Cu₂WS₄ and a control Cu₂WS₄ sample that contains no cells (black) at 0–0.3  V. (j) Correlations of single-cell Δi_ph obtained on a Cu₂WS₄ photocathode at 0–0.3  V with local MBH (b) or SH (c) concentration at the laser focus of the same cell. Blue dots, individual adapted cells. Open squares, binned and averaged results. The yellow shaded areas indicate cells with lower hydrogenase levels. (k) Schematic of dominant electron-transport pathways for bioplastic formation in biohybrid systems. All the panels are reproduced with permission from ref. 209. Copyright 2023, Nature Publishing Group.

The authors then examined the capability of R. eutropha to accept electrons from photoelectrodes by directly interfacing with Cu₂WS₄ to construct integrated biohybrids (Fig. 14a, bottom panel), a photovoltaic cathode material characterized by visible-light absorption and a conduction band edge conducive to the reduction of protons, MBH, SH, and other common cellular redox proteins. Strikingly, compared with bare Cu₂WS₄, a Cu₂WS₄ photocathode integrated with adapted R. eutropha cells shows greatly enhanced steady-state photocathodic current in either N₂, air, or CO₂ environment during bulk measurements (Fig. 14g). The independence of gas condition suggests that the measured current reflects electron transfer at the cell–semiconductor interface rather than downstream electron movements involved in CO₂ fixation. To further quantify a single cell's electron-uptake capability, a key performance indicator for microbe–semiconductor biohybrids, Fu et al. integrated photoelectrochemical mapping into a multimodal imaging platform to clarify this puzzle (Fig. 14b, Mode III-i). By sparsely dispersing adapted R. eutropha cells on a Cu₂WS₄ film annealed on a transparent conductive indium tin oxide (ITO) substrate, individual cells were easily identifiable with wide-field transmission and/or fluorescence imaging (Fig. 14h). The single cell's current was measured by illuminating the semiconductor locally via chopping off the 405 nm laser at various applied potentials. Based on the statistic results of many cells, the majority of cells (∼77%) exhibited an increase in photocathodic current (Δi_ph<  0; Fig. 14i), consistent with bulk measurements (Fig. 14g). The nanoampere photocurrent enhancement based on single-cell measurements suggests the underestimation of the turnover rates of hydrogenases or the domination of other non-H₂-mediated pathways in the photocathodic current formation. Further experiments based on BiVO₄ with a conduction-band energy level (E_CB) below the proton reduction potential show that upon being surrounded by adapted R. eutropha cells, clear photocathodic currents were detected, confirming the existence of non-H₂-mediated electron-transport pathways that probably dominates the nanoampere-level single-cell photocathodic current on Cu₂WS₄. Hydrogenases, beyond metabolizing H₂, may also participate in electron transfer involving other redox mediators.²¹³ Thus, following the discovery of non-H₂-mediated electron transfer pathways between R. eutropha and semiconductors, researchers delved into the role of hydrogenases in these pathways. By examining single-cell-level correlations between a cell's hydrogenase level and Δi_ph, it was found that the magnitude of Δi_ph increases with the local cellular MBH and SH concentrations (Fig. 14j), suggesting the stronger electron-uptake capability in cells at higher hydrogenase levels. However, neither MBH nor SH is in direct contact with the photoelectrode to accept photogenerated electrons, and the authors hypothesized that redox mediators at the R. eutropha surface should be involved in shuttling electrons from the photoelectrodes to the hydrogenase (Fig. 14k). The hypothesis was further confirmed by the integrated biohybrid of R. eutropha and CdS, in which photoanodic current enhancement was also observed. Interestingly, the cell-induced photoanodic current was found to persist for both ΔMBH and ΔSH strains, indicating that both types of hydrogenases are not important for electron outflow (Fig. 14k, step iv). Taken together, at the microbe–semiconductor interface, non-H₂-based redox mediators on the cell surface are crucial for both electron outflow and uptake (Fig. 14k, steps ii-a and ii-b), whereas MBH and SH are pivotal solely for electron uptake (Fig. 14k, step iii). Overall, this advanced imaging platform, coupled with its analytical framework, can elucidate electron-transport mechanisms across an array of biohybrids and promote the engineering of optimal biohybrid systems for various reactions such as CO₂ conversion, N₂ fixation, and pollutant degradation.

6. Imaging non-fluorescent entities

As mentioned above, SMFM imaging has revolutionized our understanding of heterogeneous catalysis.^188,214,215 Nevertheless, it can only interrogate systems or processes involving fluorescent substances, whereas a variety of chemical reactions do not involve fluorescent species. Developing novel SMFM imaging techniques for investigating nonfluorescent entities has been a long-lasting challenge in this field. To address this issue, Mao et al. developed a new imaging technique based on competitive adsorption, namely, a competition-enabled imaging technique with super-resolution (COMPEITS; Fig. 15a), which allows the quantitative super-resolution imaging of non-fluorescent processes.²¹⁶Fig. 15a and b illustrate the concept demonstration of COMPEITS in the context of photocatalytic water decontamination using BiVO₄ as the photocatalyst. In the COMPEITS experiments, the fluorogenic AR oxidation by holes generated in BiVO₄ under 405 nm laser illumination is employed as the auxiliary reaction, in which the fluorescent products Rf molecules, with fluorescence excited by the 532 nm laser, are individually imaged and localized at nanometer resolution. Fig. 15b(i) illustrates the 2D histogram of the detected fluorescent Rf molecules on a representative BiVO₄ photocatalyst, showing clear activity heterogeneity on BiVO₄. After introducing the competitive hydroquinone (HQ) oxidation, the number of detected AR oxidation products (n_p) decreases, which indicates the suppression of AR oxidation reaction (Fig. 15b(ii)), suggesting the appearance of competition. By quantifying the extent of suppression, the nonfluorescent HQ molecules can be imaged at the same nanometer resolution as the fluorescent reaction, yielding super-resolution spatial information of HQ oxidation (Fig. 15b(iii)). To derive the adsorption affinity of nonfluorescent HQ molecules K_HQ, K_AR is derived first by titrating the fluorogenic reaction rate v_AR as a function of [AR]. Subsequently, by introducing HQ with varied concentrations and building on the competitive Langmuir–Hinshelwood adsorption mode, K_HQ can be derived based on the following equation:Here, k_AR is the (specific) rate constant and v_AR is the (specific) rate of the AR oxidation reaction; K_AR and K_HQare the adsorption equilibrium constants for AR and HQ on the catalyst surface, respectively. Most excitingly, based on the relation , Δ(n_p⁻¹) was found to be proportional to K_HQ at fixed [AR] and directly reflects the HQ-binding affinity. Building on this relationship, the authors obtained the so-called COMPEITS images (Fig. 15b(iv)) that immediately show the HQ adsorption strength on individual BiVO₄ nanoparticles. Clearly, HQ adsorbs more strongly on the basal {010} facets than the lateral {110} facets. Even within the lateral facets, HQ adsorption is weaker at four corners than in the center lateral facets.

Fig. 15 Application of COMPEITS technique. (a) The COMPEITS setup based on wide-field fluorescence microscopy in a photoelectrocatalytic microfluidic cell via two-laser epifluorescence illumination. CE, counter electrode; RE, reference electrode. (b) 2D histograms of the number of fluorescent events n_p over 22.5 min without HQ (i) and with 250 μM HQ (ii), and the image derived from Δn_p between (i) and (ii) (iii). COMPEITS image derived from Δ(n⁻¹_p) between (i) and (ii) (iv). The white/null pixels represent the occasional negative values (for (iii) and (iv)) or infinities due to 1/0 (for (iv)). (c) 2D dependences of K_HQ on L and ξ for the basal {010}. Each circle represents one particle of a total of 42. The upper left and lower right panels show the corresponding 1D projections of K_HQ data onto the L and ξ axes, respectively. (Panels a–c) are reproduced with permission from ref. 216. Copyright 2019, Nature Publishing Group. (d) COMPEITS image for CTAB adsorption on Au nanorod (top) and its corresponding SEM image (middle). White/null pixels: occasional negative values or infinities from 1/0. The green dashed and magenta lines suggest the dissection of the nanorod. 1D projection of the adCOMPEITS image for the entire nanorod (bottom). (e) Facet and subfacet differences in adsorption affinity K and cooperativity h of CTAB. (f) Fractions of Au {110} and Au {111} facets vs. [CTAB]. (Panels d–f) are reproduced with permission from ref. 221 Copyright 2021, Nature Publishing Group. (g) Side view of the optimized structure of a C₁₆ ligand–alkane pair adsorbed on Au {110} at 1/16 ML coverage (left), and the side (lower right) and top (upper right) views of lowest-energy binding structures of C₈xTAB molecule on Au {110} in the lying-down configurations at the low-coverage limit. (h) Binding energies (BE) and differential binding energies (dBE) of xTAB ligand–alkane pairs on Au {111} and Au {110} as a function of the alkyl chain length. The purple and green vertical lines denote the smallest chain length required for positive adsorption cooperativity on Au {111} and Au {110}, respectively. The subscripts 1/16 and 2/16 in the legends represent the corresponding ML for different Au facets. (i) Competition titration of the initial rates of the fluorogenic auxiliary reaction with increasing [CTAB]. Magenta and orange dashed lines: fits of low- and high-concentration regimes, respectively. Black line: fit results. Red line: the weighting factor W₁vs. [CTAB]. (Panels g–i) are reproduced with permission from ref. 226. Copyright 2024, American Chemical Society.

Owing to the same nanometer resolution of COMPEITS technique in analyzing nonfluorescent molecules, the authors further quantitatively investigate the effect of facet and morphology on HQ adsorption, which is a key parameter defining the photocatalytic activity of photocatalysts. Statistic results of many particles reveal that the K_HQ for both basal {010} and lateral {110} (K_HQ^{010} and K_HQ^{110}) show a strong dependence on the particle size L and the particle shape parameter ξ (ξ = S/L, Fig. 15a). In particular, both K_HQ^{010} and K_HQ^{110} decrease asymptotically with increasing particle size L, and asymptotically with particle shape transition from biconical to plate-like with increasing ξ (Fig. 15c). Based on the facet-dependent K, the authors further derived the particle morphology design principles for optimal reactant chemisorption on BiVO₄ nanoparticles. For BiVO₄ particles with a size smaller than 2.3 μm, the optimal shape is plate like, whereas for particles larger than 9 μm, a bipyramid-like shape is better. When the particle size falls in the range of 2.3–9 μm, the optimal shape for reactant adsorption is either plate like or bipyramid like, but not a truncated bipyramid. The particle-size-/shape-decoupled information obtained by COMPEITS imaging provides unprecedented insights into the rational design of optimal photocatalysts for micropollutant degradation. Most significantly, COMPEITS could, in principle, image a broad range of nonfluorescent processes at nanometer resolution, in situ, and under operando conditions. Of course, COMPEITS has some limitations including the requirement of an auxiliary fluorescent reaction as a reporter, the limited capability to monitor the dynamic process of nonfluorescent molecules, and the long imaging duration for obtaining sufficient data for analysis.

In addition to photocatalysts, COMPEITS imaging is also applicable to studying nonfluorescent molecular adsorption on metal nanocatalysts.²¹⁷ On metal nanoparticles, the adsorption of molecules can stabilize their solution dispersion, control their morphology during synthesis, enhance their surface functionality, and/or limit their catalytic properties.^217–222 To this end, Ye et al. leveraged the COMPEITS technique to investigate the adsorption affinity and cooperativity of small molecules/ions and polymer ligands on single Au nanospheres, nanoplates, and nanorods under ambient solution conditions.²¹⁷ Excitingly, by quantifying the adsorption affinities of various molecules, they revealed both positive and negative adsorption cooperativity. To quantitatively probe the adsorption cooperativity, the authors derived the Hill coefficient h via the Hill adsorption model, where for positive cooperativity, h > 1, and for negative cooperativity, h < 1. Specifically, cetyltrimethylammonium bromide (CTAB) adsorption on Au was found to be positively correlated (h = 2.2 ± 0.1) owing to the attractive hydrophobic interactions between the alkyl chains of CTA⁺.²²³ In contrast, polyvinylpyrrolidone (PVP) adsorption on Au displays a negative cooperativity (h = 0.57 ± 0.09) because the direct electrostatic repulsions between positively charged PVP chains at pH ∼7.4 (N-alkyl pyrrolidone has a base dissociation constant p^K_b of ∼3.5) or that hydrophilic PVP chains prefer interactions with water than with themselves.^224,225 Interestingly, halide ions such as I⁻ ions show no adsorption cooperativity, which was attributed to the fact that small ligands are less likely to feel each other on the surfaces.

More excitingly, the adsorption cooperativity of various molecules also varied at different sites on the same nanoparticle. For example, by examining CTAB adsorption on penta-twinned Au nanorods with the large {110} side (S) and two tips (T) covered by {111} facets, they found that the adsorption affinity of CTAB molecules, i.e., K_CTAB, was larger on the {110} than {111} facets (K^{110} > K^{111}), (Fig. 15d and e). On the contrary, the adsorption cooperativity shows an opposite trend, with h_T (2.3 ± 0.2) > h_S (1.8 ± 0.2). Further dissection of side {110} facets into inner (I), middle (M), and outer (O) regions (Fig. 15d) suggests the presence of sub-particle adsorption heterogeneity. Interestingly, CTAB adsorption on different segments of Au follows the order of K_I > K_M > K_O (Fig. 15e), which was attributed to the high defect density of the inner segment during colloidal synthesis owing to the fast reduction kinetics in the initial stage. As the growth proceeds, the reduction rate decays and results in lower defect density for the middle and outer segments. Regarding the adsorption cooperativity, it follows a similar trend as the adsorption affinity, i.e., h_I > h_M > h_O. With a larger K, the adsorption density of CTAB molecules is higher and the inter-distance between molecules is shorter, which should render more adsorbate–adsorbate interactions within the same facet and thus overall stronger cooperativity.

Provided the adsorption affinity and cooperativity, the density of adsorbed ligand ρ on any facet at any [CTAB] can be depicted as , where ρ_max is the ligand's maximal packing density on the facet. Given K^{110} > K^{111} whereas ρ_max^{110} < ρ_max^{111} (56% vs. 91%), the authors proposed the existence of a crossover behavior in terms of ρ. At low CTAB concentrations, ρ^{110} > ρ^{111}, whereas at high ligand concentrations, ρ^{110} < ρ^{111}. They then designed colloidal synthesis experiments to prove the crossover behavior as in colloidal synthesis, surfaces with a high density of ligands are of high possibility to be preserved in the final products. Excitingly, as [CTAB] was increased from 0.26 to 3.12 mM, the shape of Au products evolved from irregular to plate like. Using electrochemical Pb underpotential deposition, they quantified the proportions of {110} and {111} facets in products obtained at various [CTAB] values. Specifically, the proportion of {110} facets gradually decreased from 98% to 20% at elevated [CTAB]; meanwhile, the proportion of {111} facets increased from 5% to 90%. In particular, the two curves intersect at roughly 2 mM CTAB (Fig. 15f), confirming the crossover behavior of CTAB adsorption and the feasibility of achieving facet control in colloidal Au synthesis by simply tuning the CTAB concentration.

Despite the experimental observation of cooperative adsorption of CTAB molecules on various Au surfaces, the molecular basis for CTAB's affinity differences between the two facets and the associated different extents of cooperativity remains unclear. Recently, Xu et al. reported a combined experimental and computational study of the adsorption behaviors of alkyl-trimethylammonium bromides (xTAB) with variable alkyl chain length x on Au nanoparticles.²²⁶ The authors established two different models for xTAB adsorption on Au {111} and Au {110} surfaces at different xTAB concentrations (Fig. 15g). One is the standing-up configuration, where a ligand–alkane pair arranged in a head-to-tail configuration and occurs in the high-xTAB-concentration range (Fig. 15g, left). Another is a lying-down model, which occurs at low xTAB concentrations (Fig. 15g, right). Subsequently, using DFT, they calculated the binding energies (BE) of xTAB on the Au {111} and Au {110} surfaces in both standing-up and lying-down configurations. Specifically, they studied both low-coverage limit (1/16 monolayer (ML)) and the 2/16 ML where a second molecule is introduced to the surface with a molecule already adsorbed at 1/16 ML. Fig. 15h summarizes the binding energies of the standing-up configuration. For C₆ and larger xTAB molecules on Au {110} and the close-packed {111} facets, the dBE (defined as the energy gained or lost) at 2/16 ML is more negative than the BE at 1/16 ML coverage. On the more open Au {110} facet, in all the cases, the 2/16 ML dBE is more negative than the low-coverage-limit BE. Therefore, on both facets, the adsorption cooperativity for sufficiently large xTAB molecules should be positive, consistent with the previous experimental observations on CTAB.²²¹ In addition, for C₈ and larger xTAB molecules in the low-concentration range, the ligand–alkyl pair binds more strongly on Au {110} than on Au {111}; and the second ligand–alkyl pair binds more strongly on Au {111} than on Au {110} in the high-concentration range, in agreement with the experimentally observed CTAB adsorption crossover behavior (Fig. 15e) where the Au {110} facet is preferred at low CTAB concentrations and the Au {111} face dominates at high CTAB concentrations. As for the lying-down configuration, xTAB (C₄) molecules bind more strongly on Au {110} than on Au {111} at low coverage limits. This is the same trend observed for the xTAB molecules in the standing structures. Moreover, in all these cases, the dBE of 2/32 ML is smaller than the BE of 1/32 ML coverage, suggesting that the interaction between the two xTAB molecules is inherently repulsive and should lead to negative adsorption cooperativity.

Additionally, the authors further demonstrated the precision of the constructed model by experimentally probing the concentration-dependent ligand adsorption based on COMPEITS titration experiments. Specifically, in the [CATB] range of ∼10⁻⁹–10⁻⁵ M, the fluorogenic Rz reduction rate v_R first decreases in the range of ∼10⁻⁹–10⁻⁸ M and then increases in the range of ∼10⁻⁸–10⁻⁷, followed by another decrease at [CTAB] higher than 10⁻⁷ M and eventually approaching zero (Fig. 15i). This decay–rise–decay behavior at various [CTAB] conditions implies that two distinctive adsorption behaviors of CTAB molecules should be involved. To explain the behavior of v_R over the entire [CTAB] range, the authors used a modified equation to empirically combine the adsorption behavior of two different ligands. In the equation, the authors introduced a weighting factor W₁, when [L] → 0, W₁ → 1, representing low-concentration adsorption; when [L] → ∞, W₁ → 0, representing high-concentration adsorption (Fig. 15i, red line). Here exists a critical concentration P that divides the low- and high-concentration-regime behaviors. The equation satisfactorily explains the competitive titration over the entire [CTAB] range (Fig. 15i, black line), yielding K₁ = (4.0 ± 1) × 10⁸ M⁻¹, h₁ = 0.75 ± 0.04, and K₂ = (7.2 ± 0.5) × 10⁵ M⁻¹, h₁ = 1.7 ± 0.1. Therefore, at concentrations below P = 7.3 ± 0.9 nM, CTAB adsorption exhibits high affinity (K₁) with negative cooperativity (h₁ < 1), confirming the computational prediction of a lying-down adsorption configuration. At concentrations above P, CTAB adsorption switches to low affinity (K₂) with positive cooperativity (h₂ > 1), which is consistent with the standing-up adsorption configuration. This switching behavior of adsorption affinity and cooperativity is unprecedented and occurs over a very narrow concentration width (Q = 1.7 ± 0.5 nM) for CTAB, suggesting that on the surface of the Au nanoparticles, the adsorbed CTAB molecules undergo a concerted change in adsorption conformation from lying to standing. This work demonstrates a paradigm for gaining molecular-scale insights into adsorbate–surface interactions, which will guide researchers in the fields of colloidal synthesis and catalysis and beyond.

7. Conclusions and outlook

In this paper, we review recent advancements in the SMFM imaging of catalytic processes on photocatalytic nanomaterials at the single-molecule/single-particle level. With the nanometer spatial resolution and millisecond temporal resolution, SMFM has been proven to be a powerful and versatile tool for studying surface reactions on single nanocatalysts, yielding insights into photocatalytic reaction kinetics and dynamics, active site distributions, identification of intermediate species, reaction reactivity fluctuations, and charge carrier behaviors. This information aids in comprehending catalytic reaction mechanisms, establishing precise structure–activity relationships, and guiding catalyst design. Nevertheless, SMFM is still facing several major challenges in applying it to various catalytic reactions. First, most studies are based on fluorogenic model reactions and investigating non-fluorescent reaction processes remains a grand challenge. This dilemma is due to the nature of SMFM that relies on detecting fluorescence signals for imaging. However, many catalytic reactions of great significance are not fluorescent or fluorescently labeled. Owing to the development of the new imaging technique COMPEITS,⁴² studying non-fluorescent systems is now feasible, which still needs further exploration. Second, the applicable scenarios are limited. As most fluorescent probes utilized for single-molecule detection typically necessitate a buffer solution and ambient environment,¹³ it is difficult to study catalytic processes in strong acidic/alkaline solutions and/or under high-temperature and high-pressure conditions. Moreover, studying catalytic reactions involving gaseous species is also limited. Third, the temporal resolution needs to be improved. Although SMFM excels in elucidating the kinetic mechanisms of catalytic reactions, its capability to probe reaction intermediates and molecular structural transformation is low. This limitation is attributed to not only the limited chemical information provided by fluorescence signals but also the insufficient time resolution, typically at the microsecond level that is much larger than the sub-picosecond timescales for molecular structural transformations.^41,227 Fourth, the raw data of imaging experiments can be contaminated by the intrinsic photoluminescence of photocatalysts or PSF distortion by the plasmonic effect.^12,108 As the intensity of single-molecule fluorescence signals is intrinsically low, the photoluminescence of photocatalysts under light excitation makes it rather difficult to precisely extract and localize single-molecule events for catalysis study. Furthermore, the plasmonic effects can distort the PSF, altering the spatial information obtained from single molecules and leading to inaccuracies in localization and analysis.¹² Addressing these two obstacles is crucial for ensuring the reliability and validity of single-molecule fluorescence measurements. Fifth, data processing is a critical step in rationalizing the SMFM results.¹³ The obtained SMFM images contain all the pertinent information regarding the molecule's extractable parameters, including its spatial position and occurrence timing. Typically, the number of images obtained from an SMFM experiment can be tens of thousands, or even hundreds of thousands for sophisticated systems, making it very time-consuming to process and analyze the results.

To address the above challenges, future endeavors are anticipated to advance this versatile technique and unlock additional opportunities in new fields. Our vision extends to progress in the following areas.

(1) Improvement in spatiotemporal resolution. The spatial resolution of SMFM per frame is determined by the signal-to-noise ratio, which can be affected by factors such as the pixel size of the EMCCD camera, background noise, and particularly, the emission intensity of the fluorescent probe. Strengthening experimental setups, including employing more sensitive cameras and intense excitation lasers, may prove effective. Furthermore, engineering the fluorescent probe to show improved brightness and reinforced resistance to photobleaching provides another viable strategy. In addition, there is a pressing need to improve the temporal resolution of SMFM to capture the reaction species and intermediates with short lifetimes, which requires the advancement of high-speed cameras.

(2) Study of non-fluorescent reactions. As we discussed above, the newly developed imaging technique COMPEITS allows us to study non-fluorescent reactions/molecules via competitive adsorption using single-molecule fluorescent imaging.⁴² With its ability to provide spatially resolved insights into the behaviors of unlabeled, non-fluorescent entities under operando conditions, COMPEITS can unveil optimal binding sites, enabling the predictions of ideal size, shape, and morphology for catalytic nanomaterials. However, COMPEITS has some limitations, including the requirement of target materials to possess the capability of catalyzing both fluorogenic probe and target reactions, the inaccessibility to the reaction kinetics of the target reaction, the potential perturbation of the auxiliary reaction on the target reaction, among others. Further improvement in COMPEITS and new technique development are expected to overcome these technical challenges.

(3) Combination with other techniques. Integrating microscopy and spectroscopy modalities with SMFM may provide unprecedented insights into heterogeneous catalysts, which combines the capabilities of microscopy in quantifying the molecular adsorption behaviors and spectroscopy in identifying molecular structural fingerprints. The integrated microscopy-spectroscopy platform can provide informative messages on adsorption kinetics and affinity, chemical composition, structural dynamics, catalytic activities, and other emergent functionalities. Various imaging techniques have been explored for integrating with SMFM, including in situ high-resolution electron microscopy,²²⁸ X-ray scattering spectroscopy,²²⁹ stimulated Raman scattering microscopy,²³⁰ single-particle photoluminescence imaging,²³¹ and atomic force microscopy.²³² The synchronous imaging enabled by multiple analytical tools can help address the limitations of each technique while enhancing its strengths. Most importantly, the as-obtained scientific messages may revolutionize our understanding of photocatalysis.

(4) Integration of deep learning with SMFM. Deep learning has emerged as a powerful tool in various scientific fields including medicine, astronomy, and biology, all of which rely heavily on imaging and microscopy. In the context of SMFM, deep learning could enable the precise extraction and super-localization of single-molecule events, facilitate rapid data analysis, overcome bottlenecks associated with large datasets, and leverage mathematical models for signal simulation. In addition, neural networks are versatile to address various challenges in single-molecule studies without the need for individualized development.²³³ For example, Möckl and co-workers introduced a background network (BGnet) to improve the image quality for single-molecule localization and tracking by accurately estimating the fluorescence background in optical microscopy images, which was demonstrated to be effective even for fluorescence signals with complex PSF shapes.²³⁴

Data availability

This manuscript is a review paper and contains no research results, software, and/or codes. No new data were generated or analyzed as part of this review.

Conflicts of interest

Authors declare no competing interests.

Acknowledgements

The work was supported by the National University of Singapore start-up grant, Centre for Hydrogen Innovations (grant no. CHI-P2023-04), Ministry of Education (grant no. 23-0646-A0001), and National Research Foundation, Singapore (grant no. U2311D4005).

References

1. X. Zheng, Z. Ye, Z. Akmal, C. He, J. Zhang and L. Wang, Chem. Soc. Rev., 2024, 53, 656–683.
2. M. S. Faculak, A. M. Veatch and E. J. Alexanian, Science, 2024, 383, 77–81.
3. S. Nishioka, F. E. Osterloh, X. Wang, T. E. Mallouk and K. Maeda, Nat. Rev. Dis. Primers, 2023, 3, 42.
4. Y. Qi, B. Zhang, G. Zhang, Z. Zheng, T. Xie, S. Chen, G. Ma, C. Li, K. Domen and F. Zhang, Joule, 2024, 8, 193–203.
5. M. Wang, H. Zhou and F. Wang, Joule, 2024, 8, 604–621.
6. T. Wang, C. Nie, Z. Ao, S. Wang and T. An, J. Mater. Chem., 2020, 8, 485–502.
7. C.-C. Wang, J.-R. Li, X.-L. Lv, Y.-Q. Zhang and G. Guo, Energy Environ. Sci., 2014, 7, 2831–2867.
8. A. M. Sadanandan, J.-H. Yang, V. Devtade, G. Singh, N. Panangattu Dharmarajan, M. Fawaz, J. Mee Lee, E. Tavakkoli, C.-H. Jeon, P. Kumar and A. Vinu, Prog. Mater. Sci., 2024, 142, 101242.
9. X. Xiao, S. Tu, M. Lu, H. Zhong, C. Zheng, X. Zuo and J. Nan, Appl. Catal., B, 2016, 198, 124–132.
10. K. Takanabe, Top. Curr. Chem., 2016, 371, 73–103.
11. C. Yan, X. Mei, X. Gong and W. Xu, Ind. Chem. Mater., 2024, 2, 85–99.
12. K. A. Willets, A. J. Wilson, V. Sundaresan and P. B. Joshi, Chem. Rev., 2017, 117, 7538–7582.
13. Y. Xiao and W. Xu, Chem, 2023, 9, 16–28.
14. W. Li, G. S. Kaminski Schierle, B. Lei, Y. Liu and C. F. Kaminski, Chem. Rev., 2022, 122, 12495–12543.
15. Z. Yang, A. Sharma, J. Qi, X. Peng, D. Y. Lee, R. Hu, D. Lin, J. Qu and J. S. Kim, Chem. Soc. Rev., 2016, 45, 4651–4667.
16. B. Brenner, C. Sun, F. M. Raymo and H. F. Zhang, Nano Convergence, 2023, 10, 14.
17. F. C. Hendriks, F. Meirer, A. V. Kubarev, Z. Ristanovic, M. B. J. Roeffaers, E. T. C. Vogt, P. C. A. Bruijnincx and B. M. Weckhuysen, J. Am. Chem. Soc., 2017, 139, 13632–13635.
18. R. Ye, M. Zhao, X. Mao, Z. Wang, D. A. Garzon, H. Pu, Z. Zhao and P. Chen, Nat. Commun., 2021, 12, 4287.
19. L. Wang, M. S. Frei, A. Salim and K. Johnsson, J. Am. Chem. Soc., 2019, 141, 2770–2781.
20. F. Balzarotti, Y. Eilers, K. C. Gwosch, A. H. Gynna, V. Westphal, F. D. Stefani, J. Elf and S. W. Hell, Science, 2017, 355, 606–612.
21. Q. Qiao, W. Liu, Y. Zhang, J. Chen, G. Wang, Y. Tao, L. Miao, W. Jiang, K. An and Z. Xu, Angew. Chem., Int. Ed., 2022, 61, e202208678.
22. F. Wang, L. Liu, H. Yu, Y. Wen, P. Yu, Z. Liu, Y. Wang and W. J. Li, Nat. Commun., 2016, 7, 13748.
23. M. Shen, T. Ding, W. H. Rackers, C. Tan, K. Mahmood, M. D. Lew and B. Sadtler, J. Am. Chem. Soc., 2021, 143, 11393–11403.
24. U. Jeong, D. Jeong, S. Go, H. Park, G.-h. Kim, N. Kim, J. Jung, W. Kim, M. Lee, C. Choi and D. Kim, Chem. Mater., 2023, 35, 5572–5581.
25. Y. Xiao and W. Xu, Chin. J. Chem., 2021, 39, 1459–1470.
26. M. B. Roeffaers, B. F. Sels, I. H. Uji, F. C. De Schryver, P. A. Jacobs, D. E. De Vos and J. Hofkens, Nature, 2006, 439, 572–575.
27. K. Naito, T. Tachikawa, M. Fujitsuka and T. Majima, J. Phys. Chem. C, 2008, 112, 1048–1059.
28. T. Tachikawa, N. Wang, S. Yamashita, S. C. Cui and T. Majima, Angew. Chem., Int. Ed., 2010, 49, 8593–8597.
29. G. Chen, N. Zou, B. Chen, J. B. Sambur, E. Choudhary and P. Chen, ACS Cent. Sci., 2017, 3, 1189–1197.
30. W. Xu, J. S. Kong, Y. T. Yeh and P. Chen, Nat. Mater., 2008, 7, 992–996.
31. X. Zhou, N. M. Andoy, G. Liu, E. Choudhary, K. S. Han, H. Shen and P. Chen, Nat. Nanotechnol., 2012, 7, 237–241.
32. W. Xu, H. Shen, Y. J. Kim, X. Zhou, G. Liu, J. Park and P. Chen, Nano Lett., 2009, 9, 3968–3973.
33. J. B. Sambur, T. Y. Chen, E. Choudhary, G. Chen, E. J. Nissen, E. M. Thomas, N. Zou and P. Chen, Nature, 2016, 530, 77–80.
34. M. J. K. Ow, J. J. Ng, J. X. Yong, B. Y. L. Quek, E. K. L. Yeow and Z. Zhang, ACS Appl. Nano Mater., 2020, 3, 3163–3167.
35. M. Xiao, R. Jiang, F. Wang, C. Fang, J. Wang and J. C. Yu, J. Mater. Chem. A, 2013, 1, 5790–5805.
36. S. Witzel, A. S. K. Hashmi and J. Xie, Chem. Rev., 2021, 121, 8868–8925.
37. Y. Shi, Z. Lyu, M. Zhao, R. Chen, Q. N. Nguyen and Y. Xia, Chem. Rev., 2021, 121, 649–735.
38. M. Choi, N. P. Siepser, S. Jeong, Y. Wang, G. Jagdale, X. Ye and L. A. Baker, Nano Lett., 2020, 20, 1233–1239.
39. Q. Zhang, L. Han, H. Jing, D. A. Blom, Y. Lin, H. L. Xin and H. Wang, ACS Nano, 2016, 10, 2960–2974.
40. Y. Kang, P. Yang, N. M. Markovic and V. R. Stamenkovic, Nano Today, 2016, 11, 587–600.
41. P. Chen, X. Zhou, N. M. Andoy, K. S. Han, E. Choudhary, N. Zou, G. Chen and H. Shen, Chem. Soc. Rev., 2014, 43, 1107–1117.
42. X. Mao, C. Liu, M. Hesari, N. Zou and P. Chen, Nat. Chem., 2019, 11, 687–694.
43. W. Xu, J. S. Kong, Y.-T. E. Yeh and P. Chen, Nat. Chem., 2008, 7, 992–996.
44. T. Chen, Y. Zhang and W. Xu, J. Am. Chem. Soc., 2016, 138, 12414–12421.
45. X. Zhou, W. Xu, G. Liu, D. Panda and P. Chen, J. Am. Chem. Soc., 2010, 132, 138–146.
46. Y. Zhang, P. Song, T. Chen, X. Liu, T. Chen, Z. Wu, Y. Wang, J. Xie and W. Xu, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10588–10593.
47. D. Saha, S. Barakat, S. E. Van Bramer, K. A. Nelson, D. K. Hensley and J. Chen, ACS Appl. Mater. Interfaces, 2016, 8, 34132–34142.
48. J. J. Martin and A. F. Armington, J. Cryst. Growth, 1983, 62, 203–206.
49. N. M. Andoy, X. Zhou, E. Choudhary, H. Shen, G. Liu and P. Chen, J. Am. Chem. Soc., 2013, 135, 1845–1852.
50. H. Lee, S. E. Habas, S. Kweskin, D. Butcher, G. A. Somorjai and P. Yang, Angew. Chem., Int. Ed., 2006, 45, 7824–7828.
51. G. A. Somorjai and Y. Li, Introduction to Surface Chemistry and Catalysis, John Wiley & Sons, 2010.
52. M. Zhao and P. Chen, Nano Lett., 2020, 20, 2939–2940.
53. H. Shen, X. Zhou, N. Zou and P. Chen, J. Phys. Chem. C, 2014, 118, 26902–26911.
54. D. L. Floyd, S. C. Harrison and A. M. van Oijen, Biophys. J., 2010, 99, 360–366.
55. H. P. Lu, L. Xun and X. S. Xie, Science, 1998, 282, 1877–1882.
56. W. Xu, J. S. Kong and P. Chen, J. Phys. Chem. C, 2009, 113, 2393–2404.
57. N. Zou, X. Zhou, G. Chen, N. M. Andoy, W. Jung, G. Liu and P. Chen, Nat. Chem., 2018, 10, 607–614.
58. L. Zhou, D. F. Swearer, C. Zhang, H. Robatjazi, H. Zhao, L. Henderson, L. Dong, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Science, 2018, 362, 69–72.
59. U. Aslam, V. G. Rao, S. Chavez and S. Linic, Nat. Catal., 2018, 1, 656–665.
60. P. Christopher and M. Moskovits, Annu. Rev. Phys. Chem., 2017, 68, 379–398.
61. C. Zhan, X.-J. Chen, J. Yi, J.-F. Li, D.-Y. Wu and Z.-Q. Tian, Nat. Rev. Chem, 2018, 2, 216–230.
62. Y. Sivan, J. Baraban, I. W. Un and Y. Dubi, Science, 2019, 364, eaaw9367.
63. W. Li, J. Miao, T. Peng, H. Lv, J. G. Wang, K. Li, Y. Zhu and D. Li, Nano Lett., 2020, 20, 2507–2513.
64. F. Tam, G. P. Goodrich, B. R. Johnson and N. J. Halas, Nano Lett., 2007, 7, 496–501.
65. S. Khatua, P. M. R. Paulo, H. Yuan, A. Gupta, P. Zijlstra and M. Orrit, ACS Nano, 2014, 8, 4440–4449.
66. M. Kim, H. Kwon, S. Lee and S. Yoon, ACS Nano, 2019, 13, 12100–12108.
67. X. Lu, G. Ye, D. Punj, R. C. Chiechi and M. Orrit, ACS Photonics, 2020, 7, 2498–2505.
68. J. H. Yoon, F. Selbach, L. Langolf and S. Schlücker, Small, 2018, 14, 1702754.
69. J. A. Faucheaux, A. L. D. Stanton and P. K. Jain, J. Phys. Chem. Lett., 2014, 5, 976–985.
70. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, J. Phys. Chem. B, 2003, 107, 668–677.
71. N. Hooshmand, P. K. Jain and M. A. El-Sayed, J. Phys. Chem. Lett., 2011, 2, 374–378.
72. J.-E. Park, Y. Lee and J.-M. Nam, Nano Lett., 2018, 18, 6475–6482.
73. B. Gao, G. Arya and A. R. Tao, Nat. Nanotechnol., 2012, 7, 433–437.
74. X. Wang, Z. Ye, J. Hua, L. Wei, S. Lin and L. Xiao, CCS Chem., 2022, 4, 1074–1086.
75. E. Cortés, W. Xie, J. Cambiasso, A. S. Jermyn, R. Sundararaman, P. Narang, S. Schlücker and S. A. Maier, Nat. Commun., 2017, 8, 14880.
76. H. Zhang, J. Wei, X.-G. Zhang, Y.-J. Zhang, P. M. Radjenovica, D.-Y. Wu, F. Pan, Z.-Q. Tian and J.-F. Li, Chem, 2020, 6, 689–702.
77. S. Linic, U. Aslam, C. Boerigter and M. Morabito, Nat. Mater., 2015, 14, 567–576.
78. L. K. Khorashad, L. V. Besteiro, M. A. Correa-Duarte, S. Burger, Z. M. Wang and A. O. Govorov, J. Am. Chem. Soc., 2020, 142, 4193–4205.
79. J. Gargiulo, R. Berté, Y. Li, S. A. Maier and E. Cortés, Acc. Chem. Res., 2019, 52, 2525–2535.
80. G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Light: Sci. Appl., 2020, 9, 108.
81. R. F. Hamans, M. Parente and A. Baldi, Nano Lett., 2021, 21, 2149–2155.
82. S. Ezendam, J. Gargiulo, A. Sousa-Castillo, J. B. Lee, Y. S. Nam, S. A. Maier and E. Cortés, ACS Nano, 2024, 18, 451–460.
83. A. Holewinski, J.-C. Idrobo and S. Linic, Nat. Chem., 2014, 6, 828–834.
84. N. Arora, A. Mehta, A. Mishra and S. Basu, Appl. Clay Sci., 2018, 151, 1–9.
85. T. Dang-Bao, D. Pla, I. Favier and M. Gómez, Catalysts, 2017, 7, 207.
86. X. Qu, B. Zhao, W. Zhang, J. Zou, Z. Wang, Y. Zhang and L. Niu, J. Phys. Chem. Lett., 2022, 13, 830–837.
87. Y. Chen, Y. Zhu, H. Sheng, J. Wang, C. Zhang, Y. Chen, W. Huang and G. Lu, ACS Catal., 2022, 12, 2938–2946.
88. Y. Wang, Y. Liang, H. Sheng, J. Wang, J. Wang, S. He, M. Guan, Y. Chen and G. Lu, Chem.–Eur. J., 2022, 28, e202103709.
89. C. Zhang, F. Jia, Z. Li, X. Huang and G. Lu, Nano Res., 2020, 13, 3183–3197.
90. H. Sheng, J. Wang, J. Huang, Z. Li, G. Ren, L. Zhang, L. Yu, M. Zhao, X. Li, G. Li, N. Wang, C. Shen and G. Lu, Nat. Commun., 2023, 14, 1528.
91. A. D. Dunkelberger, B. S. Simpkins, I. Vurgaftman and J. C. Owrutsky, Annu. Rev. Phys. Chem., 2022, 73, 429–451.
92. M. J. Hülsey, C. W. Lim and N. Yan, Chem. Sci., 2020, 11, 1456–1468.
93. J. T. Hugall, A. Singh and N. F. van Hulst, ACS Photonics, 2018, 5, 43–53.
94. R. Chikkaraddy, B. de Nijs, F. Benz, S. J. Barrow, O. A. Scherman, E. Rosta, A. Demetriadou, P. Fox, O. Hess and J. J. Baumberg, Nature, 2016, 535, 127–130.
95. K. Santhosh, O. Bitton, L. Chuntonov and G. Haran, Nat. Commun., 2016, 7, ncomms11823.
96. Y. Zhang, Q.-S. Meng, L. Zhang, Y. Luo, Y.-J. Yu, B. Yang, Y. Zhang, R. Esteban, J. Aizpurua, Y. Luo, J.-L. Yang, Z.-C. Dong and J. G. Hou, Nat. Commun., 2017, 8, 15225.
97. C. Climent, J. Galego, F. J. Garcia-Vidal and J. Feist, Angew. Chem., Int. Ed., 2019, 58, 8698–8702.
98. O. Bitton, S. N. Gupta, L. Houben, M. Kvapil, V. Křápek, T. Šikola and G. Haran, Nat. Commun., 2020, 11, 487.
99. P. T. Lyu, L. X. Yin, Y. T. Shen, Z. Gao, H. Y. Chen, J. J. Xu and B. Kang, J. Am. Chem. Soc., 2023, 145, 18912–18919.
100. P. T. Lyu, X. R. Liu, L. X. Yin, P. Wu, C. Sun, H. Y. Chen, J. J. Xu and B. Kang, Nano Lett., 2023, 23, 2269–2276.
101. L. Su, G. Lu, B. Kenens, S. Rocha, E. Fron, H. Yuan, C. Chen, P. Van Dorpe, M. B. Roeffaers, H. Mizuno, J. Hofkens, J. A. Hutchison and I. H. Uji, Nat. Commun., 2015, 6, 6287.
102. S. Repo, T. A. Paldanius, V. P. Hytönen, T. K. M. Nyholm, K. K. Halling, J. Huuskonen, O. T. Pentikäinen, K. Rissanen, J. P. Slotte, T. T. Airenne, T. A. Salminen, M. S. Kulomaa and M. S. Johnson, Chem. Biol., 2006, 13, 1029–1039.
103. E. A. Padlan, X-ray crystallography of antibodies, Adv. Protein Chem., 1996, 49, 57–133.
104. W. L. Barnes, J. Mod. Opt., 1998, 45, 661–699.
105. S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402.
106. A. Biebricher, A. Paul, P. Tinnefeld, A. Gölzhäuser and M. Sauer, J. Biotechnol., 2004, 112, 97–107.
107. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
108. R. Baiyasi, S. A. H. Jebeli, Q. Zhang, L. Su, J. Hofkens, H. Uji-i, S. Link and C. F. Landes, ACS Photonics, 2019, 6, 699–708.
109. F. Alonso, Y. Moglie and G. Radivoy, Acc. Chem. Res., 2015, 48, 2516–2528.
110. V. V. Rostovtsev, L. G. Green, V. V. Fokin and K. B. Sharpless, Angew. Chem., Int. Ed., 2002, 41, 2596–2599.
111. C. W. Tornøe, C. Christensen and M. Meldal, J. Org. Chem., 2002, 67, 3057–3064.
112. M. J. K. Ow, J. J. Ng, J. X. Yong, B. Y. L. Quek, E. K. L. Yeow and Z. Zhang, ACS Appl. Nano Mater., 2020, 3, 3163–3167.
113. S. Ye, I. E. Stewart, Z. Chen, B. Li, A. R. Rathmell and B. J. Wiley, Acc. Chem. Res., 2016, 49, 442–451.
114. S. Ye, Z. Chen, Y.-C. Ha and B. J. Wiley, Nano Lett., 2014, 14, 4671–4676.
115. M. R. Decan and J. C. Scaiano, J. Phys. Chem. Lett., 2015, 6, 4049–4053.
116. P. Zhang, S. Lee, H. Yu, N. Fang and S. H. Kang, Sci. Rep., 2015, 5, 11447.
117. L. Huang, Q. Liu, W. Wu, G. Gao, X. Zheng, J. Wang and S. Dong, Nat. Commun., 2023, 14, 5594.
118. R. Ye, X. Mao, X. Sun and P. Chen, ACS Catal., 2019, 9, 1985–1992.
119. K. Naito, T. Tachikawa, M. Fujitsuka and T. Majima, J. Phys. Chem. B, 2005, 109, 23138–23140.
120. K. Naito, T. Tachikawa, M. Fujitsuka and T. Majima, J. Phys. Chem. C, 2008, 112, 1048–1059.
121. T. Tachikawa and T. Majima, J. Am. Chem. Soc., 2009, 131, 8485–8495.
122. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
123. J. H. Pan, X. Zhang, A. J. Du, D. D. Sun and J. O. Leckie, J. Am. Chem. Soc., 2008, 130, 11256–11257.
124. J. M. Macak, M. Zlamal, J. Krysa and P. Schmuki, Small, 2007, 3, 300–304.
125. B. B. Lakshmi, P. K. Dorhout and C. R. Martin, Chem. Mater., 1997, 9, 857–862.
126. K. Naito, T. Tachikawa, M. Fujitsuka and T. Majima, J. Am. Chem. Soc., 2009, 131, 934–936.
127. T. Tachikawa, N. Wang, S. Yamashita, S. C. Cui and T. Majima, Angew. Chem., Int. Ed., 2010, 49, 8593–8597.
128. T. Tachikawa and T. Majima, Langmuir, 2009, 25, 7791–7802.
129. T. Tachikawa, S. Yamashita and T. Majima, J. Am. Chem. Soc., 2011, 133, 7197–7204.
130. W. K. Wang, J. J. Chen, Z. Z. Lou, S. Kim, M. Fujitsuka, H. Q. Yu and T. Majima, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18827–18833.
131. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
132. M. Wang, Z. Wang, B. Zhang, W. Jiang, X. Bao, H. Cheng, Z. Zheng, P. Wang, Y. Liu, M.-H. Whangbo, Y. Li, Y. Dai and B. Huang, ACS Catal., 2020, 10, 13031–13039.
133. N. Yang, S. Zhang, Y. Xiao, Y. Qi, Y. Bao, P. Xu, S. Jin and F. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202308729.
134. J. Yang, D. Wang, H. Han and C. Li, Acc. Chem. Res., 2013, 46, 1900–1909.
135. G. M. Carroll, D. K. Zhong and D. R. Gamelin, Energy Environ. Sci., 2015, 8, 577–584.
136. R. H. Wilson, J. Appl. Phys., 1977, 48, 4292–4297.
137. Z. Nilsson, M. Van Erdewyk, L. Wang and J. B. Sambur, ACS Energy Lett., 2020, 5, 1474–1486.
138. M. Shen, W. H. Rackers and B. Sadtler, Chem. Biomed. Imaging, 2023, 1, 692–715.
139. P. Saha, M. M. Rahman and C. M. Hill, J. Phys. Chem. C, 2023, 127, 9059–9066.
140. W. W. Gärtner, Phys. Rev., 1959, 116, 84–87.
141. J. B. Sambur and P. Chen, J. Phys. Chem. C, 2016, 120, 20668–20676.
142. W. Zhang, H. He, Y. Tian, H. Li, K. Lan, L. Zu, Y. Xia, L. Duan, W. Li and D. Zhao, Nano Energy, 2019, 66, 104113.
143. Y. Ma, X. Wang, Y. Jia, X. Chen, H. Han and C. Li, Chem. Rev., 2014, 114, 9987–10043.
144. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
145. H. Jang, Y. Seok, Y. Choi, S. H. Cho, K. Watanabe, T. Taniguchi and K. Lee, Adv. Funct. Mater., 2021, 31, 2006788.
146. K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, Science, 2016, 353, aac9439.
147. Y. Liu, Y. Huang and X. Duan, Nature, 2019, 567, 323–333.
148. M. Y. Li, Y. Shi, C. C. Cheng, L. S. Lu, Y. C. Lin, H. L. Tang, M. L. Tsai, C. W. Chu, K. H. Wei, J. H. He, W. H. Chang, K. Suenaga and L. J. Li, Science, 2015, 349, 524–528.
149. X. Mao and P. Chen, Nat. Mater., 2022, 21, 331–337.
150. R. Li, F. Zhang, D. Wang, J. Yang, M. Li, J. Zhu, X. Zhou, H. Han and C. Li, Nat. Commun., 2013, 4, 1432.
151. A. Nipane, S. Jayanti, A. Borah and J. T. Teherani, J. Appl. Phys., 2017, 122, 194501.
152. H. Yu, A. Kutana and B. I. Yakobson, Nano Lett., 2016, 16, 5032–5036.
153. Z. Wu and Z. Ni, Nanophotonics, 2017, 6, 1219–1237.
154. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. M. Ajayan, B. I. Yakobson and J. C. Idrobo, Nano Lett., 2013, 13, 2615–2622.
155. C. Xie, D. Yan, H. Li, S. Du, W. Chen, Y. Wang, Y. Zou, R. Chen and S. Wang, ACS Catal., 2020, 10, 11082–11098.
156. P. Yang, J. Li, D. G. Vlachos and S. Caratzoulas, Angew. Chem., Int. Ed., 2024, 63, e202311174.
157. Z. Lin, B. R. Carvalho, E. Kahn, R. Lv, R. Rao, H. Terrones, M. A. Pimenta and M. Terrones, 2D Mater., 2016, 3, 022002.
158. T. X. Huang, X. Cong, S. S. Wu, K. Q. Lin, X. Yao, Y. H. He, J. B. Wu, Y. F. Bao, S. C. Huang, X. Wang, P. H. Tan and B. Ren, Nat. Commun., 2019, 10, 5544.
159. T. X. Huang, B. Dong, S. L. Filbrun, A. A. Okmi, X. Cheng, M. Yang, N. Mansour, S. Lei and N. Fang, Sci. Adv., 2021, 7, eabj4452.
160. W. Xu, J. S. Kong, Y. T. Yeh and P. Chen, Nat. Mater., 2008, 7, 992–996.
161. W. Xu, H. Shen, G. Liu and P. Chen, Nano Res., 2010, 2, 911–922.
162. M. Wu, J. J. Shi, M. Zhang, Y. M. Ding, H. Wang, Y. L. Cen and J. Lu, Nanoscale, 2018, 10, 11441–11451.
163. J. Zhang, P. Zhou, J. Liu and J. Yu, Phys. Chem. Chem. Phys., 2014, 16, 20382–20386.
164. J. G. Smith, I. Chakraborty and P. K. Jain, Angew. Chem., Int. Ed., 2016, 55, 9979–9983.
165. M. Chen, D. Kumar, C.-W. Yi and D. W. Goodman, Science, 2005, 310, 291–293.
166. W. Yu, M. D. Porosoff and J. G. Chen, Chem. Rev., 2012, 112, 5780–5817.
167. M. Bowker, Catal. Lett., 2012, 142, 1411.
168. D. Astruc, F. Lu and J. R. Aranzaes, Angew. Chem., Int. Ed., 2005, 44, 7852–7872.
169. K. Sytwu, M. Vadai and J. A. Dionne, Adv. Phys.: X, 2019, 4, 1619480.
170. P. Pechukas, Annu. Rev. Phys. Chem., 1981, 32, 159–177.
171. Z. Li, R. Devasenathipathy, J. Wang, L. Yu, Y. Liang, H. Sheng, Y. Zhu, H. Li, H. Uji-i, X. Huang and G. Lu, Nano Res., 2023, 16, 8817–8826.
172. Y. Aoki, T. Ishida and T. Tatsuma, ACS Appl. Nano Mater., 2022, 5, 4406–4412.
173. X. Xu, C. Fang, T. Bi, Z. Cui, G. Zhao, X. Jiang and J. Hu, Chem.–Eur. J., 2020, 26, 10787–10794.
174. H.-l. Liu, F. Nosheen and X. Wang, Chem. Soc. Rev., 2015, 44, 3056–3078.
175. T. Chen, F. Tong, J. Enderlein and Z. Zheng, Nano Lett., 2020, 20, 3326–3330.
176. M. Chen, Z. Ye, L. Wei, J. Yuan and L. Xiao, J. Am. Chem. Soc., 2022, 144, 12842–12849.
177. S. Link and M. A. El-Sayed, J. Phys. Chem. B, 1999, 103, 8410–8426.
178. K. J. Major, C. De and S. O. Obare, Plasmonics, 2009, 4, 61–78.
179. J. Zhu, Nanoscale Res. Lett., 2009, 4, 977.
180. S. K. Cushing, J. Li, F. Meng, T. R. Senty, S. Suri, M. Zhi, M. Li, A. D. Bristow and N. Wu, J. Am. Chem. Soc., 2012, 134, 15033–15041.
181. Z. Zheng, T. Tachikawa and T. Majima, J. Am. Chem. Soc., 2014, 136, 6870–6873.
182. N. Zou, G. Chen, X. Mao, H. Shen, E. Choudhary, X. Zhou and P. Chen, ACS Nano, 2018, 12, 5570–5579.
183. H. Lee, Y. Park, K. Song and J. Y. Park, Acc. Chem. Res., 2022, 55, 3727–3737.
184. S. K. Dutta, S. K. Mehetor and N. Pradhan, J. Phys. Chem. Lett., 2015, 6, 936–944.
185. J. Li and N. Wu, Catal. Sci. Technol., 2015, 5, 1360–1384.
186. T. Lin, T. Yang, Y. Cai, J. Li, G. Lu, S. Chen, Y. Li, L. Guo, S. A. Maier, C. Liu and J. Huang, Nano Lett., 2023, 23, 5288–5296.
187. N. Wang, T. Tachikawa and T. Majima, Chem. Sci., 2011, 2, 891–900.
188. T. Tachikawa, T. Yonezawa and T. Majima, ACS Nano, 2013, 7, 263–275.
189. J. W. Ha, T. P. Ruberu, R. Han, B. Dong, J. Vela and N. Fang, J. Am. Chem. Soc., 2014, 136, 1398–1408.
190. Y. Zhang, J. M. Lucas, P. Song, B. Beberwyck, Q. Fu, W. Xu and A. P. Alivisatos, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8959–8964.
191. L. Collado, A. Reynal, F. Fresno, M. Barawi, C. Escudero, V. Perez-Dieste, J. M. Coronado, D. P. Serrano, J. R. Durrant and V. A. de la Peña O'Shea, Nat. Commun., 2018, 9, 4986.
192. S. He, J. Huang, J. L. Goodsell, A. Angerhofer and W. D. Wei, Angew. Chem., Int. Ed., 2019, 58, 6038–6041.
193. L. Du, G. Shi, Y. Zhao, X. Chen, H. Sun, F. Liu, F. Cheng and W. Xie, Chem. Sci., 2019, 10, 9605–9612.
194. Y. Liu, K. Zhang, X. Tian, L. Zhou, J. Liu and B. Liu, ACS Appl. Mater. Interfaces., 2021, 13, 7680–7687.
195. J. Liang, X. Yang, Y. Wang, P. He, H. Fu, Y. Zhao, Q. Zou and X. An, J. Mater. Chem. A, 2021, 9, 12898–12922.
196. Y. Ni, R. Wang, W. Zhang, S. Shi, W. Zhu, M. Liu, C. Yang, X. Xie and J. Wang, Chem. Eng. J., 2021, 404, 126528.
197. S. Wu, J. K. Lee, P. C. Lim, R. Xu and Z. Zhang, Nanoscale, 2022, 14, 5612–5624.
198. J.-Y. Li, L. Yuan, S.-H. Li, Z.-R. Tang and Y.-J. Xu, J. Mater. Chem. A, 2019, 7, 8676–8689.
199. X. Sheng, T. Xu and X. Feng, Adv. Mater., 2019, 31, e1805132.
200. J. Zhang, M. Dai, S. Zhang, M. Dai, P. Zhang, S. Wang and Z. He, Sol. RRL, 2022, 6, 2200243.
201. H. Yi, D. Huang, L. Qin, G. Zeng, C. Lai, M. Cheng, S. Ye, B. Song, X. Ren and X. Guo, Appl. Catal., B, 2018, 239, 408–424.
202. S. Wu, J.-K. Lee, J. W. E. Tan, J. X. Chan, R. Xu and Z. Zhang, Small, 2024, 20, 2307057.
203. J. An, X. Song, W. Wan, Y. Chen, H. Si, H. Duan, L. Li and B. Tang, ACS Catal., 2021, 11, 6872–6882.
204. S. Cestellos-Blanco, H. Zhang, J. M. Kim, Y.-x. Shen and P. Yang, Nat. Catal., 2020, 3, 245–255.
205. N. Kornienko, J. Z. Zhang, K. K. Sakimoto, P. Yang and E. Reisner, Nat. Nanotechnol., 2018, 13, 890–899.
206. D. K. Dogutan and D. G. Nocera, Acc. Chem. Res., 2019, 52, 3143–3148.
207. Y. Taniguchi, P. J. Choi, G. W. Li, H. Chen, M. Babu, J. Hearn, A. Emili and X. S. Xie, Science, 2010, 329, 533–538.
208. E. Debroye, J. Van Loon, H. Yuan, K. P. Janssen, Z. Lou, S. Kim, T. Majima and M. B. Roeffaers, J. Phys. Chem. Lett., 2017, 8, 340–346.
209. B. Fu, X. Mao, Y. Park, Z. Zhao, T. Yan, W. Jung, D. H. Francis, W. Li, B. Pian, F. Salimijazi, M. Suri, T. Hanrath, B. Barstow and P. Chen, Nat. Chem., 2023, 15, 1400–1407.
210. F. Reinecke and A. Steinbuchel, J. Mol. Microbiol. Biotechnol., 2009, 16, 91–108.
211. C. Liu, B. C. Colon, M. Ziesack, P. A. Silver and D. G. Nocera, Science, 2016, 352, 1210–1213.
212. Y. Kohlmann, A. Pohlmann, A. Otto, D. Becher, R. Cramm, S. Lutte, E. Schwartz, M. Hecker and B. Friedrich, J. Proteome Res., 2011, 10, 2767–2776.
213. K. K. Sakimoto, A. B. Wong and P. Yang, Science, 2016, 351, 74–77.
214. Z. Ristanovic, A. V. Kubarev, J. Hofkens, M. B. J. Roeffaers and B. M. Weckhuysen, J. Am. Chem. Soc., 2016, 138, 13586–13596.
215. J. B. Sambur, T. Y. Chen, E. Choudhary, G. Q. Chen, E. J. Nissen, E. M. Thomas, N. M. Zou and P. Chen, Nature, 2016, 530, 77–80.
216. X. W. Mao, C. M. Liu, M. Hesari, N. M. Zou and P. Chen, Nat. Chem., 2019, 11, 687–694.
217. R. Ye, M. Zhao, X. W. Mao, Z. H. Wang, D. A. Garzón, H. T. Pu, Z. H. Zhao and P. Chen, Nat. Commun., 2021, 12, 4287.
218. S. Ghosh and L. Manna, Chem. Rev., 2018, 118, 7804–7864.
219. N. Singh, U. Sanyal, J. L. Fulton, O. Y. Gutiérrez, J. A. Lercher and C. T. Campbell, ACS Catal., 2019, 9, 6869–6881.
220. T. H. Yang, Y. F. Shi, A. Janssen and Y. N. Xia, Angew. Chem. Int. Ed., 2020, 59, 15378–15401.
221. S. E. Lohse, N. D. Burrows, L. Scarabelli, L. M. Liz-Marzán and C. J. Murphy, Chem. Mater., 2014, 26, 34–43.
222. D. A. Reed, B. K. Keitz, J. Oktawiec, J. A. Mason, T. Runcevski, D. J. Xiao, L. E. Darago, V. Crocellá, S. Bordiga and J. R. Long, Nature, 2017, 550, 96–100.
223. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1169.
224. D. R. Lide, CRC Handbook of Chemistry and Physics, CRC press, 2004.
225. K. M. Koczkur, S. Mourdikoudis, L. Polavarapu and S. E. Skrabalak, Dalton Trans., 2015, 44, 17883–17905.
226. L. Xu, R. Ye, M. Mavrikakis and P. Chen, ACS Cent. Sci., 2024, 10, 65–76.
227. P. Chen, X. Zhou, H. Shen, N. M. Andoy, E. Choudhary, K.-S. Han, G. Liu and W. Meng, Chem. Soc. Rev., 2010, 39, 4560–4570.
228. F. C. Hendriks, S. Mohammadian, Z. Ristanović, S. Kalirai, F. Meirer, E. T. C. Vogt, P. C. A. Bruijnincx, H. C. Gerritsen and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2018, 57, 257–261.
229. M. Filez, M. Vesely, I. Garcia-Torregrosa, M. Gambino, Ö. Attila, F. Meirer, E. A. Katrukha, M. B. J. Roeffaers, J. Garrevoet, L. C. Kapitein and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2021, 60, 13803–13806.
230. K.-L. Liu, A. V. Kubarev, J. Van Loon, H. Uji-i, D. E. De Vos, J. Hofkens and M. B. J. Roeffaers, ACS Nano, 2014, 8, 12650–12659.
231. T. Tachikawa, T. Ochi and Y. Kobori, ACS Catal., 2016, 6, 2250–2256.
232. K. Wenderich, A. Klaassen, I. Siretanu, F. Mugele and G. Mul, Angew. Chem., Int. Ed., 2014, 53, 12476–12479.
233. L. Möckl, A. R. Roy and W. E. Moerner, Biomed. Opt Express, 2020, 11, 1633–1661.
234. L. Möckl, A. R. Roy, P. N. Petrov and W. E. Moerner, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 60–67.

---

Footnote

† These authors contributed equally to this work.

---