Electronic structure and transport in the potential Luttinger liquids CsNb₃Br₇S and RbNb₃Br₇S

Abstract

The crystal structures of ANb₃Br₇S (A = Rb and Cs) have been refined by single crystal X-ray diffraction, and are found to form highly anisotropic materials based on chains of the triangular Nb₃ cluster core. The Nb₃ cluster core contains seven valence electrons, six of them being assigned to Nb–Nb bonds within the Nb₃ triangle and one unpaired d electron. The presence of this surplus electron gives rise to the formation of correlated electronic states. The connectivity in the structures is represented by one-dimensional [Nb₃Br₇S]⁻ chains, containing a sulphur atom capping one face (μ₃) of the triangular niobium cluster, which is believed to induce an important electronic feature. Several types of studies are undertaken to obtain deeper insight into the understanding of this unusual material: the crystal structure, morphology and elastic properties are analysed, as well the (photo-)electrical properties and NMR relaxation. Electronic structure (DFT) calculations are performed in order to understand the electronic structure and transport in these compounds, and, based on the experimental and theoretical results, we propose that the electronic interactions along the Nb chains are sufficiently one-dimensional to give rise to Luttinger liquid (rather than Fermi liquid) behaviour of the metallic electrons.

---

Introduction

Metal-rich niobium halides are well known in chemistry, typically appearing with the octahedral Nb₆ cluster core, as in Nb₆X₁₄ (X = Cl, Br),^1–3 or with a triangular Nb₃ cluster core in the structure of Nb₃X₈ (X = Cl, Br, I).^4,5 The electronic structure of Nb₆X₁₄ is well described with eight metal-centred molecular orbitals (MOs) being occupied by 16 electrons. Nb₃X₈ (X = Cl, Br, I) compounds appear as layered structures based on close-packed halide arrangements in which ¾ of the octahedral voids in every second interlayer are occupied by niobium atoms. However, each niobium atom in the crystal structure is displaced away from the centre of its coordination octahedron to form trigonal clusters (shown in Fig. 1), each containing seven electrons in metal-centred states.⁶ A magnetic-to-nonmagnetic phase transition has been shown upon cooling in Nb₃Cl₈ with interlayer charge transfer between Nb₃ trimers in adjacent layers,⁷ although such charge transfer was not observed in other studies.^8,9

Fig. 1 Projection of arrangement of Nb₃ clusters within one interlayer of the structure of Nb₃X₈.

The valence electron count (VEC) in compounds containing triangular Nb₃ clusters compounds is between 6 and 8; for instance, VEC = 6 for Nb₃Br₇S¹⁰ and Nb₃O₂Cl₅,¹¹ VEC = 7 for Nb₃X₈ (X = Cl, Br, I) and CsNb₃Br₇S,¹² and VEC = 8 for NaNb₃Cl₈.^9,13,14 The compounds with seven valence electrons can have interesting magnetic behaviour, especially in combination with the two-dimensional polar Kagome lattice structure of Nb₃X₈.^8,9,15–17 MO calculations on the seven-electron cluster [Nb₃X₁₃]⁵⁻, adapted from the Nb₃X₈ structure, revealed that six electrons can be assigned to Nb–Nb bonding within the Nb₃ cluster and that the HOMO level is a half-filled 2a₁ orbital.⁶

Compounds A₃[Nb₆SBr₁₇] with A = Rb, Tl, K, Cs^18,19 contain a sulphur-centred, trigonal prismatic [Nb₆S] core which has been reported to contain only weak Nb–Nb interactions between adjacent Nb₃-triangles (Fig. 2 at left).¹⁸ The chain structure of CsNb₃SBr₇ is based on similar [Nb₃S] clusters, shown in Fig. 2 on the right. Both compounds contain seven valence electrons per Nb₃ cluster.

Fig. 2 The [Nb₆S] cluster core in the structure of A₃[Nb₆SBr₁₇] (left), and a section of the infinite [Nb₃S] chain in ANb₃Br₇S (right).

Triangular [Nb₃]⁸⁺ clusters consisting of an Nb–Nb bonded arrangement are of fundamental interest. In isolation, each cluster has seven valence electrons and thus one unpaired d electron in a 2a₁ orbital. Such unpaired electrons in Nb clusters have recently become the source of significant research attention due to their formation of various long-range ordered states, for example by charge disproportionation between layers in Nb₃Cl₈,⁷ and the formation of a Mott insulating state in GaNb₄S₈.²⁰

The structure of CsNb₃Br₇S was reported in 1993 to contain [Nb₃]⁸⁺ clusters, each of which is capped with a (μ₃) sulphur atom to form the motif of a tetrahedron (Fig. 2, right). These clusters are arranged in chains parallel to the c-axis, with alternating positions of the clusters above and below the central sulphur chain. The chains have an outer shell of bromide ions, and voids in the crystal structure between the chains are filled by caesium ions. The extended Hückel method was used to predict that CsNb₃Br₇S is a semimetal, with the Nb d orbitals forming bands which cross the Fermi level.¹²

We have revisited this material, which shows an interesting crystal morphology of cleavable rods. The synthesis and crystal structure of CsNb₃Br₇S is revised in order to confirm its structure and electronic properties. In addition, the synthesis and structure of the closely related compound RbNb₃Br₇S is reported for the first time. The elastic properties and NMR relaxation of CsNb₃Br₇S are investigated, electric conductivity measurements along the [Nb₃S]_n chain direction are performed for both compounds, and theoretical investigations of the electronic structure are performed using density functional theory (DFT).

Our studies suggest that CsNb₃Br₇S and RbNb₃Br₇S have conducting electrons which can be described as (Tomonaga–) Luttinger liquids, rather than the more usual Fermi liquids. Luttinger liquids are a type of one-dimensional paramagnetic quantum fluid, characterized by their separate transport of charge density waves (CDWs) and spin density waves (SDWs).^21,22 They can be identified by their characteristic spectral function and by the power-law response of various physical properties as a function of temperature.²¹

Experimental

Synthetic procedures

ANb₃Br₇S compounds with A = Rb and Cs were prepared by solid-state reactions starting from mixtures of ABr (99.0% Merck), NbBr₅ (99.9% ABCR GmbH), niobium powder (99.9% ABCR GmbH) and sulphur (99.9% Carl Roth GmbH) in stoichiometric proportions with total masses of 100 to 200 mg per batch. The starting materials were homogenised by grinding under an argon atmosphere and fused in silica tubing. Loaded ampoules were heated at 800 °C for 24 h (heating and cooling rates of 2 K min⁻¹). Short-term reactions and fast cooling rates yielded a furry, crystalline material consisting of fine needle-like crystals. Long-term reactions with slow cooling rates gave longer, rod-shaped crystals. Both compounds ANb₃Br₇S (A = Rb, Cs) appear as black crystals with metallic lustre and are stable in air for weeks, as confirmed by X-ray powder diffraction.

Crystallography

Carefully selected black needle-shaped single-crystals of RbNb₃Br₇S and CsNb₃Br₇S were mounted on a Rigaku XtaLab Synergy-S X-ray diffractometer using Cu-Kα (λ = 1.54184 Å) and Mo-Kα (λ = 0.71073 Å) radiation, respectively. The single crystals were kept under N₂ cooling at 100 K during the data collection. Corrections for absorption effects were applied with CrysAlisPro 171.41.64.93a (Rigaku Oxford Diffraction, 2020). Crystal structures were solved by the integrated space group and crystal-structure determination routine of SHELXT²³ and full-matrix least-squares structure refinements with SHELXL-2014²³ implemented in Olex2 1.3-ac4.²⁴ The structure of RbNb₃Br₇S was refined as a racemic twin with a Flack parameter 0.50(3).

Details of the crystal structure investigations can be obtained from the joint CCDC/FIZ Karlsruhe online deposition service: https://www.ccdc.cam.ac.uk/structures/by quoting the deposition numbers CCDC 2048759 for RbNb₃Br₇S and CCDC 2048757 for CsNb₃Br₇S.†

Electron microscopy

Electron micrographs were recorded on a JEOL 8900 Superprobe spectrometer. The samples were coated with carbon prior to the measurements.

Electrical characterisation

Conductivity measurements were performed in a Lake Shore Cryotronics CRX-6.5K probe station with a Keithley 2636B source meter unit. Rod-shaped crystals of CsNb₃Br₇S and RbNb₃Br₇S were transferred into the chamber under protective gas and contacted with silver paste on a silicon substrate with 770 nm oxide layer. The conductive silver pads at each end of the crystals were connected to the circuit with tungsten tips (Fig. S1, ESI†). The chamber was kept under vacuum (<5 × 10⁻⁵ mbar) and the temperature was varied between 20 K and 300 K. Before each measurement, sufficient time was allowed for the sample to reach the chosen temperature. Two-point conductivity measurements were performed by varying the applied source–drain voltage from −1 V to 1 V while detecting the current. Time-resolved photocurrent measurements used a picosecond pulsed laser driver (Taiko PDL M1, PicoQuant) together with a laser head 779 nm (pulse length <500 ps); the crystals were illuminated at 40 mW laser output power using the continuous wave mode under a constant bias of 1 V.

Nuclear magnetic resonance spectroscopy

¹³³Cs NMR data were collected at 65.5 MHz (B₀ = 11.7 T) and 52.4 MHz (B₀ = 9.4 T) using Bruker Avance III spectrometers. The ¹³³Cs magic-angle spinning (MAS) spectra were acquired on a polycrystalline sample at 11.7 T by Bloch decay, using a 2.5 mm MAS probe with spinning rates of 10.00, 20.00 and 30.00 kHz. The chemical shift is referenced to external 0.1 M CsCl(aq) at 0.0 ppm. T₁ relaxation times were measured by fitting inversion-recovery data to a mono-exponential decay function.

⁹³Nb NMR spectra were acquired at 97.9 MHz (B₀ = 9.4 T) on a Bruker Avance III 400 using a 4 mm MAS probe. The wideband uniform-rate smooth-truncation (WURST) quadrupolar Carr–Purcell–Meiboom–Gill (QCPMG) pulse sequence was used to acquire six individual spectra on a non-spinning sample at variable transmitter offsets, which were subsequently assembled into the 1.8 MHz spectrum. All NMR spectra were acquired at ambient temperature without temperature regulation.

Computational methods

Density functional theory (DFT) calculations were performed using the software packages Abinit (v. 9)²⁵ and Quantum Espresso. Calculations of the elastic tensor and Γ-point phonon frequencies were performed in Abinit using norm-conserving pseudopotentials from the Abinit library, a 4 × 4 × 4 Monkhorst–Pack grid of k-points,²⁶ a 34 Ha plane-wave basis set energy cutoff, and the PBE exchange–correlation functional.²⁷

Calculations of the electronic band structure with antiferromagnetic ordering and a Hubbard U term²⁸ (U = 5 eV and J = 0.2 eV on the Nb sites)²⁹ and with spin–orbit coupling were performed in Abinit using the projector-augmented wave (PAW) method³⁰ with pseudopotentials from the GBRV library,³¹ a Monkhorst–Pack grid of k-points with real-space basis vectors [0 2 4] [4 0 4] and [4 2 0],²⁶ a 128 Ha plane-wave basis set energy cutoff within the PAW spheres and a 24 Ha cutoff outside.

We also performed calculations without spin polarization to construct a tight-binding model based on Wannier functions. For these calculations we employed Wannier90³² and Quantum Espresso³³ using ultrasoft pseudopotentials also from the GBRV library³³ with a 4 × 2 × 6 Monkhorst–Pack grid, and a plane-wave energy and density cutoff of 72 Ry and 864 Ry, respectively.

All the calculations stated above were performed with PBE exchange–correlation functional²⁷ with the DFT-D3 dispersion correction,³⁴ and Methfessel–Paxton cold smearing of the electronic states.³⁵ Special points in and paths through the Brillouin zone were chosen following Hinuma et al.³⁶ All computational parameters were chosen following convergence studies. The band structures produced by Abinit and by Quantum Espresso with these parameters were compared and found to be essentially identical.

Results and discussion

Crystal structures

The crystal structures of ANb₃Br₇S (A = Rb, Cs) were solved and refined from single-crystal X-ray diffraction data. The structure of CsNb₃Br₇S was confirmed to agree with the previously reported data on the same compound with the monoclinic space group P2₁/c (No. 14).¹² The structure of the new compound RbNb₃Br₇S was refined with the orthorhombic space group Pmc2₁ (No. 26). Both crystal structures contain the same arrangement of triangular Nb₃ clusters face-capped (μ₃) by sulphur atoms, and linked into chains via bromide and sulphide ions along the crystallographic a direction for A = Rb, and along c direction for A = Cs. The [Nb₃SBr₇]⁻ cluster units in both structures are linked into chains by three inner (i) edge capping bromides, six shared (6/2) outer (a–a) bromides, and one terminal outer (a) bromide, forming the structural unit [Nb₃SBr₃ⁱBr_6/2^a–aBr^a]⁻, which can be seen in Fig. 3.

Fig. 3 Section of a single chain in the structure of CsNb₃Br₇S along the crystallographic c-direction. Niobium atoms are shown blue, sulphur yellow, and bromide atoms brown.

The difference between the two crystal structures with A = Cs and Rb is expressed in the different symmetries of the orthorhombic and monoclinic space groups. This can be explained by the different radii and coordination patterns of alkali ions in the structures. The caesium ion is situated in a nearly regular cube-octahedral environment of bromides, and Rb is surrounded by an irregular twelvefold arrangement of bromide ions. These environments with bromide ions, which are also linked to the niobium clusters, cause shifts of adjacent clusters along the one-dimensional chain of the structure (Fig. 4).

Fig. 4 Comparison of crystal structures of CsNb₃Br₇S (P2₁/c, left) and RbNb₃Br₇S (Pmc2₁, right) with their unit cells. Bromides are omitted in the drawings for better clarity. Cs (dark grey) and Rb (light grey) atoms are shown.

The distances between the three crystallographically distinct niobium atoms are about 290 pm within Nb₃ cluster triangles and about 310 pm between adjacent triangles (see Table 1 for details). Despite the similarity of these interatomic distances, previously reported electronic structure calculations (extended Hückel) on CsNb₃Br₇S had revealed comparable Nb–Nb crystal orbital overlap populations (0.25) within Nb₃ triangles and weak (0.09) overlap populations between adjacent triangles.

Table 1 Selected interatomic distances (pm) in ANb₃Br₇S (A = Rb, Cs) compounds. The A = Rb compound contains two independent Nb₃ clusters in the structure

Compound	RbNb3Br7S	CsNb3Br7S
a Within cluster triangle (Δ). b Between cluster triangles (′).
Nb–Nb Δ^a	289.3(3), 290.3(3)	290.71(7)
	289.3(3), 290.3(3)	290.01(7)
	281.2(3) 288.6(3)	286.63(7)
Nb–Nb ′^b	310.2(3)	310.74(5)
Nb–S Δ	238.8(6) 248.4(8)	238.3(2)
	238.8(6) 248.4(8)	246.0(2)
	233.0(8) 250.7(9)	246.1(2)
Nb–S ′	257.2(6)	262.9(2)
	265.6(5)	263.5(2)

---

The cohesion between adjacent cluster chains in the structure is dominated by ionic (Br–A) bonding, as expressed by the appearance of differently shifted chain arrangements in the crystal structures of ANb₃Br₇S with A = Rb and Cs along the chain directions (Fig. 4). The primary growth direction of needle-shaped crystal rods coincides with the direction of the [Nb₃SBr₃ⁱBr_6/2^a–aBr^a]⁻ chains (Fig. 5). This pronounced growth direction suggests a one-dimensional character of the material, as supported by the fraying behaviour of crystal rods shown below, and later quantitatively evaluated by the elastic properties (directional Young's modulus).

Fig. 5 Comparison of crystal structures of RbNb₃Br₇S (Pmc2₁, bottom) and CsNb₃Br₇S (P2₁/c, top) with their unit cells. Nb (blue), S (yellow), Br (brown), Cs (dark grey) and Rb (light grey) atoms are shown.

Electron microscopy and elastic properties

The morphology of synthesized CsNb₃Br₇S crystals is shown in SEM micrographs in Fig. 6. CsNb₃Br₇S forms rods with fairly uniform dimensions of about 500 μm length and 10 μm diameter. As Fig. 6a shows, each rod could be assumed to be a single crystal, but a magnified view suggests that this is not always clear. This morphology can be readily explained by a highly anisotropic crystal structure, and our XRD studies on single crystals confirm the long axis of the rods to coincide with the crystallographic c-axis. Fig. 6b shows fraying of a rod, an interesting feature indicating that the material is at least somewhat flexible, and that the cohesive forces along the a and b axes might be expected to have van der Waals character; except in this case they are instead ionic interactions between the bromides of the cluster and A cations.

Fig. 6 SEM micrographs of (a) CsNb₃Br₇S crystals, showing their pronounced rod-like morphology, (b) fraying of a rod of CsNb₃Br₇S and (c) their high degree of uniformity on the micron scale.

In order to examine the origins of this fraying behaviour further, and to determine to what extent the elastic properties of CsNb₃Br₇S can be considered one-dimensional, its elastic tensor was calculated using DFPT (eqn (S1), ESI†). The vdW-D3 dispersion correction of Grimme was employed to ensure that van der Waals forces would be accounted for in the model. The easiest way to visualize the elastic anisotropy is through the directional Young's modulus (Y_ii), which describes the resistance of the material to uniaxial stress in a given direction. This is shown in Fig. 7; CsNb₃Br₇S is found to be stiffest along the c-axis, with a directional Young's modulus of 74 GPa. While c is the stiffest direction, the Young's modulus also shows significant peaks coinciding with a (24 GPa) and b (34 GPa), indicating that the mechanical bonding between [Nb₃Br₇S]⁻ chains through the Cs⁺ cations is significant. These results demonstrate that, although CsNb₃Br₇S is highly anisotropic, its elasticity is decidedly not one-dimensional.

Fig. 7 The calculated directional Young's modulus (Y_ii) of CsNb₃Br₇S, shown as a green surface. The view is along the a-axis (analogous to Fig. 2).

Electrical properties

Both CsNb₃Br₇S and RbNb₃Br₇S exhibit ohmic behaviour in the measured temperature range between 20 and 300 K. Fig. 8 shows the dark current obtained at room temperature for two different CsNb₃Br₇S crystals. Conductivities of 0.35 S cm⁻¹ for CsNb₃Br₇S and 1.65 S cm⁻¹ for RbNb₃Br₇S are measured with a two-point measurement. The inset in Fig. 9 shows the temperature-dependent electrical conductivity in the range of 20 K to 300 K for CsNb₃Br₇S, indicating a temperature-activated behaviour. The same trend of a decreasing conductivity with decreasing temperature is observed for RbNb₃Br₇S, cf. Fig. S2 (ESI†).

Fig. 8 Dark currents I of CsNb₃Br₇S crystals on silicon with 770 nm dioxide layer at 300 K with an applied source–drain voltage U_SD of −1 V to 1 V.

Fig. 9 Double logarithmic plot of the electrical conductivity of CsNb₃Br₇S versus set temperature in a range of 20 K to 300 K with a power law fit (black) following σ(T) = cT^α with α = 4.4. In the inset: electrical conductivity of CsNb₃Br₇S versus temperature in a range of 20 K to 300 K.

The electrical conductivity of CsNb₃Br₇S (Fig. 9, inset) and RbNb₃Br₇S (Fig. S2, right, ESI†) show a general increase with increasing temperature. As shown in Fig. 9, above 50 K (CsNb₃Br₇S) and 30 K (RbNb₃Br₇S), the electrical conductivity (σ) as a function of temperature can be fitted to a power law (σ(T) = cT^α for some constants α and c), and therefore is consistent with a Luttinger liquid.^21,37 At lower temperatures, the conductivity cannot be fit to an Arrhenius curve, suggesting that it is not a simple semiconductor in that regime.

Photoelectric properties

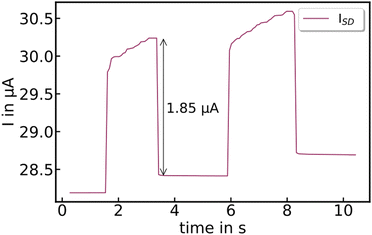
When the crystals are illuminated with 779 nm CW-laser pulses, both compounds show a photoresponse, see Fig. 10. This photocurrent consists of a steep and fast increase, followed by a slower second component. We attribute the first rise to photoexcited charge carriers, and the second increase to the effect of concomitant heating of the crystal (compare with Fig. 8). The photocurrent is strongly temperature-activated, ranging from a few nA at 20 K to several tens of μA at room temperature.

Fig. 10 Photoresponse of a CsNb₃Br₇S crystal to a 779 nm laser at 200 K.

Nuclear magnetic resonance

The ¹³³Cs MAS NMR spectrum exhibits a single peak at 330 ppm (Fig. S3, ESI†), near the upper edge of the chemical shift range for diamagnetic samples. The peak position is not far from that of CsBr (258 ppm),³⁸ consistent with the similar local Cs environment. The narrowness of the central peak indicates a small quadrupolar interaction, and the full extent of the spinning sideband envelope corresponds to a quadrupole coupling constant around 250 kHz, typical for crystalline materials.³⁹ The spinning sidebands at slower spinning rates are symmetrically distributed about the central peak, implying that there is no appreciable anisotropy in the Cs chemical shielding. No changes were observed in the central peak position or lineshape upon increasing the spinning rate, despite the accompanying temperature increase of about 25 °C.⁴⁰ The most unique feature of the ¹³³Cs NMR response is its anomalously short spin–lattice relaxation time: while most insulating and semiconducting solids have ¹³³Cs T₁ values in the range of 30–60 s^41,42 – with values up to 900 s having been reported⁴³ – the T₁ of CsNb₃Br₇S was measured to be 165 ms at 11.7 T. Such a short relaxation time is often indicative of nuclear interactions with unpaired electron spins, however, no evidence of a contact shift or electron–dipolar coupling is observed. Instead, this may be considered evidence for a Luttinger liquid, which exhibits extremely fast spin–lattice relaxation in certain magnetic field regimes.⁴⁴ A second T₁ measurement at 9.4 T yielded similarly rapid relaxation of 185 ms. Attempts to record a ⁹³Nb NMR spectrum were partially successful, yielding a broad signal spanning nearly 1.8 MHz (not shown), reflective of the large quadrupole moment of ⁹³Nb and its asymmetric local environments; however, the ⁹³Nb T₁s are similarly short (<200 ms) and the T₂ value estimated from the echo train is around 2 ms. These observations from NMR support the designation of CsNb₃Br₇S as a Luttinger liquid.

Electronic structure

The electronic structure of CsNb₃Br₇S was examined further using density functional theory (DFT). The results are in qualitative agreement with earlier calculations (both extended Hückel⁶ and DFT⁴⁵) showing semimetallicity (specifically, zero band gap semiconductor behaviour) due to crossings of the Fermi level near the B (0 0 ½) and A (−½ 0 ½) points of the Brillouin zone (Fig. 11 and 12). The band gap remains extremely small (<0.1 eV) between B (0 0 ½) and D (0 ½ ½), and between A (−½ 0 ½), and E (−½ ½ ½).

Fig. 11 The calculated electronic band structure of nonmagnetic CsNb₃Br₇S (a), and corresponding atom-centred (b) and bond-centred (c and d) maximally localized Wannier functions (shown at Γ). Blue spheres represent Nb atoms. Special points in and paths through the Brillouin zone were chosen following literature.³⁶

Fig. 12 The calculated electronic band structure of CsNb₃Br₇S with an antiferromagnetic arrangement of magnetic moments on the Nb triangles along each chain (shown at right). Special points in and paths through the Brillouin zone were chosen following literature.³⁶

In order to understand the nature of the electronic states near the Fermi level, we constructed maximally localized Wannier functions⁴⁶ from the DFT wavefunctions (Fig. 11) in two ways. We first include all the bands with strong Nb d character (see Fig. S5, ESI†) in the energy window. This way we obtain Wannier functions that have a form like Nb d orbitals (Fig. 11b), with additional of p-orbital tails coming from the hybridization with Br and S (open magenta circles in Fig. 11). In this model, the largest absolute value for the hopping integral inside one trimer is around 1.2 eV, while the largest hopping for contiguous trimers can be as high as 0.7 eV, which underlines a non-negligible contribution of inter-trimer hybridization in the electronic structure.

The importance of considering contiguous trimers is more evident if we include only the 4 states around the Fermi energy in the energy window during the wannierization (full green circles in Fig. 11). Fig. 11(c and d) shows the result of the spread minimization, with the Wannier functions being centered between the Nb trimers. The hopping integrals (t) of the tight-binding model corresponding to the bond-centred Wannier functions (Table S1, ESI†) indicate that nearest-neighbour intra-chain hopping (t ≈ −0.2 eV) is significantly favored over inter-chain hopping (t′ ≈ −0.01 eV).

The predicted electronic conduction in CsNb₃Br₇S is not unsurprising given the presence of unpaired electrons in each [Nb₃]⁸⁺ cluster, which leads to each [Nb₃Br₇S]⁻ chain having one unpaired electron per Nb₃ cluster. However, the measured temperature-activated electrical conductivity is inconsistent with a conventional metal or semimetal, but not with a Luttinger liquid. Together with the power law dependence of the electronic conductivity on temperature and short NMR T₁ relaxation times, our findings indicate that CsNb₃Br₇S is a Luttinger liquid above ca. 30 K. The values of the Luttinger parameter α extracted from the electronic conductivity (α = 4.4 for CsNb₃Br₇S and α = 4.2 for RbNb₃Br₇S) indicate that the electron–electron interactions are repulsive in nature, and that the chains contain strong impurities, i.e. discontinuities or barriers in the chains which require quantum tunnelling for electronic transport.⁴⁷ The presence of strong impurities precludes further modelling of the Luttinger electronic interaction parameters from the available data.

A metallic one-dimensional chain of electrons has several possible mechanisms of gap opening upon cooling. At low temperature, electronic correlations will favour the formation of a charge-ordered singlet (Peierls) or triplet (Mott) insulator, and which state forms depends on the relative energetics.⁴⁸ Below 30 K, as the conductivity no longer follows a power law, we expect a gap to have opened in the CDW and SDW continuum corresponding to the Luttinger liquid. We can therefore consider several mechanisms of gap opening in CsNb₃Br₇S.

The first is the Peierls distortion, which is a CDW instability that, for example, forms alternating long and short bonds (as in polyacetylene). We would expect this mechanism to lead to variations in the Nb–Nb bond lengths, either within the Nb₃ trimers as has been reported in Nb₃Cl₈⁴⁹ or between them.

In our structure refinement (at 100 K) each Nb₃ cluster in CsNb₃Br₇S is crystallographically identical; any Peierls distortion would lower the crystallographic symmetry and would be easily detectable using single-crystal X-ray diffraction. Therefore, we conclude that there is no Peierls distortion or charge disproportionation in CsNb₃Br₇S at 100 K, although there may be at lower temperatures.

Instead of forming bound pairs of electrons in a Peierls insulator, exchange coupling in combination with electronic correlations can create a Mott insulator via a SDW instability. Here, a Mott insulator would correspond to a state where each cluster has one localized electron with antiferromagnetic spin alignment with respect its neighbours along the chain (Fig. 12). However, in a Mott insulator, the magnetic susceptibility would be expected to show temperature dependence corresponding to an antiferromagnet or a paramagnet with antiferromagnetic correlations, which is seen only below 30 K in CsNb₃Br₇S, and the material could be a Mott insulator below that temperature. Above 30 K, CsNb₃Br₇S shows temperature independent paramagnetic behaviour (TIP), and a magnetic-to-nonmagnetic charge transition seen in Nb₃Cl₈ is absent in CsNb₃Br₇S (Fig. S4, ESI†).

Spin–orbit coupling presents a third mechanism for opening a band gap. Previous studies have shown that, while in the absence of SOC, CsNb₃Br₇S is a topological nodal straight-line semimetal, inclusion of SOC introduces a small gap of ca. 5 meV at the crossing points. Note that due to the combination of P and T symmetries, the semimetal state in the absence of SOC has a well-defined, nontrivial Z₂ invariant,⁵⁰ and the gapped phase in the presence of SOC is also expected to be topological.⁴⁵ Such a gap is small, but still would be expected to lead to semiconducting behaviour for a Fermi liquid at low temperature. However, our calculations indicate that, while there is such a gap near B (0 0 ½), the bands cross the Fermi level near A (−½ 0 ½) (Fig. 13). There is a small amount of dispersion of the electronic bands along a, which can be attributed to weak interchain interactions, and which leads to the formation of conducting electronic states.

Fig. 13 The calculated electronic band structure of nonmagnetic CsNb₃Br₇S, calculated with spin–orbit coupling on a fine grid of k-points along Γ–B (0 0 c*) (blue) and Γ–A (−½ 0 c*) (orange). Special points in and paths through the Brillouin zone were chosen following literature.³⁶

Therefore, the nature of CsNb₃Br₇S at temperatures below 30 K, where the Luttinger liquid state breaks down, cannot be definitively determined from the available data. The calculated phonon energies at Γ (Table S2, ESI†) do not show an instability related to dimerization; the lowest energy phonon which involves modulation of the Nb–Nb distances has a frequency of 38.67 cm⁻¹ (4.6 meV). This indicates that the rough scale of the energy barrier which the CDW instability would need to overcome in order to create a Peierls distortion is small. The upturn in the magnetic susceptibility at low temperatures (Fig. S4, ESI†) suggests a potential Mott insulating state. Further low-temperature structural and magnetic investigation is therefore required to determine the ground states of CsNb₃Br₇S and RbNb₃Br₇S at temperatures approaching absolute zero.

Conclusions

The previously given crystal structure of CsNb₃Br₇S is confirmed by single crystal X-ray diffraction studies and the new compound RbNb₃Br₇S is reported with a slightly distinct structure. Structure determinations on these compounds are challenging, due to the formation of twins and fraying character of needle-like rods parallel to the direction of infinite [Nb₃Br₇S]⁻ chains. Crystals of both compounds appear black with metallic lustre but show semiconducting behaviour. Refinement of the crystal structure reveals a one-dimensional nature, due to the presence of [Nb₃Br₇S]⁻ chains. However, different arrangements of chains in the structure of ANb₃Br₇S with A = Rb, Cs due to different ionic radii of A cations reflect significant ionic (A–Br) interaction between adjacent chains. This is also expressed by the calculated elastic properties (directional Young's modulus) of CsNb₃Br₇S in which the chain direction (c-axis) is the stiffest direction (74 GPa), but stiffness maxima also coincide with a and b, indicating that the ionic bonding between [Nb₃Br₇S]⁻ chains through Cs cations is significant. Electronic structure calculations indicate that CsNb₃Br₇S is a one-dimensional metal. At temperatures above 30 K, the experimental data indicates that the CDWs and SDWs are fluid, and the material behaves as a Luttinger liquid. The increase in conductivity with temperature in the Luttinger liquid phase indicates repulsive interactions between electrons. Below 30 K, a band gap could open through formation of a Peierls (CDW ordered) or Mott (SDW correlated) insulator.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support of this Research by the German Research Foundation (DFG) through grant ME 914/32-1 and SCHE1905/9-1 (project no. 426008387) is gratefully acknowledged. C. P. R. and S. F. W. were supported by ETH Zurich and by the European Union and Horizon 2020 through a Marie Sklodowska–Curie Fellowship, Grant Agreement No. 101030352 (C. P. R.) and by Grant No. 810451 (S. F. W.). A. C. was supported by ETH Zurich. Computational resources were provided by ETH Zurich, by the Swiss National Supercomputing Center (CSCS) under project IDs s1128 and eth3, and by the state of Baden–Württemberg through bwHPC and the DFG through grant INST 40/575-1 FUGG (JUSTUS 2 cluster). S. K. is supported by grants from the Natural Sciences and Engineering Research Council (NSERC) of Canada, and the Canada Foundation for Innovation (CFI). We thank Dr Arun Krishnamurthy and Mr Mojtaba Abbasi (University of Manitoba) for the solid-state NMR measurements.

Notes and references

1. A. Simon, H. G. Schnering, H. Wöhrle and H. Schäfer, Z. Anorg. Allg. Chem., 1965, 339, 155–170.
2. R. Allen and J. Sheldon, Aust. J. Chem., 1965, 18, 277–283.
3. M. B. Robin and N. A. Kuebler, Inorg. Chem., 1965, 4, 978–985.
4. H. Schäfer and H. G. Schnering, Angew. Chem., 1964, 76, 833–868.
5. A. Simon and H. G. Von Schnering, J. Less-Common Met., 1966, 11, 31–46.
6. H.-J. Meyer, Z. Anorg. Allg. Chem., 1994, 620, 81–84.
7. Y. Haraguchi, C. Michioka, M. Ishikawa, Y. Nakano, H. Yamochi, H. Ueda and K. Yoshimura, Inorg. Chem., 2017, 56, 3483–3488.
8. J. P. Sheckelton, K. W. Plumb, B. A. Trump, C. L. Broholm and T. M. McQueen, Inorg. Chem. Front., 2017, 4, 481–490.
9. C. M. Pasco, I. El Baggari, E. Bianco, L. F. Kourkoutis and T. M. McQueen, ACS Nano, 2019, 13, 9457–9463.
10. S. Abrahams, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 426–437.
11. F. Gulo and C. Perrin, Mater. Res. Bull., 2000, 35, 253–262.
12. H.-J. Meyer, Z. Anorg. Allg. Chem., 1994, 620, 863–866.
13. J. R. Kennedy and A. Simon, Inorg. Chem., 1991, 30, 2564–2567.
14. C. C. Torardi and R. E. McCarley, Inorg. Chem., 1985, 24, 476–481.
15. Z. Sun, H. Zhou, C. Wang, S. Kumar, D. Geng, S. Yue, X. Han, Y. Haraguchi, K. Shimada, P. Cheng, L. Chen, Y. Shi, K. Wu, S. Meng and B. Feng, Nano Lett., 2022, 22, 4596–4602.
16. Y. Feng and Q. Yang, J. Mater. Chem. C, 2023, 11, 5762–5769.
17. C.-G. Duan, J. Hong, F. Sui, K. Wang, X. Han, Y. Zheng, W.-Y. Tong, X. Deng, Z. Guan and B. Tian, Physical Sciences, 2023, preprint,  DOI:10.21203/rs.3.rs-3457733/v1.
18. H. Womelsdorf and H.-J. Meyer, Angew. Chem., Int. Ed. Engl., 1994, 33, 1943–1944.
19. H. Womelsdorf and H.-J. Meyer, Z. Anorg. Allg. Chem., 1996, 622, 2083–2088.
20. S. Jakob, H. Müller, D. Johrendt, S. Altmannshofer, W. Scherer, S. Rayaprol and R. Pöttgen, J. Mater. Chem., 2007, 17, 3833–3838.
21. D. Baeriswyl and L. Degiorgi, Strong interactions in low dimensions, Springer Science & Business Media, 2007.
22. F. D. M. Haldane, J. Phys. C: Solid State Phys., 1981, 14, 2585.
23. G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
24. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
25. X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J.-M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet, N. Brouwer, F. Bruneval, G. Brunin, T. Cavignac, J.-B. Charraud, W. Chen, M. Côté, S. Cottenier, J. Denier, G. Geneste, P. Ghosez, M. Giantomassi, Y. Gillet, O. Gingras, D. R. Hamann, G. Hautier, X. He, N. Helbig, N. Holzwarth, Y. Jia, F. Jollet, W. Lafargue-Dit-Hauret, K. Lejaeghere, M. A. L. Marques, A. Martin, C. Martins, H. P. C. Miranda, F. Naccarato, K. Persson, G. Petretto, V. Planes, Y. Pouillon, S. Prokhorenko, F. Ricci, G.-M. Rignanese, A. H. Romero, M. M. Schmitt, M. Torrent, M. J. van Setten, B. Van Troeye, M. J. Verstraete, G. Zérah and J. W. Zwanziger, Comput. Phys. Commun., 2020, 248, 107042.
26. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
28. B. Amadon, F. Jollet and M. Torrent, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155104.
29. D. B. Migas, A. B. Filonov, V. E. Borisenko and N. V. Skorodumova, J. Alloys Compd., 2020, 821, 153527.
30. M. Torrent, N. A. W. Holzwarth, F. Jollet, D. Harris, N. Lepley and X. Xu, Comput. Phys. Commun., 2010, 181, 1862–1867.
31. K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452.
32. G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J.-M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi and J. R. Yates, J. Phys.: Condens. Matter, 2020, 32, 165902.
33. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
34. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Phys. Chem., 2010, 132(15), 154104.
35. M. Methfessel and A. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616.
36. Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184.
37. M. Bockrath, D. H. Cobden, J. Lu, A. G. Rinzler, R. E. Smalley, L. Balents and P. L. McEuen, Nature, 1999, 397, 598–601.
38. S. Mooibroek, R. E. Wasylishen, R. Dickson, G. Facey and B. A. Pettitt, J. Magn. Reson., 1986, 66, 542–545.
39. J. E. C. Wren, B. J. Greer, V. K. Michaelis, C. S. Higman and S. Kroeker, Inorg. Chem., 2015, 54, 9853–9861.
40. K. Levin and S. Kroeker, Solid State Nucl. Magn. Reson., 2019, 101, 101–109.
41. A. Karmakar, A. Bhattacharya, G. M. Bernard, A. Mar and V. K. Michaelis, ACS Mater. Lett., 2021, 3, 261–267.
42. A. Karmakar, S. Mukhopadhyay, P. G. B. Gachod, V. A. Mora-Gomez, G. M. Bernard, A. Brown and V. K. Michaelis, Chem. Mater., 2021, 33, 6078–6090.
43. A. Karmakar, G. M. Bernard, A. Meldrum, A. O. Oliynyk and V. K. Michaelis, J. Am. Chem. Soc., 2020, 142, 10780–10793.
44. M. Jeong, D. Schmidiger, H. Mayaffre, M. Klanjšek, C. Berthier, W. Knafo, G. Ballon, B. Vignolle, S. Krämer, A. Zheludev and M. Horvatić, Phys. Rev. Lett., 2016, 117, 106402.
45. Q. Yuan, Z. Wang, Z. Wang, X. Shi and G. Wang, New J. Phys., 2022, 24, 093033.
46. N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475.
47. C.-H. Hsu, P. Stano, Y. Sato, S. Matsuo, S. Tarucha and D. Loss, Phys. Rev. B, 2019, 100, 195423.
48. H. Fehske and G. Hager, in Metal-to-Nonmetal Transitions, ed. R. Redmer, F. Hensel and B. Holst, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 1–21.
49. Y. Haraguchi, C. Michioka, M. Ishikawa, Y. Nakano, H. Yamochi, H. Ueda and K. Yoshimura, Inorg. Chem., 2017, 56, 3483–3488.
50. Y. Kim, B. J. Wieder, C. L. Kane and A. M. Rappe, Phys. Rev. Lett., 2015, 115, 036806.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2048757 and 2048759. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp00293h

---