Coexistence of ferromagnetism and charge density waves in monolayer LaBr2†
Jun
Zhou
 a,
Zishen
Wang
a,
Zishen
Wang
 bc,
Shijie
Wang
bc,
Shijie
Wang
 a,
Yuan Ping
Feng
a,
Yuan Ping
Feng
 *bc,
Ming
Yang
*bc,
Ming
Yang
 *d and
Lei
Shen
*d and
Lei
Shen
 *e
*e
aInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis #08-03, Singapore 138634, Republic of Singapore
bDepartment of Physics, National University of Singapore, Singapore 117551, Singapore. E-mail: phyfyp@nus.edu.sg
cCentre for Advanced Two-Dimensional Materials (CA2DM), National University of Singapore, Singapore 117546, Singapore
dDepartment of Applied Physics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong SAR, China. E-mail: mingyang@polyu.edu.hk
eDepartment of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore. E-mail: shenlei@nus.edu.sg
First published on 23rd June 2023
Abstract
Charge density waves (CDWs), a common phenomenon of periodic lattice distortions, often suppress ferromagnetism in two-dimensional (2D) materials, hindering their magnetic applications. Here, we report a novel CDW that generates 2D ferromagnetism instead of suppressing it, through the formation of interstitial anionic electrons as the charge modulation mechanism. Via first-principles calculations and a low-energy effective model, we find that the highly symmetrical monolayer LaBr2 undergoes a 2 × 1 CDW transition to a magnetic semiconducting T′ phase. Concurrently, the delocalized 5d1 electrons of La in LaBr2 redistribute and accumulate within the interstitial space in the T′ phase, forming anionic electrons, also known as 2D electride or electrene. The strongly localized nature of anionic electrons promotes a Mott insulating state and full spin-polarization, while the overlap of their extended tails yields ferromagnetic direct exchange between them. Such transition introduces a new magnetic form of CDWs, offering promising opportunities for exploring novel fundamental physics and advanced spintronics applications.
New conceptsFerromagnetism in two-dimensional materials is often suppressed by charge density waves (CDWs) due to the periodic charge density redistribution and band gap opening. Here, we report a new form of CDWs in monolayer LaBr2, in which CDWs promote magnetism instead of suppressing it. The CDW distortions in LaBr2 result in the redistribution of valence electrons into the interstitial sites, forming localized anionic electrons. The localized anionic electron bands lead to a Mott transition with full spin polarization of the anionic electrons. The coexistence of ferromagnetism and CDWs in a 2D material represents an exceptional system with sharp differences from conventional CDWs. It plays a crucial role in understanding the fundamental principles of condensed matter physics, and their unique properties offer promising opportunities for applications in advanced electronic and spintronic devices. |
Introduction
Charge density waves (CDWs) are a widely observed quantum ordering phenomenon in crystals, which feature real-space periodic lattice distortions and charge density modulation as well as reciprocal-space band gap opening (CDW gap).1 The CDW changes a material's properties profoundly and may compete with other quantum ordering phenomena in the same system, attracting tremendous research interest.2–5 One well-known example is the competition between CDWs and magnetism. CDW gaps decrease the density of states (DOS) at the Fermi level (EF), while the Stoner criterion for a spontaneous spin polarization requires high DOS at EF. Therefore, their coexistence is rare.6,7 Their mutual suppression has been used to explain the debated existence of the magnetism in some two-dimensional (2D) materials.8–10Currently, only several well-known CDWs are reported because the CDW pattern and the underlying mechanism depend critically on the d-electron count of the transition metal (TM) ions.11–16 The 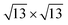 (David star), 2 × 1 (zigzag-chain) and 2 × 2 (diamond-chain) clustering of metal ions are the most common CDW patterns observed in transition metal dichalcogenides (TMDs) with d1, d2, and d3 TM ions, respectively.16 Correspondingly, while Fermi surface nesting commonly responds to the structural instability of d1 TMDs, the real-space local chemical bonding between the TM ions is responsible for the formation of CDWs in d2 and d3 TMDs.16–19
(David star), 2 × 1 (zigzag-chain) and 2 × 2 (diamond-chain) clustering of metal ions are the most common CDW patterns observed in transition metal dichalcogenides (TMDs) with d1, d2, and d3 TM ions, respectively.16 Correspondingly, while Fermi surface nesting commonly responds to the structural instability of d1 TMDs, the real-space local chemical bonding between the TM ions is responsible for the formation of CDWs in d2 and d3 TMDs.16–19
On the other hand, electrides, in which excess electrons act as anions (named anionic electrons), are attracting increasing interest as the spatial electron-ion separation promotes exotic physical and chemical properties.20–24 The recent two exciting developments of this field are the anionic electrons (AEs) as magnetic centers25–28 and monolayer electrides (named electrenes).29–33 In particular, the magnetic electrenes,34–39 such as LaBr2, have attracted immense interest recently because of their various exotic properties, such as half-metallicity,40 bimerons,41 negative piezoelectric coefficient,42 and valley polarization.43,44 The emergence of anionic electrons is explained by a mechanism based on Pauli expulsion, in which valence electrons are “squeezed out” by core electrons when the interatomic distance is sufficiently small.45–47 While for the electrides with medium interatomic distances (still within the chemical bonding range), the metal ions form multi-center chemical bonds, and their excess electrons are confined at the center of their clustered “cages”.45 However, the multi-center bonding picture may not be applicable for electrides with large cavities as their large interatomic distances may prevent chemical bonding, whose mechanism needs further investigation.48 While the periodic charge modulation in conventional CDWs occurs by changing the occupancy of atomic orbitals, the existence of electrides demonstrates the feasibility of localized electrons at interstitial sites. The coexistence of CDWs and magnetism in 2D electrides represents an exceptional system with sharp differences from conventional CDWs. It plays a crucial role in understanding the fundamental principles of condensed matter physics, and their unique properties offer promising opportunities for applications in advanced electronic and spintronic devices. However, it has not been reported to the best of our knowledge.
In this work, we report a new concept of CDWs which generate a ferromagnetic state in the T-phase monolayer LaBr2, showing two significantly different behaviors from the T-phase TMDs. One is that the 2 × 1 CDW lattice distortions do not open gaps at EF but increase the DOS at the Fermi energy due to the formation of isolated anionic electron bands. Such high DOS leads to spontaneous spin splitting, yielding a coexistence of CDW and magnetism. The other one is that LaBr2 has a formal d1 configuration for La ions but it forms a 2 × 1 CDW, rather than the conventional David star as in TMDs. Our results open up a new magnetic CDW form and a material platform, offering promising opportunities for further fundamental research and spintronic applications.
Results and discussion
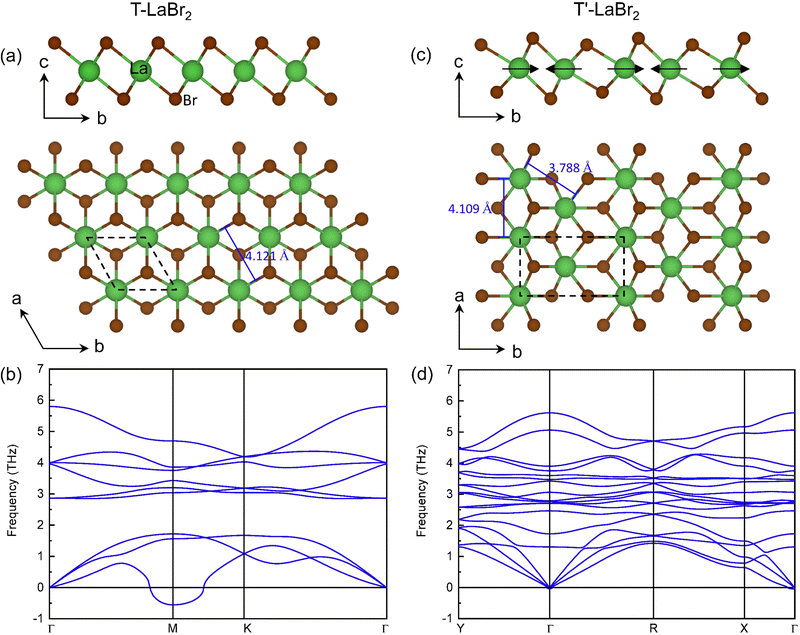
The optimized structure of T-phase LaBr2 is shown in Fig. 1(a), which has lattice parameters of a = b = 4.121 Å. It contains three atomic layers with middle La atoms octahedrally coordinated with the top and bottom Br atoms (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1). However, this phase is subject to dynamical instability [Fig. 1(b)]. The minimum imaginary phonon frequency locates at the high-symmetry point M, corresponding to a CDW vector of q = ΓM, which indicates real-space 2 × 1 CDW distortion along one of its in-plane lattice vectors. It is noted that similar period-doubling distortions have been reported in T-phase group-VI TMDs.13 However, one important difference between them is the d electron count of the metal ions, that is, d1 of La in LaBr2 while d2 of TM ions in group-VI TMDs. The typical CDW of the d1 group-V TMDs is the David Star, in contrast with the 2 × 1 CDW here. Such differences suggest that the existing mechanisms of the lattice instabilities for TMDs are not applicable for the CDW in LaBr2.
m1). However, this phase is subject to dynamical instability [Fig. 1(b)]. The minimum imaginary phonon frequency locates at the high-symmetry point M, corresponding to a CDW vector of q = ΓM, which indicates real-space 2 × 1 CDW distortion along one of its in-plane lattice vectors. It is noted that similar period-doubling distortions have been reported in T-phase group-VI TMDs.13 However, one important difference between them is the d electron count of the metal ions, that is, d1 of La in LaBr2 while d2 of TM ions in group-VI TMDs. The typical CDW of the d1 group-V TMDs is the David Star, in contrast with the 2 × 1 CDW here. Such differences suggest that the existing mechanisms of the lattice instabilities for TMDs are not applicable for the CDW in LaBr2.
According to the CDW vector of the T-phase LaBr2, a 2 × 1 supercell structure (T′ phase) is constructed by moving every pair of La ions closer to each other along the b axis, as indicated by the arrows in Fig. 1(c). The optimized structure (P21/m) has lattice parameters of a = 4.109 Å and b = 7.428 Å. The distance between the clustered La atoms decreases from 4.121 Å in the T phase to 3.788 Å. With the 2 × 1 distortions, the T′ phase is dynamically stable as only negligible imaginary phonon frequencies are found around the Γ point [see Fig. 1(d)].49 The total energy of T′ LaBr2 is 37.86 meV per formula unit (f.u.) lower than that of the T phase.
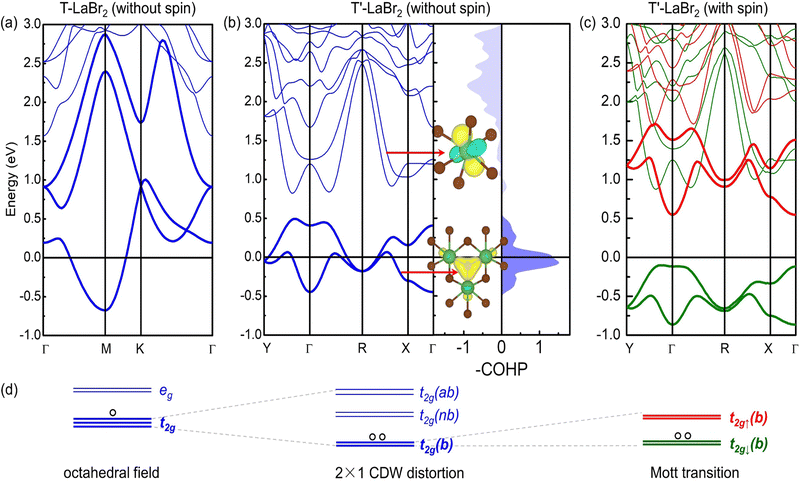
The band structures of the T and T′ LaBr2 are shown in Fig. 2(a)–(c). The T phase is nonmagnetic and metallic, the latter of which is a prerequisite for a charge density wave transition. The La ions in the T phase are octahedrally coordinated, which splits the five-fold degenerate d orbitals into doubly degenerate eg and triply degenerate t2g states [Fig. 2(d)]. The three-fold t2g states (the three bands near the Fermi level of T LaBr2) span from around −0.88 eV to 2.67 eV. The 5d1 electrons from La partially occupy such wide bands and are not subject to spin polarization.
The 2 × 1 CDW distortions in the T′-phase LaBr2 can be understood by the chemical bonding among La ions, leading to a split of t2g orbitals into bonding, non-bonding, and anti-bonding states. This can be clearly seen from the crystal orbital Hamilton population (COHP) analysis for the La–La interactions in T′ LaBr2. As shown in Fig. 2(b), the large positive -COHP values in the energy range of around −0.5 to 0.5 eV suggest the bonding states of the corresponding bands (highlighted by bold blue lines). In the energy range of around 0.8 to 1.7 eV, the negligible –COHP values indicate the non-bonding states. This can be further supported by the constructed maximally localized Wannier functions (MLWFs). The t2g-like MLWF on the La ion [upper inset in Fig. 2(b)] illustrates the minimal interaction between the La ions for the states in this energy range. The large negative -COHP values in the energy range of around 1.7 to 3.0 eV imply the anti-bonding states.
The three-center bonding among the clustered La ions is further revealed by crystal orbital bond index (COBI) analysis. The integrated COBI is as high as 0.097 for the three La ions, comparable with the value (0.099) of the multi-center bonds in GeTe.50 Interestingly, the bonding states are well isolated with a gap of 0.32 eV from the non-bonding states. Similar transition from wide bands to well-separated states has also been shown in simple metals by strong compression, leading to the formation of anionic electrons.51 The isolated bands are a signature of electrides, as the AEs are localized at interstitial sites and hybridize marginally with the atomic states.35,52 Notably, the MLWF for the bonding states [lower inset in Fig. 2(b)] further confirms the three-center bonding among the La ions. And this interstitially centered MLWF also suggests the formation of anionic electrons. Thus, we propose the formation of electride states as the mechanism for the 2 × 1 CDW distortions in the T′-phase LaBr2. The inapplicability of the Fermi surface nesting picture for the CDW in this system is shown in Fig. S3 of ESI.† Further evidence of its electride nature by the projected density of states, band decomposed charge density and electron localization function can also be found in Fig. S2 of the ESI.†
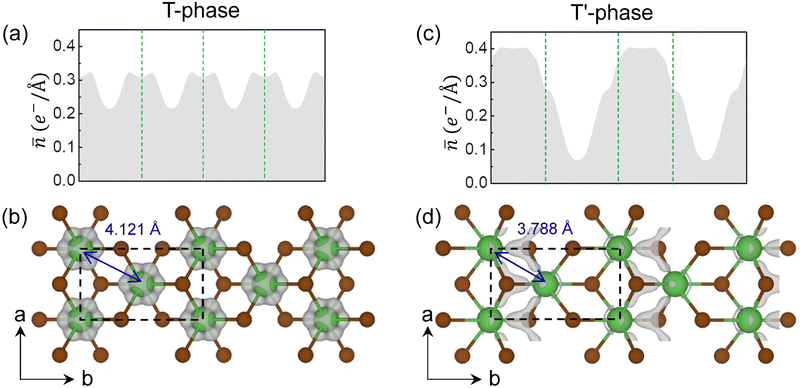
To directly show the charge density modulation after the CDW transition, we simulated the partial charge density of the excess electrons of T and T′-phase LaBr2 by integrating the states with the same energy window from the Fermi level to –1.0 eV. As the planar averaged partial charge along the b axis shows in Fig. 3(a), the excess electrons in T-phase LaBr2 are somewhat uniformly distributed with peaks around the La ions, further supported by the three-dimensional (3D) visualization in Fig. 3(b) and the large bandwidth in Fig. 2(a). With the 2 × 1 CDW distortions, the profile of the planar averaged charge density changes significantly. The excess electrons are more localized in the T′-phase LaBr2 and the peaks of charge density locate at the interstitial region between the clustered La atoms, in line with its distribution in the 3D visualization in Fig. 3(c) and (d) and the small bandwidth in Fig. 2(c). And it is noticeable that the excess electrons locate mainly at the interstitial sites as anionic electrons in T′-phase LaBr2. These results clearly demonstrate the formation of anionic electrons as the charge density modulation for the CDW transition in T-phase LaBr2. In contrast, the Mo d2 electrons in T′ MoS2 remain on Mo atoms without anionic electrons (Fig. S4 in the ESI†).
We further study the magnetic properties of T′-phase LaBr2. As shown in Fig. 2(b), the isolated bonding bands have a reduced bandwidth of 0.93 eV and the correspondingly increased DOS at the Fermi level (see more details in Fig. S7 of the ESI†) causes electronic instability. The electronic structure of T′ LaBr2 calculated with the spin polarization [Fig. 2(c)] shows a full spin-splitting of the anionic electron bands (1 μB per f.u.) with a band gap of 0.65 eV [calculated by HSE06]. It is noted that the T′ LaBr2 is metallic under pure GGA calculations, which, together with the bandgap opening by HSE06, indicates a Mott transition and the strong correlation nature of the anionic electrons.
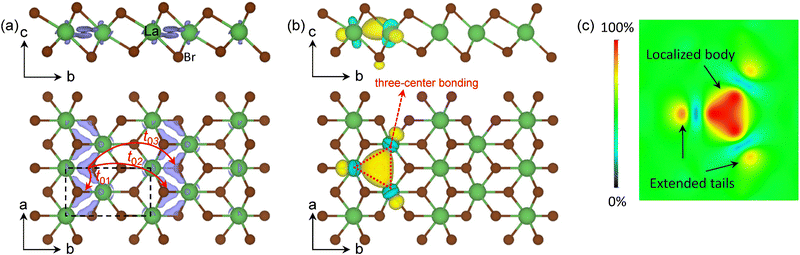
The schematic energy level diagrams shown in Fig. 2(d) summarize the transition process from the nonmagnetic metallic T phase to the magnetic Mott insulating T′ LaBr2. As the spin density of the T′-LaBr2 is shown in Fig. 4(a), the main contribution to the magnetic moments is from the two AEs at the interstitial sites between the clustered La atoms. The clustered distribution of La atoms leads to quasi-one-dimensional (1D) magnetic AE stripes. Due to the CDW distortions, the clustered La atoms are not in the same plane along the c axis and accordingly the two magnetic AEs have different heights, as shown in Fig. 4(a).
The atomic-orbital-free magnetic anionic electrons possess a unique dual localized and extended nature as well as a direct exchange coupling from the overlap of the wave functions, which has been reported in H-phase LaBr2 monolayer.34 Similar properties would be expected for the magnetic anionic electrons in CDW distorted LaBr2. Considering that Coulomb interaction on the non-atomic interstitial sites and their nonlocal direct exchange cannot be fully captured by conventional density functional theory simulations, we adopt a low-energy effective model for the two anionic electron bands. The Hamiltonian based on the second quantization is given by
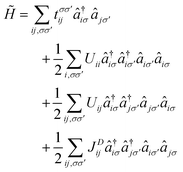 | (1) |
The interactions up to the third nearest neighboring anionic electrons are considered, whose hopping paths are indicated by the red arrows in Fig. 4(a). The calculated hopping parameters are t01 = 126.45 meV, t02 = 42.25 meV, and t03 = 25.91 meV, respectively. The localized nature of the anionic electrons produces a large on-site Coulomb interaction of 2.14 eV on the interstitial site (not on La). The off-site Coulomb interactions are U01 = 1.53 eV, U02 = 0.87 eV, and U03 = 0.84 eV, respectively. The comparable Coulomb interactions between the on-site and off-site interactions are a result of the weak screening from other bands to the well isolated anionic electron bands [see Fig. 2(b)]. The extended nature of the aniconic electrons is reflected by the significant off-site direct exchanges of JD02 = 1.57 meV and JD03 = 1.29 meV at 6.50 Å and 7.43 Å, respectively, which are beyond the spatial limit of atomic-orbital overlap in conventional direct-exchange systems. These results suggest that our proposed magnetic mechanism for magnetic anionic electrons is general for magnetic electrides.34 Compared with the nearest off-site parameters of H-phase LaBr2 (t01 = 12.50 meV, JD01 = 21.9 meV),34 the ones of the T′ phase (t01 = 126.45 meV, JD01 = 53.80 meV) are considerably larger. This can be understood by the fact that T′ LaBr2 has shorter nearest neighboring sites (2.41 Å vs. 4.14 Å) and a larger bandwidth of the anionic electron bands (0.93 eV vs. 0.50 eV) than that of the H phase.
In the limit U00 > Uij ≫ tij, the Anderson's model can be applied to determine the overall isotropic exchange interactions of T′ LaBr2 as follows.
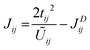 | (2) |
Conclusions
In this work, we show that highly symmetric monolayer LaBr2 is subject to a structural instability to a 2 × 1 CDW into T′ LaBr2, which possesses unexpected magnetic states, demonstrating the formation of interstitial anionic electrons as the CDW charge density modulation, in sharp contrast with the traditional CDW systems. The anionic electron states in T′ LaBr2 have an unconventional orbital-free magnetism, coexisting with CDW. This exotic system may provide an exciting platform to explore new fundamental physics and advanced applications to the fields of 2D ferromagnetism, CDWs, tunable electrides, phase transition, electron-phonon coupling, superconductivity, and spintronic devices. We found that the magnetism and CDW phases also co-exist in LaCl2 and LaI2 (Fig. S10, ESI†). Considering that lanthanoid (II) halides are a large group of materials, more materials with similar phenomena are expected to exist.Computational methods
All the calculations were performed by the density functional theory (DFT) based Vienna ab initio Simulation Package (VASP 6.1.0)54,55 with the Perdew–Burke–Ernzerhof (PBE) approximation for the exchange-correlation functional and the frozen-core all-electron projector augmented wave (PAW) method for the electron-ion interaction.56 The cutoff energy for the plane wave expansion was set to 420 eV. Γ-centered 21 × 21 × 1 and 21 × 11 × 1 k-point grids were applied for the T and T′ LaBr2, respectively. GGA with a Hubbard U value of 5.5 eV was used for La to push the unoccupied 4f orbitals of Lanthanum away from the Fermi level.57–59 It is noted that Hubbard U was applied neither on the La valence 5d orbitals nor the anionic electrons. Different U values have been tested, which leads to negligible differences.34 The structures were fully relaxed until the energy and force were converged to 10−6 eV and 0.001 eV Å−1, respectively. The vacuum layer was set to around 25 Å to eliminate the interaction between the images resulting from the periodic boundary conditions. The spin polarized band structure of T′ LaBr2 was simulated by HSE06.60 Phonon dispersions were calculated by the finite displacement approach with a 2 × 2 × 1 supercell. Ab initio molecular dynamics (MD) simulations were performed at 300 K for 6000 steps with a time step of 1 fs using a Nose heat bath scheme.61 The energy above the hull was obtained by constructing a phase diagram with the material data from Materials Project.62 The Wannier function was constructed from the results of the DFT calculations using the procedure of maximal localization by the Wannier90 package as implemented in VASP. The interstitial-centered MLWF has been shown to be more localized and reproduced the dual nature of the anionic electron,34 which was used for further constrained random-phase approximation (cRPA) calculations.63 The crystal orbital Hamilton population (COHP) analysis and crystal orbital bond index (COBI) analysis were performed by LOBSTER.64,65 It is found that the spin-orbital coupling (SOC) has negligible effects on the electronic properties (Fig. S9, ESI†).Author contributions
J. Z. and L. S. conceived the idea. J. Z. performed the calculations, wrote the manuscript under the guidance of M. Y., Y. P. F., and L. S. All authors contributed to the discussion and the revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Ministry of Education, Singapore, under its MOE Tier 1 (Awards R-144-000-441-114, R-144-000-413-114, and A-0005241-01-00) and Tier 2 (Award MOE2019-T2-2-030). M. Y. acknowledges the funding support (project ID: 1-BE47, ZE0C, ZE2F and ZE2X) from The Hong Kong Polytechnic University. We acknowledge the computational resources supported by the National Supercomputing Centre (NSCC) Singapore and Centre of Advanced 2D Materials (CA2DM) HPC infrastructure.References
- G. Grüner, Rev. Mod. Phys., 1988, 60, 1129 CrossRef.
- H. Kim, J. H. Shim, S. Kim, J. H. Park, K. Kim and B. I. Min, Phys. Rev. Lett., 2020, 125, 157001 CrossRef CAS PubMed.
- C. Chen, B. Singh, H. Lin and V. M. Pereira, Phys. Rev. Lett., 2018, 121, 226602 CrossRef CAS PubMed.
- X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344–1347 CrossRef CAS PubMed.
- A. F. Kusmartseva, B. Sipos, H. Berger, L. Forro and E. Tutis, Phys. Rev. Lett., 2009, 103, 236401 CrossRef CAS PubMed.
- K. K. Kolincio, M. Roman and T. Klimczuk, Phys. Rev. Lett., 2020, 125, 176601 CrossRef CAS PubMed.
- E. C. Stoner, Proc. R. Soc. London, Ser. A, 1938, 165, 372–414 Search PubMed.
- P. M. Coelho, K. Nguyen Cong, M. Bonilla, S. Kolekar, M.-H. Phan, J. Avila, M. C. Asensio, I. I. Oleynik and M. Batzill, J. Phys. Chem. C, 2019, 123, 14089–14096 CrossRef CAS.
- A. O. Fumega, M. Gobbi, P. Dreher, W. Wan, C. González-Orellana, M. Peña-Díaz, C. Rogero, J. Herrero-Martín, P. Gargiani, M. Ilyn, M. M. Ugeda, V. Pardo and S. Blanco-Canosa, J. Phys. Chem. C, 2019, 123, 27802–27810 CrossRef CAS.
- G. Duvjir, B. K. Choi, I. Jang, S. Ulstrup, S. Kang, T. Thi Ly, S. Kim, Y. H. Choi, C. Jozwiak, A. Bostwick, E. Rotenberg, J. G. Park, R. Sankar, K. S. Kim, J. Kim and Y. J. Chang, Nano Lett., 2018, 18, 5432–5438 CrossRef CAS PubMed.
- Z. Wang, J. Zhou, K. P. Loh and Y. P. Feng, Appl. Phys. Lett., 2021, 119, 163101 CrossRef CAS.
- K. Zhang, C. Si, C.-S. Lian, J. Zhou and Z. Sun, J. Chem. Phys. C, 2020, 8, 9742–9747 CAS.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033 CrossRef CAS.
- L. J. Li, E. C. O'Farrell, K. P. Loh, G. Eda, B. Ozyilmaz and A. H. Castro Neto, Nature, 2016, 529, 185–189 CrossRef CAS PubMed.
- V. N. Strocov, M. Shi, M. Kobayashi, C. Monney, X. Wang, J. Krempasky, T. Schmitt, L. Patthey, H. Berger and P. Blaha, Phys. Rev. Lett., 2012, 109, 086401 CrossRef PubMed.
- M. H. Whangbo and E. Canadell, J. Am. Chem. Soc., 1992, 114, 9587–9600 CrossRef CAS.
- D. Pasquier and O. V. Yazyev, Phys. Rev. B, 2019, 100, 201103(R) CrossRef.
- S. Qiao, X. Li, N. Wang, W. Ruan, C. Ye, P. Cai, Z. Hao, H. Yao, X. Chen, J. Wu, Y. Wang and Z. Liu, Phys. Rev. X, 2017, 7, 041054 Search PubMed.
- K. Rossnagel, J. Phys.: Condens. Matter, 2011, 23, 213001 CrossRef CAS PubMed.
- J. Wang, X. Sui, S. Gao, W. Duan, F. Liu and B. Huang, Phys. Rev. Lett., 2019, 123, 206402 CrossRef CAS PubMed.
- Z. Liu, G. Zhao, B. Liu, Z. F. Wang, J. Yang and F. Liu, Phys. Rev. Lett., 2018, 121, 246401 CrossRef PubMed.
- C. Park, S. W. Kim and M. Yoon, Phys. Rev. Lett., 2018, 120, 026401 CrossRef CAS PubMed.
- Y. Zhang, B. Wang, Z. Xiao, Y. Lu, T. Kamiya, Y. Uwatoko, H. Kageyama and H. Hosono, npj Quantum Mater., 2017, 2, 45 CrossRef.
- J. L. Dye, Science, 2003, 301, 607–608 CrossRef CAS PubMed.
- T. Yu, M. Hirayama, J. A. Flores-Livas, M.-T. Huebsch, T. Nomoto and R. Arita, Phys. Rev. Mater., 2021, 5, 044203 CrossRef CAS.
- X. Sui, J. Wang, C. Yam and B. Huang, Nano Lett., 2021, 21, 3813–3819 CrossRef CAS PubMed.
- H. Tamatsukuri, Y. Murakami, Y. Kuramoto, H. Sagayama, M. Matsuura, Y. Kawakita, S. Matsuishi, Y. Washio, T. Inoshita, N. Hamada and H. Hosono, Phys. Rev. B, 2020, 102, 224406 CrossRef CAS.
- T. Inoshita, N. Hamada and H. Hosono, Phys. Rev. B, 2015, 92, 201109 CrossRef (R).
- X. Yang, K. Parrish, Y.-L. Li, B. Sa, H. Zhan and Q. Zhu, Phys. Rev. B, 2021, 103, 125103 CrossRef CAS.
- S. Bae, W. Espinosa-García, Y. G. Kang, N. Egawa, J. Lee, K. Kuwahata, M. Khazaei, K. Ohno, Y. H. Kim, M. J. Han, H. Hosono, G. M. Dalpian and H. Raebiger, Adv. Funct. Mater., 2021, 31, 2100009 CrossRef CAS.
- W. Li, Y. You and J.-H. Choi, J. Phys. Chem. C, 2020, 124, 25316–25321 CrossRef CAS.
- D. L. Druffel, A. H. Woomer, K. L. Kuntz, J. T. Pawlik and S. C. Warren, J. Chem. Phys. C, 2017, 5, 11196–11213 CAS.
- J. S. Oh, C. J. Kang, Y. J. Kim, S. Sinn, M. Han, Y. J. Chang, B. G. Park, S. W. Kim, B. I. Min, H. D. Kim and T. W. Noh, J. Am. Chem. Soc., 2016, 138, 2496–2499 CrossRef CAS PubMed.
- J. Zhou, Y. P. Feng and L. Shen, Phys. Rev. B, 2020, 102, 180407 CrossRef CAS (R).
- J. Zhou, L. Shen, M. Yang, H. Cheng, W. Kong and Y. P. Feng, Chem. Mater., 2019, 31, 1860–1868 CrossRef CAS.
- J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 86 CrossRef PubMed.
- J. Zhou, X. Song, M. Yang, J. Chai, N. L. M. Wong, L. Shen, S. Wang and Y. P. Feng, J. Mater. Chem. C, 2021, 9, 16576–16580 RSC.
- J. He, Y. Chen, Z. Wang, M. Yang, T. Yang, L. Shen, X. Xu, Y. Jiang, J. Chai and L. M. Wong, J. Mater. Chem. C, 2022, 10, 7674–7679 RSC.
- X. Zhang, W. Meng, Y. Liu, X. Dai, G. Liu and L. Kou, J. Am. Chem. Soc., 2023, 145, 5523–5535 CrossRef CAS PubMed.
- Q. Chen, X. Zheng, P. Jiang, Y.-H. Zhou, L. Zhang and Z. Zeng, Phys. Rev. B, 2022, 106, 245423 CrossRef CAS.
- W. Sun, W. Wang, H. Li, X. Li, Z. Yu, Y. Bai, G. Zhang and Z. Cheng, npj Comput. Mater., 2022, 8, 159 CrossRef CAS.
- M. Noor-A-Alam and M. Nolan, ACS Appl. Electron. Mater., 2022, 4, 850–855 CrossRef CAS PubMed.
- P. Zhao, Y. Ma, C. Lei, H. Wang, B. Huang and Y. Dai, Appl. Phys. Lett., 2019, 115, 261605 CrossRef.
- P. Jiang, L. Kang, Y.-L. Li, X. Zheng, Z. Zeng and S. Sanvito, Phys. Rev. B, 2021, 104, 035430 CrossRef CAS.
- X. Dong and A. R. Oganov, in Correlations in Condensed Matter under Extreme Conditions: A tribute to Renato Pucci on the occasion of his 70th birthday, eds. G. G. N. Angilella and A. La Magna, Springer International Publishing, Cham, 2017, pp. 69–84 DOI:10.1007/978-3-319-53664-4_6.
- M. S. Miao and R. Hoffmann, J. Am. Chem. Soc., 2015, 137, 3631–3637 CrossRef CAS PubMed.
- M. S. Miao and R. Hoffmann, Acc. Chem. Res., 2014, 47, 1311–1317 CrossRef CAS PubMed.
- S. G. Dale, A. Otero-de-la-Roza and E. R. Johnson, Phys. Chem. Chem. Phys., 2014, 16, 14584–14593 RSC.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. Hempelmann, P. C. Muller, C. Ertural and R. Dronskowski, Angew. Chem., Int. Ed., 2022, 61, e202115778 CAS.
- B. Rousseau and N. W. Ashcroft, Phys. Rev. Lett., 2008, 101, 046407 CrossRef PubMed.
- T. Tada, S. Takemoto, S. Matsuishi and H. Hosono, Inorg. Chem., 2014, 53, 10347–10358 CrossRef CAS PubMed.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- M. Topsakal and R. M. Wentzcovitch, Comput. Mater. Sci., 2014, 95, 263–270 CrossRef CAS.
- J. Hubbard, Proc. R. Soc. A, 1963, 276, 238–257 Search PubMed.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B, 1998, 57, 1505 CrossRef CAS.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- C. Edmiston and K. Ruedenberg, Rev. Mod. Phys., 1963, 35, 457–464 CrossRef CAS.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00150d |
| This journal is © The Royal Society of Chemistry 2023 |