Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of molecular hydration in solution via changes in magnetic anisotropy†
Marcus J.
Giansiracusa
 a,
Michele
Vonci
a,
Yasmin L.
Whyatt
a,
Michele
Vonci
a,
Yasmin L.
Whyatt
 a,
Carys
Williams
a,
Kevin
Mason
a,
Carys
Williams
a,
Kevin
Mason
 b,
David
Parker
b,
David
Parker
 *c,
Eric J. L.
McInnes
*c,
Eric J. L.
McInnes
 *a and
Nicholas F.
Chilton
*a and
Nicholas F.
Chilton
 *a
*a
aDepartment of Chemistry, The University of Manchester, Manchester, M13 9PL, UK. E-mail: eric.mcinnes@manchester.ac.uk; nicholas.chilton@manchester.ac.uk
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK
cDepartment of Chemistry, Hong Kong Baptist University, Kowloon Tong, Hong Kong. E-mail: davidparker@hkbu.edu.hk
First published on 20th March 2023
Abstract
The hydration behaviour of coordination complexes is important for understanding their roles as bio-imaging agents. Determination of hydration is difficult, and various optical and NMR-based techniques have been used. Here we use EPR spectroscopy to unambiguously demonstrate that a t-butyl-pyridyl-functionalised ErIII DOTA derivative coordinates water, while its methylphosphinate analogue does not.
Hydration of lanthanide complexes in vivo is a crucial consideration for the performance of inorganic biomedical imaging agents, whether optical1–3 or in magnetic resonance imaging (MRI),4 and thus determination of hydration behaviour in aqueous media is key when developing new probes. This is important, not only due to the changes in nuclear relaxation times associated with metal coordination in MRI,5–7 but also due to the profound influence hydration can have on magnetic anisotropy, and hence on spectral features.6,8,9 A common approach to this task involves luminescence lifetime determination, where the optical lifetime of the metal-localised excited state is determined in water, and then remeasured in deuterated water: the relative quenching effect of the O–D vs. O–H stretching modes then allows an approximation of the hydration number to be made.10,11 However, this method is only pertinent for luminescent complexes and gives no indication of the structure of the complex. Another method to determine hydration involves nuclear magnetic resonance (NMR) spectroscopy, where a change in symmetry alters the diamagnetic spectrum, whereas a change in magnetic anisotropy for paramagnetic complexes can drastically alter the pseudocontact shifts; each situation allows the hydration state and relative structure to be inferred.
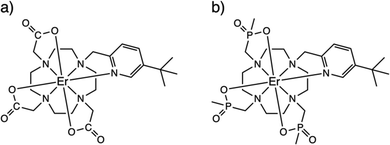
However, the NMR experiment may be confounded by the lack of solubility in a non-coordinating solvent or there may be fast exchange between the hydrated and non-hydrated structures, not to mention the inherent difficulties of solid-state paramagnetic NMR spectroscopy to provide a reference non-hydrated spectrum.12 Here, we highlight a different method, viz electron paramagnetic resonance (EPR) spectroscopy, to determine hydration via the change in magnetic anisotropy between solid and solution forms of a pair of prototype PARASHIFT reagents.9,13 Using cryogenic EPR spectroscopy, we directly probe the ground Kramers doublets of [ErL1] (1, where {L1}3- = 1,4,7,10-tetraazacyclododecane-1-5-((tert-butyl)pyridin-2-yl)methyl-4,7,10-triacetate) and [ErL2] (2, where {L2}3- = 1,4,7,10-tetraazacyclododecane-1-5-((tert-butyl)pyridin-2-yl)methyl-4,7,10-tri(methylphosphinate)),14Fig. 1, in their solid and frozen solution phases (subsequently 1solid, 1solution, 2solid and 2solution). We have chosen these ErIII complexes because often ErIII is not as well sensitised for emission as TbIII or EuIII, because ErIII is strongly paramagnetic, and because ErIII has an odd number of unpaired electrons and as such has a ground state Kramers doublet which is usually EPR active in low symmetry. Using EPR spectroscopy and computational methods, we show unequivocally that 1 binds water in aqueous media while 2 does not. Our results are consistent with the NMR-based determinations of hydration behaviour for the YIII and YbIII analogues of 1 and 2.13 The use of EPR spectroscopy to probe hydration effects is equally applicable to any half-integer lanthanide ion (i.e. also CeIII, NdIII, SmIII, GdIII, DyIII or YbIII), however sometimes fast spin-lattice relaxation can broaden spectral lines beyond detection or EPR intensity can be weak owing to small components of EPR-allowed ΔmS = ±1 states in the ground Kramers doublet; the latter effect is less likely in lower-symmetry complexes.
The ErIII complexes 1 and 2, as described previously,13,14 are both N4O3Npy chelates based on the archetypal DOTA ligand.15,16 Functionalisation of one arm to possess a 3-tert-butyl-pyridyl group is to provide a strong and distal “reporter” NMR signal, while substitution of the carboxylate groups for phosphinates in L2 is designed to provide more steric bulk and prevent solvent coordination. While neither 1solid nor 2solid have been crystallographically characterised, they are presumed to be isostructural with the YbIII analogues [YbL1] and [YbL2] which crystallise in P21/c and P21, respectively.13 The two enantiomers of [YbL1] are related by symmetry in the unit cell (the Λ-λλλλ and Δ-δδδδ forms, where the capital Λ or Δ refers to the helicity of the exocyclic groups, via the NCCO(Npy) torsion angles, and the lower case λ or δ refers to the NCCN torsions in the 12-N4 ring), while the two enantiomers of [YbL2] crystallise as independent molecules in the asymmetric unit.13
In order to probe directly the ability of L2 to protect the coordination sphere of 2 from hydration, in comparison to the less sterically demanding ligand L1 in 1, we have performed cryogenic EPR spectroscopic measurements on 1solid, 1solution, 2solid and 2solution. The Q-band EPR spectrum of 1solid at 5 K shows three clear features at ca. 0.2, 0.8 and 1.2 T (blue trace, Fig. 2): this is a prototypical rhombic signal of an effective spin S = 1/2, where each feature corresponds to a unique g-value (g3, g2 and g1, respectively). In the case of ErIII in low symmetry, the ground state is a Kramers doublet owing to crystal field splitting of the 4I15/2 term. We observe no hyperfine coupling to the I = 7/2 nuclear spin of 167Er (23% natural abundance), likely as it is within the linewidth of the transitions that are broadened by spin-lattice relaxation and strain effects owing to distributions of molecular structure.17 Simulation of the spectrum in PHI18 using an effective spin S = 1/2 model yields effective g-values of g1 = 1.96, g2 = 3.14 and g3 = 12.96. Dissolution of 1solid in H2O:glycerol 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, flash freezing at 5 K and repetition of the EPR experiment for 1solution yields a completely different spectrum (green trace, Fig. 2). In this case, the features have collapsed into half the field range of 1solid below 0.8 T. The spectrum is somewhat ambiguous: the second feature at ca. 0.4 T could either be one g feature alone (and hence the third would be assumed to be out of the field range of the measurement, and thus have g1 < 1.5), or there could be a shoulder at ca. 0.5 T corresponding to the third g feature. Hence, we have considered both possibilities: model 1 (purple trace, Fig. 2), assuming all three g-values can be observed, can be simulated with an S = 1/2 model with g-values of g1 = 4.6, g2 = 6.59 and g3 = 9.33; model 2 (yellow trace, Fig. 2), assuming only two g-values are observed, gives g-values of
2, flash freezing at 5 K and repetition of the EPR experiment for 1solution yields a completely different spectrum (green trace, Fig. 2). In this case, the features have collapsed into half the field range of 1solid below 0.8 T. The spectrum is somewhat ambiguous: the second feature at ca. 0.4 T could either be one g feature alone (and hence the third would be assumed to be out of the field range of the measurement, and thus have g1 < 1.5), or there could be a shoulder at ca. 0.5 T corresponding to the third g feature. Hence, we have considered both possibilities: model 1 (purple trace, Fig. 2), assuming all three g-values can be observed, can be simulated with an S = 1/2 model with g-values of g1 = 4.6, g2 = 6.59 and g3 = 9.33; model 2 (yellow trace, Fig. 2), assuming only two g-values are observed, gives g-values of 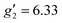 and
and 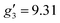 (where the unobserved g-value is fixed to
(where the unobserved g-value is fixed to 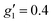 ). Model 1 gives three g-values for which the sum is quite large (>20), and so it is worthwhile to check that this is physically valid. To do so, we build a crystal field model Hamiltonian of the 4I15/2 term of ErIII, parameterised by the values predicted from a complete active space self-consistent field spin-orbit (CASSCF-SO) calculation on a solution-phase structural model of 1solution (see below), and vary the crystal field parameters to fit the effective g-values of the ground Kramers doublet to match those obtained in the model 1 simulation. We obtain g1 = 4.6, g2 = 6.5 and g3 = 9.3, suggesting this model is entirely possible (note that the fitted crystal field parameters have no meaning; the model only illustrates that this is a physically possible set of g-values for an ErIII complex).
). Model 1 gives three g-values for which the sum is quite large (>20), and so it is worthwhile to check that this is physically valid. To do so, we build a crystal field model Hamiltonian of the 4I15/2 term of ErIII, parameterised by the values predicted from a complete active space self-consistent field spin-orbit (CASSCF-SO) calculation on a solution-phase structural model of 1solution (see below), and vary the crystal field parameters to fit the effective g-values of the ground Kramers doublet to match those obtained in the model 1 simulation. We obtain g1 = 4.6, g2 = 6.5 and g3 = 9.3, suggesting this model is entirely possible (note that the fitted crystal field parameters have no meaning; the model only illustrates that this is a physically possible set of g-values for an ErIII complex).
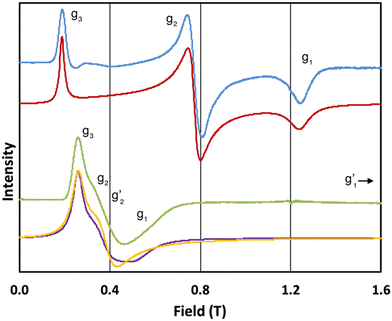 | ||
Fig. 2 Q-band EPR spectra of 1solid (blue line, 33.993 GHz) and 1solution (green line, 34.092 GHz) at 5 K. Simulations use the parameters in Table 1. For 1solid (red line) anisotropic Lorentzian linewidths (collinear with g1–3) of 2.9, 2.4 and 4.4 GHz, respectively were included. For 1solution model 1 (purple line) anisotropic Lorentzian linewidths (collinear with g1–3) of 8.2, 11.5 and 6.5 GHz, respectively, and g-strains of 1, 0.8 and 0.4, respectively, were used. For 1solution model 2 (yellow line) an arbitrarily small 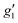 of 0.4 was used, and anisotropic Lorentzian linewidths (collinear with of 0.4 was used, and anisotropic Lorentzian linewidths (collinear with 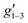 ) of 15, 10 and 8.4 GHz, respectively. ) of 15, 10 and 8.4 GHz, respectively. | ||
The 5 K Q-band spectrum of 2solid, shows two resonances at ca. 0.2 and 0.8 T (blue trace, Fig. 3), however the resonance at ca. 0.8 T does not resemble a g1 = g2 feature, indicative that this system has rhombic and not axial symmetry, consistent with the molecular structure and the results for 1solid. Simulation gives g-values of g2 = 2.91 and g3 = 13.67; the third g-value is out of the field range of the instrument, and hence g1 <1.5, and is fixed to 0.4 for the simulation. In contrast to 1, the frozen H2O:glycerol sample 2solution shows a very similar spectrum to its solid-state counterpart (green trace, Fig. 3), and simulations give similar g-values of g2 = 3.5 and g3 = 12.58 (g1 < 1.5). These spectra immediately demonstrate that the ground state Kramers doublet, and hence the magnetic anisotropy, of 1 changes from the solid-state when in the aqueous phase, while it is practically unchanged for 2. The gross spectral changes for 1, but similar spectra for 2, on dissolution are consistent with hydration in the former case and not the latter.
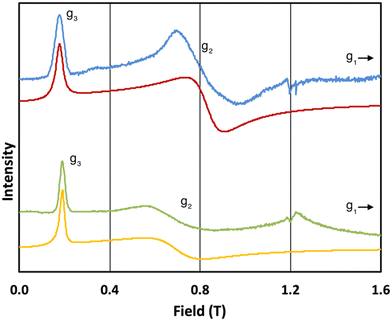 | ||
| Fig. 3 Q-band EPR spectra of 2solid (blue line, 34.180 GHz) and 2solution (green line, 34.016 GHz) at 5 K. Simulations use parameters in Table 1. For 2solid (red line) an arbitrarily small g1 of 0.4 was used, and anisotropic Lorentzian linewidths (collinear with g1–3) of 15, 5.3 and 7.2 GHz, respectively. For 2solution (yellow line) an arbitrarily small g1 of 0.4, and anisotropic Lorentzian linewidths (collinear with g1–3) of 15, 13 and 4.2 GHz, respectively, were used. (The sharp features at ca. 1.2 T are impurities in the cavity, and the broad feature in the experimental data for 2solution centred at 1.2 T is due to the silica capillary.) | ||
To test this hypothesis we sought to affirm the basis of the spectral changes via computational methodologies. First, we performed CASSCF-SO calculations in OpenMolcas19 using the crystalline geometries of [YbL1] and [YbL2] with YbIII substituted for ErIII (see Methods). These calculations provide a good approximation of the crystal field splitting of the ground 4I15/2 spin-orbit multiplet for these model complexes (the calculated principal effective g-values of all Kramers doublets arising from the 4I15/2 term are given in Tables S2–S4, ESI†). For 1, the calculated ground Kramers doublet g-values are in fair agreement with those found experimentally for 1solid (Table 1), particularly given the structural approximation (noting that YbIII is slightly smaller than ErIII) and that effective g-values are extremely sensitive to small changes to the orbital composition of the ground doublet and hence structure.20 Further discrepancies arise in calculated effective g-values due to the approximations inherent in CASSCF-SO (including the lack of dynamic correlation), but are usually <1 for a known structure;20 we also note that such minimal active space CASSCF-SO methods tend to over-estimate axiality of the ground Kramers doublet,21–24 which we also observe here. For 2, there are two surrogate molecular structures arising from the crystal structure of [YbL2] – the Λ-λλλλ and Δ-δδδδ forms – and calculated ground state g-values for both are in fair agreement with the experimental spectrum for 2solid (Table 1). The calculations predict one g-value <1, which would be outside the experimental field range, in agreement with experiment.
| Experimental | Calculated | ||||||
|---|---|---|---|---|---|---|---|
| g 1 | g 2 | g 3 | g 1 | g 2 | g 3 | Model | |
| 1solid | 1.96 | 3.14 | 12.96 | 1.32 | 2.39 | 14.26 | [YbL1] (ref. 13) |
| 1solution | 4.6 or < 1.5 | 6.59 or 6.33 | 9.33 or 9.31 | 1.94 | 5.46 | 11.60 | 1Asolution |
| 0.93 | 5.77 | 11.15 | 1Bsolution | ||||
| 2solid | <1.5 | 2.91 | 13.67 | 0.84 | 1.59 | 15.24 | [YbL2]-Λ-λλλλ (ref. 13) |
| 0.91 | 1.77 | 15.19 | [YbL2]-Δ-δδδδ (ref. 13) | ||||
| 2solution | <1.5 | 3.5 | 12.58 | 0.29 | 0.71 | 16.17 | 2Asolution |
| 0.63 | 3.11 | 13.37 | 2Bsolution | ||||
To determine pseudo-solution model structures for 1 and 2, we surrounded the Δ-δδδδ forms of each compound in a droplet of 70 water molecules, and then optimised the geometry with the semi-empirical PM6 method in MOPAC.25,26 We have done this under two conditions: A) where the whole ensemble is relaxed; and B) where only the solvent is relaxed. This led to two different solvent arrangements, and we found that when the whole ensemble was relaxed for 1 a water molecule coordinated to the ErIII ion, but not in the case of 2. Thus, we generated four structures, 1Asolution, 1Bsolution, 2Asolution and 2Bsolution, each of which was further optimised at the density-functional theory (DFT) level (see Methods; Fig. 4 and Fig. S1–S4, ESI†). We find an Er–OH2 distance of 2.507 Å for 1Asolution, which is close to the sum of ionic radii for ErIII and O,27 and consistent with Er–OH2 bond lengths in ErIII complexes,28 and a longer distance of 2.983 Å for 1Bsolution. These are far shorter than the closest Er–OH2 distances in 2Asolution and 2Bsolution which are 3.874 and 4.057 Å, respectively. We then performed CASSCF-SO calculations on the entire ensembles (Tables S5–S8, ESI†). The results for both 1Asolution and 1Bsolution unambiguously show that the close approach of H2O in 1 has a significant effect on the magnetic anisotropy of the ground Kramers doublet compared to the solid-state structure, increasing g2 by 3.2 and decreasing g3 by 2.9 on average, towards the experimental values. We find that 1Asolution seems to support the model 1 simulations of 1solution, where g1 increases from the crystal structure, while 1Bsolution seems to support the model 2 simulations of 1solution where g1 is <1.5. From these results we cannot definitively conclude which simulation of the experimental spectrum is more accurate, however it is clear that the close approach or coordination of a water molecule to ErIII in 1solution leads to a drastic change in magnetic anisotropy. On the other hand, the not-so-close approaches of H2O to ErIII in 2 lead to smaller changes compared to the solid-state structures, where we see both g2 and g3 changing by ±1.3 on average. Here, the best agreement with experiment is for 2Bsolution, where the nearest water molecule is further away from the ErIII ion than in 2Asolution.
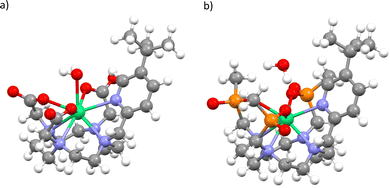 | ||
| Fig. 4 Optimised structure of 1Asolution (a) and 2Asolution (b). Note: most explicit water not shown, see Fig. S1 and S3 (ESI†). | ||
Thus, we have confirmed using EPR spectroscopy that the trimethylphosphinate ligand L2 in compound 2 effectively protects the coordination sphere of the bound erbium ion from hydration, whereas the triacetate ligand L1 in compound 1 is not sufficiently bulky to prevent water coordination, and this compound is certainly hydrated in aqueous solution. This work highlights the utility of EPR as a complimentary technique to NMR and luminescence methods for determination of hydration and solution structure.
We thank EPSRC (EP/N007034/1), The Royal Society (URF191320) and the ERC (ERC-2019-STG-851504) for funding. We thank the Computational Shared Facility at The University of Manchester for access to the CSF3. We thank the EPSRC EPR National Facility for access to EPR spectroscopy (EP/W014521/1 and EP/V035231/1). The data that support the findings of this study are openly available in FigShare at https://doi.org/10.48420/21740702.
EJLM, DP and NFC conceived the project. KM synthesised the compounds. NFC measured EPR spectra. MJG, MV, YLW, CW and NFC performed calculations. NFC wrote the manuscript with input from all authors.
Conflicts of interest
There are no conflicts to declare.Notes and references
- J.-C. G. Bünzli and S. V. Eliseeva, in Lanthanide Luminescence, eds. P. Hänninen and H. Härmä, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 7, pp. 1–45 Search PubMed.
- M. Hasegawa, H. Ohmagari, H. Tanaka and K. Machida, J. Photochem. Photobiol., C, 2022, 50, 100484 CrossRef CAS.
- N. Kofod, R. Arppe-Tabbara and T. J. Sørensen, J. Phys. Chem. A, 2019, 123, 2734–2744 CrossRef CAS PubMed.
- P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Chem. Rev., 1999, 99, 2293–2352 CrossRef CAS PubMed.
- T. Kushnir and G. Navon, J. Magn. Reson., 1984, 56, 373–384 CAS.
- R. B. Lauffer, Chem. Rev., 1987, 87, 901–927 CrossRef CAS.
- L. M. De León-Rodríguez, A. F. Martins, M. C. Pinho, N. M. Rofsky and A. D. Sherry, J. Magn. Reson. Imaging, 2015, 42, 545–565 CrossRef PubMed.
- D. Parker, E. A. Suturina, I. Kuprov and N. F. Chilton, Acc. Chem. Res., 2020, 53, 1520–1534 CrossRef CAS PubMed.
- P. K. Senanayake, N. J. Rogers, K.-L. N. A. Finney, P. Harvey, A. M. Funk, J. I. Wilson, D. O’Hogain, R. Maxwell, D. Parker and A. M. Blamire, Magn. Reson. Med., 2017, 77, 1307–1317 CrossRef PubMed.
- T. Kimura and G. R. Choppin, J. Alloys Compd., 1994, 213–214, 313–317 CrossRef.
- A. Beeby, I. M. Clarkson, R. S. Dickins, S. Faulkner, D. Parker, L. Royle, A. S. de Sousa, J. A. G. Williams and M. Woods, J. Chem. Soc., Perkin Trans. 2, 1999, 493–504 RSC.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- K. Mason, N. J. Rogers, E. A. Suturina, I. Kuprov, J. A. Aguilar, A. S. Batsanov, D. S. Yufit and D. Parker, Inorg. Chem., 2017, 56, 4028–4038 CrossRef CAS PubMed.
- A. M. Funk, K.-L. N. A. Finney, P. Harvey, A. M. Kenwright, E. R. Neil, N. J. Rogers, P. K. Senanayake and D. Parker, Chem. Sci., 2015, 6, 1655–1662 RSC.
- D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. K. Howard, Chem. Rev., 2002, 102, 1977–2010 CrossRef CAS PubMed.
- S. Aime, M. Botta and G. Ermondi, Inorg. Chem., 1992, 31, 4291–4299 CrossRef CAS.
- M. Vonci, K. Mason, E. R. Neil, D. S. Yufit, E. J. L. McInnes, D. Parker and N. F. Chilton, Inorg. Chem., 2019, 58, 5733–5745 CrossRef CAS PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513 CrossRef CAS PubMed.
- K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. Schau-Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe, O. Waldmann, L. F. Chibotaru, J. Bendix and J. Dreiser, Chem. Sci., 2014, 5, 1650–1660 RSC.
- E. Rousset, M. Piccardo, M.-E. Boulon, R. W. Gable, A. Soncini, L. Sorace and C. Boskovic, Chem. – Eur. J., 2018, 24, 14768–14785 CrossRef CAS PubMed.
- J. G. C. Kragskow, J. Marbey, C. D. Buch, J. Nehrkorn, M. Ozerov, S. Piligkos, S. Hill and N. F. Chilton, Nat. Commun., 2022, 13, 825 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- J. J. P. Stewart, MOPAC2016, Stewart Computational Chemistry Search PubMed.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. J. Giansiracusa, M. Vonci, W. Van den Heuvel, R. W. Gable, B. Moubaraki, K. S. Murray, D. Yu, R. A. Mole, A. Soncini and C. Boskovic, Inorg. Chem., 2016, 55, 5201–5214 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods, synthetic procedures and characterisation, electronic structure calculations. See DOI: https://doi.org/10.1039/d3cc00601h |
| This journal is © The Royal Society of Chemistry 2023 |