Open Access Article
Open Access ArticleQuantitative investigation of CeO2 surface proton conduction in H2 atmosphere†
Taku
Matsuda
,
Ryo
Ishibashi
,
Yoshiki
Koshizuka
,
Hideaki
Tsuneki
and
Yasushi
Sekine
 *
*
Department of Applied Chemistry, Waseda University, 3-4-1, Okubo, Shinjuku, Tokyo, 169-8555, Japan. E-mail: ysekine@waseda.jp
First published on 2nd September 2022
Abstract
This report is the first describing a study quantitatively analysing aspects of oxide surface protonics in a dry H2 atmosphere. Elucidating surface protonics is important for electrochemical and catalytic applications. In this study, AC impedance spectroscopy was used to investigate surface conduction properties of porous CeO2 at low temperatures (423–573 K) and in a dry H2 atmosphere. Results demonstrated that the conductivity increased by several orders of magnitude when H2 was supplied. Dissociative adsorption of H2 contributes to conduction by forming proton–electron pairs. Also, H/D isotope exchange studies confirmed protons as the dominant conduction carriers. Furthermore, H2 adsorption equilibrium modelling based on the Langmuir mechanism was applied to explain the H2 partial pressure dependence of conductivity. For the first time, the obtained model explains the experimentally obtained results both qualitatively and quantitatively. These findings represent new insights into surface protonics in H2 atmosphere.
The phenomenon of surface protonics has potential applications in proton-conducting fuel cells,1 proton exchange membranes2 and electrochemical gas sensors.3 This phenomenon is defined as proton transfer at oxide surfaces. Moreover, surface protonics plays an important role in heterogeneous catalysis.4–17 Surface proton conduction is observed in the presence of H2O or H2 at temperatures of room temperature to 773 K.18–31 Because adsorption plays an important role, porous samples at low temperatures are preferred; for H2O adsorption, multilayers are formed. It is noteworthy that no multilayer is formed in the adsorption of H2, thereby leading to a difference in surface proton transport behaviour: in an H2O atmosphere, free protons and mainly hydronium ions move through the chemisorbed and physisorbed water layers on the oxide, respectively according to the Grotthuss and vehicle mechanisms.29 Which mechanism prevails depends on the water layer thickness in relation to temperature and relative humidity.29 However, in an H2 atmosphere, dissociative adsorption of H2 produces proton–electron pairs. The produced protons are transferred on the surface lattice oxygen by a hopping mechanism.31 The presence of a metal (e.g. Pt) is regarded as necessary for H2 dissociation and spillover.
The evaluation of surface proton conduction is of great importance. For that evaluation, AC impedance spectroscopy is a promising technique because it allows separation of the electrical properties into components (e.g. bulk and grain boundaries), and facilitates their subsequent quantified. To date, many reports have described studies using AC impedance measurements to characterise surface proton conduction properties in an H2O atmosphere.18–30 Earlier reports described that surface proton conductivity under an H2O atmosphere can be quantified using an equivalent circuit suitable for the analysis.28–30 The equivalent circuit included surface components parallel to the bulk and grain boundary components, thereby allowing direct assessment of surface proton transport in the adsorbed water layer.
However, the evaluation of surface proton conduction under a dry H2 atmosphere has been reported only qualitatively.31 It has not yet reached the stage of quantitative evaluation. Therefore, a more general theory of surface proton conduction under a dry H2 atmosphere must be found.
This study investigated surface proton conduction properties induced by dry H2 supply on porous CeO2 by AC impedance measurements. Then a model was proposed to interpret those properties in terms of H2 partial pressure dependence. This study provides new insights into surface proton conduction in H2 atmosphere on an oxide surface. As the sample to be measured, we selected CeO2 (JRC-CEO-1), because surface protonic transport on CeO2 has been widely studied25–28 and CeO2 as a surface proton-conducting oxide is important for catalysis and fuel cell applications.4–12,27 Experimental procedures are described in ESI.†
First, the H2 supply effects on conductivity for porous CeO2 were investigated at various temperatures by AC impedance measurement. The obtained data were analysed using a parallel RQ equivalent circuit presented in Fig. S1 (ESI†). The temperature dependence of the CeO2 conductivity with and without H2 supply is presented in Fig. 1. From these data, we inferred that the H2 supply increased the conductivity by several orders of magnitude. The marked increase in conductivity is not attributable to oxygen vacancy formation, as explained in the discussion of ESI† (see Fig. S2 and S3). A change in the activation energy was also observed before and after H2 supply, as shown in Table 1, suggesting a change in the conduction mechanism or conductive carriers. According to earlier reports, porous samples with relative density of around 60% provide information related to conduction with adsorbed species.28,31 As shown in Fig. S4 in ESI,† SEM observations confirmed the presence of numerous pores in samples with relative density of approximately 60%.
| Condition (—) | Activation energy (eV) |
|---|---|
| Ar only (>573 K) | 1.33 |
| Ar only (<573 K) | 0.18 |
| 5%H2/Ar (>500 K) | 1.48 |
| 5%H2/Ar (<500 K) | 0.24 |
The increase in conductivity can therefore be attributed to the dissociative adsorption of H2 and the formation of conducting species, as presented in eqn (1)–(3).
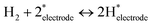 | (1) |
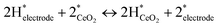 | (2) |
 | (3) |
Therein, * denotes adsorption site. Hydrogen spillover has been reported earlier.32,33
Dissociative adsorption of H2 is thought to have occurred on the Pt electrode. It then spilled over onto CeO2, giving rise to proton and electron pairs. On various reducible oxides (e.g. CeO2, TiO2, WO3), protons are said to bind to surface lattice oxygen; electrons reduce metal cations near O–H bonds.34 Protons move over the oxide surface, whereas electrons move via the conduction band.
Next, the H/D isotope effect was investigated to identify the dominant conducting carrier in the H2 atmosphere. As a result, the H/D isotope effect was identified at each measured temperature, as shown in Table 2 and in Fig. S5 in ESI.† Those findings are explainable by the different barriers posed by the hopping mechanism against the transfer of protons and deuterons. The deuteron transfer barrier is well known to be higher than the proton transfer barrier because of the different energies of the O–H and O–D ground states. According to classical theory, the theoretical value of the H/D isotope effect on the hopping proton/deuteron conductivity σD+/σH+ is expected to be  (≒0.71),35,36 as calculated using the following equation.37
(≒0.71),35,36 as calculated using the following equation.37
 | (4) |
| Temp (K) | σ D/σH (—) |
|---|---|
| 573 | 0.79 |
| 548 | 0.67 |
| 523 | 0.59 |
| 498 | 0.72 |
| 473 | 0.69 |
| 448 | 0.68 |
| 423 | 0.69 |
In that equation, D denotes diffusivity; m stands for the mass of the diffusing species. As Table 2 shows, the theoretical value closely approximates the experimentally obtained values. It can therefore be inferred that protons are the dominant conduction carrier in the H2 atmosphere and that they are transferred via the hopping mechanism. The possibility of proton conduction in the bulk was ruled out; in general, the diffusivity of hydrogen in CeO2 is low,38 and considerably high temperatures (above 1050 K) are required for CeO2 to exhibit the bulk proton conduction.39 So we attributed the measured proton conductivity only to the oxide surface and not to the bulk.
Next, to elucidate the surface protonics in an H2 atmosphere further, the effects of the H2 partial pressure dependence were investigated. As Fig. 2 shows, the conductivity increased concomitantly with increasing H2 partial pressure. At the low H2 partial pressure region, the slope was 0.13. It then saturated gradually with increasing H2 partial pressure, indicating a relation between conductivity and H2 coverage. Based on these results, an H2 adsorption equilibrium model was proposed to interpret the H2 partial pressure dependence of conductivity.
As explained in the preceding section, dissociative adsorption of H2 and spillover lead to the formation of protons on the CeO2 surface, as shown particularly by eqn (1)–(3). For simplicity, eqn (1) and (2) were combined. The reaction on the Pt electrode was omitted.
 | (5) |
The total equation for eqn (3) and (5) and the equilibrium constant Ktotal can be written as
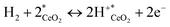 | (6) |
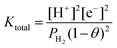 | (7) |
 | (8) |
Then, rearranging eqn (8) yields the following equation.
 | (9) |
This equation represents the H2 partial pressure dependence of proton concentration. However, the relation between H2 partial pressure and coverage is not considered. The H2 partial pressure dependence is explainable by the Langmuir adsorption model. The Langmuir adsorption model includes the assumption that the adsorption sites are homogeneous without interactions and that no interaction exists between neighbouring adsorbed molecules. The model also describes the adsorption of molecules on a solid surface as a function of gas pressure at a constant temperature. Applying the Langmuir adsorption model to eqn (5) gives the following equation.
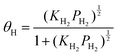 | (10) |
Therein, KH2 denotes the Langmuir adsorption constant. The H2 atom coverage represented in the eqn (10) can be assumed to be similar to θ. Then, substituting the coverage in the eqn (9) yields the following equation.
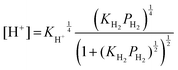 | (11) |
In that equation, KH+ is the equilibrium constant for eqn (5). The carrier concentration such as that of protons is related to the conductivity.
| σ = zFcμ | (12) |
Therein, z, F, c, and μ respectively denote the charge number, Faraday's constant, carrier concentration, and mobility.
Substituting the proton concentration expressed in eqn (11) into eqn (12) yields the following equation.
 | (13) |
Therefore, the following can be inferred from eqn (13); (1) At low H2 partial pressures,  . Then the proton conductivity is proportional to the power of 1/4 of the H2 pressure. (2) At high H2 partial pressures,
. Then the proton conductivity is proportional to the power of 1/4 of the H2 pressure. (2) At high H2 partial pressures,  . Then the proton conductivity is independent of the H2 partial pressure. These conclusions show close agreement with the experimentally obtained results. Furthermore, to explain the dependence of conductivity on H2 partial pressure quantitatively rather than qualitatively, eqn (13) can be rearranged as shown below.
. Then the proton conductivity is independent of the H2 partial pressure. These conclusions show close agreement with the experimentally obtained results. Furthermore, to explain the dependence of conductivity on H2 partial pressure quantitatively rather than qualitatively, eqn (13) can be rearranged as shown below.
 | (14) |
The values of A and KH2 are obtainable by the slope and intercept of  . The relation between
. The relation between  is shown in Fig. 3.
is shown in Fig. 3.
As expected, a linear relation was confirmed. The values of A and KH2 were calculated respectively as 2.5 × 10−9 S cm−1 and 4.8 × 102 atm−1. Substituting these values in the eqn (13) enables calculation of the value of σH+ at the H2 partial pressure. A comparison of the experimentally obtained data with the calculated data is presented in Fig. 4. The calculated σH+ showed good correspondence with the experimentally obtained results, thereby proving the model validity.
 | ||
| Fig. 4 H2 partial pressure dependence of conductivity for CeO2 at 473 K: experimentally obtained data and calculated data. | ||
In summary, AC impedance measurements were taken to characterise the electrical properties of porous CeO2 in a dry H2 atmosphere. A marked increase in conductivity with H2 supply was observed, suggesting the formation of conductive carriers (protons and electrons) by dissociative adsorption of H2 as shown in Fig. 5. The H/D isotope effect was also observed, indicating protons as the dominant conductive carriers. Furthermore, the proposed H2 adsorption equilibrium model quantitatively describes the H2 partial pressure dependence of the conductivity. The model presented herein provides new insights into surface protonics in a dry H2 atmosphere. The development of surface protonics in a dry H2 atmosphere and the establishment of a method for measuring and evaluating such protonics are expected to be applied to various catalytic reactions such as ammonia synthesis in a dry H2 atmosphere in the future.
Conflicts of interest
The authors have no conflicts of interest.References
- S. Kim, H. Park, M. Martin and Z. Munir, Adv. Mater., 2008, 20, 556–559 CrossRef CAS.
- A. Shabanikia, M. Javanbakht, H. Salar Amoli, K. Hooshyari and M. Enhessari, J. Electrochem. Soc., 2014, 161, 1403–1408 CrossRef.
- M. Sakthivel and W. Weppner, J. Phys. D: Appl. Phys., 2007, 40, 7210–7216 CrossRef CAS.
- M. Torimoto, S. Ogo, Y. Hisai, N. Nakano, A. Takahashi, Q. Ma, J. G. Seo, H. Tsuneki, T. Norby and Y. Sekine, RSC Adv., 2020, 10, 26418–26424 RSC.
- A. Takahashi, R. Inagaki, M. Torimoto, Y. Hisai, T. Matsuda, Q. Ma, J. G. Seo, T. Higo, H. Tsuneki, S. Ogo, T. Norby and Y. Sekine, RSC Adv., 2020, 10, 14487–14492 RSC.
- K. Murakami, Y. Tanaka, R. Sakai, Y. Hisai, S. Hayashi, Y. Mizutani, T. Higo, S. Ogo, J. G. Seo, H. Tsuneki and Y. Sekine, Chem. Commun., 2020, 56, 3365–3368 RSC.
- K. Yamada, S. Ogo, R. Yamano, T. Higo and Y. Sekine, Chem. Lett., 2020, 49(3), 303–306 CrossRef CAS.
- K. Takise, A. Sato, S. Ogo, J. G. Seo, K. Imagawa, S. Kado and Y. Sekine, RSC Adv., 2019, 9, 27743–27748 RSC.
- M. Torimoto, K. Murakami and Y. Sekine, Bull. Chem. Soc. Jpn., 2019, 92(10), 1785–1792 CrossRef CAS.
- K. Takise, A. Sato, K. Murakami, S. Ogo, J. G. Seo, K. Imagawa, S. Kado and Y. Sekine, RSC Adv., 2019, 9, 5918–5924 RSC.
- R. Inagaki, R. Manabe, Y. Hisai, Y. Kamite, T. Yabe, S. Ogo and Y. Sekine, Int. J. Hydrogen Energy, 2018, 43(31), 14310–14318 CrossRef CAS.
- R. Manabe, S. Okada, R. Inagaki, K. Oshima, S. Ogo and Y. Sekine, Sci. Rep., 2016, 6, 38007 CrossRef CAS PubMed.
- M. Kosaka, T. Higo, S. Ogo, J. G. Seo, K. Imagawa, S. Kado and Y. Sekine, Int. J. Hydrogen Energy, 2020, 45(1), 738–743 CrossRef CAS.
- T. Yabe, K. Yamada, K. Murakami, K. Toko, K. Ito, T. Higo, S. Ogo and Y. Sekine, ACS Sustainable Chem. Eng., 2019, 7(6), 5690–5697 CrossRef CAS.
- A. Gondo, R. Manabe, R. Sakai, K. Murakami, T. Yabe, S. Ogo, M. Ikeda, H. Tsuneki and Y. Sekine, Catal. Lett., 2018, 148(7), 1929–1938 CrossRef CAS.
- K. Murakami, R. Manabe, H. Nakatsubo, T. Yabe, S. Ogo and Y. Sekine, Catal. Today, 2018, 303, 271–275 CrossRef CAS.
- R. Manabe, H. Nakatsubo, A. Gondo, K. Murakami, S. Ogo, H. Tsuneki, M. Ikeda, A. Ishikawa, H. Nakai and Y. Sekine, Chem. Sci., 2017, 8, 5434–5439 RSC.
- S. Kim, H. J. Avila-Paredes, S. Wang, C. T. Chen, R. A. Souza, M. Martin and Z. A. Munir, Phys. Chem. Chem. Phys., 2009, 11, 3035–3038 RSC.
- B. Scherrer, M. V. F. Schlupp, D. Stender, J. Martynczuk, J. G. Grolig, H. Ma, P. Kocher, T. Lippert, M. Prestat and L. J. Gauckler, Adv. Funct. Mater., 2013, 23, 1957–1964 CrossRef CAS.
- M. T. Colomer, Adv. Mater., 2006, 18, 371–374 CrossRef CAS.
- H. J. Avila-Paredes, J. Zhao, S. Wang, M. Pietrowski, R. A. de Souza, A. Reinholdt, Z. A. Munir, M. Martin and S. Kim, J. Mater. Chem., 2010, 20, 990–994 RSC.
- S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Solid State Ionics, 2012, 207, 21–28 CrossRef CAS.
- S. Miyoshi, Y. Akao, N. Kuwata, J. Kawamura, Y. Oyama, T. Yagi and S. Yamaguchi, Chem. Mater., 2014, 26, 5194–5200 CrossRef CAS.
- R. Sato, S. Ohkuma, Y. Shibuta, F. Shimojo and S. Yamaguchi, J. Phys. Chem. C, 2015, 119, 28925–28933 CrossRef CAS.
- G. Gregori, M. Shirpour and J. Maier, Adv. Funct. Mater., 2013, 23, 5861–5867 CrossRef CAS.
- M. Shirpour, G. Gregori, R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2011, 13, 937–940 RSC.
- Y. Xing, Y. Wu, L. Li, Q. Shi, J. Shi and S. Yun, ACS Energy Lett., 2019, 4, 2601–2607 CrossRef CAS.
- R. Manabe, S. Ø. Stub, T. Norby and Y. Sekine, Solid State Commun., 2018, 270, 45–49 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Phys. Chem. C, 2017, 121, 12817–12825 CrossRef CAS.
- S. Ø. Stub, E. Vøllestad and T. Norby, J. Mater. Chem. A, 2018, 6, 8265–8270 RSC.
- Y. Hisai, K. Murakami, Y. Kamite, Q. Ma, E. Vøllestad, R. Manabe, T. Matsuda, S. Ogo, T. Norby and Y. Sekine, Chem. Commun., 2020, 56, 2699–2702 RSC.
- K. Mori, N. Hashimoto, N. Kamiuchi, H. Yoshida, H. Kobayashi and H. Yamashita, Nat. Commun., 2021, 12, 3884 CrossRef CAS.
- F. Yang, B. Hu, W. Xia, B. Peng, J. Shen and M. Muhler, J. Catal., 2018, 365, 55–62 CrossRef CAS.
- W. C. Conner and J. L. Falconer, Chem. Rev., 1995, 95, 759–788 CrossRef CAS.
- J. Bigeleisen, J. Chem. Phys., 1949, 17, 675–678 CrossRef CAS.
- T. Scherban, W. K. Lee and A. S. Nowick, Solid State Ionics, 1988, 28-30, 585–588 CrossRef.
- T. Scherban, Y. Baikov and E. Shalkova, Solid State Ionics, 1993, 66, 159–164 CrossRef CAS.
- N. Sakai, K. Yamaji, T. Horita, H. Yokokawa, Y. Hirata, S. Sameshima, Y. Nigara and J. Mizusaki, Solid State Ionics, 1999, 125, 325–331 CrossRef CAS.
- Y. Nigara, K. Kawamura, T. Kawada, J. Mizusaki and M. Ishigame, J. Electrochem. Soc., 1999, 146, 2948–2953 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc03687h |
| This journal is © The Royal Society of Chemistry 2022 |