Open Access Article
Open Access ArticleOrigin of the N-coordinated single-atom Ni sites in heterogeneous electrocatalysts for CO2 reduction reaction†
Yu
Wang‡
 a,
Liming
You
a and
Kun
Zhou
a,
Liming
You
a and
Kun
Zhou
 *ab
*ab
aEnvironmental Process Modelling Centre, Nanyang Environment and Water Research Institute, Nanyang Technological University, 1 CleanTech Loop, Singapore 637141, Singapore. E-mail: kzhou@ntu.edu.sg
bSchool of Mechanical and Aerospace Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore
First published on 7th October 2021
Abstract
Heterogeneous Ni–N–C single-atom catalysts (SACs) have attracted great research interest regarding their capability in facilitating the CO2 reduction reaction (CO2RR), with CO accounting for the major product. However, the fundamental nature of their active Ni sites remains controversial, since the typically proposed pyridinic-type Ni configurations are inactive, display low selectivity, and/or possess an unfavorable formation energy. Herein, we present a constant-potential first-principles and microkinetic model to study the CO2RR at a solid–water interface, which shows that the electrode potential is crucial for governing CO2 activation. A formation energy analysis on several NiNxC4−x (x = 1–4) moieties indicates that the predominant Ni moieties of Ni–N–C SACs are expected to have a formula of NiN4. After determining the potential-dependent thermodynamic and kinetic energy of these Ni moieties, we discover that the energetically favorable pyrrolic-type NiN4 moiety displays high activity for facilitating the selective CO2RR over the competing H2 evolution. Moreover, model polarization curves and Tafel analysis results exhibit reasonable agreement with existing experimental data. This work highlights the intrinsic tetrapyrrolic coordination of Ni for facilitating the CO2RR and offers practical guidance for the rational improvement of SACs, and this model can be expanded to explore mechanisms of other electrocatalysis in aqueous solutions.
Introduction
The high dependence of non-renewable fossil resources in modern economics has resulted in increasing concerns regarding energy and the environment. A promising solution to address this issue is to electrochemically convert waste CO2 to fuels to achieve a carbon-neutral cycle.1–3 Unfortunately, due to its sluggish kinetics and the concomitant hydrogen evolution reaction (HER), the feasibility of implementing such a CO2 reduction reaction (CO2RR) process on industrial scales suffers from the coupled problems of poor energy efficiency and low product selectivity. In particular, electrodes composed of earth-abundant metals generally exhibit low activity and/or selectivity for facilitating the CO2RR. Research on developing effective CO2RR catalysts has brought about the advent of a new class of heterogeneous electrocatalysts, namely, M–N–C single-atom catalysts (SACs), which feature atomically dispersed single-metal-atom sites.4–8 These metal sites exhibit unique electronic and structural properties compared with their bulk counterparts, thereby endowing M–N–C SACs with outstanding catalytic performance.9Ni–N–C, one of the most represented CO2RR SACs, has been established to possess great potential for facilitating selective CO2-to-CO conversion. Determining the role of coordination environments is beneficial for implementing strategic improvements to CO2RR catalysts. While significant efforts have been expended to investigate the fundamental nature of the active Ni sites through employing physical characterizations and modern quantum mechanics methods, a common consensus pertaining to such an issue has not been reached.3,9,16,17 Several pioneering studies have proposed a pyridinic-type NiN4 moiety (referred to as “α-NiN4” herein) in which a central Ni atom is coordinated by four pyridinic N atoms, and CO2RR processes on such a moiety were explored through comprehensive density functional theory (DFT) calculations.6–8 It should also be noted that pyridinic-type MN4 is a prototypical moiety that has been successfully established for describing the oxygen reduction reaction (ORR) on various M–N–C SACs.18–22 However, a detailed examination of the computational results of the CO2RR on α-NiN4 indicates a failure to reproduce the observed CO2RR activities of Ni–N–C SACs since large theoretical overpotentials ηt (>1.6 V) are involved.6–8
Recently, a variety of hybrid pyridinic N and C coordination environments with respect to the Ni sites have been proposed. For instance, Zhao et al. demonstrated that a pyridinic-type NiN1C3 moiety (referred to as “α-NiN1C3” herein) is considerably active for facilitating the CO2RR with a small ηt value of 0.48 V and exhibits high selectivity toward CO over H2.10 Such a hybrid moiety was also suggested in a recent grand canonical DFT study by Li and co-workers;23 their calculations also revealed that the charge capacity and the formation of hydrogen bonds between the adsorbates and the surrounding water molecules play vital roles in facilitating the activation of CO2. In contrast, Hossain et al. showed that pyridinic-type NiN2C2 and NiN3C1 moieties (referred to as “α-NiN2C2” and “α-NiN3C1” herein) are responsible for facilitating the CO2RR at an electrode potential of −0.8 V.24
While previous studies have predicted that Ni moieties containing fewer N atoms, i.e., α-NiNxC4−x (x = 1–3), exhibit excellent CO2RR activity, a general situation in which the formation energy of an MN4 moiety is much lower than those of MNxC4−x (x = 1–3) moieties has been overlooked.25–27 From a thermodynamics perspective, the predominant moieties of M–N–C SACs are expected to have the formula of MN4 instead of MNxC4−x (x = 1–3). Indeed, the research of Li et al. indicated that no Ni–C bond exists in the Ni–N–C SACs they synthesized on the basis of the C K-edge X-ray absorption spectroscopy (XAS) characterization of the Ni–N–C SACs and a control N–C system.6 Moreover, numerous experimental and computational studies on the ORR occurring on M–N–C SACs have demonstrated that the dispersed metal sites are mainly contributed by MN4.18–22 Therefore, none of the commonly studied α-NiNxC4−x moieties are responsible for the excellent CO2RR performance of Ni–N–C SACs. This situation presents an ambiguity regarding the structure–activity of the Ni sites of heterogeneous Ni–N–C SACs, which requires the development of (operando) characterization techniques and modelling approaches with high sensitivity and resolution.
In this study, we addressed this ambiguity by employing first-principles calculations and microkinetic modelling to investigate pyrrolic-type NiNxC4−x (β-NiNxC4−x) moieties as well as α-NiNxC4−x moieties, in tandem with a constant-potential method and the explicit treatment of solvents. β-NiNxC4−x moieties were explored because pyrrolic-type moieties have been demonstrated to inherently exist (or coexist with pyridinic-type moieties) in heterogeneous M–N–C SAC,28–32 but little is known of their CO2RR mechanisms. Remarkably, we demonstrated that the electrode potential is crucial for governing CO2 activation, and in contrast to other moieties that are inactive and/or exhibit low-selectivity, the β-NiN4 moiety not only possesses a favourable formation energy but also exhibits considerable activity and selectivity for CO2-to-CO conversion.
Results and discussion
Structural models of Ni–N–C SACs and their formation energy
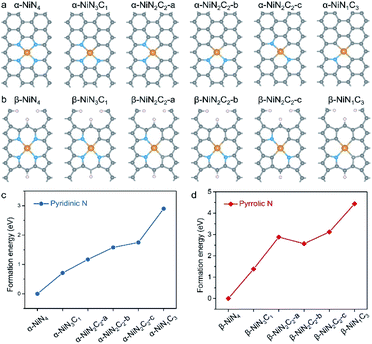
Good knowledge of the active structure of a catalyst is a solid foundation for understanding its catalytic nature.33,34 It has been established that the local coordination environment of a single-atom metal site is essential for determining its catalytic performance.35,36 We began by constructing the potential configurations of single-atom Ni sites and evaluating their formation energy values. For the local structure of the Ni sites of Ni–N–C SACs, the central Ni atom adopts a (quasi-)planar tetracoordination configuration, and as mentioned earlier, the ligand species can be either pyridinic N, pyrrolic N, or C. Interestingly, the prototypical α-NiNxC4−x can be conveniently constructed by creating a double-vacancy in the basal plane of graphene and replacing certain C atoms with N atoms (Fig. 1a), which may explain why α-NiNxC4−x moieties are typically chosen as structural models for XAS fitting and DFT calculations in existing literature.6–15,23,24In contrast, the construction of the β-NiNxC4−x moieties requires more skilful manipulation of the C atoms to create pyrrolic-type coordination environments (Fig. 1b), and according to previous studies,28–30 the unsaturated C atoms have been terminated by H atoms. Such pyrrolic-type moieties have been demonstrated to typically exist within the micropores of graphene nanosheets. α-NiN2C2 exhibits three possible configurations that correspond to different combinations of its N and C ligands; each of these configurations have been explored in various studies, such as α-NiN2C2-a,10 α-NiN2C2-b,12,23 and α-NiN2C2-c.24 Similarly to α-NiN2C2, β-NiN2C2 also corresponds to three possible configurations. In this work, only the configurations with a relative low formation energy were adopted in the later CO2RR calculations for NiN2C2.
The relative formation energy of the α-NiNxC4−x and β-NiNxC4−x moieties are presented in Fig. 1c and d, in which the formation energy values of α-NiN4 and β-NiN4 are set to be zero. For both the α-NiNxC4−x and β-NiNxC4−x moieties, the formation energy increases significantly as the number of N atoms decreases. In particular, the difference in formation energy values between NiN1C3 and NiN4 reaches up to 2.90 eV for the pyridinic-type configuration and 4.44 eV for the pyrrolic-type configuration. These results suggest that compared with N, the C ligand is not a good support for anchoring single-atom Ni species.
Please note that such formation energy calculations were performed to provide a general demonstration of the single-atom Ni sites based on a thermodynamics criterion, and they do not indicate whether the sites are pyridinic or pyrrolic. Additionally, they do not exclude the presence of energetically unfavourable NiNxC4−x (x = 1–3) moieties existing in nature. Indeed, the local structure of the single metal site should be determined by a synthesis parameter, such as the precursor materials, synthetic atmosphere, and pyrolysis temperature. However, the favourable formation energy of NiN4 over that of NiNxC4−x (x = 1–3) provides clear evidence that in principle, the predominant Ni moieties of Ni–N–C SACs are expected to correspond to the formula of NiN4.
CO2 reduction reaction on the pyrrolic-type NiN4
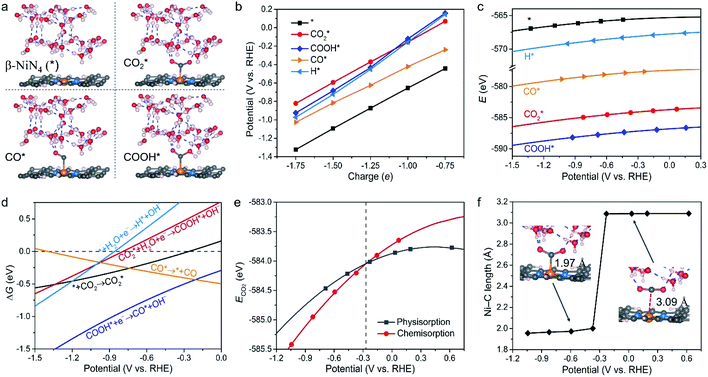
We next assessed the intrinsic CO2RR activities of the Ni moieties by employing a constant-potential/hybrid-solvent model. First, the constant-potential method considers the surface charge effect to determine potential-dependent energy values. Please note that the surface charge of an electrocatalyst is essential for assessing its chemical reactivity.23,24,37–39 Secondly, the explicit solvent model of the electrochemical interface allows the interactions between intermediates and the surrounding water molecules to be captured. Thirdly, the implicit solvation model accurately describes long-range electrostatic interactions and takes advantage of the fact that the electrostatic potential goes to zero in the electrolyte region. More details can be found in the Methods section.Taking β-NiN4, a Ni moiety with a favourable formation energy, as an example, the geometric structures of its CO2RR reaction species are shown in Fig. 2a. For each species, five individual simulations with system charge values of −1.75e, −1.5e, −1.25e, −1e, and −0.75e were conducted. Based on these calculations, the electrode potential (U) of each species for a given charge can be determined (Fig. 2b). A wider range of charge values (nine groups from −0.25e to −2.25e) has also been sampled, and negligible difference was found between the results (Fig. S1†). Due to the non-identical electronic structures of these species, the same charge does not correspond to the same value of U. However, the total energy of each species can be described as a continuous function of U by fitting five potential–energy points (Fig. 2c and Table S1†). With these potential–energy curves, the energy of these species for a specific value of U can be obtained, and the corresponding free energy changes ΔG of the reaction steps can be determined by further considering contributions of the zero-point energy, enthalpy, and entropy (Fig. 2d).
It can be observed from Fig. 2d that CO2 adsorption on β-NiN4 (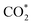 formation step) is exothermic in nature below U = −0.26 V and is more energetically favourable than the competing H* formation above U = −1.20 V. This suggests that β-NiN4 can efficiently activate CO2 molecules at typical working potentials while maintaining high selectivity for the CO2RR compared with the HER over a wide range of U. The conversion of
formation step) is exothermic in nature below U = −0.26 V and is more energetically favourable than the competing H* formation above U = −1.20 V. This suggests that β-NiN4 can efficiently activate CO2 molecules at typical working potentials while maintaining high selectivity for the CO2RR compared with the HER over a wide range of U. The conversion of 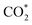 to COOH* (COOH* formation step) is the potential-limiting step, which becomes exothermic at U = −0.79 V. Subsequently, COOH* is reduced to CO* (CO* formation step) with a negative ΔG value, and the adsorbed CO molecule can be easily released from the β-NiN4 surface. A more appropriate comparison of the onset potentials and overpotentials with experimental data can be established based on microkinetic modelling, as discussed later.
to COOH* (COOH* formation step) is the potential-limiting step, which becomes exothermic at U = −0.79 V. Subsequently, COOH* is reduced to CO* (CO* formation step) with a negative ΔG value, and the adsorbed CO molecule can be easily released from the β-NiN4 surface. A more appropriate comparison of the onset potentials and overpotentials with experimental data can be established based on microkinetic modelling, as discussed later.
Specifically, we determined that the consideration of U is crucial for reproducing the experimentally observed chemisorption of CO2 on the Ni sites of Ni–N–C SACs. As shown in Fig. 2e and f, the adsorption of CO2 on β-NiN4 preferentially adopts a chemisorption configuration when the U is lower than −0.27 V, while a physisorption configuration is dominant above this potential value. Chemisorption configurations can be distinguished from physisorption configurations by the formation of a Ni–C bond. For example, a CO2 molecule is bent when adsorbed onto β-NiN4 while forming a Ni–C bond (1.97 Å) at U = −0.59 V (q = −1.5e), but it remains straight with a Ni–C distance of 3.09 Å at U = 0.03 V (q = −0.25e), which is within the range of typical vdW interactions. Please note that the different adsorption configurations were obtained by employing different initial structures (i.e., different Ni–C distances). The surrounding water molecules are also essential for the chemisorption of CO2 since the hydrogen bonds between them stabilize the 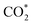 intermediates.23 The removal of the surrounding water molecules can also result in the adsorption of CO2 transiting from chemisorption to physisorption.
intermediates.23 The removal of the surrounding water molecules can also result in the adsorption of CO2 transiting from chemisorption to physisorption.
Comparison of the CO2RR performance of different Ni moieties
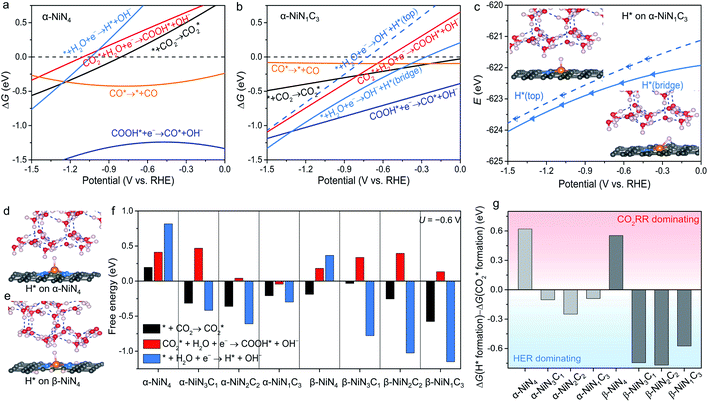
The constant-potential results of other Ni moieties are shown in Fig. 3a, b, S2 and S3†, and their energy–potential relationships are summarized in Tables S2–S8.† For α-NiN4, another Ni moiety exhibiting a favourable formation energy, its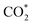 and COOH* formation steps are only exothermic at very negative potentials (−0.81 and −1.10 V, respectively), as shown in Fig. 3a. This suggests that α-NiN4 is inactive for facilitating the CO2RR.
and COOH* formation steps are only exothermic at very negative potentials (−0.81 and −1.10 V, respectively), as shown in Fig. 3a. This suggests that α-NiN4 is inactive for facilitating the CO2RR.
While the 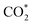 and COOH* formation steps of α-NiN1C3 are more energetically favourable than its H* formation step, the latter surpasses the
and COOH* formation steps of α-NiN1C3 are more energetically favourable than its H* formation step, the latter surpasses the 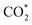 formation step below U = −0.45 V (Fig. 3b). On α-NiN1C3, the location of H* with the lowest energy is the Ni–C bridge site instead of the Ni top site (Fig. 3c), which differs from both α-NiN4 and β-NiN4 that preferentially adopt the Ni-top H* configuration (Fig. 3d and e). Although it appears that H* could be weakly adsorbed onto the Ni top sites of α-NiN1C3,23 the strong binding of H* on the Ni–C bridge sites prevents the reduction of CO2, thereby resulting in poor CO2RR selectivity. Meanwhile, strong H* adsorption on the bridge sites has also been identified in other Ni moieties that involve the hybrid C and N coordination (Fig. S4†).
formation step below U = −0.45 V (Fig. 3b). On α-NiN1C3, the location of H* with the lowest energy is the Ni–C bridge site instead of the Ni top site (Fig. 3c), which differs from both α-NiN4 and β-NiN4 that preferentially adopt the Ni-top H* configuration (Fig. 3d and e). Although it appears that H* could be weakly adsorbed onto the Ni top sites of α-NiN1C3,23 the strong binding of H* on the Ni–C bridge sites prevents the reduction of CO2, thereby resulting in poor CO2RR selectivity. Meanwhile, strong H* adsorption on the bridge sites has also been identified in other Ni moieties that involve the hybrid C and N coordination (Fig. S4†).
Fig. 3f shows the values of ΔG for the three key reaction steps, i.e., 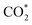 formation, COOH* formation, and H* formation, of the studied Ni moieties at U = −0.60 V, at which a partial current density of CO can be detected experimentally for Ni–N–C SACs.10–15 The results for the CO* formation and CO desorption steps are excluded since the two steps are typically exothermic. At U = −0.60 V,
formation, COOH* formation, and H* formation, of the studied Ni moieties at U = −0.60 V, at which a partial current density of CO can be detected experimentally for Ni–N–C SACs.10–15 The results for the CO* formation and CO desorption steps are excluded since the two steps are typically exothermic. At U = −0.60 V, 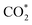 formation on α-NiN4 remains endothermic by 0.20 eV, and COOH* formation is endothermic by 0.41 eV. These results indicate that α-NiN4 displays a low activity for facilitating the CO2RR, which is consistent with previous studies.
formation on α-NiN4 remains endothermic by 0.20 eV, and COOH* formation is endothermic by 0.41 eV. These results indicate that α-NiN4 displays a low activity for facilitating the CO2RR, which is consistent with previous studies.
Although the 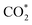 formation steps of the α- and β-NiNxC4−x (x = 1–3) moieties correspond to negative ΔG values, their H* formation steps are highly exothermic. Since H* formation is more energetically favourable than
formation steps of the α- and β-NiNxC4−x (x = 1–3) moieties correspond to negative ΔG values, their H* formation steps are highly exothermic. Since H* formation is more energetically favourable than 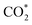 formation, the α- and β-NiNxC4−x (x = 1–3) moieties are expected to facilitate the HER preferentially instead of the CO2RR at U = −0.60 V. Evidently, such a situation directly contradicts the experimental observation of Ni–N–C SACs exhibiting high selectivity for the CO2RR. Hence, apart from α-NiN4, Ni moieties with hybrid C and N coordination environments, i.e., the α- and β-NiNxC4−x (x = 1–3) moieties, cannot be responsible for the excellent CO2RR performance of Ni–N–C SACs.
formation, the α- and β-NiNxC4−x (x = 1–3) moieties are expected to facilitate the HER preferentially instead of the CO2RR at U = −0.60 V. Evidently, such a situation directly contradicts the experimental observation of Ni–N–C SACs exhibiting high selectivity for the CO2RR. Hence, apart from α-NiN4, Ni moieties with hybrid C and N coordination environments, i.e., the α- and β-NiNxC4−x (x = 1–3) moieties, cannot be responsible for the excellent CO2RR performance of Ni–N–C SACs.
Remarkably, β-NiN4 exhibits a negative ΔG value for 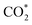 formation (−0.19 eV) and a positive ΔG value for H* formation (0.40 eV), as shown in Fig. 3f, which indicates that at U = −0.60 V, CO2 molecules can be activated effectively over β-NiN4, and the competing HER process is suppressed. Please note that the difference in energy between
formation (−0.19 eV) and a positive ΔG value for H* formation (0.40 eV), as shown in Fig. 3f, which indicates that at U = −0.60 V, CO2 molecules can be activated effectively over β-NiN4, and the competing HER process is suppressed. Please note that the difference in energy between 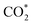 formation and H* formation is as large as 0.59 eV (Fig. 3g); such a value implies that β-NiN4 possesses high selectivity toward the CO2RR. Moreover, for COOH* formation, it can be shown from Fig. 3f that aside from α-NiN1C3 (−0.04 eV), the other Ni moieties exhibit positive ΔG values at U = −0.60 V; however, the ΔG values of α-NiN2C2, β-NiN4, and β-NiN1C3 are only slightly positive, indicating that COOH* formation on these three moieties is still feasible. Overall, the above results have established that among these Ni moieties, only β-NiN4 has a favourable formation energy value and is active and selective toward the CO2RR. Such characteristics of β-NiN4 may potentially account for the experimentally observed high CO2RR performance of Ni–N–C SACs.
formation and H* formation is as large as 0.59 eV (Fig. 3g); such a value implies that β-NiN4 possesses high selectivity toward the CO2RR. Moreover, for COOH* formation, it can be shown from Fig. 3f that aside from α-NiN1C3 (−0.04 eV), the other Ni moieties exhibit positive ΔG values at U = −0.60 V; however, the ΔG values of α-NiN2C2, β-NiN4, and β-NiN1C3 are only slightly positive, indicating that COOH* formation on these three moieties is still feasible. Overall, the above results have established that among these Ni moieties, only β-NiN4 has a favourable formation energy value and is active and selective toward the CO2RR. Such characteristics of β-NiN4 may potentially account for the experimentally observed high CO2RR performance of Ni–N–C SACs.
Kinetics and free energy diagrams
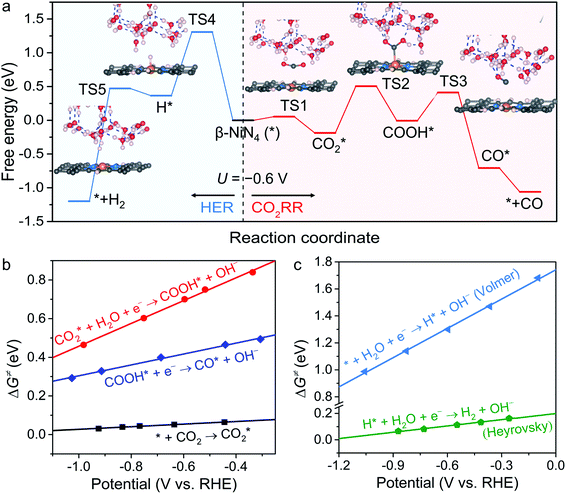
To obtain more insight into the CO2RR occurring on the active β-NiN4 moiety, we further explored the kinetics of the key reaction steps involved, and the thermodynamic and kinetic energy values were compiled in a free energy diagram (Fig. 4a). The potential dependence of the kinetic barrier ΔG‡(U) was determined through multiple barrier calculations at varying potentials (Fig. 4b and c). According to our calculations, at U = −0.60 V, β-NiN4 exhibits a small barrier of 0.05 eV for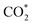 formation and a moderate barrier of 0.69 eV for COOH* formation, while it displays a quite high barrier of 1.31 eV for H* formation (Volmer reaction). After the formation of the COOH* or H* intermediates, the subsequent protonation steps are kinetically feasible, e.g., ΔG‡(−0.6 V) = 0.42 eV for the reduction of COOH* to CO* and ΔG‡(−0.6 V) = 0.10 eV for the reduction of H* to H2 (Heyrovsky reaction). By extrapolating these thermodynamic and kinetic energy values, we thereby conclude that at U = −0.60 V, the efficient conversion of CO2 to CO on β-NiN4 can be achieved.
formation and a moderate barrier of 0.69 eV for COOH* formation, while it displays a quite high barrier of 1.31 eV for H* formation (Volmer reaction). After the formation of the COOH* or H* intermediates, the subsequent protonation steps are kinetically feasible, e.g., ΔG‡(−0.6 V) = 0.42 eV for the reduction of COOH* to CO* and ΔG‡(−0.6 V) = 0.10 eV for the reduction of H* to H2 (Heyrovsky reaction). By extrapolating these thermodynamic and kinetic energy values, we thereby conclude that at U = −0.60 V, the efficient conversion of CO2 to CO on β-NiN4 can be achieved.
The kinetic barriers of a prototypical Ni moiety, α-NiN1C3, were also investigated. The geometric structures of its transition states are shown in Fig. S5.† As expected, at U = −0.60 V, α-NiN1C3 was predicted to exhibit a relatively favourable ΔG‡ value for COOH* formation (0.39 eV) compared with β-NiN4. However, upon considering the lowest-energy location of the H* intermediate (i.e., H* adsorption on the Ni–C bridge sites), the value of ΔG‡ for H* formation (0.36 eV) was found to be lower than that for COOH* formation. Therefore, the kinetic results have also established the poor CO2RR selectivity of α-NiN1C3, which has already been identified by the above thermodynamic calculations.
Microkinetic modelling
Finally, we constructed a microkinetic model to further examine the CO2RR performance of the active β-NiN4 moiety and to provide a qualitative comparison with existing experimental data of Ni–N–C SACs. Fig. 5a shows the reaction steps of the CO2RR (i = 1–5) and HER (i = 6, 7) processes considered in our model. The terms CO2(aq) and CO2(dl) represent CO2 molecules within the electrolyte and at the catalyst–electrolyte interface, respectively. The term ki is the rate constant of the step i, which depends directly on the potential-based kinetic barrier ΔG‡(U) in accordance with the transition state theory, and k−i is the rate constant for the reverse reaction. The CO partial current density can be estimated by solving these rate equations at a steady state. Further details are summarized in the Methods section.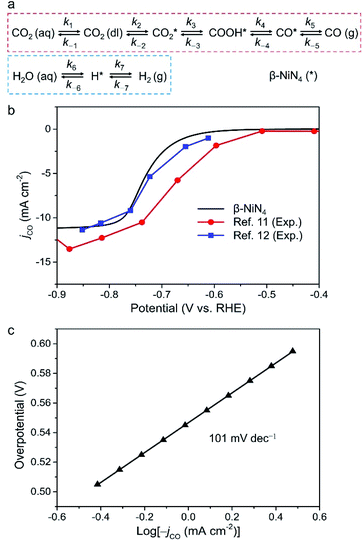 | ||
| Fig. 5 (a) Schematic plot of reaction steps considered in the microkinetic modelling. (b) Simulated partial CO current density of β-NiN4 compared with existing experimental data (catalyst loading: 1.0 mg cm−2 in ref. 11 and 0.75 mg cm−2 in ref. 12). For the polarization curve simulation, eρNi = 10.5 μC cm−2 was adopted; the term ρNi is the density of active single-Ni-atom sites. (c) Tafel plot of β-NiN4. | ||
Fig. 5b displays the model partial CO current density (jCO) as a function of the electrode potential. The onset-potential of β-NiN4 was calculated to be −0.55 V, beyond which the value of jCO increases continuously with U and reaches 10 mA cm−2 at U = −0.77 V. Such a curve is consistent with its experimentally measured counterparts.11,12 Please note that the current density is highly dependent on the catalyst morphology and electrochemical measurement parameters (e.g., electrode material, catalyst mass loading, and CO2 diffusion rate), and the present calculation was performed to provide a qualitative demonstration of CO2RR activity as the effective density of active Ni sites (ρNi) is unknown experimentally, even though the Ni content and loading can be determined.
A Tafel analysis was further conducted (Fig. 5c). According to our calculations, the Tafel slope of β-NiN4 was estimated to be ∼101 mV dec−1, which is in reasonable agreement with the typical values for Ni–N–C SACs in experiments (∼108 mV dec−1).6,8,10,11 The polarization curve for the competing HER is shown in Fig. S6,† in which the poor HER activity of β-NiN4 is revealed (U = −1.57 V at 10 mA cm−2). This also implies that the experimentally observed concomitant H2 production at U < −0.7 V may be attributed to the HER occurring on the N-neighbouring C sites of Ni–N–C SACs, considering that the N-doped graphene nanosheets are active for facilitating the HER.11
Conclusions
In summary, we have presented a fundamental understanding of the CO2RR occurring on heterogeneous Ni–N–C SACs by considering twelve possible single-atom Ni moieties. We discovered that an intrinsic tetrapyrrolic coordination environment with respect to Ni, i.e., β-NiN4, can boost the CO2RR activity, which rationalizes existing experimental observations. Such an understanding is based on the first-principles and microkinetic modelling of reaction processes at a solid–water interface, in which a constant-potential/hybrid-solvent model was adopted. According to an analysis of the formation energy, the predominant Ni moieties in Ni–N–C SACs are expected to correspond to the formula of NiN4. After determining the potential-dependent thermodynamic and kinetic energy values of the studied Ni moieties, we found that among them, only β-NiN4 exhibits considerable activity for the selective CO2-to-CO conversion compared with the competing H2 production. Specifically, its theoretical polarization curve and Tafel plot show reasonable agreement with existing experimental data. Our work discloses the activity origin of an important model SAC, offers practical guidance for the rational design of electrocatalysts, and serves as a prime example for future studies exploring the underlying mechanisms of other heterogeneous electrocatalysis in aqueous solutions.Methods
First-principles computations
The first-principles calculations were performed with Vienna Ab initio Simulation Package (VASP),40,41 and the projector-augmented wave approach was employed to describe the ion–electron interactions.42 The electronic exchange–correlation energy was modelled using the BEEF-vdW functional,43 which accurately describes vdW interactions while retaining a good description of chemisorption of adsorbates on surfaces. All calculations included spin polarization and were performed using a cutoff energy of 400 eV with a Gaussian smearing of 0.1 eV for slabs and 0.01 eV for gas-phase species. The k-space samplings were set as 3 × 3 × 1. The optimized lattice parameters of the α-NiNxC4−x slabs were a = 8.39 Å and b = 12.43 Å, and those of the β-NiNxC4−x slabs were a = 8.12 Å and b = 12.02 Å. For all slabs, the distance of the vacuum space was set as ∼25 Å to minimize interactions between periodic images. The lowest energy location of each intermediate was reported.Formation energy calculations
The formation energy of a NiNxC4−x (x = 1, 2, 3, or 4) moiety is defined as:| Eform = ENiNxC4−x − NCμC − NNμN − NHμH − μNi | (1) |
Constant-potential/hybrid-solvent model
A constant-potential/hybrid-solvent model was employed to determine the potential-dependent thermodynamic and kinetic energy values of reactions at the catalyst–solvent interface. A water bilayer containing 24 H2O molecules was constructed to explicitly describe the interactions between intermediates and the surrounding water molecules. The Poisson–Boltzmann implicit solvation model was utilized to establish the relationship between the system charge and electrode potential U, as implemented in the VASPsol.44,45 This model takes advantage of the fact that the electrostatic potential goes to zero in the electrolyte region. The effective surface tension parameter was set as zero as the cavitation energy is negligible.45 For an electrochemical system, the electrostatic potential is analogous to the workfunction. We added additional electrons (a net charge) and subsequently calculated the workfunction of the charged slab (Φslab), which is reflected by the Fermi level with respect to the electrostatic potential in the electrolyte region. After determining the value of Φslab, the electrode potential of the slab on the standard hydrogen electrode (SHE) scale, USHE, can be calculated by| USHE = Φslab/e − U0 | (2) |
Potential-dependent kinetic barrier
For adsorbates, the zero-point energy (EZPE), enthalpy (∫CpdT), and entropy (−TS) contributions to free energy were calculated by vibrational frequencies calculations, in which all 3N degrees of freedom are treated as harmonic vibrational motions. For molecules, these contributions were obtained from the NIST database. Electronic energy corrections were applied to the calculations of EDFT of CO2 (+0.33 eV) and H2 (+0.09 eV) molecules because of the errors residing in the description of the OCO backbone and H2 from the BEEF-vdW functional.53 Based on the above constant potential simulations and free energy contributions, the free energy change (ΔG) for each reaction step can be determined by the following equation:| ΔG = ΔE + ΔEZPE + Δ∫CpdT − TΔS | (3) |
The potential dependence of the kinetic barrier, ΔG‡(U), was obtained via multiple barrier calculations at varying potentials (different system charges). The transition state was determined using the climbing-image nudged elastic band (CI-NEB) approach54 with a given charge and has been further verified by vibrational frequency calculations (only one imaginary frequency). The values of ΔG‡ have been corrected by considering the zero-point energy, but no configurational entropies were included according to the transition state theory.
Microkinetic model
The rate equation of each species in the CO2RR process is summarized in eqn (4)–(9), and they are presented as follows: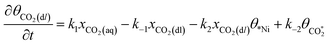 | (4) |
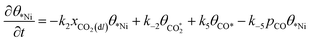 | (5) |
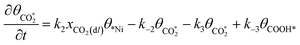 | (6) |
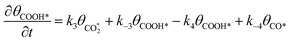 | (7) |
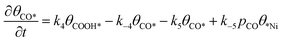 | (8) |
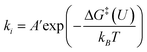 | (9) |
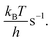 The current density is calculated by
The current density is calculated by| j = 2eρNiTOF | (10) |
Author contributions
Y. W. performed the calculations. Y. W., L. Y., and K. Z. analysed the data and wrote the paper. K. Z. supervised the study.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Yu-Jia Tang for many fruitful discussions. The authors acknowledge financial support from the Nanyang Environment and Water Research Institute (Core Fund), Nanyang Technological University, Singapore. The calculations were performed on computer clusters at High Performance Computing Centre at Nanyang Technological University.References
- Y. Y. Birdja, E. Pérez-Gallent, M. C. Figueiredo, A. J. Göttle, F. Calle-Vallejo and M. T. Koper, Nat. Energy, 2019, 4, 732–745 CrossRef CAS.
- S. Zhang, Q. Fan, R. Xia and T. J. Meyer, Acc. Chem. Res., 2020, 53, 255–264 CrossRef CAS PubMed.
- M. Li, H. Wang, W. Luo, P. C. Sherrell, J. Chen and J. Yang, Adv. Mater., 2020, 32, 2001848 CrossRef CAS PubMed.
- A. S. Varela, N. Ranjbar Sahraie, J. Steinberg, W. Ju, H.-S. Oh and P. Strasser, Angew. Chem., Int. Ed., 2015, 54, 10758–10762 CrossRef CAS PubMed.
- J. Gu, C.-S. Hsu, L. Bai, H. M. Chen and X. Hu, Science, 2019, 364, 1091–1094 CrossRef CAS PubMed.
- X. Li, W. Bi, M. Chen, Y. Sun, H. Ju, W. Yan, J. Zhu, X. Wu, W. Chu and C. Wu, J. Am. Chem. Soc., 2017, 139, 14889–14892 CrossRef CAS PubMed.
- W. Ju, A. Bagger, G.-P. Hao, A. S. Varela, I. Sinev, V. Bon, B. R. Cuenya, S. Kaskel, J. Rossmeisl and P. Strasser, Nat. Commun., 2017, 8, 944 CrossRef PubMed.
- H. B. Yang, S.-F. Hung, S. Liu, K. Yuan, S. Miao, L. Zhang, X. Huang, H.-Y. Wang, W. Cai and R. Chen, Nat. Energy, 2018, 3, 140–147 CrossRef CAS.
- Q. Qu, S. Ji, Y. Chen, D. Wang and Y. Li, Chem. Sci., 2021, 12, 4201–4215 RSC.
- C. Zhao, Y. Wang, Z. Li, W. Chen, Q. Xu, D. He, D. Xi, Q. Zhang, T. Yuan and Y. Qu, Joule, 2019, 3, 584–594 CrossRef CAS.
- K. Jiang, S. Siahrostami, T. Zheng, Y. Hu, S. Hwang, E. Stavitski, Y. Peng, J. Dynes, M. Gangisetty and D. Su, Energy Environ. Sci., 2018, 11, 893–903 RSC.
- T. Möller, W. Ju, A. Bagger, X. Wang, F. Luo, T. N. Thanh, A. S. Varela, J. Rossmeisl and P. Strasser, Energy Environ. Sci., 2019, 12, 640–647 RSC.
- Y. N. Gong, L. Jiao, Y. Qian, C. Y. Pan, L. Zheng, X. Cai, B. Liu, S. H. Yu and H. L. Jiang, Angew. Chem., Int. Ed., 2020, 59, 2705–2709 CrossRef CAS PubMed.
- H. Yang, Q. Lin, C. Zhang, X. Yu, Z. Cheng, G. Li, Q. Hu, X. Ren, Q. Zhang, J. Liu and C. He, Nat. Commun., 2020, 11, 593 CrossRef CAS PubMed.
- Z. Chen, X. Zhang, W. Liu, M. Jiao, K. Mou, X. Zhang and L. Liu, Energy Environ. Sci., 2021, 14, 2349–2356 RSC.
- Y. Li and A. I. Frenkel, Acc. Chem. Res., 2021, 8738–8748 Search PubMed.
- T. N. Nguyen, M. Salehi, Q. V. Le, A. Seifitokaldani and C. T. Dinh, ACS Catal., 2020, 10, 10068–10095 CrossRef.
- H. T. Chung, D. A. Cullen, D. Higgins, B. T. Sneed, E. F. Holby, K. L. More and P. Zelenay, Science, 2017, 357, 479–484 CrossRef CAS PubMed.
- J. Li, M. Chen, D. A. Cullen, S. Hwang, M. Wang, B. Li, K. Liu, S. Karakalos, M. Lucero and H. Zhang, Nat. Catal., 2018, 1, 935–945 CrossRef CAS.
- S. Kattel and G. Wang, J. Phys. Chem. Lett., 2014, 5, 452–456 CrossRef CAS PubMed.
- J. Sun, Y.-H. Fang and Z.-P. Liu, Phys. Chem. Chem. Phys., 2014, 16, 13733–13740 RSC.
- Y. Wang, Y.-J. Tang and K. Zhou, J. Am. Chem. Soc., 2019, 141, 14115–14119 CrossRef CAS PubMed.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777 CrossRef CAS PubMed.
- M. D. Hossain, Y. Huang, H. Y. Ted, W. A. Goddard III and Z. Luo, Nat. Commun., 2020, 11, 1–14 Search PubMed.
- J. M. Ziegelbauer, T. S. Olson, S. Pylypenko, F. Alamgir, C. Jaye, P. Atanassov and S. Mukerjee, J. Phys. Chem. C, 2008, 112, 8839–8849 CrossRef CAS.
- S. Kattel, P. Atanassov and B. Kiefer, J. Phys. Chem. C, 2012, 116, 8161–8166 CrossRef CAS.
- Y. Li, X. Liu, L. Zheng, J. Shang, X. Wan, R. Hu, X. Guo, S. Hong and J. Shui, J. Mater. Chem. A, 2019, 7, 26147–26153 RSC.
- A. Zitolo, V. Goellner, V. Armel, M.-T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937–942 CrossRef CAS PubMed.
- A. Zitolo, N. Ranjbar-Sahraie, T. Mineva, J. Li, Q. Jia, S. Stamatin, G. F. Harrington, S. M. Lyth, P. Krtil and S. Mukerjee, Nat. Commun., 2017, 8, 1–11 CrossRef CAS PubMed.
- J. Li, M. T. Sougrati, A. Zitolo, J. M. Ablett, I. C. Oğuz, T. Mineva, I. Matanovic, P. Atanassov, Y. Huang and I. Zenyuk, Nat. Catal., 2021, 4, 10–19 CrossRef CAS.
- T. Mineva, I. Matanovic, P. Atanassov, M.-T. Sougrati, L. Stievano, M. Clémancey, A. Kochem, J.-M. Latour and F. Jaouen, ACS Catal., 2019, 9, 9359–9371 CrossRef CAS.
- S. Wagner, H. Auerbach, C. E. Tait, I. Martinaiou, S. C. Kumar, C. Kübel, I. Sergeev, H. C. Wille, J. Behrends and J. A. Wolny, Angew. Chem., Int. Ed., 2019, 58, 10486–10492 CrossRef CAS PubMed.
- Q. Wang, C. Cai, M. Dai, J. Fu, X. Zhang, H. Li, H. Zhang, K. Chen, Y. Lin, H. Li, J. Hu, M. Miyauchi and M. Liu, Small Sci., 2021, 1, 2000028 CrossRef.
- M. Li, Y. Ma, J. Chen, R. Lawrence, W. Luo, M. Sacchi, W. Jiang and J. Yang, Angew. Chem., Int. Ed., 2021, 60, 11487–11493 CrossRef CAS PubMed.
- A. Chen, X. Zhang, L. Chen, S. Yao and Z. Zhou, J. Phys. Chem. C, 2020, 124, 22471–22478 CrossRef CAS.
- D. Gao, T. Liu, G. Wang and X. Bao, ACS Energy Lett., 2021, 6, 713–727 CrossRef CAS.
- Y. Huang, R. J. Nielsen and W. A. Goddard III, J. Am. Chem. Soc., 2018, 140, 16773–16782 CrossRef CAS PubMed.
- D. Kim, J. Shi and Y. Liu, J. Am. Chem. Soc., 2018, 140, 9127–9131 CrossRef CAS PubMed.
- C. Choi, G. H. Gu, J. Noh, H. S. Park and Y. Jung, Nat. Commun., 2021, 12, 4353 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- K. Mathew, V. C. Kolluru, S. Mula, S. N. Steinmann and R. G. Hennig, J. Chem. Phys., 2019, 151, 234101 CrossRef PubMed.
- H. Reiss and A. Heller, J. Phys. Chem., 1985, 89, 4207–4213 CrossRef CAS.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef.
- J.-S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402–406 CrossRef CAS PubMed.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668 CrossRef CAS PubMed.
- N. G. Hörmann, O. Andreussi and N. Marzari, J. Chem. Phys., 2019, 150, 041730 CrossRef PubMed.
- Z. Duan and G. Henkelman, ACS Catal., 2019, 9, 5567–5573 CrossRef CAS.
- C. Guo, X. Fu and J. Xiao, J. Phys. Chem. C, 2020, 124, 25796–25804 CrossRef CAS.
- F. Studt, F. Abild-Pedersen, J. B. Varley and J. K. Nørskov, Catal. Lett., 2013, 143, 71–73 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational methods, supporting figures, and supporting tables. See DOI: 10.1039/d1sc04094d |
| ‡ Current address: Jiangsu Collaborative Innovation Centre of Biomedical Functional Materials, Jiangsu Key Laboratory of New Power Batteries, School of Chemistry and Materials Science, Nanjing Normal University, 1 Wenyuan Road, Nanjing 210023, China. |
| This journal is © The Royal Society of Chemistry 2021 |