Covalent photofunctionalization and electronic repair of 2H-MoS2via nitrogen incorporation†
Helena
Osthues
 a,
Christian
Schwermann
a,
Christian
Schwermann
 a,
Johann A.
Preuß
a,
Johann A.
Preuß
 b,
Thorsten
Deilmann
b,
Thorsten
Deilmann
 a,
Rudolf
Bratschitsch
a,
Rudolf
Bratschitsch
 b,
Michael
Rohlfing
a and
Nikos L.
Doltsinis
b,
Michael
Rohlfing
a and
Nikos L.
Doltsinis
 *a
*a
aInstitute for Solid State Theory and Center for Multiscale Theory and Computation, Westfälische Wilhelms-Universität Münster, Wilhelm-Klemm-Str. 10, 48149 Münster, Germany. E-mail: nikos.doltsinis@wwu.de; Fax: +49 251 83 33669; Tel: +49 251 83 33582
bInstitute of Physics and Center for Nanotechnology, Westfälische Wilhelms-Universität Münster, Wilhelm-Klemm-Str. 10, 48149 Münster, Germany
First published on 13th August 2021
Abstract
A route towards covalent functionalization of chemically inert 2H-MoS2 exploiting sulfur vacancies is explored by means of (TD)DFT and GW/BSE calculations. Functionalization via nitrogen incorporation at sulfur vacancies is shown to result in more stable covalent binding than via thiol incorporation. In this way, defective monolayer MoS2 is repaired and the quasiparticle band structure as well as the remarkable optical properties of pristine MoS2 are restored. Hence, defect-free functionalization with various molecules is possible. Our results for covalently attached azobenzene, as a prominent photo-switch, pave the way to create photoresponsive two-dimensional (2D) materials.
1 Introduction
Molybdenum disulfide (MoS2) and other transition metal dichalcogenides (TMDCs) have attracted widespread attention over the last decade in the field of two-dimensional (2D) materials. Similar to graphene, atomically thin sheets of the layered van der Waals crystals can be exfoliated mechanically, which, in the monolayer (ML) limit, possess a direct band gap and exhibit strong photoluminescence (PL), which is in the visible range for MoS2.1,2 TMDCs are therefore promising materials for potential applications in optoelectronic devices.3,4Covalent chemical functionalization is critical to robustly tailor the electronic and optical properties of nanomaterials and to give them new functionalities required for various applications. MoS2 in its stable semiconducting 2H-phase is chemically inert due to the lack of dangling bonds in the basal plane. Therefore sulfur vacancies, the predominant type of defect5 in mechanically exfoliated and chemical vapor deposition (CVD) grown MoS2 with the lowest formation energy,6,7 are used as reactive centers for the attachment of nucleophilic functional groups, mostly thiols.8–12 This yields a hypervalent structure as the sulfur atom of the deprotonated thiol-group fills the vacancy and binds to the three surrounding Mo atoms and the molecular rest. Recently, other protocols for covalent functionalization via carbon–sulfur-bonding were also developed.13–15
The reactivity of sulfur vacancies in MoS2 has been long known and exploited to catalyze hydrodesulfurization,16 and dissociation of the C–S bond at sulfur vacancies has been shown for different alkanethiols.12,17,18 Elimination of defects is crucial to improve optical and transport properties of TMDCs. This has been achieved by treatment with acids19,20 and thiol-containing molecules. The decomposition of thiol derivatives can be triggered by electrical stimulation18 and thermal annealing13,21,22 for the purpose of filling and repairing surface defects. However, theoretical investigations controversially debate the stability of the C–S bond.23,24
Amino acids have been shown to induce simultaneous exfoliation and covalent functionalization of 2H-MoS2. XPS measurements and density functional theory (DFT) calculations suggest that the –NH groups bind at S-vacancies.25,26
Covalent functionalization using light-switchable molecules provides, for instance, the opportunity to interactively and reversibly alter the surface's electrical and optical properties. Azobenzene (AB) derivatives have been widely studied and applied in photoresponsive devices exploiting their light-induced isomerization accompanied by a pronounced change in molecular properties such as length or dipole moment.27,28 Photo-tunable doping with proximal azobenzene derivatives alters the photoluminescence properties of monolayer MoS2.29
In this work, ab initio calculations are performed to investigate the potential of nitrogen incorporation for defect-free functionalization of MoS2. DFT binding energies are calculated to analyze the stability of the functionalized monolayer. Band structures and UV-vis absorption spectra based on the GW/BSE approach within the LDA+GdW approximation30,31 reveal the electronic and optical properties.
2 Computational details
2.1 Geometry optimizations
Geometry optimizations used an in-house modified version of CPMD 3.15.132 using a plane-wave basis with 70 Ry cutoff energy, the PBE density functional33 and normconserving Goedecker–Teter–Hutter pseudopotentials.34–36 van der Waals interactions were included by employing D3 dispersion correction with Becke–Johnson damping (BJ).20,37–39 The 2D geometries in this work are calculated using hexagonal periodic boundary conditions with a 29 Å lattice constant vertical to the surface. The experimental value40 of 3.16 Å was used for the MoS2 lattice constant. The Brillouin zone was sampled by a Monkhorst–Pack mesh41 of 9 × 9 × 1 k-points and its equivalent for larger supercells. For example, for the 3 × 3 MoS2 supercell a 3 × 3 × 1 k-grid was used. Geometry optimizations were considered converged when all ionic forces were below 5 × 10−4 a.u. For potential energy bond scans, harmonic restraint potentials with a force constant of 3 a.u. were added to enforce a given bond length. Restrained geometry optimizations are carried out at the Γ-point using a 5 × 5 MoS2 supercell, which is large enough to neglect interactions between molecules in neighboring unit cells. For large supercells, the energy discrepancy due to coarse k-sampling is small, especially for the energy differences calculated in this work.2.2 GdW/BSE calculations
The DFT(LDA) eigenvalues and eigenvectors needed for the LDA+GdW calculations30,31 were calculated using a basis of localized Gaussian orbitals (for detailed information see ESI†). Spin–orbit interaction was taken into account via normconserving and separable pseudopotentials.42–44 All band structure calculations employed a 3 × 3 MoS2 supercell, i.e. a 9.48 Å × 9.48 Å × 29 Å cell. Quasiparticle energy calculations used a 6 × 6 × 1 k-grid in the first Brillouin zone, which corresponds to a 18 × 18 × 1 k-grid for a 1 × 1 MoS2 unit cell, and an energy cutoff of the auxiliary plane wave basis of 2.5 Ry. The Bethe–Salpeter equation (BSE) was solved for four valence and six conduction bands and its equivalent for larger supercells. The exchange part of the electron–hole interaction kernel is calculated using a Gaussian basis set to handle the strongly localized molecular orbitals efficiently.2.3 TDDFT calculations
For time-dependent DFT (TDDFT) calculations, the CP2K 6.1 program package45 was utilized, which employs a mixed Gaussian and plane-wave basis set. A TZVP (DZVP-SR for Mo) basis set46 and a plane-wave cutoff of 450 Ry were chosen together with the PBE functional. Optical spectra were computed via the linear-response (LR) TDDFT formalism in the Tamm–Dancoff approximation.47 Absorption was calculated for a 6 × 6 × 1 MoS2 supercell at the Γ-point. All virtual orbitals were included in the calculation of the first 1000 excited states. An artificial Lorentzian function of 0.035 eV half-width is applied to the excitation energies to simulate the broadening in experimental measurements.2.4 Visualisation
Molecular structures and orbitals were visualized using ADF 2018.20648 and VMD.493 Results and discussion
3.1 Optimized geometries
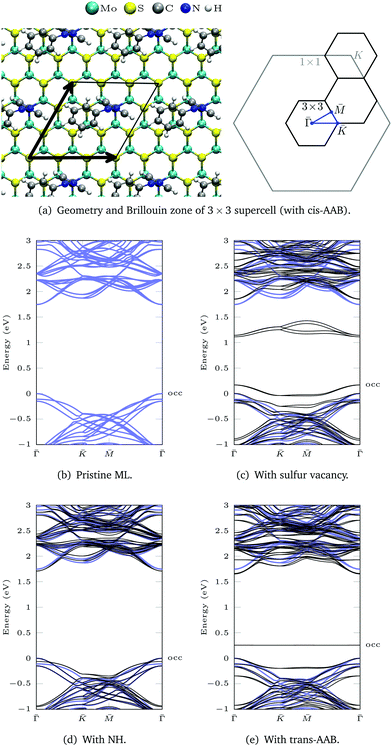
Fig. 1 shows the optimized geometries of the systems we studied and compared. Although we consider low-energy structures in vacuum only, calculations of this type have proven valuable for predictions of measurements under realistic experimental conditions.20,50 Most publications on the functionalization of the basal plane of 2H-MoS2 (Fig. 1a) discuss bonding between a surface sulfur atom and a carbon atom of the attached molecule. Fig. 1d shows how MoS2 can be functionalized with azobenzene in this way. In our work, an alternative linkage via Mo–N–C is studied, where a sulfur vacancy (Fig. 1b) is filled with a nitrogen atom, which binds not only to the three surrounding molybdenum atoms but additionally needs another single bond to be saturated. Saturation can be achieved with hydrogen (Fig. 1c), in the simplest case, or other molecules such as azobenzene (Fig. 1e and f).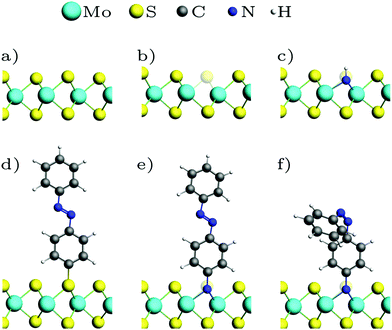 | ||
| Fig. 1 Optimized geometries: (a) MoS2 ML, (b) with sulfur vacancy, (c) with NH, (d) with trans-azobenzene (AB), (e) with trans-aminoazobenzene (AAB), (f) with cis-AAB in the vacancy. Note that the systems are fully periodic, for a top view see e.g.Fig. 3a. | ||
In a pristine MoS2 monolayer, the calculated Mo–S distance is 2.40 Å, which is in good agreement with experimentally measured value of 2.42 Å.40 Attaching azobenzene to a sulfur atom leaves the position of Mo and S atoms almost unchanged. The C–S bond length is 1.81 Å. NH (Fig. 1c) binds to the three neighboring Mo in equal distances of 2.10 Å in a vertical orientation to the basal plane. Replacing the hydrogen atom with azobenzene (Fig. 1e) slightly breaks the threefold symmetry, the N–Mo distances being 2.17 Å, 2.19 Å and 2.19 Å. The N–C bond is again oriented vertically, with a bond length of 1.46 Å, which is significantly larger than the 1.39 Å in the amino group of isolated aminoazobenzene (AAB), and almost as long as the C–N bond in methylamine with 1.48 Å, for example.
3.2 Binding energies
The binding energy for amino-containing molecules is calculated as follows:| Eb = −EML(vac) − Emol + EML+mol + EH2 | (1) |
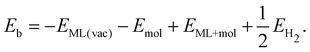 | (2) |
| Molecule | Binding type | E b (eV) |
|---|---|---|
| Methanethiol | C–S | −1.57 |
| p-Thioazobenzene | C–S | −1.46 |
| p-Hydroxyazobenzene | C–O | −0.24 |
| Ammonia | Mo–N | −1.73 |
| Methylamine | Mo–N | −2.03 |
| p-Aminoazobenzene | Mo–N | −1.13 |
| Glycine | Mo–N | −1.12 |
Breaking the C–S bond in hypervalent functionalized systems gives pristine ML. The reaction energy for the repair of the sulfur vacancy can be calculated as
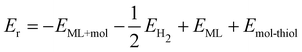 | (3) |
Furthermore, we can probe the stability of the adsorbate with respect to rupture of the C–X bond, where X = (N, S, O) is the atom filling the sulfur vacancy, by potential hypersurface scans. For azobenzene bound via N, the energy rises steeply with increasing N–C distance, with the asymptotic limit being around 3 eV (Fig. 2). In contrast, hypervalent binding via sulfur or oxygen gives much flatter bond scans with maximum values of approximately 0.5 eV, i.e. thermodynamically accessible energy, which has been confirmed experimentally during thermal annealing.13,21,22 Thus, functionalization via N results in much higher stability than functionalization via O or S. The main difference between bonding via the chalcogens or nitrogen is that, in the former case, there is an odd number of electrons which gives pristine ML and an azobenzene radical after bond breaking. For nitrogen bonding, which is described by an even number of electrons, removing the molecule results in two dangling bonds – both at the nitrogen, which is left within the ML, and at the molecular rest.
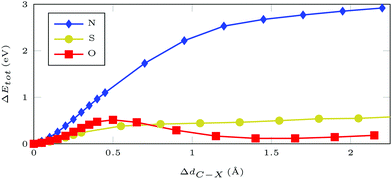 | ||
| Fig. 2 Total DFT energy differences for a 5 × 5 MoS2 supercell with AB attached at an atom of type X = (N/S/O) filling a sulfur vacancy. Geometries were optimized with restrained C–X distance. | ||
3.3 Electronic band structure
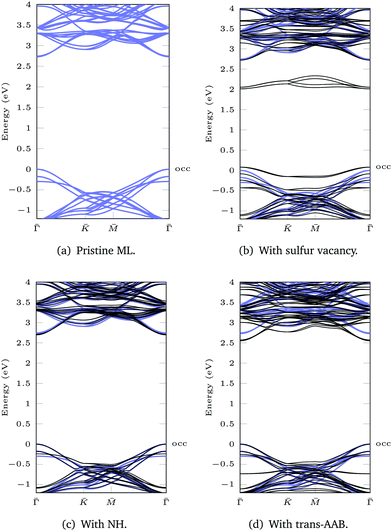
The DFT(LDA) band structures corresponding to the different functionalization types (Fig. 1) are calculated using a 3 × 3 MoS2 ML supercell and the respective 2D surface Brillouin zone (Fig. 3a). In the LDA band structure of the pristine ML (Fig. 3b), there is a direct gap of 1.74 eV at![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) , which contains (due to backfolding) the
, which contains (due to backfolding) the ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) -point of the 1 × 1 unit cell. DFT(LDA) is known to underestimate the band gap, but as the dispersions are reproduced well in most cases, the DFT calculations can be used as a starting point for more accurate methods based on many-body perturbation theory.
-point of the 1 × 1 unit cell. DFT(LDA) is known to underestimate the band gap, but as the dispersions are reproduced well in most cases, the DFT calculations can be used as a starting point for more accurate methods based on many-body perturbation theory.
Sulfur vacancies are the predominant type of defect in MoS2.5–7 If a sulfur atom is missing, defect states appear within the band gap (Fig. 3c) that are located at the sulfur vacancies.50 In our calculation these states are not completely flat, which is due to interactions between neighboring vacancies. For one vacancy in each 3 × 3 supercell, the distance between neighboring defect sites is only 9.48 Å.
The dangling bonds at a sulfur vacancy can be saturated by inserting imino (NH) in the vacancy. Compared to the defective ML, the defect states disappear and the band structure deviates only slightly from pristine ML in the shown energy range (Fig. 3d). The type of bonding is similar for atomic nitrogen (compare geometries in Fig. S15 and charge density differences in Fig. S16, ESI†). Yet, in the deprotonated case there is a defect band above the ML valence bands in our DFT calculation (Fig. S17, ESI†), which can be exploited for p-type doping.6,51,52 In contrast, NH3 only weakly bonds to the surface53 which is reflected by large Mo–N bond lengths (Fig. S15, ESI†) and multiple defect states within the MoS2 band gap (Fig. S17, ESI†).
For AAB bound via Mo–N, the gap between the ML bands is reduced by 0.09 eV compared to the pristine ML (Fig. 3e). The main difference between MoS2 functionalized with trans-AAB and cis-AAB can be found in the molecular orbitals (see the flat bands in Fig. 3e and Fig. S20, ESI†). In Fig. 4a, the band structures for the isolated molecules are compared with the functionalized ML. Orange points indicate the result of a Mulliken analysis,54 their size reflecting to what extend the wave functions are located at the molecule. The valence band maximum (VBM) corresponds to the highest occupied molecular orbital (HOMO) of AAB which is mostly formed by electrons at the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond (Fig. S18, ESI†). The other molecular orbitals can also be identified in the band structure of the functionalized system.
N double bond (Fig. S18, ESI†). The other molecular orbitals can also be identified in the band structure of the functionalized system.
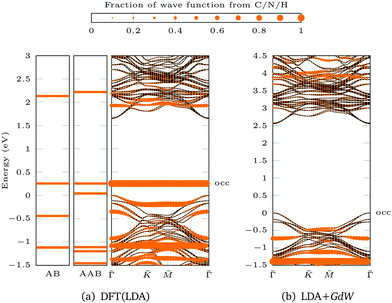 | ||
| Fig. 4 Population analysis for trans-AAB-ML bandstructures in Fig. 3e and 5d: the size of the orange points is proportional to the part of the wave function stemming from C/N/H atoms. The valence band maximum of the ML is set to 0 eV. The highest occupied (occ) band of the functionalized system is labeled. (a) LDA band structures of AB (left), AAB (center) and trans-AAB-ML (right). (b) LDA+GdW band structures of trans-AAB-ML. Note the different energy scales. | ||
Attaching AB to the ML via C–S bond introduces states within the band gap of the ML (Fig. S13, ESI†). These states are located at the C–S bond and the Mo atoms below as presented in the density isosurface plotted in Fig. S14 (ESI†). Detailed analysis of the band structure and calculated absorption of C–S functionalized MoS2 can be found in the literature.13,55–57 In this work, we focus on the electronic structure of MoS2 functionalized by insertion of nitrogen into a sulfur vacancy.
Based on the DFT(LDA) calculations the GW method in the LDA+GdW approximation is employed to calculate the so-called quasiparticle corrections. In LDA+GdW calculations the HOMO–LUMO gap of isolated molecules increases. In the case of trans-AAB from 1.9 eV to 5.9 eV. In all calculations, the LDA+GdW Hamiltonian was diagonalized, therefore the final quasiparticle wave functions are linear combinations of the DFT wave functions. This is important as the molecular and ML orbitals are hybridized and the quasiparticle corrections are different for molecular and MoS2 states. The hybridization hinders the determination of the energy difference between HOMO and lowest unoccupied molecular orbital (LUMO) for the trans-AAB-ML system (Fig. 4b). The HOMO is roughly 0.5 eV lower in energy than the ML VBM, and the LUMO is at around 3 eV. Hence, the HOMO–LUMO gap is smaller than the gap of the isolated molecule, which is due to the screening of the ML. The molecule itself increases the polarizability of the environment surrounding the ML and hence the band gap is reduced by 0.2 eV compared to the pristine ML (Fig. 5a and d). The gap is 0.03 eV lower if the bound AAB changes from trans to cis configuration (Fig. S21, ESI†). For MoS2, the band dispersion is reproduced reasonably well in LDA, but the band gap of the ML increases from 1.74 eV in LDA to 2.73 eV in LDA+GdW.‡ This is roughly four times less pronounced compared to the AAB states, because in the ML additional charges can be screened more efficiently by polarization of the surrounding electron density.
For the ML with vacancy (Fig. 5b) and NH-functionalization (Fig. 5c) a similar band gap widening can be noted.
3.4 Optical properties
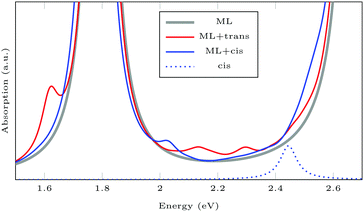
Fig. 6 shows the absorption spectra calculated using GdW/BSE. The pristine MoS2 ML has two characteristic spin–orbit-split absorption peaks, A and B, at 2.13 eV and 2.29 eV. If one sulfur atom is missing, there are multiple peaks at lower energies. For larger supercells, i.e. larger distances between two vacancies, these excitations converge to one absorption peak at approximately 1.8 eV.58 They can be attributed to transitions into the defect states within the band gap. Filling the vacancy with NH repairs the defects and low-lying transitions disappear. The excitations are slightly broadened and shifted by approximately −0.03 eV (8 nm) compared to pristine ML. If the ML is functionalized with AAB, all peaks are broadened. The energy shift for the A exciton is −0.04 eV compared to pristine MoS2. In the shown energy range there is only one transition originating from the molecular HOMO. It is located at 2.00 eV with very small oscillator strength, which can be identified as the HOMO–LUMO excitation of (amino-)azobenzene. The excitation energy is significantly smaller than the experimental value, which is roughly 2.7 eV.59 The difference is mostly due to the small unit cell. For gas-phase AAB in a 3 × 3 supercell (without Mo and S atoms), the first excited state of the molecule is at 2.14 eV. For cis-AAB binding to the surface decreases the energy of the HOMO–LUMO excitation by 0.21 eV. A thorough investigation of this effect requires a larger supercell, but it is computationally extremely demanding to study the intramolecular transitions for this system, as a vast number of MoS2-type bands have to be included to take into account a sufficient number of AAB-type bands. This problem is exacerbated for larger supercells.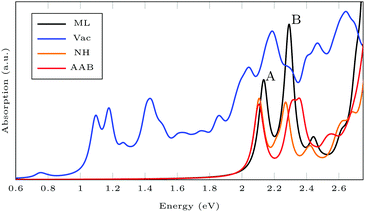 | ||
| Fig. 6 Exciton absorption spectrum (GdW/BSE) of pristine MoS2 monolayer (ML), with sulfur vacancy (Vac), NH and trans-aminoazobenzene (AAB) in a vacancy. | ||
Isomerization in AB derivatives proceeds via excited electronic states, therefore these states have to be analyzed in detail in order to probe the switchability of AB derivatives attached to MoS2. Since they are based on two-point functions only, LR-TDDFT calculations in the adiabatic approximation are less costly and analytical nuclear forces are widely available. TDDFT with GGA functionals is known to underestimate excitation energies in semiconducting solids,60 but here, we focus on the influence of the covalently bound surface on the intramolecular excitations. Spin–orbit coupling (SOC) is neglected to further reduce the computational effort. The splitting into A and B exciton is due to SOC as one can see when comparing the BSE results with and without SOC (see Fig. 7). The energy for the first excitation(s) is too high in BSE, whereas it is too low in TDDFT, compared to the experimental value of about 1.97 eV.61 In both BSE and TDDFT, this excitation is a transition from the valence band maximum with Mo-dxy/dx2−y2 type to the conduction band minimum with Mo-dz2 type.
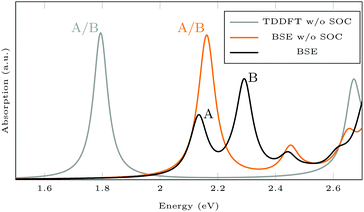 | ||
| Fig. 7 Absorption spectra calculated using GdW/BSE and TDDFT. The splitting into A and B exciton is due to spin–orbit coupling (SOC). | ||
For isolated AAB, the lowest TDDFT excitations are at 2.33 eV and 2.45 eV for trans and cis, respectively. The AAB-functionalized ML shows additional peaks compared to pristine MoS2 (see Fig. 8). For ML + trans-AAB the intramolecular HOMO–LUMO transition can be identified at 2.33 eV. The absorption spectrum is very similar to the pristine ML, but there is an additional peak at 1.62 eV, which is an excitation from the molecular HOMO−1 to the lowest MoS2 state. This excitation energy from molecule to ML is likely to be underestimated as TDDFT with GGA functional PBE struggles with charge transfer excitations.§ For ML + cis-AAB the HOMO–LUMO excitation energy cannot be determined exactly as hybridization of the LUMO with MoS2 conduction bands splits the excitation into many transitions with different energies. The small peak at 2.0 eV is a charge transfer excitation from molecule to ML.
The analysis of the TDDFT spectra reveals two challenges for ab initio simulations of the first excited intramolecular excitation: (1) hybridization makes it difficult to identify the excitation of interest and treat it separately. (2) Errors in the ordering of excited potential energy surfaces falsifies excited states molecular dynamics when using GGA functionals.
4 Conclusions
We have demonstrated defect-free functionalization of MoS2via incorporation of nitrogen atoms at sulfur vacancies. Increased stability of N–Mo bound azobenzene as opposed to common C–S bonding is demonstrated by DFT calculations. Defect states within the band gap of monolayer MoS2 are removed by our functionalization approach. This is verified by LDA+GdW band structure calculations. Photoabsorption of functionalized MoS2 resembles that of pristine ML as shown by GdW/BSE. Hence, our work shows that MoS2 can be functionalized while keeping its remarkable properties. Stable attachment of azobenzene derivatives is the key to photoresponsive 2D materials with exciting optical properties.In this work, we solely focus on point defects. For other types of defects,62–66 restoring the electronic band structure of pristine MoS2 by functionalization is more challenging and will be the subject of future studies.
As far as the photoswitchability of covalently attached AAB on MoS2 is concerned, theoretical treatment within LR-TDDFT faces the problem that, due to mixing between molecular and substrate orbitals, it is impossible to single out one particular excited state in which photoisomerization proceeds. An investigation of switching efficiency would thus require a nonadiabatic dynamical treatment taking into account a large manifold of excited states. Due to the charge transfer character of many relevant states, a hybrid functional (possibly range-separated) would have to be used to ensure the correct state ordering. All in all, this would, however, entail an enormous computational cost.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. O. and J. A. P. gratefully acknowledge the Graduate School of Molecules and Interfaces WWU Münster for financial support. T. D. acknowledges financial support from the German Research Foundation (DFG Projects No. DE 2749/2-1). The authors also thank T. Stiehm, R. Schmidt, R. Schneider, J. Kern, and S. Michaelis de Vasconcellos for fruitful discussions. The computations were carried out using resources provided by the ZIV of the University of Münster (PALMA II HPC cluster).Notes and references
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Nano Lett., 2010, 10, 1271 CrossRef CAS PubMed.
- K. F. Mak and J. Shan, Nat. Photonics, 2016, 10, 216 CrossRef CAS.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699 CrossRef CAS PubMed.
- J. Hong, Z. Hu, M. Probert, K. Li, D. Lv, X. Yang, L. Gu, N. Mao, Q. Feng and L. Xie, et al. , Nat. Commun., 2015, 6, 6293 CrossRef CAS PubMed.
- H.-P. Komsa, J. Kotakoski, S. Kurasch, O. Lehtinen, U. Kaiser and A. V. Krasheninnikov, Phys. Rev. Lett., 2012, 109, 035503 CrossRef PubMed.
- W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. M. Ajayan, B. I. Yakobson and J.-C. Idrobo, Nano Lett., 2013, 13, 2615 CrossRef CAS PubMed.
- S. S. Chou, M. De, J. Kim, S. Byun, C. Dykstra, J. Yu, J. Huang and V. P. Dravid, J. Am. Chem. Soc., 2013, 135, 4584 CrossRef CAS PubMed.
- D. M. Sim, M. Kim, S. Yim, M.-J. Choi, J. Choi, S. Yoo and Y. S. Jung, ACS Nano, 2015, 9, 12115 CrossRef CAS PubMed.
- K. Cho, M. Min, T.-Y. Kim, H. Jeong, J. Pak, J.-K. Kim, J. Jang, S. J. Yun, Y. H. Lee and W.-K. Hong, et al. , ACS Nano, 2015, 9, 8044 CrossRef CAS PubMed.
- S. Bertolazzi, S. Bonacchi, G. Nan, A. Pershin, D. Beljonne and P. Samor, Adv. Mater., 2017, 29, 1606760 CrossRef PubMed.
- S. Bertolazzi, M. Gobbi, Y. Zhao, C. Backes and P. Samor, Chem. Soc. Rev., 2018, 47, 6845 RSC.
- X. S. Chu, A. Yousaf, D. O. Li, A. A. Tang, A. Debnath, D. Ma, A. A. Green, E. J. Santos and Q. H. Wang, Chem. Mater., 2018, 30, 2112 CrossRef CAS.
- M. Vera-Hidalgo, E. Giovanelli, C. Navo and E. M. Pérez, J. Am. Chem. Soc., 2018, 141, 3767 CrossRef PubMed.
- R. Quirós-Ovies, M. Vázquez Sulleiro, M. Vera-Hidalgo, J. Prieto, I. J. Gómez, V. Sebastián, J. Santamara and E. M. Pérez, Chem. – Eur. J., 2020, 26, 6629 CrossRef PubMed.
- A. Aoshima and H. Wise, J. Catal., 1974, 34, 145 CrossRef CAS.
- S. L. Peterson and K. H. Schulz, Langmuir, 1996, 12, 941 CrossRef CAS.
- M. Makarova, Y. Okawa and M. Aono, J. Phys. Chem. C, 2012, 116, 22411 CrossRef CAS.
- M. Amani, D.-H. Lien, D. Kiriya, J. Xiao, A. Azcatl, J. Noh, S. R. Madhvapathy, R. Addou, K. Santosh and M. Dubey, et al. , Science, 2015, 350, 1065 CrossRef CAS PubMed.
- C. Schwermann, T. Stiehm, P. Tonndorf, R. Schneider, R. Schmidt, J. Kern, S. M. de Vasconcellos, R. Bratschitsch and N. Doltsinis, Phys. Chem. Chem. Phys., 2018, 20, 16918 RSC.
- Z. Yu, Y. Pan, Y. Shen, Z. Wang, Z.-Y. Ong, T. Xu, R. Xin, L. Pan, B. Wang and L. Sun, et al. , Nat. Commun., 2014, 5, 5290 CrossRef CAS PubMed.
- Y. Park, S. Shin, Y. An, J.-G. Ahn, G. Shin, C. Ahn, J. Bang, J. Baik, Y. Kim and J. Jung, et al. , ACS Appl. Mater. Interfaces, 2020, 12, 40870 CrossRef CAS PubMed.
- Q. Li, Y. Zhao, C. Ling, S. Yuan, Q. Chen and J. Wang, Angew. Chem., Int. Ed., 2017, 56, 10501 CrossRef CAS PubMed.
- A. Förster, S. Gemming, G. Seifert and D. Tománek, ACS Nano, 2017, 11, 9989 CrossRef PubMed.
- E. Satheeshkumar, A. Bandyopadhyay, M. Sreedhara, S. K. Pati, C. Rao and M. Yoshimura, ChemNanoMat, 2017, 3, 172 CrossRef CAS.
- S. Kumari, A. Chouhan, O. P. Sharma, S. Kuriakose, S. A. Tawfik, M. J. Spencer, S. Walia, H. Sugimura and O. P. Khatri, ACS Appl. Mater. Interfaces, 2020, 12, 30720 CrossRef CAS PubMed.
- Molecular Switches, ed. B. L. Feringa and R. W. Browne, Wiley-VCH, Weinheim, 2011 Search PubMed.
- Smart Light-Responsive Materials: Azobenzene-Containing Polymers and Liquid Crystals, ed. Y. Zhao and T. Ikeda, Wiley-VCH, Weinheim, 2009 Search PubMed.
- J. Li, J. Wierzbowski, Ö. Ceylan, J. Klein, F. Nisic, T. L. Anh, F. Meggendorfer, C.-A. Palma, C. Dragonetti and J. V. Barth, et al. , Appl. Phys. Lett., 2014, 105, 241116 CrossRef.
- M. Rohlfing, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205127 CrossRef.
- M. Drüppel, T. Deilmann, J. Noky, P. Marauhn, P. Krüger and M. Rohlfing, Phys. Rev. B, 2018, 98, 155433 CrossRef.
- CPMD, http://www.cpmd.org/, Copyright IBM Corp 1990–2015, Copyright MPI für Festkörperforschung Stuttgart 1997–2001.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- D. G. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197 CrossRef CAS PubMed.
- T. Böker, R. Severin, A. Müller, C. Janowitz, R. Manzke, D. Voß, P. Krüger, A. Mazur and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235305 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- L. Kleinman and D. Bylander, Phys. Rev. Lett., 1982, 48, 1425 CrossRef CAS.
- D. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 2980 CrossRef PubMed.
- L. Hemstreet, C. Fong and J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4238 CrossRef PubMed.
- CP2K version 6.1, the CP2K developers group, 2018, CP2K is freely available from https://www.cp2k.org/.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- M. E. Casida, THEOCHEM, 2009, 914, 3 CrossRef CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- S. W. Han, G.-B. Cha, K. Kim and S. C. Hong, Phys. Chem. Chem. Phys., 2019, 21, 15302 RSC.
- A. Azcatl, X. Qin, A. Prakash, C. Zhang, L. Cheng, Q. Wang, N. Lu, M. J. Kim, J. Kim and K. Cho, et al. , Nano Lett., 2016, 16, 5437 CrossRef CAS PubMed.
- C. Hu, C. Yuan, A. Hong, M. Guo, T. Yu and X. Luo, Appl. Phys. Lett., 2018, 113, 041602 CrossRef.
- H. Li, M. Huang and G. Cao, Phys. Chem. Chem. Phys., 2016, 18, 15110 RSC.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- L. Gao, Z.-D. Yang and G. Zhang, Chem. Phys., 2017, 490, 29 CrossRef CAS.
- M. Palummo, A. D'Auria, J. Grossman and G. Cicero, J. Phys.: Condens. Matter, 2019, 31, 235701 CrossRef CAS PubMed.
- L. O. Jones, M. A. Mosquera, M. A. Ratner and G. C. Schatz, ACS Appl. Mater. Interfaces, 2020, 12, 4607 CrossRef CAS PubMed.
- M. Drüppel, PhD thesis, University of Münster, 2017.
- Y. Hirose, H. Yui and T. Sawada, J. Phys. Chem. A, 2002, 106, 3067 CrossRef CAS.
- N. T. Maitra, J. Chem. Phys., 2016, 144, 220901 CrossRef PubMed.
- A. Arora, N. K. Wessling, T. Deilmann, T. Reichenauer, P. Steeger, P. Kossacki, M. Potemski, S. M. de Vasconcellos, M. Rohlfing and R. Bratschitsch, Phys. Rev. B, 2020, 101, 241413 CrossRef CAS.
- E. Mitterreiter, et al. , Nat. Commun., 2021, 12, 3822 CrossRef CAS PubMed.
- F. Bertoldo, et al. , ACS Nano, 2021, 15, 2858 CrossRef CAS PubMed.
- W. Liao, K. Xie, L. Liu, X. Wang, Y. Luo, S. Liang, F. Liu and L. Jiang, J. Energy Chem., 2021, 62, 359 CrossRef.
- J.-A. Ke, S. Garaj and S. Gradečak, ACS Appl. Mater. Interfaces, 2019, 11, 26228 CrossRef CAS PubMed.
- J. Xie, et al. , Adv. Mater., 2013, 85, 5807 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational details, graphical representation of binding energies, comparison of N/NH/NH3 functionalization, MoS2 + AB and MoS2 + cis-AAB band structures and absorption spectrum. See DOI: 10.1039/d1cp02313f |
| ‡ As polarisation effects are included in LDA+GdW more vacuum is needed between the layers to exactly calculate the band gap. The gap is approximately 0.2 eV larger for infinite interlayer distance, i.e. 2.9 eV.31 |
| § Unfortunately, the use of (range-separated) hydrid functionals is computationally prohibitive in this case. |
| This journal is © the Owner Societies 2021 |