Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A machine learning based intramolecular potential for a flexible organic molecule†
Daniel J.
Cole
 *a,
Letif
Mones
*a,
Letif
Mones
 b and
Gábor
Csányi
b and
Gábor
Csányi
 b
b
aSchool of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
bEngineering Laboratory, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK. E-mail: gc121@cam.ac.uk
First published on 13th May 2020
Abstract
Quantum mechanical predictive modelling in chemistry and biology is often hindered by the long time scales and large system sizes required of the computational model. Here, we employ the kernel regression machine learning technique to construct an analytical potential, using the Gaussian Approximation Potential software and framework, that reproduces the quantum mechanical potential energy surface of a small, flexible, drug-like molecule, 3-(benzyloxy)pyridin-2-amine. Challenges linked to the high dimensionality of the configurational space of the molecule are overcome by developing an iterative training protocol and employing a representation that separates short and long range interactions. The analytical model is connected to the MCPRO simulation software, which allows us to perform Monte Carlo simulations of the small molecule bound to two proteins, p38 MAP kinase and leukotriene A4 hydrolase, as well as in water. We demonstrate that our machine learning based intramolecular model is transferable to the condensed phase, and demonstrate that the use of a faithful representation of the quantum mechanical potential energy surface can result in corrections to absolute protein–ligand binding free energies of up to 2 kcal mol−1 in the example studied here.
1 Introduction
The interplay of the intramolecular, or internal, energy of a molecule and the non-bonded energetics that determine its interactions with its environment plays a crucial role in simulations of protein folding,3 crystal structure prediction,4 protein–ligand binding,5 and many more. In particular, oral drugs are typically flexible, containing on average 5.4 rotatable bonds,6 and are therefore capable of populating many free energy minima both in solution and when bound to their target. Computational analysis has revealed that the majority of ligands bind in a conformation within 0.5 kcal mol−1 of a local energy minimum.7 To be successful, docking or any other method used in computer-aided structure-based drug design must be able to accurately predict both the bioactive conformation of the molecule and the free energy change that accompanies its binding from solution.The potential energy surfaces of organic molecules for practical applications are typically modelled using transferable molecular mechanics force fields such as AMBER,8 CHARMM,9 GROMOS10 or OPLS.11 When combined with molecular dynamics (MD) or Monte Carlo (MC) sampling, these force fields may be used to predict, for example, liquid properties of small molecules,12,13 structural propensities of peptides,14,15 and protein–ligand binding free energies,16,17 all with reasonable accuracy. The intramolecular component of the force field is typically modelled by harmonic bond and angle potentials to represent two- and three-body terms, respectively, an anharmonic torsional term to model dihedral rotations, and Coulomb and Lennard-Jones terms to account for interactions between atoms separated by three or more bonds.8,18,19 Details vary between these transferable force fields, but the fixed functional form is common to all. Thus, no matter how carefully the force field is parameterized, accuracy will ultimately be limited by the choice of this functional form.
For the description of intramolecular energetics, quantum mechanics (QM) is seemingly preferable and is frequently used in computational enzymology applications.20 However, the computational cost associated with QM simulations is high, particularly for free energy predictions which require extensive (alchemical and/or conformational) sampling.21 In order to make a calculation tractable, the level of QM theory (basis set and exchange-correlation functional, for example) is often compromised, which again raises questions over the final accuracy.22
Alternatively, one can construct direct fits to the high dimensional QM potential energy surface of the molecule. There is a wide range of methods available for fitting bond, angle and dihedral parameters of the MM force field to QM energies, gradients and Hessian matrices,23–28 and these often include extended functional forms such as cross-terms to account for coupling between internal coordinates.29 However, for larger, more flexible molecules, longer-range atomic interactions beyond the 1–4 interaction are also crucial in determining molecular conformation. For these molecules, a consistent, accurate approach to approximating the QM potential energy surface is key. If shown to be fast enough, such an approach would provide a means to connect QM calculations to long time scales. It would also be amenable to systems requiring accurate descriptions of strong correlation, such as metalloproteins, or molecules in electronic excited states, which are extremely challenging for current MM force fields. Rather than relying on human intuition to decide on the functional form of the potential energy surfaces of these molecules, it is preferable to harness recent advances in machine learning inspired techniques.
There are several neural network and kernel based techniques recently developed for material systems that can predict quantum energies and forces with remarkable accuracy.30–35 Since these potentials need to be trained on only a few thousand (well dispersed) configurations, the underlying quantum mechanical data can be of high accuracy while maintaining affordable computational expense. These techniques have been successfully used to reproduce the atomization energies36–39 and QM potential energy surfaces40–42 of a range of organic molecules. With accurate energies and forces, the opportunity arises to begin to use machine learning based potentials in molecular dynamics simulations of organic molecules.43,44 So far these studies have tended to focus on gas phase dynamics, however a recent study showed that neural-network potentials (within a QM/MM type approach) are capable of predicting the structural conformations of drugs in protein binding pockets, as well as conformational components of binding free energies.45 Interestingly, this study showed that conformational binding energies can be over-estimated by molecular mechanics force fields by several kcal mol−1. But otherwise, relatively little is known about the performance of these machine learning based potentials in the condensed phase, where free energy basins that are unpopulated in the gas phase may emerge.46 Such considerations are especially important for free energy simulations in computer-aided drug design involving molecules with multiple degrees of freedom where accurate sampling of conformational space is required.
In this work, we investigate the feasibility of using machine learning in developing accurate representations of the potential energy surface of a flexible, “drug-like” molecule for potential use in, for example, structure-based lead optimization efforts. We employ the Gaussian Approximation Potential (GAP)47 framework that is based on a sparse Gaussian process regression technique, which is formally equivalent to kernel ridge regression.48,49 GAP uses both QM energy and gradient information and although it was originally developed for material systems, it has been used successfully to describe molecular properties.36,37 Here we use it to create a potential energy surface for 3-(benzyloxy)pyridin-2-amine (3BPA, Fig. 1). Although still somewhat smaller than typical drug-like molecules (molecular weight of 200, three rotatable bonds, and three hydrogen bond donors/acceptors), it represents a challenging test case for machine learning due to its internal flexibility. The high effective dimensionality of the configurational manifold of the molecule requires a relatively large amount of training data extensively sampled from the potential energy surface. To address these challenges, we developed an iterative protocol to gradually improve the reconstructed potential, and applied sparsification techniques to cope with the relatively large amount of training data. Despite its small size, 3BPA has been identified in two separate fragment screens as an efficient ligand for p38 MAP kinase1 and leukotriene A4 hydrolase.2 In the former study, although its binding affinity was found to be greater than 1 mM in an enzyme bioassay, 3BPA has a clearly defined binding mode to the hinge region of the ATP binding site of the kinase (Fig. 1(b)).1 While in the latter, the same compound binds near the bottom of the substrate binding cleft of leukotriene A4 hydrolase with sub-mM affinity (Fig. 1(c)).2 To investigate the binding of 3BPA in these two environments, we have interfaced GAP with the MCPRO software.18 MCPRO is a tool for structure-based lead optimization through the use of free energy perturbation (FEP) theory combined with Monte Carlo sampling of protein–ligand binding modes. It has been used for the successful computationally guided design of inhibitors of targets including HIV-1 reverse transcriptase50 and macrophage migration inhibitory factor,51 and has recently been applied to the fragment-based design of inhibitors of the Aurora A kinase–TPX2 protein–protein interaction.52 As we will show, our interface between GAP and MCPRO allows us to perform Monte Carlo simulations of 3BPA in a range of environments, which allows us to evaluate the completeness of the training and transferability of the intramolecular potential to the condensed phase. Furthermore, we will demonstrate that, unlike QM, the machine learning based potential is fast enough to be used for extensive sampling of the molecule’s potential energy surface, and may be used, for example, to evaluate a correction to the binding free energy that is computed using a molecular mechanics force field.
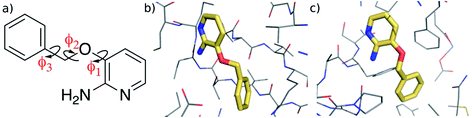 | ||
| Fig. 1 (a) 3-(Benzyloxy)pyridin-2-amine (3BPA). (b) Bound to p38 MAP kinase (PDB: 1W7H).1 (c) Bound to leukotriene A4 hydrolase (PDB: 3FTY).2 | ||
2 Computational methods
2.1 Creating a Gaussian approximation potential
We now briefly outline the Gaussian Approximation Potential (GAP)47 framework, and how we apply it to create a potential energy surface for 3BPA that reproduces quantum mechanical energies to within 1.0 kcal mol−1 root mean square (RMS) error. GAP has been applied to many different materials and compounds,53–63 and has been described in detail elsewhere,64,65 and so we summarize here only the main features. Although the probabilistic and linear regression viewpoints are entirely equivalent, we follow the latter here because it is likely to be more familiar, and we will not be making use of the uncertainty estimates and parameter optimization techniques that follow naturally from the former.The main idea of potential energy surface fits, and the way in which they go beyond conventional force fields, is that the potential energy is explicitly written as a generic function of all atomic degrees of freedom, without making assumptions about separability (e.g. into body ordered terms such as bond and angle potentials). Thus the fit to the potential energy is high dimensional. The basis functions for the fit have to be of a kind that allows systematic convergence to the a priori unknown target potential energy surface, and this has consequences for the attainable accuracy as a function of the amount of input data, for transferability to configurations far away from the distribution from which the training configurations were drawn, as well as for the overall cost of evaluation of the potential energy fit. Typically the high dimensional fits are significantly more expensive to evaluate than the short range terms of a conventional force field, though they are still of course much cheaper than a QM calculation, or the evaluation of the electrostatic potential of a large system that includes a protein and explicit solvent molecules.
Let us denote the conformations of a molecule by the letters  ,
,  , etc., irrespective of how they are represented numerically. The target function, which in our case is the QM potential energy, is written as a linear combination of basis functions:
, etc., irrespective of how they are represented numerically. The target function, which in our case is the QM potential energy, is written as a linear combination of basis functions:
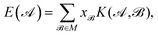 | (1) |
The approximation can be significantly improved by choosing a numerical representation of conformations and a kernel function that respect the basic physical symmetries of the potential energy of a molecule. These are translation, global rotation, and permutation symmetries. The first two apply to any physical system, and we factor them out of the representation by transforming the set of Cartesian coordinates into the vector of all interatomic distances, R = {‖ri − rj‖}i<j. Note how the dimensionality of this representation scales with the square of the number of atoms, n, but this is of little consequence, since all our samples will lie on the 3n dimensional manifold. Alternatively, one could work with the well-known internal coordinates of the z-matrix, and this choice would not increase the dimensionality. However, the potential energy function is clearly a much less regular function of the internal coordinates, because changing some angles would correspond to much more drastic changes in Cartesian coordinates than changing others.
The complete permutation symmetry group of 3BPA has only eight elements, and so we simply sum the kernel function over the action of the group over one of its arguments, resulting in a permutationally invariant kernel,
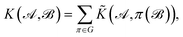 | (2) |
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) , and results in a permutationally invariant potential energy. In the present work, we use a Gaussian base kernel (often called a “squared exponential” kernel to distinguish this choice from Gaussian probability distributions) which, in terms of the interatomic distance representations, is given by:
, and results in a permutationally invariant potential energy. In the present work, we use a Gaussian base kernel (often called a “squared exponential” kernel to distinguish this choice from Gaussian probability distributions) which, in terms of the interatomic distance representations, is given by: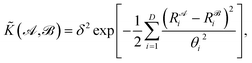 | (3) |
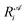 is the ith element of the vector of interatomic distances of conformation
is the ith element of the vector of interatomic distances of conformation 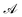 ,
, 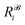 is the corresponding element for conformation
is the corresponding element for conformation 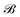 , D is the number of elements in the representation vector, δ is an energy scale parameter and θi are length scale parameters (one for each dimension of the representation vector).
, D is the number of elements in the representation vector, δ is an energy scale parameter and θi are length scale parameters (one for each dimension of the representation vector).
The coefficients in the ansatz (1) are determined by regularized least squares regression using energies and forces computed using quantum chemistry techniques on a diverse set of conformations (see below for further details). Given N conformations with n atoms in each, we have N(3n + 1) pieces of data, leading to the same number of linear equations when (1) is substituted either directly (for the energy) or by taking its derivative with respect to atomic positions (to obtain the forces). Let us collect the M unknown coefficients in (1) into a vector x, concatenate all the available data (energies e and forces f) into the vector y = [e f], and let L be the linear operator connecting this data vector with the energies of the input configurations, so that y = Le. Note that L consists of two blocks; the upper block is just the identity, and the lower block is the negative differential operator. With this, the regularized least squares problem is linear and can be written as:
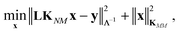 | (4) |
| x* = [KMM + (LKNM)TΛ−1LKNM]−1(LKNM)TΛ−1y, | (5) |
We note that the method of Chmiela et al. for generating potential energy surfaces of small organic molecules66 uses the same kernel ridge regression technique with the following differences: (i) they include only gradient observables (i.e. forces) while GAP reconstructs the surface using both potential energies and forces, (ii) they use the same number of basis functions as there are data, which corresponds to M = 3Nn above, (iii) their basis functions for the potential energy are derivatives of a base kernel (such as a Gaussian) with respect to atomic positions, rather than the base kernel itself, and (iv) they use the inverse of interatomic distances as the arguments of the kernel. We have found no significant advantage to any of these variations, and note that (ii) would result in a larger linear problem, thus significantly increasing the computational cost. We typically find that M ≪ 3Nn is sufficient.
Beyond the basic framework outlined above, we used one additional twist, inspired by the form of empirical organic force fields. There, the energy is typically separated into larger bonded terms (i.e. terms involving up to 1–4 bonded interactions) and smaller non-bonded interactions (the electrostatic and Lennard-Jones interactions computed for all other atom pairs). We adapted this strategy for the multi-dimensional kernel fit by describing the total energy as the sum of two separate terms, both having the same form as (1), with the only difference between them being that for the first, only interatomic distances spanning bond positions 1–4 are included in the configuration vector R, whereas for the second, all interatomic distances are included. The fit for both terms is carried out together with an extra weight factor of 0.1 included for the second term (using the δ parameter), corresponding to the smaller (non-bonded) energy it is describing.
2.2 Generating training data
The goal of the GAP training procedure was to recreate the QM potential energy surface of 3BPA at the MP2/6-311G(2d,p) level of theory. This choice represents a compromise between accuracy and computational expense; one energy and force evaluation requires approximately 1 CPU hour, which makes it feasible to generate thousands of data points. However, accurate characterization of the multidimensional potential energy surface requires extensive sampling, which is not practical with an expensive QM method, so we used the following protocol.Preliminary work indicated that training data extracted from MM molecular dynamics (MD) simulations was not representative of the QM potential energy surface. Instead, we performed several independent MD simulations in the gas phase using MP2 but with a smaller, cheaper basis set (6-31G). The simulations were carried out at temperatures of 300, 600 and 1200 K for 30 ps per trajectory using a Langevin thermostat with a collision frequency of 5 ps−1. The computational cost was approximately 1000 CPU hours for each trajectory. Altogether we collected 3000 independent configurations of 3BPA at 300 K, 1000 configurations at 600 K, and 1000 configurations at 1200 K. The energies and forces were then recomputed at the MP2/6-311G(2d,p) level of theory for each of these 5000 configurations.
The original training set included 3000 configurations (1000 configurations at each of the three temperatures), while for the test we used 2000 configurations collected from the MD simulation performed at 300 K. The representative configurations for eqn (1) were generated as follows. We picked 250 configurations from the original small basis set MD run, and for each of these, we displaced each of the atoms, in turn, by 0.5 Å along each Cartesian direction. This results in M = 27 × 3 × 250 = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 configurations and corresponding basis functions. Note that we do not need QM energies or forces for these configurations, since they do not enter the fit, just serve to generate basis functions. We found that this procedure worked significantly better than just picking all representative configurations randomly from the MD trajectory itself.
250 configurations and corresponding basis functions. Note that we do not need QM energies or forces for these configurations, since they do not enter the fit, just serve to generate basis functions. We found that this procedure worked significantly better than just picking all representative configurations randomly from the MD trajectory itself.
The diagonal elements in Λ were set to be 10−6, and the length scale parameter θi was chosen to be 20 times the range of the data distribution in each dimension of the configuration vector R. The time required to construct the fit is approximately 5 CPU hours on a modern CPU using our current software implementation. The RMS errors of the fitted potential on the 2000 test configurations were 0.57 kcal mol−1 for the energy and 0.95 kcal mol−1 Å−1 for the forces.
We then ran simulations with the fitted potential both in water solution and bound to leukotriene A4 hydrolase (see below). These latter simulations revealed a number of samples with very high energy when evaluated with the QM method. Therefore, 300 such configurations were added to the training set, and the potential was refitted. Such iterative fitting has been used before,53,56,59 and is expected to be an important technique for creating transferable machine learning potentials. The new GAP model had a similar RMS error on the test sets (0.65 kcal mol−1 and 0.95 kcal mol−1 Å−1 for energies and forces, respectively) and was stable in subsequent simulations (see Results section). Both GAP models are available as ESI (XML),† which may be evaluated using the QUIP software67 and LAMMPS.68 In what follows, we refer to the two versions of our machine learned intramolecular potentials as GAP-v1 and GAP-v2.
2.3 Interfacing GAP and MCPRO
GAP is implemented in a modified version of MCPRO (version 2.3) to allow Monte Carlo sampling of 3BPA in water or bound to a protein. The total potential energy (EMM) of a receptor–ligand complex is broken down as follows:| EMM = EL + ER + ERL | (6) |
| EL = (1 − λ)EGAP + λEMM | (7) |
| ΔGGAP = ΔGMM + ΔGA − ΔGB | (8) |
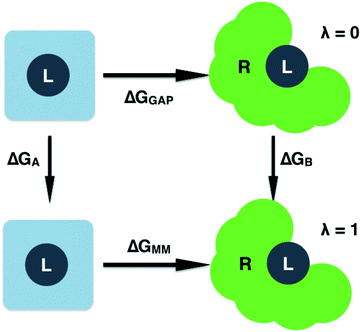 | ||
| Fig. 2 Free energy cycle used to compute the GAP correction to the MM binding free energy. Simulations are performed on the ligand (L) in water and bound to the receptor (R). | ||
3 Results
We begin by examining in more detail the training data used in the construction of the GAP. As shown in Fig. 1, 3BPA has three flexible dihedral angles connecting the two saturated six-membered rings. As such, the relatively large accessible conformational space poses a challenge for machine learning techniques. Fig. 3(a) shows the 2D distribution of the dihedral angles ϕ1 and ϕ2 sampled during the QM dynamics used to train GAP-v1 (3000 configurations). The equivalent 2D distribution for the ϕ2 and ϕ3 dihedral angles is given in Fig. S3.† The use of high temperatures allows a thorough sampling of conformational space in this case. The white circles show the positions of the corresponding dihedral angles in the two crystal structures studied here.1,2 The compound bound to p38 MAP kinase adopts a conformation that is well sampled by our training data (ϕ1 = 334°, ϕ2 = 204°). Interestingly, on the other hand, the conformation in the leukotriene A4 hydrolase crystal structure is in a seemingly disallowed region of conformational space (ϕ1 = 168°, ϕ2 = 116°). Closer inspection reveals that, in this conformation, the –NH2 group on the aminopyridine is in unphysical close contact with the –CH2– linker (Fig. 1(c) and S2†). This is, therefore, likely an artefact of the crystal structure refinement. By visual inspection, we were able to orient 3BPA within the leukotriene A4 hydrolase binding site with a conformation that is more consistent with the QM dynamics (ϕ1 ∼ 270°, ϕ2 ∼ 270°). We therefore used this bound conformation as the starting point for our MC simulations.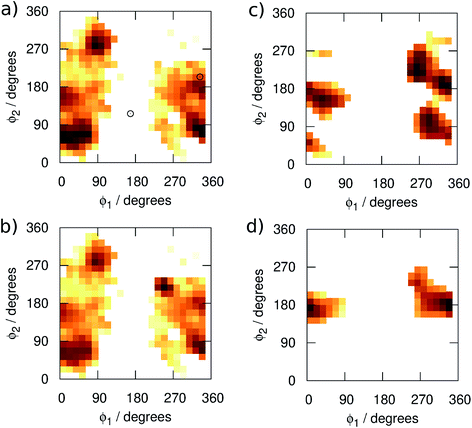 | ||
| Fig. 3 Distribution of the dihedral angles (plotted as log(pϕ1,ϕ2)) sampled in (a) training set 1, (b) training set 2, (c) MC simulations with GAP-v2, and (d) MC simulations with OPLS. | ||
Next, we ran MC simulations of 3BPA in three different environments, using GAP-v1 to describe its intramolecular energetics, and the OPLS/CM1A force field to describe its interactions with the proteins and water. As discussed in the Introduction, 3BPA is capable of occupying a range of potentially environment-dependent conformations, and so it is important to validate not only the gas phase potential energy surface, but also the conformations adopted in the condensed phase. Hence, 300 configurations of 3BPA were saved from each trajectory, and its energetics were recomputed at the MP2/6-311G(2d,p) level of theory in vacuum. Table 1 shows the RMS errors in the GAP for 3BPA in water, and bound to the two proteins. The errors are less than 1 kcal mol−1 in water and bound to p38 MAP kinase, which is consistent with the reported accuracy of the GAP for the test set described in the Computational Methods section. However, despite the reorientation of 3BPA in the binding pocket of leukotriene A4 hydrolase, the RMS error in the GAP is extremely high (19 kcal mol−1). This result is consistent with a lack of training data in the region of conformational space close to ϕ1 = 270°, ϕ2 = 270° (Fig. 3(a)). Therefore, 300 configurations were extracted from MC simulations of 3BPA bound to leukotriene A4 hydrolase and were added to the original training set to produce the dihedral angle distribution shown in Fig. 3(b).
| Water | p38 MAP kinase | Leukotriene A4 hydrolase | |
|---|---|---|---|
| a Excluding one outlying configuration. b Configurations were sampled from the GAP-v2 trajectories, and the MM and QM energies were shifted to align the mean energies. | |||
| GAP-v1 | 0.83 | 0.60 | 19.04 |
| GAP-v2 | 1.42 (0.93a) | 0.95 | 1.13 |
| OPLS/CM1Ab | 11.87 (4.85a) | 3.36 | 3.45 |
MC simulations of the second iteration of the GAP (GAP-v2) were run in the three environments and the errors are summarized in Table 1. Now, the errors are close to 1 kcal mol−1 in all three environments. Fig. 4(a) further reveals a very good correlation between the GAP and QM intramolecular energies, although there is one significant outlier whose phenyl and pyridine rings approach too close (Fig. 4(a), inset). Removal of this configuration from the ensemble of 3BPA in water reduces the error in the GAP still further from 1.42 kcal mol−1 to 0.93 kcal mol−1. Further iterative training of the GAP would prevent sampling of this configuration during the MC simulations. Fig. 3(c) (and Fig. S3(c)†) shows the distribution of dihedral angles sampled during these three MC simulations, and reveals that all areas of conformational space are now well-represented by the training data. Fig. 3(d) (and Fig. S3(d)†) shows the equivalent distribution obtained using the MM force field, which appears to have a stronger preference for a single energy basin (close to ϕ1 = 0°, ϕ2 = 180°), which contrasts with the GAP dynamics and original QM training data. Fig. S4† confirms that duplicate runs with different starting conditions sample similar dihedral distributions, which indicates that conformational differences are associated with differences in the underlying potential energy surfaces rather than sampling limitations.
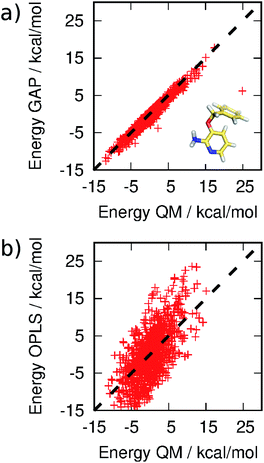 | ||
| Fig. 4 Correlation between (a) GAP and (b) OPLS and QM energies of 3BPA sampled from MC simulations. Not all OPLS MM data are displayed for clarity. The mean energy of each distribution has been shifted to zero. | ||
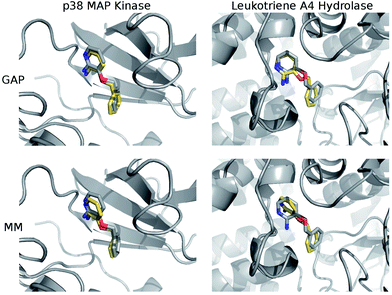
The structures of the protein–ligand complexes sampled during MC simulations are in good agreement with the crystal structures of 3BPA bound to p38 kinase and leukotriene A4 hydrolase. Fig. 5 shows representative structures from the MC simulations overlaid on the original crystal structures (ESI†). Both GAP and MM retain the binding mode indicated by the crystal structure of p38 MAP kinase. As discussed, we have identified a binding mode of 3BPA to leukotriene A4 hydrolase that appears to be consistent with both QM dynamics and the observed electron density map.2 We emphasize that the crystallographically-assigned structure of 3BPA is not physically reasonable due to severe steric clashes (Fig. S2†), although alternative (and multiple) binding modes are possible. The alternative binding mode proposed here is stable throughout the GAP simulation, which is a good indication that GAP is able to capture a range of conformations of this flexible molecule. The alternative binding mode is not stable in the MM simulation, and there is a rotation of the pyridine ring of 3BPA, which breaks the hydrogen bond between the amine group and the backbone of the Pro374 residue. However, in the duplicate MM run (Fig. S4†), the bound conformation is stable for longer before the hydrogen bond is broken, and so longer simulations would be required to establish the equilibrium populations of these binding modes.
It should be emphasized that reproduction of the total QM energy for a flexible molecule of this size (15 heavy atoms) to an accuracy of 1 kcal mol−1 is a significant task. For comparison, we have computed the MM energies of the configurations of 3BPA extracted from the GAP-v2 MC simulations in the three different environments. Table 1 and Fig. 4(b) summarize the accuracy of OPLS/CM1A, which is expected to be typical of standard small molecule force fields, in comparison with the QM data. As expected, the MM force field is significantly less accurate than the machine learning potential. These improvements in intramolecular energetics are expected to carry over into improved thermodynamic quantities, such as binding free energies.
Having validated the ability of GAP to reproduce the underlying QM potential energy surface of 3BPA, we now investigate one possible application of machine learning based intramolecular potentials such as these. Free energy calculations have extremely high (conformational and/or alchemical) sampling requirements and, as such, are inaccessible to accurate QM calculation, relying instead on MM force fields. As discussed in the Computational Methods section, our implementation of GAP in the MCPRO software allows us to estimate corrections to protein–ligand binding free energies using free energy perturbation theory. In particular, the intramolecular energetics of the ligand were smoothly altered from GAP to OPLS/CM1A and the free energy cycle shown in Fig. 2 was employed to compute the correction to the binding free energy, ΔGA − ΔGB (eqn (8)). Note that we have not computed the absolute binding free energies here. Focussing first on the binding of 3BPA to p38 MAP kinase, both GAP-v1 and GAP-v2 give a correction to the MM binding free energy of close to 1 kcal mol−1 (Table 2). That is, we expect the standard MM force field to over-estimate binding, in this case, due to inaccuracies in the treatment of intramolecular energetics of the ligand in water and in the protein binding site. It is reassuring that the two versions of GAP agree on the magnitude of the correction; one would not expect the addition of extra training configurations to substantially affect the energetics of the molecule in either water or the p38 kinase binding site. The correction to the binding of 3BPA to leukotriene A4 hydrolase is larger, which is consistent with the inability of the MM force field to produce a binding mode that is consistent with the experimental electron density map (Fig. 5).
| p38 MAP kinase | Leukotriene A4 hydrolase | |
|---|---|---|
| GAP-v1 | +1.3 | — |
| GAP-v2 | +1.0 | +2.0 |
4 Conclusions
In this paper, we have reported the first construction, training and application of the Gaussian approximation potential to an organic molecule with significant conformational flexibility. The potential is a full dimensional fit of the molecular potential energy surface, with squared-exponential basis functions corresponding to conformations from a MD run. The potential can be systematically improved by adding more training data (energies and gradients) and more basis functions. Iterative training was used, whereby further sampled configurations are collected from a run with a previous version of the potential. It should be emphasized that machine learning based potentials are only as accurate as the underlying QM method used for training.For this study, we have chosen the MP2/6-311G(2d,p) level of QM theory, which provides a reasonable balance between accuracy and computational expense for this molecule. The same training methods are potentially applicable to suitably benchmarked density functional theory (DFT) methods, including extensions to model, for example, strong electronic correlations and electronic excited states if required. In this regard, it has recently been shown that transfer learning can be employed to train a machine learning potential using sparse gold standard coupled-cluster theory at the complete basis set limit,41 and similar extensions would be interesting to study in the context of GAP.
Here, the GAP was trained using just 3300 QM calculations in total. In comparison, computation of the thermodynamic quantities reported in this paper required around 108 evaluations of the ligand intramolecular energetics, which would have been infeasible using even a very inaccurate QM/MM approach. Interestingly, using the FEP set-up described here (ESI†), GAP is only a factor of three times slower than the OPLS force field. There are two reasons for this. First, the speed of machine learning potentials is usually compared with evaluation of force field terms for small molecules, whereas in the condensed phase, long-ranged electrostatic interactions become a significant computational overhead. Second, the ligand is not moved at every Monte Carlo step in the condensed phase (see ESI Methods†), so evaluation of the intramolecular energetics can be skipped when not required. The second version of the GAP is able to reproduce QM energies to a high accuracy of close to 1 kcal mol−1 following training on a gas phase QM MD data set, supplemented by configurations of the ligand taken from the binding site of leukotriene A4 hydrolase. We envisage iterative fitting approaches such as this being a key feature of future machine learning potentials to fill any gaps in the training data, especially if corrections can be automated and made on-the-fly. It is encouraging that substantial improvements could be made to version 2 of the GAP with only 300 extra training configurations and minimal changes to its behavior in the water and p38 kinase environments.
We have chosen to demonstrate the application of the GAP to the computation of corrections to the MM binding free energy of 3BPA with two proteins. The GAP is used to describe the intramolecular energetics of the ligand only. It should be emphasized that there are still inaccuracies in protein dynamics and protein–ligand interactions due to the use of standard MM force fields for these components of the total energy. However, a wide range of parallel work is being devoted to deriving these components from QM data, either within the confines of the MM functional form73,74 or using expanded machine learning data sets.42,44 By making use of free energy perturbation theory, we estimate the corrections to MM binding free energies to be close to 1 and 2 kcal mol−1 for p38 kinase and leukotriene A4 hydrolase, respectively. For comparison, a recent study of 138 experimentally-verified FEP predictions of relative free energies of binding found that the accuracy of the computed results is close to 1 kcal mol−1.16 The computation of absolute binding free energies is expected to be less accurate than relative free energies, nevertheless it appears that substantial accuracy gains are achievable by improving the description of intramolecular energetics. Of course, in computer-aided drug design one is typically interested in the relative binding free energies of a congeneric series of ligands, and similar free energy cycles could be employed also in these applications. We note in this regard that a full evaluation of the accuracy of GAP for correcting protein–ligand binding free energies will require evaluation of a significantly larger validation set for which accurate experimental data are available (only approximate binding affinities of the 3BPA fragment are available1,2). Our goal is first to optimize the balance between accuracy and the size of the training dataset (which affects the computational time required to evaluate and train the potential). This is expected to be even more crucial as we move to drug-like compounds that typically have an even more complex potential energy surface than 3BPA, and thus potentially require more basis functions in the fit. A significant design choice is then whether to (i) construct a new fit for each different candidate molecule, which is expected to be most accurate, but requires new QM calculations for each new molecule, or (ii) construct a fit optimized for several molecules simultaneously, which will still be less general than a transferable organic force field but might not need reparameterizing for a new molecule within the same class. Both routes are worth investigating further.40,42 However, we have demonstrated here the feasibility of constructing a full potential energy surface for a molecule of significant flexibility, shown that it is transferable to condensed phase environments outside the training dataset, and employed it for the first time in binding free energy calculations. Having established the accuracy of this molecule-specific machine learning based potential for a flexible organic molecule, future applications such as computational enzymology, simulation of metals in biology, and construction of ground and excited state potential energy surfaces for photochemistry applications are envisaged.
Conflicts of interest
G. C. is listed as an author of a related patent, US 8843509.Acknowledgements
The authors are grateful to Graeme Robb for helpful discussion. This research made use of the Rocket High Performance Computing service at Newcastle University.References
- M. J. Hartshorn, C. W. Murray, A. Cleasby, M. Frederickson, I. J. Tickle and H. Jhoti, J. Med. Chem., 2005, 48, 403–413 Search PubMed.
- D. R. Davies, B. Mamat, O. T. Magnusson, J. Christensen, M. H. Haraldsson, R. Mishra, B. Pease, E. Hansen, J. Singh, D. Zembower, H. Kim, A. S. Kiselyov, A. B. Burgin, M. E. Gurney and L. J. Stewart, J. Med. Chem., 2009, 52, 4694–4715 Search PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 Search PubMed.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 439–459 Search PubMed.
- D. L. Mobley and M. K. Gilson, Annu. Rev. Biophys., 2017, 46, 531–558 Search PubMed.
- M. Vieth, M. G. Siegel, R. E. Higgs, I. A. Watson, D. H. Robertson, K. A. Savin, G. L. Durst and P. A. Hipskind, J. Med. Chem., 2004, 47, 224–232 Search PubMed.
- K. T. Butler, F. J. Luque and X. Barril, J. Comput. Chem., 2009, 30, 601–610 Search PubMed.
- W. D. Cornell, P. Ciepiak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 Search PubMed.
- B. R. Brooks, C. L. Brooks, A. D. Mackerell, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 Search PubMed.
- B. A. C. Horta, P. F. J. Fuchs, W. F. van Gunsteren and P. H. Hünenberger, J. Chem. Theory Comput., 2011, 7, 1016–1031 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 Search PubMed.
- D. Shivakumar, E. Harder, W. Damm, R. A. Friesner and W. Sherman, J. Chem. Theory Comput., 2012, 8, 2553–2558 Search PubMed.
- L. S. Dodda, J. Z. Vilseck, K. J. Cutrona and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 4273–4282 Search PubMed.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 Search PubMed.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. Mackerell Jr, Nat. Methods, 2017, 14, 71–73 Search PubMed.
- L. Wang, Y. Wu, Y. Deng, B. Kim, L. Pierce, G. Krilov, D. Lupyan, S. Robinson, M. Dahlgren, J. Greenwood, D. L. Romero, C. Masse, J. L. Knight, T. Steinbrecher, T. Beuming, W. Damm, E. Harder, W. Sherman, M. Brewer, R. Wester, M. Murcko, L. Frye, R. Farid, T. Lin, D. L. Mobley, W. L. Jorgensen, B. J. Berne, R. A. Friesner and R. Abel, J. Am. Chem. Soc., 2015, 137, 2695–2703 Search PubMed.
- D. J. Cole, J. Tirado-Rives and W. L. Jorgensen, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 966–971 Search PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Comput. Chem., 2005, 26, 1689–1700 Search PubMed.
- A. D. Mackerell Jr, J. Comput. Chem., 2004, 25, 1584–1604 Search PubMed.
- R. Lonsdale, K. E. Ranaghan and A. J. Mulholland, Chem. Commun., 2010, 46, 2354–2372 Search PubMed.
- J.-L. Fattebert, E. Lau, B. J. Bennion, P. Huang and F. C. Lightstone, J. Chem. Theory Comput., 2015, 11, 5688–5695 Search PubMed.
- D. J. Cole and N. D. M. Hine, J. Phys.: Condens. Matter, 2016, 28, 393001 Search PubMed.
- S. Grimme, J. Chem. Theory Comput., 2014, 10, 4497–4514 Search PubMed.
- V. Barone, I. Cacelli, N. De Mitri, D. Licari, S. Monti and G. Prampolini, Phys. Chem. Chem. Phys., 2013, 15, 3736–3751 Search PubMed.
- A. E. A. Allen, M. C. Payne and D. J. Cole, J. Chem. Theory Comput., 2018, 14, 274–281 Search PubMed.
- L.-P. Wang, K. A. McKiernan, J. Gomes, K. A. Beauchamp, T. Head-Gordon, J. E. Rice, W. C. Swope, T. J. Martínez and V. S. Pande, J. Phys. Chem. B, 2017, 121, 4023–4039 Search PubMed.
- A. T. Hagler, J. Chem. Theory Comput., 2015, 11, 5555–5572 Search PubMed.
- J. T. Horton, A. E. A. Allen, L. Dodda and D. J. Cole, J. Chem. Inf. Model., 2019, 59, 1366–1381 Search PubMed.
- J. Cerezo, G. Prampolini and I. Cacelli, Theor. Chem. Acc., 2018, 137, 80 Search PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 Search PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 Search PubMed.
- A. P. Bartók, M. J. Gillan, F. R. Manby and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 054104 Search PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 Search PubMed.
- T. T. Nguyen, E. Szekely, G. Imbalzano, J. Behler, G. Csányi, M. Ceriotti, A. W. Götz and F. Paesani, J. Chem. Phys., 2018, 148, 241725 Search PubMed.
- A. P. Bartók, J. Kermode, N. Bernstein and G. Csányi, Phys. Rev. X, 2018, 8, 041048 Search PubMed.
- A. P. Bartók, S. De, C. Poelking, N. Bernstein, J. R. Kermode, G. Csányi and M. Ceriotti, Sci. Adv., 2017, 3, e1701816 Search PubMed.
- M. J. Willatt, F. Musil and M. Ceriotti, Phys. Chem. Chem. Phys., 2018, 20, 29661–29668 Search PubMed.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, J. Chem. Phys., 2018, 148, 241722 Search PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 Search PubMed.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903 Search PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 Search PubMed.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 Search PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 Search PubMed.
- S.-L. J. Lahey and C. N. Rowley, Chem. Sci., 2020, 11, 2362–2368 Search PubMed.
- V. T. Lim, C. I. Bayly, L. Fusti-Molnar and D. L. Mobley, J. Chem. Inf. Model., 2019, 59, 1957–1964 Search PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 Search PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning series), MIT Press, Cambridge MA, 2005 Search PubMed.
- D. J. MacKay, Information Theory, Inference and Learning Algorithms, Cambridge University Press, Cambridge, UK, 2003 Search PubMed.
- M. Bollini, R. A. Domaoal, V. V. Thakur, R. Gallardo-Macias, K. A. Spasov, K. S. Anderson and W. L. Jorgensen, J. Med. Chem., 2011, 54, 8582–8591 Search PubMed.
- P. Dziedzic, J. A. Cisneros, M. J. Robertson, A. A. Hare, N. E. Danford, R. H. G. Baxter and W. L. Jorgensen, J. Am. Chem. Soc., 2015, 137, 2996–3003 Search PubMed.
- D. J. Cole, M. Janecek, J. E. Stokes, M. Rossmann, J. C. Faver, G. J. McKenzie, A. R. Venkitaraman, M. Hyvönen, D. R. Spring, D. J. Huggins and W. L. Jorgensen, Chem. Commun., 2017, 53, 9372–9375 Search PubMed.
- V. L. Deringer and G. Csányi, Phys. Rev. B, 2017, 95, 094203 Search PubMed.
- F. C. Mocanu, K. Konstantinou, T. H. Lee, N. Bernstein, V. L. Deringer, G. Csányi and S. R. Elliott, J. Phys. Chem. B, 2018, 122, 8998–9006 Search PubMed.
- F. Maresca, D. Dragoni, G. Csányi, N. Marzari and W. A. Curtin, npj Comput. Mater., 2018, 4, 69 Search PubMed.
- V. L. Deringer, D. M. Proserpio, G. Csányi and C. J. Pickard, Faraday Discuss., 2018, 211, 45–59 Search PubMed.
- V. L. Deringer, N. Bernstein, A. P. Bartók, M. J. Cliffe, R. N. Kerber, L. E. Marbella, C. P. Grey, S. R. Elliott and G. Csányi, J. Phys. Chem. Lett., 2018, 9, 2879–2885 Search PubMed.
- J. Mavračić, F. C. Mocanu, V. L. Deringer, G. Csányi and S. R. Elliott, J. Phys. Chem. Lett., 2018, 9, 2985–2990 Search PubMed.
- V. L. Deringer, C. J. Pickard and G. Csányi, Phys. Rev. Lett., 2018, 120, 156001 Search PubMed.
- S. Fujikake, V. L. Deringer, T. H. Lee, M. Krynski, S. R. Elliott and G. Csányi, J. Chem. Phys., 2018, 148, 241714 Search PubMed.
- P. Rowe, G. Csányi, D. Alfè and A. Michaelides, Phys. Rev. B, 2018, 97, 054303 Search PubMed.
- M. A. Caro, V. L. Deringer, J. Koskinen, T. Laurila and G. Csányi, Phys. Rev. Lett., 2018, 120, 166101 Search PubMed.
- D. Dragoni, T. D. Daff, G. Csányi and N. Marzari, Phys. Rev. Mater., 2018, 2, 013808 Search PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 Search PubMed.
- M. Ceriotti, M. J. Willatt and G. Csányi, in Handbook of Materials Modeling, 2018 Search PubMed.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Sci. Adv., 2017, 3, e1603015 Search PubMed.
- https://github.com/libAtoms/QUIP .
- http://lammps.sandia.gov .
- M. Udier-Blagović, P. Morales De Tirado, S. A. Pearlman and W. L. Jorgensen, J. Comput. Chem., 2004, 25, 1322–1332 Search PubMed.
- L. Wang, B. J. Berne and R. A. Friesner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1937–1942 Search PubMed.
- D. J. Cole, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2014, 10, 565–571 Search PubMed.
- J. Michel, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2009, 113, 13337–13346 Search PubMed.
- D. J. Cole, J. Z. Vilseck, J. Tirado-Rives, M. C. Payne and W. L. Jorgensen, J. Chem. Theory Comput., 2016, 12, 2312–2323 Search PubMed.
- A. E. A. Allen, M. J. Robertson, M. C. Payne and D. J. Cole, ACS Omega, 2019, 4, 14537–14550 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational methods, convergence of free energies, analysis of crystallographic structure of 3BPA in a complex with leukotriene A4 hydrolase, and additional dihedral distribution plots (PDF). QM training data, configurations from MC simulations, representative protein–ligand structures, input files for GAP simulations (ZIP). See DOI: 10.1039/d0fd00028k |
| This journal is © The Royal Society of Chemistry 2020 |