 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural properties, Judd–Ofelt calculations, and near infrared to visible photon up-conversion in Er3+/Yb3+ doped BaTiO3 phosphors under excitation at 1500 nm
M. Vega *ab,
P. Alemanyc,
I. R. Martind and
J. Llanos*b
*ab,
P. Alemanyc,
I. R. Martind and
J. Llanos*b
aDepartamento de Química, Facultad de Ciencias, Universidad de Chile, Casilla 635, Santiago, Chile. E-mail: mvega02@ucn.cl; Tel: +56 55 235 5606
bDepartamento de Química, Universidad Católica del Norte, Avda. Angamos 0610, Antofagasta, Chile. E-mail: jllanos@ucn.cl
cDepartament de Ciència de Materials i Química Física, Institut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona, 08028 Barcelona, Spain
dDepartamento de Física, Instituto de Materiales y Nanotecnología (IMN), Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
First published on 7th February 2017
Abstract
The structural and up-conversion properties of BaTiO3 phosphors doped with Er3+/Yb3+ have been studied. All phases were synthesized using the sol–gel process and characterized by X-ray powder diffraction (PXRD), Raman spectroscopy, optical absorption spectroscopy (Judd–Ofelt theory), and scanning electron microscopy (SEM). Photoluminescence (PL) and time-resolved luminescence measures were employed to monitor the photon upconversion (UC) process in the synthetized phosphors. The results of PXRD show that all synthesized phases crystallize in a perovskite structure, where rare earth ions replace both Ba2+ and Ti4+ cations. Raman spectra confirm the coexistence of both cubic and tetragonal phases. Photon UC was studied under excitation at 1500 nm. The emission spectrum shows a strong emission at 975 nm (4I11/2 → 4I15/2) and a weak emission at 660 nm (4F9/2 → 4I15/2). To unravel the mechanism of photon UC, the dependence of the emission intensity on the pump power of the incident laser was also measured. Furthermore, the decay curves for the 975 nm emission upon excitation at 1500 and 800 nm were also recorded. These results of our study point towards a GSA/ESA type mechanism for photon UC in this material.
1. Introduction
The conversion of sunlight directly into electricity using photovoltaic devices is one of the most attractive options for renewable energy generation, mainly due to the zero emission of polluting gases as well as the permanent resource availability over wide geographical areas. Most of the commercial solar panels use semiconductor materials such as silicon and their efficiency is largely determined by the magnitude of the band gap.1 The overall efficiency is, however, limited by many different factors, including among them spectral losses. Although photons with energies above the band gap are also absorbed, they relax the excess energy as heat (thermalization). On the other hand, photons with energies below the band gap are not absorbed at all and do not contribute to the generation of electricity (transmission).1,2 For this reason, photon conversion arises as an attractive option to reduce spectral losses and increase the efficiency of solar cells.3–6 Among photon conversion phenomena, upconversion (UC) can transform photons from the infrared region of the solar spectrum into photons in the visible region, a process that may increase the efficiency of solar energy harvesting by reducing transmission losses.3–7UC consists in the successive absorption of two or more long wavelength (IR) photons and the subsequent emission of a photon with a shorter wavelength (Vis).8,9 The conversion process requires the participation of a luminescent material having multiple energy levels with the appropriate energy spacing. In this respect, lanthanide ions offer interesting features for UC materials, since the energy levels within the 4f shell range from the near infrared to the ultraviolet part of the electromagnetic spectrum. Among lanthanide ions, Pr3+, Nd3+, Dy3+, Ho3+, Er3+ and Tm3+ have been investigated as activators for upconversion materials in solar cells.10,11
In optical materials doped with one single type of activator ion, one of the important parameters affecting the UC process is the absorption cross section of the rare earth ions. Since many activator ions exhibit low absorption, upconverting materials doped with just one type of activator ion, show relatively low efficiencies.7,8,12 To increase the overall efficiency of the UC process, sensitizer ions with sufficient absorption in the infrared region, are often included as co-dopants. Due to its range of absorption in the near infrared region (900–1100 nm) corresponding to the 2F5/2–2F7/2 transition, Yb3+ is usually used as a sensitizer ion. Furthermore, the 2F5/2–2F7/2 transition for Yb3+ coincides with f–f transitions of several lanthanide ions (Er3+, Tm3+ and Ho3+) used in UC materials, facilitating an efficient energy transfer from the sensitizer Yb3+ ions to the activator ions.10,12
On the other hand, fluorides due to their low phonon energies9,13 have been found to be among the most efficient matrices for UC materials. However, do to toxicity problems and their poor chemical, thermal and mechanical stability, application of fluorides in technological devices has had a limited success.14 In comparison with fluorides, oxides exhibit larger phonon energies, but excellent chemical, thermal and mechanical stabilities. An interesting oxide in this respect is barium titanate (BaTiO3). Its relatively low phonon energy (around 700 cm−1) together with a good insulating behavior and excellent physical and chemical stabilities make it an excellent candidate for the development of new upconversion phosphors.15
In all these systems, Ln3+ ions due to their ionic size are expected to occupy the A2+ sites in the ABO3 lattice and, therefore, the excess positive charge must be compensated. However, it is also possible to replace some of the B4+ ions by Ln3+, keeping the overall charge neutrality. In a previous paper16 we reported on the effects of Eu3+ substitution on the luminescent and magnetic properties of BaTiO3. We observed that at low concentrations the rare earth cations replace the Ti4+ sites, whereas both sites, Ba2+ and Ti4+, are replaced when the concentration of lanthanide cations is increased.
In the present paper, we report on the synthesis of BaTiO3 based phosphor, codoped with Er3+ and Yb3+ via the sol–gel process and the measurement of its IR to visible up-conversion luminescent properties recorded under a 1500 nm excitation.
2. Experimental
2.1. Synthesis
Parent reagents, tetrabutyl titanate (TBT) (97%), erbium nitrate (99.9%), ytterbium nitrate (99.9%), and barium acetate (≥99%) were purchased from Aldrich Chemical Co. and used as received. In a typical procedure, a solution of the stoichiometric amount of Ba(CH3COO)2 in 20 mL of acetic acid was aggregated drop-wise to a solution of 2 mL of TBT diluted using 8 mL of acetylacetone. This mixture was heated to 323 K on a hot plate for 2 h under continuous stirring to form the titania sol. Following this, a solution of the respective amounts of Er(NO3)3·5H2O and Yb(NO3)3·5H2O in 5 mL of deionized water were added to the titania sol and heated to 373 K on a hot plate for 24 h to form a brown powder corresponding to the dry barium erbium–ytterbium titanate. Finally, the product obtained was ground in an agate mortar, placed in an alumina boat and annealed for 2 h at 1273 K in a muffle furnace. All synthetic processes were carried out in air.2.2. Characterization
To check the phase purity, powder X-ray diffraction (PXRD) data were collected using a Bruker D8 Advance diffractometer fitted with a graphite monochromator using CuKα radiation (λ = 1.54057 Å) in the range 10° ≤ 2θ ≤ 60°, operated at 40 kV and 30 mA. Raman spectra were collected using a Renishaw research Ramanscope 1000 spectrometer equipped with a Peltier-cooled CCD detector and with Leica microscopes. An excitation line of 785 nm was used and did not reveal any significant dispersion. SEM images were obtained using a TESCAN VEGA 3 microscope.The optical absorption spectrum was measured by using a Agilent Cary 5000 UV-Vis-NIR spectrophotometer. The samples were compressed in order to prepare pellets with a diameter of 6 mm and a thickness about 0.24 mm.
Upconversion spectra were recorded by exciting samples using a commercial 1500 nm laser (Alcatel 1933 SMG) with a maximum power of 80 mW. The laser was focused on the samples using a lens with a 30 mm focal length. The emitted light was focused on the entrance slit of a CCD spectrograph (Andor Shamrock 303i) using a lens with a focal length of 50 mm.
Luminescence decay curves were obtained by exciting samples using a 10 ns pulsed optical parametric oscillator laser (EKSPLA/NT342/3/UVE). The emission was focused on the entrance of a spectrograph coupled to a photomultiplier (R928 Hamamatsu in the Vis range or 5509-73 Hamamatsu for the NIR range) connected to a digital storage oscilloscope (Tektronix 2430).
3. Results and discussion
3.1. X-Ray diffraction
The powder diffraction patterns contain sharp and well-defined peaks, indicating good crystallinity for all samples. However, minor shifts in the peak positions were observed when the Er3+ and Yb3+ cations were incorporated into the host BaTiO3 matrix. Comparing the d-values with the standard patterns (JCPDS 075-0462),17 all reflections in the diffractograms can be indexed in the cubic perovskite-type structure of BaTiO3, as shown in Fig. 1. As the concentration of dopant ions increases, the crystal structure is maintained. However, at high dopant concentrations (BaTiO3:Er3+ 9%–Yb3+ 10%) the appearance of minority phases related to either precursor materials (BaCO3) or a secondary phase (Er2Ti2O7) can be observed.Incorporation of Ln3+ ions in the structure can occur in both cationic sites (Ba2+ and Ti4+), depending on the ionic radius of the rare earth. Tsur et al.18 have reported that for BaTiO3, Ba2+ ions are being replaced by ions with ionic radii ≥ 0.94 Å, whereas the Ti4+ ions are being replaced by rare earth ions with ionic radius ≤ 0.87 Å. Meanwhile, ions with ionic radii in the range between these values can replace both sites. The ionic radii of Ba2+ and Ti4+ are 1.42 and 0.61 Å, respectively, while those of Er3+ and Yb3+ are 0.89 and 0.87 Å, respectively.19 Therefore, according to Tsur et al. the Er3+ cation should be able to replace both sites indistinctly, while Yb3+ ions would replace only the Ti4+ ones.18
The effect of substitution on the cell volume can be seen in Fig. 2. In general, one can observe that, at low concentrations of both dopants, the cell volume does not show a systematic variation. This is due to random distribution of Er3+ ions in the cationic sites. Moreover, at high concentrations of both dopants a progressive decrease in unit cell volume is observed. Since the Yb3+ ions only replace Ti4+ ions, at high concentrations of Yb3+ these sites are mostly occupied. For this reason, as the Er3+ ion concentration increases in codoped samples, these ions occupy mostly Ba2+ sites, causing a steady decline in the volume of the unit cell. The values of lattice constants and volume of the unit cell for various dopings are summarized in Table 1.
| Sample | a (Å) | V (Å3) |
|---|---|---|
| BaTiO3:Er3+ 1%–Yb3+ 1% | 4.012(9) | 64.57 |
| BaTiO3:Er3+ 1%–Yb3+ 5% | 4.013(8) | 64.62 |
| BaTiO3:Er3+ 1%–Yb3+ 10% | 4.021(7) | 65.02 |
| BaTiO3:Er3+ 5%–Yb3+ 1% | 4.009(12) | 64.47 |
| BaTiO3:Er3+ 5%–Yb3+ 5% | 4.015(5) | 64.72 |
| BaTiO3:Er3+ 5%–Yb3+ 10% | 4.016(9) | 64.78 |
| BaTiO3:Er3+ 9%–Yb3+ 1% | 4.013(1) | 64.62 |
| BaTiO3:Er3+ 9%–Yb3+ 5% | 4.015(9) | 64.73 |
| BaTiO3:Er3+ 9%–Yb3+ 10% | 4.014(4) | 64.67 |
3.2. Raman spectroscopy
While XRD shows only the presence of the cubic phase, it is known that in BaTiO3 cubic and tetragonal perovskite phases may coexist.20 A way of confirming the presence of the tetragonal phase is to visualize small differences in the local symmetry of the crystal lattice. In the cubic phase Ti4+ ions occupy the center of octahedra formed by six neighboring O2− ions, resulting in a local Oh symmetry. In the tetragonal phase, one of these O2− ions is, however, slightly displaced in the direction of the c axis, resulting in a local C4v symmetry, a difference that can be easily monitored by means of Raman spectroscopy.Raman spectra for three different samples of BaTiO3:Er3+/Yb3+ phosphors with varying contents in Er3+/Yb3+ ions are shown in Fig. 3. In them, the five characteristic bands of the BaTiO3 phase, which have been widely reported in literature,20–26 can be observed: a sharp peak at 304 cm−1 [B1, E (TO + LO)] and broad bands at about 181 cm−1 [A1 (TO), E (LO)], 255 cm−1 [A1 (TO2)], 515 cm−1 [A1, E (TO)], and 719 cm−1 [A1, E (LO)]. The sharpness of the peak around 304 cm−1, which is characteristic of the tetragonal BaTiO3 phase, is reduced its and becomes indistinct when the tetragonal phase is not dominant.25 As it can be seen in Fig. 3, this is, however, not the case in our samples, confirming the presence of the tetragonal case. In the recorded spectra, the bands at 255 and 515 cm−1 did not show significant changes, while the intensity of those at 181, 304, and 719 cm−1 increases clearly with the concentration of dopant ions. The band at 718 cm−1, which can be ascribed to the presence of defects in the BaTiO3 lattice is clearly indicative that the formation of the tetragonal phase improves by incorporation of the rare earth cations into the host structure.23 The observed changes in the Raman spectra corroborate thus the coexistence of both, the cubic and tetragonal phases in the analyzed samples.
 | ||
| Fig. 3 Raman spectra for bare BaTiO3 and BaTiO3 doped with different concentrations of Er3+ and Yb3+ ions. | ||
3.3. Scanning electronic microscopy
SEM images for BaTiO3:Er3+ 5%–Yb3+ 1% are shown in Fig. 4. The image on the left was generated by secondary electrons (SE) while that on the right by backscattering electrons (BSE). The formation of agglomerates of micron size without a defined morphology is mainly appreciated in these figures. It is also possible to observe the presence of smaller particles both between grains and on the surface of these. From the BSE image it can be deduced that the sample is homogeneous in composition, which was corroborated by energy dispersive X-ray (EDX) analysis. No large morphological changes between samples as the concentration of the dopant ions is varied were observed. | ||
| Fig. 4 SEM micrography for a BaTiO3:Er3+ 5%–Yb3+ 1% sample. Right: Backscattering and Left: secondary electrons. | ||
3.4. Optical absorption and Judd–Ofelt analysis
Judd–Ofelt (JO) theory to describe the intensity of f–f transitions in rare-earth ions27,28 has become a centerpiece of rare-earth spectroscopy and nowadays it is being considered a fundamental stage in the characterization of luminescent materials.29–31 The great appeal of JO theory is that it allows the prediction oscillator strengths in absorption and luminescence, luminescence branching ratios, and excited-state radiative life-times just by using only three empirical parameters, Ω(λ) (λ = 2, 4, 6), that may be easily determined by fitting calculated intensities to those obtained from an absorption spectrum with known absolute absorption cross sections.31 Unfortunately the application of JO theory to powder samples is not straightforward and for this reason, quantitative studies for micro- or nanostructured optical materials in the literature are still scarce. To solve these inconveniences an alternative method based on the use of relative optical absorption spectra and the subsequent calibration of oscillator strengths through the use of a radiative lifetime has been devised.32–34From the theoretical point of view, the oscillator strength fcal associated to an f–f optical transition is given by
 | (1) |
 | (2) |
Most of the intensities of 4fN–4fN optical transitions have electric-dipole character, although some of them also present magnetic dipole character. For these, Smd can be expressed in terms of the intermediate coupling coefficients associated to the fN[SL]J and fN[S′L′]J′ states as well as the matrix elements of the (L + 2S) operator between these states and Smd can be thus readily calculated, using for instance, the RELIC program31 or using tabulated values calculated for the same transition in other host matrices.
In a standard JO analysis the three intensity parameters Ωλ (λ = 2, 4, 6) are being determined by fitting the experimental oscillator strengths fexp to the calculated ones, fcalc, where the experimental oscillator strengths have been extracted from an optical absorption spectrum using
 | (3) |
Besides general problems related to the determination of oscillator strengths from optical absorption spectra (base line corrections, separation of overlapping bands, determination of the band barycenters, etc.) when trying to apply the standard procedure to powder samples one encounters the problems that both the active ion concentration and sample thickness are not straightforward quantities to be quantified accurately. An alternative procedure,34 that has also been employed to perform a JO analysis using absorbances derived from a diffuse reflection spectrum33 is to follow a two step procedure, performing first a relative JO analysis using the absorption spectrum in terms of optical densities and in a second step, to calibrate the relative JO intensity parameters by using the measured lifetime for a pure radiative transition.
In this procedure, the relative purely electric-dipole line strength
 | (4) |
| Ωλ = CJOΩrelλ | (5) |
The proportionality constant CJO is afterwards determined through the comparison of the calculated and measured lifetimes of a selected predominantly radiative transition. For such a transition, the total transition probability, which is inversely proportional to the lifetime is given by
| AT = Aed + Amd = τrad−1 ≈ τexp−1 | (6) |
 | (7) |
To determine the proportionality constant CJO one has thus to subtract first the magnetic dipole contribution (calculated using data tabulated in ref. 36) from the total transition probability to obtain the electric dipole probability. Then CJO can be simply obtained by combining eqn (2) and (5).
The measured absorption spectrum for a BaTiO3:9% Er3+/1% Yb3+ sample is shown in Fig. 5. The areas below the peaks have been obtained from this spectrum by numerical integration after correction for the baseline. In the 400–1600 nm range, the refraction index for the BaTiO3 host37 can be satisfactorily described by Cauchy's equation
 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123.4 nm2 yielding values between 2.66 and 2.27 for wavelengths in the range from 400 to 1600 nm. The measured lifetime for the 4I13/2 level is found to be τexp = 4.61 ms, and the corresponding spontaneous emission probability AT = 216.9 s−1.
123.4 nm2 yielding values between 2.66 and 2.27 for wavelengths in the range from 400 to 1600 nm. The measured lifetime for the 4I13/2 level is found to be τexp = 4.61 ms, and the corresponding spontaneous emission probability AT = 216.9 s−1.
According to Carnall et al.36 the magnetic dipole contribution to the oscillator strength for the 4I15/2 → 4I13/2 transition is given by fmd = n × 30.82. Since at the wavelength for this transition the refractive index of pure BaTiO3 is 2.26, we can estimate an oscillator strength due to magnetic dipole fmd = 70 × 10−8 for our sample. Using eqn (9)
 | (9) |
Judd–Ofelt intensity parameters Ωλ (λ = 2, 4, 6) can be extracted from the experimental data by fitting the fexp values in Table 2 to a set of fcalc values obtained from eqn (2) using the RELIC program.31 For this purpose, we have used the crystal field and spin–orbit coupling parameters for Er3+ in aqueous solution given by Carnall in ref. 35: F(2) = 440.8, F(4) = 66.8, F(6) = 7.3, and ζ = 2380, all in units of cm−1. The resulting JO intensity parameters are Ω2 = 1.3 × 10−20, Ω4 = 0.9 × 10−20, and Ω6 = 0.4 × 10−20 cm2. Using these parameters and eqn (2) we can estimate the oscillator strengths, fcalc, given in Table 2. The associated absolute RMS value is 3.6 × 10−7.
The Ωλ parameters found for Er3+ in BaTiO3:9% Er3+/1% Yb3+ are in the range found for Er3+ in other mixed crystalline oxides.29 Since the intensity of f–f transitions arises from the admixture of odd-parity crystal-field components their JO intensity parameters should depend on the type and symmetry of the ligands in a given material, although as noted by Hehlen et al.31 it is difficult to establish clear correlations because the influence of the coordinating environment on the well-shielded 4f electrons is quite small. Besides this, comparison of Ωλ values reported in the literature is also hindered by the use of different procedures in their calculation, such as fitting the intensity parameters using optimized wavefunctions for the given material vs. using tabulated data obtained for another material, the types of transitions included in the fit, and the numerical details used in the fitting procedure. An additional difficulty in correlating JO parameters with structural features arises from the additivity of JO Ωλ values29 since in the presence of several non-equivalent sites in the host matrix one obtains an average value for each Ωλ parameter. In general, Ω2 has been found to scale with the degree of covalency between the rare earth cation and the coordinating ligands.29,31,38 The small value found here is in concordance with those found for oxides with a strong ionic character. The Ω4 and Ω6 parameters have been found to decrease with increasing rigidity of the matrix.39 According to this trend, the small values found here would be associated with the high rigidity of BaTiO3, similar to that of other mixed crystalline oxides.
The calculated line strengths fcalc obtained from the fitted JO intensity parameters have been used to calculate spontaneous emission probabilities via eqn (7). The most relevant results are summarized in Table 3 where radiative lifetimes
 | (10) |
| βJ′→J = τradA(J′ → J) | (11) |
| Transition | λ (nm) | Aed (s−1) | Amd (s−1) | τrad (μs) | βJ′→J (%) |
|---|---|---|---|---|---|
| 4I13/2 → 4I15/2 | 1537 | 107 | 117 | 3898 | 100 |
| 4I11/2 → 4I13/2 | 2754 | 28 | 32 | 4115 | 25 |
| 4I15/2 | 975 | 183 | — | 75 | |
| 4I9/2 → 4I11/2 | 4545 | 2 | 4 | 2498 | 1 |
| 4I13/2 | 1715 | 61 | — | 15 | |
| 4I15/2 | 811 | 334 | — | 84 | |
| 4I9/2 → 4I9/2 | 3387 | 5 | 12 | 318 | 1 |
| 4I11/2 | 1940 | 90 | 24 | 4 | |
| 4I13/2 | 1138 | 150 | — | 5 | |
| 4I15/2 | 660 | 2859 | — | 90 | |
| 4S3/2 → 4F9/2 | 3052 | 1 | — | 430 | 0 |
| 4I9/2 | 1605 | 117 | — | 5 | |
| 4I11/2 | 1186 | 54 | — | 2 | |
| 4I13/2 | 829 | 642 | — | 28 | |
| 4I15/2 | 538 | 1510 | — | 65 | |
| 2H11/2 → 4S3/2 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
0 | 0 | 91 | 0 |
| 4F9/2 | 2463 | 33 | 1 | 0 | |
| 4I9/2 | 1426 | 141 | 11 | 1 | |
| 4I11/2 | 1085 | 142 | 806 | 9 | |
| 4I13/2 | 779 | 212 | 257 | 4 | |
| 4I15/2 | 517 | 9366 | 0 | 86 |
3.5. Upconversion emission
UC spectra of the co-doped samples with different concentrations of Er3+ and Yb3+ are shown in Fig. 6. All spectra were obtained by exciting at 1500 nm. The emission spectra of BaTiO3:Er3+–Yb3+ phosphors show emission bands at 975 nm and 660 nm, which correspond to the electronic 4I11/2 → 4I15/2 and 4F9/2 → 4I15/2 transitions of the Er3+ ion, respectively. Moreover, at 975 nm the 2F5/2 → 2F7/2 transition corresponding to Yb3+ ions is also present. | ||
| Fig. 6 Up-conversion spectra (excitation at 1500 nm) for BaTiO3 based phosphors as a function of Er3+ and Yb3+ contents. | ||
Comparing the intensity of the 975 nm band in the emission spectra for samples with different rare earth ion content (Fig. 7) it can be seen that in all cases, the sample doped with Er3+ at 5% that presents a maximal emission, being BaTiO3:Er3+ 5%–Yb3+ 1% the composition yielding the highest photon UC (Fig. 6a). It is also observed that as the concentration of Yb3+ ion increases, the emission intensity decreases. This observation can be explained considering an increase of energy transfer and non-radiative processes that compete with luminescence as the concentration of sensitizer Yb3+ ions is increased.
 | ||
| Fig. 7 Relative intensity of up-conversion emission as a function of Er3+ and Yb3+ ion concentrations using λexc. = 1500 nm. | ||
As it is clearly visible in Fig. 6, the most intense emission corresponds to the 975 nm band, which corresponds precisely to the most interesting emission for applications in solar cells since it corresponds to the absorption band of silicon. Inclusion of BaTiO3:Er3+–Yb3+ phosphors in these cells could then contribute to increase their photocurrent by harvesting also photons with a wavelength of 1500 nm.
To study the mechanism behind photon UC in BaTiO3:Er3+–Yb3+ we have also studied the dependence of the intensity for the emissions at 975 and 660 nm as a function of the pump power of the incident laser. It is well-known that the upconversion intensity is directly related to the intensity of the infrared excitation by the following expression:
| IUC ∝ IIRn | (12) |
 | ||
| Fig. 8 Logarithm of the up-conversion emission intensity (excitation at 1500 nm) as a function of the logarithmic pump power of the excitation source. | ||
The discrepancy between the actual values of the slope (1.8 and 2.3) and the number of photons involved in the process (2 and 3) is due to the known effect that the slope of the curve is gradually decreasing as the laser power increases, a phenomenon described by Pollnau et al.42 as a saturation in the upconversion process at high power. According to this interpretation, a high pump power would increase the competition between the linear decay and upconversion for the depletion of the intermediate excited states, resulting in a significantly reduced slope.
The dynamics of the 975 nm emission was studied by measuring the corresponding decay curves. Fig. 9 shows the decay curves for excitation at 1500 and 800 nm. In both cases, a rapid rise time is observed after excitation with the laser, followed by a rapid decline. This behavior is indicative of a GSA/ESA mechanism for the UC process in which after excitation by a pulsed laser at 1500 nm, the Er3+ ion is immediately excited to the 4I13/2 level by absorbing a photon and afterwards to the 4I9/2 level by absorbing a second 1500 nm photon. In this process, the population of the 4I9/2 level increases rapidly as a result of successive two-photon absorption, similar to what would be observed if this level is excited directly. Therefore, as it can be seen in Fig. 9, there is an immediate rise time after pulse excitation at 1500 nm, confirming the proposed upconversion mechanism. Subsequently a non-radiative relaxation to the 4I11/2 level takes place, from where the emission of a photon of wavelength 975 nm leads to the fundamental 4I15/2 state. In the same way, absorption of a third photon contributes to an increase in the population of the 4S3/2 level. Due to the small energy gap, Er3+ ions in the 4S3/2 state relax very quickly through a non-radiative process to the 4F9/2 levels from where they relax radiatively to the 4I15/2 ground state emitting a red photon (660 nm). Moreover, from the 4I11/2 level of the Er3+ ions, Yb3+ ions may be excited by resonant energy transfer processes. As observed in Fig. 10, the emission band by exciting at 800 nm of co-doped BaTiO3:Er3+–Yb3+ is broader than the emission band of doped BaTiO3:Er3+. It is due to the presence of the Er3+:4I11/2 → 4I15/2 and Yb3+:2F5/2 → 4F7/2 transitions in the codoped sample, confirming the energy transfer from the Er3+ to the Yb3+ ions.
As can be seen ion Fig. 6, the UC emission intensity decreases with increasing Yb3+ ion concentration. A possible explanation for this result is the excitation of Yb3+ ions from 4I11/2 level of Er3+ (see Fig. 10) followed by a final transfer to traps in the matrix.43 The complete diagram for the proposed photon UC mechanism is shown in Fig. 11.
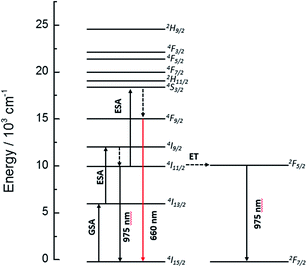 | ||
| Fig. 11 Energy level diagram for the Er3+ and Yb3+ ions, indicating the suggested upconversion mechanisms taking place upon 1500 nm laser excitation. | ||
4. Conclusions
Er3+/Yb3+ doped BaTiO3 phosphors were synthesized through a sol–gel method and their photon upconversion behavior was studied by excitation at 1500 nm. The results of PXRD measures show the existence of solid solutions for all phases in which the Er3+ and Yb3+ cations replace both the Ba2+ and Ti4+ sites. Raman spectroscopy corroborates the coexistence of the cubic and the tetragonal phases.Our analysis of the optical properties of the new phosphors shows that their upconversion emission spectra are dominated by the emission at 975 nm (4I11/2 → 4I15/2), which has a potential use to increase the efficiency of Si solar cells by reducing transmission losses. The best UC behavior was observed for samples with a BaTiO3:Er3+ 5%–Yb3+ 1% composition. A detailed analysis shows that the emission at 975 nm is the result of a successive two-photon absorption of 1500 nm radiation. Finally, the decay curves of the emission at 975 nm by exciting at 1500 nm and 800 nm are in good agreement with a GSA/ESA mechanism for photon upconversion in these materials.
Acknowledgements
The authors acknowledge Conicyt-Chile for the financial support (Anillo Grant ACT 1204). J. Ll, I. R. M. and P. A. acknowledge Fondecyt (Grant 1130248) for the international cooperation as well as MINECO and EU-FEDER (projects MAT2013-46649-C4-4-P, MAT2015-71070-REDC, MAT2016-75586-C4-4-P and CTQ2015-64579-C3-3-P). M. V. acknowledges CONICYT for a doctoral fellowship.References
- B. S. Richards, Sol. Energy Mater. Sol. Cells, 2006, 90, 2329 CrossRef CAS.
- M. A. Green, Phys. E, 2002, 14, 65 CrossRef CAS.
- B. M. van der Ende, L. Aarts and A. Meijerink, Phys. Chem. Chem. Phys., 2009, 11, 11081 RSC.
- W. G. J. H. M. van Sark, J. de Wild, J. K. Rath, A. Meijerink and R. E. I. Schropp, Nanoscale Res. Lett., 2013, 8, 81 CrossRef PubMed.
- X. Huang, S. Han, W. Huang and X. Liu, Chem. Soc. Rev., 2013, 42, 173 RSC.
- P. Ramasamy, P. Manivasakan and J. Kim, RSC Adv., 2014, 4, 34873 RSC.
- C. Strümpel, M. McCann, G. Beaucarne, V. Arkhipov, A. Slaoui, V. Svtcek, C. del Cañizo and I. Tobias, Sol. Energy Mater. Sol. Cells, 2007, 91, 238 CrossRef.
- F. Auzel, Chem. Rev., 2004, 104, 139–173 CrossRef CAS PubMed.
- A. Shalav, B. S. Richards and M. A. Green, Sol. Energy Mater. Sol. Cells, 2007, 91, 829 CrossRef CAS.
- H. Lian, Z. Hou, M. Shang, D. Geng, Y. Zhang and J. Lin, Energy, 2013, 57, 270 CrossRef CAS.
- W. Yang, X. Li, D. Chi, H. Zhang and X. Liu, Nanotechnology, 2014, 25, 482001 CrossRef PubMed.
- F. Wang and X. Liu, Chem. Soc. Rev., 2009, 38, 976 RSC.
- H.-Q. Wang, M. Batentschuk, A. Osvet, L. Pinna and C. J. Brabec, Adv. Mater., 2011, 23, 2675 CrossRef CAS PubMed.
- D. R. Gamelin and H. Güdel, Top. Curr. Chem., 2001, 214, 1 CrossRef CAS.
- D. P. Dutta, A. Ballal, J. Nuwad and A. K. Tyagi, J. Lumin., 2014, 148, 230 CrossRef CAS.
- S. Fuentes, N. Barraza, E. Veloso, R. Villarroel and J. Llanos, J. Alloys Compd., 2013, 569, 52 CrossRef CAS.
- J. Long, L. Yang and X. Wei, J. Alloys Compd., 2013, 549, 336 CrossRef CAS.
- Y. Tsur, T. D. Dunbar and C. A. Randall, J. Electroceram., 2001, 7, 25 CrossRef CAS.
- S. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- U. D. Venkateswaran, V. M. Naik and R. Naik, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14256 CrossRef CAS.
- Z. Yao, H. Liu, Y. Liu, Z. Wu, Z. Shen, Y. Liu and M. Cao, Mater. Chem. Phys., 2008, 109, 475 CrossRef CAS.
- A. Garrido-Hernández, A. García-Murillo, F. d. J. Carrillo-Romo, L. A. Cruz-Santiago, G. Chadeyron, A. d. J. Morales-Ramírez and S. Velumani, J. Rare Earths, 2014, 32, 1016 CrossRef.
- P. Hermet, M. Veithen and P. Ghosez, J. Phys.: Condens. Matter, 2009, 21, 215901 CrossRef CAS PubMed.
- E. Chávez, S. Fuentes, R. A. Zárate and L. Padilla-Campos, J. Mol. Struct., 2010, 984, 131 CrossRef.
- H. Hayashi, T. Nakamura and T. Ebina, J. Phys. Chem. Solids, 2013, 74, 957 CrossRef CAS.
- D. Caruntu, T. Rostamzadeh, T. Costanzo, S. S. Parizi and G. Caruntu, Nanoscale, 2015, 7, 12955 RSC.
- B. R. Judd, Phys. Rev., 1962, 127, 750 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511 CrossRef CAS.
- C. Görller-Walrand and K. Binnemans, Spectral intensities of f–f transitions, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr and L. Eyring, North-Holland, 1998, vol. 25, p. 101 Search PubMed.
- B. M. Walsh, Judd–Ofelt theory: principles and practices, in Advances in Spectroscopy for Lasers and Sensing, ed. B. Di Bartolo and O. Forte, Springer, Netherlands, 2006, p. 403 Search PubMed.
- M. P. Hehlen, M. G. Brik and K. W. Krämer, J. Lumin., 2013, 136, 221 CrossRef CAS.
- W. Luo, J. Liao, R. Li and X. Chen, Phys. Chem. Chem. Phys., 2010, 12, 3276 RSC.
- G. Yao, C. Lin, Q. Meng, P. S. May and M. T. Berry, J. Lumin., 2015, 160, 276 CrossRef CAS.
- E. Cantelar, M. Marin-Dobrincic, T. Jardiel, A. C. Caballer and F. Cussó, Opt. Mater., 2015, 41, 122 CrossRef CAS.
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4424 CrossRef CAS.
- W. T. Carnall, The absorption and fluorescence spectra of rare earth ions in solution, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner Jr and L. Eyring, North Holland, 1979, vol. 3, p. 171 Search PubMed.
- S. M. Wemple, M. Didomenico and I. Camlibel, J. Phys. Chem. Solids, 1968, 29, 1797 CrossRef.
- D. E. Henrie, R. L. Fellows and G. R. Choppin, Coord. Chem. Rev., 1976, 18, 199 CrossRef CAS.
- C. K. Jorgensen and R. Reisfeld, J. Less-Common Met., 1983, 93, 107 CrossRef.
- B. M. van der Ende, L. Aarts and A. Meijerink, Phys. Chem. Chem. Phys., 2009, 11, 11081 RSC.
- W. Yu, Y. Tian, M. Xing, Y. Fu, H. Zhang and X. Luo, Mater. Res. Bull., 2016, 80, 223 CrossRef CAS.
- M. Pollnau, D. R. Gamelin, S. R. Lüthi, H. U. Güdel and M. P. Helen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337 CrossRef CAS.
- M. A. Hernández-Rodríguez, M. H. Imanieh, L. L. Martín and I. R. Martín, Sol. Energy Mater. Sol. Cells, 2013, 116, 171 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |





