Structure and properties of 1-amino-2-nitroguanidinium nitrate†
Xinghui Jin,
Bingcheng Hu*,
Zuliang Liu and
Chunxu Lv
School of Chemical Engineering, Nanjing University of Science and Technology, Jiangsu, Nanjing 210094, China. E-mail: hubingcheng210094@163.com
First published on 15th May 2014
Abstract
A nitrogen-rich energetic material 1-amino-2-nitroguanidinium nitrate (ANGN) was synthesized and fully characterized by nuclear magnetic resonance, infrared spectroscopy, mass spectroscopy and elemental analysis. Its thermal behavior and detonation properties were also investigated to give a better understanding of its physical and chemical properties. The results show that the calculated critical temperature of thermal explosion, entropy of activation, enthalpy of activation, free energy of activation, detonation pressure and detonation velocity are 319.8 K, 130.24 J mol−1 K−1, 155.45 kJ mol−1, 106.45 kJ mol−1 43.0 GPa and 9775 m s−1, respectively. It is predicted that ANGN possesses excellent energetic properties compared to those of RDX and HMX, and can be considered as a potential energetic material.
1 Introduction
Significant progress has been achieved in the development of novel nitrogen-rich high-energy density materials (HEDMs) with high performance and decreased sensitivity as well as environmental compatibility during the last few decades.1–4 Unfortunately, in most cases, the requirements of insensitivity (such as oxygen balance, sensitivity to impact, sensitivity to friction, thermal shock, electrostatic discharge) and high detonation properties are often contradictory to each other, which make the design and synthesis of new HEDMs an interesting and enormous challenge.5 To solve these problems, one possible approach is to design and synthesize energetic salts which were often prepared by neutralization or metathesis reactions with N-protonated cations and O-deprotonated anions. This is primarily because salt-based energetic materials often possess advantages over non-ionic molecules since these salts tend to exhibit lower vapor pressures and higher densities than their atomically similar non-ionic analogues. Moreover, production of these energetic salts always involves the combination of different energetic cations and anions and makes it possible to balance the requirements of low sensitivity and high detonation properties.6,7 Thus, nitrogen-rich energetic salts as a family of environmentally benign high energy density materials (HEDMs), have became one of the hottest topics in the field of HEDM.8–10Guanidine, aminoguanidine, diaminoguanidine and triaminoguanidine were often considered as the nitrogen-rich cations in the previous research.11 However, little research was reported on 1-amino-2-nitroguanidine (ANG) which possesses better energetic properties (such as density, detonation velocity, detonation pressure and so on) than guanidine and its derivatives.12,13 Herein, a nitrogen-rich energetic salt 1-amino-2-nitroguanidinium nitrate (ANGN Scheme 1) was synthesized and fully characterized. Its crystal structure, thermal behavior and detonation properties were also investigated to give a better understanding of its physical and chemical properties.
2 Experimental
2.1 Materials
1-amino-2-nitroguanidine was prepared according to ref. 14.ANGN was prepared as the following procedure: to a vigorously stirred suspension of 1-amino-2-nitroguanidine (1.19 g, 0.01 mol) in water (10 mL) was added 65% nitric acid (1.5 mL, 0.02 mol). The solution was stirred at 60 °C for 1 h and then cooled to the room temperature. The ANGN was crystallized (1.72 g, 94.5%) as white blocks. M.p. 138–149 °C. IR ν/cm−1: 3395, 3290, 1645, 1580, 1470, 1385, 1281, 1215, 1050, 915, 823. δH (d6-DMSO, 500 MHz): 9.49 (s, 1H), 8.31 (s, 5H); δC (d6-DMSO, 125 MHz): 159. m/z (ESI): 62 [M − H]−, 120 [M + H]+. CH6O5N6: calcd/%. C 6.59, H 3.30, N 46.15, found C 6.48, H 3.39, N 46.22%.
2.2 Experimental equipments and conditions
BrukerAvance III 500 MHz spectrometer was used for 1H NMR and 13C NMR spectra of ANGN; IR spectrum was obtained from a Thermo Nicolte IS10 IR instrument; ESI-MS results were obtained from a Finnigan TSQ Quantum Mass Spectrometer. Elemental analysis was completed on a Perkin-Elmer PE-2400. TG-DTG-DSC curves were obtained on a NETZSCH STA 409 PC/PG coupling system with an initial mass of 3.0 mg placed in alumina crucibles (nitrogen atmosphere with the flow rate of 30 mL min−1). The crystal data were collected with a Bruker SMART APEX II CCD X-ray diffractometer using graphite-monochromated Mo-Kα radiation (λ = 0.071073 nm).†3 Results and discussion
3.1 Crystal structure
Single crystal suitable for X-ray measurements were obtained by slow evaporation of a nitric acid solution of ANGN. A white crystal with dimensions 0.3 mm × 0.2 mm × 0.2 mm was chosen for X-ray determination. The structure was solved by direct methods (SHELXTL-97) and refined by full-matrix-block least-squares methods on F2 with anisotropic thermal parameters for all non-hydrogen atoms. Crystal data and refinement results were summarized in Table 1. It is also fascinating that the crystal density measured in our group is 1.85 g cm−1 while the data is 1.91 g cm−1 in ref. 12. It is certainly due to the different temperatures of analysis, 173 K in ref. 12 vs. 293 K in this paper and the current X-ray analysis will make it more useful in predicting properties for practical applications. This also results in the difference of the detonation properties directly (P, detonation pressure and D, detonation velocity) since density is an important data for an energetic material according to Kamlet–Jacobs equations. The following investigation also proved this fact.| Chemical formula | CH6N6O5 |
| Formula weight/g mol−1 | 182.12 |
| Temperature/K | 293 (2) |
| Wavelength/Å | 0.71073 |
| Crystal system | Triclinic |
| Space group | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| Crystal colour | White |
| a/Å | 7.1750 (14) |
| b/Å | 7.2020 (14) |
| c/Å | 7.8560 (16) |
| α/° | 66.12 (3) |
| β/° | 65.34 (3) |
| γ/° | 68.51 (3) |
| Volume/Å3 | 327.69 (11) |
| Z | 2 |
| Dcalc/g cm−3 | 1.85 |
| Absorption coefficient/mm−1 | 0.180 |
| F(000) | 188.0 |
| θ range/° | 2.99–25.39 |
| Index ranges | 0 ≤ h ≤ 8, −8 ≤ k ≤ 8, −8 ≤ l ≤ 9 |
| Reflections collected | 1210 |
| Goodness-of-fit on F2 | 1.000 |
| Final R indices [I > 2σ(I)] | R1 = 0.0466, wR2 = 0.1389 |
| R indices (all data) | R1 = 0.0413, wR2 = 0.1320 |
| Largest diff. peak and hole/e Å−3 | 0.271, −0.245 |
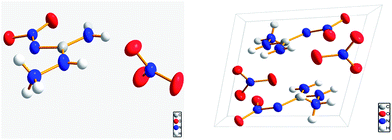
Fig. 1 shows the molecular structure and the three-dimensional packing diagram of ANGN. It is evident that the ANGN structure was made up of one ANG cation and one nitrate anion. The ANG cation and the nitrate anion distributed in different planes, and the whole molecule presents an almost perpendicular conformation.
3.2 Thermal behavior
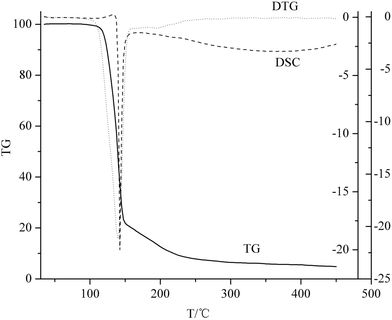
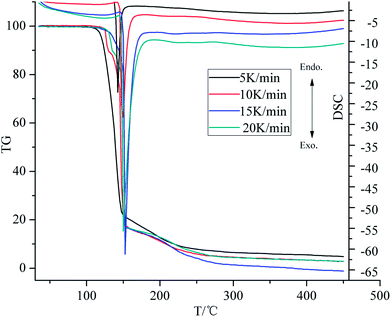
Fig. 2 shows the TG-DTG-DSC curves of title compound with the initial temperature 30 °C up to 450 °C at the heating rate of 5 K min−1. From the figure, two steps were observed by TG curve. The first step, which is the main stage process, starts from 100 to 150 °C with 77.5% weight loss while the second step starts from 150 to 240 °C with about 22.5% weight loss. Correspondingly, there appear an evident sharp peak at about 140 °C and a faint peak at around 200 °C in the DTG curve, which also demonstrated that the decomposition reaction was a two stage process. As for the DSC curve, there is a faint endothermic peak (140 °C) and an evident sharp exothermic peak (142 °C) which makes it have a number of potential applications in melt cast explosive, primary explosive, gas generating composition, low characteristic signal propellant, and so on. The two peaks belong to the melt and decomposition of ANGN, respectively.Fig. 3 shows the TG-DSC curves of the decomposition process of ANGN salt at different heating rates of 5, 10, 15 and 20 K min−1. It was found that, with the increase of the heating rate, the decomposition temperatures and the exothermic peaks of ANGN salt shifted to higher temperatures. On the other hand, the endothermic peaks and the exothermic peaks in DSC curves clearly appear as the heating rate increased.
3.3 Non-isothermal decomposition kinetics
In order to obtain the relative kinetic parameters such as activation energy (Ea), pre-exponential constant (A), entropy of activation (ΔS≠), enthalpy of activation (ΔH≠), and free energy of activation (ΔG≠), two thermal analysis kinetic methods were jointly employed. The equations were written as follows:(1) Kissinger Equation:15
 | (1) |
(2) Ozawa–Flynn–Wall Equation:16
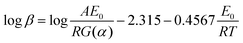 | (2) |
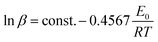 | (3) |
The activation energy and pre-exponential factor can easily be calculated based on the straight line that was obtained by plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. reciprocal of the temperature (T−1).
β vs. reciprocal of the temperature (T−1).
The data β, Tpi and the kinetic parameters obtained by Kissinger and Ozawa methods were summarized in Table 2. It is obviously seen from the table that the values of Tpi of the exothermic peak shifted to higher temperatures as the heating rate increased. On the other hand, the values of E calculated by Kissinger method (Ek = 158.6 kJ mol−1) agrees well with that obtained by Ozawa's method (E0 = 157.6 kJ mol−1) and both of the linear correlation coefficients are very close to 1. All the data obtained above indicates that the result is credible.
| β (°C min−1) | Tpi (°C) | Kissinger method | Ozawa method | |||
|---|---|---|---|---|---|---|
| Ek (kJ mol−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ak (s−1) Ak (s−1) |
rk | E0 (kJ mol−1) | r0 | ||
| 5 | 142.0 | 158.6 | 19.7 | 0.999 | 157.6 | 0.999 |
| 10 | 148.3 | |||||
| 15 | 151.9 | |||||
| 20 | 154.3 | |||||
The corresponding parameters such as the entropy of activation (ΔS≠), the enthalpy of activation (ΔH≠), and the free energy of activation (ΔG≠) could be calculated by eqn (4)–(6) based on the calculated values of Ea and A.19,20
 | (4) |
| ΔH≠ = Ea − RT | (5) |
| ΔG≠ = ΔH≠ − TΔS≠ | (6) |
In order to get the values of ΔS≠, ΔH≠ and ΔG≠, the value of Tp0 must be known firstly according to eqn (4)–(6). Then the next important work is to calculate the value of Tp0 which could be calculated by eqn (7).21
| Tpi = Tp0 + bβi + cβi2 + dβi3 | (7) |
Based on the above-described equations, the value of Tp0, ΔS≠, ΔH≠, and ΔG≠ were calculated as 378.45 K, 130.24 J mol−1 K−1, 155.45 kJ mol−1 and 106.45 kJ mol−1, respectively.
3.4 Critical ignition temperature
The critical temperature is another important parameter since it is necessary to give a better understanding of the thermal stability and to insure the safe storage involving explosives, propellants and pyrotechnics. It can be defined as follows: the lowest temperature to which a specific charge may be heated without undergoing thermal runaway.22 The value of Tb of 319.8 K was calculated by the following equation:23
 | (8) |
3.5 Energetic properties
Computations were performed with the Gaussian 03 suite of programs.24 The geometric optimization of the structures were based on single crystal structures, where available, and frequency analyses are carried out using B3LYP functional with 6-31+G(d,p) basis set, and single energy points were calculated at the MP2(full)/6-311++G(d,p) level. All of the optimized structures were characterized to be true local energy minima on the potential energy surface without imaginary frequencies.Detonation velocity (D) and detonation pressure (P) are two important parameters when an energetic material was designed or synthesized. Previous studies have proved that the Kamlet–Jacobs equations can be considered as the most reliable approach to estimate the detonation properties of an energetic material.25
D = 1.01(N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 1/2Q1/2)1/2(1 + 1.3ρ) 1/2Q1/2)1/2(1 + 1.3ρ)
| (9) |
P = 1.558ρ2N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 1/2Q1/2 1/2Q1/2
| (10) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) , the average molecular weight of these gases; Q, the heat of detonation (cal g−1). Values of N,
, the average molecular weight of these gases; Q, the heat of detonation (cal g−1). Values of N, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) , and Q could be obtained using the following equations that summarized in Table 3.
, and Q could be obtained using the following equations that summarized in Table 3.
| Parameters | Stoichiometric ratio | ||
|---|---|---|---|
| c ≥ 2a + b/2 | 2a + b/2 > c ≥ b/2 | b/2 > c | |
| a, b, c and d stand for the number of C, H, O and N atoms in the explosive molecule respectively. M in the formula is the molecular weight of the explosive (g mol−1); ΔHf is the heat of formation of the explosive (kJ mol−1). | |||
| N | (b + 2c + 2d)/4M | (b + 2c + 2d)/4M | (b + d)/2M |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) |
4M/(b + 2c + 2d) | (56d + 88c − 8b)/(b + 2c + 2d) | (2b + 28d + 32c)/(b + d) |
| Q × 10−3 | (28.9b + 94.05a + 0.239ΔHf)/M | [28.9b + 94.05(c/2 − b/4) + 0.239ΔHf]/M | (57.8c + 0.239ΔHf)/M |
According to the above-described equations, the heat of formation is an essential parameter to calculate the detonation properties of an energetic material. Then the next important task is to determine the heat of formation (ΔH0f) of ANGN using Born–Haber energy cycle (Fig. 4) and eqn (11)–(13):26
| ΔH0f (ionic salt 298 K) = ∑ΔH0f (cation, 298 K) + ∑ΔH0f (anion, 298 K) − ΔHL | (11) |
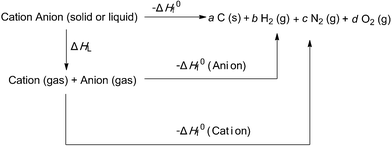 | ||
| Fig. 4 Born–Haber cycle for the formation of energetic salts. a, b, c, d are the number of moles of the respective products. | ||
The value of ΔHL could be predicted by the formula suggested by Jenkins et al.:
| ΔHL = UPOT + [p(nM/2 − 2) + q(nX/2 − 2)]RT | (12) |
| UPOT (kJ mol−1) = γ(ρ/M)1/3 + δ | (13) |
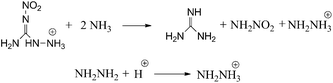
Isodesmic reactions (Scheme 2) and protonation reactions were employed (Scheme 2) in this paper to obtain the heat of formation (ΔH0f) of the cations, anions and the parent ions (heat of formation of H+ is 1530 kJ mol−1).27
Then the enthalpy of the isodesmic reaction (ΔH0f) is obtained by combining the MP2/6-311++G** energy difference for the reaction, the zero-point energies (B3LYP/6-31+G**), and other thermal factors (B3LYP/6-31+G**). Thus, the detonation properties of the title salt (Table 4) can be calculated based on the above-described equations and schemes. For a comparison, detonation properties of two well-known energetic material RDX (hexahydro-1,3,5-trinitro-1,3,5-triazine) and HMX (1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane) were also listed in Table 4. It is seen that detonation properties of the title energetic salt ANGN is superior to that of RDX and HMX.
| Compd. | da | Tmb | Tdc | ΔH0f, cationd | ΔH0f, anione | ΔH0f, latticef | ΔH0f, saltg | Ph | Di | OBj |
|---|---|---|---|---|---|---|---|---|---|---|
| a Density (g cm−3).b Melting point (°C).c Thermal degradation (°C).d Calculated molar enthalpy of formation of the cation (kJ mol−1).e Calculated molar enthalpy of formation of the anion (kJ mol−1).f Calculated molar lattice energy (kJ mol−1).g Calculated molar enthalpy of formation of the salt (kJ mol−1).h Detonation pressure (GPa).i Detonation velocity (m s−1).j Oxygen balance (OB), for the compound with molecular formula CaHbNcOd (without crystal water), OB (%) = 1600 (d − 2a − b/2)/Mw (%). | ||||||||||
| ANGN | 1.85 | 140 | 142 | 862 | −308 | 533 | 22 | 43.0 | 9775 | 0 |
| RDX28 | 1.82 | — | 230 | — | — | — | — | 35.2 | 8997 | −21.6 |
| HMX28 | 1.91 | — | 287 | — | — | — | — | 39.6 | 9320 | −21.6 |
Finally, it should be pointed out that we use isodesmic reactions (Scheme 2) and protonation reactions to calculate the heat of formation of the title compound in this paper instead of the atomization energy method that cited in ref. 12. However, the calculated results from the two methods show that the heat of formation of the cation, anion and the salt are 862 kJ mol−1 (ref. 12, 877 kJ mol−1), −308 kJ mol−1 (ref. 12, −313.6 kJ mol−1) and 22 kJ mol−1 (ref. 12, 22.2 kJ mol−1), respectively. The values are approximately the same which indicates that the isodesmic reaction and protonation reactions are of a feasible way to evaluate the heat of formation of an energetic salt. The detonation properties (P, detonation pressure and D, detonation velocity) calculated in this paper (P, 43.0 GPa; D, 9775 km s−1) also shows some difference from ref. 12 (P, 42.7 GPa; D, 9551 km s−1). This may be due to the different density that calculated from the crystal structure.
3.6 NBO analysis
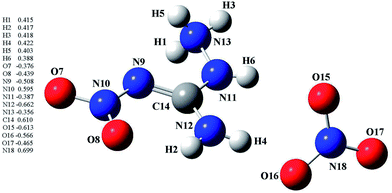
In order to give a better understanding of the chemical and physical properties of ANGN, the molecular orbital and the natural bond orbital (NBO) analyses based on the optimized structure (B3LYP/6-311+G(d,p)) were carried out by using Gaussian 03 program. As were shown in Fig. 5, NBO analysis indicated that the positive charge is delocalised over the C and H atoms in 1-amino-2-nitroguanidinium group (ranges from −0.356–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.662 e) and the negative charge is mostly delocalised over the N and O atoms except N10 and N18 (ranges from 0.388–0.610 e). This may be caused by the effect of the O atoms in the –NO2 group and NO3− anion.
−0.662 e) and the negative charge is mostly delocalised over the N and O atoms except N10 and N18 (ranges from 0.388–0.610 e). This may be caused by the effect of the O atoms in the –NO2 group and NO3− anion.
The highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) of ANGN were shown in Fig. 6. According to the molecule structure and calculated data, there are 95 molecule orbits in this system including 48 unoccupied ones. It also can be seen from Fig. 6 that the electron density of HOMO is mainly focus on the NO3− anion, while that of LUMO is mainly on the –NO2 group of the 1-amino-2-nitroguanidium. The results indicate that the group of –NO2 and –NH2 make an important difference to some properties of the title compound.
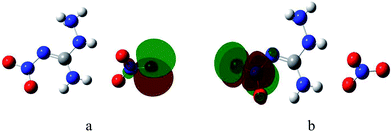 | ||
| Fig. 6 The highest occupied molecular orbital (HOMO, a) and the lowest unoccupied molecular orbital (LUMO, (b)) of ANGN. | ||
Since the gap energy of the highest occupied molecular orbitals and the lowest unoccupied molecular orbitals (ΔE) is an important parameter to measure the stability of the energetic material, the molecular energy (Etotal), the highest occupied molecular orbital energy (EHOMO), the lowest unoccupied molecular orbital energy (ELUMO) and their gaps (ΔE) were calculated. They were obtained as −745.8411766, −0.21153, −0.11045 and 0.10108 Hartree, respectively. It indicates that ANGN has a better thermal stability.
4 Conclusions
A nitrogen-rich energetic material 1-amino-2-nitroguanidinium nitrate (ANGN) was synthesized. The following conclusions about ANGN can be drawn:(1) The single-crystal X-ray diffraction indicates that ANGN was crystallized in a triclinic system, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) .
.
(2) The thermal behavior of ANGN presents one main decomposition stage in the temperature range 100–250 °C with about 95% mass loss.
(3) The calculated thermal dynamic parameters of ANGN were obtained as follows: Ek, 158.6 kJ mol−1; E0, 157.6 kJ mol−1; ΔS≠, 130.24 J mol−1 K−1; ΔH≠, 155.45 kJ mol−1 and ΔG≠, 106.45 kJ mol−1.
(4) The calculated detonation velocity and detonation pressure of ANGN are 9775 m s−1 and 43.0 GPa respectively. It indicates that ANGN has superior detonation properties to that of RDX and HMX, and can be considered as a potential energetic material.
Acknowledgements
This study was supported by the National Defense Advanced Research Projects (no. J-KY-2012-1317) and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).References
- Q. Wu, W. H. Zhu and H. M. Xiao, RSC Adv., 2014, 4, 3789 RSC.
- X. H. Jin, B. C. Hu, H. Q. Jia, Z. L. Liu and C. X. Lv, Quim. Nova, 2014, 37, 74 CrossRef CAS PubMed.
- Y. Q. Wu, F. L. Huang and Z. Y. Zhang, RSC Adv., 2012, 2, 4152 RSC.
- X. H. Jin, B. C. Hu, W. Lu, S. J. Gao, Z. L. Liu and C. X. Lv, RSC Adv., 2014, 4, 6471 RSC.
- G. H. Tao, Y. Guo, D. A. Parrish and J. M. Shreeve, J. Mater. Chem., 2010, 20, 2999 RSC.
- H. X. Gao, R. H. Wang, B. Twamley, M. A. Hiskey and J. M. Shreeve, Chem. Commun., 2006, 4007 RSC.
- Y. Q. Zhang, Y. Guo, Y. H. Joo, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2010, 16, 10778 CrossRef CAS PubMed.
- X. H. Jin, B. C. Hu, H. Q. Jia, Z. L. Liu and C. X. Lv, Aust. J. Chem., 2014, 67, 277 CAS.
- T. Altenburg, T. M. Klapötke, A. Penger and J. Stierstorfer, Z. Anorg. Allg. Chem., 2010, 636, 463 CrossRef CAS.
- D. Srinivas, V. D. Ghule and K. Muralidharan, RSC Adv., 2014, 4, 7041 RSC.
- Y. H. Joo, B. Twamley and J. M. Shreeve, Chem.–Eur. J., 2009, 15, 9097 CrossRef CAS PubMed.
- N. Fischer, T. M. Klapötke and J. Stierstorfer, Z. Naturforsch, 2012, 67b, 573 CrossRef.
- N. Fischer, T. M. Klapötke, K. Lux, F. A. Martin and J. Stierstorfer, Crystals, 2012, 2, 675 CrossRef CAS PubMed.
- R. A. Henry, R. C. Makosky and G. B. L. Smith, J. Am. Chem. Soc., 1951, 73, 474 CrossRef CAS.
- H. E. Kissinger, Anal. Chem., 1957, 29, 1702 CrossRef CAS.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881 CrossRef CAS.
- J. M. Salla, J. M. Morancho, A. Cadenato and X. Ramis, J. Therm. Anal. Calorim., 2003, 72, 719 CrossRef CAS.
- J. H. Yi, F. Q. Zhao, S. Y. Xu, L. Y. Zhang, H. X. Gao and R. Z. Hu, J. Hazard. Mater., 2009, 165, 8539 CrossRef PubMed.
- M. Najafi and A. K. Samangani, Propellants, Explos., Pyrotech., 2011, 36, 487 CrossRef CAS.
- R. Z. Hu, S. P. Chen, S. L. Gao, F. Q. Zhao, Y. Luo, H. X. Gao, Q. Z. Shi, H. A. Zhao, P. Yao and J. Li, J. Hazard. Mater., 2005, 117, 103 CrossRef CAS PubMed.
- K. Z. Xu, H. Zhang, P. Liu, J. Huang, Y. H. Ren, B. Z. Wang and F. Q. Zhao, Propellants, Explos., Pyrotech., 2012, 37, 653 CrossRef CAS.
- T. L. Zhang, R. Z. Hu, Y. Xie and F. P. Li, Thermochim. Acta, 1994, 244, 171 CrossRef CAS.
- J. Q. Zhang, H. X. Gao, L. H. Su, R. Z. Hu, F. Q. Zhao and B. Z. Wang, J. Hazard. Mater., 2009, 167, 205 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, Gaussian 03, Gaussian Inc, Pittsburgh, PA, 2003 Search PubMed.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23 CrossRef CAS PubMed.
- H. D. B. Jenkins, D. Tudeal and L. Glasser, Inorg. Chem., 2002, 41, 2364 CrossRef CAS PubMed.
- Y. G. Huang, Y. Q. Zhang and J. M. Shreeve, Chem.–Eur. J., 2011, 17, 1538 CrossRef CAS PubMed.
- Q. H. Zhang, J. H. Zhang, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2013, 19, 11000 CrossRef CAS PubMed.
Footnote |
| † CCDC 989437. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra03462g |
| This journal is © The Royal Society of Chemistry 2014 |