Open Access Article
Open Access ArticleStructure sensitivity of the electrochemical hydrogenation of cis,cis-muconic acid to hexenedioic acid and adipic acid†
Deep M.
Patel‡
 ab,
Prathamesh T.
Prabhu‡
ab,
Prathamesh T.
Prabhu‡
 ab,
Geet
Gupta
ab,
Marco Nazareno
Dell'Anna
ab,
Geet
Gupta
ab,
Marco Nazareno
Dell'Anna
 ab,
Samantha
Kling
ab,
Huy T.
Nguyen
ab,
Jean-Philippe
Tessonnier
ab,
Samantha
Kling
ab,
Huy T.
Nguyen
ab,
Jean-Philippe
Tessonnier
 *ab and
Luke T.
Roling
*ab and
Luke T.
Roling
 *ab
*ab
aDepartment of Chemical and Biological Engineering, Iowa State University, Ames, IA 50011, USA. E-mail: roling@iastate.edu; tesso@iastate.edu
bCenter for Biorenewable Chemicals (CBiRC), Ames, IA 50011, USA
First published on 29th December 2023
Abstract
The global market of fossil carbon-derived adipic acid (AA) was over 3 million tons in 2022, emitting 3.1 million tons of the potent greenhouse gas N2O. Alternative biomass-derived feedstocks offer a sustainable option to replace fossil carbon, but alternative pathways for AA synthesis are also required to curb the substantial emissions associated with the process. A novel and sustainable approach to synthesize AA is by coupling biomanufacturing and electrocatalysis. Biologically-produced cis,cis-muconic acid (ccMA) from sugars and lignin monomers has recently gained significant attention as a precursor to AA, as it can be electrochemically hydrogenated to AA using water-derived (instead of fossil-derived) hydrogen and electricity generated from wind energy. For the first time in literature, we demonstrate appreciable electrochemical production of AA using supported palladium nanoparticles. The performance of this system contrasts with that of palladium foil or platinum-based catalysts, which produced little AA. Density functional theory calculations on model surfaces of palladium and platinum suggest that the reduction of ccMA to trans-3-hexenedioic acid occurs through an outer sphere proton-coupled electron transfer mechanism, while subsequent reduction to AA preferentially occurs on surface terrace sites. Our calculations also explain the exceptional performance of palladium nanoparticles compared to palladium- and platinum-based foils, attributing the more favorable activation energy barriers found on palladium terraces to the relatively moderate binding strength of adsorbed species. These results suggest structure-sensitive catalyst design strategies that maximize the exposure of terrace atoms for further improvement of the ccMA electrochemical hydrogenation process.
Introduction
Replacing fossil hydrocarbons with renewable feedstocks such as lignocellulosic biomass has recently gained significant traction in chemical production.1–4 However, the decarbonization of the chemical industry also requires significant process innovation to reduce water and energy usage and minimize waste production, in accordance with the United Nations Sustainable Development Goals.5 Adipic acid (AA) production from petroleum-based cyclohexane is one of the largest chemical processes in terms of annual volumetric turnover, and is accordingly one of the most significant greenhouse gas (GhG) emitting processes.6–8 The global production of AA exceeded 3 million tons in 2022 with an annual growth of 3–5%; this production emits 3.1 million tons of N2O, a greenhouse gas 300 times more potent than CO2.9,10 About 75% of AA produced is utilized in the synthesis of Nylon-6,6, a commodity polymer broadly used in the packaging, textile, and automotive industries.11–14 Due to the unmatched chemical and mechanical properties and the large market size of nylons, it is difficult to replace nylon with a bio-based polymer like polylactic acid.15 Therefore, innovation is needed to make nylon synthesis more sustainable.The current commercial approach to synthesize AA is through oxidation of petroleum-derived cyclohexane in the presence of air and nitric acid.16,17 Recent efforts to develop greener routes for AA production have focused on replacing cyclohexane with lignin-derived phenol;18 however, the overall process to obtain ketone-alcohol oil from phenol is costly and environmentally unfriendly.19cis,cis-Muconic acid (ccMA) has gained significant attention as a biomass-derived platform intermediate to synthesize AA.20–24 Recent studies have shown promising results to sustainably produce high concentrations of ccMA in a single-step batch fermentation process.25,26 Notably, PTT Global Chemical has reported ccMA titers as high as 81.5 g L−1 from lignocellulosic biomass, motivating further research on developing sustainable pathways for its conversion to commodity chemicals.27ccMA, a C6-diunsaturated dicarboxylic acid, can be thermocatalytically hydrogenated to AA on conventional Re, Pt, and Pd-based catalysts with appreciable turnover frequencies (TOFs) and nearly 100% selectivity to AA at >90% conversion of MA.28–31 However, the thermocatalytic pathway requires a high pressure of H2 (4–10 bar)30 typically produced by methane steam reforming, another GhG emission-intensive process.
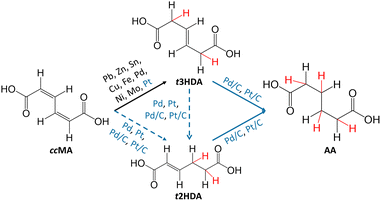
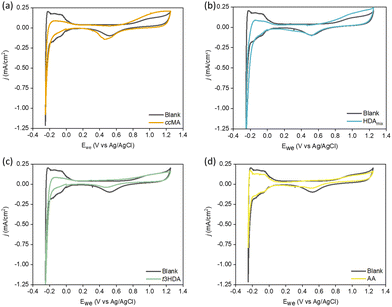
Electrocatalysis is of emerging significance due to its operation at ambient reaction conditions, its ability to utilize renewably-sourced electricity for generating current, the relative ease of modulating the reaction driving force through the cell potential, and the use of water as a source of hydrogen.32,33 However, as summarized in Fig. 1, previous studies have shown that ccMA electrochemical hydrogenation (ECH) to AA was surprisingly challenging, and instead selectively produced the monounsaturated diacid trans-3-hexenedioic acid (t3HDA).33–35 Such monounsaturated acids have been recently shown to find applications in synthesizing performance-advantaged nylons.36
In this study, we demonstrate for the first time that ccMA ECH can be driven to form AA with high selectivity on commercial Pd/C under acidic conditions. These results contrast with results on commercial Pt/C, which yielded smaller concentrations of AA with slower kinetics, and Pd and Pt foils, which only produced t3HDA. Density functional theory (DFT) calculations suggest that the exceptional activity on Pd/C could be due to an abundance of terrace sites, which bind adsorbed species relatively moderately and exhibit the lowest activation energies for ccMA ECH to AA. Our results further suggest an interplay between processes occurring in the outer sphere, forming monounsaturated diacids, and the further reaction of those species on the catalyst surface to form AA. Interestingly, the proposed electrochemical pathway is different from the previously proposed thermocatalytic pathway on Pd/C, which highlights the reaction environment-sensitive nature of the ccMA reduction mechanism.31 Our cyclic voltammograms combined with DFT calculations further show that the effect of coadsorbed organic molecules on HER onset potential is sensitive to the identity of the catalyst surface. Overall, this work is the first report on hydrogenating ccMA to AA using protons in solution as a green alternative to fossil-fuel derived H2 gas, demonstrating the promise of using ECH to open new pathways for the sustainable production of monomers from biomass-derived feedstocks.
Results and discussion
Screening Pd and Pt catalyst geometries for electrochemical hydrogenation of cis,cis-muconic acid
Since Pd and Pt-based catalysts33,34 were observed to achieve substantial conversions and TOFs of MA to AA via thermocatalytic hydrogenation,29,30 we started by screening different geometries (foils vs. nanoparticles) of Pd- and Pt-based catalysts for ccMA ECH through chronoamperometry (CA) in acidic media (Fig. 2 and Fig. S1–S3†). During this screening process, we found surprisingly high activity on Pd nanoparticles (TOFMA: 1.1 s−1, ccMA conversion after 1 h: 91%) with high selectivity (>95%, faradaic efficiency (FE): 18%) at −0.4 V vs. Ag/AgCl (VAg/AgCl). Based on the constant voltage bulk electrolysis experiments for higher catalyst loading (10 mg), we observe 100% conversion and selectivity to AA on Pd/C and Pt/C (Fig. S4†). These observations, combined with DFT calculations in the following section, identify t3HDA and t2HDA as reaction intermediates to form AA. Such high yield of AA on Pd/C suggests that the final process design for synthesizing bio-based AA might not require complicated downstream separation processes.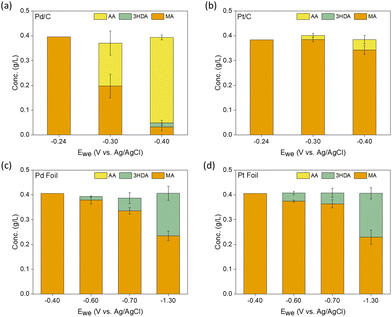 | ||
| Fig. 2 Concentration (g L−1) of reactants and products in solution after 1 hour of chronoamperometry (CA) experiments performed at varying working potentials (Ewe) on (a) Pd/C, (b) Pt/C, (c) Pd foil, and (d) Pt foil. The error bars represent the standard error from triplicates. In addition to these products, we observed a small concentration (0.1 g L−1) of muconolactone (not shown here for simplicity) that remained constant throughout the course of the reaction on all materials and at all potentials (see Methods section and Fig. S1–S3† for more details). Notation: MA: muconic acid, 3HDA: trans-3-hexenedioic acid, AA: adipic acid. | ||
Pt nanoparticles were considerably less active (TOFMA: 0.1 s−1, ccMA conversion after 1 h: 12%) and less selective for ECH (AA selectivity: >90%, FE: 3%) than Pd nanoparticles. In contrast to the results on nanoparticles, Pd and Pt foils did not produce any AA, yielding t3HDA as the only hydrogenation product with poor FE (<5%), in good agreement with previous observations.34
The relatively low FE observed for the best catalytic performance (18% on Pd/C) suggests that ∼80% of the cathodic current is being used in the production of H2 gas. While this observation provides a motivation for future studies to fine-tune reaction conditions for Pd/C to reduce HER,37 or design catalyst materials with high hydrogen overpotential,38 the co-produced H2 could be stored locally and used in fuel cells to compensate for the intermittent nature of wind energy.39–41
We performed constant-current experiments to verify that the observed product distribution in Fig. 2 is not an artifact of differences in mass-transfer kinetics across different materials. As shown in Fig. S5,† at a current density of 5 mA cm−2 we observe high selectivity and conversion of ccMA to AA on Pd nanoparticles. In contrast, on foils we observe t3HDA as a sole product with low ccMA conversion (<10% after 1 h) on Pd foil. Increasing the current densities from 5 mA cm−2 to 50 mA cm−2 and 100 mA cm−2 on Pd foil enhanced the production of the hydrogenation reaction but had no effect on its product selectivity, i.e., t3HDA remained the sole product on Pd foil. These observations suggest that mass-transfer kinetics are not affecting the product distributions.
Density functional theory calculations for cis,cis-muconic acid hydrogenation on (111) and (533) surfaces of Pd and Pt
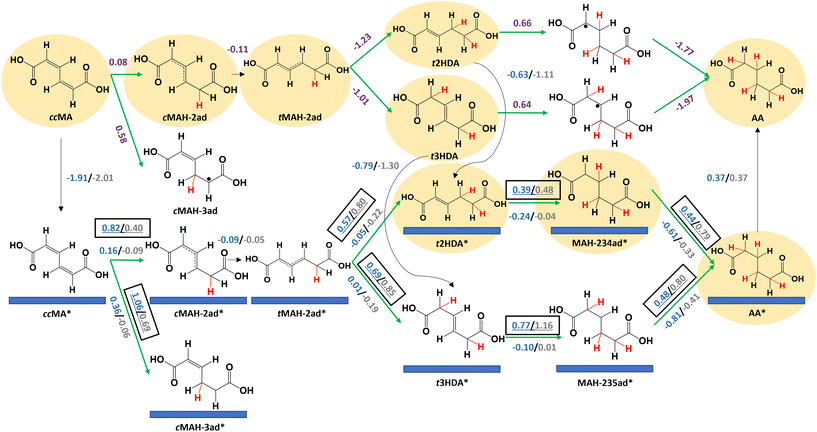
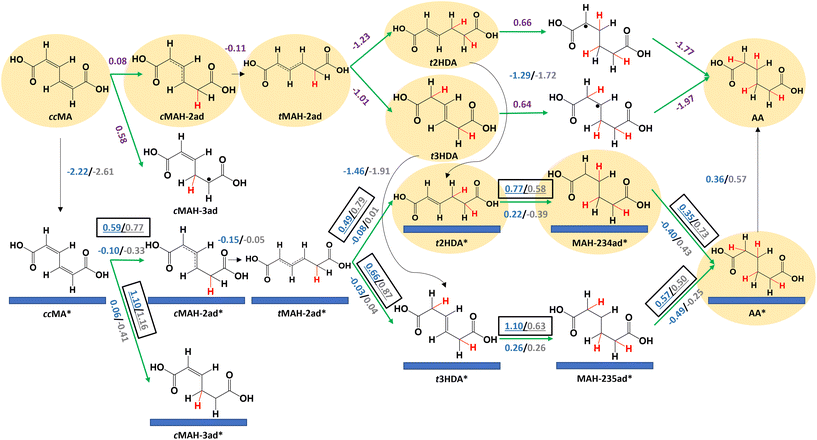
We performed DFT calculations to understand the different activities of ccMA ECH on foils and nanoparticles. We first investigated the reaction mechanism on Pd(111) and Pt(111) surfaces to understand reaction energetics on highly coordinated terrace surface sites. Fig. 3 summarizes the key elementary steps along with the corresponding reaction free energies (ΔG) and activation free energies (Ga); energetics are calculated at −0.14 V vs. the reversible hydrogen electrode (VRHE), equivalent to −0.40 VAg/AgCl at the relevant experimental conditions. A summary of all the elementary steps that were considered is provided in Fig. S6.† Adsorption of ccMA is thermodynamically favorable on (111) surfaces, with adsorption free energies of −1.91 eV for Pd(111) and −2.01 eV for Pt(111). However, the activation free energies for ccMA* hydrogenation to its preferred single-hydrogenation intermediate (cMAH-2ad*, Fig. 3) were relatively high (Pd: 0.82 eV, Pt: 0.40 eV). We therefore anticipate that the first hydrogenation will more readily occur through a non-catalytic outer-sphere mechanism in the solution (ΔG = 0.08 eV) at the considered potential. Although the radical cMAH-2ad species could adsorb on the surface (Pd: −1.83 eV, Pt: −2.18 eV), we anticipate that it also is more readily hydrogenated in solution to trans-2-hexenedioic acid (t2HDA) or t3HDA because of the similarly large activation free energies on the surface to form t2HDA* (Pd: 0.57 eV, Pt: 0.80 eV) or t3HDA* (Pd: 0.69 eV, Pt: 0.85 eV), whereas the formation of t2HDA or t3HDA in solution are highly favored energetically (more than 1 eV energetically downhill). This comparison of activation energies on the surface with free energies in solution provides only a qualitative picture of the relative reactivities of the surface and solution processes. We do not exclude the prospect of the surface forming t2HDA* or t3HDA* solely on the basis of the calculations, as calculating appropriate activation energies in the solution phase would be computationally expensive to perform accurately. We do note, however, the activation energies required to perform ECH to t2HDA or t3HDA on the surface (each requiring overcoming a barrier of at least 0.80 eV for an elementary hydrogenation step) are much larger than anticipated activation barriers for H3O+ dissociation (∼0.08 eV)42 and therefore we anticipate surface-mediated steps to be relatively difficult. These conclusions are consistent with our recent experimental studies showing that these steps can occur as outer-sphere PCET processes, with similar rates and selectivity for Pb, Bi, Pd, and Pt foils suggesting that the step is not directly surface-mediated.33,35The reaction free energies for further reduction of t2HDA (0.66 eV) and t3HDA (0.64 eV) in solution are substantially more positive. In these cases, the activation energies of surface-mediated t2HDA* hydrogenation on Pd(111) (0.39 eV) and Pt(111) (0.48 eV) are both lower than the solution-phase reaction free energy. We therefore anticipate the most favorable ECH of t2HDA occurs by adsorbing on the (111) surface (−0.63 eV for Pd, −1.11 eV for Pt) before the third and fourth elementary hydrogenations. The activation free energies for t3HDA* ECH are relatively higher (Pd: 0.77 eV; Pt: 1.16 eV), making the solution-phase reaction energetics more competitive. However, given that we observe AA on nanoparticles but not on foils (Fig. 2), we believe that t3HDA ECH most likely is a surface-catalyzed process. We further note that a more favorable pathway for t3HDA* ECH to AA may occur by isomerization on the surface to t2HDA*, with maximum activation free energies corresponding to H-abstraction (0.58 eV on Pd(111) and 1.04 eV on Pt(111)). t2HDA* will more readily undergo further ECH than desorb, explaining why it is not observed experimentally.
We note that Pt(111) generally binds species more strongly than Pd(111); for example, t2HDA and t3HDA bind stronger on Pt(111) by 0.48 eV and 0.51 eV, respectively. We also find that the activation free energy barriers are 0.1–0.4 eV higher on Pt(111) than on Pd(111) for steps after t2HDA* or t3HDA* adsorption, explaining the relatively poor experimental ECH activity to AA on Pt surfaces. This behavior is related to the tendency of stronger binding surfaces such as Pt to favor bond breaking, leading bond-making ECH steps to have higher barriers on such surfaces.43 This result is qualitatively similar to that in previous literature for benzaldehyde ECH, which suggested that Pd/C is significantly more active than Pt/C due to relatively low activation barriers for ECH of organic species on Pd.44
Finally, we calculate a slightly positive desorption free energy of 0.37 eV for AA* on Pd(111) and Pt(111), which is relatively weaker than the other species and easily overcome at the reaction conditions.34 Moreover, this adsorption strength is likely overestimated, as it is calculated according to Hess's law to close the thermodynamic cycle (see Methods section).45 Overall, the reaction energetics suggest the most favorable ECH pathway occurs by ccMA forming t2HDA/t3HDA in solution with AA produced by surfaces, and that the higher activity of Pd(111) stems from its overall lower activation energies along that pathway. Alternative free energy diagrams comparing Pd(111) and Pt(111) surface energetics are provided in Fig. S7 and S8.†
We next calculated reaction energetics on Pd(533) and Pt(533) surfaces to understand the effects of undercoordinated atoms at step edges on ccMA ECH (Fig. 4). As was the case on (111) surfaces, the reaction energetics suggest that ccMA ECH to t2HDA/t3HDA occurs through an outer-sphere mechanism due to the high activation energies associated with the corresponding surface reactions. The adsorption free energies of t2HDA (Pd(533): −1.29 eV; Pt(533): −1.72 eV) and t3HDA (Pd(533): −1.46 eV; Pt(533): −1.91 eV) are more favorable than on the corresponding (111) surfaces. However, the activation energies associated with the subsequent surface-mediated steps are substantially higher than on the corresponding (111) surfaces, again consistent with the principle that stronger-binding surfaces generally have higher barriers for bond-making steps. We therefore anticipate that stepped surfaces are relatively inactive for ccMA ECH (in particular, the ECH of t2HDA and t3HDA) due to their strong-binding nature. Free energy diagrams comparing Pd(533) and Pt(533) surface energetics are provided in Fig. S9 and S10.†
Our current computational approach does not differentiate between the energetics of Langmuir–Hinshelwood-type or Eley–Rideal-type mechanisms,46,47 for the purpose of simplicity within the scope of this work. The quantification of relative flux through these mechanisms is limited by our model, including crucial effects such as quantifying surface coverage effects and solvent–adsorbate interactions. We note that dissociation of H3O+ will have a small activation barrier42 (∼0.08 eV) relative to other calculated barriers, and therefore, we believe that its implicit treatment by focusing primarily on reaction free energies of solution phase steps is appropriate.48 We have not explicitly accounted for the effect of solvent, counterions, electrical double layer, surface charge effects, or coverage effects (e.g., effects of coadsorbed H*/other ions, water molecules, and organic species) in our surface calculations to maintain a reasonable computational cost in this mechanistic study. We acknowledge that this might impact the quantitative nature of our assessment, and note that some of these effects (e.g., interfacial electric field) might have appreciable effects on the absolute reaction energetics.49,50
Determining the relative barriers for trans-2-hexenedioic acid vs. trans-3-hexenedioic acid hydrogenation for adipic acid production
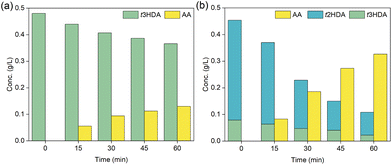
Our DFT results in Fig. 3 and 4 suggest that the hydrogenation of ccMA to AA proceeds sequentially through pathways that involve monounsaturated intermediates t2HDA and t3HDA. Therefore, to experimentally understand and validate these concepts, we performed constant-current bulk electrolysis experiments at −100 mA starting with t3HDA and t2HDA model solutions on Pd/C (Fig. 5).Since t2HDA is not commercially available, we synthesized it through base-catalyzed isomerization of t3HDA following a procedure reported previously.51 This method produces a mixture (HDAmix) of t2HDA (70–80%) and t3HDA (10–20%). Higher t2HDA concentrations could not be achieved due to the reaction's thermodynamic equilibrium. Separation of t2HDA also proved to be challenging as both isomers show similar chemical and physical properties. Nevertheless, the significantly higher concentration of t2HDA in the mixture compared to t3HDA enabled us to study its reactivity for the first time.
From Fig. 5, we note that both HDA intermediates were readily hydrogenated to AA on Pd/C with no trace of other hexenedioic acid isomers, which indicates that t2HDA to t3HDA isomerization (or vice versa) in solution is unlikely under ECH conditions. The reaction rate was also significantly faster for the t2HDA and t3HDA mixture compared to pure t3HDA, which is in line with DFT-calculated lower activation energies (eV) for t2HDA* hydrogenation (Pd(111): 0.39, Pd(533): 0.77) compared to t3HDA* hydrogenation (Pd(111): 0.77, Pd(533): 1.10) on Pd.
Understanding the effect of organic intermediates on hydrogen desorption characteristics at Pd- and Pt-based materials
Previously, Singh et al.52 quantified the adsorption of organics based on the charge calculation in the underpotential deposited hydrogen (HUPD) region using a Pt wire electrode. They observed competitive adsorption between organics including phenol, benzaldehyde, and cyclohexanol vs. H+ at low concentrations of organics (0.01 M), and almost all the HUPD sites were blocked at higher concentrations. Further, Yu et al.53 recently showed that biomass-based organic molecules like furfural can exhibit coverage-dependent competitive adsorption with H*, due to differences in the adsorption geometries of furfural. Therefore, we calculated adsorption free energies of H* to determine how they change in the presence of organics. Our DFT results show that the adsorption of H* becomes less favorable on each surface in the presence of ccMA*, t2HDA*, and t3HDA*, with the following ranges of destabilization on each surface: Pd(111) 0.38–0.46 eV; Pd(533) 0.14–0.46 eV; Pt(111) 0.22–0.30 eV; Pt(533) 0.18–0.29 eV. To experimentally investigate this effect at foils and nanoparticles, we performed cyclic voltammetry (CV) measurements using respective model solutions, explained in detail in the Experimental section. The potential was swept between −0.25 VAg/AgCl and 1.25 VAg/AgCl, where ccMA and its intermediates are not active for ECH. Fig. 6 shows the HUPD adsorption/desorption peaks in the 0.0 to −0.25 VAg/AgCl range on Pt foil.CVs performed on the model solutions containing ccMA (Fig. 6a), HDAmix (Fig. 6b), and t3HDA (Fig. 6c) showed suppression of Hdesorption peaks. In comparison, the model solution containing AA (Fig. 6d) did not show any changes in the CV. The low solubility limit of ccMA and its intermediates limits the complete blockage of Pt sites. Unlike Pt foil, Pd foil (Fig. S11†) does not show any facet-specific Hadsorption/desorption peaks, but only one prominent peak for Hdesorption. Overall, from Fig. S11–S13,† we observe a similar trend across all materials with approximately the same percent suppression of HUPD peak for strong binding organics such as MA and HDA. These CVs combined with DFT calculations hint at the presence of competitive adsorption between H+ and respective organic species, except in cases of weakly binding organics like AA.
To determine the relative interplay between ccMA ECH and HER at foils and NPs, we performed linear sweep voltammetry (LSV) for respective model solutions at Pd/Pt foils and Pd/Pt carbon-supported nanoparticles (Fig. S14†). The LSV currents were normalized by the metallic surface area calculated using CO chemisorption for the supported metal nanoparticles, and the geometric surface area for the foils. The current transients observed for blank samples were purely HER. Comparing the onset potentials of HER in the presence and absence of organics on Pt foils (Fig. S14a†) and Pt NPs (Fig. S14b†), we note that the presence of organics does not change the onset potential of HER on either of these Pt-based materials.
Together, these observations suggest that the presence of organics or the structure of Pt and Pd surface do not significantly impact the thermodynamic driving force for HER under acidic conditions on the Pt and Pd surfaces studied in this work. Overall, while these observations on Pt surfaces are in line with previous AIMD calculations by Yuk et al. which showed that Pt(111) does not have a strong impact of the presence of an organic on the HER activity, our observations contrast with their findings on Pd(111) which showed suppression of HER activity in the presence of strong binding organics.54 Finally, we did not detect any differences in the onset potential of HER for blank solutions on Pd- and Pt-based materials (Fig. S14†).
Implications for catalyst design
Our computational results demonstrated that while t3HDA most likely forms via an outer-sphere electrochemical process, the subsequent formation of AA likely occurs on the surface as the activation energy barriers are significantly lower for those ECH steps. Further, the structure sensitivity of t3HDA activation is significant, as terraces (e.g., (111) surface facets) are likely to be much more active for AA formation than undercoordinated step edges due to the overbinding nature of step edges. Our experimental results showed that Pd/C (and, to a lesser extent, Pt/C) nanoparticles were active for AA formation, in contrast to the corresponding foils that yielded only t3HDA. We therefore anticipate the commercial Pd/C and Pt/C catalysts contain a relatively high fraction of terrace-like atoms on their surfaces, while the foils contain a high proportion of undercoordinated step atoms.We investigated the nature of Pd and Pt metal foils and supported nanoparticles using X-ray diffraction (XRD) (Fig. 7). We note that XRD is not a surface-sensitive technique and that its information depth typically ranges between 1 and 10 μm.55 However, prior studies have shown excellent correlations between XRD and surface-sensitive techniques (e.g., EBSD) in the case of commercial Pd and Pt foils.55,56 Here, we combine our X-ray diffractograms with TEM images (Fig. S15†) and previous EBSD-based arguments for these materials to comment on the exposed surface facets. The X-ray diffractograms of foils showed mainly (220) step reflections with trace amounts of (111) and (200) terrace reflections, which is characteristic of the orientation of its fcc structure. These reflections are consistent with XRD and EBSD results obtained independently by other groups; the predominance of high-index facets was attributed to the sheer forces applied during the cold rolling of Pd foils.55–57 Further, Yule et al. recently showed that HER is relatively more facile on higher index facets such as (411), compared to that on lower-index facets including (100), (111), and (110).58 Combining this observation with our X-ray diffractograms and the high FE of HER (>95%) on our polycrystalline foils, we anticipate a relatively larger fraction of higher index facets on our polycrystalline Pd and Pt foils. As an additional validation, we compared the CV of our polycrystalline Pt foil (Fig. 6) with those reported by Marković et al.,59 which suggest that our polycrystalline Pt foil has (100), (111), and (110) type facets. Specifically, we observe a slightly larger current density for the (110) characteristic peak at −0.22 VAg/AgCl compared to that for other coupled characteristic peaks of (111) and (100) facets in the range of −0.01 to −0.12 VAg/AgCl, which supports our claim of relative abundance of steps compared to terraces on polycrystalline foils.
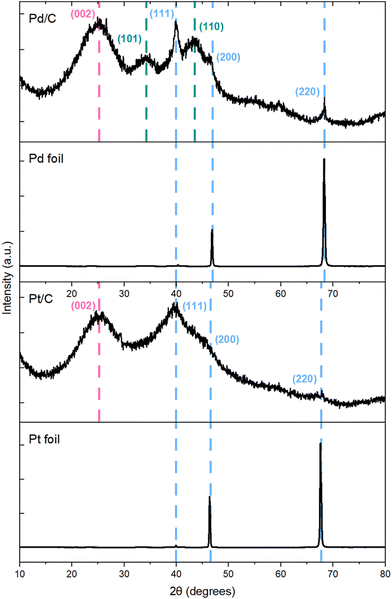 | ||
| Fig. 7 X-ray diffractograms of Pd/C, Pd foil, Pt/C, and Pt foil before reaction. Color code: metal (blue), carbon (pink), PdO (green). | ||
In contrast, our X-ray diffractograms for Pd/C and Pt/C display reflections higher along the (111), and (200) facets, which are characteristic of the fcc crystal of Pd (or Pt), consistent with literature.60 Combining these X-ray diffractograms with the d-spacing determined from the TEM image of Pd/C (Fig. S15†), we infer that our Pd/C and Pt/C have relatively higher exposure of terraces than the corresponding foils. Overall, these observations are therefore consistent with our DFT-predicted notion that the improved activity of our nanoparticle catalysts is due to a high exposure of terrace sites on those materials. Combining this prediction with our CA results (Fig. 2), our experimental and computational work suggest that terraces are more active than steps for MA ECH to AA. This finding contrasts with previous literature,61 which suggested that the ECH of aliphatic ketones is more favorable on undercoordinated sites of Pt-group metals than on the respective terraces.
We performed preliminary tests to determine the recyclability of the Pd/C catalyst, using the same catalyst for 3 consecutive ECH runs held at a constant potential of −0.40 VAg/AgCl for 1 hour. These showed that the catalyst deactivates over time (Fig. S16†), consistent with literature on Pd/C for formic acid electro-oxidation.62 Mitigating this deactivation is beyond the scope of the present work and will be a topic of future studies.
Our results demonstrate the benefit of structure-sensitive catalyst design strategies for these reactions. The higher activity of (111) facets motivates the exploration and use of catalyst materials selectively exposing such faces, such as Pd octahedra.63 Future catalyst design efforts should also explore the effects of adsorbate binding; our calculations suggested that weaker binding of adsorbates is beneficial for reducing activation energies for AA formation, though it is still to be determined whether weakening binding relative to that on Pd(111) would continue to enhance activity by lowering activation energies, given the need to activate C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (i.e., finding the peak of an activity “volcano” plot). Finally, improved catalysts would continue to mitigate HER activity while reducing dependence on precious metal components.
C bonds (i.e., finding the peak of an activity “volcano” plot). Finally, improved catalysts would continue to mitigate HER activity while reducing dependence on precious metal components.
Conclusions
The use of electrocatalysis to drive the next generation of sustainable chemical transformations requires atomic-scale innovation and insight to design systems with suitable activity and selectivity to desired products. We here provide the first report in the literature of appreciable AA production from ccMA ECH using Pd nanoparticles. This contrasts with small to no AA activity on Pt nanoparticles, and production of only t3HDA on Pd and Pt foils. Using computations, we obtain an atomic-scale understanding of ccMA ECH towards t2HDA, t3HDA, and AA at terraces and undercoordinated steps of Pd and Pt. DFT-calculated reaction energetics suggest that the initial reduction of ccMA → t2HDA/t3HDA might be happening through an outer-sphere mechanism; this is corroborated by the lack of significant change observed experimentally in the onset potential of ccMA ECH on foils or nanoparticles of Pd and Pt. In contrast, the subsequent reduction of the monounsaturated acids to AA likely proceeds through a surface-mediated pathway at the catalyst surface. DFT calculation combined with constant-current bulk electrolysis experiments further suggest that t2HDA reacts faster than t3HDA to form AA, which may explain the lack of t2HDA observed in bulk electrolysis products. DFT calculations predict that terraces are more active than steps for the formation of AA due to the substantially lower activation energies found on (111) surfaces; this combined with XRD analysis suggests the higher activity of Pd/C nanoparticles relative to foil is due to a relative abundance of terrace-like surface atoms compared to foils. Experimental CVs suggest the presence of competitive adsorption between H+ and organics at metal–electrolyte interface; LSVs show no detectable change in the HER onset in the presence of organics on Pt- or Pd-based materials. Together, these results suggest structure-sensitive catalyst design strategies employing selective exposure of terrace atoms and modulation of surface binding strength to further reduce activation energy barriers and yield high ECH activity.Experimental details
Computational details
Plane-wave DFT calculations were performed using the Vienna ab initio simulation package (VASP).64,65 Electron–ion interactions were quantified by projector augmented wave (PAW) potentials.66,67 Exchange correlations were calculated using Perdew–Burke–Ernzerhof (PBE) functionals.68 The zero-damped DFT-D3 method was implemented to apply dispersion corrections.69,70 Dipole corrections were applied in the z-direction normal to the surface.71 The kinetic energy cutoff was set to 400 eV, with electronic convergence calculated to 10−4 eV.Calculations on (111) surfaces were performed using a 5 × 5 × 4 periodic unit cell; those on (533) surfaces were performed with a 4 × 5 × 4 periodic unit cell. Metal atoms in the bottom two layers of all the slabs were fixed at their respective bulk positions; all other atoms, including adsorbates, were fully relaxed. A 4 × 4 × 1 Monkhorst–Pack k-point grid72 was used for these surface calculations; the grid was gamma-centered on (111) surfaces. At least 14 Å of vacuum spacing was used between periodic images. DFT-calculated lattice constants of bulk Pd and Pt were used to construct all slab models (experimental values73 are provided in parentheses, all values in Å): Pd 3.89 (3.89), Pt 3.92 (3.92). For geometric optimization, ionic forces on each atom were converged to 0.02 eV Å−1. Transition states and activation energies for surface-mediated elementary steps were evaluated using the climbing image nudged elastic band method;74,75 seven interpolated images and a force convergence criterion of 0.05 eV Å−1 were used to calculate activation energies.
The Gaussian 09 simulation package was used to determine solution phase Gibbs free energies.76 The QB3 variant of complete basis set (CBS) extrapolation method was used; optimizations were performed with the “verytight” convergence criteria.77,78 The SMD variant of the polarizable continuum model (PCM) with integral equation formalism variant was used to model the presence of water (solvent).79
Gibbs free energies of all species were referenced to the gas phase free energies of ccMA and H2, and the energy of clean slabs:
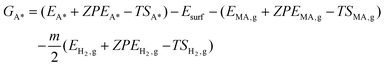 | (1) |
Here, Ei are DFT-calculated total energies, ZPEi are calculated zero-point energies, and Si are calculated entropies. Systems denoted with A* contain species A adsorbed on the surface; systems with subscript “g” refer to respective gas-phase quantities (all the required quantities are provided in Tables S1–S6†). Esurf is the total energy of the clean slab. The harmonic oscillator approximation was used to calculate ZPE and S. The temperature (T) is 298 K, in accordance with experimental conditions. The constant m corresponds to the stoichiometric coefficient for H2.
Assuming equilibrium between H2(g) and proton/electron pairs, the computational hydrogen electrode model80 was used to apply a linear correction to the free energies of faradaic elementary steps:
| A* + (H+ + e−) → B* | (2) |
| ΔG(URHE) = GB* − GA* + |e|URHE | (3) |
| Ga(URHE) = Ga(U0,RHE) + β*(URHE − U0,RHE) | (4) |
Here, U0,RHE is the onset potential (with the reference to the RHE) for coadsorption of H* (relative to H2(g)) in the presence of the reactant molecule for the respective hydrogenation step on a modeled catalyst surface. We assume the value of the symmetry factor (β) to be 0.5, noting potential limitations of this assumption.81
Electrode potentials experimentally referenced to the Ag/AgCl electrode were converted to a reference vs. the RHE using the following expression: URHE = UAg/AgCl + 0.197 + 0.059 × pH. All DFT calculations for H+/e− transfer steps are accordingly presented at 298 K and URHE = −0.14 V to match the electrode potential of −0.40 V vs. Ag/AgCl for the bulk electrolysis experiments at pH 1. All elementary reaction energetics are provided in Tables S5–S6.† Due to differences in DFT methods used for calculating solution-phase reaction energetics (hybrid functionals in Gaussian 09) and those at metal surfaces (PBE functionals with plane-wave basis) in Fig. 3 and 4, the thermodynamic cycle must be closed via Hess's law for consistency. We calculated the adsorption energy of ccMA* relative to a gas-phase ccMA reference; these and all subsequent surface-mediated steps were calculated using VASP relative to the common references. We also calculated the energetics of species from ccMA to AA using Gaussian 09 as described above. To maintain consistency of the thermodynamic cycle, we then applied Hess's law to implicitly determine the desorption energies of t2HDA, t3HDA, and AA such that the path to forming each of these species (whether via the surface or solution) has the same net energy change from the ccMA starting point to the given end point. We recognize that this will overestimate the binding strength of ccMA, t2HDA, t3HDA, and AA, as a gas-phase reference for ccMA is more unstable than the “true” reference state, though calculating the appropriate reference energy of ccMA is nontrivial due in part to the low solubility of ccMA in solution. The conclusions of this work are unaffected by the absolute magnitudes of adsorption/desorption energies.
Materials
cis,cis-Muconic acid (ccMA, 97%), adipic acid (AA, 99%), dimethylmalonic acid (DMA, TraceCERT® grade for qNMR), deuterium oxide (D2O, 99.9 atom% D), potassium sulfate (K2SO4, 99%), sulfuric acid-d2 (96–98 wt% in D2O, 99.5 atom% D) were purchased from Millipore Sigma. trans-3-Hexenedioic acid (t3HDA, 98%) was purchased from Tokyo Chemical Industries. Graphitic carbon felt (0.125 in. thick, 99%) was purchased from Fisher Scientific. Palladium and platinum foils (0.001 in. thick, 99%) were purchased from Fisher Scientific. Pd/C (5 wt%) and Pt/C (5 wt%) powders with average metal particle size ∼3 nm were purchased from Millipore Sigma. pH 1 model solutions were prepared by first dissolving a desired amount of ccMA, t3HDA, or AA in deionized (DI) water by ultrasonication; upon dissolution, 18.2 M sulfuric acid (H2SO4) was added to obtain an electrolyte concentration of 0.1 M. t2HDA is not commercially available, and therefore, we synthesized it through base-catalyzed isomerization of t3HDA with purity up to 70–80% t2HDA along with t3HDA. Deionized (DI) water (18.2 MΩ cm, Barnstead™ E-Pure™) was used for all experiments in this work.Electrochemical measurements and reactions
Dissolution of ccMA in H2SO4 at pH 1 is notoriously challenging due to its poor solubility,33 rapid isomerization to ctMA,82 and progressive acid-catalyzed lactonization to muconolactone.82,83 We dissolved 50 mg of ccMA in 100 mL of water to remain below the solubility limit of 1 g L−1 at pH 1. We found that accelerating the dissolution process with the help of ultrasound mitigated isomerization to ctMA, and maintaining the temperature at less than 30 °C limited the lactonization process. As such, we managed to consistently prepare stock solutions with <12–18% ctMA and Mlac. Mlac was omitted from the product distribution in Fig. 2, 5, and Fig. S1–S3† as it did not interfere with the hydrogenation reaction and its concentration remained consistent throughout all chronoamperometry experiments. All Mlac was consumed when we performed ccMA ECH at higher catalyst loadings (Fig. S4†).All electroanalytical measurements and bulk electrolysis were performed using a BioLogic SP-150e potentiostat coupled with a VMP3 10A booster. The uncompensated solution resistance was measured by potentiostatic electrochemical impedance spectroscopy (PEIS) and an 85% iR compensation was applied by the electrochemical workstation to all measurements. A single-compartment 3-electrode setup was used for all electroanalytical measurements (PEIS, LSV, CV). The solution was purged with argon gas before and during measurements. An Ag/AgCl electrode (Pine Research Instrumentations) and a Pt coil served as reference and counter electrodes, respectively. The working electrode consisted of either Pt or Pd foils (2 × 2 cm), or 1 mg of commercial 5 wt% Pt/C or Pd/C ink drop-casted on a glassy carbon electrode.
Bulk electrolysis was performed using a single-compartment ElectroCell MicroFlow Cell® (Amherst, NY) equipped with a Fisherbrand GP1000 peristaltic pump and operated as a loop reactor. A schematic and photographs of the experimental setup are provided in the ESI (Fig. S17†). Pd and Pt foils were attached to a graphite electrode (ElectroCell) using double-sided conductive Cu tape. Pt/C and Pd/C inks were drop casted on a carbon felt (0.125 in) and pressed against the graphite electrode for electrical contact using a PTFE mesh that also served as a turbulence promoter. Platinized titanium was used as a counter electrode, while Ag/AgCl connected to a PTFE separator was used as a reference electrode. The electrode working area was confined to a maximum of 10 cm2 using EPDM rubber gaskets, which provided additional sealing. The electrode gap was 4 mm and the pump was set to deliver a flow rate of 3 mL s−1, ensuring turbulent conditions.84 Samples were drawn at regular intervals to record the progress of the reaction. The aliquots were dried in air overnight and then redissolved in an internal standard solution containing DMA dissolved in D2O. The samples were then analyzed by 1H-NMR using a Bruker 600 MHz spectrometer to identify the product conversion. All calculations were performed on a weight fraction basis.
XRD measurements were performed using a Siemens D500 X-ray diffractometer with a diffracted beam monochromator. To accurately determine possible changes in the HUPD region upon addition of the diacids, we performed the CVs presented in Fig. S11† using 40 wt% Pt/C instead of 5 wt% Pt/C.
Catalyst turnover frequencies were calculated using the rate of the reaction during the first 15 min (TOF = ccMA molecules converted per second per active surface metal site). The catalyst's active sites were calculated from pulsed CO chemisorption using Micromeritics Autochem II 2920. Total active sites were estimated from the cumulative CO adsorbed and considering the stoichiometric coefficient (1 mol of CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mol of Pt/Pd).
2 mol of Pt/Pd).
Author contributions
Deep M. Patel: investigating and validating theoretical calculations on Pd and Pt surfaces; writing – original draft, editing and review. Prathamesh T. Prabhu: investigating and validating electrochemical experiments; writing – editing and review. Geet Gupta: investigating and validating theoretical calculations for the solution phase. Marco Nazareno Dell'Anna: investigating and validating electrochemical experiments; Samantha Kling: investigating and validating electrochemical experiments; Huy Nguyen: investigating and validating electrochemical experiments; Jean-Philippe Tessonnier: conceptualizing, investigating, and supervising the electrochemical experiments; writing – review and editing. Luke T. Roling: conceptualizing, investigating, and supervising the theoretical calculations; writing – review and editing.Conflicts of interest
All authors of this paper declare that they have no conflicts of interest associated with this work.Acknowledgements
This material is supported by the National Science Foundation under award number EFMA-2132200. LTR acknowledges the Building a World of Difference Faculty Fellowship at Iowa State University. The computations reported in this paper are partially supported by HPC@ISU equipment at Iowa State University, some of which has been purchased through funding provided by NSF under MRI grant numbers 1726447 and 2018594. This research used the Theory and Computation facility of the Center for Functional Nanomaterials (CFN), which is a U.S. Department of Energy Office of Science User Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704.References
- D. Vincent Sahayaraj, A. Lusi, A. J. Kohler, H. Bateni, H. Radhakrishnan, A. Saraeian, B. H. Shanks, X. Bai and J.-P. Tessonnier, Energy Environ. Sci., 2023, 16, 97–112 RSC.
- B. H. Shanks and P. L. Keeling, Green Chem., 2017, 19, 3177–3185 RSC.
- B. H. Shanks, Ind. Eng. Chem. Res., 2010, 49, 10212–10217 CrossRef CAS.
- T. J. Schwartz, B. J. O'Neill, B. H. Shanks and J. A. Dumesic, ACS Catal., 2014, 4, 2060–2069 CrossRef CAS.
- B. X. Lee, F. Kjaerulf, S. Turner, L. Cohen, P. D. Donnelly, R. Muggah, R. Davis, A. Realini, B. Kieselbach, L. S. MacGregor, I. Waller, R. Gordon, M. Moloney-Kitts, G. Lee and J. Gilligan, J. Public Health Policy, 2016, 37, 13–31 CrossRef PubMed.
- J. Iglesias, I. Martínez-Salazar, P. Maireles-Torres, D. Martin Alonso, R. Mariscal and M. López Granados, Chem. Soc. Rev., 2020, 49, 5704–5771 RSC.
- A. Castellan, J. C. J. Bart and S. Cavallaro, Catal. Today, 1991, 9, 237–254 CrossRef CAS.
- H. Lü, W. Ren, P. Liu, S. Qi, W. Wang, Y. Feng, F. Sun and Y. Wang, Appl. Catal., A, 2012, 441–442, 136–141 CrossRef.
- J. Rios, J. Lebeau, T. Yang, S. Li and M. D. Lynch, Green Chem., 2021, 23, 3172–3190 RSC.
- E. Skoog, J. H. Shin, V. Saez-Jimenez, V. Mapelli and L. Olsson, Biotechnol. Adv., 2018, 36, 2248–2263 CrossRef CAS PubMed.
- S. M. Zhou, K. Tashiro and T. Li, Polym. J., 2001, 33, 344–355 CrossRef CAS.
- W. Deng, Q. Zhang and Y. Wang, J. Energy Chem., 2015, 24, 595–607 CrossRef.
- T. Debuissy, E. Pollet and L. Avérous, J. Polym. Sci., Part A: Polym. Chem., 2017, 55, 1949–1961 CrossRef CAS.
- X. Zhang, Y. Liu, J. Wang, Y. Zhao and Y. Deng, J. Microbiol., 2020, 58, 1065–1075 CrossRef CAS PubMed.
- Fortune Business Insights, Food Service Market Size, Share & COVID-19 Impact Analysis, Market Research Report, 2022.
- M. T. Musser, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co., Hoboken, NJ, USA, 2000 Search PubMed.
- S. R. Nicholson, N. A. Rorrer, T. Uekert, G. Avery, A. C. Carpenter and G. T. Beckham, ACS Sustainable Chem. Eng., 2023, 11, 2198–2208 CrossRef CAS.
- S. Gundekari, B. Biswas, T. Bhaskar and K. Srinivasan, Biomass Bioenergy, 2022, 161, 106448 CrossRef CAS.
- M. Lang and H. Li, ChemSusChem, 2022, 15, e202101531 CrossRef CAS PubMed.
- B. H. Shanks and L. J. Broadbelt, ChemSusChem, 2019, 12, 2970–2975 CrossRef CAS PubMed.
- A. E. Settle, L. Berstis, N. A. Rorrer, Y. Roman-Leshkóv, G. T. Beckham, R. M. Richards and D. R. Vardon, Green Chem., 2017, 19, 3468–3492 RSC.
- B. Hočevar, A. Prašnikar, M. Huš, M. Grilc and B. Likozar, Angew. Chem., Int. Ed., 2021, 60, 1244–1253 CrossRef PubMed.
- A. Corona, M. J. Biddy, D. R. Vardon, M. Birkved, M. Z. Hauschild and G. T. Beckham, Green Chem., 2018, 20, 3857–3866 RSC.
- D. R. Vardon, M. A. Franden, C. W. Johnson, E. M. Karp, M. T. Guarnieri, J. G. Linger, M. J. Salm, T. J. Strathmann and G. T. Beckham, Energy Environ. Sci., 2015, 8, 617–628 RSC.
- G. Wang, S. Øzmerih, R. Guerreiro, A. C. Meireles, A. Carolas, N. Milne, M. K. Jensen, B. S. Ferreira and I. Borodina, ACS Synth. Biol., 2020, 9, 634–646 CrossRef CAS PubMed.
- T. Liu, B. Peng, S. Huang and A. Geng, Bioresour. Technol. Rep., 2020, 9, 100395 CrossRef.
- R. Sillers, R. Hermann, M. Spencer, R. Udani and R. R. Yocum, US 2021/0277429 A1, 2021.
- X. She, H. M. Brown, X. Zhang, B. K. Ahring and Y. Wang, ChemSusChem, 2011, 4, 1071–1073 CrossRef CAS PubMed.
- S. Capelli, A. Rosengart, A. Villa, A. Citterio, A. Di Michele, C. L. Bianchi, L. Prati and C. Pirola, Appl. Catal., B, 2017, 218, 220–229 CrossRef CAS.
- S. Capelli, D. Motta, C. Evangelisti, N. Dimitratos, L. Prati, C. Pirola and A. Villa, ChemCatChem, 2019, 11, 3075–3084 CrossRef CAS.
- A. E. Settle, N. S. Cleveland, C. A. Farberow, D. R. Conklin, X. Huo, A. A. Dameron, R. W. Tracy, R. Sarkar, E. J. Kautz, A. Devaraj, K. K. Ramasamy, M. J. Watson, A. M. York, R. M. Richards, K. A. Unocic, G. T. Beckham, M. B. Griffin, K. E. Hurst, E. C. D. Tan, S. T. Christensen and D. R. Vardon, Joule, 2019, 3, 2219–2240 CrossRef CAS.
- M. Suastegui, J. E. Matthiesen, J. M. Carraher, N. Hernandez, N. Rodriguez Quiroz, A. Okerlund, E. W. Cochran, Z. Shao and J.-P. Tessonnier, Angew. Chem., Int. Ed., 2016, 55, 2368–2373 CrossRef CAS PubMed.
- M. N. Dell'Anna, M. Laureano, H. Bateni, J. E. Matthiesen, L. Zaza, M. P. Zembrzuski, T. J. Paskach and J.-P. Tessonnier, Green Chem., 2021, 23, 6456–6468 RSC.
- J. E. Matthiesen, J. M. Carraher, M. Vasiliu, D. A. Dixon and J.-P. Tessonnier, ACS Sustainable Chem. Eng., 2016, 4, 3575–3585 CrossRef CAS.
- M. N. Dell'Anna, G. Gupta, P. T. Prabhu, T.-H. Chu, L. T. Roling and J.-P. Tessonnier, Green Chem., 2023, 25, 10387–10397 RSC.
- S. Abdolmohammadi, D. Gansebom, S. Goyal, T. H. Lee, B. Kuehl, M. J. Forrester, F. Y. Lin, N. Hernández, B. H. Shanks, J.-P. Tessonnier and E. W. Cochran, Macromolecules, 2021, 54, 7910–7924 CrossRef CAS.
- J. T. Bender, A. S. Petersen, F. C. Østergaard, M. A. Wood, S. M. J. Heffernan, D. J. Milliron, J. Rossmeisl and J. Resasco, ACS Energy Lett., 2023, 8, 657–665 CrossRef CAS.
- K. S. Exner, Curr. Opin. Electrochem., 2021, 26, 100673 CrossRef CAS.
- D. Wei, X. Shi, P. Sponholz, H. Junge and M. Beller, ACS Cent. Sci., 2022, 8, 1457–1463 CrossRef CAS PubMed.
- M. A. Khan, T. A. Al-Attas, N. G. Yasri, H. Zhao, S. Larter, J. Hu and M. G. Kibria, Sustainable Energy Fuels, 2020, 4, 5568–5577 RSC.
- H. Luo, J. Barrio, N. Sunny, A. Li, L. Steier, N. Shah, I. E. L. Stephens and M.-M. Titirici, Adv. Energy Mater., 2021, 11, 2101180 CrossRef CAS.
- Q. Yu and J. M. Bowman, J. Chem. Theory Comput., 2016, 12, 5284–5292 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- N. Singh, U. Sanyal, G. Ruehl, K. A. Stoerzinger, O. Y. Gutiérrez, D. M. Camaioni, J. L. Fulton, J. A. Lercher and C. T. Campbell, J. Catal., 2020, 382, 372–384 CrossRef CAS.
- J. Park and L. T. Roling, AIChE J., 2020, 66, e17036 CrossRef CAS.
- B. Tran, Y. Cai, M. J. Janik and S. T. Milner, J. Phys. Chem. A, 2022, 126, 7382–7398 CrossRef CAS PubMed.
- J. Ekspong, E. Gracia-Espino and T. Wågberg, J. Phys. Chem. C, 2020, 124, 20911–20921 CrossRef CAS.
- S. A. Akhade, N. J. Bernstein, M. R. Esopi, M. J. Regula and M. J. Janik, Catal. Today, 2017, 288, 63–73 CrossRef CAS.
- J. Li, J. H. Stenlid, T. Ludwig, P. S. Lamoureux and F. Abild-Pedersen, J. Am. Chem. Soc., 2021, 143, 19341–19355 CrossRef CAS PubMed.
- H. J. Peng, M. T. Tang, J. Halldin Stenlid, X. Liu and F. Abild-Pedersen, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- J.-P. Tessonnier, B. H. Shanks, E. W. Cochran, J. E. Hadel, M. N. Dell'Anna, P. Carter and D. Gansebom, WO-2022061275-A1, 2022.
- N. Singh, U. Sanyal, J. L. Fulton, O. Y. Gutiérrez, J. A. Lercher and C. T. Campbell, ACS Catal., 2019, 9, 6869–6881 CrossRef CAS.
- I. K. M. Yu, F. Deng, X. Chen, G. Cheng, Y. Liu, W. Zhang and J. A. Lercher, Nat. Commun., 2022, 13, 7154 CrossRef CAS PubMed.
- S. F. Yuk, M.-S. Lee, S. A. Akhade, M.-T. Nguyen, V.-A. Glezakou and R. Rousseau, Catal. Today, 2022, 388–389, 208–215 CrossRef CAS.
- K. Hayashi, S. Kameoka and A.-P. Tsai, Mater. Trans., 2021, 62, 1089–1096 CrossRef CAS.
- M. Yuan, K. Lee, D. G. Van Campen, S. Liguori, M. F. Toney and J. Wilcox, Ind. Eng. Chem. Res., 2019, 58, 926–934 CrossRef CAS.
- A. L. Cabrera, E. Morales-Leal, J. Hasen and I. K. Schuller, Catal. Lett., 1994, 30, 11–23 CrossRef CAS.
- L. C. Yule, E. Daviddi, G. West, C. L. Bentley and P. R. Unwin, J. Electroanal. Chem., 2020, 872, 114047 CrossRef CAS.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
- F. Sanchez, D. Motta, A. Roldan, C. Hammond, A. Villa and N. Dimitratos, Top Catal., 2018, 61, 254–266 CrossRef CAS PubMed.
- C. J. Bondue, F. Calle-Vallejo, M. C. Figueiredo and M. T. M. Koper, Nat. Catal., 2019, 2, 243–250 CrossRef CAS.
- M. Smiljanić, M. Bele, L. Moriau, F. Ruiz-Zepeda, M. Šala and N. Hodnik, J. Phys. Chem. C, 2021, 125, 27534–27542 CrossRef.
- M. Jin, H. Zhang, Z. Xie and Y. Xia, Energy Environ. Sci., 2012, 5, 6352–6357 RSC.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, Florida, 97th edn, 2016 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Wallingford CT, 2013 Search PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. Rendón-Calle, Q. H. Low, S. H. L. Hong, S. Builes, B. S. Yeo and F. Calle-Vallejo, Appl. Catal., B, 2021, 285, 119776 CrossRef.
- J. M. Carraher, T. Pfennig, R. G. Rao, B. H. Shanks and J.-P. Tessonnier, Green Chem., 2017, 19, 3042–3050 RSC.
- J. M. Carraher, P. Carter, R. G. Rao, M. J. Forrester, T. Pfennig, B. H. Shanks, E. W. Cochran and J.-P. Tessonnier, Green Chem., 2020, 22, 6444–6454 RSC.
- S. J. C. Weusten, J. van der Schaaf and M. T. de Groot, J. Electroanal. Chem., 2022, 918, 116481 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional chronoamperometric results, DFT-calculated free energy diagrams, experimental CVs, LSVs, and supporting DFT energetics. See DOI: https://doi.org/10.1039/d3gc03021k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |