Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Extension of the D3 and D4 London dispersion corrections to the full actinides series†
Lukas
Wittmann‡
 a,
Igor
Gordiy‡
a,
Igor
Gordiy‡
 a,
Marvin
Friede‡
a,
Marvin
Friede‡
 a,
Benjamin
Helmich-Paris
a,
Benjamin
Helmich-Paris
 b,
Stefan
Grimme
b,
Stefan
Grimme
 a,
Andreas
Hansen
a,
Andreas
Hansen
 *a and
Markus
Bursch
*a and
Markus
Bursch
 *bc
*bc
aMulliken Center for Theoretical Chemistry, Universität Bonn, Beringstr. 4, 53115 Bonn, Germany. E-mail: hansen@thch.uni-bonn.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: bursch@kofo.mpg.de
cFACCTs GmbH, 50677, Köln, Germany
First published on 17th July 2024
Abstract
Efficient dispersion corrections are an indispensable component of modern density functional theory, semi-empirical quantum mechanical, and even force field methods. In this work, we extend the well established D3 and D4 London dispersion corrections to the full actinides series, francium, and radium. To keep consistency with the existing versions, the original parameterization strategy of the D4 model was only slightly modified. This includes improved reference Hirshfeld atomic partial charges at the ωB97M-V/ma-def-TZVP level to fit the required electronegativity equilibration charge (EEQ) model. In this context, we developed a new actinide data set called AcQM, which covers the most common molecular actinide compound space. Furthermore, the efficient calculation of dynamic polarizabilities that are needed to construct CAB6 dispersion coefficients was implemented into the ORCA program package. The extended models are assessed for the computation of dissociation curves of actinide atoms and ions, geometry optimizations of crystal structure cutouts, gas-phase structures of small uranium compounds, and an example extracted from a small actinide complex protein assembly. We found that the novel parameterizations perform on par with the computationally more demanding density-dependent VV10 dispersion correction. With the presented extension, the excellent cost-accuracy ratio of the D3 and D4 models can now be utilized in various fields of computational actinide chemistry and, e.g., in efficient composite DFT methods such as r2SCAN-3c. They are implemented in our freely available standalone codes (dftd4, s-dftd3) and the D4 version will be also available in the upcoming ORCA 6.0 program package.
1 Introduction
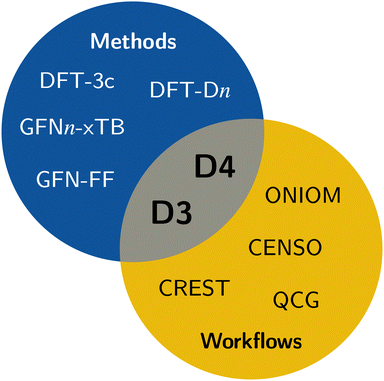
In computational chemistry, mean-field (MF) methods are very often the method of choice for the computation of the electronic and geometric structure of large systems. Some prominent members are Hartree–Fock theory, Kohn–Sham (KS) density functional theory (DFT), and semi-empirical extended tight-binding (TB) methods. However, a general problem of mean-field methods is the inability to describe long-range correlation effects, which are important to obtain correct energetic properties and geometries for many chemical problems.1 The most significant long-range correlation effect is the London dispersion interaction,2–5 which is not only important for non-covalent interactions (NCI),6,7 but also crucial for an accurate description of general thermochemistry,8,9 and even polarized systems that are expected to be dominated by electrostatic interactions (e.g., water clusters).10–13 Therefore, dedicated London dispersion corrections are necessary. This also applies to classical methods like force fields, where long-range dispersion effects need to be explicitly taken into account.14 Some of the popular models to describe long-range dispersion effects are the D315,16 and D417–19 corrections, Vydrov's and van Voorhis' VV1020 model, including rVV1021 and NL,22,23 the exchange-dipole moment (XDM) method,24–26 or the Tkatchenko–Scheffler (TS) method.27,28 Specifically, the efficient DFT-Dn approach has proven to be reliable in countless quantum chemical applications and workflows.29,30 It is also very often already out-of-the-box combined with modern density functionals of all rungs.31–33Due to the ever-growing interest in larger systems with hundreds to thousands of atoms, the need for efficient methods is increasing. In this regime of computational chemistry, method selection is significantly influenced by cost considerations. Popular choices are QM/MM schemes,34 combining a higher-level method in the areas of interest with a lower-level method for the surroundings; composite methods,35–41 augmenting fast DFT methods with systematic corrections; or semi-empirical methods42–44 that significantly reduce the computational cost by introducing systematic approximations. In these approaches, the usage of, e.g., the density-based DFT-NL scheme is not applicable because (i) it requires a reasonably accurate electron density and (ii) it is computationally expensive. Nonetheless, describing long-range dispersion effects is crucial, especially for larger systems, which are the primary application of efficient computational methods. Hence, there is a need for cost-effective dispersion corrections like the D3 and D4 models, which are employed in contemporary efficient methods including the GFN-FF force-field14 and the extended tight-binding GFNn-xTB methods.45–47 Accordingly, all workflows and tasks utilizing these efficient methods also depend on the availability of the respective D3 or D4 parameterizations. This, for example, includes conformer generation with the sophisticated conformer–rotamer-ensemble sampling tool CREST,48,49 fast transition-state sampling,50 or QM/MM approaches like ONIOM34,51,52 (see Fig. 1).
Due to the progress of modern computational chemistry, the investigation of very large systems has become possible, which has naturally extended the field of application to the complex field of biochemistry.53–56 The rich chemistry of actinides, in particular, has attracted attention due to their unique chemical properties, applications and role in nature.57 This part of (bio)chemistry studies, e.g., the efficient disposal of nuclear waste from nuclear power plants and dismantled nuclear weapons,58–61 environmental effects of naturally occurring or accidentally released actinides,62,63 the interactions of metals with organic species, for example, on metalloenzymes and biomimetic compounds,64–67 the metabolic and biological processes involving actinides68–70 – like their interaction with proteins,71 also in humans.70,72,73 In analytical (bio)chemistry, actinides are also already used,74 for example for bio-imaging75,76 by using nanoparticles,77 or radioimmunoassays.78 Moreover, actinides find utility in medicine, particularly in nuclear medicine,79 where they are utilized for, e.g., radiopharmaceutical imaging and therapeutic applications.80,81
However, due to the danger posed by the radioactivity of these elements and heavy metals in general, laboratory testing can be difficult. Therefore, theoretical research becomes invaluable in this context. Computational studies offer a safe and environmentally friendly alternative, enabling the prediction and avoidance of potential risks and hazardous substances before their large-scale application.82 The theoretical investigation can help to obtain a deeper understanding of the structure and reactivity of various bioorganic compounds, allowing for a systematic construction of biomimetics, which is the imitation of models, systems, and elements of nature for the purpose of solving complex human problems. In many cases, theoretical approaches are already accurate enough to allow comparison with experimental findings. Numerous theoretical works have been successfully published, offering valuable insights into various issues.83,84 The scope of application already ranges from investigations of the coordination chemistry of actinides,85 their oxides and nitrides,86–88 surface adsorption processes,89 to the investigation of complex properties,90 up to larger complexes and materials.91 Also, already more far-reaching problems like the optimization of radioactive waste transmutation were investigated theoretically.92 Even the role of dispersion interactions for actinide chemistry has already been investigated in some studies, which showed better agreement with the experiment.93
The efficient quantum chemical investigation of large actinide structures using mean-field methods is greatly limited by the availability of efficient dispersion corrections. The density-dependent schemes of Vydrov and van Voorhis and the XDM dispersion correction can be used combined with higher, much more expensive levels of theory, but no efficient solutions for semi-empirical methods are available.
With this work, we aim to extend our DFT-D3 and -D4 schemes to the full actinides series. This expansion will not only allow the existing DFT-D3 and -D4 density functionals to be applied to actinides but will also facilitate the adaptation of composite methods and various semi-empirical approaches to the entire series. We will begin by detailing the theory and implementation, followed by a description of the parameterization protocol. The final section will showcase the efficacy of the current dispersion correction schemes.
2 Theory and implementation
2.1 Dispersion correction schemes
In most dispersion-corrected methods, including our D3 and D4 schemes, the total electronic energy consists of the energy from the underlying mean-field approach and an additive contribution from the dispersion energy94| Etotal = EMF + Edisp. | (1) |
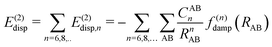 | (2) |
2.2 DFT-D3
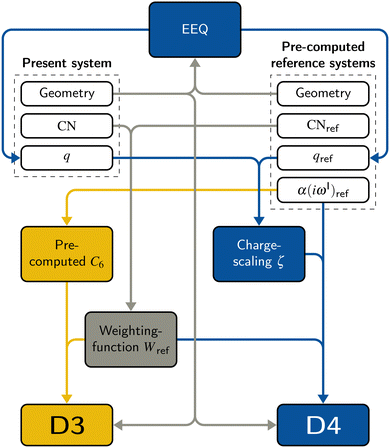
The DFT-D3 approach extends and improves its predecessor DFT-D2,102 notably by explicitly considering the structural environment through the use of a so-called fractional coordination number CN. This adaptation recognizes that atoms in different bonding or hybridization states possess distinct coordination numbers, which aligns well with chemical intuition. A simplified flowchart of the DFT-D3 scheme is shown in Fig. 2.To obtain the system-specific dispersion coefficients, reference dispersion coefficients CAB6,ref(CNA,CNB) of the reference systems AmHn and BkHl, are used. The values for m, n, k, and l are set individually for each reference system utilized. In principle, any realistic system can serve as a reference. For instance, structures such as P2H2 (m = 2, n = 2) or C2H4 (m = 2, n = 4) are already employed. These are pre-computed for every possible pair and obtained by a modified expression (eqn (4)) of the Casimir-Polder integration103 (eqn (3)) of electric dipole polarizabilities at imaginary frequency αA(iωI) for many reference systems. In the following, iωI is used interchangeably with iω for the imaginary part of ω = ωR + iωI.
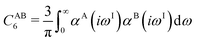 | (3) |
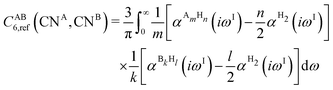 | (4) |
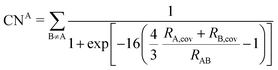 | (5) |
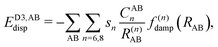 | (6) |
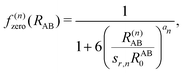 | (7) |
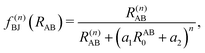 | (8) |
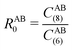 , the pair-wise cutoff radius, which is interchangeably called van-der-Waals radius in this work. The zero-damping scheme uses fixed a6 = 14 and a8 = 16, and one method-specific parameter sr,n, while BJ-damping utilizes the two method-specific parameters a1 and a2.
, the pair-wise cutoff radius, which is interchangeably called van-der-Waals radius in this work. The zero-damping scheme uses fixed a6 = 14 and a8 = 16, and one method-specific parameter sr,n, while BJ-damping utilizes the two method-specific parameters a1 and a2.
2.3 DFT-D4
A simplified flowchart of the DFT-D4 scheme is shown in Fig. 2. The DFT-D4 model further improves DFT-D3 by introducing an atomic partial charge dependence of the atomic reference polarizabilities αA(iωI) through the charge-scaling function ζ(zA,zA,ref).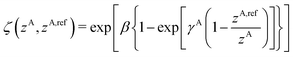 | (9) |
| αA,ref(iωI, zA) = αA,ref(iωI)ζ(zA,zA,ref) | (10) |
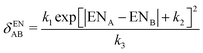 | (11) |
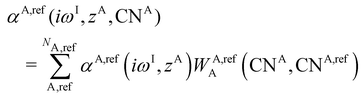 | (12) |
The final energy expression of the DFT-D4 model is given by eqn (13).
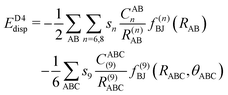 | (13) |
2.4 Electronegativity equilibration charges
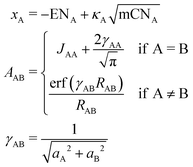
The partial charges used in the polarizability scaling are obtained with the classical electronegativity equilibration charge (EEQ) model. It is based on electronegativity equilibration of Gaussian-type charge densities.110 This is done by minimizing the following isotropic electrostatic (IES) energy expression (eqn (14)) with respect to the atomic charges. In the following, the equations are given in matrix notation, where capital bold letters indicate matrices and non-capital bold letters vectors. The individual atomic partial charges qA are the elements of the vector q.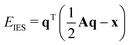 | (14) |
For each element A, four parameters are used: electronegativity ENA, hardness JAA, coordination number scaling parameter κA, and width of Gaussian charge distribution aA. These parameters are obtained by parameterization against accurate reference charges (DFT Hirshfeld level) using a dataset as described in Section 4.3. To obtain EEQ partial charges from these equations, the method of constrained Lagrangian optimization is employed under the constraint that the sum of the partial charges conserves the total charge qtotal of the system.
2.5 Dynamic purely imaginary-frequency polarizabilities
In order to evaluate the dispersion coefficients in eqn (3) and (4), the isotropic polarizabilities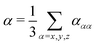 | (15) |
ααβ(iωI) = − 〈〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α; α;![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β〉〉ωI β〉〉ωI | (16) |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α. For self-consistent field (SCF) theories, the linear response function in eqn (16) is evaluated from the first electronic derivative of the dipole operator V[1] and the second electronic derivative matrices E[2] and S[2] by
α. For self-consistent field (SCF) theories, the linear response function in eqn (16) is evaluated from the first electronic derivative of the dipole operator V[1] and the second electronic derivative matrices E[2] and S[2] by〈〈![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) α; α;![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β〉〉ω = −(V[1])†α(E[2] − (ωR + iωI)S[2])−1V[1]β, β〉〉ω = −(V[1])†α(E[2] − (ωR + iωI)S[2])−1V[1]β, | (17) |
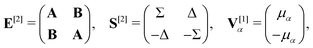 | (18) |
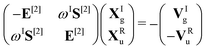 | (19) |
Alternatively, polarizabilities at purely imaginary frequencies can also be computed approximately by truncated moment expansions in order to avoid complex algebra.115–117 However, we have not introduced such approximations because the imaginary-frequency dynamic polarizabilities can be computed as efficiently as the ones with real frequencies without introducing any computational overhead.
The usage of purely-imaginary frequencies provides a powerful mathematical tool to simplify calculations and provide more stable numerical results. The usage of those was already shown to offer very accurate treatment of quantum many-body correlations,118–120 like dispersion-energy coefficients.121 They enable controllable simulation of equilibrium properties, nuclear quantum phenomena, and other non-adiabatic effects – often disadvantages of ab initio methods like quantum Monte Carlo approaches.122–124
3 Computational details
Quantum chemical calculations were performed with xtb 6.5.1, xtb-python 22.1, ORCA 5.0.4125,126 and the development version of ORCA 6.0. For calculations involving actinide elements, a locally-dense basis set approach is used for the actinide only. The def-TZVP127 and ma-def-TZVP128 basis for the actinides were used and implemented into the development version of ORCA 6.0. PBE0-NL/def2-SVP129 (def-TZVP for the actinide) was generally employed for geometries. For the creation of the hydride reference structures, PBE0/def2-TZVP (def-TZVP for the actinide) was used. Hirshfeld population analysis130 single points were calculated using ωB97M-V/def2-TZVPP131 (ma-def-TZVP for the actinide). The final benchmarking studies use DefGrid3 grid, geometries were obtained using def2-TZVP (ma-def-TZVP for the actinide) and single-point energies are calculated using ma-def2-TZVP basis (ma-def-TZVP for the actinide). Matching general-purpose auxiliary basis sets were automatically constructed on the fly using ORCA's AutoAux.132 The RIJCOSX133–135 approximation was used for all calculations. The DefGrid2 option was applied for the numerical integration grid as well as TightSCF convergence criteria as implemented in ORCA. For all calculations, the matching def2 (def for the actinide) effective small core potentials (ECPs)127,128,136,137 for heavy elements with Z > 36 were generally employed. The matching ECPs for the actinides already account for relativistic effects. The quality of the ECPs was tested against scalar relativistic, all-electron (ZORA) calculations for the geometries and dynamic purely-imaginary frequency polarizabilities and provide very similar results. These results for the actinium hydrides can be found in the ESI.†The SCF frequency-dependent polarizabilities were implemented into the development version of ORCA 6.0. For the calculation of the frequency-dependent polarizabilities of the reference systems, unrestricted PBE38/ma-def2-TZVP138 was used with tight convergence criteria (TightSCF) and DefGrid3 grid. PBE38 was chosen due to its robustness and successful application in previous parameterizations of the DFT-D dispersion corrections.15,139 This also ensures the greatest possible consistency with the existing parameterization of other elements. For every system, 23 frequency-dependent polarizabilities were calculated between iωImin = 10−6 and iωImax = 10.0.
DFT-NL was calculated using the ORCA native, non-self-consistent, post-SCF implementation. DFT-D3 and -D4 dispersion corrections were calculated using development versions of simple-dftd3 1.0.0 and dftd4 3.6.0, as well as the development version of ORCA 6.0.
All new functionalities implemented in the development version of ORCA will be made available in the upcoming version of ORCA 6.0.
4 Parameterization
This chapter is divided into parameterization of DFT-D3 and DFT-D4 for a better overview, although some parameters are used in both models.4.1 Parameterization of DFT-D3
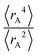 Expectation values.
The ratio of
Expectation values.
The ratio of 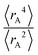 is used for the recursive calculation of the pairwise dipole–quadrupole CAB8 dispersion coefficients. The individual expectation values at the four-component relativistic PBE/Dyall-AE4Z140–142 levels of theory were used as provided in the framework of D3 parameterizations of super heavy elements.143–145 The respective
is used for the recursive calculation of the pairwise dipole–quadrupole CAB8 dispersion coefficients. The individual expectation values at the four-component relativistic PBE/Dyall-AE4Z140–142 levels of theory were used as provided in the framework of D3 parameterizations of super heavy elements.143–145 The respective 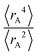 expectation values can be found in Section B.2 of the ESI.†
expectation values can be found in Section B.2 of the ESI.†
4.2 Parameterization of DFT-D4
The dynamic purely-imaginary frequency polarizabilities were obtained as described in Section 3. For D3, the described modified Casimir-Polder expression (eqn (4)) was used to obtain the atom pair-wise dispersion coefficients CAB6. Both, the dynamic purely-imaginary frequency polarizabilities and the atom pair-wise parameters can be found in Section C.4 of the ESI.†
4.3 Parameterization of EEQ
For the parameterization of the EEQ model, a set of actinide structures called AcQM was created. The set contains in total 2537 structures. The first part of 1283 structures contain realistic actinide complexes that were created using the Architector152,153 combined with our ArchitectorWrapper package,154 as described in our recent LnQM set.155 The structures were generated with only stable oxidation states of the central actinide with coordination numbers ranging from four to 10. The second part contains 1254 structures of smaller hydrides, fluorides, chlorides, oxides, and sulfides as well as various mindless structures. Mindless structures are randomly generated artificial molecules, that extend the structural space beyond conventional chemical intuition and thus including much more diverse structures. This helps to make the parameterization and model more robust. These structures were created by a program that randomly places 1–8 atoms from the first five periods of the periodic table (excluding any transition metals) together with a single actinide in close vicinity to each other. This procedure is described in detail in ref. 156; additionally, some examples are given in the ESI.† A first crude optimization of the structures using the respective lanthanide homolog was done using GFN2-xTB, followed by the described (Section 3) DFT geometry optimization. The AcQM set with the PBE0-NL optimized structures and the ωB97M-V Hirshfeld partial charges is provided in the ESI,† and on GitHub at https://github.com/grimme-lab/acqm.The EEQ model was parameterized against the obtained Hirshfeld charges using a modified simplex algorithm157,158 with the loss function given in the ESI.† Here, only the systems with total charges ranging from −1 to +1 are used to ensure the reliability of the reference Hirshfeld charges. The obtained parameters are given in Section D.3 of the ESI.†
The parameterization yields a mean absolute error (MAE) of 0.21e− and a root mean squared error (RMSE) of 0.25e− for all actinide charges of the AcQM set against the reference Hirshfeld charges (Fig. 3).
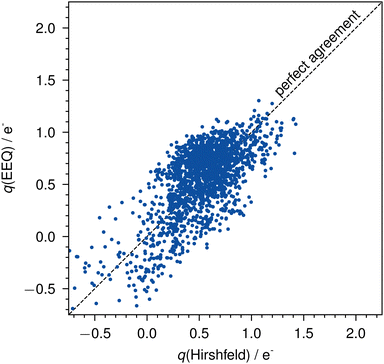 | ||
| Fig. 3 Errors of the EEQ model against Hirshfeld charges on the AcQM set. The dashed line indicates perfect agreement. | ||
5 Results and discussion
We tested the extension of the D3 and D4 models through multiple case studies focusing on various actinide compounds. As only the DFT-D4 extension is implemented in ORCA, the geometries are only tested with D4. With this, we aim to qualitatively assess the performance, especially to show the relative effect of utilizing dispersion correction schemes, while using experimental data as a reference where applicable. An in-depth quantitative analysis is not our goal and also not feasible due to a lack of experimental and, above all, accurate theoretical reference data. Studies investigating the general performance of dispersion corrections can be found in, e.g., ref. 29 and 159–162.Additionally, the density-dependent non-local dispersion correction DFT-NL will also be evaluated as a comparison. Generally, D3 and NL are found to perform similarly,161,163 However, NL sometimes offers an advantage when it comes to metallic systems where the electronic structure changes significantly – such as in ionization reactions.164 D4 seems to be able to keep up with NL in most cases and may offer better performance for general thermochemistry and larger systems compared to NL.33,161,165
NL requires reasonably accurate electron densities to obtain good results, which requires an expensive converged SCF density from, e.g., density functional theory. This means that the addition of NL in retrospect is not possible if no electron density is saved, and thus, requires the calculation to be re-done. It is important to note that NL only includes dipole–dipole interactions (C6) and no dipole–quadrupole (C8) or many-body effects (e.g., C9). The DFT-NL implementation in ORCA uses the non-local part of the VV10 functional,20 which requires a functional specific parameter b. This parameter can be obtained from parameterization on non-covalent interaction (NCI) benchmark sets like the NCIBLIND10,166 S66 × 8167–169 and S22 × 5.170,171 The parameterization of b can in principle absorb some of the missing higher-order interactions but could also lead to overestimated dipole–dipole contributions.172,173
For the following test calculations, the common B3LYP174,175 and PBE0 functionals are used.
5.1 Dissociation curves
Dissociation curves for actinium3+ with argon, and for neutral nobelium with neon are calculated using B3LYP, without dispersion correction, with NL, D3, and D4. The Ac3+–Ar dissociation curve is shown in Fig. 4, the No–Ne dissociation curve is shown in Fig. 5.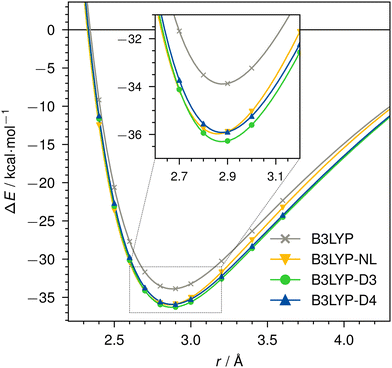 | ||
| Fig. 4 Dissociation curve of Ac3+–Ar for B3LYP/def2-TZVP without dispersion correction, with NL, D3, or D4. | ||
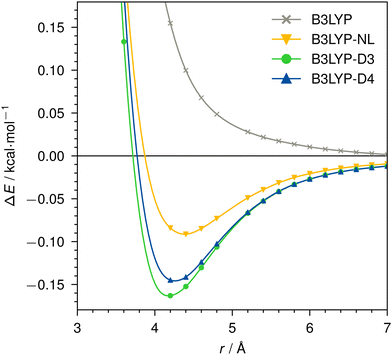 | ||
| Fig. 5 Dissociation curve of No–Ne for B3LYP/def2-TZVP without dispersion correction, with NL, D3, or D4. | ||
For the threefold positive actinide ion, both D4 and NL yield very similar dispersion energies. In contrast, D3 tends to slightly over-bind in this case when compared to D4 and NL. This is expected due to the missing charge dependency of D3, which D4 incorporates. This decreases the dynamic atomic polarizabilities and, thus, the Cn coefficients, particularly, in cases with fewer electrons compared to the neutral state. The density dependency of NL inherently accounts for this atomic charge dependency. Even though the NL correction can be prone to under-bind simple diatomic cases due to the missing higher-order contributions,1 we find excellent agreement in this instance. The minimum of the Ac3+–Ar dimer is identical for all cases, as the interaction energy is comparably large and already well described by the density functional itself. The missing dispersion contribution plays only a minor role.
For the neutral No–Ne case, no attractive interaction is found without applying a dispersion correction. This behavior is analogous to, e.g., the Kr–Kr dimer shown in ref. 95. With dispersion correction, the interaction of the two atoms is correctly predicted as attractive and shows the expected behavior of a vdW dimer. While we find very similar result for D3 and D4, NL provides a noticeably less attractive dispersion interaction. For B3LYP in the No–Ne case, the total dispersion contribution at 2.2 Å is −0.6 kcal mol−1, of which −0.2 kcal mol−1 is due to dipole–dipole (C6) and −0.4 kcal mol−1 due to dipole–quadrupole (C8) interaction. The bond–distance minimum of the dimer is identical with D3 and D4, NL however predicts a 0.2 Å longer bond.
5.2 Uranium molecular compounds
Uranium halogenide compounds of the type UXn with X = {F, Cl} and n = {3, 4, 5, 6} are used to evaluate bond distances.176 The resulting bond distances with the experimental reference can be found in Table 1.| Bond | Structure | Exp. | B3LYP | PBE0 | ||||
|---|---|---|---|---|---|---|---|---|
| — | NL | D4 | — | NL | D4 | |||
| U–F | UF6 | 1.999, 1.997177,178 | 2.007 | 2.002 | 2.007 | 1.989 | 1.986 | 1.988 |
| UF5 | — | 2.027 | 2.021 | 2.026 | 2.009 | 2.006 | 2.009 | |
| UF4 | — | 2.065 | 2.058 | 2.064 | 2.048 | 2.046 | 2.048 | |
| UF3 | — | 2.071 | 2.061 | 2.070 | 2.060 | 2.057 | 2.058 | |
| U–Cl | UCl6 | 2.420, 2.461179 | 2.469 | 2.456 | 2.464 | 2.436 | 2.430 | 2.434 |
| UCl5 | — | 2.484 | 2.472 | 2.479 | 2.454 | 2.448 | 2.453 | |
| UCl4 | — | 2.508 | 2.496 | 2.504 | 2.482 | 2.476 | 2.480 | |
| UCl3 | 2.549180 | 2.553 | 2.536 | 2.548 | 2.412 | 2.393 | 2.404 | |
Unsurprisingly, U–F distances are hardly changed by using D4, compared to plain B3LYP or PBE0. The covalent bonds are already well described by the semi-local correlation functionals. For cases, where the dispersion is already well covered by the density functional, we find no deterioration of performance upon using D4 dispersion correction and the equilibrium bond distances mainly depend on the employed density functional. The short-range damping function of the non-local NL correction does not damp covalent bonds entirely and thus predicts slightly smaller bond distances compared to D4, for all U–F distances. For the longer U–Cl distances, the D4 damping function allows small amounts of dispersion interactions and thus leads to slightly smaller covalent bonds upon employing D4. However, the majority of the dispersion contribution is due to dispersion interactions between the Cl ligands. For UCl6, the total D4 dispersion contribution is −19.0 kcal mol−1, of which −10.3 kcal mol−1 is only due to the Cl–Cl pair-wise dispersion interactions. This can be analyzed by using DFT-D4's feature to calculate a pairwise decomposition of the dispersion energy. For DFT-NL, the same as with U–F is observed: NL predicts a stronger dispersion interaction compared to D4 and thus yields smaller bond distances.
5.3 Crystal structures
As a further test, a systematic investigation of geometries was carried out using molecular crystal cutouts. The structures were obtained from the Cambridge Structural Database (CSD).181 The unit cell of the respective crystals was used to create a cluster of molecules. We mainly used cases where the 5f sub-shell is either fully empty, fully singly, or fully doubly occupied (i.e., 5f0, 5f7, or 5f14), as otherwise larger amounts of static correlation effects may be present.182Each structure was optimized using B3LYP and PBE0 with each no dispersion correction, D4, or NL dispersion corrections. The heavy-atom best-fit RMSD (hRMSD) of the obtained geometries compared to the experimental structures was calculated using quaternions.183 The resulting hRMSD in Å are given in Table 2. A value below 0.40 Å can be considered as a very good agreement for such large structures.
| CCSD-ID | Formula | B3LYP | PBE0 | ||||
|---|---|---|---|---|---|---|---|
| — | NL | D4 | — | NL | D4 | ||
| 1047312184,185 | ThC21H28Si2 | 0.29 | 0.03 | 0.15 | 0.41 | 0.03 | 0.14 |
| 1100351186 | NpC20H28O8 | 0.29 | 0.39 | 0.08 | 0.93 | 0.32 | 0.78 |
| 1100378187 | UC10H14O7 | 0.46 | 0.27 | 0.28 | 0.45 | 0.27 | 0.28 |
| 1100552188 | UC15H21O8 | 0.23 | 0.34 | 0.35 | 0.24 | 0.28 | 0.31 |
| 1553027189,190 | U2C30H28O6N4Cl4 | 0.75 | 0.73 | 0.70 | 0.70 | 0.66 | 0.64 |
| 1554548191,192 | ThC32H37N4Cl | 0.15 | 0.07 | 0.08 | 0.13 | 0.07 | 0.07 |
| 1554554193,194 | ThC46H56O2N4 | 0.29 | 0.32 | 0.30 | 0.21 | 0.30 | 0.29 |
| 1557708195,196 | AmC16H32O4Br3 | 0.51 | 0.46 | 0.48 | 0.53 | 0.48 | 0.49 |
| 1841778197,198 | AmC27H38S6N5 | 0.67 | 0.47 | 0.49 | 0.65 | 0.50 | 0.49 |
| 2168159199,200 | CmO18N6 | 0.32 | 0.27 | 0.30 | 0.28 | 0.26 | 0.28 |
| 713927201–203 | UC6O8H9 | 0.14 | 0.13 | 0.13 | 0.13 | 0.13 | 0.13 |
| 726784204,205 | NpC13H15O5N2 | 0.24 | 0.22 | 0.27 | 0.23 | 0.35 | 0.26 |
| 793245206,207 | UC16H21O6N | 0.33 | 0.33 | 0.26 | 0.33 | 0.33 | 0.32 |
| Mean | 0.37 | 0.34 | 0.33 | 0.41 | 0.34 | 0.36 | |
The mean hRMSD for both functionals improves by using the D4 or NL dispersion correction. B3LYP-D4 is found to perform slightly better than its NL counterpart; PBE0-D4 and -NL deliver very similar results.
D4 improves almost every structure compared to B3LYP. The single exception (1100552) still exhibits a good hRMSD of 0.35 Å. D4 is also found to systematically improve the geometries of plain PBE0, only two structures (1100552 and 1554554) are slightly worse with PBE0-D4 compared to uncorrected PBE0.
5.4 Bioorganic complex
As mentioned in the introduction, QM/MM schemes are a popular choice for treating large structures, especially for biochemical modeling. With those schemes, the structure of interest is partitioned into two regions that are treated with different methods. The more important part is calculated using a higher-level, more expensive method. As a demonstration, we use the inner Cm3+-4OL§-complex of a large siderocalin complex (4ZHF)208,209 as a cutout. The inner complex is used unchanged and does not require any cutting and capping of chemical bonds, as the complex is an individual molecule that is bound non-covalently to the protein. This structure was obtained from the protein data bank (PDB).210,211 The complex is shown in Fig. 6.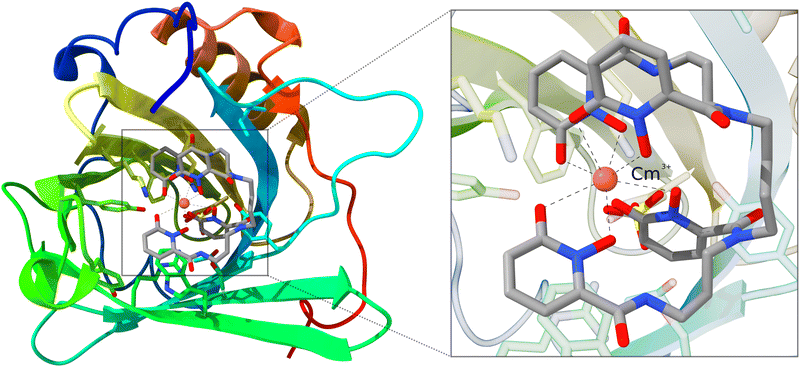 | ||
| Fig. 6 Structure of the Cm3+-siderocalin complex; the inner Cm3+-4OL is highlighted and enlarged on the right. Hydrogen atoms are hidden for better visibility. | ||
This cutout is optimized with plain B3LYP, combined with D4, and NL. The calculations with PBE0 could not be converged. The optimized bond distances between Cm3+ and the oxygens of the 4OL ligand, as well as the intermolecular distance of the benzene moieties of the 4OL ligand are given in Table 3; an overlay of the resulting optimized structures is shown in Fig. 7. The bond distances between the central Cm3+ and the oxygens of the 4OL ligand are found to be systematically smaller by employing NL or D4 dispersion corrections. The distances between the benzene moieties of the 4OL ligand are also smaller by employing NL or D4 dispersion corrections. This can also be seen in the overlay of the optimized structures in Fig. 7. In addition, the anisotropy in the distance between the two pairs of ring moieties is lost with any of the calculated geometries compared to the experimental crystal structure.
| Bond | Exp. | B3LYP | ||
|---|---|---|---|---|
| — | NL | D4 | ||
| Cm3+–O(1–6) | 2.539 | 2.469 | 2.441 | 2.447 |
| H6C6–C6H6 (left) | 5.281 | 6.254 | 5.555 | 5.163 |
| H6C6–C6H6 (right) | 7.090 | 6.253 | 5.588 | 5.138 |
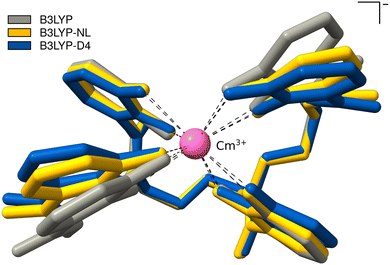 | ||
| Fig. 7 PBE0-D4/def2-SVP Optimized structures of Cm3+-4OL with B3LYP, B3LYP-NL, and B3LYP-D4. Hydrogen atoms are omitted for clarity. | ||
Compared to the crystallographic results of Allred et al., we find too small mean bond distances by B3LYP-D4 or -NL. The distance between the left ring moieties improves upon employing a dispersion correction, whereas the right ring moieties become too small. The used cutout is a rough approximation, as the surrounding protein is not incorporated at all. This is also the reason for the missing anisotropy in the distance between the two pairs of ring moieties which could also be caused by crystal packing in the experimental X-ray structure. The missing description of dispersion interactions offers good error compensation in this case for the mean distance between the two pairs of ring moieties, which is the reason why the agreement with the experiment worsens upon employing a dispersion correction, however, the anisotropy is still lost. The inclusion of the protein will likely slightly increase the Cm3+-4OL and H6C6–C6H6 distances and could also introduce the anisotropy due to attractive dispersion interactions with the surrounding protein. Given the current lack of advanced semi-empirical methods tailored for actinides, implementing a QM/MM-type scheme is not straightforward and would require substantial effort. Our tests on crystal structures indicate that dispersion corrections typically enhance accuracy considerably. Consequently, we expect similar improvements in this case when a comprehensive description of the entire structure is employed.
5.5 Role of actinide dispersion interaction
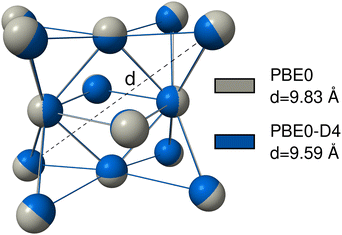
For many transition metal complexes and clusters, it is crucial to have a robust description of metal–non-metal dispersion to correctly model those systems.212 This is, for example, the case for transition metal–alkane interactions in σ-complexes,213 or in the formation of the Grubbs II catalyst.214 However, the metal–metal dispersion interaction can also be important. This was found for gold nanoparticles,215 zinc, cadmium, and mercury clusters,216 for interactions of metals and clusters with surfaces217 or for the description of adsorption processes on metal surfaces218,219 or in bulk metal crystals.220,221 To show that this is also the case for the actinides, we provide examples where dispersion interactions involving actinides, either actinide–non-actinide or actinide–actinide, are significant and must be taken into account.The actinide–actinide dispersion interaction is evaluated using a nobelium cluster consisting of 14 nobelium atoms, which is optimized using PBE0/def2-SVP with D4, NL, and without any dispersion correction. Nobelium offers the advantage of an electronically simple 7s2 5f14 closed-shell configuration. To quantify the results, the cluster and its cross-diagonal distance, as shown in Fig. 8, is calculated with PBE0, PBE0-D4, and PBE0-NL. The non-dispersion corrected geometry yields the largest distance of d = 9.83 Å, while the D4 and NL geometries yield a very similar result with d = 9.59 Å and d = 9.55 Å, respectively.
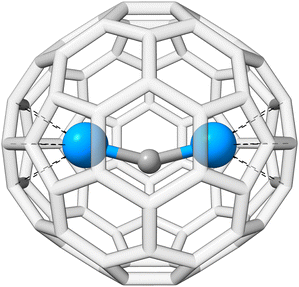
The actinide–non-actinide dispersion interaction is investigated using diuranium carbide U2C inside a Ih(7)–C80 fullerene cage, which was recently experimentally stabilized by Zhang et al.222 The U2C@C80 cluster is shown in Fig. 9. For this, the respective interaction energy of the process U2C + C80 → U2C@C80 is calculated. We find an interaction energy of −244.3 kcal mol−1 for PBE0/ma-def2-TZVP, −292.3 kcal mol−1 with NL, and −277.1 kcal mol−1 with D4; −175.7, −250.7, and −232.8 kcal mol−1 were found for the respective B3LYP/ma-def2-TZVP analogues. In all cases, the dispersion contribution is substantial, exceeding −33 kcal mol−1 and accounting for more than 10% (up to 30% for B3LYP-NL) of the total interaction energy. NL yields a slightly larger dispersion contribution compared to D4, which could potentially originate from the missing many-body term in NL. The dispersion contribution to the interaction energy of DFT-D4 reveals that 80% stem from the UU2C–C80 interaction, while only the remaining 20% arise from to CU2C–C80 interaction.
6 Conclusions
Generally applicable and efficient dispersion corrections are an indispensable and integral part of various contemporary quantum chemical methods. Nevertheless, many heavy elements like actinides were barely considered during the development of efficient methods. This stands in stark contrast to the rich and diverse chemistry of the actinides, which holds significant importance across various domains of chemical research. As a consequence, the prominent D3 and D4 dispersion corrections lacked a complete and consistent parameterization for the actinides. In this work, we extended the D3 and D4 London dispersion corrections to the full actinides series, francium, and radium. To keep intrinsic consistency with the existing version for the rest of the periodic table, the original parameterization strategy of the D4 model was only slightly modified. Accordingly, reference Hirshfeld atomic partial charges were generated at the sophisticated ωB97M-V/ma-def-TZVP level to fit the required electronegativity equilibration charge model that is a key component of the D4 model. To facilitate this, a new actinide data set called AcQM was created that covers the most common chemical compound space of molecular actinide chemistry. The new parameter set was assessed for the computation of various dissociation curves of actinide atoms and ions, geometry optimizations of experimentally determined crystal structure cutouts and gas-phase structures of small uranium compounds, and an example extracted from a small actinide complex protein assembly. We find that the novel parameterizations perform on par with the computationally more demanding density-dependent NL variant of the VV10 dispersion correction for both geometric and energetic properties. On the other hand, in agreement with the literature on transition metals, we find that the actinide–actinide and actinide–non-actinide dispersion interaction can play an important role in many relevant actinide systems. With the presented extension to the actinides, the excellent cost-accuracy ratio of the D3 and D4 models can now be utilized to improve the accuracy of density functional, semi-empirical quantum mechanical, and force field methods for the description of actinide complexes. Without this extension, a robust description of the actinide chemical space would not be possible due to many relevant cases that require a good description of dispersion interactions. This development also facilitates the incorporation of efficient composite DFT methods, such as r2SCAN-3c, previously applied to other elements, into actinide research. These fast methods are crucial for investigating large actinide complexes, particularly, in the framework of QM/MM techniques. Moreover, they expedite the adaptation of established computationally demanding workflows and tasks, like conformer generation and high-throughput transition state sampling, to the field of actinide chemistry.All extensions presented in this work are implemented in our freely available standalone codes, and the DFT-D4 parameterization as well as the efficient algorithm to compute dynamic polarizabilities will be available in the upcoming ORCA 6.0 program package.
Author contributions
Conceptualization: L. W., S. G., A. H. and M. B.; data curation: L. W., I. G. and M. F.; formal analysis: L. W., I. G. and M. F.; funding acquisition: S. G., A. H. and M. B.; investigation: L. W., I. G. and M. F.; methodology: S. G., A. H. and M. B.; project administration: A. H. and M. B.; resources: L. W., I. G., M. F., B. H.-P., S. G., A. H. and M. B.; software: L. W., I. G., M. F. and B. H.-P.; supervision: S. G., A. H. and M. B.; validation: L. W., I. G., M. F., B. H.-P., S. G., A. H. and M. B.; visualization: L. W.; writing – original draft: L. W., I. G., M. F. and B. H.-P.; writing – review & editing: L. W., I. G., M. F., B. H.-P., S. G., A. H. and M. B.Data availability
All obtained parameters for the presented DFT-D3 and -D4 extensions, the parameters for the EEQ model, and the investigation of relativistic effects have been included as part of the ESI.† The full AcQM set is additionally included as part of the ESI,† but can also be found on GitHub at https://github.com/grimme-lab/acqm.Conflicts of interest
M. B., B. H.-P. and S. G. are affiliated with the FACCTs GmbH which licenses the ORCA program package for commercial use.Acknowledgements
The German Science Foundation (DFG) is gratefully acknowledged for financial support of S. G. Further, S. G. and M. B. gratefully acknowledge financial support from the Max Planck Society through the Max Planck fellow program. The authors would like to sincerely thank the University of Bonn for granting access to the Marvin Computing Cluster. The authors would also like to thank Jan-Michael Mewes, Christian Hölzer and Thomas Froitzheim for fruitful discussions. Open Access funding provided by the Max Planck Society.Notes and references
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- R. Eisenschitz and F. London, Z. Phys., 1930, 60, 491–527 CrossRef CAS.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier, 2011, pp. 577–616 Search PubMed.
- J. Brandenburg, J. Bates, A. Ruzsinszky, J. Sun and J. Perdew, Abstracts of Papers of the American Chemical Society, 2016 Search PubMed.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- L. Goerigk, Non-Covalent Interactions in Quantum Chemistry and Physics, Elsevier, 2017, pp. 195–219 Search PubMed.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372 CrossRef CAS.
- S. Yoo and S. S. Xantheas, J. Chem. Phys., 2011, 134, 121105 CrossRef PubMed.
- K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2008, 4, 232–242 CrossRef CAS PubMed.
- Z. Ma, Y. Zhang and M. E. Tuckerman, J. Chem. Phys., 2012, 137, 044506 CrossRef PubMed.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- R. Sabatini, T. Gorni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 CrossRef.
- O. A. Vydrov and T. Van Voorhis, Phys. Rev. Lett., 2009, 103, 063004 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101 CrossRef PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chemie, 2022, 134, e202205735 CrossRef.
- N. Jacob, Y. Zaid, J. C. A. Oliveira, L. Ackermann and J. Wencel-Delord, J. Am. Chem. Soc., 2022, 144, 798–806 CrossRef CAS PubMed.
- S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101 CrossRef CAS PubMed.
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed.
- L. Wittmann, H. Neugebauer, S. Grimme and M. Bursch, J. Chem. Phys., 2023, 159, 224103 CrossRef CAS PubMed.
- C. Plett, A. Katbashev, S. Ehlert, S. Grimme and M. Bursch, Phys. Chem. Chem. Phys., 2023, 25, 17860–17868 RSC.
- E. Caldeweyher and J. G. Brandenburg, J. Phys.: Condens. Matter, 2018, 30, 213001 CrossRef PubMed.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- J. G. Brandenburg, E. Caldeweyher and S. Grimme, Phys. Chem. Chem. Phys., 2016, 18, 15519–15523 RSC.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 014103 CrossRef PubMed.
- T. Bredow and K. Jug, Theor. Chem. Acc., 2004, 113, 1–14 Search PubMed.
- W. Thiel, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 4, 145–157 Search PubMed.
- A. S. Christensen, T. Kubař, Q. Cui and M. Elstner, Chem. Rev., 2016, 116, 5301–5337 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker, C. Plett, S. Spicher, P. Steinbach, P. A. Wesołowski and F. Zeller, J. Chem. Phys., 2024, 160, 114110 CrossRef CAS PubMed.
- S. Dohm, M. Bursch, A. Hansen and S. Grimme, J. Chem. Theory Comput., 2020, 16, 2002–2012 CrossRef CAS PubMed.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- C. E. Tzeliou, M. A. Mermigki and D. Tzeli, Molecules, 2022, 27, 2660 CrossRef CAS PubMed.
- B. Pullman, Isr. J. Chem., 1975, 14, 69–78 CrossRef CAS.
- C. F. Matta, Quantum biochemistry, John Wiley & Sons, 2010 Search PubMed.
- Q. Cui, J. Chem. Phys., 2016, 145, 140901 CrossRef PubMed.
- J.-C. G. Bunzli and V. K. Pecharsky, Handbook on the Physics and Chemistry of Rare Earths: Including Actinides, Elsevier, 2016 Search PubMed.
- R. E. Wilson, S. De Sio and V. Vallet, Nat. Commun., 2018, 9, 622 CrossRef PubMed.
- J. Veliscek-Carolan, J. Hazard. Mater., 2016, 318, 266–281 CrossRef CAS PubMed.
- J. A. Laub and K. D. Vogiatzis, J. Phys. Chem. A, 2023, 127, 5523–5533 CrossRef CAS PubMed.
- A. Francis, J. Alloys Compd., 1998, 271–273, 78–84 CrossRef CAS.
- R. C. Ewing, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3432–3439 CrossRef CAS PubMed.
- R. C. Thompson, Radiat. Res., 1982, 90, 1 CrossRef CAS PubMed.
- K. Maher, J. R. Bargar and G. E. Brown, Inorg. Chem., 2012, 52, 3510–3532 CrossRef PubMed.
- J. Suh, Acc. Chem. Res., 1992, 25, 273–279 CrossRef CAS.
- Y.-W. Lin, Molecules, 2019, 24, 2743 CrossRef PubMed.
- S. Safi, M. C. Charbonnel, G. Creff, A. Jeanson, S. Mostapha, J. Roques, E. Simoni, P. Solari, C. Vidaud and C. Den Auwer, MRS Online Proc. Libr., 2012, 1444, mrss12–1444 Search PubMed.
- A. Garai and P. Delangle, J. Inorg. Biochem., 2020, 203, 110936 CrossRef CAS PubMed.
- J. G. Hamilton, Rev. Mod. Phys., 1948, 20, 718–728 CrossRef CAS.
- E. Ansoborlo, O. Prat, P. Moisy, C. Den Auwer, P. Guilbaud, M. Carriere, B. Gouget, J. Duffield, D. Doizi, T. Vercouter, C. Moulin and V. Moulin, Biochimie, 2006, 88, 1605–1618 CrossRef CAS PubMed.
- É. Ansoborlo, B. Amekraz, C. Moulin, V. Moulin, F. Taran, T. Bailly, R. Burgada, M.-H. Hengé-Napoli, A. Jeanson, C. Den Auwer, L. Bonin and P. Moisy, C. R. Chim, 2007, 10, 1010–1019 CrossRef.
- G. Creff, C. Zurita, A. Jeanson, G. Carle, C. Vidaud and C. Den Auwer, Radiochim. Acta, 2019, 107, 993–1009 CrossRef CAS.
- S. Y. Tolmachev, M. E. Ketterer, D. Hare, P. Doble and A. C. James, Proc. Radiochem., 2011, 1, 173–181 CrossRef.
- E. Vergucht, B. De Samber, A. Izmer, B. Vekemans, K. Appel, S. Tolmachev, L. Vincze and F. Vanhaecke, Anal. Bioanal. Chem., 2014, 407, 1559–1566 CrossRef PubMed.
- R. Bulman, Coord. Chem. Rev., 1980, 31, 221–250 CrossRef CAS.
- D. Hare, S. Tolmachev, A. James, D. Bishop, C. Austin, F. Fryer and P. Doble, Anal. Chem., 2010, 82, 3176–3182 CrossRef CAS PubMed.
- N. Archipowa, L. Wittmann, J. Köckenberger, F. J. Ertl, J. Gleixner, M. Keller, M. R. Heinrich and R. J. Kutta, J. Phys. Chem. B, 2023, 127, 9532–9542 CrossRef CAS PubMed.
- R. M. Pallares and R. J. Abergel, Nanoscale, 2020, 12, 1339–1348 RSC.
- S. J. Goldsmith, Semin. Nucl. Med., 1975, 5, 125–152 CrossRef CAS PubMed.
- E. R. Birnbaum, M. E. Fassbender, M. G. Ferrier, K. D. John and T. Mastren, The Heaviest Metals: Science and Technology of the Actinides and Beyond, 2019, p. 445 Search PubMed.
- T. I. Kostelnik and C. Orvig, Chem. Rev., 2018, 119, 902–956 CrossRef PubMed.
- I. Kopp, P. Cieslik, K. Anger, T. Josephy, L. Neupert, G. Velmurugan, M. Gast, H. Wadepohl, S. A. Brühlmann, M. Walther, K. Kopka, M. Bachmann, H. Stephan, M. Kubeil and P. Comba, Inorg. Chem., 2023, 62, 20754–20768 CrossRef CAS PubMed.
- N. Kaltsoyannis, Chem. Soc. Rev., 2002, 32, 9–16 RSC.
- G. Schreckenbach and G. A. Shamov, Acc. Chem. Res., 2009, 43, 19–29 CrossRef PubMed.
- A. J. Freeman and J. B. Darby, The actinides: Electronic structure and related properties, Academic Press, 1974 Search PubMed.
- V. Cocalia, K. Gutowski and R. Rogers, Coord. Chem. Rev., 2006, 250, 755–764 CrossRef CAS.
- X.-D. Wen, R. L. Martin, G. E. Scuseria, S. P. Rudin and E. R. Batista, J. Phys. Chem. C, 2013, 117, 13122–13128 CrossRef CAS.
- X.-D. Wen, R. L. Martin, T. M. Henderson and G. E. Scuseria, Chem. Rev., 2012, 113, 1063–1096 CrossRef PubMed.
- A. Kovács, R. J. M. Konings, J. K. Gibson, I. Infante and L. Gagliardi, Chem. Rev., 2015, 115, 1725–1759 CrossRef PubMed.
- P. Grover, M. S. Oakley and G. Schreckenbach, J. Phys. Chem. C, 2024, 128, 3033–3042 CrossRef CAS.
- L. Belkhiri, B. Le Guennic and A. Boucekkine, Magnetochemistry, 2019, 5, 15 CrossRef CAS.
- P. Söderlind, G. Kotliar, K. Haule, P. M. Oppeneer and D. Guillaumont, MRS Bull., 2010, 35, 883–888 CrossRef.
- A. Golovkina, D. Ovsyannikov and S. Olaru, Cybern. Phys., 2018, 210–215 Search PubMed.
- M. S. Christian, E. R. Johnson and T. M. Besmann, J. Phys. Chem. A, 2021, 125, 2791–2799 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- A. Salam, Non-Relativistic QED Theory of the van der Waals Dispersion Interaction, Springer International Publishing, 2016 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- P. Xu, M. Alkan and M. S. Gordon, Chem. Rev., 2020, 120, 12343–12356 CrossRef CAS PubMed.
- S. M. Gatica, M. M. Calbi, M. W. Cole and D. Velegol, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 205409–205417 CrossRef.
- O. Anatole von Lilienfeld and A. Tkatchenko, J. Chem. Phys., 2010, 132, 234109–234120 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. B. G. Casimir and D. Polder, Phys. Rev., 1948, 73, 360–372 CrossRef CAS.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300 CrossRef CAS.
- Y. Muto, Nippon Sugaku-Buturigakkwaishi, 1943, 17, 629–631 CAS.
- H. Schröder, A. Creon and T. Schwabe, J. Chem. Theory Comput., 2015, 11, 3163–3170 CrossRef PubMed.
- D. G. A. Smith, L. A. Burns, K. Patkowski and C. D. Sherrill, J. Phys. Chem. Lett., 2016, 7, 2197–2203 CrossRef CAS PubMed.
- J. Witte, N. Mardirossian, J. B. Neaton and M. Head-Gordon, J. Chem. Theory Comput., 2017, 13, 2043–2052 CrossRef CAS PubMed.
- D. C. Ghosh and N. Islam, Int. J. Quantum Chem., 2009, 110, 1206–1213 CrossRef.
- S. A. Ghasemi, A. Hofstetter, S. Saha and S. Goedecker, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045131 CrossRef.
- P. Norman, A. Jiemchooroj and B. E. Sernelius, J. Chem. Phys., 2003, 118, 9167–9174 CrossRef CAS.
- T. Saue and H. J. A. Jensen, J. Chem. Phys., 2003, 118, 522–536 CrossRef CAS.
- J. Kauczor, P. Jørgensen and P. Norman, J. Chem. Theory Comput., 2011, 7, 1610–1630 CrossRef CAS PubMed.
- J. Kauczor and P. Norman, J. Chem. Theory Comput., 2014, 10, 2449–2455 CrossRef CAS PubMed.
- P. W. Langhoff and M. Karplus, J. Chem. Phys., 1970, 53, 233–250 CrossRef CAS.
- F. Visser, P. E. S. Wormer and P. Stam, J. Chem. Phys., 1983, 79, 4973–4984 CrossRef CAS.
- P. W. Fowler, P. Jørgensen and J. Olsen, J. Chem. Phys., 1990, 93, 7256–7263 CrossRef CAS.
- S. Weiss and R. Egger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 245301–245307 CrossRef.
- I. Kylänpää, J. Balachandran, P. Ganesh, O. Heinonen, P. R. C. Kent and J. T. Krogel, Phys. Rev. Mater., 2017, 1, 065408–065417 CrossRef.
- J. Shee, S. Zhang, D. R. Reichman and R. A. Friesner, J. Chem. Theory Comput., 2017, 13(6), 2667–2680 CrossRef CAS PubMed.
- D. M. Bishop and J. Pipin, Int. J. Quantum Chem., 1993, 45, 349–361 CrossRef CAS.
- J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume and K. Varga, Rev. Mod. Phys., 2013, 85, 693–749 CrossRef.
- N. M. Tubman, I. Kylänpää, S. Hammes-Schiffer and D. M. Ceperley, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 042507–042512 CrossRef.
- Y. Yang, I. Kylänpää, N. M. Tubman, J. T. Krogel, S. Hammes-Schiffer and D. M. Ceperley, J. Chem. Phys., 2015, 143, 124308–124318 CrossRef PubMed.
- ORCA – an ab initio, density functional and semiempirical program package, V. 5.0.1, F. Neese, MPI für Kohlenforschung, Mülheim a. d. Ruhr (Germany), 2021 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, e1606 Search PubMed.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2010, 128, 295–305 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2007, 117, 491 Search PubMed.
- K. G. Dyall, Theor. Chem. Acc., 2012, 131, 1217 Search PubMed.
- written by H. J. A. Jensen, R. Bast, A. S. P. Gomes, T. Saue and L. Visscher, with contributions from, I. A. Aucar, V. Bakken, C. Chibueze, J. Creutzberg, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, L. Halbert, E. D. Hedegård, T. Helgaker, B. Helmich-Paris, J. Henriksson, M. van Horn, M. Iliaš, C. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, N. H. List, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, A. Papadopoulos, Y. C. Park, J. K. Pedersen, M. Pernpointner, J. V. Pototschnig, R. di Remigio, M. Repisky, K. Ruud, P. Sałek, B. Schimmelpfennig, B. Senjean, A. Shee, J. Sikkema, A. Sunaga, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, M. L. Vidal, S. Villaume, O. Visser, T. Winther, S. Yamamoto and X. Yuan, DIRAC, a relativistic ab initio electronic structure program, Release DIRAC22, 2022 DOI:10.5281/zenodo.6010450, see also https://www.diracprogram.org.
- L. Trombach, S. Ehlert, S. Grimme, P. Schwerdtfeger and J.-M. Mewes, Phys. Chem. Chem. Phys., 2019, 21, 18048–18058 RSC.
- P. Jerabek, O. R. Smits, J.-M. Mewes, K. A. Peterson and P. Schwerdtfeger, J. Phys. Chem. A, 2019, 123, 4201–4211 CrossRef CAS PubMed.
- O. R. Smits, J. Mewes, P. Jerabek and P. Schwerdtfeger, Angew. Chem., Int. Ed., 2020, 59, 23636–23640 CrossRef CAS PubMed.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2008, 15, 186–197 CrossRef PubMed.
- A. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221 CrossRef CAS.
- A. F. Holleman, Lehrbuch der Anorganischen Chemie, De Gruyter, 1964, p. 2146 Search PubMed.
- J. Huheey, E. Keiter, R. Keiter and O. Medhi, Inorganic Chemistry: Principles of Structure and Reactivity, Pearson Education, 2006 Search PubMed.
- L. C. Allen, J. Am. Chem. Soc., 1989, 111, 9003–9014 CrossRef CAS.
- A. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221 CrossRef CAS.
- M. G. Taylor, D. J. Burrill, J. Janssen, E. R. Batista, D. Perez and P. Yang, Nat. Commun., 2023, 14, 2786 CrossRef CAS PubMed.
- Architector, https://github.com/lanl/Architector.
- ArchitectorWrapper, https://github.com/grimme-lab/ArchitectorWrapper.
- C. Hölzer, I. Gordiy, S. Grimme and M. Bursch, J. Chem. Inf. Model., 2024, 64, 825–836 CrossRef PubMed.
- M. Korth and S. Grimme, J. Chem. Theory Comput., 2009, 5, 993–1003 CrossRef CAS PubMed.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- M. H. Wright, Direct Search Methods: Once Scorned, Now Respectable, Addison Wesley Longman, Harlow, United Kingdom, 1996, pp. 191–208 Search PubMed.
- S. Ehrlich, J. Moellmann and S. Grimme, Acc. Chem. Res., 2012, 46, 916–926 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2012, 9, 308–315 CrossRef PubMed.
- L. Goerigk, J. Chem. Theory Comput., 2014, 10, 968–980 CrossRef CAS PubMed.
- M. A. Iron and T. Janes, J. Phys. Chem. A, 2019, 123, 3761–3781 CrossRef CAS PubMed.
- T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591 CrossRef CAS PubMed.
- D. E. Taylor, J. G. Ángyán, G. Galli, C. Zhang, F. Gygi, K. Hirao, J. W. Song, K. Rahul, O. A. von Lilienfeld, R. Podeszwa, I. W. Bulik, T. M. Henderson, G. E. Scuseria, J. Toulouse, R. Peverati, D. G. Truhlar and K. Szalewicz, J. Chem. Phys., 2016, 145, 124105 CrossRef PubMed.
- J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438 CrossRef PubMed.
- B. Brauer, M. K. Kesharwani, S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2016, 18, 20905–20925 RSC.
- G. Santra, E. Semidalas, N. Mehta, A. Karton and J. M. L. Martin, Phys. Chem. Chem. Phys., 2022, 24, 25555–25570 RSC.
- P. Jurečka, J. Šponer, J. Černý and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993 RSC.
- L. Gráfová, M. Pitoňák, J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2010, 6, 2365–2376 CrossRef PubMed.
- J. C. Sancho-García, A. J. Pérez-Jiménez and Y. Olivier, J. Chem. Phys., 2015, 142, 054702 CrossRef PubMed.
- M. Bursch, S. Grimme and A. Hansen, Acc. Chem. Res., 2023, 57, 153–163 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- G. Beridze and P. M. Kowalski, J. Phys. Chem. A, 2014, 118, 11797–11810 CrossRef CAS PubMed.
- B. Weinstock and R. H. Crist, J. Chem. Phys., 1948, 16, 436–441 CrossRef CAS.
- H. M. Seip, J.-O. Lundgren, P. Klæboe and T.-M. Enari, Acta Chem. Scand., 1965, 19, 1955–1968 CrossRef CAS.
- Y. S. Ezhov, S. A. Komarov, V. G. Sevastyanov and V. I. Bazhanov, J. Struct. Chem., 1993, 34, 473–474 CrossRef.
- V. I. Bazhanov, Y. S. Ezhov and S. A. Komarov, J. Struct. Chem., 1991, 31, 986–987 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- H. Neugebauer, H. T. Vuong, J. L. Weber, R. A. Friesner, J. Shee and A. Hansen, J. Chem. Theory Comput., 2023, 19, 6208–6225 CrossRef CAS PubMed.
- E. A. Coutsias, C. Seok and K. A. Dill, J. Comput. Chem., 2004, 25, 1849–1857 CrossRef CAS PubMed.
- H. Braunschweig, M. A. Celik, K. Dück, F. Hupp and I. Krummenacher, Chem. – Eur. J., 2015, 21, 9339–9342 CrossRef CAS PubMed.
- H. Braunschweig, M. A. Celik, K. Dück, F. Hupp and I. Krummenacher, CCDC 1047312: Experimental Crystal Structure Determination, 2015, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/cc144t8csid=DataCite.
- B. Allard, S. Dhabanandana, J. Krogh-Moe, J. Songstad and Â. Pilotti, Acta Chem. Scand., 1972, 26, 3492–3504 CrossRef CAS.
- N. W. Alcock and D. J. Flanders, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 1480–1483 CrossRef.
- M. Lenner, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1979, 35, 2396–2398 CrossRef.
- S. Schöne, T. Radoske, J. März, T. Stumpf, M. Patzschke and A. Ikeda-Ohno, CCDC 1553027: Experimental Crystal Structure Determination, 2017, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc1p41njsid=DataCite.
- S. Schöne, T. Radoske, J. März, T. Stumpf, M. Patzschke and A. Ikeda-Ohno, Chem. – Eur. J., 2017, 23, 13574–13578 CrossRef PubMed.
- S. Hohloch, M. E. Garner, B. F. Parker and J. Arnold, Dalton Trans., 2017, 46, 13768–13782 RSC.
- S. Hohloch, M. E. Garner, B. F. Parker and J. Arnold, CCDC 1554548: Experimental Crystal Structure Determination, 2017, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc1p5mq6 sid=DataCite.
- S. Hohloch, M. E. Garner, B. F. Parker and J. Arnold, CCDC 1554554: Experimental Crystal Structure Determination, 2017, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc1p5mxdsid=DataCite.
- S. Hohloch, M. E. Garner, B. F. Parker and J. Arnold, Dalton Trans., 2017, 46, 13768–13782 RSC.
- S. S. Galley, J. M. Sperling, C. J. Windorff, M. Zeller, T. E. Albrecht-Schmitt and S. C. Bart, CCDC 1557708: Experimental Crystal Structure Determination, 2019, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc1p8xnjsid=DataCite.
- S. S. Galley, J. M. Sperling, C. J. Windorff, M. Zeller, T. E. Albrecht-Schmitt and S. C. Bart, Organometallics, 2019, 38, 606–609 CrossRef CAS.
- S. K. Cary, J. Su, S. S. Galley, T. E. Albrecht-Schmitt, E. R. Batista, M. G. Ferrier, S. A. Kozimor, V. Mocko, B. L. Scott, C. E. Van Alstine, F. D. White and P. Yang, CCDC 1841778: Experimental Crystal Structure Determination, 2018, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc1ztj6jsid=DataCite.
- S. K. Cary, J. Su, S. S. Galley, T. E. Albrecht-Schmitt, E. R. Batista, M. G. Ferrier, S. A. Kozimor, V. Mocko, B. L. Scott, C. E. Van Alstine, F. D. White and P. Yang, Dalton Trans., 2018, 47, 14452–14461 RSC.
- M. L. Tarlton, S. Skanthakumar, V. Vallet and R. E. Wilson, CCDC 2168159: Experimental Crystal Structure Determination, 2022, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccdc.csd.cc2bs4mxsid=DataCite.
- M. L. Tarlton, S. Skanthakumar, V. Vallet and R. E. Wilson, Chem. Commun., 2022, 58, 11997–12000 RSC.
- L. Serezhkina, E. Peresypkina, A. Virovets and N. Neklyudova, CCDC 713927: Experimental Crystal Structure Determination, 2011, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccrywxgsid=DataCite.
- L. B. Serezhkina, E. V. Peresypkina, A. V. Virovets and N. A. Neklyudova, Russ. J. Inorg. Chem., 2010, 55, 1020–1025 CrossRef CAS.
- L. B. Serezhkina, E. V. Peresypkina, Y. A. Medvedkov, A. V. Virovets and V. N. Serezhkin, Russ. J. Inorg. Chem., 2013, 58, 1465–1469 CrossRef CAS.
- N. N. Krot, I. A. Charushnikova, M. S. Grigor'ev, A. A. Bessonov and I. N. Polyakova, CCDC 726784: Experimental Crystal Structure Determination, 2011, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccsd8n2sid=DataCite.
- N. N. Krot, I. A. Charushnikova, M. S. Grigorev, A. A. Bessonov and I. N. Polyakova, Radiochemistry, 2010, 52, 12–16 CrossRef CAS.
- T. Kawasaki, T. Nishimura and T. Kitazawa, CCDC 793245: Experimental Crystal Structure Determination, 2011, https://www.ccdc.cam.ac.uk/services/structure_request?id=doi:10.5517/ccvmfkfsid=DataCite.
- T. Kawasaki, T. Nishimura and T. Kitazawa, Bull. Chem. Soc. Jpn., 2010, 83, 1528–1530 CrossRef CAS.
- B. E. Allred, P. B. Rupert, S. S. Gauny, D. D. An, C. Y. Ralston, M. Sturzbecher-Hoehne, R. K. Strong and R. J. Abergel, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10342–10347 CrossRef CAS PubMed.
- B. Allred, P. Rupert, S. Gauny, D. An, C. Ralston, M. Sturzbecher-Hoehne, R. Strong and R. Abergel, Siderocalin-mediated recognition and cellular uptake of actinides, 2015 DOI:10.2210/pdb4ZHF/pdb.
- C. Zardecki, S. Dutta, D. S. Goodsell, R. Lowe, M. Voigt and S. K. Burley, Protein Sci., 2021, 31, 129–140 CrossRef PubMed.
- H. M. Berman, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- A. Hansen, C. Bannwarth, S. Grimme, P. Petrović, C. Werlé and J.-P. Djukic, ChemistryOpen, 2014, 3, 177–189 CrossRef CAS PubMed.
- Q. Lu, F. Neese and G. Bistoni, Phys. Chem. Chem. Phys., 2019, 21, 11569–11577 RSC.
- M. Bursch, E. Caldeweyher, A. Hansen, H. Neugebauer, S. Ehlert and S. Grimme, Acc. Chem. Res., 2019, 52, 258–266 CrossRef CAS PubMed.
- J. B. A. Davis, F. Baletto and R. L. Johnston, J. Phys. Chem. A, 2015, 119, 9703–9709 CrossRef CAS PubMed.
- R. Hatz, V. Hänninen and L. Halonen, J. Phys. Chem. A, 2014, 118, 5734–5740 CrossRef CAS PubMed.
- G. Pacchioni, Phys. Chem. Chem. Phys., 2013, 15, 1737–1757 RSC.
- R. J. Maurer, V. G. Ruiz and A. Tkatchenko, J. Chem. Phys., 2015, 143, 102808 CrossRef PubMed.
- F. R. Rehak, G. Piccini, M. Alessio and J. Sauer, Phys. Chem. Chem. Phys., 2020, 22, 7577–7585 RSC.
- A. A. Adeleke and E. R. Johnson, Phys. Rev. B, 2023, 107, 064101 CrossRef CAS.
- K. Tonigold and A. Groß, J. Comput. Chem., 2012, 33, 695–701 CrossRef CAS PubMed.
- X. Zhang, W. Li, L. Feng, X. Chen, A. Hansen, S. Grimme, S. Fortier, D.-C. Sergentu, T. J. Duignan, J. Autschbach, S. Wang, Y. Wang, G. Velkos, A. A. Popov, N. Aghdassi, S. Duhm, X. Li, J. Li, L. Echegoyen, W. H. E. Schwarz and N. Chen, Nat. Commun., 2018, 9, 2753 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: All parameters for the DFT-D3, DFT-D4, and EEQ extensions, investigation of relativistic effects, and the complete AcQM set. See DOI: https://doi.org/10.1039/d4cp01514b |
| ‡ These Authors contributed equally. |
| § N,N'-butane-1,4-diylbis[1-hydroxy-N-(3-[(1-hydroxy-6-oxo-1,6-dihydropyridin-2-yl)carbonyl]aminopropyl)-6-oxo-1,6-dihydropyridine-2-carboxamide] |
| This journal is © the Owner Societies 2024 |