Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gaseous inhibition of the transsulfuration pathway by cystathionine β-synthase†
Neil R.
McFarlane
 a,
Jiangli
Gui
a,
Julianna
Oláh
a,
Jiangli
Gui
a,
Julianna
Oláh
 b and
Jeremy N.
Harvey
b and
Jeremy N.
Harvey
 *a
*a
aDepartment of Chemistry, KU Leuven, Celestijnenlaan 200f-box 2404, B-3001 Leuven, Belgium. E-mail: neilrory.mcfarlane@kuleuven.be; jeremy.harvey@kuleuven.be
bDepartment of Inorganic and Analytical Chemistry Budapest University of Technology and Economics H-1111 Budapest, Műegyeten rakpart 3, Hungary. E-mail: olah.julianna@vbk.bme.hu
First published on 30th May 2024
Abstract
The transsulfuration pathway plays a key role in mammals for maintaining the balance between cysteine and homocysteine, whose concentrations are critical in several biochemical processes. Human cystathionine β-synthase is a heme-containing, pyridoxal 5′-phosphate (PLP)-dependent enzyme found in this pathway. The heme group does not participate directly in catalysis, but has a regulatory function, whereby CO or NO binding inhibits the PLP-dependent reactions. In this study, we explore the detailed structural changes responsible for inhibition using quantum chemical calculations to validate the experimentally observed bonding patterns associated with heme CO and NO binding and molecular dynamics simulations to explore the medium-range structural changes triggered by gas binding and propagating to the PLP active site, which is more than 20 Å distant from the heme group. Our results support a previously proposed mechanical signaling model, whereby the cysteine decoordination associated with gas ligand binding leads to breaking of a hydrogen bond with an arginine residue on a neighbouring helix. In turn, this leads to a shift in position of the helix, and hence also of the PLP cofactor, ultimately disrupting a key hydrogen bond that stabilizes the PLP in its catalytically active form.
Introduction
In mammals, the transsulfuration pathway plays a key role in sulfur metabolism and in intracellular redox regulation.1 At the heart of the transsulfuration pathway is the regulation of homocysteine and cysteine concentrations. Their concentrations are crucial from two opposing perspectives: homocysteine in high concentrations is toxic in mammals,2 and cysteine plays an important part in many biochemical processes including the production of the antioxidant glutathione,3 the biogenesis of iron–sulfur clusters,4 and in the folding and stability of cellular proteins via structural disulfide bonds,5 among many others. There is also some recent evidence that cysteine has a cytoprotective function on tumour growth.6The transsulfuration pathway formally begins with homocysteine, which can react with serine to form cystathionine via a β-elimination reaction with catalysis by cystathionine β-synthase (CBS) (see Fig. 1).
 | ||
| Fig. 1 The canonical reaction found in hCBS, where serine reacts with homocysteine to form cystathionine with water condensation via a β-elimination reaction. | ||
In all organisms, CBS is a pyridoxal 5′-phosphate (PLP) dependent enzyme, but in higher organisms such as humans (henceforth hCBS), it also contains a peripheral heme group. The broad mechanistic and kinetic features of reactions occurring in PLP-dependent enzymes are fairly well understood (see Fig. S1 for the observed reactions, ESI†).7–9 Besides the regulation of homocysteine concentration via the canonical reaction of hCBS (shown in Fig. 1), this enzyme can also catalyse various side-reactions leading to production of H2S (shown in Fig. S1, ESI†).10,11 While traditionally considered as purely a toxic gas,12 there is increasing evidence that H2S plays a regulatory role in critical biochemical processes involved in vasodilation and neuromodulation.13–18 The importance of H2S as an intracellular signalling molecule is a subject of increasing interest, potentially joining CO and NO as the third endogenous gas signalling molecule.19
hCBS exhibits various mechanisms of allosteric regulation and inhibition, based on binding of commonly-occurring intracellular molecules.20 One regulatory pathway which remains challenging to understand is the binding of small gas molecules to the aforementioned peripheral heme group. In hCBS, the heme group is known to not be directly involved in catalysis, and is located in a hydrophobic pocket near the surface of the enzyme approximately 20 Å away from the catalytic core.21 The heme group is 6-coordinate, and has a coordination sphere of a distal histidine and a proximal cysteine. The heme may exist in either the ferric or ferrous redox states, but is ferric in the basal state,20 where ferrous heme has been found to be approximately 2-fold less active than ferric heme.22 Given the different activities of the electronic states, the heme group in hCBS has been suggested to be redox-active and has accordingly been designated as a heme redox sensor protein.22–24
When reduced to the ferrous state, the heme group may bind either CO or NO, with both causing complete inhibition of hCBS.21 Upon CO binding, UV-vis. Spectroscopy shows a blue shift of the Soret absorption maximum from 450 nm to 422 nm.25,26 Similarly, NO binding causes a larger UV-vis. Blue shift from 450 nm to ∼390 nm.27–29 Compared to those reported for CO binding, the equilibrium dissociation constants for NO binding were initially predicted to be rather a lot higher than for CO binding.27,28 However, more recent refinement of these values shows that the equilibrium dissociation constants for both gases are similar in magnitude, at KD = 0.8 μM and KD = 0.23 μM for CO and NO, respectively.29 Relative to another heme signalling protein which binds both CO and NO, soluble guanylate cyclase (sGC), these equilibrium dissociation constants are slightly lower for CO (KD = 260 μM for sGC), and many orders of magnitude higher for NO (KD = 53 nM–850 pM for sGC).30 The above dissociation constants for hCBS do not take into account the fact that it is a homodimer, with binding to the heme group in one chain potentially being able to affect the binding strength in the other chain. While there is evidence of such allosteric effects for bonding of CO, with different KD1 and KD2 being reported,25,26,29 we have not attempted to model these effects here. In any case, whether NO or CO binds to hCBS, the heme group is quickly oxidised back to the ferric state by O2, resulting in total recovery of enzymatic activity.31
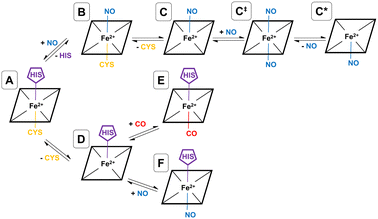
As shown by EPR spectroscopy, CO binding is associated with decoordinatation of proximal cysteine in a two-step fashion (A → D → E), where the initial loss of cysteine (A → D) is the rate-limiting step (see Fig. 2). The final inhibitory state, E, is found to be hexa-coordinate with proximal CO and distal histidine.26,32 Also based on EPR spectroscopy, the NO binding pathway has been shown to occur in two steps (A → B → C), starting with concerted displacement of the distal histidine by incoming NO (A → B), followed by (again rate-limiting) decoordination of proximal cysteine (B → C). In this case, the final inhibitory state, C, is determined to be penta-coordinate, with a proximal NO, and both amino acids decoordinated (see Fig. 2).26,27,32 Given the mechanism for CO binding, we suggest that it is feasible that D could bind to NO rather than CO equivalent, forming a different hexa-coordinate heme group with proximal NO and distal histidine (F) (see Fig. 2).
NO also binds to heme in a somewhat similar protein, soluble guanylate cyclase, and in that case, the NO-bound form is also suggested to be pentacoordinate, with NO binding being accompanied by histidine sidechain decoordination. There is also some evidence that the NO-bound form involves a proximal NO ligand, i.e., bound on the same side as the departing histidine sidechain. We have previously suggested33 that this proximal NO state could be formed by reaction of a second NO equivalent with the initially formed penta-coordinate Fe(II)–NO system with a distal NO, to form a transient hexa-coordinate NO–Fe(II)–NO system (C‡) that would then lose the first NO to yield the isomeric penta-coordinate NO–Fe(II) (C*) (see Fig. 2). We suggested that this proximal NO binding (whose formation might be plausible during a short period of elevated NO partial pressure) could be associated with slower return to the initial state, as under low NO conditions, access to hexa-coordinate C‡ would be difficult. It is possible that a similar mechanism occurs also for hCBS, where experiment does not allow a conclusive assignment of the bound NO state to a C or C* form. If C* is indeed formed, this could explain the reported lower rate of NO dissociation (∼0.003 s−1) compared to that of CO (∼0.5 s−1) in hCBS, as has already been suggested.29
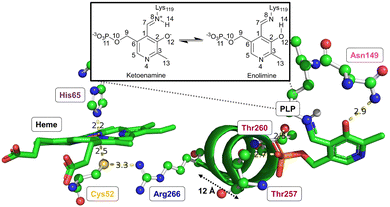
Both CO or NO binding to the heme group can inhibit hCBS, and it has been shown that this is due to conformational changes in the PLP-dependent active site upon gas binding to the heme site, ultimately leading to mechanical signalling between the two sites. However, the detailed way in which this signalling occurs and the way in which it causes the inhibition are not yet fully understood. The environment of the heme group and how it is structurally related to the PLP environment is shown in Fig. 3.
The proximal Cys52 forms a salt bridge with Arg266, where Arg266 is at one end of a short α-helix 8, and at the other end, Thr260 and Thr257 exhibit strong hydrogen bonding with the phosphate group of PLP.20,34–36 Mutation of both Arg266 and Thr260/Thr257 has been shown to reduce enzymatic activity.35,37–39 As well as the suggested mechanical signalling between the heme group and PLP cofactor, a form of electronic coupling between the heme group, α-helix 8 and the PLP cofactor has been suggested40 to play a role in this inhibition, but the nature of this coupling is unclear,‡ and we will focus here on the mechanical signalling hypothesis.
In the mechanical signalling model,41 the active ketoenamine form of PLP and its protonated Schiff base nitrogen is stabilised by hydrogen bonding between Asn149 and the pyridoxine ring oxygen atom, as shown in Fig. 3. The protonation of the Schiff base nitrogen atom makes the imine carbon atom more susceptible to nucleophilic attack.7,8,41 In case the PLP centre undergoes tautomerisation, an inactive enolimine form with a neutral imine nitrogen is obtained.41 Fluorescence spectroscopy experiments show that upon binding of CO/NO, the PLP cofactor changes character from the ketoenamine to enolimine form.41 This was suggested to be due to helix 8 motion caused by breaking of the Cys52–Arg266 salt bridge, with the strong hydrogen bonds between Thr257/Thr260 and the phosphate group of PLP leading to movement of the PLP group that cause disruption of the Asn149–O−(PLP) hydrogen bond and hence the shift of the tautomerisation equilibrium towards the inactive enolimine form. The experimental technique does not however provide access to detailed atomistic insight into the structural changes in helix 8 and the PLP site.
The goal of this study is to investigate the structural changes occurring upon CO or NO binding to the heme group. To do so, we first explore the free energy landscape associated with CO and NO binding, using quantum-chemical methods, to obtain accurate microscopic models of the C, E and F inhibited forms of the heme group. Based on these models, extended MD simulations of the inhibited forms are performed to study the motion of α-helix 8 following breakage of the Cys52–Arg266 salt bridge, and what effect this has on the structure surrounding the PLP active site.
Computational details
Quantum chemical calculations
In all calculations, the heme ring was modelled as an Fe-porphin ring,42,43 and cysteine and histidine were modelled as hydrosulfide and imidazole, respectively. To provide adiabatic spin-state energetics,42 each of the heme derivatives shown in Fig. 2 (excluding C‡ and C*, which is identical to C with the modelling approach used) were geometry optimised in their low-, medium-, and high-spin states using the hybrid B3LYP functional44,45 where Fe(II) was described using the def2-TZVP basis set and all other atoms with the def2-SVP basis set46 (TZVP/SVP basis in Table S1, ESI†). The D3 dispersion correction with the Becke–Johnson damping function was used for all optimisations.47,48 Using second-derivative calculations, no imaginary frequencies were found, thus all heme derivatives were found to be stable minima on their corresponding potential energy surface. These optimisations and frequency analyses were performed with the Gaussian 16 program (see Table S6 for convergence criteria for these optimisations, ESI†).49 See the data availability statement for the geometries for the optimised species for the various spin states.To identify the electronic ground states, single-point DLPNO-CCSD(T1) calculations were performed on the optimised geometries of the heme derivatives using the ORCA quantum chemistry program package (see Table S7 (ESI†) for the accuracy settings for all DLPNO-CCSD(T1) calculations).50 The coupled-cluster expansion was based on hybrid B3LYP-D3 Kohn–Sham orbitals44,45 obtained using the TZVP/SVP basis set combination (see Table S1, ESI†).46 The density-fitting approximation was used to solve Coulomb integrals, and numerical chain-of-sphere integration was used for the Hartree–Fock exchange integrals.51 As previously shown,52 test calculations using Hartree–Fock orbitals for the coupled-cluster expansion showed very similar relative energies. Scalar relativistic effects were also considered through the zero-order regular approximation (ZORA).53–55 The ZORA recontracted versions of the def2 basis sets were used within this approximation.56 As auxiliary basis sets, the normal def2 family of basis sets and the segmented all-electron relativistically contracted (SARC) were used.46,56
On the calculated electronic ground state for each species, a higher-level DLPNO-CCSD(T1) calculation was performed, where two-point complete basis set limit extrapolation57 (details in ESI†) was applied with respect to the heme iron using two basis set combinations, TZVPP(Fe(II))/TZVP(N,O,S,C)/SVP(H) & QZVPP(Fe(II))/TZVP(N,O,S,C)/SVP(H) (see Table S1, ESI†).46 All other parameters for the DLPNO-CCSD(T1) calculations remained the same as already outlined above.
To evaluate the Gibbs free energy changes associated with the steps of the reaction pathways, two terms were added to the complete basis set extrapolated DLPNO-CCSD(T1) electronic energy. The first is the statistical mechanics Gibbs free energy correction for each of the species at standard state (1 M) taken from a frequency analysis of a hybrid B3LYP-D3 calculation performed using the TZVPP/TZVP/SVP basis set combination. The translational contribution to the Gibbs free energy was removed for decoordinated amino acid models, hydrosulfide and imidazole, since these remain bound to the protein even upon dissociation from the heme group. The second is the Gibbs free energy of solvation for each of the species, which was calculated by the difference in hybrid B3LYP-D3 electronic energy between a vacuum and implicitly solvated model using a CPCM implicit solvent model with a protein-representative dielectric constant of ε = 4. We have also evaluated Gibbs free energy changes associated with the steps of the reaction pathways using a selection of DFT functionals – see Table S2 (ESI†) and the accompanying text.
Molecular dynamics simulations
To the best of our knowledge, there exist 8 crystal structures of hCBS in the basal state (pdb-id: 1JBQ, 1M54, 4COO, 4L0D, 4L3V, 4L27, 4L28, 5MMS).20,24,34,58,59 On the basis of having the best resolution (2.00 Å), being the wild-type form of hCBS, and having all residues modelled in the relevant domains, 4COO was used as the starting point in this work. For a detailed comparison of all available crystal structures for hCBS, see Table S8 (ESI†). hCBS is a biological homodimer and was modelled as such. 4COO contains all three domains of hCBS: the N-terminal heme domain, the central catalytic domain, and the C-terminal regulatory domain.34 Since the C-terminal regulatory domain is not the main focus of this work and its inclusion would surely increase computational expense, it was excluded from modelling – a previously successful methodology for catalytic domain focused modelling work.60 There are 64 missing residues at the N-termini for both chains which were not added due to uncertainty in their secondary structures. With these considerations in mind, both chains, residues 43–381, were used for modelling throughout, giving a total of 676 residues. Within this selection, there are a few residues with missing atoms – these were added back using SCWRL.61The parameters for the covalently-bound PLP cofactor were generated using CGenFF62 and deemed to be satisfactory for the purposes of this work (see ESI† for parameters). To include the heme group in the system topology, the native support within CHARMM36 was used.63 Where relevant, the distal His65 and proximal Cys52 were bonded to the heme group by inclusion of a specbond.dat file. All other atoms also used the native support within CHARMM36.63 The protonation states of all titratable amino acid side-chains were assigned based on their pKa predicted by PropKa64 and set accordingly within the system topology (see ESI† for the protonation states of all amino acids).
Prior to production MD, equilibration was performed for species A (see Fig. 2), using the TIP3P water model,65 and periodic boundary conditions with a rhombic dodecahedron unit cell, where the protein was at least 20 Å from the box edge. The total charge of the system was neutralised and set to a realistic physiological concentration of NaCl (0.15 M).66 To remove any initial bad contacts, an energy minimisation was performed and NVT and NPT equilibrations were performed for 1000 ps each, using the velocity-rescaling thermostat67 and Parrinello–Rahman barostat,68 thus equilibrating the system at 300 K and 1 bar. Lastly, positional restraints on all atoms were sequentially relaxed, and two 1000 ns simulations were performed using different starting velocities in the NPT ensemble with Parrinello–Rahman pressure coupling.68
In order to simulate a given inhibitory pathway (A → C, A → F, and A → E – see Fig. 2), the final geometry from the trajectory of A was extracted and structurally modified to represent the relevant bonding for C, E, or F, and the specbond.dat file was updated appropriately. Any CO or NO molecules were introduced appropriately by making slight structural modifications to the amino acids they displace to avoid any severe steric clashes and were bonded to the heme group using the specbond.dat file. These modifications were performed for both monomers, so for each trajectory, there are two heme and PLP groups to be modified. In all cases, the proximal Cys52 was protonated upon decoordination from the heme iron. An energy minimisation was used to mitigate any bad contacts caused by the crude structural modifications. Following this, NVT and NPT equilibrations were performed for 1000 ps each, using the velocity-rescaling thermostat67 and Parrinello–Rahman barostat.68 Once each of the systems were sufficiently equilibrated, all positional restraints were sequentially relaxed, and simulations for each inhibitory state in the NPT ensemble with Parrinello–Rahman pressure coupling68 were performed. For each pathway, two 1000 ns simulations were performed using different starting velocities. All MD simulations were performed with GROMACS.69,70
Results and discussion
Quantum chemical calculations
In good agreement with previous ab initio and DFT studies,71–74F has a clear doublet ground state, and this is also the case for C, again in agreement with previous work.75 As already mentioned, there are no computational studies of species B to the best of our knowledge, though the corresponding ferric species has been studied, and found to have a clear low-spin form (in that case, a singlet).76 This suggests that B should be low-spin (i.e. a doublet), which we indeed find, with a large spin state gap to the closest-lying spin state (sextet) of 20.5 kcal mol−1. We calculate a stable singlet ground state for species E, in positive agreement with numerous previous computational studies.71,74,77
Moving now to the gas-free heme adducts, it is well established from previous experimental78 and computational42 work that D has a quintet ground state with a close-lying triplet, and this is also found here, albeit with a larger quintet-triplet gap than in some previous studies,42 perhaps due to the use of local coupled-cluster with a relatively small basis set. For species A there is, to the best of our knowledge, no previous experimental or computational work on the electronic nature of the ground state. We find the ground spin state of A to be a singlet, albeit with a relatively small spin state gap to the triplet of 4.2 kcal mol−1.
As well as the inherent uncertainties coming from the level of electronic structure theory used, our computational approach is limited in accuracy due to three aspects, which we discuss here. First, dissociation of histidine and/or cysteine sidechains from the heme group does not involve formation of a separate molecule, since the sidechains remain part of the whole protein-heme system. Hence, within the ideal-gas-like treatment of statistical mechanics, it is not clear how to treat the dissociated species, as this will not have a large relative translational partition function. In our calculations, we (somewhat arbitrarily) treat it as having no translational freedom. The rotational and vibrational parts of the partition function are computed using the usual rigid-rotor/harmonic oscillator approaches. Since the dissociated sidechain does have some range of possible motion, this may underestimate the entropy (and hence overestimate the Gibbs energy) of the dissociated states, but this may be partly compensated for by including the full rotational partition function (the sidechain will in reality have some degree of constraint on its rotational motion).
A second approximation involves the use of a continuum solvent with a generic dielectric permittivity of 4 to describe the medium surrounding the heme model used in our quantum chemical calculations. The initial species A is an anion, but dissociation of cysteine leads to neutral species, so solvation does affect our calculated Gibbs energies to some extent, and the polarity of the medium may not be well captured by a single dielectric constant. We have checked that varying the dielectric constant to that of water does not impact the calculated relative Gibbs energies in a major way (for example, species C moves from −0.4 to −2.9 kcal mol−1, with the difference being of the order of the estimated error in the quantum-chemical method used), but this approach does still introduce some additional error in our estimated Gibbs energies. We note that the departing cysteine sidechain is treated as anionic HS− in our calculations. The cysteine sidechain has a pKa near 7, so that when using a standard state for the proton concentration corresponding to pH 7 (i.e. using ΔG°′ rather than ΔG°, see ref. 82) the standard Gibbs energies of the anionic thiolate and neutral thiol forms are almost equal, and we therefore do not need to account for the differential solvation energies of the two forms. As an additional test for the accuracy of this assumption and of the solvation treatment, we did however compute the pKa of H2S at the same level of theory used here, obtaining a value of 4.7, reasonably close to the experimental value of 7. Cysteine residue have pKa values ranging from 3.5 to 12 depending on the protein environment and reactivity,83 so our prediction is in reasonable qualitative agreement.
A third aspect relates to the conformational rearrangement of the overall protein structure, α-helix 8, and the PLP cofactor following CO or NO coordination, that will be discussed below. This rearrangement is spontaneous and will hence lead to a favourable contribution to the reaction free energy. As the inhibition by CO and NO is observed to be total, the free energy gain associated with relaxation of the structure after CO or NO coordination must be significant, since otherwise a small portion of the protein would remain in its active form. Assuming inhibition by a factor of 100, the Gibbs energy change should be −RT ln 100 or 2.7 kcal mol−1, but the precise value is unclear. Of course, relaxation cannot be too favourable, because otherwise the protein would not be stable in the active form, even in the absence of CO or NO binding.
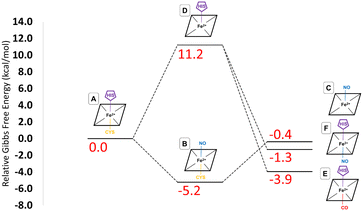
These provisos noted, we can compare our results with experimental observations. The pathway leading to inhibition by CO is believed to follow the route A → D → E. According to our calculations, the first step is endoergic in Gibbs energy terms (+11.2 kcal mol−1), and the second step is exoergic (−15.1 kcal mol−1) (see Fig. 4). We note that our calculations do not address energy barriers. As previously argued,72 gaseous ligand binding, as in the second step, can be expected to be quite fast so will have a low barrier. Decoordination of cysteine (with concomitant protonation) in the first step will likely have a larger barrier, consistent with the slow (k ≅ 10−3 s−1, equivalent to a free energy barrier of 21.5 kcal mol−1 at 298 K in terms of the Eyring equation) observed binding of CO to ferrous hCBS.32 The net free energy change from A to E is calculated to be −3.9 kcal mol−1. Given the many sources of uncertainty mentioned above, this is consistent with the observed binding affinity and KD = 0.8 μM, which implies ΔG°′ = −8.3 kcal mol−1.
Experimentally, NO has been observed to inhibit hCBS by binding through the pathway, A → B → C. The alternative pathway via intermediate D as for CO is presumably much less favourable, given the difference in the observed kinetics. The first step A ≥ B is calculated to be exogenic (−5.2 kcal mol−1) and will have a barrier which we have not studied here. Presumably, given the observed fast binding of NO, this barrier is relatively low, but the reason for the difference with CO, for which this pathway is not observed, is less clear. The second step is predicted as endoergic (+4.8 kcal mol−1), leading to an overall predicted binding free energy of −0.4 kcal mol−1, which differs by 8.7 kcal mol−1 from the value indicated by the experimental dissociation constant of KD = 0.23 μM, which means that ΔG°′ = −9.1 kcal mol−1. Formation of C requires dissociation of both the cysteine and histidine sidechains, so is twice subject to the uncertainty mentioned above relating to the translational entropy of the dissociated ligand. In case some portion of the translational entropy does still contribute to the dissociation Gibbs energy, this would account for some of the mismatch between the calculated and experimental ΔG°′. The conformational change would also account for some of the difference and bearing in mind possible inaccuracies local CCSD(T), the computed values are overall roughly consistent with experiment.
The suggested endpoint of NO binding based on experiment is species C, while the a priori plausible F species not experimentally observed. Our calculations suggest that F would be more stable (see Fig. 4), but given the errors in our computational approach, and the small difference in computed Gibbs energies, this is not a major inconsistency.
To conclude this section, the quantum chemical calculations are consistent with the experimental observations and provide us with a solid basis for assigning the bonding pattern to be used in the MD simulations addressing the conformational changes in structure upon NO or CO coordination, which will be discussed next.
To confirm the quality of the CGenFF parameters for PLP generated herein with respect to their validity for studying the inhibitory pathways A → C, A → E, and A → F, simulations of the resting state, A, were performed first. The core of our hypothesis is that when Cys52 decoordinates from the heme group, it is quickly protonated, and the strong salt bridge between Cys52 and Arg266 (see Fig. 3) would be broken as a direct consequence. Rupture of this salt bridge may cause some mechanically induced signalling pathway to PLP via α-helix 8 and enable the tautomerisation to the enolimine form of PLP, thus inhibiting the enzyme's activity. For this hypothesis to be supported, the salt bridge must of course be stable in the basal state A, so two separate simulations (1000 ns each) were performed for this state, with the Cys52 still coordinated to heme. These trajectories indeed show stable structures, as evidenced by a flat overall root mean square deviation (RMSD) for the protein as a whole (Fig. S2a & b, ESI†), an intact Cys52-Arg266 hydrogen bond throughout the simulation (Fig. S4, ESI†), and a largely unbroken hydrogen-bonding network around the PLP cofactor. For this latter aspect, we will first define a criterion for a hydrogen bond: the distance between the heavy atoms of the donor and acceptor must be <3.5 Å, and the donor-hydrogen-acceptor angle must be >100°.84 Using this criterion, returning to the simulations of the basal state A, we find a stable Asn149–O−(PLP) hydrogen bond throughout the simulations, with the hydrogen bond being observed for an average of 84% of the simulation time (Fig. S8, S9, S16, S17 and Table S5, ESI†). We do note some slight weakening occurring during one of the replica simulations for one of the homodimeric chains, where the hydrogen bond is observed for 73% of simulation time (Fig. S8, S9, S17 and Table S5, ESI†). Besides this key hydrogen bond, we also expect that strong hydrogen bonds are formed between the PLP phosphate group and the residues at the N-terminus of α-helix 8, ultimately coupling the positioning of α-helix 8 to the PLP cofactor. For these hydrogen bonds, we do not use the criteria described above due to the large number of possible donor–acceptor pairs complicating analysis and instead use only the donor–acceptor distances. However, the stability and minimal fluctuation of these donor–acceptor distances indicates that these hydrogen bonds are, as expected, very stable throughout the simulations (Fig. S24–S27, ESI†).
We now turn to simulations of the inhibited forms C and E resulting from binding of NO and CO, respectively, as well as of the possible modified inhibited form F, in which NO binds to the heme group but the histidine residue also remains bonded to the heme iron. We have performed two 1000 ns simulations of each of the final inhibitory states (C, E, and F), representing the pathways A → C, A → E, and A → F. From a MD standpoint, the topologies of E and F are very similar and are generated by modification of the topology of A, such that heme-Cys52 bond is broken, and a distal CO or NO (for E and F, respectively) molecule is introduced. While similar, the forcefield parameters are also slightly different for the hexa-coordinate heme groups. Again, from modification of a topology of A, generation of a topology for C requires that both the heme-Cys52 and heme-His65 bonds are broken, and that a distal NO molecule is introduced, resulting in a penta-coordinate heme group. For all simulations of C, E, and F, Cys52 has been protonated as we expect this would be the case given the proximity to bulk solvent and the typical pKa of cysteine sidechains. Moreover, the experimental study of the coupling between the heme group and the PLP cofactor suggested that cysteine protonation is an essential step in the inhibition pathway.41
As no structures are available for the inhibited form, it was not clear which structural changes compared to species A would be likely to be observed, nor on which timescale they could be expected to occur, though minor conformational change could certainly be expected to be visible on the microsecond timescale of the MD simulations. We monitored a range of structural coordinates relating to α-helix 8, the heme group and the PLP cofactor for each of the species C, E and F, each of the chains in the homodimers, and each of the independent simulations.
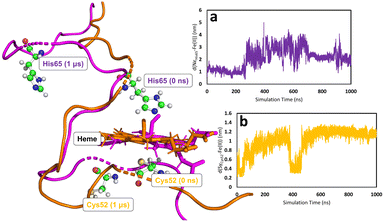
In all simulations, the Cys52-Arg266 interaction is found to break almost immediately upon modifying the heme group topology. This is expected since the cysteine is protonated as part of the change in topology. (see Fig. S5, S6 & S7 for C, E, and F, respectively, ESI†). The forcefield partial charge on the coordinated sulfur atom in species A is −0.8 but is only −0.23 in the neutral cysteine form, leading to much weaker electrostatic interactions. After the initial instantaneous increase in d(SγCys52–N1ηArg266), slower and higher-amplitude variations are also observed, associated with the fact that the proximal Cys52 is part of a loop region of the secondary protein structure. Consequently, upon decoordination from heme, Cys52 (and His65 for the case of C) is free to move as its position is no longer defined by the coordination sphere of the heme group. On the other hand, the position of the heme group is in some way locked by interaction of the propionate side-chains with Arg51 and Arg224,85 which are not part of the flexible loop region, so that despite the loss of the ligand, the heme group remains reasonably well anchored. Motion of Cys52 following decoordination occurs in all simulations of C, E, and F, but the direction of translation of Cys52 is not systematic, presumably due to the flexibility of the loop region. Similar freedom of movement is seen for His65 for simulations of C, again with no discernible pattern. Fig. 5 shows the types of large-scale motions which are observed for both Cys52 and His65 when they have decoordinated from heme to form C.
None of the simulations of species C, E and F show rapid or major changes in the positions of the heme group, α-helix 8 or the PLP cofactor, as shown by the moderate overall RMSD values for the trajectories, with respect to their species A–derived reference points (Fig. S2 & S3, ESI†). Nevertheless, close inspection of these trajectories does show evidence for structural change consistent with the mechanical signalling hypothesis. The main metric showing this is the previously mentioned Asn149–O−(PLP) hydrogen bond. Considering the three species C, E and F, the two chains of the homodimer, and the two independent MD simulations for each case, there are 12 time series to be analysed. Again, using the criteria defined above, in a way that is not seen for the simulations of A, in three of these time series, the Asn149–O−(PLP) hydrogen bond is unambiguously disrupted in a major way, with it being observed for 38, 25, and 13% of simulation times (Fig. S10, S11, S14, S15, S19, S22, S23 and Table S5, ESI†). In a further three time series, the hydrogen bond shows some weakening in a similar fashion to that which was observed in one of the replica simulations of A, where the hydrogen bond is observed for 75, 71, and 79% of simulation times (Fig. S10, S11, S14, S15, S18, S19, S22 and Table S5, ESI†). The remaining six simulations do not show convincing evidence of hydrogen bond elongation. Since our MD simulations cannot account for the tautomeric change in the PLP cofactor, any weakening of the hydrogen bonding must be due to the mechanical signalling through α-helix 8. We note that the lack of clear changes in hydrogen bonding in some of the timeseries may be due to insufficient sampling, evidenced by the fact that there is no clear pattern concerning the differences between species C, E and F. In fact, the species showing the least evidence for weakening of the interaction, E (Fig. S12, S13, S20, S21 and Table S5, ESI†), is treated in an extremely similar way within the forcefield to the related species F, which shows clear elongation of the Asn149–O−(PLP) hydrogen bond in some of the time series (Fig. S14 and S15, ESI†), strengthening the suggestion that the differences between simulations are indeed due to insufficient sampling.
Other structural metrics relating to the PLP cofactor are stable throughout the simulation. For example, the strong hydrogen bonds between the PLP phosphate group and the α-helix 8 N-terminus are largely unbroken throughout (Fig. S24–S39, ESI†) (some of the changes in distance shown in these plots arise due to switching of hydrogen bonds between the different phosphate oxygens). The α-helix is thereby firmly attached to the PLP cofactor, and motion of the α-helix leads to the above-mentioned weakening of the interaction of the PLP cofactor with Asn149. See the data availability statement for initial GROMACS geometry files for each of the species A, C, E, F as well as selected forcefield parameters.
The elongation of the Asn149–O−(PLP) hydrogen bond is associated with other slight structural changes relating to the position of α-helix 8 and the PLP cofactor. Some insight into these changes can be obtained by comparing a typical species A structure and a typical structure in which the hydrogen bond is surely broken (Fig. 6). This comparison is somewhat artificial since the choice of the two structures is necessarily arbitrary, but it has the benefit of providing an overall picture of the changes arising with the mechanical coupling mechanism. In Fig. 6, the two structures are aligned based on the positions of the α-carbons of all amino acids, so that their protein backbones are maximally close to each other. As can be seen, there is a clear change in the relative position of α-helix 8 and the PLP cofactor with respect to Asn149, confirming that indeed α-helix 8 does play a role in mechanically induced signalling between the heme group and PLP cofactor.
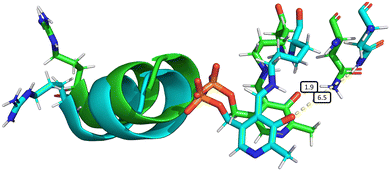 | ||
| Fig. 6 Overall structural changes following decoordination of Cys52 and rotation of Arg266. The initial structure at 0 ns is shown in green and a snapshot after 1000 ns is shown in blue (species F, chain A). The bond length d(NδAsn149–O12PLP) is highlighted in the figure, increasing from 1.9 Å (at 0 ns) to 6.5 Å (at 1000 ns). This figure was generated by α-carbon backbone alignment in PyMOL.86 | ||
In principle, biased simulation techniques together with free energy evaluation methods could be used to quantify the differences arising when switching from the Cys-heme bound species A to the free Cys species C, E and F. This would however be rather challenging to model, given the extensive small structural differences between the various species, and the lack of a clearly identified reaction coordinate associated with the mechanical coupling. Hence this has not been attempted here.
Conclusions
In this work, we have aimed to investigate in more detail the role of a peripheral heme group found in hCBS that does not directly engage in catalytic activities, but instead exerts regulatory control over the enzyme. This regulatory function manifests when CO or NO gas molecules bind to the heme group, leading to complete inhibition of PLP-dependent reactions.Initially, we validated the CO/NO bonding models proposed by EPR spectroscopy through detailed quantum chemical studies, analysing the Gibbs free energy changes associated with the inhibitory pathways. Despite noted limitations in computational accuracy, our findings demonstrated positive agreement with previous calculations on related heme derivatives, often employing more sophisticated quantum chemical methods, and our calculated Gibbs energies are consistent with observed thermodynamics, giving confidence in the atomistic models for the basal and ligand-bound states.
Using forcefields with bonding patterns identified using the quantum chemical calculations, several 1000 ns molecular dynamics simulations on the various inhibitory species were performed. Through these simulations, we sought to investigate in greater detail the proposed mechanical signalling model, which suggests that the rupture of the Cys52-Arg266 salt bridge, triggered by gas binding, initiates a cascade of allosteric changes. We find that motion of α-helix 8 (which Arg266 is a part of) which happens following breakage of the Cys52-Arg266 salt bridge leads to destabilisation of the active ketoenamine form of PLP. This destabilization arises from the elongation of a crucial hydrogen bond between Asn149 and a pyridoxine ring oxygen atom, suggesting a lowered barrier to tautomerization which produces the inactive enolimine form of PLP.
Our findings underscore the intriguing regulatory role of CO and NO in hCBS, indicating that both gases have the potential to inhibit the enzyme both experimentally and theoretically. Moreover, reactions catalysed by hCBS at the PLP active site cause production of H2S, yet further indicating the emerging theme of complex interplay between CO, NO and H2S as signalling molecules.
Data availability
The data referenced throughout this have been uploaded as part of the electronic supplementary material and files for replicating quantum chemical calculations and molecular dynamics simulations are available via the KU Leuven Research Data Repository, see https://doi.org/10.48804/EBWSWB.Author contributions
Neil R. McFarlane: conceptualisation, data curation, formal analysis, visualisation, writing – original draft, writing – review & editing; Jiangli Gui: data curation, formal analysis, visualisation; Julianna Oláh: conceptualisation, supervision, writing – review & editing; Jeremy N. Harvey: conceptualisation, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support through KU Leuven – Budapest University of Technology and Economics joint research funding (CELSA/19/017). J. O. thanks the National Research Development and Innovation Office (NKFIH) of Hungary for funding through grant K146661.Notes and references
- J. I. Sbodio, S. H. Snyder and B. D. Paul, Br. J. Pharmacol., 2019, 176, 583–593 CrossRef CAS PubMed.
- J. Perła-Kaján, T. Twardowski and H. Jakubowski, Amino Acids, 2007, 32, 561–572 CrossRef PubMed.
- Y. Chen, H. G. Shertzer, S. N. Schneider, D. W. Nebert and T. P. Dalton, J. Biol. Chem., 2005, 280, 33766–33774 CrossRef CAS PubMed.
- R. Lill and U. Mühlenhoff, Annu. Rev. Cell Dev. Biol., 2006, 22, 457–486 CrossRef CAS PubMed.
- C. S. Sevier and C. A. Kaiser, Nat. Rev. Mol. Cell Biol., 2002, 3, 836–847 CrossRef CAS PubMed.
- H.-F. Zhang, R. I. K. Geltink, S. J. Parker and P. H. Sorensen, Trends Cell Biol., 2022, 32, 800–814 CrossRef CAS PubMed.
- A. Salvà, J. Donoso, J. Frau and F. Muñoz, J. Phys. Chem. A, 2003, 107, 9409–9414 CrossRef.
- E. F. Oliveira, N. M. F. S. A. Cerqueira, P. A. Fernandes and M. J. Ramos, J. Am. Chem. Soc., 2011, 133, 15496–15505 CrossRef CAS PubMed.
- J. Liang, Q. Han, Y. Tan, H. Ding and J. Li, Front. Mol. Biosci., 2019, 6, 4 CrossRef CAS PubMed.
- A. P. Landry, J. Roman and R. Banerjee, Curr. Opin. Struct. Biol., 2021, 71, 27–35 CrossRef CAS PubMed.
- T. Chiku, D. Padovani, W. Zhu, S. Singh, V. Vitvitsky and R. Banerjee, J. Biol. Chem., 2009, 284, 11601–11612 CrossRef CAS PubMed.
- R. J. Reiffenstein, W. C. Hulbert and S. H. Roth, Annu. Rev. Pharmacol. Toxicol., 1992, 32, 109–134 CrossRef CAS PubMed.
- K. Abe and H. Kimura, J. Neurosci., 1996, 16, 1066–1071 CrossRef CAS PubMed.
- R. Hosoki, N. Matsuki and H. Kimura, Biochem. Biophys. Res. Commun., 1997, 237, 527–531 CrossRef CAS PubMed.
- W. Zhao, J. Zhang, Y. Lu and R. Wang, EMBO J., 2001, 20, 6008–6016 CrossRef CAS PubMed.
- W. Zhao and R. Wang, Am. J. Physiol.: Heart Circ. Physiol., 2002, 283, H474–H480 CrossRef CAS PubMed.
- M. Whiteman, J. S. Armstrong, S. H. Chu, S. Jia-Ling, B.-S. Wong, N. S. Cheung, B. Halliwell and P. K. Moore, J. Neurochem., 2004, 90, 765–768 CrossRef CAS PubMed.
- C. Szabo, Biochem. Pharmacol., 2018, 149, 5–19 CrossRef CAS PubMed.
- R. Wang, FASEB J., 2002, 16, 1792–1798 CrossRef CAS PubMed.
- M. Meier, M. Janosik, V. Kery, J. P. Kraus and P. Burkhard, EMBO J., 2001, 20, 3910–3916 CrossRef CAS PubMed.
- S. Singh, P. Madzelan and R. Banerjee, Nat. Prod. Rep., 2007, 24, 631–639 RSC.
- S. Taoka, S. Ohja, X. Shan, W. D. Kruger and R. Banerjee, J. Biol. Chem., 1998, 273, 25179–25184 CrossRef CAS PubMed.
- R. Banerjee and C. Zou, Arch. Biochem. Biophys., 2005, 433, 144–156 CrossRef CAS PubMed.
- S. Taoka, B. W. Lepore, Ö. Kabil, S. Ojha, D. Ringe and R. Banerjee, Biochemistry, 2002, 41, 10454–10461 CrossRef CAS PubMed.
- S. Taoka, M. West and R. Banerjee, Biochemistry, 1999, 38, 2738–2744 CrossRef CAS PubMed.
- M. Puranik, C. L. Weeks, D. Lahaye, Ö. Kabil, S. Taoka, S. B. Nielsen, J. T. Groves, R. Banerjee and T. G. Spiro, J. Biol. Chem., 2006, 281, 13433–13438 CrossRef CAS PubMed.
- S. Taoka and R. Banerjee, J. Inorg. Biochem., 2001, 87, 245–251 CrossRef CAS PubMed.
- C. Gherasim, P. K. Yadav, O. Kabil, W.-N. Niu and R. Banerjee, PLoS One, 2014, 9, e85544 CrossRef PubMed.
- J. B. Vicente, H. G. Colaço, M. I. S. Mendes, P. Sarti, P. Leandro and A. Giuffrè, J. Biol. Chem., 2014, 289, 8579–8587 CrossRef CAS PubMed.
- G. Wu, I. Sharina and E. Martin, Front. Mol. Biosci., 2022, 9, 1007768 CrossRef CAS PubMed.
- S. Carballal, P. Madzelan, C. F. Zinola, M. Graña, R. Radi, R. Banerjee and B. Alvarez, Biochemistry, 2008, 47, 3194–3201 CrossRef CAS PubMed.
- S. Carballal, E. Cuevasanta, I. Marmisolle, O. Kabil, C. Gherasim, D. P. Ballou, R. Banerjee and B. Alvarez, Biochemistry, 2013, 52, 4553–4562 CrossRef CAS PubMed.
- A. M. Rozza, M. Papp, N. R. McFarlane, J. N. Harvey and J. Oláh, Chem. – Eur. J., 2022, 28, e202200930 CrossRef CAS PubMed.
- T. J. McCorvie, J. Kopec, S.-J. Hyung, F. Fitzpatrick, X. Feng, D. Termine, C. Strain-Damerell, M. Vollmar, J. Fleming, J. M. Janz, C. Bulawa and W. W. Yue, J. Biol. Chem., 2014, 289, 36018–36030 CrossRef CAS PubMed.
- P. K. Yadav, P. Xie and R. Banerjee, J. Biol. Chem., 2012, 287, 37611–37620 CrossRef CAS PubMed.
- R. Evande, S. Ojha and R. Banerjee, Arch. Biochem. Biophys., 2004, 427, 188–196 CrossRef CAS PubMed.
- S. Singh, P. Madzelan, J. Stasser, C. L. Weeks, D. Becker, T. G. Spiro, J. Penner-Hahn and R. Banerjee, J. Inorg. Biochem., 2009, 103, 689–697 CrossRef CAS PubMed.
- A. T. Smith, Y. Su, D. J. Stevens, T. Majtan, J. P. Kraus and J. N. Burstyn, Biochemistry, 2012, 51, 6360–6370 CrossRef CAS PubMed.
- A. Bhatt and Md. E. Ali, J. Biomol. Struct. Dyn., 2022, 40, 12690–12698 CrossRef CAS PubMed.
- A. Bhatt, A. Mukhopadhyaya and Md. E. Ali, J. Phys. Chem. B, 2022, 126, 4754–4760 CrossRef CAS PubMed.
- C. L. Weeks, S. Singh, P. Madzelan, R. Banerjee and T. G. Spiro, J. Am. Chem. Soc., 2009, 131, 12809–12816 CrossRef CAS PubMed.
- M. Radoń, J. Chem. Theory Comput., 2014, 10, 2306–2321 CrossRef PubMed.
- Md. E. Ali, B. Sanyal and P. M. Oppeneer, J. Phys. Chem. B, 2012, 116, 5849–5859 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- Z. Benedek, P. Timár, T. Szilvási and G. Barcza, J. Comput. Chem., 2022, 43, 2103–2120 CrossRef CAS PubMed.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- F. Neese and E. F. Valeev, J. Chem. Theory Comput., 2011, 7, 33–43 CrossRef CAS PubMed.
- J. B. Vicente, H. G. Colaço, F. Malagrinò, P. E. Santo, A. Gutierres, T. M. Bandeiras, P. Leandro, J. A. Brito and A. Giuffrè, Oxid. Med. Cell. Longevity., 2017, 2017, e8940321 Search PubMed.
- J. Ereño-Orbea, T. Majtan, I. Oyenarte, J. P. Kraus and L. A. Martínez-Cruz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E3790–E3799 CrossRef PubMed.
- S. Gupta, S. Kelow, L. Wang, M. D. Andrake, R. L. Dunbrack and W. D. Kruger, J. Biol. Chem., 2018, 293, 13921–13931 CrossRef CAS PubMed.
- G. G. Krivov, M. V. Shapovalov and R. L. Dunbrack Jr., Proteins: Struct., Funct., Bioinf., 2009, 77, 778–795 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. MacKerell, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- J. Huang and A. D. MacKerell, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- G. A. Ross, A. S. Rustenburg, P. B. Grinaway, J. Fass and J. D. Chodera, J. Phys. Chem. B, 2018, 122, 5466–5486 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- N. Strickland and J. N. Harvey, J. Phys. Chem. B, 2007, 111, 841–852 CrossRef CAS PubMed.
- A. Lábas, D. K. Menyhárd, J. N. Harvey and J. Oláh, Chem. – Eur. J., 2018, 24, 5350–5358 CrossRef PubMed.
- J. Oláh and J. N. Harvey, J. Phys. Chem. A, 2009, 113, 7338–7345 CrossRef PubMed.
- M. Radoń and K. Pierloot, J. Phys. Chem. A, 2008, 112, 11824–11832 CrossRef PubMed.
- C. Rovira, K. Kunc, J. Hutter, P. Ballone and M. Parrinello, J. Phys. Chem. A, 1997, 101, 8914–8925 CrossRef CAS.
- D. A. Scherlis, C. B. Cymeryng and D. A. Estrin, Inorg. Chem., 2000, 39, 2352–2359 CrossRef CAS PubMed.
- S. Liu, S. Xia, D. Yue, H. Sun and H. Hirao, Inorg. Chem., 2022, 61, 17494–17504 CrossRef CAS PubMed.
- L. Pauling and C. D. Coryell, Proc. Natl. Acad. Sci. U. S. A., 1936, 22, 210–216 CrossRef CAS PubMed.
- D. G. Liakos, Y. Guo and F. Neese, J. Phys. Chem. A, 2020, 124, 90–100 CrossRef CAS PubMed.
- M. Feldt, Q. M. Phung, K. Pierloot, R. A. Mata and J. N. Harvey, J. Chem. Theory Comput., 2019, 15, 922–937 CrossRef CAS PubMed.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, J. Chem. Theory Comput., 2022, 18, 3538–3548 CrossRef CAS PubMed.
- M. R. Gunner, T. Murakami, A. S. Rustenburg, M. Işık and J. D. Chodera, J. Comput.-Aided Mol. Des., 2020, 34, 561–573 CrossRef CAS PubMed.
- D. W. Bak, T. J. Bechtel, J. A. Falco and E. Weerapana, Curr. Opin. Chem. Biol., 2019, 48, 96–105 CrossRef CAS PubMed.
- E. N. Baker and R. E. Hubbard, Prog. Biophys. Mol. Biol., 1984, 44, 97–179 CrossRef CAS PubMed.
- V. Guallar and B. Olsen, J. Inorg. Biochem., 2006, 100, 755–760 CrossRef CAS PubMed.
- L. Schrödinger and W. DeLano, PyMOL (version 2.4.0)https://www.pymol.org/pymol, 2020 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01321b |
| ‡ Ref. 40 indeed shows very large changes in electron density distribution when performing comparative density functional theory calculations on the heme group, α-helix 8 and the PLP cofactor as separate fragments and in structures as found in hCBS, but these large changes seem to be due to artefacts associated with the gas-phase nature of the DFT calculations performed, which involve a fragment with large negative charge (the PLP cofactor) being brought into close proximity of the model for α-helix 8. |
| This journal is © the Owner Societies 2024 |