Spectroscopic characterization of carbon monoxide activation by neutral chromium carbides

Abstract

Spectroscopic characterization of carbon monoxide activation by neutral metal carbides is of essential importance for understanding the structure–reactivity relationships of catalytic sites, but has been proven to be very challenging owing to the difficulty in size selection. Here, we report a size-specific infrared-vacuum ultraviolet spectroscopic study of the reactions between carbon monoxide with neutral chromium carbides. Quantum chemical calculations were carried out to identify the low-lying structures and to interpret the experimental features. The results reveal that the most stable structure of CrC₃(CO)₂ consists of a CCO ketenylidene unit and that of CrC₄(CO)₂ has a semi-bridging CO with a very low CO stretching vibrational frequency at 1821 cm⁻¹. The electron structure analyses show that this semi-bridging CO is highly activated through the delocalized Cr–C–C three-center two-electron (3c–2e) interaction between the antibonding orbitals of CO and the metal carbide skeleton. The formation of these metal carbide carbonyls is found to be both thermodynamically exothermic and kinetically facile in the gas phase. The present findings have important implications for the mechanical understanding of the catalytic processes with isolated metal atoms/clusters dispersed on supports.

---

1. Introduction

The activation of carbon monoxide (CO) is essential in various catalytic processes (i.e., Fischer–Tropsch synthesis,^1,2 hydroformylation,^3,4 and alcohol synthesis⁵), which are important technologies in modern chemical and energy industries. The study of CO activation can help to clarify the mechanism of homogeneous and heterogeneous catalytic reactions. CO is usually activated by transition metals in terms of π-backdonation from the metal to CO, according to the Blyholder model.^6–12 CO molecules bond to transition metals in various manners, such as terminal, bridging, semi-bridging, and side-on-bonded modes.¹² Interestingly, recent studies demonstrated that transition-metal-free B₂(NHC)₂ molecules can also activate CO by backdonation of π and π* orbitals of the B–B triplet bond with a remarkable low C–O stretching frequency (1926 cm⁻¹),^13–15 providing intriguing insights into the CO activation by nonmetallic compounds.

Transition metal carbides are widely used to activate CO in many systems.^16–19 For instance, FeC_n has been proven to exhibit higher catalytic activity than the Fe-based catalysts.^20–26 Various metal carbide carbonyls have been synthesized in the condensed phase, showing higher nuclearity than the species containing only carbonyl ligands.^27–29 The gas-phase investigation of size-specific metal carbide carbonyl complexes provides insights into the structure–reactivity relationship that is difficult to extract from the bulk experiments. Recently, the NiC(CO)_n⁻ (n = 3–5) anions were prepared and studied by photoelectron spectroscopy, highlighting the pivotal roles played by metal carbides in C–C bond formation.³⁰ The study of the reaction between neutral transition metal carbides and carbon monoxide at the molecular level has been proven to be a challenging experimental target due to the difficulty in mass selection. Here, we synthesized neutral chromium carbide carbonyl compounds in a laser vaporization cluster source and measured the infrared spectra of CrC₃(CO)₂ and CrC₄(CO)₂ by infrared-vacuum ultraviolet (IR-VUV) spectroscopy. Experimental spectra in conjunction with quantum chemical calculations reveal that the most stable structure of CrC₃(CO)₂ consists of a CCO ketenylidene unit and that of CrC₄(CO)₂ has a semi-bridging CO. The electron structure analyses show that the semi-bridging CO is highly activated through the delocalized Cr–C–C three-center two-electron (3c–2e) interaction between the antibonding orbitals of CO and the metal carbide skeleton.

2. Experimental and theoretical methods

The experiment was performed using the IR-VUV apparatus, which has been described in detail in previous reports.^31–33 The neutral chromium carbide carbonyl complexes were prepared using the laser-vaporization cluster source in a pulsed supersonic expansion of 99.99% CO. The second harmonic of a Nd:YAG laser (532 nm) was employed to ablate the pure chromium target, with a pulse energy of 4.0 mJ. The reaction gas was introduced by a Parker pulse valve (Series 009), with a pulse width of 190 μs. The molecular beams that passed through a 4-mm-diameter skimmer were ionized by a VUV laser and then were detected by a reflectron time of flight mass spectrometer (TOF-MS).

The VUV light with the wavelength of 193 nm was produced by an ArF excimer laser (EX5A/500, Gamlaser, USA), with an energy of 7 mJ per pulse. The infrared laser was delivered by a potassium titanyl phosphate/potassium titanyl arsenate optical parametric oscillator/amplifier system (OPO/OPA, LaserVision) pumped by another seeded Nd:YAG laser (Continuum, Surelite EX). The OPO/OPA system was tunable from 700 to 7000 cm⁻¹, with a line width of 1 cm⁻¹.

The pulse valve, the vaporization laser, and the VUV light were operated at 20 Hz. The tunable IR light pulse was introduced at approximately 50 ns prior to the VUV pulse in a crossed manner and operated at 10 Hz. When the resonant vibrational transition was irradiated by the IR laser light and caused vibrational predissociation, a depletion of the selected neutral cluster mass signal was detected. The infrared spectra were recorded by the difference between the mass spectral signals without and with an infrared laser (IR laser OFF minus IR laser ON). The IR spectra of size-specific neutral CrC_n(CO)₂ (n = 3 and 4) complexes were successfully measured by a depletion spectrum of the ion signal intensity as a function of IR wavelength. The absence of IR spectra of other chromium carbide carbonyls could be due to either the low IR pulse energy or the low VUV photon energy. Typical spectra were recorded by scanning the IR wavelength in steps of 2 cm⁻¹ and averaging over 1800 laser shots at each wavelength. The infrared wavelength was calibrated using a commercial wavelength meter (HighFinesse GmbH, WS6-200 VIS IR).

Geometric optimization and frequency calculations of CrC_n(CO)₂ (n = 3 and 4) were performed using the Gaussian 16 program package³⁴ at the BLYP-D3(BJ)/def2-TZVPP level of theory. The harmonic vibrational frequencies were scaled by a factor of 0.991 in order to account for the method dependent systematic errors.³⁵ The resulting stick spectra were convoluted by a Gaussian line shape function with an 8 cm⁻¹ width at half-maximum (FWHM). For the possible isomerization paths, the transition states were optimized in the Berny algorithm. Intrinsic reaction coordinates (IRC) of all the transition states were carried out to confirm that the transition states connected to the initial and final states. The B2PLYPD3/def2-TZVPP single-point energy calculations on the BLYP-D3(BJ)/def2-TZVPP optimized structures were carried out to determine relative energies. The adaptive natural density partitioning (AdNDP)³⁶ bonding analysis was performed at the BLYP-D3(BJ)/def2-TZVPP level of theory by using the Multiwfn software.³⁷

3. Results and discussion

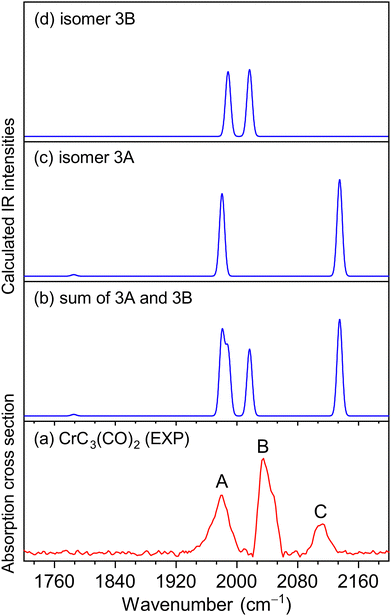
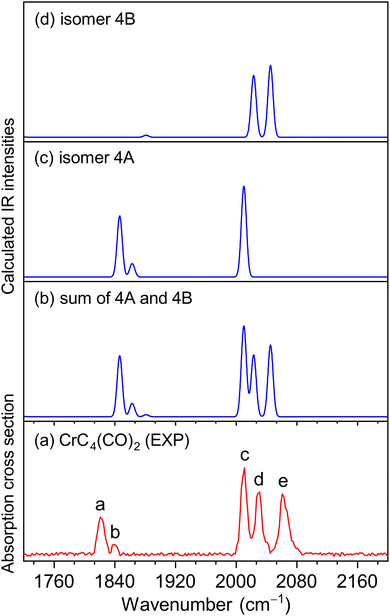
The experimental IR spectra of neutral CrC₃(CO)₂ and CrC₄(CO)₂ complexes in the CO stretching region are shown in Fig. 1a and 2a, respectively. Table 1 lists the corresponding band positions. Three peaks were observed in the experimental spectrum of CrC₃(CO)₂ at 1981, 2033, and 2113 cm⁻¹ (labeled A, B, and C), and five peaks were observed in the experimental spectrum of CrC₄(CO)₂ at 1821, 1839, 2011, 2031, and 2061 cm⁻¹ (labeled a, b, c, d, and e), respectively. The number of infrared absorption peaks of CrC₃(CO)₂ and CrC₄(CO)₂ is more than the number of CO groups in the corresponding molecules, indicating their complexity of the structure and the diversity of isomers.

Fig. 1 Comparison of the experimental and calculated IR spectra of neutral CrC₃(CO)₂. (a) Experimental IR spectrum of CrC₃(CO)₂. (b) The simulated total IR spectrum of a 1 (3A):1 (3B) mixture of isomers and (c and d) simulated IR spectrum of each individual isomer calculated at the BLYP-D3(BJ)/def2-TZVPP level of theory, with the harmonic vibrational frequencies scaled by 0.991.

Fig. 2 Comparison of the experimental and calculated IR spectra of neutral CrC₄(CO)₂. (a) Experimental IR spectrum of CrC₄(CO)₂. (b) The simulated total IR spectrum of a 1 (4A):1 (4B) mixture of isomers and (c) and (d) simulated IR spectrum of each individual isomer calculated at the BLYP-D3(BJ)/def2-TZVPP level of theory, with the harmonic vibrational frequencies scaled by 0.991.

Table 1 Comparison of the experimental band positions (cm⁻¹) of neutral CrC_n(CO)₂ (n = 3 and 4) complexes to the calculated values of isomer 3A, 3B, 4A, and 4B obtained at the BLYP-D3(BJ)/def2-TZVPP level of theory, with IR intensities listed in parentheses in km mol⁻¹ and the calculated harmonic vibrational frequencies scaled by a factor of 0.991

Species	Isomer	Calcd	Exptl	Mode
CrC3(CO)2	3A	1786 (19)	—	Antisymmetric stretching mode of C(3)C(4)C(5) groups
		1981 (1046)	1981 (band A)	Stretching mode of C(1)O(1) group
		2135 (1223)	2113 (band C)	Stretching mode of C(2)O(2) group
	3B	1988 (821)	1981 (band A)	Antisymmetric stretching mode of C(1)O(1) and C(2)O(2) groups
		2017 (846)	2033 (band B)	Symmetric stretching mode of C(1)O(1) and C(2)O(2) groups
CrC4(CO)2	4A	1846 (576)	1821 (band a)	Stretching mode of C(1)O(1) group
		1863 (126)	1839 (band b)	Symmetric stretching mode of C(3)C(4)C(5)C(6) groups
		2010 (857)	2011 (band c)	Stretching mode of C(2)O(2) group
	4B	1720 (3)	—	Antisymmetric stretching mode of C(3)C(4)C(5)C(6) groups
		1881 (19)	—	Symmetric stretching mode of C(3)C(4)C(5)C(6) groups
		2023 (583)	2031 (band d)	Antisymmetric stretching mode of C(1)O(1) and C(2)O(2) groups
		2045 (677)	2061 (band e)	Symmetric stretching mode of C(1)O(1) and C(2)O(2) groups

---

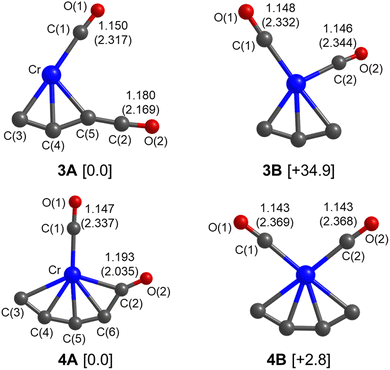
Quantum chemical calculations were performed to understand the experimental spectra and geometric/electronic structures of CrC₃(CO)₂ and CrC₄(CO)₂. The optimized structures of CrC₃(CO)₂ and CrC₄(CO)₂ are shown in Fig. 3. The calculated IR spectra of CrC₃(CO)₂ and CrC₄(CO)₂ are compared with the corresponding experimental ones in Fig. 1 and 2, respectively. Here, the two types of isomers are named nA and nB, respectively, in which n denotes the n in the CrC_n(CO)₂ molecular formulas.

Fig. 3 Optimized equilibrium geometries of isomers 3A, 3B, 4A and 4B at the BLYP-D3(BJ)/def2-TZVPP level of theory (O, red; C, gray; Cr, blue). All isomers are in ⁵A electronic states. Bond lengths (Å) and Mayer bond orders of the CO groups are given in regular font and in parentheses, respectively. Relative energies (in brackets) are calculated at the B2PLYPD3//BLYP-D3(BJ)/def2-TZVPP level of theory and listed in kcal mol⁻¹. Atoms are labeled for discussion.

As shown in Fig. 3, all the isomers of CrC_n(CO)₂ (n = 3 and 4) are in quintet electronic states, in which two CO molecules are bound to the fan-like chromium carbide basic skeletons. In the most stable isomer of CrC₃(CO)₂ (labeled 3A), one CO is bound terminally to the Cr atom and the other CO is bound terminally to the C atom with the formation of a ketenylidene. The 3B isomer consists of two terminal carbonyls bound to the Cr atom, which lies 34.9 kcal mol⁻¹ higher in energy than isomer 3A. In the calculated IR spectrum of isomer 3A (Fig. 1c), the 1981 cm⁻¹ band is attributed to the stretching mode of the C(1)O(1) group (Table 1), which is in excellent agreement with the experimental band A (1981 cm⁻¹); the 2135 cm⁻¹ band is due to the stretching mode of the C(2)O(2) group, which is consistent with the experimental band C (2113 cm⁻¹). In the calculated IR spectrum of isomer 3B (Fig. 1d), the antisymmetric and symmetric stretching modes of C(1)O(1) and C(2)O(2) groups are predicted at 1988 and 2017 cm⁻¹ (Table 1), respectively, which are in accordance with the experimental bands A and B. The best agreement between the experimental and simulated IR spectra is obtained when assuming a ratio of a 1 (3A):1 (3B) mixture of isomers (Fig. 1b).

For CrC₄(CO)₂, the most stable isomer (labeled 4A) consists of one terminal CO bound to the Cr atom and one semi-bridging CO bound to the Cr and C atoms (Fig. 3). Isomer 4B comprises two terminal CO bound to the Cr atom, which lies slightly higher than isomer 4A by 2.8 kcal mol⁻¹. In the calculated IR spectrum of isomer 4A (Fig. 2c), the 1846 cm⁻¹ band is attributed to the stretching mode of C(1)O(1) group (Table 1), which is in agreement with experimental band a (1821 cm⁻¹); the 1863 cm⁻¹ band is due to the symmetric stretching mode of C(3)C(4)C(5)C(6) groups, which is consistent with experimental band b (1839 cm⁻¹); the 2010 cm⁻¹ band is due to the stretching mode of the C(2)O(2) group, which agrees well with experimental band c (2011 cm⁻¹). In the calculated IR spectrum of isomer 4B (Fig. 2d), the antisymmetric and symmetric stretching modes of C(1)O(1) and C(2)O(2) groups are predicted at 2023 and 2045 cm⁻¹ (Table 1), respectively, which are in accordance with experimental bands d and e (2031 and 2061 cm⁻¹). The best agreement between the experimental and simulated IR spectra is obtained when assuming a ratio of a 1 (4A):1 (4B) mixture of isomers (Fig. 2b).

The coexistence of isomers 3A/3B and 4A/4B is quite interesting, which inspired us to explore their possible formation mechanisms. Since all of the identified isomers contain the CrC_n core structure as shown in the CrC_n(CO)_m (n = 1–4 and m = 0–2) series in the mass spectrum (Fig. S1, ESI†), the target clusters are likely generated by the CrC_n + mCO → CrC_n(CO)_m reactions. As a pure chromium target was used in the experiment, the formation processes of CrC_n(CO)_m in the laser vaporization source are proposed as follows: the laser-vaporized Cr atoms with high internal energy react with the CO molecules to form chromium carbonyls, chromium carbides, and chromium oxides. The chromium carbides are cooled by soft collision of the CO carrier gas and react with CO to form chromium carbide carbonyls.³⁸

Based on the above reaction processes, we first discuss the electronic ground states and the most stable structures of the CrC₃ and CrC₄ carbides. Neutral chromium carbides have been studied theoretically, with different conclusions.^39–41 In order to determine the electronic ground state and the most stable structure of chromium carbides, test calculations were performed for CrC₃ by using several representative methods and the results are given in Table S1 (ESI†). The BLYP-D3(BJ)/def2-TZVPP calculated results show that CrC₃ has a ³B₁ electronic ground state with a fan-like structure, consistent with the BPW91/6-311+G(d) results.³⁹ However, a ⁵Π electronic ground state with a linear structure was suggested at the BLYP/DNP level of theory.⁴⁰ Due to these different results calculated by different computational methods, it is necessary to perform higher level calculations to verify the electronic ground state of CrC₃. The MN15-L⁴² functional was proposed to be a nice density functional theory (DFT) functional with good performance in calculating the relative energies of different electronic states in a recent benchmark study⁴³ and thus was employed in this work. The MN15-L/def2-TZVPP calculations show that CrC₃ has a ⁵B₂ electronic ground state with a fan-like structure. This result holds true for the B2PLYPD3/def2-TZVPP and CCSD(T)//BLYP-D3(BJ)/def2-TZVPP calculations (Table S1, ESI†). We therefore infer that CrC₃ has a ⁵B₂ ground state with a fan-like structure. For CrC₄, theoretical studies yielded consistent results of a ⁵B₂ electronic ground state with a fan-like structure.^39,40

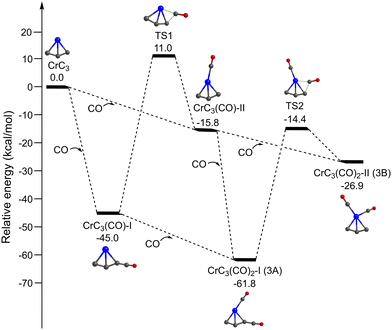
Fig. 4 shows the potential energy profiles of the generation of isomers 3A and 3B starting from quintet CrC₃. The CrC₃ carbide reacts with the first CO molecule to form CrC₃(CO)-I and CrC₃(CO)-II, which is predicted to be exothermic by 45.0 and 15.8 kcal mol⁻¹, respectively. The energy barrier for the CrC₃(CO)-II → CrC₃(CO)-I isomerization is calculated to be 26.8 kcal mol⁻¹, which might be sufficiently large so that the CrC₃(CO)-II isomer could be kinetically trapped by the soft expansion of the cold molecular beam prior to its rearrangement to the global minimum-energy structure CrC₃(CO)-I.⁴⁴ The addition of the second CO to CrC₃(CO)-I and CrC₃(CO)-II forms CrC₃(CO)₂-I (isomer 3A) and CrC₃(CO)₂-II (isomer 3B), respectively, which is predicted to be exothermic by 16.8 and 11.1 kcal mol⁻¹. CrC₃(CO)₂-I (isomer 3A) could also be produced by CO addition to CrC₃(CO)-II, with an exothermic value of 46.0 kcal mol⁻¹. The energy barrier for the 3B → 3A isomerization is 12.5 kcal mol⁻¹, which is sufficiently large so that both 3A and 3B could be simultaneously captured in a cold molecular beam. The lowest dissociation energy of one CO from 3A and 3B is predicted to be 16.8 and 11.1 kcal mol⁻¹, respectively, indicating that the absorption of at least 3 and 2 photons around 2000 cm⁻¹ is required to overcome the dissociation limit of 3A and 3B. This implies that the IR-induced depletion efficiency of isomer 3A is lower than that of isomer 3B, which might account for the weaker intensity of experimental band C than that in the simulated IR spectrum of isomer 3A.

Fig. 4 Potential energy profiles of the CrC₃ + 2CO → CrC₃(CO)₂ reaction calculated at the B2PLYPD3//BLYP-D3(BJ)/def2-TZVPP level of theory. Energies are given in kcal mol⁻¹. All the molecules are in a quintet state.

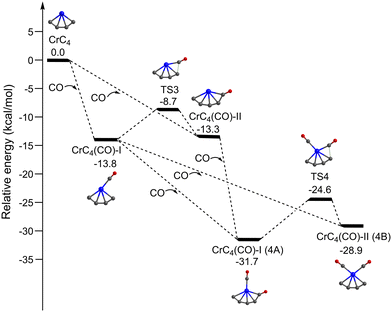
Fig. 5 shows the potential energy profiles of the generation of isomers 4A and 4B starting from quintet CrC₄. The CrC₄ carbide reacts with the first CO molecule to form CrC₄(CO)-I and CrC₄(CO)-II, which is predicted to be exothermic by 13.8 and 13.3 kcal mol⁻¹, respectively. The energy barrier for the CrC₄(CO)-II → CrC₄(CO)-I isomerization is predicted to be 4.6 kcal mol⁻¹. Similar to the CrC₃ system, CrC₄(CO)-I and CrC₄(CO)-II could co-exist in the cold molecular beam. The addition of the second CO to CrC₄(CO)-I could form CrC₄(CO)₂-I (isomer 4A) and CrC₄(CO)₂-II (isomer 4B), which is predicted to be exothermic by 17.9 and 15.1 kcal mol⁻¹, respectively. CrC₄(CO)₂-I (isomer 4A) can also be produced by the CO addition to CrC₄(CO)-II with an exothermic value of 18.4 kcal mol⁻¹. The energy barrier for the 4B → 4A isomerization is 4.3 kcal mol⁻¹, similar to that of the CrC₄(CO)-II → CrC₄(CO)-I isomerization. It can be concluded that these calculated results support the coexistence of isomers 3A/3B and 4A/4B in the present experimental conditions.

Fig. 5 Potential energy profiles of the CrC₄ + 2CO → CrC₄(CO)₂ reaction calculated at the B2PLYPD3//BLYP-D3(BJ)/def2-TZVPP level of theory. Energies are given in kcal mol⁻¹. All the molecules are in a quintet state.

The Kohn–Sham α-orbitals of isomers 3A, 3B, 4A, and 4B are shown in Fig. S2–S5 (ESI†), respectively. It can be seen that the terminal-coordination CO molecules are bound to the Cr atoms by the interactions of σ donation and π* back donation, following the Blyholder model. The highest occupied molecular orbital (HOMO) of isomer 3A shows that the CCO ketenylidene group is mainly an in-plane π orbital, which is similar to that in the titanium ketenylidene complexes (OTiCCO(CO)_n−2) that were analyzed in detail.⁴⁵ The most significant observation in this work is a remarkably low CO stretching frequency of 1821 cm⁻¹ of semi-bridging CO in isomer 4A, which is 322 cm⁻¹ lower than the CO stretching vibration frequency of free CO (2143 cm⁻¹),⁴⁶ indicative of a substantial activation of CO. Therefore, we mainly analyze the electronic structure of this semi-bridging CO in isomer 4A. The most important occupied MOs of isomer 4A are shown in Fig. 6. The singly occupied molecular orbital (SOMO) is a π-type bond characteristic with chromium to terminal carbonyl donation. The SOMO+1, SOMO+2, and SOMO+3 are mainly the d orbitals of the Cr atom. The HOMO (α) and HOMO (β) contain the π_⊥* orbitals of semi-bridging CO that accept the d electron of the Cr atom and the electron of an adjacent carbon atom, forming a Cr–C–C three-center two-electron (3c–2e) bond.^47,48 This delocalized 3c–2e bond is also confirmed by AdNDP bonding analysis as shown in Fig. S6 (ESI†). HOMO-2 is mainly the π orbital of the CrC₄ group that comprises a back donation interaction with the π_‖* orbital of CO. HOMO-14 indicates that the lone pair electrons of CO are mainly donated to the carbon chain to form a σ bond. Thus, both HOMO and HOMO-2 feature extensively delocalized 3c–2e interaction between the π antibonding orbitals of CO and the CrC₄ group, which leads to a remarkable activation of the C–O bond. The bonding mode of the semi-bridging CO in isomer 4A is similar to that in the CO-B₂(NHC)₂ molecule,¹⁵ in which the π antibonding orbitals of CO both form polycentric bonds and receive backdonation from the π orbitals of other atoms. The slight difference is that the lone pair of CO in isomer 4A of CrC₄(CO)₂ is mainly donated to the C atom and that in CO–B₂(NHC)₂ is divided equally between the two B atoms. The smaller ring tension and the stronger electron donating capacity of the atoms in isomer 4A make the CO group more active than that in CO–B₂(NHC)₂. As a result, the semi-bridging CO in isomer 4A of CrC₄(CO)₂ shows a much lower CO stretching frequency (1821 cm⁻¹) than that in CO–B₂(NHC)₂ (1926 cm⁻¹).

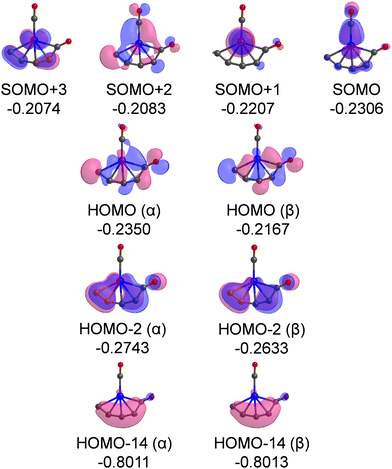Fig. 6 Plots of the most important occupied MOs of isomer 4A. The isovalue of the orbital is set to 0.03. Relative energies are listed in Hartree.

The high degree of CO activation in isomer 4A of CrC₄(CO)₂ is reminiscent of chemisorbed CO on the Co-based and Fe-based catalysts involved in Fischer–Tropsch synthesis.^8,49,50 Spectral studies have shown that the infrared absorption peak of CO adsorbed on the surface of Co-based catalysts is in the range of 1780–1880 cm⁻¹,⁵⁰ which covers the infrared absorption peak position of semi-bridging CO in isomer 4A (1821 cm⁻¹). Interestingly, the C–O bond length, CO stretching vibration frequency, and CO dissociation energy of semi-bridging CO in isomer 4A are also close to those in the Fe_n(CO) (n = 10–20) clusters as studied theoretically.⁵¹ Note that the terminal CO groups in the 3A, 3B, and 4B isomers exhibit a lower degree of activation than the semi-bridging CO group in the 4A isomer. The difference in the CO activation ability of the 3A and 4A structures may provide insights into understanding the catalytic activity of iron carbides.^21–26 The present findings would have important implications for rational design and chemical control of the catalysts with unique structures and properties.

4. Conclusions

In this work, the neutral CrC₃(CO)₂ and CrC₄(CO)₂ clusters were prepared by a laser-vaporization supersonic expansion cluster source and characterized by infrared-vacuum ultraviolet (IR-VUV) spectroscopy combined with quantum chemical calculations. The results indicate that the CrC₃(CO)₂ and CrC₄(CO)₂ molecules have the structures of two CO molecules bound to the fan-like CrC₃ and CrC₄ basic skeletons, respectively. The measured infrared spectrum of CrC₃(CO)₂ is a mixture of an isomer with two COs terminally coordinating to Cr and an isomer with one CO bonded to Cr and the other forming a ketenylidene. The measured infrared spectrum of CrC₄(CO)₂ is a mixture of an isomer with two terminal COs and an isomer with one terminal CO and the other semi-bridging CO. The electron structure analyses show that this semi-bridging CO is highly activated through the interaction of two antibonding orbitals with the metal carbide skeleton to form the delocalized Cr–C–C three-center two-electron (3c–2e) interaction. The present system serves as a model for clarifying the pivotal roles played by neutral metal carbides in the CO activation and stimulates systematical studies on various reactions of neutral metal clusters and small molecules under the conditions of interest.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors gratefully acknowledge the Dalian Coherent Light Source (DCLS) for support and assistance. This work was supported by the National Natural Science Foundation of China (Grant No. 22125303, 92361302, 92061203, 22373102, 22103082, 22273101, 22288201, and 21327901), the National Key Research and Development Program of China (2021YFA1400501), the Youth Innovation Promotion Association of the Chinese Academy of Sciences (CAS) (2020187), Innovation Program for Quantum Science and Technology (2021ZD0303304), CAS (GJJSTD20220001), Dalian Institute of Chemical Physics (DICP DCLS201702), and International Partnership Program of CAS (121421KYSB20170012).

References

1. A. Y. Khodakov, W. Chu and P. Fongarland, Chem. Rev., 2007, 107, 1692–1744.
2. K. T. Rommens and M. Saeys, Chem. Rev., 2023, 123, 5798–5858.
3. R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732.
4. S. S. Nurttila, P. R. Linnebank, T. Krachko and J. N. H. Reek, ACS Catal., 2018, 8, 3469–3488.
5. G. Liu, G. Yang, X. Peng, J. Wu and N. Tsubaki, Chem. Soc. Rev., 2022, 51, 5606–5659.
6. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774.
7. M. F. Zhou, L. Andrews and C. W. Bauschlicher, Chem. Rev., 2001, 101, 1931–1961.
8. A. Fielicke, P. Gruene, G. Meijer and D. M. Rayner, Surf. Sci., 2009, 603, 1427–1433.
9. G. Bistoni, S. Rampino, N. Scafuri, G. Ciancaleoni, D. Zuccaccia, L. Belpassi and F. Tarantelli, Chem. Sci., 2016, 7, 1174–1184.
10. G. Frenking, I. Fernandez, N. Holzmann, S. Pan, I. Krossing and M. Zhou, JACS Au, 2021, 1, 623–645.
11. J. J. Turner, M. W. George, M. Poliakoff and R. N. Perutz, Chem. Soc. Rev., 2022, 51, 5300–5329.
12. A. Fielicke, Chem. Soc. Rev., 2023, 52, 3778–3841.
13. P. L. Arnold, Nature, 2013, 502, 458–459.
14. H. Braunschweig, T. Dellermann, R. D. Dewhurst, W. C. Ewing, K. Hammond, J. O. C. Jimenez-Halla, T. Kramer, I. Krummenacher, J. Mies, A. K. Phukan and A. Vargas, Nat. Chem., 2013, 5, 1025–1028.
15. H. Zhang, Z. Cao, W. Wu and Y. Mo, Angew. Chem., Int. Ed., 2018, 57, 13076–13081.
16. R. B. Levy and M. Boudart, Science, 1973, 181, 547–549.
17. H. H. Hwu and J. G. G. Chen, Chem. Rev., 2005, 105, 185–212.
18. S. T. Hunt, M. Milina, A. C. Alba-Rubio, C. H. Hendon, J. A. Dumesic and Y. Roman-Leshkov, Science, 2016, 352, 974–978.
19. X. Zhang, M. Zhang, Y. Deng, M. Xu, L. Artiglia, W. Wen, R. Gao, B. Chen, S. Yao, X. Zhang, M. Peng, J. Yan, A. Li, Z. Jiang, X. Gao, S. Cao, C. Yang, A. J. Kropf, J. Shi, J. Xie, M. Bi, J. A. van Bokhoven, Y.-W. Li, X. Wen, M. Flytzani-Stephanopoulos, C. Shi, W. Zhou and D. Ma, Nature, 2021, 589, 396–401.
20. P. Patterson, Appl. Catal., A, 2003, 251, 449–455.
21. J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2009, 114, 1085–1093.
22. E. de Smit, F. Cinquini, A. M. Beale, O. V. Safonova, W. van Beek, P. Sautet and B. M. Weckhuysen, J. Am. Chem. Soc., 2010, 132, 14928–14941.
23. J. Ohata, A. Teramoto, H. Fujita, S. Takemoto and H. Matsuzaka, J. Am. Chem. Soc., 2021, 143, 16105–16112.
24. S. Ahmad, I. Ashraf, M. A. Mansoor, S. Rizwan and M. Iqbal, Nanomaterials, 2021, 11, 776.
25. X. Liu, J. Liu, Y. Yang, Y.-W. Li and X. Wen, ACS Catal., 2021, 11, 2156–2181.
26. H. Yu, L. Wang, Y. Yu, G. Yang and M. Zhang, Chem. Eng. J., 2023, 469, 143947.
27. C. Femoni, M. C. Iapalucci, G. Longoni, J. Wolowska, S. Zacchini, P. Zanello, S. Fedi, M. Ricco, D. Pontiroli and M. Mazzani, J. Am. Chem. Soc., 2010, 132, 2919–2927.
28. S. Kuppuswamy, J. D. Wofford, C. Joseph, Z.-L. Xie, A. K. Ali, V. M. Lynch, P. A. Lindahl and M. J. Rose, Inorg. Chem., 2017, 56, 5998–6012.
29. C. Cesari, C. Femoni, M. C. Iapalucci and S. Zacchini, Inorg. Chim. Acta, 2023, 544, 121235.
30. J. Yang, S. Du, B. Ju, Z. Zhang, G. Li, J. Zou, J. Cao, Q. Jing, H. Xie and L. Jiang, J. Phys. Chem. A, 2023, 127, 10450–10456.
31. B. B. Zhang, Y. Yu, Z. J. Zhang, Y. Y. Zhang, S. K. Jiang, Q. M. Li, S. Yang, H. S. Hu, W. Q. Zhang, D. X. Dai, G. R. Wu, J. Li, D. H. Zhang, X. M. Yang and L. Jiang, J. Phys. Chem. Lett., 2020, 11, 851–855.
32. G. Li, C. Wang, Q. M. Li, H. J. Zheng, T. T. Wang, Y. Yu, M. Z. Su, D. Yang, L. Shi, J. Y. Yang, Z. G. He, H. Xie, H. J. Fan, W. Q. Zhang, D. X. Dai, G. R. Wu, X. M. Yang and L. Jiang, Rev. Sci. Instrum., 2020, 91, 034103.
33. G. Li, C. Wang, H.-j Zheng, T.-j Wang, H. Xie, X.-m Yang and L. Jiang, Chin. J. Chem. Phys., 2021, 34, 51–60.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016.
35. J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700.
36. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
37. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
38. U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071.
39. H.-J. Zhai, L.-S. Wang, P. Jena, G. L. Gutsev and C. W. Bauschlicher, J. Chem. Phys., 2004, 120, 8996–9008.
40. Q.-M. Ma, Z. Xie, Y. Liu and Y.-C. Li, Solid State Commun., 2010, 150, 1439–1444.
41. V. T. Tran, C. Iftner and M. F. A. Hendrickx, J. Phys. Chem. A, 2013, 117, 5613–5619.
42. H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293.
43. D. Zhang and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 4416–4428.
44. K. D. Jordan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24383–24385.
45. C. Wang, Q. M. Li, X. T. Kong, H. J. Zheng, T. T. Wang, Y. Zhao, G. Li, H. Xie, J. Y. Yang, G. R. Wu, W. Q. Zhang, D. X. Dai, M. F. Zhou, X. M. Yang and L. Jiang, J. Phys. Chem. Lett., 2021, 12, 1012–1017.
46. G. J. Jiang, W. B. Person and K. G. Brown, J. Chem. Phys., 1975, 62, 1201–1211.
47. B. J. Morris-Sherwood, C. B. Powell and M. B. Hall, J. Am. Chem. Soc., 2002, 106, 5079–5083.
48. J. C. Green, M. L. H. Green and G. Parkin, Chem. Commun., 2012, 48, 11481–11503.
49. J. T. Lyon, P. Gruene, A. Fielicke, G. Meijer and D. M. Rayner, J. Chem. Phys., 2009, 131, 184706.
50. C. J. Weststrate, J. van de Loosdrecht and J. W. Niemantsverdriet, J. Catal., 2016, 342, 1–16.
51. P. Limon, A. Miralrio, R. Gomez-Balderas and M. Castro, J. Phys. Chem. A, 2020, 124, 9951–9962.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00011k

---