Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The dynamic nature of natural and fatty acid modified calcite surfaces
Per M.
Claesson
 *a,
Natalia A.
Wojas
*b,
Robert
Corkery
a,
Andra
Dedinaite
*a,
Natalia A.
Wojas
*b,
Robert
Corkery
a,
Andra
Dedinaite
 cd,
Joachim
Schoelkopf
e and
Eric
Tyrode
cd,
Joachim
Schoelkopf
e and
Eric
Tyrode
 a
a
aKTH Royal Institute of Technology, Department of Chemistry, Division of Surface and Corrosion Science, Teknikringen 29, SE-100 44 Stockholm, Sweden. E-mail: percl@kth.se
bRISE Research Institutes of Sweden, Division of Bioeconomy and Health – Material and Surface Design, Drottning Kristinas väg 61B, SE-114 28 Stockholm, Sweden
cKTH Royal Institute of Technology, School of Engineering Sciences in Chemistry, Biotechnology and Health, Engineering Pedagogics, SE-100 44 Stockholm, Sweden
dRISE Research Institutes of Sweden, Division Bioeconomy and Health, Department Chemical Process and Pharmaceutical Development, Box 5604, SE-114 86 Stockholm, Sweden
eOmya International AG, Baslerstrasse 42, CH-4665 Oftringen, Switzerland
First published on 27th December 2023
Abstract
Calcium carbonate, particularly in the form of calcite, is an abundant mineral widely used in both human-made products and biological systems. The calcite surface possesses a high surface energy, making it susceptible to the adsorption of organic contaminants. Moreover, the surface is also reactive towards a range of chemicals, including water. Consequently, studying and maintaining a clean and stable calcite surface is only possible under ultrahigh vacuum conditions and for limited amounts of time. When exposed to air or solution, the calcite surface undergoes rapid transformations, demanding a comprehensive understanding of the properties of calcite surfaces in different environments. Similarly, attention must also be directed towards the kinetics of changes, whether induced by fluctuating environments or at constant condition. All these aspects are encompassed in the expression “dynamic nature”, and are of crucial importance in the context of the diverse applications of calcite. In many instances, the calcite surface is modified by adsorption of fatty acids to impart a desired nonpolar character. Although the binding between carboxylic acid groups and calcite surfaces is strong, the fatty acid layer used for surface modification undergoes significant alterations when exposed to water vapour and liquid water droplets. Therefore, it is also crucial to understand the dynamic nature of the adsorbed layer. This review article provides a comprehensive overview of the current understanding of both the dynamics of the calcite surface as well as when modified by fatty acid surface treatments.
1. Introduction
It is easy to be overwhelmed by the amount of literature on calcium carbonate, focused not only on chemistry and physics but also on the history of art, architecture, geology, and mineralogy.1 One may wonder why this simple chemical compound, CaCO3, is so diverse and useful. Starting from the beginning of history, CaCO3 catalyzes the Formose reaction, a vital biological process that potentially contributed to the origin of life, as it leads to the formation of complex sugars, such as ribose, a building block of RNA.2 CaCO3 is also the primary constituent for the growth and degradation of bones, teeth and shells.1 It is a key material in exoskeletons that supports and protects many organisms and constitutes tissues for storing calcium ions and light perception.1,3–5 Interestingly, CaCO3 contributes to a positive global carbon dioxide balance, as it is a buffer for acid rain. Calcium carbonate also has other positive environmental effects as it picks up toxic compounds (such as heavy metals) and minimizes bacterial activity in water.6Calcium carbonate is a prevalent component found in various rock formations, including chalk, metamorphic marble, and limestone. These rocks have been utilized by human civilisations for millennia. Some of the oldest known limestone and marble objects date back to the Paleolithic Age, spanning from 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 12
000 to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 BC. In ancient Egypt, limestone was extracted and processed to create an array of construction materials, decorative columns, ornamental pieces, jewellery, and vases. In ancient Rome, marble held great significance, and it was regarded as an ornamental stone used for decorative inlays, architectural elements, and sculptures. Additionally, chalk emerged as a popular white powdered pigment for paints and primers during the Anglo-Saxon era. During the High Renaissance, renowned artists such as Michelangelo and Bernini crafted iconic marble statues, and towards the end of the 16th century, a new painting technique arose in Europe – pastel painting.1 In an intriguing connection, the Taj Mahal, constructed in the 17th century, showcases the use of white marble. However, the yellowing colour observed today is a result of atmospheric pollutants that have affected its appearance. The most stable polymorph of CaCO3, the transparent calcite mineral, has unique polarizing properties, and there are claims that Vikings may have used calcite as a navigation aid during cloudy days, even though the validity of this belief has been questioned.7
000 BC. In ancient Egypt, limestone was extracted and processed to create an array of construction materials, decorative columns, ornamental pieces, jewellery, and vases. In ancient Rome, marble held great significance, and it was regarded as an ornamental stone used for decorative inlays, architectural elements, and sculptures. Additionally, chalk emerged as a popular white powdered pigment for paints and primers during the Anglo-Saxon era. During the High Renaissance, renowned artists such as Michelangelo and Bernini crafted iconic marble statues, and towards the end of the 16th century, a new painting technique arose in Europe – pastel painting.1 In an intriguing connection, the Taj Mahal, constructed in the 17th century, showcases the use of white marble. However, the yellowing colour observed today is a result of atmospheric pollutants that have affected its appearance. The most stable polymorph of CaCO3, the transparent calcite mineral, has unique polarizing properties, and there are claims that Vikings may have used calcite as a navigation aid during cloudy days, even though the validity of this belief has been questioned.7
CaCO3 currently plays an important role in a wide range of industrial applications. There are two commonly used types of granulates: ground calcium carbonate (GCC) and precipitated calcium carbonate (PCC). GCC is obtained by grinding sedimentary rocks, primarily limestone and chalk.8 On the other hand, PCC is prepared by carbonating calcium hydroxide (Ca(OH)2), derived from slaked burnt lime, in water.9 Both GCC and PCC are extensively used as nano- and micro-sized particles, offering a large surface area that enhances the functional properties of other materials.10 Calcium carbonate stands out as a highly cost-effective, nontoxic material with high chemical purity that conforms to food legislation standards.1 These remarkable properties have led to the widespread use of CaCO3 as an additive in numerous industries. It finds application in sectors such as paper and board production, construction, polymers, and environmentally friendly solutions, where it is used in the strengthening of soils, water purification processes, and as a sorbent for exhaust gasses.1,11–16 Moreover, it is also utilized in consumer goods, including food and pharmaceuticals.
However, the use of calcium carbonate is not without its challenges. The surface of the material is dynamic and reactive, undergoing physical changes when exposed to air and solvents. These changes lead to alterations in surface properties, as well as processes like dissolution and recrystallization. Fortunately, on calcite surfaces, the rates of these processes occur on time scales that allow for their observation using surface-sensitive experimental techniques.6 Calcite surfaces can be cleaved to form relatively flat surfaces, making them suitable for demanding techniques such as X-ray reflectivity (XRR), and vibrational sum frequency spectroscopy (VSFS). These features make calcite particularly interesting for fundamental studies. Curiously, it has been observed that cleavage in liquids results in smoother surfaces compared to cleavage in air.17 The authors speculated that this could be attributed to the lubricating effect of the liquid during cleavage. It can be further conjectured that the adsorption of the liquid leads to a decrease in surface energy, facilitating the formation of smoother surfaces. The dynamic changes occurring on the calcium carbonate surface,6,18–20 although of fundamental scientific interest, can pose challenges in practical applications. The evolving heterogeneous surface properties under ambient air or water exposure can potentially lead to deterioration in the functionality of calcium carbonate.
In some applications, untreated, bare CaCO3 cannot be directly used, especially when combined with low surface energy organic materials.21 For instance, the hydrophilic nature of the calcium carbonate surface poses compatibility issues with nonpolar polymers. To address this problem, surface modification techniques are employed. However, even this process can introduce surface heterogeneities,21 adding further complexity to the material. Despite extensive research over the years, these issues surrounding calcium carbonate are not fully understood. Therefore, it is crucial to enhance our comprehension of the dynamic nature of both pure and modified calcium carbonate. Such understanding can pave the way for improving industrial processes and developing novel applications, bridging the gap between scientific knowledge and practical implementation.20
Compared to GCC and PCC, organisms produce and use calcium carbonate in a much more sophisticated manner. In these organisms, the biomineralization of calcite is carefully regulated by adsorption of biomacromolecules onto specific surface planes. This adsorption stimulates the growth of given surface planes while inhibiting the growth of others, ultimately enabling precise control over the shape of the calcium carbonate structures. Although this fascinating scientific area is not covered in this article, we refer the reader to valuable reviews that delve into various aspects of this topic.22–25 We also note recent reports describing the use of vibrational spectroscopy26 and scanning probe methods27 in relation to biomineralization. Similarly, this review does not encompass the synthesis of calcium carbonate particles with controlled morphology and size, as an excellent review article on this subject has recently been published.28
This review article is structured as follows. In Section 2, we provide a brief overview of the different forms of calcium carbonate. Subsequently, the focus shifts to calcite in the following sections. Section 3 discusses calcite surfaces when exposed to air and liquids, exploring topics such as restructuring, surface energy, and adsorption of organic molecules and water. Particular emphasis is given to calcite surfaces in contact with water. Moving on to Section 4, we consider surface-modified calcite, with a specific focus on surfaces carrying a layer of carboxylic acids. Throughout the article, we highlight the dynamic nature of both calcite and modified calcite surfaces, drawing insights from experiments and modelling. We note that the term “dynamic nature” encompasses both structural differences of calcite surfaces in different environments, as well as kinetic changes occurring in a constant environment, such as e.g. supersaturated or undersaturated aqueous solutions.
2. Different forms of calcium carbonate
Calcium carbonate is commonly described as consisting of three different anhydrous crystalline forms: trigonal calcite with a rhombohedral unit cell, orthorhombic aragonite, and hexagonal vaterite. Calcite is the most stable form at normal pressure and temperature but can be converted to aragonite at higher pressures. However, this classification of CaCO3 into three anhydrous forms is a simplification. At higher pressures, calcite can undergo a range of transformations, leading to structures known as calcite I, calcite II, calcite III, and so on.29 The transition from calcite I to calcite II occurs at a pressure slightly below 1.5 GPa,30 while calcite III is observed in the pressure range of 2.5 to 15 GPa.31 The form typically found under normal temperature and pressure conditions is calcite I, and in this work, we will refer to calcite I simply as calcite.In addition to the anhydrous forms, calcium carbonate also exists in hydrated forms, including the crystalline hexahydrate, crystalline monohydrate, crystalline hemihydrate, and amorphous forms. Their appearance is sensitive to local conditions such as supersaturation, temperature and impurities. Although these forms are metastable, they play an important role in the precipitation pathway of calcium carbonate.32 The crystal structure of the hexahydrate form, known as ikarite, was determined in the 1970,33 followed by the characterization of the monohydrate34 and hemihydrate35 forms in later studies.
The focus of this review is on calcite, a brittle or quasi-brittle material, where the term quasi-brittle indicates a gradual loss of stress beyond the initial cracking. Calcite has a Mohs scale hardness index of 3, and is anisotropic, meaning that its optical and mechanical properties depend on the direction relative to the crystal planes. Even though the values for the Young's modulus reported in early sources vary somewhat, advancements in techniques and modelling have led to greater agreement in recent theoretical and experimental studies. It is clear that the modulus is lower perpendicular to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) plane than parallel to this plane. For instance, in the [421] direction that is orthogonal to the (10
4) plane than parallel to this plane. For instance, in the [421] direction that is orthogonal to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) plane, the Young's modulus has been reported to be about 60 GPa while along the [010] direction within this plane, the Young's modulus is approximately 70 GPa.36,37 Furthermore, calcite thermally decomposes into calcium oxide and carbon dioxide at about 800 °C, a reaction that has also been extensively studied.38
4) plane, the Young's modulus has been reported to be about 60 GPa while along the [010] direction within this plane, the Young's modulus is approximately 70 GPa.36,37 Furthermore, calcite thermally decomposes into calcium oxide and carbon dioxide at about 800 °C, a reaction that has also been extensively studied.38
3. Natural calcite surfaces
Calcite possesses a trigonal rhombohedral structure, belonging to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group and point group
c space group and point group ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 2/m.39 Calcite can most easily be cleaved along the (10
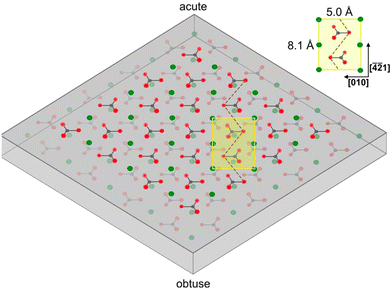
2/m.39 Calcite can most easily be cleaved along the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane,40,41 resulting in two identical surfaces, which contain both calcium ions and carbonate ions in two different orientations, with termination by oxygen atoms.42 The atomic structure of calcite depicted in Fig. 1, provides further insight into this arrangement.
4) surface plane,40,41 resulting in two identical surfaces, which contain both calcium ions and carbonate ions in two different orientations, with termination by oxygen atoms.42 The atomic structure of calcite depicted in Fig. 1, provides further insight into this arrangement.
3.1. Surface restructuring due to cleavage in ultra-high vacuum
When a solid surface is cleaved, the environment of the surface groups by necessity changes, which can lead to alterations of the surface structure due to variations in the intermolecular forces. In the case of calcite, the structure of the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) plane at the surface may not be identical to the (1 × 1) unit cell with dimension 5.0 × 8.1 Å2 containing two calcium atoms and two carbonate groups found in the bulk.43,44 Information related to this issue can be obtained using high vacuum surface sensitive techniques as well as atomistic modelling.
4) plane at the surface may not be identical to the (1 × 1) unit cell with dimension 5.0 × 8.1 Å2 containing two calcium atoms and two carbonate groups found in the bulk.43,44 Information related to this issue can be obtained using high vacuum surface sensitive techniques as well as atomistic modelling.
Stipp and co-workers utilized low-energy electron diffraction (LEED) and X-ray photoelectron spectroscopy (XPS) to investigate surface relaxation of pristine calcite cleaved under high vacuum conditions (P ≈ 10−10 mbar).45,46 Their findings revealed that the LEED patterns from the calcite surface did not show any statistically significant difference in lattice parameters compared to bulk calcite. However, weak diffraction patterns were observed, indicating the potential twisting of CO3 groups located at the surface.6 Additionally, shifts in photoelectron peaks were observed directly after fracturing, providing evidence for surface bond restructuring. The photoelectron peak for carbon, which is primarily influenced by surface carbonate groups (S-CO3), showed a shoulder at the high energy binding side, suggesting that some surface bicarbonate (S-CO3H) groups were formed. Moreover, indications of carbide-like bonds between calcium and carbon atoms at the surface was also found from the carbon peak, suggesting a surface relaxation that facilitates further interaction between calcium and carbon. This bond formation was proposed to occur due to the loss of oxygen coordination for calcium (with 6 oxygen atoms in the bulk and 5 at the surface).
Assuming a pure ionic bonding scenario, this loss in coordination for calcium results in a positive charge of +1/3 at the vacant oxygen site over the calcium atom. Yet, the presence of a slight covalent character in the Ca–carbonate bond should reduce this charge to some extent.46 Similarly, the charge over a vacant oxygen site associated with the carbonate anion is −1/3 or slightly less negative.46 Indeed, the magnitude of the effective charge reported by Heberling et al. is 0.25.47 This simplified picture accounts for the inhomogeneous charge distribution in the carbonate anion, which is taken into account in modelling studies. A successful model proposed by Dove et al., describes calcite by considering electrostatic interactions, assigning a charge of +1.64203 to the calcium ion, +1.04085 to carbon in the carbonate ion, and −0.894293 to each oxygen atom in carbonate.48 This charge distribution has been applied in various studies, including investigations on water vapour adsorption as a function of relative humidity conducted by Rahaman et al.49 Another successful model by Pavese et al. employs the following charges: calcium (+2), carbon (+1.134), oxygen (−1.045).50 This particular model has been utilized by Kerisit et al. in their theoretical study of adsorption to calcite.41
Importantly, when a vacuum-cleaved calcite surface is exposed to air, hydrocarbons appear on the surface while the carbide-like peak disappears. On the other hand, exposure to water enhances the S-CO3H peak.45,46 These observations provide evidence for surface reactions of calcite with components present in air and water, as well as rapid adsorption of hydrocarbons.
Atomistic simulations by Wright et al. shed light on the orientation of CO3 groups located at the surface plane of calcite. They found a slight rotation towards the bulk compared to the orientation in the bulk crystal, with a torsional angle shift of approximately 20°. This shift in orientation gradually decreases in the first four layers below the surface reaching bulk values afterwards.51 However, the magnitude of the shifts reported varies in different studies. Furthermore, shifts in the position of the calcium ions located at the surface have been reported. For instance, Wright et al. described a downward shift of the calcium ions of 0.75 Å,51 while Bruno et al. reported a much smaller shift of 0.07 Å at 0 K.52 The discrepancies mentioned above likely arise from the use of different force fields and modelling approaches.
Non-contact mode atomic force microscopy (AFM) studies conducted in ultrahigh vacuum at low temperatures reveal that the cleavage surface (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) plane retains the surface symmetry found in the bulk. However, the unit cell is doubled in size, containing four calcium atoms and four carbonate groups. This (2 × 1) cell has dimension of 10 × 8.1 Å2,43,44 suggesting a more significant restructuring of the calcite surface than considered in modelling studies.
4) plane retains the surface symmetry found in the bulk. However, the unit cell is doubled in size, containing four calcium atoms and four carbonate groups. This (2 × 1) cell has dimension of 10 × 8.1 Å2,43,44 suggesting a more significant restructuring of the calcite surface than considered in modelling studies.
3.2. Surface energy in air and water
When the high surface energy calcite surface is exposed to air or water, adsorption of various species readily occurs to minimize the surface energy. In contact with water, dissolution and redeposition processes also take place. All of this has made the determination of the surface energy of different pristine calcite surface planes a challenge both from the experimental and theoretical (using simulation methods) point of view. Experimental studies face difficulties in controlling the environment to minimize the effects of adsorption, while modelling studies require accurate force fields to account for all interactions in the system. Thus, it is not surprising that the values reported are far from consistent.53,54 However, it is generally agreed that the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane of calcite has the lowest surface energy, both in dry and wet conditions. Experimental values obtained after cleavage in the dry state range from 0.23 to 0.35 J m−2,53–55 while atomistic modelling typically reports higher values in the range of 0.32 to 0.86 J m−2.41,42,51,52,56 Contributing factors to these discrepancies are certainly the use of different experimental methods and modelling approaches. However, it is remarkable that the range of values obtained experimentally in dry state differs so significantly from those in simulations. Røyne et al. suggest that one reason could be the difficulty of obtaining absolutely dry and clean calcite surfaces.53
4) surface plane of calcite has the lowest surface energy, both in dry and wet conditions. Experimental values obtained after cleavage in the dry state range from 0.23 to 0.35 J m−2,53–55 while atomistic modelling typically reports higher values in the range of 0.32 to 0.86 J m−2.41,42,51,52,56 Contributing factors to these discrepancies are certainly the use of different experimental methods and modelling approaches. However, it is remarkable that the range of values obtained experimentally in dry state differs so significantly from those in simulations. Røyne et al. suggest that one reason could be the difficulty of obtaining absolutely dry and clean calcite surfaces.53
Adsorption of water generally lowers the surface energy. Subcritical crack propagation studies suggest an upper limit of 0.15 J m−2 for the surface energy of the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane when wetted by water.53 In contrast, Donnet et al. report lower values down to 0.04 J m−2 based on solubility data for small calcite particles.57 Atomistic simulations, on the other hand, suggest higher values ranging from 0.16 to 0.29 J m−2 for the (10
4) surface plane when wetted by water.53 In contrast, Donnet et al. report lower values down to 0.04 J m−2 based on solubility data for small calcite particles.57 Atomistic simulations, on the other hand, suggest higher values ranging from 0.16 to 0.29 J m−2 for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane.40–42,51 Røyne et al. propose that relaxation effects at wet calcite surfaces play a significant role, but they are difficult to account for in atomistic modelling.53 We note that several reports attempt to calculate the calcite–water interfacial energy based on the calcite–air (or vacuum) surface energy and measured water contact angles. However, this approach is, in our opinion, unreliable since the high-energy calcite surface readily adsorbs molecules present in the air, leading to an increase in the water contact angle.
4) surface plane.40–42,51 Røyne et al. propose that relaxation effects at wet calcite surfaces play a significant role, but they are difficult to account for in atomistic modelling.53 We note that several reports attempt to calculate the calcite–water interfacial energy based on the calcite–air (or vacuum) surface energy and measured water contact angles. However, this approach is, in our opinion, unreliable since the high-energy calcite surface readily adsorbs molecules present in the air, leading to an increase in the water contact angle.
The cosine of the contact angle, θ, can be determined when the interfacial energies (interfacial tensions), γ, are known:
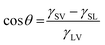 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ calculated from eqn (1) exceeds 1. This result is clearly unreasonable. However, it implies that water should spread on the calcite surface with a zero contact angle. This is consistent with water vapour adsorption isotherms on calcite, as discussed in Section 3.5. Nevertheless, reported contact angles of water on calcite vary significantly in the literature, ranging from 10°20 to above 70°.58 This inconsistency cannot be explained by surface roughness, as an increased roughness would lower the contact angle if the corresponding angle on a perfectly flat surface is below 90°. Instead, it reflects the challenge of obtaining clean calcite surfaces due to the strong adsorption of adventitious molecules. This topic is discussed further in Section 3.3.
θ calculated from eqn (1) exceeds 1. This result is clearly unreasonable. However, it implies that water should spread on the calcite surface with a zero contact angle. This is consistent with water vapour adsorption isotherms on calcite, as discussed in Section 3.5. Nevertheless, reported contact angles of water on calcite vary significantly in the literature, ranging from 10°20 to above 70°.58 This inconsistency cannot be explained by surface roughness, as an increased roughness would lower the contact angle if the corresponding angle on a perfectly flat surface is below 90°. Instead, it reflects the challenge of obtaining clean calcite surfaces due to the strong adsorption of adventitious molecules. This topic is discussed further in Section 3.3.
Most studies concerned with macroscopic calcite surfaces utilize the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane. Unless stated otherwise, this is the surface plane considered in this perspective article. Calcite particles, on the other hand, are more complex and may contain other surface planes with higher surface energy.52
4) surface plane. Unless stated otherwise, this is the surface plane considered in this perspective article. Calcite particles, on the other hand, are more complex and may contain other surface planes with higher surface energy.52
3.3. Adsorption of airborne organic molecules, carbon dioxide, and carbon monoxide
Adsorption leads to a lowering of the surface energy as described by the Gibbs adsorption equation. Given that calcite surface planes have higher surface energy compared to surfaces of organic materials (e.g., hydrocarbon materials have a surface energy of the order of 0.02 to 0.03 J m−2), it is expected that organic materials will adsorb to calcite to reduce the surface energy. This constitutes a challenge when studying chemically pure calcite surfaces since molecules from the environment readily adsorb and modify the surface properties. The most direct approach to minimize this effect is to cleave and investigate calcite under high vacuum conditions. However, one obvious drawback is that most of the production and applications of calcite occur in less controlled environments rather than in high vacuum. As a result, high vacuum studies do not directly correlate with industrial applications and environmental processes. Nonetheless, they do provide a fundamental understanding of calcite surfaces. This dilemma is not unique to calcite, but it is faced by all surface scientists investigating high-energy surfaces. In this regard, it is important to mention the thorough and pioneering work carried out by Stipp and co-workers.45 They used XPS to study calcite cleaved in air and high vacuum (≈ 10−10mbar). While surfaces cleaved in air and analysed as quickly as possible showed carbon contamination corresponding to about two monolayers of carbon atoms, surfaces cleaved in high vacuum showed no contamination when analysed immediately after cleavage. However, both in air and in high vacuum, adsorption of adventitious carbon was found to increase over time. Stipp's opinion on this issue is made apparent by her statement: “in air or water, a host of species is available for reaction, so investigation of a pristine surface is impossible”.46In more recent studies, the impact of specific functional groups found in organic compounds that adsorb to calcite has been considered both from a theoretical and experimental point of view. These studies are focused on describing the equilibrium structure in different environments. Ataman et al. used DFT calculations and concluded that the adsorption strength varied as carboxylic acids > alcohols ≈ water > aldehydes > benzene ≈ carbon dioxide > ethane.59 This trend was further supported by XPS desorption experiments, although the number of molecules studied was more limited compared to the DFT calculations.59 The observed behaviour can be rationalized by considering the interplay of electrostatic interactions, hydrogen bonds and dispersion interactions (Fig. 2). The same study considered the low coverage situation in their calculations, where interactions between adsorbed molecules could be ignored. The adsorption energy was found to increase with the size of the side group, primarily due to larger dispersion interactions with the surface.59
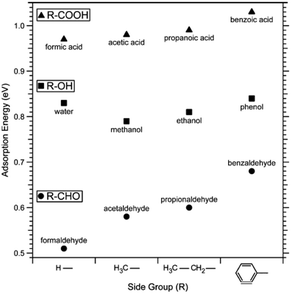 | ||
| Fig. 2 Adsorption energy of a series of carboxylic acids, alcohols, aldehydes and water determined by DFT calculations. Reprinted with permission from Attaman et al., J. Phys. Chem., C 120, 16586. Copyright 2016 American Chemical Society.59 | ||
Another study explored the adsorption energies for ethanol and acetic acid and found they increased with coverage, indicating favourable interactions between the adsorbed molecules.60 On the other hand, the adsorption energy for water remained relatively independent of surface coverage, while it decreased with coverage for acetone.59 The different situations arise from a competition between dispersion interactions, which enhances the adsorption energy, and steric hindrance, which reduces it. Considering the hydrophilic nature of the calcite surface, it may seem surprising that small alcohols adsorb as strong as, or even stronger than, water. This observation has been rationalized by considering that a single ethanol molecule can interact both electrostatically with calcium sites and via hydrogen bonds with carbonate sites. In contrast, a single water molecule, due to its smaller size, can only participate in one of these interactions.61 Furthermore, DFT calculations combined with XPS desorption studies have also been used to investigate the adsorption of various amine and sulphur-containing small molecules. The data showed that the amine group binds significantly stronger to calcite compared to cyanide and thiol groups.62 The strong adsorption of amines was attributed to electrostatic interactions with calcium sites and the formation of hydrogen bonds to carbonate sites. The predicted orientations of the studied molecules on the calcite surface can be found in the articles by Ataman et al.59,62
To better understand the effect of organic molecules on crystal growth inhibition, computer modelling was employed to investigate the adsorption of small organic molecules with different functional groups on planar surfaces and at growth steps.63 The findings revealed that molecules with carboxylic acid, hydroxy aldehyde, amide and amine groups adsorb strongly on dry surfaces and edges. In the presence of a water monolayer, wherein each calcium site is occupied by a water molecule, all functional groups were found capable of displacing water both on the planar surface and at step edges. Notably, for formic acid, the simulation suggests that the carboxylic acid group on the planar surface interacts with two calcium sites, with the carbonyl oxygen displaying stronger interaction with a calcium site compared to the hydroxyl oxygen.
In a separate study focused on carbon dioxide adsorption on the dominant calcite surface plane, it was found that CO2 adsorption does not alter the arrangement of ions on the calcite surface, owing to an insignificant change in surface energy.64 The same study suggests that CO2 adsorption occurs over calcium sites and involves one of the oxygen atoms of carbon dioxide while the other oxygen atom points away from the surface. The adsorption is driven by electrostatic interactions. Likewise, under ultrahigh vacuum conditions at temperatures below 100 K, infrared reflection adsorption spectroscopy (IRRAS) shows CO adsorption. Non-contact mode AFM studies supported the conclusion that CO adsorbs on top of calcium sites.43 Surprisingly, density functional theory (DFT) calculations presented in the same study suggested that the carbon atom in CO points toward the surface, which contrasts with the findings reported for CO2.
3.4. Adsorption from organic liquids
In contrast to adsorption from vapor, adsorption from a pure liquid always leads to maximum coverage of the liquid molecules at the calcite surface. X-ray reflectivity (XRR) measurements have been used for investigating adsorption from organic liquids. In some studies, the calcite crystal was cleaved after immersion in the liquid of interest, thus allowing adsorption to occur on pristine calcite surfaces. The wet surface was then transferred into an XRR cell held at the saturation level of the liquid vapour to avoid or minimize evaporation.17,65 In the case of methanol, ethanol, and isopropanol, the total adsorbed layer thickness was found to be just above 2 nm, with a density that decreases away from the calcite surface.17,65 The XRR data for ethanol is shown in Fig. 3. Note the ethanol-depleted region just outside the first adsorbed ethanol layer.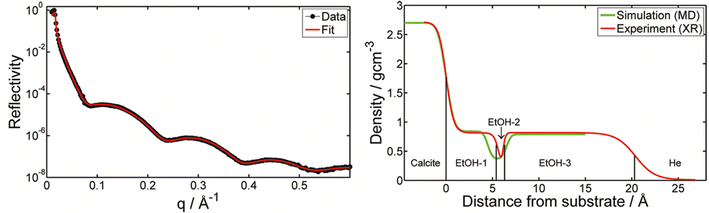 | ||
| Fig. 3 Left: The XRR data for ethanol adsorption from ethanol saturated He atmosphere with the theoretical fit. Right: The density distribution of ethanol normal to the calcite surface derived from XRR as well as calculated from MD simulations. Reprinted with permission from Pasarín et al., Langmuir, 28, 2545. Copyright 2012 American Chemical Society.65 | ||
Simulations presented in the same articles show that the alcohols form distinct layers with the highest density next to the surface. The simulations also show that the oxygen atom in the alcohols coordinates with calcium ions on the calcite surface, effectively replacing the oxygen coordination lost at the surface plane due to cleavage. Additionally, a hydrogen bond forms between the alcohol OH-group and the carbonate on the calcite surface. The hydrocarbon part of the alcohols is preferentially oriented away from the surface, and the ordering appears to decrease with branching, as concluded by comparing results for n-propanol and iso-propanol.
For pentanol and octanoic acid, with longer hydrocarbon chains than the alcohols discussed above, only a single monolayer was observed. The thickness of the layer was found to be of similar size, albeit slightly lower, than the length of the molecule.17 For both alcohols and carboxylic acids, the driving forces for adsorption were identified as being electrostatic interactions between oxygen atoms in the functional groups and surface calcium atoms, and hydrogen bonding between the functional groups and surface carbonate oxygens.
3.5. Water vapour adsorption
From previous sections, we have learned that water adsorbs strongly to calcite but not more strongly than alcohols and carboxylic acids. Water vapour adsorption is nevertheless discussed separately as water is always present in air, and its presence on calcite surfaces leads to processes such as dissolution and recrystallization.In Fig. 4, we have replotted the water vapour adsorption isotherm determined on freshly prepared calcite particles,60 along with two measurements conducted on commercial calcite powder samples.66,67 It is important to note that the data reported in each study were obtained using different cross-section areas for adsorbed water. Thus, to enable a meaningful comparison, we recalculated the data using the cross-sectional area of 12.5 Å2 suggested by Okhrimenko et al.60 Additionally, the data was converted into monolayers of water using the information provided in the original articles.
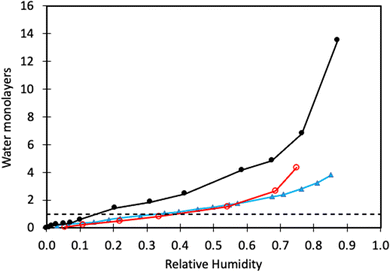 | ||
| Fig. 4 Water adsorption isotherm determined on freshly prepared calcite crystals (black filled circles, data taken from Okhrimenko et al.60). Water adsorption isotherms on commercial calcite powder (red unfilled circles are data from Gustafsson et al.,66 and filled blue triangles are data from Rezaei Gomari et al.67). The solid lines are guides to the eye, and the dashed line marks monolayer coverage. | ||
We note that a water monolayer is formed at a significantly lower relative humidity (RH) for freshly prepared calcite powder (10 to 20% RH) compared to commercial samples where monolayer coverage is reached at RH ≈ 40%. This disparity could be attributed, at least in part, to difficulties in completely removing organic contaminants from commercial samples. At higher humidity levels, all studies show the formation of water multilayers, which distinguishes water from alcohols and carboxylic acids, where an approximate monolayer coverage is maintained until the vapour saturation pressure is approached.60 This difference arises from the strong water–water interaction resulting from hydrogen bonding. In contrast, in alcohols and carboxylic acids, the polar group is anchored to the surface and hidden by the non-polar part of the molecule. As a result, subsequent layer adsorption for these molecules relies on weaker dispersion forces. The adsorption enthalpy of water on calcite powder has been measured using calorimetry techniques.68 The adsorption is, as expected, strongly exothermic with the differential enthalpy ranging from about −130 kJ mol−1 at low coverage to approaching the value for the enthalpy of condensation of bulk water (i.e., −44 kJ mol−1) at high coverage. At this stage, the surface accommodated roughly 5 water molecules per nm2. The integral heat of adsorption was found to be about −96 kJ mol−1,68 which is of the same order of magnitude as predicted by simulations for adsorption of water molecules.41,42,49 Synchrotron X-ray reflectivity measurements indicate a water layer thickness of 19.9 Å in humid N2 (close to water saturation),69 whereas another study reports a layer thickness of 15.5 Å over a surprisingly broad range of RH values.70
In the atomistic simulation conducted by Leeuw and Parker, the equilibrium structure at the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane covered with a monolayer of water was considered.42 They found that the oxygen atom of the water molecule coordinated with calcium ions, while the water hydrogens formed hydrogen bonds with carbonate oxygens in such a way that each carbonate oxygen was coordinated to two water hydrogens from two different water molecules. In another simulation, Rahaman et al. investigated the effect of relative humidity in the range of 50% to 100%.49 At 100% RH, they found two water density peaks at distances of 2.1 Å and 3.2 Å from the calcite surface. The peak at 2.1 Å was attributed to water adsorbed on calcium sites, with the water oxygen towards the surface, while the peak at 3.2 Å was associated with water hydrogen bonded to carbonate oxygen atoms. Reducing the relative humidity from 100% to 50% had minimal impact on the number of water molecules at distances less than about 3 Å, see Fig. 5.49
4) surface plane covered with a monolayer of water was considered.42 They found that the oxygen atom of the water molecule coordinated with calcium ions, while the water hydrogens formed hydrogen bonds with carbonate oxygens in such a way that each carbonate oxygen was coordinated to two water hydrogens from two different water molecules. In another simulation, Rahaman et al. investigated the effect of relative humidity in the range of 50% to 100%.49 At 100% RH, they found two water density peaks at distances of 2.1 Å and 3.2 Å from the calcite surface. The peak at 2.1 Å was attributed to water adsorbed on calcium sites, with the water oxygen towards the surface, while the peak at 3.2 Å was associated with water hydrogen bonded to carbonate oxygen atoms. Reducing the relative humidity from 100% to 50% had minimal impact on the number of water molecules at distances less than about 3 Å, see Fig. 5.49
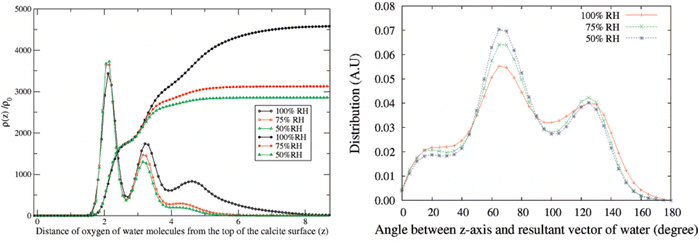 | ||
| Fig. 5 Left: Density distribution of water molecules normal to the calcite surface at different humidity levels. The integrals of the density distributions are also shown. Right: The angle distribution of adsorbed water molecules. Reprinted with permission from Rahaman et al., J. Phys Chem. C, 2008, 112, 2109. Copyright 2008 American Chemical Society.49 | ||
In the aforementioned simulations, it was assumed that water physically adsorbs onto the calcite surface without undergoing any reactions or dissolving the surface. These two issues will now be discussed.
There is supporting evidence for the reactive adsorption of water molecules to calcite based on XPS and time-of-flight secondary ion mass spectroscopy (TOFS-SIMS) studies. In particular, TOFS-SIMS reveals the presence of H and OH on the calcite surface, with stronger signals observed at step edges.46 It was suggested that water molecules dissociate at the calcite surface, leading to OH binding to calcium sites and H binding to CO3 sites.46 Similarly, FTIR spectra of calcium carbonate powder also suggest the same surface reaction with water.71,72 However, synchrotron X-ray reflectivity measurements in humid N2 do not show evidence for calcite surface modification by adsorbed water vapour, suggesting physisorption.69 Hence, while some experiments suggest dissociative adsorption of water to calcite, not all findings align with this conclusion.
Atomistic simulations by Kerisit et al. indicate a preference for physical water adsorption, with no water dissociation observed at the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane.41 However, they also found that dissociative water adsorption could occur at some step edges, releasing CO2 in the process. Further, ab initio simulations by Lardge et al. suggest that dissociative water adsorption occurs over vacant carbonate sites, resulting in the formation of bicarbonate and a hydroxide ion. In contrast, associative water adsorption was found over calcite vacancies.73 For both types of vacancies, the water adsorption energy was more negative, indicating a more favourable interaction compared to the perfect calcite (10
4) surface plane.41 However, they also found that dissociative water adsorption could occur at some step edges, releasing CO2 in the process. Further, ab initio simulations by Lardge et al. suggest that dissociative water adsorption occurs over vacant carbonate sites, resulting in the formation of bicarbonate and a hydroxide ion. In contrast, associative water adsorption was found over calcite vacancies.73 For both types of vacancies, the water adsorption energy was more negative, indicating a more favourable interaction compared to the perfect calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane.
4) surface plane.
3.6. Morphological changes of calcite surfaces in humid air
In the presence of water vapor the calcite surface changes due to dissolution and redeposition, leading to morphological changes that readily can be followed. A powerful method to directly visualize such changes is AFM, and this technique has been used for a long time to study calcite surfaces in air.18 Already in early investigations, it was established that the morphology of calcite rapidly changes in contact with air. For instance, Stipp et al. noted nucleation along step edges on the surface but also on the flat terraces.18 They called “hillocks” the small new structures that extend above the surface, and also noted the development of small holes or trenches on other areas. Clearly, in some areas, calcite dissolves to give rise to trenches and in others, the dissolved ions deposit to form hillocks. The process is facilitated by water that hydrates calcium ions and converts some carbonate ions to bicarbonate ions.18 A recent publication by Wojas et al. emphasized structural changes on the calcite surface at different relative humidity values from <3% to about 95%.20 They followed the development of hillocks and trenches as a function of time and found that the dissolution and redeposition process occurs more rapidly at higher humidity values. This is illustrated in Fig. 6, where data obtained at 50% RH are shown. It was observed that samples exposed to dry air with RH < 3% showed no hillocks or trenches even after 21 hours, consistent with the finding that the adsorbed amount of water at this humidity is below a monolayer (as shown in Fig. 4). Indeed, force measurements conducted at <3% RH are consistent with van der Waals forces without evidence for capillary condensation between tip and sample, whereas capillary forces were observed at 75% RH and became the dominant interaction at higher humidity levels.20 At 25% RH, both trenches and hillocks appeared, and their number and size increased with exposure time. However, the height of the hillocks (6–7 Å) and the depth of the trenches (3–4 Å) were found to be independent of exposure time. At higher humidity levels, the dissolution and reprecipitation processes occurred more rapidly, but the increase in hillock heights was relatively small (see Fig. 7).20 This behaviour is consistent with previous studies, although they reported slightly larger hillock heights of about 10–15 Å.74,75 Further, the depth of the trenches were essentially independent of humidity (Fig. 7).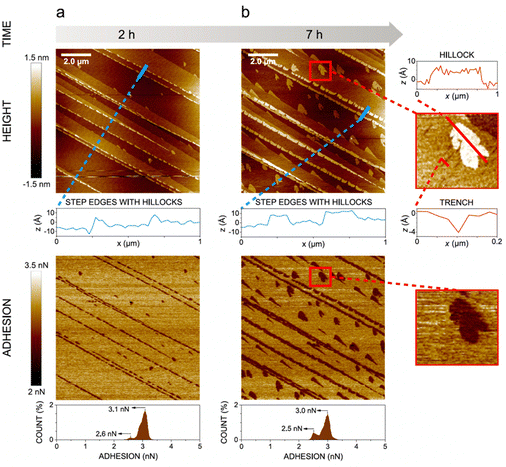 | ||
| Fig. 6 AFM height and adhesion images with height profile and adhesion histograms for a freshly cleaved calcite surface within (a) 2 h and (b) 7 h of exposure to nitrogen gas at 50% RH. Scan size 10 × 10 μm2. Figures reproduced from Wojas et al., J. Colloid Interface Sci., 2019, 541, 42.20 | ||
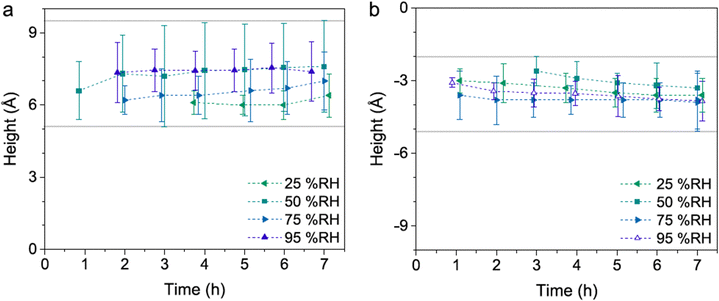 | ||
| Fig. 7 Height difference between hillocks and the surrounding terrace (a) and the surrounding terrace and trenches (b). Data are reported for different humidity levels and exposure times. Figures from Wojas et al., J. Colloid Interface Sci., 2019, 541, 42.20 | ||
The hillocks were also found to display a lower tip-sample adhesion and larger deformation under the tip's load compared to the surrounding calcite areas. This was attributed to lower van der Waals forces caused by the incorporation of water in the hillock domains, as supported by Hamaker constant calculations. These calculations suggested that the hillocks may contain approximately 50% water, indicating the presence of hydrated forms of calcium carbonate. If this were the case, one would expect that the height of the hillocks would decrease when the relative humidity is lowered to very low values. Indeed, it was observed that hillocks formed at high humidity that had a height of 6–7 Å, reduced to 3–4 Å when dried in an atmosphere of less than 3% RH, and restored when humidity was reintroduced to its original value.20 This observation further supports the idea that the hillocks consist of hydrated forms of calcium carbonate (monohydrate, hexahydrate or amorphous hydrate),20,75,76 stabilized by the underlying calcite surface.75 Although this hypothesis has not been confirmed by physical–chemical analysis, there is evidence of compositional differences between the hillocks and the surrounding terrace. Surface potential measurements using Kelvin probe force microscopy at 45% RH revealed that the hillocks, though still negative, have a relatively more positive surface potential than the surrounding terrace.74 Moreover, the hillocks display internal surface potential heterogeneities, with larger values at the edges compared to the centre (Fig. 8). In contrast, dissolution pits exhibited no surface potential differences relative to the terrace. It was argued that the absolute surface potential on the hillocks was lower (i.e., less negative) compared to the terraces because of formation of hydrated amorphous calcium carbonate. This formation appears to reduce the surface dipole moment due to a less ordered interface and also shields the dipole moment from the underlying calcite crystal.74
 | ||
| Fig. 8 Height (left) and surface potential (right) on a calcite surface with hillocks at a RH level of 45% measured using Kelvin probe force microscopy. The image size is 3 × 3 μm2. The surface potential difference between the hillocks and the terrace is about 120 mV, with the former displaying the less negative values. Reprinted with permission from Na et al., Environ. Sci. Technol., 41, 6491. Copyright 2007 American Chemical Society.74 | ||
Baltrusaitis and Grassian also explored the calcite surface with AFM at 70% RH, and they suggested that newly formed structures were due to hydrated amorphous calcium carbonate.77 They report that hillocks grow preferentially parallel to step edges, whereas trenches tend to grow perpendicular to such edges. At this specific humidity level, the growth rate of the hillocks varied between 2 and 4 nm min−1, depending on the growth direction. A similar growth rate was reported by Kendall and Martin at 80% RH.75 In contrast, the trenches grew at approximately half of this rate.77 Additionally, Baltrusaitis and Grassian found evidence for the formation of another layer on top of the hydrated amorphous calcium carbonate that appeared after about 70 min exposure to RH 70% and displayed an anisotropic growth. Interestingly, this layer was more readily formed at lower temperatures (5 °C) compared to higher temperatures (23 °C), and it was hypothesized that this top layer may consist of vaterite rather than calcite.77
Furthermore, it has been observed that the presence of foreign ions can influence the rate of restructuring. For instance, the presence of cadmium ions was found to inhibit the process, while lead ions did not have the same effect.76 This difference was attributed to the preferential interaction of Cd2+ with step-edges, which are particularly prone to participate in dissolution–redeposition processes.
3.7. Nanowear
We have seen that calcite surfaces undergo spontaneous changes when exposed to gases and liquids. In processes and applications of calcite the surface may also be exposed to stresses that induces additional changes. Such changes are considered in this section.Calcite is a quasi-brittle material, and stress–strain curves have been reported for high-quality synthetic calcite single crystals subjected to uniaxial stress in unconfined samples.78 This work shows an initial elastic (or pseudo-elastic) deformation phase up to a stress of 2 to 4 MPa, with a corresponding strain of about 0.5% (depending on sample size and compression direction). Beyond this stress and strain range, the crystal undergoes plastic deformation primarily through twinning until fracturing occurs at strain levels of approximately 3–6%. It is worth noting that micro-cracks were also observed during the plastic deformation phase.
In a recent study, the local wear of calcite surfaces was examined under different conditions. The experiments involved using AFM to assess the wear in both dry (RH < 5%) and humid (RH = 75%) air. Different applied loads were tested along the [421] direction,79 ranging from 100 to 300 nN. Although these loads might seem small, it is important to consider the pressure exerted by the AFM tip (radius about 10 nm), which locally reaches several GPa. Thus, the applied load is sufficient to induce both plastic deformation and cracks, leading to localized fracture of the calcite surface. Indeed, the data shown in Fig. 9 supports this view. The results show that wear is limited when the load is 100 nN, but it is much more significant at 200 nN and 300 nN, where wear particles accumulate at the edge of the worn area. In the case of dry air, the wear scar reaches a depth of about 4 nm at the highest load. In contrast, the situation in humid air differs in two aspects. Firstly, the wear scar is shallower, which may indicate increased surface plasticity in the presence of the adsorbed water layer. Secondly, the wear debris is not only pushed to the side of the worn area but is also found within the worn area itself. This collection of wear particles in the worn area can be attributed to capillary forces between the wear debris and the calcite substrate.
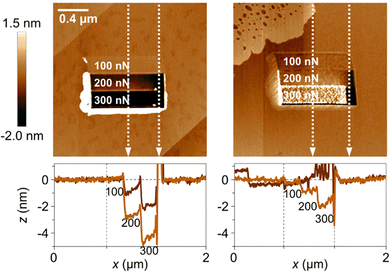 | ||
| Fig. 9 Top row: Topography measurements recorded after the wear measurement, with the worn area shown in the middle of the figures. The load used in the different regions are provided in the figures. The image size is 2 × 2 μm2. Bottom row: Height scans along the vertical white dashed lines. The left column contains data at low humidity (RH < 5%), and the right column data at high humidity (RH = 75%). Figures from Wojas et al., Langmuir., 2021, 37, 9826.79 | ||
A closer inspection of the topography image hints at the presence of recrystallized calcite on the surface. This becomes even more apparent in the adhesion image presented in Fig. 10.79 As mentioned earlier, the recrystallized patches exhibit a lower adhesion between the tip and the sample. It should be noted that these patches are completely removed in the worn area, even at a low load of 100 nN, where the wear depth is minimal. Clearly, the adhesion between the redeposited material and the calcite surface is lower than the cohesion within the calcite crystal itself. Although this finding aligns with the hypothesis that the hillocks consist of hydrated forms of CaCO3, it is important to note that it does not serve as conclusive proof. Hausner et al. also observed the removal of certain hillocks when subjected to a combined action of load and shear. Additionally, they demonstrated that these hillocks reappeared when the surface was left undisturbed in humid air.76
 | ||
| Fig. 10 An image of the tip-sample adhesion after wear measurements in dry (<5% RH) air. The redeposited hillocks are completely removed from the worn area. The image size is 2 × 2 μm2. Figure from Wojas et al., Langmuir., 2021, 37, 9826.79 | ||
3.8. Solubility in bulk water
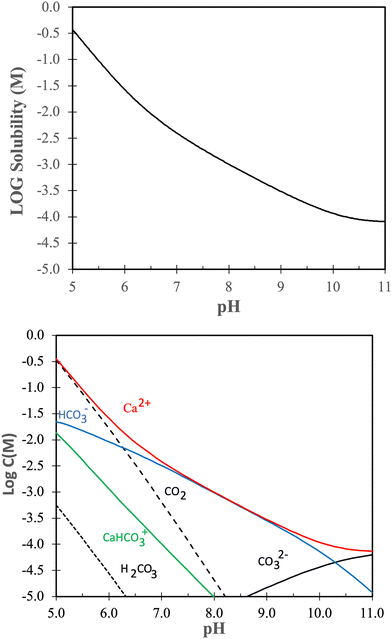
Dissolution and redeposition on calcite surfaces is intimately related to the solubility of calcite under various conditions. Thus, in this section we look further into the solubility of calcite.The solubility product of calcite is given by:
| Ksp = aCa2+aCO32− | (2) |
Without going into further detail, it is established that the solubility of calcite increases with decreasing temperature and increasing pressure.81,82 The temperature dependence is a consequence of the dissolution reaction being exothermic,83 leading to a decrease in solubility with increasing temperature according to the van’t Hoff equation. The negative entropy change during calcite dissolution is attributed to ion hydration, which orders the solvent molecules.84 Higher pressure enhances the solubility due to increased stresses in the crystal structure. This effect is particularly noticeable at grain boundaries, where the local chemical potential is higher, leading to a local undersaturation of the solution and consequently increased local solubility.85
The solubility of calcite increases with increasing CO2 pressure, which can be understood from the reaction between calcite and carbon dioxide:81,86
| CaCO3(s) + CO2 + H2O ⇔ Ca2+ + 2HCO3− |
| CaCO3(s) + H+ ⇔ Ca2+ + HCO3− |
3.9. The calcite–water interface structure
Calcite and water commonly interact in nature and in applications. It is thus worthwhile to consider in detail how water is arranged at calcite surfaces. In this section we mostly consider modelling studies where dissolution and redeposition processes are not taken into account, but an understanding of the equilibrium situation at a perfect calcite surface is elucidated.The structure of the calcite water interface has been investigated using both simulations and experiments. For instance, Kerisit and Parker used MD simulations to explore the structure and energetics of a 20 Å thick water layer on the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane of calcite.87 As expected, they found an oscillatory water density profile where the two closest peaks were observed at distances of 2.2 Å and 3.2 Å. The peak located at 2.2 Å was identified as being due to water adsorbed on calcium sites with the water oxygen towards the surface, while the peak at 3.2 Å was attributed to water hydrogen bonded to carbonate oxygen atoms. This finding aligns well with the simulations conducted by Rahaman et al., which investigated water vapour adsorption at relative humidity ranging from 100% to 50%.49 It also agrees well with the surface X-ray diffraction experiments by Heberling et al.,47 who reported water layers at distances of 2.36 ± 0.06 Å and 3.24 ± 0.12 Å from the plane of the calcium ions, as well as the study by Brugman et al., which identified two peaks at distances of 2.36 ± 0.03 Å and 3.17 ± 0.08 Å.88 The latter study also found that these two water layers were strongly ordered, whereas the subsequent layer was completely disordered.88 The simulations by Kerisit and Parker indicated that water–water hydrogen bonds were completely broken within the layer associated with adsorption to calcium sites, while they were partially broken within the layer associated with carbonate sites.87 The free energy of adsorption on calcium sites was determined to be −2.8 kJ mol−1, slightly lower than the −2.4 kJ mol−1 on the carbonate sites. Interestingly, these values are more than a factor of 10 lower than the enthalpy of adsorption found by the same group for water adsorption from vapour.41 This suggests a large entropy change due to water adsorption, as mentioned by the authors.87 Additionally, synchrotron X-ray reflectivity measurements revealed that the roughness of the calcite–water interface increases over time due to dissolution.69 Vibrational sum frequency spectroscopy (VSFS) has also been used to investigate the calcite surface in contact with pure water. From the lack of signal observed in the OH stretching region, it was concluded that the first and second water layers have opposite orientations but interestingly similar vibrational frequencies.89 These studies also indicate that the calcite surface itself carries a negligible surface charge. However, the latter conclusion is incompatible with zeta potential measurements, and repulsive double-layer forces observed between calcite surfaces, summarized below in Sections 3.11, and 3.13, respectively.
4) surface plane of calcite.87 As expected, they found an oscillatory water density profile where the two closest peaks were observed at distances of 2.2 Å and 3.2 Å. The peak located at 2.2 Å was identified as being due to water adsorbed on calcium sites with the water oxygen towards the surface, while the peak at 3.2 Å was attributed to water hydrogen bonded to carbonate oxygen atoms. This finding aligns well with the simulations conducted by Rahaman et al., which investigated water vapour adsorption at relative humidity ranging from 100% to 50%.49 It also agrees well with the surface X-ray diffraction experiments by Heberling et al.,47 who reported water layers at distances of 2.36 ± 0.06 Å and 3.24 ± 0.12 Å from the plane of the calcium ions, as well as the study by Brugman et al., which identified two peaks at distances of 2.36 ± 0.03 Å and 3.17 ± 0.08 Å.88 The latter study also found that these two water layers were strongly ordered, whereas the subsequent layer was completely disordered.88 The simulations by Kerisit and Parker indicated that water–water hydrogen bonds were completely broken within the layer associated with adsorption to calcium sites, while they were partially broken within the layer associated with carbonate sites.87 The free energy of adsorption on calcium sites was determined to be −2.8 kJ mol−1, slightly lower than the −2.4 kJ mol−1 on the carbonate sites. Interestingly, these values are more than a factor of 10 lower than the enthalpy of adsorption found by the same group for water adsorption from vapour.41 This suggests a large entropy change due to water adsorption, as mentioned by the authors.87 Additionally, synchrotron X-ray reflectivity measurements revealed that the roughness of the calcite–water interface increases over time due to dissolution.69 Vibrational sum frequency spectroscopy (VSFS) has also been used to investigate the calcite surface in contact with pure water. From the lack of signal observed in the OH stretching region, it was concluded that the first and second water layers have opposite orientations but interestingly similar vibrational frequencies.89 These studies also indicate that the calcite surface itself carries a negligible surface charge. However, the latter conclusion is incompatible with zeta potential measurements, and repulsive double-layer forces observed between calcite surfaces, summarized below in Sections 3.11, and 3.13, respectively.
Perhaps the most powerful way to elucidate the calcite–water interface is to combine surface X-ray diffraction (SXRD) measurements with simulation methods. Such an approach was recently reported,88 and allowed comparing the calcite surface and hydration water structure observed experimentally, with similar data and additional molecular insight obtained by simulations. The structural data from this study agreed well with previous experimental and theoretical findings, suggesting a satisfactory current understanding of the calcite–water interface structure. Brugman et al. provided detailed information on the positions of the atoms in the two uppermost calcite layers and the water molecules above these layers, presenting results from three different simulation approaches along with SXRD data.88 The study also highlighted that density functional theory (DFT) calculations yielded better agreement with SXRD data than force field simulations. The dominant orientations of water molecules above calcite sites and above carbonate sites are illustrated in Fig. 12.
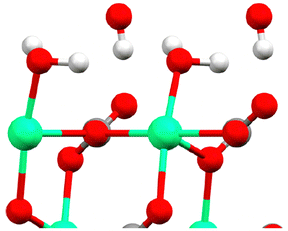 | ||
| Fig. 12 The topmost calcite surface with calcium in green oxygen in red and carbon in grey (hardly seen as covered by an oxygen in this perspective). The water molecules above calcium and carbonate sites are illustrated in their dominant orientation. Here hydrogen is shown in white. The figure is reproduced from Brugman et al., J. Phys. Chem. C, 2020 124, 18564.88 | ||
3.10. Water dynamics at the calcite surface
Even though the structure of the calcite–water interface seems to be largely resolved, the same is not true for the dynamics of the water layer. For instance, Kerisit and Parker reported water residence times of 300 ps and 53 ps in the first and second layers,87 whereas the simulations by Brugman et al. suggest a residence time of 4 ns at the calcite surface.88 MD simulations have revealed that water diffusion next to the calcite surface is anisotropic and slower than in bulk water (2.3 × 10−9 m2 s−1 at 25 °C). Specifically, the diffusion coefficient normal to the surface was found to be around 0.2 × 10−9 m2 s−1 in the first two layers, while parallel to the surface, it was higher, at approximately 0.6 × 10−9 m2 s−1 in the first layer and 0.9 × 10−9 m2 s−1 in the second layer.87 This observation of greater mobility along the surface compared to perpendicular to it was also noted in the MD simulations conducted by Rahaman et al.493.11. Electrical aspects of calcite–water interfaces
An important aspect of calcite surfaces in contact with aqueous solutions is that surface reactions and ion adsorption may occur. This will change the initially uncharged (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane, and under most conditions the calcite surface will acquire a net charge. This section consider this aspect of the dynamic calcite surface.
4) surface plane, and under most conditions the calcite surface will acquire a net charge. This section consider this aspect of the dynamic calcite surface.
The electrical properties of calcite surfaces have been extensively studied, but the data obtained so far lack consistency. A comprehensive review published in 2017 provides an excellent resource for interested readers, as it includes numerous references on this topic.90 From the available studies, we can conclude that two main factors contribute to the divergent results. Firstly, the slow equilibration between gas, liquid, and solid47 phases can lead to studies being conducted before equilibrium is established. Secondly, the propensity of many compounds, both ionic and non-ionic, to adsorb onto calcite surfaces makes it difficult to achieve perfectly clean samples, which further complicates the experimental process.
To better understand the surface charge of calcite in contact with aqueous solutions, it is necessary to consider all possible surface reactions. Surface complexation models, such as the one developed by Heberling et al., who considers close to twenty surface species,47 have been instrumental in this regard. According to Heberling et al., the potential determining ions are Ca2+ and CO32−, rather than H+ and OH−. They identify surface-Ca-OH and surface-CO3H as the most prominent surface groups. This finding is qualitatively consistent with the proposal made by Stipp already in 1999.46 The complexation of ions appears not to occur directly on the surface (except for H+ and OH−) but rather 4–6 Å above the plane defined by the calcium ions, i.e. they are outer sphere complexes located at the outer Helmholtz plane.47 Their work demonstrated the importance of working with equilibrated calcite–solution–gas systems and reported that equilibration takes between 1 day and 1 month, depending on the specific conditions. Fig. 13 shows the variation of the zeta-potential as a function of pH, determined in equilibrated systems using calcite powder dominated by the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface. The observed pH-dependence stems from the increased solubility of calcite at lower pH values, leading to higher concentrations of calcium ions. In contrast, measurements of zeta-potentials as a function of pH for a constant calcium ion concentration demonstrate that the zeta-potential is unaffected by pH, which is a consequence of calcium and carbonate ions being potential determining.90
4) surface. The observed pH-dependence stems from the increased solubility of calcite at lower pH values, leading to higher concentrations of calcium ions. In contrast, measurements of zeta-potentials as a function of pH for a constant calcium ion concentration demonstrate that the zeta-potential is unaffected by pH, which is a consequence of calcium and carbonate ions being potential determining.90
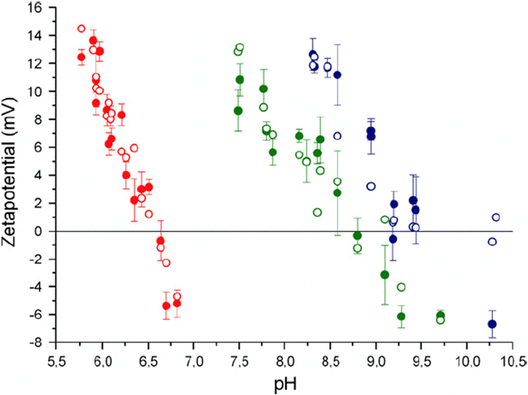 | ||
Fig. 13 Zeta potential of calcite powder dominated by (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface planes. Data were recorded at p(CO2) = 1 (red-filled symbols), p(CO2) = 10−3.44 (green-filled symbols) corresponding to the typical CO2 pressure in the atmosphere, and p(CO2) = 10−5.2 (blue-filled symbols). The unfilled points are calculated using their surface complexation model. Reproduced with permission from Heberling et al., J. Colloid Interface Sci. 2011, 354, 843. Copyright 2011 Elsevier.47 4) surface planes. Data were recorded at p(CO2) = 1 (red-filled symbols), p(CO2) = 10−3.44 (green-filled symbols) corresponding to the typical CO2 pressure in the atmosphere, and p(CO2) = 10−5.2 (blue-filled symbols). The unfilled points are calculated using their surface complexation model. Reproduced with permission from Heberling et al., J. Colloid Interface Sci. 2011, 354, 843. Copyright 2011 Elsevier.47 | ||
The measured data in equilibrated systems are in good agreement with the proposed surface complexation model and show that the isoelectric point decreases linearly with the logarithm of the CO2 pressure.47 Zeta-potential measurements performed by the same authors prior to reaching equilibrium were remarkably different from those depicted in Fig. 13, emphasizing the importance of working with properly equilibrated systems.
3.12. Dissolution and redeposition at calcite surfaces in contact with water
We have seen that the calcite surface in the presence of water vapour is highly dynamic, and this dynamism becomes even more pronounced when calcite is in contact with bulk water. In supersaturated solutions, precipitation occurs on the calcite surface, whereas in undersaturated solutions, dissolution of calcite takes place. These processes have been extensively investigated due to their relevance in industrial processes where precipitation, known as scaling, is undesirable. However, they are also vital for many life forms as they play a fundamental role in biomineralization. This has inspired many scientific studies, particularly focusing on biomineralization pathways and how nature uses specific adsorption of biomolecules on certain crystal planes to control the crystal growth process in different crystallographic directions.91–93In recent years, there has been a particular focus on comprehending dissolution and growth mechanisms, requiring a detailed understanding of local surface events. AFM has proven to be a very suitable tool for investigating such dissolution and redeposition processes, and the interested reader is referred to a detailed review by Ruiz-Agudo and Putnis in 2012,94 for further information than provided here. We note that the overall rate of dissolution depends on two key factors: the surface reaction rate, where calcium and carbonate ions are liberated from the crystal, and the mass transport away from the surface region. Thus, the dissolution rate depends both on the degree of undersaturation and the flow conditions. Extensive data summarized by Arvidson et al., emphasize that the dissolution rate of single crystals is significantly slower than that of calcite powder, primarily due to a lower number of defects present on the single crystal surface.95 Their data also demonstrate a rapid increase in dissolution rate as the pH decreases below 6, while the solubility rate remains nearly independent of pH at higher pH values.
Dissolution mainly occurs at high-energy locations on the surface, such as step edges (illustrated in Fig. 14), where the constituents have a low coordination number. On the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane, there are two obtuse edges (with an angle of 102°) and two acute ones (with an angle of 78°), as shown in Fig. 1 and 18. AFM studies have revealed that dissolution at obtuse edges is approximately 2 to 4 times faster, depending on solution pH, compared to dissolution at acute edges.96 This difference has been attributed to a combination of larger steric hindrance and stronger hydration at acute edges.94Ab initio simulations support the variation in hydration at these two types of edges.73 During dissolution, the step edges recede on the surface at a constant rate and tend to remain straight97 until a crystal plane is completely dissolved. Particularly important are the kink sites where the coordination is only half of that in bulk, and dissolution is achieved by advancements of such sites on the surface.
4) surface plane, there are two obtuse edges (with an angle of 102°) and two acute ones (with an angle of 78°), as shown in Fig. 1 and 18. AFM studies have revealed that dissolution at obtuse edges is approximately 2 to 4 times faster, depending on solution pH, compared to dissolution at acute edges.96 This difference has been attributed to a combination of larger steric hindrance and stronger hydration at acute edges.94Ab initio simulations support the variation in hydration at these two types of edges.73 During dissolution, the step edges recede on the surface at a constant rate and tend to remain straight97 until a crystal plane is completely dissolved. Particularly important are the kink sites where the coordination is only half of that in bulk, and dissolution is achieved by advancements of such sites on the surface.
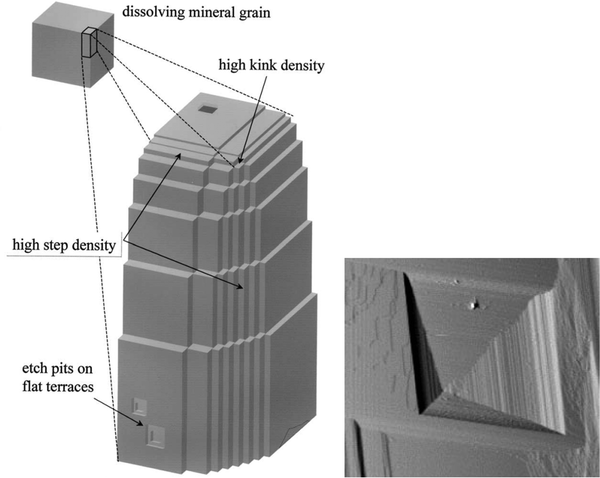 | ||
| Fig. 14 Left: An illustration of step edges, kinks and etch pits. Reproduced with permission from Arvidson et al., Geochim. Comochim. Acta. 2003, 67, 1623. Copyright 2003 Elsevier.95 Right: An AFM image of an etch pit reproduced with permission from Shiraki et al., Aquat. Geochem., 2000, 6, 87. Copyright 2000 Kluwer Academic Publisher.96 The etch pit is about 3 μm wide. | ||
Another mechanism of dissolution in calcite involves the formation of etch pits, which are depressions on the surface, typically exhibiting a rhombohedral structure (see Fig. 14). It has been noted that shallow and temporary etch pits, approximately one layer deep of about 3 Å, tend to form at point defects and impurities. On the other hand, deeper pits tend to form preferentially at dislocations.98 However, such pits also appear in defect-free locations.94 During dissolution, the etch pits become deeper and wider. Under near-equilibrium conditions, triangular-shaped pits, rather than rhombohedral ones, have been found.99 The relative importance of different dissolution mechanisms depends on the degree of undersaturation of the solution.100 It has been proposed that dissolution of pre-existing steps is the main mechanism not far away from equilibration. However, as the degree of undersaturation increases, the formation and spreading of etch pits become more important.100
The growth of calcite crystals in supersaturated solutions has also been followed by AFM, and it is emphasized that the process depends on the degree of supersaturation, solution composition, and the local topography of the initial calcite crystal.94 The degree of supersaturation (and undersaturation), denoted by σ, is defined as:101
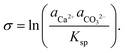 | (3) |
 | ||
| Fig. 15 AFM images of calcite surfaces in contact with solutions of different degrees of supersaturation, σ. (A) Low supersaturation (σ = 0.4) where spiral structures grow by the advancement of step edges. (B) Intermediate supersaturation (σ = 1.0) where both spiral and surface nucleation structures are found. (C) High supersaturation (σ = 1.6) where surface nucleation is predominant. These structures have a height of 0.3 nm, corresponding to one monolayer. Adapted by permission from Teng et al., Geochim. Cosmochim. Acta, 2000, 64, 2255. Copyright 2000 Elsevier.101 | ||
The growth occurs through the incorporation of calcium and carbonate ions into the crystal structure. It has been observed that, for a specific degree of supersaturation, the growth rate is fastest when the activity of calcium and carbonate ions is equal. Interestingly, the decrease in growth rate away from stoichiometry is unsymmetrical. Further analysis of this phenomenon has indicated that the incorporation of calcium ions is less favourable compared to that of carbonate ions. This is attributed to the stronger interaction of calcium ions with water molecules.102
3.13. Calcite surfaces under confinement
So far, we have considered a single surface in contact with water, and discussed many of the complex processes that occur. However, in many natural and industrial situations calcite surfaces come very close together. This results in additional processes related to surface interactions and pressure changes.In recent years, the complex processes occurring at calcite surfaces in contact with water have also been investigated by direct force measurements using techniques such as AFM85,103–107 and the surface forces apparatus (SFA).85,108,109 The difference between these measurements and those reported previously is that the focus has shifted to events taking place between two calcite surfaces under compression and in close contact. For instance, Røyne et al. measured interactions between two calcite surfaces and found evidence for a repulsive hydration force. This means that a compressive force was needed to dehydrate the surfaces.103 The range of this force was a few nanometres, and its presence was argued to be consistent with the decreasing strength of calcite when in contact with water.53 Diao et al. also reported a hydration force between calcite and silica, with a measurable range of 1–2 nm.104 One can add that based on simulation and experimental work discussed previously in this article, there should be at least two strongly bound layers of water on calcite, and thus a strong repulsive hydration force could be expected when the calcite surfaces are less than four water layers apart.
An adhesion force, attributed to van der Waals forces, has been observed between the calcite surfaces in air and ethylene glycol. In contrast, in water, no adhesion was found due to the presence of the hydration force.103 The study of calcite–calcite adhesion was later extended to include the effect of NaCl concentration (0–1.2 M) and applied load. At low NaCl concentration (<100 mM), no or a very small adhesion was found. However, at higher NaCl concentrations, an adhesion force that increased with salinity was noted. The appearance of calcite–calcite adhesion was suggested to be due to a reduction in the hydration force and the appearance of ion–ion correlation forces.105 The adhesion force was also found to increase with applied compressive force, which could be convincingly explained by an increased contact area resulting from the compression of surface asperities and subsequent recrystallization.105 Repulsive double-layer forces between calcite and silica have also been reported.104
Recently, a very interesting article discussed the relationship between pressure solution (i.e. the increase in calcite solubility with pressure), and the action of load and shear in an SFA.85 These experiments utilized single-crystal calcite surfaces and saturated solutions. Application of pressure resulted in local solubilization and redeposition of dissolved ions on unstressed locations. Measurements of crystal thickness as a function of sliding speed showed that pressure-induced dissolution was enhanced, particularly at low sliding speeds below 0.02 μm s−1 at a load of 2 mN, corresponding to a pressure of approximately 6 MPa. This also resulted in a marked decrease in friction force at slower sliding speeds at a constant load, deviating from the expected logarithmic dependence for a shear-assisted slip process.85 For this to happen, the contact time needs to be larger than the dissolution time, highlighting why pressure dissolution enhancement was more pronounced at slow sliding speeds.85 It was observed that the change in friction was reversible, which is a strong argument for pressure solution rather than morphological changes on the surfaces. Additionally, in the same study, it was observed that redeposition of calcium carbonate slightly increased the friction force. AFM measurements used for studying specific ion effects on friction forces in saturated solutions revealed that MgCl2 reduced the friction by promoting pressure dissolution. The effect was attributed to the strong hydration of Mg2+ ions, which could disrupt the hydration of the calcite surface.85
4. Modified calcite surfaces
As described above, the calcite surface is dynamic, changing by interactions with water vapour and airborne molecules. Thus, the efficiency of any surface modification process will depend on the initial state of the calcite surface. Indeed, controlling the moisture level throughout the process is crucial, as emphasized in studies on composites of coated calcium carbonate and low-density polyethylene, where the effects of different drying methods have been evaluated.110 As we have seen, many functional groups bind strongly to calcite, offering numerous options for surface modification of this mineral.28,111 However, long-chain fatty acids and their salts are by far the most commonly used chemicals for surface modification of calcium carbonate powders, which are typically used as fillers.112 This review focuses on this class of compounds. The fatty acids can exist in both acid and carboxylate forms. While stearic acid has a pKa in aqueous solution of about 4.8–5.2, the apparent pKa at a surface can be vastly different.113,114For a comprehensive discussion on many other surface modification agents, particularly in relation to calcium carbonate nanoparticles, we refer to the recent review by Niu et al.28 When calcium carbonate is used as a filler material, the aim of surface modification is to achieve good dispersibility and compatibility between the particle and the polymer matrix. This results in the formation of a strong interphase region around the particles. It is then expected that, for a given volume fraction of particles, materials with improved mechanical properties can be obtained by reducing the particle size, as this increases the interphase volume.115
4.1. Surface modification processes
Industrial surface modifications of calcite using fatty acids employ two main approaches: dry methods and wet methods. In both cases, the aim is to achieve full monolayer coverage with the carboxylic acid group anchored to the surface and the hydrocarbon chain exposed to the environment. This gives rise to a non-polar surface that facilitates mixing into a non-polar polymer matrix.In the dry process, calcite particles and the fatty acid are mixed at or above the melting temperature of the fatty acid. There are several technical variations of this method, and, for example, two different set-ups are described in the work of Cao et al.116 and Jeong et al.117 For obtaining good results with this method, an efficient mixing process and stringent control of the dosage of the carboxylic acid is required.118 In many cases, ball milling is utilized, and the process parameters also need to be carefully optimized.119
In the wet process, the adsorption is instead facilitated using a liquid, such as water, alcohol, or chloroform, which enables the transport of the fatty acid to the calcite surface. Typically, a dispersion of calcite powder is mixed with a solution containing the fatty acid. For instance, Mihajlovic et al. used a slurry of calcite in water at 50 °C and mixed it with a chloroform solution containing stearic acid.11 However, many other conditions have also been employed. Ball milling may be utilized to achieve a more efficient and homogeneous surface modification.120
We note that ball milling reduces the particle size,119 which means that some pristine, not contaminated surfaces are created during the process. This may, in fact, be important as calcite surfaces exposed to air contain adsorbed species that need to be displaced for effective surface modification. One common and simple way to determine the surface modification efficiency is to measure the floatability of the modified powder sample, and the results are then reported in terms of the active ratio, AR, defined as:
 | (4) |
However, all the above surface modification processes have their limitations. In particular, it is challenging to precisely control the dosage of carboxylic acid required to form a monolayer. A too-low dosage gives rise to voids in the adsorbed layer, while a too-high dosage can result in the formation of bilayer patches, both of which hinder the achievement of a homogeneous non-polar surface. Voids in the adsorbed layer can also occur when calcite particles remain in contact during the surface modification process, thus hampering the formation of a monolayer at and near the contact points.
For more fundamental studies, the mentioned approaches lack sufficient control. In addition, flat surfaces are preferred over particles in fundamental studies. One method to control the adsorption process is to utilize vapour deposition of the fatty acid, where control of temperature and deposition time can be used to build carboxylic acid layers with different packing densities.79,122
4.2. Dry process and particle surfaces
In a dry surface modification process, all added surface modification agent remains in the system. Thus, dosage is a critical issue, and the fate of all parts of the added molecules has to be considered.In the dry method, it is assumed that the fatty acid dissociates upon attachment to the surface, with the carboxylate anion attaching to calcium sites and that the released protons associate with carbonate sites, thus forming bicarbonate surface sites.123 This method often involves temperatures above 100 °C,112 but in an interesting study by Mihajlovic et al., a temperature of 70 °C with a vibrating mill mixer was utilized.123 They analysed bare and modified calcite using thermogravimetric analysis (TGA, see Fig. 16) and differential thermal analysis (DTA).
 | ||
| Fig. 16 TGA curves for calcite modified by stearic acid. The data is shown for calcite powder and samples with different degree of coverage given within brackets. CD-0.5 (0.52), CD-1 (1.00), CD-1.5 (1.53), CD-2 (2.16), CD-3 (3.25), CD-4 (4.44). Figure reproduced with permission from Mihajlovic et al., Powder Technol., 2013, 245, 208. Copyright 2013 Elsevier.123 | ||
The weight loss below 200 °C was primarily due to the removal of physisorbed water and weakly bound organic species. The strongly bound stearic acid was found to desorb at higher temperatures in the range of 200–400 °C. DTA curves showed a wide exothermic peak of relatively low intensity at around 120 °C, attributed to physisorbed water and weakly bound stearic acid. There was also a smaller exothermic peak at 220–250 °C and a larger one above 300 °C, indicating combustion of strongly bound stearic acid. Interestingly, the larger peak shifted from 311 °C at low coverage to 342 °C at the highest coverage.123 However, in the case of calcite nanoparticles coated with stearic acid using an emulsion method, the peak shifted in the opposite direction towards lower temperature as coverage increased.10 The reason for this opposite trend is not clear. TGA measurements suggest that the area per molecule for stearic acid in the monolayer on calcite modified with the dry method is approximately 0.28 nm2,67 which suggests that the all-trans chain conformation is not achieved using this method.
Since the aim of the surface modification process is to obtain a non-polar surface dominated by the dispersive component of the surface energy, it is of interest to measure this quantity and some reports can be found. For instance, the dispersive component of the surface energy of ground calcium carbonate modified with stearic acid using a dry method, was reported to be about 35 mJ m−2 based on inverse gas chromatography measurements.117 In an earlier study, the dispersive component to the surface energy at monolayer coverage was reported to be about 23 mJ m−2 based on the spreading pressure of octane, with the polar component of 18 mJ m−2 calculated from the spreading pressure of benzene, giving a total surface energy of about 41 mJ m−2.118 For comparison, the surface energy of a perfect hydrocarbon surface is completely given by the dispersive component and amounts to about 25 mJ m−2.
In the dry method, the added stearic acid must remain in the system, and thus at high loading, more than a monolayer coverage is obtained. However, even when more than a monolayer is formed, the active ratio (eqn (4)) is not reduced. This suggests that the excess stearic acid, not bound to the surface in the chemisorbed monolayer, gets dispersed in the aqueous phase during the floatability experiment. In one study, the active ratio achieved by the dry method was found to be slightly less than that obtained by a wet method using a similar loading of stearic acid.123
4.3. Wet aqueous emulsion process and particle surfaces
The water present in the aqueous emulsion process provides a pathway for the carboxylic acids to dissociate prior to adsorption and also to form self-assembled aggregates, both of which distinguish it from a dry process.The emulsion process involves an alkaline aqueous solution of the fatty acid, prepared by first heating to approximately 80–90 °C and then adding sodium hydroxide with a slight excess compared to the acid. Thus, the acid form is converted to the carboxylate form, and the temperature should be above the Krafft point so micellar-like aggregates can be formed. Once the emulsion has been formed, the calcite particles are added. An example of a laboratory procedure using stearin is provided in some detail by Shi et al.124 They analysed the coated particles with FTIR and noted that only the carboxylate form with an absorption peak at 1575 cm−1 was detected, whereas the peak from the acid form at 1709 cm−1 was not observed, which is consistent with the use of an alkaline medium in the modification process. It was also noted that at high dosages of stearin, more than monolayer coverage was obtained. Therefore, a distinction was made between chemisorbed stearate directly attached to the calcite surface and physically adsorbed calcium stearate, CaSt2, formed as a result of calcium ions being released from calcite to the solution where these ions can react with two stearate molecules. This leads to precipitation of CaSt2 due to its low solubility. A similar distinction was made by Mihajlovic et al. based on DTA curves.123 Consistent with this observation, thermogravimetric analysis confirmed that nearly all the added stearin was found on the particles.124
When in contact with an aqueous solution, the under-coordination of surface calcium atoms leads to the formation of ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Ca-OH surface groups.47 It has been proposed that these groups react with the fatty acid according to:124,125
Ca-OH surface groups.47 It has been proposed that these groups react with the fatty acid according to:124,125
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) CaOH + R–COOH → CaOH + R–COOH → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Ca–OOC–R + H2O Ca–OOC–R + H2O |
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) CaOH + R–COO− → CaOH + R–COO− → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Ca–OOC–R + OH− Ca–OOC–R + OH− |
In conclusion, the most plausible structure of the modification layer, in this case, is an incomplete chemisorbed layer next to the calcite surface, with physisorbed calcium stearate accumulated on top to a degree dictated by the dosage. Therefore, it is important to avoid excessive dosage if monolayer coverage is desired. Another approach is to first modify the particles and then remove some of the coating chemicals by extraction to achieve the optimum adsorption. This method was employed by Li et al., who used Soxhlet extraction with ethanol.10 However, the process took several days, which makes it impractical for large quantities.
4.4. Wet solvent process and particle surfaces
The wet solvent method involves using good solvents for the fatty acids, such as acetone, heptane, or toluene. The intension here is to have the carboxylic acids dissolved as individual molecules, which is different from the aqueous emulsion process. Dissociation of the carboxylic acid group also occurs to much lower extent in low dielectric media than in water.Osman and Suer dissolved stearic acid in toluene and examined its adsorption on calcite under varying concentrations at room temperature.112 Similar to the methods mentioned above, TGA showed peaks assigned to physically adsorbed, intercalated or partial bilayer, and chemisorbed molecules on calcium sites. However, in this case, no calcium stearate was detected.112 The estimated area per molecule in the adsorbed layer was about 0.2 nm2, which closely matched the cross-section area of stearic acid and the area per calcium site.118 The FTIR analysis showed the characteristic methylene and methyl peaks from stearic acid, with peak positions consistent with those observed for crystalline stearic acid. This led to the conclusion that the adsorbed stearic acid molecules predominantly adopted the all-trans alkyl chain conformation, indicating a tight chain packing. In contrast, when using oleic acid and valeric acid as coating agent, the asymmetric methylene vibration peak shifted to higher wavenumbers. This red shift was attributed to a larger number of gauche defects in these layers caused by the presence of a double bond (oleic acid) or a short hydrocarbon chain (valeric acid). The FTIR spectra also detected characteristic bands of bicarbonate groups, and the intensity of these bands increased as a result of surface treatment.112 This suggests that stearic acid dissociates upon adsorption from toluene, with the stearate anion being adsorbed on calcium sites and the released proton associating with surface carbonate sites. It was proposed that the reaction was insensitive to the actual anion residing on the calcite surface and the following surface modification reactions for stearic acid were suggested:
| Ca(OH)HCO3 + C17H35COOH → Ca(HCO3)OOCC17H35 + H2O |
| 2Ca(CO3)2 + 2C17H35COOH → 2Ca(HCO3)OOCC17H35 + 2CO2 + O2 |
The adsorption of stearin from acetone has also been reported, and a Langmuir-like adsorption isotherm was observed.124 The maximum adsorbed amount aligned well with the expected value for a vertically oriented monolayer. Thus, in this case, full monolayer coverage was achieved, and no physisorbed molecules were detected above this monolayer. Unfortunately, no spectroscopic analysis was conducted, so it remains unclear whether the adsorbed layer exclusively consisted of the carboxylate form, the acid form, or a mixture of both.
In some cases ball milling has been utilized with the modification agent dispersed in a good solvent.111
4.5. Vapour deposition and flat surfaces
A convenient method for controlling the surface coverage of fatty acids on calcite is through vapour deposition, as recently described by Wojas et al.79 This technique allows for precise control over the adsorbed amount by adjusting the temperature and deposition time. Previous studies had proposed that at low coverage, stearic acid molecules adsorb parallel to the surface.123 However, as depicted in the AFM images reported by Wojas et al., Fig. 17, the structure of the adsorbed stearic acid layer obtained by vapour deposition is more complex, first forming islands that later merge to a complete monolayer as the coverage increases.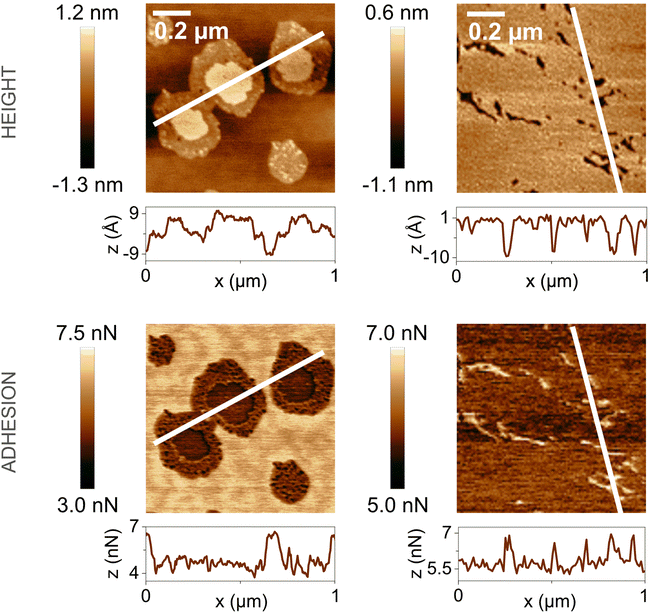 | ||
Fig. 17 AFM images of topography (top) and adhesion (bottom) showing the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface plane after exposure to stearic acid vapour for 20 min at 85 °C (left) and 105 °C (right). Line profiles along the white lines are shown below each image. Figures reproduced from Wojas et al., Langmuir., 2023, 39, 14840.122 4) surface plane after exposure to stearic acid vapour for 20 min at 85 °C (left) and 105 °C (right). Line profiles along the white lines are shown below each image. Figures reproduced from Wojas et al., Langmuir., 2023, 39, 14840.122 | ||
In the AFM images taken after stearic acid vapour exposure for 20 min at 85 °C, the patches of stearic acid are distinguished by larger height and lower tip-sample adhesion than the surrounding calcite surface. It is also clear that the patches consist of an inner region where the molecules are oriented close to vertically to the surface and an outer region with a more parallel orientation. The formation of these patches instead of a uniformly distributed, sparsely packed monolayer is attributed to favourable interactions between the adsorbed molecules. On the other hand, when the calcite surface was exposed to stearic acid vapour for 20 min at 105 °C, a nearly complete monolayer was formed. In this case, the monolayer thickness could not be determined from the AFM measurements. However, once a complete monolayer has formed, the adsorbed amount and the layer thickness can be determined using XPS and the substrate-overlayer model.122 The results from such an analysis are shown in Table 1.
| Exposure time [h] | Layer thickness [nm] | Lower limit | Upper limit | ||
|---|---|---|---|---|---|
| Molecules/area [nm−2] | Area/molecule [nm2] | Molecules/area [nm−2] | Area/molecule [nm2] | ||
| 1 | 2.7 | 5.2 | 0.19 | 6.2 | 0.16 |
| 4 | 2.8 | 4.9 | 0.20 | 5.9 | 0.17 |
| 24 | 2.9 | 5.3 | 0.19 | 6.3 | 0.16 |
In the XPS analysis, a complication arises due to the presence of adventitious carbon adsorbed on the uncoated calcite surface, as discussed in previous sections. To address this issue, calculations were performed for two limiting situations. The lower limit assumes that none of the adventitious carbon is removed during stearic acid adsorption, while the upper limit assumes complete removal of this carbon as stearic acid adsorbs. The true situation is likely somewhere in between. Considering that the area per molecule of a stearic acid chain in all-trans conformation is approximately 0.20 nm2, it appears that a tightly packed monolayer, possibly with a few physisorbed molecules on top, forms during long exposure times to stearic acid vapour.
The binding of the stearic acid molecules to the calcite surface was investigated with vibrational sum frequency spectroscopy, VSFS, an inherently surface-specific technique. VSFS spectra in the CH stretching region taken in the SSP polarization combination (S polarization of sum frequency and visible beam and P polarization of the infrared beam) are shown in Fig. 18, recorded at three different azimuthal angles (Ψ).
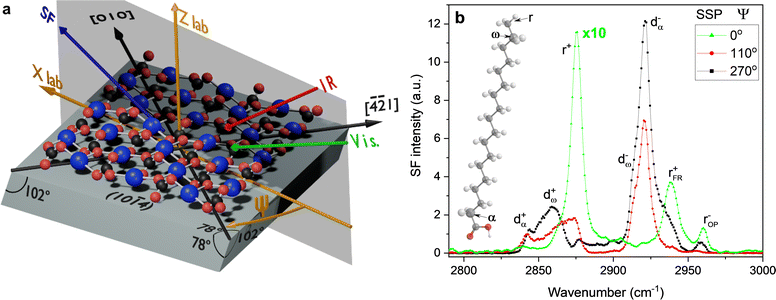 | ||
Fig. 18 (a) Schematic of the experimental geometry and coordinate system relative to the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface. The red and black spheres depict oxygen and carbon atoms from the carbonate group, and the blue spheres represent calcium atoms. The azimuthal angle (Ψ) is defined between the plane of incidence of the laser beams and the [010] direction, which is perpendicular to the [ 4) surface. The red and black spheres depict oxygen and carbon atoms from the carbonate group, and the blue spheres represent calcium atoms. The azimuthal angle (Ψ) is defined between the plane of incidence of the laser beams and the [010] direction, which is perpendicular to the [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1] direction and the optical c axis. The incident IR and visible lasers and emitted sum frequency beam signal are shown in the diagram as red, green, and blue arrows, respectively. Zlab corresponds to the axis of rotation in the laboratory frame. (b) Sum frequency spectra of a stearic acid-modified calcite surface, obtained by 24 h exposure to stearic acid vapour at 105 °C, collected under the SSP polarization combination at selected azimuthal angles. Proposed assignments are included in the figure (see also Appendix 1). The molecular model of stearic acid depicts the α- and ω-CH2 groups in the alkyl chain. The spectrum at Ψ = 0° was multiplied by 10 for ease of comparison. Figures reproduced from Wojas et al., Langmuir., 2023, 39, 14840.122 1] direction and the optical c axis. The incident IR and visible lasers and emitted sum frequency beam signal are shown in the diagram as red, green, and blue arrows, respectively. Zlab corresponds to the axis of rotation in the laboratory frame. (b) Sum frequency spectra of a stearic acid-modified calcite surface, obtained by 24 h exposure to stearic acid vapour at 105 °C, collected under the SSP polarization combination at selected azimuthal angles. Proposed assignments are included in the figure (see also Appendix 1). The molecular model of stearic acid depicts the α- and ω-CH2 groups in the alkyl chain. The spectrum at Ψ = 0° was multiplied by 10 for ease of comparison. Figures reproduced from Wojas et al., Langmuir., 2023, 39, 14840.122 | ||
The spectra presented in Fig. 18 exhibit notable differences depending on the azimuthal angle. This is because the stearic acid monolayer is not isotropic in the plane of the surface. Instead, the fatty acids have a preferential tilt along a certain direction at the 10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4 surface, which is a characteristic feature of epitaxially grown monolayers.126 In the original article,122 plots illustrating the dependence of vibration amplitudes on the azimuthal angle further emphasize the in-plane anisotropy of the monolayer. It is important to note that this angular dependence was observed across all regions of the surface, indicating that the azimuthal order extends throughout. Furthermore, it is worth mentioning that no signal was detected from the methylene groups not adjacent to the methyl or carboxylic acid group, where symmetry is necessarily broken. This finding implies that the alkyl chains adopt an all-trans conformation,127 which is consistent with the high packing density deduced from the XPS data (Table 1).
4 surface, which is a characteristic feature of epitaxially grown monolayers.126 In the original article,122 plots illustrating the dependence of vibration amplitudes on the azimuthal angle further emphasize the in-plane anisotropy of the monolayer. It is important to note that this angular dependence was observed across all regions of the surface, indicating that the azimuthal order extends throughout. Furthermore, it is worth mentioning that no signal was detected from the methylene groups not adjacent to the methyl or carboxylic acid group, where symmetry is necessarily broken. This finding implies that the alkyl chains adopt an all-trans conformation,127 which is consistent with the high packing density deduced from the XPS data (Table 1).
The binding of the stearic acid to the calcite surface was also investigated by employing VSFS, and spectra obtained at different polarization combinations are shown in Fig. 19.
 | ||
| Fig. 19 Sum frequency spectra of a 24 h stearic acid-modified calcite surface in the double-bond/fingerprint region collected under the SSP, PPP, SPS, SSS, and SPP polarization combinations at Ψ = 240°. Proposed assignments and sketches of the carboxylic and carboxylate groups are included in the figure. Figures reproduced from Wojas et al., Langmuir., 2023, 39, 14840.122 | ||
Importantly, vibrational characteristics for both the protonated COOH group and the unprotonated carboxylate, COO−, form of the headgroup were found. Thus, it is clear that the vapour deposition of stearic acid leads to a monolayer composed of a mixture of stearic acid and stearate anions.
4.6. Transformations of adsorbed fatty acid layers in contact with bulk water
The stability of fatty acid monolayers on calcite under different conditions is not only of fundamental interest but also has practical relevance for biomineralization as well as storage, transportation, and use of surface-modified calcite samples. The influence of adsorbed stearic acid on the growth of calcite in supersaturated solutions and the subsequent dissolution of calcite in undersaturated solutions was investigated by Ricci et al. employing the 10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4 surface and AFM.128 They utilised vapour deposition to control the stearic acid content on the surface. The study found that the presence of stearic acid on the surface slowed down the kinetics of the calcite restructuring process. In supersaturated solutions, calcite was observed to grow around and eventually engulf the stearic acid patches, demonstrating how organic material can be incorporated into growing crystals. Interestingly, when the surface was exposed to undersaturated solutions, such engulfed stearic acid patches emerged again as the calcite surface redissolved.
4 surface and AFM.128 They utilised vapour deposition to control the stearic acid content on the surface. The study found that the presence of stearic acid on the surface slowed down the kinetics of the calcite restructuring process. In supersaturated solutions, calcite was observed to grow around and eventually engulf the stearic acid patches, demonstrating how organic material can be incorporated into growing crystals. Interestingly, when the surface was exposed to undersaturated solutions, such engulfed stearic acid patches emerged again as the calcite surface redissolved.
Furthermore, the study revealed that the stearic acid layer itself underwent restructuring. At low coverage in air, the monolayer patches were found to be 1.1–1.4 nm thick and exhibited lower adhesion compared to the surrounding calcite surface, in agreement with the data reported in previous sections.122 However, there is a discrepancy between the deformation images reported by Ricci et al. and those by Wojas et al.122 In the former,128 the calcite surfaces and stearic acid patches were observed to have similar deformations. In contrast, Wojas et al. reported a higher deformation for the stearic acid patches when compared to the surrounding bare calcite. This difference could potentially be attributed to variations in the applied peak forces used in the respective AFM experiments.
When the stearic acid-coated calcite surface was immersed in a supersaturated solution, the stearic acid monolayer patches underwent a transformation into bilayer and multilayer patches. This process is driven by surface energy minimization, where the hydrophobic tails of the stearic acid avoid contact with the aqueous solution. Additionally, a calcite surface that was nearly fully covered with a stearic acid monolayer was also found to rapidly convert to bilayer and multilayer patches upon exposure to supersaturated aqueous solutions.128
4.7. Transformations of adsorbed fatty acid layers below a water droplet
In the previous section we have seen that the stability of fatty acid monolayers on calcite is poor in contact with bulk water. Here we consider the case where a small droplet covers part of the surface. The difference is that that now the water reservoir is small, and this may limit the amount of fatty acid that can dissolve in the aqueous phase.Recently a study considered the fate of octanoic acid and stearic acid layers on calcite 10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4 surfaces when exposed for 30 seconds to small droplets of pure water and aqueous droplets saturated with octanoic acid (i.e. strongly undersaturated solutions with respect to calcium and carbonate ions).129 This scenario is relevant for the storage and transportation of modified calcite in humid conditions. Similar to the findings of Ricci et al.,128 it was found that under the pure water droplet, the initial closely-packed stearic acid monolayer transformed into bilayer and multilayer patches with heights ranging from 4.4 to 6.7 nm.129 Thus, it is clear that surface energy minimization leads to bilayer and multilayer structures in contact with both supersaturated and undersaturated solutions. Octanoic acid is significantly more soluble in water (≈0.8 g kg−1) than stearic acid (≈0.003 g kg−1).129 As a consequence, a considerable amount of octanoic acid dissolved in the droplet and partially redeposited when the droplet was removed. Nevertheless, the restructuring of the calcite surface was found to be slowed down on octanoic acid covered calcite.
4 surfaces when exposed for 30 seconds to small droplets of pure water and aqueous droplets saturated with octanoic acid (i.e. strongly undersaturated solutions with respect to calcium and carbonate ions).129 This scenario is relevant for the storage and transportation of modified calcite in humid conditions. Similar to the findings of Ricci et al.,128 it was found that under the pure water droplet, the initial closely-packed stearic acid monolayer transformed into bilayer and multilayer patches with heights ranging from 4.4 to 6.7 nm.129 Thus, it is clear that surface energy minimization leads to bilayer and multilayer structures in contact with both supersaturated and undersaturated solutions. Octanoic acid is significantly more soluble in water (≈0.8 g kg−1) than stearic acid (≈0.003 g kg−1).129 As a consequence, a considerable amount of octanoic acid dissolved in the droplet and partially redeposited when the droplet was removed. Nevertheless, the restructuring of the calcite surface was found to be slowed down on octanoic acid covered calcite.
Interestingly, no evidence was found for the restructuring into bilayer and multilayer patches of octanoic acid or stearic acid monolayers below droplets of saturated aqueous octanoic acid solutions.129 The reason for this is that octanoic acid readily adsorbs with the hydrophobic tails oriented towards the initial monolayer and the carboxylic acid group exposed to solution. Therefore, there is no driving force for restructuring the initial carboxylic acid monolayer to achieve a low interfacial energy with the aqueous solution, as this is achieved by the adsorption of octanoic acid.
4.8. Transformations of adsorbed fatty acid layers at the modified calcite–water–vapour three-phase line
Another pathway for disruption of an adsorbed fatty acid layer in contact with a water droplet is transport of fatty acids from the calcite surface to the aqueous–air interface. Such a pathway may be particularly important for a long chain fatty acid with low water solubility. Thus, here we consider events occurring close to the calcite–water–air three phase line.Octanoic acid and stearic acid are surface active molecules that readily accumulate at air–water interfaces. Consequently, the calcite–water–air three-phase line is expected to be particularly disruptive for the monolayer. Indeed, this was observed in AFM images of the region close to the three-phase line after the removal of the deposited water droplet, as illustrated in Fig. 20.
 | ||
| Fig. 20 AFM deformation images of the region close to the water droplet edge, imaged in air after removal of the droplet. Left: Octanoic acid-coated calcite, image size 10 × 10 μm2. Right: Stearic acid-coated calcite, image size 40 × 40 μm2. The position of the three-phase line is indicated by the white arrow, and the droplet covered the lower left side of the image. Figures reproduced from Wojas et al., Langmuir., 2021, 37, 14135.129 | ||
In the case of octanoic acid-coated calcite, the region below the droplet exhibited multilayer structures, which displayed a larger deformation than the surrounding area. Close to the three-phase contact line, there was a noticeable accumulation of such structures. Additionally, bare calcite was found in the region next to the three-phase line, demonstrating the complete removal of octanoic acid in such areas. Further, the deformation in the region below the droplet was slightly lower than in the region not exposed to water, suggesting partial desorption of octanoic acid.129
For stearic acid-coated calcite, a similar situation was observed. Large and soft aggregates were present near the three-phase line. Below the droplet, the monolayer transformed into an array of bilayer and multilayer patches, but the limited solubility of the longer chain fatty acid had prevented desorption. However, a wide region of bare calcite with low deformation was found next to the three-phase line. This suggests that stearic acid in this region had been transferred from the calcite surface to the air–water interface of the droplet. These findings have been discussed in terms of water evaporation and pinning of the three-phase contact line, resulting in capillary flow of the carboxylic acids to the contact line.129
4.9. Wettability of carboxylic acid modified calcite surfaces
The changes occurring on the modified calcite surfaces due to exposure to water droplets have a large impact on the wettability. For instance, on octanoic acid-modified calcite, the water contact angle decreased from approximately 110° to 70° during the first 30 seconds after placing the droplet. In contrast, the change for the less soluble stearic acid was only from about 110° to 100°.129 This latter result may seem counterintuitive since the structure of the stearic acid layer beneath the droplet completely transformed during the 30 seconds of the measurements. However, the intact monolayer outside the droplet prevents excessive spreading. Conversely, the hydrophilic region formed on the droplet side of the three-phase line, resulted in a low receding contact angle of about 20° with both carboxylic acids.To gain further insights, it is valuable to compare the evolution of the contact angle and droplet base diameter on stearic acid-modified calcite with that of an intrinsic non-polar surface, like polystyrene, as the droplet evaporates. Data from such experiments lasting for 20 min, are provided in Fig. 21.
 | ||
| Fig. 21 Contact angle (a) and droplet base diameter change (b) on stearic acid-modified calcite and polystyrene. The data becomes scattered when the droplet becomes very small, as seen after about 17 minutes. Figures adopted from Wojas et al., Langmuir., 2021, 37, 14135.129 | ||
For polystyrene, the contact angle (CA) initially decreases as the surface groups reorient, while the base diameter (BD) remains constant. After 5 minutes, the contact angle stabilizes at around 80°, and the base diameter decreases as the droplet recedes due to evaporation. However, the situation is markedly different for stearic acid-modified calcite. The contact angle continuously decreases as the monolayer structure converts into bilayer and multilayer structures, and stearic acid molecules are transported to the air–water interface. Due to the presence of a stearic acid-free region near the three-phase line, the droplet becomes pinned, and the base diameter remains constant until the droplet reduces to a very small size.
Clearly, the hydrophobic character of the calcite surface modified by carboxylic acids is locally compromised when exposed to water droplets.
5. Summary
We have summarized the pioneering studies of calcite surfaces in ultrahigh vacuum. At the surface, the coordination of both calcium and carbonate groups is reduced compared to the bulk crystal, leading to the restructuring of the surface to minimize the free energy. There is, however, no consensus in the literature regarding the extent of the restructuring. In particular, we note that non-contact mode AFM data suggest that the surface unit cell contains four calcium atoms and four carbonate groups rather than two of each as found in the bulk material. The reduced coordination at the surface facilitates adsorption of various compounds on both calcium and carbonate sites. The adsorption strength of different functional groups has been investigated both theoretically and experimentally, revealing that water adsorbs strongly to calcite surfaces but not as strongly as, for example, carboxylic acid groups. While the pure calcite surface should be theoretically fully wetted by water, experimental observations often show otherwise due to the fact that organic materials readily adsorb to calcite surfaces.When exposed to humid air, calcite surfaces undergo changes facilitated by water adsorption, leading to dissolution and redeposition. AFM studies have shown that shallow trenches (about a monolayer deep) and low hillocks (about one nanometre in height) form on the surfaces, with the height of the latter structures varying reversibly with relative humidity, implying that they must contain water. The hillocks are then believed to consist of hydrated forms of calcium carbonate, yet their exact chemical composition and structure remain unclear.
Calcite surfaces undergo dramatic changes in undersaturated and supersaturated solutions. In undersaturated solutions, pits form, and step edges dissolve, whereas in supersaturated solutions, step edges grow, and deposition occurs. The dominant mechanism depends on the degree of undersaturation and supersaturation, respectively. The understanding of the dynamic nature of pure calcite surfaces is considered to be well-developed, and there is a growing body of knowledge on how the adsorption of organic species can modify calcite growth in supersaturated solutions, as it is of paramount importance for biomineralization.
In contrast, we believe the understanding of the dynamic nature of surface-modified calcite is less comprehensive. Surface modification by fatty acid adsorption has been observed to slow down calcite recrystallization. However, when in contact with bulk water and water droplets, fatty acid monolayers rapidly transform into bilayer and multilayer structures. The situation at the water-surface modified calcite–air three-phase line is particularly severe, as even non-soluble fatty acids can be transported to the air–water interface, resulting in the formation of hydrophilic regions near the three-phase line. This leads to a vastly different wetting behaviour compared to intrinsic hydrophobic materials.
In the realm of hydrophobic surface-modified calcite, several questions remain unanswered and warrant further investigation. The impact of organic matter adsorption from air prior to surface modification with fatty acids needs exploration. Does the nature of the adsorbed organic matter affect the efficiency of the fatty acid surface modification? The dynamic response of a fatty acid monolayer on calcite to liquid water is now well established, but questions regarding its response to relative humidity and potential structural changes require elucidation. Is the non-polar layer on the calcite surface unaffected, becomes less ordered, or does it partly or fully convert to similar structures as observed in contact with liquid water? If such changes do occur, what is the time scale of these events? Additionally, developing more robust surface modification chemicals for calcite, surpassing the limitations of fatty acid monolayers in contact with water, may be necessary. Advancements in computing capabilities and experimental techniques provide promising prospects for answering these and many other questions related to the dynamics of calcite surfaces and particularly modified calcite surfaces.
Author contributions
Claesson was the overall responsible and main writer of the manuscript. Tyrode was the main discussion partner during manuscript preparation. All co-authors made considerable contributions through discussions and their insights, including AFM and wetting (Wojas), structural analysis (Corkery), surface forces and solution speciation (Dedinaite), surface modification and industrial applications (Schoelkopf), and vibrational spectroscopy (Tyrode).Conflicts of interest
There are no conflicts of interest to declare.Appendix 1
Peak assignments in the VSFS spectrum shown in Fig. 18 and 19.| Abbreviation | Wavenumber (cm−1) | Assignment |
|---|---|---|
| r + | ≈2873 | Symmetric stretch of terminal methyl group |
| r FM + | ≈2940 | Fermi resonance associated with the symmetric stretch of the terminal methyl group |
| r OP − | ≈2960 | Out of phase antisymmetric stretch of terminal methyl group |
| d ω + | ≈2865 | Symmetric stretch of the methylene group adjacent to the methyl group |
| d α + | ≈2842 | Symmetric stretch of the methylene group adjacent to the carboxylic acid group |
| d − ω | ≈2912 | Antisymmetric stretch of the methylene group adjacent to the methyl group |
| d α − | ≈2921 | Antisymmetric stretch of the methylene group adjacent to the carboxylic acid group |
| δ CH3 + | ≈1380 | Symmetric methyl deformation |
| δ CH3 − | ≈1460 | Antisymmetric methyl deformation |
| δ CH2 | ≈1469 | Methylene deformation |
| δ α-CH2 | ≈1410 | Deformation of the methylene group next to the carboxylic acid group |
v
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O
|
≈1680 | Carbonyl stretch of the COOH group |
v
asym![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) COO− COO−
|
≈1545 and 1590 | Asymmetric carboxylate stretches |
v
sym![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) COO− COO−
|
≈1420 | Symmetric carboxylate stretch |
v
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) calcite calcite
|
≈1432 | Antisymmetric carbonate stretch from the calcite surface |
Acknowledgements
NW, PC and ET acknowledge financial support from Omya International AG. Patrick Gane (Aalto University) is acknowledged for many stimulating and challenging discussions throughout the past years. Your knowledge and ideas have been invaluable and greatly inspiring.References
- J. Geyssant, in Calcium carbonate: from the Cretaceous period into the 21st century, ed. F. W. Tegethoff, Birkhäuser, Basel, 2001, ch. I, pp. 1–52 Search PubMed.
- R. M. Hazen, in Progress in biological chirality, ed. G. Palyi, C. Zucchi and L. Caglioti, Elsevier, Oxford, 2004, ch. 11, pp. 137–151 Search PubMed.
- J. Gomez-Morales, G. Falini and J. M. Garcia-Ruiz, Crystals, 2019, 9, 409 CrossRef CAS.
- G. Falini, S. Fermani and S. Goffredo, Semin. Cell Dev. Biol., 2015, 46, 17–26 CrossRef PubMed.
- J. Aizenberg, A. Tkachenko, S. Weiner, L. Addadi and G. Hendler, Nature, 2001, 412, 819–822 CrossRef CAS PubMed.
- S. L. S. Stipp, Mol. Simul., 2002, 28, 497–516 CrossRef CAS.
- C. Roslund and C. Beckman, Appl. Opt., 1994, 33, 4754–4755 CrossRef CAS PubMed.
- E. Huwald, in Calcium carbonate: from the Cretaceous period into the 21st century, ed. F. W. Tegethoff, Birkhäuser, Basel, 2001 Search PubMed.
- N. Erdogan and H. A. Eken, Physicochem. Probl. Miner. Process., 2017, 53, 57–68 CAS.
- Y. Li, Z.-F. Zhao, Y.-T. R. Lau, Y. Lin and C.-M. Chan, J. Colloid Interface Sci., 2010, 345, 168–173 CrossRef CAS PubMed.
- S. Mihajlovic, Z. Sekulic, A. Dakovic, D. Vucinik, V. Jovanovic and J. Stojanovic, Ceram.-Silik., 2009, 53, 268–275 CAS.
- N. Matijakovic, G. Magnabosco, F. Scarpino, S. Fermani, G. Falini and D. Kralj, Crystals, 2019, 9, 16 CrossRef.
- K. S. Lee, J. H. Jung, S. I. Keel, J. H. Yun, J. H. Min and S. S. Kim, Sci. Total Environ., 2012, 429, 266–271 CrossRef CAS PubMed.
- J.-H. Huh, Y.-H. Choi, H.-J. Lee, W. J. Choi, C. Ramakrishna, H.-W. Lee, S.-H. Lee and J.-W. Ahn, J. Korean Ceram. Soc., 2016, 53, 1–6 CrossRef CAS.
- P. A. C. Gane, K. Dimic-Misic, N. Barac, M. Imani, D. Janackovic, P. Uskokovic and E. Barcelo, Appl. Sci., 2020, 10, 3927 CrossRef CAS.
- W.-S. Ng, M.-L. Lee and S.-L. Hii, World Acad. Sci. Eng. Technol., 2012, 6, 188–194 Search PubMed.
- S. S. Hakim, M. H. M. Olsson, H. O. Sørensen, N. Bovet, J. Bohr, R. Feidenhans’l and S. L. S. Stipp, Sci. Rep., 2017, 7, 7592 CrossRef CAS PubMed.
- S. L. S. Stipp, W. Gutmannsbauer and T. Lehmann, Am. Mineral., 1996, 81, 1–8 CAS.
- W. Sekkal and A. Zaoui, Sci. Rep., 2013, 3, 1587 CrossRef CAS PubMed.
- N. A. Wojas, A. Swerin, V. Wallqvist, M. Järn, J. Schoelkopf, P. A. C. Gane and P. M. Claesson, J. Colloid Interface Sci., 2019, 541, 42–55 CrossRef CAS PubMed.
- G. Wypych, Handbook of fillers, ChemTec Publishing, Toronto, 4th edn, 2016 Search PubMed.
- N. K. Dhami, M. S. Reddy and A. Mukherjee, Front. Microbiol., 2013, 4, 314 Search PubMed.
- P. U. P. A. Gilbert, K. D. Bergmann, N. Boekelheide, S. Tambutté, T. Mass, F. Marin, J. F. Adkins, J. Erez, B. Gilbert, V. Knutson, M. Cantine, J. O. Hernandez and A. H. Knoll, Sci. Adv., 2022, 8, eabl9653 CrossRef CAS PubMed.
- V. Achal, A. Mukherjee, D. Kumari and Q. Zhang, Earth Sci. Rev., 2015, 148, 959–970 CrossRef.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- H. Liu, H. Jiang, X. Liu and X. Wang, Exploration, 2023, 20230033 CrossRef.
- B. Khurshid, E. Lesniewska, L. Polacchi, M. L’Héronde, D. J. Jackson, S. Motreuil, J. Thomas, J.-F. Bardeau, S. E. Wolf, D. Vielzeuf, J. Perrin and F. Marin, Acta Biomater., 2023, 168, 198–209 CrossRef CAS PubMed.
- Y.-Q. Niu, J.-H. Liu, C. Aymonier, S. Fermani, D. Kralj, G. Falini and C.-H. Zhou, Chem. Soc. Rev., 2022, 51, 7883–7943 RSC.
- R. Belkofsi, O. Adjaoud and I. Belabbas, Modell. Simul. Mater. Sci. Eng., 2018, 26, 065004 CrossRef.
- D. Vo Thanh and A. Lacam, Phys. Earth Planet. Inter., 1984, 34, 195–203 CrossRef.
- M. Merlini, M. Hanfland and W. A. Crichton, Earth Planet. Sci. Lett., 2012, 333–334, 065004 Search PubMed.
- J. R. Clarkson, T. J. Price and C. J. Adams, J. Chem. Soc., Faraday Trans., 1992, 88, 243–249 RSC.
- B. Dickens and W. E. Brown, Inorg. Chem., 1970, 480–486 CrossRef CAS.
- I. P. Swainson, Am. Mineral., 2008, 93, 1014–1018 CrossRef CAS.
- Z. Zou, W. J. E. M. Habraken, G. Matveeva, A. C. S. Jensen, L. Bertinetti, M. A. Hood, C.-Y. Sun, P. U. P. A. Gilbert, I. Polishchuk, B. E. A. Pokroy, J. Mahamid, Y. Politi, S. Weiner, P. Werner, S. Bette, R. Dinnebier, U. Kolb, E. Zolotoyabko and P. Fratzl, Science, 2019, 363, 396–400 CrossRef CAS PubMed.
- C. Luo, X. Yang and J. Li, Mater. Today, 2022, 15, 4613 CAS.
- Z. Kabcinska, L. Yate, M. Wencka, R. Krzyminiewski, K. Tadyszak and E. Coy, J. Phys. Chem. C, 2017, 121, 13357–13369 CrossRef.
- C. Rodriguez-Navarro, E. Ruiz-Agudo, A. Luque, A. B. Rodriguez-Navarro and M. Ortega-Huertas, Am. Mineral., 2009, 94, 578–593 CrossRef CAS.
- E. N. Maslen, V. A. Streltsov and N. R. Streltsova, Acta Cryst., 1993, B49, 636–641 CAS.
- B. Kvamme, T. Kuznetsova and D. Uppstad, J. Mater. Chem., 2009, 46, 756–762 CAS.
- S. Kerisit, S. C. Parker and J. H. Harding, J. Phys. Chem. B, 2003, 107, 7676–7682 CrossRef CAS.
- N. H. de Leeuw and S. C. Parker, J. Phys. Chem. B, 1998, 102, 2914–2922 CrossRef CAS.
- T. M. Hafshejani, W. Wang, J. Heggermann, A. Nefedov, S. Heissler, Y. Wang, P. Rahe, P. Thissen and C. Wöll, Phys. Chem. Chem. Phys., 2021, 23, 7696–7702 RSC.
- J. Schütte, P. Rahe, L. Tröger, S. Rode, R. Bechstein, M. Reichling and A. Kühnle, Langmuir, 2010, 26, 8295–8300 CrossRef PubMed.
- S. L. Stipp and M. F. Hochella Jr., Geochim. Cosmochim. Acta, 1991, 55, 1723–1736 CrossRef CAS.
- S. L. S. Stipp, Geochim. Cosmochim. Acta, 1999, 63, 3121–3131 CrossRef CAS.
- F. Heberling, T. P. Trainor, J. Lützenkirchen, P. Eng, M. A. Denecke and D. Bosbach, J. Colloid Interface Sci., 2011, 354, 843–857 CrossRef CAS PubMed.
- M. T. Dove, B. Winkler, M. Leslie, M. J. Harris and E. K. H. Salje, Am. Mineral., 1992, 77, 244–250 CAS.
- A. Rahaman, V. H. Grassian and C. J. Margulis, J. Phys. Chem. C, 2008, 112, 2109–2115 CrossRef CAS.
- A. Pavese, M. Catti, S. C. Parker and A. Wall, Phys. Chem. Miner., 1996, 23, 89–93 CrossRef CAS.
- K. Wright, R. T. Cygan and B. Slater, Phys. Chem. Chem. Phys., 2001, 3, 839–944 RSC.
- M. Bruno, F. R. Massaro, L. Pastero, E. Costa, M. Rubbo, M. Prencipe and D. Aquilano, Cryst. Growth Design, 2013, 13, 1170–1179 CrossRef CAS.
- A. Røyne, J. Bisschop and D. K. Dysthe, J. Geophys. Res., 2011, 116, B044204 CrossRef.
- J. J. Gilman, J. Appl. Phys., 1960, 31, 2208–2218 CrossRef CAS.
- A. T. Santhanam and Y. P. Gupta, Int. J. Rock Mech. Min. Sci., 1968, 5, 253–259 CrossRef.
- S. Hwang, M. Blanco and W. A. Goddard III, J. Phys. Chem. B, 2001, 105, 10746–10753 CrossRef CAS.
- M. Donnet, P. Bowen and J. Lemaitre, J. Colloid Interface Sci., 2009, 340, 218–224 CrossRef CAS PubMed.
- P. B. Kowalczuk, C. Akkaya, M. Ergun, M. J. Janicki, O. Sahbaz and J. Drzymala, Physiochem. Probl. Miner. Process., 2017, 53, 192–201 CAS.
- E. Ataman, M. P. Andersson, M. Ceccato, N. Bovet and S. L. S. Stipp, J. Phys. Chem. C, 2016, 120, 16586–16596 CrossRef CAS.
- D. V. Okhrimenko, J. Nissenbaum, M. P. Andersson, M. H. M. Olsson and S. L. S. Stipp, Langmuir, 2013, 29, 11062–11073 CrossRef CAS PubMed.
- D. J. Cooke, R. J. Gray, K. K. Sand, S. L. S. Stipp and J. A. Elliott, Langmuir, 2010, 26, 14520–14529 CrossRef CAS PubMed.
- E. Ataman, M. P. Andersson, M. Ceccato, N. Bovet and S. L. S. Stipp, J. Phys. Chem. C, 2016, 120, 16597–16607 CrossRef CAS.
- N. H. de Leeuw and T. G. Cooper, Cryst. Growth Design, 2004, 4, 123–133 CrossRef CAS.
- L. Tao, Z. Li, G.-C. Wang, B.-Y. Cui, X.-T. Yin and Q. Wang, Mater. Res. Express, 2019, 6, 025035 CrossRef.
- I. S. Pasarın, M. Yang, N. Bovet, M. Glyvradal, M. M. Nielsen, J. Bohr, R. Feidenhans’l and S. L. S. Stipp, Langmuir, 2012, 28, 2545–2550 CrossRef PubMed.
- R. J. Gustafsson, A. Orlov, C. L. Badger, P. T. Griffiths, R. A. Cox and R. M. Lambert, Atmos. Chem. Phys., 2005, 5, 3415–3421 CrossRef CAS.
- K. A. Rezaei Gomari, R. Denoyel and A. A. Hamouda, J. Colloid Interface Sci., 2006, 297, 470–479 CrossRef CAS PubMed.
- T. Z. Forbes, A. V. Radha and A. Navrotsky, Geochim. Cosmochim. Acta, 2011, 75, 7893–7905 CrossRef CAS.
- R. P. Chiarello, R. A. Wogelius and N. C. Sturchio, Geochim. Cosmochim. Acta, 1993, 57, 4103–4110 CrossRef CAS.
- J. Bohr, R. A. Wogelius, P. M. Morris and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 5985–5999 CrossRef CAS.
- W. Neagle and C. H. Rochester, J. Chem. Soc., Faraday Trans., 1990, 86, 181–183 RSC.
- S. I. Kuriyavar, R. Vetrivel, S. G. Hedge, A. V. Ramaswamy, D. Chakrabarty and S. Mahapatra, J. Mater. Chem., 2000, 10, 1835–1840 RSC.
- J. S. Lardge, D. M. Duffy, M. J. Gillan and M. Watkins, J. Phys. Chem. C, 2010, 114, 2664–2668 CrossRef CAS.
- C. Na, T. A. Kendall and S. T. Martin, Environ. Sci. Technol., 2007, 41, 6491–6497 CrossRef CAS PubMed.
- T. A. Kendall and S. T. Martin, J. Phys. Chem. A, 2007, 111, 505–514 CrossRef CAS PubMed.
- D. B. Hausner, R. J. Reeder and D. R. Strongin, J. Colloid Interface Sci., 2007, 305, 101–110 CrossRef CAS PubMed.
- J. Baltrusaitis and V. H. Grassian, Surf. Sci., 2009, 603, L99–L104 CrossRef CAS.
- C. Parlangeau, A. Dimanov, O. Lacombe, S. Hallais and J.-M. Daniel, Solid Earth, 2019, 10, 307–316 CrossRef.
- N. A. Wojas, I. Dobryden, V. Wallqvist, A. Swerin, M. Järn, J. Schoelkopf, P. A. C. Gane and P. M. Claesson, Langmuir, 2021, 37, 9826–9837 CrossRef CAS PubMed.
- L. N. Plummer and E. Busenberg, Geochim. Cosmochim. Acta, 1982, 46, 1011–1040 CrossRef CAS.
- B. Coto, C. Martos, J. L. Pena, R. Rodriguez and G. Pastor, Fluid Phase Equilib., 2012, 324, 1–7 CrossRef CAS.
- J. B. Fein and J. V. Walther, Geochim. Cosmochim. Acta, 1987, 51, 1665–1673 CrossRef CAS.
- A. V. Radha, T. Z. Forbes, C. E. Killian, P. U. P. A. Gilbert and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16438–16443 CrossRef CAS PubMed.
- M. Kellermeier, P. Raiteri, J. K. Berg, A. Kempter, J. D. Gale and D. Gebauer, ChemPhysChem, 2016, 17, 3535–3541 CrossRef CAS PubMed.
- B. Fu, Y. Diao and R. M. Espinosa-Marzal, J. Colloid Interface Sci., 2021, 601, 254–264 CrossRef CAS PubMed.
- E. R. Segnit, H. D. Holland and C. J. Biscardi, Geochim. Cosmochim. Acta, 1962, 26, 1301–1331 CrossRef CAS.
- S. Kerisit and S. C. Parker, J. Am. Chem. Soc., 2004, 126, 10152–10161 CrossRef CAS PubMed.
- S. J. T. Brugman, P. Raiteri, P. Accordini, F. Megens, J. D. Gale and E. Vlieg, J. Phys. Chem. C, 2020, 124, 18564–18575 CrossRef CAS.
- H. Söngen, S. J. Schlegel, Y. M. Jaques, J. Tracey, S. Hosseinpour, D. Hwang, R. Bechstein, M. Bonn, A. S. Foster, A. Kühnle and E. H. G. Backus, J. Phys. Chem. Lett., 2021, 12, 7605–7611 CrossRef PubMed.
- D. Al Mahrouqi, J. Vinogradov and M. D. Jackson, Adv. Colloid Interface Sci., 2017, 240, 60–76 CrossRef CAS PubMed.
- P. J. M. Smeets, K. R. Cho, R. G. E. Kempen, N. A. J. M. Sommerdijk and J. J. De Yoreo, Nat. Mater., 2015, 14, 394–399 CrossRef CAS PubMed.
- C.-L. Chen, J. Qi, R. N. Zuckermann and J. J. DeYoreo, J. Am. Chem. Soc., 2011, 133, 5214–5217 CrossRef CAS PubMed.
- N. A. J. M. Sommerdijk and G. de With, Chem. Rev., 2008, 108, 4499–4550 CrossRef CAS PubMed.
- E. Ruiz-Agudo and C. V. Putnis, Mineral. Mag., 2012, 76, 227–253 CrossRef CAS.
- R. S. Arvidson, I. E. Ertan, J. E. Amonette and A. Luttge, Geochim. Cosmochim. Acta, 2003, 67, 1623–1634 CrossRef CAS.
- R. Shiraki, P. A. Rock and W. H. Casey, Aquat. Geochem., 2000, 6, 87–108 CrossRef CAS.
- Y. Liang, D. R. Baer, J. M. McCoy and J. P. LaFemina, J. Vac. Sci. Technol., 1996, A14, 1368–1375 CrossRef.
- Y. Liang, D. R. Baer, J. M. McCoy, J. E. Amonette and J. P. LaFemina, Geochim. Cosmochim. Acta, 1996, 60, 4883–4887 CrossRef CAS.
- M. Xu, X. Hu, K. G. Knauss and S. R. Higgins, Geochim. Cosmochim. Acta, 2010, 74, 4285–4297 CrossRef CAS.
- H. H. Teng, Geochim. Cosmochim. Acta, 2004, 68, 253–262 CrossRef CAS.
- H. H. Teng, P. M. Dove and J. J. De Yoreo, Geochim. Cosmochim. Acta, 2000, 64, 2255–2266 CrossRef CAS.
- C. Perdikouri, C. V. Putnis, A. Kasioptas and A. Putnis, Cryst. Growth Design, 2009, 9, 4344–4350 CrossRef CAS.
- A. Røyne, K. N. Dalby and T. Hassenkam, Geophys. Res. Lett., 2015, 42, 4786–4794 CrossRef.
- Y. Diao and R. M. Espinosa-Marzal, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12047–12052 CrossRef CAS PubMed.
- S. Javadi and A. Røyne, J. Colloid Interface Sci., 2018, 532, 605–613 CrossRef CAS PubMed.
- Y. Diao and R. M. Espinosa-Marzal, J. Geophys. Res. Solid Earth, 2019, 124, 5607–5628 CrossRef CAS.
- Y. Diao and R. M. Espinosa-Marzal, Nat. Commun., 2018, 9, 2309 CrossRef PubMed.
- J. Dziadkowiec, S. Javadi, J. E. Bratvold, O. Nilsen and A. Røyne, Langmuir, 2018, 34, 7248–7263 CrossRef CAS PubMed.
- Y. J. Diao, A. Q. Li and R. M. Espinosa-Marzal, Geochim. Cosmochim. Acta, 2020, 280, 116–129 CrossRef CAS.
- I. Özen and S. Süleyman, Powder Technol., 2015, 270, 320–328 CrossRef.
- Deepika, S. K. Hait, J. Christopher, P. Hodgson and D. K. Tuli, Powder Technol., 2013, 235, 581–589 CrossRef CAS.
- M. A. Osman and U. W. Suter, Chem. Mater., 2002, 14, 4408–4415 CrossRef CAS.
- J. R. Kanicky, A. F. Poniatowski, N. R. Mehta and D. O. Shah, Langmuir, 2000, 16, 172–177 CrossRef CAS.
- A. Sthoer and E. Tyrode, J. Phys. Chem. C, 2019, 123, 23037–23048 CrossRef CAS.
- R. A. Vaia and H. D. Wagner, Mater. Today, 2004, 7, 32–37 CrossRef CAS.
- Z. Cao, M. Daly, L. Clémence, L. M. Geever, I. Major, C. L. Higginbotham and D. M. Devine, Appl. Surf. Sci., 2016, 378, 320–329 CrossRef CAS.
- S.-B. Jeong, Y.-C. Yang, Y.-B. Chae and B.-G. Kim, Mater. Trans., 2009, 50, 409–414 CrossRef CAS.
- E. Fekete, B. Pukanszky, A. Toth and I. Bertoti, J. Colloid Interface Sci., 1990, 135, 200–208 CrossRef CAS.
- M. Ucurum, O. Bayram, O. Y. Toraman, H. Kilic and S. Yalcin, Physicochem. Probl. Miner. Process., 2018, 54, 688–700 CAS.
- I. Acar and O. Acisli, Appl. Surf. Sci., 2018, 457, 208–213 CrossRef CAS.
- Y. Sheng, B. Zhou, C. Wang, X. Zhao, Y. Deng and Z. Wang, Appl. Surf. Sci., 2006, 253, 1983–1987 CrossRef CAS.
- N. A. Wojas, E. Tyrode, R. Corkery, M. Ernstsson, V. Wallqvist, M. Järn, A. Swerin, J. Schoelkopf, P. A. C. Gane and P. M. Claesson, Langmuir, 2023, 39, 14840–14852 CrossRef CAS PubMed.
- S. R. Mihajlovic, D. R. Vucinic, Z. T. Sekulic, S. Z. Milicevic and B. M. Kolonja, Powder Technol., 2013, 245, 208–216 CrossRef CAS.
- X. Shi, R. Rosa and A. Lazzeri, Langmuir, 2010, 26, 8474–8482 CrossRef CAS PubMed.
- P. Fenter and N. C. Sturchio, Geochim. Cosmochim. Acta, 1999, 63, 3145–3152 CrossRef CAS.
- D. A. Beattie, R. Fraenkel, S. A. Winget, A. Petersen and C. D. Bain, J. Phys. Chem. B, 2006, 110, 2278–2292 CrossRef CAS PubMed.
- P. Guyot-Sionnest, J. H. Hunt and Y. R. Shen, Phys. Rev. Lett., 1987, 59, 1597–1600 CrossRef CAS PubMed.
- M. Ricci, J. J. Segura, B. W. Erickson, G. Fantner, F. Stellacci and K. Voitchovsky, Langmuir, 2015, 31, 7563–7571 CrossRef CAS PubMed.
- N. A. Wojas, A. Swerin, V. Wallqvist, M. Järn, J. Schoelkopf, P. A. C. Gane and P. M. Claesson, Langmuir, 2021, 37, 14135–14146 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |