Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unravelling the electrochemical impedance spectroscopy of silicon half cells with commercial loading†
Frederik T.
Huld
 *ab,
Zhixin
Yu
*ab,
Zhixin
Yu
 *a and
Fengliu
Lou
*b
*a and
Fengliu
Lou
*b
aDepartment of Energy and Petroleum Engineering, University of Stavanger, Kjølv Egelands hus, Kristine Bonnevies vei, 4021, Stavanger, Norway. E-mail: frederik.huld@uis.no; zhixin.yu@uis.no
bBeyonder, Stokkamyrveien 30, N-4313, Sandnes, Norway. E-mail: frederik@beyonder.no; fengliu@beyonder.no
First published on 23rd June 2023
Abstract
Silicon (Si) is an important anode material for lithium ion batteries (LIBs), and increasing the loading of Si electrodes is an important step towards commercialization. However, half cells commonly used for Si studies are limited by polarization of the lithium (Li) counter electrode, especially at high Si loading. To study the interplay between Si and Li electrodes, a set of electrochemical impedance spectroscopy (EIS) spectra are generated using cycled Si half cells at four different potentials in the charge–discharge profile, and then repeated using symmetric Si/Si and Li/Li cells assembled from half cells cycled to equivalent stages in the cycle. Distribution of relaxation times (DRT) analysis is used to design equivalent circuits (ECs) for both Si/Si and Li/Li symmetric cells incorporating both electrolyte and electrode-related diffusion, and these are applied to the half cells. The results demonstrate that the behaviour of half cells is dominated by the solid electrolyte interphase (SEI) impedances at the Li counter electrode at the low and high potentials where the Li+ mobility signal in Si is limited, while the Si electrode is dominant at intermediate potentials where the signal from mobile Li+ is strong. EIS studies of Si half cells should therefore be performed at intermediate potentials, or as symmetric cells.
1 Introduction
Silicon (Si) is widely touted as the future of lithium (Li) ion storage materials due to its large theoretical capacity of 3579 mA h g−1.1 However, issues of stability have limited its use in commercial lithium-ion batteries (LiBs).2,3 These issues arise in large part due to the extreme swelling (300%) experienced by the material during charging which causes rapid solid electrolyte interphase (SEI) growth.4 This in turn quickly uses up cyclable lithium and electrolyte, leading to cell failure after only a few cycles.2,3,5,6 Understanding and mitigating these failure mechanisms has resulted in a large amount of research in recent years, with published strategies ranging from coatings on nanomaterials, to nanostructuring, to use of dopants and heteroatoms.5,7–11 However, in order to achieve good performance Si electrodes in the literature often contain very low loading.12 This makes it difficult to assess the suitability of these materials for commercial applications where the loading requirements are much higher. Higher loading of Si in the electrode exacerbate the issues of swelling and poor conductivity. As a result testing of these materials at high loading is a relatively unexplored area of research.12–14 A further issue affecting high loading Si electrodes is the almost ubiquitous use of Li counter electrodes (CE). Li is highly polarizable and forms dendrites above 1 mA cm−2, which makes it difficult to produce reliable data.15,16 Despite these disadvantages the use of Si/Li half cells in the literature is unlikely to cease, and it is therefore important to understand the interplay of the electrodes in these systems.An established and sensitive method for studying the electrochemistry of Si is electrochemical impedance spectroscopy (EIS).17 Unfortunately, this sensitivity means that distinguishing between features and noise is very difficult, and the design of the cell and the experiment surroundings is very important. For instance, performing EIS directly on half cells will result in the generated spectrum containing information from both the working and counter electrodes (WE and CE, respectively), as well as the electrolyte and separator located in between them. This can be avoided by introducing a reference electrode (RE) into the cell in proximity with the WE, but this increases the construction complexity and cost, and requires consideration of the RE electrode chemistry.15 The use of symmetric cells (where both the WE and CE are identical) is also an option, but these cells cannot be cycled, and can therefore not easily be used for cycling studies. Therefore, in much of the high loading Si literature EIS is used as a complementary technique in full-cell or half-cell (vs. Li/Li+) setup to show e.g. the increase in resistance of a cell before and after cycling.13,14 Equivalent circuits (ECs) have been designed to describe the behaviour of Si electrodes at low loading.18–20 These ECs vary considerably in the literature, but more recent work has shown that the inclusion of a finite-length Warburg diffusion element (Wo) is useful for describing the diffusion behaviour of Li+ ions within the Si material.18,21 A similar diffusion element, the finite-space Warburg (Ws) has also been shown to be useful for describing Li+ diffusion through thin films such as SEI layers formed on the Li CE.21 Recently, the use of distribution of relaxation times (DRT) analysis has also been employed to deconvolve the data generated by impedance experiments.18,22,23 This technique gives information on the number of processes occurring in the data, and is a useful technique for designing ECs. A peak in the DRT spectrum corresponds to a polarization process and the position (in Hz), size (in Ω cm2), and shape gives information on the electrochemistry of the process.18,22–24
Si has very different behaviour during charging and discharging, and EIS offers the possibility of helping to understand these differences.18 Amorphous Si cycled in the region 0.05 to 1.5 V vs. Li/Li+ displays two electrochemical phases. During lithiation, Li reacts with Si to form Li2Si at around 0.25 V. As the potential is decreased to about 0.07 V Li2Si reacts to form Li3.5Si. Delithiation reverses this reaction, with Li3.5Si forming Li2Si at about 0.28 V, and the resulting Li2Si forming pure Si at about 0.48 V and higher.25–27 The ECs of Si half cells at these potentials are not necessarily all the same, especially when considering the effect of the Li CE.
In this work, we will construct and test a commercially available Si material in electrodes with high loading in both half-cell and symmetric configuration to investigate the changes to the EIS spectrum at different potentials. This comparison will be used to differentiate between effects occurring due to the Si WE and those due to the Li CE in half cells. The EIS spectra will be collected at the potentials at which each phase is at equilibrium using a constant-current constant-voltage (CCCV) step to ensure that the phase is allowed to run to completion and the electrode consists mainly of the product of the desired phase. The symmetric cells will be assembled from half cells which have been cycled to each of these points in the cycle. DRT analysis will be used to inform the design of the ECs used in this work, and these will be used to elucidate the behaviour of the high loading Si electrodes in half cells.
2 Experimental
2.1 Electrode preparation
Si electrode slurries were prepared in an overhead stirrer (Dispermat LC30). The slurry consisted of 5% carboxymethylcellulose (CMC, Walcocel 10000), 2% KOH/citric acid buffer (pH 3), 0.5% carbon nanotubes (CNT, Lanxi Zhide), 9.5% carbon black (C65, Imerys), 80% Si powder (SCC55, Group 14), and 3% SBR (BM-451B, Zeon). The slurry was made by sequential addition of powders and stirring in a ball mill at 2500 rpm for 15 minutes, followed by a stirring step of 2 h at 2500 rpm. The final addition consisted of SBR, which was mixed slowly at 700 rpm for 15 minutes. Electrodes containing higher concentrations of Si material were found to be too brittle after cycling to be disassembled and reassembled. Carbon black was found to increase the stability of the electrode while having a negligible effect on the electrochemistry.The slurry was coated onto 10 μm copper foil using a doctor blade with a blade height of 130 μm and dried at room temperature overnight. This resulted in an electrode loading of 3.38 mg cm−2 and a thickness of 59.6 μmm. The electrolyte uptake and porosity were 89% and 35.6%, respectively. Details of these experiments may be found in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 The reversible gravimetric capacity of the Si material in the 0.05–1 V range was 1290 mA h g−1 at a current density of 0.179 mA cm−2, yielding an area capacity of 3.49 mA h cm−2 for these electrodes. 15 mm diameter electrodes were cut from the electrode sheet for coin cell assembly.
28 The reversible gravimetric capacity of the Si material in the 0.05–1 V range was 1290 mA h g−1 at a current density of 0.179 mA cm−2, yielding an area capacity of 3.49 mA h cm−2 for these electrodes. 15 mm diameter electrodes were cut from the electrode sheet for coin cell assembly.
2.2 Coin cell assembly, disassembly, and reassembly
All assembly, disassembly and reassembly was performed in an Argon-filled glove box. CR2032 coin cells (stainless steel, MTI) were assembled by placing the Si electrode (15 mm dia.) in the cap (the o-ring and the cap are glued together in MTI's coin cell parts), followed by electrolyte (25 μl, TC-E8593, TINCI) to wet the electrode surface. This was then covered with two layers of paper separator (19 mm dia., Tf4030), followed by a further 25 μl of electrolyte. Next, the Li electrode (16 mm dia, 750 μm thick, Sigma Aldrich) was placed on top of the separator followed by the spacer (0.5 mm), the spring, and finally the base.Disassembly was performed using a decrimping machine (Hohsen), taking care not to short-circuit or damage the electrodes.
Reassembly was performed in almost the same manner as for half-cells, using fresh coin cell parts, separator, and electrolyte. For Si/Si symmetric cells the 0.5 mm spacer was replaced with a 1 mm spacer to account for the thickness of the Si electrodes.
2.3 Cycling and EIS procedures
Once assembled, coin cells were placed on the cycling machine (BTS 4000, Neware) and discharged to 1.5 V before being resting for 12 h. Following this rest the cells were cycled once at 1/20C (0.179 mA cm−2) and twice at 1/10C (0.358 mA cm−2) for a total of three cycles. The voltage limits were 0.05–1.5 V.The EIS cycling procedure was started immediately at the end of the formation, and is given in Table 1. The C-rate for each step in Table 1 was 1/10C. EIS experiments were performed at the end of each CCCV step. A plot of this procedure can be seen in Fig. S1 in the ESI.†
| Step type | Stop potential (V) | Step time (h) |
|---|---|---|
| CCCV | 0.2 | 20 |
| CCCV | 0.07 | 20 |
| CC | 0.05 | — |
| Rest | — | 0.3 |
| CCCV | 0.3 | 20 |
| CCCV | 0.48 | 20 |
| CC | 1.5 | — |
EIS spectra were collected on an Autolab potentiostat (Metrohm) connected using two-electrode setup to a coin cell holder from Neware. Spectra were collected using Nova 2.13 software at the open circuit voltage (OCV) using an amplitude of 5 mV in the frequency (f) range of 10−2 to 105 Hz, at 15 points per decade. EIS spectra for symmetric cells were collected after resting for 24 h.
DRT analysis was performed in Python using the Gaussian Process (GP) GP-DRT method described by Liu and Ciucci (2019).22 This models the DRT based on the assumption that the peaks in the DRT spectrum are normal distributions. Fitting was performed using the impedance.py package in Python.29
3 Results and discussion
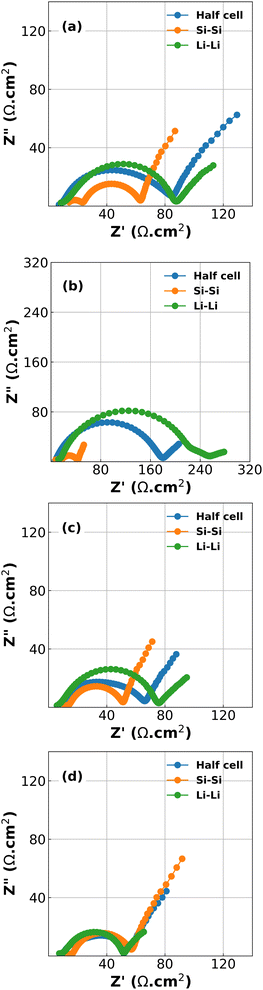
Inspection of the formation cycles are shown in Fig. S2 in the ESI.† These reveal an initial Coulombic efficiency (ICE) of 86%. The subsequent cycles at 1/10C had CEs of 98.6% and 99.7% indicating a relatively stable electrode suitable for short experiments. However, it should be noted that there was a significant capacity drop between each delithiation cycle and the subsequent lithiation (87.3% and 90.1% between cycles 1 to 2 and 2 to 3, respectively), indicating that a large polarization process exists during lithiation.Results of the EIS spectra for half-cells, Si/Si symmetric cells and Li/Li symmetric cells at each of the 4 stop potentials are given in Fig. 1. In all cases the Kronig–Kramers relations showed that the data was acceptable quality, with the residuals of the Kronig–Kramers and data not exceeding 1%.23,30 As expected, the spectra show that there is a large difference in EIS response both as a function of potential, and also between half cells and symmetric cells.18 While one might expect that the EIS spectra of the half cells should be equal to half the sum of the Si/Si and Li/Li symmetric cells there is a non-linear relationship between the components of the cell and the EIS spectrum, especially as a function of voltage.31 This is shown in Fig. S3 in the ESI.†
The plots in Fig. 1 reveal two challenges: the first is that large changes are happening at the Li CE (green lines) as a function of voltage, an electrode which is often considered to behave in a constant manner. The second is that deconvolution of the half cell impedance from that of the individual electrodes is not straightforward.
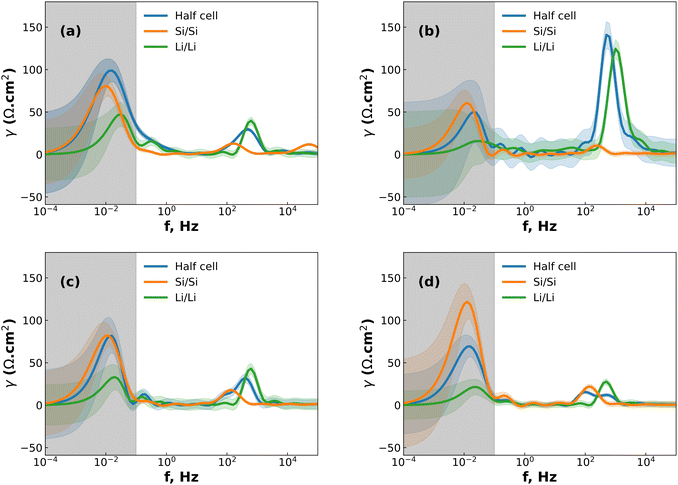
While DRT can give information about the polarization processes that appear in the impedance spectrum, the analysis is limited by the necessity that the data is complete (i.e. that the impedance is real as f = 2πω → 0).23 For LIBs this presents a difficulty since low-frequency diffusion means that the EIS data rarely converges and the timescales required means that experiments are often limited to 10−2 to 10−3 Hz in the low-frequency region. One possible workaround is to “pre-process” the EIS data by removing the diffusive tail.18,23 This is done by modelling the diffusive region using an EC and then simply subtracting it from the data in a manner similar to applying a baseline in e.g. X-ray diffraction. However – and similarly to the application of a baseline in other techniques – the choice of baseline has an influence on the rest of the data, especially for features close to where the baseline is large. A different method can be used, whereby the data is assumed to converge to the real axis even if the spectrum is incomplete.22 The DRT spectrum can then be calculated without the need to choose a baseline. It is important to note that the DRT peak characteristics (size, shape and position) which appears in the low-frequency region as a result of this assumption is not an accurate description of the polarization process. The GP method employed here uses this assumption of convergence to the real axis, and while we present the full DRT spectrum (including the peak in the diffusive region) we do not use the DRT spectrum to extrapolate information about the low-frequency polarization processes.22 The results of DRT deconvolution for half cell and symmetric cells at each of the four stop potentials can be seen in Fig. 2. The large peak in the low-frequency diffusion region is an artefact due to the method extrapolating beyond the data as well as data not converging to the real axis and should therefore not be included when discussing the DRT analysis. For clarity, this region has been greyed out. In each plot in Fig. 2 the Si/Si and Li/Li symmetric cells consist of one peak at about 102 and 103 Hz, respectively. These correspond to the Li+ diffusion through the solid electrode and the SEI, respectively.18,23,24 The half cells consist of either a broad, shouldered peak (as in the case of 2a to 2c), or two distinct but overlapping peaks (Fig. 2d). This indicates that the half cell behaviour is comprised of both Li and Si contributions, but due to their close proximity these may not be resolvable by fitting separate loops in the EC. Interestingly, at 0.07 V (Fig. 2b) the Li/Li symmetric cells and the half cells show a very large polarization, indicating that the impedance at this potential is strongly dominated by the Li CE behaviour. A final small peak exists in the low frequency range at about 10−1 Hz which may be due to diffusion of Li+ in the electrolyte. The breadth of these peaks indicates that they are likely best described by using constant phase elements (Q) rather than capacitive elements (C). Q is given by:
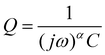 | (1) |
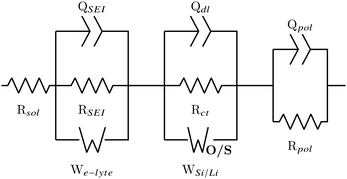
From the analysis of the DRT plots it is possible to conclude that the cells consists of three loops: the first describes the double-layer constant phase element QSEI and layer resistance RSEI along with a Warburg diffusion W describing the electrolyte–SEI interface; the second loop describes the solid electrode behaviour, with Qdl and Rct describing the double-layer pseudo-capacitance and charge transfer polarization of the electrode/SEI interface, respectively;32 and the final loop describes the polarization process of the cell.18 For large cells with low impedance and contact resistances (between electrode material and current collector) induction effects also come into play, but for coin cells these can mostly be ignored. The cell resistance is the total resistance at f → ∞, analogous to the iR-drop seen in the first few seconds of a galvanostatic charge–discharge (GCD) curve.18 This is commonly referred to as the solution resistance Rsol, and because it is a series resistance it is not included in the DRT plots.
The DRT analysis results in two ECs to describe the behaviour of the Si/Si, Li/Li and half cell spectra, one incorporating a finite space Warburg Wo which describes the Li+ solid state diffusion, and the other incorporating a finite length Warburg Ws which describes the diffusion of Li+ through the SEI. The EC is shown in Fig. 3, with Wo/s representing either the finite space or the finite length Warburg. The EC with the lowest χ2 was chosen to represent the half cell data. It should be noted that the χ2 for both circuits was often very small (∼10−6), and the difference between χ2 values varied by less than an order of magnitude.
At intermediate potentials (0.2 and 0.3 V) the solid-state diffusion behaviour is dominant over the thin-film behaviour, while at low and high potentials (0.07 and 0.48 V) the opposite is true. This could be because the highly lithiated and highly delithiated states have limited space for solid-state diffusion, and so the thin-film behaviour becomes dominating, either as a result of the SEI on the Si WE, or on the Li CE, or both. This matches the expectation from previous research, which showed that the SEI cracks both during lithiation and delithiation.18
In cases where the exponent α of the constant phase element Q is equal to 1, eqn (1) becomes equivalent to that of a capacitor. This will in turn decrease the number of parameters needed for fitting of the data and give more easily interpreted results.
Analysis of the fitted results of the Si/Si EC and half cells within the relevant stop potentials (0.2 and 0.3 V) reveals that the QSEI parameter for the symmetric cells can be replaced with capacitors, but the same parameter for the half cells cannot. This is likely due to interference of the signal from the Li side of the half cell. The same result is seen in the high and low potentials (0.07 and 0.48 V) for the Ws EC, with the Li/Li QSEI behaving as a pure capacitor, and the half-cell showing mixed behaviour. This result is notable because it reduces the number of parameters needed to describe the symmetric cells, while simultaneously showing that the QSEI parameter of the half cells is made of a mixture of the two SEI layers.
From the results of the fitting it is possible to draw some conclusions as to the behaviour of Si during lithiation and delithiation, and how this affects the impedance response. This is shown schematically in Fig. 4. Starting from the fully delithiated state and lithiating: at 0.2 V – which corresponds to the equilibrium position of the Si → Li2Si phase – there is both enough space and sufficient Li+ ions in the Si for the ions to move freely and be measurable by EIS on the coin cell level even in the half cell format. At 0.07 V where most of the electrode consists of Li3.5Si, the high concentration of Li+ in the electrode reduces the number of mobile ions, and therefore the diffusion of Li+ through thin films such as SEI become dominating in the EIS spectrum. Further, the long timescales of the CCCV experiment mean that a thick SEI layer is able to grow on the Li CE, which then generates a strong impedance response. During delithiation the situation is very similar, with the end of the Li3.5Si → Li2Si phase (at 0.3 V) showing a strong impedance signal from Li+ mobility in the Si, and the highly delithiated Li2Si → Si phase at 0.48 V showing very little signal from the Li+ in the Si, allowing the surface diffusion effects to dominate once again. This is similar to the ion mobility effects seen in LEDs.33 The decreased impedance of the Li CE is likely due to the decreased overpotential during deposition (i.e. during delithiation of the Si electrode) vs. stripping (i.e. during lithiation of the Si electrode).34
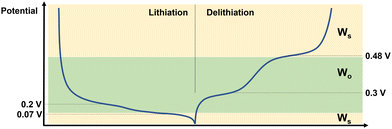 | ||
| Fig. 4 Schematic describing the behaviour of Si half cells at different points in the charge–discharge curve. The dominant diffusion behaviour is denoted on the right hand side. | ||
The results obtained in this work show that it is necessary to exercise caution when studying the behaviour of high loading Si half cells. At or near the fully lithiated and delithiated states the Li CE contributes significantly to the impedance of the cell, and so SEI impedances from the Li CE can easily be misidentified as belonging to the Si WE. Should an EIS spectrum be desired e.g. at the end-of life, it is therefore recommended to either use symmetric cells (by using at least two cycled cells), or to perform EIS at one or more potentials in the cycle, with emphasis on the intermediate potentials where the Li CE contribution is limited.
4 Conclusion
A set of Si electrodes with commercial level loadings were analysed by means of EIS, both as half cells and their Si/Si and Li/Li symmetric cell equivalents. The cells were tested at four different potentials corresponding to the equilibrium potentials of the lithiation and delithiation phases. Analysis of the resulting EIS spectra by DRT showed that the half cells are described by a combination of the Si/Si and Li/Li symmetric cells, and that these are in turn best described by different ECs. The Si/Si symmetric cells are shown to fit a finite-length Warburg describing the solid-state diffusion of Li+ in Si, while the Li/Li cells are best described by a finite-space Warburg corresponding to the diffusion of Li+ through the SEI. The half cells are described either by the Si/Si or the Li/Li EC depending on the stop potential, with the high and low potentials showing Li/Li character, and the intermediate potentials showing Si/Si behaviour. Further analysis showed that both the Si/Si and Li/Li symmetric cell ECs could be simplified by replacing the two-parameter constant phase element QSEI with a single-parameter capacitive element CSEI, but that the mixing of signals meant this could not be extended to the half cells. This work shows the importance of EIS as a technique for studying Si electrodes with high loading, as well the importance of carefully considering the behaviour of both electrodes in half cell EIS.Author contributions
F. T. Huld: conceptualization; data curation; software; formal analysis; investigation; visualization; methodology; writing – original draft; writing – review and editing. Z. Yu: supervision; project administration; writing – review and editing. F. Lou: resources; supervision; funding acquisition; project administration; writing – review and editing.Conflicts of interest
F. T. Huld and F. Lou declare that they are employees and stockholders of Beyonder AS, a Norwegian battery company. The remaining authors do not declare a conflict of interest.References
- M. T. McDowell, S. W. Lee, W. D. Nix and Y. Cui, Adv. Mater., 2013, 25, 4966–4985 CrossRef CAS PubMed.
- M. Obrovac, Curr. Opin. Electrochem., 2018, 9, 8–17 CrossRef CAS.
- V. Vanpeene, J. Villanova, A. King, B. Lestriez, E. Maire and L. Roué, Adv. Energy Mater., 2019, 9, 1803947 CrossRef.
- M. N. Obrovac and L. J. Krause, J. Electrochem. Soc., 2007, 154, A103 CrossRef CAS.
- F. T. Huld, S. Y. Lai, W. M. Tucho, R. Batmaz, I. T. Jensen, S. Lu, O. E. Eleri, A. Y. Koposov, Z. Yu and F. Lou, ChemistrySelect, 2022, 7, e202202857 CrossRef CAS.
- J. P. Pender, G. Jha, D. H. Youn, J. M. Ziegler, I. Andoni, E. J. Choi, A. Heller, B. S. Dunn, P. S. Weiss, R. M. Penner and C. B. Mullins, ACS Nano, 2020, 14, 1243–1295 CrossRef CAS PubMed.
- X. Shen, Z. Tian, R. Fan, L. Shao, D. Zhang, G. Cao, L. Kou and Y. Bai, J. Energy Chem., 2018, 27, 1067–1090 CrossRef.
- R. Teki, M. K. Datta, R. Krishnan, T. C. Parker, T.-M. Lu, P. N. Kumta and N. Koratkar, Small, 2009, 5, 2236–2242 CrossRef CAS PubMed.
- R. Batmaz, F. M. Hassan, D. Higgins, Z. P. Cano, X. Xiao and Z. Chen, J. Power Sources, 2018, 407, 84–91 CrossRef CAS.
- A. Ulvestad, M. O. Skare, C. E. Foss, H. Krogsæter, J. F. Reichstein, T. J. Preston, J. P. Mæhlen, H. F. Andersen and A. Y. Koposov, ACS Nano, 2021, 15, 16777–16787 CrossRef CAS PubMed.
- L. Luo, H. Yang, P. Yan, J. J. Travis, Y. Lee, N. Liu, D. Molina Piper, S.-H. Lee, P. Zhao, S. M. George, J.-G. Zhang, Y. Cui, S. Zhang, C. Ban and C.-M. Wang, ACS Nano, 2015, 9, 5559–5566 CrossRef CAS PubMed.
- Z. Chen, C. Wang, J. Lopez, Z. Lu, Y. Cui and Z. Bao, Adv. Energy Mater., 2015, 5, 1401826 CrossRef.
- Y. Wang, H. Xu, X. Chen, H. Jin and J. Wang, Energy Storage Mater., 2021, 38, 121–129 CrossRef.
- J. Lu, J. Liu, X. Gong, S. Pang, C. Zhou, H. Li, G. Qian and Z. Wang, Energy Storage Mater., 2022, 46, 594–604 CrossRef.
- F. La Mantia, C. Wessells, H. Deshazer and Y. Cui, Electrochem. Commun., 2013, 31, 141–144 CrossRef CAS.
- M. Ender, J. Illig and E. Ivers-Tiffée, J. Electrochem. Soc., 2017, 164, A71–A79 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001 Search PubMed.
- K. Pan, F. Zou, M. Canova, Y. Zhu and J.-H. Kim, J. Power Sources, 2020, 479, 229083 CrossRef CAS.
- D. A. Lozhkina, A. M. Rumyantsev and E. V. Astrova, Semiconductors, 2020, 54, 383–391 CrossRef CAS.
- F. Paloukis, C. Elmasides, F. Farmakis, P. Selinis, S. G. Neophytides and N. Georgoulas, J. Power Sources, 2016, 331, 285–292 CrossRef CAS.
- M. Levi, Solid State Ionics, 2001, 143, 309–318 CrossRef CAS.
- J. Liu and F. Ciucci, Electrochim. Acta, 2020, 331, 135316 CrossRef CAS.
- J. Illig, M. Ender, T. Chrobak, J. P. Schmidt, D. Klotz and E. Ivers-Tiffée, J. Electrochem. Soc., 2012, 159, A952–A960 CrossRef CAS.
- J. P. Schmidt, T. Chrobak, M. Ender, J. Illig, D. Klotz and E. Ivers-Tiffée, J. Power Sources, 2011, 196, 5342–5348 CrossRef CAS.
- K. Ogata, E. Salager, C. Kerr, A. Fraser, C. Ducati, A. Morris, S. Hofmann and C. Grey, Nat. Commun., 2014, 5, 3217 CrossRef CAS PubMed.
- B. Key, M. Morcrette, J.-M. Tarascon and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 503–512 CrossRef CAS PubMed.
- K. Kitada, O. Pecher, P. C. M. M. Magusin, M. F. Groh, R. S. Weatherup and C. P. Grey, J. Am. Chem. Soc., 2019, 141, 7014–7027 CrossRef CAS PubMed.
- Y.-S. Wu, C.-C. Yang, S.-P. Luo, Y.-L. Chen, C.-N. Wei and S. J. Lue, Int. J. Hydrogen Energy, 2017, 42, 6862–6875 CrossRef CAS.
- M. Murbach, B. Gerwe, N. Dawson-Elli and L.-K. Tsui, J. Open Source Software, 2020, 5, 2349 CrossRef.
- M. Schönleber and E. Ivers-Tiffée, Electrochem. Commun., 2015, 61, 45–48 CrossRef.
- C. H. Chen, J. Liu and K. Amine, J. Power Sources, 2001, 96, 321–328 CrossRef CAS.
- Z. C. Huertas, D. Settipani, C. Flox, J. R. Morante, T. Kallio and J. J. Biendicho, Sci. Rep., 2022, 12, 137 CrossRef PubMed.
- J. C. deMello, N. Tessler, S. C. Graham and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12951–12963 CrossRef CAS.
- J. Seok, C. N. Gannett, S.-H. Yu and H. D. Abruña, Anal. Chem., 2021, 93, 15459–15467 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00181d |
| This journal is © The Royal Society of Chemistry 2023 |