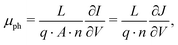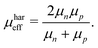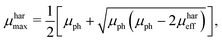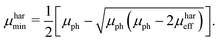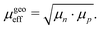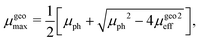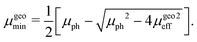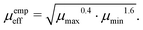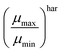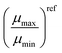DOI:
10.1039/D3YA00125C
(Paper)
Energy Adv., 2023,
2, 1390-1398
On the relationship of the effective mobility and photoconductance mobility in organic solar cells†
Received
21st March 2023
, Accepted 19th July 2023
First published on 22nd July 2023
Abstract
The efficiency of organic solar cells has increased significantly in the recent years due to the continued improvement in material properties, including the charge carrier mobilities within the bulk heterojunction. However, common strategies to measure the mobility of electrons and holes, such as the space-charge-limited-current approach, rely on purpose-made single carrier diodes, which are operated in the injection regime. Alternatively, impedance spectroscopy measurements can yield an effective mobility as well as a photoconductance mobility for solar cells under realistic operating conditions. There exist various theoretical interpretations that relate the experimentally determined values of the effective mobility with the mobility of the individual charge carriers (i.e. electrons and holes). Furthermore, the relationship between the effective and photoconductance mobility has not been clarified yet. This study shows how the effective and photoconductance mobilities can be combined in a system of equations to calculate the individual mobilities of the faster and slower carriers. Finally, these considerations are applied to determine individual carrier mobilities in several blend systems, including fullerene-based P3HT:PC60BM solar cells, as well as non-fullerene devices based on PM6:Y11-N4, PM6:Y5, PPDT2FBT:Y6, PM6:Y11, PM6:N4, and PM6:Y6. These results were validated with mobility values obtained via the space-charge-limited-current approach.
1. Introduction
The field of organic solar cells has experienced significant improvements in recent years. Organic photovoltaics (OPV) distinguish themselves with the potential of a low priced, solution based, scalable production, and their applicability on lightweight, flexible substrates, which are unique selling points of all types of organic electronic technologies.1–5 There is a considerable commercial potential for OPVs, if certain thresholds in device stability, power conversion efficiency (PCE ≥ 15%) and production cost are achieved.6,7 One of these aforementioned thresholds has recently been exceeded in laboratory scale devices (PCE > 19%),8–13 which can mostly be attributed to the successful use of non-fullerene acceptors (NFA) that were developed through continuous efforts to replace the hitherto ubiquitous fullerene-based acceptors, such as PC60BM.14–24 In particular, solar cells based on the polymer donor PM6 and the NFA Y6 are representative of this recent performance increase.25–27 Furthermore, numerous different synthetic strategies have been employed and investigated in search for viable NFAs in the past.28–33 Organic solar cells typically have a two-component active layer in a bulk-heterojunction (BHJ) configuration, consisting of a donor and acceptor material with a large donor–acceptor (D:A) interface (cf.Fig. 1).34 The need for this configuration arises due to the small dielectric constant of organic semiconductors (εr ≈ 3), which leads to the formation of bound excitons.35,36 The excitons can split into free charge carriers at the D:A interface, owing to the energy level differences. Matching these different energy levels at the D:A interface is critical for the efficient generation and extraction of free electrons and holes, which affects the overall performance of the organic solar cell. It is a common approach to treat the BHJ active layer as an effective medium, and some device characterization analyses operate on the basis of an effective charge carrier mobility μeff that replaces individual mobilities of electrons and holes.37 The need for dedicated, single carrier diodes to determine the mobilities of the individual carriers through space-charge-limited-current (SCLC) measurements, which have to be studied at voltages that are outside of the typical operating range of solar cells, can be avoided by this strategy. Moreover, the effective mobility μeff has been successfully used for the quantification of recombination and extraction dynamics.38,39
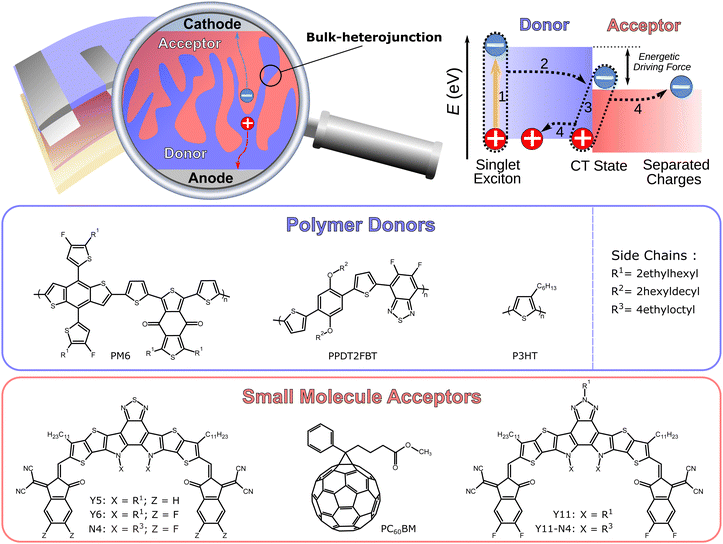 |
| | Fig. 1 Schematic depiction of an organic solar cell and its bulk-heterojunction active layer consisting of a donor polymer and acceptor small molecule. The relevant energy levels involved in the photogeneration: (1) formation of exciton via photon absorption; (2) exciton diffusion to the donor:acceptor (D:A) interface and charge transfer (CT) state; (3) charge separation; (4) extraction of free charge carriers to the electrodes. Chemical structures of the polymer donors PM6, PPDT2FBT, and P3HT as well as the small molecule acceptors Y5, Y6, N4, PC60BM, Y11, and Y11-N4. | |
The experimentally attainable effective mobility μexpeff of charge carriers in organic solar cells has hitherto been referred to as a mean value between the slower and faster carrier mobilities (μmin and μmax).37 This study provides an overview of the various descriptions of the effective mobility and proposes a combination of experimental measurements which yield relevant mobility values, followed by the investigation of different types of blend systems over a wide range of light intensities. Devices with active layers based on P3HT:PC60BM, PM6:Y11-N4, PM6:Y5, PPDT2FBT:Y6, PM6:Y11, PM6:N4, and PM6:Y6, the latter with varying electron transport layers and thicknesses (cf.Fig. 1 and Fig. S1 in the ESI†), were investigated, demonstrating the general applicability of the aforementioned approach.
2. Fundamental principles
Measuring individual carrier mobilities in complete solar cells at operating conditions poses a significant challenge, since injection/extraction and transport of both negative and positive charge carriers occur simultaneously. Let us consider the total current density in a solar cell in the presence of an electric field as the sum of the current densities resulting from the movement of electrons and holes:| | | Jtot = Jn + Jp = q·n·μn·E + q·p·μp·E, | (1) |
where q is the elementary charge, E is the electric field within the active layer, n and p are the charge carrier densities for electrons and holes, and μn,p are the respective mobilities. Considering the relationship of the average charge carrier density nav = n = p, which is relevant for higher light intensities when the excess carrier density significantly exceeds the dark carrier density, the following expression can be obtained:| | | Jtot = q·E·nav·(μn + μp) = 2q·E·nav·μeff, | (2) |
where the effective mobility is introduced due to the inability to distinguish between the faster and slower carrier mobilities. As suggested by eqn (2), the effective mobility encompasses the transport properties of both charge carriers; its relationship to the individual carrier mobilities remains at the focus of numerous studies. Experimentally the effective mobility can be accessed by taking into account the relationship of the current density J, charge carrier density nav, and the internal voltage Vint under steady-state conditions:| | 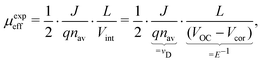 | (3) |
where vD is the charge carrier velocity, E is the electric field within the active layer, q is the elementary charge, L is the active layer thickness, VOC is the open-circuit voltage, and Vcor is the applied voltage corrected for the series resistance Rs (Vcor = Vapp − J·Rs).36,39 The current density J and the associated internal voltage Vint can be easily obtained via standard J–V-characteristics. In contrast, the determination of the charge carrier density nav relies on more sophisticated measurement techniques, such as charge extraction, transient photovoltage/photocurrent, or impedance/capacitance spectroscopy.40–46 Nevertheless, the necessary values to calculate the effective mobility according to eqn (3) can be obtained for solar cells under realistic operating conditions. Notably, determination of the effective mobility is not possible in the vicinity of the open-circuit voltage due to the denominator in eqn (3) approaching zero. Under the assumption of the equality between the excess electron and hole densities, as well as in absence of strong doping and dark charge injection, the sum of the electron and hole mobilities at the open-circuit condition can be obtained from the device quasi-steady-state photoconductivity σph.47 Specifically, the relationship between the photoconductance Gph and the charge carrier density n gives:| | 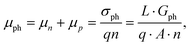 | (4) |
where μph is the photoconductance mobility, q is the elementary charge, A is the active area, and L is the active layer thickness. Furthermore, with 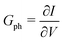 , we obtain:
, we obtain:| | 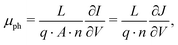 | (5) |
which, upon comparison with eqn (3), results in the equivalence:under the condition that ∂J/∂V = J/Vint and μn = μp. Thus, eqn (6) relies on the approximation of the J–V-curve at V = Vint (or V = VOC); the relationship is not applicable beyond these voltages. Nonetheless, eqn (6) is important, since the effective mobility μexpeff is not defined at VOC, as can be seen by the numerator (J = 0) and the denominator (Vint = 0) in eqn (3). Therefore, in previous studies μexpeff (VOC) was obtained via linear interpolation or extrapolation of the experimentally determined values of μexpeff at voltages close to open-circuit, or was left undetermined under these conditions.36,39
The relationship between the effective mobility and independently measured carrier mobilities has been previously rationalised in terms of the encounter limited and morphology dependent recombination models, which represent the bimolecular carrier recombination coefficient k as a function of mobility.48 As such, depending on the size of the domains within a bulk heterojunction, k has been found to correlate with an arithmetic, harmonic, or geometric mean of the individual carrier mobilities. For the detailed description of this topic we refer the reader to more dedicated review articles.37,48 In the framework of this paper, we focus on the various definitions of the effective mobility in terms of the respective means of the electron and hole mobilities.
One fundamental interpretation of the effective mobility relies on the harmonic mean of μn and μp:
| | 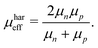 | (7) |
Here, it is assumed that under steady state conditions the flux of electrons leaving the device must be the same as the flux of holes.
49 Importantly, the combination of the definition of the effective mobility
via the harmonic mean
μhareff and the photoconductance mobility
μph depicted above (
cf.eqn (4)) allows determining the individual mobilities of the two types of charge carriers. This is possible, since there are now two unknown variables, namely
μn and
μp, and two equations. Instead of
μn and
μp, the variables
μmax and
μmin are chosen, since the suggested method does not allow to identify the type of charge carrier. The solution of the proposed system of equations yields:
| | 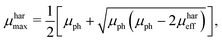 | (8) |
| | 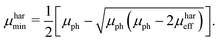 | (9) |
Hence, if the proposed relationship between the effective mobility
μhareff and the photoconductance mobility
μph is reliable, it should be possible, according to
eqn (8) and (9), to calculate the maximum and minimum mobility (
μharmax and
μharmin) for an appropriately tested solar cell.
Another interpretation of the effective mobility in relation to the individual mobilities of the two types of charge carriers is based on their geometric mean:50–52
| | 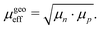 | (10) |
In this case, the solutions to the system of equations to determine the maximum and minimum mobilities have to be adjusted accordingly. Thus, the respective expressions for individual mobilities change as follows:
| | 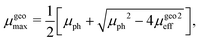 | (11) |
| | 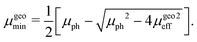 | (12) |
There also exist empirical estimates for the effective mobility, which put a more significant weight on the smaller carrier mobility:
53| | 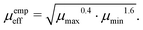 | (13) |
The different interpretations of the photoconductance and effective mobility in relationship to the different ratios of
μp/
μn are depicted in
Fig. 2. In the plots shown in
Fig. 2(a), different values for
μp and
μn have been used to calculate
μph,
μhareff,
μgeoeff, and
μempeff, respectively. However, it should be noted that space-charge effects that can have an influence particularly once significantly imbalanced mobilities are present, have not been considered in these examples.
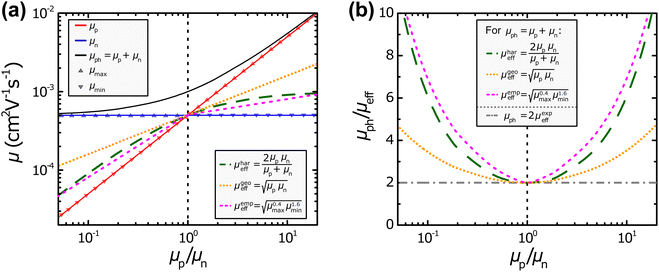 |
| | Fig. 2 (a) Different definitions of the effective mobility μeff and photoconductance mobility μph as well as (b) the resulting ratio μph/μeff in relation to the ratio of the hole and electron mobility μp/μn. | |
One of the obvious aspects that is shared by all the aforementioned definitions of the effective mobility is that they are all equal to the value of the individual mobilities in the presence of balanced charge transport (μeff = μp = μn). This also highlights the need for the factor “2” for the harmonic case, because otherwise the harmonic effective mobility μhareff would converge to half of the individual mobilities.49 Furthermore, the effective mobilities all follow, to a varying extent, the smaller individual mobility μmin, as should be expected from the equations listed above. In particular, the harmonic and empirical effective mobilities (μhareff and μempeff) exhibit rather similar values throughout the different mobility ratios μp/μn. In contrast, the geometric effective mobility μgeoeff shows more pronounced deviations to the other two types of definitions of the effective mobility, specifically at more imbalanced ratios of μp/μn. Under such conditions, the geometric effective mobility μgeoeff yields values that are noticeably larger than the minimum mobility μmin. In Fig. 2(b), the ratios between the photoconductance mobility μph as described in eqn (4) and the various definitions of the effective mobility (i.e. μhareff, μgeoeff, μempeff; cf.eqn (7), (10) and (13), respectively) are visualized at different mobility ratios μp/μn. The case of a linear relationship between the photoconductance and effective mobility (μph = 2μexpeff, cf.eqn (6)) has also been included in form of the horizontal, dash-dotted line. This visualization also depicts the convergence of all the different definitions for the balanced mobilities (μp/μn = 1). In addition, Fig. 2(b) shows the necessary ratios of μph/μeff to obtain μmin and μmaxvia the relationships derived in eqn (8) and (9) for the harmonic definition as well as the relationships derived in eqn (11) and (12) for the geometric definition of the effective mobility. No results can be expected for the individual mobilities, if the ratio μph/μeff < 2, regardless of what exact definition is chosen for the effective mobility. As we will see later, there are several experimental examples, for which μph/μeff < 2 is the case, leading to undefined μmin and μmax.
3. Results and discussion
In this study, nine different organic solar cells were investigated over a wide range of light intensities to test the hypothesis presented above in Section 2. Namely, solar cells based on P3HT:PC60BM, PM6:Y11-N4, PM6:Y5, PPDT2FBT:Y6, PM6:Y11, PM6:N4, and PM6:Y6, the latter with varying electron transport layers and thicknesses, were fabricated (cf.Fig. 1). The photovoltaic parameters of the tested devices, including the open-circuit voltage VOC, the short-circuit current density JSC, the fill factor FF, and power conversion efficiency PCE under 1 sun illumination as well as the BHJ thickness L, are listed in Table 1. The effective mobilities at varying light intensities and applied biases were obtained from the measured J–V-characteristics and charge carrier densities using eqn (3). The latter were determined, as described in more detail in the ESI,†via the capacitance spectra extracted from the impedance measurements (cf. Section S13 and S23 in the ESI†).45,46 The effective mobility under the open-circuit condition μexpeff (VOC) was obtained via linear interpolation of the experimentally determined values of μexpeff at voltages close to open circuit, since according to eqn (3), μexpeff (VOC) is not directly accessible. To determine the photoconductance mobilities at open circuit by means of eqn (4), the real part of the device low-frequency admittance (also known as quasi-steady-state photoconductance Gph) and the impedance-derived carrier density n were employed.45,47 The results for PM6:Y6 (PDINO, L = 100 nm) and PM6:Y11-N4 in Fig. 3 serve well as a representation for the overall trends exhibited by the other blends (cf. Fig. S1 in the ESI†). The values of the photoconductance mobility μph (black squares) and the interpolated values of μexpeff (VOC) (red circles), as well as other derived mobilities, are all visualized. Quite surprisingly, a relatively good agreement between the effective mobility at open circuit and half of the photoconductance mobility (μexpeff (VOC) ≈ 0.5μph) was observed over a relatively wide range of charge carrier densities, which according to eqn (6) implies rather balanced electron and hole mobilities (cf. Fig. S1 of the ESI†). The only exception to this trend was PM6:N4, where a noticeable divergence at lower charge carrier densities is evident.
Table 1 Photovoltaic parameters obtained from the J–V-characteristics and active layer thickness of the studied solar cells in order of their PCE
| Solar cell |
V
OC (mV) |
J
SC (A m−2) |
FF |
PCE (%) |
L (nm) |
| P3HT:PC60BM |
725.0 |
72.3 |
0.6245 |
3.27 |
90 |
| PM6:Y11-N4 |
835.5 |
155.0 |
0.6179 |
8.00 |
80 |
| PM6:Y5 |
973.5 |
164.0 |
0.5301 |
8.46 |
100 |
| PPDT2FBT:Y6 |
685.7 |
263.4 |
0.5763 |
10.41 |
80 |
| PM6:Y11 |
863.1 |
250.7 |
0.5253 |
11.37 |
90 |
| PM6:N4 |
779.5 |
234.2 |
0.6550 |
11.96 |
110 |
| PM6:Y6 (PDINO) |
815.3 |
258.4 |
0.6788 |
14.30 |
100 |
| PM6:Y6 (PDINO) |
825.5 |
272.0 |
0.6476 |
14.54 |
90 |
| PM6:Y6 (PDINN) |
815.9 |
270.9 |
0.7044 |
15.57 |
100 |
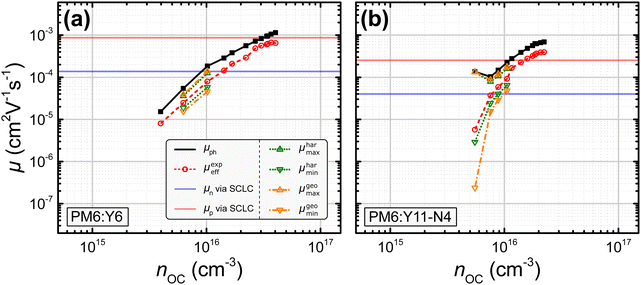 |
| | Fig. 3 Experimentally determined values for μph (black squares; cf.eqn (4)) and μexpeff (VOC) (red circles; cf.eqn (3)) for a PM6:Y6 and a PM6:Y11-N4 organic solar cell. Calculation of the maximum and minimum mobilities determined via the harmonic and geometric approach (μharmax, μharmin: green dots, cf.eqn (8) and (9); μgeomax, μgeomin: orange dash-dots, cf.eqn (11) and (12)). The electron (μn: blue) and hole (μp: red) SCLC mobilities are shown as horizontal lines due to the unknown charge carrier density at which they were measured. Results for other investigated devices can be found in the ESI† (cf. Fig. S1). | |
The values of μharmax and μharmin (green dots) as well as μgeomax and μgeomin (orange dash-dots) for the studied blends were calculated by inserting the experimentally determined μph and μexpeff either into eqn (8) and (9) or into eqn (11) and (12). The first set of equations is used, if the experimentally determined effective mobility μexpeff is interpreted as the harmonic mean and the second set of equations is used, if μexpeff is interpreted as the geometric mean. Interestingly, in case of the PM6:Y6 device, neither of these assumptions provided a continuous range of μmax and μmin values, as it was possible to obtain finite values only for a few data points. One explanation for this observation could be the relatively balanced charge carrier mobilities under the employed measurement conditions; then, even small deviations caused by measurement noise could push the ratio below the threshold of μph/μeff < 2. Indeed, rather balanced mobilities have been reported for the PM6:Y6 blend.54 In contrast, for the PM6:Y11-N4 solar cell it was possible to obtain finite values for both μmax and μmin at low to medium light intensities (cf.Fig. 3). In all cases where μmax and μmin could be obtained (i.e. μph/μeff ≥ 2), a greater imbalance between the individual mobilities was calculated when using μgeoeff in comparison to μhareff. This observation is in agreement with Fig. 2(b), where a given ratio μph/μeff would result in a more imbalanced ratio μp/μn, if μgeoeff was used rather than μhareff. Interestingly, this line of reasoning also means that a hypothetical calculation of μmin and μmax based on μempeff (cf.Fig. 2) should yield even smaller ratios of μp/μn compared to the approach relying on μhareff.
All studied blends can be divided into two categories exemplified by the two cells in Fig. 3. Specifically, the PM6:Y5, PM6:Y11, and various PM6:Y6 devices are comparable to the PM6:Y6 solar cell discussed in detail above, whereas the P3HT:PC60BM, PM6:N4, and PPDT2FBT:Y6 solar cells are comparable to the PM6:Y11-N4 device (cf. Fig. S1 in the ESI†). The first category of blends only sporadically yielded finite values for μmax and μmin, while the latter category consistently yielded them, especially at lower charge carrier densities.
The individual mobilities of the studied blends determined via the SCLC method for single carrier diodes were added to Fig. 3 and Fig. S1 in the ESI† as a reference in the form of horizontal lines (μn: blue; μp: red). In general, SCLC mobilities are assumed to be obtained at charge carrier densities of n ≈ 1015–1016 cm−3.55 In case of the PM6:Y6 device shown in Fig. 3(a), the SCLC mobilities (μn = 1.3 × 10−4 cm2 V−1 s−1; μp = 8.4 × 10−4 cm2 V−1 s−1) are generally larger than the minimum and maximum mobilities determined via the harmonic and geometric approach at a charge carrier density of n = 1016 cm−3 (μharmin = 5.8 × 10−5 cm2 V−1 s−1; μharmax = 1.3 × 10−4 cm2 V−1 s−1; μgeomin = 4.6 × 10−5 cm2 V−1 s−1; μgeomax = 1.4 × 10−4 cm2 V−1 s−1). These deviations are not too surprising as only a few data points yielded finite values of μmin and μmax. However, in case of the PM6:Y11-N4 device shown in Fig. 3(b), the SCLC mobilities (μn = 4.0 × 10−5 cm2 V−1 s−1; μp = 2.5 × 10−4 cm2 V−1 s−1) more or less match the minimum and maximum mobilities determined via the harmonic and geometric approach at a charge carrier density of n = 1016 cm−3 (μharmin = 6.5 × 10−5 cm2 V−1 s−1; μharmax = 1.6 × 10−4 cm2 V−1 s−1; μgeomin = 4.8 × 10−5 cm2 V−1 s−1; μgeomax = 1.8 × 10−4 cm2 V−1 s−1). Depending on the chosen charge carrier density, the reference SCLC mobilities of the other blend systems also show a reasonable agreement with the different determined values for μmin and μmax (cf. Fig. S1 in the ESI†), with the exception of the P3HT:PC60BM solar cell, where the SCLC mobilities exceed the determined values for μmin and μmax. The values for μmin, μmax, and their ratios are listed in Table 2 for all investigated blend systems; the reference SCLC mobilities can be found in Section S24 of the ESI.† It turns out that the SCLC derived ratios for P3HT:PC60BM, PM6:Y5, PPDT2FBT:Y6, PM6:Y11-N4, and PM6:N4 match well with the ratios determined via the harmonic and geometric approaches. In contrast, the SCLC derived ratios for PM6:Y6 and PM6:Y11 diverge from the ratios determined by the harmonic and geometric approach to a varying degree, which as mentioned previously might be caused by the few data points yielding finite values of μmin and μmax.
Table 2 Mobility ratios determined from the experimental methods in this study and reference mobilities for the studied blends. The reference mobilities were determined via the SCLC method
| Blend |
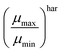
|

|
μ
refmin (cm2 V−1 s−1) |
μ
refmax (cm2 V−1 s−1) |
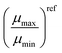
|
Ref. |
| P3HT:PC60BM |
1.94–34.94 |
2.57–339.61 |
2.0 × 10−4 |
3.0 × 10−3 |
15.0 |
56 and 57
|
| PM6:Y11-N4 |
2.46–45.73 |
3.65–568.07 |
0.4 × 10−4 |
2.5 × 10−4 |
6.25 |
S20 |
| PM6:Y5 |
1.59–2.69 |
1.93–4.17 |
3.3 × 10−4 |
7.3 × 10−4 |
2.1 |
S21 |
| PPDT2FBT:Y6 |
1.41–2.68 |
1.63–4.15 |
1.5 × 10−4 |
3.5 × 10−4 |
2.3 |
S22 |
| PM6:Y11 |
2.45 |
3.62 |
1.2 × 10−4 |
1.6 × 10−4 |
1.3 |
S23 |
| PM6:N4 |
3.71–89.66 |
6.78–2098.70 |
0.1 × 10−4 |
1.6 × 10−4 |
16.0 |
58
|
| PM6:Y6 |
1.68–3.52 |
2.09–6.27 |
1.3 × 10−4 |
8.4 × 10−4 |
6.5 |
58
|
We note that mobilities reported in the literature for blends of organic semiconductors are generally determined via the SCLC technique, which relies on specifically fabricated single-carrier diodes that do not function as a solar cell and are typically operated at larger applied voltages. Thus, deviations between the SCLC derived parameters and the values determined in the scope of this study can also be caused by the difference in the applied conditions.26
Nonetheless, the observed agreement for most studied blend systems between the reference mobility ratios measured via SCLC and the ratios obtained via the effective mobility/photoconductance mobility analysis presented in this study has an important implication, validating these approaches relative to each other. It must be noted that the respective charge carrier densities, at which the mobilities are determined for both methods are quite close. Although the presented approach is unable to distinguish the sign of the faster/slower charge carriers, it allows both determining the values of μmin and μmax and checking if carrier mobilities are balanced (in which case μexpeff = 0.5 μph applies). As a result, this provides a new way to determine individual carrier mobilities in functioning solar cells at operating conditions, as well as rationalising the device performance due to a potentially present mobility imbalance.
4. Conclusions
In summary, we employed impedance spectroscopy measurements in a series of organic solar cells with different blend systems to determine both the effective and photoconductance mobilities (μeff and μph). Furthermore, we demonstrated the possibility to determine the slower and faster mobilities (μmin and μmax) by solving systems of equations for μeff and μph. For the studied solar cells, the values for μmin, μmax, and their ratio obtained by this approach match for the most part with the individual electron and hole mobilities, and their ratios, measured independently via the SCLC technique. The determination of finite values for μmin and μmax in a continuous range of light intensities was possible in the blends with higher mobility imbalance. In contrast, for the blends with rather balanced mobilities, finite values of μmin and μmax could not be obtained continuously. Importantly, this condition corresponds to the relationship between the effective and photoconductance mobilities: μexpeff ≈ 0.5 μph. This opens up an avenue to determine the effective mobility for such systems under open-circuit conditions without relying on interpolation or extrapolation.
Conflicts of interest
The authors declare that there is no conflict of interest regarding the publication of this article.
Acknowledgements
This work has been funded by the Alexander-von-Humboldt Stiftung [Sofja-Kovalewskaja-Award]. J. V. acknowledges funding by the Alexander-von-Humboldt Stiftung [Feodor-Lynen-Rückkehrstipendium] and by a Brückenstipendium of the University of Potsdam. H. Y. W. acknowledges the financial support from the National Research Foundation of Korea [2019R1A6A1A11044070].
References
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Polymer photovoltaic cells: enhanced efficiencies via a network of internal donor-acceptor heterojunctions, Science, 1995, 270, 1789–1791 CrossRef CAS.
- Y. J. Cheng, S. H. Yang and C. S. Hsu, Synthesis of conjugated polymers for organic solar cell applications, Chem. Rev., 2009, 109, 5868–5923 CrossRef CAS.
- G. Li, R. Zhu and Y. Yang, Polymer solar cells, Nat. Photonics, 2012, 6, 153–161 CrossRef CAS.
- Y. Lin and X. Zhan, Oligomer molecules for efficient organic photovoltaics, Acc. Chem. Res., 2016, 49, 175–183 CrossRef CAS PubMed.
- L. Lu, T. Zheng, Q. Wu, A. M. Schneider, D. Zhao and L. Yu, Recent advances in bulk heterojunction polymer solar cells, Chem. Rev., 2015, 115, 12666–12731 CrossRef CAS PubMed.
- S. B. Darling and F. You, The case for organic photovoltaics, RSC Adv., 2013, 3, 17633–17648 RSC.
- J. Guo and J. Min, A Cost Analysis of Fully Solution-Processed ITO-Free Organic Solar Modules, Adv. Energy Mater., 2019, 9, 1802521 CrossRef.
- Y. Lin, Y. Firdaus, F. H. Isikgor, M. I. Nugraha, E. Yengel, G. T. Harrison, R. Hallani, A. El-Labban, H. Faber and C. Ma,
et al., Self-assembled monolayer enables hole transport layer-free organic solar cells with 18% efficiency and improved operational stability, ACS Energy Lett., 2020, 5, 2935–2944 CrossRef CAS.
- M. Zhang, L. Zhu, G. Zhou, T. Hao, C. Qiu, Z. Zhao, Q. Hu, B. W. Larson, H. Zhu and Z. Ma,
et al., Single-layered organic photovoltaics with double cascading charge transport pathways: 18% efficiencies, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed.
- Y. Cui, Y. Xu, H. Yao, P. Bi, L. Hong, J. Zhang, Y. Zu, T. Zhang, J. Qin and J. Ren,
et al., Single-Junction Organic Photovoltaic Cell with 19% Efficiency, Adv. Mater., 2021, 33, 2102420 CrossRef CAS PubMed.
- Y. Wei, Z. Chen, G. Lu, N. Yu, C. Li, J. Gao, X. Gu, X. Hao, G. Lu and Z. Tang,
et al., Binary organic solar cells breaking 19% via manipulating the vertical component distribution, Adv. Mater., 2022, 34, 2204718 CrossRef CAS.
- H. Yao and J. Hou, Recent Advances in Single-Junction Organic Solar Cells, Angew. Chem., 2022, 134, e202209021 Search PubMed.
- W. Gao, F. Qi, Z. Peng, F. R. Lin, K. Jiang, C. Zhong, W. Kaminsky, Z. Guan, C. S. Lee and T. J. Marks,
et al., Achieving 19% Power Conversion Efficiency in Planar-Mixed Heterojunction Organic Solar Cells Using a Pseudosymmetric Electron Acceptor, Adv. Mater., 2022, 34, 2202089 CrossRef CAS.
- Y. Lin, J. Wang, Z. G. Zhang, H. Bai, Y. Li, D. Zhu and X. Zhan, An electron acceptor challenging fullerenes for efficient polymer solar cells, Adv. Mater., 2015, 27, 1170–1174 CrossRef CAS.
- Y. Cui, H. Yao, L. Hong, T. Zhang, Y. Tang, B. Lin, K. Xian, B. Gao, C. An and P. Bi,
et al., Organic photovoltaic cell with 17% efficiency and superior processability, Natl. Sci. Rev., 2020, 7, 1239–1246 CrossRef CAS PubMed.
- A. Karki, J. Vollbrecht, A. J. Gillett, P. Selter, J. Lee, Z. Peng, N. Schopp, A. L. Dixon, M. Schrock and V. Nádaždy,
et al., Unifying charge generation, recombination, and extraction in low-offset non-fullerene acceptor organic solar cells, Adv. Energy Mater., 2020, 10, 2001203 CrossRef CAS.
- C. B. Nielsen, S. Holliday, H. Y. Chen, S. J. Cryer and I. McCulloch, Non-fullerene electron acceptors for use in organic solar cells, Acc. Chem. Res., 2015, 48, 2803–2812 CrossRef CAS PubMed.
- A. Kuzmich, D. Padula, H. Ma and A. Troisi, Trends in the electronic and geometric structure of non-fullerene based acceptors for organic solar cells, Energy Environ. Sci., 2017, 10, 395–401 RSC.
- G. Zhang, J. Zhao, P. C. Chow, K. Jiang, J. Zhang, Z. Zhu, J. Zhang, F. Huang and H. Yan, Nonfullerene acceptor molecules for bulk heterojunction organic solar cells, Chem. Rev., 2018, 118, 3447–3507 CrossRef CAS PubMed.
- J. Hou, O. Inganäs, R. H. Friend and F. Gao, Organic solar cells based on non-fullerene acceptors, Nat. Mater., 2018, 17, 119–128 CrossRef CAS.
- Y. Xu, H. Yao, L. Ma, J. Wang and J. Hou, Efficient charge generation at low energy losses in organic solar cells: a key issues review, Rep. Prog. Phys., 2020, 83, 082601 CrossRef CAS PubMed.
- J. Lee, S. J. Ko, H. Lee, J. Huang, Z. Zhu, M. Seifrid, J. Vollbrecht, V. V. Brus, A. Karki and H. Wang,
et al., Side-chain engineering of nonfullerene acceptors for near-infrared organic photodetectors and photovoltaics, ACS Energy Lett., 2019, 4, 1401–1409 CrossRef CAS.
- R. Ma, T. Liu, Z. Luo, Q. Guo, Y. Xiao, Y. Chen, X. Li, S. Luo, X. Lu and M. Zhang,
et al., Improving open-circuit voltage by a chlorinated polymer donor endows binary organic solar cells efficiencies over 17%, Sci. Chin. Chem., 2020, 63, 325–330 CrossRef CAS.
- Q. Ma, Z. Jia, L. Meng, J. Zhang, H. Zhang, W. Huang, J. Yuan, F. Gao, Y. Wan and Z. Zhang,
et al., Promoting charge separation resulting in ternary organic solar cells efficiency over 17.5%, Nano Energy, 2020, 78, 105272 CrossRef CAS.
- J. Yuan, Y. Zhang, L. Zhou, G. Zhang, H. L. Yip, T. K. Lau, X. Lu, C. Zhu, H. Peng and P. A. Johnson,
et al., Single-junction organic solar cell with over 15% efficiency using fused-ring acceptor with electron-deficient core, Joule, 2019, 3, 1140–1151 CrossRef CAS.
- A. Karki, J. Vollbrecht, A. L. Dixon, N. Schopp, M. Schrock, G. M. Reddy and T. Q. Nguyen, Understanding the High Performance of over 15% Efficiency in Single-Junction Bulk Heterojunction Organic Solar Cells, Adv. Mater., 2019, 31, 1903868 CrossRef CAS.
- A. Karki, J. Vollbrecht, A. J. Gillett, S. S. Xiao, Y. Yang, Z. Peng, N. Schopp, A. L. Dixon, S. Yoon and M. Schrock,
et al., The role of bulk and interfacial morphology in charge generation, recombination, and extraction in non-fullerene acceptor organic solar cells, Energy Environ. Sci., 2020, 13, 3679–3692 RSC.
- C. Yao, C. Peng, Y. Yang, L. Li, M. Bo and J. Wang, Larger VH (Hole Distribution Volume)/VM (Molecular Volume) Induced Higher Charge Mobility of Group IVA Element-Based Host Materials for Potentially Highly Efficient Blue OLEDs. The, J. Phys. Chem. C, 2018, 122, 22273–22279 CrossRef CAS.
- C. Yao, C. Peng, Y. Yang, L. Li, M. Bo and J. Wang, Elucidating the key role of fluorine in improving the charge mobility of electron acceptors for non-fullerene organic solar cells by multiscale simulations, J. Mater. Chem. C, 2018, 6, 4912–4918 RSC.
- C. Yao, Y. Yang, L. Li, M. Bo, C. Peng and J. Wang, Quad-rotor-shaped non-fullerene electron acceptor materials with potential to enhance the photoelectric performance of organic solar cells, J. Mater. Chem. A, 2019, 7, 18150–18157 RSC.
- Y. Yang, C. Yao, L. Li, M. Bo, J. Zhang, C. Peng, Z. Huang and J. Wang, Non-fullerene electron acceptors constructed by four strong electron-withdrawing end groups: Potential to improve the photoelectric performance of organic solar cells by theoretical investigations, Dyes Pigm., 2020, 181, 108542 CrossRef CAS.
- C. Yao, Y. Yang, L. Li, M. Bo, J. Zhang, C. Peng, Z. Huang and J. Wang, Elucidating the key role of the cyano (- C≡ N) group to construct environmentally friendly fused-ring electron acceptors, J. Phys. Chem. C, 2020, 124, 23059–23068 CrossRef CAS.
- Y. Yang, C. Yao, L. Li, M. Bo, M. He and J. Wang, Isomerization of two-dimensional non-fullerene electron acceptor materials for developing high-performance organic solar cells, J. Mater. Chem. C, 2022, 10, 11286–11295 RSC.
- N. S. Sariciftci, Polymeric photovoltaic materials, Curr. Opin. Solid State Mater. Sci., 1999, 4, 373–378 CrossRef CAS.
- M. P. Hughes, K. D. Rosenthal, N. A. Ran, M. Seifrid, G. C. Bazan and T. Q. Nguyen, Determining the dielectric constants of organic photovoltaic materials using impedance spectroscopy, Adv. Funct. Mater., 2018, 28, 1801542 CrossRef.
- J. Vollbrecht, J. Lee, S. J. Ko, V. V. Brus, A. Karki, W. Le, M. Seifrid, M. J. Ford, K. Cho and G. C. Bazan,
et al., Design of narrow bandgap non-fullerene acceptors for photovoltaic applications and investigation of non-geminate recombination dynamics, J. Mater. Chem. C, 2020, 8, 15175–15182 RSC.
- S. Shoaee, M. Stolterfoht and D. Neher, The Role of Mobility on Charge Generation, Recombination, and Extraction in Polymer-Based Solar Cells, Adv. Energy Mater., 2018, 8, 1703355 CrossRef.
- M. C. Heiber, T. Okubo, S. J. Ko, B. R. Luginbuhl, N. A. Ran, M. Wang, H. Wang, M. A. Uddin, H. Y. Woo and G. C. Bazan,
et al., Measuring the competition between bimolecular charge recombination and charge transport in organic solar cells under operating conditions, Energy Environ. Sci., 2018, 11, 3019–3032 RSC.
- J. Vollbrecht, V. V. Brus, S. J. Ko, J. Lee, A. Karki, D. X. Cao, K. Cho, G. C. Bazan and T. Q. Nguyen, Quantifying the nongeminate recombination dynamics in nonfullerene bulk heterojunction organic solar cells, Adv. Energy Mater., 2019, 9, 1901438 CrossRef.
- C. Shuttle, A. Maurano, R. Hamilton, B. O’regan, J. C. de Mello and J. Durrant, Charge extraction analysis of charge carrier densities in a polythiophene/fullerene solar cell: Analysis of the origin of the device dark current, Appl. Phys. Lett., 2008, 93, 183501 CrossRef.
- J. W. Ryan and E. Palomares, Photo-Induced Charge Carrier Recombination Kinetics in Small Molecule Organic Solar Cells and the Influence of Film Nanomorphology, Adv. Energy Mater., 2017, 7, 1601509 CrossRef.
- K. Nakano, Y. Chen and K. Tajima, Quantifying charge carrier density in organic solar cells by differential charging techniques, AIP Adv., 2019, 9, 125205 CrossRef.
- C. M. Proctor, C. Kim, D. Neher and T. Q. Nguyen, Nongeminate recombination and charge transport limitations in diketopyrrolopyrrole-based solution-processed small molecule solar cells, Adv. Funct. Mater., 2013, 23, 3584–3594 CrossRef CAS.
- E. Von Hauff, Impedance spectroscopy for emerging photovoltaics, J. Phys. Chem. C, 2019, 123, 11329–11346 CrossRef CAS.
- J. Vollbrecht and V. V. Brus, On charge carrier density in organic solar cells obtained via capacitance spectroscopy, Adv. Electron. Mater., 2020, 6, 2000517 CrossRef CAS.
- J. Vollbrecht, N. Tokmoldin, B. Sun, V. V. Brus, S. Shoaee and D. Neher, Determination of the charge carrier density in organic solar cells: A tutorial, J. Appl. Phys., 2022, 131, 221101 CrossRef CAS.
- N. Tokmoldin, J. Vollbrecht, S. M. Hosseini, B. Sun, L. Perdigón-Toro, H. Y. Woo, Y. Zou, D. Neher and S. Shoaee, Explaining the Fill-Factor and Photocurrent Losses of Nonfullerene Acceptor- Based Solar Cells by Probing the Long-Range Charge Carrier Diffusion and Drift Lengths, Adv. Energy Mater., 2021, 11, 2100804 CrossRef CAS.
- A. Wagenpfahl, Mobility dependent recombination models for organic solar cells, J. Phys.: Condens. Matter, 2017, 29, 373001 CrossRef PubMed.
- S. Albrecht, J. R. Tumbleston, S. Janietz, I. Dumsch, S. Allard, U. Scherf, H. Ade and D. Neher, Quantifying charge extraction in organic solar cells: the case of fluorinated PCPDTBT. The, J. Phys. Chem. Lett., 2014, 5, 1131–1138 CrossRef CAS PubMed.
- S. Schiefer, B. Zimmermann and U. Würfel, Determination of the intrinsic and the injection dependent charge carrier density in organic solar cells using the Suns-VOC method, J. Appl. Phys., 2014, 115, 044506 CrossRef.
- D. Neher, J. Kniepert, A. Elimelech and L. Koster, A new figure of merit for organic solar cells with transport-limited photocurrents, Sci. Rep., 2016, 6, 1–9 CrossRef.
- A. Armin, J. Subbiah, M. Stolterfoht, S. Shoaee, Z. Xiao, S. Lu, D. J. Jones and P. Meredith, Reduced Recombination in High Efficiency Molecular Nematic Liquid Crystalline: Fullerene Solar Cells, Adv. Energy Mater., 2016, 6, 1600939 CrossRef.
- P. Kaienburg, U. Rau and T. Kirchartz, Extracting Information about the Electronic Quality of Organic Solar-Cell Absorbers from Fill Factor and Thickness, Phys. Rev. Appl., 2016, 6, 024001 CrossRef.
- Q. An, X. Ma, J. Gao and F. Zhang, Solvent additive-free ternary polymer solar cells with 16.27% efficiency, Sci. Bull., 2019, 64, 504–506 CrossRef CAS PubMed.
- C. Tanase, E. J. Meijer, P. W. M. Blom and D. M. de Leeuw, Unification of the Hole Transport in Polymeric Field-Effect Transistors and Light-Emitting Diodes, Phys. Rev. Lett., 2003, 91(21), 216601 CrossRef CAS PubMed.
- V. D. Mihailetchi, H. Xie, B. Boer, L. A. de, Koster and P. W. Blom, Charge transport and photocurrent generation in poly (3-hexylthiophene): methanofullerene bulk-heterojunction solar cells, Adv. Funct. Mater., 2006, 16, 699–708 CrossRef CAS.
- F. Laquai, D. Andrienko, R. Mauer and P. W. Blom, Charge carrier transport and photogeneration in P3HT:PCBM photovoltaic blends, Macromol. Rapid Commun., 2015, 36, 1001–1025 CrossRef CAS.
- L. Perdigón-Toro, L. Q. Phuong, F. Eller, G. Freychet, E. Saglamkaya, J. I. Khan, Q. Wei, S. Zeiske, D. Kroh and S. Wedler,
et al., Understanding the Role of Order in Y-Series Non-Fullerene Solar Cells to Realize High Open-Circuit Voltages, Adv. Energy Mater., 2022, 12, 2103422 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00125c |
| ‡ Current address: Institut für Solarenergieforschung GmbH, Emmerthal, Germany. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Nurlan
Tokmoldin
*a,
Nurlan
Tokmoldin
 *a,
Bowen
Sun
a,
Elifnaz
Saglamkaya
a,
Lorena
Perdigón-Toro
a,
Seyed Mehrdad
Hosseini
a,
Jae Hoon
Son
b,
Han Young
Woo
*a,
Bowen
Sun
a,
Elifnaz
Saglamkaya
a,
Lorena
Perdigón-Toro
a,
Seyed Mehrdad
Hosseini
a,
Jae Hoon
Son
b,
Han Young
Woo
 b,
Safa
Shoaee
b,
Safa
Shoaee
 ac and
Dieter
Neher
ac and
Dieter
Neher
 a
a
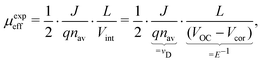
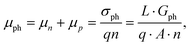
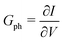 , we obtain:
, we obtain: