Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using small angle neutron scattering to explore porosity, connectivity and accessibility, towards optimised hierarchical solid acid catalysts†
Matthew E.
Potter
 *a,
Alice E.
Oakley
*a,
Alice E.
Oakley
 a,
Joshua J. M.
Le Brocq
a,
Lauren N.
Riley
a,
Marina
Carravetta
a,
Joshua J. M.
Le Brocq
a,
Lauren N.
Riley
a,
Marina
Carravetta
 a,
Stephen M.
King
a,
Stephen M.
King
 b,
Cara M.
Doherty
b,
Cara M.
Doherty
 c,
Bart D.
Vandegehuchte
d and
Robert
Raja
c,
Bart D.
Vandegehuchte
d and
Robert
Raja
 *a
*a
aUniversity of Southampton, Chemistry Department, Southampton, Hants SO17 1BJ, UK. E-mail: M.E.Potter@soton.ac.uk; R.Raja@soton.ac.uk
bISIS Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Harwell Campus, Didcot, Oxon, OX11 0QX, UK
cCSIRO Manufacturing, Private Bag 10, Clayton South, Victoria, Australia
dTotalEnergies, OneTech Belgium, Zone Industrielle Feluy C, B-7181 Seneffe, Belgium
First published on 20th September 2023
Abstract
The significant interest in developing hierarchical materials to overcome the traditional limitations of microporous catalysts, has led to a wide range of synthesis protocols being developed. In this work we modify traditional synthetic procedures known to yield highly crystalline microporous materials, by adding a hydrocarbon surfactant, leading to the formation of hierarchical solid-acid zeotypes; silicoaluminophosphates. We show for the first time, that small angle neutron scattering can build a qualitative description of the porosity in hierarchical materials, probing the exact nature of the micropores and mesopores within our system, that can be adapted to any hierarchical system. When combined with positron annihilation lifetime spectroscopy and porosimetry measurements we gain greater insight by exploring the accessibility and interconnectivity of the micropores and mesopores. We show that by varying the quantity of mesoporogen the size and nature of the mesopores can be finely tuned. Further, small angle neutron scattering reveals that mesopores are lined with a silica layer, that strongly influences the accessibility of the micropores. As such we show that our hierarchical materials contain distinct micropores housing stronger Brønsted acid sites, whilst the mesopores are lined with weaker silanol groups. This is complemented with a catalytic study focussing on n-butane isomerisation and ethanol dehydration that highlights the advantages and disadvantages of this design and further probes the influence of these bimodal porous systems on catalytic performance.
Introduction
Porous materials are widely used in industrial catalysis, where microporous frameworks (zeotypes), in particular, are central to many processes.1–3 Due to their improved surface areas, porous materials can form more isolated active sites,4,5 while still possessing a high density of accessible active sites. Porosity also plays a major role in controlling both diffusion and chemical kinetics.6–8 In the former, the size and density of pores influence, not only the speed at which reactants reach the active sites, but also the rate at which products leave, a vital factor for improving catalyst lifetime.9–11 Chemical kinetics are also heavily influenced by the system's porosity, as the constrained micropores are known to affect both reaction rate and the choice of chemical pathway.12–14 As a result of this, there is clear incentive to further optimise these materials to overcome the traditional disadvantages of microporous materials, such as being limited to smaller reagents15 and deactivation due to pore-blockage.16 By their very nature mesoporous materials, particularly siliceous materials, such as the well-known SBA-15 (9 nm pore diameter) and MCM-41 (3 nm pore diameter), do not suffer with such issues. Indeed, such species often possess higher surface areas and pore volumes than similar microporous materials, leading to increasingly isolated active species. Several studies comparing the activity of microporous and mesoporous materials have confirmed similar levels of activity, though, as expected the mesoporous species favoured larger, bulkier products.17 To consolidate the advantages of microporous and mesoporous systems, whilst minimising the drawbacks, interest in hierarchical zeotype materials has grown rapidly.Hierarchical materials possess multiple levels of porosity, typically containing both microporous (≤2 nm) and mesoporous (2–50 nm) features.18–21 There are now multiple approaches to introduce mesoporosity into microporous materials, which are loosely categorised as either ‘top-down’ or ‘bottom-up’ processes.22,23 In a top-down process the microporous material is modified post-synthetically to create mesopores, typically by eroding the framework in a controlled manner, commonly through desilication or dealumination.22–24 In contrast, bottom-up processes form mesopores alongside the microporous framework, by introducing a mesopore templating agent to the synthesis mixture, which is then removed post-synthesis.22,23 Having such a large variety of methods to create hierarchical materials means that the benefits and drawbacks of each approach must be carefully evaluated.
Over the last two decades research into hierarchical aluminophosphates (AlPOs) has surged, driven by the desire for improved methanol-to-olefin catalysts.25–27 AlPOs are microporous materials that are iso-structural to zeolites, often with identical framework topologies.28,29 Unlike zeolites, AlPOs are made of alternating AlO4 and PO4 tetrahedral units bound together by Al–O–P bonds, instead of primarily SiO4 species with Si–O–Si bonds as found in zeolites. In zeolites, replacing a Si4+ framework species with Al3+ is a well understood method to create acid sites.30,31 Similarly, AlPOs can substitute Si4+ into the framework to create silicon-substituted aluminophosphates (SAPOs).32 Si4+ can either exclusively substitute for a framework P5+via type II substitution to create isolated active sites, or can form silicon islands by replacing adjacent Al and P pairs, through a combination of type II and III substitution.32,33 Both methods lead to protons binding to a framework oxygen, adjacent to the dopant Si, forming Brønsted acid sites (BAS) for acid catalysis. More recently we have shown that the inclusion of a surfactant (DMOD; dimethyloctadecyl[(3-(trimethoxysilyl)propyl] ammonium chloride)) successfully forms hierarchical SAPO species, which showed improved catalytic activity in the production of ε-Caprolactam.34 The catalytic improvement was partially due to the mesopores preventing the build-up of bulkier coke precursors within the micropores, though another key factor was the surfactant choice.34,35 The DMOD surfactant has a polar alkoxysilane head, which interacts with the synthesis gel, while the hydrocarbon tails will interact with neighbouring DMOD species, similar to swelling agents. As a result, it was shown that post-calcination, the silane head-group of DMOD remained, forming a layer of silica around the mesopores.34 This introduced a greater range of acid sites into the hierarchical SAPO systems that could perform the catalytic rearrangement.
The significant potential of hierarchical AlPOs is clear, though to understand the synthesis procedure, and optimise the catalytic behaviour, it would be desirable to control the mesopore properties.36 To this end, further studies modifying the synthesis protocol are required. In this work we focus on how the DMOD quantity added in the synthesis of SAPO-5 influences the porosity and catalytic behaviour. While catalytic behaviour can be routinely tested, porosity is often harder to probe. Physisorption methods are routinely used to explore the porosity of the system.32,37 While many methods exist to quantify the surface area, pore widths and even pore shapes, physisorption can ultimately only provide information on the accessible open space. It cannot give details on the surface composition or inaccessible voids. Small angle scattering techniques with neutrons (SANS) or X-rays (SAXS), however, produce signals based on the contrast between phases, and does not require a molecular probe.38 These two phases could, for example, be the empty pore and the framework walls, therefore providing useful and complementary insights into porosity.39 Loosely, the intensity of both SANS and SAXS comes from the square of the difference in scattering length density (SLD; ρ) between the two phases, what is termed ‘contrast’, as well as the number (N) and sizes (volume, V) of the pores:38,40
| I(Q) α (ρA− ρB)2NV2 |
We have previously found that the introduction of DMOD for the creation of hierarchically porous SAPO-37 resulted in increased catalytic performance in the Beckmann rearrangement of cyclohexanone oxime to ε-caprolactam.34,48 In this work, we have systematically studied the introduction of DMOD for creating hierarchically porous SAPO-5 catalysts, by incorporating varying quantities of the mesopore templating agent (DMOD) into a well-established synthetic procedure that was previously reported34,48 for creating highly crystalline microporous SAPO-5 (MP-SAPO-5). By using complementary structural (SANS) physicochemical (N2 Physisorption), textural (PALS) and acid site characterisation (ssNMR) techniques, we will build a holistic understanding of the porosity in our hierarchical systems. This combined with our catalytic findings on n-butane isomerisation and ethanol dehydration will provide significant insight into the design of hierarchical materials, their limitations, and future potential.
Materials and methods
Synthesis
For microporous SAPO-5, pseudo boehmite (AlOOH, 3.0 g), phosphoric acid (H3PO4, 5.75 g, 85 wt% in water) and deionised water (22.5 mL) were added to a Teflon beaker and stirred for 4 hours. Triethylamine (C6H15N, 5.06 g) and colloidal silica gel (SiO2, 1.5 g, 40 wt% in water) were added dropwise sequentially to the gel and then stirred for 2 hours. The gel was then transferred into PTFE lined autoclaves and heated in the oven at 200 °C for 24 hours. On removal and cooling the samples were washed with 500 mL of deionised water and dried overnight at 70 °C before being calcined at 550 °C for 16 hours, under a flow of air, with a ramp rate of 2.5 °C min−1.For hierarchical SAPO-5, an identical procedure was followed, except the surfactant; DMOD (40 wt% in methanol) was added to the reaction mixture with TEA and colloidal silica gel. The gel compositions for the materials are listed below (Table 1).
| System | Molar gel ratio |
|---|---|
| MP-SAPO-5 | 2Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2P 2P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2TEA 2TEA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53H2O 53H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.34Si 0.34Si |
| HP-SAPO-5_0.1 | 2Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2P 2P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2TEA 2TEA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53H2O 53H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.34Si 0.34Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1DMOD 0.1DMOD |
| HP-SAPO-5_0.2 | 2Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2P 2P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2TEA 2TEA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53H2O 53H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.34Si 0.34Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2DMOD 0.2DMOD |
| HP-SAPO-5_0.3 | 2Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2P 2P![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2TEA 2TEA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53H2O 53H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.34Si 0.34Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3DMOD 0.3DMOD |
Small angle neutron scattering (SANS)
SANS data were collected on the LOQ small-angle diffractometer49 at the ISIS Neutron and Muon Source, Didcot, UK.50 This is a fixed-geometry “white beam” time-of-flight instrument which utilizes neutrons with wavelengths 2.2 ≤ λ ≤ 10 Å. Data are simultaneously recorded on two, two-dimensional, position-sensitive, neutron detectors situated at 0.5 and 4 m from the samples, to simultaneously probe scattering vectors in the range ∼0.007 ≤ Q ≤ 1.4 Å−1, where:Q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 2π/d θ = 2π/d |
0.15 g of dried SAPO-5 samples were densely packed into cylindrical, 1 mm pathlength, synthetic quartz cuvettes (Starna Type 21/Hellma Type 404). Where required 0.3 mL of D2O/H2O mixtures were added to these samples, which were sonicated for 15 minutes, ensuring that the SAPO-5 catalysts were fully saturated. Four different solvents were used (Table 2).
| Liquids | D2O (wt%) | H2O (wt%) | SLD (Å−2) | Contrast to AlPO4 (Å−4) | Contrast to SiO2 (Å−4) |
|---|---|---|---|---|---|
| D2O | 100 | 0 | 6.4 × 10−6 | 5.29 × 10−12 | 8.41 × 10−12 |
| A | 69.2 | 30.8 | 4.1 × 10−6 | 0 | 0.36 × 10−12 |
| B | 60.9 | 39.1 | 3.5 × 10−6 | 0.36 × 10−12 | 0 |
| H2O | 0 | 100 | −0.6 × 10−6 | 22.1 × 10−12 | 16.8 × 10−12 |
SANS data were collected on all four SAPO-5 catalysts, under ‘dry’ conditions.
Further measurements were made on HP-SAPO-5_0.3, dispersed in the liquids in Table 2, to explore the accessibility and the origin of the features shown. An empty cuvette and the pure solvents were also measured as backgrounds. Scattering data on each sample or background were accumulated for a total of 120 minutes to gather data of high statistical precision. Transmission (neutron absorption) data were accumulated for 10 minutes.
Each ‘raw’ 2D data set was then corrected for the detector efficiencies and spatial linearity, sample transmission and background scattering, and reduced to 1D differential scattering cross-section data (∂Σ/∂Ω vs. Q) using the MantidPlot framework (version 4.1.0).51,52
These data were then placed on an absolute scale (cm−1) by comparison with the scattering from a standard sample (a solid blend of hydrogenous and perdeuterated polystyrene) measured under the same instrument configuration in accordance with established procedures.53 In common with the accepted convention in SANS, we shall henceforth refer to (∂Σ/∂Ω) as ‘intensity’, I(Q). To derive meaningful structural information from the reduced data, as opposed to a fully quantitative structural refinement, optimised model-fitting was conducted using the SasView program (version 4.2.2).54 Further details of this are provided in the ESI.†
n-Butane isomerisation catalysis
Catalytic butane isomerisation measurements were performed using a fixed bed reactor, containing 0.3 g of calcined material, pelletised and sieved between 300–500 μm. The sample was dried at 400 °C for 1 hour under a 80 mL min−1 flow of nitrogen in the reactor prior to the reaction. After this the gas flow was changed to 5 mL min−1 of 10% n-butane in nitrogen, at 300 °C under atmospheric pressure. Samples were taken every 15 minutes using an online PerkinElmer Arnel 4035 gas chromatogram (GC), equipped with a FID (Flame Ionised Detector) and an Alumina Sulfate PLOT column, 50 m × 0.53 mm. The peak areas were then used to calculate conversion and selectivity, normalised based on a molar basis.Ethanol dehydration catalysis
Catalysis was performed using a custom-built flow reactor provided by Cambridge Reactor Design. 0.3 g of calcined catalyst was used for each reaction, sieved between 300–500 μm. The sample was dried at 400 °C for 1 hour under a 25 mL min−1 flow of nitrogen prior to the reaction. The initial temperature measured was 140 °C, at which point the nitrogen flow was kept at 25 mL min−1, and a liquid flow of 10 μL min−1 of 10 vol% heptane (internal standard) in ethanol was flown. After 40 minutes, 250 μL of the vaporized output was injected as a gas into a PerkinElmer Clarus 460 GC with a FID, with a HP1 cross linked methylsiloxane (30 m × 0.32 mm × 1 μm film thickness) column. All results shown are the average of three consistent samples. The temperature was then subsequently increased by 20 °C, and resampled after 40 minutes as required.Powder diffraction
Powder X-ray diffraction was performed on a Bruker D2 Phaser diffractometer using a 1D LYNXEYE detector and 0.6 mm slits, with Cu Kα1 radiation. Patterns were run over a 2θ range of 5–40° with a scan speed of 3° min−1 and an increment of 0.01°.Nitrogen physisorption
BET surface area measurements were performed at −196 °C, on a sample dried under 20 mTorr of vacuum at 120 °C overnight. Analysis was performed on a Micromeritics Gemini 2375 surface area analyser. Surface area was calculated using the BET model,55 while the pore width distribution was calculated with the BJH model.56Positron annihilation lifetime spectroscopy (PALS)
Samples were degassed overnight at 120 °C prior to being loaded into an analysis cell. A positron point source (3.5 MBq 22NaCl sealed in Mylar envelope) was placed in the centre of the 3 mm thick packed sample. The samples were measured at room temperature under vacuum (5 × 10−6 torr) using Ortec EG&G Spectrometers with a resolution of 230 ps. A minimum of 5 files with 4.5 × 106 integrated counts were collected for each sample and the resulting time spectra were fit using LT-v9 software.57 The data was fit to 5 components and a source component (1.48 ns, 3.4%). Three of the longer lifetime components were assigned to micro and mesopores. The lifetimes were converted to average pore sizes using the Relative Tao-Eldrup relationship.58,59 The pore size distributions were prepared using the PAScual software.60Inductively coupled plasma – mass spectrometry (ICP-MS)
10 mg of samples were first digested in 1 mL of concentrated HNO3, 1 mL of concentrated HCl and 0.75 mL of concentrated HF. The samples were heated overnight at 120 °C to ensure that complete digestion occurred. Samples were then diluted into 60 mL of deionised water and then diluted 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 into 3% HNO3 in deionised water. These samples were then run on a High Resolution ICP-MS Thermo ELEMENT 2XR, with appropriate standards for quantification.
100 into 3% HNO3 in deionised water. These samples were then run on a High Resolution ICP-MS Thermo ELEMENT 2XR, with appropriate standards for quantification.
Solid state nuclear magnetic resonance (ssNMR)
Samples were packed into 4 mm pencil-style zirconium oxide rotors and acquired at a spinning rate of 8 kHz using a 4 mm RevolutionNMR probe. 1H, 27Al, and 31P spectra were acquired in triple resonance mode, and29 Si in double resonance on a Bruker Avance Neo widebore Spectrometer, using a 9.4 T field, in air. The sample 1H, 27Al, and 31P, and 29Si T1 relaxation time was assessed using a saturation recovery pulse technique, which was used for the respective direct acquisitions.Scanning electron microscopy (SEM)
SEM images were acquired at the Southampton Biomedical Imaging Unit, using an FEI Quanta 250 FEG scanning electron microscope. Samples were sputter coated with platinum prior to imaging.Temperature programmed desorption (TPD)
TPD measurements were obtained at TotalEnergies OneTech Belgium, Feluy using an Autochem II 2920 device from Micromeritics. In a typical experiment, 0.5 g of sample is heated up to 600 °C (10 °C min−1) and maintained for 2 h under 50 mL min−1 of pure He. Next, the sample is cooled down to 150 °C (10 °C min−1), and after 30 min the gas feed is changed from pure He to 30 mL min−1 of a mixture of 10 vol% NH3 in helium. This condition is maintained for 8 h after which the gas feed is again switched to 50 mL min−1 He. After 1.17 h required for detector stabilisation and the removal of physisorbed NH3, the sample is heated up to 260 °C (10 °C min−1) and maintained for 1 h to fully resolve the first, low-temperature peak signal. Finally, the sample is further heated up to 600 °C (10 °C min−1) and maintained for 40 min to resolve the second, high-temperature peak signal. Only the latter peak signal was considered for acidity quantification.Results and discussions
Confirming the catalysts structural and textural integrity
The integrity of the hierarchical (HP) and microporous (MP) SAPO-5 systems was initially confirmed using powder XRD (Fig. S1†), which exclusively showed peaks attributable to the expected AlPO-5 (AFI) framework.61 Some subtle variations in peak width and position can be seen, suggesting slight variations in the unit cell parameters, and in particle size. This is likely due to the incorporation of disordered mesopores within the hierarchical systems, causing a relaxation or distortion of the idealised unit cell. No other peaks are present, confirming the phase-purity of the systems.In MP-SAPO-5, 1.4 wt% of Si is present in the framework, due to the colloidal silica dopant undergoing isomorphous substitution in the framework (Table S1†). The ratio of phosphorus and silicon to aluminium shows some deviation from unity, suggesting a mixture of type II and type III Si substitution has occurred. ICP analysis also shows that introducing DMOD to the synthesis leads to a significant increase in the Si content of the final material, with HP-SAPO-5_0.1 possessing considerably more Si than MP-SAPO-5 (6.1 and 1.4 wt% respectively). Further, adding larger quantities of DMOD yields even higher Si loadings with HP-SAPO-5_0.2 and HP-SAPO-5_0.3 containing 9.8 and 11.2 wt% of silicon, respectively (Table S1†). As the amount of colloidal silica (non DMOD silica source) does not vary during the synthesis, and resulted in only 1.4 wt% of Si in MP-SAPO-5, then most of the Si in the HP-SAPO-5 systems must be attributed to the silane headgroups. It is likely that these are lining the mesoporous walls post-calcination, leading to a silica layer.34 As the DMOD ratio increases, the molar ratio of silicon and phosphorus to aluminium notably deviates from unity, again suggesting type II substitution is less prevalent.32,62
N2 physisorption was initially used to explore the porosity of the systems, here MP-SAPO-5 shows a classic type I isotherm, showing the system is primarily microporous as expected (Fig. 1A).63 A subtle hysteresis occurs after P/P0 = 0.5, which has previously been attributed to inter-crystalline voids and surface roughness.8,33,64
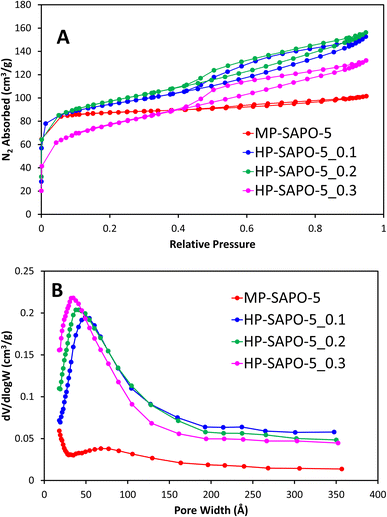 | ||
| Fig. 1 Showing the N2 physisorption isotherms (A) and the corresponding BJH pore distribution plots (B) for microporous and hierarchical SAPO-5. | ||
The pore volumes and surface areas of MP-SAPO-5 agree with previous work, again showing that the majority of the pore volume is due to the micropores (Table 3).33 The three HP-SAPO-5 systems show similar surface areas to MP-SAPO-5, but present a type IV isotherm, supporting the systems being hierarchical, possessing both micropores and mesopores (Fig. 1A).63 The H4 hysteresis shown is commonly associated with narrow slit-like pores or hollow spheres, suggesting hindered accessibility to the mesopores.63 The HP-SAPO-5 species have lower micropore volumes than the MP-SAPO-5, but larger mesopore volumes, resulting in a larger total pore volume compared to MP-SAPO-5.
| System | Surface area (m2 g−1) | Micropore volume (cm3 g−1) | Mesopore volume (cm3 g−1) | Total pore volume (cm3 g−1) | Average mesopore width (Å) |
|---|---|---|---|---|---|
| MP-SAPO-5 | 303 | 0.12 | 0.04 | 0.16 | N/A |
| HP-SAPO-5_0.1 | 315 | 0.09 | 0.14 | 0.23 | 49 |
| HP-SAPO-5_0.2 | 260 | 0.09 | 0.16 | 0.24 | 38 |
| HP-SAPO-5_0.3 | 265 | 0.05 | 0.16 | 0.21 | 32 |
This suggests that varying the quantity of DMOD does not significantly affect the total pore volumes or surface areas, though clearly influences the mesopore volume at the expense of the micropore volume, suggesting some micropores may be becoming blocked. The pore size distribution (Fig. 1B) shows that the quantity of DMOD also influences the pore size, as the maximum, and average pore width decreases with increased DMOD. We note that our BET data is not suitable to describe the small pore region (<15 Å), however we can see a preference for smaller mesopores in the HP systems, as the initial data points (17 Å) increase with increasing DMOD quantity, again suggesting a tendency towards smaller mesopores. The hierarchical species also show a subtle feature around 200–250 Å, typically assigned to intracrystalline voids. Overall, the physisorption confirms the hierarchical nature of the HP-SAPO-5 systems. Further these findings suggest that the mesopore size can be tailored within a narrow range by careful addition of DMOD.
Positron annihilation lifetime spectroscopy (PALS) was used in combination with the N2 physisorption data to probe the porosity of the MP-SAPO-5 and three HP-SAPO-5 systems. While N2 physisorption is well suited to probing longer length scales such as mesopores and macropores, PALS can provide complementary evidence over smaller (micropore) length scales. PALS identified three distinct lifetimes (Fig. 2); τ3, τ4 and τ5, relating to positron decay within the catalyst pores. These lifetimes were in the range of 0.86 to 1.01 ns, 4.0 to 5.2 ns and 30 to 48 ns, respectively in the four SAPO-5 systems. Using the Tao–Eldrup relationship58,59 these lifetimes were converted into average pore diameters (Table 4). The three lifetimes (τ3, τ4 and τ5) have previously been linked to different regions and locations within a hierarchical SAPO-37 species, also prepared using a DMOD surfactant.34τ3 corresponds to positrons which decay within the local microporous structure, specifically the d3 value matches the diameters of the 6-membered rings, which make up the secondary building units of the AlPO-5 framework.65 There is some indication that the d3 value increases as DMOD is increased, however, the changes fall within the range of uncertainty.
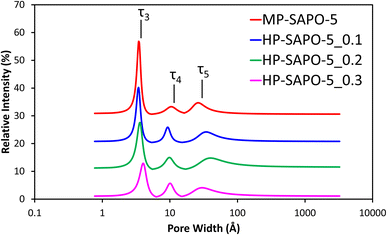 | ||
| Fig. 2 Fitted pore-size distributions of the four SAPO-5 materials from PALS experimental data. Each data set is incrementally increased by 10% for clarity. | ||
| System | Lifetime (ns) | Intensity (%) | Average pore diameter (Å) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| τ 3 | τ 4 | τ 5 | I 3 | I 4 | I 5 | d 3 | d 4 | d 5 | |
| MP-SAPO-5 | 0.86 ± 0.04 | 5.16 ± 0.34 | 30.3 ± 1.2 | 26.8 ± 3.7 | 3.3 ± 0.3 | 4.7 ± 0.1 | 2.8 ± 0.1 | 10.6 ± 0.3 | 25.8 ± 0.7 |
| HP-SAPO-5_0.1 | 0.87 ± 0.05 | 4.02 ± 0.10 | 41.3 ± 1.1 | 20.2 ± 3.0 | 5.9 ± 1.0 | 4.2 ± 0.4 | 2.8 ± 0.2 | 9.4 ± 0.1 | 32.9 ± 0.8 |
| HP-SAPO-5_0.2 | 0.94 ± 0.16 | 4.33 ± 0.33 | 47.6 ± 3.6 | 17.6 ± 7.3 | 5.0 ± 0.4 | 4.8 ± 0.1 | 3.1 ± 0.6 | 9.7 ± 0.4 | 37.8 ± 3.0 |
| HP-SAPO-5_0.3 | 1.01 ± 0.11 | 4.70 ± 0.24 | 36.4 ± 1.6 | 12.9 ± 3.0 | 5.7 ± 0.3 | 4.1 ± 0.1 | 3.4 ± 0.4 | 10.2 ± 0.3 | 29.6 ± 1.1 |
This may be an indication that the mesopores in the HP-SAPO-5 systems are disrupting the local framework structure. We also note that the intensity of the τ3 lifetime (I3) significantly decreases with increased DMOD in the synthesis. This is in good agreement with the BET findings, which also suggested that the micropore volume decreases with increasing DMOD. The τ4 lifetime has previously been attributed to positron decay within intracrystalline defects and within the main micropore channel itself. Given that the micropore diameter of SAPO-5 is 7.3 Å, it is likely that τ4 is an average of these two features. The growing quantity of defects may be due to the crystalline microporous MP-SAPO-5 system being perturbed by mesopores. This is evidenced again by the intensity of τ4 (I4) increasing from 3.3% in MP-SAPO-5, to between 5.0 and 5.9% with the HP-SAPO-5 series. Finally the τ5 lifetime, which represents positron decay in the mesopores,11,34 is notably larger in the HP systems, also shows some variation from the HP systems compared to the MP-SAPO-5 system. Despite not purposefully having mesopores engineered into MP-SAPO-5, it still has a τ5 signal. This is due to inherent properties of the system, such as intraparticle porosity, particle agglomeration or defect sites. Notably the lifetime of the τ5 signal for MP-SAPO-5 and the average pore diameter (d5) are significantly lower than those present in the three HP-SAPO-5 samples. This change is due to the of enhanced mesoporosity in the HP systems, extending the PALS lifetime (τ5),11,34 as the positrons reside in large pore diameters (d5), supporting our nitrogen physisorption findings. In contrast the MP systems only possess intraparticle porosity and surface roughness. However, we note that the uncertainties associated with this lifetime are much larger than the others, likely due to an increased spread in the sizes of the mesopores. Despite this we note that the inclusion of DMOD in the synthesis (HP-SAPO-5) increases the pore diameter relative to the microporous (MP-SAPO-5) system, supporting mesopore formation. Thus, combining the nitrogen physisorption with the PALS data, highlights the influence of DMOD inclusion, perturbing the local environment and promoting mesopore formation.
SEM confirms the highly crystalline nature of MP-SAPO-5, primarily exhibiting hexagonal crystals, roughly 2–3 μm in size, in excellent agreement with the hexagonal P6/mcc unit cell (Fig. S2†). In contrast the HP-SAPO-5 systems are mainly composed of larger aggregates species (Fig. S3 to S5†), despite being phase pure and having the expected surface area and pore volumes. The surface roughness of the HP-SAPO-5 systems appears more variable, with some areas resembling the MP-SAPO-5, whilst others do not. This suggests that the addition of DMOD also significantly influences the surface texture and roughness of the system.
Contrasting acid sites
The 31P and 27Al environments were probed using solid state NMR measurements, to confirm the AlPO structure had formed. All four SAPO-5 species showed a single 31P peak (Fig. S6A†), centred at −30 ppm, attributed to the expected tetrahedral P(OAl)4 environment.64,66 Similarly the 27Al NMR spectra (Fig. S6B†) all showed a single dominant feature centred at 35 ppm, attributed to the framework Al(OP)4 species.64,67In some cases, a small shoulder feature was visible in the 27Al spectra at roughly 10 ppm. This is assigned to small quantities of extra-framework AlO6 species.64,67 Overall these features confirm the integrity of the intended AlPO framework.
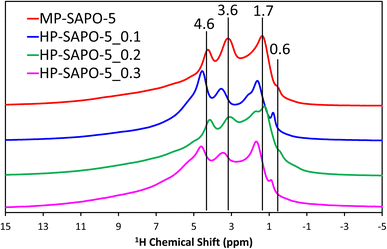
The 29Si NMR spectra (Fig. S6C†) for the microporous MP-SAPO-5 species show a dominant feature at −109 ppm, due to Si(OSi)4 species within silicon islands. This suggests that silicon has incorporated into the framework via a combination of type II and type III substitution, as expected from the ICP findings.8,32,62,64,68,69 A feature at −88 ppm is also present, representing isolated Si(OAl)4 species, indicative of type II substitution, with some potential signals between −94 and −97 ppm due to Si(OSi)1(OAl)3 on the periphery of silicon islands.8,32,64 The addition of DMOD to the synthesis gel appeared to increase the relative intensity of the main −109 ppm feature, compared to the −88 ppm signal. As such we see evidence from the 29Si NMR that some of the colloidal silica species underwent successful framework substitution in MP-SAPO-5. However, in contrast the DMOD did not undergo successful framework substitution. This supports our hypothesis that the Si from the DMOD surfactant is in a highly-siliceous phase, with limited contact with the AlPO framework.341H NMR (Fig. 3) was able to give more direct evidence on the acidity of the system, showing a range of environments.
The microporous MP-SAPO-5 species shows three main signals at 4.6, 3.6 and 1.7 ppm. The former is associated with water within the framework material, whereas the 3.6 ppm signal is due to the presence of BAS, indicative of isomorphous silicon substitution into the framework.34,70 The 1.7 ppm signal is typically assigned to the Si–OH species, suggesting some silanol defects are present, due to silicon islanding or incomplete silicon substitution, as seen in the 29Si NMR signal.34,70 Another subtle feature at 0.6 ppm is also present in the microporous MP-SAPO-5 which is due to the presence of terminal P–OH groups, which are ever-present on the surface of AlPO materials.34,70 There is also a shoulder peak around 6.0 ppm, which we attribute to being either bulk water or hydrogen-bonded silanol species.68 We note in the HP-SAPO-5 systems that there is a shift in peak positions to higher chemical shifts. This has previously been attributed to the presence of mesopores changing the confinement of the different species, however the shift is not significant enough to change the signal assignments.70 More noticeable is the change in the relative intensities of the Si–OH and BAS signals. These signals are at similar intensities in the MP-SAPO-5 species but increasing quantities of DMOD show a transition to the Si–OH signal becoming dominant. This finding further supports the hypothesis that the DMOD surfactant is creating a silica layer, rich with silanols.34
The acidity of the four systems were probed using ammonia temperature probe desorption (NH3-TPD, Table S2†). The measurements showed the presence of chemisorbed NH3 species, ascribed to moderate-strong acid sites, all desorbing within the 370–390 °C region.71 However, there were few discernible trends between the four systems, possibly due to the wide variety of species present. We note that adding DMOD to the system (HP-SAPO-5 species) increased the quantity of NH3 desorbed in this region, from 188 μmol gsample−1 to between 245–330 μmol gsample−1 (Table S2†). This confirms that the addition of DMOD noticeably increases the total acidity of the systems. We also note that the total acidity of the microporous (MP-SAPO-5) system is significantly lower than the theoretical acidic quantity, if all Si present had formed isolated acid sites via type II substitution (498 μmol gsample−1). This supports our Si NMR findings, which show that a significant quantity of Si(OSi)4 species are present.32
Catalysis findings
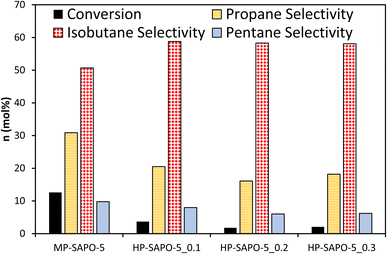
The four SAPO-5 catalysts were tested for their activity in the acid-catalysed isomerisation of n-butane (Fig. 4 and S7†). Typically, this reaction is initiated by strong BAS, regardless of whether the mono- or bi-molecular mechanism is dominant, as both require the activation of a C–H bond.72 Given that both the n-butane reactant and iso-butane product readily fit within the 7.3 Å cylindrical pores of the AlPO-5 framework, the micropore geometry should not hinder the reaction. This means that the catalysis data here should be a useful indicator for the nature of the active sites and their accessibility.Despite possessing framework acid sites, all three HP-SAPO-5 systems were relatively inactive, achieving <5 mol% conversion in all cases, mostly converting to isobutane (Fig. 4 and S7†).
In contrast the MP-SAPO-5 was much more active, achieving roughly 12 mol% conversion of n-butane, primarily to isobutane. This cracking behaviour is typically associated with strong acid sites.72 This suggests that despite the HP-SAPO-5 systems possessing a greater quantity of acid sites, they are weaker than those in MP-SAPO-5. This would suggest that the stronger BAS due to framework silicon substitution (MP-SAPO-5) are being blocked or weakened by the presence of the silanol species from DMOD. This hypothesis aligns with our recent work on the Beckmann rearrangement, a reaction known to require weaker acid sites.8,64 Previously we showed that a hierarchically porous SAPO-37 system (prepared with DMOD) featured improved activity compared to the analogous microporous SAPO-37 system,48 which was attributed to the increased quantity of silanol species. However, we must consider the differences in the two processes, as the Beckmann rearrangement is known to require much weaker strength acid sites for optimal performance.8 In principle, the Beckmann rearrangement could be activated by weaker silanol species, whereas the n-butane isomerisation is unlikely to be. Despite this, the significant differences in conversion are surprising, especially given the higher acid site density of the HP-SAPO-5 systems.
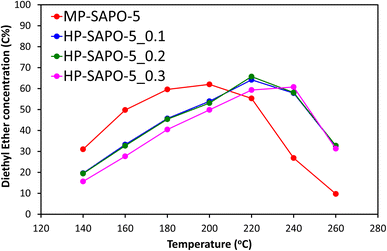
The four materials for the acid-catalysed dehydration of ethanol to ethylene (Fig. 5 and S8†), a reaction where SAPO-5 has shown reasonable activity,33 and which does not exclusively require stronger acid sites. We have previously shown that this reaction proceeds via a two-step mechanism in SAPO materials.73 The initial step sees ethanol molecules rapidly combine to form the diethyl ether (DEE) intermediate, which then decomposes to give ethylene, with the latter step being rate-limiting.73 The materials were tested under identical conditions, over a range of 140–260 °C to observe the changes in the reaction profile. We see that the introduction of DMOD reduces the overall activity of the system, as seen by increased ethanol output (Fig. S8A†), with increased temperature lowering the ethanol output. This again shows that the extra Si species from the DMOD surfactant are either not contributing to the reactivity or are hindering it.
Further we observe the reverse trend for ethylene (Fig. S8B†), where greater quantities of DMOD led to lower quantities of the final product; ethylene, again with higher temperatures improving the activity, forming more ethylene. The DEE profile is more enlightening (Fig. 5), as each SAPO-5 system goes through a maximum DEE value, with the temperature of this maximum depending on the DMOD concentration. MP-SAPO-5 reaches a maximum DEE concentration at 200 °C, with HP-SAPO-5_0.1 and HP-SAPO-5_0.2 both reaching the maxima at 220 °C. Finally, HP-SAPO-5_0.3 reaches its maximum DEE value at 240 °C, again highlighting the difference in activity and acidity in these four systems. Despite the HP-SAPO-5 species possessing a greater number of acid sites than the MP-SAPO-5 species, in both reactions (n-butane isomerisation and ethanol dehydration) they exhibited inferior catalytic activity. To rationalise these findings further we explored the porosity of these systems further using SANS measurements.
Probing porosity with SANS
The SANS data from the four bare dried SAPO-5 catalysts show a variety of features over the wide Q range studied (0.007 to 1.4 Å−1, corresponding to distances between 900 and 5 Å, Fig. 6). Stark differences can be seen between the MP-SAPO-5 and three HP-SAPO-5 systems. In the low Q range (<0.01 Å−1) the MP-SAPO-5 instantly diverges from the three HP-SAPO-5 systems as Q increases, decaying at a faster rate, to a higher power of Q. This faster decay in MP-SAPO-5 is indicative of scattering from surfaces that are less rough, as seen in the SEM images (Fig. S2–S5†).40 The MP-SAPO-5 data is then largely featureless below 0.5 Å−1, whereas two oscillations can be seen in the HP-SAPO-5 systems at Q values of roughly 0.02 and 0.04 Å−1. It is only beyond these oscillations, in the 0.1 to 0.4 Å−1Q range, that the three HP-SAPO-5 systems differ from one another. This corresponds to length scales of 60 to 15 Å, the mesopore region, where those samples prepared with an increased DMOD ratio exhibit slightly greater intensity. After these features, all four datasets loosely converge onto a similar background with two notable defined peaks at Q values of 0.52 and 0.92 Å−1 (d values of 12.6 and 7.0 Å respectively).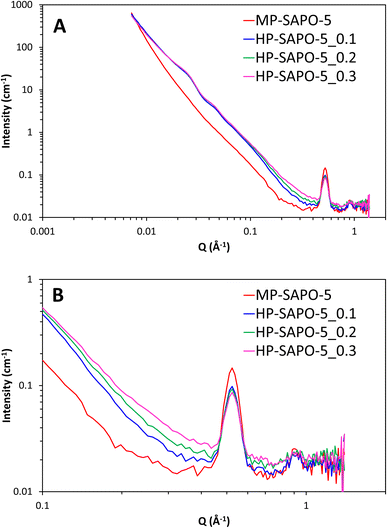 | ||
| Fig. 6 SANS data of the four dried, bare, SAPO-5 species over full Q range (A) and zoomed in on high Q range (B). | ||
To interpret these data in a methodical manner we started by modelling the simpler MP-SAPO-5 system. This system is better defined, and only contains the microporous SAPO (principally AlPO4) phase, making it a logical starting point before tackling the more complex HP-SAPO-5 systems.
The MP-SAPO-5 system was modelled in SasView54 using a weighted summation of terms, as is common in small angle scattering analysis.74,75 Here a power law term for the interfacial scattering from the pores, a fractal term, which importantly includes a structure factor (S(Q)) and accounts for micropores (where the aggregates are comprised of homogeneous but polydisperse ‘building blocks’: the pores), and two Gaussian functions to model the defined diffraction peaks (Fig. S9†) were summed. This requires 14 parameters, however many are confined, such as the Gaussian peak positions (0.50 to 0.55 Å−1 and 0.90 to 0.95 Å−1) and also the power law exponent (3 to 4) and fractal dimension (2 to 3).
We emphasise here that the SAPO structures studied are complex species, and the standard summation approach chosen is used to understand the characteristics of the systems, and is not meant to be a full structure refinement. Other combinations of these terms were examined, but all resulted in inferior fits (Table S3 and Fig. S10†). What this highlighted was a subtle complexity to the scattering in the intermediate-Q region. The detail of the fitting is provided in the ESI.†
The only structural parameters fixed during parameter optimisation were the SLD's of the AlPO4 framework (4.1 × 10−6 Å−2) and the empty pores (0.0 × 10−6 Å−2; air).
At low-Q the scattering decayed as ∼Q−4 in accordance with Porod's law,76 indicating a well-defined interface at the supra-mesoscopic level, as might be expected. In the intermediate-Q (mesoscopic) regime, the model envisages fractal aggregates of roughly 61 Å in size, assembled from units of mean radius 14 Å (with a lognormal polydispersity of 30%). These values likely represented a combination of the distances between the centre of the micropores within the hexagonal AlPO-5 system, and the intracrystalline porosity seen in the PALS data (Fig. 2 and Table 4). The fractal dimension of the aggregates, 2.54, is typical of porous materials (between 2 and 3), and close to the value expected from weakly-segregated or percolating networks (2.5).40 The two Gaussian peaks were centred at 0.523 and 0.911 Å−1, corresponding to d values of 12.01 and 6.90 Å. These two values are in excellent agreement with both our experimental, and theoretical d spacings for the 100 and 110 Bragg peaks in the AFI framework at 2θ = 7.4° (11.9 Å) and 12.9° (6.9 Å) with Cukα X-radiation. It is possible that these features could also be associated with the microporosity of the system, however we feel that the exact positions, and shape, provide firm evidence that these features are diffraction peaks from the crystalline planes within the unit cell, reinforcing our XRD findings. However the presence of these diffraction peaks makes it highly challenging to resolve any other features in this region, or to deduce the surface area of the sample by application of Porod's law.40,76 Overall this model produced a good fit to the SANS data, with intuitive values that reflect the expected AlPO-5 framework.
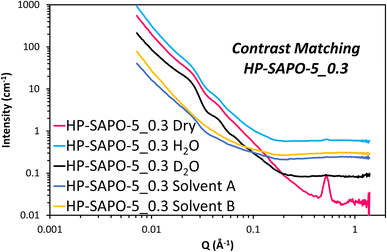
The HP-SAPO-5 systems are more complex, owing to the hierarchical mesopores present, and the potential presence of a SiO2 third phase, likely lining those mesopores. Attempting to model the HP-SAPO-5 systems with the same (2 Gaussian + power law + fractal aggregate) model used on the MP-SAPO-5 gave poor fits (Table S4 and Fig. S11†). Most notably, large deviations were seen in the oscillations in the low Q region (0.01 to 0.06 Å) and the ‘mesoporous region’ of 0.1 to 0.4 Å. To better understand these features a contrast matching (CM-SANS) study was undertaken on HP-SAPO-5_0.3 (Fig. 7). The intention was to vary the SLD of the void space, as outlined in Table 2, and see what effect this had on mesopore scattering.
As expected, the addition of H2O and D2O mixtures had a dramatic effect on the SANS data (Fig. 7), though we particularly focussed on their influence on the oscillations in the low Q region (0.01 to 0.06 Å). Solvent A had a SLD of 4.1 × 10−6 Å−2, intended to contrast match the AlPO4 phase, while solvent B had a SLD of 3.5 × 10−6 Å−2 to match any SiO2 phases. This is, however, a narrow range of solvents to work with. Fig. 7 shows the low Q oscillations were successfully contrast-matched with solvent B, but remained with solvent A, suggesting that these features are indeed associated with the SiO2 phase, and are accessible, at least to a small probe molecule like water. Given that the SiO2 phase is believed to coat the inside of the mesopores, adding a core–shell term to the model, with a void space core, a SiO2 shell and AlPO4 as the continuous matrix would seem an intuitive approach for characterising the structure of HP-SAPO-5_0.3. This was considered for the low Q (0.01 to 0.06 Å) region, but subsequently rejected, as regardless of the SLD of the core (D2O, H2O, air, etc.), the oscillations occur at the same Q values. Whereas, in a spherical core–shell model, changing the SLD of the core, whilst keeping the SLD of the shell and solvent constant, would change the position of the oscillations (Fig. S12†), which is not seen here. The constant position of these oscillations, despite the varying SLD of the core, lends itself to a crystallographic explanation. Ordered mesoporous silica species such as SBA-15, SBA-16 and MCM-41 show features in similar Q regions arising from diffraction peaks of the ordered mesopores.77–79 As such, we have incorporated two additional Gaussian peaks into the model to account for these low-Q oscillations (Table S5 and Fig. S13†), which greatly improved the fit in the 0.01 to 0.06 Å region. The centre of these peaks were found to be at Q ∼ 0.022 (d = 286 Å) and 0.044 Å−1 (d = 143 Å) separated by a factor of 2, again strengthening the belief that the mesopores possess some ordered packing.39,77–79 Therefore, we believe that these oscillations are in fact Bragg reflections. If this is the case, this would suggest that the distribution of SiO2, and therefore the mesopores, is not completely random, as originally expected. However, considering the breadth of these peaks (particularly compared to other systems), we cannot claim more than the existence of partial long-range order. The position of these peaks was also invariant of the DMOD quantity added.
We now focus on the 0.1 to 0.4 Å−1 region, in the scattering from dry HP-SAPO-5 systems. We expect that DMOD surfactant forms spherical mesopores in our HP-SAPO-5 systems from the H4 hysteresis shape. Attempts to introduce a simple sphere model, in this Q region, reproduced the experimental data well, however this model suggested that even the largest radii were below 13 Å (Table S6 and Fig. S14†). Thus far there is no indication on the shape of the mesopores in the HP-SAPO-5 systems. As such their contributions are initially modelled as a sphere to minimise parameters in the model.
The diameter of the spheres modelled were considered too small to be realistic, given our N2 physisorption and PALS findings. To improve both the accuracy and realism, a core–shell sphere term was used instead, with the aim of describing regular or lined mesopores, with an empty void space core, a SiO2 shell and an AlPO4 solvent. Again, this leads to multiple parameters, but many are fixed or constrained, and are therefore not all freely optimised. In all cases this produced radii in the 20 to 23 Å region (Table S7 and Fig. S15†), in good agreement with the 32 to 50 Å mesopore width (diameter) from N2 physisorption (Table 3 and Fig. 1) and the 25 to 37 Å values from PALS (Fig. 2 and Table 4). Further the mesopore size decreased on adding greater quantities of DMOD, also in agreement with N2 physisorption findings.
The inclusion of the core–shell sphere term to the model led to excellent fits for all three HP-SAPO-5 systems (Fig. 8 and S16). The final parameters of the fully fitted models are shown in Table S7† and summarised in Table 5. Notably the SLD used for the SiO2 shell (3.6 × 10−6 Å−2) is that of bulk silica, suggesting the silica layer is non-porous, this supports the theory that access to the mesopores is strained, as seen in our nitrogen physisorption measurements.
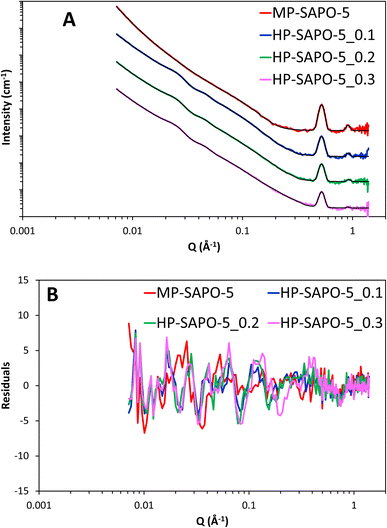 | ||
| Fig. 8 (A) Final fits of SAPO-5 materials, each data set has been successively incremented by a factor of 10 for ease of comparison. (B) Showing the residuals to the fits. | ||
| Parameter | MP-SAPO-5a | HP-SAPO-5_0.1b | HP-SAPO-5_0.2b | HP-SAPO-5_0.3b |
|---|---|---|---|---|
| a For in-depth fitting parameters of the 2 Gaussian, power law and fractal model see Table S3 in the ESI. b For in-depth fitting parameters of the 4 Gaussian, power law, fractal and core–shell sphere model see Table S7 in the ESI. | ||||
| 1st Gaussian position (Å) | 12.01 | 12.01 | 12.01 | 11.99 |
| 2nd Gaussian position (Å) | 6.90 | 6.84 | 6.79 | 6.91 |
| 3rd Gaussian position (Å) | — | 273 | 273 | 273 |
| 4th Gaussian position (Å) | — | 140 | 143 | 143 |
| Core–shell sphere scale | — | 0.031 | 0.036 | 0.039 |
| Core radius (Å) | — | 23.5 | 22.6 | 20.1 |
| Shell thickness (Å) | — | 20.1 | 20.7 | 17.3 |
In our HP-SAPO-5 systems the power law and fractal law terms showed little deviation from each other and the original MP-SAPO-5 system (Tables S3 and S7, and Fig. S17†).
We note that the power term remains close to 4, while the fractal exponent varies slightly from 2.5 in MP-SAPO-5, to between 2.7 and 2.8 in the HP-SAPO-5 systems. This deviation is likely due to the presence of mesopores segregating the pore network further.40 Further we note that the fractal aggregate (correlation length) has also increased from 62 to around 103 Å, possibly due to the mesopores again leading to greater segregation between the microporous region.
The fully fitted models confirm the trends seen in the raw data, such as the mesoporous region being more pronounced with greater DMOD quantities (Fig. 6). This is reflected in the scale (magnitude) of the core–shell sphere term, which is proportional to the pore volume, increasing with increasing DMOD ratio. This agrees with the physisorption data, namely that more DMOD leads to more mesopores, and thus more mesopore volume. SANS mesopore width, decreases with increasing DMOD quantities, as is also seen in the physisorption data. These values are also in relatively good agreement, with the physisorption data returning values of 49, 38 and 32 Å for the pore-widths of the 0.1, 0.2 and 0.3 HP-SAPO-5 species respectively. Similarly, here, the SANS analysis calculates values of 47, 45 and 40 Å, suggesting that the analysis is reasonable. The core–shell sphere term in all cases predicts the thickness of the silica shell is between 17–21 Å in all cases, without an obvious trend. This suggests a substantial silica shell is present in these systems, and could block the reactants from accessing the micropores, as also seen by the decreasing micropore volume, and/or the acid active sites (as seen from ssNMR) within the micropores.
These SANS findings have allowed us to interpret our catalysis findings (Fig. 4, 5, S7 and S8†), where the three HP-SAPO-5 species all performed notably worse than the MP-SAPO-5. We can now attribute this to a combination of two main factors. Firstly, the introduction of mesopores creates an alternative void for the reagents to occupy, however as these possess only weak silanol sites, this region cannot perform catalytic transformation. Secondly, the presence of the non-porous silica lining appears to distort the microporous features (as seen by PALS), and further will hinder access to the stronger BAS within the micropores. It is likely that the extent of micropore blockage is larger in this work, compared to our previous works as we have used a 1D channel system, SAPO-5, while our previous work focussed on 3D cage structures; in SAPO-34 and SAPO-37.34,48 This study therefore shows that while hierarchical materials can improve on catalytic activity over traditional microporous analogues,34,48 care must be exercised in the design and surface chemistries of the mesopores created. This reinforces the need for intelligent design of hierarchical systems, requiring systems to be tailored for specific applications. Further, while this synthesis method was not beneficial for the studied reactions, many possible applications do exist where combining a mesoporous silica surface with micropores in an AlPO framework is beneficial. Having distinct mesoporous and microporous regions with differing active sites permits tethering active sites onto the silica, while having separate active sites in the AlPO pore, creating two unique distinct catalytic environments in one system, which could be exploited for cascade or domino catalysis.80
Conclusions
Hierarchical AlPOs have the potential to combine the traditional catalytic selectivity of microporous AlPOs with faster diffusion rates and catalytic lifetime, towards improved catalyst performance. We have shown that by including a mesoporous surfactant, DMOD, into the synthesis procedure one can not only form hierarchical materials, but also control their properties, by adjusting the quantity of surfactant added. We emphasise here, that unlike the MP-SAPO-5 synthesis, where ssNMR shows some silicon had successfully substituted into the framework, there was no evidence that DMOD successfully went into the framework, instead contributes primarily to the formation of mesopores. Through a combination of acid site characterization, physicochemical techniques and SANS we have demonstrated new synthetic methods to control not just the quantity, but also the size of mesopores formed within an AlPO system. Using the unique insights from SANS we were able to correlate the properties of the mesopore to the catalytic performance of the system, providing useful information on catalyst design. Here the presence of a silica shell, coating the mesopores, was found to strongly influence the catalytic behaviour, while simultaneously offering a wide range of possibilities in tandem catalysis.Author contributions
M. E. P. wrote the manuscript and performed the material synthesis, SANS and catalysis experiments. A. E. O. also helped performed SANS experiments. J. J. L. B. aided with the ssNMR measurements. L. N. R. performed initial synthesis studies. M. C. collected ssNMR data. S. M. K. helped with SANS analysis and performing the SANS experiments. C. M. D. performed and analysed the PALS data. B. V. helped write, review and edit the manuscript. R. R. helped with funding acquisition, supervision and to review and edit the manuscript. All authors have approved and contributed to the final manuscript.Conflicts of interest
The authors declare that this study received funding from TotalEnergies OneTech Belgium. The funder had the following involvement in the study: discussion and interpretation of data, as well as the decision to submit and support in writing the publication.Acknowledgements
MEP, AOE, JJMLB, MC and RR acknowledge the TotalEnergies “Consortium on metal nanocatalysts” project for funding. The authors would like to thank the Science & Technology Facilities Council for the provision of neutron beamtime (experiment RB1920060, DOI: 10.5286/ISIS.E.RB1920060-1). This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no. 654000. CMD acknowledges the Veski Inspiring Women fellowship for support. ICP analysis was performed at the National Oceanography Centre, Southampton with the kind help of Dr Matthew Cooper. SEM imaging was performed at the Biological Imaging Unit at Southampton General Hospital.Notes and references
- J. Shi, Y. Wang, W. Yang, Y. Tang and Z. Xie, Chem. Soc. Rev., 2015, 44, 8877–8903 RSC
.
- E. T. Vogt and B. M. Weckhuysen, Chem. Soc. Rev., 2015, 44, 7342–7370 RSC
.
- V. Blay, B. Louis, R. Miravalles, T. Yokoi, K. A. Peccatiello, M. Clough and B. Yilmaz, ACS Catal., 2017, 7, 6542–6566 CrossRef CAS
.
- Y. Liu, Z. Li, Q. Yu, Y. Chen, Z. Chai, G. Zhao, S. Liu, W. C. Cheong, Y. Pan, Q. Zhang, L. Gu, L. Zheng, Y. Wang, Y. Lu, D. Wang, C. Chen, Q. Peng, Y. Liu, L. Liu, J. Chen and Y. Li, J. Am. Chem. Soc., 2019, 141, 9305–9311 CrossRef CAS PubMed
.
- N. R. Altvater, R. W. Dorn, M. C. Cendejas, W. P. McDermott, B. Thomas, A. J. Rossini and I. Hermans, Angew Chem. Int. Ed. Engl., 2020, 59, 6546–6550 CrossRef CAS PubMed
.
- D. Fu, O. van der Heijden, K. Stanciakova, J. E. Schmidt and B. M. Weckhuysen, Angew Chem. Int. Ed. Engl., 2020, 59, 15502–15506 CrossRef CAS PubMed
.
- Z. Guo, X. Li, S. Hu, G. Ye, X. Zhou and M. O. Coppens, Angew. Chem., 2019, 132, 1564–1567 CrossRef
.
- M. E. Potter, A. J. O'Malley, S. Chapman, J. Kezina, S. H. Newland, I. P. Silverwood, S. Mukhopadhyay, M. Carravetta, T. M. Mezza, S. F. Parker, C. R. A. Catlow and R. Raja, ACS Catal., 2017, 7, 2926–2934 CrossRef CAS
.
- M. Milina, S. Mitchell, P. Crivelli, D. Cooke and J. Pérez-Ramírez, Nat. Commun., 2014, 5, 3922 CrossRef
.
- T. Willhammar, J. Sun, W. Wan, P. Oleynikov, D. Zhang, X. Zou, M. Moliner, J. Gonzalez, C. Martinez, F. Rey and A. Corma, Nat. Chem., 2012, 4, 188–194 CrossRef CAS PubMed
.
- J. Kenvin, S. Mitchell, M. Sterling, R. Warringham, T. C. Keller, P. Crivelli, J. Jagiello and J. Pérez-Ramírez, Adv. Funct. Mater., 2016, 26, 5621–5630 CrossRef CAS
.
- J. Jae, G. A. Tompsett, A. J. Foster, K. D. Hammond, S. M. Auerbach, R. F. Lobo and G. W. Huber, J. Catal., 2011, 279, 257–268 CrossRef CAS
.
- J. Han, Z. Liu, H. Li, J. Zhong, W. Zhang, J. Huang, A. Zheng, Y. Wei and Z. Liu, ACS Catal., 2020, 10, 8727–8735 CrossRef CAS
.
- J. M. Thomas, R. Raja, G. Sankar and R. G. Bell, Acc. Chem. Res., 2001, 34, 191–200 CrossRef CAS PubMed
.
- X. Ji, L. Xu, X. Du, X. Lu, W. Lu, J. Sun and P. Wu, Catal. Sci. Technol., 2017, 7, 2874–2885 RSC
.
- I. Pinilla-Herrero, U. Olsbye, C. Márquez-Álvarez and E. Sastre, J. Catal., 2017, 352, 191–207 CrossRef CAS
.
- C. Perego and R. Millini, Chem. Soc. Rev., 2013, 42, 3956–3976 RSC
.
- K. Na, C. Jo, J. Kim, K. Cho, J. Jung, Y. Seo, R. J. Messinger, B. F. Chmelka and R. Ryoo, Science, 2011, 333, 328–332 CrossRef CAS PubMed
.
- Q. Tian, Z. Liu, Y. Zhu, X. Dong, Y. Saih, J.-M. Basset, M. Sun, W. Xu, L. Zhu, D. Zhang, J. Huang, X. Meng, F.-S. Xiao and Y. Han, Adv. Funct. Mater., 2016, 26, 1881–1891 CrossRef CAS
.
- T. C. Keller, S. Isabettini, D. Verboekend, E. G. Rodrigues and J. Pérez-Ramírez, Chem. Sci., 2014, 5, 677–684 RSC
.
- C. M. Parlett, K. Wilson and A. F. Lee, Chem. Soc. Rev., 2013, 42, 3876–3893 RSC
.
- A. Feliczak-Guzik, Microporous Mesoporous Mater., 2018, 259, 33–45 CrossRef CAS
.
- D. P. Serrano, J. M. Escola and P. Pizarro, Chem. Soc. Rev., 2013, 42, 4004–4035 RSC
.
- D. Verboekend and J. Pérez-Ramírez, Catal. Sci. Technol., 2011, 1 Search PubMed
.
- J. W. Zhong, J. F. Han, Y. X. Wei, P. Tian, X. W. Guo, C. S. Song and Z. M. Liu, Catal. Sci. Technol., 2017, 7, 4905–4923 RSC
.
- D. Xi, Q. Sun, X. Chen, N. Wang and J. Yu, Chem. Commun., 2015, 51, 11987–11989 RSC
.
- Q. Sun, N. Wang, R. Bai, G. Chen, Z. Shi, Y. Zou and J. Yu, ChemSusChem, 2018, 11, 3812–3820 CrossRef CAS PubMed
.
- H. O. Pastore, S. Coluccia and L. Marchese, Annu. Rev. Mater. Res., 2005, 35, 351–395 CrossRef CAS
.
- M. Hartmann and L. Kevan, Chem. Rev., 1999, 99, 635–664 CrossRef CAS PubMed
.
- P. N. Plessow, A. Smith, S. Tischer and F. Studt, J. Am. Chem. Soc., 2019, 141, 5908–5915 CrossRef CAS PubMed
.
- P. Losch, H. R. Joshi, O. Vozniuk, A. Grunert, C. Ochoa-Hernandez, H. Jabraoui, M. Badawi and W. Schmidt, J. Am. Chem. Soc., 2018, 140, 17790–17799 CrossRef CAS PubMed
.
- M. E. Potter, ACS Catal., 2020, 10, 9758–9789 CrossRef CAS
.
- M. E. Potter, M. E. Cholerton, J. Kezina, R. Bounds, M. Carravetta, M. Manzoli, E. Gianotti, M. Lefenfeld and R. Raja, ACS Catal., 2014, 4, 4161–4169 CrossRef CAS
.
- S. Chapman, M. Carravetta, I. Miletto, C. M. Doherty, H. Dixon, J. D. Taylor, E. Gianotti, J. Yu and R. Raja, Angew Chem. Int. Ed. Engl., 2020, 59, 19561–19569 CrossRef CAS PubMed
.
- L. H. Chen, M. H. Sun, Z. Wang, W. Yang, Z. Xie and B. L. Su, Chem. Rev., 2020, 120, 11194–11294 CrossRef CAS PubMed
.
- D. Jin, L. Li, G. Ye, H. Ding, X. Zhao, K. Zhu, M.-O. Coppens and X. Zhou, Catal. Sci. Technol., 2018, 8, 5044–5061 RSC
.
- C. Schlumberger and M. Thommes, Adv. Mater. Interfaces, 2021, 8, 2002181 CrossRef CAS
.
- C. G. Windsor, J. Appl. Crystallogr., 1988, 21, 582–588 CrossRef CAS
.
- A. Holewinski, M. A. Sakwa-Novak and C. W. Jones, J. Am. Chem. Soc., 2015, 137, 11749–11759 CrossRef CAS PubMed
.
-
Y. B. Melnichenko, Small-Angle Scattering from Confined and Interfacial Fluids, 2016 Search PubMed
.
- B. Smarsly, C. Goltner, M. Antonietti, W. Ruland and E. Hoinkis, J. Phys. Chem. B, 2001, 105, 831–840 CrossRef CAS
.
- M. Erko, D. Wallacher, A. Brandt and O. Paris, J. Appl. Crystallogr., 2009, 43, 1–7 CrossRef
.
- P. S. Singh, V. K. Aswal, S. G. Chaudhri and W. Schwieger, Microporous Mesoporous Mater., 2018, 259, 99–110 CrossRef CAS
.
- L. Ludescher, R. Morak, C. Balzer, A. M. Waag, S. Braxmeier, F. Putz, S. Busch, G. Y. Gor, A. V. Neimark, N. Husing, G. Reichenauer and O. Paris, Langmuir, 2019, 35, 11590–11600 CrossRef CAS PubMed
.
- A. Christoulaki, A. Chenneviere, I. Grillo, L. Porcar, E. Dubois and N. Jouault, J. Appl. Crystallogr., 2019, 52, 745–754 CrossRef CAS PubMed
.
- Z. Mileeva, D. K. Ross, D. Wilkinson, S. M. King, T. A. Ryan and H. Sharrock, Carbon, 2012, 50, 5062–5075 CrossRef CAS
.
- M. Juneau, R. Liu, Y. Peng, A. Malge, Z. Ma and M. D. Porosoff, ChemCatChem, 2020, 12, 1826–1852 CrossRef CAS
.
- S. H. Newland, W. Sinkler, T. Mezza, S. R. Bare, M. Carravetta, I. M. Haies, A. Levy, S. Keenan and R. Raja, ACS Catal., 2015, 5, 6587–6593 CrossRef CAS
.
- R. K. Heenan, J. Penfold and S. M. King, J. Appl. Crystallogr., 1997, 30, 1140–1147 CrossRef CAS
.
- https://www.isis.stfc.ac.uk .
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS
.
- https://www.mantidproject.org .
- G. D. Wignall and F. S. Bates, J. Appl. Crystallogr., 1987, 20, 28–40 CrossRef CAS
.
- https://www.sasview.org .
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS
.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS
.
- J. Kansy, Nucl. Instrum. Methods Phys. Res., Sect. A, 1996, 374, 235–244 CrossRef CAS
.
- S. J. Tao, J. Chem. Phys., 1972, 56, 5499–5510 CrossRef CAS
.
- M. Eldrup, D. Lightbody and J. N. Sherwood, Chem. Phys., 1981, 63, 51–58 CrossRef CAS
.
- C. Pascual-Izarra, A. W. Dong, S. J. Pas, A. J. Hill, B. J. Boyd and C. J. Drummond, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 603, 456–466 CrossRef CAS
.
- A. J. Mora, A. N. Fitch, M. Cole, R. Goyal, R. H. Jones, H. Jobic and S. W. Carr, J. Mater. Chem., 1996, 6, 1831–1835 RSC
.
- I. Pinilla-Herrero, C. Márquez-Álvarez and E. Sastre, Catal. Sci. Technol., 2017, 7, 3892–3901 RSC
.
- Z. Alothman, Materials, 2012, 5, 2874–2902 CrossRef CAS
.
- M. E. Potter, S. Chapman, A. J. O'Malley, A. Levy, M. Carravetta, T. M. Mezza, S. F. Parker and R. Raja, ChemCatChem, 2017, 9, 1897–1900 CrossRef CAS
.
- B. Zhu, L. Zou, C. M. Doherty, A. J. Hill, Y. S. Lin, X. Hu, H. Wang and M. Duke, J. Mater. Chem., 2010, 20, 4675–4683 RSC
.
- S. E. Ashbrook, M. Cutajar, C. J. Pickard, R. I. Walton and S. Wimperis, Phys. Chem. Chem. Phys., 2008, 10, 5754–5764 RSC
.
- S. Antonijevic, S. E. Ashbrook, S. Biedasek, R. I. Walton, S. Wimperis and H. Yang, J. Am. Chem. Soc., 2006, 128, 8054–8062 CrossRef CAS PubMed
.
- G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Phys. Chem. B, 1997, 101, 5249–5262 CrossRef CAS
.
- G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Phys. Chem., 1996, 100, 6722–6730 CrossRef CAS
.
- G. Paul, C. Bisio, I. Braschi, M. Cossi, G. Gatti, E. Gianotti and L. Marchese, Chem. Soc. Rev., 2018, 47, 5684–5739 RSC
.
- G. V. A. Martins, G. Berlier, C. Bisio, S. Coluccia, H. O. Pastore and L. Marchese, J. Phys. Chem. C, 2008, 112, 7193–7200 CrossRef CAS
.
- M. E. Potter, J. J. M. Le Brocq, A. E. Oakley, E. B. McShane, B. D. Vandegehuchte and R. Raja, Catalysts, 2020, 10 Search PubMed
.
- M. E. Potter, L.-M. Armstrong and R. Raja, Catal. Sci. Technol., 2018, 8, 6163–6172 RSC
.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS
.
- G. Beaucage, J. Appl. Crystallogr., 1996, 29, 134–146 CrossRef CAS
.
- G. Porod, Kolloid-Z., 1951, 124, 83–114 CrossRef CAS
.
- S. Jähnert, D. Müter, J. Prass, G. A. Zickler, O. Paris and G. H. Findenegg, J. Phys. Chem. C, 2009, 113, 15201–15210 CrossRef
.
- M. Schoeffel, N. Brodie-Linder, F. Audonnet and C. Alba-Simionesco, J. Mater. Chem., 2012, 22, 557–567 RSC
.
- M. Impéror-Clerc, P. Davidson and A. Davidson, J. Am. Chem. Soc., 2000, 122, 11925–11933 CrossRef
.
- M. J. Climent, A. Corma, S. Iborra and M. J. Sabater, ACS Catal., 2014, 4, 870–891 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Including further characterisation data on the sample's structural integrity, acidity and catalytic behaviour. Further details of SANS fitting and alternative models are also shown. See DOI: https://doi.org/10.1039/d3ta04763f |
| This journal is © The Royal Society of Chemistry 2023 |