Semi-quantitative determination of active sites in heterogeneous catalysts for photo/electrocatalysis
Jing
Ren
a,
Haoyuan
Chi
 a,
Ling
Tan
ac,
Yung-Kang
Peng
a,
Ling
Tan
ac,
Yung-Kang
Peng
 b,
Guangchao
Li
d,
Molly
Meng-Jung Li
d,
Yufei
Zhao
b,
Guangchao
Li
d,
Molly
Meng-Jung Li
d,
Yufei
Zhao
 *a and
Xue
Duan
a
*a and
Xue
Duan
a
aState Key Laboratory of Chemical Resource Engineering, Beijing University of Chemical Technology, 100029 Beijing, P. R. China. E-mail: zhaoyufei@mail.buct.edu.cn
bDepartment of Chemistry, City University of Hong Kong, Hong Kong SAR, Hong Kong
cState Key Laboratory of Vanadium and Titanium Resources Comprehensive Utilization, ANSTEEL Research Institute of Vanadium & Titanium (Iron & Steel), Chengdu 610031, China
dDepartment of Applied Physics, The Hong Kong Polytechnic University, Hong Kong
First published on 10th January 2023
Abstract
Catalysis is a widely applied process due to its predominant role in the chemical industry. Developing highly active exposed facets via defect engineering is considered to be the most promising strategy for optimizing the electrical and optical properties of catalysts to improve their catalytic activity. Therefore, quantitative determination and calculation of the concentration of defect structures related to the highly exposed active crystal plane provided an efficient route for elucidating the catalytic active sites, and has attracted increasing attention. This work not only summarizes the existing defect characterization methods and the calculation methods of defect concentrations reported in recent years but also proposes a semi-quantitative method based on X-ray absorption fine structure (XAFS) and related methods for the determination and classification of active sites related to the active surface, which can be applied for the semi-quantitative calculation of defect concentrations in widely used metals and metal oxides. In addition, we emphasize the deficiencies of current defect concentration quantitative methods and look forward to the future development of defect characterization methods under working conditions. This review further reveals the structure–activity relationship between the content of active sites and the reaction performance.
1. Introduction
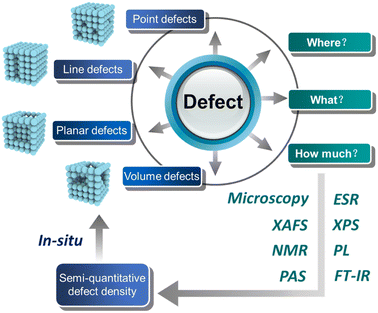
Heterogeneous metal or metal oxide catalysts play a key role in the chemical industry, in which more than 85% of chemical processes involve at least one catalytic step.1 It is well known that heterogeneous catalysts provide a wide range of active sites such as edges, corners, and facets (cf. homogeneous catalysts with well-defined active sites). Therefore, the precise recognition of the active sites of catalysts and the development of high-performance heterogeneous materials are crucial to achieving a green and sustainable society. Early research work reported that the performance of catalysts is highly correlated with the elemental composition, and the active center of catalysts is contributed by some elements, which are relatively crude.2–4 With the development in the preparation of catalysts and characterization tools, the current focus has been geared to the surface features of catalysts such as corners, edges, and related defect sites, which are believed to determine the observed activity/selectivity.5,6 Taking the active crystal surface of the catalyst as an example, some crystal surfaces with high indexes have a higher surface energy because of the existence of more suspended bonds, so they form an open surface structure and exhibit a higher catalytic activity.7,8 There is no doubt that defects inevitably exist in all imperfect crystalline materials, and when they appear on the crystal surface, they can significantly regulate the electronic structure of the surface, bringing about changes in their physicochemical properties. Therefore, the defect structure on the active crystal surface has the structural particularity of the active crystal surface.A defect is a place in a material where atoms or molecules arranged in perfect periodic are broken or destroyed, which has been regarded to play a prominent role in determining the catalytic activity, and it can be divided into four types according to the size: zero-dimensional point defects (such as vacancies and dopings), one-dimensional linear defects (such as spiral and edge dislocations) mainly existing as edges or corners, two-dimensional planar defects (such as grain boundaries and twin boundaries) that can also be regarded as facets, and three-dimensional volume defects (such as lattice disorders and voids)9 (Fig. 1). On the one hand, the formation of defects can further reduce the coordination number of adjacent atoms and provide unsaturated sites for the reactants to adsorb and transform. On the other hand, the existence of defects will change the electronic structure of the material to promote the interaction between the active site and the reactant intermediates, which regulates the catalytic performance.10 Thus, the defect engineering of nanomaterials has been widely applied in the field of heterogeneous catalysis.11,12 Previous studies have shown that defect engineering can not only affect the physicochemical properties of heterogeneous materials,13,14 but also improve the catalytic performance of photo/electrocatalytic materials.15–20 Recently, in order to enhance the efficiency of atom utilization, single-atom catalysts have also come into existence in the research field, and the introduction of defects on the supports of single-atom catalysts can effectively stabilize the single metal atoms and prevent the aggregation of active sites,21–23 benefiting the catalysis.
Among the catalysts involved in the chemical production process, heterogeneous metal or metal oxide catalysts have become essential in most refining and petrochemical processes. Metal (hydrogen) oxides represented by layered double hydroxides (LDHs) such as NiO, ZnO, and TiO2 have attracted extensive research attention due to their excellent photo/eletrocatalytic performance. For instance, transition metal (such as Ni, Co and Fe)-containing LDHs are the most promising materials for electrocatalytic oxygen evolution reactions (OERs).24,25 The catalytic performance of LDHs can be further improved by introducing defects via exfoliation,26 etching,27 and plasma processes.28 With the help of defect engineering, the overpotential of LDHs for OERs has decreased from more than 300 mV to about 190 mV at 10 mA cm−2, as reported by Sun and coworkers.29 Density function theory (DFT) revealed that vacancy-related defects (O vacancies or metal vacancies) can facilitate the adsorption of H2O30 and, hence, reduce the activation barrier for OERs.31 For the photo/electrocatalytic CO2 reduction reaction, the electronic structure of the catalyst and the adsorption configuration of the intermediates are changed by regulating the defects, which promotes the formation of C2+ products.32,33 The presence of defects in the electrocatalytic N2 reduction can also improve the intrinsic activity and stability of the catalyst.34 In the photolysis water-coupled benzyl alcohol oxidation, the defects can be used as active sites of the reaction and also effectively inhibit the photogenerated electron–hole recombination.35 Therefore, defect engineering is an efficient strategy to prepare catalysts in improving photo/electrocatalysis. In view of these encouraging results, researchers began to study the defects in more depth and detail. However, how to determine the catalytic active site qualitatively or semi-quantitatively is still a challenge at this stage. Therefore, it is crucial to develop a route to identify the key active site of the target catalysts, particularly in in situ or operando conditions.36–39
At present, defects can be well characterized by electron microscopy and spectroscopy analyses such as transmission electron microscopy (TEM), aberration-corrected high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), X-ray absorption fine structure (XAFS), electron spin resonance (ESR), positron annihilation spectroscopy (PAS), nuclear magnetic resonance (NMR), X-ray photoelectron spectroscopy (XPS), and photoluminescence spectroscopy (PL). Some peers have summarized the synthesis and characterization methods of defects.12 The catalytic performance as well as the selectivity of a given reaction is known to change with the number/type of defects. Note that the appearance of certain defects generates positive/negative effects. For example, our group found that the selectivity of methane increases and that of H2 decreases with the increase in defects in NiAl-LDH40 from photocatalytic CO2 reduction. Furthermore, Zhao and co-workers investigated the concentration ratio between bulk and surface defects in TiO2 and concluded that bulk defects will lead to the recombination of carriers, resulting in a decreased photocatalytic activity.41 Therefore, understanding the relationship between defect concentration and performance can help us rationally design smart catalysts.
Herein, we summarize the current representative work of constructing defects on the exposed active facet to improve photo/electrocatalytic activity, and quantification of the defects via various characterizations such as TEM, XAFS, NMR, PAS, ESR, XPS, PL, and FT-IR, as shown in Fig. 1. On the basis of previous works on quantifying defects, we also propose a semi-quantitative defect concentration method based on highly active facets using XAFS and related methods, and provide a description on the location, type and concentration of defect sites. By using this calculation, we can obtain the concentration information of defects in the target facet, which is helpful to accurately quantify the role of defect sites in the reaction process using in situ technology and to design efficient catalysts via defect engineering in the future.
2. Advanced methods for determining and semi-quantifying defects
2.1. Electron microscopy
The electron microscope is an indispensable microscopic tool in the field of materials science, which can clearly and intuitively show the morphology of the nanomaterials at atomic-level resolution. With the use of TEM, scanning tunneling microscopy (STM), and HAADF-STEM, we can unambiguously identify the thickness, size, exposed facets, surface defects, etc., of the nanomaterials. For example, long-range and local structural details of electrodes and solid electrolyte materials were revealed using advanced TEM techniques, which provides a new view on the energy conversion and storage.42 Moreover, the morphology, multiphase distribution, and even the atomic arrangement around the structural defect regions of nanostructured materials can also be distinguished from (S)TEM images. Recently, Wang and co-workers have covered the visualized observation of the morphology of SnS2, and the presence of defect regions in the structure.43 As shown in Fig. 2A, the lattice spacing of pristine SnS2 is about 0.587 nm, which corresponds well to the (001) facet of SnS2 (0.585 nm). While the discontinuous lattice fringes can be clearly observed in the HRTEM image of SnS2 featuring Al doping (Fig. 2B), it can be inferred that the fractional crooked fringes observed in the fuzzy region may donate the existence of defects. These consequences represent that Al doping successfully introduced defects in the (001) crystal plane of SnS2. By observing the HRTEM images, it can also be clearly found that β-Ni(OH)2 ultra-thin nanosheets are distributed with nanopores of size 3–4 nm, further indicating the wide existence of defects in some traditional materials.44 To gain insights into the defects of the material, Xie's group used HAADF-STEM to reveal the microstructure of Bi2O3 with rich oxygen vacancies.45 The apparent lattice disorder in Fig. 2C verified the existence of a metal coordination unsaturated structure in the material. Furthermore, the fast-scanning Aarhus STM and time-lapsed sequential STM images allow us to detect the presence of defects and monitor the diffusion behavior of some small molecules such as H2O46,47 and O2.37,38 For instance, as shown in Fig. 2D–F, Besenbacher's team successfully tracked the diffusion behavior of a single O2 molecule on O vacancies of TiO2(110) by STM technology.38 They observed that the diffusion of O2 molecules only along the (001) direction and the O2 hopping rates are related to the content of O vacancies on the surface: the oxygen jumping rate increases with the increase in the content of O vacancies at an appropriate temperature. Using STEM, Dou's team revealed that the O vacancies on the TiO2(110) surface promote HER processes in alkaline media.46 The O vacancy concentration decreased with the increase in surface depth (Fig. 2D–F). In the HER process, H2O molecules preferentially adsorbed onto the O vacancy surface, and one O vacancy could induce two Ti3+ (Fig. 2G and H). The O vacancies and Ti3+ ions in the surface region determine the conductivity and the number of electrocatalytic active sites of TiO2. | ||
| Fig. 2 HRTEM images of (A) pristine SnS2 and (B) SnS2 featuring Al doping43 copyright © 2021 Elsevier B.V. (C) HAADF-STEM images of VO-rich-Bi2O3 nanosheets, the scale bar is 2 nm.45 Copyright © 2019, Springer Nature Limited. STEM image of cross-sectional TiO2(110) single crystal (D) and large region (E). (F) Concentration of O vacancies increased from inner to surface regions. (G) STM image of the TiO2 surface in the empty state. (H) STM image of the same region of (G), but in the filled state46 copyright © 2018 American Chemical Society. | ||
As the most intuitive and clear evidence, microscopy plays an indispensable role in estimating the presence and location of defects in heterogeneous catalysts. In last several years, the development of in situ electron microscopy has also led to its application in many fields such as ion migration in lithium-ion batteries,48,49 the interaction between metal nanoparticles and oxide support under redox conditions,39,50,51 and the structural transformation of metals in the gas phase52 or during heating up.53 Even though electron microscopy cannot accurately quantify the concentration of defects at present, it is still making an important contribution to the study of the transition process of defects under working conditions.
2.2. X-ray absorption fine structure (XAFS)
X-ray absorption fine structure (XAFS) spectrum is one of the most powerful tools for determining the local structures. Therefore, via the X-ray absorption fine structure (EXAFS) analysis, the following information such as the coordination number, bond length, defect concentration, and disorder degree of the coordination atoms around the central absorption atom can be accurately obtained. Compared with EXAFS, X-ray absorption near edge structure (XANES) is more ingenious to spatial structure information and can obtain valency and symmetry information qualitatively and effectively. Via combination with the AFM and TEM information, the defect concentration and the density of the defect can be accurately obtained as follows:Taking layered double hydroxides (LDHs), layered materials consisting of brucite-like positively charged laminates, and negatively charged interlaminar anions and water molecules,56 as examples, our group synthesized the defect-containing ultrathin LDH photocatalyst for photocatalytic phenol oxidation. We used XAFS technology to study the local structure of defective NiFe-LDH synthesized by a co-precipitation method, as shown in Fig. 3A.54 As can be seen from the R-space of Ni shown in Fig. 3B, the coordination number of the first shell (Ni–O) and the second shell (Ni–Ni/Fe) of NiFe-LDH nanosheets (NNi–O = 5.3, NNi–Ni/Fe = 5.4) are much lower than that of the NiFe-LDH bulk counterpart (NNi–O = 6, NNi–Ni/Fe = 6). The same result can be also observed in Fe K-edge EXAFS (Fig. 3C), further indicating the presence of O, Ni and Fe vacancies (VOH, VNi, and VFe) in NiFe-LDH nanosheets. However, the quantification of defects and the provision of their location on the LDH/nanoparticles are both unclear.
 | ||
| Fig. 3 (A) Structural model of NiFe-LDH nanosheets and NiFe-LDH bulk; R space of the (B) Ni and (C) Fe K-edge EXAFS spectra.54 Copyright © 2020 Royal Society of Chemistry. (D) R space of Ni K-edge EXAFS spectra. (E) Schematic illustration of the basic unit cell of monolayer NiAl-LDH.55 Copyright © 2019 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
In order to further explore the relationship between the defect concentration and performance, our group prepared bulk, few-layer, and monolayer NiAl-LDH nanosheets (denoted as b-NiAl-LDH, f-NiAl-LDH, and m-NiAl-LDH, respectively) for photoreduction of CO2.55 The coordination numbers of Ni and O decreased with the decrease in the thickness of NiAl-LDH, indicating that the Ni and O vacancies increased sequentially, and the selectivity of the target product CH4 also increased sequentially (Fig. 3D). It is easy to find that the selectivity of target product CH4 and the quantity of Ni vacancies and O vacancies are closely related.
According to the coordination number information obtained by XAFS and the detail of the basic unit cells, a method for quantifying defect concentration was summarized. Taking m-NiAl-LDH as an example (Fig. 3E), the surface area of one LDH cell can be calculated as 1.2 nm × 1.2 nm × sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60° = 1.247 nm2. The cell parameter c of LDHs is related to interlayer anions, and different interlayer anions lead to different layer thicknesses and eventually lead to differences in c; therefore, the volume of the LDHs can be obtained as follows: surface area of the cell × thickness (nm), where the thickness is measured by atomic force microscopy (AFM) results (1 nm). The corresponding oxygen number in this m-NiAl-LDH model is referred to as 32, and the metal (Ni and Al) atom number is 16. As obtained from the EXAFS results of m-NiAl-LDH, the corresponding coordination number of the first Ni–O shell is 5.5, compared with the pure LDH with a coordination number of 6.0, the ratio of the defect concentration of the Ni–O shell in m-NiAl-LDH is proposed to be around (5.5 − 6)/6 = 8.3%. Therefore, in the whole model, the defect intensity of O vacancies can be inferred as follows: oxygen vacancies density (nm−3) = ratio of the defect concentration × the total oxygen number in the model per nm3 = 8.3% × 32/(1.247 nm2 × 1 nm) = 2.14 nm−3. The above-mentioned equation can also be extended to calculate the metal vacancies density, and the metal vacancies density (nm−3) in m-NiAl-LDH can be obtained as: the ratio of the defect concentration × the total metal number in the model per nm3 = (6.0 − 5.0)/6.0 × 16/(1.247 nm2 × 1 nm) = 2.14 nm−3. Accordingly, the defect density of O and Ni vacancies in f-NiAl-LDH was calculated to be 1.80 nm−3 and 1.20 nm−3, respectively. Defect density provides a guideline for regulating the selectivity/activity of catalytic reactions and exploring the corresponding structure–activity relationship. In addition, our proposed method can also be applied to other LDH materials such as CoFe-LDH,57–59 ZnAl-LDH,60 and NiFe-LDH.61,62 The concentrations of oxygen defects and metal defects for other LDHs in recent reports were also calculated, and the results are presented in Table 1. It is worth noting that the concentration of oxygen defects and metal defects ranges from 0.05 to 10.69 nm−3, and is closely related to the types of metal elements that compose the LDH laminate. Then, a defect location site description can be defined as follows: material-defect type-active exposed facet-concentration, like NiAl-LDH-VO-(001)-2.14 nm−3. This semi-quantitative calculation method of defect concentration provides guidance for accurate defect engineering design to achieve better performance control.
60° = 1.247 nm2. The cell parameter c of LDHs is related to interlayer anions, and different interlayer anions lead to different layer thicknesses and eventually lead to differences in c; therefore, the volume of the LDHs can be obtained as follows: surface area of the cell × thickness (nm), where the thickness is measured by atomic force microscopy (AFM) results (1 nm). The corresponding oxygen number in this m-NiAl-LDH model is referred to as 32, and the metal (Ni and Al) atom number is 16. As obtained from the EXAFS results of m-NiAl-LDH, the corresponding coordination number of the first Ni–O shell is 5.5, compared with the pure LDH with a coordination number of 6.0, the ratio of the defect concentration of the Ni–O shell in m-NiAl-LDH is proposed to be around (5.5 − 6)/6 = 8.3%. Therefore, in the whole model, the defect intensity of O vacancies can be inferred as follows: oxygen vacancies density (nm−3) = ratio of the defect concentration × the total oxygen number in the model per nm3 = 8.3% × 32/(1.247 nm2 × 1 nm) = 2.14 nm−3. The above-mentioned equation can also be extended to calculate the metal vacancies density, and the metal vacancies density (nm−3) in m-NiAl-LDH can be obtained as: the ratio of the defect concentration × the total metal number in the model per nm3 = (6.0 − 5.0)/6.0 × 16/(1.247 nm2 × 1 nm) = 2.14 nm−3. Accordingly, the defect density of O and Ni vacancies in f-NiAl-LDH was calculated to be 1.80 nm−3 and 1.20 nm−3, respectively. Defect density provides a guideline for regulating the selectivity/activity of catalytic reactions and exploring the corresponding structure–activity relationship. In addition, our proposed method can also be applied to other LDH materials such as CoFe-LDH,57–59 ZnAl-LDH,60 and NiFe-LDH.61,62 The concentrations of oxygen defects and metal defects for other LDHs in recent reports were also calculated, and the results are presented in Table 1. It is worth noting that the concentration of oxygen defects and metal defects ranges from 0.05 to 10.69 nm−3, and is closely related to the types of metal elements that compose the LDH laminate. Then, a defect location site description can be defined as follows: material-defect type-active exposed facet-concentration, like NiAl-LDH-VO-(001)-2.14 nm−3. This semi-quantitative calculation method of defect concentration provides guidance for accurate defect engineering design to achieve better performance control.
| No. | Sample | Thickness (nm) | N M–O | V O (nm−3) | N M–M | V M (nm−3) | Reference |
|---|---|---|---|---|---|---|---|
| Bulk NiAl-LDH | 27 | N Ni–O = 6.0 | V O-(001) = 0 | N Ni–M = 6.0 | V M-(001) = 0 | ||
| 1 | Fewlayer NiAl-LDH | 5 | N Ni–O = 5.7 | V O-(001) = 0.26 | N Ni–M = 5.6 | V M-(001) = 0.17 | 55 |
| Monolayer NiAl-LDH | 1 | N Ni–O = 5.5 | V O-(001) = 2.14 | N Ni–M = 5.0 | V M-(001) = 2.14 | ||
| 2 | CoFe-LDH | 4.5 | N Fe–O = 6.0 | V O-(001) = 0 | N Fe–M = 5.7 | V M-(001) = 0.14 | 57 |
| NiCoFe-LDH | 3.3 | N Fe–O = 5.2 | V O-(001) = 1.04 | N Fe–M = 4.1 | V M-(001) = 1.23 | ||
| 3 | Bulk NiFe-LDH | 20 | N Fe–O = 6.0 | V O-(001) = 0 | N Fe–Ni = 6.0 | V M-(001) = 0 | 61 |
| Monolayer NiFe-LDH | 1 | N Fe–O = 5.9 | V O-(001) = 0.43 | N Fe–Ni = 5.8 | V M-(001) = 0.43 | ||
| Ultrafine NiFe-LDH | 0.6 | N Fe–O = 5.8 | V O-(001) = 1.43 | N Fe–Ni = 5.5 | V M-(001) = 1.78 | ||
| 4 | Pristine CoFe-LDH | 27.5 | N Co–O = 4.9 | V O-(001) = 0.17 | N Co–M = 5.3 | V M-(001) = 0.05 | 58 |
| H2O-plasma exfoliated-CoFe LDH | 1.54 | N Co–O = 4.7 | V O-(001) = 3.61 | N Co–M = 4.4 | V M-(001) = 2.22 | ||
| 5 | Bulk CoFe-LDH | 20.6 | N Fe–O = 4.7 | V O-(001) = 0.27 | N Fe–M = 4.4 | V M-(001) = 0.17 | 59 |
| Ultrathin CoFe-LDH | 0.6 | N Fe–O = 4.5 | V O-(001) = 10.69 | N Fe–M = 3.6 | V M-(001) = 8.55 | ||
| 6 | Monolayer NiFe-LDH | 0.8 | N Fe–O = 5.9 | V O-(001) = 0.53 | N Fe–M = 5.7 | V M-(001) = 0.80 | 62 |
| Porous monolayer NiFe-LDH | 0.8 | N Fe–O = 5.7 | V O-(001) = 1.60 | N Fe–M = 5.1 | V M-(001) = 2.41 |
The above-mentioned calculation can also be applicable to other catalysts such as ZnO, NiO, and TiO2. Chergui and co-workers quantitatively analyzed the oxygen and Zn vacancies for colloidal ZnO nanoparticles with different sizes.63 With the help of EXAFS, the peak intensity of the first shell (Zn–O) of the three samples with different sizes is similar to the R space spectrum, indicating that the number of their oxygen vacancies is comparable. However, the relative intensity of the second shell (Zn–Zn) peak decreases with the size of ZnO, indicating that the number of Zn vacancies increases with the decrease in ZnO transverse size. Besides, Passerini and co-workers also performed EXAFS to obtain the quantitative structural information of Fe/Co-doped ZnO.64 They found that Fe doping leads to more cation and oxygen vacancies in ZnO than Co-doped ZnO. With the introduction of O and Zn defects, the optical properties and ferromagnetism of ZnO materials were improved.65 Some papers also give the fitting results of EXAFS, and then combined with the crystal cell information of ZnO, we can calculate the defect density of Zn and O vacancies accordingly. The volume of the ZnO cell can be obtained as follows: a × b × c × sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120° = 0.324927 nm × 0.324927 nm × 0.520544 nm × sin
120° = 0.324927 nm × 0.324927 nm × 0.520544 nm × sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120° = 0.0476 nm3. The number of O and Zn atoms in the ZnO unit model is 2, and the coordination number of oxygen and Zn is 4 and 12, respectively. As obtained from the EXAFS results of ZnO, the defect density of the Zn–O shell in ZnO was calculated to be around (4 − NO)/4 × 2/0.0476 nm−3 and the defect density of the Zn–Zn shell in ZnO is thus around (12 − NZn)/12 × 2/0.0476 nm−3. The calculated results of the ZnO defect density are listed in Table 2.
120° = 0.0476 nm3. The number of O and Zn atoms in the ZnO unit model is 2, and the coordination number of oxygen and Zn is 4 and 12, respectively. As obtained from the EXAFS results of ZnO, the defect density of the Zn–O shell in ZnO was calculated to be around (4 − NO)/4 × 2/0.0476 nm−3 and the defect density of the Zn–Zn shell in ZnO is thus around (12 − NZn)/12 × 2/0.0476 nm−3. The calculated results of the ZnO defect density are listed in Table 2.
| No. | Sample | N M–O | V O (nm−3) | N M–M | V M (nm−3) | Reference |
|---|---|---|---|---|---|---|
| Standard ZnO | N Zn–O = 4 | V O = 0 | N Zn–Zn = 12 | V Zn = 0 | ||
| 1 | ZnO doping Ni 5% | N Zn–O = 3.3 | V O = 7.35 | N Zn–Zn = 11.5 | V Zn = 1.75 | 65 |
| ZnO doping Ni 12.5% | N Zn–O = 2.8 | V O = 12.61 | N Zn–Zn = 10.9 | V Zn = 3.85 | ||
| 2 | ZnO aliquot 1 | — | — | N Zn–Zn = 6.7 | V Zn = 18.56 | 79 |
| ZnO aliquot 2 | — | — | N Zn–Zn = 8.7 | V Zn = 11.55 | ||
| ZnO aliquot 3 | — | — | N Zn–Zn = 11.5 | V Zn = 1.75 | ||
| Standard NiO | N Ni–O = 6 | V O = 0 | N Ni–Ni = 12 | V Ni = 0 | ||
| 3 | NiO from Ni(CH3COO)2 | N Ni–O = 5.7 | V O = 2.76 | N Ni–Ni = 10.7 | V Ni = 5.99 | 72 |
| NiO from Ni(acac)2 | N Ni–O = 5.5 | V O = 4.60 | N Ni–Ni = 7.5 | V Ni = 20.72 | ||
| NiO from Ni(acac)2 without TOPO | N Ni–O = 6 | V O = 0 | N Ni–Ni = 10.3 | V Ni = 7.83 | ||
| 4 | NiAl-275 | N Ni–O = 5.5 | V O-(110) = 4.60 | N Ni–M = 7.2 | V M-(110) = 22.10 | 69 |
| NiAl-600 | N Ni–O = 5.8 | V O-(110) = 1.84 | N Ni–M = 10.1 | V M-(110) = 8.75 | ||
| NiAl-800 | N Ni–O = 6.0 | V O-(110) = 0 | N Ni–M = 10.7 | V M-(110) = 5.99 | ||
| 5 | NiO/SiO2 | N Ni–O = 6.0 | V O = 0 | N Ni–Ni = 11.6 | V Ni = 1.84 | 73 |
| NiO/Ti-anat | N Ni–O = 5.3 | V O = 6.45 | N Ni–Ni = 10.9 | V Ni = 5.06 | ||
| NiO/Ti-P25 | N Ni–O = 5.2 | V O = 7.37 | N Ni–Ni = 10.4 | V Ni = 7.37 | ||
| 6 | Fe-doped NiOx nanotubes | N Ni–O = 5.2 | V O = 7.37 | N Ni–Ni = 10.2 | V Ni = 8.29 | 74 |
| 7 | NiO-10% oxygen | N Ni–O = 6 | V O = 0 | N Ni–Ni = 11.8 | V Ni = 0.92 | 75 |
| NiO-40% oxygen | N Ni–O = 6 | V O = 0 | N Ni–Ni = 11.4 | V Ni = 2.76 | ||
| NiO-70% oxygen | N Ni–O = 6 | V O = 0 | N Ni–Ni = 11 | V Ni = 4.60 | ||
| 8 | Bulk NiO | N Ni–O = 6 | V O = 0 | N Ni–Ni = 12 | V Ni = 0 | 76 |
| 25 nm NiO | N Ni–O = 5.5 | V O = 4.60 | N Ni–Ni = 10.6 | V Ni = 6.45 | ||
| 5 nm NiO | N Ni–O = 5.4 | V O = 5.52 | N Ni–Ni = 10.4 | V Ni = 7.34 | ||
| 9 | Mono-NiTi-MMO | N Ni–O = 5.7 | V O-(110) = 2.76 | N Ni–Ni = 7.7 | V Ni-(110) = 19.80 | 68 |
The study of O and Ni defects in NiO materials also makes an important contribution to the interpretation of the structure–activity relationship. Langell and co-workers used XAFS to study the coordination environment of bulk, 25 nm, and 5 nm NiO nanomaterials.66 Gutiérrez and co-workers revealed from the XAFS results that the resistivity of NiO films is intimately in connection with the Ni defects.67 Therefore, the quantification of defect density is instructive for NiO defect engineering. By fitting the R space, the defect densities of O vacancies and Ni vacancies can also be calculated from the coordination number results obtained by XAFS. The volume of the NiO cell can be obtained as follows: a × b × c = 0.41684 nm × 0.41684 nm × 0.41684 nm = 0.0724 nm3. The number of O and Ni atoms in the NiO unit model is 4, and the coordination number of O and Ni is 6 and 12, respectively. As obtained from the EXAFS results of NiO, the defect density of the Ni–O shell in NiO was calculated to be around (6 − NO)/6 × 4/0.0724 nm−3 and the defect density of the Ni–Ni shell in NiO is around (12 − NNi)/12 × 4/0.0724 nm−3. Via calcination of the NiTi-LDH monolayer precursor, the (110) facet-exposed NiO can be obtained.68 Together with the results of AFM, TEM, and XAFS, the synthesized NiO(110) facet contains abundant O and Ni defects, which promote water adsorption and later charge transfer process in the OER. Our group also successfully synthesized NiO enclosed by the (110) facet using a NiAl-LDH precursor.69Via the calculation of defect concentration in Table 2, it was found that the photocatalytic selectivity of CO2 reduction to CH4 increased with the increase in metal defect concentration in NiO. Quantifying defects in NiO can provide a new perspective for exploring the relationship between the structure and the performance.
Based on this method, we can quantitatively calculate the number of metal defects and oxygen defects per cubic nanometer of metal (hydrogen) oxides. The defect concentrations of the most widely reported materials such as LDHs, NiO, and ZnO for photo/eletrocatalysis in recent years were thus calculated, as shown in Fig. 4. It is not difficult to find that the concentration of defects affects the catalytic performance of the material. The proposed method solves the problem of defect quantification to some extent and helps understand the structure–activity relationship between defect concentration and catalytic performance. With the development and application of in situ XAFS, the real atomic and electronic structures of catalysts can be monitored under working conditions.77,78 It is promising that in situ techniques can be used to reveal the active sites of catalysts and accurately quantify the concentration of defects.
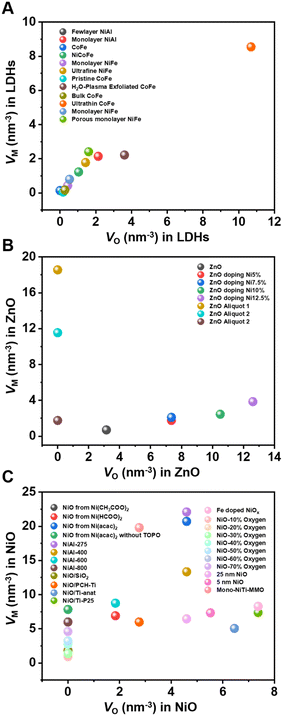 | ||
| Fig. 4 Oxygen defect and metal defect density in (A) LDHs; (B) NiO; and (C) ZnO.55,57–59,61,62,68–76 | ||
However, this quantitative method is limited to XAFS results, which only show the changes in the overall material coordination environment, and it is difficult to distinguish which defects cause the changes. Therefore, the defect density calculated by this method cannot represent the density of a certain type of defect. In addition, the coexistence of multiple metal oxides and amorphous phases also set up obstacles for the selection of appropriate cell elements, which hinders the accurate calculation of defect density, and still needs to be explored in the future.
2.3. Nuclear magnetic resonance (NMR)
NMR is a mighty characterization technique for materials containing a large number of spin-active nuclei. By this technique, we can acquire information about the regional structure of materials, like the micro-arrangement of cations. It also makes up for some light metal elements such as Mg and Al, which are difficult to characterize by XAFS to a certain extent. Taking 25Mg-NMR as an example, although the development has been challenged by low sensitivity due to low gyromagnetic ratio and natural abundance, combined with large quadrupole moment of isotopes, they have gained much research interest in Mg-containing LDH structures. By studying the 1H and 25Mg NMR spectra of MgAl-LDH with different Al contents, Grey's team first revealed the arrangement order of cations in the material.80 When the ratio of Mg to Al was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with a “honeycomb” ordering, the arrangement of Mg and Al was perfectly ordered, while in the case of low Al contents, cations were randomly arranged in the case of no Al3+–Al3+ close contacts. Inspired by this work, Massiot's group used 1H and 27Al NMR spectroscopy to identify and quantify the defect in cation arrangement of MgAl-LDH.81 The cation distribution of MgAl-LDH was predicted by 1H solid-state NMR technology combined with DFT theoretical calculations, as shown in Fig. 5A, and the optimized model of LDH intercalated with nitrate as shown in Fig. 5B was proposed. The ascendant peak of 3.8 ppm in Fig. 5A was identified as the Mg2AlOH species, while the shoulder peak at 4.6 ppm corresponded to interlaminar or adsorbed water. The little peak at 1.6 ppm was contributed by the Mg3OH. The defect concentrations of different Mg to Al content ratios can be estimated according to the fitting and integration of 1H NMR spectra, as shown in Fig. 5C, and the specific calculation formula is as follows:81
1 with a “honeycomb” ordering, the arrangement of Mg and Al was perfectly ordered, while in the case of low Al contents, cations were randomly arranged in the case of no Al3+–Al3+ close contacts. Inspired by this work, Massiot's group used 1H and 27Al NMR spectroscopy to identify and quantify the defect in cation arrangement of MgAl-LDH.81 The cation distribution of MgAl-LDH was predicted by 1H solid-state NMR technology combined with DFT theoretical calculations, as shown in Fig. 5A, and the optimized model of LDH intercalated with nitrate as shown in Fig. 5B was proposed. The ascendant peak of 3.8 ppm in Fig. 5A was identified as the Mg2AlOH species, while the shoulder peak at 4.6 ppm corresponded to interlaminar or adsorbed water. The little peak at 1.6 ppm was contributed by the Mg3OH. The defect concentrations of different Mg to Al content ratios can be estimated according to the fitting and integration of 1H NMR spectra, as shown in Fig. 5C, and the specific calculation formula is as follows:81
 | ||
| Fig. 5 (A) Solid-state 1H NMR spectra of Mg/Al-2-LDH. (B) Schematic illustration of Mg/Al-2-LDH. (C) Quantitative fitting of the 1H echo-MAS NMR spectra of LDH.81 Copyright © 2011 American Chemical Society. | ||
Al defects:
Mg defects:
According to this quantitative method, when the ratio of Mg to Al is 2, the disorder percentages of Al and Mg are ∼10% and 5%, respectively. The ability to responsibly quantify the degree of cation ordering in LDH materials also plays an important role in accurately controlling and optimizing the structure and properties of LDH-based nanocomposites at the molecular level.
Some paramagnetic materials such as Ni2+-containing LDHs can also be characterized by 2H NMR spectroscopy after deuteration. Peng's team, for the first time, resolved different types of hydrogen atoms such as Ni3OD, Ni2AlOD and interlayer water in NiAl-LDH using 2H NMR spectroscopy, and confirmed the order of Al3+ ions by quantitative NMR analysis of LDHs with disparate Al ratios.82 Moreover, the 2H MAS NMR spectra can be extended to explore the local structural information of multifarious different paramagnetic LDHs. Recently, they have synthesized CaAl-LDH nanosheets using salt and urea without any additional water, and the obtained CaAl-LDH gives oxygen defects with the formation of AlO4, as evidenced by NMR, explaining the improved performance in F anion removal.83 The development of NMR spectroscopy makes it possible to study the microchemical environmental structure (like degree of disorder and coordination structure) in the future, especially for Mg and Al-containing structures that are difficult to characterize by XAFS.
However, NMR active molecules (e.g., 13C-acetone for 13C, pyridine for 15N, and trimethylphosphine oxide (TMPO) and trimethylphosphine (TMP) for 31P) can serve as probes to study the microenvironments of active sites on solid surfaces.84–86 Among them, TMP bearing a wide 31P response range has been demonstrated to be a promising probe for differentiating (from peak position) and quantifying (from peak area) active sites on various solid surfaces.87 In general, the stronger their interaction, the lower the electron density of TMP 31P nucleus and hence the shift of the 31P signal (δ31P) towards downfield (or positive ppm). Peng and co-workers first used this molecule to study various ZnO surfaces, namely, (100), Zn-terminated (002) (Zn-(002)), O-terminated (002) (O-(002)) surfaces using plate- and rod-like ZnO crystallites.88 Distinct TMP-31P NMR spectra observed for these two shapes (Fig. 6A) suggest that the nature of surface three-coordinated Zn (Zn3C) atoms and Vo-associated protons varies with their host surfaces. The presence of TMP-Zn3C (I and II) and TMP-proton (III and IV) species were further confirmed by DFT calculations (Fig. 6B). Since one can obtain the amount of these TMP adsorbed sites (I to IV) from the area of their δ31P signal, not only the distribution but also the concentration of Zn3C, Vo, and hydroxyl groups can be provided for each sample (Fig. 6C). This allows for a reliable correlation of surface sites to their photocatalytic activities in both qualitative and quantitative manners. Therefore, the photocatalytic oxidation of surface hydroxyl groups to OH radicals was revealed.89
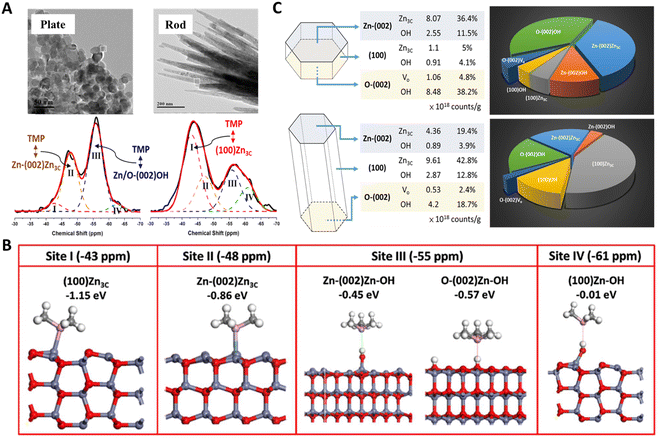 | ||
| Fig. 6 (A) 31P NMR spectra of TMP-adsorbed plate-/rod-like ZnO crystallites. (B) DFT simulation of the adsorption configuration and energy of TMP on Zn3C (I and II) and proton (III and IV) species. (C) Distribution, concentration, and percentage of various surface features on plate-/rod-like ZnO revealed by TMP-31P NMR.88 Copyright © 2016 American Chemical Society. | ||
Recently, the same group also studied the surface effect of CeO2 shapes in two enzymatic reactions (Fig. 7A).92,93 A CeO2 cube terminated by the (100) facet was found to display high activity in H2O2 conversion,92 while it is nearly inactive in dephosphorylation reactions.93 Interestingly, CeO2 octahedron with the (111) exposure shows a total reverse trend in both reactions. The chemical state of surface Ce revealed by TMP-31P NMR suggested that Ce has stronger Lewis acidity on the (111) facet of the octahedron (more Ce4+ like) while weaker Lewis acidity on the (100) facet of the cube (more Ce3+ like) (Fig. 7C).94 One can thus easily achieve ca. 1000% (for cube in H2O2 conversion) and 4500% (for octahedron in dephosphorylation) increase for pristine CeO2 if its terminal facet is wisely selected for a given reaction. In addition to the facet effect, the electronic effect of “surfactant” (e.g., fluorine) imposed on surface five-coordinated Ti (Ti5c) was also revealed by TMP-31P NMR (Fig. 7B).90 As HF, a structure-directing agent can efficiently stabilize the high-energy (001) facet of anatase TiO2 (cf. thermodynamic stable (101)), and the percentage of exposed (001)/(101) facet can thus be tuned by added HF. TMP-31P NMR spectra revealed that the 0HF sample has ∼90% of Ti5C on the most stable (101) facet (−36 ppm) and less than 10% of Ti5C on the high-energy (001) facet with higher acidity (−29 ppm). While for 2HF and 6HF, the presence of surface F observably shifts the chemical state of Ti5C on the (101) and (001) facets to −31 and −22.5 ppm and produces extra surface features such as acidic proton (−2.6 ppm, TMPH+) and oxygen vacancy (−42.5 ppm). This technique also demonstrated its power in monitoring the change in Ti5c chemical state in the course of F removal (NaOH wash) and later sulfate modification (Fig. 7D).91 As TiO2 surfaces can be comprehensively mapped, the key Ti5c site dictating TiO2 facet activity in Pechmann condensation,91 dephosphorylation reaction,95 photocatalytic hydrogen evolution,96 and water splitting97 was thus revealed.
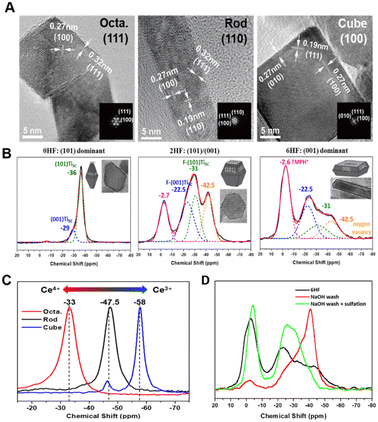 | ||
| Fig. 7 (A) TEM images of CeO2 terminated with the (111), (110), and (100) facets, respectively, and schematic illustration of H2O2 conversion (left) and dephosphorylation reaction (right). (B) TEM and TMP-31P NMR spectra of different TiO2 facets.90 Copyright © 2017 Springer Nature Limited. (C) TMP-31P NMR spectra of CeO2 shapes. (D) TMP-31P NMR spectra of NaOH- and sulfate-modified samples.91 Copyright © 2018 Royal Society of Chemistry. | ||
Moreover, TMP-31P NMR can be used to identify different Al species, Zheng's group used DFT calculations in combination with 31P NMR experiments, where TMP was the probe molecule to conduct a comprehensive study on the existence of tri-coordinated EFAL-Al3+ species in the zeolitic catalysts, which is usually undetectable by conventional one – and two-dimensional 1H and/or 27Al solid-state NMR.98 In addition to TMP, TMPO as a31P probe molecule is preferentially attached to acid sites on solid catalysts, thus providing qualitative and quantitative information on Brønsted and Lewis acid sites.85 The development of NMR and the expansion of various probe molecules has enabled the quantitative study of the types, densities and intensities of various sites,99,100 which is a powerful means to identify the surface characteristics of catalysts.
The combination of NMR with other complementary techniques has allowed researchers to investigate surface active sites and their connection to structural flexibility and defect formation. For instance, Tsang's group used Raman, XPS, XAFS, and 93Nb NMR to gain new insights into the structure-acidity correlations of nanosize niobium oxides with nonstoichiometric structural variety.101 Besides, combining NMR with in situ techniques can provide valuable information about dynamic changes in active sites under catalyst working conditions. For example, Li and co-workers used solid-state NMR, in situ synchrotron X-ray powder diffraction, and infrared spectroscopy to show that traditional Brønsted acid sites (Si–O(H)–Al) on silicoaluminophosphate zeolites can be transformed into Frustrated Lewis Pairs via breaking the Al–O bond in the framework upon adsorption of polar small molecules.102 Similar active site transformations can also be promoted at elevated temperatures.103 These findings highlight the importance of using combined characterizations and in situ techniques for active site identification.
2.4. Positron annihilation spectroscopy (PAS)
PAS is favored by researchers because it can non-destructively study the internal microstructure and defect state of species. Researchers often employ coincidence Doppler broadening (CDB) and positron lifetime of positron annihilation spectroscopy (PAS) to study the defective structure of heterogeneous materials. In the CDB spectrum, the low electron density at the vacancy defect leads to a decrease in the average momentum of the annihilated electron and a narrow spectral line, while the positron lifetime in the PAS test corresponds to defects of different sizes.PAS technology can be used to accurately locate defect types (like isolated or double or triple defects) that cannot be clearly identified by XAFS technique. Xie's team successfully prepared ultrathin BiOCl nanosheets that nearly exposed the active (001) facet, and used PAS technology to reveal that the main component of the defect changed from single-defect  to triple vacancy-associated defect
to triple vacancy-associated defect  as the thickness of the nanosheets decreased to the atomic scale.104 As shown in Fig. 8A and D, both the ultrathin BiOCl nanosheets and nanoplates yield four lifetime components in the PAS spectrum. The two longer lifetimes (τ3, 550–590 ps, and τ4, 2.2–2.5 ns) correspond to large defect clusters and positron annihilation between material interfaces, respectively. Based on the theoretically calculated positron lifetime (Fig. 8E), the shortest lifetime (τ1, about 250 ps) observed in the PAS spectrum can correspond to positron annihilation trapped in a single isolated bismuth vacancy (Fig. 8B), while another lifetime (τ2, about 325 ps) was attributed to
as the thickness of the nanosheets decreased to the atomic scale.104 As shown in Fig. 8A and D, both the ultrathin BiOCl nanosheets and nanoplates yield four lifetime components in the PAS spectrum. The two longer lifetimes (τ3, 550–590 ps, and τ4, 2.2–2.5 ns) correspond to large defect clusters and positron annihilation between material interfaces, respectively. Based on the theoretically calculated positron lifetime (Fig. 8E), the shortest lifetime (τ1, about 250 ps) observed in the PAS spectrum can correspond to positron annihilation trapped in a single isolated bismuth vacancy (Fig. 8B), while another lifetime (τ2, about 325 ps) was attributed to  associated with Bi3+-oxygen vacancies (Fig. 8C). Obviously, the Bi3+-oxygen triple vacancies mainly exist in the ultrathin nanosheets, while
associated with Bi3+-oxygen vacancies (Fig. 8C). Obviously, the Bi3+-oxygen triple vacancies mainly exist in the ultrathin nanosheets, while  mainly exists in the nanoplates by analyzing their PAS results. The combination of PAS technology with XAFS and other representation technologies can accurately determine the type of defects and calculate the density of the defects semi-quantitatively, thus giving a deeper understanding of the defects.
mainly exists in the nanoplates by analyzing their PAS results. The combination of PAS technology with XAFS and other representation technologies can accurately determine the type of defects and calculate the density of the defects semi-quantitatively, thus giving a deeper understanding of the defects.
 | ||
Fig. 8 (A) PAS spectra of ultrathin BiOCl nanosheets and nanoplates. (B and C) Schematic illustrations of trapped positrons of  defects and associated defects defects and associated defects  (D) Positron lifetime parameters of ultrathin BiOCl nanosheets and nanoplates. (E) Calculated positron lifetime values of BiOCl.104 Copyright © 2013 American Chemical Society. (D) Positron lifetime parameters of ultrathin BiOCl nanosheets and nanoplates. (E) Calculated positron lifetime values of BiOCl.104 Copyright © 2013 American Chemical Society. | ||
Recently, some researchers have found that bulk vacancy defects and surface vacancy defects have discrepant effects on catalysis. Zhao and co-workers explored for the first time the relationship between bulk/surface defects in TiO2 and the corresponding photocatalytic efficiency.41 The different concentration ratio of bulk defects to surface defects in anatase TiO2 was realized by vapor-induced hydrothermal hydrolysis of titanium butoxide at 120 °C, 180 °C (denoted as TiO2-120, TiO2-180) and calcination of TiO2-180 at 480 °C (denoted as TiO2-480). The intensity (I) of the positron lifetime reflects their relative concentration. The ratio of I1 to I2 (I1/I2) performed by PAS represents the ratio of the concentration of volume defects to surface defects. I1/I2 decreases from 1.01 for TiO2-120 to 0.45 for TiO2-180, manifesting a decline of the concentration ratio of bulk-to-surface defects. TiO2-120 with the highest ratio shows the lowest photocurrent response, which is because of the recombination of charge carriers in the bulk defects. This phenomenon may attribute to interfacial defects from bulk defects in TiO2, which is confirmed by the positron lifetime that τ1 for TiO2 is larger than that for TiO2-120. This work indicated that controlling the content ratio of bulk-to-surface defects is highly essential for photocatalysis. It is well known that catalysis happens on the surface, the PAS also provides information about the defects on the surface, while XAFS and NMR always provide a statistical result no matter from the surface or bulk structure.
The defect structure information of metal catalysts can also be obtained by PAS. Wei and co-workers reported a Ru–Ni catalyst (denoted as Ru0.8-Ni/H–Al2O3) that anchored Ru clusters to the defect sites of Ni nanoparticles (denoted as Ni/H–Al2O3) prepared by topotactic reduction of the NiAl-LDH precursor.105 The materials obtained from Ni/H–Al2O3 annealed at 500 °C and 550 °C were denoted as NiA500/H–Al2O3 and NiA550/H–Al2O3, respectively. Based on the CDB spectra of the samples distributed along a straight line obtained by PAS, it can be inferred that these samples mainly have Ni defects. After anchoring Ru clusters, the increase in τ2 from 381.5 ps to 424.8 ps could be attributed to the appearance of Ru–Ni interface, improving the electron density on Ni vacancy clusters. A similar I2/I1 ratio observed between Ni/H–Al2O3 (1.40) and Ru0.8-Ni/H–Al2O3 (1.30) manifested that the concentration of newly formed Ru–Ni interface defects is close to that of original Ni vacancy clusters. Hence, most Ru atoms may anchor onto vacancy clusters. The ratio of I2/I1 decreases with the increase in annealing temperature, indicating that the concentration of Ni vacancy clusters decreases. The I2/I1 ratios of Ni/H–Al2O3, NiA500/H–Al2O3, and NiA550/H–Al2O3 catalysts were positively correlated with the turnover frequency of C1 (TOFC1) and CH4 (TOFCH4), which suggested that vacancy clusters were the active sites for the cleavage of both C–C bond and C–O bonds in an ethanol steam reforming reaction. This work thus highlights the significance of quantifying concentration to probe catalytic reactions. PAS technology can only obtain the ratio of bulk-to-surface defects and the types of surface defects, which are limited in quantifying defect concentration. However, PAS plays an irreplaceable role in accurately locating defect types, which can be used as an auxiliary means to accurately quantify defect concentration in combination with other technologies such as XAFS and NMR.
2.5. Electron paramagnetic resonance (EPR)
EPR is a widely used technique that can qualitatively and quantitatively measure the unpaired electrons included in atoms or molecules and explore the structural features of their surroundings via the spin transitions of unpaired electrons.Eichel's group studied the photoluminescence behaviour of ZnO films at different temperatures and calculated the defect density through EPR.106 As shown in Fig. 9A, a single line is observed at g = 1.9588 in the corresponding EPR spectrum of the bulk ZnO powder (bottom), which indicates the presence of singly charged oxygen vacancy VO. For nano-sized ZnO (top), accessional resonance lines appear at g = 2.0028, while the intensity of resonance lines at g = 1.9588 increases after UV irradiation of both nano-sized and bulk ZnO for 10 minutes (Fig. 9B), and the intensity of resonance lines at g = 2.0028 remains unchanged. Therefore, it is inferred that the resonance line at g = 2.0028 represents a defect on the ZnO surface. Similarly, Liu and colleagues synthesized a series of oxygen vacancy-rich Fenton-like catalysts CuFeO2 by a cryogenic hydrothermal method, and used the EPR technology to compare the defect structure of these materials in depth.107 As shown in Fig. 9C, all catalysts have a distinct EPR signal at g = 2.003, which indicates that oxygen vacancies are formed on the catalyst surface and that CuFeO2@MRPs-200 contains the most abundant oxygen vacancies. The presence of oxygen vacancies not only promotes the charge transfer ability, but also promotes the activation of H2O2 to ˙OH, thus improving the ability of the material to catalyze rhodamine B degradation. Wang and co-workers also studied the Ti3+ species in anatase nanocrystals using EPR (Fig. 9D).108 The “Ti3+ reversible diffusion mechanism” was used to control the location and concentration of Ti3+ defects by regulating temperature. The TiO2 with the highest concentration of Ti3+ shows the best photocatalytic decomposition activity of methylene blue. This work emphasized that the reasonable distribution of Ti3+ subsurface/bulk defects is significant to high visible light-driven photocatalysis. In addition, the ESR can also be extended to recognize S vacancies. Peng's group used in situ EPR technology to reveal that the S vacancies of CdS-CNT samples increased with the CO2RR, which strongly supported the continuous generation of S vacancies on the surface of CdS-CNT during the electrochemical reduction of CO2.109
 | ||
| Fig. 9 (A) EPR spectrum of different-sized ZnO. (B) Defect concentration (VO) at g = 1.9588 before and after irradiation.106 Copyright © 2009 Royal Society of Chemistry. (C) EPR spectra of CuFeO2, CuFeO@MRPs-100, CuFeO2@MRPs-200 and CuFeO2@MRPs-400.107 Copyright © 2021 Elsevier Ltd. (D) EPR spectrum of P25, TiO2−x and TiO2−x-T.108 Copyright © 2015 Elsevier B.V. | ||
In general, the EPR can be a very intuitive means to observe unpaired electrons and defects, but the intensity of signal peak increases with the extension of scanning time, resulting in the deviation of using paramagnetic resonance to quantify the defect concentration, which is more useful as a qualitative tool. This limitation suggests that this technique should be used with other techniques for a comprehensive surface understanding.
2.6. X-ray photoelectron spectroscopy (XPS)
XPS can provide not only the elemental composition and valence information on the catalyst surface, but also the defect structure and chemical bond information of various compounds. The quantification of defects is also of great importance for a more in-depth study of defect effects in order to improve the performance of TiO2. Sung and co-workers by XPS analysis (Fig. 10A and B) reported that Cu doping increases the concentration of oxygen vacancies in TiO2 nanorods.110 The concentration of oxygen vacancies of pristine and Cu doping TiO2 nanorods was estimated based on the following formula:110| VO (%) = {[(the atomic number ratio of Ti × 4) − (the atomic number ratio of OL × 2)]}/2 × 100 |
 | ||
| Fig. 10 (A) XPS of pure TiO2 nanorods and (B) TiO2 nanorods with Cu doping.110 Copyright © 2010 American Chemical Society. (c) XPS of VO-rich ZnO.112 Copyright © 2012 American Chemical Society. (D) XPS valence band spectra of black TiO2 samples.113 Copyright © 2018 Elsevier Inc. | ||
Three forms of oxygen can be observed in the O 1s XPS spectra, namely, lattice oxygen (OL, 530.3 eV), surface hydroxyl oxygen (O–OH, 532.1 eV) and adsorbed oxygen (OS, 533.6 eV). The OL corresponds to lattice oxygen, and it is considered to be an element sensitivity factor. After doping Cu, the concentration of oxygen vacancies increases from 31.2% for pristine TiO2 nanorods to 37.66% for Cu-doped TiO2 nanorods, which suggests that Cu doping facilitates the generation of oxygen vacancies in TiO2. In addition, Dai and co-workers also investigated the variation in oxygen vacancy concentration in ZnO prepared at different annealing temperatures.111 According to the results of XPS fitting calculations, the concentration of oxygen vacancies decreases with the increase in annealing temperature, and the experimental results also indicate that ZnO materials with more oxygen vacancies have a longer absorption wavelength and a narrower band gap, resulting in the highest photodegradation activity for 2,4-dichlorophenol. Besides, Zeng and co-workers promoted the activation of CO2 to produce CO by introducing oxygen vacancies on ZnO surfaces.112 According to the XPS results shown in Fig. 10C, the integrated area ratios of 531.7 eV and 530.2 eV peaks are 0.30, 0.57 and 0.76, respectively, by fitting the ZnO nanosheets with three different oxygen defect contents (pristine, poor and rich). Moreover, XPS valence band spectroscopy can not only explore the surface defects of materials, but also reveal the electronic structure of materials. Ohno and coworkers investigated the concentrations of Ti3+ on the surface of TiO2 and estimated the valence band maxima of the material to be about 1.6 eV based on linear extrapolation (Fig. 10D).113 The concentration of oxygen defects on the TiO2 surface decreased with the increase in Ti3+ concentration, and the photocatalytic activity of TiO2 reached the best when the concentration of Ti3+ was 22.6%. The quantitative analysis of the relative concentration of vacancy defects is thus critical to optimize the catalyst performance.
XPS is one of the most powerful tools for researching the surface properties of materials, allowing for detailed information about surface defects and electronic structures. However, its limitation is that the surface of many offline samples is easy to be oxidized and modified or adsorbed some small molecules. Therefore, the in situ technique can be developed to better understand the real surface information of the catalyst. Together with other representative techniques such as XAFS and PAS, one can better obtain a more comprehensive information of the defects.
2.7. Photoluminescence (PL) spectra
PL is widely used to characterize the bulk defect structure of metal oxide semiconductors. After absorbing the photon, the semiconductor material generates photoexcited electrons and holes in the conduction and valence bands, respectively. The excited electron–hole pairs will recombine at the defect center, resulting in trap-state luminescence.Uyar and coworkers used the atomic layer deposition method with different deposition cycle numbers to prepare ZnO quantum dots (QDs) or nanocoating (NC) for the photodegradation of methylene blue (MB).114 They found that Zn interstitials (Znis) were dominant when the number of cycles was small, and oxygen vacancy (VO) was gradually introduced as the cycle progresses. Analytical experiments for each defect were performed for each sample (Fig. 11A and B), and the relevant concentrations of ZniS and VO were estimated by calculating the area of each peak, corresponding to the defect-related transitions. For illuminating the effect of Zni and VO on photocatalytic activity, photoluminescence (PL) spectra were employed to quantify the density of defects.
 | ||
| Fig. 11 (A) Luminescence spectra of ZnO with different numbers of cycles. (B) Schematic diagram of defect attribution. (C) Photocatalytic activities of different samples. (D) Defect density and corresponding decay constant. (E) Spectral locations of deconvoluted peaks and ascribed emission mechanism.114 Copyright © 2014 Royal Society of Chemistry. | ||
The percentage increase in defect density was calculated by each peak's area of PL spectra based on the following formula:114
| %increase for b emission = b′ = (AbfromPZ1QD − AbfromPZ2,PZ3,PZ4NC) × 100/AbfromPZ1QD |
Via analysis of the relation between photocatalytic activity (Fig. 11C) and the percentage increase in defect density (Fig. 11D), they concluded that VO is more efficient than Zni-related defects for photocatalysis. In addition, importing oxygen vacancies into ZnO for the enhanced CO2 reduction activity was reported by Zeng and coworkers.115 The recombination of two-electron-trapped oxygen vacancies and photogenerated holes in the PL spectra also confirms that ZnO with the rich oxygen vacancies has a higher PL intensity. The introduction of oxygen vacancies regulates the valence and conduction structures of ZnO, enhances the activation of CO2 and promotes the electrocatalytic reduction of CO2 to CO.
PL has been widely used to evaluate the defect structures due to its simple operation. However, the result could be interfered by bulk defects and vary with the excitation wavelength, indicating that PL testing alone is not enough to provide a comprehensive view on the structure–activity relationship. Therefore, it is strongly suggested to combine this technique with XPS, XAFS and other technologies for a better understanding of defect sites. Meanwhile, the recent development of in situ PL technique116 also makes it possible to measure the defective structure (or surface temperature) of materials under reactive conditions.
2.8. Fourier-transform infrared (FTIR) spectroscopy
The chemical bonds or functional groups in the material that absorbs infrared light at different frequencies will show specific positions, giving information about the vibrational properties of the adsorbed hydroxyl groups and metal–O (appearing at around 650–450 cm−1) of the catalyst. The bond force constant (k) determines the position and intensity of the IR absorption peak, indicating the change in the type and strength of the bond. Zhu and co-workers studied the variation in the VO concentration on the ZnO surface by FTIR spectroscopy and found that the increase in VO concentration leads to a decrease in Zn–O bond strength (k value), along with the position of IR absorption peak shifts to a lower wave number.117 Therefore, the defect concentration of the samples can be judged according to the infrared peak shift degree, providing a new view on the determination of the defect state. When other metallic elements such as Mn118,119 and Eu120 entering the ZnO lattice, the IR absorption peak of the Zn–O bond in the fingerprint region will also change accordingly, which can be used to judge the successful doping of elements or not. It should be noted that the limitation of using FTIR spectroscopy to obtain defect information is that it is difficult to distinguish whether the change in fingerprint region is solely caused by defects when the catalyst composition and the surface state is complex. In situ FTIR techniques have been developed to monitor intermediates and active species in photo/electrocatalytic reaction processes,121,122 combined with other characterizations, and we can have a deeper understanding of the changes of catalyst and reactant molecules in the reaction process.3. Summary and perspectives
In summary, defect engineering has become a key strategy to regulate the structure and properties of catalysts with the development of catalytic reactions in chemical production. This review focuses on a variety of representational methods to reveal the defects and summarizes from different perspectives on where, what and how much of the defects. Our method for calculating the defect concentration on the exposed facet based on XAFS characterization also provides a new path for semi-quantifying the defect concentration of common catalytic materials. However, although considerable progress has been made in the study of defects, there are still some problems to be solved in terms of defect characterization technology and catalytic mechanism under working conditions.(1) Due to the differences in the application scope of various characterization techniques, the characteristics of identifying defects are also different. Individual technology is limited by its own detection mechanism, making the obtained information unsatisfactory. For example, the VO density and VM density calculated based on the coordination number information obtained by XAFS are the average results of the whole individual phase, and the specific types of defects (like the surface of bulk state) cannot be well distinguished. 31P NMR can be used to obtain information such as defect types on specific facets of materials, but the results are more limited to the surface of materials. Therefore, to have a comprehensive understanding of the defect structure, we need to combine different representation techniques.
(2) The defect concentration obtained in the off-line state cannot truly reflect the defect state in the reaction process, and it is crucial to capture the defect information in the catalytic condition. Some in situ characterization techniques such as in situ XAFS, in situ ESR, in situ TEM, in situ NMR, and in situ XPS remain to be applied to reveal the dynamic evolution process of defects, so as to accurately understand and quantify defects. However, in situ characterization is faced with many challenges. First of all, the equipment and instruments need to be upgraded, and it is urgent to develop in situ reaction devices suitable for liquid, light irradiation or gas environment, or high-temperature experiments. Second, the signal received in the in situ reaction process is much weaker than that in the off-line process, so it is necessary to design the concentration of catalyst active components reasonably to monitor the reaction process.
(3) The relationship between defects, reaction intermediates, and the reaction process has not been clarified. Given that transient processes such as charge transfer are also difficult to capture using in situ techniques, theoretical calculations (like DFT) will need to be developed next to better comprehend the catalytic processes. The development of transient time-resolved DFT calculation can also make up for the shortcomings of current characterization techniques and assist the understanding of defects in the catalytic process.
This review summarizes the current characterization of semi-quantified metals and metal oxide active sites under off-line conditions, and proposes a method to calculate the defect concentration using XAFS characterization and related methods, which provides some guidance for future defect engineering applications. The development of in situ technology and DFT will allow us to have a deeper understanding of defects and provide insights for the design of catalysts with high activity.
Author contributions
Jing Ren wrote and outlined the draft of the manuscript under the guidance of Yufei Zhao; Haoyuan Chi and Ling Tan contributed to investigate and data collation; Yung-Kang Peng, Guangchao Li and Molly Meng-Jung Li participated in data analysis and summary; Xue Duan developed the idea and supervised the project.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This research was supported by the National Natural Science Foundation of China (22278030, 22090032, 22090030, 22288102, 22011530162), Major Program of Qingyuan Innovation Laboratory (Grant No. 001220005). We would like to thank the Space Exploration Program and the Qian Xuesen Laboratory, China Academy of the Space Technology.References
- J. C. Vedrine, ChemSusChem, 2019, 12, 577–588 CrossRef CAS PubMed.
- J. N. Armor, Appl. Catal., 1991, 78, 141–173 CrossRef CAS.
- A. Chauvel, B. Delmon and W. F. Hölderich, Appl. Catal., A, 1994, 115, 173–217 CrossRef CAS.
- M. Misono and N. Nojiri, Appl. Catal., 1990, 64, 1–30 CrossRef CAS.
- G. A. Somorjai, Annu. Rev. Phys. Chem., 1994, 45, 721–751 CrossRef CAS.
- G. Ertl, Advances in Catalysis, Academic Press, 2000, vol. 45, pp. 1–69 Search PubMed.
- C. Xiao, B.-A. Lu, P. Xue, N. Tian, Z.-Y. Zhou, X. Lin, W.-F. Lin and S.-G. Sun, Joule, 2020, 4, 2562–2598 CrossRef CAS.
- Z.-Y. Zhou, N. Tian, J.-T. Li, I. Broadwell and S.-G. Sun, Chem. Soc. Rev., 2011, 40, 4167–4185 RSC.
- Y. Sun, S. Gao, F. Lei and Y. Xie, Chem. Soc. Rev., 2015, 44, 623–636 RSC.
- J. Ren, L. Tan, Y. Zhao and Y.-F. Song, CIESC J., 2021, 72, 398–424 CAS.
- S. Bai, N. Zhang, C. Gao and Y. Xiong, Nano Energy, 2018, 53, 296–336 CrossRef CAS.
- Z. Xiao, C. Xie, Y. Wang, R. Chen and S. Wang, J. Energy Chem., 2021, 53, 208–225 CrossRef CAS.
- K. Zhong, R. Bu, F. Jiao, G. Liu and C. Zhang, Chem. Eng. J., 2022, 429, 132310 CrossRef CAS.
- J. Huang, C. Fu, J. Chen, N. Senthilkumar, X. Peng and Z. Wen, CCS Chem., 2022, 4, 566–583 CrossRef CAS.
- J. Zhu and S. Mu, Adv. Funct. Mater., 2020, 30, 2001097 CrossRef CAS.
- Y.-C. Zhang, S. Ullah, R. Zhang, L. Pan, X. Zhang and J.-J. Zou, Appl. Catal., B, 2020, 277, 119247 CrossRef CAS.
- B. Zhou, R. Gao, J.-J. Zou and H. Yang, Small, 2022, 18, 2202336 CrossRef CAS PubMed.
- Y.-C. Zhang, N. Afzal, L. Pan, X. Zhang and J.-J. Zou, Adv. Sci., 2019, 6, 1900053 CrossRef.
- Y. Liu, J.-g. Guo, Y. Wang, Y.-j. Hao, R.-h. Liu and F.-t. Li, Green Energy Environ., 2021, 6, 244–252 CrossRef.
- J. W. Zuzeng Qin, B. Li, T. Su and H. Ji, Acta Phys.-Chim. Sin., 2021, 37, 2005027 Search PubMed.
- Y. Zhang, L. Guo, L. Tao, Y. Lu and S. Wang, Small Methods, 2019, 3, 1800406 CrossRef.
- P. Rao, D. Wu, T.-J. Wang, J. Li, P. Deng, Q. Chen, Y. Shen, Y. Chen and X. Tian, eScience, 2022, 2, 399–404 CrossRef.
- Y. Guo, M. Wang, Q. Zhu, D. Xiao and D. Ma, Nat. Catal., 2022, 5, 766–776 CrossRef CAS.
- C. Chen, L. Tao, S. Du, W. Chen, Y. Wang, Y. Zou and S. Wang, Adv. Funct. Mater., 2020, 30, 1909832 CrossRef CAS.
- H. Du, J. Fan, C. Miao, M. Gao, Y. Liu, D. Li and J. Feng, Trans. Tianjin Univ., 2021, 27, 24–41 CrossRef CAS.
- Y. Wang, Y. Zhang, Z. Liu, C. Xie, S. Feng, D. Liu, M. Shao and S. Wang, Angew. Chem., Int. Ed., 2017, 56, 5867–5871 CrossRef CAS PubMed.
- P. Zhou, Y. Wang, C. Xie, C. Chen, H. Liu, R. Chen, J. Huo and S. Wang, Chem. Commun., 2017, 53, 11778–11781 RSC.
- R. Liu, Y. Wang, D. Liu, Y. Zou and S. Wang, Adv. Mater., 2017, 29, 1701546 CrossRef PubMed.
- D. Zhou, X. Xiong, Z. Cai, N. Han, Y. Jia, Q. Xie, X. Duan, T. Xie, X. Zheng, X. Sun and X. Duan, Small Methods, 2018, 2, 1800083 CrossRef.
- X. Jia, X. Zhang, J. Zhao, Y. Zhao, Y. Zhao, G. I. N. Waterhouse, R. Shi, L.-Z. Wu, C.-H. Tung and T. Zhang, J. Energy Chem., 2019, 34, 57–63 CrossRef.
- Q. Xie, Z. Cai, P. Li, D. Zhou, Y. Bi, X. Xiong, E. Hu, Y. Li, Y. Kuang and X. Sun, Nano Res., 2018, 11, 4524–4534 CrossRef CAS.
- Z. Ni, H. Liang, Z. Yi, R. Guo, C. Liu, Y. Liu, H. Sun and X. Liu, Coord. Chem. Rev., 2021, 441, 213983 CrossRef CAS.
- H. Zhang and M. M.-J. Li, Curr. Opin. Green Sustainable Chem., 2022, 36, 100646 CrossRef CAS.
- S. Chen, X. Liu, J. Xiong, L. Mi, X.-Z. Song and Y. Li, J. Mater. Chem. A, 2022, 10, 6927–6949 RSC.
- Q. Yang, T. Wang, Z. Zheng, B. Xing, C. Li and B. Li, Appl. Catal., B, 2022, 315, 121575 CrossRef CAS.
- T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102 CrossRef CAS PubMed.
- R. Schaub, E. Wahlström, A. Rønnau, E. Lægsgaard, I. Stensgaard and F. Besenbacher, Science, 2003, 299, 377–379 CrossRef CAS PubMed.
- E. Wahlstrom, E. K. Vestergaard, R. Schaub, A. Ronnau, M. Vestergaard, E. Laegsgaard, I. Stensgaard and F. Besenbacher, Science, 2004, 303, 511–513 CrossRef PubMed.
- F. F. Tao and M. Salmeron, Science, 2011, 331, 171–174 CrossRef CAS PubMed.
- L. Tan, S. M. Xu, Z. Wang, Y. Xu, X. Wang, X. Hao, S. Bai, C. Ning, Y. Wang, W. Zhang, Y. K. Jo, S. J. Hwang, X. Cao, X. Zheng, H. Yan, Y. Zhao, H. Duan and Y. F. Song, Angew. Chem., Int. Ed., 2019, 58, 11860–11867 CrossRef CAS PubMed.
- M. Kong, Y. Li, X. Chen, T. Tian, P. Fang, F. Zheng and X. Zhao, J. Am. Chem. Soc., 2011, 133, 16414–16417 CrossRef CAS PubMed.
- X. Liu and L. Gu, Small Methods, 2018, 2, 1800006 CrossRef.
- Q. Sun, Z. Gong, Y. Zhang, J. Hao, S. Zheng, W. Lu, Y. Cui, L. Liu and Y. Wang, J. Hazard. Mater., 2022, 421, 126816 CrossRef CAS PubMed.
- J. Xie, X. Zhang, H. Zhang, J. Zhang, S. Li, R. Wang, B. Pan and Y. Xie, Adv. Mater., 2017, 29, 1604765 CrossRef.
- S. Chen, H. Wang, Z. Kang, S. Jin, X. Zhang, X. Zheng, Z. Qi, J. Zhu, B. Pan and Y. Xie, Nat. Commun., 2019, 10, 788 CrossRef CAS.
- H. Feng, Z. Xu, L. Ren, C. Liu, J. Zhuang, Z. Hu, X. Xu, J. Chen, J. Wang, W. Hao, Y. Du and S. X. Dou, ACS Catal., 2018, 8, 4288–4293 CrossRef CAS.
- R. Schaub, P. Thostrup, N. Lopez, E. Lægsgaard, I. Stensgaard, J. K. Nørskov and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 266104 CrossRef CAS PubMed.
- X. Li, A. Gao, Z. Tang, F. Meng, T. Shang, S. Guo, J. Ding, Y. Luo, D. Xiao, X. Wang, D. Su, Q. Zhang and L. Gu, Adv. Funct. Mater., 2021, 31, 2010291 CrossRef CAS.
- J. Lee, Y. Gong, L. Gu and B. Kang, ACS Energy Lett., 2021, 6, 789–798 CrossRef CAS.
- H. Frey, A. Beck, X. Huang, J. A. van Bokhoven and M. G. Willinger, Science, 2022, 376, 982–987 CrossRef CAS PubMed.
- A. Beck, X. Huang, L. Artiglia, M. Zabilskiy, X. Wang, P. Rzepka, D. Palagin, M. G. Willinger and J. A. van Bokhoven, Nat. Commun., 2020, 11, 3220 CrossRef CAS PubMed.
- X. Huang, T. Jones, A. Fedorov, R. Farra, C. Coperet, R. Schlogl and M. G. Willinger, Adv. Mater., 2021, 33, e2101772 CrossRef PubMed.
- H. Fan, L. Qiu, A. Fedorov, M. G. Willinger, F. Ding and X. Huang, ACS Nano, 2021, 15, 17895–17906 CrossRef CAS PubMed.
- J. Wang, Y. Xu, J. Li, X. Ma, S.-M. Xu, R. Gao, Y. Zhao and Y.-F. Song, Green Chem., 2020, 22, 8604–8613 RSC.
- L. Tan, S.-M. Xu, Z. Wang, Y. Xu, X. Wang, X. Hao, S. Bai, C. Ning, Y. Wang, W. Zhang, Y. K. Jo, S.-J. Hwang, X. Cao, X. Zheng, H. Yan, Y. Zhao, H. Duan and Y.-F. Song, Angew. Chem., Int. Ed., 2019, 58, 11860–11867 CrossRef CAS PubMed.
- Q. Wang and D. O'Hare, Chem. Rev., 2012, 112, 4124–4155 CrossRef CAS PubMed.
- X. Hao, L. Tan, Y. Xu, Z. Wang, X. Wang, S. Bai, C. Ning, J. Zhao, Y. Zhao and Y.-F. Song, Ind. Eng. Chem. Res., 2020, 59, 3008–3015 CrossRef CAS.
- R. Liu, Y. Wang, D. Liu, Y. Zou and S. Wang, Adv. Mater., 2017, 29, 1701546 CrossRef PubMed.
- Y. Wang, Y. Zhang, Z. Liu, C. Xie, S. Feng, D. Liu, M. Shao and S. Wang, Angew. Chem., Int. Ed., 2017, 56, 5867–5871 CrossRef CAS PubMed.
- Y. Zhao, Y. Zhao, G. I. N. Waterhouse, L. Zheng, X. Cao, F. Teng, L.-Z. Wu, C.-H. Tung, D. O'Hare and T. Zhang, Adv. Mater., 2017, 29, 1703828 CrossRef PubMed.
- Y. Zhao, X. Zhang, X. Jia, G. I. N. Waterhouse, R. Shi, X. Zhang, F. Zhan, Y. Tao, L.-Z. Wu, C.-H. Tung, D. O'Hare and T. Zhang, Adv. Energy Mater., 2018, 8, 1703585 CrossRef.
- X. Zhang, Y. Zhao, Y. Zhao, R. Shi, G. I. N. Waterhouse and T. Zhang, Adv. Energy Mater., 2019, 9, 1900881 CrossRef.
- T. Rossi, T. J. Penfold, M. H. Rittmann-Frank, M. Reinhard, J. Rittmann, C. N. Borca, D. Grolimund, C. J. Milne and M. Chergui, J. Phys. Chem. C, 2014, 118, 19422–19430 CrossRef CAS.
- G. Giuli, A. Trapananti, F. Mueller, D. Bresser, F. d'Acapito and S. Passerini, Inorg. Chem., 2015, 54, 9393–9400 CrossRef CAS PubMed.
- A. K. Rana, Y. Kumar, P. Rajput, S. N. Jha, D. Bhattacharyya and P. M. Shirage, ACS Appl. Mater. Interfaces, 2017, 9, 7691–7700 CrossRef CAS PubMed.
- M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483–4490 CrossRef CAS.
- A. Gutiérrez, G. Domínguez-Cañizares, J. A. Jiménez, I. Preda, D. Díaz-Fernández, F. Jiménez-Villacorta, G. R. Castro, J. Chaboy and L. Soriano, Appl. Surf. Sci., 2013, 276, 832–837 CrossRef.
- Y. Zhao, X. Jia, G. Chen, L. Shang, G. I. N. Waterhouse, L.-Z. Wu, C.-H. Tung, D. O'Hare and T. Zhang, J. Am. Chem. Soc., 2016, 138, 6517–6524 CrossRef CAS PubMed.
- Z. Wang, S.-M. Xu, L. Tan, G. Liu, T. Shen, C. Yu, H. Wang, Y. Tao, X. Cao, Y. Zhao and Y.-F. Song, Appl. Catal., B, 2020, 270, 118884 CrossRef CAS.
- A. K. Rana, Y. Kumar, P. Rajput, S. N. Jha, D. Bhattacharyya and P. M. Shirage, ACS Appl. Mater. Interfaces, 2017, 9, 7691–7700 CrossRef CAS PubMed.
- B. L. Caetano, C. V. Santilli, F. Meneau, V. Briois and S. H. Pulcinelli, J. Phys. Chem. C, 2011, 115, 4404–4412 CrossRef CAS.
- M. Kuwa, M. Harada, R. Sato and T. Teranishi, ACS Appl. Nano Mater., 2020, 3, 2745–2755 CrossRef CAS.
- D. Delgado, R. Sanchís, J. A. Cecilia, E. Rodríguez-Castellón, A. Caballero, B. Solsona and J. M. L. Nieto, Catal. Today, 2019, 333, 10–16 CrossRef CAS.
- G. Wu, W. Chen, X. Zheng, D. He, Y. Luo, X. Wang, J. Yang, Y. Wu, W. Yan, Z. Zhuang, X. Hong and Y. Li, Nano Energy, 2017, 38, 167–174 CrossRef CAS.
- A. Gutiérrez, G. Domínguez-Cañizares, J. A. Jiménez, I. Preda, D. Díaz-Fernández, F. Jiménez-Villacorta, G. R. Castro, J. Chaboy and L. Soriano, Appl. Surf. Sci., 2013, 276, 832–837 CrossRef.
- M. A. Peck and M. A. Langell, Chem. Mater., 2012, 24, 4483–4490 CrossRef CAS.
- T. Ding, X. Liu, Z. Tao, T. Liu, T. Chen, W. Zhang, X. Shen, D. Liu, S. Wang, B. Pang, D. Wu, L. Cao, L. Wang, T. Liu, Y. Li, H. Sheng, M. Zhu and T. Yao, J. Am. Chem. Soc., 2021, 143, 11317–11324 CrossRef CAS PubMed.
- S. Fang, X. Zhu, X. Liu, J. Gu, W. Liu, D. Wang, W. Zhang, Y. Lin, J. Lu, S. Wei, Y. Li and T. Yao, Nat. Commun., 2020, 11, 1029 CrossRef CAS PubMed.
- B. L. Caetano, C. V. Santilli, F. Meneau, V. Briois and S. H. Pulcinelli, J. Phys. Chem. C, 2011, 115, 4404–4412 CrossRef CAS.
- P. J. Sideris, U. G. Nielsen, Z. Gan and C. P. Grey, Science, 2008, 321, 113–117 CrossRef CAS PubMed.
- S. Cadars, G. Layrac, C. Gérardin, M. Deschamps, J. R. Yates, D. Tichit and D. Massiot, Chem. Mater., 2011, 23, 2821–2831 CrossRef CAS.
- G. Yu, F. Hu, H. Huo, W. Ding and L. Peng, Chem. Phys. Lett., 2018, 706, 47–52 CrossRef CAS.
- L. Jin, Y. Sun, X. Zhou, J. Wen, F. Wang, X. Ning, Y. Wen, D. Wu and L. Peng, ACS Sustainable Chem. Eng., 2022, 10, 12955–12961 CrossRef CAS.
- Y.-K. Peng and S. C. E. Tsang, Nano Today, 2018, 18, 15–34 CrossRef CAS.
- X. Yi, H.-H. Ko, F. Deng, S.-B. Liu and A. Zheng, Nat. Protoc., 2020, 15, 3527–3555 CrossRef CAS PubMed.
- A. Zheng, S.-B. Liu and F. Deng, Chem. Rev., 2017, 117, 12475–12531 CrossRef CAS PubMed.
- A. Zheng, S.-J. Huang, S.-B. Liu and F. Deng, Phys. Chem. Chem. Phys., 2011, 13, 14889–14901 RSC.
- Y. K. Peng, L. Ye, J. Qu, L. Zhang, Y. Fu, I. F. Teixeira, I. J. McPherson, H. He and S. C. Tsang, J. Am. Chem. Soc., 2016, 138, 2225–2234 CrossRef CAS PubMed.
- Y.-K. Peng, Y. Fu, L. Zhang, I. F. Teixeira, L. Ye, H. He and S. C. E. Tsang, ChemCatChem, 2017, 9, 155–160 CrossRef CAS.
- Y. K. Peng, Y. Hu, H. L. Chou, Y. Fu, I. F. Teixeira, L. Zhang, H. He and S. C. E. Tsang, Nat. Commun., 2017, 8, 675 CrossRef PubMed.
- Y. K. Peng, H. L. Chou and S. C. Edman Tsang, Chem. Sci., 2018, 9, 2493–2500 RSC.
- Z. Tan, J. Zhang, Y.-C. Chen, J.-P. Chou and Y.-K. Peng, J. Phys. Chem. Lett., 2020, 11, 5390–5396 CrossRef CAS PubMed.
- Z. Tan, T.-S. Wu, Y.-L. Soo and Y.-K. Peng, Appl. Catal., B, 2020, 264, 118508 CrossRef.
- Z. Tan, G. Li, H.-L. Chou, Y. Li, X. Yi, A. H. Mahadi, A. Zheng, S. C. Edman Tsang and Y.-K. Peng, ACS Catal., 2020, 10, 4003–4011 CrossRef CAS.
- Q. Wang, X. Yi, Y.-C. Chen, Y. Xiao, A. Zheng, J. L. Chen and Y.-K. Peng, Angew. Chem., Int. Ed., 2021, 60, 16149–16155 CrossRef CAS PubMed.
- Y.-K. Peng, B. Keeling, Y. Li, J. Zheng, T. Chen, H.-L. Chou, T. J. Puchtler, R. A. Taylor and S. C. E. Tsang, Chem. Commun., 2019, 55, 4415–4418 RSC.
- Y. Li, Y.-K. Peng, L. Hu, J. Zheng, D. Prabhakaran, S. Wu, T. J. Puchtler, M. Li, K.-Y. Wong, R. A. Taylor and S. C. E. Tsang, Nat. Commun., 2019, 10, 4421 CrossRef PubMed.
- X. Yi, K. Liu, W. Chen, J. Li, S. Xu, C. Li, Y. Xiao, H. Liu, X. Guo, S.-B. Liu and A. Zheng, J. Am. Chem. Soc., 2018, 140, 10764–10774 CrossRef CAS PubMed.
- Y.-K. Peng and S.-c. E. Tsang, Magn. Reson. Lett., 2022, 2, 9–16 CrossRef CAS.
- X. Chen, Y.-y. Fu, B. Yue and H. He, Chin. J. Magn. Reson., 2021, 38, 491–502 Search PubMed.
- H. T. Kreissl, M. M. J. Li, Y.-K. Peng, K. Nakagawa, T. J. N. Hooper, J. V. Hanna, A. Shepherd, T.-S. Wu, Y.-L. Soo and S. C. E. Tsang, J. Am. Chem. Soc., 2017, 139, 12670–12680 CrossRef CAS PubMed.
- G. Li, C. Foo, X. Yi, W. Chen, P. Zhao, P. Gao, T. Yoskamtorn, Y. Xiao, S. Day, C. C. Tang, G. Hou, A. Zheng and S. C. E. Tsang, J. Am. Chem. Soc., 2021, 143, 8761–8771 CrossRef CAS PubMed.
- G. Li, T. Yoskamtorn, W. Chen, C. Foo, J. Zheng, C. Tang, S. Day, A. Zheng, M. M.-J. Li and S. C. E. Tsang, Angew. Chem., Int. Ed., 2022, 61, e202204500 CAS.
- M. Guan, C. Xiao, J. Zhang, S. Fan, R. An, Q. Cheng, J. Xie, M. Zhou, B. Ye and Y. Xie, J. Am. Chem. Soc., 2013, 135, 10411–10417 CrossRef CAS PubMed.
- H. Chen, S. He, X. Cao, S. Zhang, M. Xu, M. Pu, D. Su, M. Wei, D. G. Evans and X. Duan, Chem. Mater., 2016, 28, 4751–4761 CrossRef CAS.
- J. J. Schneider, R. C. Hoffmann, J. Engstler, S. Dilfer, A. Klyszcz, E. Erdem, P. Jakes and R. A. Eichel, J. Mater. Chem., 2009, 19, 1449–1457 RSC.
- M. Wang, C. Liu, H. Shi, T. Long, C. Zhang and B. Liu, Chemosphere, 2021, 283, 131191 CrossRef CAS PubMed.
- X. Xin, T. Xu, J. Yin, L. Wang and C. Wang, Appl. Catal., B, 2015, 176–177, 354–362 CrossRef CAS.
- B. Qin, Y. Li, H. Wang, G. Yang, Y. Cao, H. Yu, Q. Zhang, H. Liang and F. Peng, Nano Energy, 2019, 60, 43–51 CrossRef CAS.
- M. You, T. G. Kim and Y.-M. Sung, Cryst. Growth Des., 2010, 10, 983–987 CrossRef CAS.
- J. Wang, Z. Wang, B. Huang, Y. Ma, Y. Liu, X. Qin, X. Zhang and Y. Dai, ACS Appl. Mater. Interfaces, 2012, 4, 4024–4030 CrossRef CAS PubMed.
- Z. G. Geng, X. D. Kong, W. W. Chen, H. Y. Su, Y. Liu, F. Cai, G. X. Wang and J. Zeng, Angew. Chem., Int. Ed., 2018, 57, 6054–6059 CrossRef CAS PubMed.
- S. Liu, S. Yuan, Q. Zhang, B. Xu, C. Wang, M. Zhang and T. Ohno, J. Catal., 2018, 366, 282–288 CrossRef CAS.
- F. Kayaci, S. Vempati, I. Donmez, N. Biyikli and T. Uyar, Nanoscale, 2014, 6, 10224–10234 RSC.
- Z. G. Geng, X. D. Kong, W. W. Chen, H. Y. Su, Y. Liu, F. Cai, G. X. Wang and J. Zeng, Angew. Chem., Int. Ed., 2018, 57, 6054–6059 CrossRef CAS PubMed.
- B. Terlingen, T. Arens, T. P. van Swieten, F. T. Rabouw, T. Prins, M. M. de Beer, A. Meijerink, M. Ahr, E. M. Hutter, C. van Lare and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2022, 61, e202211991 CrossRef CAS PubMed.
- Y. Zheng, C. Chen, Y. Zhan, X. Lin, Q. Zheng, K. Wei, J. Zhu and Y. Zhu, Inorg. Chem., 2007, 46, 6675–6682 CrossRef CAS PubMed.
- S. Yildirimcan, K. Ocakoglu, S. Erat, F. M. Emen, S. Repp and E. Erdem, RSC Adv., 2016, 6, 39511–39521 RSC.
- N. D. Raskar, D. V. Dake, V. A. Mane, E. Stathatos, U. Deshpande and B. Dole, J. Mater. Sci.: Mater. Electron., 2019, 30, 10886–10899 CrossRef CAS.
- O. Sacco, P. Franco, I. De Marco, V. Vaiano, E. Callone, R. Ceccato and F. Parrino, J. Mater. Sci. Technol., 2022, 112, 49–58 CrossRef.
- L. Tan, S.-M. Xu, Z. Wang, X. Hao, T. Li, H. Yan, W. Zhang, Y. Zhao and Y.-F. Song, Cell Rep. Phys. Sci., 2021, 2, 100322 CrossRef CAS.
- T. Li, L. Tan, Y. Zhao and Y.-F. Song, Chem. Eng. Sci., 2021, 245, 116839 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |