Investigating structure and dynamics of unentangled poly(dimethyl-co-diphenyl)siloxane via molecular dynamics simulation†
Weikang
Xian
a,
Jinlong
He
a,
Amitesh
Maiti
b,
Andrew P.
Saab
b and
Ying
Li
 *a
*a
aDepartment of Mechanical Engineering, University of Wisconsin-Madison, Madison, WI 53706-1572, USA. E-mail: yli2562@wisc.edu; Fax: +1 608 890 3966; Tel: +1 608 265 0577
bLawrence Livermore National Laboratory, Livermore, California 94550, USA
First published on 29th May 2023
Abstract
Polysiloxane is one of the most important polymeric materials in technological use. Polydimethylsiloxane displays glass-like mechanical properties at low temperatures. Incorporation of phenyl siloxane, via copolymerization for example, improves not only the low-temperature elasticity but also enhances its performance over a wide range of temperatures. Copolymerization with the phenyl component can significantly change the microscopic properties of polysiloxanes, such as chain dynamics and relaxation. However, despite much work in the literature, the influence of such changes is still not clearly understood. In this work, we systematically study the structure and dynamics of random poly(dimethyl-co-diphenyl)siloxane via atomistic molecular dynamics simulations. As the molar ratio ϕ of the diphenyl component increases, we find that the size of the linear copolymer chain expands. At the same time, the chain-diffusivity slows down by over an order of magnitudes. The reduced diffusivity appears to be a result of a complex interplay between the structural and dynamic changes induced by phenyl substitution.
1 Introduction
Since Hermann Staudinger published the first article on polymerization1 a century ago, polymeric materials have become a ubiquitous component in industrial applications such as transportation,2 biomedical engineering3,4 and aerospace engineering,5,6 owing to their rich chemical and mechanical properties. Silicone is one of the most widely used polymers because of its extraordinary thermal, mechanical, and electrical stability,7,8 in addition to excellent bio-compatibility that earns increasing attention in biomedical devices.9–11 Thus, silicone is used in sealants, adhesives, lubricants, medicine, cooking utensils, thermal insulation, electrical insulation, etc.It is often a requirement that the silicone materials serve with long-lasting lifetime, from months to decades in many applications, despite strong environmental strains like mechanical stress,8 chemical erosion,12 high-energy radiation,13,14 and change of temperature.15–18 In particular, silicone's ability to sustain extreme temperatures is of great importance in aerospace applications.18–20 At the same time, one needs to be aware that periodic cycles of fluctuating temperature can significantly change the mechanical properties of polysiloxane due to temperature-induced semicrystallization.21,22
Efforts in improving the properties of silicone materials have been longstanding and researchers have developed various controllable methods to enhance their properties. Cross-linking process augments the moduli of the silicone materials by connecting polymer chains into a permanent elastic network that can not only sustain mechanical loading but also enables recovery to the original state upon unloading.8 The addition of filler-like silica particles may increase the toughness of the silicone materials, to protect against rupture and fatigue.23 Polysiloxane with improved properties can also be developed through copolymerization. For example, Shen et al. synthesized polystyrene-block-polydimethylsiloxane copolymer as a potential substitute for silica to reinforce polysiloxane;24 polysiloxane–polyethylene oxide copolymer can be used as a drug-releasing system with tunable phase properties.25–27 Moreover, siloxane copolymers with phenyl units, like poly-dimethyl–diphenyl siloxane copolymer, have been found to maintain rubbery-like elastic properties at low temperature22,28 because the inclusion of the phenyl units greatly impedes the crystallization process.17 It was shown that only 3.3 mol% of diphenyl siloxane is sufficient to suppress crystallization.29,30
The outstanding low-temperature performance of the methyl-co-phenyl siloxane copolymers has attracted ongoing efforts to understand the interplay between microstructure, microscale dynamics, and macroscopic mechanical properties.17,22,28–30 Two typical poly dimethyl-co-diphenyl siloxane random copolymers that are widely used31,32 are shown in Fig. 1(a) and (b). Recently, Zhu et al. showed the influence of the phenyl units on the atomic structures of the methyl-co-phenyl polysiloxane, with moderately high phenyl ratios of 31.6 mol% and 30.7 mol% for PDMS-co-PMPS and PDMS-co-PDPS, respectively.33 However, most of the previous works focus on exploring the structural and mechanical properties separately and pay less attention to their connection. Consequently, the interplay between the two properties is not well understood, especially for cases with high phenyl content, thus leaving an understanding of the influence of the phenyl content on the properties of the copolymer somewhat unclear.
The aim of this work is to clarify the structure–property interplay of the poly-dimethyl–diphenyl siloxane copolymer. Here we use Molecular Dynamics (MD) simulation, as a proven, powerful, and flexible method that enables direct probing of microscopic information that is usually difficult, if not impossible, to obtain by experimental techniques. The rest of this article is arranged as follows. In Section II, the method and the theory are introduced. The results of the microstructure and the dynamic properties of the copolymers are shown in Section III. The structure–property relation is analyzed and discussed in Section IV, which is followed by a final conclusion.
2 Method and theory
In this section, we first provide some details of the setup of the MD simulations. We then briefly introduce an augmented version of the Rouse model as a theoretical tool for analyzing results from the MD simulations. The Rouse model simplifies the description of chain dynamics in terms of collective variables called normal modes, from which relevant relaxation times can be extracted. In addition, we compute coherent dynamic structure factors.2.1 Molecular dynamics simulation
To generate the molecular structures for the copolymers, we used a self-avoiding random walk algorithm.34 We explored copolymers with molar ratio ϕ of the diphenyl component varying from 0 to 0.6. Periodic supercell representations of condensed amorphous structures of these copolymers were generated by a Monte Carlo procedure35,36 as implemented in the AMORPHOUS CELL module within Materials Studio.37 For simulations reported here, we used Nc = 100 (except Nc = 90 for ϕ = 0.3) chains with N = 50 monomers each. Given the relatively large system size, it was not possible to fully relax the constructed amorphous structures within Materials Studio. Thus, to thoroughly equilibrate the systems and perform extensive MD simulations we migrated the semi-relaxed structures to the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) platform developed by Sandia National Laboratories that enables efficient massive parallel computation.38 All simulations reported here employed PCFF force field39–42 that was developed to cover a broad range of organic polymers in terms of properties like cohesive energies and heat capacities. It is widely used to understand the dynamics of polymeric systems.43,44 The cutoff distance for the non-bonded pairwise interactions was set as 1.0 nm, with tail corrections added to the pairwise interactions to account for the contributions of long-range van der Waals interactions to the total energy and pressure.45 The long-range Coulombic interactions were calculated by a particle–particle particle–mesh solver (PPPM).46 Periodic boundary condition was applied in all three directions. The equilibrium temperature was set as 550 K for all the systems. This choice of high temperature was mandated by the need to achieve system relaxation and equilibration within reasonable simulations times, especially for systems with high molar ratio ϕ where chain dynamics gets markedly slowed down by the side group of the diphenyl component, as will be shown in the following sections. Although in the real application, such temperature could cause potential degradation of the siloxane copolymer,47 bond-breaking reactions are automatically excluded in these simulations due to the inherent non-reactive nature of the classical forcefield employed here. We performed NPT simulations with the Nose–Hoover thermostat and barostat.48,49 A constant timestep of 0.2 fs was employed to ensure the numerical stability of the simulations. For each system, a semi-relaxed structure from Materials Studio was first equilibrated in an NVT ensemble for 100 million steps (20 ns) at T = 600 K. This was followed by cooling down to the target temperature of 550 K within 1 million steps (0.2 ns). The next step involved NPT equilibration for another 100 million steps (20 ns). In the final production step, the simulations were run in an NPT ensemble for up to 300 ns (for ϕ = 0.6). The rescaled internal end-to-end distances of the beginning and ending stages of the production step were checked and the results are shown in Fig. S1 (ESI†). The temperature damping factors of the thermostat were set to 20 fs for both NVT and NPT ensemble. The pressure damping parameter of the barostat was set to 200 fs for the NPT ensemble. In the NVT ensemble and the first NPT equilibration, an additional drag of 0.2 was used to dampen the fluctuations of the temperature and the pressure. Snapshots of the simulation boxes are shown in Fig. 1(c) and (d). As the molar ratio ϕ increases, the dimethyl groups are progressively replaced by the diphenyl groups in a random fashion. All chains in a system share a specific sequence. The sequences are provided in Table S1 in the ESI.† Generally, the structural and dynamic characteristics of the copolymer are dependent on the sequence such that it seems that systems with multiple different sequences50 are a better choice because systems with specific sequences might introduce statistical uncertainties or even spurious correlations in the structural and dynamic characteristics. However, the intrinsic limited spatial scale of the MD simulation restricts the available numbers of chains in the simulation (100 chains in the current study) such that the introduction of different sequences itself might introduce additional uncertainties, contradicting the goal to decrease the uncertainties. In addition, there is no abnormality shown in the structural and dynamic characteristics presented in the remaining of this work. For example, a linear dependence of the glass transition temperature on ϕ, as will be shown, reflects the random packing of the two distinct constituents of the copolymer,51 suggesting no local heterogeneity presented in the systems of the MD simulations.52 All the chains are well dispersed and there is no discernible phase separation within the simulation boxes. Parameters of the equilibrated systems are listed in Table 1.| Molar ratio ϕ | Molecular weight (g mol−1) | Density ρ (g cm−3) |
|---|---|---|
| 0.0 | 3709.83 | 0.75(0.93/0.95) |
| 0.2 | 4951.27 | 0.85 |
| 0.3 | 5569.92 | 0.89 |
| 0.4 | 6192.70 | 0.92 |
| 0.6 | 7434.14 | 0.96 |
2.2 Classic dynamics
Relaxation of linear polymer chains in the melt state is well-described by the Rouse and Reptation models, applicable to unentangled short-chain and entangled long-chain systems, respectively.54–56 The Rouse model treats a linear flexible polymer chain as a string of beads connected by harmonic springs. Every bead represents a Kuhn monomer that usually consists of a few chemical monomers. In a theta-solvent, where the assumption of the Gaussian chain is valid, the separation between the Kuhn monomers is defined as Kuhn length. Rouse dynamics describes the Brownian motion of different length scales, from a single Kuhn bead to an entire chain.Although a modified version of the Rouse model is used in the current work as described in the next subsection, the classic Rouse model is briefly reviewed here. In the Rouse dynamics, the relaxation of chains is decomposed into a set of independent collective modes p, ranging from 1 to NR − 1, for a chain with NR Kuhn monomers. While mode p = NR − 1 corresponds to the relaxation of a Kuhn segment, mode p = 1 represents the relaxation of the whole chain. A characteristic relaxation time of the whole chain is given as τR in eqn (1), where ξCM is the friction coefficient of the center-of-mass of the chain and 〈R2〉 is the size of the chain, usually quantified by the mean-squared radius of gyration.57–59kB is the Boltzmann constant and T the absolute temperature.
 | (1) |
Relaxation times for the other modes are given by τp = τR/p2, corresponding to portions of the chain that have (NR − 1)/p Kuhn segments. In the case of homopolymers where there is only one type of monomer, the friction coefficient of the CM is ξCM = NRξ, where ξ is the friction coefficient of a Kuhn monomer. After the full relaxation of the chain that is at time t > τR, all the internal correlations of different modes decay and the chain simply diffuses in the space. The motion of the CM of the chain is diffusive in such case, which is described by the mean-squared displacement g3(t) according to eqn (2), where RCM is the position of the CM. The linearity between g3 and t can be used to examine the diffusivity of a system as will be shown in the next section.
 | (2) |
2.3 Normal mode analysis
It has been shown that the Rouse-like internal relaxations have respective characteristic times corresponding to different length scales by computer simulation.60–63 It is of great importance to extract these characteristic times from the results of the MD simulations. The Rouse model essentially transforms the physical coordinates of the Kuhn monomers into normalized (i.e., Fourier-transformed) space where all the normal modes are independent of each other. The normalization of the coordinates is defined as in eqn (3)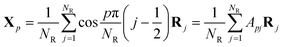 | (3) |
 . An important quantity used in the analysis of Rouse dynamics is the autocorrelation of normal modes, as defined in eqn (4)
. An important quantity used in the analysis of Rouse dynamics is the autocorrelation of normal modes, as defined in eqn (4) | (4) |
The denominator in eqn (4) is given as 〈Xp〉2 = (b2/8N)sin(pπ/2N) where b is the Kuhn length. The Rouse model predicts that the autocorrelation Cp(t) decays exponentially with respective characteristic times i.e., Cp(t) = exp(−t/τp).
In practice, however, it is difficult to apply the normalization of eqn (3) directly to the physical coordinates of the trajectory from MD simulations because of the short-range interaction of the chemical monomers, which can lead to a worm-like bending stiffness, leading to the prediction by the Rouse model deviated from the results from MD simulation.62,63 Therefore, a chemical monomer does not necessarily represent a Kuhn monomer. Although it is possible to remap the chemical structure by a Kuhn scale, the remapping can pose an additional challenge in that the remapped monomer does not necessarily retain unambiguous physical coordinates for eqn (3). To apply the normalization procedure successfully, therefore, we still use the physical coordinates of the chemical monomer in eqn (3) but with an addition stretched exponential64 to the autocorrelation as in eqn (5).
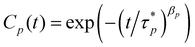 | (5) |
To further clarify, the autocorrelations of different modes are still calculated by eqn (4) from the MD trajectories but are fitted by eqn (5) to acquire the parameters  and the βp that are then used to estimate the effective relaxation time using eqn (6), where Γ represents the gamma function.
and the βp that are then used to estimate the effective relaxation time using eqn (6), where Γ represents the gamma function.
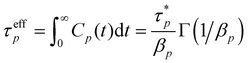 | (6) |
2.4 Dynamic structure factor
MD simulations and normal mode analysis become even more powerful when used in conjunction with experiments. Over the years, significant advances have been made in techniques such as dielectric spectroscopy and neutron scattering, which are widely used in the experimental study of relaxation of polymeric materials.65–68 In such studies, the dynamics of a single chain can be characterized by the coherent dynamic structure factor defined as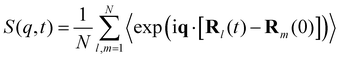 | (7) |
 . It is straightforward to substitute Rouse dynamics results from an MD trajectory into eqn (7). However, such a procedure can be inconsistent because of a mismatch between the physical monomers and the Kuhn monomers, as mentioned in the previous section. Accordingly, in this work we use a modified expression for S(q,t) as in eqn (8), where Apj and Cp(t) are defined in eqn (3) and (5), respectively.58,64
. It is straightforward to substitute Rouse dynamics results from an MD trajectory into eqn (7). However, such a procedure can be inconsistent because of a mismatch between the physical monomers and the Kuhn monomers, as mentioned in the previous section. Accordingly, in this work we use a modified expression for S(q,t) as in eqn (8), where Apj and Cp(t) are defined in eqn (3) and (5), respectively.58,64 | (8) |
3 Results
In this section, we present detailed results on the structural and dynamic properties of the copolymer systems as a function of the diphenyl molar ratio ϕ. First, the structural properties are illustrated through intra- and inter-chain radial distribution functions (RDFs), together with the analysis of gyration tensors and distribution of pore size (PSD). In the second part of this section, we study the dynamics properties by tracking the relaxation of the copolymer chains. Analyses of mean-squared displacement (MSD), normal mode (NM), and coherent dynamic structure factor (DSF) are used to provide insight into the dynamics properties. In order to validate our MD model, we first compared the total structure factor of PDMS at 298 K at which experimental data by wide-angle X-ray scattering is available.69,70 The comparison is shown in Fig. S2 (ESI†). In addition, different pairs of radial distribution functions were also compared and detailed in Fig. S3 (ESI†). The agreements suggested by the comparison confirm that our simulation protocol captures the essential atomistic structural characteristic. There is no experimental data that can be used for a direct comparison of other systems with nonzero ϕ. We also evaluated the characteristic ratio of PDMS from simulations at 298 K. The values are 5.52 ± 0.25 and 6.41 ± 0.25 for N = 20 and N = 50 systems respectively, as shown in Fig. S5 (ESI†), in agreement with reported values C = 5.2871,72 and C = 6.16 calculated by eqn (25) and by data in Table 2 in the ref. 73. The two PDMS systems at 298 K were equilibrated as shown in Fig. S4 (ESI†). Glass transition temperatures Tg of different systems were also evaluated according to the method proposed by Patrone et al.,74 shown in Fig. S6 (ESI†) and then compared with experimental data collected from the literature demonstrated in Fig. S7 (ESI†).47,75–77 It is worth noting that MD simulation generally tends to overestimate the values of Tg because the computationally permissible cooling rates are often orders of magnitude higher than the experimental values.78,79 Therefore, direct comparisons of Tg values estimated from MD simulation and those from experiments are not always quantitatively satisfactory. On the other hand, the evaluation of Tg by experimental techniques is subject to many factors such as the materials, boundary conditions, and types of techniques74,80 such that the estimated values of Tg are usually given with noticeable ranges of variation. Therefore, the estimation of the Tg presented in this work does not aim at predicting the Tg precisely. Nevertheless, the results of Tg estimated from our simulations show qualitative agreement with the experimental values, as shown in Fig. S7 (ESI†), suggesting the setup of the simulation indeed captures the dependence of the Tg on ϕ. Using a lower cooling rate might result in a more physical estimation of the Tg but such a choice requires extra computational cost and does not guarantee an accurate estimation because the cooling rate is still limited by the intrinsic tempo scale of the MD simulation. In addition, the thermal expansion coefficient α was estimated based on the density-temperature relation shown in Fig. S6(a) (ESI†). Fig. S8 (ESI†) shows that a linear fitting yields α = 8.91 × 10−4 K−1 that agrees well with the experimental value of 9.07 × 10−4 K−1.81 Molecular weights of the copolymer systems and their density are listed in Table 1.3.1 Structural properties
The intra-chain RDFs are shown in Fig. 2. The first three plots are for the backbone atoms and the rest are for the side groups. The first peak in (b), at around 1.7 Å, represents the covalent Si–O bonding which is consistent with the range of 1.54 Å to 1.71 Å of α-tridymite.82 The second peak is from the Si–O–Si–O dihedral-like interaction. The first peaks of the Si–Si and O–O pairs at around 3.2 Å correspond to Si–O–Si and O–Si–O angle-like interactions. As the molar ratio ϕ increases, the locations of these peaks corresponding to bonded interaction remain essentially unchanged. However, the peak heights increase as ϕ goes from 0 to 0.6, suggesting that phenyl incorporation leads to backbone re-organization into a more ordered and rigid intra-chain structure. Such increasingly rigid arrangements of the copolymer chains are also suggested by the RDFs between the side group pairs from (d) to (f), as their peak height increase with the molar ratio ϕ as well. It should be noted that the center-of-mass of the respective methyl and phenyl groups are used in the calculation of the RDFs of the side group pairs. The rest of the peaks beyond 6 Å in (a) to (c) are from weaker long-distance interactions, as their amplitudes are much smaller than those of the bonded interactions. Nonetheless, the slight rightward shifts of their locations suggest expansions of the backbone.The inter-chain RDFs are shown in Fig. 3. In (a) to (c), the peaks, of the first four systems, have values less than unity. This suggests that the local densities of the pairs are sparser than the densities in bulk. On the other hand, the ϕ = 0.6 systems have peaks that slightly exceed unity implying that the local densities of the backbones are higher than the densities in bulk. In addition, as the ϕ increases, the peaks shift rightward, suggesting that the inter-chain packing of the polymer expands. This is likely to compensate for a more rigid intra-chain arrangement with increasing ϕ as discussed previously. Side-group pairs are shown at the bottom of Fig. 3. For all the Me–Me, Me–Ph, and Ph–Ph pairs, the amplitudes are smaller than unity. The decrease in peak amplitudes with increasing molar ratio ϕ is consistent with the expansion of the inter-chain packing of the backbones. We note that there are no Me–Ph and Ph–Ph pairs in the ϕ = 0 system.
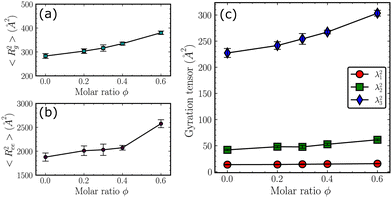
Although the intra-chain RDFs in Fig. 2 show the dependence of the local structures of the copolymer chains on the molar ratio ϕ, the overall topology of the chains remains unclear. To obtain a more detailed picture of the overall structures of the chains, the mean squared radius of gyration 〈Rg2〉 and mean squared end-to-end distance 〈Ree2〉 are calculated and shown in Fig. 4(a) and (b). As the molar ratio ϕ increases, the 〈Rg2〉 increases monotonically, suggesting an overall expansion of the chains. Such a trend is more obvious for the 〈Ree2〉. Additionally, the three principal eigenvalues of the gyration tensors are shown in Fig. 4(c). For all the ϕ, the λ3 is significantly larger than the other two, indicating that the shape of the overall topology can be depicted as a prolate ellipsoid. The increase of all the first and the second eigenvalues indeed corresponds to the overall expansion that is attributed to the increasing amount of bulky diphenyl side groups along the backbone.
Fig. 3 suggests that the inter-chain packing of the backbones becomes looser (i.e., expands outward) as the molar ratio ϕ increases. However, as shown in Table 1, the material density increases with increasing molar ratio ϕ. A possible cause is that lighter methyl groups are being replaced by heavier phenyl components as ϕ increases. To obtain deeper insight, we studied the distributions of pore sizes in all the systems.83,84 In the analysis of the PSD, a probe is located at a random position. For a given point within the simulation box, the probe volume is defined as the maximum spherical void space that includes the given point but does not overlap any physical atoms with their van der Waals radius. The maximum size of the probe at the specific position is recorded. Following this, the position of the probe is changed by an offset and the procedure is repeated until the whole simulation box is exhausted. The derived distributions of the pore size fully describe the way the system free volume changes with molar ratio ϕ. The normalized probability distribution functions are shown in Fig. 5(a). As the molar ratio ϕ increases, there is a slight leftward shift of PSD peak positions, accompanied by an increase in peak height and corresponding narrowing of the distribution. In Fig. 5(b), the symbols represent the PSD peak values for various ϕ, while the 70% confidence limits are indicated by the 15th and 85th percentiles. Although the maximum pore sizes are similar for all the systems, the distribution narrows as ϕ increases, suggesting that the copolymer system becomes more ordered. In addition, the volume fraction, defined as the sum of the volume of the pores over the sum of the simulation boxes, is plotted against the ϕ and is shown as a function of ϕ in Fig. 5(c). All the results were averaged over ten different frames. The amplitudes of the errors are smaller than the sizes of the symbols. As ϕ increases, the volume fraction decreases, suggesting an overall decrease in the free volume of the copolymer system. This decrease in porosity is also consistent with the increase in density as listed in Table 1.
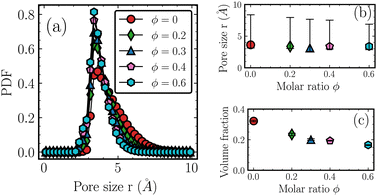 | ||
| Fig. 5 Distribution of pore size. (a) Normalized probability distribution function. As the molar ratio ϕ increases, the peak slightly shifts toward the left, and the distribution narrows. (b) The peak values of the PSDs as a function of ϕ along with 70% confidence bounds. (c) The volume fraction of pores as a function of the ϕ with standard deviation marked. The narrowing of the pore size and the decrease of the free volume are consistent with an increase in material density as shown in Table 1. | ||
3.2 Dynamics properties
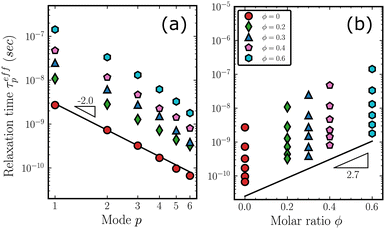
To elucidate the dynamics of the copolymer as a whole, we track the motion of the polymer chains. The results for MSD functions g3 are given in Fig. S9 in (ESI†). Fig. 6(a) plots g3/6t as a function of time to estimate diffusion coefficients. In the initial stages of the MD simulations, we find a steady decrease in g3/6t because of the chain relaxations. However, as the chains achieve full relaxation and enter the regime of Fickian diffusion (Fig. S9, ESI†), the values saturate to plateaus, as indicated by the black dashed lines. Relaxation of the first three systems of lower diphenyl content is much faster than the systems with higher molar ratios, as suggested by their early saturation. For the higher ϕ systems, the relaxation process can take tens of nanoseconds. However, we believe that these systems have also entered the Fickian regime within the simulation time of Fig. 6(a). In Fig. 6(b), the corresponding diffusion coefficients, Dc, is estimated by averaging the last 100 data points of each curve in Fig. 6(a) and plotted against the molar ratio ϕ. The diffusion coefficient of PDMS (ϕ = 0) is 3.05 cm2 s−1 and is consistent with the value of 3.08 cm2 s−1 derived from experimental measurements85,86 as detailed in the ESI.† The small fluctuations indicated by the error bar (standard deviation of the estimated Dc) suggest convergence of the diffusion coefficients. The slope of the fitting line is −2.7 as indicated, i.e., it follows the equation Dc(ϕ) = Dc(0) × 10−2.7ϕ. This shows that the dynamics of the copolymer chain are slowed down by more than 40 times as the molar ratio ϕ increases from 0 to 0.6, resulting in a significant increase in relaxation times.While MSD summarizes the overall motion of the copolymer chains, normal mode analysis provides useful insights into the understanding of internal relaxations. We performed the normalization of eqn (3) and calculated the effective relaxation time according to eqn (6). The detailed fittings are available in Fig. S10 in ESI.† The estimated τeffp are plotted in Fig. 7(a) and (b) against the mode index p and the molar ratio ϕ, respectively. For clarity, only the first 6 modes are displayed. In Fig. 7(a), the slope of the solid line is approximately −2, corresponding to the Rouse model's prediction τp = τR/p2. In Fig. 7(b), τeffp increases monotonically with increasing molar ratio ϕ. For each ratio, the highest point represents the Rouse time τp=1 = τR. Interestingly, the slope of the solid lines in Fig. 7(b) is 2.7, suggesting that it is not only applicable to the dynamics of the chain as a whole in the MSD but also approximately describes the trend of relaxation times of higher internal modes (p> 2).
To further analyze the patterns of chain relaxation, we computed the dynamic structure factors S(q,t) using eqn (7) on MD trajectories. Five q values were used in the calculation. According to Doi and Edwards,87 the term within the first bracket of RHS of eqn (8) dominates the decay of the dynamic structure factor, for q values q2Rg2 ≪ 1. A rough estimation with Rg2 ≈ 300 Å2 gives the lower bound of the magnitude qmin ≈ 0.05 Å−1. On the other hand, it is not physical to have q > l−1 where l ≈ 1.6 Å is the chemical bond length between all the atoms in the polymer, which sets an upper bound of qmax ≈ 0.6 Å−1. For the analysis of the dynamics below, we focus on low q values, ranging from 0.05 to 0.13, to show the overall relaxation at the chain level. In the short time range at the beginning, the dynamic structure factors were computed every 0.01 ns while a coarser interval of 0.2 ns was used in the long time range. The results are shown in Fig. 8 as open symbols for all systems. Additionally, theoretical curves of the dynamic structure factor S(q,t) were computed by the modified model given by eqn (8), as represented by the solid lines, for a direct comparison. The diffusion coefficients estimated by MSD are used to capture the motion of the CM in the first square bracket in eqn (8) while the autocorrelation Cp(t) in the second square bracket is adopted from the NMA without any extra fitting. For pure PDMS (ϕ = 0) the decays predicted by the modified model match well with the dynamic structure factors calculated from MD. For this system, the DSFs decay to zeros for all q, suggesting that the chains are fully relaxed at all the length scales. For the ϕ = 0.2 system, the agreement between the results from MD and the modified model still holds. The DSFs also decay to zero, but only for q = 0.13 and q = 0.11 within the simulation time. Noticeably, the times at which full decay of DSFs takes place for the ϕ = 0.2 system (≈30 ns) are much longer compared to those for the ϕ = 0 system (≈10 ns). While the DSFs for the q = 0.09 and q = 0.07 start to approach zero, the factor for the smallest value q = 0.05 is obviously far away from the full decay. The comparison between ϕ = 0 and ϕ = 0.2 systems clearly shows that the relaxation process significantly decelerates with increasing ϕ. The magnitude of the slowdown becomes larger with increasing molar ratio ϕ, as shown in the rest of Fig. 8. For ϕ values of 0.3 and higher, S(q,t) does not decay to zero for the small q within the simulation time up to 300 ns (for ϕ = 0.6).
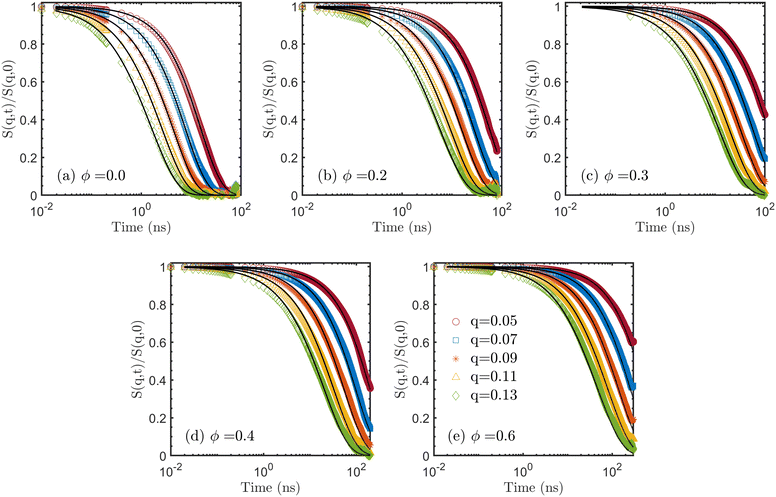 | ||
| Fig. 8 Dynamic structure factor. q is from 0.05 to 0.13 with a step size of 0.02 in calculating the dynamic structure factor. The symbols are the results of using eqn (7) on trajectories from MD simulations. The solid curves are estimations according to eqn (8). There is no fitting involved. | ||
3.3 Discussion
We have shown that the molar ratio ϕ changes not only the structure but also the dynamics of the copolymers significantly. The different systems’ friction coefficients (ξ) are shown in Fig. 9, as estimated by the three methods we used. The friction coefficients from the DSF are calculated based on the fitting as shown in Fig. S11 in ESI.† Despite small deviations, all three methods derive notably similar values of the friction coefficient, with log(ξ) increasing with ϕ with a slope of 2.7 and R2 of the linear fitting is 0.976. | ||
| Fig. 9 Monomeric friction coefficients. The coefficients are estimated from all three analyses. The scaling factor of 2.7 is indicated. | ||
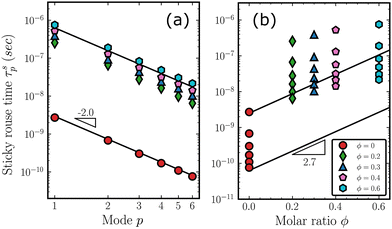
It is intuitive to attribute the deceleration in chain relaxation to presumably strong attractive interaction between the Ph–Ph and Me–Ph groups in the copolymer (nonzero ϕ) systems as compared to much weaker Me–Me interaction in pure PDMS. The attractive interaction between the phenyl and methyl groups could arise due to the methyl groups bonded to silicon atoms being less electronegative than carbon, and thus serving as electron density donors,88 while strong phenyl–phenyl attraction could result from aromatic–aromatic ring interactions. Such a picture of pairwise interaction between the sides group is similar to associative polymers which have segments that can form interaction with finite bond life with their neighbors. Generally, different associative polymers with transient bonds that have a wide range of lifetimes show distinct dynamics.89 For example, systems with strong ionic bonds that have high binding energy might display elastic behavior because the ionic bonds can effectively serve as crosslinking points for the system to maintain network integrity. Such an associative system can be used as a self-healing polymer.90,91 On the other hand, systems with weaker bonds only lead to decelerated dynamics of relaxation. As the T-shaped aromatic–aromatic interaction has an activation energy of 3.63 kcal mol−1,92,93 which is comparable to the thermal energy of 1.09 kcal mol−1 at T = 550 K, the systems in this study could be categorized as weakly associative polymer. According to Hansen and Shen,94 such systems can be described well by the sticky Rouse model.
To shed further light on the above discussion, we have used a single-chain sticky Rouse model to explore the effect of random diphenyl substitutions on overall chain relaxation times. A brief description of the sticky Rouse model is included in the ESI.† In the sticky Rouse model, a single chain is placed in an effective hydrodynamics medium, while inter-chain packing details are completely ignored. Since the ratio of the friction coefficient in the sticky Rouse model determines the relative strength of the binding of the associative beads compared to the regular beads, we varied the portion of associative beads from 0 to 0.6, to investigate how the relaxation times change as a function of ϕ. For the system with ϕ = 0, the base friction coefficient ξl is assigned a value of 0.65 × 10−12 kg s−1, as according to Fig. 9. For an imaginary ϕ = 1.0 system, on the other hand, the value is taken as ξh = 102.7ξl. For the cases in between, the appropriate fraction of associative beads is randomly defined and each bead is assigned corresponding friction coefficient values. Rouse-like relaxation times are then calculated by eqn (S6) (ESI†). The resulting system relaxation times computed by the single-chain sticky Rouse model for various p modes and ϕ values are shown in Fig. 10. All results in Fig. 10 are averages of 50 different random sequences. In Fig. 10(a), the relaxation times are shown as a function of the mode p. The solid lines with a slope of −2.0 indicate that the relaxation times of the single-chain sticky Rouse model are consistent with the classic Rouse model. However, as Fig. 10(b) shows, the relaxation times of the nonzero ϕ systems deviate significantly from the log-linear relation of Fig. 9 for each mode p. Such deviation does not depend on the arrangement of the associative beads along the chain, showing that the single-chain sticky Rouse model with a binary combination of regular and associative beads cannot reproduce the friction coefficient result of Fig. 9 derived from the extensive MD simulations. This demonstrates that the observed chain dynamics of the copolymer system cannot be described by pre-assigned friction coefficients of specific side chains in an effective medium, but arise from a complex interplay between 3D packing structure and various interactions. The nontrivial dynamics are expected because of the synergic effect that the randomness of the copolymer's sequences introduces. While self-diffusion and collective diffusion of block copolymers have been theoretically and experimental studied,95 the theory of dynamics of random copolymer is developed. Although theoretical frameworks based on which the block copolymers have been studied can be modified to describe “blocky” random copolymers, it is still premature to apply a similar analysis to understand the truly random copolymer.96 It is worth noting that the dependence of the relaxation of random copolymers on the contents of their constituent, quantified by the diffusion coefficients, has been experimentally observed.97–99 But the dependence has not been identified in quantitative ways because of the limitation shown in the experiments. On the contrary, the dependence of the PDMS-co-PDPS, summarized by the power law with an exponent of 2.7, is systematically studied in the current work, which is not available in the experimental literature. The influence of temperature on the dependence is also expected since the dynamics of linear polymer chains are essentially dependent on temperature even for the homopolymers. However, the role of temperature can not be unequivocally determined in the scope of the current work because of the chosen high temperature (550 K), assuming all the melts are sufficiently above the values of Tg. It is of interest to study the copolymers in super-cooled states, in glass states, and even in the transitional states although the topics are completely out of the scope of the current work and require further studies.
4 Conclusions
In this article, we systematically studied the influences of the molar ratio ϕ of the diphenyl component on the structure and the dynamics of the unentangled poly(dimethyl-co-diphenyl) siloxane copolymer by atomistic MD simulation. The change of the intra-chain RDFs suggests that increasing ϕ results in a more rigid and ordered structure of the copolymer chains, although partially compensated by the expanded inter-chain packing shown by the inter-chain RDFs. The change in the orderliness was further confirmed by the distribution of pore size that narrows with unchanged maximum size, as ϕ increases. The PSD also confirmed that the increased density is attributed to the decrease in the free volume of the copolymer. In terms of dynamics, we first extracted the diffusion coefficients of copolymer systems by analyzing their MSD. Moreover, the hierarchical relaxation related to the different length scales of the copolymer structure was revealed by the NM and DSF. All three approaches confirmed a relation of ξ(ϕ) = ξ(0) × 102.7ϕ, regarding the friction coefficient that governs the dynamics of the copolymer. Additionally, we found that, by using a single-chain sticky Rouse model, the change of the dynamics of the copolymer with respect to ϕ is not merely attributed to the variation of local friction. The slowed-down dynamics are a consequence of a complex interplay of various interactions.Author contributions
Weikang Xian: computational implementation, data analysis, and original draft writing. Jinlong He: computational assistance and validation. Amitesh Maiti: supervision and draft revision. Andrew P. Saab: supervision and draft revision. Ying Li: computational implementation, supervision, conceptualization, and draft editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at LLNL was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344. Y. L. also would like to thank the support from the National Science Foundation (CMMI-2314424, CMMI-2316200, CAREER-2323108).Notes and references
- H. Staudinger, Ber. Dtsch. Chem. Ges, 1920, 53, 1073 CrossRef
.
- J. M. Garces, D. J. Moll, J. Bicerano, R. Fibiger and D. G. McLeod, Adv. Mater., 2000, 12, 1835–1839 CrossRef CAS
.
- J. E. Puskas and Y. Chen, Biomacromolecules, 2004, 5, 1141–1154 CrossRef CAS PubMed
.
- H. Tian, Z. Tang, X. Zhuang, X. Chen and X. Jing, Prog. Polym. Sci., 2012, 37, 237–280 CrossRef CAS
.
- X. Zhang, Y. Chen and J. Hu, Prog. Aerosp. Sci., 2018, 97, 22–34 CrossRef
.
- Y. Liu, H. Du, L. Liu and J. Leng, Smart Mater. Struct., 2014, 23, 023001 CrossRef CAS
.
- E. Yilgör and I. Yilgör, Prog. Polym. Sci., 2014, 39, 1165–1195 CrossRef
.
- S. C. Shit and P. Shah, Natl. Acad. Sci. Lett., 2013, 36, 355–365 CrossRef CAS
.
- M. Razavi, R. Primavera, A. Vykunta and A. S. Thakor, Mater. Sci. Eng., C, 2020, 111615 Search PubMed
.
- M. Razavi, R. Primavera, A. Vykunta and A. S. Thakor, Mater. Sci. Eng., C, 2021, 119, 111615 CrossRef CAS PubMed
.
- D. Campoccia, L. Montanaro and C. R. Arciola, Biomaterials, 2013, 34, 8533–8554 CrossRef CAS PubMed
.
- N. Yoshimura, S. Kumagai and S. Nishimura, IEEE Trans. Dielectr. Electr. Insul., 1999, 6, 632–650 CAS
.
- A. S. Palsule, S. J. Clarson and C. W. Widenhouse, J. Inorg. Organomet. Polym. Mater., 2008, 18, 207–221 CrossRef CAS
.
- A. Maiti, W. Small, M. Kroonblawd, J. Lewicki, N. Goldman, T. Wilson and A. Saab, J. Phys. Chem. B, 2021, 125, 10047–10057 CrossRef CAS PubMed
.
- H. Chang, Z. Wan, X. Chen, J. Wan, L. Luo, H. Zhang, S. Shu and Z. Tu, Appl. Therm. Eng., 2016, 104, 472–478 CrossRef CAS
.
- F. Wu, B. Chen, Y. Yan, Y. Chen and M. Pan, Polymers, 2018, 10, 522 CrossRef PubMed
.
- L. Qu, Z. Xie, G. Huang and Z. Tang, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 1652–1659 CrossRef CAS
.
- K. Polmanteer and M. Hunter, J. Appl. Polym. Sci., 1959, 1, 3–10 CrossRef CAS
.
- P. Jha, L. W. Mason and J. D. Way, J. Membr. Sci., 2006, 272, 125–136 CrossRef CAS
.
- L. Tao, G. Chen and Y. Li, Patterns, 2021, 2, 100225 CrossRef CAS PubMed
.
- U. Kumar, T. Kato and J. M. Frechet, J. Am. Chem. Soc., 1992, 114, 6630–6639 CrossRef CAS
.
- H. Li and J. Magill, Polymer, 1978, 19, 829–836 CrossRef CAS
.
- E. Warrick, O. Pierce, K. Polmanteer and J. Saam, Rubber Chem. Technol., 1979, 52, 437–525 CrossRef CAS
.
- L. Shen, T.-p Wang, F.-Y. Lin, S. Torres, T. Robison, S. H. Kalluru, N. B. Hernández and E. W. Cochran, ACS Macro Lett., 2020, 9, 781–787 CrossRef CAS PubMed
.
- G. Kickelbick, J. Bauer, N. Hüsing, M. Andersson and A. Palmqvist, Langmuir, 2003, 19, 3198–3201 CrossRef CAS
.
- D. Li, C. Li, G. Wan and W. Hou, Colloids Surf., A, 2010, 372, 1–8 CrossRef CAS
.
- M. Fauquignon, E. Ibarboure, S. Carlotti, A. Brûlet, M. Schmutz and J.-F. Le Meins, Polymers, 2019, 11, 2013 CrossRef CAS PubMed
.
- S. Wang and J. Mark, J. Mater. Sci., 1990, 25, 65–68 CrossRef CAS
.
- A. Zlatanic, D. Radojcic, X. Wan, J. M. Messman and P. R. Dvornic, Macromolecules, 2017, 50, 3532–3543 CrossRef CAS
.
- A. Zlatanic, D. Radojcic, X. Wan, J. M. Messman, D. E. Bowen and P. R. Dvornic, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 1122–1129 CrossRef CAS
.
- T. M. Alam, PDPS Copolym., 2002, 1–23 Search PubMed
.
- W. E. Cady, E. S. Jessop and B. M. McKinley, 1982.
- L. Zhu, X. Cheng, W. Su, J. Zhao and C. Zhou, Polymers, 2019, 11, 1989 CrossRef CAS PubMed
.
-
K. Binder, Monte Carlo and molecular dynamics simulations in polymer science, Oxford University Press, 1995 Search PubMed
.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478 CrossRef CAS
.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1986, 19, 379–387 CrossRef CAS
.
-
Biovia Materials Studio, Dassault Systemes, 2022, https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio Search PubMed
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen,
et al.
, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
- H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987 CrossRef CAS
.
- H. Sun, Macromolecules, 1995, 28, 701–712 CrossRef CAS
.
- J. R. Hill and J. Sauer, J. Phys. Chem., 1994, 98, 1238–1244 CrossRef CAS
.
- J.-R. Hill and J. Sauer, J. Phys. Chem., 1995, 99, 9536–9550 CrossRef CAS
.
- S. Y. Lim, T. T. Tsotsis and M. Sahimi, J. Chem. Phys., 2003, 119, 496–504 CrossRef CAS
.
- N. C. Karayiannis, V. G. Mavrantzas and D. N. Theodorou, Macromolecules, 2004, 37, 2978–2995 CrossRef CAS
.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS
.
-
R. W. Hockney and J. W. Eastwood, Computer simulation using particles, CRC Press, 2021 Search PubMed
.
- C. Chou and M.-H. Yang, J. Therm. Anal. Calorim., 1993, 40, 657–667 CrossRef CAS
.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed
.
- G. Smith, W. Paul, M. Monkenbusch, L. Willner, D. Richter, X. Qiu and M. Ediger, Macromolecules, 1999, 32, 8857–8865 CrossRef CAS
.
- T. G. Fox, Bull. Am. Phys. Soc., 1952, 1, 123 Search PubMed
.
- C.-C. Huang, M.-X. Du, B.-Q. Zhang and C.-Y. Liu, Macromolecules, 2022, 55, 3189–3200 CrossRef CAS
.
- M. Beevers, S. Mumby, S. Clarson and J. Semlyen, Polymer, 1983, 24, 1565–1570 CrossRef CAS
.
- P. E. Rouse Jr, J. Chem. Phys., 1953, 21, 1272–1280 CrossRef
.
- P.-G. De Gennes, J. Chem. Phys., 1971, 55, 572–579 CrossRef
.
- M. Doi and S. Edwards, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 1789–1801 RSC
.
-
M. Rubinstein, R. H. Colby, et al., Polymer physics, Oxford university Press, New York, 2003, vol. 23 Search PubMed
.
- Y. Li, M. Kröger and W. K. Liu, Soft Matter, 2014, 10, 1723–1737 RSC
.
- C. Svaneborg and R. Everaers, Macromolecules, 2020, 53, 1917–1941 CrossRef CAS
.
- M. Mondello and G. S. Grest, J. Chem. Phys., 1997, 106, 9327–9336 CrossRef CAS
.
- W. Paul, G. D. Smith and D. Y. Yoon, Macromolecules, 1997, 30, 7772–7780 CrossRef CAS
.
- V. A. Harmandaris, V. G. Mavrantzas and D. N. Theodorou, Macromolecules, 1998, 31, 7934–7943 CrossRef CAS
.
- J. Padding and W. J. Briels, J. Chem. Phys., 2001, 114, 8685–8693 CrossRef CAS
.
- J. Padding and W. J. Briels, J. Chem. Phys., 2002, 117, 925–943 CrossRef CAS
.
-
F. Kremer and A. Schönhals, Broadband dielectric spectroscopy, Springer Science & Business Media, 2002 Search PubMed
.
- F. Kremer, J. Non-Cryst. Solids, 2002, 305, 1–9 CrossRef CAS
.
- B. Frick and D. Richter, Science, 1995, 267, 1939–1945 CrossRef CAS PubMed
.
-
D. Richter, M. Monkenbusch, A. Arbe and J. Colmenero, Neutron Spin Echo in Polymer Systems, 2005, pp.1–221 Search PubMed
.
- S. W. Sides, J. Curro, G. S. Grest, M. J. Stevens, T. Soddemann, A. Habenschuss and J. Londono, Macromolecules, 2002, 35, 6455–6465 CrossRef CAS
.
- A. Habenschuss, M. Tsige, J. G. Curro, G. S. Grest and S. K. Nath, Macromolecules, 2007, 40, 7036–7043 CrossRef CAS
.
- A. L. Frischknecht and J. G. Curro, Macromolecules, 2003, 36, 2122–2129 CrossRef CAS
.
- P.-N. Tzounis, S. D. Anogiannakis and D. N. Theodorou, Macromolecules, 2017, 50, 4575–4587 CrossRef CAS
.
- L. Fetters, D. Lohse, D. Richter, T. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639–4647 CrossRef CAS
.
- P. N. Patrone, A. Dienstfrey, A. R. Browning, S. Tucker and S. Christensen, Polymer, 2016, 87, 246–259 CrossRef CAS
.
- G. Deshpande and M. E. Rezac, Polym. Degrad. Stab., 2002, 76, 17–24 CrossRef CAS
.
- G. Babu, S. Christopher and R. Newmark, Macromolecules, 1987, 20, 2654–2659 CrossRef CAS
.
- C. Wang, G. Fytas and J. Zhang, J. Chem. Phys., 1985, 82, 3405–3412 CrossRef CAS
.
- J. Han, R. H. Gee and R. H. Boyd, Macromolecules, 1994, 27, 7781–7784 CrossRef CAS
.
- J. Buchholz, W. Paul, F. Varnik and K. Binder, J. Chem. Phys., 2002, 117, 7364–7372 CrossRef CAS
.
- S. Napolitano, E. Glynos and N. B. Tito, Rep. Prog. Phys., 2017, 80, 036602 CrossRef PubMed
.
- H. Shih and P. Flory, Macromolecules, 1972, 5, 758–761 CrossRef CAS
.
-
N. Wiberg, A. Holleman and E. Wiberg, Holleman-Wiberg's Inorganic Chemistry, Elsevier Science, 2001 Search PubMed
.
- L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257 CrossRef CAS
.
- L. D. Gelb and K. Gubbins, Langmuir, 1999, 15, 305–308 CrossRef CAS
.
-
L. Leger, H. Hervet, P. Auroy, E. Boucher and G. Massey, Rheology Series, Elsevier, 1996, vol. 5, pp.1–16 Search PubMed
.
- J. Hintermeyer, A. Herrmann, R. Kahlau, C. Goiceanu and E. Rossler, Macromolecules, 2008, 41, 9335–9344 CrossRef CAS
.
-
M. Doi, S. F. Edwards and S. F. Edwards, The theory of polymer dynamics, Oxford university press, 1988, vol. 73 Search PubMed
.
- O. Loveday and J. Echeverra, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed
.
- Z. Shen, H. Ye, Q. Wang, M. Kröger and Y. Li, Macromolecules, 2021, 54, 5053–5064 CrossRef CAS
.
- R. P. Wool, Soft Matter, 2008, 4, 400–418 RSC
.
- K. Yu, A. Xin, H. Du, Y. Li and Q. Wang, NPG Asia Mater., 2019, 11, 1–11 CrossRef
.
- S. Tsuzuki, T. Uchimaru, K. Matsumura, M. Mikami and K. Tanabe, Chem. Phys. Lett., 2000, 319, 547–554 CrossRef CAS
.
- M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887–10893 CrossRef CAS PubMed
.
- D. R. Hansen and M. Shen, Macromolecules, 1975, 8, 343–348 CrossRef CAS
.
- G. H. Fredrickson and F. S. Bates, Annu. Rev. Mater. Sci., 1996, 26, 501–550 CrossRef CAS
.
- G. H. Fredrickson and L. Leibler, Macromolecules, 1995, 28, 5198–5208 CrossRef CAS
.
- M. E. Schimpf and J. C. Giddings, J. Polym. Sci., Part B: Polym. Phys., 1990, 28, 2673–2680 CrossRef
.
- A. Losch, R. Salomonovic, U. Steiner, L. J. Fetters and J. Klein, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 1821–1831 CrossRef CAS
.
- T. Cosgrove, V. Rodin, M. Murray and R. Buscall, J. Polym. Res., 2007, 14, 175–180 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Structural properties, thermal properties, mean-squared displacement, normal mode analysis, dynamic structure factor, and interaction energy. See DOI: https://doi.org/10.1039/d3sm00509g |
| This journal is © The Royal Society of Chemistry 2023 |