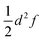Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The Marcus dimension: identifying the nuclear coordinate for electron transfer from ab initio calculations†
Adam
Šrut
 a,
Benjamin J.
Lear
*b and
Vera
Krewald
a,
Benjamin J.
Lear
*b and
Vera
Krewald
 *a
*a
aDepartment of Chemistry, Theoretical Chemistry, TU Darmstadt, Peter-Grünberg-Straße 4, 64287 Darmstadt, Germany. E-mail: vera.krewald@tu-darmstadt.de
bDepartment of Chemistry, The Pennsylvania State University, University Park, PA 16802, USA. E-mail: bul14@psu.edu
First published on 8th August 2023
Abstract
The Marcus model forms the foundation for all modern discussion of electron transfer (ET). In this model, ET results in a change in diabatic potential energy surfaces, separated along an ET nuclear coordinate. This coordinate accounts for all nuclear motion that promotes electron transfer. It is usually assumed to be dominated by a collective asymmetric vibrational motion of the redox sites involved in the ET. However, this coordinate is rarely quantitatively specified. Instead, it remains a nebulous concept, rather than a tool for gaining true insight into the ET pathway. Herein, we describe an ab initio approach for quantifying the ET coordinate and demonstrate it for a series of dinitroradical anions. Using sampling methods at finite temperature combined with density functional theory calculations, we find that the electron transfer can be followed using the energy separation between potential energy surfaces and the extent of electron localization. The precise nuclear motion that leads to electron transfer is then obtained as a linear combination of normal modes. Once the coordinate is identified, we find that evolution along it results in a change in diabatic state and optical excitation energy, as predicted by the Marcus model. Thus, we conclude that a single dimension of the electron transfer described in Marcus–Hush theory can be described as a well-defined nuclear motion. Importantly, our approach allows the separation of the intrinsic electron transfer coordinate from other structural relaxations and environmental influences. Furthermore, the barrier separating the adiabatic minima was found to be sufficiently thin to enable heavy-atom tunneling in the ET process.
1 Introduction
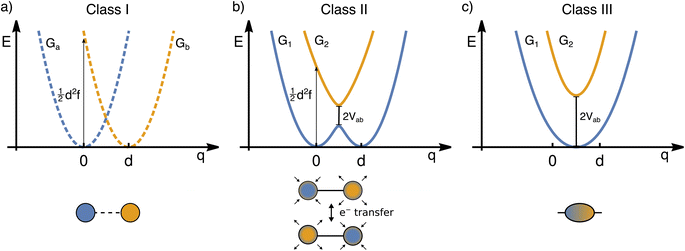
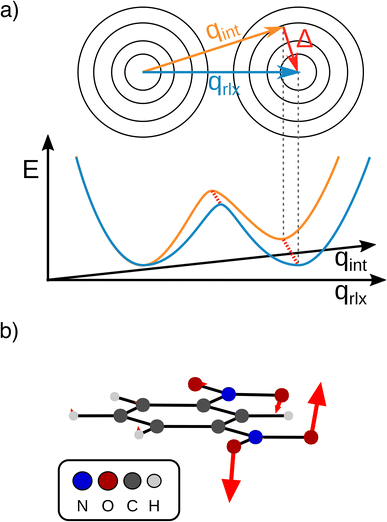
The transfer of electron density is implicated in nearly every chemical transformation and hence there has been a long-standing and intense interest in developing models for describing, predicting, and quantifying the pathways of electron transfer (ET). For the past 60 years, the dominant model has been the classical Marcus–Hush theory.1,2The theory originally described by Marcus treats ET between two separated redox sites (i.e., intermolecular ET), giving rise to two electronic states a and b. These states are represented on a reaction coordinate diagram by two harmonic potential energy surfaces (PES) as shown in Fig. 1a. The electron transfer occurs when the nuclei (internal and solvent) are distorted such that the two surfaces have the same energy, at which point there is some probability of ET. This can be represented using Fermi's golden rule3,4
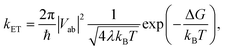 | (1) |
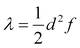 .
.
The insight that would be gained by obtaining a precise description of the ET coordinate is made clear when considering systems with large degrees of electronic coupling. Hush expanded Marcus' theory for such systems, retaining the connection between the electron transfer coordinate, the barrier to electron transfer, the curvature of the PES, and the displacement along the ET coordinate. Again, it was common to combine the effects of curvature and separation into a reorganization energy, though some treatments explicitly considered the spring constant and separation.5
Large electronic coupling mixes the diabatic states Ga and Gb and produces two adiabatic states: a ground state G1 and an excited state G2 (Fig. 1b and c). Thus, for significant coupling, ET will occur adiabatically, in which case the pre-exponential factor will reduce to a nuclear frequency along the ET coordinate νq. The resulting classical expression for the ET rate will be:6
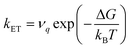 | (2) |
The ET coordinate is also implicated in other effects of electronic coupling, namely that increasing electronic coupling produces a movement of the ground state PES minima towards one another along the ET coordinate. If the coupling is strong enough, the minima merge, and the molecule has a single stable configuration with the unpaired electron delocalized over the redox sites. The shape of the ground state PES is the basis for the dominant classification scheme for mixed valence systems proposed by Robin and Day.7 In this classification, systems with minimal coupling (i.e., diabatic) are termed Class I, systems with a single minimum are termed Class III, and the intermediate case is termed Class II. Movement along q away from the minimum in Class III therefore implies a greater extent of localisation, whereas movement along q between the minima in Class II leads to electron transfer.
While electronic coupling in these complexes is often discussed without reference to the PES spring constant and minima separation, it is also true that the final shape of the surface depends not only on the magnitude of the electronic coupling, but also on the curvature and separation along the ET coordinate.8 It is well established that solvation has a pronounced influence on the shape of the potential and can even lead to a switch in Class.9,10 Having a direct way of identifying the shape of the PES would therefore be of great value for disentangling these different contributors, comparing the properties of different chemical systems in more detail, and quantifying environmental effects.
The lack of attention paid to the spring constant and separation between PES minima comes from both experimental and theoretical limitations. Experimentally, the IVCT band can be used to estimate the magnitude of electronic coupling,9,11 although it contains limited information about the spring constant and the separation of the PES minima. Vibronic progressions and resonance Raman experiments can shed some light on these, although some contributing motions may not be captured. The donor–acceptor distance, which is not identical to the separation of the adiabatic minima on the nuclear coordinate q, can be evaluated from the change in dipole moment upon IVCT excitation.12,13 Deducing the electronic coupling from changes in the dipole moment is hampered by the fact that estimating the change in dipole moment in the absence of coupling is difficult.14,15 Finally, even if the approach were valid, what would be measured is not the ET coordinate directly, but a separation along it. Therefore, any specific chemical information about the nuclear motions involved is not obtained.
On the theory side, one can perform a linear interpolation between the reactants and transition state, or the reactants and the products, as is common in light-induced ET to understand which nuclear motions are implicated in ET. However, this approach is also restricted to Class II systems where two well defined minima and a transition state exist. For MV systems that are sensitive to the solvation environment, a linear interpolation approach would not be able to evaluate any solvent-induced change in nuclear motion or the decoupling of solvent and solute motion. Finally, as shown below, a linear interpolation approach may furthermore contain motions that are not required for the ET process and thus render a coordinate with superfluous motions.
Considering the state of the art in ET research, there remains a need for a general method to describe the ET coordinate quantitatively. Ideally such a method would capture details such as the nature of nuclear motion promoting ET, the spring constant associated with this motion, and the separation of minima along potential energy surfaces associated with this coordinate. Additionally, it would be easily expandable to include additional dimensions of electron transfer, e.g. to evaluate the relevance of higher-lying excited states. Herein, we describe one such approach based upon quantum chemical calculations, demonstrating it for organic mixed valence systems.
The method we propose can identify the ET coordinate of a MV system regardless of its Robin–Day Class, which is achieved with a sampling procedure covering a representative set of thermally populated nuclear configurations and subsequent analysis of the electronic structures in this ensemble. The coordinate we identify appears to be an intrinsic property of the mixed valent molecule and can be used to predict the barrier height or reorganization energy of the system. We demonstrate that this intrinsic motion is separable from structural relaxations that do not contribute to driving ET and from environmental influences. We also show that, while this approach largely substantiates the Marcus–Hush model, it also raises some questions regarding interpretation of the model and reveals some of its limitations.
2 Methodology
For many years, computational predictions of spectroscopic properties of MV compounds were hampered by the fact that most theoretical methods tend to favour either a localized or a delocalized description. Solutions to this problem were found and discussed in seminal work by Martin Kaupp and coworkers.16 Herein, we use local hybrid functionals that are designed to strike a balance between correcting the self-interaction error and an accurate description of exchange–correlation17,18 and have been shown to perform extraordinarily well in the prediction of spectroscopic properties of MV compounds.19–21Theoretical studies on MV systems often assume a direct pathway between two well-defined structures, either the adiabatic minima22 or an adiabatic minimum and a totally symmetric structure.23 Powerful approaches to recover the potential energy curves from Marcus theory using the energy gap between the diabatic states have been established.24,25 To identify the diabatic states, one can either use constrained DFT,26,27 where they result directly from the calculation, or use a diabatization procedure.28 However, both of these approaches will be challenging for strongly coupled systems and will not provide information about the curvature of the potential energy curves.
To assess the interplay between the geometric and electronic structure of a MV system, it is clear that the picture derived from a single nuclear configuration will not represent reality. Therefore, a sampling procedure is needed that covers a set of thermally populated nuclear configurations with their associated electronic structures. The nuclear ensemble method29 presents a simple and powerful method for simulating vibrationally resolved electronic spectra,30,31 for obtaining the initial conditions for non-adiabatic dynamics,32 or for exploring phase space properties.33 The most common way to generate a nuclear ensemble is ab initio molecular dynamics which, however, comes with a great computational cost.34
A significantly less demanding method for moderately sized molecules is the so-called Wigner sampling,35 which is achieved by approximating the PES by a harmonic potential and evaluating the Wigner function36 for thermally accessible vibrational states. The Wigner sampling method showed great performance when predicting absorption spectra37 and capturing temperature effects in the intersystem crossing of 2-nitronaphthalene.38 A strength of Wigner sampling is that it offers a more realistic sampling than ab initio molecular dynamics for high-frequency vibrational modes, because it accounts for the zero-point energy.37 However, it does not capture the decreasing spacing between levels and altered nature that is expected for an anharmonic oscillator and so undersamples anharmonic low-frequency modes. While we use Wigner sampling here, it is conceivable that other sampling methods will perform equally well as long as a representative set of geometric and electronic structures is used.
To the best of our knowledge, a unified strategy towards a coordinate that describes electron transfer (Class II) or localisation (Class III) and that can be used to disentangle intra-molecular motion from solvent motion is missing in state-of-the-art theoretical research of MV systems. Our approach for identifying the intramolecular ET coordinate starts from an optimized geometry that represents an adiabatic minimum of the system and the Hessian matrix obtained from a frequency calculation. The phase space of the system under study is sampled using the Wigner sampling method as implemented in the SHARC package39 at room temperature. The system can be placed in vacuum or in implicit solvation; while the inclusion of explicit solvation is not discussed here this should be equally feasible with the Wigner method or other sampling approaches.37 The central sampling idea is illustrated in Fig. 2a where the potential energy surface is approximated around the adiabatic minimum by a harmonic potential. A representative set of nuclear configurations is selected by evaluating the Wigner function for the relevant vibrational states whose thermal populations are estimated in Monte Carlo fashion.39 The next step is to run time-dependent DFT (TD-DFT) calculations with a small number of excited states for each selected geometry.
For each of the structures, it can be easily evaluated where the unpaired electron is localized: the position of this electron is defined as the weighted average of the spin populations si on specified molecular fragments, as illustrated in Fig. 2b and given in eqn (3). The electron position is a unitless scalar number that takes value between 1 and 3, noting that the choice of integers for the fragments is up to the user. The quantity can be thought of as a centroid of the spin density.
| epos.− = 1 × s1 + 2 × s2 + 3 × s3. | (3) |
To identify the ET coordinate, the electronic properties, i.e., the electron position or the excitation energy as discussed in more detail in the results section, are correlated with the distortion in the direction of vibrational modes. To obtain these displacements, a transformation from Cartesian coordinates to normal coordinates is carried out according to eqn (4), where C is a transformation matrix (obtained from the frequency calculation at the adiabatic minimum), M is a diagonal matrix of atomic masses, r is a vector of Cartesian coordinates, and r0 is the equilibrium configuration,
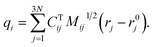 | (4) |
3 Choice of model systems
As test cases, we have chosen meta-dinitrobenzene (m-DNB˙−), para-dinitrobenzene (p-DNB˙−), 2,6-dinitronaphthalene (2,6-DNN˙−), and 2,7-dinitronaphthalene (2,7-DNN˙−), see Fig. 3. These molecules have been well characterized experimentally and computationally so that the IVCT bands and ET rates are known. They served as model compounds for exploring the adiabatic ET rate40 or for development of reliable electronic structure methods for MV systems.23 These extensive studies render the four dinitrocompounds as ideal test cases for our proof-of-concept study.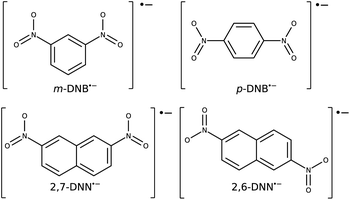 | ||
| Fig. 3 Structures and charge states of the studied mixed valence systems for which we demonstrate our approach. | ||
The Robin–Day classification of these compounds depends on the solvation environment.41 In vacuum, all four compounds are expected to be Class III, while when placed in a dielectric continuum of acetonitrile, m-DNB˙− and 2,7-DNN˙− transition to Class II.16 Alcohol solvents, which are capable of hydrogen bonding, show a very strong localization effect and high ET barriers.41
4 Computational details
All calculations were carried out using the TURBOMOLE package.42 The local hybrid functional43–45 LH20t19 was employed; in the ESI† we show additional tests using the BLYP35 (ref. 46) functional. Calculations used the def2-TZVP basis set47 for the carbon, nitrogen and oxygen atoms, and the def2-SVP basis set47 for hydrogen atoms. The resolution of identity approximation for computation of the Coulomb integrals48 was used. The convergence criterion for the self-consistent field method was set to 10−8Eh. As the integration grid, m3 in TURBOMOLE notation was used to obtain the energy. Solvation effects were modelled implicitly using a conductor-like screening model49 (COSMO) with acetonitrile (ACN) as the modeled solvent. The five lowest excited states were determined using TD-DFT without the Tamm–Dancoff approximation and the same settings as described above. The phase space of all studied molecules was sampled using the Wigner sampling method as implemented in the SHARC package39 at 300 K. 500 structures were generated as representative of the ensemble. Any scans performed along linear interpolation coordinates or the electron transfer coordinates identified with our approach used the LH20t/def2-TZVP electronic structure method described above and a step size of 0.002 or 0.005 Å. To evaluate the electronic structure progression along the Marcus dimension, CASSCF and CASSCF/NEVPT2 calculations were performed using the ORCA suite of programs;50 the respective computational details are given in the ESI.†To summarise, the calculations were carried out in the following order: (I) geometry optimization of the ground state and frequency calculation with DFT in vacuum or considering solvation effects implicitly if desired.‡ (II) Wigner sampling of 500 geometries at 300 K. (III) Single-point calculations of each sampled geometry with TD-DFT. (IV) Fitting of normal coordinates to the electron position or the excitation energy. (V) Linear combination of normal modes using the coefficients obtained from (IV) into the Marcus dimension. (VI) Scan along the Marcus dimension with TD-DFT.
5 Results and discussion
5.1 Electron transfer driven by vibrational modes
The ET coordinate represents nuclear movements associated with the transfer of the unpaired electron between the redox centres in the mixed-valent system. An intuitive concept of the ET coordinate is an anti-symmetric vibrational mode.51–53 In organic MV systems, the unpaired electron is often found on a multi-atom functional group, i.e. more delocalised than in inorganic complexes where the redox sites are mostly restricted to metal ions. Therefore, the ET coordinate cannot be conceived of as intuitively as in many inorganic complexes.54 Herein, we present a method for obtaining the ET coordinate from ab initio calculations representing an ensemble.Our task is to find an association between the distortions in the direction of each vibrational mode with a property that is very sensitive to progression along the ET coordinate. Considering the Marcus–Hush model and the Robin–Day classification, appropriate electronic properties are the electron position in Class III cases, and the excitation energy in Class II cases. In Class III systems, even a small movement along the ET coordinate away from the adiabatic minimum can lead to a non-negligible degree of electron localisation on one of the redox centers. The electron position is thus an intuitive property to be correlated with vibrational motions. This is, however, not the case in Class II systems, where in the vicinity of the adiabatic minimum the unpaired electron stays localized on the respective redox center. A significant change of the electron position will occur only near the top of the barrier.
Instead, the property that can uniquely define the ET coordinate in Class II systems is the excitation energy to the first excited state. As the system progresses from the adiabatic minimum to the top of the barrier, the excitation energy will decrease. The nuclear configuration with the lowest excitation energy will thus correspond to the top of the barrier, as can be readily seen from the Marcus model (Fig. 1). We note that this approach is conceptually similar to following the energy gap between the diabatic states to obtain the ET coordinate.9,25 Class III systems cannot be treated this way because the excitation energy increases with the absolute value of nuclear displacements along the ET coordinate. Consequently, the information whether a negative or positive displacement of any vibrational mode pushes ET forwards or backwards, i.e. to the acceptor or donor, is lost. The calculated ground state electronic structure of the mixed valence state can be used to assign the molecule as Class II or III, thereby indicating which approach is appropriate.
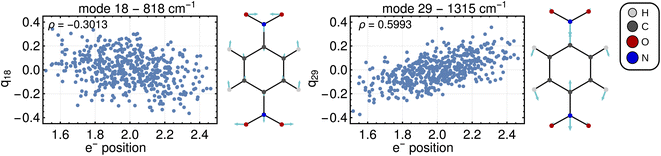
Computing the correlation between a normal coordinate and the relevant ET property will reveal which vibrational modes contribute to the unique ET dimension. To this end, we plotted the relevant ET properties against the normal coordinates, see Fig. 4 for a Class III case and Fig. S2† for a Class II case. We focus here on the Class III case because we are not aware of alternative methods to gain insight into the ET coordinate for Class III systems. In the Class III example shown in Fig. 4, a correlation with the electron position can be seen for some normal coordinates. The two most strongly pronounced correlations are those with the antisymmetric stretching of C–N bonds (mode 29) which is apparent at first glance, and the correlation with the ONO bending motion (mode 18) that is less clear. The importance of these modes for the ET dimension agrees with chemical expectations, i.e., the ET is associated with changing the distance between redox center (NO2 group) and bridging unit (benzene ring). Very similar observations are made for a Class II system where, as explained above, the correlation is established using the excitation energy (see Fig. S2†).
In both cases, there is no ultimate measure for deciding whether or how much these modes contribute to the overall ET dimension. In other words, it is not clear how much they contribute to the reorganization energy λ. Correlating the normal coordinate with the relevant ET property can only identify the relative importance of the vibrational modes. This finding underscores the need for a unified ET coordinate for which one would then know the spring constant f and the separation of the minima d, and therefore λ.
5.2 Marcus dimension of the electron transfer
As shown above, the ET coordinate cannot be assigned to a single normal mode. A general approach towards composing the sought after ET dimension from the vibrational modes is to quantify how well aligned each mode is with the Marcus–Hush model. A linear combination of all vibrational modes should therefore result in a unique ET dimension, as proposed by Rudolph Marcus and refined in the Marcus–Hush model.1 We call this coordinate obtained from ab initio calculations the Marcus dimension in the following.The correct combination of vibrational modes is obtained by a multi-component fit of all vibrational modes to the electron position for a Class III system, or to the excitation energy for a Class II system, see eqn (5a) and (5b), respectively. This procedure will account for all vibrational degrees of freedom. The independent variables in the multi-component fit are the displacements in the direction of the vibrational modes (qj) and the dependent variable is either the electron position (epos.−) or the excitation energy (ΔED0−D1):
| b0 + b1 × q1,i + … + b3N−6 × q3N−6,i = epos.,i− | (5a) |
| b0 + b1 × q1,i + … + b3N−6 × q3N−6,i = ΔEDi0−D1 | (5b) |
The coefficients bj are used to construct the Marcus dimension as a linear combination of vibrational modes, which are vectors of Cartesian displacements of individual atoms. The resulting Marcus dimension will therefore also take the form of a vector of Cartesian displacements.
Fig. 5 shows the result of the fit for p-DNB˙− (panel a) and m-DNB˙− (panel b) as examples. By comparison of Fig. 5a with 4 we can again identify mode 29 as the most prominent motion for the Marcus dimension in p-DNB˙−. We emphasize that there are other modes with substantial contributions to the ET coordinate that are not expected among the chemically intuitive motions for the ET process. The role of these modes is thus to cancel out the motions of atoms that are not important for the Marcus dimension. The remaining modes have small, but non-zero, contributions which would be overlooked if the Marcus dimension was determined only from the correlation plots in Fig. 4.
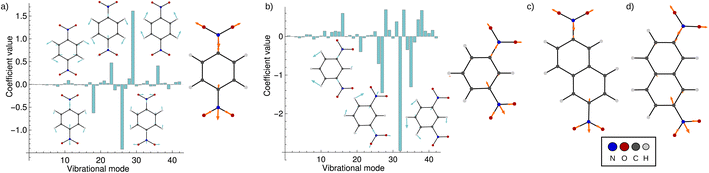 | ||
| Fig. 5 Coefficients obtained from the multi-component fit, including sketches of the normal modes with the largest coefficients. The resulting Marcus dimensions as linear combinations of the normal modes with expansion coefficients obtained from the multi-component fit are shown as sketches. (a) Results for p-DNB˙−, where the fit used the electron position according to eqn (5a). (b) Results for m-DNB˙−, where the fit used the excitation energy according to eqn (5b). (c) Obtained Marcus dimension for 2,6-DNN˙− (fit using the electron position). (d) Obtained Marcus dimension for 2,7-DNN˙− (fit using the excitation energy). | ||
The fact that many modes contribute in non-negligible amounts shows that the Marcus dimension should not be thought of as a single anti-symmetric normal mode. Therefore, it is not possible to fully equate the absorption in a specific infra-red or Raman region with the ET coordinate: some important contributors to the Marcus dimension may be infra-red or Raman silent, or they may appear outside of the region of interest. In addition, there may be irrelevant absorption bands in the energetic region of interest.
The obtained Marcus dimensions for the remaining dinitroradical anions are plotted in panels (c) and (d) of Fig. 5. The Marcus dimension is a motion localized on the nitro groups and the carbon atoms they are attached to. The most prominent parts of the motions are C–N bond stretches and N–O bond stretches. All motions are anti-symmetric which agrees with the ET coordinate described by the Marcus model,51–53 and very similar amongst each other, which is expected for structurally and electronically similar compounds. We emphasize here that our procedure elucidates the participation of each atom in the reaction coordinate without making any prior assumptions, other than assuming the validity of the Marcus–Hush model.
Upon repeating the whole procedure in vacuum, where all studied systems belong to Class III, qualitatively the same motions are obtained (see Fig. S3†). It is important to note that even though m-DNB˙− and 2,7-DNN˙− switch from a localized to a delocalized system, the Marcus dimension obtained by our approach is identical. The results support our ansatz of using the electron position or the excitation energy as dependent variables in the multi-component fit, which clearly gives equivalent results. Moreover, these findings provide additional confirmation that the motion identified with our procedure is the intrinsic electron transfer coordinate in the respective molecule.
5.3 Scan along the Marcus dimension
As further evidence that the dimensions found above correspond to those originally proposed in the Marcus model and that the ET results from nuclear motion along this dimension, an unrelaxed scan was performed along the vibrational coordinate shown in Fig. 5. In practice, the Marcus dimension is obtained as a vector of Cartesian displacements from the equilibrium configuration. This vector can be normalized and progress along the Marcus dimension can be measured in terms of the displacement of the nuclei from their equilibrium position.First, we show the results for p-DNB˙−, a Class III system. The potential energy surfaces of the ground and the first excited states are plotted in Fig. 6a, where the localization or delocalization of the unpaired electron is illustrated by natural transition orbitals. The scan results in two nested parabolic-like surfaces with different curvatures. The adiabatic minimum is characterized by an electron delocalized over the entire molecule. Any motion along the Marcus dimension will lead to a degree of localization of the electron on one of the nitro groups. This localization is reversed in the excited state. We therefore conclude that the system behaves according to Marcus theory of ET and that the identified ET coordinate is correct.
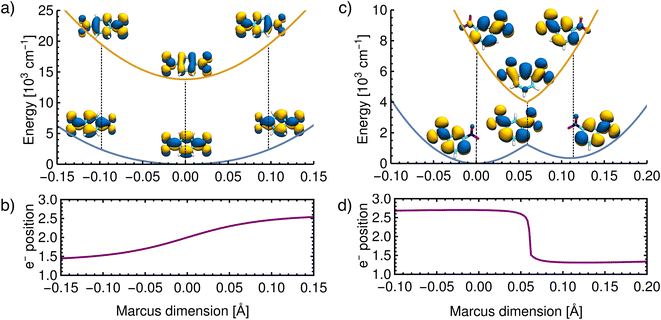 | ||
| Fig. 6 Reconstructed potential energy curves from geometries displaced in the direction of the Marcus dimension using the electronic energies. (a) Results for p-DNB˙− in ACN. The scan was performed with a step size of 0.005 Å. (b) The electron position for p-DNB˙−. (c) Results for m-DNB˙− in ACN. The scan was performed with a step size of 0.002 Å. (d) The electron position for m-DNB˙−. The change of the electron position in the ground and excited states is illustrated in the upper panels using natural transition orbitals and quantified in the lower panels according to eqn (3). | ||
Moving on to a Class II system, m-DNB˙− in ACN (see Fig. 6c), the ground state energy profile is a double-well potential and the excited state is a harmonic-like potential with the minimum centered just above the top of the ground state barrier. The qualitative agreement of the ab initio energy profiles with the Marcus model is a necessary, but not sufficient, condition to demonstrate that this dimension is the ET coordinate. The motion along the Marcus dimension should result in a change of the diabatic state. In other words, by overcoming the ground state barrier the unpaired electron has to be transferred to the other center. At the equilibrium configuration (position 0 Å in Fig. 6d), the unpaired electron is localized on the left-hand side nitro group in the ground state and on the right-hand side one in the excited state. At the top of the barrier, the unpaired electron is delocalized over the entire molecule. Once the barrier is overcome, the electron is localized on the right-hand side nitro group in the ground state and on the left-hand side one in excited state. This behaviour agrees exactly with the Marcus–Hush model, and hence the Marcus dimension we obtained from the multi-component fit is the dimension that facilitates electron transfer.
There are, however, two aspects in the Class II case that display some deviations from the Marcus model: there is a cusp at the top of the barrier, and the double-well potential is not symmetrical. These two aspects are discussed below.
The scan in Fig. 6c shows that the ground state potential does not change smoothly at the top of the barrier; instead, it exhibits a cusp. The same is seen in the excited state where the energy minimum takes the shape of a cusp. This appears to be a direct result of our approach, considering that the size of the scan steps is 0.002 Å and it is therefore unlikely that the curvature was missed due to a too widely spaced grid. This observation does not agree with the Marcus model, where the potential curves are smooth everywhere. The top of the barrier is in the region of an avoided crossing so that a multideterminant method might be necessary. In the ESI,† we compare the scans of the potential energy curves obtained from DFT with wavefunction methods (CASSCF, CASSCF/NEVPT2), showing that the cusp might be an artifact of using a single reference method. However, a proper description of the potential curves requires a strongly correlated method due to the expected importance of dynamic correlation. This is relatively easily captured with an appropriately chosen density functional, but when using wavefunction methods it appears that very large active spaces in combination with a perturbative treatment will be needed.
We now move on to discuss the energetic asymmetry in the double-well potential shown in Fig. 7c. Since the m-DNB˙− is a symmetrical system, both adiabatic minima in the double-well potential must have the same energy. The initial minimum (position 0 Å in Fig. 6c) was found by geometry optimization and is therefore described properly. Displacing the molecular geometry along the Marcus dimension results in the second minimum which is 350 cm−1 higher in energy. Of course the obtained potential could be symmetrized easily, but we do not expect to gain any additional insight from a symmetrized potential. In fact, we interpret the offset between the minima as the stabilisation that would be achieved by nitro group twisting, which implies that the electron transfer itself does not require twisting of the nitro group (see Fig. 5).
In other words, the Marcus dimension contains only the motions that directly promote the ET and neglects the motions that lead to the most stable conformer: our approach separates the intrinsic electron transfer coordinate from structural relaxation and environmental influences. This idea is illustrated in Fig. 7a, showing the Marcus dimension qint as an orange arrow and an orthogonal relaxation to reach the second adiabatic minimum as a red arrow. The blue arrow qrlx represents the direct, relaxed connection of the adiabatic minima, which would be obtained from a linear interpolation of Cartesian coordinates (LICC) and includes motions that do not contribute to electron transfer (here: twisting of the nitro groups). The separability of the intrinsic ET dimension from orthogonal structural relaxations is demonstrated in Fig. 7b. A linear interpolation from the endpoint of the intrinsic electron transfer coordinate to the optimized minimum, i.e. the motion associated with the red arrow, is found to be exclusively nitro group twisting and thus confirms the above interpretation. This finding is readily rationalised: in the initial minimum, the π system of the donor nitro group with the unpaired electron is conjugated with the π system of the benzene ring; only once the unpaired electron has been transferred to the acceptor nitro group can the system gain energy by rotation about the C–N bond to again enable stabilisation via π system conjugation. While for the cases studied here, there clearly are two separable motions, one can imagine cases where the intrinsic coordinate directly connects the two minima and no significant structural relaxation is seen, e.g. when the electron is placed in a non-bonding orbital at the acceptor site. The offset of the two minima discussed in Fig. 6c is then explained by choosing an adiabatic minimum which is a relaxed structure as a reference.
A more detailed comparison of the motions obtained by LICC vs. our approach is shown in the ESI.† We note here that the barrier of the Marcus dimension is ca. 200 cm−1 higher than that obtained from LICC. This relatively small difference supports the above reasoning that our approach does not reveal the minimum energy pathway. This is not a surprising result since the only constraint enforced in the fit is a correspondence to the Marcus–Hush model.
Our findings suggest that the minima along qint are actually spatially very close to each other in the many-dimensional space of atomic nuclei: they have to move by only 0.12 Å to reach the other adiabatic minimum. In contrast, the barrier obtained along the LICC path is wider (0.2 Å), again in line with separability of the intrinsic ET dimension from unrelated structural relaxation as shown schematically in Fig. 7a. Considering that the barrier is rather thin and the height agrees with literature expectations,55,56 heavy-atom tunneling might be an important process for the ET. This has been discussed in early work,57–59 and modern measurements found that heavy-atom tunneling in organic compounds to be important for many reactions.60–62 It may therefore be worthwhile to reconsider the importance of heavy-atom tunneling for intramolecular electron transfer. For the two Class II systems studied here, we estimated the transmission coefficients through the barrier as 0.34 for m-DNB˙− and 0.13 for 2,7-DNN˙−, respectively (see ESI† for details). These perhaps unexpectedly high values suggest that ET might be observable even at very low temperatures. In contrast, the transmission coefficients through the barrier obtained by LICC are significantly lower (m-DNB˙−: 0.04). Having a tool at hand that facilitates the evaluation of whether heavy-atom tunneling is relevant for intramolecular ET is an additional demonstration of the utility of being able to specify the ET coordinate and to quantify the electronic structure evolution along it.
5.4 Parameterization of the Marcus model
With the procedure described above, the Marcus model can now be recovered in the potential obtained from an ab initio calculation. To this end, an analytical potential is parameterized to the Marcus–Hush theory so that it matches as closely as possible to the ab initio potential. Before discussing the results, we note that in view of the idea in Fig. 7a, the experimental findings may be dependent on the experimental conditions, i.e. does the experiment allow the system to thermally relax, measuring the ET along the blue and red arrows in Fig. 7a, or is the measurement sufficiently rapid to separate intrinsic ET and vibronic relaxation?63There are four quantities that ultimately characterize the ab initio potential energy surfaces: (i) the excitation energy at the adiabatic minimum, (ii) the height of the barrier, (iii) the excitation energy at the top of the barrier, and (iv) the distance between the adiabatic minimum and the top of the barrier. These are depicted in both panels of Fig. 8. The Marcus model has three parameters: the potential coupling Vab, the separation of the minima of the diabatic states d, and their force constants f. Only the potential coupling 2Vab can be read immediately from the scan; it is the excitation energy at the top of the barrier. With the knowledge of the potential coupling we can relate other quantities obtained from the scan to the Marcus model. A more detailed discussion on how to choose the input values for the parameterization and description of the entire procedure is given in the ESI.†
The resulting parameters of the Marcus model will depend on the choice of parameterization procedure (sketched in Fig. 8). If the parameterization uses the potential coupling, the height of the barrier, and separation of the adiabatic minimum from the top of the barrier (parameterization A, Fig. 8a), the obtained potential energy curves will agree better with the ground (D0) than with the excited state (D1), see Fig. 8a. This is due to the fact that the reorganization energy from the ab initio scan does not enter the parameterization. In contrast, if the parameterization uses the reorganization energy, the separation of the adiabatic minimum and the top of the barrier, and the potential coupling (parameterization B, Fig. 8b), the shape of the potential curves for both ground and excited state will be better represented. However, the height of the barrier will not agree with the ab initio potential.
The results illustrate that the Marcus model faithfully captures the general shape of the potential curves but does not result in quantitative agreement with the ab initio potential. This is reflected in the parameters obtained for the barrier height ΔG and the reorganization energy λ, see Table 1. A disagreement might be expected given the offset between intrinsic and relaxed ET coordinates, and that the Marcus model assumes harmonic diabatic states which might not be the case in a real system for which the anharmonicities of the diabatic states enter the ab initio potential. In addition, the electronic structures at the top of the barrier are not described perfectly, but since the error introduced by the electronic structure method cannot be avoided or removed, the predicted shapes of the potential energy curves cannot be expected to agree exactly with the shapes in the Marcus model. We note that parameterizing the Marcus model for a specific system is not a straightforward procedure; in most cases it can be expected that a compromise between describing well either the barrier height or the reorganisation energy will need to be found to best represent the system.
| Class II system | ΔG [cm−1] | λ [cm−1] | 2Vab [cm−1] | d [Å] | |
|---|---|---|---|---|---|
| A | m-DNB˙− | 1233 | 9652 | 2752 | 0.125 |
| 2,7-DNN˙− | 1644 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386 386 |
2111 | 0.135 | |
| B | m-DNB˙− | 737 | 7434 | 2752 | 0.129 |
| 2,7-DNN˙− | 970 | 7510 | 2111 | 0.138 | |
| Ab initio scan | m-DNB˙− | 1233 | 7434 | 2752 | 0.120 |
| 2,7-DNN˙− | 1644 | 7510 | 2111 | 0.132 |
Perhaps the most surprising result is the separation of the diabatic states d, which is unexpectedly low in all cases. Prior experimental studies of dinitroradical anions40,64 made use of the generalized Mulliken–Hush formula12 to estimate the donor–acceptor separation from the transition dipole moments, evaluated either experimentally64 or by using semi-empirical calculations.40 The values ranged from 2 to 6 Å and it was noted that these were significantly shorter than the distance between the redox centers.
At first glance, such a discussion of distances raises the question whether we need to resolve the fact that these distances are much longer than the distances on the order of tenths of an Ångström we find. We note that the distances measured by dipole moment are fundamentally different from the ones we find by ab initio scans. The former are attempts at measuring the ‘real-space’ distance of electron transfer, while our approach identifies the distance in a multidimensional space expressed as the Marcus dimension. Nevertheless, one might be tempted to ascribe the results obtained from transition dipole moments to the distance along the Marcus coordinate. However, a simple thought experiment can show this is not reasonable. If we choose even the shortest distance (d = 2 Å) and use reasonable values for the reorganization energy 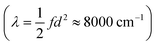 and coupling (2Vab ≈ 2500 cm−1),23,55,65 the remaining parameter is the spring constant f which becomes 11 kcal mol−1 Å−2. This is a unreasonably small spring constant that would result in an extremely low frequency along the ET coordinate. For instance, if we assume only a single N atom is moving, we can ascribe a mass of 14 amu, and the spring constant yields a frequency of 100 cm−1. On the other hand, our separations are associated with frequencies on the order of 1000 cm−1, which is in better agreement with expectations for the nuclear motions associated with ET.
and coupling (2Vab ≈ 2500 cm−1),23,55,65 the remaining parameter is the spring constant f which becomes 11 kcal mol−1 Å−2. This is a unreasonably small spring constant that would result in an extremely low frequency along the ET coordinate. For instance, if we assume only a single N atom is moving, we can ascribe a mass of 14 amu, and the spring constant yields a frequency of 100 cm−1. On the other hand, our separations are associated with frequencies on the order of 1000 cm−1, which is in better agreement with expectations for the nuclear motions associated with ET.
5.5 ET rate constant
In systems that conform to the Marcus model, the ET rate can in principle be assessed with the Marcus equation (eqn (1)).3,4 The expression is based on Fermi's golden rule and is thus valid only for small values of the potential coupling Vab. Another assumption employed in the Marcus equation is that all vibrational motions involved in the ET are small in frequency (ℏω ≪ 2kBT); this is the so-called high temperature limit.3 The Marcus equation is widely used to predict the ET rate in proteins,66 the rate of the photoinduced ET,67 or the rate of the inter-system crossing.68For large potential couplings Vab, the ET can be assumed to happen only adiabatically, i.e., once the nuclei reach the top of the barrier the probability of the electron tunneling is close to one.4 In this case, the pre-exponential factor will reduce to a nuclear frequency along the ET coordinate νq and the ET rate can be calculated according to eqn (2). The nuclear frequency νq is a well defined concept only in the harmonic potential. In the double-well potential this value has to be estimated, and we propose to use the harmonic approximation at the adiabatic minimum to obtain the force constant and subsequently the harmonic frequency (see Sec. S7† for more details). Regardless of how νq is estimated, the value is approximately 1013 s−1.
A comparison of ET rates according to the Marcus equation with the adiabatic rates is shown in Table 2. The adiabatic, i.e. classical, rate was computed using the barrier height from the scanned potential and the harmonic frequency at the adiabatic minimum. The parameters for the Marcus equation were taken from parameterization procedure A.
The ET rates listed in Table 2 favor the description with the more simplistic eqn (2) over that with the Marcus equation (eqn (1)). We can identify two reasons for this finding: (I) both systems under study have large potential coupling values Vab, which are outside the scope of the Marcus equation. (II) The nuclear frequency in the Marcus dimension is larger than 2kBT. Note that the Marcus dimension is confined mainly to the stretching of C–N and N–O bonds which have frequencies of ca. 1000 cm−1.
For systems with large potential coupling Vab, the ET mechanism is adiabatic and the ET rate should be assessed classically (i.e., with eqn (2)). Since the biggest error is introduced by the electronic structure method, choosing a different method of estimating the nuclear frequency νq would improve the value of the ET rate only through error cancellation. Classical treatment of ET is only possible for high temperatures; heavy-atom tunneling which might drive ET at low temperatures should in principle be possible due to the very narrow barrier. Another case where the classical theory will fail is a photoinduced ET which is, however, beyond the scope of this paper.
6 Conclusions
We propose a method for identifying the nuclear coordinate that promotes electron transfer in mixed valence systems by exploiting properties postulated by Marcus–Hush theory in the analysis of a thermally representative ensemble of ab initio calculations. As the characteristic electron transfer property, the electron position is chosen for Class III systems with complete delocalisation of the unpaired electron, and the excitation energy is chosen for Class II systems where a small barrier separates two adiabatic minima with localisation of the unpaired electron on one of the redox centers. The electron transfer coordinate, also termed Marcus dimension, is obtained as a linear combination of vibrational modes. We find that the Marcus dimension is not simply equivalent to the absorption in a certain IR or Raman region; the ab initio analysis shows that active and silent modes across all energies contribute.The method was demonstrated on a set of organic radical compounds with two nitro groups as the redox centers. The Marcus dimension was found to be a chemically intuitive antisymmetric motion mostly restricted to the redox centres (nitro groups) and the atoms of the bridging unit (aromatic core) that they are attached to. The motion is qualitatively very similar for structurally similar compounds, and is retained even after an environmentally induced change from Class II (m-DNB˙− and 2,7-DNN˙− in ACN) to Class III (both in vacuum). We have thus shown that our approach identifies the nuclear coordinate that is the electron transfer pathway in Class II compounds and leads to a higher degree of charge localization in Class III compounds. Scans along the Marcus dimension clearly demonstrate that the expected potential shapes are obtained, and furthermore provide the basis for recovering the Marcus model from ab initio calculations. To the best of our knowledge, this is the first approach for identifying the electron transfer coordinate that is applicable across all Robin–Day Classes.
The Marcus dimension we identify for Class II compounds appears to be an intrinsic property of the molecule, which implies separability of the transition from one adiabatic minimum to the other into the electron transfer process and ET-innocent structural relaxations or environmental contributions. This is demonstrated explicitly for the examples studied here and by comparison with the previously employed linear interpolation of Cartesian coordinates approach. The usefulness of the presented approach lies in extracting the exact nuclear motion that is responsible for promoting ET, which does not have to coincide with the lowest energy pathway. It may be possible to devise an experimental test for our suggestion of separable electron transfer and structural relaxation events, e.g. using frozen solution or solid state experiments that prevent structural relaxation and/or ultrafast spectroscopies that probe electronic structures prior to structural relaxation.63
The ab initio scans along the Marcus dimension show a small separation of the minima. The parameterization of the Marcus model provides acceptable agreement with experiment, and we note that other approaches may produce better results22,25 especially for weakly coupled systems. The parameterization results in similar separations of the diabatic states of ca. 0.12–0.13 Å, i.e., much thinner barriers for electron transfer than had been previously suggested. This small distance in the multi-dimensional space of atomic nuclei suggests that heavy-atom tunneling may be a relevant contributor to intramolecular electron transfer. We estimated transmission coefficients of 0.34 for m-DNB˙− and 0.13 for 2,7-DNN˙−. Low temperature experiments may confirm this finding in future, which would be one way of obtaining experimental support for the concept of the Marcus dimension introduced here.
With a method for identifying the Marcus dimension of electron transfer in any mixed valence system for which TD-DFT calculations on a representative ensemble can be obtained, a more rigorous and quantitative discussion of electron transfer is now possible, likely also extending to proton-coupled electron transfer. It provides an opportunity to evaluate ET mechanisms involving molecular orbitals or electronic states proposed in the literature, e.g. incoherent hopping vs. coherent superexchange mechanisms, or two-state vs. multi-state models.6,54 Our approach is the first to provide the spring constant of the nuclear motion and the separation of the adiabatic minima. Individual access to all parameters of the Marcus model holds promise for disentangling electronic structure behaviour arising from the electronic coupling, the curvature of the PES and the separation of the minima, as well as decoupling and quantifying the intramolecular and solvent contributions to the ET coordinate.
Data availability
We provide extensive ESI† and have now made available the script used to fit the data and generate the Marcus dimension, https://git.rwth-aachen.de/ak-krewald/mdlcnm.Author contributions
Conceptualization: V. K., B. J. L. and A. S.; data generation: A. S.; analysis and interpretation: A. S., B. J. L. and V. K.; writing: V. K., B. J. L. and A. S.; supervision: V. K.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Lichtenberg II high performance computer of TU Darmstadt for computational resources. AS thanks the Merck'sche Gesellschaft für Kunst und Wissenschaft e.V. for financial support. BJL thanks the HPC Europa3 programme for financial support.References
- N. S. Hush, Coord. Chem. Rev., 1985, 64, 135–157 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- B. S. Brunschwig and N. Sutin, Coord. Chem. Rev., 1999, 187, 233–254 CrossRef CAS.
- B. S. Brunschwig, C. Creutz and N. Sutin, Chem. Soc. Rev., 2002, 31, 168–184 RSC.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1968, 10, 247–422 CrossRef.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2685 CrossRef CAS PubMed.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Phys. Chem., 1996, 100, 13148–13168 CrossRef CAS.
- C. Creutz, in Mixed Valence Complexes of d5-d6 Metal Centers, John Wiley & Sons, Ltd, 1983, pp. 1–73 Search PubMed.
- C. Creutz, M. D. Newton and N. Sutin, J. Photochem. Photobiol., A, 1994, 82, 47–59 CrossRef CAS.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS.
- J. P. Launay, Chem. Soc. Rev., 2001, 30, 386–397 RSC.
- J. R. Reimers and N. S. Hush, in Electric Field Perturbation of Electronic (Vibronic) Absorption Envelopes: Application to Characterization of Mixed-Valence States, ed. K. Prassides, Springer Netherlands, Dordrecht, 1991, pp. 29–50 Search PubMed.
- D. H. Oh, M. Sano and S. G. Boxer, J. Am. Chem. Soc., 1991, 113, 6880–6890 CrossRef.
- M. Parthey and M. Kaupp, Chem. Soc. Rev., 2014, 43, 5067–5088 RSC.
- J. Jaramillo, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 1068–1073 CrossRef CAS.
- T. M. Maier, A. V. Arbuznikov and M. Kaupp, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, 1–32 Search PubMed.
- M. Haasler, T. M. Maier, R. Grotjahn, S. Gückel, A. V. Arbuznikov and M. Kaupp, J. Chem. Theory Comput., 2020, 16, 5645–5657 CrossRef CAS PubMed.
- S. Klawohn, M. Kaupp and A. Karton, J. Chem. Theory Comput., 2018, 14, 3512–3523 CrossRef CAS PubMed.
- S. Gückel, J. B. G. Gluyas, S. G. Eaves, P. Safari, D. S. Yufit, A. N. Sobolev, M. Kaupp and P. J. Low, Chem.–Eur. J., 2019, 25, 8837–8853 CrossRef PubMed.
- A. Koch, D. Kinzel, F. Dröge, S. Gräfe and S. Kupfer, J. Phys. Chem. C, 2017, 121, 16066–16078 CrossRef CAS.
- M. Renz, M. Kess, M. Diedenhofen, A. Klamt and M. Kaupp, J. Chem. Theory Comput., 2012, 8, 4189–4203 CrossRef CAS PubMed.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218–2224 CrossRef CAS.
- J. K. Hwang and A. Warshel, J. Am. Chem. Soc., 1987, 109, 715–720 CrossRef CAS.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- H. Oberhofer and J. Blumberger, J. Chem. Phys., 2009, 131, 064101 CrossRef PubMed.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Chem. Theory Comput., 2011, 7, 2831–2841 CrossRef CAS PubMed.
- J. P. Bergsma, P. H. Berens, K. R. Wilson, D. R. Fredkin and E. J. Heller, J. Phys. Chem., 1984, 88, 612–619 CrossRef CAS.
- R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1–14 Search PubMed.
- Š. Sršeň, J. Sita, P. Slavíček, V. Ladányi and D. Heger, J. Chem. Theory Comput., 2020, 16, 6428–6438 CrossRef PubMed.
- S. Mai, H. Gattuso, M. Fumanal, A. Muñoz-Losa, A. Monari, C. Daniel and L. González, Phys. Chem. Chem. Phys., 2017, 19, 27240–27250 RSC.
- F. Kossoski and M. Barbatti, J. Chem. Theory Comput., 2018, 14, 3173–3183 CrossRef CAS PubMed.
- S. Mai, H. Gattuso, A. Monari and L. González, Front. Chem., 2018, 6, 495 CrossRef CAS PubMed.
- L. Sun and W. L. Hase, J. Chem. Phys., 2010, 133, 044313 CrossRef PubMed.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- J. P. Zobel, M. Heindl, J. J. Nogueira and L. González, J. Chem. Theory Comput., 2018, 14, 3205–3217 CrossRef CAS PubMed.
- J. P. Zobel, J. J. Nogueira and L. González, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915 RSC.
- S. Mai, M. Richter, M. Heindl, M. F. S. J. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, L. M. Ibele, S. Kropf, M. Oppel, P. Marquetand and L. González, SHARC2.1: Surface Hopping Including Arbitrary Couplings — Program Package for Non-Adiabatic Dynamics, 2019, https://sharc-md.org Search PubMed.
- S. F. Nelsen, M. N. Weaver, A. E. Konradsson, J. P. Telo and T. Clark, J. Am. Chem. Soc., 2004, 126, 15431–15438 CrossRef CAS PubMed.
- J. P. Telo, M. C. B. Shohoji, B. J. Herold and G. Grampp, J. Chem. Soc., Faraday Trans., 1992, 88, 47–51 RSC.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- H. Bahmann and M. Kaupp, J. Chem. Theory Comput., 2015, 11, 1540–1548 CrossRef CAS PubMed.
- S. Klawohn, H. Bahmann and M. Kaupp, J. Chem. Theory Comput., 2016, 12, 4254–4262 CrossRef CAS PubMed.
- T. M. Maier, H. Bahmann and M. Kaupp, J. Chem. Theory Comput., 2015, 11, 4226–4237 CrossRef CAS PubMed.
- M. Renz, K. Theilacker, C. Lambert and M. Kaupp, J. Am. Chem. Soc., 2009, 131, 16292–16302 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, 1–15 Search PubMed.
- B. J. Lear, S. D. Glover, J. C. Salsman, C. H. Londergan and C. P. Kubiak, J. Am. Chem. Soc., 2007, 129, 12772–12779 CrossRef CAS PubMed.
- N. Sutin, in Theory of Electron Transfer Reactions: Insights and Hindsights, John Wiley & Sons, Ltd, 1983, pp. 441–498 Search PubMed.
- J. R. Reimers and N. S. Hush, Chem. Phys., 1996, 208, 177–193 CrossRef CAS.
- A. Heckmann and C. Lambert, Angew. Chem., Int. Ed., 2012, 51, 326–392 CrossRef CAS PubMed.
- J. P. Telo, A. S. Jalilov and S. F. Nelsen, J. Phys. Chem. A, 2011, 115, 3016–3021 CrossRef CAS PubMed.
- H. Hosoi and Y. Masuda, J. Mol. Liq., 2001, 90, 279–286 CrossRef CAS.
- J. Jortner and M. Bixon, J. Chem. Phys., 1988, 88, 167–170 CrossRef CAS.
- V. Levich, R. Dogonadze, E. German, A. Kuznetsov and Y. Kharkats, Electrochim. Acta, 1970, 15, 353–367 CrossRef CAS.
- M. D. Purugganan, C. V. Kumar, N. J. Turro and J. K. Barton, Science, 1988, 241, 1645–1649 CrossRef CAS PubMed.
- T. Schleif, M. Prado Merini, S. Henkel and W. Sander, Acc. Chem. Res., 2022, 55, 2180–2190 CrossRef CAS PubMed.
- C. Castro and W. L. Karney, Angew. Chem., Int. Ed., 2020, 59, 8355–8366 CrossRef CAS PubMed.
- J. Meisner and J. Kästner, Angew. Chem., Int. Ed., 2016, 55, 5400–5413 CrossRef CAS PubMed.
- S. Rafiq, B. Fu, B. Kudisch and G. D. Scholes, Nat. Chem., 2021, 13, 70–76 CrossRef CAS PubMed.
- S. F. Nelsen, A. E. Konradsson, M. N. Weaver and J. P. Telo, J. Am. Chem. Soc., 2003, 125, 12493–12501 CrossRef CAS PubMed.
- S. F. Nelsen, M. N. Weaver, J. I. Zink and J. P. Telo, J. Am. Chem. Soc., 2005, 127, 10611–10622 CrossRef CAS PubMed.
- H. B. Gray and J. R. Winkler, Q. Rev. Biophys., 2003, 36, 341–372 CrossRef CAS PubMed.
- V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759–833 CrossRef CAS PubMed.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Predicted spectra from the nuclear ensemble approach, correlation plots for m-DNB˙−, Marcus dimensions found for studied systems in vacuum, scans along the Marcus dimension in acetonitrile, wavefunction calculations, calculation of phonon masses and harmonic frequencies for the Marcus dimension, parameterization of the Marcus model, estimation of transmission coefficients, coordinates of the calculated adiabatic minima and of obtained ET dimensions. See DOI: https://doi.org/10.1039/d3sc01402a |
| ‡ As stated elsewhere in the text, the concept is expected to be easily translatable to explicit solvation environments using QM-MD, QM/MM-MD or other approaches for sampling a representative ensemble via snapshots. |
| This journal is © The Royal Society of Chemistry 2023 |