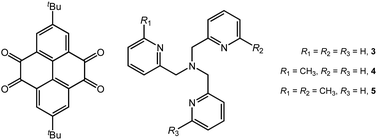
Tuning the magnetic properties of dinuclear cobalt–tetraoxolene compounds: from valence tautomerism to ferromagnetic coupling

Abstract

The reaction of a non-innocent ligand 2,7-di-tert-butyl-pyrene-4,5,9,10-tetraone (pyrene^Q–Q, Q = quinone), Co₂(CO)₈, and tris(2-pyridylmethyl)amine derivatives (Me_ntpa) gave rise to a series of dinuclear cobalt–tetraoxolene compounds formulated as {[Co(Me_ntpa)]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂·S (Sq = semiquinone; n = 0, S = 2C₆H₅CH₃ for 3; n = 1 for 4; n = 2, S = 2CHCl₃ for 5). Magnetic measurements and single-crystal X-ray diffraction studies revealed that compound 3 underwent incomplete valence tautomeric transition, while compounds 4 and 5 maintained in the steady electronic structure of {Co^II-HS–pyrene^Sq–Sq–Co^II-HS} in the whole temperature range. Remarkably, strong ferromagnetic interactions in both 4 and 5 were confirmed by experimental and theoretical studies. Theoretical calculations showed that the successive introduction of methyl groups enhanced the steric rigidity of tpa, and hence the {Co^II-HS–pyrene^Sq–Sq–Co^II-HS} state was stabilized sterically and electronically, which in turn altered the energetic order and gap among the different electronic states, which resulted in distinct magnetic properties.

---

Introduction

Molecule-based materials displaying switchable physical and chemical properties are potentially applicable in molecular switches, information storage devices, displays, and sensors;^1–7 thus, they have attracted widespread attention. In particular, there exists an escalating interest in designing novel molecule-based materials with switchable magnetic properties among the scientific community. Exemplary cases include spin-crossover (SCO) compounds and valence tautomeric (VT) compounds. The former typically refer to transition-metal compounds featuring 3d⁴–3d⁷ electronic configurations that can switch between low-spin (LS) and high-spin (HS) states, and the latter engage in a successive intramolecular electron transfer and spin transition process. Interestingly, the switching of magnetic properties in both cases can be controlled by external stimuli, such as heat, light, pressure, electric field, magnetic field, soft X-ray, hard X-ray, and others.^8–17

Over the past two decades, a plethora of VT compounds with new structures and properties have been reported in which the central metal ions are mainly focused on V, Mn, Fe, Co, Ni, Cu, and Ru with Co being the most common.^18–26 Specifically, cobalt–dioxolene compounds are perhaps the most well explored VT system, where the dioxolene ligands can interconvert between the catecholate (Cat²⁻) and semiquinonate (Sq˙⁻) oxidation states with the concomitant change of cobalt spin state from Co^III-LS to Co^II-HS together with variations in bond lengths as well as optical, electrical, and magnetic properties. Apart from valence tautomerism, the cobalt–dioxolene system itself is quite intriguing as it engenders magnetic coupling between radical ligands and metal ions, which provides valuable insight for designing materials with conductivity and magnetism that are indispensable for future technologies.²⁷ In fact, introducing strong magnetic coupling between paramagnetic metal ions and radical ligands has long been adopted as an effective strategy to establish long-range magnetic ordering and slow down magnetic relaxation in single-molecule magnets (SMMs).^28,29

In the cobalt–dioxolene system, the nitrogen-containing ancillary ligands have a profound impact on VT transition behaviours and should be thoroughly considered when designing VT compounds. For example, if the ancillary ligand has a rigid structure or contains bulky substituents, the increasing steric strain will favour longer Co–N bond lengths, thereby stabilizing Co^II-HS and lowering the VT transition temperature. In addition, substitution on the ancillary ligand can alter the Co^III/II redox potential, thus dictating the charge distribution within the cobalt–dioxolene scaffold. In 2008, Beni et al. reported that the VT transition behaviour can be controlled by introducing methyl groups into the 6-position of pyridine rings of the tripod-type ligand tris(2-pyridylmethyl)amine (tpa).³⁰ They revealed that the VT transition temperature of [Co(Me_ntpa)(diox)]PF₆·sol (n = 0, 2, and 3; diox = 3,5-di-tert-butyl-1,2-dioxolene; sol = ethanol and toluene) gradually decreased with increasing number of methyl groups. Thereafter, methyl-substituted tpa ancillary ligands had been widely utilized to obtain desirable VT properties but majority of the related studies were focused on mononuclear VT compounds with limited reports concerning dinuclear VT systems, especially those with two-step VT behaviours. One such case was based upon the redox-active bis(dioxolene) ligand 3,3,3′,3′-tetramethyl-1,1′-bis(indane-5,5′,6,6′-tetrol) (spiroH₄), with which a series of dinuclear cobalt compounds [Co₂(spiro)(Me_ntpa)₂]²⁺ (n = 0, 1, 2, and 3), [Co₂(spiro)(tpa)₂]³⁺ and [Co₂(spiro)(tpa)₂]⁴⁺ were synthesized.^31–33 Magnetic susceptibility measurement indicated that [Co₂(spiro)(Me₂tpa)₂]²⁺ exhibited a rare two-step incomplete VT transition in the temperature range of 2–320 K, while the rest displayed distinct magnetic properties.

Very recently, we reported two dinuclear cobalt–tetraoxolene compounds {[CoL₂]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂·solvent (pyrene^Sq–Sq = semiquinone form of 2,7-di-tert-butyl-pyrene-4,5,9,10-tetraone (pyrene^Q–Q, Scheme 1); L = 1,10-phenanthroline (phen) for 1, and 2,2′-bipyridine (bpy) for 2).³⁴ Due to the difference in steric rigidity and π-accepting capability of phen and bpy, compound 1 exhibited a one-step partial VT transition, while 2 showed a rare two-step VT transition. Importantly, the study manifests that two-step VT transition is accessible in a fully π-conjugated tetraoxolene system featuring efficient electronic communication between the two dioxolene halves, and the π-expanded tetraoxolene core exhibits a rare diradical character likely stabilized by coupling interaction with the Co^II-HS ions. Despite the ubiquity of radical-bridged paramagnetic systems present in the literature, diradical coupled systems are considerably less common presumably due to their intrinsic high reactivity. Such a unique system provides us an ideal platform to construct a more thorough understanding of the correlation between molecular and electronic structures, which offers chemical insights beyond the narrow scope of valence tautomerism. We envision that the structural modulation of the ancillary ligand can serve as a convenient strategy to control the overall electronic distribution with the intention to tune the VT behaviour and magnetic exchange interactions within the system. In this regard, we synthesized three new dinuclear cobalt–tetraoxolene compounds {[Co(Me_ntpa)]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂·S (n = 0 and S = 2C₆H₅CH₃ for compound 3, n = 1 for compound 4, and n = 2 and S = 2CHCl₃ for compound 5) using the same redox-active pyrene-based tetraoxolene ligand (Scheme 1). Whereas the previous report leans more towards the discovery of a novel two-step VT complex, the present work delves into the maneuvering/tuning of the electronic structure of VT compounds via ancillary ligand derivatization. These compounds were thoroughly investigated by single-crystal X-ray diffraction, magnetic and photomagnetic measurements, and DFT studies. Compound 3 features an incomplete VT transition, while 4 and 5 retain the {Co^II-HS–pyrene^Sq–Sq–Co^II-HS}²⁺ electronic states in the entire measured temperature range. Remarkably, 4 and 5 display large ground spin states enabled by two Co^II-HS ions bridged by a strongly ferromagnetically coupled diradical dianion. Detailed experimental and theoretical studies have been carried out, which reveals how subtle changes around the cobalt coordination sites can profoundly affect the charge distribution both sterically and electronically and how these compounds behave differently from those incorporating more traditional tetraoxolene ligands with little or no magnetic/electronic communications.

Scheme 1 Structures of ligands used in this work.

Results and discussion

Synthesis

Compounds 3–5 are obtained by one-pot synthesis starting from pyrene^Q–Q and Co₂(CO)₈ in the presence of tetradentate N-donor co-ligands. We propose that pyrene^Q–Q is reduced to pyrene^Sq–Sq by Co₂(CO)₈, and the zero-valent cobalt in Co₂(CO)₈ disproportionates to produce Co(II) ions and the diamagnetic [Co(CO)₄]⁻ anion at the same time.^35,36 Dark-brown plate-shaped crystals suitable for X-ray diffraction measurement can be obtained by layer diffusion in C₆H₅CH₃/CH₂Cl₂ or C₆H₅CH₃/CHCl₃ using 14 mM Co₂(CO)₈, 14 mM pyrene^Q–Q, and 28 mM Me_ntpa, respectively. Desolvated samples were obtained by heating the fresh crystals in a vacuum. It should be emphasized that the as-synthesized crystals desolvate and turn into dull powders readily after being removed from the solvent. Moreover, excess reactants or prolonged reaction time leads to the formation of large amounts of amorphous unidentified impurities. In any case, these impurities mixed with crystals easily in the growing process and needed to be washed with the mother liquor before subsequent measurements. We also note that compounds 3–5 in the solid state are sufficiently air stable and can be stored immersed in the mother liquor under ambient conditions for weeks, whereas solutions of 3–5 are air sensitive and need to be handled under an inert atmosphere.

Infrared and electronic absorption spectroscopy

The infrared spectra for the three compounds were measured at room temperature using KBr pellets (Fig. S1†). All compounds show a strong band at around 1885 cm⁻¹, which corresponds to the C≡O stretching vibration of the [Co(CO)₄]⁻ anion,^36,37 and a medium band at around 1606 cm⁻¹ associated with pyridyl C–N stretching vibration of the Me_ntpa ligand.^38,39 In the literature, the characteristic semiquinone C–O stretching vibration is generally found in the range of 1400–1550 cm⁻¹ and the fully reduced catecholate C–O stretching band is observed within the range of 1250–1300 cm⁻¹.^40–42 In compound 3, the bands at 1480 cm⁻¹ and 1276 cm⁻¹ can be ascribed to C–C ring and C–O stretching bands of the catecholate ligand.^36,37 In addition, the weak bands in the region between 1450 and 1400 cm⁻¹ are identified as the C–O stretching band of the semiquinone group.^32,43 The coexistence of semiquinone and catecholate characters implies that compound 3 is intrinsically mixed valence at room temperature, consistent with the single-crystal structure and magnetic data (vide infra). For compounds 4 and 5, the two obvious bands at around 1440 and 1470 cm⁻¹ can be assigned to the semiquinonate C–O stretching vibrations. The band at 1200–1300 cm⁻¹ could be due to the C–N stretching vibrations of the auxiliary ligand. Importantly, in contrast to 3, the band at 1276 cm⁻¹ belonging to catecholate C–O stretching is absent in 4 and 5, which indicates that both 4 and 5 are in the {Co^II-HS–pyrene^Sq–Sq–Co^II-HS}²⁺ spin state. The calculated frequencies (Table S1†) by the DFT method are in good agreement with our above assignments.

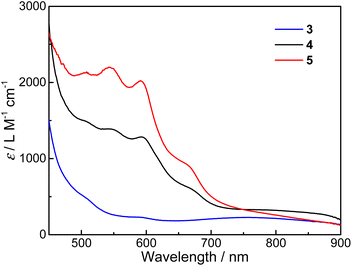
UV-vis absorption spectra for the three compounds dissolved in desiccative CH₃CN were measured at room temperature (Fig. 1, see Fig. S2† for solid-state UV-vis diffuse reflectance spectra). At first sight, the absorption spectrum of 3 is more characteristic of Co^III-LS–Cat species, which shows a weak and broad absorption band around 750 nm that can be assigned to the ligand-to-metal charge transfer (LMCT) transitions.⁴⁴ In addition, the weak band between 550 and 630 nm can be assigned to the metal-to-ligand charge transfer (MLCT) transitions arising from Co^II-HS–Sq species in minor proportions. In contrast, the spectra of 4 and 5 appear to resemble that of the congener compound 2 incorporating a bipyridine ancillary ligand as reported previously. Both 4 and 5 possess several strong absorption bands between 500 and 700 nm, which correspond to the MLCT transitions from Co^II-HS to the π* orbital of semiquinone.^45,46 The broad shoulders between 700 and 900 nm can be attributed to internal semiquinone ligand transitions within the pyrene^Sq–Sq ligand.^30,32,47 The assignments of LMCT and MLCT bands are in reasonable agreement with TD-DFT results except for internal semiquinone transitions, which are more problematic for DFT calculations (Fig. S3–S5†). These features indicate that compounds 4 and 5 are predominantly {Co^II-HS–pyrene^Sq–Sq–Co^II-HS}²⁺ in MeCN at room temperature. Closer scrutiny of the electronic absorption spectra reveals that the bands of compound 5 between 500 and 700 nm undergo a slight blue shift compared to 4, which may be due to the electron-donating and/or steric effects of the methyl group on the Me_ntpa ligand. Overall, the electronic absorption of 4 and 5 is substantially stronger than that of 3, which further confirms their {Co^II-HS–pyrene^Sq–Sq–Co^II-HS}²⁺ electronic structures.

Fig. 1 UV-vis absorption spectra of 3–5 in CH₃CN at room temperature.

Structural description

Single-crystal X-ray crystallographic studies revealed that compound 3 crystallized in the monoclinic space group P2₁/c (Table S2†). The asymmetric unit is composed of half a cationic species {[Co(tpa)]₂(pyrene^Cat–Sq)}²⁺ (room temperature, RT), a [Co(CO)₄]⁻ counter-ion, and a C₆H₅CH₃ molecule. As shown in Fig. 2, each cobalt atom is coordinated with three pyridyl-N atoms and one tertiary amine N atom of the tpa ligand and two cis-oriented O atoms from the tetraoxolene ligand, thus forming a slightly distorted octahedral coordination geometry. At 100 K, the Co–O and Co–N bond lengths range from 1.868(2) to 1.879(2) Å and from 1.920(3) to 1.965(3) Å, respectively, consistent with a Co^III-LS metal center.¹¹ The C1–O1 and C2–O2 bond lengths are 1.358(4) and 1.352(4) Å, respectively, which fall in the range of 1.33–1.39 Å typically observed for catecholate ligands.^48,49 The octahedral distortion parameters are Σ = 32.81° and Θ = 88.85° (Table S3†), where Σ is the deviation of a metal ion from an ideal octahedron, while Θ indicates the distortion of the MX₆ geometry from a perfect octahedron to a trigonal tetrahedron.⁵⁰ Metrical oxidation state (MOS) by least-squares fitting of dioxolene C–C and C–O bond lengths reveals a MOS value of −1.8 (catecholate and semiquinone have a MOS of around −2 and −1, respectively).^51,52 Cobalt oxidation state is further established as +3 by charge balance considerations and bond valence sum (BVS) calculations (Table S4†).^53–55 Together, the charge distribution of 3 at 100 K can be unambiguously assigned as {Co^III-LS(tpa)–pyrene^Cat–Cat–Co^III-LS(tpa)}²⁺. At 298 K, the Co–N bond lengths vary from 1.967(3) to 2.008(3) Å and the Co–O bond lengths are 1.896(3) and 1.930(3) Å. The C1–O1 and C2–O2 bond lengths are 1.342(4) and 1.330(4) Å, respectively, corresponding to a MOS value of −1.6. BVS analysis reveals a decrease of the apparent oxidation state of cobalt (Table S4†). Distortion parameters Σ and Θ are calculated to be 49.7° and 135.9° (Table S3†), indicating higher degree of geometry distortion. At 360 K, the Co–N and Co–O bond lengths further increase to 1.997(4)–2.061(4) and 1.933(3)/1.976(3) Å, respectively, elongated by 0.087 and 0.081 Å compared to 100-K data. The octahedral distortion parameters are Σ = 62.32° and Θ = 175.6°, larger than those at 100 K and 298 K (Table S3†), consistent with the transition from Co^III to Co^II with more deviation from octahedron geometry. The C1–O1 and C2–O2 bond lengths are 1.301(6) Å and 1.327(5) Å, respectively. This is further confirmed by oxidation state analysis, which reveals a MOS value of −1.4, borderline between catecholate and semiquinone. The oxidation state of cobalt ion is established based on charge balance and BVS calculations (Table S4†). Therefore, the electronic structure of the cation in 3 is best described as {Co^III-LS(tpa)–pyrene^Cat–Sq–Co^II-HS(tpa)}²⁺ at 360 K. That is to say, 3 undergoes an incomplete VT conversion between a {Co^III-LS(tpa)–pyrene^Cat–Cat–Co^III-LS(tpa)}²⁺ and a {Co^III-LS(tpa)–pyrene^Cat–Sq–Co^II-HS(tpa)}²⁺ electronic state, in which Co^III-LS–Cat and Co^II-HS–Sq components are crystallographically indistinguishable as a result of rapid electronic transfer or crystal disorder (Scheme 2).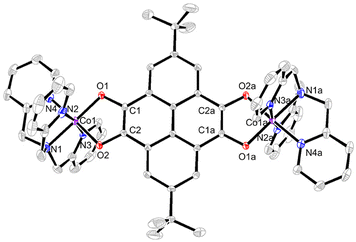

Fig. 2 Perspective view of the dinuclear cation of 3 with 50% thermal ellipsoids. Hydrogen atoms, solvent molecules, and counter-ions are omitted for clarity. Symmetry code: (a) −x, −y, 1 − z.

Scheme 2 One-step VT transition of compound 3.

Compound 4 also crystallized in the monoclinic space group P2₁/c (Table S5†). The asymmetric unit is composed of half a cationic species {[Co(Metpa)]₂(pyrene^Sq–Sq)}²⁺, and a [Co(CO)₄]⁻ anion (Fig. S6a†). The cation is also centrosymmetric and the cobalt ion is six-coordinated with three pyridyl-N atoms and one tertiary amine N atom from the Metpa ligand and two cis-oriented O atoms from the tetraoxolene ligand, giving rise to a distorted octahedral coordination geometry. At 100 K, the Co–N and Co–O bond distances are 2.074(6)–2.150(3) and 2.006(6)–2.076(8) Å, respectively, consistent with Co^II-HS centers.²⁷ The C1–O1 and C2–O2 bond lengths range from 1.274(9) to 1.290(7) Å, which are within the range of 1.26–1.32 Å for Sq ligands.^42,56 The octahedral distortion parameters are Σ = 94.58° and Θ = 285.5° (Table S6†). The MOS value of the tetraoxolene ligand is −1.05, assigning the ligand oxidation state as semiquinone. Cobalt oxidation state is further verified as divalent by charge balance considerations and BVS calculations (Table S7†). Therefore, the electronic structure of 4 is {Co^II-HS(Metpa)–pyrene^Sq–Sq–Co^II-HS(Metpa)}²⁺ at 100 K, ruling out the occurrence of VT transition.

Compound 5 crystallized in the triclinic space group P1̄, distinct from the above two compounds where a two-fold screw axis is present along the c axis (Table S5†). The asymmetric unit is composed of half a cationic species {[Co(Me₂tpa)]₂(pyrene^Sq–Sq)}²⁺, a [Co(CO)₄]⁻ anion, and a CHCl₃ molecule (Fig. S6b†). The central cobalt ion locates in a distorted octahedral coordination environment with an average Co–N distance of 2.171 Å and an average Co–O bond length of 2.072 Å. Furthermore, the C–O bond distances are 1.291(4) and 1.272(4) and the intra-ring C1–C2 distance is 1.449(5) Å. The octahedral distortion parameters are Σ = 104.8° and Θ = 267.1°, commensurate with a larger deviation from octahedral geometry (Table S6†). These metrics closely resemble those of compound 4. The calculated MOS value (−0.96) and BVS calculations (Table S7†) indicate that compound 5 is analogous to 4, with an electronic structure of {Co^II-HS(Me₂tpa)–pyrene^Sq–Sq–Co^II-HS(Me₂tpa)}²⁺ at 100 K.

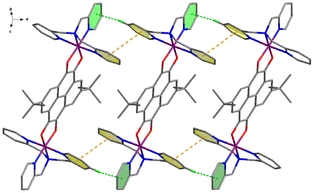
In the crystal lattices, the cations of compounds 3–5 stack in a different style. As shown in Fig. 3, the cationic species of 3 at 100 K parallelly stack along the a-axis direction, interacting with each other through two kinds of intermolecular interactions, i.e., π_py⋯π_py and C_py–H⋯π_py. The centroid⋯centroid distance of π_py⋯π_py interaction increases from 3.867 Å at 100 K to 4.008 Å at 360 K, and the C_py–H⋯π_py distance varies from 3.554 Å (156.7°) at 100 K to 3.785 Å (151.9°) at 360 K, respectively (Table S8†). These one-dimensional (1D) supramolecular chains then arrange parallel to the a-axis through weak inter-chain van der Waals interactions, forming 1D void channels that are occupied by anions and guest solvent molecules (Fig. S7†).

Fig. 3 One-dimensional supramolecular chain formed with the cationic species of compound 3.

Different from compound 3, the cationic species of compounds 4 and 5 interact with each other to form two-dimensional (2D) layers. As for compound 4 (Fig. 4a), the cation {Co^II-HS(Metpa)–pyrene^Sq–Sq–Co^II-HS(Metpa)}²⁺ interacts with adjacent ones through two sets of π_py⋯π_py and C_py–H⋯π_py interactions, which are d₁ and d₃ and d₂ and d₃. At 100 K, the centroid⋯centroid distances of d₁ and d₂ are 3.748 and 3.667 Å, and the d₃ value (C_py–H⋯π_py) is 4.081 Å and 138.5°. Such layers are stacked along the a-axis directions, generating ladder-shaped 1D channels that are resided by anions and guest solvent molecules (Fig. S8†). On the other hand, for compound 5 (Fig. 4b), the intermolecular interactions are more interesting. Besides the intermolecular π_py⋯π_py (d₁ = 3.666 Å at 100 K), the cation {Co^II-HS(Me₂tpa)–pyrene^Sq–Sq–Co^II-HS(Me₂tpa)}²⁺ shows two-fold C_py–H⋯π_py (d₂) and C_py–H⋯π_pyrene (d₃) interactions. At 100 K, the d₂ distance and angle are 4.030 Å and 139.5°, and those of d₃ are 3.734 Å and 171.5°, respectively. This 2D layer stacks in the ABCABC mode via weak inter-layer van der Waals interactions, resulting in the formation of irregular parallelogram channels that encapsulate anions and solvent molecules (Fig. S9†).

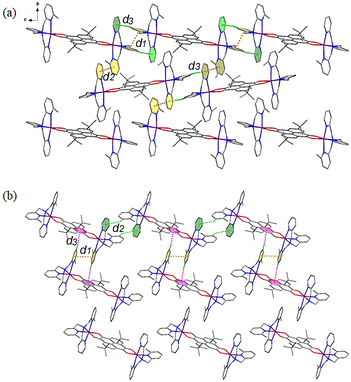Fig. 4 Perspective view of the intermolecular interactions between the cationic species in compounds 4 (a) and 5 (b).

Magnetic properties

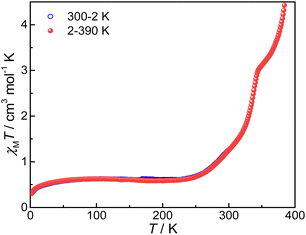
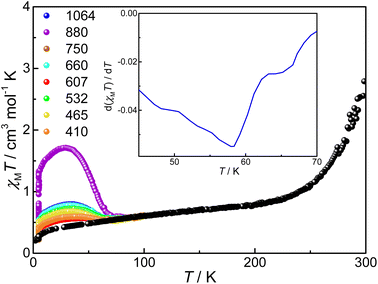
Magnetic susceptibilities of compound 3 were measured on a SQUID magnetometer in the temperature range of 300–2–390 K; the sample was cooled from 300 K to 2 K and then heated to 390 K (Fig. 5).

Fig. 5 χ _M T versus T plot for compound 3. Applied field: 5000 Oe.

The χ_MT value is 1.23 cm³ mol⁻¹ K at 300 K, much lower than those of 4 and 5 (5.62 and 5.52 cm³ mol⁻¹ K, respectively, vide infra). Without a good grasp of the χ_MT value of the pure {Co^II-HS–pyrene^Sq–Sq–Co^II-HS} state, accurate determination of the HS-Co^II–Sq/LS-Co^III–Cat fraction is not feasible. Nevertheless, given the close resemblance among compounds 3, 4, and 5, we deduce that the HS-Co^II–Sq fraction is more than half if the χ_MT values of 4 and 5 are treated as references for the {Co^II-HS–pyrene^Sq–Sq–Co^II-HS} state. Upon lowering temperature, the χ_MT value gradually decreases and attains a value of 0.55 cm³ mol⁻¹ K and 0.54 cm³ mol⁻¹ K at 200 K and 30 K, respectively. The non-zero χ_MT value at temperatures below 200 K most likely comes from a small, trapped fraction of HS-Co^II–Sq and temperature independent paramagnetism (TIP) of Co^III, as commonly seen for other VT cobalt–dioxolene complexes.^32,33,57 In the heating cycle, compound 3 undergoes an incomplete and reversible VT transition between 2 and 300 K. When the temperature exceeds 300 K, the sample begins to lose guest solvent molecules (Fig. S10†), and the χ_MT versus T plot shows a point of inflection that is followed by the second-step VT transition. The χ_MT value is 2.99 cm³ mol⁻¹ K at 345 K, which rises abruptly to 4.37 cm³ mol⁻¹ K at 390 K, indicating that the occurrence of VT transition in compound 3 is incomplete. Because the loss of guest solvent molecules ends at approximately 440 K (Fig. S10†), the VT transition in the high-temperature range may be induced by both desolvation and temperature. When we measured back from 390 K to 2 K, the curve did not overlap with that of the heating, which may be caused by the loss of solvent and crystallinity (Fig. S11†).

The magnetic susceptibilities of compounds 4 and 5 were measured in the 2–300 K temperature range and are shown in Fig. 6. At 300 K, the χ_MT values of 4 and 5 are 5.62 and 5.52 cm³ mol⁻¹ K, respectively, which are much larger than the expected spin-only value (4.50 cm³ mol⁻¹ K) for two HS-Co^II ions (S = 3/2, 1.875 cm³ mol⁻¹ K) and two organic radicals (S = 1/2, 0.375 cm³ mol⁻¹ K) located on the pyrene bridge,^32,33 implying significant orbital contribution or presence of strong ferromagnetic exchange at room temperature.^58–63 Upon temperature decrease, no VT transition occurs, while instead, the χ_MT value gradually increases to a maximum of 7.96 cm³ mol⁻¹ K at 24 K and 8.87 cm³ mol⁻¹ K at 32 K for 4 and 5, respectively. This could be due to ferromagnetic coupling between the HS-Co^II ions and the pyrene radicals.^{45,46,60–62} The sharp decrease at lower temperature is indicative of magnetic anisotropy (D), depopulation of low-lying excited states and/or intermolecular antiferromagnetic interactions.^63,64 Indeed, the magnetization (M) vs. isothermal field (H) plots show that the M values are 6.76Nμ_B for 4 and 6.32Nμ_B for 5 at 2 K under 7 T field, which indicate the near saturation for two Co(II) ions with effective spin S_eff = 1/2 ^65,66 and two radicals (Fig. S12 and S13†). 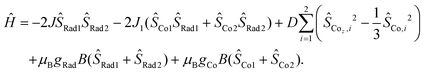To unravel the intramolecular magnetic exchange mechanism, the magnetic susceptibility data of compounds 4 and 5 were fitted using the PHI program⁶⁷ based on the following spin Hamiltonian (eqn (1)):

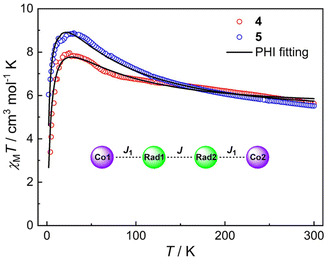Fig. 6 Magnetic susceptibilities of compounds 4 and 5 under an applied field of 5000 Oe. Solid black lines represent the fitting results by the PHI program based on eqn (1). Inset: the magnetic coupling parameters of 4 and 5.

The first two terms in Ĥ correspond to the isotropic radical⋯radical and Co⋯radical magnetic exchanges. Note that the long-range coupling interactions are omitted to avoid overparameterization. The third term describes the axial zero-field splitting parameter. The last two terms represent Zeeman interactions, where μ_B stands for the Bohr magneton, and g_Co and g_Rad correspond to electronic Landé factor for Co^II and pyrene radical, respectively. To avoid overparameterization, g_Rad is fixed to 2.0. Reasonable fits can be obtained with temperature-independent paramagnetism (TIP) introduced and intermolecular magnetic interactions taken into account within the molecular field model (zJ′ term) (Table 1). These results indicate ferromagnetic exchange interactions between HS-Co^II ions and pyrene radicals (J = 27.7 cm⁻¹ and J = 40.9 cm⁻¹ for 4 and 5, respectively) with coupling constants comparable to other Co^II-semiquinonato systems reported in the literature.^60,68,69 Remarkably, semiquinone moieties within the pyrene ligand are strongly ferromagnetically coupled (J = 160.9 cm⁻¹ and J = 161.7 cm⁻¹ for 4 and 5, respectively), which resemble the coupling constant (J = 116 cm⁻¹) in a similar dinuclear Fe^II compound.⁷⁰ Similar coupling parameters were also obtained by Density Functional Theory (DFT) calculations (vide infra), lending credence to the fitting results. The large positive D values are commonly observed for octahedral Co^II ions arising from low-lying excited states and spin–orbit coupling, substantiating the presence of magnetic anisotropy, as suggested by the M ∼ H plots at different temperatures (Fig. S12 and S13†).

Table 1 Parameters obtained from PHI fitting and DFT calculations for compounds 4 and 5

	PHI fitting		DFT calculations
	4	5	4	5
g Co	2.10	2.00	—	—
D (cm^−1)	44.9	20.0	—	—
J (cm^−1)	160.9	161.7	173	181
J 1 (cm^−1)	27.7	40.9	83	83
TIP(cm^3 mol^−1)	6.9 × 10^−4	7.0 × 10^−4	—	—
zJ′ (cm^−1)	−0.06	−0.01	—	—

---

Photomagnetic studies

Photo-induced VT transition experiments were carried out with compound 3. Its ground sample was exposed to 410, 465, 532, 607, 660, 750, 880, and 1064 nm lasers, respectively, until the χ_MT values saturate at 5 K, among which the photoconversion efficiency is the largest under excitation at 880 nm, similar to what we have observed for desolvated compound 2 where bpy was used instead of tpa derivatives (Fig. 7).³⁴ Under laser irradiation at 880 nm at 5 K, the χ_MT value slowly increases from 0.29 to 1.33 cm³ mol⁻¹ K, corresponding to a conversion of 24%. The significant increase of χ_MT value indicates a clear photoinduced VT transition, i.e., intramolecular electron transfer from pyrene^Cat–Cat to LS-Co^III, and simultaneously the electron-gaining LS-Co^III is converted to HS-Co^II. The lower conversion ratio is reasonable and can be attributed to limited penetration of laser due to low sample opacity as well as the significant energy difference between the ground state {Co^III-LS–pyrene^Cat–Cat–Co^III-LS} and photoinduced metastable state {Co^III-LS–pyrene^Cat–Sq–Co^II-HS}.⁴⁶ After the light is switched off and the sample is heated at a rate of 1 K min⁻¹, the χ_MT value firstly increases to 1.71 cm³ mol⁻¹ K at 29 K due to the non-Curie nature of the photoinduced HS-Co^II ion,⁴⁶ and then decreases rapidly, which coincides with the unirradiated curve at 86 K. The T_LIESST value (the critical temperature of light-induced excited spin-state trapping) is estimated to be 55 K according to the d(χ_MT)/dT versus T plot (Fig. 7, inset).

Fig. 7 Photo-induced χ_MT data for the ground sample of compound 3 with different lights at 5 K. Black balls: the χ_MT data of the ground sample of compound 3 on adhesive tape. Inset: d(χ_MT)/dT versus T plot.

Computational study

To compare the metal–ligand interaction strengths between cobalt ions and tpa ligands, ligand field analysis has been carried out using the ab initio ligand field theory implemented in the ORCA computational program.⁷¹ The calculated ligand-field splitting of cobalt ions is shown in Fig. 8. The d-orbital splitting is characteristic of an elongated octahedron with a large splitting of e_g orbitals stemming from the longer bond lengths to the axial tpa nitrogen atoms (Co–N2 and Co–N3) than equatorial ones. Overall, the successive introduction of methyl groups to the tpa ligand results in a slight decrease in the ligand field splitting (10D_q) from 8718 cm⁻¹ to 8289 cm⁻¹, in good agreement with the stronger preference for HS-Co^II upon introducing the steric demanding methyl group. The mutual repulsion between d electrons is quantified by the Racah B parameter, which is calculated to be 1068 cm⁻¹, 1071 cm⁻¹, and 1060 cm⁻¹ for 3, 4, and 5, respectively, suggesting similar metal–ligand bond covalence among the three compounds.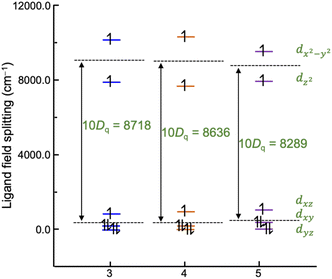

Fig. 8 Comparison of the ligand-field splitting of compounds 3–5. The ligand field parameter 10D_q has been extracted from the AILFT calculations with a CAS (7,5) along with the NEVPT2 correction.

To gain a deeper insight into the electronic structure and magnetic behaviour of the compounds 3–5, a DFT computational study has been performed. As follows from the results of calculations, the ground state of compound 3 is presented by the diamagnetic {Co^III-LS(tpa)–pyrene^Cat–Cat–Co^III-LS(tpa)} species (Tables S10 and S11†). The calculated bond lengths in the coordination sites and dioxolene moieties of this state (Fig. S16†) closely reproduce the X-ray structure of compound 3 at 100 K. The electronic state {Co^III-LS(tpa)–pyrene^Cat–Sq–Co^II-HS(tpa)} on the quintet PES is destabilized as compared to the ground state by 2.8 kcal mol⁻¹. According to the spin density distribution (Fig. 9), the unpaired electrons are localized at the cobalt ion and the dioxolene moiety adjacent to this metal centre and interact ferromagnetically (Table S12†). The {Co^II-HS(tpa)–pyrene^Sq–Sq–Co^II-HS(tpa)} electronic state is predicted to have a relative energy of 7.4 kcal mol⁻¹ and is therefore unlikely to form in an accessible temperature range. Therefore, the DFT calculations predict a {Co^III-LS(tpa)–pyrene^Cat–Cat–Co^III-LS(tpa)} ground state with a thermally induced VT transition to the {Co^III-LS(tpa)–pyrene^Cat–Sq–Co^II-HS(tpa)}, consistent with experimental results.

Fig. 9 Spatial structure and spin density distribution (contour value = 0.03 e Å⁻³) of compound 3 in the {Co^III-LS(tpa)–pyrene^Cat–Sq–Co^II-HS(tpa)} (top) and {Co^II-HS(tpa)–pyrene^Sq–Sq–Co^II-HS(tpa)} (bottom) charge distributions, as calculated by the DFT UTPSSh/6-311++G(d,p) method. Hydrogen atoms and counter-ions are omitted for clarity.

Calculations for compound 4 revealed the {Co^III-LS(Metpa)–pyrene^Cat–Cat–Co^III-LS(Metpa)}, {Co^III-LS(Metpa)–pyrene^Cat–Sq–Co^II-HS(Metpa)}, and {Co^II-HS(Metpa)–pyrene^Sq–Sq–Co^II-HS(Metpa)} charge distributions to be approximately isoenergetic (Tables S11 and S12†). However, taking zero-point harmonic vibrations into account results in stabilization of the {Co^II-HS(Metpa)–pyrene^Sq–Sq–Co^II-HS(Metpa)} state due to the entropic term. As thermally induced VT is an entropy-driven process, no VT transition is expected in compound 4, which will exist in the form of {Co^II-HS(Metpa)–pyrene^Sq–Sq–Co^II-HS(Metpa)} electronic structure. The calculated bond lengths in the metal coordination sites of this electromer exceed 2 Å (Fig. S17†) and are consistent with X-ray data at 100 K. Commensurate with the experimental data (vide supra), the estimated values of the J parameters (Tables 1 and S12†) indicate ferromagnetic exchange interactions between the HS-Co^II and semiquinone radical, while spin coupling within the redox-active pyrene ligand bears strong ferromagnetic nature. Magnetic orbital analysis confirmed that unpaired electrons of the HS-Co^II ion and Sq interact ferromagnetically (Fig. S18†). The only antiferromagnetic pathway exhibits a small overlap integral (S_αβ = 0.075) arising from the interactions of d_xz + d_yz orbitals on HS-Co^II and semiquinone π orbital. Close inspection of the magnetic orbitals reveals a symmetry mismatch between the two components. There is no straightforward way to explain the strong ferromagnetic coupling between the two dioxolene halves by magnetic orbital calculations. The pyrene-based tetraoxolene diradical belongs to the type of non-Kekulé delocalized molecules.⁷² For structurally symmetric tetraoxolene diradicals plausible predications can be made according to the distributions of their degenerate nonbonding molecular orbitals (NBMOs).⁷³ Whereas diradicals with disjoint (sharing no atoms in common) NBMOs show no strong spin-state preference,⁷⁴ those with nondisjoint NBMOs usually have a triplet ground state due to less electron repulsion in the triplet state than in the singlet state (electron pairing). The NBMOs of the pyrene^Sq–Sq diradical in 4 and 5 are of nondisjoint type (Fig. S19†), which makes the ferromagnetically coupled spin state (triplet) more favoured.

A subsequent increase in steric bulkiness of the tpa ligand created by methyl groups in the pyridine rings (compound 5) leads to further elongation of the coordination bond distances (Fig. S20†), thus lowering the stability of the electromers {Co^III-LS(Me₂tpa)–pyrene^Cat–Cat–Co^III-LS(Me₂tpa)} and {Co^III-LS(Me₂tpa)–pyrene^Cat–Sq–Co^II-HS(Me₂tpa)} bearing the low-spin metal ions. As a result, the high-spin electronic state {Co^II-HS(Me₂tpa)–pyrene^Sq–Sq–Co^II-HS(Me₂tpa)} corresponds to the ground state of compound 5, and no VT transitions are expected. Variation of the number of methyl substituents in the ancillary ligands does not exert significant impact on the computed J values: ferromagnetic interactions are predicted for the Co^II-HS–Sq1 and Sq1–Sq2 pairs (Table S12†). Similar to the results obtained for 4, analysis of the corresponding orbitals (Fig. S18†) indicates the ferromagnetic nature of the exchange between the HS-Co^II ion and Sq moieties (S_αβ = 0.057 for the major antiferromagnetic pathway).

As in previous works,^33,34,75,76 it can be stated that differences in magnetic behaviors of compounds 3–5 are mostly conditioned by the steric rigidity of the cobalt coordination sites. The latter can be controlled by the number of methyl groups in the pyridine rings of the tpa ligand. Along with steric factors, electronic effects of the ancillary ligand also take place. As the ancillary ligand changes from tpa (compound 3) to bpy (compound 2) to phen (compound 1),³⁴ the {Co^II–pyrene^Sq–Sq–Co^II}²⁺ and {Co^III–pyrene^Cat–Sq–Co^II}²⁺ electromers decrease in energy relative to the {Co^III–pyrene^Cat–Cat–Co^III}²⁺ electromer (Fig. 10). As a result, one-step, two-step, and partial VT interconversions are possible for {[Co(tpa)]₂(pyrene)}²⁺, {[Co(bpy)]₂(pyrene)}²⁺, and {[Co(phen)]₂(pyrene)}²⁺ species, respectively. Insertion of methyl groups into the tpa ligands, i.e., compounds 4 and 5, hinders the formation of Co–N bonds at shorter lengths, as typically required for the LS-Co^III ion (Fig. S17 and S20†), thus stabilizing the {Co^II–pyrene^Sq–Sq–Co^II}²⁺ charge distributions with no VT transitions. Surprisingly, the type of the ancillary ligands virtually does not affect the magnetic exchange interactions. Nevertheless, a recent study integrating detailed theoretical and experimental results has shown that the exchange in Co(II)–semiquinonate systems is not simply ferromagnetic or antiferromagnetic in nature and contains significant contributions from spin–orbit coupling.²⁷

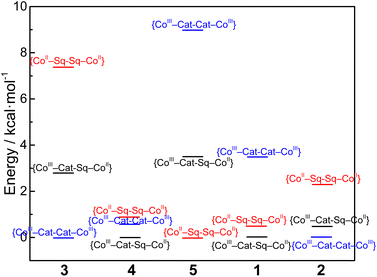Fig. 10 Plots of relative energies calculated for compounds 1–5 with different charge distributions (no entropic considerations).

Conclusion

To conclude, three dinuclear cobalt–tetraoxolene compounds with ancillary tpa-type ligands have been synthesized and characterized. Variable-temperature magnetic susceptibility and single-crystal X-ray diffraction measurements indicate that modulating the steric hindrance of ancillary ligands by variations in the number of methyl groups can manipulate the charge distribution and magnetic properties of the studied compounds. Compound 3 exhibits incomplete VT transition in the high temperature range, whereas compounds 4 and 5 retain the electronic structures of {Co^II-HS-pyrene^Sq–Sq-Co^II-HS} in the entire measured temperature range. Remarkably, 4 and 5 exhibit significant ferromagnetic coupling interactions arising from the magnetic coupling between Co^II and semiquinone radical together with the strong magnetic interaction between the two dioxolene halves. Theoretical calculations were carried out to rationalize the above observations, revealing that successive introduction of methyl substituents can increase the steric rigidity of the cobalt coordination sites, which stabilizes the {Co^II-HS-pyrene^Sq–Sq-Co^II-HS} state both sterically and electronically. This in turn alters the energetic order and gap among the different electronic states, which results in distinct magnetic behaviors. Comparison between compounds with spiro-conjugated tetraoxolene ligands³³ and those in the present work implies the pivotal role of the bridging redox-active ligand in the nature and strength of the exchange interactions, which indirectly affects the relative stabilities of the electromers. Strong ferromagnetic spin coupling in pyrene compounds likely arises from efficient electronic communication of polycyclic π-conjugated system of the redox-active ligand that stabilizes the {Co^II–pyrene^Sq–Sq–Co^II}²⁺ charge distribution. In the case of compounds with tetraoxolene comprising a spiro linker, the electronic coupling is virtually absent, which does not offer additional stabilization of the electromers bearing non-interacting semiquinone moieties. On the other hand, diradicals featuring the triplet group state represent a popular research frontier in molecular magnetism. The pyrene-based ligand possesses diradicaloid feature with strong ferromagnetic coupling and such systems can potentially serve as single-molecule magnets. The present work offers new chemical insights beyond the scope of valence tautomerism alone and lays a solid foundation for future application of π-conjugated redox-active ligands in designing magnetically switchable systems with molecular precision.

Experimental

Materials and methods

All reagents were purchased from commercial sources and used without further purification. Elemental analyses of C, H, and N were performed on a EUROVECTER EA3000 analyzer. Thermogravimetric analysis (TGA) was carried out from 318 to 1073 K on a Hitachi TG-DTA 7200 instrument with a heating rate of 10 K min⁻¹ under N₂ flow. Fourier transform infrared (FT-IR) spectra were measured on a Thermo IS5 FT-IR spectrometer with KBr pellets in the range of 4000–400 cm⁻¹. Solid-state UV-Vis spectra were measured on a TU-1901 dual-beam UV-visible spectrophotometer with BaSO₄ as the reference in the range of 200–800 nm. We noted that both compounds were highly air sensitive and hence all the solution characterization was carried out under nitrogen. UV-vis spectra in CH₃CN at a concentration of 1 mM were recorded on a TU-1901 dual-beam UV-visible spectrophotometer in the range of 450–900 nm.

Single-crystal X-ray diffraction

Single-crystal X-ray diffraction (SCXRD) data of 3–5 were collected on a Rigaku Oxford XtaLAB PRO diffractometer with Mo Kα radiation at different temperatures. All structures were solved by direct methods and further refined by full-matrix least-squares techniques on F² with the SHELXT package.⁷⁷ Non-H atoms were refined anisotropically, and all H atoms were generated geometrically and refined isotropically. The single crystal of 3 was sealed in a capillary containing mother liquor for structural determination. Attempts to define all highly disordered solvent molecules in 3–5 were unsuccessful, so the reflection contributions of highly disordered solvent molecules were removed using SQUEEZE embedded in PLATON.⁷⁸

Magnetic measurements

Variable-temperature magnetic susceptibilities were measured on a Quantum Design MPMS XL7 magnetometer under a magnetic field of 5000 Oe in the temperature range of 300–2–390 K (2–300 K for compounds 4 and 5) with a sweeping rate of 2 K min⁻¹. The crystals of 3–5 are, respectively, sealed in an NMR tube with the mother liquor for magnetic measurements. Photomagnetic experiments were performed for ca. 4 mg of freshly made compound 3 adhered to commercial Scotch tape. In terms of the LIESST effect, the sample was exposed to 410, 465, 532, 607, 660, 750, 880, and 1064 nm lasers with the power at the sample surface adjusted to 18 mW cm⁻² at 5 K until the χ_MT value reached a constant, and then the light was switched off and the magnetic susceptibilities were collected with the temperature increasing at 1 K min⁻¹.

Ab initio AILFT calculations

Ab initio calculations were performed using the ORCA quantum chemistry software version 4.2.1.⁷⁹ A state average-CASSCF (Complete Active Space Self-Consistent Field) method^80–82 with an active space composed of seven active electrons in five active d-orbitals (CAS (7,5)) along with the implemented Ab Initio Ligand Field Theory (AILFT) module was employed to analyze the local ligand field. With this active space, all 10 quartet and 40 doublet states were computed in the configuration interaction procedure. The def2-TZVP basis set is employed on the metal ion and def2-SVP for the rest of the atoms.⁸³ On top of the converged CASSCF wave function, NEVPT2 (n-electron valence state perturbation theory) calculations were performed to account for dynamic correlation effects.^84–87 Since the AILFT is restricted to monomeric systems, one of the Co(II) centers has been replaced by Zn(II).

Density functional theory (DFT) calculations

The DFT calculations were performed using the Gaussian 16 (Revision A.03) program package with the UTPSSh functional^88,89 and the standard 6-311++G(d,p) basis set including diffuse and polarization functions on all atoms. This methodology was shown to provide a good reproduction of the energetic characteristics and magnetic properties of magnetically bistable transition metal compounds,^90–92 in particular cobalt compounds with redox-active ligands.^33,34,47,75 As calculated (Mulliken, Lowdin, NBO, Hirshfeld, and AIM) charges do not provide reliable conclusions about the oxidation state of the central ion in compounds with redox-active ligands,⁹³ the charge distributions of compounds 3–5 were assigned to the corresponding electronic states on the basis of spin density distribution and analysis of the bond lengths. It has been earlier demonstrated^{33,34,47,75,93} that calculations of cationic structures of such types of compounds had led to the significant underestimation of energies of the low-spin electromers. Therefore, the calculations have been performed with inclusion into the computational scheme of outer-sphere counter-ions. The stationary points on the potential energy surfaces were localized by full geometry optimization with calculation of force constants and were checked for the stabilities of the DFT wavefunction. The estimation of exchange coupling parameter J (in cm⁻¹) was carried out by calculation of all possible charge distributions in the framework of the “broken symmetry” (BS) formalism⁹⁴ with the use of the generalized spin-projection method developed by Yamaguchi.⁹⁵ For the search of the BS states, the Gaussian 16 procedure (Guess = Fragment = N) has been employed. This technique implies a possibility to assume spin states and signs along with charges for separate parts of a molecule on the stage of generation of the initial guess. To investigate the nature of the Co^II-HS–Sq exchange interactions, the analysis of the corresponding orbitals in the electromers {Co^III-LS(Metpa)–pyrene^Cat–Sq–Co^II-HS(Metpa)} and {Co^III-LS(Me₂tpa)–pyrene^Cat–Sq–Co^II-HS(Me₂tpa)} was performed. Structural visualizations were prepared using the ChemCraft software [Chemcraft: version 1.7, 2013. https://www.chemcraftprog.com.] with the calculated atomic coordinates as input parameters.

Synthesis of {[Co(tpa)]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂·2C₆H₅CH₃ (3)

A toluene solution (5 mL) of Co₂(CO)₈ (0.0239 g, 0.07 mmol) was placed at the bottom of a test tube, and then a dichloromethane solution (5 mL) of tpa (0.0407 g, 0.14 mmol) and pyreneQ₂ (0.0262 g, 0.07 mmol) was carefully layered on the top under a N₂ atmosphere. After two days dark-brown plate-shaped crystals were formed. The crystals were removed and immersed in a 5 ml vial containing the mother liquor. Then the crystals were rinsed several times with the mother liquor, and the floating unreacted flocs were removed from the solution using a pipette, leaving the crystals at the bottom (yield: 17.5 mg, ∼36% based on Co₂(CO)₈). Note that fresh samples were transferred to filter paper for 1–2 minutes to absorb extra solvent and then characterized. Desolvated samples obtained by heating the as-synthesized crystals in a vacuum at 80 °C for 6 h were used for elemental analysis. IR (cm⁻¹) for 3: 440, 468, 502, 554, 614, 645, 698, 731, 747, 768, 844, 883, 905, 1051, 1131, 1147, 1276, 1287, 1311, 1362, 1402, 1442, 1462, 1481, 1564, 1606, 1667, 1882. Elemental analysis (%) for desolvated sample of 3: C: 57.39; H: 4.34; N: 8.03. Calcd for C₆₈H₅₈Co₄N₈O₁₂: C: 57.72; H: 4.13; N: 7.92.

Synthesis of {[Co(Metpa)]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂ (4)

A chloroform solution (5 mL) of Co₂(CO)₈ (0.0239 g, 0.07 mmol) was placed at the bottom of a test tube, and then a buffer layer of chloroform/toluene (v/v = 1 : 4, 5 mL) was added. A toluene solution (5 mL) of Metpa (0.0426 g, 0.14 mmol) and pyreneQ₂ (0.0262 g, 0.07 mmol) was carefully layered on the top under a N₂ atmosphere. After about one week dark-brown plate-shaped crystals were formed. The crystals were purified by the same procedure as that of 3 (yield: 10.3 mg, ∼18.4% based on Co₂(CO)₈). Note that fresh samples were transferred to filter paper for 1–2 minutes to absorb extra solvent and then characterized. Desolvated samples obtained by heating the as-synthesized crystals in a vacuum at 80 °C for 6 h were used for elemental analysis. IR (cm⁻¹) for 4: 468, 491, 555, 645, 669, 697, 767, 842, 858, 891, 964, 979, 1021, 1052, 1099, 1157, 1239, 1282, 1366, 1441, 1467, 1574, 1606, 1885. Elemental analysis (%) for desolvated sample of 4: C: 58.34; H: 4.31; N: 7.40. Calcd for C₇₀H₆₂Co₄N₈O₁₂: C: 58.26; H: 4.33; N: 7.76.

Synthesis of {[Co(Me₂tpa)]₂(pyrene^Sq–Sq)}[Co(CO)₄]₂·2CHCl₃ (5)

A chloroform solution (5 mL) of Co₂(CO)₈ (0.0239 g, 0.07 mmol) was put at the bottom of a test tube, and then a buffer layer of chloroform/toluene (v/v = 1 : 4, 5 mL) was added. A toluene solution (5 mL) of Me₂tpa (0.0446 g, 0.14 mmol) and pyreneQ₂ (0.0262 g, 0.07 mmol) was carefully layered on the top under a N₂ atmosphere. After about one week dark-brown plate-shaped crystals were formed. The crystals were purified by the same procedure as that of 3 (yield: 14.2 mg, ∼25% based on Co₂(CO)₈). Note that fresh samples were transferred to filter paper for 1–2 minutes to absorb extra solvent and then characterized. Desolvated samples obtained by heating the as-synthesized crystals in a vacuum at 80 °C for 6 h were used for elemental analysis. IR (cm⁻¹) for 5: 466, 483, 555, 646, 669, 697, 736, 786, 843, 890, 1020, 1053, 1098, 1164, 1240, 1271, 1283, 1368, 1441, 1467, 1537, 1576, 1606, 1885. Elemental analysis (%) for the desolvated sample of 5: C: 58.97; H: 4.41; N: 7.85. Calcd for C₇₂H₆₆Co₄N₈O₁₂: C: 58.78; H: 4.52; N: 7.62.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grants 92061106, 21971016, and 22101021). The technical support from the staff at the Analysis & Testing Center, Beijing Institute of Technology is also appreciated A. A. S. thanks the Ministry of Science and Higher Education of the Russian Federation (State assignment in the field of scientific activity, project No. FENW-2023-0017).

References

1. S. Sanvito, Molecular spintronics, Chem. Soc. Rev., 2011, 40, 3336–3355.
2. T. Tezgerevska, K. G. Alley and C. Boskovic, Valence tautomerism in metal complexes: Stimulated and reversible intramolecular electron transfer between metal centers and organic ligands, Coord. Chem. Rev., 2014, 268, 23–40.
3. A. Lannes, Y. Suffren, J. B. Tommasino, R. Chiriac, F. Toche, L. Khrouz, F. Molton, C. Duboc, I. Kieffer, J.-L. Hazemann, C. Reber, A. Hauser and D. Luneau, Room temperature magnetic switchability assisted by hysteretic valence tautomerism in a layered two-dimensional manganese-radical coordination framework, J. Am. Chem. Soc., 2016, 138, 16493–16501.
4. M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu, H. J. Shepherd and A. Bousseksou, Switchable molecule-based materials for micro- and nanoscale actuating applications: Achievements and prospects, Coord. Chem. Rev., 2016, 308, 395–408.
5. O. Sato, Dynamic molecular crystals with switchable physical properties, Nat. Chem., 2016, 8, 644–656.
6. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Molecular-scale electronics: from concept to function, Chem. Rev., 2016, 116, 4318–4440.
7. J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Molecular magnetism, quo vadis? A historical perspective from a coordination chemist viewpoint, Coord. Chem. Rev., 2017, 339, 17–103.
8. R. M. Buchanan and C. G. Pierpont, Tautomeric catecholate-semiquinone interconversion via metal-ligand electron transfer. Structural, spectral, and magnetic properties of (3,5-di-tert-butylcatecholato)(3,5-di-tert-butylsemiquinone) (bipyridyl)cobalt(III), a complex containing mixed-valence organic ligands, J. Am. Chem. Soc., 1980, 102, 4951–4957.
9. D. M. Adams and D. N. Hendrickson, Pulsed laser photolysis and thermodynamics studies of intramolecular electron transfer in valence tautomeric cobalt o-quinone complexes, J. Am. Chem. Soc., 1996, 118, 11515–11528.
10. C. Roux, D. M. Adams, J. P. Itié, A. Polian, D. N. Hendrickson and M. Verdaguer, Pressure-induced valence tautomerism in cobalt o-quinone complexes: An X-ray absorption study of the low-spin [Co^III(3,5-DTBSQ)(3,5-DTBCat)(phen)] to high-spin [Co^II(3,5-DTBSQ)₂(phen)] interconversion, Inorg. Chem., 1996, 35, 2846–2852.
11. R. D. Schmidt, D. A. Shultz, J. D. Martin and P. D. Boyle, Goldilocks effect in magnetic bistability: Remote substituent modulation and lattice control of photoinduced valence tautomerism and light-induced thermal hysteresis, J. Am. Chem. Soc., 2010, 132, 6261–6273.
12. O. Sato, S. Hayami, Z.-Z. Gu, K. Takahashi, R. Nakajima and A. Fujishima, Photo-induced reverse valence tautomerism in a metastable Co compound, Chem. Phys. Lett., 2002, 355, 169–174.
13. B. Li, F.-L. Yang, J. Tao, O. Sato, R.-B. Huang and L.-S. Zheng, The effects of pressure on valence tautomeric transitions of dinuclear cobalt complexes, Chem. Commun., 2008, 45, 6019–6021.
14. A. Droghetti and S. Sanvito, Electric field control of valence tautomeric interconversion in cobalt dioxolene, Phys. Rev. Lett., 2011, 107, 047201.
15. I. N. Markevtsev, M. P. Monakhov, V. V. Platonov, A. S. Mischenko, A. K. Zvezdin, M. P. Bubnov, G. A. Abakumov and V. K. Cherkasov, Field-induced spin phase transition in a Co complex, J. Magn. Magn. Mater., 2006, 300, e407–e410.
16. G. Poneti, M. Mannini, L. Sorace, P. Sainctavit, M.-A. Arrio, E. Otero, J. C. Cezar and A. Dei, Soft-X-ray-induced redox isomerism in a cobalt dioxolene complex, Angew. Chem., Int. Ed., 2010, 49, 1954–1957.
17. T. M. Francisco, W. J. Gee, H. J. Shepherd, M. R. Warren, D. A. Shultz, P. R. Raithby and C. B. Pinheiro, Hard X-ray-induced valence tautomeric interconversion in cobalt-o-dioxolene complexes, J. Phys. Chem. Lett., 2017, 8, 4774–4778.
18. A. Caneschi and A. Dei, Valence tautomerism in a o-Benzoquinone Adduct of a Tetraazamacrocycle Complex of manganese, Angew. Chem., Int. Ed., 1998, 37, 3005–3007.
19. N. Shaikh, S. Goswami, A. Panja, X.-Y. Wang, S. Gao, R. J. Butcher and P. Banerjee, New route to the mixed valence semiquinone-catecholate based mononuclear Fe^III and catecholate based dinuclear Mn^III complexes: First experimental evidence of valence tautomerism in an iron complex, Inorg. Chem., 2004, 43, 5908–5918.
20. E. Evangelio and D. Ruiz-Molina, Valence tautomerism: New challenges for electroactive ligands, Eur. J. Inorg. Chem., 2005, 2005, 2957–2971.
21. A. Panja, Unusual structural features in tetrabromocatechol-chelated dinuclear manganese(III) complex: Synthesis, electrochemistry and thermally induced valence tautomerism, Inorg. Chem. Commun., 2012, 24, 140–143.
22. I. Ando, T. Fukuishi, K. Ujimoto and H. Kurihara, Oxidation states and redox behavior of ruthenium ammine complexes with redox-active dioxolene ligands, Inorg. Chim. Acta, 2012, 390, 47–52.
23. M. K. Biswas, S. C. Patra, A. N. Maity, S.-C. Ke, N. D. Adhikary and P. Ghosh, Electronic structures of ruthenium and osmium complexes of 9,10-phenanthrenequinone, Inorg. Chem., 2012, 51, 6687–6699.
24. M. K. Biswas, S. C. Patra, A. N. Maity, S.-C. Ke, T. Weyhermüller and P. Ghosh, 9,10-Phenanthrenesemiquinone radical complexes of ruthenium(III), osmium(III) and rhodium(III) and redox series, Dalton Trans., 2013, 42, 6538–6552.
25. J. Bendix and K. M. Clark, Delocalization and valence tautomerism in vanadium tris(iminosemiquinone) complexes, Angew. Chem., Int. Ed., 2016, 55, 2748–2752.
26. N. Kundu, M. Maity, P. B. Chatterjee, S. J. Teat, A. Endo and M. Chaudhury, Reporting a unique example of electronic bistability observed in the form of valence tautomerism with a copper(II) helicate of a redox-active nitrogenous heterocyclic ligand, J. Am. Chem. Soc., 2011, 133, 20104–20107.
27. G. K. Gransbury, M.-E. Boulon, R. A. Mole, R. W. Gable, B. Moubaraki, K. S. Murray, L. Sorace, A. Soncini and C. Boskovic, Single-ion anisotropy and exchange coupling in cobalt(II)-radical complexes: insights from magnetic and ab initio studies, Chem. Sci., 2019, 10, 8855–8871.
28. S. Demir, I. R. Jeon, J. R. Long and T. D. Harris, Radical ligand-containing single-molecule magnets, Coord. Chem. Rev., 2015, 289–290, 149–176.
29. C. A. Gould, E. Mu, V. Vieru, L. E. Darago, K. Chakarawet, M. I. Gonzalez, S. Demir and J. R. Long, Substituent effects on exchange coupling and magnetic relaxation in 2,2′-bipyrimidine radical-bridged dilanthanide complexes, J. Am. Chem. Soc., 2020, 142, 21197–21209.
30. A. Beni, A. Dei, S. Laschi, M. Rizzitano and L. Sorace, Tuning the charge distribution and photoswitchable properties of cobalt–dioxolene complexes by using molecular techniques, Chem. – Eur. J., 2008, 14, 1804–1813.
31. K. G. Alley, G. Poneti, J. B. Aitken, R. K. Hocking, B. Moubaraki, K. S. Murray, B. F. Abrahams, H. H. Harris, L. Sorace and C. Boskovic, A two-step valence tautomeric transition in a dinuclear cobalt complex, Inorg. Chem., 2012, 51, 3944–3946.
32. K. G. Alley, G. Poneti, P. S. D. Robinson, A. Nafady, B. Moubaraki, J. B. Aitken, S. C. Drew, C. Ritchie, B. F. Abrahams, R. K. Hocking, K. S. Murray, A. M. Bond, H. H. Harris, L. Sorace and C. Boskovic, Redox activity and two-step valence tautomerism in a family of dinuclear cobalt complexes with a spiroconjugated bis(dioxolene) ligand, J. Am. Chem. Soc., 2013, 135, 8304–8323.
33. G. K. Gransbury, B. N. Livesay, J. T. Janetzki, M. A. Hay, R. W. Gable, M. P. Shores, A. Starikova and C. Boskovic, Understanding the origin of one- or two-step valence tautomeric transitions in bis(dioxolene)-bridged dinuclear cobalt complexes, J. Am. Chem. Soc., 2020, 142, 10692–10704.
34. J.-P. Wang, W.-T. Liu, M. Yu, X.-Y. Ji, J.-L. Liu, M.-Z. Chi, A. A. Starikova and J. Tao, One-step versus two-step valence tautomeric transitions in tetraoxolene-bridged dinuclear cobalt compounds, Inorg. Chem., 2022, 61, 4428–4441.
35. R. M. Buchanan, B. J. Fitzgerald and C. G. Pierpont, Semiquinone radical anion coordination to divalent cobalt and nickel. Structural features of the bis(3,5-di-tert-butyl-1,2-semiquinone)cobalt(II) tetramer, Inorg. Chem., 1979, 18, 3439–3444.
36. M. Zhou and L. Andrews, Matrix Infrared spectra and density functional calculations of Co(CO)_x⁻ (x = 1, 2, 3, 4) anions, J. Phys. Chem. A, 1998, 102, 10250–10257.
37. C. E. Plečnik, S. Liu, J. Liu, X. Chen, E. A. Meyers and S. G. Shore, Lanthanide−transition-metal carbonyl complexes. 1. syntheses and structures of ytterbium(II) solvent-separated ion pairs and isocarbonyl polymeric arrays of tetracarbonylcobaltate, Inorg. Chem., 2002, 41, 4936–4943.
38. A. Panja, N. C. Jana, A. Bauzá, A. Frontera and C. Mathonière, Solvent-triggered cis/trans isomerism in cobalt dioxolene chemistry: Distinguishing effects of packing on valence tautomerism, Inorg. Chem., 2016, 55, 8331–8340.
39. A. Panja and A. Frontera, Valence-tautomerism-driven aromatic nucleophilic substitution in cobalt-bound tetrabromocatecholate ligands – Influence of positive charge at the ligand backbone on phenoxazinone synthase activity, Eur. J. Inorg. Chem., 2018, 2018, 924–931.
40. E. Evangelio, D. N. Hendrickson and D. Ruiz-Molina, Intramolecular electron transfer in the mixed-valence [Co(3,5-DTBCat)(3,5-DTBSQ)(bpy)] complex: Beyond valence tautomerism, Inorg. Chim. Acta, 2008, 361, 3403–3409.
41. J. Dai, S. Kanegawa, Z. Li, S. Kang and O. Sato, A Switchable Complex ligand exhibiting photoinduced valence tautomerism, Eur. J. Inorg. Chem., 2013, 2013, 4150–4153.
42. W.-Q. Cheng, G.-L. Li, R. Zhang, Z.-H. Ni, W.-F. Wang and O. Sato, Synthesis, crystal structure and valence tautomerism of a 4,4′-bipyridine-bridged one-dimensional chiral cobalt complex, J. Mol. Struct., 2015, 1087, 68–72.
43. G.-L. Li, S. Kanegawa, Z.-S. Yao, S.-Q. Su, S.-Q. Wu, Y.-G. Huang, S. Kang and O. Sato, Influence of intermolecular interactions on valence tautomeric behaviors in two polymorphic dinuclear cobalt complexes, Chem. – Eur. J., 2016, 22, 17130–17135.
44. O. Drath, R. W. Gable, G. Poneti, L. Sorace and C. Boskovic, One dimensional chain and ribbon cobalt–dioxolene coordination polymers: A new valence tautomeric compound, Cryst. Growth Des., 2017, 17, 3156–3162.
45. A. Madadi, M. Itazaki, R. W. Gable, B. Moubaraki, K. S. Murray and C. Boskovic, Electronic lability in a dinuclear cobalt–bis(dioxolene) complex, Eur. J. Inorg. Chem., 2015, 2015, 4991–4995.
46. O. Drath, R. W. Gable, B. Moubaraki, K. S. Murray, G. Poneti, L. Sorace and C. Boskovic, Valence tautomerism in one-dimensional coordination polymers, Inorg. Chem., 2016, 55, 4141–4151.
47. T. Tezgerevska, E. Rousset, R. W. Gable, G. N. L. Jameson, E. C. Sañudo, A. Starikova and C. Boskovic, Valence tautomerism and spin crossover in pyridinophane–cobalt–dioxolene complexes: an experimental and computational study, Dalton Trans., 2019, 48, 11674–11689.
48. C. G. Pierpont, Studies on charge distribution and valence tautomerism in transition metal complexes of catecholate and semiquinonate ligands, Coord. Chem. Rev., 2001, 216–217, 99–125.
49. Y. Mulyana, A. Nafady, A. Mukherjee, R. Bircher, B. Moubaraki, K. S. Murray, A. M. Bond, B. F. Abrahams and C. Boskovic, New family of ferric spin clusters incorporating redox-active ortho-dioxolene ligands, Inorg. Chem., 2009, 48, 7765–7781.
50. R. Ketkaew, Y. Tantirungrotechai, P. Harding, G. Chastanet, P. Guionneau, M. Marchivie and D. J. Harding, OctaDist: a tool for calculating distortion parameters in spin crossover and coordination complexes, Dalton Trans., 2021, 50, 1086–1096.
51. O. Carugo, C. B. Castellani, K. Djinović and M. Rizzi, Ligands derived from o-benzoquinone: statistical correlation between oxidation state and structural features, J. Chem. Soc., Dalton Trans., 1992, 5, 837–841.
52. S. N. Brown, Metrical oxidation states of 2-amidophenoxide and catecholate ligands: Structural signatures of metal–ligand π bonding in potentially noninnocent ligands, Inorg. Chem., 2012, 51, 1251–1260.
53. N. E. Brese and M. O'Keeffe, Bond-valence parameters for solids, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
54. G. J. Palenik, Bond valence sums in coordination chemistry using oxidation state independent R₀ values. A simple method for calculating the oxidation state of manganese in complexes containing only Mn−O bonds, Inorg. Chem., 1997, 36, 4888–4890.
55. R. M. Wood and G. J. Palenik, Bond Valence sums in coordination chemistry. A simple method for calculating the oxidation state of cobalt in complexes containing only Co−O bonds, Inorg. Chem., 1998, 37, 4149–4151.
56. I. Imaz, D. Maspoch, C. Rodríguez-Blanco, J. M. Pérez-Falcón, J. Campo and D. Ruiz-Molina, Valence-tautomeric metal–organic nanoparticles, Angew. Chem., Int. Ed., 2008, 47, 1857–1860.
57. M. Affronte, A. Beni, A. Dei and L. Sorace, Valence tautomerism interconversion triggers transition to stable charge distribution in solid polymeric cobalt–polyoxolene complexes, Dalton Trans., 2007, 45, 5253–5259.
58. M. Graf, G. Wolmershäuser, H. Kelm, S. Demeschko, F. Meyer and H.-J. Krüger, Temperature-induced spin-transition in a low-spin cobalt(II) semiquinonate complex, Angew. Chem., Int. Ed., 2010, 49, 950–953.
59. S.-Q. Su, S.-Q. Wu, M. L. Baker, P. Bencok, N. Azuma, Y. Miyazaki, M. Nakano, S. Kang, Y. Shiota, K. Yoshizawa, S. Kanegawa and O. Sato, Quenching and restoration of orbital angular momentum through a dynamic bond in a Cobalt(II) complex, J. Am. Chem. Soc., 2020, 142, 11434–11441.
60. A. Caneschi, A. Dei, D. Gatteschi and V. Tangoulis, Antiferromagnetic coupling in a six-coordinate high spin cobalt(II)−semiquinonato complex, Inorg. Chem., 2002, 41, 3508–3512.
61. I. A. Gass, S. Tewary, A. Nafady, N. F. Chilton, C. J. Gartshore, M. Asadi, D. W. Lupton, B. Moubaraki, A. M. Bond, J. F. Boas, S.-X. Guo, G. Rajaraman and K. S. Murray, Observation of ferromagnetic exchange, spin crossover, reductively induced oxidation, and field-induced slow magnetic relaxation in monomeric cobalt nitroxides, Inorg. Chem., 2013, 52, 7557–7572.
62. A. Witt, F. W. Heinemann, S. Sproules and M. M. Khusniyarov, Modulation of magnetic properties at room temperature: coordination-induced valence tautomerism in a cobalt dioxolene complex, Chem. – Eur. J., 2014, 20, 11149–11162.
63. Y. Cui, Y. Xu, X. Liu, Y. Li, B.-L. Wang, Y. Dong, W. Li and S. Lei, Field-induced single-ion magnetic behavior in two mononuclear cobalt(II) complexes, Chem. – Asian J., 2019, 14, 2620–2628.
64. J.-H. Wang, J.-W. Dai, Z.-Y. Li and M. Yamashita, Strong antiferromagnetic coupling of the cobalt(II)–semiquinone radical in a dinuclear complex with 2,2′-bipyrimidine ligands, New J. Chem., 2020, 44, 8471–8476.
65. J. M. Herrera, A. Bleuzen, Y. Dromzée, M. Julve, F. Lloret and M. Verdaguer, Crystal structures and magnetic properties of two octacyanotungstate(IV) and (V)-cobalt(II) three-dimensional bimetallic frameworks, Inorg. Chem., 2003, 42, 7052–7059.
66. X. Lin, J. Tao, R.-B. Huang and L.-S. Zheng, Ferromagnetic interactions in a bis(μ-end-on azido)cobalt(II) linear trimer, Inorg. Chem. Commun., 2009, 12, 154–156.
67. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.
68. A. G. Starikov, A. A. Starikova, M. G. Chegerev, S. M. Aldoshin, A. V. Metelitsa and V. I. Minkin, Spin-state-switching rearrangements of bis(dioxolene)-bridged CrCo complexes: A DFT study, Eur. J. Inorg. Chem., 2021, 2021, 4113–4121.
69. G. Novitchi, S. Shova and C. Train, Investigation by chemical substitution within 2p-3d-4f clusters of the cobalt(II) role in the magnetic behavior of [vdCoLn]₂ (vd = Verdazyl Radical), Inorg. Chem., 2022, 61, 17037–17048.
70. H. Cui, Z.-B. Hu, C. Chen, H. Ruan, Y. Fang, L. Zhang, Y. Zhao, G. Tan, Y. Song and X. Wang, A high-spin diradical dianion and its bridged chemically switchable single-molecule magnet, Chem. Sci., 2021, 12, 9998–10004.
71. S. K. Singh, J. Eng, M. Atanasov and F. Neese, Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective, Coord. Chem. Rev., 2017, 344, 2–25.
72. M. Abe, Diradicals, Chem. Rev., 2013, 113, 7011–7088.
73. H. Ikeda, Y. Matsui, I. Akimoto, K.-I. Kan'no and K. Mizuno, X-ray-triggered thermoluminescence and density functional theory characterization of a gem-diphenyltrimethylenemethane biradical, Aust. J. Chem., 2010, 63, 1342–1347.
74. E. R. Davidson and W. T. Borden, Some aspects of the potential surface for singlet trimethylenemethane, J. Am. Chem. Soc., 1977, 99, 2053–2060.
75. A. A. Starikova, M. G. Chegerev, A. G. Starikov and V. I. Minkin, A DFT computational study of the magnetic behaviour of cobalt dioxolene complexes of tetraazamacrocyclic ligands, Comput. Theor. Chem., 2018, 1124, 15–22.
76. M. G. Chegerev and A. A. Starikova, Electronic lability of quinonoid-bridged dinuclear 3d-metal complexes with tetradentate N-donor bases, Eur. J. Inorg. Chem., 2021, 2021, 2684–2695.
77. A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, A new tool for crystal structure determination and refinement, J. Appl. Crystallogr., 1999, 32, 115–119.
78. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
79. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
80. B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173.
81. S. Per, H. Anders, R. Björn and L. Bernard, A comparison of the super-CI and the Newton-Raphson Scheme in the complete active space SCF method, Phys. Scr., 1980, 21, 323.
82. P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, The complete active space SCF (CASSCF) method in a newton–raphson formulation with application to the HNO molecule, J. Chem. Phys., 1981, 74, 2384.
83. D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-electron scalar relativistic basis sets for third-row tansition metal atoms, J. Chem. Theor. Comput., 2008, 4, 908–919.
84. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory., J. Chem. Phys., 2001, 114, 10252–10264.
85. C. Angeli, R. Cimiraglia and J.-P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350, 297–305.
86. C. Angeli and R. Cimiraglia, Multireference perturbation CI IV. selection procedure for one-electron properties, Theor. Chem. Acc., 2001, 105, 259–264.
87. C. Angeli, R. Cimiraglia and J.-P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117, 9138–9153.
88. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids, Phys. Rev. Lett., 2003, 91, 146401.
89. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119, 12129–12137.
90. A. Bannwarth, S. O. Schmidt, G. Peters, F. D. Sönnichsen, W. Thimm, R. Herges and F. Tuczek, Fe^III Spin-crossover complexes with photoisomerizable ligands: experimental and theoretical studies on the ligand-driven light-induced spin change effect, Eur. J. Inorg. Chem., 2012, 2012, 2776–2783.
91. J. Cirera and F. Paesani, Theoretical prediction of spin-crossover temperatures in ligand-driven light-induced spin change systems, Inorg. Chem., 2012, 51, 8194–8201.
92. J. Cirera, M. Via-Nadal and E. Ruiz, Benchmarking Density functional methods for calculation of state energies of first row spin-crossover molecules, Inorg. Chem., 2018, 57, 14097–14105.
93. V. I. Minkin, A. G. Starikov and A. A. Starikova, Computational insight into magnetic behavior and properties of the transition metal complexes with redox-active ligands: a DFT approach, Pure Appl. Chem., 2018, 90, 811–824.
94. L. Noodleman, Valence bond description of antiferromagnetic coupling in transition metal dimers, J. Chem. Phys., 1981, 74, 5737–5743.
95. M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, A general algorithm for calculation of Heisenberg exchange integrals J in multispin systems, Chem. Phys. Lett., 2006, 432, 343–347.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional tables (crystallographic data, bond lengths and angles, parameters of intermolecular interactions and data of theory calculation) and figures (IR spectra, UV-Vis spectra, packing arrangements, TGA plots and other figures) (PDF). CCDC 2224738, 2224741, 2224744, 2287990 and 2158906. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3qi01706k

‡ These authors contributed equally to this work.

---