Halogen bonding between metal-bound I₃⁻ and unbound I₂: the trapped I₂⋯I₃⁻ intermediate in the controlled assembly of copper(I)-based polyiodides

Abstract

Crystallization of [CuI(CNXyl)₃] (1) with I₂ (exhibiting strong halogen bond donor properties), at different molar ratios between the reactants, resulted in a series of (XylNC)Cu^I crystal polyiodides formed along with gradual accumulation of iodine, namely [Cu(I₃)(CNXyl)₃] (two crystalline polymorphs 2^I and 2^II), [Cu(I₃)(CNXyl)₃]·½I₂ (2·½I₂) and [Cu(CNXyl)₃](I₅) (3); all these compounds were studied by X-ray diffractometry. Molecular electrostatic potential (MEP) surface plots were also calculated using density functional theory (DFT) for isolated molecules of 2 and I₂, showing electrophilic and nucleophilic sites. Halogen bonding in 2·½I₂ was additionally elucidated for both crystal and cluster models, including combined quantum theory of atoms-in-molecules (QTAIM) and one-electron potential (OEP) projections. For model clusters, DFT energetic analysis, quantum theory of atoms-in-molecules, combined with the noncovalent interaction index plot (QTAIM/NCIplot), natural bond orbital (NBO) donor–acceptor charge transfer analysis, and Wiberg bond index (WBI) analysis were used. In the structure of 2·½I₂, the presence of an I₂⋯I₃⁻ halogen bonded linkage gives a key toward the understanding of the precise mechanism for the generation of I₅⁻ (and then I₈²⁻) ligands from I₂ and metal-coordinated I₃⁻.

---

1. Introduction

Polyhalides are a subject of intensive studies,^1–3 in view of their broad application as, for instance, electrolytes for batteries and dye sensitized solar cells,^1,2 mildly selective oxidants for organic synthesis,² and synthons for the construction of metal–organic frameworks.⁴ In particular, polyhalides (especially polyiodides) of various transition metals are utilized for the design of coordination networks⁴ and fabrication of semiconductive materials;⁵ halogen–halogen closed-shell bonding interactions have been widely studied theoretically.^6–12

The ability to generate polyatomic anions, namely polyiodide anions, is a characteristic feature of iodine as an element.^1,3,13,14 In the formulation of polyiodides I_mⁿ⁻, there is always a problem whether I_mⁿ⁻ can be considered as a single entity or as a composite of the building blocks I₂, I⁻, and I₃⁻, linked by noncovalent interaction(s), including halogen bonding (abbreviated as HaB).

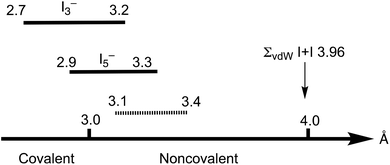
The Cambridge Structural Database (CSD) analysis of the I–I distances in such systems³ revealed a continuum in the distribution of iodine–iodine separations, spanning from approx. 2.7 Å (the distances that are typical of the I₂ molecule) to those larger than 4 Å (Bondi van der Waals radii¹⁵ sum ∑(I + I) 3.96 Å; Rowland van der Waals radii^16,17 sum ∑(I + I) 4.06 Å); values larger than 4 Å exceed the optimistic expectations for noncovalent interactions (Fig. 1). As follows from the recent CSD analysis,¹³ the iodine–iodine covalent bond for the most widespread and studied polyiodide, I₃⁻, is in the range of 2.7–3.2 Å, while it is 2.9–3.3 Å for the less common I₅⁻.

Fig. 1 Iodine–iodine distances in polyiodides.

Starting from approximately 3.2 Å and further, up to ca. 4 Å, lies the region of various noncovalent interactions. Although the interval 3.2–4.0 Å is specific for I⋯I intermolecular bonds, the accurate assignment of contacts in the 3.0–3.6 Å range is often rather ambiguous,³ and the area 3.1–3.4 Å is the so-called “no man's land” with an overlap of covalent and noncovalent contacts.¹³ This large variability of iodine–iodine interactions hampers a clear assignment of I–I contacts to primary or secondary bonding (in other words HaB) thus blurring, in turn, the accurate difference between covalent and noncovalent contacts.

In the framework of our ongoing project focused on noncovalent interactions in organometallics, in particular HaB including iodine and polyiodides,^18,19 we studied the [CuI(CNXyl)₃] cocrystals with such a strong iodine-based HaB donor (exhibiting two 180°-directing σ-hole donor sites) as I₂.²⁰ We obtained a series of (XylNC)Cu^I polyiodides, whose structural features are outlined in section 2.2. In this series, the change in the composition of the product occurs in accordance with the change in the ratio of the reagents. A transition from a coordinated triiodide to a semicoordinated pentaiodide via an intermediate I₈²⁻ was observed and studied in detail. In one of these structures (section 2.2.2), we identified a I₂⋯I₃⁻ entity present between metal-bound I₃⁻ and unbound I₂. Despite all difficulties in the identification of noncovalent bonding in I₂⋯I₃⁻ outlined above, our experimental and appropriate theoretical data explicitly confirmed the existence of HaB in the I₂⋯I₃⁻ linkage and, thus, our results indicate that we trapped the hitherto unreported I₂⋯I₃⁻ intermediate in the generation of pentaiodide. All our findings are consequently detailed in the sections that follow.

2. Results and discussion

2.1. Cocrystal growth

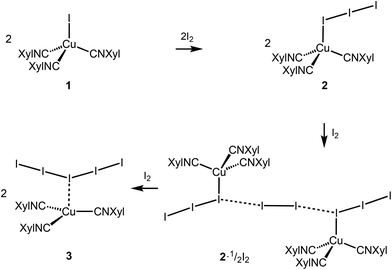
Copper complexes (first of all, Cu^II species) demonstrate very rich and versatile polyiodide chemistry, reviewed in ref. 4, while copper(I) polyiodides are far less studied and all these reports are briefly surveyed in the ESI (section S2.1†).

The copper(I) iodide complexes [CuI(CNXyl)₃] (1) and [Cu(I)₃(CNXyl)₃] (2) chosen for this study were prepared by known procedures.²¹ The solvent-dependent crystallization of 2 yielded 2^I (from CH₂Cl₂) and 2^II (from CH₂Cl₂/MeNO₂, 1 : 1 v/v) polymorphic forms (Scheme 1); the structure of 2^II is identical to that obtained previously.²¹ Crystallization of 2^I with I₂ (2 : 1 molar ratio) in CH₂Cl₂ afforded crystals of the adduct [Cu(I₃)(CNXyl)₃]·½I₂ (2·½I₂). The latter was also obtained when 1 was crystallized with a 1.5-fold excess of I₂ in CH₂Cl₂. Crystallization of 1 with a 3-fold excess of I₂ from CH₂Cl₂ furnished [Cu(CNXyl)₃](I)₅ (3); these crystals were also obtained when 2 was crystallized with I₂ (1 : 2 molar ratio) in CH₂Cl₂. The indicated crystallizations gave crystals suitable for XRD studies, which were performed for all these species.

Scheme 1 Synthetic scheme and compound numbering.

2.2. X-ray diffraction studies

2.2.1. Structures of 1 and 2^I–II. The XRD structures of 1 and 2^I–II (Fig. 2) are not unusual and they are considered in details in the ESI (sections S2.2 and S2.3†).

Fig. 2 View of the molecular packing for 2^I and 2^II (CCDC no 1841442), demonstrating a short I⋯I contact in polymorph 2^I (top panel) and Cu⋯I contact in polymorph 2^II (bottom panel).

2.2.2. Crystal and molecular structures of 2·½I₂. The structure of this adduct is central in the context of this work and we discuss it in more details with particular focus on I₃⁻⋯I₂ short contacts. Appropriate theoretical calculations of the HaB situation in this structure are detailed later in section 2.3.

The structural parameters of complex 2 in 2·½I₂ (τ₄ = 0.85 ²²) are close to those in 2^II: ∠(Cu1–I1–I2) 94.399(15)° and ∠(I1–I2–I3) 178.502(17)°. The bond distances within the I₃⁻ ligand (I1–I2 2.8204(4), I2–I3 3.0520(5) Å) are normal and agree well with those in the previously reported structures of 2^II and 2·CHI₃.²¹ The Cu1–I1 bond length is 2.9015(7) Å, what is somehow longer than those in other structures apparently because of the effect of HaB, which is discussed later.

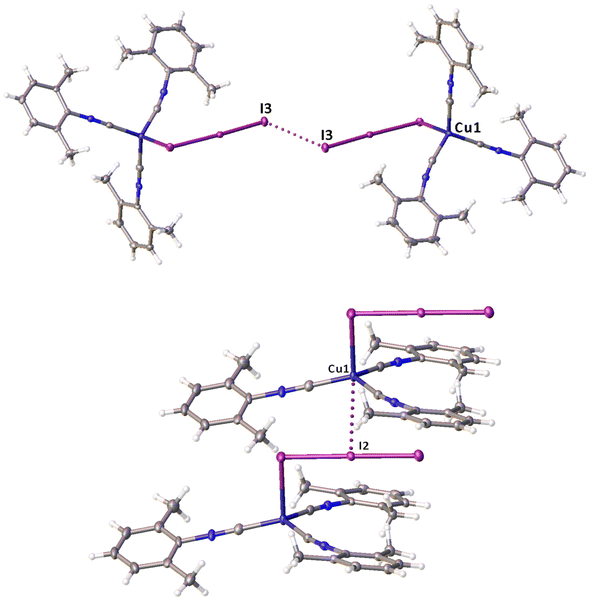
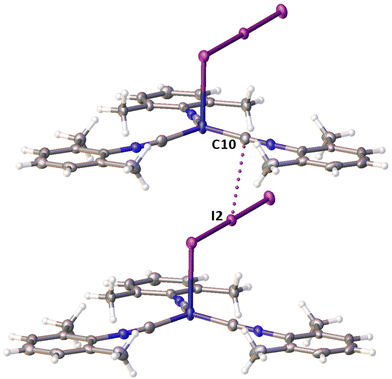
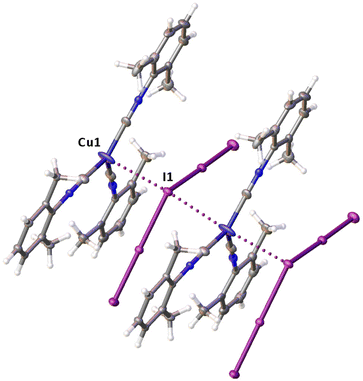
Noncovalent contacts (Table S3†) include Type-I halogen–halogen²³ interactions (induced by packing effects) between the I3 atoms from different molecules (Fig. 3), and the lone pair–π-hole interaction between the I2 atom and the π-system (C10) of the isocyano groups (Fig. 4). Intermolecular contact I4⋯I1 between I₂ and I₃⁻ moieties fulfill the IUPAC criteria for the identification of Type-II halogen–halogen²³ interactions (or, in other words, the true HaB) (d(I1–I4) = 3.3658(6) Å vs. Bondi ∑(I + I) = 3.96 Å, ∠(I4–I4–I1) = 174.23(2)°).²³ This is the shortest contact between iodine atoms in the structure of 2·½I₂. This interatomic separation (3.3658(6) Å) lies on the borderline between the values typical for I₅⁻ (2.9–3.3 Å)¹³ and the area of the “no man's land” range (3.1–3.4 Å;¹³Fig. 1) with an overlap of covalent and noncovalent contacts.

Fig. 3 Two types of I⋯I contacts in the structure of 2·½I₂.

Fig. 4 The I⋯C contact in the structure of 2·½I₂.

If we consider only covalent and Type-II noncovalent interactions and put aside packing-driven Type-I contacts, the observed HaB-based adduct I₃⁻⋯I₂⋯I₃⁻ is relevant to the metal-bound dianion I₈²⁻. The Type-I contact I3⋯I3 is longer than the true I1⋯I4 HaB and it is certainly weaker than the HaB; this conclusion was confirmed by the analysis of the computation results (section 2.4). Considering all these, one can formulate the supramolecular organization of 2·½I₂ as the 1D-chain built by the copper(I)-ligated I₈²⁻; a similar outstretched Z-shaped polyiodide geometry has been previously reported.²⁴

On moving from the structures of 2^I–II to that of 2·½I₂, the Cu–I bond is further lengthened (by approx. 0.18 and 0.06 Å, correspondingly, for two polymorphs) and the coordination polyhedron is more deviated from the tetrahedral geometry (the Δ∑(∠C–Cu–C) was increased by 13–17 and 1°, respectively). The weak contact Cu⋯I in 2·½I₂, as compared to that in 2^II, became shorter (by 0.06 Å). As compared to 2^I–II, in 2·½I₂, an additional I₂ molecule appeared and a new HaB contact I4⋯I1 between the I₂ and I₃⁻ ligand was identified (3.3658(6) Å).

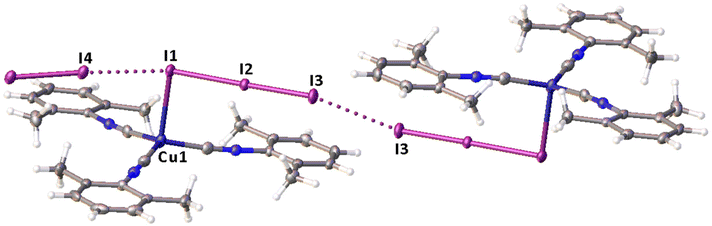
Remarkably, although many examples of different polyiodide sequences, including the I₈²⁻ moiety, are known, predominantly they belong to the category of metal-free polyiodides. To prove the novelty of our findings, namely the noncovalent nature of the I₂⋯I₃⁻ linkage, we performed the CSD search of metal-bound polyiodides exhibiting structures similar to 2·½I₂, namely those built by I₂ and coordinated I₃⁻via relatively short (3.1–3.4 Å) I₂⋯I₃⁻ contacts. In the nickel(II) triiodide complex (KUGBAS,¹⁹R_w 2.20%) the ligated I₃⁻ forms a relatively short I⋯I (3.3503(6) Å; N_c = d/(∑_vdW Bondi) = 0.85) contact with I₂. The other iodine center of I₂ forms a slightly longer contact (3.4547(8) Å; N_c 0.87) with another complex via the terminal uncomplexed iodine of the I₃⁻ ligand (Fig. 5) and, hence, the supramolecular organization of KUGBAS includes the extended chains {(μ-I¹,I³-I₃⁻)·(μ-I¹,I²-I₂)}_n. Notably, the I₂ molecule behaves as a bifunctional HaB donor toward two accepting I₃⁻ moieties. No detailed discussion of the supramolecular organization of the structure was provided in the corresponding article.¹⁹

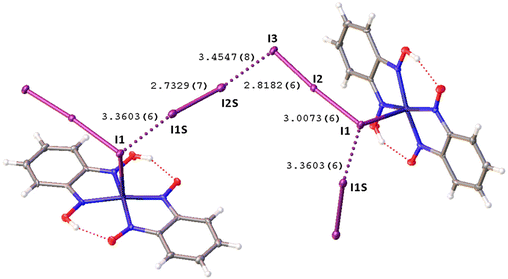Fig. 5 View of the supramolecular organization of KUGBAS bearing coordinated I₃⁻; HaBs are given by dotted lines, interatomic distances (Å) are given for selected iodine–iodine bonds and contacts.

Another structure, [Ru(I₃)(ClI₂)(CNBu-t)₄]·I₂ (ZAGTEJ),²⁵ contains both I₃⁻ and ClI₂⁻ ligands and it includes the {I₃⁻·I₂·ClI₂⁻} moieties featuring rather strong I⋯Cl (3.056(9) Å) and I⋯I (3.309(5) Å) noncovalent interactions (Fig. S5†). However, the R_w (13%) value is too high and this prevents an accurate examination of its geometric characteristics and complicates appropriate computational works. The same group studied the structures of cocrystals of Ru^II–halide species with molecular halogens and identified the polyhalide (X⋯X′₂)_n and the oligomeric X⋯X′₂⋯X linkages involving the halide X ligands.²⁶

We also performed CSD search for the known uncoordinated I₅⁻ and I₈⁻ systems, although these systems were only relevant but not strictly related to our observations (see the ESI, section S1†). In summary, the analysis of structural parameters of I₅⁻ from CSD indicates that I₅⁻ demonstrates a noticeable difference in the covalent distances for the terminal (2.7–3.0 Å) and internal (3.0–3.4 Å) I–I bonds. At the same time, the extreme cases of unsymmetric L-shaped I₅⁻ can be considered as the supramolecular adducts {I₃⁻·I₂}.

The bond length analysis for the I₈²⁻ CSD structures allowed the formulation of these structures as the associates {I₃⁻⋯I₂⋯I₃⁻}, where interatomic distances within the structural units (namely, I₂ and I₃⁻) are attributed to covalent bonding (2.74–3.12 Å) and the shortest separations between these units are in the 3.27–3.44 Å range, i.e. lie in the “no man's land” region (3.1–3.4 Å) (see the Introduction section).

A very similar bond length distribution was observed for the fragment {I₃⁻⋯I₂⋯I₃⁻} in 2·½I₂ (see above), therefore coordinated {I₃⁻·I₂·I₃⁻} and uncomplexed (for details of the latter see the ESI†) moieties demonstrate certain structural similarities. However, this work is the first where coordinated polyiodides {I₃⁻⋯I₂⋯I₃⁻} were detected in the solid state and structurally characterized.

2.2.3. Structure of 3. The crystal structure of this ionic complex consists of cation [Cu(CNXyl)₃]⁺ and the pentaiodide anion, I₅⁻ (Fig. 6; detailed consideration of this structure is given in the ESI, section 2.5†). The complex exhibits a trigonal planar geometry, while the pentaiodide anion exhibit a V-shaped geometry that is typical for I₅⁻.^27–29 On moving from 2·½I₂ to 3, the d(Cu–I) bond length is drastically lengthened (by 0.49 Å) that results in the cationic planar (∑(∠C–Cu–C) 360°) complex [Cu(CNXyl)₃]⁺, which forms two equivalent Cu⋯I semicoordination bonds (3.42515(11) Å) with two I₅⁻ anions.

Fig. 6 Semicoordinative Cu⋯I contacts (dotted lines) in the structure of 3.

2.3 Theoretical DFT study of halogen bonding in the structure of 2·½I₂

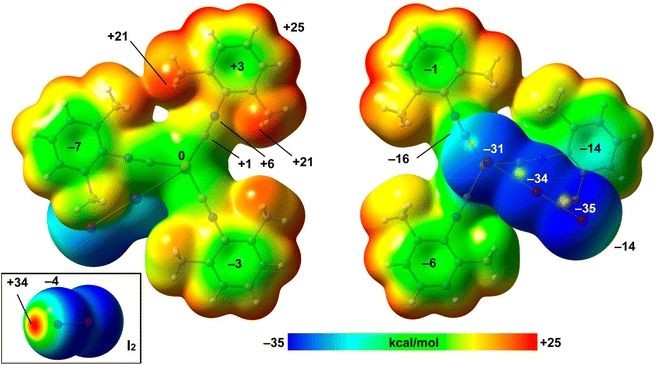
The structure of the 2·½I₂ adduct was studied in detail with a particular focus on the HaB.

2.3.1. MEP surfaces. Initially, we computed the molecular electrostatic potential (MEP) surfaces of 2 and I₂ to rationalize the assemblies observed in the solid-state structure of 2·½I₂. To this end, it is relevant to investigate the MEP differences among the negative belts of the three iodide atoms of the coordinated I₃⁻, since the I₂ molecule bridges the I1-atom (Cu^I-coordinated iodine) from one molecule to the I3-atom (I₃⁻-end), see Fig. 5. Moreover, it is also relevant to study the electronic nature of the Cu-coordinated isocyanide group to rationalize the I⋯C contact represented in Fig. 4. Fig. 7 shows the MEP surfaces using two different orientations of complex 2 (I₃⁻ ligand down and up). The MEP maximum is located at the aromatic H-atoms (+25 kcal mol⁻¹) followed by the methyl groups (+21 kcal mol⁻¹). The MEP minimum is located at the coordinated I₃⁻ ligand, as expected, being the belt of the most nucleophilic uncoordinated I-end (−35 kcal mol⁻¹). Interestingly, the MEP values on the extension of both I–I bonds of the I₃⁻ ligand are significantly less negative (−16 and −14 kcal mol⁻¹) than those at the electron belts (−31 to −35 kcal mol⁻¹). This explains the directionality of the I₂⋯I₃⁻ interaction observed in the X-ray structure of 2·½I₂, where the I₂ σ-holes point to the negative belts. Moreover, the small differences between the negative belts of the three I-atoms in I₃ also suggests that the HaB preference observed in 2·½I₂ is likely modulated by other interactions in the X-ray structure.

Fig. 7 MEP surfaces (two opposite orientations) of compound 2 and iodine (bottom-left). The energies at selected points of the surfaces are given in kcal mol⁻¹. Isosurface 0.001 a.u. the PBE-D3/def2-TZVP level of theory.

The MEP values over the aromatic rings are in general modest, ranging from slightly positive (+3 kcal mol⁻¹) to slightly negative (−7 kcal mol⁻¹). The MEP value at the Cu-atom is zero and over the C≡N bonds is slightly positive, thus disclosing that the I⋯C interaction is favored electrostatically. The MEP surface of I₂ is also included in Fig. 7 (bottom-left), evidencing a deep σ-hole (+34 kcal mol⁻¹) and a very modest negative belt (−4 kcal mol⁻¹).

2.3.2. Crystal and cluster model theoretical calculations. To have more arguments supporting the occurrence of I₃⁻⋯I₂ HaB in the structure of 2·½I₂, we conducted an additional theoretical study that utilized the crystal model and the calculations were performed under time-demanding, the so-called “true”, periodic conditions. For relevant calculations we also used a model cluster approach, which proved to be useful for molecular crystals.

Thus, to closely interrogate the systems and to verify the nature of the I⋯I interactions, we performed DFT calculations under periodic boundary conditions (the crystal model, PBE³⁰-D3^31,32 level of theory and DZVP-MOLOPT-SR-GTH³³ bases within the Gaussian/plane wave (GPW)³⁴ methodology in CP2K) for the 2·½I₂ crystal. In addition, we also performed calculations for the isolated heterotrimeric (2)₂·(I₂) cluster exhibiting the I⋯I interactions, namely gas-phase DFT calculations (the cluster model, PBE³⁰-D3³¹ level of theory and def2-TZVP^35,36 basis) in Gaussian 09, both approaches are based on the experimentally determined coordinates.

The QTAIM analysis for the crystal and cluster models demonstrated the presence of bond critical points (3, −1) (BCP) between the iodine centers of I₂ and the iodine atoms of the I₃ group (Table 1). Consideration of the negative values of the BCP sign(λ₂)ρ(r) values indicates the attractive nature of the I⋯I interaction,³⁷ although with some covalence contribution in view of the negative energy density and the balance of the Lagrangian kinetic energy G(r) and the potential energy density V(r) (−G(r)/V(r) < 1) on the corresponding critical points.³⁸ Remarkably, the sign(λ₂)ρ(r), ∇²ρ(r), G(r), and V(r) values are almost the same for the crystal and cluster models.

Table 1 Parameters in (3, −1) bond critical points (the electron density with sign of λ₂ sign(λ₂)ρ(r) in e bohr⁻³, Laplacian of electron density ∇²ρ(r) in e bohr⁻⁵, the local electronic energy density H_b, local electronic potential energy density V(r), and local electronic kinetic energy density G(r) in hartrees per bohr³) corresponding to the I⋯I XBs in the cluster and crystal models

Model	sign(λ2)ρ(r)	∇^2ρ(r)	V(r)	G(r)	H b
Cluster	−0.0216	0.0373	−0.0101	0.0097	−0.0004
Crystal	−0.0205	0.0371	−0.0093	0.0091	−0.0002

---

One-electron potential analysis. Laplacian of electron density ∇²ρ(r),³⁹ and electron localization function (ELF)⁴⁰ are widely used to locate the electron concentration regions such as, for instance, electron pairs. A quantity, closely related to the Laplacian of the electron density, is the one-electron potential (OEP),^41,42 which accurately represents the potential governing the motion of a single electron in an electron system⁴³ and, therefore, OEP serves as a useful tool for the localization of electron pairs. Hamilton⁴⁴ (for relevant recent work see ref. 45) has revealed topological similarities between ∇²ρ(r) and OEP, as reflected in the valence shell structures of light atoms. Differences arise in heavy atoms (elements beyond the third row) for which the valence shells are generally missing in ∇²ρ(r), but are present in OEP. Notably, the OEP approach is better than the ELF method since the former does not directly depend on wavefunction, and its results can be compared for calculations with and without pseudopotentials using electron density function (EDF) for core electrons.⁴⁶

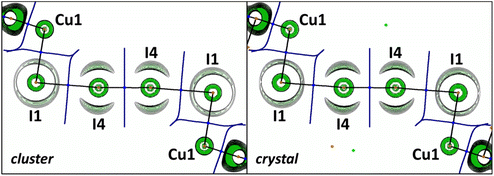
The OEP value can be used, instead of the Laplacian distribution, to reveal noncovalent features of polyiodide chains in the studied crystal. Similar to the previous reports,^20,47 we observed a toroidal shape of the OEP around the I4 atom covalently bound to the neighboring (also I4) atoms (Fig. 8). This shape is specific for an anisotropic electron density distribution around the nucleus: the nucleophilic region of the valence shell is localized at the equator, while the electrophilic region is located at the continuation of the covalent σ-bond. For the I1⋯I4 halogen bond the nucleophilic and electrophilic regions of the iodine atoms in the crystal agree well with those obtained in the gas-phase cluster model.

Fig. 8 OEP distribution in the plane of the polyiodide chain computed for cluster (left) and crystal (right) models of [Cu(I₃)(CNXyl)₃]·½I₂. Contour lines are drawn at OEP values from −0.4 to 0.0 with 0.02 step, the color range is from green (−0.4) to white (0.0). QTAIM ρ(r) topological pale brown nuclear (3, −3), blue bond (3, −1), orange ring (3, +1), and light green cage (3, +3), critical points are drawn with black bond paths and dark blue interatomic surface projections.

The electrostatic potential features of the observed interactions. Interatomic surfaces in gradient fields of electron density (ρ) and electrostatic potential (φ) allow the identification of the atomic ρ- and φ-basins, respectively. The former defines chemically bonded atoms, while the latter determines electrically neutral atomic fragments within a common electron–nuclear system. The analysis of the superposition of these gradient fields provides useful information about the electrostatic potential features of atomic interactions along the bond paths.

Fig. 9 shows that the ρ- and φ-basin boundaries of atoms coincided completely within the bonds in I2 and I3⁻. In the case of I1⋯I4 noncovalent interactions, the boundary of the φ-basin of I4 spreads through the region of the ρ-basin of I1. This suggests that some fraction of the electrons belonging to I1 in the triiodide anion is attracted to the I4 nucleus in the I₂ molecule. According to ref. 23, this is a conventional case for Type-II HaB. Thus, consideration of mutual arrangement of the zero-flux boundaries of ρ- and φ-basins provides the specific information about the kind of I⋯I interactions in the polyiodide chain in the studied crystal.

Fig. 9 Superposition of the electrostatic potential gradient field (orange) and electron density gradient field (grey) in the plane of polyiodide chain for cluster model of [Cu(I₃)(CNXyl)₃]·½I₂. Interatomic surfaces projections are in blue and brown for ρ- and φ-basins respectively. QTAIM ρ(r) topological bond (3, −1) critical points are drawn in dark blue. Type-II halogen bond occurred between the I1 and I4 atoms.

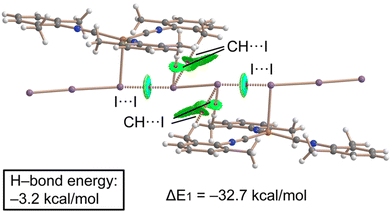
Combined QTAIM/NCIPlot analysis and dimerization energy. In (2)₂·(I₂), each contact is characterized by a CP bond (red sphere) and bond path (dashed bond) interconnecting both I-atoms (Fig. 10), according to the combined QTAIM and NCIplot analyses. The QTAIM values at the bond CP, as discussed earlier in this section, are typical of a noncovalent interaction. The QTAIM/NCIPlot analysis of the HaB heterotrimer also evidences the formation of secondary CH⋯I interactions involving the methyl groups of the XylNC ligands and the negative belts of the I₂ molecule. The dimerization energy is large (ΔE₁ = −32.7 kcal mol⁻¹) in line with the strong electrophilicity of the I₂ molecule and strong nucleophilicity of the I₃⁻ ligand, as demonstrated by the MEP surface analysis. We also estimated the strength of the CH⋯I H-bonds using the V_r predictor,⁴⁸ which is −3.2 kcal mol⁻¹ for the four contacts altogether, thus confirming the dominant role of the HaB, in line with the blue color of the HaB RDG isosurface compared to the green color of the HBs.

Fig. 10 Combined QTAIM/NCIPlot analyses of (2)₂·(I₂). The dimerization energies computed at the PBE-D3/def2-TZVP are given. Only intermolecular contacts are represented by bond CPs and RDG isosurfaces.

The same calculations were performed for the (2)₂ dimers with other interactions extracted from the 2·½I₂ adduct, for details see the ESI.†

NBO and WBI analyses in a natural atomic partitioning scheme. To further study the σ-hole nature of the HaB in (2)₂·(I₂), we performed the natural bond orbital (NBO) analysis in the natural atomic partitioning scheme focusing on the second order perturbation analysis.⁴⁹ This computational tool is very convenient to study donor–acceptor interactions from an orbital viewpoint.⁵⁰ Interestingly, we have found two symmetrically equivalent electron transfer from lone pair (LP) orbitals located at the coordinated iodine atoms and to the σ antibonding orbital of the I₂ molecule (σ*) with a concomitant stabilization energy of E⁽²⁾ = 9.04 kcal mol⁻¹ (Fig. 11) for each LP(I) → σ*(I–I) interaction, thus confirming the σ-hole HaB nature of the I₃⁻⋯I₂⋯I₃⁻ contacts.

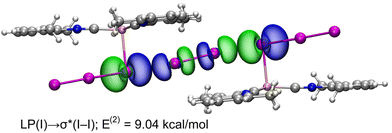Fig. 11 Representation of the NBOs corresponding to the LP → σ* donor–acceptor interactions in (2)₂·(I₂). The isosurface used for the MOs is 0.006 a.u.

The Wiberg bond index (WBIs)^51–53 was also calculated using the natural atomic partitioning scheme for the I⋯I interaction in the cluster model. The WBI is 0.16 and therefore the interaction can be considered as noncovalent but with some covalence.

Therefore, different approaches—QTAIM and OEP analyses in both crystal and cluster modes, combining QTAIM/NCIplot analysis, dimerization energies, NBO charge transfer and Wiberg indexes—clearly demonstrate the noncovalent nature of the I1⋯I4 contact, although with some covalence contribution. The analysis of electrostatic potential features of this contact allowed this attribution to Type-II²³ HaB. The I₈²⁻ units in the structure of 2·½I₂ can be interpreted as the associates {I₃⁻·I₂·I₃⁻}, where one uncomplexed I₂ and two I₃⁻ ligands are linked by relatively strong HaBs.

3. Conclusions

The addition of various amounts of molecular iodine to the copper(I) isocyanide complex [CuI(CNXyl)₃] provided a series of copper polyiodide complexes and their adducts, namely [Cu(I₃)(CNXyl)₃], [Cu(I₃)(CNXyl)₃]·½I₂, and [Cu(CNXyl)₃](I₅) (Scheme 1). In this series, we observed a change in the ligation of (poly)iodide anions to the metal site—a gradual transition from the coordinated iodide, to triiodide, followed by the generation and stabilization of the semicoordinated pentaiodide. In a more general sense, we performed the systematic and controllable creation of metal complexes exhibiting increasing polyiodide content. Polyiodide containing products, like our systems, are often encountered unexpectedly or unreliably and often relegated to the ESI† of other publications. This work, in contrast, demonstrates the controllable design of metal complexes with increasing polyiodide content based on the molar ratio of iodine added during the synthesis. This stepwise addition of iodine to give polyiodides allows the systematic assembly of a HaB network centered on Cu^I-bound I₃⁻. We consider this as an advancement in the supramolecular assembly of coordination complexes in pursuit of other (e.g., analyzed in recent reviews^54,55) higher dimensional networks utilizing HaB. Considering that polyiodide-based materials have been utilized in e.g. photovoltaics,⁵⁶ the result of this work may be useful for controllable assembly of appropriate polyiodides.

In the [Cu(I₃)(CNXyl)₃]·½I₂ cocrystals, we identified the unit I₈²⁻, which is built by two coordinated triiodides connected by a bridge of molecular iodine via relatively strong HaBs. The geometric parameters of the HaB indicate its intermediate position between covalent bonds and noncovalent interactions. Theoretical methods within different approaches—QTAIM analysis in both crystal and cluster modes and OEP analysis along with the analysis of Wiberg indexes—allowed the conclusion on the predominantly noncovalent character of HaB, although with small contribution of the covalence. Therefore, the I₈²⁻ units in the structure of [Cu(I₃)(CNXyl)₃]·½I₂ can be treated as the associates {I₃⁻·I₂·I₃⁻}, where I₂ molecules and I₃⁻ ligands are linked by relatively strong HaBs.

The most significant findings of this study include the trapping of the halogen-bonded compound [Cu(I₃)(CNXyl)₃]·½I₂, and a theoretical confirmation of the noncovalent nature of the I₂⋯I₃⁻ linkage (as an intermediate between the I₃⁻ ligand to I₅⁻ or I₈²⁻ ligands) in this structure. This entity includes Type-II halogen–halogen interactions or, in other words, the true HaB, and it represents a previously unreported intermediate in the generation of metal-bound pentaiodides. In the context of this study, it is noteworthy that although the studies focused on the bonding situation in polyiodides are known,^1–3,6–12 no single work is devoted to metal-involving transformation of I₈²⁻ to I₅⁻. We believe that the identification of HaB in the structure of [Cu(I₃)(CNXyl)₃]·½I₂ is key to understanding the precise mechanism of the generation of I₅⁻ (and then I₈²⁻) ligands from I₂ and metal-coordinated I₃⁻. The HaB-involving mechanism is predictable but has not yet received experimental support; our finding provides the means for its confirmation.

4. Experimental section

4.1. Reagents, instrumentation, and methods

Solvents, CuI, xylylisocyanide, and I₂ were obtained from commercial sources and used as received, apart from CH₂Cl₂, which was purified by the conventional distillation over CaCl₂. The complexes [CuI(CNXyl)₃] (1) and [Cu(I)₃(CNXyl)₃] (2) were prepared by the known procedures,²¹ while the synthesis of 3 is given below in this section.

The high-resolution mass spectra were obtained on a Bruker micrOTOF spectrometer equipped with an electrospray ionization (ESI) source and MeOH was used as the solvent. The instrument was operated in the positive ion mode using an m/z range of 50–3000. The most intensive peak in the isotopic pattern is reported. Infrared spectra (4000–400 cm⁻¹) were recorded on a Shimadzu IRAffinity-1 FTIR spectrophotometer in KBr pellets. NMR spectra were recorded on Bruker AVANCE III 400 spectrometers in CDCl₃ at ambient temperature (at 400 and 100 MHz for ¹H and ¹³C NMR, respectively). Chemical shifts are given in δ-values [ppm] referenced to the residual signals of the undeuterated solvent (CHCl₃): δ 7.27 (¹H) and 77.0 (¹³C).

4.1.1. Synthesis of 3. Method A. Complex [CuI(CNXyl)₃] (19 mg, 0.03 mmol) and I₂ (17 mg, 0.07 mmol) were dissolved in CH₂Cl₂ at room temperature and left to stand for 30 min. Then the resulting homogeneous brown solution was evaporated at 20–25 °C under reduced pressure (20 mbar) until dryness to give a brown residue of 3. The yield of 3 is 35 mg, 96%.

Method B. A solution of [CuI(CNXyl)₃] (190 mg, 0.3 mmol) was mixed with a saturated solution of I₂ in CH₂Cl₂ (2 mL) and the resulting solution was left for slow evaporation at room temperature to 0.5 mL. The formed brown crystals were separated by decantation and dried in air at room temperature. The yield of 3 is 236 mg, 72%.

The obtained compound is rather unstable and it releases molecular iodine on keeping the sample at room temperature. HRESI⁺, m/z: 325.0774 ([M − I₅ − CNXyl]⁺, calcd 325.0761). FTIR, ν_max (KBr)/cm⁻¹: 2162 s ν(C≡N). ¹H NMR (CDCl₃, δ): 2.53 (s, 6H, CH₃), 7.17 (d, ³J_H,H = 7.5 Hz, 2H, m-H from xylyl), 7.29 (t, ³J_H,H = 7.5 Hz, 1H, p-H from xylyl). ¹³C{¹H} NMR (CDCl₃, δ): 19.12 (CH₃), 125.65 (t, ¹J_C,N = 10.0 Hz, ipso-C from xylyl), 128.14 (m-C from xylyl), 129.92 (o-C from xylyl), 135.69 (p-C from xylyl), 150.99 (broad, C_isocyanide).

4.2. Crystal growth

Crystals of 1 were obtained by slow evaporation of its CH₂Cl₂ solution at RT. Crystals of 2^I were obtained by slow evaporation of a solution of 2 in CH₂Cl₂ at RT. Crystals of 2·½I₂ were grown by the dissolution of a mixture of 2^I and I₂ (molar ratio 2 : 1) in CH₂Cl₂ at RT followed by the slow evaporation of this solution at RT. Crystals of 3 were grown by the dissolution of a mixture of 1 and I₂ (1 : 3 molar ratio) in CH₂Cl₂ at RT followed by slow evaporation of this solution at RT. The crystallization of 1 gives colorless crystals, while 2^I, 2·½I₂, and 3 are brown.

4.3. X-ray diffraction studies

Single-crystal X-ray diffraction experiments were carried out on “Xcalibur”, Eos (1, 2^I, and 3) and “SuperNova” (2·½I₂) diffractometers with monochromated MoKα radiation. Crystals were kept at 100(2) K during data collection. Structures have been solved using ShelXT⁵⁷ (structure solution program using Intrinsic Phasing) and refined by means of the ShelXL⁵⁸ program incorporated into the OLEX2 program package.⁵⁹ Crystallographic details are summarized in Table S1.† CCDC numbers 2211053–2211056 contain the supplementary crystallographic data for this paper.†

4.4. Computational details

Single-point DFT calculations were performed under periodic boundary conditions using the mixed Gaussian/plane-wave (GPW)³⁴ basis set with a 350 Ry and a 50 Ry relative plane-wave cut-offs for the auxiliary grid and the PBE³⁰-D3^31,32 functional and the DZVP-MOLOPT-SR-GTH basis for the crystal (1 × 1 × 1 cell) model [Cu(I₃)(CNXyl)₃]·½I₂ was performed using the CP2K-8.1 program.^33,60–65 The 1.0 × 10⁻⁶ Hartree convergence was achieved for the self-consistent field cycle in the Γ-point approximation. This methodology has been previously used for the study of the related halogen-bonded systems.²¹ The gas-phase study for the heterotrimeric cluster ([Cu(I₃)(CNXyl)₃])₂·(I₂) was performed at the same PBE-D3 level of theory in Gaussian-09⁶⁶ with the def2-TZVP^35,36 basis set. One-electron potential (OEP)^67–69 analysis and the quantum theory of atoms in molecules (QTAIM) analysis^38,70,71 of the electron density as well as analysis of the electrostatic potential and electron density gradient fields⁷² were performed and visualized using Multiwfn 3.8.⁷³ The pseudopotential core areas were modelled using the inner code of Multiwfn 3.8 using electron density function (EDF)⁴⁶ for both OEP and QTAIM analyses. Wiberg bond indexes in the natural atomic partitioning scheme were calculated for cluster models using the GENNBO utility in NBO 7.0⁷⁴ based on 0.47 files generated in Multiwfn 3.8. Other cluster calculations were performed at the PBE³⁶-D3^37,38/def2-TZVP^41,42 level of theory using the Gaussian-16 program⁷⁵ and the X-ray coordinates. The QTAIM/NCIPlot analysis was performed using the AIMAll program.⁷⁶ The MEP calculations were performed at the same level of theory and plotted using the 0.001 a.u. isosurface.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Russian Science Foundation projects 22-13-00078 (experimental part and XRD analysis) and 22-73-00021 (theoretical calculations under periodic conditions and for cluster mode). The QTAIM/NCIPlot calculations were funded by the MICIU/AEI of Spain (project PID2020-115637GB-I00 FEDER funds). Measurements were performed at the Center for Magnetic Resonance, the Center for X-ray Diffraction Studies, the Center for Chemical Analysis and Materials Research, and the Computing Center (all belonging to Saint Petersburg State University). This article is in commemoration of the 300th anniversary of St Petersburg State University's founding.

References

1. P. H. Svensson and L. Kloo, Synthesis, Structure, and Bonding in Polyiodide and Metal Iodide−Iodine Systems, Chem. Rev., 2003, 103, 1649–1684.
2. H. Haller and S. Riedel, Recent Discoveries of Polyhalogen Anions – from Bromine to Fluorine, Z. Anorg. Allg. Chem., 2014, 640, 1281–1291.
3. L. Kloo, in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 233–249.  DOI:10.1016/B978-0-08-097774-4.00109-1.
4. S. A. Adonin, M. N. Sokolov and V. P. Fedin, Polyhalide-bonded metal complexes: Structural diversity in an eclectic class of compounds, Coord. Chem. Rev., 2018, 367, 1–17.
5. J. He, P. Cao, C. Wu, J. Huang, J. Huang, Y. He, L. Yu, M. Zeller, A. D. Hunter and Z. Xu, Highly Polarizable Triiodide Anions (I3−) as Cross-Linkers for Coordination Polymers: Closing the Semiconductive Band Gap, Inorg. Chem., 2015, 54, 6087–6089.
6. G. R. Desiraju and R. Parthasarathy, The nature of halogen.cntdot..cntdot..cntdot.halogen interactions: are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms?, J. Am. Chem. Soc., 1989, 111, 8725–8726.
7. V. G. Tsirelson, P. F. Zhou, T.-H. Tang and R. F. W. Bader, Topological definition of crystal structure: determination of the bonded interactions in solid molecular chlorine, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 143–153.
8. C. F. Matta, N. Castillo and R. J. Boyd, Characterization of a Closed-Shell Fluorine−Fluorine Bonding Interaction in Aromatic Compounds on the Basis of the Electron Density, J. Phys. Chem. A, 2005, 109, 3669–3681.
9. N. Castillo, C. F. Matta and R. J. Boyd, Fluorine−Fluorine Spin−Spin Coupling Constants in Aromatic Compounds: Correlations with the Delocalization Index and with the Internuclear Separation, J. Chem. Inf. Model., 2005, 45, 354–359.
10. T. T. T. Bui, S. Dahaoui, C. Lecomte, G. R. Desiraju and E. Espinosa, The Nature of Halogen⋯Halogen Interactions: A Model Derived from Experimental Charge-Density Analysis, Angew. Chem., Int. Ed., 2009, 48, 3838–3841.
11. P. Politzer, J. S. Murray and T. Clark, Halogen bonding and other σ-hole interactions: a perspective, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
12. E. Aubert, E. Espinosa, I. Nicolas, O. Jeannin and M. Fourmigué, Toward a reverse hierarchy of halogen bonding between bromine and iodine, Faraday Discuss., 2017, 203, 389–406.
13. M. Savastano, Words in supramolecular chemistry: the ineffable advances of polyiodide chemistry, Dalton Trans., 2021, 50, 1142–1165.
14. A. J. Blake, W.-S. Li, V. Lippolis, M. Schröder, F. A. Devillanova, R. O. Gould, S. Parsons and C. Radek, Template self-assembly of polyiodide networks, Chem. Soc. Rev., 1998, 27, 195–206.
15. A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
16. R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391.
17. S. S. Batsanov, van der Waals Radii of Elements, Inorg. Mater., 2001, 37, 871–885.
18. Z. M. Bikbaeva, D. M. Ivanov, A. S. Novikov, I. V. Ananyev, N. A. Bokach and V. Y. Kukushkin, Electrophilic-Nucleophilic Dualism of Nickel(II) toward Ni center dot center dot center dot l Noncovalent Interactions: Semicoordination of Iodine Centers via Electron Belt and Halogen Bonding via sigma-Hole, Inorg. Chem., 2017, 56, 13562–13578.
19. Z. M. Efimenko, A. S. Novikov, D. M. Ivanov, A. V. Piskunov, A. A. Vereshchagin, O. V. Levin, N. A. Bokach and V. Y. Kukushkin, The (Dioximate)NiII/I2 System: Ligand Oxidation and Binding Modes of Triiodide Species, Inorg. Chem., 2020, 59, 2316–2327.
20. F. Bertolotti, A. V. Shishkina, A. Forni, G. Gervasio, A. I. Stash and V. G. Tsirelson, Intermolecular Bonding Features in Solid Iodine, Cryst. Growth Des., 2014, 14, 3587–3595.
21. M. A. Kinzhalov, D. M. Ivanov, A. A. Melekhova, N. A. Bokach, R. M. Gomila, A. Frontera and V. Y. Kukushkin, Chameleonic Metal-bound Isocyanides: π-Donating CuI-center Imparts a Nucleophilicity to the Isocyanide Carbon toward Halogen Bonding, Inorg. Chem. Front., 2022, 9, 1655–1665.
22. A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Coordination polymers and molecular structures among complexes of mercury(II) halides with selected 1-benzoylthioureas, Polyhedron, 2015, 90, 47–57.
23. G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Definition of the halogen bond (IUPAC Recommendations 2013), Pure Appl. Chem., 2013, 85, 1711.
24. P. K. Hon, T. C. W. Mak and J. Trotter, Synthesis and structure of 1-methyl-1,3,5,7-tetraazaadamantan-1-ium octaiodide, [(CH2)6N4CH₃]2I8. A new outstretched Z configuration for the polyiodide ion I82, Inorg. Chem., 1979, 18, 2916–2918.
25. M. E. G. Mosquera, P. Gomez-Sal, I. Diaz, L. M. Aguirre, A. Ienco, G. Manca and C. Mealli, Intriguing I2 Reduction in the Iodide for Chloride Ligand Substitution at a Ru(II) Complex: Role of Mixed Trihalides in the Redox Mechanism, Inorg. Chem., 2016, 55, 283–291.
26. M. E. G. Mosquera, I. Egido, C. Hortelano, M. López-López and P. Gómez-Sal, Comparison of halogen bonding networks with Ru(ii) complexes and analysis of the influence of the XB interactions on their reactivity, Faraday Discuss., 2017, 203, 257–283.
27. J. Y. Lu and V. Schauss, A Novel Nanostructured Open-Channel Coordination Polymer with an Included Fused-Polyiodide Ring, Eur. J. Inorg. Chem., 2002, 2002, 1945–1947.
28. M. C. Aragoni, M. Arca, F. Demartin, F. A. Devillanova, A. Garau, F. Isaia, V. Lippolis, S. Rizzato and G. Verani, [Ni(L)(MeCN)]²⁺ complex cation as a template for the assembly of extended I3−·I5− and I5−·I7− polyiodide networks {L = 2,5,8-trithia[9](2,9)-1,10-phenanthrolinophane}. Synthesis and structures of [Ni(L)(MeCN)]I8 and [Ni(L)(MeCN)]I12, Inorg. Chim. Acta, 2004, 357, 3803–3809.
29. C. A. L. Filgueiras, A. Horn Jr., J. M. S. Skakle and J. L. Wardell, Tetra-methyl-ammonium pentaiodide, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2001, 57, o338–o340.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
32. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
33. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128.
34. B. G. Lippert, J. Hunter and M. Parrinello, A hybrid Gaussian and plane wave density functional scheme, Mol. Phys., 1997, 92, 477–488.
35. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
36. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
37. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506.
38. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems, J. Chem. Phys., 2002, 117, 5529–5542.
39. R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, Properties of atoms in molecules: atomic volumes, J. Am. Chem. Soc., 1987, 109, 7968–7979.
40. V. Tsirelson and A. Stash, Determination of the electron localization function from electron density, Chem. Phys. Lett., 2002, 351, 142–148.
41. W.-T. Chan and I. P. Hamilton, Correspondence between the one-electron potential and the Laplacian of the electron density as indicators of proton affinity, Chem. Phys. Lett., 1999, 301, 53–58.
42. V. Tsirelson and A. Stash, On functions and quantities derived from the experimental electron density, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 418–426.
43. G. Hunter, Conditional probability amplitudes in wave mechanics, Int. J. Quantum Chem., 1975, 9, 237–242.
44. I. P. Hamilton, Discussion. Comment on “Are the Bader laplacian and the Bohm quantum potential equivalent?”, Chem. Phys. Lett., 1998, 297, 261–262.
45. S. Sadjadi, C. F. Matta and I. P. Hamilton, Bonding and metastability for Group 12 dications, J. Comput. Chem., 2021, 42, 40–49.
46. W. Zou, Z. Cai, J. Wang and K. Xin, An open library of relativistic core electron density function for the QTAIM analysis with pseudopotentials, J. Comput. Chem., 2018, 39, 1697–1706.
47. E. V. Bartashevich, I. D. Yushina, A. I. Stash and V. G. Tsirelson, Halogen Bonding and Other Iodine Interactions in Crystals of Dihydrothiazolo(oxazino)quinolinium Oligoiodides from the Electron-Density Viewpoint, Cryst. Growth Des., 2014, 14, 5674–5684.
48. E. Espinosa, E. Molins and C. Lecomte, Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 1998, 285, 170–173.
49. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: New vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241.
50. E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
51. K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096.
52. C. Trindle, Bond index description of delocalization, J. Am. Chem. Soc., 1969, 91, 219–220.
53. C. Trindle and O. Sinanoglu, Local orbital and bond index characterization of hybridization, J. Am. Chem. Soc., 1969, 91, 853–858.
54. L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Halogen Bonding in Supramolecular Chemistry, Chem. Rev., 2015, 115, 7118–7195.
55. P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Halogen Bonding in Supramolecular Chemistry, Angew. Chem., Int. Ed., 2008, 47, 6114–6127.
56. A. V. Novikov, A. N. Usoltsev, S. A. Adonin, A. A. Bardin, D. G. Samsonenko, G. V. Shilov, M. N. Sokolov, K. J. Stevenson, S. M. Aldoshin, V. P. Fedin and P. A. Troshin, Tellurium complex polyhalides: narrow bandgap photoactive materials for electronic applications, J. Mater. Chem. A, 2020, 8, 21988–21992.
57. G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
58. G. Sheldrick, SADABS-2008/1-Bruker AXS area detector scaling and absorption correction, Bruker AXS, Madison, Wisconsin, USA, 2008.
59. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
60. M. Frigo and S. G. Johnson, The Design and Implementation of FFTW3, Proc. IEEE, 2005, 93, 216–231.
61. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, cp2k: atomistic simulations of condensed matter systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
62. U. Borštnik, J. VandeVondele, V. Weber and J. Hutter, Sparse matrix multiplication: The distributed block-compressed sparse row library, Parallel Comput., 2014, 40, 47–58.
63. O. Schütt, P. Messmer, J. Hutter and J. VandeVondele, in Electronic Structure Calculations on Graphics Processing Units, 2016, pp. 173–190.  DOI:10.1002/9781118670712.ch8.
64. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
65. T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103.
66. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09W, 2009. https://www.gaussian.com/(accessed on 30 December 2013).
67. A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403.
68. B. Silvi and A. Savin, Classification of chemical bonds based on topological analysis of electron localization functions, Nature, 1994, 371, 683–686.
69. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The Electron Localization Function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.
70. R. F. W. Bader and T. T. Nguyen-Dang, in Adv. Quant. Chem, ed. P.-O. Löwdin, Academic Press, 1981, vol. 14, pp. 63–124.
71. R. F. W. Bader, A quantum theory of molecular structure and its applications, Chem. Rev., 1991, 91, 893–928.
72. I. Mata, E. Molins, I. Alkorta and E. Espinosa, Topological Properties of the Electrostatic Potential in Weak and Moderate N⋯H Hydrogen Bonds, J. Phys. Chem. A, 2007, 111, 6425–6433.
73. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
74. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, 2018.
75. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
76. T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019. ( https://aim.tkgristmill.com).

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2211053–2211056. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi02634a

---