Open Access Article
Open Access ArticleUnravelling the thermo-responsive evolution from single-chain to multiple-chain nanoparticles by thermal field-flow fractionation†
Upenyu L.
Muza
a,
Chelsea D.
Williams
b and
Albena
Lederer
 *ab
*ab
aLeibniz-Institut für Polymerforschung Dresden e.V., Hohe Str. 6, 1069 Dresden, Germany. E-mail: lederer@ipfdd.de
bStellenbosch University, Department of Chemistry and Polymer Science, Private Bag X1, Matieland 7602, South Africa
First published on 27th June 2023
Abstract
The amphiphilic block copolymer polystyrene–polyethylene oxide (PS–PEO) is shown for the first time to exhibit unique thermo-responsive transformation into single-chain nanoparticles (SCNPs), as characterized by thermal field-flow fractionation (ThFFF) with multiple detectors. In toluene, the PEO blocks are shown to fold and collapse into spheres that are stabilized by PS shells (SCNP-shells), and solvophobic interactions are prescribed as the critical determinant of the overall dynamics of formation as a function of temperature. Contrary to the typically expected random coil conformation, PS–PEO is shown to formulate SCNP–shell nanostructures. Below a critical temperature threshold of 20 °C, the SCNP–shell nanostructures are shown to collate into much larger, multiple-chain nanoparticles (MCNPs) with multiple morphologies. The associated conformational evolutions in microstructure from SCNP–shell nanostructures to MCNPs are characterized in-depth with respect to their size, shape, morphology, molar mass, and their respective distributions.
Introduction
Polymeric single-chain nanoparticles (SCNPs) are complex nanostructures with lucrative applications in catalysis, sensory, bioimaging and drug delivery.1–3 These SCNPs are produced when unit polymer chains fold or collapse upon themselves – a self-folding mimicking the well-known protein-folding. This self-folding is a result of intramolecular linkages, which can either be covalent, or noncovalent.4 Self-folding due to noncovalent linkages is predominated by solvophobic interactions, as instigated by external stimuli such as temperature, pH, and electromagnetic irradiation.5 In general, the stimuli-responsive self-folding of polymers into SCNPs represents a facile strategy for engineering complex macromolecular structures. In addition, the self-folded SCNPs can also be prompted to self-assemble into more complex supramolecular structures,6 whose molecular properties can be modulated to precision by external stimuli. Therefore, SCNPs are not just functional nanostructures, but also fundamental building blocks in the supply chain for engineering complex nanomaterials.Unlike proteins, the self-folding behavior of SCNPs is not yet well-defined. Notably, the precise definition of self-folding mechanisms is necessary for understanding the structure and formation dynamics of SCNPs, which is a critical determinant of their functionalities.7–9 Therefore, such a prelude is a critical incentive for the research and development of more comprehensive strategies for the advanced characterization of the self-folding characteristic of block copolymers into SCNPs. Block copolymers have previously been shown to self-fold into SCNPs;10,11 however, to the best of our knowledge, no reports are available on the self-folding characteristic of polystyrene–polyethylene oxide (PS–PEO) into SCNPs, as a function of the collective effect of thermo-responsive and solvophobic interactions. As such, our focus herein is on the introduction of thermal field-flow fractionation (ThFFF) with multiple detectors as an advanced analytical strategy for studying the self-folding of PS–PEO into SCNPs.
The folding process of SCNPs has been intensively investigated using dynamic light scattering (DLS), size exclusion chromatography (SEC), small angle neutron scattering as well as DOSY NMR.1,7,12 The first investigation of SCNPs with field-flow fractionation (FFF) technique was performed using asymmetrical-flow FFF (AF4) with multiple detectors.13 In contrast to AF4, where cross-flow is used as a driving force for separating according only to size, ThFFF is a separation technique that applies a thermal gradient and flow dynamics to simultaneously separate molecules according to their size and composition.14–16 The thermal gradient is a function of temperature, and temperature is a key factor in the thermodynamics and kinetics of a given sample matrix. Therefore, in addition to providing the separation force field in ThFFF, the thermal gradient can also actively manipulate the thermodynamics and kinetics of a sample matrix in question.17 As such, ThFFF is strategically chosen for fractionations and for performing temperature dependent studies, bearing in mind that the thermo-responsiveness of PS–PEO is subject to study. Moreso, ThFFF is the only FFF technique currently available that is capable of fractionating according to both size and chemical composition.18
Analyzing size dynamics is essential to understand conformational changes in macromolecules. Our studies incorporated three state-of-the-art detectors for analysing size related parameters subsequent to ThFFF fractionations. This so-called triple-detection modulation is composed of the following detectors: multi-angle light scattering (MALS), differential refractive index (dRI) and viscometer (Visco). The dRI serves as a universal concentration detector, of which concentration is required for calculations related to MALS and Visco detections. The design of the MALS is such that one of the angles can be used for the detection of dynamic light scattering (DLS). From the MALS, the intensity of the scattered light is used to determine the absolute molar mass (MW), while the radius of gyration (RG) is derivable from the angular dependency of this scattered light.19 From DLS, the fluctuation in intensity of the scattered light is a measure of Brownian motion, and thus, hydrodynamic radius (RH) is calculable from the Stokes–Einstein equation. The ratio RG/RH is important for calculating the shape factor (ρ) as defined in eqn (1). Typically, ρ values ranging around 0.7 describe hard sphere structures, while values above 1.2 are generally attributed to elongated conformations.20,21
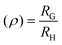 | (1) |
Intrinsic viscosity [η] is a measure of the solute's impact on solvent viscosity, and this is measurable from the Visco. [η] allows for structural elucidations, and for calculating the viscosity radius (RV) using eqn (2), where NA is the Avogadro number.22 The RV is an important size measurement when MALS and DLS are not sensitive enough for measuring smaller molecules, particularly in lower concentrations.23
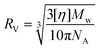 | (2) |
Results and discussion
For establishing a proof of concept, the following standards are analysed by ThFFF: PS102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (PS102) and PS102
000 (PS102) and PS102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–PEO34
000–PEO34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (PS102–PEO34), where the subscript represents the respective molar mass (Mw) in g mol−1. Unless otherwise stated, toluene is used for both sample dissolution or suspension, and as the career liquid; and all measurements relating to PS102–PEO34 were performed after an optimised equilibration time of two weeks.
000 (PS102–PEO34), where the subscript represents the respective molar mass (Mw) in g mol−1. Unless otherwise stated, toluene is used for both sample dissolution or suspension, and as the career liquid; and all measurements relating to PS102–PEO34 were performed after an optimised equilibration time of two weeks.
In a selective solvent for PS such as toluene, PS102–PEO34 is hypothesized to fold and collapse into SCNP-shell nanostructures, comparable in size to PS102. The solubility of PS in toluene is very good considering also the low difference in Hansen solubility parameters between polymer and solvent (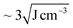 ). Compared to this, PEO at the same conditions has significantly lower solubility (
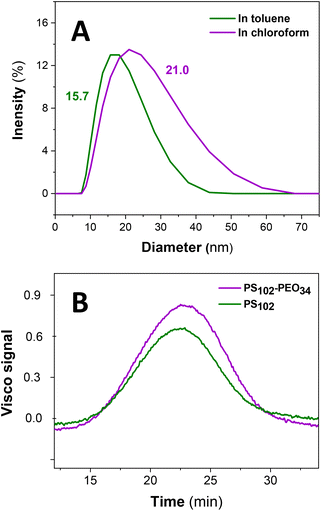
). Compared to this, PEO at the same conditions has significantly lower solubility (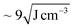 ).24 Thus, the PEO block of PS102–PEO34 is assumed to drastically fold and collapse into SCNPs that are stabilized by PS shells (SCNP–shell). Thus, the size of the PS shell dominates the overall size of the SCNP–shell nanostructures. A simple change to a better solvent for both blocks changes the SCNP structure immediately into a coil like structure. Chloroform is a common good solvent for PS as well as for PEO, leading to hydrodynamic size increase of the macromolecules from 15.7 nm in toluene to 21 nm in chloroform (see Fig. 1A). The folding process is, thus, necessary for maintaining stability of the macromolecule by minimising exposure to thermodynamically unfavourable interactions with the selective solvent. For further validation of the hypothesis, ThFFF is employed.
).24 Thus, the PEO block of PS102–PEO34 is assumed to drastically fold and collapse into SCNPs that are stabilized by PS shells (SCNP–shell). Thus, the size of the PS shell dominates the overall size of the SCNP–shell nanostructures. A simple change to a better solvent for both blocks changes the SCNP structure immediately into a coil like structure. Chloroform is a common good solvent for PS as well as for PEO, leading to hydrodynamic size increase of the macromolecules from 15.7 nm in toluene to 21 nm in chloroform (see Fig. 1A). The folding process is, thus, necessary for maintaining stability of the macromolecule by minimising exposure to thermodynamically unfavourable interactions with the selective solvent. For further validation of the hypothesis, ThFFF is employed.
A co-elution in ThFFF of PS102 and PS102–PEO34 is observed in Fig. 1B, regardless of distinct differences in chemical composition, MW and size. Such similar co-elutions were previously reported by Ngaza et al.25,26 It was demonstrated that for PS–PEO block copolymers independently on the ratios of blocksize, ThFFF separates the copolymers according to their shell properties in PS selective solvents. Notably, the two samples chosen for our study have comparable RV as outlined in Table 1, and thus uncharacteristically, an elution trend governed by hydrodynamic size is implied. Comparisons of RG and RH values are not available due to the limits of detection pertaining to size and concentration for analysing PS102 using ThFFF – MALS and – DLS. A contraction effect must be prevalent, since PS102–PEO34 is much larger in Mw (by 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1). The contraction effect is hypothesized to emanate from the lower interaction of the PEO block with toluene in comparison to the PS block, as previously discussed. Moreover, there is an apparent loss in ThFFF selectivity to PEO composition, as explained in subsequent text.
000 g mol−1). The contraction effect is hypothesized to emanate from the lower interaction of the PEO block with toluene in comparison to the PS block, as previously discussed. Moreover, there is an apparent loss in ThFFF selectivity to PEO composition, as explained in subsequent text.
| Sample | R V (nm) | T R (min) | M w (g mol−1) | Đ | dn/dc (mL g−1) |
|---|---|---|---|---|---|
| PS102 | 9.7 | 22.6 | 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.01 | 0.11 |
| PS102–PEO34 | 10.3 | 22.7 | 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.00 | 0.10 |
As previously mentioned, and further explained in the ESI section 2.2,† ThFFF is a separation technique which separates not only according to size, but also chemical composition. However, we observe the shielding of the PEO core by the PS shell, which explains why the ThFFF separations in Fig. 1B were size-based, and seemingly “blind” to the PEO composition.27 Notably, separations in ThFFF have already been proven to be insensitive to the overall chemical composition, but rather sensitive to the peripheral chemistry of the eluting analytes.26
Transmission electron microscopy (TEM) visualizes the SCNP-shell structures, as shown in Fig. 2. The sphere-like nanostructures in Fig. 2A are the most comparable in size and morphology to the hypothesized structures for the SCNP–shell nanostructures. Their narrow distribution is clearly visible by the well-defined distance between the SCNPs as a result of neighbouring PS-shells. The micrographs were generated independent of any contrasting agents owing to the sufficient contrast between PEO and PS blocks. The TEM micrograph in Fig. 2B showcases other nanostructures with multiple morphologies and a broad range of sizes. The shape and size of these large nanostructures is not comparable to typical block-copolymer nanostructures, such as micelles, polymersomes or networks.17,18,28,29
The SCNP–shell is not purely native to our sample matrix, but rather exists in a dynamic equilibrium with larger nanostructures, which can be regarded as multiple chain nanoparticles (MCNPs).6 As such, for a given concentration, the sphere–like SCNP–shell nanostructures must be prone to both size and morphological evolutions, as a function of temperature.30 For preliminary investigations into the temperature dependent dynamics of formation, size changes as a function of temperature shall be performed by DLS, prior to further analysis with multiple-detection ThFFF.
Size dynamics as a function of temperature
At sub-room temperatures, a much larger and unimodal size distribution is detected for PS102–PEO34 in the size regimes typical for aggregates or MCNPs (Fig. 3).6,17 These measured sizes correlate with the larger nanostructures observed in the TEM micrographs (Fig. 2B). On the other hand, at high temperatures (above 20 °C) the unimodal size regime previously observed for PS102–PEO34 at 20 °C transforms to a bimodal distribution. A very pronounced small size population is detected (Fig. 3). Large aggregates (above 1 μm) are observed only in the intensity % plot but are not detectable by the number %, which means that these structures are insignificant in amount (see also volume % plots in ESI Fig. SI.1†).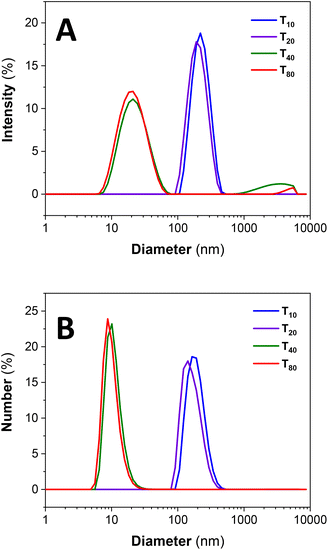 | ||
| Fig. 3 Size dynamics for PS102–PEO34 as a function of temperature (A) by intensity % and (B) number %; where the subscripts represent the measurement temperature in °C. | ||
Unimodal and large size distributions for the MCNP nanostructures disassemble into SCNP–shell nanostructures with increased temperature. Although lower in concentrations, as deduced from Number % size measurements in Fig. 3B, the larger MCNP nanostructures scatter light with higher intensity, which explains why their peak integrals by Intensity % are relatively more pronounced (Fig. 3A).
Having established key temperature limits and a solid theoretical framework for the dynamics of formation and evolution for the SCNP–shell and MCNP nanostructures, the next discussion considers ThFFF with triple-detection. Triple-detection makes use of the MALS, dRI and Visco detectors for the complementary analysis of the eluting nanostructures. Fig. 4 outlines the results from the ThFFF separation of PS102–PEO34 at ΔT 80 °C, and Fig. SI.2† shows the corresponding MALS, dRI and Visco signals.
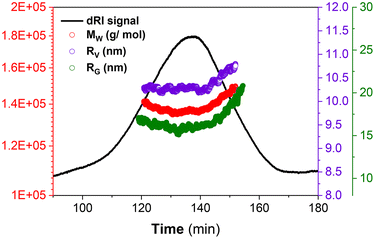
Fig. 4 shows the respective distributions in MW, RG and RV for PS102–PEO34. The measured MW (136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) is comparable to the nominal values provided by the vendor supplier of the commercial standards, and this validates the robustness of ThFFF for the reliable analysis of PS102–PEO34 regardless of conformation, shape and morphology. The high ΔT used (80 °C) doubles up as an external stimulus for providing sufficient energy for solubilisation to circumvent phase separations, which allows for accurate MW determination.
000 g mol−1) is comparable to the nominal values provided by the vendor supplier of the commercial standards, and this validates the robustness of ThFFF for the reliable analysis of PS102–PEO34 regardless of conformation, shape and morphology. The high ΔT used (80 °C) doubles up as an external stimulus for providing sufficient energy for solubilisation to circumvent phase separations, which allows for accurate MW determination.
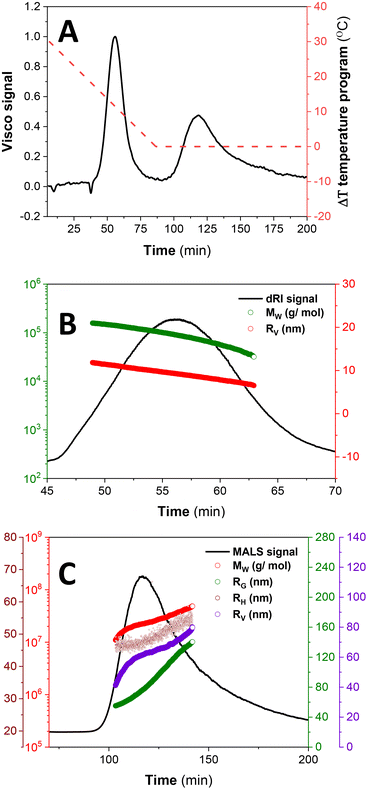
For further investigations on the effect of ΔT on the size, MW and conformational dynamics, a lower ΔT was explored using ThFFF with triple detection, and the results are summarized in Table 2 and Fig. 5. For the elution step, a ΔT of 30 °C is run for 1 min prior to a programmed linear decay to 0 °C, over 80 minutes, and thereafter, proceeds at 0 °C until the elution is complete (Fig. 5A).
| Sample | R G (nm) | R H (nm) | R V (nm) | T R (min) | M w (kg mol−1) | Đ |
|---|---|---|---|---|---|---|
| SCNP-shell | — | — | 9.2 | 55.8 | 93.8 | 1.02 |
| MCNP | 78.6 | 47.7 | 61.8 | 116.0 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739 739 |
1.00 |
Two distinct subpopulations are observed, with the first peak recording lower size (RV) and MW regimes (see Table 2 and Fig. 5B). This subpopulation is prescribed for the SCNP-shell nanostructures. Although the RV are comparable with those for separations at ΔT of 80 °C, the MW are much lower (see Table 1), and this is due to the reduced impact of temperature on the thermodynamics of solvation. No reliable RG and RH values are recorded for the first eluting subpopulation due to the combined effect of lower size (as a result of contraction effect owing to reduced solvation) and concentration limits for detection by light scattering. As such, it was not possible to calculate ρ (eqn (1)) in order to evaluate the conformation due to chain packing within the SCNP-shell nanostructures at ΔT 30 °C, relative to 80 °C.
Extremely high MW and sizes (RG, RH and RV) are recorded for the second eluting subpopulation, as expected for MCNPs (Fig. 5C). This subpopulation is attributed to the collation of SCNP-shells to form MCNPs nanostructures, as expected. The MCNP structures show a gradual increment in size as a function of elution time, in accordance with normal mode of elution in ThFFF.
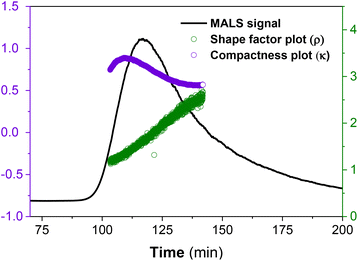
In Fig. 6, the calculated ρ distribution cut across a broad range of theoretical structural predictions, which implies that these MCNP structures are dynamic under the given ThFFF conditions. This is expected, given that the thermo-responsiveness of the MCNPs has already been established, and of which, temperature is a critical determinant of the separation mechanism in ThFFF. The compactness parameter κ is defined in eqn (3), and describes the shape of a molecule independent from MW. The κ values 1.3 and 0.5–0.7 respectively describe dense-hard spheres and linear coils.21,23
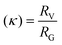 | (3) |
On average, both calculated shape parameters are in the range of hard sphere (ρ ∼ 0.7 and κ ∼ 1.3), which is consistent with the observed morphologies from the TEM micrographs in Fig. 2.
Nevertheless, we observe certain distribution in both cases due to the dynamic nature of the MCNP nanostructures (Fig. 6).
As already highlighted, size is the dominant determinant for the separation criteria, and therefore, the co-elution of divergent morphologies of comparable sizes is highly plausible. The superimposed effect of having a co-eluting and dynamic sample matrix presents a complex analytical challenge, and this further explains the calculated distributions in ρ and κ.
To probe further into the dynamic nature at play, a time-dependent ThFFF analysis is explored by comparing the results after 0- and 2-weeks equilibration, using the same temperature program for ThFFF (see ESI Fig. SI.3 and Table SI.2†). Ultimately, two weeks equilibrium time is deduced as optimum for reproducible ThFFF results.
Conclusions
Our studies have highlighted the complementarity and capability of ThFFF coupled with the MALS, dRI and Visco as an alternative analytical strategy for characterizing the evolution in conformational transformation associated with SCNP-shell nanostructures. The SCNP-shell nanostructures in question are in dynamic equilibrium with MCNPs, as fabricated from the unique thermo-responsive phase separation of PS–PEO as a function of hydrophobic interactions. The SCNP-shell nanostructures are shown to be more stable in size and morphology relative to the MCNPs. ThFFF currently presents the only provision for separating and characterizing SCNP-shell and MCNP nanostructures according to both size and chemical composition, in a single measurement. Although this study is focused on just one block copolymer, the techniques presented herein are generally applicable for analysing multiple complex nanostructures engineered from copolymers. However, such studies must be limited to non-aqueous and thermally non-degrading analytes.Author contributions
ULM: concept, data interpretation, manuscript drafting. CW: data acquisition and interpretation. AL: supervision, manuscript editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
ULM acknowledges the funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 898878 (USOME). The authors would also like to thank Dr. P Formanek for the help and assistance in generating and interpreting TEM micrographs.References
- J. Engelke, J. Brandt, C. Barner-Kowollik and A. Lederer, Strengths and Limitations of Size Exclusion Chromatography for Investigating Single Chain Folding-Current Status and Future Perspectives, Polym. Chem., 2019, 3410–3425, 10.1039/c9py00336c.
- J. Rubio-Cervilla, E. González and J. A. Pomposo, in 9 Applications of Single-Chain Polymer Nanoparticles, ed. J. A. Pomposo, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2017 Search PubMed.
- A. P. P. Kröger and J. M. J. Paulusse, Single-Chain Polymer Nanoparticles in Controlled Drug Delivery and Targeted Imaging, J. Controlled Release, 2018, 326–347, DOI:10.1016/j.jconrel.2018.07.041.
- O. Altintas, T. S. Fischer and C. Barner-Kowollik, Synthetic Methods Toward Single-Chain Polymer Nanoparticles, 2017 Search PubMed.
- J. He, L. Tremblay, S. Lacelle and Y. Zhao, Preparation of Polymer Single Chain Nanoparticles Using Intramolecular Photodimerization of Coumarin, Soft Matter, 2011, 7(6), 2380–2386, 10.1039/c0sm01383h.
- J. Wen, L. Yuan, Y. Yang, L. Liu and H. Zhao, Self-Assembly of Monotethered Single-Chain Nanoparticle Shape Amphiphiles, ACS Macro Lett., 2013, 2(2), 100–106, DOI:10.1021/mz300636x.
- J. Engelke, B. T. Tuten, R. Schweins, H. Komber, L. Barner, L. Plüschke, C. Barner-Kowollik and A. Lederer, An In-Depth Analysis Approach Enabling Precision Single Chain Nanoparticle Design, Polym. Chem., 2020, 11(41), 6559–6578, 10.1039/d0py01045f.
- S. Liao, L. Wei, L. A. Abriata and F. Stellacci, Control and Characterization of the Compactness of Single-Chain Nanoparticles, Macromolecules, 2021, 54(24), 11459–11467, DOI:10.1021/acs.macromol.1c02071.
- E. Blasco, B. T. Tuten, H. Frisch, A. Lederer and C. Barner-Kowollik, Characterizing Single Chain Nanoparticles (SCNPs): A Critical Survey. Polym. Chem., 2017, 5845–5851. 10.1039/c7py01278k.
- J. F. Thümmler, A. H. Roos, J. Krüger, D. Hinderberger, F. J. Schmitt, G. Tang, F. G. Golmohamadi, J. Laufer and W. H. Binder, Tuning the Internal Compartmentation of Single-Chain Nanoparticles as Fluorescent Contrast Agents, Macromol. Rapid Commun., 2023, 44(2), 2200618, DOI:10.1002/marc.202200618.
- T. S. Fischer, D. Schulze-Sünninghausen, B. Luy, O. Altintas and C. Barner-Kowollik, Chemisch Gesteuerte Schrittweise Entfaltung von Einzelketten- Nanopartikeln, Angew. Chem., 2016, 128(37), 11446–11450, DOI:10.1002/ange.201602894.
- T. S. Fischer, S. Spann, Q. An, B. Luy, M. Tsotsalas, J. P. Blinco, H. Mutlu and C. Barner-Kowollik, Self-Reporting and Refoldable Profluorescent Single-Chain Nanoparticles, Chem. Sci., 2018, 9(20), 4696–4702, 10.1039/c8sc01009a.
- J. Engelke, S. Boye, B. T. Tuten, L. Barner, C. Barner-Kowollik and A. Lederer, Critical Assessment of the Application of Multidetection SEC and AF4 for the Separation of Single-Chain Nanoparticles, ACS Macro Lett., 2020, 9(11), 1569–1575, DOI:10.1021/acsmacrolett.0c00519.
- M. Geisler, W. C. Smith, L. Plüschke, R. Mundil, J. Merna, S. K. R. Williams and A. Lederer, Topology Analysis of Chain Walking Polymerized Polyethylene: An Alternative Approach for the Branching Characterization by Thermal FFF, Macromolecules, 2019, 52(22), 8662–8671, DOI:10.1021/acs.macromol.9b01410.
- U. L. Muza, G. Greyling and H. Pasch, Stereocomplexation of Polymers in Micelle Nanoreactors As Studied by Multiple Detection Thermal Field-Flow Fractionation, Anal. Chem., 2018, 90(23), 13987–13995, DOI:10.1021/acs.analchem.8b03590.
- M. E. Schimpf, K. Caldwell and J. C. Giddings, in Field-Flow Fractionation Handbook, ed. M. E. Schimpf, K. Caldwell and J. C. Giddings, Wiley, New York, 1st edn, 2000 Search PubMed.
- U. L. Muza, G. Greyling and H. Pasch, Characterization of Complex Polymer Self-Assemblies and Large Aggregates by Multidetector Thermal Field-Flow Fractionation, Anal. Chem., 2017, 89(13), 7216–7224, DOI:10.1021/acs.analchem.7b01445.
- U. L. Muza and H. Pasch, Thermal Field-Flow Fractionation with Quintuple Detection for the Comprehensive Analysis of Complex Polymers, Anal. Chem., 2019, 91, 6926–6933, DOI:10.1021/acs.analchem.9b01384.
- S. Podzimek, T. Vlcek and C. Johann, Characterization of Branched Polymers by Size Exclusion Chromatography Coupled with Multiangle Light Scattering Detector. I. Size Exclusion Chromatography Elution Behavior of Branched Polymers, 2001 Search PubMed.
- W. Burchard, Solution Properties of Branched Macromolecules, Adv. Polym. Sci., 1999, 143, 113–194 CrossRef CAS.
- B. M. Tande, N. J. Wagner, M. E. Mackay, C. J. Hawker and M. Jeong, Viscosimetric, Hydrodynamic, and Conformational Properties of Dendrimers and Dendrons, Macromolecules, 2001, 34(24), 8580–8585, DOI:10.1021/ma011265g.
- M. Bohdaneckq and M. Netopilik, The Mark-Houwink-Kuhn-Sakurada Exponent of Polymers with Long Side Groups: Is A0 = l/2 a Reliable Criterion of the Theta State?, 1995, vol. 36 Search PubMed.
- A. K. Brewer and A. M. Striegel, Characterizing the Size, Shape, and Compactness of a Polydisperse Prolate Ellipsoidal Particle via Quadruple-Detector Hydrodynamic Chromatography, Analyst, 2011, 136(3), 515–519, 10.1039/c0an00738b.
- C. Özdemir and A. Güner, Solubility Profiles of Poly(Ethylene Glycol)/Solvent Systems, I: Qualitative Comparison of Solubility Parameter Approaches, Eur. Polym. J., 2007, 43(7), 3068–3093, DOI:10.1016/j.eurpolymj.2007.02.022.
- N. Ngaza and H. Pasch, Thermal Field-Flow Fractionation (Thermal FFF) and Asymmetrical Flow Field-Flow Fractionation (AF4) as New Tools for the Analysis of Block Copolymers and Their Respective Homopolymers, 2014. https://scholar.sun.ac.za Search PubMed.
- N. Ngaza, M. Brand and H. Pasch, Multidetector-ThF3 as a Novel Tool for the Investigation of Solution Properties of Amphiphilic Block Copolymers, Macromol. Chem. Phys., 2015, 216(12), 1355–1364, DOI:10.1002/macp.201500070.
- M. E. Schimpf and J. Calvin Giddings, Characterization, of Thermal Diffusion of Copolymers in Solution by Thermal Field-Flow Fractionation, J. Polym. Sci., Part B: Polym. Phys., 1990, 28, 2673–2680 CrossRef.
- S. Moreno, P. Sharan, J. Engelke, H. Gumz, S. Boye, U. Oertel, P. Wang, S. Banerjee, R. Klajn, B. Voit, A. Lederer and D. Appelhans, Light-Driven Proton Transfer for Cyclic and Temporal Switching of Enzymatic Nanoreactors, Small, 2020, 16(37), 1–11, DOI:10.1002/smll.202002135.
- S. Boye, F. Ennen, L. Scharfenberg, D. Appelhans, L. Nilsson and A. Lederer, From 1D Rods to 3D Networks: A Biohybrid Topological Diversity Investigated by Asymmetrical Flow Field-Flow Fractionation, Macromolecules, 2015, 48(13), 4607–4619, DOI:10.1021/acs.macromol.5b00824.
- G. Greyling and H. Pasch, Multidetector Thermal Field-Flow Fractionation: A Unique Tool for Monitoring the Structure and Dynamics of Block Copolymer Micelles, Macromolecules, 2016, 49(5), 1882–1889, DOI:10.1021/acs.macromol.5b02634.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3py00426k |
| This journal is © The Royal Society of Chemistry 2023 |