Open Access Article
Open Access ArticleDetermination of the optical constants of ligand-free organic lead halide perovskite quantum dots†
Andrea
Rubino
,
Gabriel
Lozano
,
Mauricio E.
Calvo
 and
Hernán
Míguez
and
Hernán
Míguez
 *
*
Instituto de Ciencia de Materiales de Sevilla (CSIC-US), C/Américo Vespucio 49, 41092 Sevilla, Spain. E-mail: h.miguez@csic.es
First published on 5th November 2022
Abstract
Precise knowledge of the optical constants of perovskite lead halide quantum dots (QDs) is required to both understand their interaction with light and to rationally design and optimize the devices based on them. However, their determination from colloidal nanocrystal suspensions, or films made out of them, remains elusive, as a result of the difficulty in disentangling the optical constants of the organic capping ligands and those of the semiconductor itself. In this work, we extract the refractive index and extinction coefficient of ligand-free methylammonium lead iodide (MAPbI3) and bromide (MAPbBr3) nanocrystals. In order to prevent the use of organic ligands in the preparation, we follow a scaffold assisted synthetic procedure, which yields a composite film of high optical quality that can be independently and precisely characterized and modelled. In this way, the contribution of the guest nanocrystals can be successfully discriminated from that of the host matrix. Using a Kramers–Kronig consistent dispersion model along with an effective medium approximation, it is possible to derive the optical constants of the QDs by fitting the spectral dependence of light transmitted and reflected at different angles and polarizations. Our results indicate a strong dependence of the optical constants on the QD size. Small nanocrystals show remarkably large values of the extinction coefficient compared to their bulk counterparts. This analysis opens the door to the rigorous modelling of solar cells and light-emitting diodes with active layers based on perovskite QDs.
Introduction
The determination of the optical constants (i.e., refractive index and extinction coefficient) of semiconductors is essential to model their interaction with light, which is also central to the optimization of the performance of optoelectronic devices. They are typically determined from the analysis of the optical response of the materials with the aid of appropriate models.1–8 As far as lead halide perovskites are concerned, several studies have focused on the characterization of their optical constants.8–17 Remarkably, a comparative analysis reveals that significant dispersion is observed for materials that are nominally the same, which is mainly attributed to differences in sample preparation.18 As far as we know, to date, all reported works have focused on the analysis of the optical constants of perovskites in the shape of thin films or single crystals. However, the determination of the complex refractive index of perovskite nanocrystals remains elusive. This contrasts with their relevance in different applied research fields, such as light-emitting diodes,19,20 solar cells,21,22 transistors,23 photodetectors24 and, more recently, X-ray detection,25 or non-linear optics,26,27 which could greatly benefit from optimized designs that require a precise knowledge of the optical constants of all materials involved, as it has been demonstrated for their bulk counterparts.15,16,28In order to perform a reliable determination of the optical constants of a material, uniform and scattering-free films are required. However, the preparation of such films out of colloidal nanocrystals, which are typically attained by ligand-assisted synthesis,29,30 is not straightforward. Furthermore, the structural configuration of the ligand network in a film made of colloidal nanocrystals is strongly dependent on the interaction between them, which depends in turn on the processing of the sample. So, even if high quality films can be obtained, since both sets of optical constants (i.e., that of the nanocrystals and the one corresponding to the ligand network) are unknown, discriminating between their relative contributions to the overall optical response of a quantum dot solid is not an easy task.31–34 On the other hand, it has been recently demonstrated that optoelectronic quality perovskite QDs can be achieved within the void network of pore size controlled metal oxide matrices.35 Moreover, these can be made in the shape of homogeneous and uniform scattering-free films,36,37 which opens the possibility to perform specular reflection and ballistic transmission measurements that allow a precise estimation of their average optical constants as reliable as those attained by ellipsometry characterization.38,39 Since in this case both the optical constants and the volume fraction of the host are known, it may be possible to differentiate the contribution from the semiconductor nanocrystals and determine their optical constants in a reliable way.
Based on this hypothesis, in this work we obtain the optical constants of ligand-free MAPbI3 and MAPbBr3 QDs embedded in porous scaffolds. The transparent porous films employed as hosts provide the necessary environmental stability required to perform reliable characterization of their optical properties without the need for ligands. A combination of a Forouhi–Bloomer model, employed to describe the spectral dependence of the complex refractive index of the QDs, and an effective medium approximation, accounting for the interaction between perovskite NCs and the porous silica matrix, is employed to fit the optical reflectance and transmittance measured at different angles from a series of QD embedded films40 and extract their optical constants. Interestingly, our analysis reveals that QD size reduction brings about an increase in the extinction coefficient. Our results not only provide information on the fundamental constants of nanosized organic lead halides, but also open the door to precise modelling of perovskite QD-based optoelectronic devices.
Results and discussion
Nanocrystal synthesis and characterization
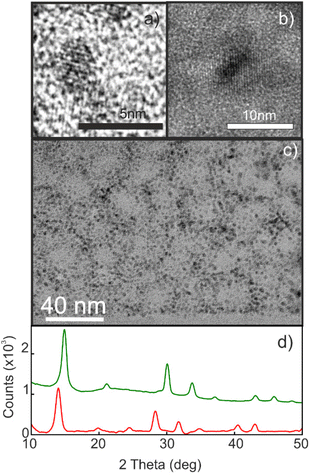
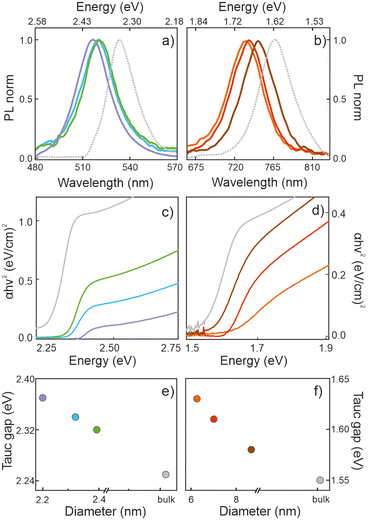
Porous silicon oxide films exhibiting plane-parallel interfaces and a high transparency, with a thickness d of ∼400 nm, were used as scaffolds for the synthesis of MAPbBr3 and MAPbI3 QDs analyzed in this work, following a procedure thoroughly described before.37Fig. 1(a and b) show the transmission electron microscopy (TEM) images of these films. Fig. 1c shows a typical TEM cross section of a focused ion beam cleaved and thinned lamella of a quantum dot filled porous silica scaffold (QD-MAPbBr3@SiO2) film, in which the semiconductor nanocrystals can be identified as dark spots inside the matrix. X-ray diffractograms confirm the presence of perovskite crystallites, as illustrated in Fig. 1d, with the main peaks associated with bromide- and iodide-based perovskites being clearly observed around 2θ = 14.9° and 2θ = 14.1°, respectively.41Fig. 2 shows the corresponding photoluminescence (PL) spectra recorded from QD-MAPbBr3@SiO2 (Fig. 2a) and QD-MAPbI3@SiO2 (Fig. 2b). The PL spectra of the thin films of the bulk perovskite materials are also shown in Fig. 2a and b, for the sake of comparison. The characteristic gradual blue-shift of the electronic band gap is observed as the size of either MAPbI3 or MAPbBr3 nanocrystals becomes smaller. The average QD diameters were estimated both from the analysis of HRTEM images and by fitting the spectral position of the luminescence peak to the Brus model,42 which offer consistent results (full details of the fittings can be found in the ESI†). The absorbance of these films was also estimated by measuring the total reflectance (RT) and transmittance (TT), and according to the formula A = 1 − RT − TT. Fig. 2c and d show the Tauc plots obtained for the different samples, which allow us to estimate the band gap energy (Eg) plotted versus the QD diameters in Fig. 2e and f.43,44 A maximum blue-shift of ∼100 meV is observed for the smallest QDs synthesized with respect to the Eg of the bulk materials in each case.Determination of the optical constants
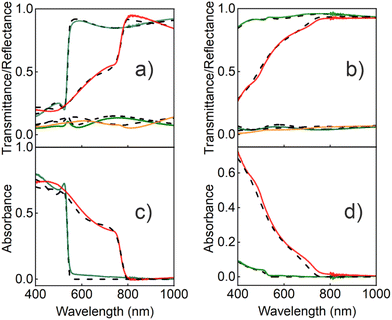
In order to extract the optical constants of the QDs, we measured the spectral dependence of light reflected and transmitted at different angles for both polarizations of the incident beam and fitted it using a model based on the transfer matrix formalism.15 This method, which has been successfully employed in recent years to calculate the optical constants of homogeneous ABX3 perovskite films or single crystals, constitutes a robust alternative to ellipsometry,15,39 and has been applied to optimize the photo-conversion performance of high-efficient perovskite solar cells prepared by solution processing or evaporation.16,28 In the present work, our model considers a system composed of a thin film (the porous silica matrix loaded with QDs) characterized by a thickness d and a complex effective refractive index, Neff = n + ik. A substrate of a refractive index 1.51 and thickness 1 mm is also assumed, while air is taken as the incoming and outgoing medium. In order to calculate the real (n) and imaginary (k) parts of Neff, we use the approach developed by Maxwell and Garnett (MG), a well-established effective medium approximation that has been successfully employed recently to attain the Neff of colloidal quantum dot solid films.31 In our case, both pores and perovskite nanocrystals are considered inclusions in the silica matrix.45 For the calculations, we first experimentally determined the volume filling fractions of both the porous scaffold (ffSiO2) and the perovskite QDs (ffQD). As the porous matrix can be analyzed independently46 before infiltrating the QDs, ffSiO2 could be set at 0.51 and the (almost dispersion-less) refractive index of the solid part of the porous network at NSiO2 = 1.49, as extracted by using a Cauchy model. Also, ffQD could be experimentally determined by means of inductively coupled plasma optical emission spectrometry (ICP-OES) for each film, as shown in Table S1 of the ESI,† where full details on this procedure can be found. Please note that the possibility to know the exact volume fraction and optical constants of the matrix, as well as the amount of nanocrystals present, implies a fundamental difference with respect to the optical analysis of the colloidal quantum dot solids. In the latter, the degree of interpenetration of the ligands surrounding the QDs is unknown, which prevents an accurate estimation of both the filling fraction and the optical constants of such organic networks, thus rendering the elucidation of the contribution of each one of the constituents to Neff unfeasible.Considering this information, a Kramers–Kronig consistent Forouhi–Bloomer dispersion model, in the Jobin Yvon parametrization (new amorphous),47 was used to account for the spectral dependence of the complex refractive index of the QDs. To find the set of parameters that fit best the optical response of the fabricated films, we combined our optical model with a genetic algorithm. Fig. 3 shows the calculated specular reflectance (R), ballistic transmittance (T) and absorbance (A = 1 − R − T) spectra for the best fitting obtained for a bulk film and for a porous silica layer scaffold loaded with 2.2 nm MAPbBr3 (Fig. 3a and c) and 6 nm MAPbI3 (Fig. 3b and d) nanocrystals, along with their corresponding experimental spectra (the results for QDs of different sizes are provided in the ESI†). A fair agreement is found and the main spectral features are faithfully reproduced. The slight divergence observed in the reflectance background can be attributed to a small fraction of diffusely scattered light due to the roughness or imperfections in the film. The full set of parameters used for the calculation can also be found in the ESI.†
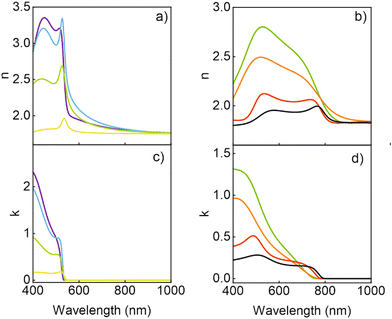
Fig. 4 shows the spectral dependence of both n and k of the MAPbBr3 and MAPbI3 QDs that provide the best fit to the experimental results. For comparison, we also show the data obtained for the corresponding bulk films, which are in accordance with the optical constants previously reported for such materials.8,10 Complementarily, the spectral dependence of the real and imaginary parts of the corresponding complex dielectric constants are shown in the ESI.† Interestingly, a remarkable increase of both the real and imaginary parts of the refractive index occurs for energies above the band gap as the nanocrystal dimensions diminish. It is worth noting that this observation is independent of the approach employed to extract the optical constants. We employed a MG approach because it is the one that assumes a low filling fraction of the inclusions, as it is the case for the scaffold supported perovskite QDs used here (see Table S1†), and hence is expected to describe our system best. In fact, among all the possible ones tested, this approach provides the best fitting to our experimental results, thus supporting the validity of this assumption. In any case, for the sake of comparison, we have modelled the effective refractive index of the porous silica film loaded with QDs using other approximations. Regardless of the quantitative differences observed, the trends observed, and hence our main conclusions, are independent of the approximation chosen to model the effective index of the QD loaded scaffolds. More details may be found in the ESI (Fig. S2),† where comparisons to the results attained employing other approaches (more specifically, Bruggeman's model and a variant of MG assuming a homogeneous matrix as the host, instead of considering the pores as inclusions) are shown.
Analysis of the results
We observed an increase in the extinction coefficient of the first excitonic transition when the size of the QD decreased, an effect that is attributed to the higher oscillator strength, f1, that results from the stronger overlap of the confined electron and hole and that has been thoroughly scrutinized before for other nanocrystalline semiconductors.48 Under strong coupling, it has been shown that the oscillator strengths of the first exciton of a nanocrystal, fnc1, and the bulk material, fb1, are related by the expression:49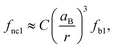 | (1) |
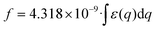 | (2) |
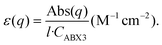 | (3) |
The ratio fnc1/fb1 is evaluated employing the first oscillator that contributes to the fitting of k and n shown in Fig. 4 for both the nanocrystals and the bulk. From them, the corresponding Abs(q), and then ε(q) as given in eqn (3), are calculated. This information is used to attain fnc1 for each QD size and fb1 using eqn (2). The results of fnc1/fb1vs. diameter for each perovskite QD sample under analysis can be seen in Fig. 5(a) and (b) (same color code as in Fig. 2), together with the expected inverse cubic dependence predicted using eqn (1). Assuming values of aB for MAPbI3 (4.6 nm) and for MAPbBr3 (3.8 nm), as reported in the literature,51 the values of the constant C attained from the fitting of the experimental data were 0.38 and 0.44, respectively, of the same order than the others reported in the literature. Please note that eqn (3) relies on the validity of the Lambert–Beer formula to account for the spatial decay of the transmitted light intensity along a homogeneous medium. However, in thin films with widths comparable to the light wavelength, the interference effects between counterpropagating light beams, which result from the partial transmission and reflection at each one of the film interfaces, may alter the commonly considered decaying exponential profile, hence limiting its applicability. In our case, this might give rise to certain deviations with respect to theoretical predictions.
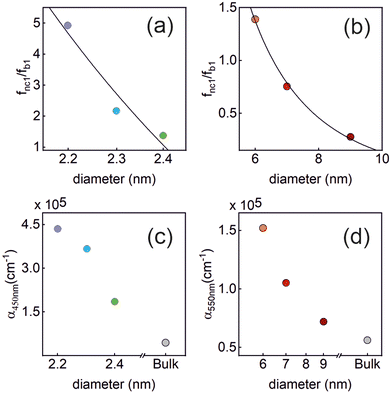 | ||
Fig. 5 Upper panels: the normalized oscillator strength of the first excitonic transition vs. the QD size, estimated for the (a) MAPbBr3 QDs, and (b) MAPbI3 QDs using the values of k extracted from our analysis. The solid line represents the theoretically expected 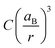 dependence. Lower panels: the absorption coefficient α vs. the QD size estimated for the (c) MAPbBr3 QDs (at λ = 450 nm), and (d) MAPbI3 QDs (at λ = 550 nm). In each plot, the color code is the same as that shown in Fig. 2. dependence. Lower panels: the absorption coefficient α vs. the QD size estimated for the (c) MAPbBr3 QDs (at λ = 450 nm), and (d) MAPbI3 QDs (at λ = 550 nm). In each plot, the color code is the same as that shown in Fig. 2. | ||
Finally, for energies higher than the band gap, the extinction coefficient k of solution dispersed quantum dots is expected to become size independent.52,53 Our observations are at odds with this prediction, as shown in Fig. 5(c) and (d), in which we have plotted the absorption coefficient α for the MAPbBr3 (at λ = 450 nm) and MAPbI3 (at λ = 550 nm) QDs according to the following expression:
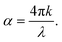 | (4) |
One possible origin for this discrepancy may be that in our case the concentration is at orders of magnitude larger than those in the diluted dispersions (typically 10−6 M) commonly employed for this analysis, where QDs barely interact with each other. In our films, nanocrystals are close enough to allow a dot-to-dot charge transport.35 Under these conditions, the neighbouring QDs are coupled through a dipolar interaction, which gives rise to an increase in the absorption cross section, and the polarization field induced by each nanoparticle may influence the surrounding nanoparticles. It has also been demonstrated that the dielectric confinement gives rise to an increase of the oscillator strength and therefore in the absorption cross section.54 For instance, as a result of these interactions, it has been shown that QD solids made out of colloidal CdSe and PbS monolayers present an absorption increase as the size of the nanocrystals and ligands decreases.32,55 Also, composite nanostructures that resemble those herein studied show an increase in the absorption of the QDs embedded in matrices with a lower dielectric constant, such as PbS in a glass matrix,56 PbS/FAPI systems57 and CsPbBr3 NCs embedded in a Cs4PbBr6 matrix.58
Conclusion
Herein, we demonstrate a method to determine the complex refractive indexes of MAPbBr3 and MAPbI3 perovskite quantum dots. To the best of our knowledge, the results attained constitute the first set of optical constants that can be considered intrinsic to these nanosized semiconductors. This achievement was possible due to the precise knowledge of the nanocrystal dielectric environment, which could be seized due to both the absence of capping ligands and the possibility to extract independently the optical constants of the host matrix in which the embedded nanocrystals are synthesized. We use a Kramers–Kronig consistent model to account for the spectral dispersion of the complex refractive index of the nanocrystals and an effective medium approximation approach to consider the effect of the porous silica matrix in which the nanocrystals are dispersed. Hence, contributions from the host and guest could be differentiated. Our analysis consistently reveals a remarkable increase of the values of both the real and the imaginary parts of the refractive index as the size of nanocrystals reduces. While the increase of the oscillator strength of the first excitonic transition grows according to the theoretical predictions; the behavior at energies well above the band gap edge is anomalous, but characteristic of QDs embedded in a vitreous host. We believe our results are both relevant from a fundamental perspective, as they provide a deeper insight into the origin of the remarkable optical properties of lead halide perovskites, and useful from an applied point of view, since they will allow a finer design and optimization of the optoelectronic devices in which perovskite QDs are already widely used.Methods
Perovskite@SiO2 composite preparation
The porous SiO2-based thin film consists of a stratification of Ludox TMA nanoparticles (30 nm) deposited by dip-coating onto a microslide glass substrate up to a 400 nm thickness with a final calcination step (400 °C). The MAPbX3 precursor solution contains a mixture of MAX and PbBr2 or PbCl2 (where X is Br or I), respectively, for bromide and iodide perovskites. Precursors were dissolved in N,N-dimethylformamide at a molar ratio of 3 to 1. Typically, for each case, the same recipes are employed for the preparation of the corresponding polycrystalline films, depositing the most concentrated precursor solution on the substrate, without the SiO2 porous layer. NC synthesis is a one-pot process conducted in a glovebox, in which the precursor solution (different concentration for each NC) is dropped on top of the silica matrix and spin coated. Finally, the composite is heated up to 100 °C for 40 min.Structural characterization
Lead determination was carried out by atomic emission spectroscopy with an inductively coupled plasma (ICP OES JASCO FT/IR-6200 IRT-5000). The microscopic analysis illustrated in Fig. 1 was performed using a FEI Talos F200S scanning/transmission electron microscope to observe the sample lamellae prepared by means of a focused ion beam (FIB, Carl Zeiss Auriga). For the composite thickness measurements, we used a profilometer.Optical characterization
The photoluminescence spectra were recorded using a spectrophotometer, using two different lasers at 450 nm and 530 nm for the excitation of MAPbBr3 and MAPbI3, respectively. The RT and TT measurements were carried out inside an integrating sphere (DRA-2500, Agilent) connected to a commercial spectrophotometer (Cary 5000 UV-Vis-NIR). For the angular characterization, we made use of an accessory of the spectrophotometer, which is the Universal Measurement Accessory, allowing the analysis of the angular optical response of the composite films.Complex refractive index determination
We fitted the optical response of the layers using an optical model based on the transfer matrix formalism. To model the spectral dependence of the nanocrystals, we used the Forouhi–Bloomer model in the Jobin–Yvon parametrization. Specifically, we considered three oscillators for MAPbI3 and two oscillators for MAPbBr3. Besides, we used an effective medium approximation to model the effective refractive index of the porous silica layer in which nanocrystals were embedded. A genetic algorithm was used to look for the parameters that provide the best fit for the experimental data. The results are shown in the ESI.†Data availability
Data for this paper are available at Digital CSIC at https://doi.org/10.20350/digitalCSIC/14799. The code for estimating the optical constants of an arbitrary layered optical material may be found at https://github.com/Multifunctional-Optical-Materials-Group.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the Spanish Ministry of Science and Innovation under grant PID2020-116593RB-I00, funded by MCIN/AEI/10.13039/501100011033, and from the Junta de Andalucía under grant P18-RT-2291 (FEDER/UE) is gratefully acknowledged.References
- J. I. Cisneros, Optical characterization of dielectric and semiconductor thin films by use of transmission data, Appl. Opt., 1998, 37, 5262–5270 CrossRef CAS.
- D. Poelman and D. F. Smet, Methods for the determination of the optical constants of thin films from single transmission measurements: a critical review, J. Phys. D: Appl. Phys., 2003, 36, 1850 CrossRef CAS.
- I. Moreels, K. Lambert, D. De Muynck, F. Vanhaecke, D. Poelman, J. C. Martins, G. Allan and Z. Hens, Composition and Size-Dependent Extinction Coefficient of Colloidal PbSe Quantum Dots, Chem. Mater., 2007, 19, 6101–6106 CrossRef CAS.
- I. Moreels, K. Lambert, D. Smeets, D. De Muynck, T. Nollet, J. C. Martins, F. Vanhaecke, A. Vantomme, C. Delerue, G. Allan and Z. Hens, Size-Dependent Optical Properties of Colloidal PbS Quantum Dots, ACS Nano, 2009, 3, 3023–3030 CrossRef CAS.
- Z. Hens and I. Moreels, Light absorption by colloidal semiconductor quantum dots, J. Mater. Chem., 2012, 22, 10406–10415 RSC.
- Y. C. Liu, J. H. Hsieh and S. K. Tung, Extraction of optical constants of zinc oxide thin films by ellipsometry with various models, Thin Solid Films, 2006, 510, 32–38 CrossRef CAS.
- R. Kerremans, C. Kaiser, W. Li, N. Zarrabi, P. Meredith and A. Armin, The Optical Constants of Solution-Processed Semiconductors—New Challenges with Perovskites and Non-Fullerene AcceptorsAdv, Opt. Mater., 2020, 8, 2000319 CrossRef CAS.
- M. S. Alias, I. Dursun, M. I. Saidaminov, E. M. Diallo, P. Mishra, T. K. Ng, O. M. Bakr and B. S. Ooi, Optical constants of CH3NH3PbBr3 perovskite thin films measured by spectroscopic ellipsometry, Opt. Express, 2016, 24, 16586–16594 CrossRef CAS.
- Y. Jiang, M. A. Green, R. Sheng and A. Ho-Baillie, Room temperature optical properties of organic–inorganic lead halide perovskites, Sol. Energy Mater. Sol. Cells, 2015, 137, 253–257 CrossRef CAS.
- P. Loeper, M. Stuckelberger, B. Niesen, J. Werner, M. Filipic, S. J. Moon, J. H. Yum, M. Topic, S. De Wolf and C. Ballif, Complex Refractive Index Spectra of CH3NH3PbI3 Perovskite Thin Films Determined by Spectroscopic Ellipsometry and Spectrophotometry, J. Phys. Chem. Lett., 2015, 6, 66–71 CrossRef.
- A. M. A. Leguy, P. Azarhoosh, M. I. Alonso, M. Campoy-Quiles, O. J. Weber, J. Yao, D. Bryant, M. T. Weller, J. Nelson, A. Walsh, M. Van Schilfgaarde and P. R. F. Barnes, Experimental and theoretical optical properties of methylammonium lead halide perovskites, Nanoscale, 2016, 8, 6317–6327 RSC.
- C. He, G. Zha, C. Deng, Y. An, R. Mao, Y. Liu, Y. Lu and Z. Chen, Refractive Index Dispersion of Organic–Inorganic Hybrid Halide Perovskite CH3NH3PbX3 (X
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Cl, Br, I) Single Crystals, Cryst. Res. Technol., 2019, 54, 1900011 CrossRef.
Cl, Br, I) Single Crystals, Cryst. Res. Technol., 2019, 54, 1900011 CrossRef. - M. I. Alonso, B. Charles, A. Francisco-López, M. Garriga, M. T. Weller and A. R. Goñi, Spectroscopic ellipsometry study of FAxMA1−xPbI3 hybrid perovskite single crystals, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2019, 37, 062901 Search PubMed.
- M. Zhao, Y. Shi, J. Dai and J. Lian, Ellipsometric study of the complex optical constants of a CsPbBr3 perovskite thin film, J. Mater. Chem. C, 2018, 6, 10450–10455 RSC.
- M. Anaya, G. Lozano, M. E. Calvo, W. Zhang, M. B. Johnston, H. J. Snaith and H. Míguez, Optical description of mesostructured organic–inorganic halide perovskite solar cells, J. Phys. Chem. Lett., 2015, 6, 48–53 CrossRef CAS PubMed.
- J. Ávila, C. Momblona, P. Boix, M. Sessolo, M. Anaya, G. Lozano, K. Vandewal, H. Míguez and H. J. Bolink, High voltage vacuum-deposited CH3NH3PbI3−CH3NH3PbI3 tandem solar cells, Energy Environ. Sci., 2018, 11, 3292–3297 RSC.
- Q. Lin, A. Armin, R. C. R. Nagiri, P. L. Burn and P. Meredith, Electro-optics of perovskite solar cells, Nat. Photonics, 2014, 9, 106–112 CrossRef.
- M. E. Calvo, Materials chemistry approaches to the control of the optical features of perovskite solar cells, J. Mater. Chem. A, 2017, 5, 20561–20578 RSC.
- G. Li, F. W. R. Rivarola, N. J. L. K. Davis, S. Bai, T. C. Jellicoe, F. de la Peña, S. Hou, C. Ducati, F. Gao, R. H. Friend, N. C. Greenham and Z. K. Tan, Highly efficient perovskite nanocrystal light-emitting diodes enabled by a universal crosslinking method, Adv. Mater., 2016, 28, 3528–3534 CrossRef CAS.
- G. Lozano, The Role of Metal Halide Perovskites in Next-Generation Lighting Devices, J. Phys. Chem. Lett., 2018, 9, 3987–3997 CrossRef CAS PubMed.
- J. Jean, Getting high with quantum dot solar cells, Nat. Energy, 2020, 5, 10–11 CrossRef CAS.
- M. Hao, Y. Bai, S. Zeiske, L. Ren, J. Liu, Y. Yuan, N. Zarrabi, N. Cheng, M. Ghasemi, P. Chen, M. Lyu, D. He, J.-H. Yun, Y. Du, Y. Wang, S. Ding, A. Armin, P. Meredith, G. Liu, H.-M. Cheng and L. Wang, Ligand-Assisted Cation-Exchange Engineering for High-Efficiency Colloidal Cs1-xFAxPbI3 Quantum Dot Solar Cells with Reduced Phase Segregation, Nat. Energy, 2020, 5, 79–88 CrossRef CAS.
- S. Zhou, G. Zhou, Y. Li, X. Xu, Y.-J. Hsu, J. Xu, N. Zhao and X. Lu, Understanding Charge Transport in All-Inorganic Halide Perovskite Nanocrystal Thin-Film Field Effect Transistors, ACS Energy Lett., 2020, 5, 2614–2623 CrossRef CAS.
- P. Ramasamy, D. H. Lim, B. Kim, S. H. Lee, M. S. Lee and J. S. Lee, All-inorganic cesium lead halide perovskite nanocrystals for photodetector applications, Chem. Commun., 2016, 52, 2067–2070 RSC.
- Q. Chen, J. Wu, X. Ou, B. Huang, J. Almutlaq, A. A. Zhumekenov, X. Guan, S. Han, L. Liang, Z. Yi, J. Li, X. Xie, Y. Wang, Y. Li, D. Fan, D. B. L. Teh, A. H. All, O. F. Mohammed, O. M. Bakr, T. Wu, M. Bettinelli, H. Yang, W. Huang and X. Liu, All-Inorganic Perovskite Nanocrystal Scintillators, Nature, 2018, 561, 88–93 CrossRef CAS PubMed.
- A. Rubino, T. Huq, J. Dranczewski, G. Lozano, M. E. Calvo, S. Vezzoli, H. Míguez and R. Sapienza, J. Mater. Chem. C, 2020, 8, 15990–15995 RSC.
- M. Athanasiou, P. Papagiorgis, A. Manoli, C. Bernasconi, M. I. Bodnarchuk, M. V. Kovalenko and G. Itskos, ACS Photonics, 2021, 8, 2120–2129 CrossRef CAS.
- J.-P. Correa-Baena, M. Anaya, G. Lozano, W. Tress, K. Domanski, M. Saliba, T. Matsui, T. J. Jacobsson, M. E. Calvo, A. Abate, M. Grätzel, H. Míguez and A. Hagfeldt, Unbroken perovskite: interplay of morphology, electro-optical properties and ionic movement, Adv. Mater., 2016, 28, 5031–5037 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X=Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS PubMed.
- J. Shamsi, A. S. Urban, M. Imran, L. De Trizio and L. Manna, Chem. Rev., 2019, 119, 3296–3348 CrossRef CAS PubMed.
- D. B. Dement, M. Puri and V. E. Ferry, Determining the Complex Refractive Index of Neat CdSe/CdS Quantum Dot Films, J. Phys. Chem. C, 2018, 122, 21557–21568 CrossRef CAS.
- P. Geiregat, Y. Justo, S. Abe, S. Flamee and Z. Hens, Giant and broad-band absorption enhancement in colloidal quantum dot monolayers through dipolar coupling, ACS Nano, 2013, 7, 987–993 CrossRef CAS PubMed.
- D. D. W. Grinolds, P. R. Brown, D. K. Harris, V. Bulovic and M. G. Bawendi, Quantum-dot size and thin-film dielectric constant: precision measurement and disparity with simple models, Nano Lett., 2015, 15, 21–26 CrossRef CAS.
- E. S. Skibinsky-Gitlin, S. Rodríguez-Bolívar, M. Califano and F. M. Gómez-Campos, Optical properties of nanocrystal films: blue shifted transitions as signature of strong coupling, Nanoscale Adv., 2020, 2, 384–393 RSC.
- A. Rubino, L. Caliò, M. E. Calvo and H. Míguez, Ligand-Free MAPbI3 Quantum Dot Solar Cells Based on Nanostructured Insulating Matrices, Sol. RRL, 2021, 2100204 CrossRef CAS.
- M. Anaya, A. Rubino, T. C. Rojas, J. F. Galisteo-López, M. E. Calvo and H. Míguez, Strong quantum confinement and fast photoemission activation in CH3NH3PbI3 perovskite nanocrystals grown within periodically mesostructured films, Adv. Opt. Mater., 2017, 5, 1601087 CrossRef.
- A. Rubino, M. Anaya, J. F. Galisteo-López, T. C. Rojas, M. E. Calvo and H. Míguez, Highly Efficient and Environmentally Stable Flexible Color Converters Based on Confined CH3NH3PbBr3 Nanocrystals, ACS Appl. Mater. Interfaces, 2018, 10, 38334–38340 CrossRef CAS PubMed.
- D. Poelman and P. F. Smet, Methods for the determination of the optical constants of thin films from single transmission measurements: a critical review, J. Phys. D: Appl. Phys., 2003, 1850, 1850–1857 CrossRef.
- S. Brittman and E. C. Garnett, Measuring n and k at the Microscale in Single Crystals of CH3NH3PbBr3 Perovskite, J. Phys. Chem. C, 2016, 120, 616–620 CrossRef CAS.
- G. A. Niklasson, C. G. Granqvist and O. Hunderi, Effective medium models for the optical properties of inhomogeneous materials, Appl. Opt., 1981, 20, 26–30 CrossRef CAS.
- J. Xie, Y. Liu, J. Liu, L. Lei, Q. Gao, J. Li and S. Yang, Study on the correlations between the structure and photoelectric properties of CH3NH3PbI3 perovskite light-harvesting material, J. Power Sources, 2015, 285, 349–353 CrossRef CAS.
- L. E. Brus, Electron–electron and electron–hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state, J. Chem. Phys., 1984, 80, 4403 CrossRef CAS.
- J. Tauc, R. Grigorovic and A. Vancu, Optical Properties and Electronic Structure of Amorphous Germanium, Phys. Status Solidi B, 1966, 15, 627–637 CrossRef CAS.
- B. D. Viezbicke, S. Patel, B. E. Davis and D. P. Birnie III, Evaluation, of the Tauc method for optical absorption edge determination: ZnO thin films as a model system, Phys. Status Solidi B, 2015, 252, 1700–1710 CrossRef CAS.
- O. Levy and E. Cherkaev, Effective medium approximations for anisotropic composites with arbitrary component orientation, J. Appl. Phys., 2013, 114, 164102 CrossRef.
- N. Hidalgo, C. López-López, G. Lozano, M. E. Calvo and H. Míguez, Characterization of Mesoporous Thin Films by Specular Reflectance Porosimetry, Langmuir, 2012, 28, 13777–13782 CrossRef CAS PubMed.
- A. R. Forouhi and I. Bloomer, Optical dispersion relations for amorphous semiconductors and amorphous dielectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7018 CrossRef CAS PubMed.
- T. Vossmeyer, L. Katsikas, M. Giersig, I. G. Popovic, K. Diesner, A. Chemseddine, A. Eychmueller and H. Weller, CdS Nanoclusters: Synthesis, Characterization, Size Dependent Oscillator Strength, Temperature Shift of the Excitonic Transition Energy, and Reversible Absorbance Shift, J. Phys. Chem., 1994, 98, 7665–7673 CrossRef CAS.
- Y. Kayanuma, Quantum-size effects of interacting electrons and holes in semiconductor microcrystals with spherical shape, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 9797 CrossRef PubMed.
- N. J. Turro, Molecular Photochemistry, W. A. Benjamin, Inc., Reading, MA, 1965 Search PubMed.
- M. Baranowski and P. Plochocka, Excitons in Metal-Halide Perovskites, Adv. Energy Mater., 2020, 10, 1903659 CrossRef CAS.
- I. Angeloni, R. Raja, A. Brescia, F. Polovitsyn, M. De Donato, G. Canepa, R. Bertoni, P. Zaccaria and I. Moreels, Disentangling the Role of Shape, Ligands, and Dielectric Constants in the Absorption Properties of Colloidal CdSe/CdS Nanocrystals, ACS Photonics, 2016, 3, 58–67 CrossRef CAS.
- S. J. Lim, M. U. Zahid, P. Le, L. Ma, D. Entenberg, A. S. Harney, J. Condeelis and A. M. Smith, Brightness-equalized quantum dots, Nat. Commun., 2015, 6, 1–10 Search PubMed.
- T. Takagahara, Effects of dielectric confinement and electron-hole exchange interaction on excitonic states in semiconductor quantum dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4569 CrossRef PubMed.
- C. Giansante, I. Infante, E. Fabiano, R. Grisorio, G. P. Suranna and G. Gigli, Darker-than-Black” PbS Quantum Dots: Enhancing Optical Absorption of Colloidal Semiconductor Nanocrystals via Short Conjugated Ligands, J. Am. Chem. Soc., 2015, 137, 1875–1886 CrossRef CAS PubMed.
- I. Moreels, D. Kruschke, P. Glas and J. W. Tomm, The dielectric function of PbS quantum dots in a glass matrix, Opt. Mater. Express, 2012, 2, 496–500 CrossRef CAS.
- S. Masi, C. Echeverría-Arrondo, K. M. M. Salim, T. T. Ngo, P. F. Mendez, E. López-Fraguas, D. F. Macias-Pinilla, J. Planelles, J. I. Climente and I. Mora-Seró, Chemi-Structural Stabilization of Formamidinium Lead Iodide Perovskite by Using Embedded Quantum Dots, ACS Energy Lett., 2020, 5, 418–427 CrossRef CAS.
- J. Xu, W. Huang, P. Li, D. R. Onken, C. Dun, Y. Guo, K. B. Ucer, C. Lu, H. Wang and S. M. Geyer, Imbedded nanocrystals of CsPbBr3 in Cs4PbBr6: kinetics, enhanced oscillator strength, and application in light-emitting diodes, Adv. Mater., 2017, 29, 1703703 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the Tauc plot analysis; the use of the Brus equation; the experimental quantification of the QD filling fraction; the modeling of the complex refractive index; the extracted dielectric constants; the comparison between different effective medium approximations. See DOI: https://doi.org/10.1039/d2nr05109e |
| This journal is © The Royal Society of Chemistry 2023 |