Fluidics for energy harvesting: from nano to milli scales
Nan
Wu
 ,
Youcef
Brahmi
and
Annie
Colin
,
Youcef
Brahmi
and
Annie
Colin
 *
*
ESPCI Paris, PSL Research University, MIE-CBI, CNRS UMR 8231, 10, Rue Vauquelin, F-75231 Paris Cedex 05, France. E-mail: annie.colin@espci.psl.eu
First published on 10th January 2023
Abstract
A large amount of untapped energy sources surrounds us. In this review, we summarize recent works of water-based energy harvesting systems with operation scales ranging from miniature systems to large scale attempts. We focus particularly on the triboelectric energy, which is produced when a liquid and a solid come into contact, and on the osmotic energy, which is released when salt water and fresh water are mixed. For both techniques we display the state of the art understanding (including electrical charge separation, electro-osmotic currents and induced currents) and the developed devices. A critical discussion of present works confirms the significant progress of these water-based energy harvesting systems in all scales. However, further efforts in efficiency and performance amelioration are expected for these technologies to accelerate the industrialization and commercialization procedure.
1 Introduction
A large amount of untapped energy sources surrounds us. They derive from human activities or come from ambient energies such as chemical, thermal, radiant and mechanical energies. Energy harvesting from environment is not recent: people have been harvesting energy for centuries at large scale with windmills and nowadays with wind turbines or photovoltaic batteries. After the radiant sources (sun, RF, etc.), mechanical energy (vibrations, wind, rain, etc.) and salted gradient are the second main environmental source of energy1–4 The mixing of 1 cm3 of sea water with 1 cm3 of river water produces an energy of 1.4 J.5 The energy of a rainwater drop falling on a surface is of the order of magnitude of 10 μJ (speed of the drops estimated to 1 m s−1). These energies are not negligible and are comparable to the energy demand for powering current electronic devices. It takes 1 mJ to send a text message and 1 μJ to measure a temperature.6,7 It seems therefore interesting to develop new techniques to recover energy from water by focusing on the mechanical energy contained in the drops of rain, in waves and in a more original way, in the osmotic energy contained in salt solutions. In such an approach, the first goal will be to be able to power sensors and embedded electronic devices, which is part of the energy harvesting field. The second goal in the longer term, if the results are there, will be to extend these devices to large scales in order to generate new renewable energy sources to fight against climate change and replace fossil fuels. Researchers estimate that the worldwide salinity gradient energy could reach 2.4–2.6 Terawatts considering all the rivers and effluents running to the sea, among which 1 Terawatt is extractable.8,9In this context, nanofluidics, microfluidics and millifluidics can have an impact in the field of research and development of new strategies to recover blue energy or energy from rain water. Nanofluidics, microfluidics and millifluidics encompasse all techniques for manipulating fluids at nanometer scale (between 1 and 1000 nanometers), micron scale (between 1 and 1000 micrometers) and millimeter scale (between 1 and 1000 millimeters), respectively.
In this review, we focus on emerging techniques for energy harvesting from fluids. In all cases, these techniques involve charge separation mechanisms and the creation of an ionic flow which is then converted into electronic flows either through a capacitive system or a faradic system. The charge separation mechanism is a basic key point in this framework. It remains to this day an open question although much progress has been made recently.10 It involves the interactions between liquids and solids and the electrification of the contact. In this context it finds its explanations in the mechanics that govern triboelectric phenomena.11,12
The remaining part of this review proceeds as follows. In the second part, we will mainly focus on triboelectric energy harvesting systems. We will start with the state of art charge separation mechanisms taking place in liquids, or at the contact between a liquid and a solid surface due to the supply of mechanical energy. Based on these principles, innovative devices for the recovery of the mechanical energy of raindrops or waves are presented. A brief discussion on economic viability is provided at the end of this part. The third part will deal with the recovery of osmotic energy from salted gradient. Here we will present the main techniques including pressure retarded osmosis, reverse electrodialysis, capacitive mixing and capacitive reverse electrolysis. Present technological challenges and economic evaluations of these techniques are discussed in this part. A comprehensive conclusion, which summarizes the present research advancement as well as encouraging perspectives in this field, is provided at the end.
2 Triboelectric energy harvesting
When two materials or a material and a fluid come into contact by friction, the materials and the fluid become electrically charged. This effect, known since ancient Greece, is called the triboelectric effect. Despite the fact that it is observed on a daily basis, it has only recently been partially explained. In the following section we will clarify this point and in particular illustrate the recent work that explains charge separation. It is possible to take advantage of this phenomenon to create an electric current. The presence of triboelectric charges on the dielectric surfaces can be a force that pushes the electrons in the electrode to flow in order to balance the electric potential drop created. Based on this observation, Wang invented TriboElectric NanoGenerators (TENGs).13,14 In the second subsection of this part we will see how these devices work by focusing on devices that consist of a liquid and a material. The last subsections are devoted to economic analysis and perspectives of TENGs.2.1 Contact electrification and charge electrification
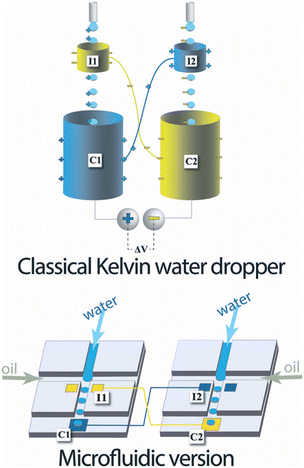 | ||
| Fig. 1 Top, classical Kelvin water dropper, bottom, representation of the microfluidic version (figures and captions reproduced from ref. 16 with permission from Royal Society of Chemistry, copyright 2013). | ||
At the end of the 20th century, this experience was redesigned to increase the recoverable energy density. Marin et al.16 proposed a microfluidic version of the device in 2013. The device consists of two microfluidic drop generators on different chips. Each chip comprises two types of electrodes: an electrode analogous to the ring of the Kelvin system close to the emission zone of the drops and an electrode further on the channel which recovers the charges. They demonstrated a successful formation of charged liquid drops by this microfluidic system.
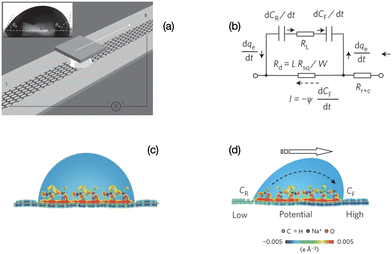 | ||
| Fig. 2 Mechanism of charge separation on graphene. (a) Illustration of the experimental set-up. A liquid droplet is sandwiched between graphene and a SiO2/Si wafer, and drawn by the wafer at specific velocities. Inset: A droplet of 0.6 M NaCl solution on a graphene surface with advancing and receding contact angles of 91.98° and 60.28°, respectively. (b) Equivalent circuit for (d). (c) Schematic illustration of the pseudo-capacitance formed by a static droplet on graphene. (d) Schematic illustration of the potential difference induced by a moving droplet (figures and captions reproduced from ref. 19 with permission from Springer Nature, copyright 2014). | ||
When the drop moves, there is a constant supply of positive charge towards the front of the drop. Thus there is a constant supply of electrons at the front interface. Similarly, there is a constant departure of electrons from the back of the drop. These two phenomena induce an electric current in the graphene and a potential difference between the front and the back, with the electric potential at the front being higher than the electric potential at the back. The density power19 is 19.2 nW cm−2 which corresponds to an efficiency of 1%.
Charge separations have also been demonstrated when a graphene-covered surface is dipped in an electrolyte20 (see Fig. 3). The sodium ions in the electrolyte adsorb rapidly on the surface. Chlorine ions move less rapidly towards the surface from which they are repelled. It therefore takes time to cancel this charge separation. During this time, the electrons in the graphene move closer to the sodium ions, creating holes in the graphene. A difference in the concentration of holes appears along the material and thus leads to the creation of a potential difference and an electric current. When the plate is removed from the liquid, the opposite phenomenon occurs, resulting in an electronic current in the opposite direction. Maximum voltages of 100 mV and maximum currents of 11 μA are measured for surfaces of 20 cm2. The powers are therefore very low. The authors consider that their work can have an impact in the field of sensors.
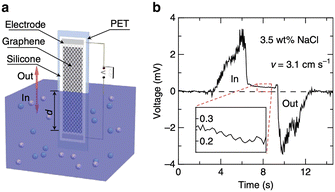 | ||
| Fig. 3 a, Schematic illustration of the experimental set-up: moving the graphene sample on a polyester terephthalate substrate vertically across the water surface within a container. All the edges of the graphene sheet and silver emulsion electrodes are protected with silicone. b, Typical voltage signals produced as a sample is inserted and pulled out of 0.6 M NaCl solution (3.5 wt%) at a velocity v = 3.1 cm s−1 (figures and captions reproduced from ref. 20, with permission from Springer Nature copyright 2014). | ||
At this stage we are not aware of any development of these graphene-liquid systems leading to real efficient devices. However, these new reflections have the merit to improve the understanding of the electrification phenomena. To conclude this section, in the above-mentioned graphene-based charge separation processes, graphene itself presents no permanent static surface charges. The electric current is generated by potential differences and dynamic concentration imbalances. In the following, we will present several charge separation mechanisms involving the creation and use of charged surfaces.
The electrification of the contact allows to create currents. Let's consider the contact between PDMS (polydimethylsiloxane) and copper lubricated by water. The set-up developed by Lin et al.26 to study this process, encompasses a PDMS layer on which a pyramid-shaped structure has been lithographically etched, a layer of water and a poly(methyl methacrylate) (PMMA) plate covered with a copper film (see Fig. 4). At initial state, a drop of DI water is placed onto the copper thin film, which is noted as electrode 1. For electrode 2, the structured side of the PDMS film is facing the electrode 1, while the other side is covered with a copper thin film. A drop of DI water is deposited onto electrode 1 on the copper surface. When the PDMS comes into contact with the liquid, the ionization of these surface groups induces the appearance of a positive surface charge in the liquid volume and a negative one on the polymer surface.
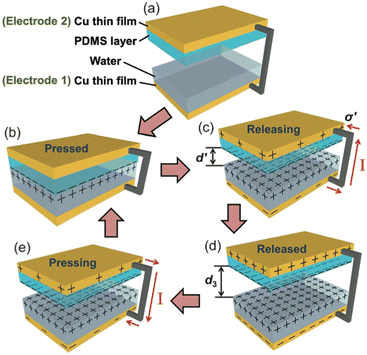 | ||
| Fig. 4 Working mechanism of the water-TENG. (a) Initial status without any external force applied. (b) External force brings the PDMS layer into contact with water. (c) Removing the PDMS layer from the water surface. (d) PDMS layer returning back to the original position. (e) External force applied makes the PDMS layer contact with water again. For simplification, both PMMA substrates are not shown (figures and captions reproduced from ref. 26) with permission from John Wiley and Sons, copyright 2013. | ||
When the PDMS is removed from the liquid, its hydrophobic character induces the charge separation. The PDMS carries a net negative surface charge and the liquid a positive charge. This charge is greater the more easily water is drained from the PDMS surface. As said before, the hydrophobic character of PDMS is fundamental to ensure charge separation. A maximum surface charge is generated when the water is completely drained from the PDMS surface in an ideal case. If the two copper films are electrically connected, a flow of electrons occurs between the copper film covered by the PDMS which is negatively charged and the copper film covered by the water drop which is positively charged so as to counterbalance the charges. When the PDMS re-enters the liquid, its charge is locally neutralized by the charge of the liquid. Thus the electrons make the opposite path, results in a capacitive current in the opposite direction. This new prototype of triboelectric contact by charge exchange between a solid surface and a liquid surface produces a current of 2.45 mA m−2, a peak voltage of 52 V and a peak power (not average) of 0.13 W m−2 which allows to power 60 LEDs simultaneously. It is worth to be noted that the measured effect strongly decreases when deionized water is replaced by salt water. The power decreases by a factor of 4 when the authors use a 0.6 M NaCl solution instead of deionized water. This explanation is suitable for a surface carrying ionizable groups but is not satisfactory on PTFE surfaces or oxide surface. In this last situation, the interaction of the ions of the solution with the surface is put forward.
Surface charge, wherever it comes from (electrons from water or ions adsorption), seems also to be at the origin of the production of charged drops. We have just seen that the contact of a drop of water on a surface can create surface electrostatic charges and induced currents. A similar mechanism can occur when a liquid flows over a surface. The electrification of the drop after its emission from a nozzle or a capillary has generated a lot of activities over the past 20 years. The surface of the nozzle or capillary27 has a surface charge.28 When liquid flows, it will first take away the released counterions which balance the surface charge and reveal a charged surface. Then through the capillary or the nozzle, a layer of counterions will build up at the liquid–wall interface. The whole wall of the tube, electrolyte in the tube is neutral. However, the tube wall and the electrolyte each carry a surface charge which is opposite. The value of the charge depends on the pH, the concentration of electrolytes, the capillary coating and little on the humidity value. This explains why the drops coming out of a capillary are charged. This natural electrification of the droplets does not come from pre-existing free charges on the capillaries but from a charge separation mechanism between a droplet and the surface of the pipette tip which carries a static electric charge. The chemical balance of the surface is not affected by the flow. This causes the upper liquid upstream of the capillary to become inversely charged. The existence of charged drops will be used in the following to generate energy producing devices.
2.2 Applications to energy harvesting devices
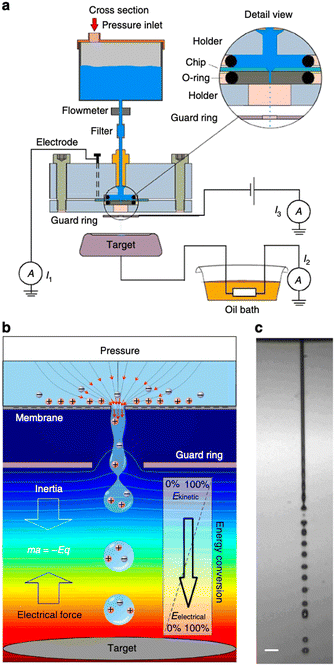 | ||
| Fig. 5 Concept of energy conversion and set-up. a, Experimental set-up. Aqueous solution is forced by applied air pressure through a 10 or 30 mm diameter circular pore in a 500 nm-thick silicon nitride membrane. A platinum electrode sputtered on the backside of the chip (30 mm pore experiments) or an inserted platinum wire (10 mm pore experiments) was connected to a picoammeter (Keithley 6485). A microjet is formed that breaks up in a droplet stream. The droplets travel through the air and arrive on a metal target placed at 7.5–25 mm distance from the pore opening. The target is connected to electrical ground via a high-load resistance. A metal guard ring with an opening of 2 mm diameter is placed at 1.5 mm (10 mm pore) or 5.0 mm (30 mm pore) from the pore exit and maintained at ground potential, or at a negative potential for inductive droplet charging. The current can be measured between ground and the platinum reservoir electrode (denoted I1), between target and ground (I2) and between metal guard ring and ground (I3). b, Conceptual illustration of the conversion principle. Water is accelerated to form a microjet that breaks up into charged droplets. On their air trajectory towards the target, the droplets are decelerated by the electrical force, converting kinetic energy into electrical energy. The background colour from red to blue indicates the voltage distribution from high to low, the lines denote equipotentials. c, Photomicrograph of the microjet from the 10 mm pore taken by double iLIF illumination. Scale bar, 40 mm (figures and captions reproduced from ref. 29 with permission from Springer Nature, copyright 2014). | ||
The authors claimed that the system displays a conversion efficiency up to 48% and may generate a power density of 160 kW m−2 if scale up holds. These figures are excellent. However, although promising, the device is far from being developed as an application. The main disadvantage of this system is that it does not provide for a surface discharge phase. Indeed, in order to produce energy in a system that induces ion flows and then capacitive electron flows, it is necessary either to imagine a process that induces reverse flows, or to set up reactions that consume the charges produced by faradaic reactions. In other words, it is necessary to manage to discharge the surfaces, to depolarize them in order to be able to cycle as in the case of triboelectric systems. Moreover, even if this problem is solved, the system will face the same energy storage problem as triboelectric systems. This system has a very small output impedance and the energy transfer efficiency will be very low. This work has not led to any application developments in the literature but as we said before it is one of the most promising.
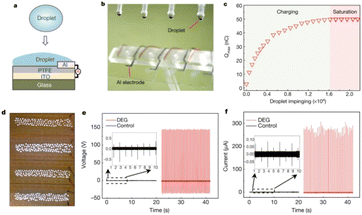 | ||
| Fig. 6 Schematic illustration of droplet-based electricity generator (DEG). (a) Schematic diagram. (b) Optical image showing four parallel DEG devices fabricated on a glass substrate. The volume of each droplet is 100.0 μl. (c) As individual droplets continue to impinge on the as-fabricated device, the amount of charge on the PTFE surface increases gradually and eventually reaches a stable value. (d) One hundred commercial LEDs can be powered when one droplet, released from a height of 15.0 cm, is in contact with the device. (e) Under the same experimental conditions (for example, the same droplet size and height of release), the output voltage measured from the DEG (in red, with the frequency of impinging droplets being set at 4.2 Hz, and the total number of droplets being about 84) is more than two orders of magnitude higher than that from the control device (in black, with a droplet frequency of 1.0 Hz, and a total of 20 impinging droplets). The negligible electricity generation from the control device is limited by the interfacial effect, although its PTFE surface is loaded with the same amount of charge as the DEG. (f) Comparison of output current from the DEG (in red) and the control device (in black) in response to continuous impinging of individual droplets (figures and captions reproduced from ref. 30 with permission from Springer Nature, copyright 2020). | ||
At this stage we are not aware of the industrial development of this device. The electrification of liquid–solid contacts, that is to say the triboelectric process, is the technique closest to applications and commercialization. We will describe these points in the next subsection.
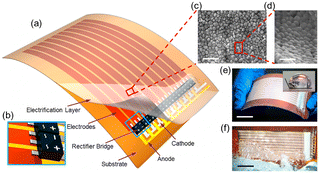 | ||
| Fig. 7 Structure of a thin-film triboelectric generator (TF-TEG). a, Schematic diagram of an integrated TF-TEG. b, Enlarged sketch of the arrayed bridge rectifiers. c, SEM image of the PTFE nanoparticles on the electrification layer (scale bar = 1 μm). d, Enlarged view of the nanoparticles at a tilted angle of 60° (scale bar = 500 nm). e, Picture of a bendable as-fabricated TF-TEG. Inset: Water contact angle on the nanostructured surface (scale bar = 25 mm). f, Picture of the TF-TEG that is interacting with the water wave (scale bar = 25 mm) (figures and captions reproduced from ref. 33 with permission from American Chemical Society, copyright 2015). | ||
When the water comes into contact with the PTFE, the latter acquires a permanent electrostatic surface charge as explained above in the text.31,49 During the following phases when the water advances on the surface, the positive ions it contains are adsorbed on the PTFE due to the existence of negative surface charge. As seawater propagates over the surface, this creates a charge gradient on the material, with the emerged part having zero charge and the dry part carrying an unbalanced negative charge. (see Fig. 8). Electrons move away from electrode A whose surface charge is neutralized by the propagating water and head towards electrodes B and C which are both negatively charged (see Fig. 8).
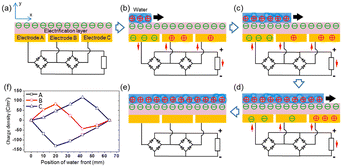 | ||
| Fig. 8 Electricity-generating process of the TF-TEG. (a) Cross-sectional view of charge distribution when the device is fully exposed from water. Charge distribution when water is propagating across (b) electrode A, (c) electrode B and (d) electrode C. (e) Charge distribution when water fully covers the electrification layer underneath. (f) Charge density on the three electrodes as the water front propagates (figures and captions reproduced from ref. 33 with permission from American Chemical Society, copyright 2015). | ||
When the water recedes, an electrical reverse current is measured using the same principle. The use of bridge rectifiers makes it possible to recover a current that always flows in the same direction. Thanks to the use of rectifier bridges, it is possible to rectify the current and to sum currents of the same sign, which opens up the possibility of device scaling up. Due to the wetting properties, static charges remain on the PTFE. (We recall that the most probable mechanism responsible for the appearance of this charge is the permanent adsorption of OH− ions). The authors measure a peak output power of 1.1 mW. This device can power a total number of 10 light emitting diodes.
In the same spirit, Wang et al.50 have developed a device which recovers the energy dissipated during the navigation on the hull of a boat. The originality of this work, which is complementary to the previous one, consists in the development of a coating that avoids the proliferation of algae and microorganisms on the triboelectric layer. The device has excellent stability and high performance. It allows several LEDs to be illuminated during navigation. Currently, many groups51,52 are studying PTFE for energy harvesting applications based on liquid–solid contact electrification. This material is one of the most promising. It is possible38 to recover 3 W m−2 in the best conditions.
| Materials | Output current (μA) | Power (μW) | Power density (W m−2) | Comments | Ref. |
|---|---|---|---|---|---|
| CYTOP | 30 | 103 | — | Water drops plus electret | 34 |
| FEP | 2.6 | 1.2 × 105 | — | Water drops, an efficiency of 7.7% | 35 |
| FEP-PTFE | 5.1 + 4.3 | 41.2 + 3.03 | — | Hybrid TENG (interfacial electrification TENG (IE-TENG) + impact-TENG) | 36 |
| HCOENPs-coated fabric-PET | 3.2 | — | 0.14 | Wearable all-fabric-based triboelectric generator | 37 |
| Graphene | 1.7 | 1.92 × 102 | — | Efficiency of 1% | 19 |
| PDMS-Cu | 2.45 × 103 m−2 | — | 0.13 | Water-TENG | 26 |
| PDMS-PTFE | 5.5 | 1.2 × 103 | 3 | Water-TENG | 38 |
| PTFE | 0.553 | 1.2 | — | Water drops | 39 |
| PTFE | 17 | 145 | — | Superhydrophobic micro–nanostructured polytetrafluoroethylene (PTFE), water drop contact electrification | 40 |
| PTFE | 12.9 + 3.8 | — | 0.59 + 0.03 | Hybrid TENG (water-TENG + disk-TENG), water flow rate 54 mL s−1 | 41 |
| PTFE | 13 | 1.1 × 103 | — | Thin-film TENG | 33 |
| PTFE-FTO | 1.8 | — | 0.01266 | Multi-unit transparent TENG, flow rate 45 mL s−1 | 42 |
| PTFE-ITO | 270 | — | 50.1 | Water drop contact electrification | 30 |
| PTFE-nylon | 0.54 | — | 1.838 | Bi-electrode freestanding mode TENG (BF-TENG) | 43 |
| PVDF-Al | 1.67 | — | 0.02653 | Unsteady peristaltic flow induced pulsatile flow-TENG (PF-TENG) | 44 |
| PVDF-Al-FEP | 6.2 | 1.34 × 104 | — | Coupled TENG and piezo ENG | 45 |
| PVDF-BOPP | 2.4 | 11.5 | — | Fluid-based TENG | 46 |
| PVP | 5.3 | — | 0.5 | Power peak to peak, water drops | 47 |
| Superhydrophobic TiO2 + SiO2 | 43 + 18 | — | 1.31 + 0.18 | Hybrid TENG (water-TENG + contact TENG), flow rate 40 mL s−1 | 48 |
2.3 Economic analysis
The levelized cost of electricity LCOE is the cost necessary to produce electricity from a process, taking into account the materials, resources needed for the production, the life time and the maintenance during the process. In 2022, The BloombergNEF report estimates LCOE for onshore wind to be 0.044 $ per kW h and 0.042 $ per kW h for solar PV without storage.53 The LCOE of storage is estimated in the same report to be 0.146 $ per kW h. The US average LCOE of wind projects built in 2021 was 0.031 $ per kW h.54 It becomes very complex to give that of gas and fossiles combustible in the context of the war in Ukraine. Before the Ukraine war in 2021, the LCEO of gas was 0.081 $ per kW h.53 The LCOE of triboelectrical generators has been estimated by Ahmed et al.55 and is comprised between 0.02 and 0.09 $ per kW h. Unsurprisingly, this figure is lower than that for renewable and fossil fuels. The triboelectric devices are made of polymers and conductive layers already very present in the industrial world. The costs of these materials are low. Efficiency and module lifetime are the most sensitive factors for the LCOE of TENG. The lowest value of the LCOE assumes a life time of 15 years. In the same work,55 the authors evaluated the Energy PayBack Time (EPBT) of a TENG, i.e. the time needed to produce the same amount of electricity (converted into equivalent primary energy) with the energy consumed during its life cycle. The two generators used have EPBT comprised between 0.1 and 0.25 year. These values are lower than those of the solar devices which are included between 0.3 and 2.5 years depending upon the different technologies. TENGs are more efficient and have a smaller energy footprint than photovoltaic cells. Indeed their manufacture does not require to purify and to treat silicon or rare elements necessary to the constructions of photovoltaic cells. These processes consume a lot of energy. A comprehensive analysis points out, that to improve these performances, more efforts should be made to increase the lifetime and the efficiency of TENGs rather than to identify cheaper materials and fabrication processes.2.4 Perspective dealing with TENG
The results presented in this section are very encouraging and show the potential for commercial applications. The performances of some of these devices are reported in Table 1. The power densities that can be obtained are variable and range according to the experimental conditions from mW m2 to 50 W m2. Couplings between different devices (e.g. PiezoENG coupling with a Water TENG45 or a Water TENG coupling with a Solid Contact TENG36,48) seem very promising. However, there is still a lot of work to be done to bring these techniques to the commercial level. There is a need to increase the energy conversion at the triboelectric layer level. This requires a better understanding of the physical mechanisms related to triboelectricity. Although triboelectric series have been established for a long time, the study of liquid–solid contacts calls for their modification. This requires research into new materials, new composites involving carbon nanotubes,56 graphene57 and systematic studies. These materials must be mechanically resistant, hydrophobic and possess a high surface charge. The energy storage at the device output has to be improved. Indeed, most of these devices have very low output impedances which strongly limit their use in the context of charging a battery or a super capacitor. The capacity of a TENG is very small of the order of 100 pF. These characteristics result in a low energy transfer efficiency, whether for charging a battery or powering electronic devices. These later generally have a much higher impedance (100 of μF). In order to transfer a maximum amount of energy, it is important to insert an electronic stage between the battery or the super capacitor that allows to adapt the impedances. This can be achieved by using N capacitors in series on charge and in parallel on discharge (basic switched capacitor convertor) or a fractal design based switched-capacitor-convertor (FSCC).58 In the last situation, a energy transfer of 94% with an impedance reduction of 750 has been demonstrated. Last but not the least, the durability of the materials has to be improved. Moreover, it should be noted, that polymer devices are easily corroded by seawater.59 Thus, some of the wave energy harvesting devices involve fully enclosed TENG devices whose review is beyond the scope of this work.60–64 The power density of some of these devices64 may reach 10.6 W m−3.In the following part, we will focus on osmotic energy harvesting. The technologies for saline gradients recovering emerged earlier and thus are more mature than the above-mentioned ones. There were already several pilot-scale attempts in industrial field, as well as other novel trials planned in the future. Considering the present energy crisis, these osmotic based energy harvesting systems might reach the threshold of economical viability soon.
3 Osmotic energy harvesting
The osmotic energy released during the process of mixing solutions of different salinity is clean and renewable energy. It is nicknamed blue energy.65,66 Naturally, a spontaneous and irreversible mixing of river water and sea water happens at the estuary, resulting in an entropy increase of the system.67 A precise and engineering control of this entropy change procedure enables the blue energy harvesting. The potential of blue energy can be estimated by thermodynamics studies. The non-expansion work released from the mixing of seawater and freshwater can be described by the Gibbs free energy of mixing ΔGmix at a constant pressure P and at absolute temperature T.| ΔGmix = Gmix − (GH + GL) | (1) |
As the Gibbs free energy is defined as 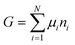 , where μi and ni represent the chemical potential and the mole number of species i for a system consists of a number of N species. The chemical potential μi is defined as
, where μi and ni represent the chemical potential and the mole number of species i for a system consists of a number of N species. The chemical potential μi is defined as 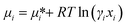 where
where 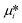 is the standard chemical potential, R perfect gas constant. γi and xi represent the coefficient of activity and the mole fraction of species i, respectively. For a system of volume V, the molar concentration is defined as ni = ciV, where ci is the molar concentration of species i. Thus the Gibbs free energy of mixing can be calculated as:68
is the standard chemical potential, R perfect gas constant. γi and xi represent the coefficient of activity and the mole fraction of species i, respectively. For a system of volume V, the molar concentration is defined as ni = ciV, where ci is the molar concentration of species i. Thus the Gibbs free energy of mixing can be calculated as:68
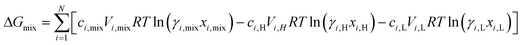 | (2) |
3.1 Pressure retarded osmosis
As an emerging energy harvesting system, the technology of pressure retarded osmosis (PRO) is attracting much attention.71,72 Semipermeable membranes, which allow the passage of water molecules and block the passage of ions, are used in the configuration of PRO systems.73 To better illustrate the power generation principle of PRO, an introductory explanation of the osmotic process across the semipermeable membrane is given in the following paragraph.The observation of osmotic phenomenon was firstly documented by Jean-Antoine Nollet. It describes the spontaneous movement of a solvent flux moving across the semipermeable membrane towards a solute of higher concentration, in the way of balancing solute concentrations on both sides of the membrane.75 The concentration difference across the membrane results in an osmosis pressure difference Δπ. Additional hydraulic pressure ΔP could be applied on the system to influence the solvent flux. Description of the water (solvent) flux Jw is an essential parameter in the description of osmotic phenomenon. It can be theoretically described as a function of the applied hydraulic pressure difference ΔP and the effective osmosis pressure difference Δπ for an ideal membrane as Jw = Ax(Δπ − ΔP). Here Ax refers to the permeability of the membrane.76
Based on the comparison between ΔP and Δπ, osmotic process can be briefly classified into four categories as illustrated in Fig. 9(a).74 The Forward osmosis (FO) corresponds to a trivial case where ΔP is zero, indicating no mechanical work in this process. In this case, water flux is driven by the osmotic driving force, penetrating the semipermeable membrane and proceeding to the draw solution side. While applying a hydraulic pressure difference on the feed solution compartment (ΔP < 0), the above-mentioned process is further assisted and accelerated in the so-called procedure of pressure assisted osmosis (PAO). In the case where ΔP > Δπ, the direction of the water flux is reversed (from draw solution to feed solution) due to the external hydraulic pressure. This procedure is named as reverse osmosis (RO) and has intriguing applications in water desalination. It is to mention that both PAO and RO are energy consuming processes. On the contrary, PRO is the only power generating process where the water molecules move from feed solution towards the pressurized draw solution under osmotic effect (0 < ΔP < Δπ). The pressurized solution is then utilized to drive turbine systems for electricity power generation. A complete description of the water flux (Jw) and the power density (W) of each osmotic process is illustrated in Fig. 9(b and c).74
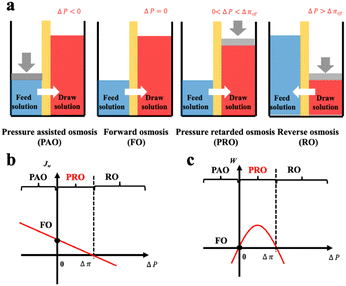 | ||
| Fig. 9 Schematic illustration a, and analysis b and c, of four classic membrane-based osmotic processes of pressure assisted osmosis (PAO), forward osmosis (FO), pressure retarded osmosis (PRO) and reverse osmosis (RO) (figures and captions reproduced from ref. 74 with permission from Elsevier, copyright 2021). | ||
Fig. 10 presents a typical configuration of the PRO plant. Feed solution and draw solution are both filtered and pumped into the PRO module. Under the osmotic effect, a water exchange flow rate (ΔQ) is created near the semipermeable membrane moving from feed water side towards draw water side. The brackish water received in the feed water chamber presents a higher flow rate of (ΔQ + QH) and a higher hydrostatic pression PH. The brackish water is then divided into two streams, where one stream is depressurized to drive turbine systems and produce electricity and the other one is delivered into a pressure exchanger to maintain the incoming pressure of draw solution.77 Here the gross power density of a PRO system can be experimentally calculated as78
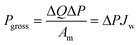 | (3) |
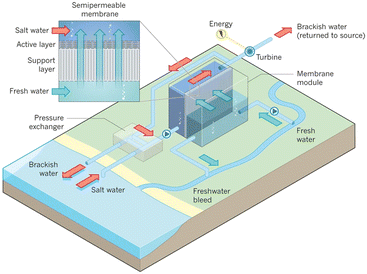 | ||
| Fig. 10 Schematic illustration of the working principle of PRO systems. Feed solution and draw solution are injected continuously into water compartments which are separated by semipermeable membranes. Driven by effective osmotic force, water flux flows across the membrane from freshwater compartment towards saltwater compartment, resulting in a concentration decrease and a flow rate increase in draw solution compartment. The pressurized water flux is then split into two fluid streams: one fluid stream is used for electricity generation by driving an installed turbine, while the other stream returns to a pressure exchanger to maintain the pressure of draw solution (figures and captions reproduced from ref. 80 with permission from Springer Nature, copyright 2012). | ||
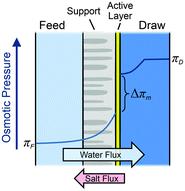 | ||
| Fig. 11 Illustration of the semipermeable membrane cross section composed of an active layer and a support layer. A qualitative presentation of osmotic pressure profile across the membrane is presented (figures and captions reproduced from with permission ref. 78 with permission from Royal Society of Chemistry, copyright 2016). | ||
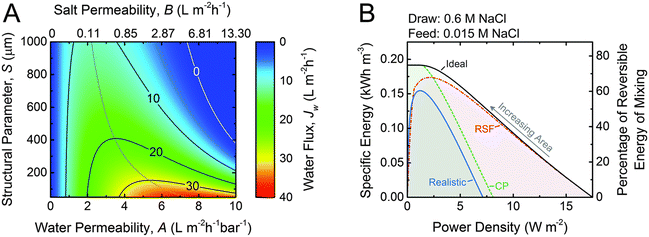 | ||
| Fig. 12 A. Coupon-scale water flux Jw as a function of the water permeability coefficient, A; NaCl permeability coefficient, B; and support layer structural parameter, S. The water permeability and salt permeability are linked by the permeability-selectivity trade-off. B. Specific energy and power density for counter-current membrane modules with increasing membrane area from right to left. Data for three types of membranes are shown: ideal (solid black line), RSF (dash dotted red line) and CP (dashed green line) and realistic (solid blue line) (figures and captions reproduced with permission from ref. 78 with permission from Royal Society of Chemistry, copyright 2016). | ||
One of the major obstacles of membrane applications is the polarization effect, which refers to the ion accumulation phenomenon near the semipermeable membrane. The internal concentration polarization (ICP) corresponds to an immobile area clogged with ions in the dense support layer.81 External concentration polarization (ECP) occurs at the interface between active layer and the draw solution (dilutive ECP) or feed solution (concentrative ECP). Concentration polarization effect deteriorates the osmotic driving force across the membrane, thus leads to lower effective membrane performances and power density output.82 In addition, the imperfection of membranes could lead to ion leakage from draw solution to feed solution, which is named as reverse salt flux (RSF).83 The trace leakage might cause more severe ICP effect in the system, lower the power density output, and could possibly promote membrane fouling problems,84 which is also one of the major limitations on PRO power density output. A theoretical analysis of the impact of ICP and RSF was conducted by Straub et al., as illustrated in Fig. 12(B). An apparent drop in power density is observed under the synergistic effect of ICP and RSF.78
Biofouling is a common problem for the industrial application of membranes. It influences severely the membrane performances in practical use, hinders the lifespan of membranes and raises additional fees for water pre-treatment.85 The mechanical strength of membranes is also the key point for the development of PRO performances and its commercialization.74
In general, ideal PRO membranes should reach the following criteria: large water permeability, high salt rejection (high membrane selectivity), low reverse flux, limited biofouling problems and reinforced mechanical strength.86 Precise engineering of the membrane's properties, including layer thickness, geometry configuration, porosity, selectivity and etc., is summarized in the following paragraph.
Flat-sheet PRO TFC membranes consist of a highly-porous support layer and an active layer to reinforce its selectivity.93 Polyamide (PA) is commonly chosen as the active layer, which is polymerized over the interface of the support layer through the phase inversion polymerization.86 Various works were realized to optimize the permeability and structure integrity, aiming to ameliorate the power density output of PRO systems.
Table 2 lists the present work of flat-sheet PRO TFC membranes in literature.
| Materials | Concentration gradient | Hydraulic pressure (bar) | Power density (W m−2) | Comments | Ref. |
|---|---|---|---|---|---|
| PA/PSf-PET | DI/0.5 M | 12 | 10 | NaOCl, NaHSO3 and heat treatment | 94 |
| PA/PI | DI/1.0 M | 15 | 7–12 | NaOCl, NaHSO3 and MeOH treatment | 123 |
| PA/PAN | DI/3.5% (w/w) | 10 | 2.6 | NaOCl and NaHSO3 treatment | 124 |
| PA/PAI | DI/3.5% (w/w) | 6 | 2.84 | PDA coating and NaOCl, NaHSO3, EtOH treatment | 96 |
| PA/PI | DI/1.0 M | 9 | 6.0 | PA blended with moderate p-xylylenediamine | 125 |
| PA/PAN | 80 mM/1.06 M | 22 | 15.2 | NaClO treatment | 126 |
| PA/PI | DI/1.0 M | 22 | 18.1 | PA modified with DMF and SDS | 127 |
| PA/PAN-PE | DI/0.5 M | 11.5 | 8.0 | PA selective layer of mTFC/pTFC | 99 |
| CTA membrane | DI/3.0 M | 48 | 60 | — | 128 |
| PA/PEI | 10 mM/1.0 M | 17.2 | 12.8 | — | 129 |
| PA/PEI | DI/1.0 M | 16.9 | 17.3 | Tiered PEI nanofibrous support with multi-walled CNTs | 100 |
| PA/PSf-PET | 10 mM/1.0 M | 18.4 | 7.1 | — | 130 |
| PA/PES | DI/0.5 M | 6 | 1.6 | CNT-embedded-PES with NaOCl and NaHSO3 treatment | 97 |
| PA/PSf | DI/1.0 M | 22 | 12.9 | PSf support layer reinforced by PVP | 98 |
| PA/PES-PET | DI/1.0 M | 25 | 12.5 | — | 131 |
| PA/PK | DI/0.6 M | 28 | 6.1 | PK reinforced by PED non-woven fabric | 132 |
| GO membrane | 17 mM/1.0 M | 6.9 | 12.8 | — | 133 |
| PA/PET | DI/1.0 M | 21 | 12.1 | PSf/GO and PSf/HNT (dual layer) nanocomposite on PET | 101 |
| PA/TR-PBO | DI/1.0 M | 15 | 17.9 | TR-PBO (thermally rearranged polybenzoxazole-co-imide) | 104 |
| PA/PAI | DI/1.0 M | 21 | 12.1 | PA incorporated with SNW-1 nanocomposite | 102 |
| PA/TR-PBO | DI/3.0 M | 27 | 87.2 | TR-PBO ESMs exposed to direct fluorination | 105 |
| PA/TR-PBO | DI/1.0 M | 21 | 26.6 | TR-PBO modified with PVA coating | 134 |
| PA/PE | DI/1.0 M | 20 | 35.7 | PA formed by toluene-assisted IP | 103 |
It was demonstrated that membrane post-treatment of PA active layer could significantly increase the power density of PRO systems. Yip et al.94 compared the performance of membranes with and without NaOCl and NaHSO3 solution immersion and heat treatment. The highest power density output is predicted to be 10 W m−2 with proper post-treatment. A detailed study on membrane post-treatment was conducted by Han et al.95 An optimal post-treatment condition was reported to generate a power density of 12 W m−2 under a hydraulic pressure of 15 bar. Integrating additives into support layer is another common strategy applied in membrane research for PRO applications. Li et al.96 realized polydopamine (PDA) modification onto the polyamide-imide (PAI) support layer. Son et al.97 successfully embedded carbon nano tubes (CNTs) into the polyethersulfone (PES) support layer, obtaining a power density output of 1.6 W m−2 at a hydraulic pressure of 6 bar, using deionized (DI) water and NaCl solution of 0.5 M. Wei et al.98 realized polysulfone (PSf) support layer reinforced by polyvinylpyrrolidone (PVP), and obtained a maximum power density of 12.9 W m−2 at hydraulic pressure of 22 bar.
Flat sheet membranes could also be prepared by electrospun polymeric supports of high porosity and tortuosity. A highly-porous support layer was realized by Bui et al.99 by electrospinning polyacrylonitrile (PAN) nanofibers onto a polyester (PET) fabric substrate. Tian et al.100 prepared tiered polyethylenimine (PEI) nanofibrous support incorporated with multi-walled CNTs. Use of such membrane in PRO system generates a power density of 17.3 W m−2. A dual layer of PSf/GO (graphene oxide) and PSf/HNT (halloysite nanotube) of nanocomposite on PET was prepared by Lim et al.101 to ameliorate water permeability.
The possibility of incorporating nano-sized materials into conventional membranes has been well developed by researchers. Gonzales et al.102 incorporated Schiff base network-1 (SNW-1) nanocomposite into the PA active layer preparation. The PRO system reached its maximum performance of 12.1 W m−2 with DI water and brine water of 1M. Kwon et al.103 realized a toluene-assisted interfacial polymerization to fabricate active layer of PA onto a polyvinyl alcohol (PVA)-coated polyethylene (PE) support. An astonishing power density of 35.7 W m−2 was reported for a hydraulic pressure of 20 bar. Recently, a Korean research group reported a novel thermally rearranged TFC membrane containing polybenzoxazole-co-imide (TR-PBO) combined with a PA layer.104 A giant power density increase towards 40 W m−2 was reported in its first work. Later, modification with fluorination on TR-PBO membranes ameliorate the output power density towards 87.2 W m−2 in PRO applications.105
There is no doubt that tremendous advances were achieved in flat-sheet PRO TFC membranes. However, most published works presented here focus on gross power densities, calculated by eqn (3). Actually, the module gross power densities presented here differ from the net power density due to the irrecoverable pumping energy input and the energy losses during electricity generation in turbine systems.106 Taken into consideration the pumping energy inputs and energy losses, the net power density in published works might be much lower than its gross value. A detailed economic analysis of PRO systems will be given later.
In conventional PRO configuration using flat-sheet membrane, a feed spacer is needed to maintain the feeding channel geometry and reinforce the mass transfer near the membrane.107 Such configuration decreases the hydraulic pressure and results in an energy loss in the PRO system.108 In addition, feed spacers might cause membrane deformation at high hydraulic pressure, inducing severe reverse solute diffusion of the membrane and leading to performance loss.86
Different from flat-sheet membranes, hollow fiber PRO TFC membranes have a self-supporting tubular shape of higher effective surface area. Such geometry avoids the use of feed spacers, thus limit the deformation failure in flat-sheet based PRO systems. The PRO module using hollow fiber membranes could also achieve a higher pack density, which could efficiently ameliorate output performances.109 The major preparation method of the hollow fiber membrane is the phase separation spinning, including non-solvent induced phase separation (NIPS) or thermal induced phase separation (TIPS).77
The first work dealing with hollow fiber TFC membranes for PRO application was realized by Chou et al.110 They successfully prepared a tubular self-supporting membrane made of PES as the supporting substrate and PA as the selective layer. A maximum power density of 10.6 W m−2 could be achieved by using the home-made hollow fiber PRO membrane with a salt concentration of 40 mM and 1 M for fresh and salt water chambers, respectively. The same group prepared a novel hollow fiber TFC membrane using PEI as the supporting substrate.111 This PEI based hollow fiber membrane presents superior mechanical strength and shows a better power density output of 20.9 W m−2 under a hydraulic pressure of 15 bar.
Similar to flat-sheet PRO TFC membranes, chemical modifications on selective layer and the supporting substrate are both widely investigated in the research field. The work of Ingole et al.112,113 proves the effectiveness of PDA coating on PES supporting substrates in PRO applications. A power density increase from 1.62 W m−2 to 3 W m−2 is realized due to the additional coating. Grafting of chemical groups on supporting substrates were also reported in literature.114,115
Ingole et al.116 prepared CA layer treated with tributyl phosphate (TBP) onto the supporting substrate of PES with PDA coating. An improved power density of 3.9 W m−2 is achieved with the same brine water and fresh water conditions used in their previous work. Zhang et al.117 reported a novel supporting substrate of PES with PDA coating, grafted with dendritic-architecture sulfonated hyperbranched polyglycerol (SHPG). A superior resistance to protein adhesion and bacterial attachment is achieved due to the high wettability of the polymer brushes. A maximum power density at hydraulic pressure of 15 bar is reported to be 18.8 W m−2.
An emerging trend nowadays is to incorporate nanocomposites into membrane preparation. Zhao et al.118 grafted carbon quantum dots (CDQs) onto the PDA coating of the PES supporting substrate by covalent bonding during the hollow fiber membrane preparation. They obtained a maximum power density of 11 W m−2 at a hydraulic pressure of 15 bar. Another work of incorporating CDQs in PA selective layer was realized later by Gai et al.119 They reported a better power density of 34.2 W m−2 at hydraulic pressure of 23 bar. Park et al.120 incorporated graphene oxide nanosheets with PES supporting substrate.
In addition, numerous research work investigated on modifications of hollow fiber membranes to limit bio-fouling problems. Synthetic sea brine solutions with complex components were used in fouling experiments and the power density of PRO systems was tracked along the procedure. Zhao et al.121 reported the use of MPC (2-methacryloyloxyethylphosphorylcholine)-PDA coating on PES support layer to enhance anti-fouling capacities of the system. Le et al.122 presented the effect of using grated zwitterionic poly(sulfobetaine) on PA selective layers.
Table 3 lists the present work of hollow fiber PRO TFC membranes in literature.
| Materials | Concentration gradient | Hydraulic pressure (bar) | Power density (W m−2) | Comments | Ref. |
|---|---|---|---|---|---|
| PA/PES | 40 mM/1 M | 9 | 10.6 | — | 110 |
| PA/PEI | 1 mM/1.0 M | 15 | 20.9 | — | 111 |
| PA/PI | DI/1.0 M | 16 | 14 | — | 123 |
| PAN-PVP/PBI-POSS | 10 mM/1.0 M | 7 | 2.5 | — | 135 |
| PA/PI | DI/1.0 M | 20 | 7.6 | PDA coating | 136 |
| PA/PES | DI/1.0 M | 20 | 24.3 | — | 137 |
| PA/P84 co-polyimide | DI/1.0 M | 21 | 12 | — | 115 |
| PAN-PVP/PBI-POSS | 10 mM/1.0 M | 15 | 5.1 | PAN/PVP with APS post-treatment | 114 |
| PA/PI | DI/1.0 M | 15 | 16.5 | — | 138 |
| PA/PES | DI/0.6 M | 6 | 1.62 | — | 112 |
| PA/PES | DI/0.6 M | 7 | 3 | PDA coating | 113 |
| PA/PES | DI/0.6 M | 8 | 3.9 | PA treated with TBP with PDA coating | 116 |
| PA/PES | DI/3.5% (w/w) | 16 | 6.7 | PES grafted with HPG | 115 |
| PA/PI | DI/1.0 M | 16.2 | 12 | — | 139 |
| PA/PES | DI/1.0 M | 18 | 11.2 | — | 140 |
| PBI/PVP/PAN triple layer | 10 mM/1 M | 22 | 6.2 | — | 141 |
| PA/PES | DI/1.0 M | 20 | 7.8 | — | 142 |
| PA/PES | DI/1.0 M | 20 | 22.1 | Pre-stabilization | 143 |
| PA/PEI | DI/1.0 M | 17 | 9.6 | Pre-wetting | 122 |
| PA/PEI | DI/1.0 M | 13 | 13 | PA modified with APTMS | 144 |
| PA/PES | Wastewater/0.81 M | 15 | 7.7 | PES with MPC- PDA coating | 121 |
| PA/PEI | DI/1.0 M | 15 | 19.2 | — | 145 |
| PA/PEI | — | 17 | 9.5 | — | 146 |
| PA/PES | DI/1.0 M | 22 | 10.7 | — | 147 |
| PA/PES | DI/1.0 M | 20 | 22 | — | 148 |
| PA/PES | DI/1.0 M | 15 | 10.7 | PA dual layer on both sides | 149 |
| PA/PEI | DI/1.0 M | 15 | 16.2 | PA with LbL deposition of PAH and PAA | 146 |
| PA/PES | DI/0.81 M | 15 | 11 | PDA coating grafted with CQDs | 118 |
| PA/PES | DI/1.0 M | 20 | 20 | PES with CaCl2 additive tuning | 150 |
| PA/PES | Wastewater/0.81 M | 20 | 18.8 | PDA coating grafted with SHPG | 117 |
| PA/PEI | DI/1.0 M | 15 | 8.9 | — | 151 |
| PA/PES | DI/1.0 M | 23 | 34.2 | PA incorporated with CDQs | 119 |
| PA/PAI | Wastewater/1.0 M | 13 | 4.3 | PAH post-treatment | 152 |
| PA/PES | DI/1.0 M | 16.5 | 14.6 | PES incorporated with GO nanosheets | 120 |
| CTA/CA T-NIPS membrane | DI/1.0 M | 18 | 5.5 | — | 153 |
| PA/PES | DI/1.0 M | 17 | 14.6 | PA incorporated with PP-SO3H | 154 |
Straub et al.78 reported a thorough energetic analysis of PRO system harvesting blue energy in river water and sea water. An estimation for energy inputs and outputs in the system was presented separately. Overall, the expected energetic inputs will most likely surpass outputs, resulting in a negative power generation. The major cause is the insufficient energy density extractable in mixing of river and sea sources. However, systems with higher concentration gradients can sufficiently overcome the energy output limit mentioned above, though technical problems including biofouling and selectivity decrease remain to be solved. Touati et al.71 confirmed the viability of open-loop PRO and close-loop PRO by using low-concentration feed solutions. However, the analysis of hybrid SWRO-PRO systems results in a negative energy generation.
Though the debate of the viability of PRO system never stops, industrial attempts using PRO prototypes continues in the globe. The first commercialized plant was conducted by Statkraft in Norway from December 2009.158 The aim of the project is to produce an 8 inch spiral wound module of 2000 m2 which is able to produce a total of 10 kW of power, corresponding to a power density of 5 W m−2.159 However, the actual performance of the PRO plant failed to reach the initial objective, delivering a total power of 2 kW, which corresponds only to 20% of the designed power.160 Due to the lack of membrane optimization and high cost in accessory systems, the sale price of a PRO plant reaches 70–100 euros per MW h and showed low economic interests, compared with the actual electricity price of 30–40 euros in Norway. The whole system was unfortunately shut down in 2013. Researchers and engineers performed another prototype experiment in Quebec, Canada.159 The main objective of the project is to carry out process optimization studies of performing water pretreatment to prevent biofouling problems. A novel project was started in Japan to install an additional prototype PRO module, using commercial CTA hollow fiber membrane modules, to the Fukuoka WRO desalination plant to form a RO-PRO joint system.159 A maximum power density of 13.3 W m−2 was achieved by a 10 inch hollow fiber membrane module. Nowadays, a similar hybrid RO-PRO project is developed jointly by Saudi Arabia and Japan, aiming to develop efficient PRO systems for energy recovery and environmentally friendly high saline water treatment used in RO desalination processes.161
Overall, stand-alone PRO systems with sources of higher salinity difference seem to be more promising due to a higher extractable energy density. The development of commercialized inexpensive PRO membranes is of key importance, which could sufficiently increase the system performances and reduce the production and maintenance costs. Considering the rising electricity price in Europe due to the lack of gas and the emerging technology development in PRO systems, the economic threshold of PRO system might be reached in the near future.
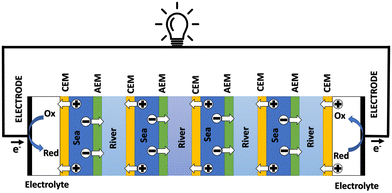
3.2 Reverse electrodialysis
Proposed by Pattle et al. in 1954,162 reverse electrodialysis (RED) is the earliest technology proposed for blue energy extraction. In a classic RED configuration, sea water and river water were injected respectively into two different compartments separated by an ionic exchange membrane (IEM). This approach corresponds to the reversed process of the electrolysis (ED), where IEMs are used with an electric current to remove salts from sea water for pure water production. Years after, no significant development has done until 70s, when Lacey in 1980 developed his model for the RED.163 To understand how an RED device works, it is necessary to understand how an ion exchange membrane behaves when it separates two salt solutions of different concentrations. This question will be answered in the following subsection.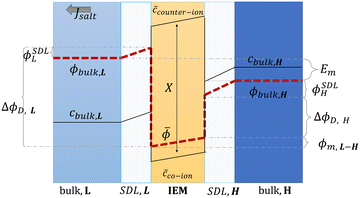 | ||
| Fig. 13 Schematic representation of concentration, c, and potential, ϕ, profile in the bulk solutions, the stagnant diffusion layers (SDLs), and in an ion exchange membrane (IEM) (figures and captions adapted from ref. 164 with permission from FIMTEC & MPRL, copyright 2016). | ||
ΔϕD,L is called the Donnan potential in the diluted solution. It comes from the difference in ion concentration at the solution–membrane interface. In this context, the equality of chemical potentials leads to:
μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ai,L) + ziFϕL = μ0i + RT ln(ai,L) + ziFϕL = μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(āi,L) + ziF ln(āi,L) + ziF![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) L L | (4) |
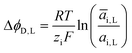 | (5) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) L are the electrical potential on the external and the internal side of the membrane in the diluted electrolyte, respectively. ΔϕD,H is the Donnan potential characterizing the concentrated solution. ϕm,L–H is the difference of potential occurring inside the membrane. ϕSDLL and ϕSDLH are the difference of potential created by stagnant double layers (boundary layer) that build up close to the membrane. These layers, also named as polarization layers, have fundamental impacts with the presence of electric current. As we will see later, they are usually considered as non-ohmic resistances in the analysis of RED systems. The modeling of all these terms is complex and requires complicated numerical simulations.
L are the electrical potential on the external and the internal side of the membrane in the diluted electrolyte, respectively. ΔϕD,H is the Donnan potential characterizing the concentrated solution. ϕm,L–H is the difference of potential occurring inside the membrane. ϕSDLL and ϕSDLH are the difference of potential created by stagnant double layers (boundary layer) that build up close to the membrane. These layers, also named as polarization layers, have fundamental impacts with the presence of electric current. As we will see later, they are usually considered as non-ohmic resistances in the analysis of RED systems. The modeling of all these terms is complex and requires complicated numerical simulations.
A simple limit can be found. In the absence of electric current through the membrane, in the case of a rigorously selective membrane, the diffusion potential vanishes. Neglecting the stagnant double layers, the open circuit voltage writes:
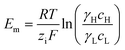 | (6) |
Under the assumption of an open circuit and neglecting the polarization layers, this equation can be generalized to a non-selective membrane by writing: 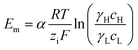 , where
, where 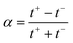 with t+ the transport number of the cation and t− the transport number if the anion. To go further and calculate α, the modeling of all these terms is required. The most widely used description comes from the Teorell–Meyer–Sievers165 theory which is a one-dimensional model that does not take into account the ions concentrations variations in the pore section of the membrane, nor the fluid transport by convection. The space charged model developed by Osterle and colleagues166 takes into account these two points. Recently, interactions with surfaces and electro-osmotic effects have been taken into account in calculations to explain the strong ionic currents generated by charged but a priori non-selective nanotubes of more than 20 nanometers in diameter.167 We will return to this point later in the text.
with t+ the transport number of the cation and t− the transport number if the anion. To go further and calculate α, the modeling of all these terms is required. The most widely used description comes from the Teorell–Meyer–Sievers165 theory which is a one-dimensional model that does not take into account the ions concentrations variations in the pore section of the membrane, nor the fluid transport by convection. The space charged model developed by Osterle and colleagues166 takes into account these two points. Recently, interactions with surfaces and electro-osmotic effects have been taken into account in calculations to explain the strong ionic currents generated by charged but a priori non-selective nanotubes of more than 20 nanometers in diameter.167 We will return to this point later in the text.
In a more pragmatic way, this description of the membrane potentials leads to propose an electrical scheme for a membrane. In the presence of different salt concentrations on both sides of the membrane, the membrane behaves like a voltage generator EOCV which is the open circuit voltage in series with a resistor and with elements that account for the polarization layers. These double layers are resistors in parallel with phase elements or simply resistors.168,169
In the following we will detail all the elements of the cell.
Electrodes. Electrodes are used in RED stacks for the conversion of osmotic-driven ionic flux into an electric current by faradaic reactions. The choice of electrodes is of great importance for the optimization of energy conversion efficiency in RED stacks.170 Several electrodes were proposed for RED systems, from participating electrodes like Ag/AgCl to inert ones like Pt, and with redox reactions ranging from hydrogen/oxygen reactions to more complex like Fe(CN)63−/Fe(CN)64−. These electrodes are classified to three main types summarized in the Table 4. The oldest electrodes162,171 were made of two metals immersed in a solution containing the metal ions. The metal (or the amalgam such as Ag/AgCl) participates directly in the red-ox reaction. Thereby, the electrodes were consumed during the process and their life span remains limited. For theses reasons, participating electrodes were dropped out in the latest development.172,173 After that, inert electrodes were proposed to avoid the regeneration problem. They interact directly with the electrolytes and forming gases which is their major drawback.174 Inert electrodes are used jointly with redox couples dissolved in the circulating electrolytes to enable the redox reactions for energy conversion. Inert electrodes present enormous applications in RED systems due to good chemical/environmental advantage. The consumed ions in one electrode will be generated in the other one, and thus leading to no net chemical reaction at the end. In the same time, because of this, the electrolyte will be conserved and no over-potential will be appear because of the gas formation. The problem with this category is the nature of the couple: for the FeCl2/FeCl3 system, low pH is needed to prevent formation of solid (hydr)oxides172 and for the Fe-complex couple, it is not stable during long time especially if exposed to light.175
| Type | Electrodes | Electrolyte | Advantage | Disadvantage | Ref. |
|---|---|---|---|---|---|
| Inert electrodes with reversible reactions | Ti–Ru/Ir mesh | K4Fe(CN)6 K3Fe(CN)6 | No electrolysis voltage losses | Sensible to light | 176 |
| Ti–Ru/Ir mesh | Fe(Cl)2/Fe(Cl)2 | No net chemical reaction | Sensible to pH | 172 | |
| Bidirectional system | |||||
| Inert electrodes with irreversible reactions | Ti-Ru/Ir mesh | NaCl | No net chemical reaction | Voltage loss | 174 |
| H2 generation | |||||
| Ti–Pt mesh | Na2SO4 | Cl2 generation | 177 | ||
| Participating electrodes | Ag/AgCl | NaCl | No net chemical reaction | Switching flows | 178 |
| Cu | CuSO4 | No electrolysis voltage losses | Electrodes regeneration | 162 | |
| Zn | ZnSO4 | 171 |
Ionic exchange membrane. The RED is a membrane based osmotic process where IEMs are considered as the main engine of the energy recovery. Membranes are usually characterized by several properties based on the amount, structure, type and the charge of the functional groups in the membrane. These proprieties are linked. IEMs are divided to three main classes: CEMs, AEMs and bipolar membranes according to the surface charge. CEMs possess negative charges with a fixed chemical group. Generally, chemical groups of strong acids, like sulphonate (–SO3−) and phosphorate (–PO3−), or weak acids like carboxyl groups (–COO−) are used in CEMs. Due to the presence of negative charges in CEMs, anions in solutions are repulsed and the cations pass. For AEMs, cations are repulsed due to the positively charged chemical groups including ammonium (–NR3+), primary amine (–NH2), secondary amine (–NRH) and tertiary amine (–NR2). Bipolar membranes have simultaneously negative and positive chemical groups and display fascinating applications in water splitting. The main characteristics of commercial membranes, i.e. the swelling degree, the ion exchange capacity, the fixed charge density, the permselectivity, and the membrane resistance are reported in the Table 5.
The swelling degree (SD) characterizes the ability of a dry membrane to absorb water. It measures the mass change ratio of a dry membrane before and after water immersion:
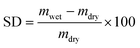 | (7) |
Ion exchange capacity (IEC) determines the number of fixed charges inside the IEM per unit of mass of a dry membrane. The fixed charges in the membrane are usually in equilibrium with the ions in the electrolytes, this equilibrium is given by the Fixed charge density (CD) and it is defined as the milliequivalents of charged groups per gram of water in the membrane. It is given by:
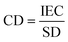 | (8) |
| Membrane | Thickness (μm) | IEC (meq g−1) | SD (%) | CD (meq g−1 H2O) | α (%) | R (Ω cm2) | Ref. |
|---|---|---|---|---|---|---|---|
| CEM | |||||||
| Neosepta CMX | 164 | 1.62 | 18 | 9.0 | 99 | 2.91 | 179 |
| Neosepta CMS | 150 | — | — | — | 97 | 1.4–1.8 | 180 |
| Neosepta CM-1 | 133 | 2.3 | 20 | 11.5 | 97.2 | 1.67 | 179 |
| Neosepta CIMS | 150 | 2.3 | 30 | 7.7 | — | 2.49 | 181 |
| Fumasep FKD | 113 | 1.14 | 29 | 3.9 | 89.5 | 2.14 | 179 |
| Fumasep FKS-20 | 20 | 1.24 | — | 99 | 1.7 | 182 | |
| Fumasep FKE | 34 | 1.36 | 12 | 11.3 | 98.6 | 2.46 | 179 |
| Selemion CSO | — | 1.04 | 16 | 6.4 | 92.3 | 2.26 | 183 |
| Selemion CMV | 101 | 2.01 | 20 | 10.1 | 98.8 | 2.29 | 179 |
| Fujifilm V1 | 125 | — | — | — | 93 | 1.6 | 184 |
| Fujifilm CEM RP1 80050-04 | 120 | 1.45 | — | — | 96 | 2.55 | 182 |
| Nafion-115 | 139 | 0.9 | — | 8 | — | — | 185 |
| Nafion-117 | 201 | 0.9 | — | 7.7 | — | — | 185 |
| Ralex CMH | 764 | 2.34 | 31 | 7.5 | 94.7 | 11.33 | 179 |
| Qianqiu CEM | 205 | 1.21 | 33 | 3.7 | 82 | 1.97 | 186 |
| Tailor-made SPEEK 65 | 72 | 1.76 | 35.6 | — | 89.1 | 1.22 | 186 |
| Tailor-made SPEEK 40 | 53 | 1.23 | 23 | — | 95.3 | 2.05 | 186 |
| AEM | |||||||
| Neosepta AM-1 | 126 | 1.77 | 19 | 9.3 | 91.8 | 1.84 | 179 |
| Neosepta AFN | 163 | 3.02 | 43 | 7 | 88.9 | 0.7 | 179 |
| Neosepta AMX | 134 | 1.25 | 16 | 7.8 | 90.7 | 2.35 | 179 |
| Neosepta ACS-8T | 150 | 1.9 | — | — | — | 2.41 | 181 |
| Fumasep fad | 74 | 0.13 | 34 | 0.4 | 86 | 0.89 | 179 |
| Fumasep fas-20 | 20 | 1.5 | 31.25 | 4.8 | 95.5 | 0.5 | 182 |
| Selemion DSV | 121 | 1.89 | 1.03 | 183.5 | 89.9 | 1.03 | 179 |
| Selemion APS | 138 | 0.29 | 147 | 0.2 | 88.4 | 0.68 | 179 |
| Selemion AMV | 110 | 2.2 | 21 | 10.5 | 95 | 2.44 | 187 |
| Fujifilm TYPE I | 115 | — | — | — | 91.9 | 1.3 | 180 |
| Fujifilm AEM RP1 80045-01 | 120 | 1.28 | — | — | 96 | 1.83 | 182 |
| Fujifilm V3B | 84 | 1.7 | 23 | 7.39 | 87 | 1.36 | 187 |
| Fuji V3A | 66 | 2.2 | 23 | 9.57 | 82 | 0.87 | 187 |
| Fujifilm V1 | 139 | 1.8 | 23 | 7.83 | 90 | 1.05 | 187 |
| Fujifilm V2 | 53 | 1.6 | 23 | 6.96 | 86 | 0.67 | 187 |
| Ralex AMH-PES | 714 | 1.97 | 56 | 3.5 | 89.3 | 7.66 | 179 |
| Qianqiu AEM | 294 | 1.33 | 35 | 3.8 | 86.3 | 2.85 | 186 |
| Tailor-made PECH A | 77 | 1.31 | 32.2 | 4.1 | 90.3 | 2.05 | 186 |
| Tailor-made PECH B2 | 77 | 1.68 | 49 | 3.4 | 87.2 | 0.94 | 186 |
| Tailor-made PECH B1 | 33 | 1.68 | 49 | 3.4 | 86.5 | 0.82 | 186 |
The membrane is a part of an electrochemical cell where the ionic current is converted to an electrical one. This current is directly affected by the conductivity of this membrane (ohm loss) and can influence the power density. This resistance is reported to a unit of area. It depends on the material's property and its structure (see Table 5).
These properties depend on the conditions of use such as the concentrations of the saline solutions, the value of the difference in salinity, the acidity, the temperature. Using a very high concentration can reduce membrane selectivity even though it gives better conductivity.169,173 A high temperature173 decreases the permselectivity of the membrane.
The characteristics of the membranes depend on the mode of production based on which IEMs are classified into homogeneous IEMs and heterogeneous IEMs.
For the first class, the membrane is prepared using just one product, generally, by polymerization of a charged/can be charged monomers or followed by grafting functional monomers on a film/dissolved polymer.188 On the other hand, heterogeneous IEMs contain two parts, an ionic exchange resin mixed with an uncharged polymer matrix without any chemical bound. Homogeneous IEMs exhibit excellent electrochemical properties, very low resistances and high permselectivity.189 Their thickness is between 1 and 30 μm. However, their production is more complicated and more expensive. In contrast, heterogeneous IEMs are easier and less expensive to prepare with a good mechanical and chemical stability especially for the AEMs in alkaline electrolyte. However, their high resistance is still a major challenge for the RED technology.179 Recently, N. D. Pismenskaya et al.189 modified an heterogeneous membrane by grafting functional quaternary ammonium groups to increase its electrochemical performance. The results are encouraging and close to that of a homogeneous IEM.
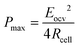 | (9) |
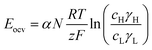 | (10) |
To develop a production cell, it is necessary to choose the number of membranes to be used. A priori, it is interesting to increase the number of membranes. Using a large number of membranes should make the whole device more compact. When the salinity of the solutions is fixed, Eocv, and Pmax increases theoretically linearly with the number of cell pairs and is independent of the flow rate. The power density should therefore not be depend upon the number of membranes.
Experimentally, H. Kim et al.196 observe a different behavior. When the stack is supplied with a constant flow, the gross and net power density decrease when the number of membranes becomes higher than.200 These phenomena are caused by the polarization of the cell. When the pairs of cells are more numerous, the local flow rate decreases in each cell which favors mixing, the appearance of a concentration gradient along the flow and the growth of the thickness of stagnant ionic layers.
In fact it comes from the polarization the open circuit potential increases with the number of cell pairs but the growth law between the two is weaker than a linear law. When the number of cells is fixed, the open circuit potential increases slightly with the flow rate. As the number of cells increases, the throughput in each cell is lower and the polarization effects along the cell but also the thickness of the depleted layers increases. Both effects induce a decrease of the open potential.
According to eqn (9), an efficient way for power density optimization is to increase the open-circuit voltage Eocv. Several research works managed to ameliorate the membrane selectivity a or increase the number of IEM pairs used in RED systems. Güler et al.186 tested several IEMs and found that the permselectivity could be independent of the thickness. H. Kim et al.196 showed that the using a big number of cell pair will affect the residence time of the ions inside and therefore the concentration polarization inside the cell will cause a diminishing of the potential compared to the theoretical value.
For the non-ohmic resistance, the challenge is always present. Vermaas et al.193 attempted to improve mixing inside the cell to reduce the boundary layer using a specific spacer with filled channels and with sub-corrugations (see Fig. 15B) without much success.
 | ||
| Fig. 15 Images obtained from a scanning electron microscope for (A) the profiled membranes (B) and profiled membranes with sub-corrugations (figures and captions reproduced from ref. 193 with permission from Elsevier, copyright 2014). | ||
Though the use of more than 45 membranes in the RED system, Pattle et al.162 reported a mild power density of 0.2 W m−2 because of the low efficiency of their stack. Numerous studies continues today in the hope of promoting output power density of RED systems. In 2007, Dlugolecki et al.179 investigated the performance of several membranes used generally in the RED, and estimated that a power density of 6 W m−2 can be achieved by commercial IEMs. A year after, a power density of 0.84 W per square metre of membrane was obtained in the work of Turek et al.177 with a high salinity gradient (around 200) and even a 0.9 W m−2 is reached by Veerman et al.190 with a salinity difference of 30 g L−1vs. 1 g L−1 of NaCl for the concentrated and the diluted solution respectively. High cell resistance hinders the electrical performance of RED systems.174 It was reported that the diminution of spacer thickness (from 485 μm to 100 μm) could effectively reduce the ohmic resistance of the system by 4.176 With these RED improvements, Vermaas et al.176 obtained a gross power density of 1.8 W m−2 using just 5 pairs of IEMs. However, for thinner spacers, a higher pressure loss was reported. A net power density of 1.2 W m−2, which remains the highest experimental net power density documented until present, was achieved in this work. The same team tried to removed the spacers and employed profiled membranes to reduce water volume (higher conductivity). While a significant ohmic resistance drop of 30% was achieved, the profiled membranes suffered from severe polarization problems which reduces the ohmic resistance around 30% but the polarization resistance was significantly higher.191 Adding sub-corrugations to disturb the uniform flow and enhance the mixing was insufficient to increase the net energy power.193
As already described, the potential Eocv between the stack's electrodes is directly related to the gradient. Daniilidis et al.173 investigated the RED stack for hypersaline solution like the Dead sea, with a concentration close to the saturation (around 5 M) with a river water of 0.01 M concentration and they obtained a gross power density 3.8 W m−2 at 25 °C and more than 6.5 W m−2 at 60 °C in 5 membrane pairs cell, even if the selectivity was lower with the increasing of the temperature and the gradient. This power density corresponds to a gross power. It's worth to note that even though this energy was experimentally measured, no pumping energy consumption was subtracted. In the same topic, and to show the effect of temperature and gradient, Tedesco et al.182 used a hypersaline solution at 5 M and a brackish solution with 0.1 M, and reached a gross power of 6 W m−2 at 40 °C in a cell with 50 membrane pairs. In this situation, the resistance of membrane pairs is low.
In fact, the recorded experimental gross power density without correction was around 4.75 W m−2 with 2–2.5 W m−2 of dissipated power due to the pressure drop inside the cell. Increasing the unit size to the double and the number of the membrane pairs had only a slight reduction in the power density caused by the non-uniform distribution of fluids concentration. The amount of the theoretical power is very huge, it is estimated to be more than 2 TW in the world rivers and oceans.8 Just a part of this power is actually exploitable by the blue energy harvesting technologies. The efficiency is defined as the ratio between the recoverable energy and the available Gibbs free energy in the water mixing of unit volume. Higher energy efficiency is achieved when the feed waters are recycled (multiple pass)176 and a lower current density is applied (due to ionic shortcut currents).190
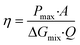 | (11) |
| Membrane | C H (M) | C L (M) | Temperature (°C) | Power density (W m2) | Efficiency | Ref. |
|---|---|---|---|---|---|---|
| Fumasep FKD/FAD | 0.507 | 0.017 | 25 | 0.93 | 18% | 190 |
| Neosepta CMX/AMX | 1.899 | 0.01 | — | 0.72 | — | 177 |
| Fumasep FKS/FAS | 0.507 | 0.017 | 25 | 2 | 32% | 176 |
| Fumasep FKS/FAS | 0.507 | 0.017 | 25 | 1.8 | 15% | 176 |
| Ralex Profiled CMH/AMH | 0.507 | 0.017 | 25 | 0.8 | <1% | 191 |
| Tailor-made SPEEK65/PECH B2 | 0.513 | 0.017 | 25 | 1.28 | — | 192 |
| Qianqiu CEM/AEM | 0.513 | 0.017 | 25 | 0.83 | — | 192 |
| Custom-made composite/Selemion CEM/ASV | 0.5 | 0.017 | 25 | 1.3 | — | 183 |
| Ralex Profiled + sub-corrugations CMH/AMH | 0.507 | 0.017 | — | 0.9 | — | 193 |
| Neosepta CMS/ACS | 5 | 0.01 | 25 | 3.8 | 7% | 173 |
| Neosepta CMS/ACS | 5 | 0.01 | 60 | 6.7 | 20% | 173 |
| Fumasep FK-20/FAS-20 | 5 | 0.1 | 40 | 4.75 | <1% | 182 |
| Fujifilm CEM 80045-04/AEM 80045-01 | 4–5 | 0.03 | 23 | 1.35 | 2–3% | 194 |
| Fujifilm CEM-80050/AEM-80045 | 0.762 | 0.005 | 20 | 0.3 | — | 195 |
| Fujifilm CEM-80050/AEM-80045 | 0.762 | 0.005 | 60 | 0.705 | — | 195 |
| Nafion/Neosepta N117/AMX | 4 | 0.5 | 25 | 1.38 | — | 185 |
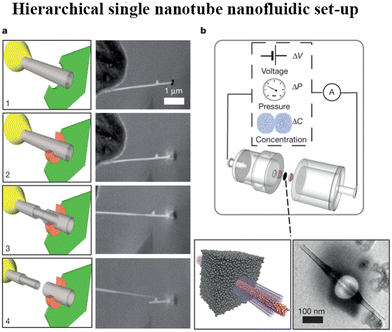 | ||
| Fig. 16 a, In situ nanomanipulation of a BNNT (left, sketch; right, scanning electron microscope (SEM) images): 1, insertion of a BNNT (grey) through a nanopore drilled in a SiN membrane (green) using a focused ion beam (FIB); 2, carbon sealing of the FIB-drilled hole using local electron-beam-induced deposition (orange); 3, telescopic retraction of internal walls of the BNNT; 4, finalized transmembrane BNNT device. b, Top, Schematic of the experimental set-up for measuring fluid transport through the single BNNT. Bottom, sketch of the final transmembrane BNNT for nanofluidic measurements (left) and its experimental realization, imaged by transmission electron microscopy (TEM) (right) (figures and captions reproduced from ref. 167 with permission from Springer Nature copyright 2013). | ||
For a BNNT placed between a 1 M and 0.01 M NaCl solution the authors measure167 an electric current of 1 nA and a power density of 4 kW m−2 for a nanotube (see Fig. 17). This point is very remarkable. This potential is created by an electrophoretic flux due to the surface charge of the nanotube. Boron Nitride surfaces bear a large surface charge.
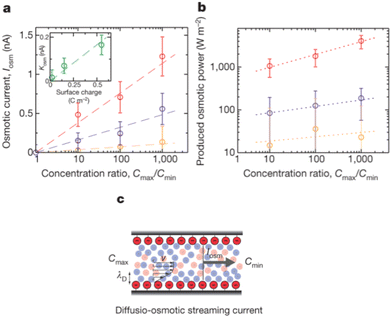 | ||
Fig. 17 a, Osmotic streaming current versus concentration difference for a t-BNNT with R, L 5 40 nm, 1250 nm and pH 5.5 (yellow), 9.5 (purple) and 11 (red). The experimental points show measurements for various salt concentrations in the two reservoirs, with Cmin and Cmax in the range 10−3–1 M. Error bars follow from the corresponding error analysis. Dashed lines are linear fits: 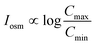 . Inset, Osmotic mobility versus surface charge. Surface charge is obtained from independent conductance measurements. The dashed line is a linear fit with proportionality factor of 0.33 for the chosen units. b, Corresponding power density (per unit surface of the BNNT) for the three values of pH. Dotted lines are a guide to the eye. In the present graph, the minimum concentration is fixed to Cmin = 10−3 M. b, Sketch of the osmotically driven streaming current under a salt concentration difference, Cmax − Cmin (figures and captions reproduced from ref. 167 with permission from Springer Nature, copyright 2013). . Inset, Osmotic mobility versus surface charge. Surface charge is obtained from independent conductance measurements. The dashed line is a linear fit with proportionality factor of 0.33 for the chosen units. b, Corresponding power density (per unit surface of the BNNT) for the three values of pH. Dotted lines are a guide to the eye. In the present graph, the minimum concentration is fixed to Cmin = 10−3 M. b, Sketch of the osmotically driven streaming current under a salt concentration difference, Cmax − Cmin (figures and captions reproduced from ref. 167 with permission from Springer Nature, copyright 2013). | ||
The ion concentration profile of the salt solution placed above this surface is given by: C±(x,z) = C∞(x)exp(−±ϕ(z)) where ϕ(z) is the electrical potential, z the vertical position normal to the surface, x the position along the direction of the surface, C∞(x) the concentration in salt far from the surface, C+(x,z) the concentration in positive counterions, C−(x,z) the concentration in negative counterions as a function of x and z. The balance along the z direction between the pressure forces acting on a fluid particle and the electrostatic forces links the pressure and concentration fields. This writes: P(x,z) = P∞ + 2kBTC∞(x)cosh(ϕ(z) − 1) the concentration gradient along the loaded surface induces thus a pressure gradient along the same surface. This pressure gradient is at the origin of a Stokes flow in the nanotube whose maximum speed is given by: 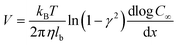 with
with  and ϕo the surface potential. The diffusion–osmotic flow drags the ions and produce an electric current by convection of the ions in excess. We recall that as the surface is charged, and as the liquid plus the surface is neutral, the liquid alone bears a charge which is opposed to the surface one. The obtained electrical current and potential drop are proportional to Δlog
and ϕo the surface potential. The diffusion–osmotic flow drags the ions and produce an electric current by convection of the ions in excess. We recall that as the surface is charged, and as the liquid plus the surface is neutral, the liquid alone bears a charge which is opposed to the surface one. The obtained electrical current and potential drop are proportional to Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C∞. This modeling is in quantitative agreement with the measurements.
C∞. This modeling is in quantitative agreement with the measurements.
A quantitative analysis of these equations shows that the power gain in the system comes from the very low electrical resistance of the nanopores. The potential difference across the nanotube is not exacerbated and remains about 100 millivolts under classic experimental conditions. The theory recovers an expression close to the one presented for the selective membrane when the radius of the nanopore goes to zero and when the surface charge is high. This study has prompted many groups to prepare membranes with nanopores to increase the performance of the RED. At this stage, all the attempts end in failure to create large-scale membranes. Fig. 18 compares the power and extrapolated on 1 m2 surfaces and the powers measured on membranes. Clearly there is no correspondence between the two and the maximum powers obtained remain below 10 W m−2. This results comes from the existence of collective effects between nano-channels that prevent the generalization and extrapolation of the results obtained on a single nanotube. When the nanotubes are too close together in the membrane, the formation of ion depletion layer results in an effective concentration difference much smaller than the imposed one. The transport of an electrolyte within a single nanotube is therefore very different from that within a membrane.197 The results obtained, although disappointing at the level of extrapolation, are nevertheless better than the powers obtained in the experiments with polymeric membranes. It is necessary to comment on this point. All the experiments conducted on large hole membranes are done on systems with very small surfaces generally smaller than 0.01 mm2. The system that allows the measurement of powers includes large volume of electrolyte and electrodes of large size. In this case the ionic resistance of the compartments is negligible compared to the resistance of the membrane, which is absolutely not the case in the RED experiments.
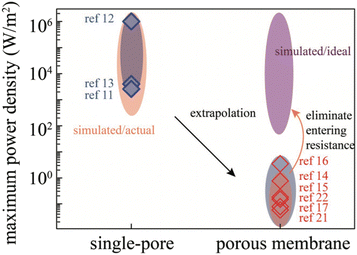 | ||
| Fig. 18 Comparison between literatures reported power density and our simulated results. The range of simulated actual power density (upper left and lower right orange ovals) is approximately in agreement with that reported by literatures (blue diamond represents reported values) for both single-pore and nanoporous membrane systems, suggesting that our intuitive resistance paradigm semiquantitatively explains the orders- of magnitude power density gap between single-pore and nanoporous membrane systems. Remarkably, by eliminating the entering resistance, the simulated ideal power density (upper right oval) of membrane materials can be brought back to the single-pore level (figures and captions reproduced from ref. 197 with permission from John Wiley and Sons, copyright 2019). | ||
It is therefore impossible to compare these data to the RED experiments. Liu et al.198 have developed a nanoporous carbon membrane via the thermal crossing of polycyclic aromatic hydrocarbons. They obtained a mechanically robust membrane of size 1 cm with 3.6 ± 1.8 nm pores and a thickness of 2.0 ± 0.5 nm. The pore density is close to 1010 pore by cm2. They carry out RED experiments on a membrane 1 micrometer in diameter. They obtain by mixing artificial seawater (0.5 M NaCl) and river water (0.01 M NaCl) a power density of 67 W m−2 for a circuit resistance of 15 MW. In the context of the experiment, the dominant resistance corresponds to the resistance of the membrane. The resistance of the electrolyte compartments is negligible. The resistance of the membrane can therefore be calculated and estimated to 0.19 Ω cm2. This figure takes into account the resistance of the membrane and the resistance of the double layer near the membrane. It forgets the ohmic resistance of the solutions and the polarization resistance due to the drop of the concentration gradient along the membrane. Note that the values reported on Table 5 are closed to this one even though they do not take into account the resistance of the double layer near the membrane. To conduct a fair comparison, calculations of magnitude's order are necessary. The power generated by this membrane in the nanofluidic system is 67 W m−2. To generate such power, a flow rate equal to 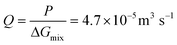 is required assuming an efficiency of 100%. This corresponds to a viscous power by unit area of
is required assuming an efficiency of 100%. This corresponds to a viscous power by unit area of 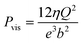 of 26 MW m−2 for a gap e of 1 μm and 26 W m−2 for a gap e of 100 μm. The ohmic resistance of a 0.01 M saline solution is equal to 7.8 Ω cm2 for a gap e equals to 100 μm. This value is much higher than the resistance of the membrane and must be added to it to calculate the performance in a device of 1 square meter. Clearly it will therefore be impossible to achieve such high performance in a device of one square meter in area. It is not possible to compare the power from nanofluidic devices and centifluidic devices with conventional membranes. An interesting study would be to measure the resistance of classical ion exchange membranes such as Nafion in nanofluidic systems.
of 26 MW m−2 for a gap e of 1 μm and 26 W m−2 for a gap e of 100 μm. The ohmic resistance of a 0.01 M saline solution is equal to 7.8 Ω cm2 for a gap e equals to 100 μm. This value is much higher than the resistance of the membrane and must be added to it to calculate the performance in a device of 1 square meter. Clearly it will therefore be impossible to achieve such high performance in a device of one square meter in area. It is not possible to compare the power from nanofluidic devices and centifluidic devices with conventional membranes. An interesting study would be to measure the resistance of classical ion exchange membranes such as Nafion in nanofluidic systems.
In the previous framework, the creation of an ionic current in nanopores of several nanometers in diameter comes from the surface charge. Another way to do this is to be inspired by nature by creating nanopores covered by a very thin selective membrane. The realization199 of robust mushroom-shaped (with stem and cap) nanochannel array membrane with an ultrathin selective layer and ultrahigh pore density, has notably allowed to obtain a power of 15 W m−2 with a 10 mM/0.5 M salt gradient. The experiments are performed on a membrane of 8000 μm2. From the data of the article, it is possible to calculate the resistance of the membrane. This resistance is 1.6 Ω cm2. As discussed previously, such feature is very close to the one of classical membranes, which is unlikely to present exceeded performances in our point of view.
To overcome this problem, monovalent ion exchange membranes were proposed to replace the usual IEMs. Guler et al.192 compared two commercial monovalent AEMs with a home-modified one, and they found that there is no significant difference on the measured gross power densities between the monovalent and the multivalent IEMs because of their high internal resistance.180,192 Moreno et al.180 tried two different strategies to minimise the negative effect of uphill transport (multivalent ions transport against the concentration gradient). The first one is using a highly cross-linked cationic monovalent membrane. This type of IEMs select the ions with the same charge based on their size (hydrated ionic radius). It blocks the multivalent ions and allows the transport of monovalent ions only. The second strategy is based on the charge rejection. A standard CEM with a thin positively charged layer on the membrane surface. A constant OCV was obtained using a mixing between NaCl and MgCl2 compared to pure NaCl solution for the monovalent CEM. Also, for the coated CEM, a slight decrease in the OCV was observed. The membrane resistance was higher due to the lower ion mobility of magnesium ions inside these membranes. Hence, the power density was lower.
In addition to this negative effect, fouling remains a tricky problem in long-term experiment, causing severe resistance increase and permselectivity hindrance. In 2012, Vermaas et al.204 established RED stacks with water feeds of naturel river water (Van Harinxmakanaal – Netherland) and natural sea water (Wadden Sea – Netherland) filtered by a 20 μm diameter filter. During the 25 day continuous test, they observed a significant resistance rise, along with a slight decrease in membrane permselectivity, which results in a power loss of 60% of the RED system. This result was confirmed by the work of Vital et al.,205 where after 54 days, the power density decrease by 25%. This fouling comes in two major parts of the RED stack, the IEMS and the spacers. For the IEM we can determine two kinds of fouling depending on the charge of the membrane: the organic and the bio-fouling, generally negatively charged, are more occurred on the AEMs. In contract of the CEM, where the main problem is scaling and the solid particles. In the other hand, the fouling in the spacer can directly detect by a drop pressure jump inside the cell204 and channel clogging, shown by Cosenza et al.,203 due to bacteria growing in the channels of the RED unit and in the dilute solution circuit, hence, The fouling is most probably in river water.
To control this fouling, various strategies are proposed at different levels: before pumping the steams, inside the RED stack, by slowing the formation of fouling and after by removing all blocking particles.
The first barrier can be a simple pretreatment a 20 μm pore size mesh filter, proposed by Vermaas et al.,204 to filtrate the biggest particles. Vital et al.205 add to this last a second filter media composed by a 50 cm layer of anthracite (1.2–2.0 mm Ø) on top of a 50 cm layer of sand (0.5–1.0 mm Ø), placed into 11 cm Ø polyvinyl chloride (PVC) pipe. An optimization of the spacers was proposed to reduce the fouling by Vermass et al.191 where they replaced the traditional spacers and IEMs by profiled membranes, and they found that the pressure drop increased four times slower and the power density remained relatively higher. He et al.206 confirmed this importance of the spacers and proposed a new type with different inlet and outlet to enhance the hydraulic performance and the power density.
Another solution is to modify the anionic exchange membrane surface to make it less attractive to biofouling. Vaselbehagh et al.207 coated a polydopamine layer on the surface of an AEM and found that it reduces bacterial attachment.
Various methods, suggest treating the IEMs with some polymer layer to make them selective for monovalent ions and to reduce the uphill effect and the fouling.180 From these methods, we can find Gao et al.208 who realized a deposition of two polymers poly(styrenesulfonate) (PSS) and poly(ethyleneimine) (PE) on the surface of an AEM to compare it with commercial one and they showed a good monovalent-anion selectivity comparable, a better anti-organic fouling potential and slightly lower gross power density due to the membrane resistance.
The last strategy is occurred when the fouling is already present. A physical cleaning is used by increasing the pressure or the flow rate for few seconds (a pulse) inside channels to destroy the substances clogging the channels. A chemical washing could be beneficial using some acid and alkaline solutions. To avoid bacteria and algae proliferation, a UV lamp could be installed. With these strategies, they were able to ensure a positive net power density value for more than 18 days using feed from oil well industry.203
| Year | σ H (mS cm−1) | σ L (mS cm−1) | Membrane area (m2) | Membrane pairs number | Gross power density (W m−2) | Ref. |
|---|---|---|---|---|---|---|
| 2016 | 150–220 | 3.4 | 48.4 | 125 | 0.8 | 194 |
| 2017 | 150–220 | 3.4 | 435 | 1125 | 0.76 | 209 |
| 2019 | 52.9–53.8 | 1.3–5.7 | 250 | 1000 | 0.38 | 210 |
| 2020 | 83.5–92.3 | 1.3–2.2 | 40 | 200 | 0.54 | 211 |
| 2021 | 51.9 ± 1 | 0.34 ± 0.05 | 179.4 | 299 | 0.62 | 181 |
| 2021 | 81.9 ± 1 | 0.34 ± 0.05 | 179.4 | 299 | 0.96 | 181 |
| 2022 | 31.4 ± 4.1 | 0.52 ± 0.02 | 3.1 + 6.2 | 32 + 64 | 0.4 | 212 |
A year after, a pilot plant is started in south of Italy with a RED unit equipped with 50 m2 of membranes, and working with natural concentrated brine from saltworks basins and brackish water from a shoreline well over a period of five months during the summer. The gross power density was around 0.75–0.85 W m−2 corresponding to 40 W with an average net power of 25 W.194 This pilot209 has scaled up to reach more than 400 m2 of total membrane area, delivering a 330 W of gross power capacity which is equivalent to around 0.76 W m−2 of power density. After that, a South Korean group built a cell with around 1000 cell pairs with a total area of 250 m2 and tested it with Ocean lava seawater and wastewater effluent from a sewage treatment plant located beside the sea in Jeju, Korea. The pilot plant was able to produce 95.8 W of power (0.38 W m−2).213 Recently, Yasukawa et al.211 obtained 0.46 W m−2 net power density with a stack of 200 pairs of IEMs, corresponding to 40 m2 of total effective membrane area, and streams from a seawater reverse osmosis (SWRO) desalination plant, Mamizu Pia (Fukuoka, Japan), and the Wagiro water treatment center (Fukuoka, Japan). The same team evaluated the performance of the RED pilot plant (RED stack) with 299 cell pairs and a 179.4 m2 membrane effective area, installed in the sea water desalination unit of Okinawa islands in Chatan town, Japan, using one-side monovalent exchange membranes to reduce the uphill effect.181 Surface water was used as the diluted solution, while the sea water and brine from the desalination process were used as concentrated solution. The maximum gross power output of 171.6 W (0.96 W m−2) for the brine/river water and 110.6 W (0.62 W m−2) for the combination sea-river solutions.
Thin homogeneous membranes with low resistance are generally of high prices (above 80 $ per m2).215 In 2007, Turek et al.216 found a very high cost equal to 6.5 $ per kW h by using an experimental power density value of 0.92 W m−2 of cell pair and considering a total investment cost of 96 $ per m2 of installed membrane. In 2010 Post et al.217 fixed a viable power density of 2 W m−2 with a membrane price of 2 $ per m2 and cost of 0.08 $ per kW h for the electricity.
Daniilidis et al.214 suggest that if the membrane technology will be developed by using cheap raw materials and manufacturing procedures in the near future, same as in the ED technology with heterogeneous membrane, allowing a membrane price below 4.3 $ per m2. A net power density of 2.7 W m−2 will be sufficient to start producing energy. And with a LCOE fixed at 0.16 $ per kW h will make RED electricity competitive against conventional and established renewable technologies. Another study was done by Toupin et al.218 on the cost of Nafion and other perfluorinated sulfonic acid (PFSA) polymer electrolyte membranes. They estimated that with a higher annual production (around 5 million m2), the cost of 1 m2 of membrane will be below 10 $ for the melt blowing method185,218 (see Fig. 19).
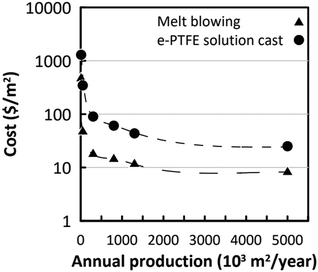 | ||
| Fig. 19 Cost estimation of PFSA electrolyte membrane produced by two different methods as a function of the total yearly production (figures and captions reproduced from ref. 185 with permission from MDPI, copyright 2020). | ||
In 2019, Giacalone et al.219 estimate the levelized cost of electricity ranging from 0.27 to 0.33 $ per kW h based on membrane cost of 15 $ per m2, and using brine and freshwater. This cost is lower than the actual electricity prices in certain countries in Europe, that achieve 0.56 $ per kW h last August in Germany. It's worth to note that with the latest events in Ukraine, the fast inflation in the world, and the energy price rise (especially for the natural gas) may make the RED competitive with other power sources.
3.3 Capmixing
Firstly proposed in 2009 by Brogioli,228 Capmixing is an emerging blue energy harvesting energy with tremendous potential. Unlike PRO and RED where energy conversion is realized through intermediate steps of mechanical turbine systems and electrochemical redox reactions, Capmixing generates electricity directly from a controlled mixing procedure.69 In a classic configuration of Capmixing illustrated in Fig. 20(A), two porous carbon electrodes are dipped into high concentration solutions at initial state.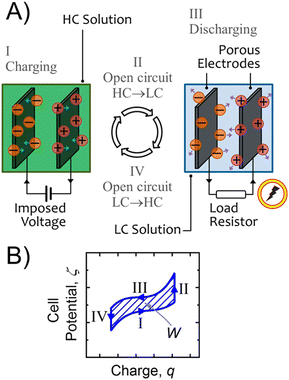 | ||
| Fig. 20 (A) Illustration of the working principle of capacitive energy extraction based on double layer expansion (CDLE) and (B) the qualitative plot of useful work W produced in an unit Capmixing cycle (figures and captions reproduced from ref. 69 with permission from American Chemical Society, copyright 2016). | ||
It is an energy consuming state where electrodes are charged by an imposed external electric source. Thus, electrical double layers (EDL) are formed near each electrode to maintain a local electron neutrality in the solution.65 In state II, the system is in open circuit state and the high concentration solution in the system is replaced by solution of lower concentration. As the ionic strength lowering of the electrolyte results in a thickness expansion of the EDL, the overall capacitance of EDL CEDL decreases.229 Considering the total charges accumulated in the electrodes q remain unchanged, the potential difference between these electrodes DE increases as predicted by the following equation q = ΔCEDLΔE. In state III, a load resistor is connected with the Capmixing system. Discharging in electrodes delivers current to produce useful work in the load resistor. At the same time, the thickness of EDL decreases due to the discharging. At final state IV, system switches into open-circuit state and fresh water is replaced by salt water to close the operation loop. As illustrated in Fig. 20(B), the produced work in state III is larger than the energy consumed in state I, a net power is harvested using this so-called capacitive energy extraction based on double layer expansion (CDLE) technology.68 In the pioneer work of CDLE, Brogioli presented this innovative configuration with a mild power density of 7 mW per square meter of electrodes harvested by two activated carbon porous electrodes.228 Later, Brogioli et al.230 analyzed the spontaneous potential and the leakage current of different activated carbon electrodes. Based on this analysis, they proposed several suitable couples of activated carbon materials that could possibly enlarge the energy extraction. Using porous carbon electrodes of A-PC-2 and NS30 (two commercial activated carbon films) in CDLE system, a remarkable power density of 50 mW m−2 was reported.
In CDLE, capacitive electrodes suffer from self-discharging problems due to faradic reactions on the surface of the carbon. Porada et al.231 summarized these reaction into three types: the first one is the conversion of quinone group on the carbon's surface with two protons to form two hydroquinone. Secondly, the carbon oxidation from carbon to CO2. And finally, the electrochemical reactions where components in the water react at the carbon surface. Some of them require molecular oxygen in solution. Brogioli et al. found that removing oxygen by bubbling nitrogen partially reduces the self-discharge.232 An alternative solution of using selective faradaic electrodes in the CDLE configuration was proposed in 2011 by Mantia et al.233 The so-called ‘Mixing entropy battery’ was experimentally demonstrated by using Na2−xMn5O10 electrode for Na+ capturing and Ag/AgCl electrode for Cl− capturing. In this conception, extracted energy from salinity difference is stored inside the bulk crystal structure of the electrode material in chemical energy form. A power density of 138 mW m−2 was reported for a salinity gradient of 0.03 M and 1.5 M of NaCl solutions. The main problems of this technique, in addition to the high cost of the electrodes is the relatively short lifespan of the Ag/AgCl electrodes and the low specific capacity of the NMO. Also, the pre-charging step promotes the energy investment.234 To overcome all that, Ye et al.234 proposed a charge-free MEB with low-cost electrode materials with Prussian blue for the cationic electrode to capture the Na+, and polypyrrole to capture the Cl− for anions.
The conventional CDLE configuration requires the external electrical charging system to enable the energy harvesting, which requires higher installation costs and reduce the system efficiency. In 2010, Sales et al.70 proposed to replace auxiliary charging process by using IEMs, so as to use the Donnan potential established across the membrane for system charging. This technology is called capacitive energy extraction based on Donnan potential (CDP). According to their work, Neosepta CEM (or AEM) was placed between the porous carbon electrode and the spacer. While fresh water and salt water were injected alternatively into the spacer, cations and anions were transported through CEM and AEM under the Donnan potential driving force, forming alternative ionic flows (Fig. 21). The initial work of CDP reported a power density of 11.6 mW m−2 for solution concentration of 10 mM and 510 mM for fresh water and salt water, respectively. Based on the principle of CDP, modifications of electrodes and membranes were conducted for performance amelioration. Hatzell et al.235 proposed to use flow electrodes containing activated carbons in CDP configuration, which significantly increased the system performance towards 50.9 mW m−2. In 2021, Hwang et al.236 realized systematic research on flow electrodes on varying particle components and concentration, the optimum flow electrodes containing expanded graphite was reported to provide a power density of 480 mW m−2. Further optimization on current collector (graphene coated Ti mesh) could even promote the system performance towards 750 mW m−2, according to the recent work of Lee et al.237
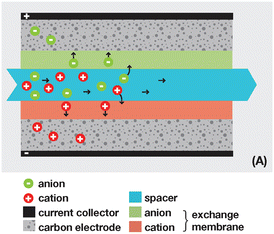 | ||
| Fig. 21 Illustration of the composition and working principle of capacitive energy extraction based on Donnan potential (CDP). IEMs are used to replace external charging sources so that anions and cations move from spacer channel into porous electrodes (figures and captions reproduced from ref. 70 with permission from American Chemical Society, copyright 2010). | ||
Another emerging strategy similar to CDP is the soft electrodes (SE), where IEMs are replaced by polyelectrolytes to form direct anionic and cationic layers onto electrodes. A pioneering work was realized in 2014 by Ahualli et al.238 by using polyelectrolyte coated carbon electrodes with a power output of 12.1 mW m−2. In 2020, Siekierka et al.239 prepared electrodes coated with EDA and PAA/PMA, reaching a maximum power of 293 mW m−2. However, it is to notice that considerable viscous loss is expected in flow electrode related systems due to the highly viscous properties of flow electrodes.
Numerous theoretical analyses of Capmixing systems were reported,232,240–242 providing guidelines for optimization of Capmixing. Further strategies, including thermal assisted Capmixing,243,244 additional charging245 and module scaling up,246,247 were also developed for performance enhancement.
3.4 CRED
An innovative configuration combining RED and Capmixing presents a higher power density output with numerous advantages compared with conventional blue energy harvesting technologies. It was firstly reported by Vermaas et al.248 in 2013, suggesting the use of capacitive electrodes in RED configurations (CRED). Such configuration allows the installation of multiple cationic and anionic membrane stacks for higher potential generation and at the same time avoids the redox reactions in the system. In their work, a layer of activated carbon is deposited on a Ti/Pt mesh to form the capacitive electrodes for adsorption and storage of ions. As larger range in voltage and accumulated charge is achieved compared with conventional Capmixing technologies, a maximum power density of 0.9 W m−2 can be achieved in cell configuration of a stack of 30 membranes with a salinity difference of 0.017 M and 0.508 M for fresh water and salt water, respectively. Zhan et al.249 proposed similar configurations using graphene hydrogel electrodes combined with a single AEM, obtaining an average power density of 0.417 W m−2 for a salinity gradient of 0.02 M/0.500 M for NaCl solution.In 2019, Zhu et al.250 proposed a novel configuration of carbonized peat moss (CPM) electrodes along with a single CEM. They obtained an average power density of 0.95 W m−2 for a salinity gradient of 0.017 M and 0.513 M for fresh water and salt water, respectively.
A novel cell design composed of a single selective membrane and two inexpensive capacitive electrodes was presented in the work of Brahmi et Colin (Fig. 22 and 23).169 A home-made slurry composed of activated carbon particles, carbon nanotubes and PVDF is homogeneously deposited onto a porous carbon electrode to form a capacitive layer. As capacitive electrodes are charged by ion adsorption while immersed in solutions, periodic water compartment switching is necessary to deblock the saturation regime. An alternative capacitive current is generated when an electrical resistance is directly connected to the system. A net power density output of 2 W m−2 was reported, with a gradient of 300 (0.017 M/5.1 M) for a simple configuration of a single cationic membrane combined with two inexpensive electrodes. It is to mention that this net power density takes into account the viscous loss in the cell and remains the maximum power density output for CRED systems.
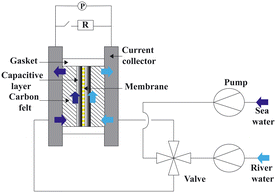 | ||
| Fig. 22 Scheme of the experimental millifluidic set up used for the salinity gradient harvesting with one membrane and a 6 mm water compartment (figures and captions reproduced from ref. 169 with permission from Elsevier, copyright 2022). | ||
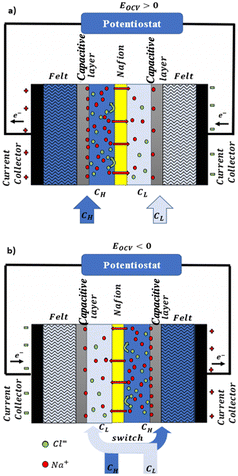 | ||
| Fig. 23 Illustration of two working regimes for a capacitive salinity-gradient cell before (a) and after (b) water compartment switch (figures and captions reproduced from ref. 169 with permission from Elsevier, copyright 2022). | ||
4 Conclusion
In this review, we mainly focus on two different types of water-based energy harvesting systems built on fluidic systems at different scales. Based on the charge separation mechanism, triboelectric energy harvesting systems converts mechanical energy into electrical energy. Osmotic energy harvesting systems realize controlled mixing procedure of solutions of different salinity to recover energies. These two systems have the advantages of being able to be miniaturized220 as well as being used on a large scale. Though they are not currently in use for electricity production due to many remaining problems, researches of system amelioration are in full development.We have shown that triboelectric systems can achieve an average power density of a few watt per meter square. The increase of efficiency of triboelectric systems requires a better understanding of charge separation mechanisms but also the implementation of efficient storage processes for the energy generated. Another promising strategy is to investigate in innovative materials. For instance, the composite polymer materials, integrated with conductive particles in order to increase their dielectric constant and their polarizability, could have an important place in future technological developments. It is of great importance to ensure the durability and recycling of these systems. Working with self-healing systems such as vitrimers251 is a prospect.
The majority of the osmotic energy harvesting systems (PRO, RED and CRED systems) obtain a power density of a few watt per meter square and an energy conversion efficiency below 35%. Though numerous attempts were realized in laboratories and in industrial applications, we now encounter with the bottleneck of performance amelioration, especially for power density and energy conversion efficiency, which remain below the commercialization threshold. The bar of 5 W m−2 of net production under industrial production conditions has still not been crossed. The key factor in technology acceleration consists of the amelioration of membrane performance and a significant membrane price reduction. Recent studies have shown that the development of these techniques will not go through the use of membranes resulting from the concepts of nanofluidics or bioinspiration which aroused great interest. To relaunch this track, it is necessary to reduce the polarization effects developed at the entry and exit of membranes with limited energy input. In order to apply these conceptions in membrane engineering, several crucial questions are raised as follows. How to stack nanochannels or slits with large surface charges in space while preventing these nanochannels from interacting with each other? How to optimize electrode arrangement in cell designs so as to avoid the ionic passage through solution compartments (of low ionic conductivity)? How to limit significant pressure drop in energy harvesting systems?
Another promising path, which remains little exploited, is the novel configuration composed of capacitive electrodes and a single membrane. It opens up a novel path of performance enhancement by working on electrode materials. In this context, the use of electrodes exhibiting faradaic surface reactions seems to be a promising track. In terms of device scaling up, it is certain that significant engineering work is required to reduce the filling time during water compartment batching. In general, there is a contribution to be made towards battery technologies to improve these processes.
All these results are very encouraging for powering electronic devices. The applications of the use of saline gradients to supply embedded sensors seem to be a relevant way and can be an important industrial outlet for this technique. The passage to large scales is more futuristic. The economic profitability of triboelectricity is proven. However, it is necessary to improve the lifetimes. The profitability of osmotic energy is less clear. It is true that currently, PRO, RED and Capmixing techniques are not profitable due to the high cost of membranes and water pre-treatments. And the debate of economic viability of osmotic energy harvesting systems has never stopped. However, these economic analyzes should not hinder research. Electricity prices increased by a factor of 20 in 1 year. In such an economic context and because of the scarcity of fossil resources, these techniques will eventually prevail even if they currently remain expensive. The IPCC report reminds us of the importance of taking actions to find solutions for limiting global environmental problems of climate change and greenhouse gas emissions. Our planet is nicknamed the blue planet. 71% of the 509 million m2 of our planet surface are covered with water,252 which corresponds to a volume of 140 million km3. It is therefore a natural idea to develop renewable energies based on salted water resources. Overall, we believe that it is important to continue scientific researches and industrial attempts on these two techniques which could eventually solve the major problem of the 21st century: the ecological transition.
Author contributions
NW, YB, AC wrote, reviewed and edited the manuscript. AC supervised the redaction of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
NW acknowledges funding from China Scholarship Council (CSC). YB acknowledges funding from the Institut Pierre-Gilles de Gennes (laboratoire d'excellence PSL).Notes and references
- S. Priya and D. J. Inman, Energy harvesting technologies, Springer, 2009, vol. 21 Search PubMed.
- M. Pruvost, W. J. Smit, C. Monteux, P. Del Corro, I. Dufour, C. Ayela, P. Poulin and A. Colin, Sci. Rep., 2020, 10, 1–14 CrossRef PubMed.
- D. Guyomar and M. Lallart, Micromachines, 2011, 2, 274–294 CrossRef.
- A. Harb, Renewable Energy, 2011, 36, 2641–2654 CrossRef.
- S. E. Skilhagen, J. E. Dugstad and R. J. Aaberg, Desalination, 2008, 220, 476–482 CrossRef.
- S. Hanson, M. Seok, Y.-S. Lin, Z. Foo, D. Kim, Y. Lee, N. Liu, D. Sylvester and D. Blaauw, IEEE J. Solid-State Circuits, 2009, 44, 1145–1155 Search PubMed.
- S. Jeong, Z. Foo, Y. Lee, J.-Y. Sim, D. Blaauw and D. Sylvester, IEEE J. Solid-State Circuits, 2014, 49, 1682–1693 Search PubMed.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS PubMed.
- A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 1–10 CrossRef.
- S. Lin, X. Chen and Z. L. Wang, Chem. Rev., 2021, 122, 5209–5232 CrossRef PubMed.
- F.-R. Fan, Z.-Q. Tian and Z. L. Wang, Nano Energy, 2012, 1, 328–334 CrossRef CAS.
- J. Tian, X. Chen and Z. L. Wang, Nanotechnology, 2020, 31, 242001 CrossRef CAS.
- Z. L. Wang, Nano Energy, 2020, 68, 104272 CrossRef CAS.
- Z. L. Wang, Mater. Today, 2017, 20, 74–82 CrossRef.
- W. Thomson, Proc. R. Soc. London, 1868, 67–72 Search PubMed.
- A. G. Marin, W. van Hoeve, P. Garcia-Sanchez, L. Shui, Y. Xie, M. A. Fontelos, J. C. Eijkel, A. van den Berg and D. Lohse, Lab Chip, 2013, 13, 4503–4506 RSC.
- J. P. Tarelho, M. P. S. dos Santos, J. A. Ferreira, A. Ramos, S. Kopyl, S. O. Kim, S. Hong and A. Kholkin, Mater. Today, 2018, 21, 1019–1041 CrossRef CAS.
- P. Dhiman, F. Yavari, X. Mi, H. Gullapalli, Y. Shi, P. M. Ajayan and N. Koratkar, Nano Lett., 2011, 11, 3123–3127 CrossRef CAS.
- J. Yin, X. Li, J. Yu, Z. Zhang, J. Zhou and W. Guo, Nat. Nanotechnol., 2014, 9, 378–383 CrossRef CAS PubMed.
- J. Yin, Z. Zhang, X. Li, J. Yu, J. Zhou, Y. Chen and W. Guo, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- S. Lin, L. Zhu, Z. Tang and Z. L. Wang, Nat. Commun., 2022, 13, 1–9 Search PubMed.
- S. Lin, L. Xu, A. Chi Wang and Z. L. Wang, Nat. Commun., 2020, 11, 1–8 CrossRef.
- Z. L. Wang and A. C. Wang, Mater. Today, 2019, 30, 34–51 CrossRef CAS.
- B. Chen, Y. Xia, R. He, H. Sang, W. Zhang, J. Li, L. Chen, P. Wang, S. Guo and Y. Yin, et al. , Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2209056119 CrossRef CAS.
- N. Miljkovic, D. J. Preston, R. Enright and E. N. Wang, Nat. Commun., 2013, 4, 1–9 Search PubMed.
- Z.-H. Lin, G. Cheng, L. Lin, S. Lee and Z. L. Wang, Angew. Chem., Int. Ed., 2013, 52, 12545–12549 CrossRef PubMed.
- D. Choi, H. Lee, D. J. Im, I. S. Kang, G. Lim, D. S. Kim and K. H. Kang, Sci. Rep., 2013, 3, 1–7 Search PubMed.
- J. H. Masliyah and S. Bhattacharjee, Electrokinetic and colloid transport phenomena, John Wiley & Sons, 2006 Search PubMed.
- Y. Xie, D. Bos, L. J. De Vreede, H. L. De Boer, M.-J. van der Meulen, M. Versluis, A. J. Sprenkels, A. van den Berg and J. C. Eijkel, Nat. Commun., 2014, 5, 1–5 Search PubMed.
- W. Xu, H. Zheng, Y. Liu, X. Zhou, C. Zhang, Y. Song, X. Deng, M. Leung, Z. Yang and R. X. Xu, et al. , Nature, 2020, 578, 392–396 CrossRef PubMed.
- Q. Sun, D. Wang, Y. Li, J. Zhang, S. Ye, J. Cui, L. Chen, Z. Wang, H.-J. Butt and D. Vollmer, et al. , Nat. Mater., 2019, 18, 936–941 CrossRef PubMed.
- H. Wu, N. Mendel, D. van den Ende, G. Zhou and F. Mugele, Phys. Rev. Lett., 2020, 125, 078301 CrossRef CAS PubMed.
- X. J. Zhao, G. Zhu, Y. J. Fan, H. Y. Li and Z. L. Wang, ACS Nano, 2015, 9, 7671–7677 CrossRef CAS.
- S. Jang, M. La, S. Cho, Y. Yun, J. H. Choi, Y. Ra, S. J. Park and D. Choi, Nano Energy, 2020, 70, 104541 CrossRef CAS.
- G. Zhu, Y. Su, P. Bai, J. Chen, Q. Jing, W. Yang and Z. L. Wang, ACS Nano, 2014, 8, 6031–6037 CrossRef CAS PubMed.
- Y. Su, X. Wen, G. Zhu, J. Yang, J. Chen, P. Bai, Z. Wu, Y. Jiang and Z. L. Wang, Nano Energy, 2014, 9, 186–195 CrossRef CAS.
- J. Xiong, M.-F. Lin, J. Wang, S. L. Gaw, K. Parida and P. S. Lee, Adv. Energy Mater., 2017, 7, 1701243 CrossRef.
- G.-Z. Li, G.-G. Wang, D.-M. Ye, X.-W. Zhang, Z.-Q. Lin, H.-L. Zhou, F. Li, B.-L. Wang and J.-C. Han, Adv. Electron. Mater., 2019, 5, 1800846 CrossRef.
- B. K. Yun, H. S. Kim, Y. J. Ko, G. Murillo and J. H. Jung, Nano Energy, 2017, 36, 233–240 CrossRef CAS.
- Z.-H. Lin, G. Cheng, S. Lee, K. C. Pradel and Z. L. Wang, Adv. Mater., 2014, 26, 4690–4696 CrossRef CAS PubMed.
- G. Cheng, Z.-H. Lin, Z.-L. Du and Z. L. Wang, ACS Nano, 2014, 8, 1932–1939 CrossRef CAS PubMed.
- Q. Liang, X. Yan, X. Liao and Y. Zhang, Nano Energy, 2016, 25, 18–25 CrossRef CAS.
- L. Zhao, L. Liu, X. Yang, H. Hong, Q. Yang, J. Wang and Q. Tang, J. Mater. Chem. A, 2020, 8, 7880–7888 RSC.
- R. K. Cheedarala, M. Shahriar, J. H. Ahn, J. Y. Hwang and K. K. Ahn, Nano Energy, 2019, 65, 104017 CrossRef CAS.
- M. Zhang, C. Bao, C. Hu, Y. Huang, Y. Yang and Y. Su, Nano Energy, 2022, 107992 CrossRef CAS.
- J. H. Ahn, J. Y. Hwang, C. G. Kim, G. H. Nam and K. K. Ahn, Nano Energy, 2020, 67, 104269 CrossRef CAS.
- S.-H. Kwon, J. Park, W. K. Kim, Y. Yang, E. Lee, C. J. Han, S. Y. Park, J. Lee and Y. S. Kim, Energy Environ. Sci., 2014, 7, 3279–3283 RSC.
- Z.-H. Lin, G. Cheng, W. Wu, K. C. Pradel and Z. L. Wang, ACS Nano, 2014, 8, 6440–6448 CrossRef PubMed.
- K. Yatsuzuka, Y. Mizuno and K. Asano, J. Electrost., 1994, 32, 157–171 CrossRef.
- B. Wang, Y. Wu, Y. Liu, Y. Zheng, Y. Liu, C. Xu, X. Kong, Y. Feng, X. Zhang and D. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 31351–31359 CrossRef PubMed.
- P. Zhao, N. Soin, K. Prashanthi, J. Chen, S. Dong, E. Zhou, Z. Zhu, A. A. Narasimulu, C. D. Montemagno and L. Yu, et al. , ACS Appl. Mater. Interfaces, 2018, 10, 5880–5891 CrossRef PubMed.
- C. Cai, B. Luo, Y. Liu, Q. Fu, T. Liu, S. Wang and S. Nie, Mater. Today, 2022, 52, 299–326 CrossRef.
- BNEF, https://about.bnef.com/blog/cost-of-new-renewables-temporarily-rises-asinflation-starts-to-bite/, 2022.
- Energy.gov, https://www.energy.gov, 2022.
- A. Ahmed, I. Hassan, T. Ibn-Mohammed, H. Mostafa, I. M. Reaney, L. S. Koh, J. Zu and Z. L. Wang, Energy Environ. Sci., 2017, 10, 653–671 RSC.
- R. Zhang and H. Olin, ACS Nanosci. Au, 2021, 2, 12–31 CrossRef.
- M. G. Stanford, J. T. Li, Y. Chyan, Z. Wang, W. Wang and J. M. Tour, ACS Nano, 2019, 13, 7166–7174 CrossRef CAS.
- W. Liu, Z. Wang, G. Wang, Q. Zeng, W. He, L. Liu, X. Wang, Y. Xi, H. Guo and C. Hu, et al. , Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- Z. L. Wang, T. Jiang and L. Xu, Nano Energy, 2017, 39, 9–23 CrossRef CAS.
- X. Wen, W. Yang, Q. Jing and Z. L. Wang, ACS Nano, 2014, 8, 7405–7412 CrossRef CAS.
- Z. L. Wang, et al. , Nature, 2017, 542, 159–160 CrossRef CAS.
- L. M. Zhang, C. B. Han, T. Jiang, T. Zhou, X. H. Li, C. Zhang and Z. L. Wang, Nano Energy, 2016, 22, 87–94 CrossRef CAS.
- S. L. Zhang, M. Xu, C. Zhang, Y.-C. Wang, H. Zou, X. He, Z. Wang and Z. L. Wang, Nano Energy, 2018, 48, 421–429 CrossRef CAS.
- M. Xu, T. Zhao, C. Wang, S. L. Zhang, Z. Li, X. Pan and Z. L. Wang, ACS Nano, 2019, 13, 1932–1939 CAS.
- N. Y. Yip, D. A. Vermaas, K. Nijmeijer and M. Elimelech, Environ. Sci. Technol., 2014, 48, 4925–4936 CrossRef CAS PubMed.
- R. S. Norman, Science, 1974, 186, 350–352 CrossRef CAS.
- J. W. Post, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2008, 42, 5785–5790 CrossRef CAS PubMed.
- Z. Jia, B. Wang, S. Song and Y. Fan, Renewable Sustainable Energy Rev., 2014, 31, 91–100 CrossRef.
- N. Y. Yip, D. Brogioli, H. V. M. Hamelers and K. Nijmeijer, Environ. Sci. Technol., 2016, 50, 12072–12094 CrossRef CAS PubMed.
- B. B. Sales, M. Saakes, J. W. Post, C. J. N. Buisman, P. M. Biesheuvel and H. V. M. Hamelers, Environ. Sci. Technol., 2010, 44, 5661–5665 CrossRef CAS.
- K. Touati and F. Tadeo, Int. J. Green Energy, 2017, 14, 337–360 CrossRef.
- S. Sarp, Z. Li and J. Saththasivam, Desalination, 2016, 389, 2–14 CrossRef CAS.
- F. Helfer, C. Lemckert and Y. G. Anissimov, J. Membr. Sci., 2014, 453, 337–358 CrossRef.
- Y. Shi, M. Zhang, H. Zhang, F. Yang, C. Y. Tang and Y. Dong, Water Res., 2021, 189, 116666 CrossRef.
- W. Y. Chia, S. R. Chia, K. S. Khoo, K. W. Chew and P. L. Show, J. Water Process. Eng., 2021, 39, 101758 CrossRef.
- Q. She, R. Wang, A. G. Fane and C. Y. Tang, J. Membr. Sci., 2016, 499, 201–233 CrossRef.
- R. R. Gonzales, A. Abdel-Wahab, S. Adham, D. S. Han, S. Phuntsho, W. Suwaileh, N. Hilal and H. K. Shon, Desalination, 2021, 500, 114841 CrossRef.
- A. P. Straub, A. Deshmukh and M. Elimelech, Energy Environ. Sci., 2016, 9, 31–48 RSC.
- S. Lin, A. P. Straub and M. Elimelech, Energy Environ. Sci., 2014, 7, 2706–2714 RSC.
- B. E. Logan and M. Elimelech, Nature, 2012, 488, 313–319 CrossRef CAS.
- S. Xu, Y. Liu, Y. Wang, M. Zhang, Q. Xiao and Y. Duan, Desalination, 2017, 412, 39–48 CrossRef CAS.
- S. Zhao and L. Zou, J. Membr. Sci., 2011, 379, 459–467 CrossRef CAS.
- Q. She, X. Jin and C. Y. Tang, J. Membr. Sci., 2012, 401–402, 262–273 CrossRef CAS.
- J. Kim, M. J. Park, M. Park, H. K. Shon, S.-H. Kim and J. H. Kim, Desalination, 2016, 389, 207–214 CrossRef CAS.
- N. Y. Yip and M. Elimelech, Environ. Sci. Technol., 2013, 47, 12607–12616 CrossRef CAS.
- M. Tawalbeh, A. Al-Othman, N. Abdelwahab, A. H. Alami and A. G. Olabi, Renewable Sustainable Energy Rev., 2021, 138, 110492 CrossRef CAS.
- S. Loeb, F. Van Hessen and D. Shahaf, J. Membr. Sci., 1976, 1, 249–269 CrossRef CAS.
- G. D. Mehta, J. Membr. Sci., 1982, 10, 3–19 CrossRef CAS.
- A. Achilli, T. Y. Cath and A. E. Childress, J. Membr. Sci., 2009, 343, 42–52 CrossRef CAS.
- N. Akther, A. Sodiq, A. Giwa, S. Daer, H. A. Arafat and S. W. Hasan, Chem. Eng. J., 2015, 281, 502–522 CrossRef CAS.
- Y. C. Kim and M. Elimelech, J. Membr. Sci., 2013, 429, 330–337 CrossRef CAS.
- S. L. Plata and A. E. Childress, Desalination, 2019, 467, 51–56 CrossRef CAS.
- N. AlZainati, H. Saleem, A. Altaee, S. J. Zaidi, M. Mohsen, A. Hawari and G. J. Millar, J. Water Process. Eng., 2021, 40, 101950 CrossRef.
- N. Y. Yip, A. Tiraferri, W. A. Phillip, J. D. Schiffman, L. A. Hoover, Y. C. Kim and M. Elimelech, Environ. Sci. Technol., 2011, 45, 4360–4369 CrossRef CAS PubMed.
- G. Han, S. Zhang, X. Li and T.-S. Chung, J. Membr. Sci., 2013, 440, 108–121 CrossRef.
- X. Li, S. Zhang, F. Fu and T.-S. Chung, J. Membr. Sci., 2013, 434, 204–217 CrossRef.
- M. Son, H. Park, L. Liu, H. Choi, J. H. Kim and H. Choi, Chem. Eng. J., 2016, 284, 68–77 CrossRef.
- J. Wei, Y. Li, L. Setiawan and R. Wang, J. Membr. Sci., 2016, 511, 54–64 CrossRef.
- N.-N. Bui and J. R. McCutcheon, Environ. Sci. Technol., 2014, 48, 4129–4136 CrossRef.
- M. Tian, R. Wang, K. Goh, Y. Liao and A. G. Fane, J. Membr. Sci., 2015, 486, 151–160 CrossRef.
- S. Lim, M. J. Park, S. Phuntsho, A. Mai-Prochnow, A. B. Murphy, D. Seo and H. Shon, J. Membr. Sci., 2018, 564, 382–393 CrossRef CAS.
- R. R. Gonzales, M. J. Park, T.-H. Bae, Y. Yang, A. Abdel-Wahab, S. Phuntsho and H. K. Shon, Desalination, 2019, 459, 10–19 CrossRef CAS.
- S. J. Kwon, K. Park, D. Y. Kim, M. Zhan, S. Hong and J.-H. Lee, J. Membr. Sci., 2021, 619, 118796 CrossRef CAS.
- J. H. Kim, S. J. Moon, S. H. Park, M. Cook, A. G. Livingston and Y. M. Lee, J. Membr. Sci., 2018, 550, 322–331 CrossRef CAS.
- S. J. Moon, J. H. Kim, J. G. Seong, W. H. Lee, S. H. Park, S. H. Noh, J. H. Kim and Y. M. Lee, J. Membr. Sci., 2020, 607, 118120 CrossRef CAS.
- H. W. Chung, J. Swaminathan, L. D. Banchik and J. H. Lienhard, Desalination, 2018, 448, 13–20 CrossRef CAS.
- Y. C. Kim and M. Elimelech, Environ. Sci. Technol., 2012, 46, 4673–4681 CrossRef CAS PubMed.
- Q. She, D. Hou, J. Liu, K. H. Tan and C. Y. Tang, J. Membr. Sci., 2013, 445, 170–182 CrossRef CAS.
- E. Sivertsen, T. Holt, W. Thelin and G. Brekke, Desalination, 2013, 312, 107–123 CrossRef CAS.
- S. Chou, R. Wang, L. Shi, Q. She, C. Tang and A. G. Fane, J. Membr. Sci., 2012, 389, 25–33 CrossRef CAS.
- S. Chou, R. Wang and A. G. Fane, J. Membr. Sci., 2013, 448, 44–54 CrossRef CAS.
- P. G. Ingole, W. Choi, K.-H. Kim, H.-D. Jo, W.-K. Choi, J.-S. Park and H.-K. Lee, Desalination, 2014, 345, 136–145 CrossRef CAS.
- P. G. Ingole, W. Choi, K. H. Kim, C. H. Park, W. K. Choi and H. K. Lee, Chem. Eng. J., 2014, 243, 137–146 CrossRef.
- F.-J. Fu, S.-P. Sun, S. Zhang and T.-S. Chung, J. Membr. Sci., 2014, 469, 488–498 CrossRef.
- X. Li, T. Cai and T.-S. Chung, Environ. Sci. Technol., 2014, 48, 9898–9907 CrossRef PubMed.
- P. G. Ingole, K. H. Kim, C. H. Park, W. K. Choi and H. K. Lee, RSC Adv., 2014, 4, 51430–51439 RSC.
- Y. Zhang, J. L. Li, T. Cai, Z. L. Cheng, X. Li and T.-S. Chung, J. Membr. Sci., 2018, 563, 521–530 CrossRef.
- D. L. Zhao, S. Das and T.-S. Chung, Environ. Sci. Technol., 2017, 51, 14016–14023 CrossRef PubMed.
- W. Gai, D. L. Zhao and T.-S. Chung, J. Membr. Sci., 2018, 551, 94–102 CrossRef CAS.
- M. J. Park, S. Lim, R. R. Gonzales, S. Phuntsho, D. S. Han, A. Abdel-Wahab, S. Adham and H. K. Shon, Desalination, 2019, 464, 63–75 CrossRef CAS.
- D. Zhao, G. Qiu, X. Li, C. Wan, K. Lu and T.-S. Chung, Water Res., 2016, 104, 389–396 CrossRef CAS PubMed.
- N. L. Le, N. M. S. Bettahalli, S. P. Nunes and T.-S. Chung, J. Membr. Sci., 2016, 505, 157–166 CrossRef CAS.
- G. Han, P. Wang and T.-S. Chung, Environ. Sci. Technol., 2013, 47, 8070–8077 CrossRef CAS PubMed.
- S. Zhang, F. Fu and T.-S. Chung, Chem. Eng. Sci., 2013, 87, 40–50 CrossRef CAS.
- X. Li, T.-S. Chung and T.-S. Chung, AIChE J., 2013, 59, 4749–4761 CrossRef CAS.
- X. Song, Z. Liu and D. D. Sun, Energy Environ. Sci., 2013, 6, 1199 RSC.
- Y. Cui, X.-Y. Liu and T.-S. Chung, Chem. Eng. J., 2014, 242, 195–203 CrossRef CAS.
- A. P. Straub, N. Y. Yip and M. Elimelech, Environ. Sci. Technol. Lett., 2014, 1, 55–59 CrossRef CAS.
- Y. Li, R. Wang, S. Qi and C. Tang, J. Membr. Sci., 2015, 488, 143–153 CrossRef CAS.
- Q. She, J. Wei, N. Ma, V. Sim, A. G. Fane, R. Wang and C. Y. Tang, J. Membr. Sci., 2016, 504, 75–88 CrossRef CAS.
- J. A. Idarraga-Mora, D. A. Ladner and S. M. Husson, J. Membr. Sci., 2018, 549, 251–259 CrossRef CAS.
- Y. Sun, L. Cheng, T. Shintani, Y. Tanaka, T. Takahashi, T. Itai, S. Wang, L. Fang and H. Matsuyama, Ind. Eng. Chem. Res., 2018, 57, 13528–13538 CrossRef CAS.
- X. Tong, X. Wang, S. Liu, H. Gao, C. Xu, J. Crittenden and Y. Chen, Carbon, 2018, 138, 410–418 CrossRef CAS.
- S. J. Moon, S. M. Lee, J. H. Kim, S. H. Park, H. H. Wang, J. H. Kim and Y. M. Lee, Desalination, 2020, 483, 114409 CrossRef CAS.
- F.-J. Fu, S. Zhang, S.-P. Sun, K.-Y. Wang and T.-S. Chung, J. Membr. Sci., 2013, 443, 144–155 CrossRef CAS.
- S.-P. Sun and T.-S. Chung, Environ. Sci. Technol., 2013, 47, 13167–13174 CrossRef PubMed.
- S. Zhang, P. Sukitpaneenit and T.-S. Chung, Chem. Eng. J., 2014, 241, 457–465 CrossRef.
- G. Han and T.-S. Chung, AIChE J., 2014, 60, 1107–1119 CrossRef.
- G. Han, Q. Ge and T.-S. Chung, Appl. Energy, 2014, 132, 383–393 CrossRef.
- S. C. Chen, C. F. Wan and T.-S. Chung, J. Membr. Sci., 2015, 479, 190–203 CrossRef.
- F.-J. Fu, S. Zhang and T.-S. Chung, Desalination, 2015, 376, 73–81 CrossRef.
- Z. L. Cheng, X. Li, Y. D. Liu and T.-S. Chung, J. Membr. Sci., 2016, 506, 119–129 CrossRef CAS.
- W. Gai, X. Li, J. Y. Xiong, C. F. Wan and T.-S. Chung, J. Membr. Sci., 2016, 516, 104–112 CrossRef CAS.
- L. Zhang, Q. She, R. Wang, S. Wongchitphimon, Y. Chen and A. G. Fane, Desalination, 2016, 389, 119–128 CrossRef CAS.
- Y. Chen, L. Setiawan, S. Chou, X. Hu and R. Wang, J. Membr. Sci., 2016, 503, 90–100 CrossRef CAS.
- N. Lieu Le, M. Quilitzsch, H. Cheng, P.-Y. Hong, M. Ulbricht, S. P. Nunes and T.-S. Chung, J. Membr. Sci., 2017, 522, 1–11 CrossRef.
- Z. L. Cheng, X. Li, Y. Feng, C. F. Wan and T.-S. Chung, J. Membr. Sci., 2017, 524, 97–107 CrossRef CAS.
- C. F. Wan, B. Li, T. Yang and T.-S. Chung, Sep. Purif. Technol., 2017, 172, 32–42 CrossRef CAS.
- G. Han, Z. L. Cheng and T.-S. Chung, J. Membr. Sci., 2017, 523, 497–504 CrossRef CAS.
- C. F. Wan, T. Yang, W. Gai, Y. D. Lee and T.-S. Chung, J. Membr. Sci., 2018, 555, 388–397 CrossRef CAS.
- Y. Chen, C. H. Loh, L. Zhang, L. Setiawan, Q. She, W. Fang, X. Hu and R. Wang, J. Membr. Sci., 2018, 548, 398–407 CrossRef CAS.
- Y. Li, S. Zhao, L. Setiawan, L. Zhang and R. Wang, J. Membr. Sci., 2018, 550, 163–172 CrossRef CAS.
- Y. H. Cho, S. D. Kim, J. F. Kim, H.-G. Choi, Y. Kim, S.-E. Nam, Y.-I. Park and H. Park, J. Membr. Sci., 2019, 579, 329–341 CrossRef CAS.
- R. R. Gonzales, Y. Yang, M. J. Park, T.-H. Bae, A. Abdel-Wahab, S. Phuntsho and H. K. Shon, Desalination, 2020, 496, 114756 CrossRef CAS.
- K. Gerstandt, K. V. Peinemann, S. E. Skilhagen, T. Thorsen and T. Holt, Desalination, 2008, 224, 64–70 CrossRef CAS.
- S. AL Mashrafi, N. Diaz-Elsayed, J. Benjamin, M. E. Arias and Q. Zhang, Desalination, 2022, 537, 115869 CrossRef CAS.
- Q. A. Khasawneh, B. Tashtoush, A. Nawafleh and B. Kan'an, Energies, 2018, 11, 3118 CrossRef CAS.
- T. N. American, Crown Princess of Norway to Open the World's First Osmotic Power Plant, https://www.norwegianamerican.com/crown-princess-ofnorway-to-open-the-worlds-first-osmotic-power-plant/, 2009 Search PubMed.
- C. Lee, S. H. Chae, E. Yang, S. Kim, J. H. Kim and I. S. Kim, Desalination, 2020, 491, 114501 CrossRef CAS.
- Osmotic Power Plant Opened, REUK.Co.Uk Search PubMed.
- M. Kurihara and H. Takeuchi, Water, 2018, 10, 48 CrossRef.
- R. E. Pattle, Nature, 1954, 174, 660–660 CrossRef CAS.
- R. E. Lacey, Ocean Eng., 1980, 7, 1–47 CrossRef CAS.
- A. Galama, J. Post, H. Hamelers, V. Nikonenko and P. Biesheuvel, J. Membr. Sci. Res., 2016, 2, 128–140 Search PubMed.
- T. Teorell, Proc. Soc. Exp. Biol. Med., 1935, 33, 282–285 CrossRef CAS.
- F. Morrison Jr and J. Osterle, J. Chem. Phys., 1965, 43, 2111–2115 CrossRef.
- A. Siria, P. Poncharal, A.-L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef PubMed.
- Z. Tang, Q.-A. Huang, Y.-J. Wang, F. Zhang, W. Li, A. Li, L. Zhang and J. Zhang, J. Power Sources, 2020, 468, 228361 CrossRef.
- Y. Brahmi and A. Colin, Energy Convers. Manage., 2022, 254, 115297 CrossRef.
- J. Veerman, M. Saakes, S. J. Metz and G. J. Harmsen, J. Appl. Electrochem., 2010, 40, 1461–1474 CrossRef.
- J. Jagur-Grodzinski and R. Kramer, Ind. Eng. Chem. Process Des. Dev., 1986, 25, 443–449 CrossRef.
- J. Veerman, M. Saakes, S. J. Metz and G. J. Harmsen, Environ. Sci. Technol., 2010, 44, 9207–9212 CrossRef PubMed.
- A. Daniilidis, D. A. Vermaas, R. Herber and K. Nijmeijer, Renewable Energy, 2014, 64, 123–131 CrossRef CAS.
- J. Veerman, R. M. de Jong, M. Saakes, S. J. Metz and G. J. Harmsen, J. Membr. Sci., 2009, 343, 7–15 CrossRef CAS.
- J. Veerman and D. Vermaas, Sustainable Energy from Salinity Gradients, Elsevier, 2016, pp. 77–133 Search PubMed.
- D. A. Vermaas, M. Saakes and K. Nijmeijer, Environ. Sci. Technol., 2011, 45, 7089–7095 CrossRef CAS PubMed.
- M. Turek, B. Bandura and P. Dydo, Desalination, 2008, 221, 462–466 CrossRef CAS.
- R. Audinos, J. Power Sources, 1983, 10, 203–217 CrossRef CAS.
- P. Dlugolecki, K. Nymeijer, S. Metz and M. Wessling, J. Membr. Sci., 2008, 319, 214–222 CrossRef CAS.
- J. Moreno, V. Díez, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2018, 550, 155–162 CrossRef CAS.
- S. Mehdizadeh, Y. Kakihana, T. Abo, Q. Yuan and M. Higa, Membranes, 2021, 11, 27 CrossRef CAS PubMed.
- M. Tedesco, E. Brauns, A. Cipollina, G. Micale, P. Modica, G. Russo and J. Helsen, J. Membr. Sci., 2015, 492, 9–20 CrossRef CAS.
- J. G. Hong and Y. Chen, J. Membr. Sci., 2014, 460, 139–147 CrossRef CAS.
- D. A. Vermaas, J. Veerman, M. Saakes and K. Nijmeijer, Energy Environ. Sci., 2014, 7, 1434–1445 RSC.
- A. H. Avci, D. A. Messana, S. Santoro, R. A. Tufa, E. Curcio, G. Di Profio and E. Fontananova, Membranes, 2020, 10, 168 CrossRef CAS PubMed.
- E. Güler, R. Elizen, D. A. Vermaas, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2013, 446, 266–276 CrossRef.
- T. Rijnaarts, J. Moreno, M. Saakes, W. M. de Vos and K. Nijmeijer, Colloids Surf., A, 2019, 560, 198–204 CrossRef CAS.
- M. Y. Kariduraganavar, R. K. Nagarale, A. A. Kittur and S. S. Kulkarni, Desalination, 2006, 197, 225–246 CrossRef CAS.
- N. D. Pismenskaya, E. V. Pokhidnia, G. Pourcelly and V. V. Nikonenko, J. Membr. Sci., 2018, 566, 54–68 CrossRef CAS.
- J. Veerman, M. Saakes, S. Metz and G. Harmsen, J. Membr. Sci., 2009, 327, 136–144 CrossRef CAS.
- D. A. Vermaas, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2011, 385–386, 234–242 CrossRef.
- E. Guler, Y. Zhang, M. Saakes and K. Nijmeijer, ChemSusChem, 2012, 5, 2262–2270 CrossRef CAS PubMed.
- D. A. Vermaas, M. Saakes and K. Nijmeijer, J. Membr. Sci., 2014, 453, 312–319 CrossRef CAS.
- M. Tedesco, C. Scalici, D. Vaccari, A. Cipollina, A. Tamburini and G. Micale, J. Membr. Sci., 2016, 500, 33–45 CrossRef CAS.
- A. H. Avci, R. A. Tufa, E. Fontananova, G. Di Profio and E. Curcio, Energy, 2018, 165, 512–521 CrossRef.
- H. Kim, S. Yang, J. Choi, J.-O. Kim and N. Jeong, Desalination, 2021, 497, 114676 CrossRef.
- J. Gao, X. Liu, Y. Jiang, L. Ding, L. Jiang and W. Guo, Small, 2019, 15, 1804279 CrossRef PubMed.
- X. Liu, M. He, D. Calvani, H. Qi, K. B. Gupta, H. J. de Groot, G. Sevink, F. Buda, U. Kaiser and G. F. Schneider, Nat. Nanotechnol., 2020, 15, 307–312 CrossRef PubMed.
- C. Li, L. Wen, X. Sui, Y. Cheng, L. Gao and L. Jiang, Sci. Adv., 2021, 7, eabg2183 CrossRef PubMed.
- A. A. Moya, J. Membr. Sci., 2020, 598, 117784 CrossRef.
- R. A. Tufa, E. Curcio, W. van Baak, J. Veerman, S. Grasman, E. Fontananova and G. D. Profio, RSC Adv., 2014, 4, 42617–42623 RSC.
- R. S. Kingsbury, F. Liu, S. Zhu, C. Boggs, M. D. Armstrong, D. F. Call and O. Coronell, J. Membr. Sci., 2017, 541, 621–632 CrossRef CAS.
- A. Cosenza, G. Campisi, F. Giacalone, S. Randazzo, A. Cipollina, A. Tamburini and G. Micale, Energies, 2022, 15, 4177 CrossRef.
- D. A. Vermaas, D. Kunteng, M. Saakes and K. Nijmeijer, Water Res., 2013, 47, 1289–1298 CrossRef PubMed.
- B. Vital, E. V. Torres, T. Sleutels, M. C. Gagliano, M. Saakes and H. V. M. Hamelers, Desalination, 2021, 518, 115277 CrossRef.
- Z. He, X. Gao, Y. Zhang, Y. Wang and J. Wang, Desalin. Water Treat., 2016, 57, 28176–28186 CrossRef.
- M. Vaselbehagh, H. Karkhanechi, R. Takagi and H. Matsuyama, J. Membr. Sci., 2017, 530, 232–239 CrossRef.
- H. Gao, B. Zhang, X. Tong and Y. Chen, J. Membr. Sci., 2018, 567, 68–75 CrossRef.
- M. Tedesco, A. Cipollina, A. Tamburini and G. Micale, J. Membr. Sci., 2017, 522, 226–236 CrossRef CAS.
- J.-Y. Nam, K.-S. Hwang, H.-C. Kim, H. Jeong, H. Kim, E. Jwa, S. Yang, J. Choi, C.-S. Kim, J.-H. Han and N. Jeong, Water Res., 2019, 148, 261–271 CrossRef CAS.
- M. Yasukawa, S. Mehdizadeh, T. Sakurada, T. Abo, M. Kuno and M. Higa, Desalination, 2020, 491, 114449 CrossRef CAS.
- C. Simões, B. Vital, T. Sleutels, M. Saakes and W. Brilman, Chem. Eng. J., 2022, 450, 138412 CrossRef.
- J.-Y. Nam, K.-S. Hwang, H.-C. Kim, H. Jeong, H. Kim, E. Jwa, S. Yang, J. Choi, C.-S. Kim, J.-H. Han and N. Jeong, Water Res., 2019, 148, 261–271 CrossRef CAS.
- A. Daniilidis, R. Herber and D. A. Vermaas, Appl. Energy, 2014, 119, 257–265 CrossRef.
- R. A. Tufa, S. Pawlowski, J. Veerman, K. Bouzek, E. Fontananova, G. di Profio, S. Velizarov, J. Goulão Crespo, K. Nijmeijer and E. Curcio, Appl. Energy, 2018, 225, 290–331 CrossRef CAS.
- M. Turek and B. Bandura, Desalination, 2007, 205, 67–74 CrossRef CAS.
- J. W. Post, C. H. Goeting, J. Valk, S. Goinga, J. Veerman, H. V. M. Hamelers and P. J. F. M. Hack, Desalin. Water Treat., 2010, 16, 182–193 CrossRef CAS.
- M. Toupin, K. Malek and A. Mokrini, World Electr. Veh. J., 2016, 8, 431–442 CrossRef.
- F. Giacalone, M. Papapetrou, G. Kosmadakis, A. Tamburini, G. Micale and A. Cipollina, Energy, 2019, 181, 532–547 CrossRef CAS.
- W.-S. Hsu, A. Preet, T.-Y. Lin and T.-E. Lin, Molecules, 2021, 26, 5469 CrossRef CAS PubMed.
- R. B. Sadeglian, O. Pantchenko, D. Tate and A. Shakouri, Appl. Phys. Lett., 2011, 99, 173702 CrossRef.
- Z.-H. Lin, W.-S. Hsu, A. Preet, L.-H. Yeh, Y.-H. Chen, Y.-P. Pao, S.-F. Lin, S. Lee, J.-C. Fan and L. Wang, et al. , Nano Energy, 2021, 79, 105440 CrossRef CAS.
- S. Roundy, P. K. Wright and J. Rabaey, Comput. Commun., 2003, 26, 1131–1144 CrossRef.
- M. Pruvost, W. J. Smit, C. Monteux, P. Poulin and A. Colin, Multifunct. Mater., 2018, 1, 015004 CrossRef CAS.
- K. E. Mueller, J. T. Thomas, J. X. Johnson, J. F. DeCarolis and D. F. Call, J. Ind. Ecol., 2021, 25, 1194–1206 CrossRef CAS.
- C. Tristán, M. Rumayor, A. Dominguez-Ramos, M. Fallanza, R. Ibáñez and I. Ortiz, Sustainable Energy Fuels, 2020, 4, 4273–4284 RSC.
- F. Giacalone, P. Catrini, A. Tamburini, A. Cipollina, A. Piacentino and G. Micale, Energy Convers. Manage., 2018, 164, 588–602 CrossRef.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef PubMed.
- P. Sharma and T. S. Bhatti, Energy Convers. Manage., 2010, 51, 2901–2912 CrossRef CAS.
- D. Brogioli, R. Ziano, R. A. Rica, D. Salerno, O. Kozynchenko, H. V. M. Hamelers and F. Mantegazza, Energy Environ. Sci., 2012, 5, 9870–9880 RSC.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS.
- D. Brogioli, R. Ziano, R. Rica, D. Salerno and F. Mantegazza, J. Colloid Interface Sci., 2013, 407, 457–466 CrossRef PubMed.
- F. La Mantia, M. Pasta, H. D. Deshazer, B. E. Logan and Y. Cui, Nano Lett., 2011, 11, 1810–1813 CrossRef PubMed.
- M. Ye, M. Pasta, X. Xie, K. L. Dubrawski, J. Xu, C. Liu, Y. Cui and C. S. Criddle, ACS Omega, 2019, 4, 11785–11790 CrossRef PubMed.
- M. C. Hatzell, K. B. Hatzell and B. E. Logan, Environ. Sci. Technol. Lett., 2014, 1, 474–478 CrossRef.
- I. Hwang, D. Lee, Y. Jung, K. Park, Y.-G. Jung, D. Kim, G.-H. Cho, S.-I. Jeon, Y.-K. Byeun, U. Paik, S. Yang and T. Song, ACS Sustainable Chem. Eng., 2021, 9, 13514–13525 CrossRef.
- D. Lee, J. S. Roh, I. Hwang, Y. Jung, H. Lee, I. W. Ock, S. Kim, S. Sun, S. Yang, H. B. Park, U. Paik and T. Song, ACS Sustainable Chem. Eng., 2022, 10, 7625–7634 CrossRef.
- S. Ahualli, M. L. Jiménez, M. M. Fernández, G. Iglesias, D. Brogioli and Á. V. Delgado, Phys. Chem. Chem. Phys., 2014, 16, 25241–25246 RSC.
- A. Siekierka, K. Smolínska-Kempisty and M. Bryjak, Desalination, 2020, 495, 114670 CrossRef CAS.
- R. A. Rica, R. Ziano, D. Salerno, F. Mantegazza and D. Brogioli, Phys. Rev. Lett., 2012, 109, 156103 CrossRef CAS PubMed.
- X. Kong, A. Gallegos, D. Lu, Z. Liu and J. Wu, Phys. Chem. Chem. Phys., 2015, 17, 23970–23976 RSC.
- M. Nasir, Y. Nakanishi, A. Patmonoaji and T. Suekane, Renewable Energy, 2020, 155, 278–285 CrossRef.
- D. Moreno and M. C. Hatzell, ACS Sustainable Chem. Eng., 2019, 7, 11334–11340 CrossRef CAS.
- S. Ahualli, M. L. Jiménez, Z. Amador, M. M. Fernández, G. R. Iglesias and A. V. Delgado, Sustainable Energy Fuels, 2021, 5, 3321–3329 RSC.
- Z. Zou, L. Liu, S. Meng and X. Bian, Energy Rep., 2022, 8, 7325–7335 CrossRef.
- G. R. Iglesias, S. Ahualli, M. M. Fernández, M. L. Jiménez and Á. V. Delgado, J. Power Sources, 2016, 318, 283–290 CrossRef CAS.
- F. Liu, T. F. W. Donkers, R. M. Wagterveld, O. Schaetzle, M. Saakes, C. J. N. Buisman and H. V. M. Hamelers, Electrochim. Acta, 2016, 187, 104–112 CrossRef CAS.
- D. A. Vermaas, S. Bajracharya, B. B. Sales, M. Saakes, B. Hamelers and K. Nijmeijer, Energy Environ. Sci., 2013, 6, 643–651 RSC.
- F. Zhan, Z. Wang, T. Wu, Q. Dong, C. Zhao, G. Wang and J. Qiu, J. Mater. Chem. A, 2018, 6, 4981–4987 RSC.
- H. Zhu, W. Xu, G. Tan, E. Whiddon, Y. Wang, C. G. Arges and X. Zhu, Electrochim. Acta, 2019, 294, 240–248 CrossRef CAS.
- M. Röttger, T. Domenech, R. van der Weegen, A. Breuillac, R. Nicolaÿ and L. Leibler, Science, 2017, 356, 62–65 CrossRef PubMed.
- B. Nath, Resonance, 2019, 24, 575–582 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |