Open Access Article
Open Access ArticleOptimization of indirect wastewater characterization: a hybrid approach based on decision trees, genetic algorithms and spectroscopy†
Daniel
Carreres-Prieto
 *a,
Juan T.
García
*a,
Juan T.
García
 *b,
José M.
Carrillo
*b,
José M.
Carrillo
 b and
Antonio
Vigueras-Rodríguez
b and
Antonio
Vigueras-Rodríguez
 b
b
aCenter for Technological Innovation in Construction and Civil Engineering (CITEEC), Universidade da Coruña, 15008, A Coruña, Spain. E-mail: daniel.carreres@udc.es
bDepartment of Mining and Civil Engineering, Universidad Politécnica de Cartagena, 30202 Cartagena, Spain. E-mail: juan.gbermejo@upct.es
First published on 16th August 2023
Abstract
The spectral response of wastewater samples allows, through the use of correlation models, to estimate the pollutant load of the samples in a simple, fast and economical way. However, the accuracy of these models can be affected by alterations in the spectral by external agents such as vibrations or temperature changes. In these cases, approximating the spectral response to trend lines can sometimes provide better estimates, while in other, it is better to work with the original spectral response. This research work proposes a methodology to accurately estimate the pollutant load of wastewater using a hybrid characterization model based on decision trees, which allows, in all cases, to obtain the best possible characterization. This model, based on the analysis of the spectral response, determines which genetic algorithm-based estimation model to make use of: the original spectral response or to the approximation of this to global or individual trend lines for each colour group, to estimate the following parameters: chemical oxygen demand (COD), biochemical oxygen demand at 5 days (BOD5), total suspended solids (TSS), total nitrogen (TN) and total phosphorus (TP) in raw and treated wastewater respectively. The study was conducted on 650 wastewater samples from 43 WWTPs. The results show that the hybrid characterization model provides the best possible fit, achieving an improvement up to 5% in raw wastewater samples, and up to 26.32% in treated wastewater with respect to the use of models that employ point values of the original spectral response, being much more significant in the case of TN.
Water impact1. Spectral response measurements from urban wastewater samples can be affected by external agents, making it difficult for models to provide accurate estimates. 2. A hybrid characterization model based on decision trees can accurately estimate pollutant load using spectral response, achieving the best possible estimate. 3. The hybrid model improves the adjustment levels of pollutant load estimates in both raw and treated wastewater samples by up to 5% and 26.32%, respectively, with a greater improvement for Total Nitrogen (TN). |
1. Introduction
Optical techniques, such as molecular spectroscopy, are reliable for monitoring sanitation systems in real-time and online.1–4 These techniques can be used in sewer networks and treatment plants.5,6 They can be used alone or in combination with other techniques to ensure accuracy7 here is a growing demand for rapid characterization analyses without pre-treatment or the addition of reagents in multiple parts of the systems. This is due to increasing quality requirements in wastewater treatment for water reuse and protection of aquatic environments.8,9 UV-VIS spectroscopy has been successfully used to determine various pollutant species in wastewater, including oxygen demand, nutrients, and solids4,10 where the use of a wide range of wavelengths calibration procedure generally generates higher correlation coefficients than individual wavelengths.11 Similar results have been observed in the research works of ref. 12 for Cr determination in water,13 combining the use of spectrophotometry with chromatography to characterize dissolved organic matter in wastewaters, or ref. 14 which also uses it to characterize dissolved organic matter in wastewater. Also noteworthy are works such as ref. 15 which, using fluorescent spectrophotometers, identify landfill leachate contamination in groundwater.The complexity of wastewater spectra makes it challenging to associate them with specific wavelengths, and the UV-VIS spectral shape lacks prominent peaks.16 This complexity arises from the diverse chemical and physical characteristics of the heterogeneous components in the water matrix, including organic and mineral substances of varying sizes.17 Consequently, the recorded absorbance represents a combination of light absorption primarily by organic compounds and light scattering by solid particles. The research of ref. 18 have identified the wavelength range of 373–374 nm as particularly suitable in the UV-VIS range for characterizing parameters such as COD, TSS, and turbidity.
To address these challenges, techniques like slope-derived spectroscopy can be employed to achieve a more concise model. Slope-derived spectroscopy is favored for its ability to eliminate irrelevant features and effectively incorporate relevant information from spectral data at different pathlengths11,16 propose the utilization of the first and second derivatives of measured spectra to identify deviations from expected patterns. These derivatives are effective in reducing noise caused by various factors. In the analysis of nitrogen species such as nitrate, nitrite, and total nitrogen, ref. 19 and 20 utilize the second derivative. The spectral response provides valuable information about the physicochemical properties of the wastewater samples.
In order to relate the information obtained from the spectral response to the pollutant load of the wastewater, characterization models are needed. Although these models can be calculated using various analysis techniques, the use of artificial intelligence allows more complex and accurate models to be obtained.21–23 Genetic algorithms are one of the most widely used techniques, by providing, through an evolutionary process analogous to that of any living being, a mathematical expression that manages to accurately estimate the response variable, and which has proven its validity as a tool for optimizing the processes of a WWTP24,25 or the estimation of pollutants.26
Another of the techniques with great use in this field are decision trees, which allow performing classification tasks and their high performance has been evidenced in works such as ref. 27 that focuses on the identification and prediction of filamentous bacteria in wastewater and sludge volume index (SVI) as a function of sludge retention time (SRT), NH4+–N and COD, or works such as ref. 28 or 29 as a tool for the optimization and improvement of purification processes.
Viable and cost-effective devices enabled for the on-line and real time quality monitoring in the visible spectra by LED are proposed by ref. 22 and 30–33 where 3D printing is making it possible to achieve low-cost, versatile spectroscopy devices.34,35 The versatility of this technology has led to the development of low-power equipment based on LED technology, such as the one developed by ref. 36, for detecting nitrates in natural waters and treated wastewater.
The spectral response of wastewater in the visible spectrum exhibits a linear relationship, with variations in slope and height depending on the pollutant load. However, external factors such as vibrations or temperature changes can introduce irregularities into certain portions of the spectral response. As a result, it is sometimes more appropriate to work with approximate linear models of the spectral response to mitigate the impact of these perturbations. On other occasions, utilizing the original spectral response is preferred. Therefore, it is crucial to have correlation models that can determine when to apply each type of model, ensuring a more accurate characterization in all scenarios.
This research work provides a methodology, over around 650 wastewater samples from 43 WWTPs, that allows to achieve a better characterization of the pollutant load, from the spectrophotometric response in the visible spectrum (380–700 nm), for the following pollutant parameters: chemical oxygen demand (COD), biochemical oxygen demand at 5 days (BOD5), total suspended solids (TSS), total nitrogen (TN) and total phosphorus (TP) in raw and treated wastewater respectively.
A total of 27 characterization models based on genetic algorithm (GA) are presented. For each pollutant parameter and type of wastewater (raw and treated), three models have been calculated: model based on point values of the spectrum (380–700 nm), model based on approximation of the spectral response to a single global trend line, and model based on the approximation to individual trend lines for each color group: (380–700 nm), violet (380–427 nm), blue (427–476 nm), cyan (476–497 nm), green (497–570 nm), yellow (570–581 nm), orange (581–618 nm), and red (618–700 nm).
In order to determine which model to apply in each case to obtain the best possible estimation, a total of 9 hybrid characterization models, as a combination of decision trees and GA, are presented for raw and treated wastewater, respectively (one for each pollutant parameter and wastewater type).
The rest of this manuscript is organized as follows:
Section 2 provides a description of the experimental campaign carried out, including a description of the equipment developed for it as well as the properties of the water, the software used for the study and its methodology.
Section 3 includes the different models for estimating the pollutant load, as well as the decision trees to select the optimal model for a certain sample. A decision tree is also shown which, based on the slope (M) and the ordinate at the origin (N) of the global trend line of the spectral response, makes it possible to determine whether a wastewater should be classified as raw or treated, a crucial aspect for the development of automatic systems for continuous monitoring of the pollutant load of water.
Finally, section 4 summarizes the general conclusions of the results achieved in this research work.
2. Materials and methods
2.1. Experimental campaign
The present research work has been carried out on 43 wastewater treatment plants (WWTPs), whose main characteristics, in term of average COD, BOD5 and TSS, are described in Table S1 in ESI.† The WWTPs are located throughout the Region of Murcia (Spain), where many of them include tertiary treatment for agricultural purposes. The samples were taken between January 11 and June 22, 2021, but the samples from the Cabezo Beaza WWTP, which were taken during the period 2019 to April 2020. A total of around 650 samples from both the inlet (raw wastewater) and outlet (treated wastewater) of the plants were collected in a homogeneous manner for 24 hours using a 500 mL h−1 in an integrated sample.Samples were not pretreated by any filtering process to replicate the conditions of future automated continuous sensor sampling.
The spectral response is closely related to the pollutant load of the wastewater. Fig. S1 (ESI†) shows the spectral response (transmittance) of eight different samples, with the values of contaminant load measured in laboratories. For instance, sample 1 is an example of raw water with a high contaminant load, and sample 8 is treated water from tertiary treatment. The tests were carried out in accordance with standard methods (SM) and International Organization for Standardization (ISO): ISO 6060:1989 for COD; SM 5210 D for BOD5; SM 2540 F for TSS; SM 4500-NC for TN, and SM 4500-P B for TP.
2.2. Spectrophotometry equipment developed
To carry out the spectral analysis of the samples, the authors have developed an LED spectrophotometry equipment37 shown in Fig. 1, which is capable, by means of a rotating disk of 33 LED lights of different emission range, to carry out the analysis of the samples over 81 wavelengths comprised between 380–700 nm (visible spectrum). The sample is manually introduced into the equipment by means of a standard spectrophotometric cuvette.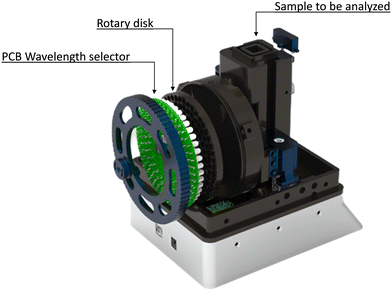 | ||
| Fig. 1 View of the equipment developed to carry out the spectrophotometric analysis in the different WWTPs. | ||
2.3. Symbolic regression
The generation of models based on genetic algorithms (GA), has been carried out through the HeuristicLab software developed by ref. 38. The modeling technique used was offspring selection (OS),38 as it is one of the techniques that provides the best results, as demonstrated by studies such as ref. 39–41 or 30–33.For the generation of the models, the ratio 66–34% has been used for the training and test data, respectively. All GA models have been calculated after eliminating outliers with a mutation rate of 20%.
Fig. S2 of the ESI† shows a simplified diagram of the process of generating the models based on genetic algorithms.
In order to introduce new characteristics (genes) that may be useful in the evolutionary process, random mutations are introduced. The new individuals generated are evaluated in terms of RMSE, and only the best ones will be the ones that will generate the next generation. The process is repeated for a certain number of generations until an individual (model) is reached that is able to best model the response variable.
2.4. Global and individual trend lines by colour groups approximation
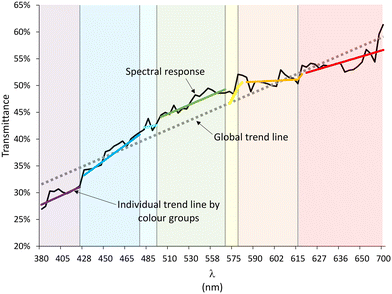
Wastewater samples respond to visible light (380–700 nm) with a line whose slope and height change based on the amount of contamination. Greater contamination leads to a steeper slope but lower overall height (less light transmitted).Fig. 2 shows the spectral response (transmittance), between 380–700 nm, of a raw wastewater sample with a COD of 779 mg l−1, which is shown in black.
Superimposed on the spectral response, the approximation of the spectral response to a global trend line (dashed line) is shown as an approximation formed by individual trend lines for each colour group of the supported visible spectrum carried by the developed equipment in Fig. S2:† violet (380–427 nm), blue (427–476 nm), cyan (476–497 nm), green (497–570 nm), yellow (570–581 nm), orange (581–618 nm) and red (618–780 nm). For clarity, each region has been delimited with its characteristic colour, where the extension of each zone corresponds to the wavelengths installed in the developed equipment.
2.5. Hybrid characterization models. Decision trees
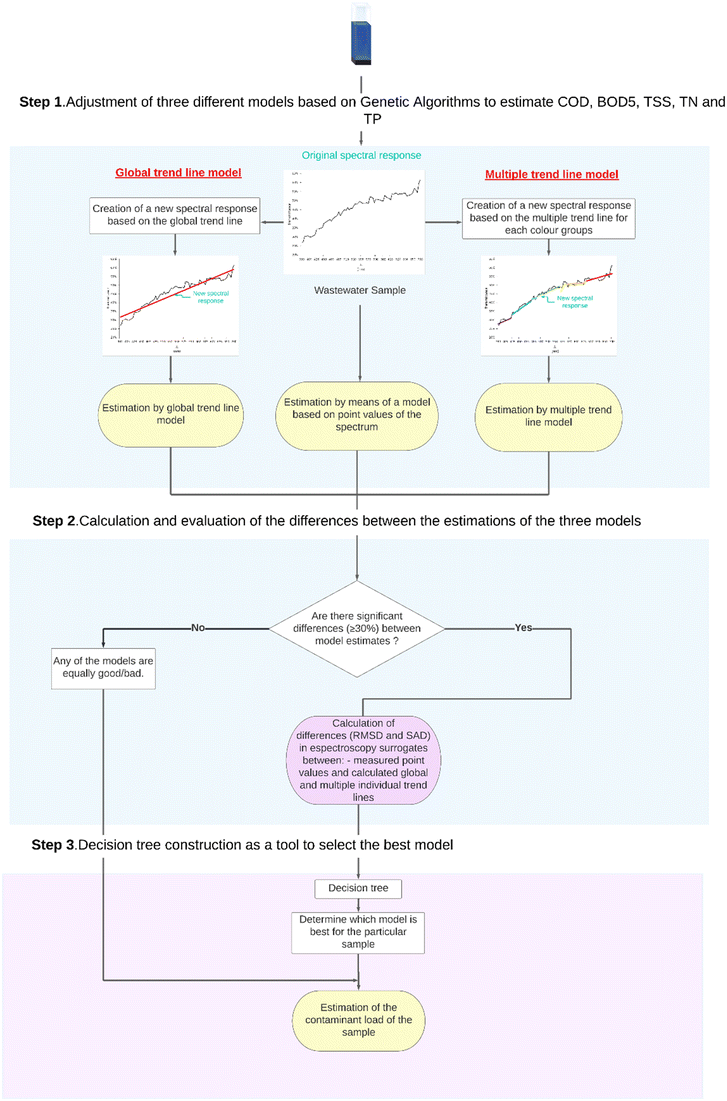
The spectral response of a wastewater sample provides very relevant information to carry out its characterization through estimation models. Depending on the characteristics of this spectral response, it may be more appropriate to apply one of these three GA models: one based on point values of the spectral response, or an approximation based on trend lines, either global (a line that fits the entire working spectrum) or from multiple trend lines for each colour group.In order to determine which model is most appropriate to apply in each specific case, the development of hybrid characterization models based on decision trees is proposed.
Decision trees, due to their characteristics, are more suitable than other artificial intelligence techniques for implementing these hybrid models, due to their requirement of classification as presented in Fig. 3. First, their computational efficiency is notably superior to other techniques in terms of the present typology of study, such as neural networks and genetic algorithms.42 This makes them an ideal choice for working with large datasets and for real-time applications.43 Once the decision tree is trained, making predictions for new instances is fast because it involves traversing the tree from the root to a leaf node based on the feature values.44 Decision trees are efficient data structures that allow for fast search and retrieval of key variables. The tree structure also enables quick access to the relevant features and their corresponding decision rules, making decision trees efficient for both training and prediction.45
In addition, decision trees are robust to irrelevant data and noise, as they tend to ignore irrelevant features during their construction. This capability simplifies data preprocessing and makes them less sensitive to alterations or outliers. On the other hand, its handling of missing data is natural, avoiding the need to eliminate instances or impute values, something problematic in other techniques such as genetic algorithms or neural networks. Furthermore, from the point of view of interpretation, decision trees are highly understandable, unlike the “black boxes” of neural networks, since they are based on a nested structure of conditionals arranged as branches of a tree. Finally, their lower consumption of computational resources makes them particularly suitable for systems with low processing capacity, which is crucial in the development of low-cost equipment for wastewater analysis.
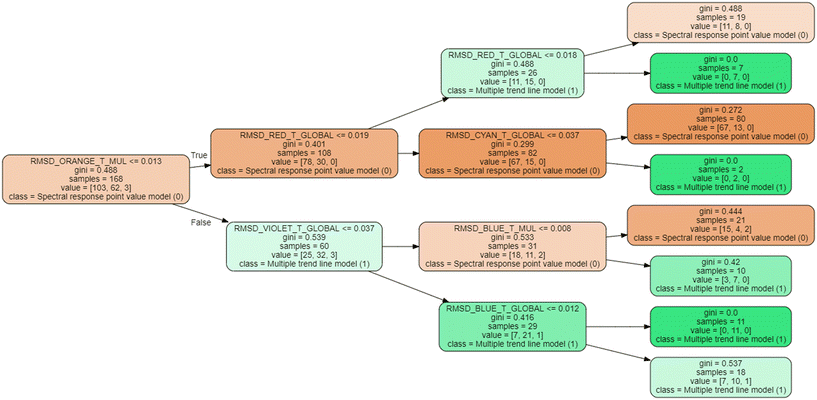
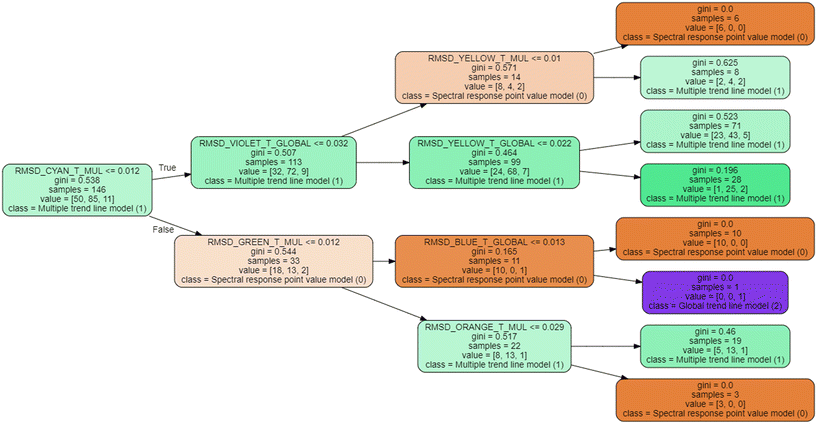
To clarify its operation, an explanatory flow diagram is shown in Fig. 3. First, significant differences among the GA predicted values of pollutants for the three cases (point value, global and multiple individual trend lines) are searched. In this case, differences equal or higher than 30% are considered significant. If this is observed, the decision trees are trained based on the values of root mean square difference (RMSD) and sum of absolute differences (SAD) between the original spectral response and its approximations to trend lines, that will determine, for each pollutant parameter and type of wastewater, which model is more appropriate to apply in each specific case to achieve the best estimates.
Decision trees have been developed by mean of the Python Sklearn library.46 Two and three decision trees have been developed to avoid overfitting. In order to achieve the best possible model, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different trees have been generated for each model, resulting from random recombination of the data into training and test data, selecting the tree with the best fit for test data, (which also implies a good fit with training data). This makes it possible to select the model with the best performance for both training and test.
000 different trees have been generated for each model, resulting from random recombination of the data into training and test data, selecting the tree with the best fit for test data, (which also implies a good fit with training data). This makes it possible to select the model with the best performance for both training and test.
2.6. Model performance indicator
The following performance indicators were used to analyze the performance of the different models presented: percent bias, PBias,47,48 measuring the average trend of the estimated values to be higher or lower than the reference value, R-squared (R2) and RMSE, indicators will be used, which are shown in eqn (1)–(3) respectively.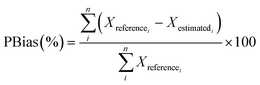 | (1) |
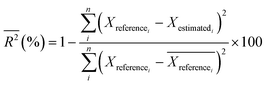 | (2) |
 | (3) |
Also, to define and train the decision trees, the root mean square difference (RMSD) and the sum of absolute differences (SAD) indicators calculated with the differences between the original spectral measurement and its approximations to trend lines, were used:
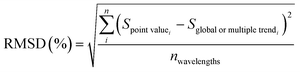 | (4) |
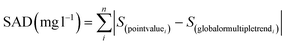 | (5) |
3. Results and discussion
This section presents the 27 different genetic algorithm correlation models used, to estimate COD, BOD5, TSS, TN and TP, 15 for raw and 12 for treated wastewater, respectively, based on:- Point values of the original spectral response (without approximation).
- Approximation of the spectral response to a global trend line.
- Approximation of the spectral response to multiple individual trend lines for each color group of the visible spectrum.
In the case of treated wastewater, the model for TP was omitted, since the concentrations of this pollutant in the effluent did not have the minimum variability to be considered statistically significant to fit a model. This explains the difference in quantity between the influent raw wastewater and effluent treated wastewater models.
For each parameter and type of wastewater, additionally a total of 9 hybrid models, based on decision trees, were also included (5 for raw wastewater and 4 for treated wastewater) to determine which of the three types of models – point value, global or multiple individual trend lines – are most appropriate in each case. Comparisons between the different techniques and the one provided by the hybrid model are also included to demonstrate that the hybrid model provides the best possible estimate in most each case.
In order to clarify the exposition, Table 1 shows, as a summary, the variables used for each of the types of characterization models that will be presented in Tables 2 and 3 of this research work, related to raw and treated wastewater, respectively.
| Variables | Model | Variables | Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ha | Gb | Pc | Sd | Ha | Gb | Pc | Sd | ||
| a Hybrid characterization model. b Model based on global trend line. c Model based on individual trend lines of the different groups of colours of the visible spectrum. d Model based on point values of the original spectral response without approximation. | |||||||||
| Transmittance 380–700 nm | ✓ | M Global | ✓ | ||||||
| Absorbance 380–700 nm | ✓ | N Global | ✓ | ||||||
| RMSDGlobal | ✓ | M Violet | ✓ | ||||||
| SADGlobal | ✓ | N Violet | ✓ | ||||||
| RMSDViolet | ✓ | M Blue | ✓ | ||||||
| SADViolet | ✓ | N Blue | ✓ | ||||||
| RMSDBlue | ✓ | M Cyan | ✓ | ||||||
| SADBlue | ✓ | N Cyan | ✓ | ||||||
| RMSDCyan | ✓ | M Green | ✓ | ||||||
| SADCyan | ✓ | N Green | ✓ | ||||||
| RMSDGreen | ✓ | M Yellow | ✓ | ||||||
| SADGreen | ✓ | N Yellow | ✓ | ||||||
| RMSDYellow | ✓ | M Orange | ✓ | ||||||
| SADYellow | ✓ | N Orange | ✓ | ||||||
| RMSDOrange | ✓ | M Red | ✓ | ||||||
| SADOrange | ✓ | N Red | ✓ | ||||||
| RMSDRed | ✓ | ||||||||
| SADRed | ✓ | ||||||||
| Pearson's coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Eqn/tree | Parameter | Modela | Training (%) | Test (%) | PBias (%) | RMSE (mg l−1) | R 2 (%) | ME (mg l−1) | SD (mg l−1) | R 2 PV (%) |
| a G: model based on global trend line; P: model based on individual trend lines of the different groups of colours of the visible spectrum; H: hybrid estimation model. b R 2 PV is the Pearson's coefficient of the GA model from point value, which is collected in eqn (8) for COD, eqn (S3)† for BOD5, eqn (S6)† for TSS, eqn (S9)† for TN and eqn (S12)† for TP. | ||||||||||
| Eqn (6) | COD | G | 72.09 | 70.55 | 2.890 | 212.91 | 70.89 | 155.77 | 145.37 | 75.88 |
| Eqn (7) | COD | P | 74.96 | 70.18 | 1.329 | 205.63 | 72.65 | 151.74 | 138.99 | |
| Fig. 4 | COD | H | — | — | −1.578 | 187.59 | 77.40 | 128.74 | 136.65 | |
| Eqn (S1)† | BOD5 | G | 66.36 | 51.47 | 0.546 | 154.67 | 60.86 | 105.89 | 112.59 | 61.50 |
| Eqn (S2)† | BOD5 | P | 67.86 | 54.17 | 0.306 | 150.54 | 62.92 | 101.52 | 111.14 | |
| Fig. S3† | BOD5 | H | — | — | 0.069 | 143.36 | 66.27 | 95.74 | 106.86 | |
| Eqn (S4)† | TSS | G | 61.90 | 70.37 | −1.434 | 88.39 | 64.81 | 68.45 | 56.01 | 72.00 |
| Eqn (S5)† | TSS | P | 67.42 | 71.95 | −1.622 | 83.17 | 68.84 | 64.4 | 52.72 | |
| Fig. S5† | TSS | H | — | — | 0.569 | 75.73 | 74.17 | 56.04 | 51.02 | |
| Eqn (S7)† | TN | G | 60.48 | 52.08 | 0.681 | 18.01 | 57.48 | 13.55 | 11.88 | 62.26 |
| Eqn (S8)† | TN | P | 68.12 | 53.86 | −0.158 | 16.89 | 62.62 | 12.77 | 11.06 | |
| Fig. S7† | TN | H | — | — | −0.234 | 16.48 | 64.40 | 12.17 | 11.13 | |
| Eqn (S10)† | TP | G | 54.77 | 61.07 | −0.975 | 2.66 | 56.66 | 2.01 | 1.74 | 58.88 |
| Eqn (S11)† | TP | P | 59.05 | 57.46 | −0.813 | 2.61 | 58.40 | 1.89 | 1.8 | |
| Fig. S9† | TP | H | — | — | 0.801 | 2.49 | 62.16 | 1.75 | 1.77 | |
| Pearson's coefficient | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Eqn/tree | Parameter | Modela | Training (%) | Test (%) | PBias (%) | RMSE (mg l−1) | R 2 (%) | ME (mg l−1) | SD (mg l−1) | R 2 PV (%) |
| a G: model based on global trend line; P: model based on individual trend lines of the different groups of colours of the visible spectrum; H: hybrid estimation model. b R 2 PV is the Pearson's coefficient of the GA model from point value, that is collected in eqn (11) for COD, eqn (S15)† for BOD5, eqn (S18)† for TSS and eqn (S21)† for TN. | ||||||||||
| Eqn (9) | COD | G | 52.26 | 16.09 | −0.472 | 12.74 | 29.39 | 9.82 | 8.12 | 48.78 |
| Eqn (10) | COD | P | 61.17 | 32.62 | 1.141 | 10.75 | 49.70 | 8.15 | 7.01 | |
| Fig. 7 | COD | H | — | — | 0.271 | 10.30 | 53.84 | 7.71 | 6.84 | |
| Eqn (S13)† | BOD5 | G | 23.84 | 20.77 | −1.234 | 1.90 | 22.78 | 1.36 | 1.33 | 35.98 |
| Eqn (S14)† | BOD5 | P | 23.13 | 41.74 | −0.553 | 1.78 | 32.27 | 1.22 | 1.3 | |
| Fig. S11† | BOD5 | H | — | — | 1.418 | 1.56 | 47.91 | 1.06 | 1.15 | |
| Eqn (S16)† | TSS | G | 28.85 | 29.45 | −3.651 | 3.66 | 28.74 | 2.88 | 2.27 | 30.07 |
| Eqn (S17)† | TSS | P | 36.04 | 27.82 | −2.357 | 3.59 | 31.42 | 2.83 | 2.22 | |
| Fig. S13† | TSS | H | — | — | 2.446 | 3.16 | 46.82 | 2.4 | 2.06 | |
| Eqn (S19)† | TN | G | 32.86 | 13.46 | 2.178 | 8.56 | 24.26 | 6.5 | 5.59 | 38.82 |
| Eqn (S20)† | TN | P | 56.98 | 31.04 | −1.701 | 7.04 | 48.88 | 5.42 | 4.5 | |
| Fig. (S15)† | TN | H | — | — | 3.541 | 5.86 | 64.55 | 4.06 | 4.23 | |
For clarity, this manuscript will only show the models related to COD, presenting the rest of the pollutant parameters (BOD5, TSS, TN and TP) in summary form in Table 2, while in the Supplementary Information all these models are presented in detail as well as their main indicators and a performance comparison with respect to the reference values measured in the laboratory and those estimated by the models.
3.1. Specific estimation model for raw wastewater samples
Table 2 shows a summary of the GA models calculated for each of the pollutants studied, indicating their Pearson's Coefficient for training and test, as well as their RMSE, PBias, R2, and the R2PV that is the Pearson's coefficient in case of considering the GA model from the point values of the original spectral response, i.e. without applying any approximation to it, as well as the mean error (ME) and standard deviation of the error (SD).As can be observe in Table 2, the use of characterization models that make use of the approximation of the spectral response to global (G) or individual trend lines for each colour group (P), provide slightly lower levels of adjustments than those obtained by models based on point values of the visible spectrum. This can be observed, for example, in the case of COD, the global model and the model based on individual lines present an R2 of 70.89% and 72.65% respectively, settings very close to those obtained by the model based on point values of the spectrum (75.88%). This is particularly relevant since, although the fit obtained is lower, these models require much fewer input variables, since they only use the values of slope (M) and ordinate at the origin (N) instead of the point values of transmittance and absorbance at the different wavelengths, which means that a smaller number of wavelengths are required for their determination.
The use of a hybrid estimation model provides the best results, up to almost 5% with respect to the best model in each case, especially in the case of BOD5, where it is observed that the hybrid model (Fig. S11†) provides an R2 of 66.27%, with respect to 61.5% of the model based on point values of the spectrum, eqn (S1).†
The different GA models mentioned above, as well as the hybrid model based on decision trees, are shown below for COD, while the rest of parameters are shown in the ESI.†
In order to clarify the exposition, the value of the slope and the ordinate at the origin of the overall trend line of the spectral response of the sample has been designated as MGlobal and NGlobal, and the values of slope and ordinate at the origin for a particular colour group as MColor, NColor, respectively.
 | (6) |
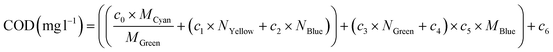 | (7) |
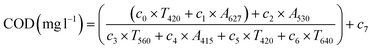 | (8) |
The high estimation of all models can be seen in the scatter plots in Fig. 5, where the scatter plot in Fig. 5C (hybrid characterization model) shows a lower dispersion of the data, which denotes an improvement in the ability to characterize the sample with respect to the exclusive use of other techniques.
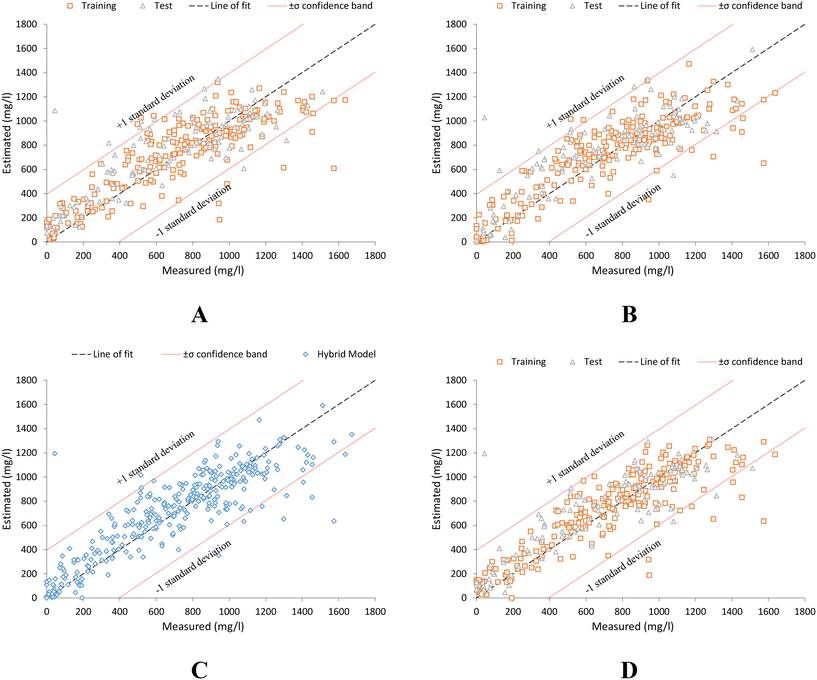 | ||
| Fig. 5 Scatter plot between laboratory measured COD values (measured) and those estimated by: (A) global model, eqn (6). (B) Individual trend model, eqn (7). (C) Hybrid estimation model. (D) Model based on spectral point values by offspring selection technique, eqn (8). | ||
Fig. 6 shows a comparison between 20 random raw water samples taken at random, between the reference values measured in the laboratory (blue), and the COD values estimated from the global (eqn (6), orange) and multiple (eqn (7), grey) trend line models, as well as with the model based on spectral point, eqn (8), and hybrid model (green chart, Fig. 4).
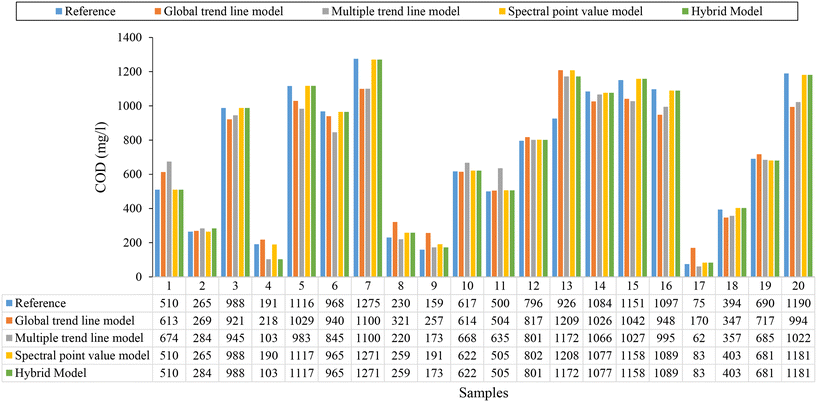 | ||
| Fig. 6 Comparison for 20 samples of raw wastewater taken at random, between reference COD values measured in the laboratory and eqn (6), (7), spectral point value model, eqn (8) and hybrid estimation model (Fig. 4). | ||
In some samples, it is observed that the model based on multiple trend lines (eqn (7), grey) provides better estimates than those provided by the model based on point values of the spectrum (yellow), as, for example, is the case of sample number 8, where for a reference value of 230 mg l−1, the model based on multiple trend lines estimates a value of 220 mg l−1, while the one based on point values of the spectrum (yellow) provides an estimate of 259 mg l−1.
The hybrid estimation model (Fig. 4), provides in most cases the best estimate, since thanks to the methodology presented in this research work, it is possible to determine which is the best model to apply in each specific case, as shown in Fig. 6 (green graph). This is identical to what happens in the rest of the hybrid models (Fig. S4, S6, S8 and S10†), as can be seen in their respective scatter plots (Fig. S5, S7, S9 and S11†) for each parameter supported in the present research work.
3.2. Specific estimation model for treated wastewater samples
Table 3 shows a summary of the different correlation models calculated for treated wastewater samples for each of the pollutant parameters considered.As can be seen in Table 3, in most parameters, models based on trend lines of the different groups of colours of the visible spectrum, do provide a much higher fit than those based on global line, and even that the models based on point values of the spectrum.
Considering the RMSE of the models presented in Table 3, it can be seen that they have a high accuracy, with a particularly low RMSE in the BOD5 and TSS models, with a value between 1.56 and 3.66 mg l−1.
As shown in Table 3, the hybrid model of characterization presents a substantial improvement in the treated water samples, achieving an improvement between 2.61% and 26.32% better fit with respect to the model based only on point values of the spectrum. This improvement is more noticeable in the case of the TN, where an R2 of 64.55% has been achieved, compared to 48.55% of the model based on multiple lines (eqn (S26)†) and 38.82% of the model based on point values of the spectrum (section S4.2†). In term of RMSE, hybrid model obtains an RMSE of 5.86 mg l−1, compared to 8.56 mg l−1 and 7.04 mg l−1 for the models based on global trend line and multiple trend lines, respectively.
The different models calculated for COD in treated wastewater are shown below, the rest of the parameters being in section S2 of ESI.†
| COD (mg l−1) = c0 × MGlobal × (c1 − c2 × NGlobal) × (c3 × MGlobal × c4 − (c5 − c6 × NGlobal)) + c7 | (9) |
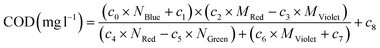 | (10) |
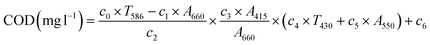 | (11) |
Fig. 8 shows the scatter plot, where the high fit of all models can be observed.
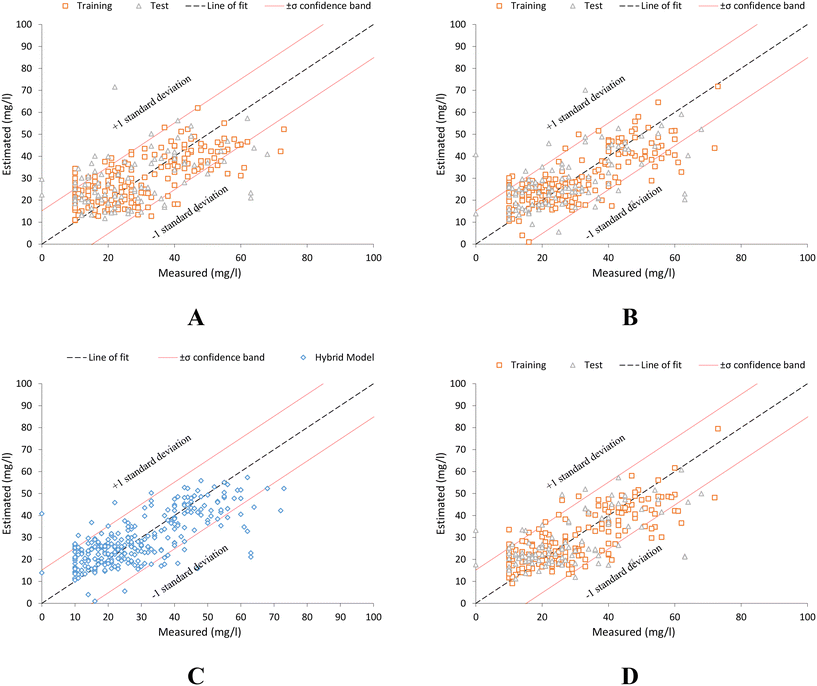 | ||
| Fig. 8 Scatter plot between laboratory measured COD in treated wastewater samples values (measured) and those estimated by: (A) global model, eqn (9). (B) Individual trend model, eqn (10). (C) Hybrid estimation model. (D) Model based on spectral point values by offspring selection technique, eqn (11). | ||
Fig. 9 shows a comparison for 20 real treated wastewater samples taken at random from the 650 samples taken at the 43 WWTPs studied in this research work.
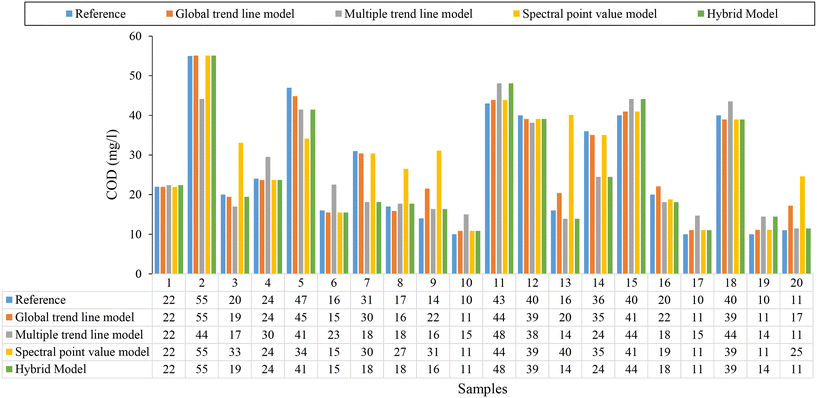 | ||
| Fig. 9 Comparison for 20 samples of treated wastewater taken at random, between reference COD values measured in the laboratory and eqn (9) and (10), spectral point value model, eqn (11) and hybrid model (Fig. 7). | ||
Although the estimation levels provided by the three are similar, the hybrid model (Fig. 7), provides the best estimates in all cases (green chart). This is identical to what occurs in the rest of the hybrid models (Fig. S11, S13 and S15†), as can be seen in their respective scatter diagrams (Fig. S12, S14 and S15†) for each supported parameter in the current research work. This high performance can be also seen in the scatter diagrams for the rest of parameters supported (Fig. S12, S14 and S16†).
Table S2 in ESI† shows an example application of the hybrid characterization model based on the decision tree shown in Fig. 7 for 20 treated wastewater samples taken at random, where it is shown that the hybrid model determines, in most cases, the most appropriate estimation model from RMSD and SAD, achieving the best possible estimation in each case.
In order to analyze the effect of external agents such as temperature changes or vibrations on the spectral response, an analysis of the performance of the different models presented in this research work in terms of RMSE has been carried out in Table S3 of the ESI.†
For this purpose, random noise has been introduced at different intensity levels: 2, 5, 10, 15 and 20%, being the latter disturbance levels higher than those that could be observed in real operating conditions. This disturbance levels were introduced by multiplying the transmittance values associated to each wastewater sample by a random, that achieves the maximum of the respective perturbation level – from 2% to 20% – and is also multiplied by the standard deviation of each of the transmittance measurements. The results obtained indicate that the use of the hybrid model allows to reach lower RMSE than using any of the models presented in this research work, up to a maximum perturbation of 10%, after which the best characterization is achieved with the models based on global trend lines.
This shows the good performance of the hybrid characterization models in the face of spectral response alterations under real operating conditions.
3.3. Wastewater type classification
In order to carry out the characterization of a water sample automatically, a preliminary step is to determine whether the sample is raw or treated wastewater, in order to decide which set of hybrid models to apply. For this reason, Fig. 10 presents a model based on decision trees, which, based on the ordinate at the origin (N) and the slope (M) of the global trend line of the spectral response, is able to determine, with an R2 of 95.46% for training and 96.8% for test, what type of wastewater it is.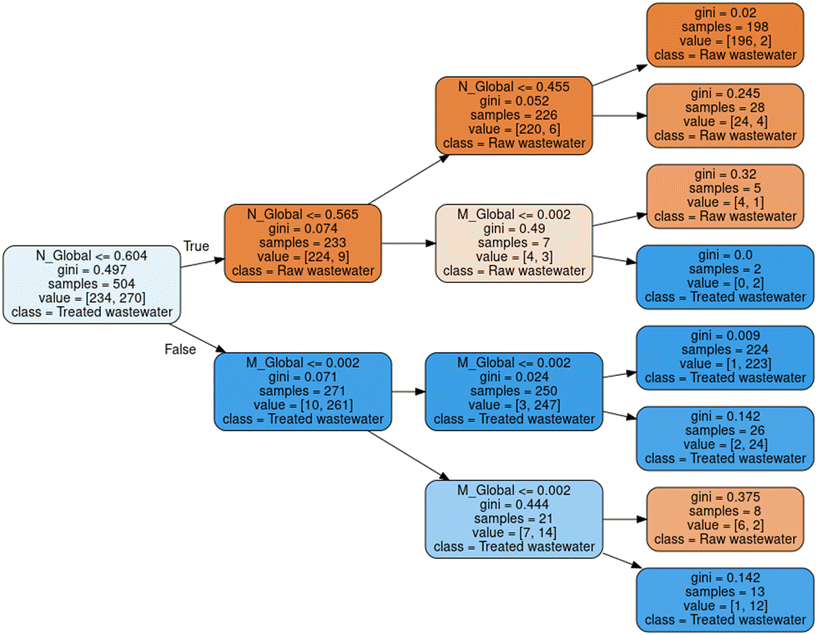 | ||
| Fig. 10 Water type classification model from the values of ordinate at the origin (N) and slope (M) of the trend lines approximated to lines. | ||
This is especially relevant in automatic characterization systems, so that they can operate indistinctly with samples of raw or treated wastewater indifferently, determining, at each moment, the best estimation model to apply.
4. Conclusions
The spectral response provides very relevant information about the properties of a sample, which can be used, with the help of correlation models, to estimate the contaminant load. However, sometimes, the spectral response of a sample, under real-time operating conditions, can be affected by external elements such as vibrations or temperature changes, which may cause irregularities in the spectral response, making it difficult for correlation models to estimate the pollutant load to provide accurate values.The present research work presents a methodology to improve the ability to estimate the pollutant load of wastewater from the spectrophotometric response, even under these conditions, achieving the best possible characterization.
This consists of a hybrid characterization model based on decision trees, which, based on the analysis of the spectral response, determines which of the following characterization models based on genetic algorithm are most appropriate to apply in each specific case:
- Model based on point values of the original spectral response (no approximation)
- Model based on the approximation of the spectral response to a single global trend line.
- Model based on the approximation of the spectral response to multiple individual trend lines for each color group of the visible spectrum.
Once significant differences are observed between the predictions of the GA models based on point value, global trend line or multiple individual trend line, a decision tree is trained using as tools the differences found between the measured spectrophotometric surrogates, i.e. absorbance and transmittance, and those obtained from the fits to the global and multiple lines (as shown in Fig. 5). The analysis of the spectral response is based on the root mean square difference (RMSD) and the sum of absolute differences (SAD) between the original spectral response and the one approximated to the global and individual trend lines for each color group of the visible spectrum (violet (380–427 nm), blue (427–476 nm), cyan (476–497 nm), green (497–570 nm), yellow (570–581 nm), orange (581–618 nm) and red (618–780 nm)), to determine, in each specific case, and for each type of pollutant and wastewater, which of the above-mentioned models to apply in each case to provide estimates closer to the reference values, achieving in almost all cases to provide the best possible estimate.
In this work, a total of 27 genetic algorithm models and 9 hybrid models based on decision trees have been calculated to estimate, in raw and treated wastewater samples, respectively, the following parameters: chemical oxygen demand (COD), biochemical oxygen demand at 5 days (BDO5), total suspended solids (TSS), total nitrogen (TN) and total phosphorus (TP), measured over around 650 wastewater samples from 43 WWTPs, taken, from both influent (raw wastewater) and effluent (treated wastewater). The models have been organized into two main categories: specific models for raw wastewater and specific models for treated wastewater.
Tests carried out in present work show that characterization models based on spectral response approximation (i.e., those based on a single overall trend line or on multiple individual trend lines for each color group) provide slightly lower levels of adjustments compared to models based on point values of the visible spectrum. However, these models require fewer input variables, since they only use slope and ordinate at the origin.
The improvement of the hybrid characterization model has allowed, in raw wastewater samples, an improvement in the adjustment levels of up to 5% with respect to using only models based on point values of the spectrum. In the case of treated wastewater samples, the improvement provided by the hybrid characterization model is up to 26.32% with respect to only using the model based on spectral point values, being this improvement much more remarkable in the case of TN, which goes from an R2 of 38.82% to 64.55% with the hybrid models. In terms of RMSE, the hybrid characterization model allows reaching values of 5.86 mg l−1, compared to 8.56 mg l−1 and 7.04 mg l−1 for the models based on global trend line and multiple trend lines, respectively.
This greater precision of the models can be seen if a comparison is made with other research studies. This can be seen in the characterization of COD in raw water samples, where the model in Fig. 4, presents an RMSE of 187.59 mg l−1, compared to 128.40 mg l−1 of ref. 49, or in the case of treated water, works such as ref. 50 and 51, or ref. 52, present RMSE levels of 40, 19 and 11 mg l−1 respectively (where they use spectrophotometric analysis in the range of 400–1700 nm and 200–500 nm), higher than the 10.30 mg l−1 reached with the model in Fig. 7 which only operates in the visible region of the spectrum (380–700 nm).
The improvement achieved with the use of hybrid models is most clearly observed in the case of treated water. In BOD5, the model in Fig. 7, trained from samples of 43 WWTPs, presents an RMSE of 1.56 mg l−1, much lower than that observed for example in the work of Inagaki et al.,55 2010 from NIR spectroscopy, with a high RMSE of 29.40 mg l−1.
In the case of TSS, the highest performance of the hybrid model is observed both in raw water samples (Fig. S5†), where an RMSE of 75.73 mg l−1 is obtained, lower than other works such as ref. 53 (83.26 mg l−1), and in treated water, where an RMSE of 3.16 mg l−1 is reached, compared to other works such as Carré et al.,18 2013 (3.5 mg l−1 from 179 wastewater samples).
For TN, the superiority of the hybrid models presented in this research work is highlighted, in raw water (Fig. S7†), the RMSE is 16.48 mg l−1, compared to 53 mg l−1 of ref. 54, while in the case of treated water (Fig. 15), the level of fit achieved is similar to that of other work such as ref. 55 with an RMSE of 5.10 mg l−1.
The higher accuracy of the hybrid models, it is worth noting that all of them have been trained with a much larger number of 43 WWTP samples, which further reinforces the robustness of the results achieved. In addition, the models presented in this research work use only wavelengths belonging to the visible region of the spectrum (380–700 nm), contrary to the other research works that make use of a wider emission range that includes the ultraviolet and near-infrared spectrum, which denotes a greater robustness of the models presented.
On the other hand, most of the works presented make use of a reduced number of samples, generally taken from the same sampling point, which limits their usability.
The use of artificial intelligence techniques such as genetic algorithms or decision trees, allow to achieve models, not only more accurate and faster to run by any system with low computing power (a key aspect in the development of low cost systems), but also more easily understandable by the user.
This methodology demonstrates the suitability of variable wavelength spectrophotometry as a technique to accurately characterize the pollutant load of wastewater, making possible to carry out a characterization under real operating conditions, achieving the best possible fit despite the fact that external agents (temperature changes, bubble formation, vibrations, etc.) may introduce certain alterations in the spectrophotometric response of the samples.
A more exhaustive comparison is shown in Table 4 of Appendix A.
Conflicts of interest
There are no conflicts to declare.Appendix A
| Source | Parameter | Type of wastewater | Number of samples | Number WWTPs/points | Device/lab technique | Wavelengths | Modeling technique | PBias (%) | RMSE (mg l−1) | R 2 (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| SPA: successive projections algorithm. GA: genetic algorithms. PLS: partial-least-square. BP-NN: back-propagation neural network. PCR: principal components regression. | ||||||||||
| Current research (Fig. 4) | COD | Raw | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | −1.578 | 187.59 | 77.40 |
| Ref. 49 | 84 | Commercial spectroscopy | 400–1000 nm | 128.40 | ||||||
| Current research (Fig. S3†) | BOD5 | Raw | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 0.069 | 143.36 | 66.27 |
| Ref. 49 | 84 | Commercial spectroscopy | 400–1000 nm | 77.81 | ||||||
| Current research (Fig. S5†) | TSS | Raw | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 0.569 | 75.73 | 74.17 |
| Ref. 49 | 84 | Commercial spectroscopy | 400–1000 nm | 83.26 | ||||||
| Current research (Fig. S7†) | TN | Raw | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | −0.234 | 16.48 | 64.40 |
| Ref. 53 | Commercial spectroscopy | 300–570 nm | PCR | 22 | 53 | |||||
| PLS | ||||||||||
| Current research (Fig. 7) | COD | Treated | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 0.271 | 10.30 | 53.84 |
| Ref. 50 | 40 | 1 | Hyperspectral camera | 400–1700 nm | SPA | — | 40.4489 | 97 | ||
| GA | ||||||||||
| Ref. 51 | 87 | 3 | Near-infrared reflectance commercial spectrometry | PLS | 19 | 97 | ||||
| Ref. 52 | 150 | — | Commercial spectroscopy | 200–500 nm | PLS | — | 10.384 | 0.945 | ||
| Ref. 52 | 150 | — | 200–500 nm | SVM | — | 11.472 | 0.931 | |||
| Ref. 52 | 150 | — | 200–500 nm | BP-NN | — | 10.650 | 0.979 | |||
| Current research (Fig. 11) | BOD5 | Treated | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 1.418 | 1.56 | 47.91 |
| Ref. 55 | BOD | 55 | 1 | NIR spectroscopy | 80 | 29.40 | ||||
| Current research (Fig. 13) | TSS | Treated | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 2.446 | 3.16 | 46.82 |
| Ref. 56 | 179 | 1 | 240–400 | Linear-PLS | — | 3.5 | ||||
| Current research (Fig. 15) | TN | Treated | 325 | 43 | LED spectrophotometer developed by the authors | 380–700 nm | Decisions tree and genetic algorithms | 3.541 | 5.86 | 64.55 |
| Ref. 55 | 55 | 1 | NIR spectroscopy | 78 | 5.10 | |||||
Acknowledgements
The author Daniel Carreres Prieto wishes to thank the financial support received from the Seneca Foundation of the Región de Murcia (Spain) through the program devoted to training novel researchers in areas of specific interest for the industry and with a high capacity to transfer the results of the research generated, entitled: “Subprograma Regional de Contratos de Formación de Personal Investigador en Universidades y OPIs” (Mod. B, Ref. 20320/FPI/17). The present research has been funded by the project MONITOCOES: New intelligent monitoring system for microorganisms and emerging contaminants in sewage networks. Reference: RTC2019-007115-5 by the Ministry of Science and Innovation – State Research Agency, within the RETOS COLABORACIÓN 2019 call, which supports cooperative projects between companies and research organizations, whose objective is to promote technological development, innovation and quality research. The developed equipment has also received funding for its industrialization through the “Proof of Concept” program of the Seneca Foundation, under the project “Equipo de MONITORización en Tiempo REAl de Contaminantes en Aguas Residuales (MONITOREA)” (21662/PDC/21). The authors wish to thank the help and availability received from the administration and technical personnel from ESAMUR during the field campaign. The present research work has also been developed under the project “Evaluation of the solids retention capacity in scuppers for runoff capture” (RETAIN-INLETS) with reference TED2021-132098B-C21, granted by the Ministry of Science and Innovation within the call for projects of Ecological Transition and Digital Transition 2021.References
- J. Altmann, L. Massa, A. Sperlich, R. Gnirss and M. Jekel, UV254 absorbance as real-time monitoring and control parameter for micropollutant removal in advanced wastewater treatment with powdered activated carbon, Water Res., 2016, 94, 240–245, DOI:10.1016/j.watres.2016.03.001.
- D. P. Mesquita, C. Quintelas, A. L. Amaral and E. C. Ferreira, Monitoring biological wastewater treatment processes: recent advances in spectroscopy applications, Rev. Environ. Sci. Biotechnol., 2017, 16(3), 395–424, DOI:10.1007/s11157-017-9439-9.
- G. V. Korshin, M. Sgroi and H. Ratnaweera, Spectroscopic surrogates for real time monitoring of water quality in wastewater treatment and water reuse, Curr. Opin. Environ. Sci. Health, 2018, 2, 12–19, DOI:10.1016/j.coesh.2017.11.003.
- R. S. Brito, H. M. Pinheiro, F. Ferreira, J. S. Matos and N. D. Lourenço, In situ UV-Vis spectroscopy to estimate COD and TSS in wastewater drainage systems, Urban Water J., 2014, 11(4), 261–273 CrossRef CAS.
- J.-J. Feng, L. Jia, Q.-Z. Liu, X.-L. Chen and J. P. Cheng, Source identification of heavy metals in sewage sludge and the effect of influent characteristics: a case study from China, Urban Water J., 2018, 15(4), 381–387, DOI:10.1080/1573062x.2018.1483525.
- J. Wasswa, N. Mladenov and W. Pearce, Assessing the potential of fluorescence spectroscopy to monitor contaminants in source waters and water reuse systems, Environ. Sci.: Water Res. Technol., 2019, 5(2), 370–382 RSC.
- O. Korostynska, A. Mason and A. I. Al-Shamma'a, Monitoring pollutants in wastewater: Traditional lab based versus modern real-time approaches, in Smart Sensors, Measurement and Instrumentation, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 1–24 Search PubMed.
- M. Lepot, A. Torres, T. Hofer, N. Caradot, G. Gruber and J.-B. Aubin, et al., Calibration of UV/Vis spectrophotometers: A review and comparison of different methods to estimate TSS and total and dissolved COD concentrations in sewers, WWTPs and rivers, Water Res., 2016, 101, 519–534, DOI:10.1016/j.watres.2016.05.070.
- Z.-M. Song, Y.-L. Xu, J.-K. Liang, L. Peng, X.-Y. Zhang and Y. Du, et al., Surrogates for on-line monitoring of the attenuation of trace organic contaminants during advanced oxidation processes for water reuse, Water Res., 2021, 190(116733), 116733, DOI:10.1016/j.watres.2020.116733.
- X. Qin, F. Gao and G. Chen, Wastewater quality monitoring system using sensor fusion and machine learning techniques, Water Res., 2012, 46(4), 1133–1144 CrossRef CAS PubMed.
- G. Langergraber, N. Fleischmann and F. Hofstädter, A multivariate calibration procedure for UV/VIS spectrometric quantification of organic matter and nitrate in wastewater, Water Sci. Technol., 2003, 47(2), 63–71, DOI:10.2166/wst.2003.0086.
- T. Li, L. Dai, Y. Huang, S. Pan, Z. Pang and J. Zou, Spectrophotometric determination of Cr(VI) in water using N, N-diethyl-p-phenylenediamine (DPD) as the indicator, J. Environ. Chem. Eng., 2021, 9(5), 1–10, DOI:10.1016/j.jece.2021.105517.
- Z. Xue, Z. Lv and L. Li, Combination of chromatographic and spectroscopic characterization based on primitive ultraviolet absorbance detection to fulfill advanced monitoring of dissolved organic matter in municipal wastewater treatment plant. Journal of Environmental, Chem. Eng., 2022, 10(3), 1–10, DOI:10.1016/j.jece.2022.107538.
- K. Komatsu, T. Onodera, A. Kohzu, K. Syutsubo and A. Imai, Characterization of dissolved organic matter in wastewater during aerobic, anaerobic, and anoxic treatment processes by molecular size and fluorescence analyses, Water Res., 2020, 171(115459), 115459, DOI:10.1016/j.watres.2019.115459.
- B.-C. Jiang, Y.-C. Tian, W.-X. Ji, M.-H. Cai, Y.-Z. Han and Y.-T. Zuo, et al., Identifying and monitoring the landfill leachate contamination in groundwater with SEC-DAD-FLD-OCD and a portable fluorescence spectrometer, ACS ES&T Water, 2022, 2(1), 165–173, DOI:10.1021/acsestwater.1c00305.
- B. Chen, H. Wu and S. F. Y. Li, Development of variable pathlength UV–vis spectroscopy combined with partial-least-squares regression for wastewater chemical oxygen demand (COD) monitoring, Talanta, 2014, 120, 325–330, DOI:10.1016/j.talanta.2013.12.026.
- UV-visible spectrophotometry of water and wastewater, ed. O. Thomas and C. Burgess, Elsevier Science, London, England, 2nd edn, 2017 Search PubMed.
- E. Carré, J. Pérot, V. Jauzein, L. Lin and M. Lopez-Ferber, Estimation of water quality by UV/Vis spectrometry in the framework of treated wastewater reuse, Water Sci. Technol., 2017, 76(3–4), 633–641, DOI:10.2166/wst.2017.096.
- M. A. Ferree and R. D. Shannon, Evaluation of a second derivative UV/visible spectroscopy technique for nitrate and total nitrogen analysis of wastewater samples, Water Res., 2001, 35(1), 327–332, DOI:10.1016/s0043-1354(00)00222-0.
- N. Suzuki and R. Kuroda, Direct simultaneous determination of nitrate and nitrite by ultraviolet second-derivative spectrophotometry, Analyst, 1987, 112(7), 1077, 10.1039/an9871201077.
- A. Niazi and R. Leardi, Genetic algorithms in chemometrics: Genetic algorithms in chemometrics, J. Chemom., 2012, 26(6), 345–351, DOI:10.1002/cem.2426.
- D. Carreres-Prieto, J. T. García, F. Cerdán-Cartagena, J. Suardiaz-Muro and C. Lardín, Implementing Early Warning Systems in WWTP. An investigation with cost-effective LED-VIS spectroscopy-based genetic algorithms, Chemosphere, 2022, 293(133610), 133610, DOI:10.1016/j.chemosphere.2022.133610.
- G. Sigmund, M. Gharasoo, T. Hüffer and T. Hofmann, Deep learning neural network approach for predicting the sorption of ionizable and polar organic pollutants to a wide range of carbonaceous materials, Environ. Sci. Technol., 2020, 54(7), 4583–4591, DOI:10.1021/acs.est.9b06287.
- N.-B. Chang, W. C. Chen and W. K. Shieh, Optimal control of wastewater treatment plants via integrated neural network and genetic algorithms, Civ. Eng. Environ. Syst., 2001, 18(1), 1–17, DOI:10.1080/02630250108970290.
- M. Otto, Chemometrics: Statistics and Computer Application in Analytical Chemistry, Wiley-VCH Verlag, Weinheim, Germany, 3rd edn, 2016 Search PubMed.
- S. Güller, G. Silahtaroğlu and O. Akpolat, Analysis waste water characteristics via data mining: A Muğla province case and external validation, Commun. Stat. Case Stud. Data Anal. Appl., 2019, 5(3), 200–213, DOI:10.1080/23737484.2019.1604192.
- N. Deepnarain, M. Nasr, S. Kumari, T. A. Stenström, P. Reddy and K. Pillay, et al., Decision tree for identification and prediction of filamentous bulking at full-scale activated sludge wastewater treatment plant, Process Saf. Environ. Prot., 2019, 126, 25–34, DOI:10.1016/j.psep.2019.02.023.
- H. Byliński, A. Sobecki and J. Gębicki, The use of artificial neural networks and decision trees to predict the degree of odor nuisance of post-digestion sludge in the sewage treatment plant process, Sustainability, 2019, 11(16), 4407, DOI:10.3390/su11164407.
- M. Dalmau, I. Rodriguez-Roda, E. Ayesa, J. Odriozola, L. Sancho and J. Comas, Development of a decision tree for the integrated operation of nutrient removal MBRs based on simulation studies and expert knowledge, Chem. Eng. J., 2013, 217, 174–184, DOI:10.1016/j.cej.2012.11.060.
- D. Carreres-Prieto, J. T. García, L. G. Castillo, J. M. Carrillo and A. Vigueras-Rodriguez, Regresión lineal multivariable versus regresión simbólica a partir de programación genética. Aplicación a la caracterización espectroscópica de aguas residuales urbanas, Ingenieria del Agua, 2022, 26(4), 261–277, DOI:10.4995/ia.2022.18073.
- D. Carreres-Prieto, J. Ybarra-Moreno, J. T. García and F. Cerdán-Cartagena, Evaluation of genetic models for COD and TSS estimation in wastewater through its spectrophotometric response, Water Sci. Technol., 2022, 85(9), 2565–2580, DOI:10.2166/wst.2022.138.
- D. Carreres-Prieto, J. Ybarra-Moreno, J. T. García and J. F. Cerdán-Cartagena, A Comparative analysis of neural networks and genetic algorithms to characterize wastewater from led spectrophotometry, J. Environ. Chem. Eng., 2023, 11(3), 110219, DOI:10.1016/j.jece.2023.110219.
- D. Carreres-Prieto, J. T. García, J. M. Carrillo and A. Vigueras-Rodríguez, Towards highly economical and accurate wastewater sensors by reduced parts of the LED-visible spectrum, Sci. Total Environ., 2023, 871(162082), 162082, DOI:10.1016/j.scitotenv.2023.162082.
- B. Baumgartner, S. Freitag and B. Lendl, 3D printing for low-cost and versatile attenuated total reflection infrared spectroscopy, Anal. Chem., 2020, 92(7), 4736–4741, DOI:10.1021/acs.analchem.9b04043.
- E. J. Carrasco-Correa, E. F. Simó-Alfonso, J. M. Herrero-Martínez and M. Miró, The emerging role of 3D printing in the fabrication of detection systems, TrAC, Trends Anal. Chem., 2021, 136(116177), 116177, DOI:10.1016/j.trac.2020.116177.
- Y.-Z. Han, W.-X. Ji, B.-C. Jiang, Y.-C. Tian, S.-Q. Shen and D. Zhou, et al., Developing a miniaturized spectrophotometer using 235 and 275 nm UVC-LEDs for fast detection of nitrate in natural water and wastewater effluents, ACS ES&T Water, 2021, 1(12), 2548–2555, DOI:10.1021/acsestwater.1c00351.
- D. Carreres-Prieto, J. T. García, F. Cerdán-Cartagena and J. Suardiaz-Muro, Spectroscopy transmittance by LED calibration, Sensors, 2019, 19(13), 2951, DOI:10.3390/s19132951.
- M. Affenzeller and S. Wagner, Offspring selection: A new self-adaptive selection scheme for genetic algorithms, in Adaptive and Natural Computing Algorithms, Springer-Verlag, Vienna, 2005, pp. 218–221 Search PubMed.
- J. H. Cho, K. Seok Sung and H. S. Ryong, A river water quality management model for optimising regional wastewater treatment using a genetic algorithm, J. Environ. Manage., 2004, 73(3), 229–242, DOI:10.1016/j.jenvman.2004.07.004.
- M. Huang, Y. Ma, J. Wan and X. Chen, A sensor-software based on a genetic algorithm-based neural fuzzy system for modeling and simulating a wastewater treatment process, Appl. Soft Comput., 2015, 27, 1–10, DOI:10.1016/j.asoc.2014.10.034.
- B. Holenda, E. Domokos, Á. Rédey and J. Fazakas, Aeration optimization of a wastewater treatment plant using genetic algorithm, Optim. Control Appl. Methods, 2007, 28(3), 191–208, DOI:10.1002/oca.796.
- S. Ziweritin, B. B. Baridam and U. A. Okengwu, A Comparative analysis of neural network and decision tree model for detecting result anomalies, Open Access Library Journal, 2022, 9(3), 1–15 Search PubMed.
- M. W. Ahmad, M. Mourshed and Y. Rezgui, Trees vs Neurons: Comparison between random forest and ANN for high-resolution prediction of building energy consumption, Energy Build., 2017, 147, 77–89, DOI:10.1016/j.enbuild.2017.04.038.
- C. C. Tsai, M. C. Lu and C. C. Wei, Decision tree-based classifier combined with neural-based predictor for water-stage forecasts in a river basin during typhoons: a case study in taiwan, Environ. Eng. Sci., 2012, 29(2), 108–116 CrossRef CAS PubMed.
- F. Ranzato and M. Zanella, Genetic adversarial training of decision trees, in Proceedings of the Genetic and Evolutionary Computation Conference, 2021, pp. 358–367 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine learning in Python, J Mach Learn Res, 2011, 12, 2825–2830 Search PubMed.
- H. V. Gupta, S. Sorooshian and P. O. Yapo, Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration, J. Hydrol. Eng., 1999, 4(2), 135–143, DOI:10.1061/(asce)1084-0699(1999)4:2(135).
- D. N. Moriasi, J. G. Arnold, M. W. Van Liew, R. L. Bingner, R. D. Harmel and T. L. Veith, Model evaluation guidelines for systematic quantification of accuracy in watershed simulations, Trans. ASABE, 2007, 50(3), 885–900 Search PubMed.
- I. Melendez-Pastor, M. Almendro-Candel, J. Navarro-Pedreño, I. Gómez, M. Lillo and E. Hernández, Monitoring urban wastewaters' characteristics by visible and short wave near-infrared spectroscopy, Water, 2013, 5(4), 2026–2036, DOI:10.3390/w5042026.
- D. Huang, Y. Tian, S. Yu, X. Wen, S. Chen and X. Gao, et al., Inversion prediction of COD in wastewater based on hyperspectral technology, J. Cleaner Prod., 2023, 385(135681), 135681, DOI:10.1016/j.jclepro.2022.135681.
- A. C. Sousa, M. M. L. M. Lucio, O. F. Bezerra, G. P. S. Marcone, A. F. C. Pereira and E. O. Dantas, et al., A method for determination of COD in a domestic wastewater treatment plant by using near-infrared reflectance spectrometry of seston, Anal. Chim. Acta, 2007, 588(2), 231–236, DOI:10.1016/j.aca.2007.02.022.
- P. Li, J. Qu, Y. He, Z. Bo and M. Pei, Global calibration model of UV-Vis spectroscopy for COD estimation in the effluent of rural sewage treatment facilities, RSC Adv., 2020, 10(35), 20691–20700, 10.1039/c9ra10732k.
- I. Melendez-Pastor, M. Almendro-Candel, J. Navarro-Pedreño, I. Gómez, M. Lillo and E. Hernández, Monitoring urban wastewaters' characteristics by visible and short wave near-infrared spectroscopy, Water, 2013, 5(4), 2026–2036, DOI:10.3390/w5042026.
- P. O. N. S. Marie-Noëlle, W. U. Jing and O. Potier, Chemometric estimation of wastewater composition for the on-line control of treatment plants, IFAC Proceedings Volumes, 2005, 38, 49–54, DOI:10.3182/20050703-6-CZ-1902.02212.
- T. Inagaki, Y. Shinoda, M. Miyazawa, H. Takamura, S. Tsuchikawa and M. Affenzeller, et al., Offspring selection: A new self-adaptive selection scheme for genetic algorithms, in Adaptive and Natural Computing Algorithms, Springer, Vienna, 2005, pp. 218–221 Search PubMed.
- E. Carré, J. Pérot, V. Jauzein, L. Lin and M. Lopez-Ferber, Estimation of water quality by UV/Vis spectrometry in the framework of treated wastewater reuse, Water Sci. Technol., 2017, 76(3–4), 633–641, DOI:10.2166/wst.2017.096.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ew00410d |
| This journal is © The Royal Society of Chemistry 2023 |