Multiple and nonlocal cation redox in Ca–Ce–Ti–Mn oxide perovskites for solar thermochemical applications†
Robert B.
Wexler
 a,
Gopalakrishnan
Sai Gautam
a,
Gopalakrishnan
Sai Gautam
 ab,
Robert T.
Bell
c,
Sarah
Shulda
c,
Nicholas A.
Strange
ab,
Robert T.
Bell
c,
Sarah
Shulda
c,
Nicholas A.
Strange
 d,
Jamie A.
Trindell
e,
Joshua D.
Sugar
e,
Eli
Nygren
cf,
Sami
Sainio
d,
Anthony H.
McDaniel
e,
David
Ginley
c,
Emily A.
Carter
d,
Jamie A.
Trindell
e,
Joshua D.
Sugar
e,
Eli
Nygren
cf,
Sami
Sainio
d,
Anthony H.
McDaniel
e,
David
Ginley
c,
Emily A.
Carter
 *a and
Ellen B.
Stechel
*a and
Ellen B.
Stechel
 *g
*g
aDepartment of Mechanical and Aerospace Engineering and the Andlinger Center for Energy and the Environment, Princeton University, Princeton, NJ 08544-5263, USA. E-mail: eac@princeton.edu
bDepartment of Materials Engineering, Indian Institute of Science, Bengaluru, Karnataka 560012, India
cNational Renewable Energy Laboratory, Golden, CO 80401, USA
dSLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
eSandia National Laboratories, Livermore, CA 94550, USA
fUniversity of California Santa Cruz, Santa Cruz, CA 95064, USA
gASU LightWorks® and the School of Molecular Sciences, Arizona State University, Tempe, Arizona 85287-8204, USA. E-mail: ellen.stechel@asu.edu
First published on 3rd May 2023
Abstract
Modeling-driven design of redox-active off-stoichiometric oxides for solar thermochemical H2 production (STCH) seldom has resulted in empirical demonstration of competitive materials. We report the theoretical prediction and experimental evidence that the perovskite Ca2/3Ce1/3Ti1/3Mn2/3O3 is synthesizable with high phase purity, stable, and has desirable redox thermodynamics for STCH, with a predicted average neutral oxygen vacancy (VO) formation energy, Ev = 3.30 eV. Flow reactor experiments suggest potentially comparable or greater H2 production capacity than recent promising Sr–La–Mn–Al and Ba–Ce–Mn metal oxide perovskites. Utilizing quantum-based modeling of a solid solution on both A and B sub-lattices, we predict the impact of nearest-neighbor composition on Ev and determine that A-site Ce4+ reduction dominates the redox-activity of Ca2/3Ce1/3Ti1/3Mn2/3O3. X-ray absorption spectroscopy measurements provide evidence that supports these predictions and reversible Ce4+-to-Ce3+ reduction. Our models predict that Ce4+ reduces even when it is not nearest-neighbor to the VO, suggesting that refinement of Ce stoichiometry has the possibility of further enhancing performance.
Broader contextSunlight is an abundant albeit low areal density source of renewable energy. Collecting and concentrating the sun's rays for its heat value can enable high-temperature endothermic reactions such as water splitting to produce clean hydrogen. Two-step thermochemical cycles with redox-active metal oxides are promising. However, technoeconomic analyses with state-of-the-art CeO2 suggest that without a new active material, achieving the US Department of Energy's Hydrogen Shot $1 per kg H2 target is unlikely. Here, we introduce a previously unknown material predicted from theoretical considerations and experimentally validated. The material is a redox-active quinary oxide perovskite, CCTM, with solid solutions of Ca/Ce and Ti/Mn on the A- and B-sites, respectively. CCTM offers promising oxygen vacancy thermodynamics and exceptional H2 yield, when reduced at moderate temperatures and cycled at relatively short reoxidation periods. Modeling reveals and experiment confirms that Ce4+ is the primary redox-active species, in contrast to other known reducible perovskites, where in all cases the active element sits on the B-site. Furthermore, even with B-site Ce4+, that element is not redox active. Hence this work reports the first perovskite with reducible A-site and reducible Ce4+, predicted entirely from theory, and subsequently validated with experiments that establish stability, reversibility, and high productivity. |
Introduction
Combating climate change calls for decarbonized production of H2 that can provide cost-effective, medium-to long-duration energy storage while also serving as a fuel1 for transportation or industrial products and processes, or a feedstock.2 However, the vast majority (95%) of commercial H2 is produced today via steam-methane reforming (SMR), which consumes fossil fuels and contributes to direct CO2 emissions (≈7 kg CO2 per kg H2 for the overall process of SMR3). Water splitting (WS) via renewable energy offers a simpler, more direct path to clean hydrogen with exceptionally low carbon intensity, albeit currently at greater expense. Given the magnitude of solar irradiance on the Earth's surface, solar thermochemical hydrogen (STCH) is potentially a cost-effective, sustainable, and carbon-neutral pathway to H2.4 However, functional STCH materials must meet an extraordinary set of requirements to be useful for large-scale hydrogen production. A STCH process that utilizes non-volatile metal oxides typically involves two steps,5 where the first is the thermal reduction (red) of a redox-active metal oxide (MOx) at high temperatures generated by concentrated solar power6 or other solar sources of high-temperature heat and low partial pressures of oxygen (i.e., at Tred and pO2 where ΔGred ≤ 0). The second step is the re-oxidation (ox) of the reduced metal oxide by steam at lower temperatures (where Tox is typically several hundred degrees K less than Tred for spontaneous WS), thereby generating hydrogen.5–7Research over the last decade has struggled to replace pure CeO2 as the state-of-the-art redox-active MOx for two-step STCH.8–10 Thermal reduction of CeO2-based redox-active materials leads to the formation of oxygen vacancies (VO) and therefore off-stoichiometric compositions, (CeO2−δ), which are re-occupied by O upon re-oxidation by steam.11 However, demonstrated solar-to-fuel conversion efficiencies (η) have plateaued between 5–8%12–14 for laboratory-scale STCH reactors running on ceria at power levels <5 kWthermal. To surpass the performance of these CeO2-based STCH reactors, researchers are exploring other redox-active metal oxides, with the ABO3 perovskites being a popular choice due to their compositional and structural flexibility.15 Specifically, research over the last decade has identified Sr–La–Mn–Al16 and Ba–Ce–Mn17 oxide perovskites, among others, as potential next-generation redox-active MOxs. However, metal-oxide perovskites have yet to supplant CeO2-based materials as the preferred redox-active MOx for STCH production.18
To create a stable and cyclable redox-active metal-oxide system at temperatures below the 1773 K needed for CeO2 is a challenge. The metal oxide must have the correct thermodynamics to be able to cycle with steam as the oxidant, the kinetics to do so rapidly, and long-term stability at both the reduction and re-oxidation temperatures. To date, theory alone has yet to design new materials that cycle under conditions milder than necessary for CeO2 with higher H2 productivity. This paper provides and discusses validating evidence for a computational methodology that has been able to achieve that, identifying a new, highly functional STCH material.
Increasing the η of metal-oxide-perovskite-based STCH toward that of the ideal Carnot cycle generally amounts to optimizing the thermodynamics of both reduction and re-oxidation; or ΔGred = ΔHred – Tred ΔSred and ΔGox = ΔHox − Tox ΔSox. For materials that undergo reduction via oxygen off-stoichiometry like CeO2 and metal-oxide perovskites, VO formation energies (Ev) of 3.4–3.9 eV correspond to optimal values of ΔHred.19 The Ev of CeO2 is too high (4.4 eV),4 hence the need for the design of off-stoichiometry metal oxides like oxide perovskites with a lower Ev. Here, we build on our previous theoretical prediction of Pnma Ca0.5Ce0.5MnO3 (CCM)20 as a promising STCH candidate based on its Ev of 3.65–3.96 eV (within the target range19) and investigate a stabilized oxide perovskite with Ca and Ce on the A-site and Ti and Mn on the B-site.
Results
Computationally predicted Ca2/3Ce1/3Ti1/3Mn2/3O3 is stable experimentally
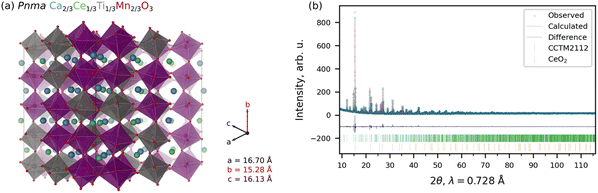
As is the convention in computational materials science, we quantify stability as the energy above the convex hull (Ehull), which is the energy change upon decomposition of a material into stable compounds at the same composition. Throughout, we performed density functional theory (DFT) calculations within the SCAN21+U22–25 framework (see Section S1 and S2 in the ESI† for additional details regarding the SCAN+U calculations and Ehull computation, respectively).26,27 Based on this convex hull construction, CCM is thermodynamically metastable, with an Ehull = 39 meV per atom at 0 K. Experimental attempts to synthesize CCM perovskite were unsuccessful, with CeO2 and Ca–Mn oxide phases predominating, and limited Ca–Ce–Mn oxide phase fraction decomposing during even gentle reduction (see Section S3 in the ESI†). We then tried to increase the stability by using the naturally abundant and highly stable CaTiO3 perovskite as a template to then add a solid solution of Ce4+ and Mn3+ on the A- and B-sites, respectively. Beginning with the previously predicted CCM, we increased the fraction of Ca on the A-site (from 1/2 to 2/3) and Ti on the B-sites (from 0 to 1/3). The resulting structure is a Pnma Ca2/3Ce1/3Ti1/3Mn2/3O3 solid solution (CCTM2112, where the numbers indicate the relative composition of the material for three formula units or numerators of the fractional A- and B-site compositions for one formula unit), matching the Pnma structure of CaTiO3. For a preliminary check on stability, we used the τ tolerance factor of Bartel et al.28 to predict whether CCTM2112 would form a perovskite. The τ value is 2.74, which gives a probability that the composition forms a perovskite structure of 94%, hence, high confidence. Additional support for this solid-solution approach came from reports of CaTi0.5Mn0.5O3−δ29 and CaTi0.2Mn0.8O3−δ,30 though, in our work, the A-site addition of Ce changes the predominant oxidation state of Mn in the fully-oxidized material from Mn4+ in the prior purely Ca-A-site perovskites to Mn3+ in CCTM2112 (see the section entitled Role of Ce4+ in Redox Activity). Independent simulation and empirical determination of the CCTM2112 crystal structure resulted in strong agreement in lattice parameters and atomic positions.To simulate an experimentally realistic CCTM2112 solid solution, we constructed an optimized special quasirandom structure (SQS)31,32 with 360 atoms (216 of which are O atoms) and lattice constants of a = 16.70 Å, b = 15.28 Å, and c = 16.13 Å, corresponding to supercell dimensions of 3 × 2 × 3, as shown in Fig. 1(a) (where optimized refers to optimization of the lattice constants and to optimization of the particular SQS to mimic the random alloy). SCAN+U calculations show that CCTM2112 has an ≈15% lower Ehull (= 33–35 meV per atom, which is comparable to kB 298.15 K ≈ 26 meV per atom) than the previously predicted CCM material, indicating improved stability. Other contributions to the stabilization of CCTM2112 probably include configuration entropy (which is >41 meV per atom at 1273 K).20 Additional details regarding the construction of the SQS for CCTM2112 (see Fig. S1 and S2, ESI†) can be found in Section S4 of the ESI.†
We performed an independent experimental determination of the CCTM perovskite structure using bulk synthesis, powder X-ray diffraction (XRD) measurements, and Rietveld refinement. CCTM was synthesized with a bulk stoichiometry of Ca0.65Ce0.35Ti0.3Mn0.7O3−δ, approaching CCTM2112. Additional synthesis details can be found in Section S3 of the ESI.† Structural refinements on the as-synthesized CCTM2112 powder using XRD data and the Rietveld method with no structural input from simulations. The XRD data and Rietveld refinement fit are shown in Fig. 1(b). For the CCTM phase, fractional occupancies of Ca, Ce, Ti, and Mn were initially allowed to refine, but did not deviate significantly from the initial 0.65–0.35–0.3–0.7 composition. No restraints were implemented since the solved structure was templated by an analogous GdFeO3-type structure (Pnma) and refined atomic positions readily converged. The final structural solution involved refinement of 30 structural parameters with weighted profile residual = 0.053 and goodness of fit equal to 0.22. Results of the CCTM phase refinement demonstrate clear random mixing of Ce and Ca on the A-site and Mn and Ti on the B-site. Fig. 1(b) shows synchrotron XRD data for the CCTM powder, with the red ticks at the bottom denoting the positions of reflections simulated from the SCAN+U-computed CCTM2112 structure using the GSAS-II code.33–35 The only impurity observed in the Rietveld refinement is <1.2 wt% CeO2 (identified by bottom row of ticks in Fig. 1(b)), which suggests a slight excess of A-site elements during synthesis and that all available Ca incorporates onto the A-site sub-lattice. The ≥98.8 wt% CCTM phase fraction and ≥1773 K extended annealing temperature during synthesis confirm the high-temperature stability of CCTM. Additional structural details from the Rietveld refinement of the CCTM and CeO2 phases are available in Tables S1–S5 and Section S6 of the ESI.†
Simulated and empirical determination of the CCTM crystal structure resulted in strong agreement. The evidence for this agreement is the comparison of the Rietveld refined Pnma lattice parameters: a = 5.61442 Å ± 0.00013 Å, b = 7.55658 Å ± 0.00018 Å, c = 5.35511 Å ± 0.00013 Å, to the simulated lattice parameters (extracted from supercell): a = 5.567 Å, b = 7.640 Å, and c = 5.377 Å, resulting in a deviation of simulation from empirical of −0.84% for a, +1.10% for b, and +0.41% for c. Small differences are expected as the composition was not identical. Additional comparison of simulated and empirically derived CCTM unit cells are included in Section S6.2 of the ESI,† which also shows an overlay of the computationally predicted structure onto the 300 K XRD data (Fig. S3, ESI†).
Ca2/3Ce1/3Ti1/3Mn2/3O3−δ splits water
We now examine the energetics of VO formation in CCTM2112 and its dependence on the VO's nearest neighbors (NNs). Inspired by our recent finding that local chemistry governs VO formation in ternary metal-oxide perovskites,36 we categorized all 216 VOs by their (NN) environment and randomly sampled one VO (i.e., we introduce one VO in the SQS, corresponding to δ = 0.014) from each of the 13 unique VO NN environments (Fig. 2(a)). This categorization also gave a tractable number of SCAN+U calculations from which to study the trends in the electronic and thermochemical properties of VOs. We define NN VO environments using xCe and xMn, where xCe = NCe/(NCa + NCe), xMn = NMn/(NTi + NMn), and x (N) is the fraction (number) of the VO's four NN A-sites and two NN B-sites occupied by Ce (xCe = 1 − xCa and NCe = 4 − NCa) and Mn (xMn = 1 − xTi and NMn = 2 − NTi), respectively. Note that the overall supercell structure maintains the same cation stoichiometry as that of bulk CCTM2112, with xCe and xMn in Fig. 2(a) strictly defining compositions that are local to the VO considered. Predictably, the VO with the highest frequency (f = 44 or 44/216 ≈ 20% of the SQS) is the one with a NN environment closest to the bulk composition allowed by the A and B site NN fractions (xCe = 0.25 and xMn = 0.5 for the VO and xCe = 1/3 and xMn = 2/3 for the bulk). Two NN VO environments do not appear in the optimized SQS for CCTM2112 (namely those for xCe = 1 and xMn ≤ 0.5), however, VOs with these NN environments are unlikely to influence significantly the macroscopic reduction of CCTM2112 due to their scarcity (xCe = 1 and xMn = 0.5, and xCe = 1 and xMn = 0 make up 0.5% and 0.1% of the random alloy, respectively).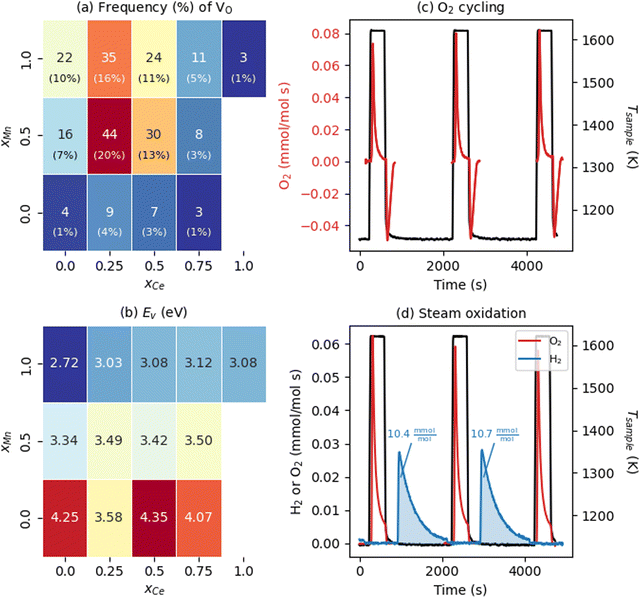 | ||
| Fig. 2 Water-splitting properties of CCTM2112. (a) Frequency (color of and text in rectangles) and probability (percentages in parentheses rounded to the nearest integer) of all unique NN VO environments in the calculated CCTM2112 360-atom cell (and, in Table S6, ESI† for the random alloy), with dark red and dark blue shading indicating higher- and lower-frequency environments, respectively. (b) NN-VO-environment dependence of calculated Ev in CCTM2112. Color of and text in rectangles correspond to Ev in eV, where the minimum Ev = 2.72 eV is dark blue and maximum Ev = 4.35 eV is dark red. (c) O2 evolution rate normalized to mole atoms in CCTM2112 (see ESI,† Section S5 for definition) measured as a function of time during heating and cooling between 1123 K and 1623 K in a constant background of 2000 ppm oxygen. (d) O2 and H2 evolution rates normalized to mole atoms in CCTM2112 measured as a function of time during two successive redox cycles where the sample temperature is raised to 1623.15 K while sweeping with high purity Ar, followed by exposure to 40 vol% H2O in Ar at 1123.15 K. The area under the gas evolution features in (c) and (d) is used to quantify the redox capacity of CCTM2112 during oxygen and steam oxidation. | ||
With this VO categorization protocol, we predict that five of the 13 VOs (shaded yellow and light blue in Fig. 2(b)), including those with the first- and third-highest frequencies (f = 44 or 44/216 ≈ 20% for xCe = 0.25 and xMn = 0.5, which is 17.6% in a random solid (Table S6, ESI†), and f = 30 or 30/216 ≈ 14% for xCe = xMn = 0.5, which is 13.2% of the sites in a random solid), have Evs within (or within 0.06 eV of) the target range of 3.4–3.9 eV (see Fig. 2(b)).19 To quantify the macroscopic reducibility of CCTM2112, we calculate the ensemble-averaged Ev, 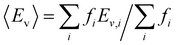 , where fi is the frequency of the ith unique NN VO environment given in Fig. 2(a), and
, where fi is the frequency of the ith unique NN VO environment given in Fig. 2(a), and 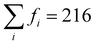 . We obtain 〈Ev〉 = 3.30 eV with a standard deviation of 0.36 eV based on the Ev values in Fig. 2(b), which overlaps with the target range for water splitting. We find that while Ev depends weakly on xCe, it systematically decreases with increasing xMn. This trend can be rationalized on the basis of crystal O2−–Mn+ bond dissociation energies Eb, an extension of molecular O–M bond dissociation energies to the solid state,36 defined as
. We obtain 〈Ev〉 = 3.30 eV with a standard deviation of 0.36 eV based on the Ev values in Fig. 2(b), which overlaps with the target range for water splitting. We find that while Ev depends weakly on xCe, it systematically decreases with increasing xMn. This trend can be rationalized on the basis of crystal O2−–Mn+ bond dissociation energies Eb, an extension of molecular O–M bond dissociation energies to the solid state,36 defined as
 | (1) |
Experiments demonstrate that CCTM2112 is a high-performance water splitter. The data presented in Fig. 2(c) and (d) were measured in a stagnation flow reactor dedicated to screening STCH materials.16,17 During dry redox cycling with O2 (Fig. 2(c)) the material is continuously exposed to ≈2000 ppm O2 while heating from a base temperature of 1123 K to 1623 K. During heating (i.e., thermal reduction) the material evolves molecular oxygen as VOs form in the crystal lattice, hence the positive rate of O2 production. Upon cooling to 1123 K, the material uptakes an equivalent amount of O2 from its surroundings as the VOS are refilled, hence the negative rate of production. CCTM2112 is also redox active under the more stringent thermodynamic conditions of water splitting, as evidenced in Fig. 2(d). Here the sample is exposed to a high purity Ar sweep gas during thermal reduction followed by exposure to a mixture of 40 vol% H2O in Ar. As with O2 redox, molecular oxygen is produced by thermal reduction. However, in the water splitting case, O atoms stripped from H2O fill VOs such that H2 evolves in the presence of steam. Finally, when reduced a second and third time (after steam re-oxidation), an equivalent amount of O2 evolves from the material at levels indicative of the first cycle. The δ calculated from the oxygen reduction in the flow reactor is δ = 0.06, with the cycling Δδ = 0.05. Due to different operating regimes, this δ for the flow reactor is approximately twice that of the soft XAS (δ = 0.033, vide infra) and four times the modeling conditions (one vacancy per 360 atom structure or δ = 0.014, vide supra). The data in Fig. 2(d) demonstrates that CCTM2112 is reversibly redox active (for several cycles) in both O2 and H2O. Furthermore, the absolute amount of O2 and H2 produced during 40 vol% steam cycling (area under blue curve = 10.4 mmol H2 per mol atom CCTM2112) exceeds that of other high-performing perovskite compounds such as BaCe0.25M0.75O3 (7.3 mmol H2 per mol atom BCM) and Sr0.4La0.6Mn0.6Al0.4O3 (8.2 mmol H2 per mol atom SLMA), and CeO2 (2.9 mmol H2 per mol atom CeO2) under similar experimental conditions (see Section S5 in the ESI† for the calculation of the H2 produced by these perovskite compounds). Note that CeO2 does poorly under these conditions, e.g., compared with thermal reduction at ≈1800 K.8 In future work, we will pursue a more thorough comparison between all of these materials in the context of “high conversion,” which is re-oxidation in a less oxidizing environment, such as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 H2
1000 H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O in the oxidizing stream. Normalizing to mole atom (see ESI† Section S5 for definition) makes these comparisons possible, without biasing one material over another.
H2O in the oxidizing stream. Normalizing to mole atom (see ESI† Section S5 for definition) makes these comparisons possible, without biasing one material over another.
Role of Ce4+ in redox activity
We aim to develop a mechanistic understanding of the high performance of CCTM2112 compared to the structurally related CTM and the Ce- and Mn-containing BCM perovskite water splitters. We therefore calculated and analyzed atomic magnetic moments (μ), which are extremely sensitive measures of oxidation- and spin-state changes. For fully oxidized CCTM2112, the mean magnetic moments in Table 1 imply that, rounded to the nearest integer, the average oxidation states of Ca, Ce, Ti, Mn, and O are 2+, 4+, 4+, 3+, and 2−, respectively, which leads to a charge neutral formula unit (see Fig. S4 in the ESI† for the μ distributions). That said, Ce also can exist as Ce3+ and Mn as Mn4+ and Mn2+ (see min/max values in Table 1), where the latter suggests that disproportionation of two Mn3+ may occur in pristine CCTM2112.| Element | Mean ± σ | Minimum | Maximum |
|---|---|---|---|
| Ca | 0.00 ± 0.00 (Ca2+) | 0.00 (Ca2+) | 0.00 (Ca2+) |
| Ce | 0.28 ± 0.23 (Ce4+) | 0.06 (Ce4+) | 0.68 (Ce3+) |
| Ti | 0.05 ± 0.02 (Ti4+) | 0.03 (Ti4+) | 0.08 (Ti4+) |
| Mn | 3.77 ± 0.24 (Mn3+) | 3.10 (Mn4+) | 4.50 (Mn2+) |
| O | 0.01 ± 0.01 (O2−) | 0.00 (O2−) | 0.05 (O2−) |
To gain greater insight into the nature of the electronic reorganization in CCTM2112 upon VO formation in the thermal reduction step of STCH, we computed the VO-induced changes in the absolute values of μCe, μMn, and μO (use of absolute values controls for changes in relative orientation, i.e., ferromagnetic or antiferromagnetic; see Fig. S5 in the ESI† for a similar analysis of μCa and μTi). We then sum these |μ| changes separately for Ce, Mn, and O to quantify the extent to which the A, B, and O sub-lattices, respectively, are reduced (positive value) or oxidized (negative value) since changes in μ roughly correspond to changes in oxidation states, excluding Ca and Ti because we observe no more than marginal spin changes on these sites. Thus, the quantification of number of electrons added/removed from a species comes from our calculated changes in |μ|. For example, when xCe = 0 and the change in |μCe| ≠ 0, a VO without a NN Ce has reduced a non-NN Ce, thus resulting in nonlocal or delocalized reduction.
Our results show that reduction occurs primarily on the A-site Ce sub-lattice (Fig. 3(a)) compared with that of Mn (Fig. 3(b)) and O (Fig. 3(c)), regardless of the VO's NNs. In particular, the Ce sub-lattice reduces by 0.75 to 2.23 electrons depending on xCe and xMn, corresponding to an average decrease in Ce oxidation state of 0.031 to 0.093 e, respectively (average reduction of the 24 Ce in the unit cell); whereas, for Mn, no obvious net reduction or oxidation occurs during the formation of the VO, with both mild reduction (≤0.35 electrons accepted) and oxidation (≤0.42 electrons donated) of Mn occurring simultaneously (see Table S7 in the ESI† for a qualitative analysis of Ce and Mn oxidation state changes upon neutral VO formation). During VO formation, the remaining O sub-lattice experiences weak-to-mild reduction (≤0.52 electrons accepted in total by the O sub-lattice containing 216 atoms in the unit cell), reminiscent of the VO-induced delocalized reduction of the O sub-lattice in the Sr2Fe2−xMoxO6 double perovskites reported by Muñoz-García et al.37 The reduction of the O sub-lattice is indicative of empty O states in the pristine material, indicating that the Os are not fully ionized as O2− (as seen by Bader charge analysis), with instead the M–O bonds exhibiting some singlet-coupled covalent character, which spin-averages the electrons on O to appear nonmagnetic.
 | ||
| Fig. 3 Multiple cation redox in CCTM2112. Dependence of VO-induced absolute magnetic moment (|μ|) changes for the (a) Ce, (b) Mn, and (c) O sub-lattices on the VO‘s NN environment, where the mole fractions, x, refer just to the NN environment. Note that we sum these |μ| changes separately for Ce, Mn, and O to quantify the extent to which the A, B, and O sub-lattices, respectively, are reduced (positive value) or oxidized (negative value) since μ changes roughly correspond to fractional oxidation state changes, reserving Ca and Ti for Fig. S5 in the ESI† because we observe marginal spin changes on these sites. XAS spectra at the (d) Ce 3d5/2 and (e) Mn 2p3/2 edge for reduced CCTM2112 and re-oxidized CCTM2112 (see Fig. S8 in the ESI† for the complete spectra). | ||
X-ray absorption (XAS) synchrotron studies provide validating evidence supporting the predicted changes in average Ce and Mn oxidation states indeed occur during reduction of CCTM2112. We confirmed that, for oxidized CCTM2112 (δ ≈ 0), the predominant oxidation states of Mn and Ce are Mn3+ and Ce4+ by comparing the XAS spectrum of oxidized CCTM2112 (Fig. 3(d) and (e)) to standards. CCTM2112 was repeatedly reduced (pO2 ≈ 1 × 10−5 bar) and re-oxidized (pO2 ≈ 0.2 bar) in dry redox cycling conditions at 1473 K with 16 hours at each condition. CCTM2112 samples after both the third reduction and third re-oxidation were characterized. XRD confirms both the reduced and re-oxidized sample retained the CCTM structure with negligible secondary phase formation (Fig. S6, ESI†). Mass change in the sample between re-oxidizing and reducing conditions is consistent with a Δδ = 0.033 ± 0.003, with near full oxidation of the re-oxidized sample (δ ≈ 0) giving the reduced sample δ = 0.033 ± 0.003. In comparison, the one VO out of 216 oxygen sites modeled here (Fig. 2) corresponds to δ = 0.014, conditions that are roughly half of the empirical reduction but still sufficiently close for comparing modeling results to observational data.
Soft XAS experiments at the Ce M-edge (i.e., X-ray-induced electron transitions from 3d to 4f orbitals) and Mn L-edge (electron transitions from 2p to 3d orbitals) were used to identify cation-specific changes in oxidation state. Increases in oxidation state result in less electron shielding of the atomic nucleus. Hence, more energy is required to excite a core electron, moving the spectrum edge position to higher energy. Ce and Mn oxidation states were benchmarked against known standards: CeO2 for Ce4+, CeAlO3 for Ce3+, MnO2 for Mn4+, Mn2O3 for Mn3+, and MnO for Mn2+. The soft XAS results for the Ce M-edge (see Fig. 3(d)) demonstrate reversible reduction of Ce (shift in edge positions at approximately 881 eV and 900 eV to lower energy upon reduction) to a fractional oxidation state of ≈3.90 ± 0.03, determined from a linear combination fit of the re-oxidized and reduced CCTM with the Ce4+ and Ce3+ standards (see Fig. S7 and S8 in the ESI†). This measured 1.1% decrease in the average Ce oxidation state ([4 − 3.9]/4 = 2.5% for δ = 0.033, ≈2.5 × 0.014/0.033 = 1.1% for δ = 0.014) agrees well with the 0.8% decrease predicted by SCAN+U calculations ([〈qox〉 − 〈qred〉]/〈qox〉 = [3.72 − 3.69]/3.72 = 0.8% for δ = 0.014, where 〈q〉 is the ensemble-averaged Ce oxidation state). Additionally, the Mn L-edge (see Fig. 3(e)) demonstrates no observable shift in edge positions (at approximately 641 eV and 652 eV), but does have evidence of Mn2+ oxidation to Mn3+ and Mn4+ reduction to Mn3+ (loss in intensity at the lower energy shoulder and higher energy side of the spectrum), supporting model predictions that simultaneous Mn oxidation and reduction occurs with modest net change in Mn oxidation state compared with that of Ce (see smaller values with positive and negative signs for Mn in Fig. 3(b) compared with larger positive values for Ce in Fig. 3(a)).
Discussion
Nonlocal Ce reduction
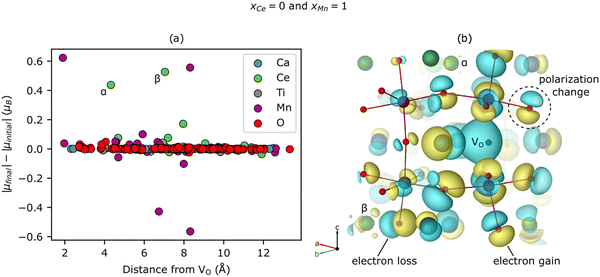
Surprisingly, we predict that Ce reduces even when it does not neighbor the VO (see ≥ 1.41 electron reduction of the Ce sub-lattice for xCe = 0 in Fig. 3(a)). To explore this phenomenon further, we study the spatial dependence of the |μ| changes induced by a VO with a Ca- and Mn-rich local environment (i.e., xCe = 0 and xMn = 1). Fig. 4(a) shows that two Ce reduce, labeled α (Δ|μ| = 0.44 μB) and β (0.53 μB), at distances of 4.32 Å (for α) and 7.04 Å (for β) from the VO. Note that Ca and Ti are not redox active and only a few O are slightly reduced or become more ionic, mostly at distances of <5 Å from the VO, which accounts for the non-zero value in Fig. 3(c) for xCe = 0 and xMn = 1. Additionally, the Mn sub-lattice is both reduced and – to a slightly lesser extent – oxidized, leading to a net mild reduction of 0.35 electrons, corresponding to a disproportionation. Given the changes for Mn are modest, experimental validation is non-trivial. Ce reduction-at-a-distance also can be seen in Fig. 4(b), which displays the difference between the electron density (ρ) of CCTM2112 with and without (i.e., in its pristine state) this same neutral VO (Δρ = ρvacancy − ρpristine), as yellow isosurfaces (indicating electron gain) emerging from and surrounding the two green Ce labeled α and β, respectively. There are a lot of cyan isosurfaces as well, which implies, in the cases where Δρ is p-like polarization rather than charge accumulation or depletion at those sites. This nonlocal reduction allows a substantial fraction of the Ce present in the material to participate in oxygen vacancy formation, and partially explains the high extent of Ce reduction in CCTM2112.Having explored the spatial dependence of VO-induced reduction, we now are able to explain the subtle xCe dependence of Ev at xMn = 0. The Ev for xCe = 0 (i.e., 4.25 eV) is the second highest value in Fig. 2(b), which we attribute to the localized reduction of Ce (≈two Ce reduced in Fig. S9 of the ESI†), and the electrostatic penalty associated with its distance (4.67–4.83 Å) from the holes localized on the VO (see, e.g., Fig. 4(b)). For xCe = 0.25, the Ev ≈ 3.58 eV (Fig. 2(b)) is anomalously low because, while the reduction of Ce remains fairly localized (two Ce reduced at distances <5 Å to the VO, Fig. S9, ESI†), these electrons are closer to the VO-generated holes and therefore electrostatically stabilize the VO. Note that strain can have an indirect effect on Ev by inducing or relaxing Jahn–Teller distortions on Mn but the strain effect is difficult to quantify.
Interestingly, Ev reaches its highest value for xCe = 0.5 (i.e., 4.35 eV; Fig. 2(b)), which we propose is the sum of (1) an electrostatic penalty for delocalized reduction of Ce (four Ce reduced by >0.27 electrons at distances of 2.36 Å to 9.48 Å from the VO, Fig. S9, ESI†) and the delocalized electrons’ resultant screening of electron–hole interactions and (2) a penalty for oxidizing the Mn (|Δμ| = −0.55 μB) at a distance of 10.01 Å from the VO. Finally, from xCe = 0.5 to xCe = 0.75, Ev decreases from 4.35 eV to 4.07 eV (Fig. 2(b)), which – considering the latter's fairly delocalized reduction of Ce (Fig. S9, ESI†) – seems to derive from the absence of oxidized Mn (i.e., Mn for which Δ|μ| < 0 μB). Therefore, we can explain the subtle xCe dependence of Ev at xMn = 0 by the nature (localized/delocalized) and location of VO-generated charge carriers interacting electrostatically with the VO.
What properties promote the high extent of Ce reduction?
Lastly, it is worth discussing an interesting question that our results provoke: why does Ce4+ function as the primary acceptor of electrons (Fig. 3(a)) if it is less reducible than Mn4+ and Mn3+? To quantify the reducibility of Ce4+, Mn4+, and Mn3+, we calculate the enthalpy changes of the following solid-state reduction reactions: CeO2 → 0.5 Ce2O3 + 0.25 O2, MnO2 → 0.5 Mn2O3 + 0.25 O2, and 0.5 Mn2O3 → MnO + 0.25 O2, respectively. Mn4+ is the most reducible cation (ΔH = 0.40 eV) followed by Mn3+ (ΔH = 1.02 eV) and then Ce4+ (ΔH = 1.82 eV). Additionally, since these reactions are normalized per one-electron reduction, their ΔHs are effectively crystal reduction potentials (Vr), which are a key factor governing Ev in ternary oxide perovskites.36 While this simple analysis suggests that Ce should not reduce, the unoccupied states closest to the Fermi level in metallic CCTM2112 are Ce 4f states (see Fig. S10 in the ESI†). Therefore, even though Ce4+ is less reducible than Mn4+ and Mn3+ in their ground-state binary oxides, Ce does reduce in CCTM2112 because there is a lower energy penalty for the structure to put the VO-donated electrons in the Ce 4f states, even if the Ce atom is physically farther from the VO. Ce4+ reduction is also accompanied by delocalization of electrons (due to the degeneracy of 4f states contributed by several Ce atoms close to the Fermi level), while Mn reduction is almost always local, evidenced by the presence or absence of Jahn–Teller distortions associated with Mn3+. The need for 4f states near the Fermi level to reduce Ce4+ in the presence of Mn3+ is consistent with the observation that Mn and not Ce reduces during thermochemical cycling of Ba(Ce,Mn)O3 (BCM) perovskites (where Ba is on the A-site, and Ce and Mn occupy the B-site)17 because BCM has a band gap and thus VO-induced reduction is driven by cation proximity and reducibility rather than the relative location of unoccupied states near the Fermi level. Thus, the density of states for CCTM2112 promotes Ce reduction, revealing a mechanism that quantum-based modeling can target to predict other formulations of Ca–Ce–Ti–Mn–O as well as other materials with enhanced Ce reduction and thus enhanced STCH performance.The high reducibility of Ce4+ in CCTM2112 is both key to its high water-splitting performance and substantially different than the behavior of CeO2 and other previously demonstrated Ce4+-containing off-stoichiometric redox-active materials. The existence of Ce4+ reduction is observed directly in both modeling and XAS. The most obvious structural distinction of CCTM2112 is the 12-fold coordination of Ce4+ on the A-site, compared to the 8-fold coordination of Ce4+ in the CeO2 fluorite structure and 6-fold coordination on the B-site of BCM. As discussed above, the redox activity of Mn on the B-site is less clear, which suggests that other electronically similar elements may be able to substitute on the B-site and enable A-site Ce4+ reduction.20 These results further suggest that a heretofore under-investigated family of Ce4+ A-site perovskites may exist with comparably high performance, across a range of alternate A-site and B-site elemental substitutions and ratios.
Conclusions
Perovskite Ca2/3Ce1/3Ti1/3Mn2/3O3 (CCTM2112) offers potential to have greater solar thermochemical H2 (STCH) production capacity than two other high-performing perovskite compounds, specifically Sr0.4La0.6Mn0.6Al0.4O3 (SLMA4664) and BaCe0.25Mn0.75O3 (BCM), and greater than CeO2 at operating temperatures of 1623.15 K for the thermal reduction step and 1123.15 K for the water-splitting step. Additionally, the more general Ca–Ce–Ti–Mn–O phase space provides possibilities for supplanting CeO2-based materials as the preferred redox-active MOx for STCH. Ce being the dominant acceptor of the electrons left behind by neutral oxygen vacancy formation, unlike other Ce-containing oxide perovskites for STCH like BCM, suggests that refinement of the Ce stoichiometry is a particularly promising avenue for future research. Finally, the electronic-structure-based mechanism that promotes Ce reduction with lower vacancy formation energies than in CeO2 reveals novel physics and redox-active materials design considerations for realizing the climate-change-mitigation potential of STCH. As such, this work does not just introduce one high-performing material but instead uses the modeling-driven and experimentally verified discovery of a new water splitter with a distinct mechanism of action to introduce a new family of water-splitting materials.Experimental details
Synchrotron powder X-ray diffraction data were acquired at the Stanford Synchrotron Radiation Lightsource (SSRL), beam line 2-1. The incident X-ray wavelength used was 0.730 Å as determined by a refinement of data from a NIST 660C LaB6 diffraction standard. CCTM powders were prepared in 0.028 inch outer diameter Kapton capillaries with 0.002 inch wall thickness and rotated (≈1 rotation per second) during data acquisition. 2D diffraction images were obtained with a Pilatus 100 K hybrid photon counting detector, and subsequently integrated into a 1D pattern using a python script developed at SSRL for beam line 2-1. The diffraction pattern used to compare the experimental XRD data to the DFT model was simulated from the “CCTM2112” model, subjected to the ADDSYM routine within PLATON.38 The XRD data was indexed using NTREOR, contained within the EXPO201439 suite of crystallographic tools. Rietveld refinements were performed using GSAS-II.33X-Ray absorption spectroscopy data was acquired at SSRL, beam line 10-1. For analysis of each sample, a thin layer of CCTM powder was spread on carbon tape. Total fluorescence yield spectra were obtained with a silicon diode AXUV100 detector at the Ce 3d and Mn 2p edges. A Mn reference spectrum was collected simultaneously with data collection at the Mn edge for all samples. Specific to this beamline, an agglomerate of chemical species resides permanently within the beam path for reference collection. The reference material does not contain Ce, so no Ce reference was available. However, the Mn references collected throughout the experiment well align ensuring the monochromator was stable and data could be directly compared. Data was analyzed with Igor Pro (Wavemetrics, Lake Oswego, Oregon, USA). For each spectrum, the average value of the pre-edge region is subtracted, and the spectrum normalized to the Mn 2p3/2 or Ce 3d5/2. Powder CCTM2112 samples were redox cycled in a laser-heated stagnation flow reactor.16,17 Approximately 100 mg of sample is placed in a shallow, loosely packed bed within the stagnation plane of the reactor flow field such that transport of gaseous species to and from the sample surface is governed by 1-D diffusion. The reactor operates at 75 Torr and the sample environment (i.e., gas flow rate, gas composition, temperature, pressure) is fully controlled using appropriate hardware and software. The gas composition in the reactor effluent is measured by mass spectrometry at a rate ∼4 Hz, which is important because the re-oxidation and reduction chemistries are inherently transient. Since the reactor flow field is well behaved, physical processes such as gas-phase dispersion, reactant mixing, and detector time lag that normally confound the extraction of material-specific behavior from the as-measured transient signal are easily resolved using numerical methods. One unique feature of the experimental system is the use of a 500 W, continuous-wave, near-IR laser to rapidly heat the material during thermal reduction. This heating method mimics the radiative environment encountered in an ultra-high temperature concentrating solar receiver and allows exploration of the effects of rapid thermal cycling, such as crystallographic and morphological instabilities, on macroscopic water splitting behavior.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge research support from the HydroGEN Advanced Water Splitting Materials Consortium, established as part of the Energy Materials Network under the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Fuel Cell Technologies Office, under award number DE-EE0008090. The authors also acknowledge the computational resources sponsored by the Department of Energy's Office of Energy Efficiency and Renewable Energy located at the National Renewable Energy Laboratory. The authors also thank Princeton University for computing resources. The National Renewable Energy Laboratory is operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under contract no. DE-AC36-08GO28308. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc, for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under contract no. DE-AC02-76SF00515. The authors thank Kevin Stone and J. R. Troxel for their skillful assistance in preparation for measurements performed at SSRL beam line 2-1. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights.References
- BESAC Subcommittee on International Benchmarking. Can the U.S. Compete in Basic Energy Sciences? (Department of Energy Office of Science, 2021). at https://science.osti.gov/-/media/bes/pdf/reports/2021/International_Benchmarking-Report.pdf.
- W.-H. Cheng, A. de la Calle, H. A. Atwater, E. B. Stechel and C. Xiang, Hydrogen from sunlight and water: A side-by-side comparison between photoelectrochemical and solar thermochemical water-splitting, ACS Energy Lett., 2021, 6, 3096–3113 CrossRef CAS.
- R. Soltani, M. A. Rosen and I. Dincer, Assessment of CO2 capture options from various points in steam methane reforming for hydrogen production, Int. J. Hydrogen Energy, 2014, 39, 20266–20275 CrossRef CAS.
- A. Bayon, A. de la Calle, E. B. Stechel and C. Muhich, Operational Limits of Redox Metal Oxides Performing Thermochemical Water Splitting, Energy Technol., 2021, 2100222 Search PubMed.
- A. Steinfeld, Solar thermochemical production of hydrogen––a review, Sol. Energy, 2005, 78, 603–615 CrossRef CAS.
- M. Romero and A. Steinfeld, Concentrating solar thermal power and thermochemical fuels, Energy Environ. Sci., 2012, 5, 9234–9245 RSC.
- B. Meredig and C. Wolverton, First-principles thermodynamic framework for the evaluation of thermochemical H2O- or CO2-splitting materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245119 CrossRef.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, High-Flux Solar-Driven Thermochemical Dissociation of CO2 and H2O Using Nonstoichiometric Ceria, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- S. Abanades and G. Flamant, Thermochemical hydrogen production from a two-step solar-driven water-splitting cycle based on cerium oxides, Sol. Energy, 2006, 80, 1611–1623 CrossRef CAS.
- J. R. Scheffe and A. Steinfeld, Oxygen exchange materials for solar thermochemical splitting of H2O and CO2: a review, Mater. Today, 2014, 17, 341–348 CrossRef CAS.
- G. Sai Gautam, E. B. Stechel and E. A. Carter, A First-Principles-Based Sub-Lattice Formalism for Predicting Off-Stoichiometry in Materials for Solar Thermochemical Applications: The Example of Ceria, Adv. Theory Simul., 2020, 3, 2000112 CrossRef CAS.
- D. Marxer, P. Furler, M. Takacs and A. Steinfeld, Solar thermochemical splitting of CO2 into separate streams of CO and O2 with high selectivity, stability, conversion, and efficiency, Energy Environ. Sci., 2017, 10, 1142–1149 RSC.
- Y. Lu, L. Zhu, C. Agrafiotis, J. Vieten, M. Roeb and C. Sattler, Solar fuels production: Two-step thermochemical cycles with cerium-based oxides, Prog. Energy Combust. Sci., 2019, 75, 100785 CrossRef.
- A. Haeussler, S. Abanades, A. Julbe, J. Jouannaux and B. Cartoixa, Solar thermochemical fuel production from H2O and CO2 splitting via two-step redox cycling of reticulated porous ceria structures integrated in a monolithic cavity-type reactor, Energy, 2020, 201, 117649 CrossRef CAS.
- M. Kubicek, A. H. Bork and J. L. M. Rupp, Perovskite oxides – a review on a versatile material class for solar-to-fuel conversion processes, J. Mater. Chem. A, 2017, 5, 11983–12000 RSC.
- A. H. McDaniel, E. C. Miller, D. Arifin, A. Ambrosini, E. N. Coker, R. O’Hayre, W. C. Chueh and J. Tong, Sr- and Mn-doped LaAlO3-δ for solar thermochemical H2 and CO production, Energy Environ. Sci., 2013, 6, 2424–2428 RSC.
- D. R. Barcellos, M. D. Sanders, J. Tong, A. H. McDaniel and R. P. O’Hayre, BaCe0.25Mn0.75O3−δ—a promising perovskite-type oxide for solar thermochemical hydrogen production, Energy Environ. Sci., 2018, 11, 3256–3265 RSC.
- R. Schäppi, D. Rutz, F. Dähler, A. Muroyama, P. Haueter, J. Lilliestam, A. Patt, P. Furler and A. Steinfeld, Drop-in fuels from sunlight and air, Nature, 2022, 601, 63–68 CrossRef PubMed.
- R. B. Wexler, E. B. Stechel and E. A. Carter, Sol. Fuels, Wiley-Scrivener, 2022 Search PubMed.
- G. Sai Gautam, E. B. Stechel and E. A. Carter, Exploring Ca–Ce–M–O (M = 3d Transition Metal) Oxide Perovskites for Solar Thermochemical Applications, Chem. Mater., 2020, 32, 9964–9982 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- G. Sai Gautam and E. A. Carter, Evaluating transition metal oxides within DFT-SCAN and SCAN+U frameworks for solar thermochemical applications, Phys. Rev. Mater., 2018, 2, 095401 CrossRef CAS.
- O. Y. Long, G. Sai Gautam and E. A. Carter, Evaluating optimal U for 3d transition-metal oxides within the SCAN+U framework, Phys. Rev. Mater., 2020, 4, 045401 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, New tolerance factor to predict the stability of perovskite oxides and halides, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- X. Qian, J. He, E. Mastronardo, B. Baldassarri, W. Yuan, C. Wolverton and S. M. Haile, Outstanding Properties and Performance of CaTi0.5Mn0.5O3–δ for Solar-Driven Thermochemical Hydrogen Production, Matter, 2021, 4, 688–708 CrossRef CAS.
- J. E. Miller, S. M. Babiniec, E. N. Coker, P. G. Loutzenhiser, E. B. Stechel and A. Ambrosini, Modified Calcium Manganites for Thermochemical Energy Storage Applications, Front. Energy Res., 2022, 10, 774099 CrossRef.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- M. Ångqvist, W. A. Muñoz, J. M. Rahm, E. Fransson, C. Durniak, P. Rozyczko, T. H. Rod and P. Erhart, ICET – A Python Library for Constructing and Sampling Alloy Cluster Expansions, Adv. Theory Simul., 2019, 2, 1900015 CrossRef.
- B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS.
- Y. Le Page, Computer derivation of the symmetry elements implied in a structure description, J. Appl. Crystallogr., 1987, 20, 264–269 CrossRef CAS.
- Y. Le Page, MISSYM 1.1 – a flexible new release, J. Appl. Crystallogr., 1988, 21, 983–984 CrossRef.
- R. B. Wexler, G. S. Gautam, E. B. Stechel and E. A. Carter, Factors Governing Oxygen Vacancy Formation in Oxide Perovskites, J. Am. Chem. Soc., 2021, 143, 13212–13227 CrossRef CAS PubMed.
- A. B. Muñoz-García, A. M. Ritzmann, M. Pavone, J. A. Keith and E. A. Carter, Oxygen Transport in Perovskite-Type Solid Oxide Fuel Cell Materials: Insights from Quantum Mechanics, Acc. Chem. Res., 2014, 47, 3340–3348 CrossRef PubMed.
- A. L. Spek, Structure validation in chemical crystallography, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- A. Altomare, C. Cuocci, C. Giacovazzo, A. Moliterni, R. Rizzi, N. Corriero and A. Falcicchio, EXPO2013: a kit of tools for phasing crystal structures from powder data, J. Appl. Crystallogr., 2013, 46, 1231–1235 CrossRef CAS.
- A. M. Deml, A. M. Holder, R. P. O’Hayre, C. B. Musgrave and V. Stevanović, Intrinsic Material Properties Dictating Oxygen Vacancy Formation Energetics in Metal Oxides, J. Phys. Chem. Lett., 2015, 6, 1948–1953 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Li–Fe–P–O2 Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20, 1798–1807 CrossRef CAS.
- S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Thermal stabilities of delithiated olivine MPO4 (M = Fe, Mn) cathodes investigated using first principles calculations, Electrochem. Commun., 2010, 12, 427–430 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Further details about the SCAN+U calculations, stability of CCTM2112, SQS construction for Pnma CCTM2112, VO NN environment statistics, magnetic moment distribution by species in pristine CCTM2112, dependence of the VO-induced magnetic moment changes by element on the VO's NN environment, qualitative Ce and Mn oxidation state changes upon VO formation, VO-induced magnetic moment changes vs. distance, and projected density of states of pristine CCTM2112;40–47 additional synthesis details, comparison of H2 produced by state-of-the-art redox-active perovskites, and XRD and XAS data from the reduced and re-oxidized CCTM powder; files containing crystal structures, total energies, magnetic moments, and projected densities of states. See DOI: https://doi.org/10.1039/d3ee00234a |
| This journal is © The Royal Society of Chemistry 2023 |