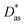Open Access Article
Open Access ArticleSuperfluid helium droplet-mediated surface-deposition of neutral and charged silver atomic species†
Berta
Fernández
 a,
Martí
Pi
a,
Martí
Pi
 bc and
María Pilar
de Lara-Castells
bc and
María Pilar
de Lara-Castells
 *d
*d
aDepartment of Physical Chemistry, University of Santiago de Compostela, E-15782 Santiago de Compostela, Spain
bDepartament FQA, Facultat de Física, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain
cInstitute of Nanoscience and Nanotechnology (IN2UB), Universitat de Barcelona, 08028 Barcelona, Spain
dInstitute of Fundamental Physics (ABINITFOT Group), Madrid, Spain. E-mail: Pilar.deLara.Castells@csic.es
First published on 2nd June 2023
Abstract
Experimental and theoretical work has delivered evidence of the helium nanodroplet-mediated synthesis and soft-landing of metal nanoparticles, nanowires, clusters, and single atoms on solid supports. Recent experimental advances have allowed the formation of charged metal clusters into multiply charged helium nanodroplets. The impact of the charge of immersed metal species in helium nanodroplet-mediated surface deposition is proved by considering silver atoms and cations at zero-temperature graphene as the support. By combining high-level ab initio intermolecular interaction theory with a full quantum description of the superfluid helium nanodroplet motion, evidence is presented that the fundamental mechanism of soft-deposition is preserved in spite of the much stronger interaction of charged species with surfaces, with high-density fluctuations in the helium droplet playing an essential role in braking them. Corroboration is also presented that the soft-landing becomes favored as the helium nanodroplet size increases.
1. Introduction
Soft-landing deposition of metal species onto solid supports is characterized by sticking probabilities close to 100% at the impact point with landing energies well below typical cohesive energies of the metal species. As shown in pioneering experimental studies carried out by A. F. Vilesov et al.1,2 soft deposition can be achieved upon synthesis of the target metal species in cold (0.4 K) 4He nanodroplets, which further serve as their carriers to the surface of interest. Further experimental evidences of the helium droplet-mediated synthesis and soft-landing deposition of metal nanoparticles,3,4 supported with molecular dynamics simulations,5 have extensively been provided by W. E. Ernst's group, including bimetallic core–shell nanoparticles of sub-10 nanometer size.6–8 A. M. Ellis and coworkers have also reported on the soft-landing of elongated metal nanowires.9,10 Experimental studies carried out by Q. Wu et al.11 have further motivated the applicability of the 4He nanodroplet-mediated surface soft-deposition technique. In this way, the authors demonstrated that a narrow size distribution, down to the subnanometer scale, of TiO2-supported gold clusters can be achieved which is stable upon exposure to CO and O2 atmospheres up to a temperature of 473 K.11 Recent experimental advances by P. Scheier's group12,13 have allowed the pickup of metal species into multiply charged helium nanodroplets, with the charges acting as nucleation centers for charged, subnanometer-sized, cluster formation.14On the theoretical side, the earliest first-principles simulations of the collision dynamics of a 4He droplet with a zero-temperature TiO2 surface15 showed the paramount importance of including nuclear delocalization on the helium droplet dynamics. Thus, in contrast with a pure classical picture predicting the splashing of helium droplets at impact, quantum simulations showed that the helium droplet spreads on a zero-temperature surface, with the spreading being consistent with the soft-landing of an embedded impurity. Further theoretical studies of both free16 and doped helium droplets17 corroborated the suitability of this picture for embedded single Au atoms and silver nanoparticles,18 including zero-temperature TiO217 and graphene16 as supports and as a “vibrating surface” made of amorphous carbon at room temperature in order to simulate experimental conditions with droplets composed of up to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 4He atoms.18 In particular, ref. 17 presented quantum and classical simulations on the collision of Au@4He300 doped droplets with a titanium dioxide surface. It was shown that the appearance of quantum density fluctuations in the superfluid 4He droplet plays a key role in assisting the soft-landing of atomic gold, dissipating its collision energy upon impact. On the contrary, no sticking was found but just a slight deviation from an elastic trajectory when the helium drop was described classically (see, e.g., ref. 19 for a recent review). The reliability of the theoretical approach was later confirmed in the experimentally probed soft-deposition of gold clusters, down to the subnanometer scale, on a titanium dioxide surface.11
000 4He atoms.18 In particular, ref. 17 presented quantum and classical simulations on the collision of Au@4He300 doped droplets with a titanium dioxide surface. It was shown that the appearance of quantum density fluctuations in the superfluid 4He droplet plays a key role in assisting the soft-landing of atomic gold, dissipating its collision energy upon impact. On the contrary, no sticking was found but just a slight deviation from an elastic trajectory when the helium drop was described classically (see, e.g., ref. 19 for a recent review). The reliability of the theoretical approach was later confirmed in the experimentally probed soft-deposition of gold clusters, down to the subnanometer scale, on a titanium dioxide surface.11
More recently, P. Scheier's group20 has experimentally shown that embedded charged C60 species scatter back upon collision with a room-temperature surface. These latest experiments have further emphasized the very complex nature of interfacial phenomena involving the interaction of helium nanodroplets with surfaces of solid materials. They have motivated us to consider the impact of the charge for metal species immersed in a superfluid helium droplet onto a zero-temperature surface, analysing the influence of the helium droplet size as well. For this purpose, we apply high-level ab initio theory combined with the He time-dependent density functional theory (He-TDDFT) method for the quantum dynamics in the collision of silver atoms and cations solvated by superfluid helium nanodroplets onto zero-temperature graphene. From an application-oriented point of view, it should be stressed that the soft-deposition of atomic metal cations onto suitable supports is a possible route towards the stabilization of single atom catalysts.21
2. High-level ab initio intermolecular potentials
2.1 He–graphene, Ag–graphene, and He–Ag interaction potentials
In this work, we have used the accurate He–graphene interaction potential reported in ref. 16, already probed by reproducing experimental data with spectroscopic accuracy (to within 0.3 cm−1). The proposed method16 (the periodic dispersionless + incremental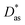 approach) extends dispersionless density functional (dlDF) theory,22,23 introducing a scheme to parametrize the dispersion interaction at the coupled cluster singles and doubles and perturbative triples (CCSD(T)) level via the method of increments.24 The same scheme has been applied to calculate the dispersion-dominated Ag–graphene interaction potential in this work. Within the incremental
approach) extends dispersionless density functional (dlDF) theory,22,23 introducing a scheme to parametrize the dispersion interaction at the coupled cluster singles and doubles and perturbative triples (CCSD(T)) level via the method of increments.24 The same scheme has been applied to calculate the dispersion-dominated Ag–graphene interaction potential in this work. Within the incremental 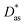 scheme, the intermonomer correlation contribution to the correlation energy calculated at the CCSD(T) level25 is identified with the dispersion contribution, fitted by means of the effective pairwise Das functional of K. Szalewicz and collaborators,23,26 and then computed on the extended system. For Ag–graphene, the calculation of the interaction energy Etotalint (see Table 1) is then reduced to,
scheme, the intermonomer correlation contribution to the correlation energy calculated at the CCSD(T) level25 is identified with the dispersion contribution, fitted by means of the effective pairwise Das functional of K. Szalewicz and collaborators,23,26 and then computed on the extended system. For Ag–graphene, the calculation of the interaction energy Etotalint (see Table 1) is then reduced to,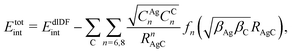 | (1) |
 method has been assessed by applying it to the Ag–coronene complex. As in ref. 25, the augmented correlation-consistent polarized triple-ζ basis of T. H. Dunning and collaborators40 (aug-cc-pVTZ) has been used for C and H atoms, while the aug-cc-pVTZ-PP basis set has been employed for silver, including a small-core (19-valence-electron) relativistic pseudopotential.43 The method provides an estimate for the interaction energy and the Ag–coronene equilibrium distance which are very close (to within 3%, see Table 1) to previous benchmarking results44 obtained using the scalar one-component Douglas–Kroll–Hess approximation45 in relativistic calculations at the second order Möller–Plesset perturbation theory (MP2) level with the ANO-RCC-VDZP basis set46,47 (see ESI†). Interestingly, the Ag–graphene interaction is less attractive (by 16%) than the Ag–coronene interaction. Similarly to the Ag2–graphene interaction,25 this behaviour is attributed to the repulsive intramonomer correlation contribution to the Ag–graphene interaction.
method has been assessed by applying it to the Ag–coronene complex. As in ref. 25, the augmented correlation-consistent polarized triple-ζ basis of T. H. Dunning and collaborators40 (aug-cc-pVTZ) has been used for C and H atoms, while the aug-cc-pVTZ-PP basis set has been employed for silver, including a small-core (19-valence-electron) relativistic pseudopotential.43 The method provides an estimate for the interaction energy and the Ag–coronene equilibrium distance which are very close (to within 3%, see Table 1) to previous benchmarking results44 obtained using the scalar one-component Douglas–Kroll–Hess approximation45 in relativistic calculations at the second order Möller–Plesset perturbation theory (MP2) level with the ANO-RCC-VDZP basis set46,47 (see ESI†). Interestingly, the Ag–graphene interaction is less attractive (by 16%) than the Ag–coronene interaction. Similarly to the Ag2–graphene interaction,25 this behaviour is attributed to the repulsive intramonomer correlation contribution to the Ag–graphene interaction.
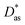 approach16 are also shown, with R being the distance between the Ag atom and a hollow site in the coronene/graphene sheet. For comparison purposes, benchmark results using the DK-MP2 approach for the Ag–coronene complex are also included.44 See text and the ESI for further details and additional dispersion-corrected density functional calculations
approach16 are also shown, with R being the distance between the Ag atom and a hollow site in the coronene/graphene sheet. For comparison purposes, benchmark results using the DK-MP2 approach for the Ag–coronene complex are also included.44 See text and the ESI for further details and additional dispersion-corrected density functional calculations
We have used the He–Ag potential reported in ref. 48, calculated at the CCSD(T) level, including corrections for the perturbative treatment of the triples excitations with a well-converged basis set encompassing a small core pseudo-potential for silver.
2.2 He–Ag+ and Ag+–graphene interaction potentials
Additionally, we have applied intermolecular ab initio interaction theory to calculate the He–Ag+ and Ag+–graphene interaction potentials. As molecular models of a single graphene sheet, we have used hydrocarbons of increasing size (see Fig. 1). This strategy avoids problems related to the description of charged systems under periodic boundary conditions.49 A systematic electron correlation method and basis set selections were carried out. In this way, the MP2 and CCSD(T) methods together with the (augmented) correlation-consistent polarized [(aug)-cc-pVXZ(-PP for Ag+), X = 2–6, denoted (a)VXZ in the following] bases have been used. For comparison purposes, dispersion-corrected DFT-D3(BJ)50,51 interaction energies have also been evaluated (see ESI†). As result, our best benchmark result for the He–Ag+ interaction was obtained with the CCSD(T) method including extrapolation to the Complete Basis Set Limit (CBS); that for Ag+-benzene with the same method and the aVDZ basis set extended with a set of 3s3p2d1f1g midbond functions (denoted aVDZmb); and in the case of the Ag+-coronene and the Ag+-circumpyrene complexes we resorted to the MP2 method and the aVDZ bases. The latter selection was carried out after observing that for the Ag+-benzene complex, the MP2/aVDZ combination delivered a potential very close to that provided by the CCSD(T)/aVDZmb combination. Previous studies of the Cs2-benzene and the Ag-benzene complexes44,52 have also shown a remarkably good agreement between the MP2 and CCSD(T) approaches when smaller bases are used in MP2 calculations to compensate for over-binding effects due to the neglect of repulsive intermonomer correlation contributions. As shown for the case of the interaction of the silver dimer with coronene (see Fig. 2 of ref. 25), the coupled MP2 method of Heßelmann and Pitonák could also be used to avoid over-binding effects.53,54 The set of 3s3p2d1f1g midbond functions was selected considering benchmark studies previously performed for the evaluation of a considerable number of interaction potentials in weak bonded complexes (see ref. 55 and 56 and references cited therein). The calculations were carried out using the ORCA suite of programs57–59 (version 5.0.1). Further computational details are provided in the ESI.†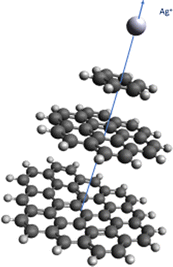 | ||
| Fig. 1 Complexes under investigation. R is defined as the distance between the Ag+ ion and the corresponding molecular center of mass and lies along the plotted axis. | ||
As can be seen in Table 1 and Fig. 2, the strength of the Ag+–coronene interaction differs by less than 3% to that predicted for the Ag+-circumpyrene complex, and hence, the corresponding potential energy curve (see ESI†) was used for the quantum dynamical simulations. For the He–Ag+ complex quantum dynamical calculations, the CCSD(T) interaction energies extrapolated to the CBS limit were used (see ESI†).
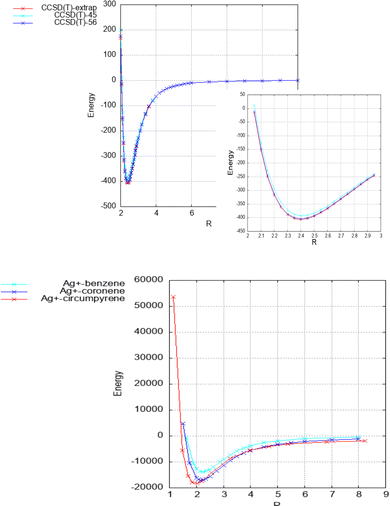 | ||
| Fig. 2 Above: He–Ag+ complex interaction potential, evaluated at the CCSD(T) level and with the set of bases described in the manuscript. Extrapolated CBS-limit results are also displayed. In the inset the area around the minimum is displayed in more detail. Below: Ag+–benzene, – coronene and – circumpyrene interaction potentials, evaluated at the MP2 level with the aVDZmb and aVDZ basis sets. See Fig. 1 for the definition of the intermolecular distance, R in Å, and text for further details. Energies are given in inverse cm. | ||
3. Quantum dynamics in the helium droplet-assisted collision process
In order to follow the superfluid helium nanodroplet-assisted collision dynamics of the silver cation with the target surface, a time-dependent density functional theory formulation (referred to as He-TDDFT) has been used.15,60,61 Due to its large mass, the solvated Ag atom or Ag+ cation (denoted M) can be represented as a classical particle with position rM(t) while the helium solvent was described by a complex effective wavefunction Ψ(r,t) such that ρ(r,t) = |Ψ(r,t)|2. In the given scenario, the helium droplet (composed by 4He atoms) follows the 3D time-dependent equation,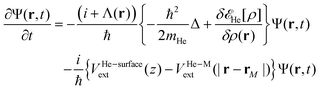 | (2) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) He[ρ] is a modification62 of the Orsay–Trento He-DFT.63 This modification allows the stabilization of the helium density when high 4He density profiles emerge during the dynamics62 due to the very attractive nature of the He–graphene interaction.16 Moreover, the modified backflow term of the Orsay–Trento functional61 has also been included to avoid the rebounding of the metal species upon impact. Hence, it is assumed that the helium droplet behaves as a Bose–Einstein condensate with all 4He atoms occupying the same single-particle wave-function (orbital). The kinetic energy term has the same form as for the case of non-interacting bosonic particles, but accounting for the He–He interaction through a Hartree-like contribution (see, e.g., ref. 64) and an ad hoc correlation density functional term with parameters derived from the properties of superfluid bulk helium. The terms VHe–M and VHe–surfaceext account for the HeN–M and laterally averaged HeN–surface pair potentials,65 assuming thus a sum of inter-atomic pairwise He–surface and He–M interactions. Finally, Λ(r) is a damping function avoiding the artificial reflection of the 4He droplet upon reaching the box boundaries (i.e., ‘absorbing’ the helium wave-function). This equation is coupled to that characterizing the metal atom and cation motions,
He[ρ] is a modification62 of the Orsay–Trento He-DFT.63 This modification allows the stabilization of the helium density when high 4He density profiles emerge during the dynamics62 due to the very attractive nature of the He–graphene interaction.16 Moreover, the modified backflow term of the Orsay–Trento functional61 has also been included to avoid the rebounding of the metal species upon impact. Hence, it is assumed that the helium droplet behaves as a Bose–Einstein condensate with all 4He atoms occupying the same single-particle wave-function (orbital). The kinetic energy term has the same form as for the case of non-interacting bosonic particles, but accounting for the He–He interaction through a Hartree-like contribution (see, e.g., ref. 64) and an ad hoc correlation density functional term with parameters derived from the properties of superfluid bulk helium. The terms VHe–M and VHe–surfaceext account for the HeN–M and laterally averaged HeN–surface pair potentials,65 assuming thus a sum of inter-atomic pairwise He–surface and He–M interactions. Finally, Λ(r) is a damping function avoiding the artificial reflection of the 4He droplet upon reaching the box boundaries (i.e., ‘absorbing’ the helium wave-function). This equation is coupled to that characterizing the metal atom and cation motions,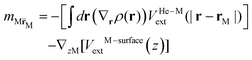 | (3) |
The initial configurations of all M@4HeN (N = 1000 and 2000) complexes are obtained via density functional calculations excluding the droplet–graphene interaction. Since the strength of the He–M interactions are larger than the He–He pair interaction, the Ag and Ag+ species locate at the droplet center. The dynamical simulations start with the M@4He1000 and M@4He2000 mass centers at 30 and 43 Å from the surface, respectively. Following the usual experimental set-ups in deposition processes, the doped droplets are provided with a collective initial velocity towards the surface plane of 200 m s−1. The metal species are provided with the same speed and added in the dynamical process, accounting for the He–graphene and corresponding Ag–graphene (or Ag+–graphene) interactions. Fig. 3 shows two-dimensional (2D) snapshots of the Ag@4He1000 droplet evolution during the first 24 ps (see Multimedia view in the ESI†). The M species motions can be followed in Fig. 4 in terms of the positions and velocity along the surface normal as a function of time.
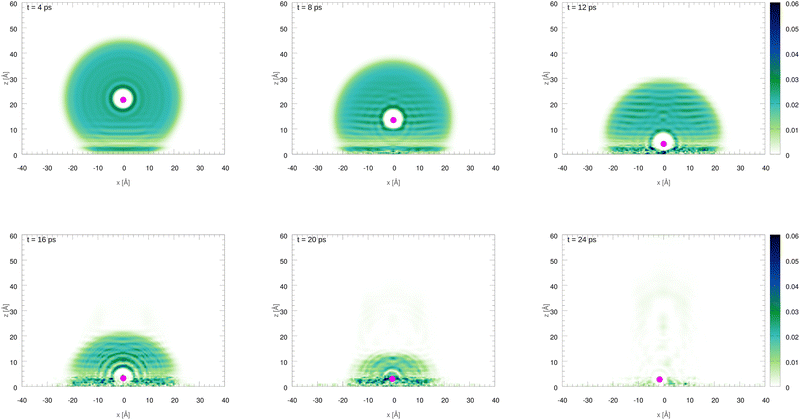 | ||
| Fig. 3 Two-dimensional (2D) snapshots showing the time evolution of the Ag@4He1000 droplet at impact with the graphene surface. The z axis is oriented along the surface normal direction. | ||
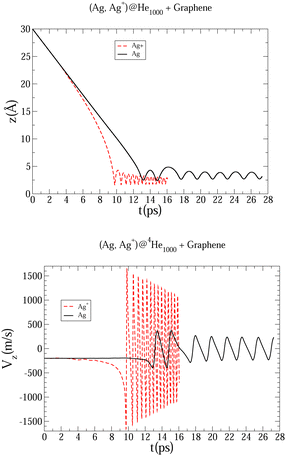 | ||
| Fig. 4 Evolution as a function of time of Ag and Ag+ positions (upper panel), and Ag and Ag+ velocity (bottom panel), considering a host helium droplet made of 1000 4He atoms. | ||
In Fig. 3 an early compression of the 4He droplet can be observed while moving towards the surface during the first 4 ps, which is caused by He–graphene dispersion forces. Due to the attractive He–Ag interaction, the Ag atom adjusts its position to the compressed helium droplet, decoupling from its center of mass, and being next accelerated towards the graphene sheet due to the long-range Ag–graphene dispersion interaction (see bottom panel in Fig. 4). In Fig. 4 (upper panel), note that the Ag atom approaches the potential minimum (at about 3.5 Å) within the graphene surface at around 12.5 ps. The 2D snapshot of this collision in Fig. 3 shows the formation of a high density helium spot below the Ag atom. This solid-like feature pushes the Ag atom back from the surface as can be seen in the panel showing the Ag velocity in Fig. 4. These high density fluctuations are unstable and disappear upon collision with either the metal species or the graphene surface. Yet they play a key role in braking the metal species. Helium density waves travelling back from the surface can also be observed in Fig. 3 as well as the evaporation-like and spreading processes of the helium drop along the surface normal and the graphene plane, respectively. After 12.5 ps, the Ag atom keeps oscillating about the minimum of the Ag–graphene potential. The helium droplet experiences an evaporation-like process each time that the Ag atom impacts with the surface, dissipating its collision energy. The helium layer located in between the Ag atom and the surface also cushions its landing motion, as shown in the snapshot at 20 ps (see Fig. 3). Finally, at 26 ps, the remaining helium droplet evaporates as a whole back from the graphene sheet, with the Ag atom having been trapped in the minimum of the Ag–graphene potential.
The described mechanism of collision energy dissipation of the Ag atom by the helium droplet is essentially the same as found for an immersed Au atom colliding with a TiO2 surface.17 The consideration of a Ag+ ion is much more challenging since the Ag+–surface interaction is much stronger. Thus, it can be observed in Table 1 that the Ag–coronene interaction is around twelve times weaker than the Ag+–coronene interaction. As a result, as can be observed in Fig. 4, the Ag+ cation experiences an earlier (ca. 9.5 vs. 12.5 ps) approach to the minimum of the Ag+–graphene potential. As can be noted in the upper panel Fig. 4, the most apparent difference between Ag and Ag+ motions, however, lies in the much larger amplitude and frequency of the latter. Moreover, due to the much higher velocity of the Ag+ cation (bottom panel of Fig. 4), higher density helium peaks are formed in the closest layers of the Ag+. As in the case of the Ag atom, these solid-like features play an essential role in braking the Ag+ motion towards the graphene sheet, causing its movement back and forth from the surface. As a consequence of these high helium density fluctuations, the amplitudes in the Ag+ motion become reduced as a function of time until the remaining helium droplet fully evaporates at ca. 15 ps (see also Fig. 5). Additionally, we note that the evaporation-like process of the helium droplet is faster when doped with the Ag+ cation than in the case of the Ag atom.
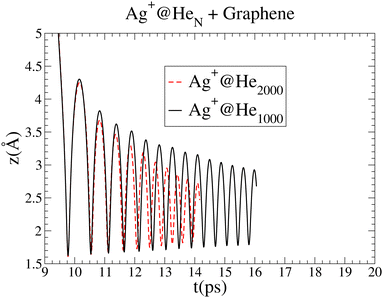 | ||
| Fig. 5 Comparison of the oscillations in the Ag+ cation motion as a function of time for droplets of 1000 and 2000 4He atoms. The graph for Ag+@4He2000 has been shifted by 6.2 ps. | ||
In spite of the major role of high-density fluctuations in the superfluid droplet 4He motion as the strength of the metal–surface interaction increases, it is remarkable that the global picture of the soft-deposition mechanism remains unaltered. The same holds true when the size of the helium droplet hosting the Ag+ ion increases from 1000 to 2000 4He atoms. Fig. 5 shows a comparison of the oscillations in the Ag+ cation motion with time for droplets of 1000 and 2000 4He atoms. The attractive region of the Ag+–graphene potential is naturally reached at a later time as the helium droplet size increases. In this way, for comparison purposes, the graph corresponding to 2000 4He atoms has been shifted by 6.2 ps. The amplitudes of the earliest oscillations are identical in both cases, but for the 4He2000 droplet, their decrease is much more pronounced as a function of time, pointing out that much more energy is being dissipated. In short, larger helium droplets favor the occurrence of soft-deposition.
4. Conclusions
Summarizing, by applying high-level ab initio theory and the quantum He-TDDFT approach, theoretical predictions are presented on the superfluid helium droplet-mediated soft-deposition of neutral and charged metal atomic species onto zero-temperature surfaces, corroborating previous work.17 Yet, due to the increase of the ion–surface interaction forces as compared with the neutral atom-surface case, high helium density fluctuations around the metal species play a much more relevant role in braking the ion upon impact with the solid support. The collision dynamics is thus much more sensitive to quantum effects for immersed charged species and, particularly, hard–core He–He correlation contributions. Classical molecular dynamics (MD) simulations using a renormalized He–He interaction to account for the fluid nature of the helium medium have proved deposition of metal nanoparticles in soft-landing conditions even on surfaces at room-temperature.18 The major role of high-density helium fluctuations for the case of charged species, however, challenges classical MD simulations, even including a renormalization of the He–He interaction,18,68 to deliver the physics of the soft-landing process at low temperature. Path Integral MD Simulations would allow the analysis of the impact of quantization as a function of the doped droplet velocity without an implicit assumption of superfluidity.69 The highly accurate results from full quantum simulations presented in this work provide a benchmark to be used in future MD simulations.The follow-up of our work with MD simulations will be useful in providing time scales for the thermalization of helium droplets on surfaces at room-temperature (RT), ultimately leading to evaporation. If thermalization is faster than soft-deposition, both neutral and charged immersed species would be back scattered. On the one hand, the numerous pieces of experimental evidence accumulated on soft-landing of neutral species on RT surfaces1,3,11,70 and large-scale MD simulations18 indicate that thermalization might be slower than soft-landing itself. On the other hand, proven back scattering of charged species immersed in charged helium droplets and further deposition on a surface orthogonally oriented with respect to the primary one20 call for a much more complex strategy in achieving soft-deposition. In particular, thermalization of the primary surface at the same temperature as the helium droplet could be an effective way to drive rebounding of the doped helium droplet as a whole towards the secondary surface. Moreover, as clearly demonstrated in this work, the enlargement of the helium droplet hosting the charged species would enhance energy dissipation on the collision with the support. Whatever the experimental strategy is, this and previous work17 point in the direction that superfluid helium droplet motion ensures soft-landing of immersed (metal coinage) atomic species independently of charge, droplet size, and chosen (graphene or titanium dioxide) support.71 Furthermore, they also suggest a possible pathway to stabilize single atom catalysts on suitable surfaces.21,49
Author contributions
All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) under grant no. PID2020-117605GB-I00/AEI/10.13039/501100011033. This publication is also based upon work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). We are also greatly thankful for the support of the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01). B. F. acknowledges Xunta de Galicia (grant number ED431C 2021/40) for further financial support. M. Pi acknowledges the Ministerio de Ciencia e Innovación Grant No. PID2020-114626GB-I00 from the MICIN/AEI/10.13039/501100011033. The CESGA supercomputer center (Spain) is acknowledged for having provided the computational resources. We also acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).Notes and references
- V. Mozhayskiy, M. N. Slipchenko, V. K. Adamchuk and A. F. Vilesov, J. Chem. Phys., 2007, 127, 094701 CrossRef PubMed.
- E. Loginov, L. F. Gómez and A. F. Vilesov, J. Phys. Chem. A, 2011, 115, 7199–7204 CrossRef CAS PubMed.
- A. Volk, P. Thaler, M. Koch, E. Fisslthaler, W. Grogger and W. E. Ernst, J. Chem. Phys., 2013, 138, 214312 CrossRef PubMed.
- P. Thaler, A. Volk, F. Lackner, J. Steurer, D. Knez, W. Grogger, F. Hofer and W. E. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155442 CrossRef.
- P. Thaler, A. Volk, M. Ratschek, M. Koch and W. E. Ernst, J. Chem. Phys., 2014, 140, 044326 CrossRef PubMed.
- M. Schnedlitz, R. Fernández-Perea, D. Knez, M. Lasserus, A. Schiffmann, F. Hofer, A. W. Hauser, M. P. de Lara-Castells and W. E. Ernst, J. Phys. Chem. C, 2019, 123, 20037–20043 CrossRef CAS PubMed.
- M. Schnedlitz, D. Knez, M. Lasserus, F. Hofer, R. Fernández-Perea, A. W. Hauser, M. Pilar de Lara-Castells and W. E. Ernst, J. Phys. Chem. C, 2020, 124, 16680–16688 CrossRef CAS PubMed.
- W. E. Ernst and A. W. Hauser, Phys. Chem. Chem. Phys., 2021, 23, 7553–7574 RSC.
- D. Spence, E. Latimer, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Phys. Chem. Chem. Phys., 2014, 16, 6903–6906 RSC.
- E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Nanoletters, 2014, 14, 2902 CrossRef CAS PubMed.
- Q. Wu, C. J. Ridge, S. Zhao, D. Zakharov, J. Cen, X. Tong, E. Connors, D. Su, E. A. Stach, C. M. Lindsay and A. Orlov, J. Phys. Chem. Lett., 2016, 7, 2910–2914 CrossRef CAS PubMed.
- L. Tiefenthaler, J. Ameixa, P. Martini, S. Albertini, L. Ballauf, M. Zankl, M. Goulart, F. Laimer, K. von Haeften, F. Zappa and P. Scheier, Rev. Sci. Instrum., 2020, 91, 033315 CrossRef CAS PubMed.
- S. Kollotzek, O. V. Lushchikova, L. Tiefenthaler, F. Zappa and P. Scheier, Int. J. Mol. Sci., 2022, 23, 3613 CrossRef CAS PubMed.
- O. V. Lushchikova, M. Gatchell, J. Reichegger, S. Kollotzek, F. Zappa, M. Mahmoodi-Darian and P. Scheier, Phys. Chem. Chem. Phys., 2023, 25, 8463–8471 RSC.
- N. F. Aguirre, D. Mateo, A. O. Mitrushchenkov, M. Pi and M. P. de Lara-Castells, J. Chem. Phys., 2012, 136, 124703 CrossRef PubMed.
- M. P. de Lara-Castells, H. Stoll, B. Civalleri, M. Causà, E. Voloshina, A. O. Mitrushchenkov and M. Pi, J. Chem. Phys., 2014, 141, 151102 CrossRef PubMed.
- M. P. de Lara-Castells, N. F. Aguirre, H. Stoll, A. O. Mitrushchenkov, D. Mateo and M. Pi, J. Chem. Phys., 2015, 142, 131101 CrossRef PubMed.
- R. Fernández-Perea, L. F. Gómez, C. Cabrillo, M. Pi, A. O. Mitrushchenkov, A. F. Vilesov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 22248–22257 CrossRef.
- M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759 CrossRef CAS PubMed.
- P. Martini, S. Albertini, F. Laimer, M. Meyer, M. Gatchell, O. Echt, F. Zappa and P. Scheier, Phys. Rev. Lett., 2021, 127, 263401 CrossRef CAS PubMed.
- X. Li, X. I. Pereira-Hernández, Y. Chen, J. Xu, J. Zhao, C.-W. Pao, C.-Y. Fang, J. Zeng, Y. Wang, B. Gates and J. Liu, Nature, 2022, 611(7935), 284–288 CrossRef CAS PubMed.
- K. Pernal, R. Podeszwa, K. Patkowski and K. Szalewicz, Phys. Rev. Lett., 2009, 103, 263201 CrossRef PubMed.
- R. Podeszwa and K. Szalewicz, J. Chem. Phys., 2012, 136, 161102 CrossRef PubMed.
- H. Stoll, J. Chem. Phys., 1992, 97, 8449–8454 CrossRef CAS.
- M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- R. Podeszwa, K. Pernal, K. Patkowski and K. Szalewicz, J. Phys. Chem. Lett., 2010, 1, 550–555 CrossRef CAS.
- K. T. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726–3741 CrossRef CAS.
- A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778–784 CrossRef.
- A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201 CrossRef PubMed.
- A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. Lett., 2016, 7, 4929–4935 CrossRef CAS PubMed.
- A. W. Hauser, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Phys. Chem. C, 2017, 121, 3807–3821 CrossRef CAS.
- M. P. de Lara-Castells, A. W. Hauser, A. O. Mitrushchenkov and R. Fernández-Perea, Phys. Chem. Chem. Phys., 2017, 19, 28621–28629 RSC.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, Phys. Chem. Chem. Phys., 2019, 21, 3423–3430 RSC.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, Mol. Phys., 2019, 117, 1746–1757 CrossRef CAS.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2020, 11, 5081–5086 CrossRef CAS PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, Phys. Chem. Chem. Phys., 2021, 23, 7908–7918 RSC.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, Front. Chem., 2021, 9, 796890 CrossRef PubMed.
- M. P. de Lara-Castells and A. O. Mitrushchenkov, J. Phys. Chem. A, 2015, 119, 11022–11032 CrossRef CAS PubMed.
- R. Dovesi, V. R. Saunderds, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunel, M. Causà and Y. Noël, CRYSTAL14 User's Manual, Universitá Torino, Torino, 2014, https://www.crystal.unito.it Search PubMed.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. Andrae, U. Haüssermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123 CrossRef CAS.
- K. Doll and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 165410 CrossRef.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS.
- J. Granatier, P. Lazar, M. Otyepka and P. Hobza, J. Chem. Theory Comput., 2011, 7, 3743–3755 CrossRef CAS PubMed.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- F. Cargnoni, T. Kuś, M. Mella and R. J. Bartlett, J. Chem. Phys., 2008, 129, 204307 CrossRef PubMed.
- R. Průcha, V. Hrubý, D. Zaoralová, E. Otyepková, V. Šedajová, J. Kolařík, R. Zboril, M. Medved and M. Otyepka, Phys. Chem. Chem. Phys., 2023, 25, 286–296 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comp. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. P. de Lara-Castells, A. W. Hauser and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2017, 8, 4284–4288 CrossRef CAS PubMed.
- A. Heßelmann, J. Chem. Phys., 2008, 128, 144112 CrossRef PubMed.
- M. Pitonák and A. Heßelmann, J. Chem. Theory Comput., 2010, 6, 168 CrossRef PubMed.
- H. Koch, B. Fernández and O. Christiansen, J. Chem. Phys., 1998, 108, 2784–2790 CrossRef CAS.
- C. R. Munteanu, J. L. Cacheiro, B. Fernández and J. Makarewicz, J. Chem. Phys., 2004, 117, 1390–1396 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- D. Mateo, D. Jin, M. Barranco and M. Pi, J. Chem. Phys., 2011, 134, 044507 CrossRef PubMed.
- F. Ancilotto, M. Barranco, F. Coppens, J. Eloranta, N. Halberstadt, A. Hernando, D. Mateo and M. Pi, Int. Rev. Phys. Chem., 2017, 36, 621 Search PubMed.
- F. Ancilotto, M. Barranco, F. Caupin, R. Mayol and M. Pi, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214522 CrossRef.
- F. Dalfovo, A. Lastri, L. Pricaupenko, S. Stringari and J. Treiner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 1193 CrossRef CAS PubMed.
- M. P. de Lara-Castells, D. López-Durán, G. Delgado-Barrio, P. Villarreal, C. Di Paola, F. A. Gianturco and J. Jellinek, Phys. Rev. A, 2005, 71, 033203 CrossRef.
- In order to obtain laterally averaged He-surface and Ag-surface potentials, the interaction energies were calculated for the atom above the “hollow”, “bridge”, and “on top” adsorption sites of the single graphene sheet. Next, the average potential was obtained from these potentials using geometrical (i.e., position density counting) weighting. The Ag+-graphene potential was calculated using molecular models of graphene and considering the “hollow” position only and thus it was not laterally averaged.
- We have also found that the Ag-graphene potential is very similar (to within 7% in the interaction energy and 0.05 Å in the equilibrium Ag-graphene distance) to that estimated for the interaction between silver and amorphous carbon as the sum of pairwise Ag-C pair interactions as reported in ref. 18.
- M. Pi, F. Ancilotto, F. Coppens, N. Halberstadt, A. Hernando, A. Leal, D. Mateo, R. Mayol and M. Barranco, 4He-DFT BCN-TLS: A Computer Package for Simulating Structural Properties and Dynamics of Doped Liquid Helium-4 Systems, see https://github.com/bcntls2016.
- D. Bonhommeau, P. T. L. Jr., C. L. Quiniou, M. Lewerenz and N. Halberstadt, J. Chem. Phys., 2007, 126, 051104 CrossRef CAS PubMed.
- A. Castillo-García, A. W. Hauser, M. P. de Lara-Castells and P. Villarreal, Molecules, 2021, 26, 5783 CrossRef PubMed.
- A. Boatwright, C. Feng, D. Spence, E. Latimer, C. Binns, A. M. Ellis and S. Yang, Faraday Discuss., 2013, 162, 113–124 RSC.
- We have considered atomic gold instead of atomic silver in our simulations. Although the Au-graphene potential is three times more attractive that the Ag-graphene potential, the simulations reveal the same physics in the process, with Au becoming engaged onto graphene after just 12 ps.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details on the calculation of ab initio intermolecular potentials. Multimedia view: movie showing the soft-deposition of atomic silver onto zero-temperature graphene. See DOI: https://doi.org/10.1039/d3cp01303k |
| This journal is © the Owner Societies 2023 |