Open Access Article
Open Access ArticleIntramolecular and intermolecular hole delocalization rules the reducer character of isolated nucleobases and homogeneous single-stranded DNA†
Jesús
Lucia-Tamudo
 *a,
Sergio
Díaz-Tendero
*a,
Sergio
Díaz-Tendero
 *abc and
Juan J.
Nogueira
*abc and
Juan J.
Nogueira
 *ab
*ab
aDepartment of Chemistry, Universidad Autónoma de Madrid, 28049, Madrid, Spain. E-mail: sergio.diaztendero@uam.es; juan.nogueira@uam.es
bInstitute for Advanced Research in Chemistry (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
cCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 9th May 2023
Abstract
The use of DNA strands as nanowires or electrochemical biosensors requires a deep understanding of charge transfer processes along the strand, as well as of the redox properties. These properties are computationally assessed in detail throughout this study. By applying molecular dynamics and hybrid QM/continuum and QM/QM/continuum schemes, the vertical ionization energies, adiabatic ionization energies, vertical attachment energies, one-electron oxidation potentials, and delocalization of the hole generated upon oxidation have been determined for nucleobases in their free form and as part of a pure single-stranded DNA. We show that the reducer ability of the isolated nucleobases is explained by the intramolecular delocalization of the positively charged hole, while the enhancement of the reducer character when going from aqueous solution to the strand correlates very well with the intermolecular hole delocalization. Our simulations suggest that the redox properties of DNA strands can be tuned by playing with the balance between intramolecular and intermolecular charge delocalization.
1. Introduction
DNA is the biomolecule in charge of storing the genetic code that expresses the characteristics of every living organism. For this reason, intense research has been carried out around its structure and functions. Moreover, DNA strands can also be employed for many technological purposes,1 including their use as nanowires,2,3 DNA-templated synthesis for new materials,4 DNA computation,5,6 and molecular detection,7–13 among others. Regarding the latter, DNA-based biosensors are becoming nowadays promising devices in sensor research, where the detection process is usually carried out by optical or electrochemical techniques. In the case of electrochemical DNA-based sensing, the devices are typically composed by an ensemble of single-stranded DNA (ss-DNA) or double-stranded DNA (ds-DNA) anchored to a metallic surface, whose most exploited application relies on the detection of specific sequences of DNA due to its capability of hybridization.7,14,15 However, other applications have been explored using DNA directly as a biosensing tool to detect, for example, heavy metals or organic molecules.8,10,16,17When using DNA as a nanowire or as an electrochemical biosensor, charge transfer processes, in which an electron or a hole is transported along the strand, become extremely relevant. In this context, understanding the redox properties and the charge distribution along the strand are of paramount importance for designing new devices with an effective transmission of the electric current. Nucleobases are the main moiety responsible for the charge transfer process in aqueous phase since the charge is held by the nucleobases of the strand.18,19 In addition, neutral nucleobases are more prone to be oxidized than to be reduced and, as a result, the charge transfer will be usually carried out by a hole rather than by an electron. Consequently, determining the one-electron oxidation potentials of nucleobases is of great importance, but also a very challenging task.20 This property can be understood as the reduction potential of the redox half-equation but in the direction of the oxidation. Many experiments and computational works have been performed in order to obtain accurate values of this property in nucleobases.20–32 Although the predicted oxidation potentials lie in large ranges, the relative order of the reducer character is well-known: G > A > T ∼ C > U. Therefore, guanine is the nucleobase more susceptible to be oxidized and, thus, the one that best hosts the positive charge of the hole.
The generation of a positively charged hole and its subsequent transfer process along a DNA strand is intimately related with the vertical ionization energy (VIE) of the nucleobases. This property is defined as the energy needed to remove an electron from the neutral species, without considering the relaxation of the geometry after the electron detachment. The vertical ionization can be seen as the first stage of the hole transfer process. VIEs for nucleobases have been computed in different media.33–36 It has been observed that the VIE of the isolated nucleobases decreases when going from the gas-phase to the aqueous phase,37 while the opposite is true in DNA strands,38 becoming a controversial issue. After ionization, the system will relax its geometry by going to the minimum of the potential energy surface (PES) of the cationic form. The adiabatic ionization energy (AIE) accounts for this relaxation within the cationic PES. In other words, the AIE is the energy difference between the cationic PES minimum and the neutral PES minimum. This property is closely related to the one-electron oxidation potential, as will be explained in Section 2.
After ionization, the charge could be located within just one nucleotide (nucleobase, essentially) or delocalized over several of them. It has been computationally shown that charge delocalization is suppressed due to the polar environment of the solvent.39 In addition, charge delocalization depends on the nature of the nucleobases and DNA sequence. Thus, theoretical calculations predicted that the charge is localized in just one nucleobase for guanine and cytosine stacks, while it is delocalized over all the nucleobases for adenine and thymine stacks. Moreover, the delocalization pattern is dependent on the number of strands in the helix.40 Therefore, it is clear that charge delocalization after ionization is a complex process that depends on many environmental factors. However, this process needs to be understood in order to get insight not only into the redox properties and reactivity of nucleobases and DNA, but also into the charge transport along DNA strands.41 This process depends on the distance between nucleobases, driving force, electronic coupling (proper π-stacking between nucleobases) and reorganization energy, as stated by the Marcus theory.42–46
Two different mechanisms have been proposed to explain charge transport phenomena along DNA strands: tunnelling and hopping.47–49 The first one is an elementary process where the charge travels along several nucleobases simultaneously.48 This mechanism is strongly dependent on the distance between nucleobases since strong π-stacking interactions are required. On the other hand, the hopping mechanism is a long-range process, in which the charge migrates from one nucleobase to another propagating the hole along the DNA strand. It shows a smoother dependence with the distance between nucleobases, but a stronger influence of the DNA-strand sequence since nucleobases with identical one-electron oxidation potentials are capable of transferring the hole one another even if other nucleobases are interspersed between them. It has been shown that the rate of charge transfer of a hole increases significantly with the number of guanine nucleobases in the strand and decreases with the distance between them.50
In this work, different redox properties, including one-electron oxidation potentials and charge delocalization, have been computationally investigated for the solvated free nucleobases and solvated ss-polyX strands (where X = A, C, G, T), which are represented in Fig. 1. First, we have assessed the validity of our computational models and methods. Then, an analysis of the effect of the environment on the VIEs and one-electron oxidation potentials has been carried out. Finally, the charge delocalization among the atoms of the isolated nucleobases and among several nucleobases of each ss-polyX strand has been studied. We clearly show that there exist a relation between charge delocalization and redox properties.
2. Methods and computational details
In order to model the redox properties of the free nucleobases and single-stranded DNA in water the same computational protocol was applied: conformational sampling achieved by classical or quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations, followed by electronic-structure calculations on ensembles of geometries performed by QM/continuum and QM1/QM2/continuum schemes, which are then used within the Marcus theory framework.The initial geometries for the dynamics of nucleobases in solution were taken from optimized structures by the CAM-B3LYP51 functional and the 6-311G(d)52,53 basis set using the 5.0.3 version of the ORCA package.54 The ss-polyX strands are composed by eight identical nucleobases and were built using the nucleic acid builder (nab) program provided by the AmberTools21 package.55–57 To prevent interactions between the edge nucleobases a protective cap was included for each DNA strand in both the 5′ and 3′ ends: (AG)4 for ss-polyA, (CT)4 for ss-polyC, (GA)4 for ss-polyG and (TC)4 for ss-polyT (see Fig. 1b). Thus, each ss-polyX strand containes 24 nucleotides. Each model was solvated within a truncated octahedron box with a buffer of 20 Å for the case of the free nucleobases and a buffer of 12 Å for the DNA strands using the tleap application also implemented in AmberTools21. The parameters required for the classical MD simulations were taken from the GAFF2,58 bsc159 and TIP3P60 force fields for free nucleobases, DNA and water molecules, respectively. The electrostatic atomic charges for the free nucleobases were taken from CHELPG calculations at CAM-B3LYP/6-311G(d) level of theory.61 The net negative charge of the DNA strands (due to the phosphate groups), was balanced by adding 22 sodium cations, described by the Joung and Cheatham parameters.62
As stated above, the configurational space for the solvated isolated nucleobases and DNA strands was explored by classical MD.63–65 These simulations were performed using the CUDA version of pmemd program implemented in the AMBER20 package.55–57 For all the systems the following protocol was employed. First, a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-steps minimization was carried out, in which the first 5000 steps were driven using the steepest-descent algorithm66 followed by another 5000 steps using the Newton–Raphson algorithm.67 Then, a constant volume (NVT) progressive heating up to 300 K was run for 500 ps. In order to regulate the temperature, the Langevin thermostat was applied with a colision frequency of 2 ps−1. After that, an additional 500 ps simulation was run at a constant temperature of 300 K (NVT ensemble). In a following step, a 1 ns simulation was run in the NPT ensemble to balance the volume of the system and reach the correct density. Finally, a production simulation of 200 ns was run in the NPT ensemble. For all the simulations carried out within the NPT ensemble, the Berendsen barostat with isotropic position scaling and a pressure relaxation time of 2 ps was employed to keep the pressure constant at 1 bar. During the full protocol the particle–mesh Ewald method68 with a grid spacing of 1.0 Å was used to compute the electrostatic interactions and a 10 Å cutoff for the non-bonded interactions was chosen. The SHAKE algorithm69–71 restrained the bonds involving hydrogen atoms and a time step of 2 fs was used during the heating, equilibration and production stages.
000-steps minimization was carried out, in which the first 5000 steps were driven using the steepest-descent algorithm66 followed by another 5000 steps using the Newton–Raphson algorithm.67 Then, a constant volume (NVT) progressive heating up to 300 K was run for 500 ps. In order to regulate the temperature, the Langevin thermostat was applied with a colision frequency of 2 ps−1. After that, an additional 500 ps simulation was run at a constant temperature of 300 K (NVT ensemble). In a following step, a 1 ns simulation was run in the NPT ensemble to balance the volume of the system and reach the correct density. Finally, a production simulation of 200 ns was run in the NPT ensemble. For all the simulations carried out within the NPT ensemble, the Berendsen barostat with isotropic position scaling and a pressure relaxation time of 2 ps was employed to keep the pressure constant at 1 bar. During the full protocol the particle–mesh Ewald method68 with a grid spacing of 1.0 Å was used to compute the electrostatic interactions and a 10 Å cutoff for the non-bonded interactions was chosen. The SHAKE algorithm69–71 restrained the bonds involving hydrogen atoms and a time step of 2 fs was used during the heating, equilibration and production stages.
After running the dynamics, different ensembles of geometries can be selected for performing electronic-structure calculations and obtain the redox properties (see below). In particular, QM/continuum and QM1/QM2/continuum schemes for the isolated nucleobases and DNA single strands, respectively, are employed. In the case of the solvated nucleobases, the QM region is comprised by just the nucleobase. However, in the case of the DNA strands, the size of the QM1 region (number of nucleobases) needed to obtain converged results must be determined. To this end, the VIE and the delocalization number (n), defined as the number of nucleobases involved in the hole delocalization, were computed for 200 equidistantly selected geometries from the classical MD trajectory for the ss-polyG strand. As will be discussed later, the electronic properties are converged for a QM1 region size of three nucleobases.
Once the size of the QM1 region was determined, the reduction free energy is computed for the isolated nucleobases and DNA strands by using the Marcus theory:
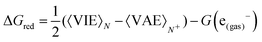 | (1) |
Finally, the last geometry of each of the QM/MM MD simulations was taken to calculate the VIEs and the VAEs of the neutral and cationic trajectories, respectively. In the case of the free nucleobases in aqueous phase, a QM/continuum scheme was applied, where the nucleobases was included in the QM region at the CAM-B3LYP/6-311G(d) level of theory and the solvent was described by the non-equilibrium CPCM continuum solvation model (NECPCM).75,76 In the case of the DNA strands, a QM1/QM2/continuum scheme was applied, where the QM1/QM2 interaction is described by an electrostatic embedding. The VIEs and VAEs are computed for the QM1 region where three nucleobases are described at the CAM-B3LYP/6-311G(d) level of theory. The remaining nucleobases were described by tight-binding DFT (DFTB), in particular with the GFN2-XTB scheme,77 in the QM2 region. Solvent effects were introduced with the ALPB model,78 suitable for XTB. Although the inclusion of water molecules in the QM region could lead to more reliable results, a very large number of water molecules could be needed to obtain converged results,79 making the calculations computationally unfeasible. In addition, previous computational work has shown that the use of implicit solvation provides accurate oxidation potentials for the nucleobases.20 To make the XTB region more affordable computationally, the DNA caps, which were included during the dynamics to avoid self-hybridization, were removed. All these calculations were performed with the ORCA 5.0.3 package.54
The free energy computed by eqn (1) can be related to the one-electron oxidation potential through the following equation:
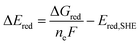 | (2) |
The delocalization of the hole created after ionization was analyzed in terms of the Lödwin charges85 by using homemade scripts. The choice of using the Lödwin charges was motivated by their reduced basis set dependency compared to other methods, for example, the Mulliken scheme. However, for the sake of comparison, the delocalization number for the single strands was also computed using the Mulliken charges and the results were virtually the same and, thus, only the analysis based on the Lödwin charges is discussed below. For the isolated nucleobases (DNA single strands), the delocalization number n is defined here as the number of atoms (nucleobases) among which the positive charge is distributed after ionization. To compute n, we first order the m atoms (nucleobases) by its charge difference between the cationic and neutral forms in increasing order. Thus, the one with the smallest charge difference will correspond to i = 1, the next one to i = 2 and the one with the highest charge will be i = m. Then, we apply the following empirical equation:
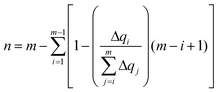 | (3) |
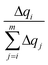 accounts for the contribution to the delocalization of each atom (nucleobase). In addition, the term (m − i + 1) indicates the number of atoms (nucleobases) over which this delocalization contribution will be taken into account. At the end, the total number of atoms (nucleobases) where the charge is delocalized, n, corresponds to the number of considered atoms (nucleobases) m minus the non-contribution to delocalization of each one. If we consider, for instance, the delocalization among three nucleobases in a DNA strand with charges (0.0/0.0/1.0), one obtains n = 1; in the opposite situation where the charge is evenly distributed among the three nucleobases (0.33/0.33/0.33), we get n = 3, i.e., maximum delocalization.
accounts for the contribution to the delocalization of each atom (nucleobase). In addition, the term (m − i + 1) indicates the number of atoms (nucleobases) over which this delocalization contribution will be taken into account. At the end, the total number of atoms (nucleobases) where the charge is delocalized, n, corresponds to the number of considered atoms (nucleobases) m minus the non-contribution to delocalization of each one. If we consider, for instance, the delocalization among three nucleobases in a DNA strand with charges (0.0/0.0/1.0), one obtains n = 1; in the opposite situation where the charge is evenly distributed among the three nucleobases (0.33/0.33/0.33), we get n = 3, i.e., maximum delocalization.
Finally, it is important to mention that static calculations (based on the optimized geometries) of the one-electron oxidation potential for all nucleosides and nucleotides were also carried out to analyze the influence of the phosphate group and the sugar on this redox property. All the neutral and cationic species of these compounds were optimized with the ORCA package using CAM-B3LYP and 6-311G(d) for consistency. Then, the one-electron oxidation potential was determined applying the static direct scheme described in a previous work.20 As can be seen in Table S1 of the ESI,† it has been found that the sugar and the phosphate do not modify the values of the one-electron oxidation potentials and, therefore, they do not have to be included in the QM region when describing DNA strands.
3. Results
3.1 Assessment of the methods
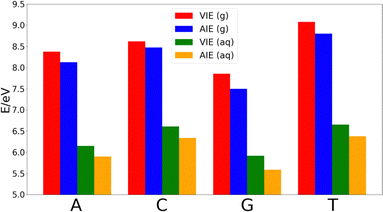
The decrease of the AIE with respect to VIE in each nucleobase is ∼0.25 eV in adenine, thymine and guanine, while cytosine shows a smaller decrease of ∼0.14 eV. Thus, the relative order of the nucleobases in terms of the VIE in the gas-phase is G < A < C < T, while the lower stabilization of cytosine makes that the difference of the AIE between this nucleobase and thymine shortens. However, the relative order of the AIEs remains unaltered with respect to the VIEs.
As Fig. 2 shows, the VIEs and AIEs decrease around 2 eV when going from gas phase to water, remaining unaltered the relative order for adenine, guanine and cytosine in both phases. However, the greater stabilization undergone for thymine due to the solvent leads to similar VIE and AIE values than those of cytosine. When comparing the change in the norm of the dipole moment going from the neutral form to the cationic one, we found Δ|μ| = 0.07 Debye for adenine, 0.09 Debye for cytosine, 0.10 Debye for guanine and 2.29 Debye for thymine. It is important to note that when going from the neutral to the charged species the change of the electrostatic interactions with the solvent is likely more important than the change in the dipole interactions. However, since the electrostatic contribution will be similar for the four nucleobases, the analysis of the change of the dipole moment is important. Moreover, although the dipole moment for charged species is not invariant with respect to the choice of the origin of the coordinate system, the dipole moment difference between the cationic and neutral species can be determined by using the same origin. Since the dipole moment of thymine undergoes a large increase when the nucleobase is ionized, its affinity for water also increases. This large increase in the polar character of thymine might be the responsible for the additional stabilization of this nucleobase with respect to the others. As a result, the relative order in both VIE and AIE is the following: G < A < C ∼ T. This is in good agreement with the previously reported values found in the literature.33–37
Since our methodology consisting of MD simulations followed by hybrid QM/classical calculations provides results for the isolated nucleobases in great agreement with previous works, it is considered valid to also reproduce the redox properties of DNA strands. However, when dealing with strands, several nucleobases must be described in the QM layer. This issue is investigated in the next section.
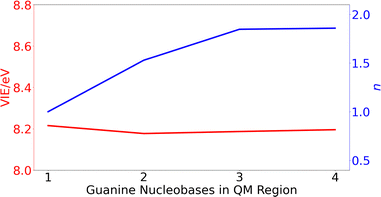 | ||
| Fig. 3 Variation of the vertical ionization energy, VIE, in eV (red) and delocalization number, n, (blue) for ss-polyG as function of the number of guanine nucleobases considered in the QM1 region. | ||
The computed results reveal that the VIE value of ∼ 8.2 eV is barely modified with the increasing number of guanines included in the QM1 region. However, the change on the delocalization number is important. As can be seen, it is necessary to include three nucleobases in the QM1 layer to achieve the converged value of 1.8. Therefore, all the results discussed below for the DNA strands were obtained by including three nucleobases in the QM1 layer. The delocalization number trend in Fig. 3 indicates that it would be desirable to perform calculations with five nucleobases in the QM1 layer to corroborate that its constant behavior when going from three to four nucleobases is maintained also for five nucleobases. However, such as calculations would be computationally very expensive, especially considering that the averaged properties are computed by considering 200 snapshots. However, as will be seen below, the delocalization number for most of the snapshots in lower than 2.5 for all the strands when three nucleobases are included in the QM1 region, indicating that it is not necessary to increase the QM1 region size.
3.2 Vertical ionization energies: isolated nucleobases vs. ss-polyX
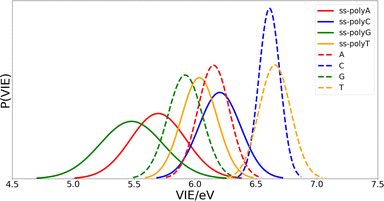
Once the optimal size of the QM1 region has been determined, the electronic properties of the DNA single strands can be computed and compared with those of the isolated nucleobases. The computed distributions of the VIEs for the free nucleobases and ss-polyX systems in aqueous phase are displayed in Fig. 4. Since the VIEs were computed for an ensemble of 200 geometries for each of the investigated systems, and not just for one geometry, one can obtain distributions rather than single values. The width of the distributions highlights the importance of introducing conformational sampling on the theoretical models, especially when describing DNA strands since their distributions are wider than those for the isolated nucleobases. An analogous plot can be found in Fig. S1 of the ESI† for the VAE.One can conclude from Fig. 4 that the reducer character of the nucleobases increases significantly when they form part of a single strand since the VIE is reduced. This means that the interaction between nucleobases favours the detachment of an electron and, therefore, the formation of a positive charge. In addition, the presence of the sugar and the phosphate functional groups could also contribute to this stabilization. However, static calculations of the one-electron oxidation potentials performed for the optimized geometries of nucleosides and nucleotides (see Table S1 of the ESI†) suggest that the contribution of these components is not significant.
Fig. 4 also shows that there exist a switch in the relative order of the VIEs when going from the isolated nucleobases to the ss-polyX. The ss-polyT system presents a smaller VIE than ss-polyC, while the VIE is smaller for the isolated cytosine than for the isolated thymine. In fact, the VIEs of adenine, cytosine and guanine decreases in 0.45 eV, 0.41 eV and 0.44 eV, respectively, when going from free form to ss-polyX, respectively. However, thymine shows a greater decrease on the VIE (0.63 eV), i.e., the cationic form of thymine suffers a larger stabilization with respect to the neutral state when it is found in a ss-DNA strand than the cationic forms of the other nucleobases. This can be related to the fact that thymine has two carbonyl groups, instead of one or zero as the other nucleobases, whose π orbitals could further contribute to the π-stacking interactions between nucleobases and the charge delocalization. This will be further analyzed below.
An analogous analysis for the VAE was also conducted (see Fig. S1 of the ESI†). In this case, the decrease of the VAE from the free form to the ss-DNA strands is smoother: adenine, cytosine, and guanine barely show this decrease (0.07, 0.08 and 0.02 eV, respectively), while thymine is the only nucleobase for which it is significant (0.23 eV). Despite this, the relative order of the VAEs for the free nucleobases and the ss-polyX in aqueous phase follow the same trends than VIE. As a result, both energetic contributions (VIE and VAE) indicate a greater stabilization of thymine from its free form to its ss-polyT system than that of the other nucleobases. Therefore, the energy gap between the neutral and the cationic PESs shortens, especially for thymine, when the nucleobases are disposed in strands.
Regarding the width of the distributions, when the system size increases, the flexibility of the system also increases reaching a larger range of geometries and, thus, presenting a larger dispersion in the values of the property investigated (in this case the VIE). This is the reason behind the larger distribution widths found for the strands than those found for the isolated nucleobases (see Fig. 4). The same explanation holds when comparing guanine and adenine with thymine and cytosine, where the former present larger distribution widths in both isolated and stranded forms than the latter.
3.3 One-electron oxidation potential: isolated nucleobases vs. ss-polyX
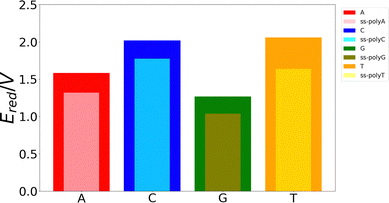
Although the VIE is a reasonable property to measure the ability of a system to be oxidized, it is just an approximate reference. Actually, the process of excitation and relaxation of the geometry within the cationic PES can be considered instantaneous and, therefore, the AIE and the oxidation potential are more reliable properties. The reduction potential of an oxidation process is commonly known as the one-electron oxidation potential, in which this study will focus on the present section. In a previous work, we have evaluated different static and dynamic protocols to determine the most efficient and accurate way to compute redox properties.20 For large systems, it was concluded that combining the Marcus theory with continuum solvation models provides accurate results avoiding large standard deviations and, therefore, the need to use a large number of snapshots in the ensemble average. Thus, as explained above, we have computed the one-electron oxidation potentials by QM/continuum and QM1/QM2/continuum calculations for the isolated nucleobases and DNA strands, respectively, within the Marcus theory where the VIE and the VAE are averaged (see eqn (1) and (2)). The ensemble averages of the oxidation potentials can be seen in Fig. 5.The values of the one-electron oxidation potentials are in agreement with those obtained for the VIEs. Firstly, the reducer character of nucleobases increases when going from solvent to the ss-polyX structure. Interactions with other neighbour residues induces a stabilization of the cationic species with respect to the free nucleobases. Secondly, the relative order of the reducer character remains invariant with respect to the one obtained for the VIEs: G > A > C ∼ T for the case of the isolated nucleobases. Similarly, changes in the one-electron oxidation potentials are also observed when moving from the free nucleobases to the ss-polyX. In particular, thymine suffers a higher increase of its reducer character (decrease of its oxidation potential). It can be seen that, although it was the least prone nucleobase to undergo oxidation in the isolated form, the larger stabilization due to the presence of the other stacked nucleobases leads to a situation in which a thymine strand is a greater reducer than the cytosine one: ss-polyG > ss-polyA > ss-polyT > ss-polyC.
3.4 Intramolecular charge delocalization: isolated nucleobases vs. ss-polyX
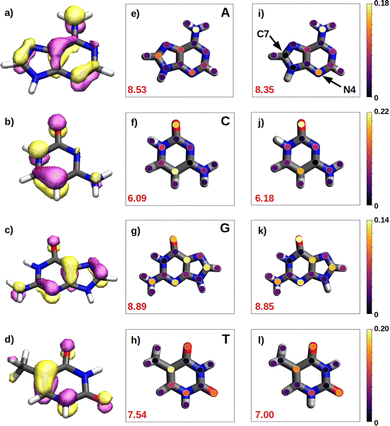
We have seen in the previous sections that the reducer character of isolated nucleobases follows the order G > A > C ∼ T. In the present section, this order will be rationalize based on the hole delocalization among the atoms of the nucleobases. The distribution of the positive charge, created upon oxidation, among the atoms of the nucleobase can provide useful information to understand the reducer character of the nucleobases. Therefore, we have computed the difference of the partial atomic charges between the neutral and cationic forms. These charge differences are plotted in Fig. 6 for the isolated nucleobases and for the nucleobases located in the single strands.A common feature observed for all the isolated nucleobases (see Fig. 6e–h) is that the atoms that hold the greater positive charge are the nitrogen atom of amino functional groups and the oxygen atom of carbonyl functional groups. Contrary, hydrogen atoms barely contribute to the storing of the positive charge. In the case of adenine, a large amount of positive charge is located in the nitrogen atom of the amino group, while the rest is delocalized among the aromatic rings, specifically, in alternated atoms, as expected from the unsaturated character of these structures. This fact can be also seen in the case of guanine, since its aromatic structure is similar to the one of adenine. However, guanine has two functional groups, amino and carbonyl, which compete for holding the positive charge on the nitrogen and oxygen atoms, respectively. The larger electronegative character of oxygen leads to a larger change in the charge on the carbonyl group than on the amino group after oxidation. In the case of pyrimidine nucleobases (cytosine and thymine), the oxygen atom in the carbonyl groups holds the greatest charge difference, closely followed by the carbon atom opposite to each carbonyl group, which surprisingly stores a large amount of positive charge in both cases. The amino group in cytosine is not relevant, opposite to the behaviour found for the purine nucleobases. All these observations are supported by the spatial location of the highest occupied molecular orbital, HOMO, of the nucleobases (see left column in Fig. 6). After oxidation, the positive charge is mainly stored among the atoms whose atomic orbitals contribute to the formation of the HOMO, from which the electron is removed.
As a rule of thumb, the larger the extension of the HOMO, the greater the reducer character. This can be characterized in a more quantitative way by computing the delocalization number, which provides the number of atoms involved in the formation of the hole: 8.89 for guanine, 8.53 for adenine, 7.54 for thymine and 6.09 for cytosine, which qualitatively agrees with the reducer character order of the nucleobases: G > A > C ∼ T. When the positive charge is accommodated among a larger number of atoms the system is stabilized in a greater extend. This explains the higher ability of guanine and adenine to be oxidized over cytosine and thymine. Moreover, as already explained, oxygen atoms in a carbonyl group are more likely to hold a greater positive charge. Thus, as a second rule, the larger the number of carbonyl groups, the greater the reducer character. This explains the predominance of guanine against adenine, and thymine against cytosine with respect to the reducer character.
It is also interesting to compute the intramolecular charge delocalization among the atoms of a single nucleobase when it is embedded in a ss-DNA. This allows us to evaluate the impact of the presence of a DNA environment. The right column of Fig. 6 shows the atomic charge distribution averaged among the three nucleobases considered in the QM1 region. As a general trend, the charge redistribution of the hole does not seem to be significantly affected by the presence of π-stacking interactions between nucleobases. The atoms holding a greater amount of positive charge are essentially the same as for the isolated nucleobases, except for adenine, in which there is a migration of the positive charge from C7 to N4. The most remarkable phenomenon when comparing the free nucleobases with the ss-polyX systems is a slight reduction of the delocalization number, except for cytosine. By analyzing the charge distribution among the atoms, it can be seen that in the strand there is a general trend to store slightly more positive charge on the functional groups, i.e., the amino and carbonyl groups, rather than on the aromatic rings. However, in general, one can conclude that the intramolecular charge distribution remains virtually constant when going from the isolated nucleobase to ss-polyX. Since the charge distribution among the atoms within a nucleobase is barely dependent on the environment, it is likely one of the main factors behind the relative reducer character of the nucleobases.
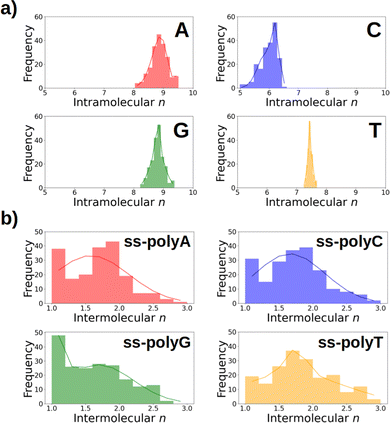
As discussed above, Fig. 6 lists the average delocalization number of the nucleobases in water and in the strand. However, additional insight can be obtained if the probability distribution of the delocalization number is analyzed. This is done in Fig. 7a, where it can be observed that this property presents relatively large oscillations along the dynamics, indicating the importance of performing a good sampling protocol instead of calculations on an arbitrarily chosen geometry. Specifically, the delocalization number oscillates 0.5 units in the case of thymine, 1.0 in guanine, and 1.5 in adenine and cytosine.
3.5 Intermolecular charge delocalization in ss-polyX
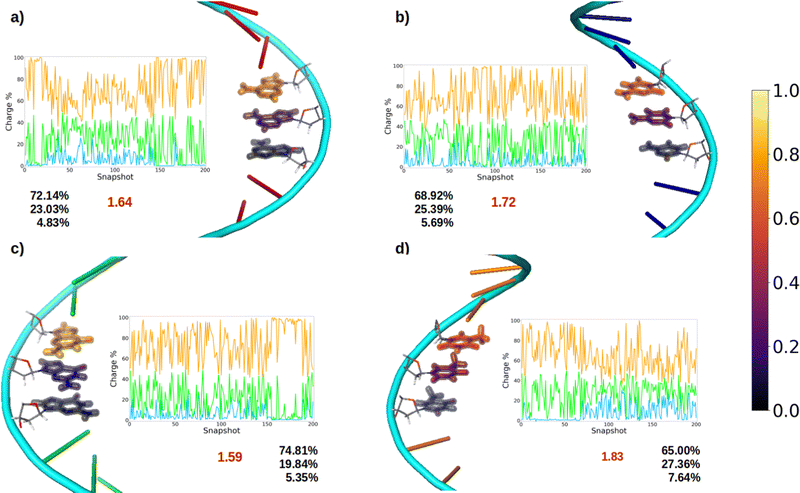
After oxidation of a DNA strand, the positive charge can be delocalized among the atoms of a single nucleobase (intramolecular delocalization), as analyzed in the previous section, but also among the different nucleobases of the strand (intermolecular delocalization). In order to analyze the intermolecular delocalization of the charge along the dynamics, the percentage of positive charge hold by each nucleobase was computed for each of the 200 selected snapshots. Then, in an arbitrary way, the first nucleobase was chosen as the one with largest percentage of charge for each snapshot, while the third one contains the lowest charge, as shown in Fig. 8. This figure also shows the evolution of the positive charge in each nucleobase among the snapshots of the different ensembles. A similar plot for the electron attachment process can be found in Fig. S2 of the ESI.†As a general trend for the four strands, ∼75% of the hole is located on one nucleobase. If one also considers the nucleobase with the second largest positive charge, ∼95% of the hole is taken into account. In this case, the delocalization number indicates the number of nucleobases involved in the hole, which is 1.83 for thymine, 1.72 for cytosine, 1.64 for adenine, and 1.59 for guanine. Therefore, the hole delocalization in single strands is not too large, a fact that supports previous theoretical work, where the positive charge was found to be mainly localized on one guanine in GC sequences.39 In addition, our results suggest that the hole transfer process along ss-polyX strands, formed by the same type of nucleobase, follows a hopping mechanism, in which the hole jumps from one nucleobase to the next one, with some contribution of tunneling, where the hole is delocalized among different nucleobases.
If the distributions of the intermolecular delocalization number are analyzed (see Fig. 7b), it can be seen that there is a significant frequency for low values of n, implying that the positive charge tends to be localized in the strand. This trend is observed in all the strands except ss-polyT, in line with its higher average intermolecular delocalization number compared to the other strands. Similarly, delocalization of the hole over more than two nucleobases is more important for ss-polyT than for the other strands. It is important to mention the broad range of values covered by the distributions of all the strands, highlighting again the importance of running dynamics to have a good sampling of the configurational space.
Finally, it is interesting to correlate the reducer character of the systems with the charge delocalization. As discussed above, the reducer character of the isolated nucleobases nicely correlates with the intramolecular charge delocalization G > A > C ∼ T. In the case of the single strands, the intermolecular charge delocalization is related with the increase of the reducer character when going from the isolated nucleobases to the DNA strands. Specifically, as shown in Fig. 5, the oxidation potential drop when the nucleobase is integrated into the strand is largest for thymine and smallest for guanine, in agreement with the intermolecular delocalization number (1.83 for thymine and 1.59 for guanine). Moreover, as discussed above, the reducer character of thymine is larger than that of cytosine when the nucleobases are embedding in the strand, while the opposite is true when the nucleobases are isolated. Again, this can be explained by the slightly larger intermolecular delocalization found for thymine (1.83) than for cytosine (1.72). Therefore, the reducer character of DNA strands depends on the balance between the intra and intermolecular hole delocalization. This suggests that the reducer ability of DNA can be tuned by modifying the rigidity of the strand. A rigid strand with strong stacking interactions will present a larger intermolecular delocalization. Therefore, it is expected that the redox properties of the nucleobases will suffer stronger modifications when going from solvent to a double strand than to a single strand due to the larger rigidity of the former one.
4. Conclusions
In this study we have computationally investigated the redox properties of isolated nucleobases and DNA single strands (ss-polyX), including VIEs, AIEs, VAEs, one-electron oxidation potentials, and hole delocalization. The electronic properties were computed by hybrid QM/continuum and QM/QM/continuum schemes within the Marcus theory and taking into account conformational sampling by QM/MM MD simulations.Purine nucleobases (adenine and guanine) show a stronger reducer character than pyrimidine ones (cytosine and thymine) in vacuum, solvent and single strands. Specifically, the relative susceptibility of the isolated nucleobases to be oxidized in vacuum is G > A > C > T. When going from vacuum to water, a large stabilization of the cationic form of thymine induces an increase of its reducer character, becoming similar as that of cytosine: G > A > C ∼ T. This stabilization is more pronounced in the DNA single strand, changing the reducer ability order between thymine and cytosine: G > A > T > C. This trend is observed for all the analyzed energetic properties (VIEs, VAEs, AIEs) as well as for the one-electron oxidation potentials. Moreover, the computed VIEs in vacuum are in pretty good agreement with the experimental data, validating the models and the computational methods employed. The VIE computations provided a broad distribution of values, especially for the DNA strands, highlighting the importance of performing conformational sampling when dealing with large systems.
The reducer ability of the different nucleobases correlates well with the intramolecular hole delocalization number, defined as the number of atoms within the nucleobase among which the positive charge upon oxidation is distributed. Purines show a larger delocalization number than pyrimidines. The charge distribution analysis agrees very well with the shape of the HOMO orbital, i.e., the atoms involved in the HOMO orbital are those that host a larger amount of positive charge. The intramolecular charge distribution is barely affected by the environment when going from the aqueous phase to the DNA strand. The most noticeable difference between both environments is a slightly smaller intramolecular delocalization found in the strand.
Finally, the delocalization of the hole along the nucleobases of the strand, named intermolecular delocalization, has also been analyzed. In the four ss-polyX systems, the hole is preferably located between one and two nucleobases. This finding suggests that the hole transfer along the single strands follows a hopping mechanism with some contribution of tunneling. Interestingly, the number of nucleobases involved in the hole delocalization nicely correlates with the increase of the reducer character of the systems when going from the isolated nucleobases to the strands. Specifically, the largest increase of the reducer ability was found for thymine, which presents a intermolecular delocalization number of 1.83, while the smallest increase was observed for guanine, whose intermolecular delocalization is 1.59.
Our results suggest that the redox properties of DNA strands and the charge transfer mechanism can be tuned by modifying the rigidity of the strand. However, this has to be further explored in future works by analyzing the electronic structure of mixed ss-polyXY and ds-DNA models.
Author contributions
J. L. T.: data curation, formal analysis, investigation, methodology, validation, softwate, visualization, writing-original draft, writing-review and editing. S. D. T. and J. J. N.: conceptualization, funding acquisition, project administration, resources, supervision, writing-review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM) and at the Red Española de Supercomputación (RES). This work was partially supported by the MICINN – Spanish Ministry of Science and Innovation – Projects PID2019-110091GB-I00 and PID2020-117806GA-I00 funded by MCIN/AEI/10.13039/501100011033, and the ‘María de Maeztu’ (CEX2018-000805-M) Program for Centers of Excellence in R & D. J. J. N. acknowledge the Comunidad de Madrid for funding through the Attraction of Talent Program (Grant ref 2018-T1/BMD-10261). J. L. T. acknowledges the FPU19/02292 grant from the Spanish Ministry of University.Notes and references
- A. Condon, Nat. Rev. Genet., 2006, 7, 565–575 CrossRef CAS PubMed.
- Y. A. Berlin, A. L. Burin and M. A. Ratner, Superlattices Microstruct., 2000, 28, 241–252 CrossRef CAS.
- C. H. Wohlgamuth, M. A. McWilliams and J. D. Slinker, Anal. Chem., 2013, 85, 8634–8640 CrossRef CAS PubMed.
- R. K. OReilly, A. J. Turberfield and T. R. Wilks, Acc. Chem. Res., 2017, 50, 2496–2509 CrossRef CAS PubMed.
- R. Braich, N. Chelyapov, C. Johnson, P. Rothemund and L. Adleman, Science, 2002, 296, 499–502 CrossRef CAS PubMed.
- X. Xiong, T. Zhu, Y. Zhu, M. Cao, J. Xiao, L. Li, F. Wang, C. Fan and H. Pei, Nat. Mach. Intell., 2022, 4, 1–11 CrossRef.
- J. Zhai, H. Cui and R. Yang, Biotechnol. Adv., 1997, 15, 43–58 CrossRef CAS PubMed.
- M. Saidur, A. A. Aziz and W. Basirun, Biosens. Bioelectron., 2017, 90, 125–139 CrossRef CAS PubMed.
- M. Minunni, S. Tombelli, M. Mascini, A. Bilia, M. C. Bergonzi and F. Vincieri, Talanta, 2005, 65, 578–585 CrossRef CAS PubMed.
- N.-N. Bu, C.-X. Tang, X.-W. He and X.-B. Yin, Chem. Commun., 2011, 47, 7689–7691 RSC.
- A. Liu, K. Wang, S. Weng, Y. Lei, L. Lin, W. Chen, X. Lin and Y. Chen, Trends Anal. Chem., 2012, 37, 101–111 CrossRef CAS.
- Z. Izadi, M. Sheikh-Zeinoddin, A. A. Ensafi and S. Soleimanian-Zad, Biosens. Bioelectron., 2016, 80, 582–589 CrossRef CAS PubMed.
- T. G. Drummond, M. G. Hill and J. K. Barton, Nat. Biotechnol., 2003, 21, 1192–1199 CrossRef CAS PubMed.
- E. Paleček, M. Fojta and F. Jelen, Bioelectrochemistry, 2002, 56, 85–90 CrossRef PubMed.
- S. Zhang, K. Wang, K.-B. Li, W. Shi, W.-P. Jia, X. Chen, T. Sun and D.-M. Han, Biosens. Bioelectron., 2017, 91, 374–379 CrossRef CAS PubMed.
- N. Dai and E. T. Kool, Chem. Soc. Rev., 2011, 40, 5756–5770 RSC.
- C. Zhou, H. Zou, C. Sun, D. Ren, J. Chen and Y. Li, Biosens. Bioelectron., 2018, 117, 678–689 CrossRef CAS PubMed.
- P. T. Kissinger, Biosens. Bioelectron., 2005, 20, 2512–2516 CrossRef CAS PubMed.
- P. Mehrotra, J. Oral Biol. Craniofac. Res., 2016, 6, 153–159 CrossRef PubMed.
- J. Lucia-Tamudo, G. Cárdenas, N. Anguita-Ortiz, S. Díaz-Tendero and J. J. Nogueira, J. Chem. Inf. Model., 2022, 62, 3365–3380 CrossRef CAS PubMed.
- V. DAnnibale, A. N. Nardi, A. Amadei and M. DAbramo, J. Chem. Theory Comput., 2021, 17, 1301–1307 CrossRef CAS PubMed.
- B. T. Psciuk, R. L. Lord, B. H. Munk and H. B. Schlegel, J. Chem. Theory Comput., 2012, 8, 5107–5123 CrossRef CAS PubMed.
- M. Faraggi, F. Broitman, J. B. Trent and M. H. Klapper, J. Phys. Chem., 1996, 100, 14751–14761 CrossRef CAS.
- S. V. Jovanovic and M. G. Simic, J. Phys. Chem., 1986, 90, 974–978 CrossRef CAS.
- C. E. Crespo-Hernández, D. M. Close, L. Gorb and J. Leszczynski, J. Phys. Chem. B, 2007, 111, 5386–5395 CrossRef PubMed.
- C. A. M. Seidel, A. Schulz and M. H. M. Sauer, J. Phys. Chem., 1996, 100, 5541–5553 CrossRef CAS.
- S. Steenken and S. V. Jovanovic, J. Am. Chem. Soc., 1997, 119, 617–618 CrossRef CAS.
- S. Steenken, S. V. Jovanovic, M. Bietti and K. Bernhard, J. Am. Chem. Soc., 2000, 122, 2373–2374 CrossRef CAS.
- J. Wang, S. Yang and Y. Zhang, Chem. Phys. Lett., 2020, 739, 136948 CrossRef CAS.
- Y. Zhang, P. Xie, S. Yang and K. Han, J. Phys. Chem. B, 2019, 123, 1237–1247 CrossRef CAS PubMed.
- Y. Paukku and G. Hill, J. Phys. Chem. A, 2011, 115, 4804–4810 CrossRef CAS PubMed.
- P. Diamantis, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2020, 16, 6690–6701 CrossRef CAS PubMed.
- C. E. Crespo-Hernández, R. Arce, Y. Ishikawa, L. Gorb, J. Leszczynski and D. M. Close, J. Phys. Chem. A, 2004, 108, 6373–6377 CrossRef.
- D. M. Close and K. T. Øhman, J. Phys. Chem. A, 2008, 112, 11207–11212 CrossRef CAS PubMed.
- P. Diamantis, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2019, 15, 2042–2052 CrossRef CAS PubMed.
- P. Slavíček, B. Winter, M. Faubel, S. E. Bradforth and P. Jungwirth, J. Am. Chem. Soc., 2009, 131, 6460–6467 CrossRef PubMed.
- D. Roca-Sanjuán, M. Rubio, M. Merchán and L. Serrano-Andrés, J. Chem. Phys., 2006, 125, 084302 CrossRef PubMed.
- E. Pluhařová, P. Slavíček and P. Jungwirth, Acc. Chem. Res., 2015, 48, 1209–1217 Search PubMed.
- A. A. Voityuk, J. Chem. Phys., 2005, 122, 204904 CrossRef PubMed.
- M. Rooman and R. Wintjens, J. Biomol. Struct. Dyn., 2014, 32, 532–545 CrossRef CAS PubMed.
- E. O’Brien, R. M. B. Silva and J. K. Barton, Isr. J. Chem., 2016, 56, 705–723 CrossRef PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1957, 26, 872–877 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem., 1963, 67, 853–857 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 979–989 CrossRef CAS.
- E. M. Boon and J. K. Barton, Curr. Opin. Struct. Biol., 2002, 12, 320–329 CrossRef CAS PubMed.
- S. Delaney and J. K. Barton, J. Org. Chem., 2003, 68, 6475–6483 CrossRef CAS PubMed.
- M. Fujitsuka and T. Majima, Phys. Chem. Chem. Phys., 2012, 14, 11234–11244 RSC.
- B. Giese, S. Wessely, M. Spormann, U. Lindemann, E. Meggers and M. E. Michel-Beyerle, Angew. Chem., Int. Ed., 1999, 38, 996–998 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, C. Jin, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O’Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2021, University of California, San Francisco, 2021.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr., A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- I. Ivani, P. D. Dans, A. Noy, A. Pérez, I. Faustino, A. Hospital, J. Walther, P. Andrio, R. Goñi and A. Balaceanu, et al. , Nat. Methods, 2016, 13, 55–58 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. of Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- V. Poltev, in Molecular Mechanics: Principles, History, and Current Status, ed. J. Leszczynski, Springer Netherlands, Dordrecht, 2016, pp. 1–48 Search PubMed.
- S. A. Adcock and J. A. McCammon, Chem. Rev., 2006, 106, 1589–1615 CrossRef CAS PubMed.
- E. Braun, J. Gilmer, H. B. Mayes, D. L. Mobley, J. I. Monroe, S. Prasad and D. M. Zuckerman, Living J. Comp. Mol. Sci., 2018, 1, 5957 Search PubMed.
- J. C. Meza, Wiley Interdiscip. Rev.: Comput. Stat., 2010, 2, 719–722 CrossRef.
- A. Galántai, J. Comput. Appl. Math., 2000, 124, 25–44 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- K. D. Hammonds and D. M. Heyes, J. Chem. Phys., 2020, 152, 024114 CrossRef CAS PubMed.
- M. Yoneya, H. J. C. Berendsen and K. Hirasawa, Mol. Simul., 1994, 13, 395–405 CrossRef CAS.
- J. E. Bartmess, J. Phys. Chem., 1994, 98, 6420–6424 CrossRef CAS.
- J. E. Bartmess, J. Phys. Chem., 1995, 99, 6755 CrossRef CAS.
- A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899 CrossRef CAS PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS PubMed.
- L. Pérez-Barcia, G. Cárdenas, J. J. Nogueira and M. Mandado, J. Chem. Inf. Model., 2023, 63, 882–897 CrossRef PubMed.
- D. G. Truhlar, C. J. Cramer, A. Lewis and J. A. Bumpus, J. Chem. Educ., 2004, 81, 596–604 CrossRef.
- D. G. Truhlar, C. J. Cramer, A. Lewis and J. A. Bumpus, J. Chem. Educ., 2007, 84, 934 CrossRef.
- A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899 CrossRef CAS PubMed.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- P.-O. Löwdin and H. Shull, Phys. Rev., 1956, 101, 1730–1739 CrossRef.
- D. Roca-Sanjuán, G. Olaso-González, M. Rubio, P. B. Coto, M. Merchán, N. Ferré, V. Ludwig and L. Serrano-Andrés, Pure Appl. Chem., 2009, 81, 743–754 CrossRef.
- E. Cauët, M. Valiev and J. H. Weare, J. Phys. Chem. B, 2010, 114, 5886–5894 CrossRef PubMed.
- N. Hush and A. S. Cheung, Chem. Phys. Lett., 1975, 34, 11–13 CrossRef CAS.
- G. Lauer, W. Schäfer and A. Schweig, Tetrahedron Lett., 1975, 16, 3939–3942 CrossRef.
- V. Orlov, A. Smirnov and Y. Varshavsky, Tetrahedron Lett., 1976, 17, 4377–4378 CrossRef.
- D. Dougherty, E. Younathan, R. Voll, S. Abdulnur and S. McGlynn, J. Electron Spectrosc. Relat. Phenom., 1978, 13, 379–393 CrossRef CAS.
- A. Padva, T. O’Donnell and P. Lebreton, Chem. Phys. Lett., 1976, 41, 278–282 CrossRef CAS.
- J. Lin, C. Yu, S. Peng, I. Akiyama, K. Li, L. K. Lee and P. R. LeBreton, J. Am. Chem. Soc., 1980, 102, 4627–4631 CrossRef CAS.
- S. Urano, X. Yang and P. R. LeBreton, J. Mol. Struct., 1989, 214, 315–328 CrossRef CAS.
- D. Dougherty and S. P. McGlynn, J. Chem. Phys., 1977, 67, 1289–1290 CrossRef CAS.
- J. Lin, C. Yu, S. Peng, I. Akiyama, K. Li, L. K. Lee and P. R. LeBreton, J. Phys. Chem., 1980, 84, 1006–1012 CrossRef CAS.
- C. Yu, S. Peng, I. Akiyama, J. Lin and P. R. LeBreton, J. Am. Chem. Soc., 1978, 100, 2303–2307 CrossRef CAS.
- D. Dougherty, K. Wittel, J. Meeks and S. P. McGlynn, J. Am. Chem. Soc., 1976, 98, 3815–3820 CrossRef CAS PubMed.
- D. M. Close, J. Phys. Chem. A, 2004, 108, 10376–10379 CrossRef CAS.
- O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Am. Chem. Soc., 2000, 122, 12304–12309 CrossRef CAS.
- O. Dolgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Phys. Chem. A, 2002, 106, 8411–8416 CrossRef CAS.
- D. M. Close, J. Phys. Chem. B, 2003, 107, 864–867 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Redox properties of different components of a nucleotide, vertical atatchment energies for systems under study and intermolecular delocalization for homogenous single-stranded DNA. See DOI: https://doi.org/10.1039/d3cp00884c |
| This journal is © the Owner Societies 2023 |