Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of core-excited ammonia: disentangling fragmentation pathways by complementary spectroscopic methods
Oksana
Travnikova
 a,
Farzad
Hosseini
ab,
Tatiana
Marchenko
a,
Farzad
Hosseini
ab,
Tatiana
Marchenko
 a,
Renaud
Guillemin
a,
Renaud
Guillemin
 a,
Iyas
Ismail
a,
Iyas
Ismail
 a,
Roba
Moussaoui
a,
Loïc
Journel
a,
Roba
Moussaoui
a,
Loïc
Journel
 a,
Aleksandar R.
Milosavljević
a,
Aleksandar R.
Milosavljević
 b,
John D.
Bozek
b,
Edwin
Kukk
ac,
Ralph
Püttner
b,
John D.
Bozek
b,
Edwin
Kukk
ac,
Ralph
Püttner
 d,
Maria Novella
Piancastelli
d,
Maria Novella
Piancastelli
 *ae and
Marc
Simon
*ae and
Marc
Simon
 a
a
aSorbonne Université, CNRS, UMR 7614, Laboratoire de Chimie Physique-Matière et Rayonnement, F-75005 Paris, France
bSynchrotron SOLEIL, L’Orme des Merisiers, Saint-Aubin, F-91192 Gif-sur-Yvette Cedex, France
cDepartment of Physics and Astronomy, University of Turku, FI-20014 Turku, Finland
dFachbereich Physik, Freie Universität Berlin, D-14195 Berlin, Germany
eDepartment of Physics and Astronomy, Uppsala University, SE-751 20 Uppsala, Sweden. E-mail: maria-novella.piancastelli@physics.uu.se
First published on 7th November 2022
Abstract
Fragmentation dynamics of core-excited isolated ammonia molecules is studied by two different and complementary experimental methods, high-resolution resonant Auger spectroscopy and electron energy-selected Auger electron–photoion coincidence spectroscopy (AEPICO). The combined use of these two techniques allows obtaining information on different dissociation patterns, in particular fragmentation before relaxation, often called ultrafast dissociation (UFD), and fragmentation after relaxation. The resonant Auger spectra contain the spectral signature of both molecular and fragment final states, and therefore can provide information on all events occurring during the core-hole lifetime, in particular fragmentation before relaxation. Coincidence measurements allow correlating Auger electrons with ionic fragments from the same molecule, and relating the ionic fragments to specific Auger final electronic states, and yield additional information on which final states are dissociative, and which ionic fragments can be produced in timescales either corresponding to the core-hole lifetime or longer. Furthermore, we show that by the combined use of two complementary experimental techniques we are able to identify more electronic states of the NH2+ fragment with respect to the single one already reported in the literature.
1. Introduction
Core excitation of molecules by monochromatic soft X-rays produces core holes, which are unstable and decay mainly by resonant Auger electron emission on a timescale of a few femtoseconds (fs, 10−15 s).1,2 When the intermediate state reached by promotion of a core electron to an unoccupied orbital is dissociative, a change in geometry possibly leading to a chemical bond breaking can occur, since the time interval between excitation and decay processes (the so-called core-hole lifetime) is long enough for light nuclei/atoms to move from their equilibrium geometry and even to grow apart until they are no longer bound. Therefore, two dynamical processes (electronic relaxation and nuclear motion) are in competition. The process in which a chemical bond is actually broken during core-hole lifetime is labelled ultrafast dissociation (UFD) (see e.g. ref. 3–8) and the resonant Auger electronic decay occurs after dissociation in the ionic fragment (fragmentation before relaxation).In resonant Auger decay, two types of final electronic cationic states are reached; (i) states with one valence hole, when the excited electron participates in the decay process (the so-called participator decay) and (ii) states with two valence holes and one excited electron, when the electron promoted to an empty orbital during excitation remains in the previously unoccupied orbital, one valence electron fills the core hole and another one is emitted (the so-called spectator decay). Some of these final states can in turn be dissociative, and eventually fragment. Thus, fragmentation after relaxation is an alternative dynamical pathway competing with the UFD. However, it should be noted that in this case the core-hole lifetime is no longer a limiting factor for the dissociation timescale of the final states, since the electronic relaxation has already taken place and the molecule is in an electronically well-defined cationic state prior to the possible dissociation (fragmentation after relaxation).
To investigate UFD, one needs to be able to explore the few-femtosecond timescale after core excitation. One way (which will not be considered here) is the use of suitable short-pulse light sources and time-resolved techniques. Another very powerful method is high-resolution electron spectroscopy, because it is possible to use the electronic decay process itself as an “internal clock” to access the ultrashort time domain. This is the basis of the so-called core-hole-clock method.9–11 Such a tool uses the decay time of a core excitation as a reference clock for other processes in the system studied. Typically, the decay of a core excitation yields a spectral signature that is characteristic of a given system. If additional processes are taking place during the core-hole decay, they will also have their own identifiable spectral signature. The core-hole lifetime can then be used as an “internal clock” to study some dynamical phenomena. If UFD is present, the decay takes place in the fragment. However, it should be emphasized that the core-hole clock is a probabilistic rather than deterministic approach, and therefore, even if UFD is present, molecular Auger decay events still occur prior to or during the UFD. The resonant Auger spectrum of the fragment will then be superimposed on the one of the intact molecule, and will be possible to assign.5–8,12,13
While the analysis of a resonant Auger spectrum can provide important information on anything which happens during core-hole lifetime, therefore e.g. on fragmentation before relaxation, the drawback is that by resonant Auger spectroscopy the nature (bound or dissociative) of the molecular final states reached after decay is not straightforward to assess, beside simple arguments on the peak shapes and substructure. In particular, the ionic fragments originating from fragmentation after decay cannot be identified, since the Auger electrons cannot carry information on processes happening after relaxation.
Another powerful technique to study fragmentation processes is electron–ion coincidence spectroscopy. The method of recording Auger electrons in coincidence with ions is called AEPICO (Auger electron–photoion coincidence) spectroscopy.14 Coincidence measurements allow correlating Auger electrons with ionic fragments from the same molecule. The ion detection, typically as a time-of-flight measurement, provides information on all ionic fragments produced, momenta and their correlation, as well as the kinetic energy release during the fragmentation. In addition, a coincidence measurement allows to relate the ionic fragments to specific Auger final electronic states and to study the interplay between electron and ion kinetic energies. Very few articles have been reported so far on ultrafast fragmentation studies through resonant Auger-ion coincidences.15,16 However, typically lower electron energy resolution and lower count rates, required in performing coincidence measurements, do not allow the same level of details on electron side, which can be derived from single-channel high-resolution resonant Auger spectra.
As mentioned, Auger electrons act as an instant probe into the chemical environment that exists at the moment of their emission during the time window of the core-hole lifetime. This information is carried also by the electrons detected in an AEPICO experiment; however, there the typically lower resolution limits our ability to extract it. On the other hand, the properties of the emitted ions do not reflect the electronic and geometrical configuration of the system at a certain moment in time in a similarly direct fashion, since their detected properties (masses, momenta) are largely formed during the entire course of the dissociation process on a much slower timescale than femtoseconds. Consequently, retrieving the initial conditions (such as timing relative to the core-excitation event) of the dissociation requires reconstruction of the entire dissociation dynamics. Therefore, the two methods (high-resolution single-channel resonant Auger spectroscopy and Auger electron–photoion coincidence technique) are complementary and their combined use is very advantageous.
We present here a study on fragmentation dynamics of core-excited isolated ammonia molecules. To achieve a complete overview of the dynamics occurring upon core excitation, in our work we have used both high-resolution resonant Auger spectroscopy and electron energy-selected AEPICO. We have exploited the complementarity of the two methods to obtain information on both different dissociation patterns, fragmentation before relaxation (UFD) and fragmentation after relaxation. While the core-hole clock method has allowed us to investigate ultrafast dissociation on the few-fs timescale, the coincidence measurements have yielded additional information on which final states are dissociative, and which ionic fragments can be produced in timescales either corresponding to the core-hole lifetime or longer.
The chosen showcase molecule is ammonia, NH3, for several reasons. The dynamics of core-excited ammonia has been extensively studied in NH3 molecules either isolated7,17,18 or adsorbed on surfaces.19 It is well known that excitation from the N 1s core level to the LUMO (lowest unoccupied molecular orbital) results in the population of a dissociative intermediate state, with a core-hole lifetime of about 6 fs.7 Previous studies have shown that the fragment produced by ultrafast dissociation and the subsequent decay is NH2+.7,17 However, in the literature there was no indication of how many fragment electronic states are populated in the decay, since there is a substantial overlap with molecular final states which cannot be resolved even with high-resolution measurements.
The main goal of the present work is to derive a complete picture of the dissociation dynamics of core-excited ammonia, both during core-hole lifetime (UFD, fragmentation before decay) or after relaxation by resonant Auger electron emission (fragmentation after decay). Furthermore, on the ground of the coincidence measurements, we can identify other electronic final states of the fragment which in the resonant Auger spectra overlap with some molecular features, but can be singled out more clearly in the AEPICO results. In the earlier work, only one final state of the NH2+ fragment pertaining to the UFD process was described in the literature.7 Our results indicate that UFD is a more efficient process in ammonia than previously reported.
We show that the NH2+ fragment appears also in coincidence events involving some of the molecular final states, therefore indicating fragmentation after relaxation. The dissociation of the NH2+ fragment proceeds until it is stripped of all hydrogens, provided that the energy left in the systems is above the corresponding ion appearance energy. However, exclusively the NH2+ ion is formed in the Auger electron kinetic energy region of the fragment lines, though the appearance of NH+ is energetically allowed.20–22 It can be mentioned that Walsh et al.17 observed NH+ fragment with H+ co-fragment, which however originates from a different minor decay channel, namely double Auger decay,23 leading to dicationic final states. The electron energies, corresponding to the double Auger decay channel, are not covered by the current measurements and cannot be disentangled easily in Auger spectra owing to the energy sharing between the two electrons.
The present results are complementary to those of a recent paper of ours,24 where we published Auger electron–ion coincidence (AEPICO) measurements on core-excited ammonia with a different setup, and showed the Auger–Doppler effect in the emission of ionic fragments deriving from UFD. While the focus of the previous work24 was mainly on the description of the Auger–Doppler effect and partitioning of the internal energy left in the system after dissociation between different degrees of freedom, this work aims at providing a more complete description of the dissociation dynamics in NH3 and disentangling different final states of the NH2+ fragment originating from UFD. We believe that such combined use of complementary spectroscopic methods allows one investigating in unprecedented detail core excitation-relaxation dynamic in isolated molecules. We will present results based on a similar approach in further publications concerning other molecules containing light atoms such as H2O.25
2. Experimental
All experiments were performed on the beamline PLEIADES26 at synchrotron SOLEIL, near Paris, France. PLEIADES uses two insertion devices. One of them is a 256 mm-period electromagnetic undulator for providing photon energies below 100 eV. The second one is an 80 mm-period Apple II type undulator for photon energies above 60 eV. Various light polarizations are available such as horizontal and vertical and tilted (magic angle (∼54.74°)) linear as well as circular and elliptical polarization.The monochromator installed at PLEIADES is a plane grating monochromator (PGM) with varied line spacing (VLS). It has four gratings with varied groove depth (VGD). Three available end-stations include a high-resolution electron spectrometer, an ion beam source crossing the photon beam of the synchrotron, and an electron–ion coincidence setup (EPICEA,27,28) for measuring high-energy electrons in coincidence with ions. The two spectrometers require somewhat different beamline settings and are operated in sequence, not simultaneously.
The high-resolution resonant Auger measurements were performed using a VG-Scienta R4000 hemispherical electron analyzer, which was operated at the pass energy of 20 eV and the entrance slit of 0.8 mm. At these analyzer settings, the achievable electron kinetic energy resolution was estimated to be 40 meV. The beamline monochromator slit was set to 20 microns and a high-flux grating containing 600 lines per mm was used. These beamline parameters resulted in a photon bandwidth of about 56 meV around 400 eV. The measurements were performed using circularly polarised light as it provides the highest flux around N K edge at the PLEIADES beamline. The electron kinetic energy was calibrated using 3a1−1 valence photoelectron line29 as well as 1st and 2nd order of the N 1s photoelectron line of NH3 recorded at the photon energy ∼50 eV above N 1s ionisation threshold. For both high-resolution resonant Auger-electron and coincidence measurements, the exact position of the top of the N 1s−14a1−1 resonance (400.66 eV30) was determined by recording a total ion yield spectrum, which mimics a photoabsorption spectrum, as a function of photon energy just below the N 1s ionization threshold of NH3. The total ion yield measurement was systematically repeated every 2–4 hours to monitor possible drifts in photon energy position using a channeltron detector, installed downstream from the hemispherical electron analyzer and the coincidence setups at the PLEIADES gas-phase end-station. Ammonia gas was introduced to the home-build gas cell at a constant flow and the pressure in the chamber was kept at 2.5 × 10−5 mbar.
The electron–ion coincidence measurements were performed with the EPICEA setup.27,28 The electron analyzer in EPICEA is a home-designed electron spectrometer. The trajectory of electrons through the analyzer consists of two half-toroidal pathways (double toroidal analyser, DTA). An ion time-of-flight (TOF) spectrometer is installed opposite to the DTA to make electron–ion coincidence measurements possible. The DTA was operated at a 180 eV pass energy providing a kinetic energy resolution of ∼1.4 eV and allowing simultaneous detection of electrons in the kinetic energy window of 22 eV. The centre of the kinetic energy window was set to 378 eV. Ammonia gas was introduced as an effusive beam through the needle and the pressure in the chamber was kept at 4.5 × 10−7 mbar. The monochromator slit was set to 5 microns for the measurements performed on top of the N 1s−14a1 resonance in NH3 and was adjusted to keep the electron count rate comparable for the two other photon energies across the resonance (+200 meV and −200 meV detunings).
Ions were detected by Roentdek 80 mm MCP and HEX-anode detector, recording ion flight times (TOFs) and radial hit positions, which were combined into a coincidence dataset together with the electron energy. Combining the ion hit positions on the detector with the deviations in the ion flight times, we could derive 3D momenta for each ion and hence obtain kinetic energy release (KER) for each dissociation event leading to the NH2+ fragment. The ions emitted in all directions (4π) were collected using the pulsed extraction field, which is applied after detection of each electron during a defined time window. In addition, non-coincident “random” triggers for ion extraction were generated during data acquisition and added to the dataset. These “randomly” generated ions create a statistical background, which was used in the analysis for the subtraction of false coincidences from the Auger electron–ion coincidence (PEPICO) maps and KER distributions.
For the coincidence measurements, electron kinetic energy calibration was performed using Ar gas by recording a series of spectra at several photon energy, which were scanned in steps so that Ar 2p lines sweep through the electron kinetic range between 375–395 eV. Ion energy was calibrated by AEPICO measurements on N2.31
3. Results and discussion
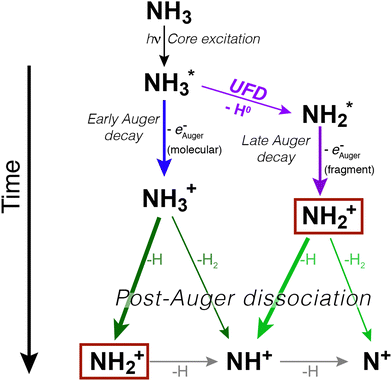
In ammonia, core excitation of an N 1s electron to the 4a1 antibonding molecular orbital populates an intermediate state, which is dissociative and known to undergo UFD. First evidence of the phenomenon was observed by resonant Auger electron spectroscopy in ref. 7. A following study reported the existence of a potential barrier of 0.17 eV at 1.2 Å in the potential energy surface (PES) of core-excited ammonia, meaning that the dissociative region of the PES of the intermediate core-excited state is not reached at the top of the resonance, but at slightly higher photon energy, to overcome such barrier.17In Fig. 1 we show a schematic representation of core excitation, resonant Auger decay and dissociation of ammonia.
We can immediately notice that the NH2+ fragment can be produced by two different pathways. Therefore, one of the challenges of the present work has been to characterize the timescale and the energetics of these two fragmentation processes. In the following we will discuss first the high-resolution resonant Auger spectra, which shed light on events taking place during core-hole lifetime (the “internal clock” mentioned above), and then the electron–ion coincidence measurements, which provide information on the energetics of all fragmentation pathways irrespective of their occurrence before or after electronic relaxation.
3.1 High-resolution resonant Auger spectroscopic analysis
In Fig. 2 we show resonant Auger spectra measured across the N 1s−1 4a1 resonance (400.66 eV). The peaks labelled 3a1−1 and 1e−1 correspond to molecular final states reached either after Auger decay of the core-excited species, or by direct valence photoionization, while the group of sharp peaks starting at 382 eV kinetic energy corresponds to a transition to fragment final states reached after UFD and subsequent Auger decay of the
core-excited species, or by direct valence photoionization, while the group of sharp peaks starting at 382 eV kinetic energy corresponds to a transition to fragment final states reached after UFD and subsequent Auger decay of the  core-excited species.7,17
core-excited species.7,17
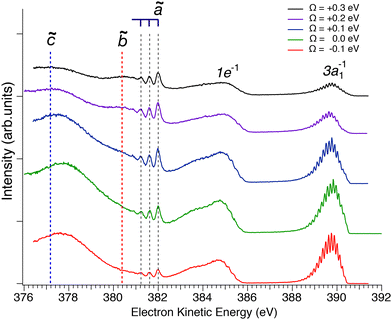 | ||
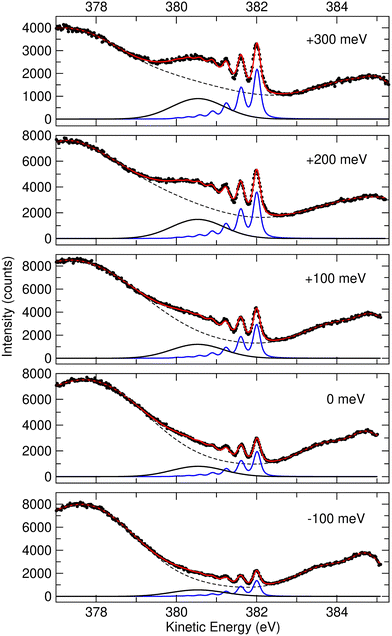
Fig. 2 Resonant Auger spectra taken at several photon energy values across the N 1s−1 4a1 resonance. The different spectra are measured at different values of detuning Ω, which is the difference between the photon energy and the energy corresponding to the highest core-excitation cross section for the N 1s−1 4a1 resonance (400.66 eV). The theoretically expected energy positions for the different Auger transitions in NH2 fragment are also indicated based on the energy differences between the states ã1A1 as well as ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 and 1B1 and ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 of the NH2+ ion with the H–N–H bond angle of 110°, which corresponds to the geometry of the core-excited fragment.32 All spectra are normalized to photon flux and acquisition time. 1A1 of the NH2+ ion with the H–N–H bond angle of 110°, which corresponds to the geometry of the core-excited fragment.32 All spectra are normalized to photon flux and acquisition time. | ||
Sharp fragment lines in Fig. 2 show non-dispersive behaviour with the photon energy, which is a signature of UFD in resonant Auger decay spectra.7 At the same time the spectroscopic feature of the 1e−1 molecular final state, corresponding to the Auger decay in the undissociated ammonia, follows the photon energy detuning across the resonance. The behaviour of the 3a1−1 molecular final state as a function of photon energy can be understood as redistribution in the population of vibrational states which would be a hint that its potential energy surface might be (nearly) parallel to the intermediate N 1s−1 4a1 core-excited state.33 One can notice that the width of the individual peaks within the vibrational progression of the 3a1−1 is significantly narrower from that of the vibrationally resolved ã1A1 state of the NH2+ fragment. This is owing to the contribution of the lifetime broadening (Γ ∼ 120 meV) in Auger decay process occurring in the fragments after UFD, while molecular Auger decay does not include lifetime broadening of core-excited state in resonant Raman conditions.24
Another noticeable observation from Fig. 2 is the appearance of the additional broad feature with the maximum at electron kinetic energy of about 380.5 eV, which was not reported in the previous work by Hjelte et al.7 The cross-section of this feature seems to follow the fragment lines of the ã1A1 state rather than molecular final states 3a1−1 and 1e−1, whose cross-section evidently drops as the photon energy is tuned away from the top of the resonance. In fact, this spectral broad feature at 380.5 eV becomes more apparent at positive detunings >200 meV, where the resonant cross-section decreases and hence molecular Auger decay signal also decreases but the probability of UFD increases owing to the barrier of 170 meV on the potential energy surface of the core-excited ammonia (see above). This suggests that the peak at 380.5 eV may also correspond to another final state of the UFD fragment. To confirm this hypothesis, we have performed a more detailed analysis of the spectra, which is presented in the following discussion.
![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 1B1 final states of the NH2+ fragment.
We performed a very detailed analysis of the spectral region of the fragment peaks by a careful fitting procedure. The results are presented in Fig. 3, which shows the Auger transitions of core-excited
1B1 final states of the NH2+ fragment.
We performed a very detailed analysis of the spectral region of the fragment peaks by a careful fitting procedure. The results are presented in Fig. 3, which shows the Auger transitions of core-excited 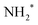 to the states ã1A1 (blue subspectrum) and
to the states ã1A1 (blue subspectrum) and ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 (black subspectrum) of NH2+ measured for different detuning relative to the peak maximum of the N 1s−1 4a1 excitation of NH3. As discussed further below, we conclude from the analysis that the initial state of the transition is (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1), that is the lowest core-excited state of NH2.
1B1 (black subspectrum) of NH2+ measured for different detuning relative to the peak maximum of the N 1s−1 4a1 excitation of NH3. As discussed further below, we conclude from the analysis that the initial state of the transition is (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1), that is the lowest core-excited state of NH2.
In a previous publication7 the most intense narrow lines around 382 eV were assigned, based on the vibrational spacing of ≈400 meV for the symmetric stretching mode, to transitions to the ã1A1 state of NH2+. Calculations predict Auger transitions to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state at about 1 eV lower kinetic energies,34,35 which were not observed in the previous work of Hjelte et al.7 As discussed above, in the present work a broad peak at around 380.5 eV becomes more and more obvious with increasing photon energy. This peak does not show much structure due to a large change of the bond angle upon the Auger transition, as discussed later. Since the Auger rates for the NH2+ fragment are independent from the excitation energy a constant intensity ratio for the transitions to the states ã1A1 and
1B1 state at about 1 eV lower kinetic energies,34,35 which were not observed in the previous work of Hjelte et al.7 As discussed above, in the present work a broad peak at around 380.5 eV becomes more and more obvious with increasing photon energy. This peak does not show much structure due to a large change of the bond angle upon the Auger transition, as discussed later. Since the Auger rates for the NH2+ fragment are independent from the excitation energy a constant intensity ratio for the transitions to the states ã1A1 and ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 of NH2+ is expected. In order to confirm this assumption and, as a consequence, the assignment of the broad peak at 380.5 eV (see black curves in Fig. 3) as transition to the state
1B1 of NH2+ is expected. In order to confirm this assumption and, as a consequence, the assignment of the broad peak at 380.5 eV (see black curves in Fig. 3) as transition to the state ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 of NH2+, we performed a least-squares curve fitting analysis of the present high-resolution spectra recorded at different photon energies in the range of 100 meV below and 300 meV above the peak maximum of the N 1s−1 4a1 resonance.
1B1 of NH2+, we performed a least-squares curve fitting analysis of the present high-resolution spectra recorded at different photon energies in the range of 100 meV below and 300 meV above the peak maximum of the N 1s−1 4a1 resonance.
In this analysis the transitions to the ã1A1 state were described with a Franck–Condon analysis by assuming Morse potentials of the core-excited and the final state. In such an analysis the intensities of the vibrational levels are calculated based on the equilibrium distances Re, vibrational energies ℏω and anharmonicities xℏω of the Morse potentials; for details, see ref. 36. The initial core-excited state 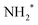 undergoes a transition to the state ã1A1 of NH2+; this Auger transition takes place in the core-excited NH2 fragment, rather than in the NH3 molecule, due to ultrafast dissociation of the N 1s−1 4a1 state of NH3. Because of this, its exact configuration and symmetry is not known. In the analysis we assumed that the initial state is the lowest core-excited state of NH2, namely (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1). The potential-energy surface of this state is not reported in literature, but can be approximated based on the Z + 1 approximation, i.e., it can be approximated with the ground state of water. The values for the ground state of H2O, namely the equilibrium distance Re = 0.958 Å,37 the vibrational energy ℏω = 475.0 meV38 and the anharmonicity xℏω = 5.3 meV38 for the symmetric stretching vibrational mode were used to generate a model potential energy curve for the lowest core-excited state of NH2. As we will show further below, these values lead to consistent results of the fit analysis; this we consider as a strong argument for the assignment of the initial state. Finally, we will use the fit result and the geometry reported in literature for the final state ã1A1 of NH2+ to derive the equilibrium distance of the core-excited NH2 state.
undergoes a transition to the state ã1A1 of NH2+; this Auger transition takes place in the core-excited NH2 fragment, rather than in the NH3 molecule, due to ultrafast dissociation of the N 1s−1 4a1 state of NH3. Because of this, its exact configuration and symmetry is not known. In the analysis we assumed that the initial state is the lowest core-excited state of NH2, namely (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1). The potential-energy surface of this state is not reported in literature, but can be approximated based on the Z + 1 approximation, i.e., it can be approximated with the ground state of water. The values for the ground state of H2O, namely the equilibrium distance Re = 0.958 Å,37 the vibrational energy ℏω = 475.0 meV38 and the anharmonicity xℏω = 5.3 meV38 for the symmetric stretching vibrational mode were used to generate a model potential energy curve for the lowest core-excited state of NH2. As we will show further below, these values lead to consistent results of the fit analysis; this we consider as a strong argument for the assignment of the initial state. Finally, we will use the fit result and the geometry reported in literature for the final state ã1A1 of NH2+ to derive the equilibrium distance of the core-excited NH2 state.
The equilibrium distance, vibrational energy and anharmonicity of the ã1A1 state were free fit parameters. The transition to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state is described with a broad Gaussian, (black subspectra in Fig. 3). The five spectra taken at different photon energies and shown in this figure were fitted simultaneously. As discussed above, we assume that the initial state of the dissociation fragment NH2 is independent from the excitation energy, and thus expect identical Auger spectra for the different excitation energies. In particular, the vibrational progressions of all spectra were described with the same Morse potentials. Moreover, the same Gaussian function was used for the transition to the
1B1 state is described with a broad Gaussian, (black subspectra in Fig. 3). The five spectra taken at different photon energies and shown in this figure were fitted simultaneously. As discussed above, we assume that the initial state of the dissociation fragment NH2 is independent from the excitation energy, and thus expect identical Auger spectra for the different excitation energies. In particular, the vibrational progressions of all spectra were described with the same Morse potentials. Moreover, the same Gaussian function was used for the transition to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state. Finally, the same intensity ratio and energy splitting for the transitions to the ã1A1 and
1B1 state. Finally, the same intensity ratio and energy splitting for the transitions to the ã1A1 and ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 states were used. The only free parameters for the NH2 transitions that were different for the spectra recorded at different photon energies are the total intensities as well as a small shift for the kinetic energy axis to account for different number of counts and small energy calibration uncertainties, respectively. The background indicated by a dashed black line is formed by resonant Auger decay to the spectator final states of molecular NH3 and possible contribution from the
1B1 states were used. The only free parameters for the NH2 transitions that were different for the spectra recorded at different photon energies are the total intensities as well as a small shift for the kinetic energy axis to account for different number of counts and small energy calibration uncertainties, respectively. The background indicated by a dashed black line is formed by resonant Auger decay to the spectator final states of molecular NH3 and possible contribution from the ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 state of the NH2+ fragment. This complex background is described by four Gaussian lineshapes as well as a quadratic function; note that these individual components have no direct physical meaning. Since the shapes of the corresponding resonant Auger transitions may depend on the photon energy, the parameters of the four Gaussian peaks in the spectra recorded at different photon energies are not linked to each other.
1A1 state of the NH2+ fragment. This complex background is described by four Gaussian lineshapes as well as a quadratic function; note that these individual components have no direct physical meaning. Since the shapes of the corresponding resonant Auger transitions may depend on the photon energy, the parameters of the four Gaussian peaks in the spectra recorded at different photon energies are not linked to each other.
The reduced χ2 for the parallel fit of the different spectra amounts to 1.90, which is significantly larger than expected for a set with about 2100 data points if only statistical deviations between the fit result and the data points occur, i.e. the fit model does not describe the physics completely. However, we consider the good agreement between the experimental data and the fit result as well as the obtained value for the reduced χ2 as clear evidence for the fact that our simplifying and restricted fit model describes well the essential physics of the analyzed spectra. Small effect that cause systematic deviations between the fit result and the experimental data and, as a consequence, the reduced χ2 larger than 1, will be discussed further below.
In the following we discuss the results of the fit analysis and start with the vibrational progression. From the fit analysis a vibrational energy of ℏω = 424(5) meV and an anharmonicity of xℏω = 13.5(1.5) meV is obtained for the symmetric stretching mode of the final state. These numbers agree well with the spacings of 390(10) meV for the lower vibrational levels observed by Hjelte et al.7 and used to assign the final state of the Auger transition to ã1A1. This assignment is, however, not unambiguous since the calculated vibrational energies for the symmetric stretching mode of the four lowest states of NH2+ vary between 401.5 meV and 408.5 meV, i.e., are very similar.29 However, from the fit analysis a change in the equilibrium distance upon the Auger decay of ΔRe = +0.081(1) Å is obtained. Using the equilibrium distance of water in the ground state as the value for the initial state of the considered Auger transition, an equilibrium distance Re = 1.039(1) Å for the final state is obtained. This result fits best to the equilibrium distances of the state ã1A1 as obtained in different calculations.34,35,39,40 However, the most convincing argument for the assignment of the vibrational progression to the transition from the (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1) state of NH2 to the ã1A1 state of NH2+ is the absence of bending vibrational levels since the difference of the bond angle of the ground state of H2O (104.52°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37) and the calculated bond angles of the ã1A1 state (108.8°,39 109°,38 108.0°,34 109.2°
37) and the calculated bond angles of the ã1A1 state (108.8°,39 109°,38 108.0°,34 109.2°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35) is very small. For all other final states, the bond angle differs much more from that of the initial state so that long vibrational progressions of the bending mode are expected. Moreover, the bond angles and equilibrium distances of the low-laying excited states of water41 also do not fit to the observed vibrational progression so that other initial states than (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1) can also be excluded.
35) is very small. For all other final states, the bond angle differs much more from that of the initial state so that long vibrational progressions of the bending mode are expected. Moreover, the bond angles and equilibrium distances of the low-laying excited states of water41 also do not fit to the observed vibrational progression so that other initial states than (1a1)1 (2a1)2 (1b2)2 (3a1)2 (1b1)2 (2A1) can also be excluded.
Since we identified in the above-presented analysis the initial and the final states unequivocally, we will use in the following the accurate results for the ã1A1 obtained from rotationally resolved photoelectron spectra35 to get deeper inside in the states involved. In the latter reference an equilibrium distance of 1.051(3) Å is reported. With this value and the change in the equilibrium distance of ΔRe = +0.081(1) Å upon the Auger decay, see above, we derive an equilibrium distance of 0.970(4) Å for the lowest core-excited state of NH2; this value is only slightly larger than for that for the Z + 1 molecule water, see above. The experimental bond angle of 109.12(27)°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 are also in excellent agreement with the different calculated results discussed above.
35 are also in excellent agreement with the different calculated results discussed above.
Willitsch et al.35 derived a spacing of 377.3(3) meV between the v′ = 0 and the v′ = 1 states. From our fit approach based on Morse potentials we obtain a splitting of ℏω − 2xℏω = 397(8) meV, which is significantly larger than the value given by Willitsch et al. Note that in our fit analysis the entire vibrational progression presented by the blue subspectra in Fig. 3 are described by the three parameters of ℏω, xℏω, and ΔRe, i.e. the fit is highly restricted. A different analysis that considers only the positions of the first two peaks result in a splitting of 383(4) meV between the vibrational levels v′ = 0 and 1, which agrees reasonably well with the value given by Willitsch et al.
This result shows clearly that our fit approach based on Morse potentials has small deficiencies, which explain the reduced χ2 of 1.90. Amongst the possible reasons for these deficiencies is a not fully correct description of the background or the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state. It is also possible that the potential energy curves of the core-excited NH2 state or the ã1A1 final state of NH2+ do not exactly match the empirical Morse potential. However, the highly restricted fit approach based on Morse potentials has two advantages, so that it makes sense to utilize it in the present data analysis. First, one obtains, based on a small number of parameters, a physically meaningful vibrational progression; in this way one can separate different contributions to the spectra. Second, this approach allows to derive geometrical changes upon electronic transitions.
1B1 state. It is also possible that the potential energy curves of the core-excited NH2 state or the ã1A1 final state of NH2+ do not exactly match the empirical Morse potential. However, the highly restricted fit approach based on Morse potentials has two advantages, so that it makes sense to utilize it in the present data analysis. First, one obtains, based on a small number of parameters, a physically meaningful vibrational progression; in this way one can separate different contributions to the spectra. Second, this approach allows to derive geometrical changes upon electronic transitions.
From the fit analysis we can also conclude that higher vibrational levels of the initial core-excited state are practically not populated since the observed Poisson-like intensity distribution of the vibrational progression is typical for a transition starting at the vibrational ground state v′′ = 0. This agrees with the conclusions also derived in our previous work.24 Indications for the populations of higher vibrational levels in the initial state are expected at higher kinetic energies, namely at ≅382.5 eV for v′′ = 1 and ≅383 eV for v′′ = 2; obviously such lines are absent in the spectrum.
In the analysis, the lines of the vibrational progression were described with Lorentzian lineshapes to account for the lifetime broadening Γ. Since the lifetime broadening of core-excited NH2 is not known, we applied Γ = 120 meV, which is the average of the N 1σg−1 and N 1σu−1 levels of N2. These lineshapes were convoluted with a Gaussian to describe the experimental resolution and the Doppler broadening due to the dissociation of NH3.24 The width of the Gaussian function was a free parameter and resulted in ΔE = 130(5) meV. This Gaussian contains three contributions, namely a photon bandwidth of 56 meV, an electron analyzer contribution of 40 meV, and a Doppler broadening ΔEDoppler of 110(8) meV (FWHM) mainly caused by the velocity of the NH2 fragment due to UFD. Using the equation ΔEDoppler [eV] = (2.48 × 1021) pz [kg m s−1] with pz being the momentum of the NH2 fragment along the detection direction of the Auger electron,24 one obtains momenta between −2.2(2) × 10−23 and +2.2(2) × 10−23 kg m s−1; these values agree well with those observed in Auger electron–ion coincidence measurements.24
Finally, we shortly address the transition to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state of NH2+, which is described with a broad Gaussian function. The equilibrium distance of this state amounts Re ≅ 1.03 Å and the bond angle α ≅ 160°.34,39,40 The large difference in the bond angle of the initial and the final state of the transition leads to a long progression of the bending mode and justifies the Gaussian function used in the fit analysis for this transition.
1B1 state of NH2+, which is described with a broad Gaussian function. The equilibrium distance of this state amounts Re ≅ 1.03 Å and the bond angle α ≅ 160°.34,39,40 The large difference in the bond angle of the initial and the final state of the transition leads to a long progression of the bending mode and justifies the Gaussian function used in the fit analysis for this transition.
3.2 Energy-selected Auger electron–ion coincidence results
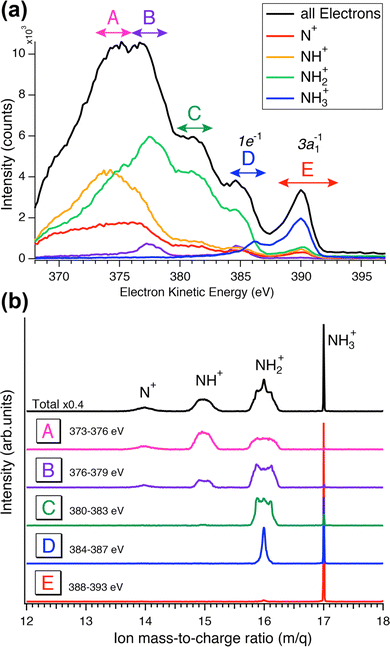
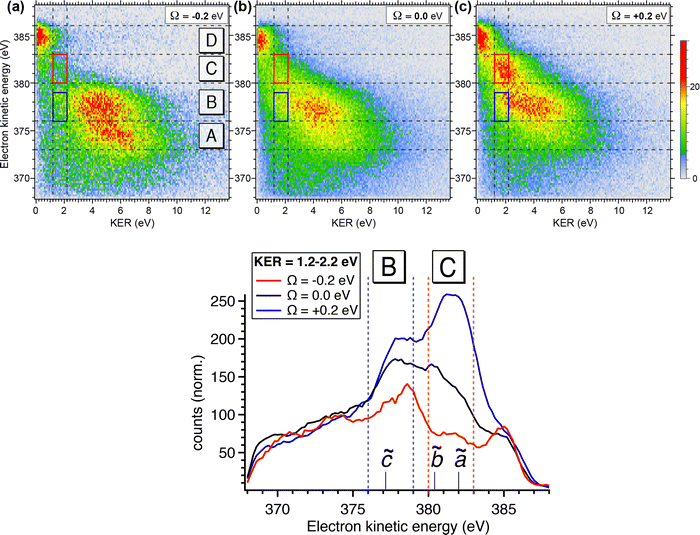
While the careful fits of the high-resolution resonant Auger spectra allow us assigning the two lowest-lying final states of the NH2+ ion, which is produced via the UFD process, the analysis of the coincidence data measured by the EPICEA setup provides complementary information on all ions emitted and their connection with specific electronic final states. An overview is presented in Fig. 4, in which an Auger decay spectrum (in black) recorded for the photon energy detuning of +200 meV from the top of the resonance is sliced into a series of Auger spectra (in colors) in coincidence with one of the ion fragments. The chosen photon energy corresponds to the value where the maximum amount of UFD is expected, due to the above-mentioned potential barrier.The different ions were detected in coincidence with the Auger electrons across the whole kinetic energy range from 367 to 389 eV and their time-of-flight mass spectrum is shown in black in Fig. 4(b). Much more detailed information can be extracted by selecting subsets of coincidence events where either the electron energy falls into a certain range, or a certain fragment ion is produced. The coloured curves in Fig. 4(a) show the spectra of Auger electrons associated to the production of either N+, NH+, NH2+ or NH3+ ions. Correspondingly, the coloured spectra in panel (b) show the ion spectra that resulted when the electron energy was filtered by the energy windows A–E (defined in Fig. 4(a)).
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 final states of UFD (see previous section). There only the NH2+ fragment is present. Another region, where solely the NH2+ fragment is observed, is region D, which corresponds to the 1e−1 molecular final state. However, the presence of the NH2+ fragment there means that the fragmentation takes place after the Auger relaxation, and not before as is the case of region C as it is explained further below. In general, this overview is a clear indication of the existence of several fragmentation processes leading to the same ion fragment but with different mechanisms and different timescales.
1B1 final states of UFD (see previous section). There only the NH2+ fragment is present. Another region, where solely the NH2+ fragment is observed, is region D, which corresponds to the 1e−1 molecular final state. However, the presence of the NH2+ fragment there means that the fragmentation takes place after the Auger relaxation, and not before as is the case of region C as it is explained further below. In general, this overview is a clear indication of the existence of several fragmentation processes leading to the same ion fragment but with different mechanisms and different timescales.
In NH3 core excitation, most of the input energy is released as kinetic energy of Auger electrons and the remaining energy can be consumed as appearance energy for ion fragments plus their kinetic energy release (KER) as follows, according to the Born–Haber cycle:
| Eph − EAuger = (IE + Ediss) + EKER = AE + EKER |
Although the relationship between KER distributions and electron kinetic energy will be explored in detail later using all three components of the ion's momentum (px, py and pz), the ion time-of-flight (TOF) spectra, which reflect only the pz component of the ion momenta, in Fig. 4 panel (b) already give the first insight into these dependencies. The peak shapes in the TOF spectra are strongly affected by the initial momentum of the ion, namely its component along the spectrometer's axis (pz). As the momentum increases, the peak broadens and can eventually split into two components. A narrow width of the TOF peaks indicates that the measured ions have a very small kinetic energy. This is the case for the NH3+ peak in all five regions, which is expected since it is the parent ion that does not receive any momentum from the KER of the dissociation. As for the NH2+ fragment ion peak shapes from E to A regions, we observe that this peak becomes broader, which means more energetic ions. Such general behaviour – beginning with little kinetic energy at and close to the ion's appearance energy, and then displaying increasing KER as the available internal energy increases (the Auger electron's energy decreases) – is commonly observed in AEPICO type of experiments.14
Furthermore, the NH2+ peak in region E, from 388 to 393 eV which corresponds to the 8 to 13 eV binding energies, is extremely weak. In this region we see mostly the NH3+ ion, indicating that the final electronic state 3a1−1 is very little or not at all dissociative, being below the appearance energy of NH2+. The appearance energy for NH2+ is reported at 15.75 eV by Qi et al.20 Note that an appearance energy is derived relative to the used photon energy of 400.86 eV, i.e., NH2+ should be visible below 400.86 − 15.75 eV = 385.11 eV, in good agreement with the findings in Fig. 4a.
The TOF spectrum (blue) for ions in coincidence with electrons in the electron kinetic energy region D, from 384 to 387 eV, shows a narrow peak for NH2+ and the NH3+ peak is still present but with lower intensity compared to region E. Here, we have less energetic Auger electrons, and thus more energy is available in the system which leads to the dissociation of the NH3+ molecular ion. Note that the appearance energy of NH2+ at ≈385.1 eV, see above, is located close to the center of region D. This agrees well with the observation in Fig. 4(a) that above this energy mainly NH3+ fragments (blue line) are formed while below this value the NH2+ fragment (green line) is dominant. In the next region, C, the broader component in the shape of the NH2+ peak provides a direct additional confirmation of its origin from UFD. In the next two regions, A and B, other fragments, NH+ and N+, are observed with their appearance energies of 16.9 eV21 and 22.6 eV,22 respectively. More in detail, for NH+, and consequently for N+, we observe two onsets, because there are two possible fragmentation processes, concerted and sequential loss of the two hydrogens, with different appearance energies, namely 16.9 eV for the simultaneous breaking of the two N–H bonds and H2 formation,21 and 21.4 eV for the N–H bond breaking in two steps (Ediss(H2) = 4.5 eV42).
![[c with combining tilde]](https://www.rsc.org/images/entities/b_char_0063_0303.gif) 1A1 final state of the NH2+ fragment.
In the following discussion, we will concentrate on the NH2+ fragment, because as stated above it can be produced by different pathways, which the combined use of both techniques has allowed us disentangling. In particular, we will focus on the manifestations of the third
1A1 final state of the NH2+ fragment.
In the following discussion, we will concentrate on the NH2+ fragment, because as stated above it can be produced by different pathways, which the combined use of both techniques has allowed us disentangling. In particular, we will focus on the manifestations of the third ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 final state of the NH2+ fragment produced via UFD, which is observed in our coincidence data and which was not experimentally observed previously in the literature.
1A1 final state of the NH2+ fragment produced via UFD, which is observed in our coincidence data and which was not experimentally observed previously in the literature.
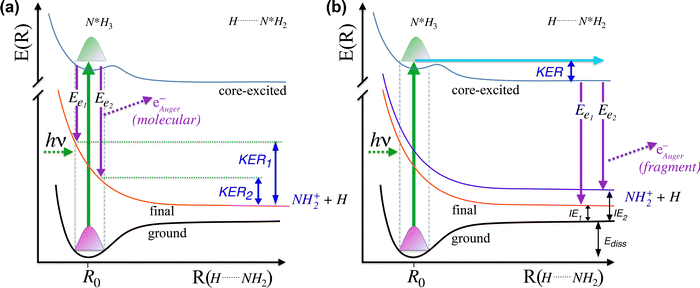
In Fig. 5 we show a schematic view of the potential energy curves along the reaction coordinate and the energetics of such different processes.
In particular, in Fig. 5(a) we show where early Auger decays occur in 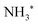 molecules and in (b) where late Auger decays take place in the
molecules and in (b) where late Auger decays take place in the 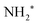 fragments following UFD. In the case of the Auger decay in the molecule, different EAuger and KER of the fragments can be expected depending on the shapes of the NH3+ PESs, which the system reaches after the decay. The emission of Auger electrons with high kinetic energy results in low or nearly zero KER in NH2+ fragments, corresponding to its appearance energy. On the other hand, less energetic Auger electrons can be emitted resulting in a larger KER after the dissociation. These two cases are shown schematically in Fig. 5(a). In general, the KER for molecular decay is a product of energy release due to dynamics in the core-excited state and dissociation in the final state. Hence, KER for molecular decay is largely determined by the potential energy surfaces of the final states, in contrast to the KER in the case of UFD, see Fig. 5(b) where it is determined solely by dissociation occurring in the core-excited state. In Fig. 5(b) two cases are shown schematically where two different NH2+ final states are reached giving rise to two different electron kinetic energies, while the KER in the fragments from which they were emitted is the same for both states.
fragments following UFD. In the case of the Auger decay in the molecule, different EAuger and KER of the fragments can be expected depending on the shapes of the NH3+ PESs, which the system reaches after the decay. The emission of Auger electrons with high kinetic energy results in low or nearly zero KER in NH2+ fragments, corresponding to its appearance energy. On the other hand, less energetic Auger electrons can be emitted resulting in a larger KER after the dissociation. These two cases are shown schematically in Fig. 5(a). In general, the KER for molecular decay is a product of energy release due to dynamics in the core-excited state and dissociation in the final state. Hence, KER for molecular decay is largely determined by the potential energy surfaces of the final states, in contrast to the KER in the case of UFD, see Fig. 5(b) where it is determined solely by dissociation occurring in the core-excited state. In Fig. 5(b) two cases are shown schematically where two different NH2+ final states are reached giving rise to two different electron kinetic energies, while the KER in the fragments from which they were emitted is the same for both states.
To obtain more detailed information, we correlate the kinetic energy of the NH2+ fragment to the kinetic energy of emitted Auger electrons and we show in Fig. 6 (top) the result as 2D energy maps for the range of electron kinetic energy between 368 eV to 388 eV. We show electron–ion correlation maps for three different photon energies across the N 1s → 4a1 resonance, and namely +200 meV, on-top (Ω = 0 eV; 400.66 eV) and −200 meV. The maps are normalized to the total number of counts and therefore reflect the number of possible dissociation pathways, or in other words their probability. The maps show well separated and distinguishable islands for different kinetic energy ranges of electrons and ions.
Looking at region C, the UFD region, which is delimited by a red box on each map, we observe a visible change in the efficiency of the UFD in this region as a function of the photon energy. The presence of the barrier on the core-excited 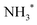 PES around the resonance would influence this efficiency. Thus, by detuning positively, we would expect higher dissociation rates owing to overcoming the potential energy barrier, which is in line with our results.
PES around the resonance would influence this efficiency. Thus, by detuning positively, we would expect higher dissociation rates owing to overcoming the potential energy barrier, which is in line with our results.
Fig. 6 (top) manifests also similar behaviour in a lower electron kinetic energy region, B, delimited by a blue box on each map. Region B is also affected by the detuning of the photon energy around the top of the resonance. These low-energy NH2+ ions in correlation with less energetic resonant Auger final states are interesting because they might be also fragments resulting from UFD. This hypothesis is based on the photon energy dependence of these cationic states as well as their KER similar to the ones obtained for the region C, see also Fig. 5(b).
The region D corresponds to the 1e−1 molecular final state. From the coincidence data reported in Fig. 4, it is evident that the NH2+ fragment is produced there. However, at variance with regions B and C, region D seems to be less sensitive to the change in photon energy, and its intensity does not peak at +200 meV detuning, but rather at the top of the resonance, indicating that UFD does not play a role, and the fragmentation takes place after the resonant Auger decay. Note that the low KER values are due to the Auger energies just below the appearance energy of NH2+ at ≈385.1 eV, see above.
The decrease of intensity in region A with increasing photon energy can be explained by taking into account the way the 2D maps are constructed. In particular, the normalization by the total number of counts implies that the number of counts is proportional to the number of possible dissociation pathways. At lower photon energy the production of NH2+ is concentrated in the low electron kinetic energy regions A and B, with relatively high KER; these processes are mainly due to molecular Auger decay. Across the resonance there are more dissociation pathways open, and therefore the intensity is spread over a larger electron kinetic energy range.
In Fig. 6 (bottom), we show electron kinetic energy spectra for ion KER distributions only between 1.2 to 2.2 eV corresponding to the red and blue boxes from the maps in Fig. 6(a). We clearly see from these spectra the photon energy dependence of these two regions, while for electrons having their energies above and below these regions the intensity of electron emissions does not change considerably as a function of the photon energy. In the electron kinetic energy region B the transition to the ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 in the NH2+ fragment is, indeed, expected at the geometry of the core-excited N*H2 (H–N–H bond angle ∼110°).32 Similarly to the
1A1 in the NH2+ fragment is, indeed, expected at the geometry of the core-excited N*H2 (H–N–H bond angle ∼110°).32 Similarly to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state,
1B1 state, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 state of NH2+ is linear at the equilibrium geometry. Therefore, extensive excitations of the bending vibrational mode are expected for the cationic final state. This results in the broad spectral profile in the resonant Auger electron spectra, similarly to the
1A1 state of NH2+ is linear at the equilibrium geometry. Therefore, extensive excitations of the bending vibrational mode are expected for the cationic final state. This results in the broad spectral profile in the resonant Auger electron spectra, similarly to the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state, which makes its identification in high-resolution single-channel electron spectroscopy measurements extremely difficult (or impossible).
1B1 state, which makes its identification in high-resolution single-channel electron spectroscopy measurements extremely difficult (or impossible).
To confirm the results shown in the 2D maps, integrated KER distributions for the different Auger energy regions are reported in Fig. 7. In region C we can clearly identify the main dissociation channel as appearing in the marked KER interval, corresponding to UFD, and with a maximum at the photon energy corresponding to +200 meV detuning. In region D the channel for the formation of the NH2+ ion just opens and the KER peaks are visible at low values owing to zero or little access energy left in the system after dissociation. Here, the trend as a function of photon energy (maximum at the top of the resonance) is consistent with early Auger decay and fragmentation after relaxation. In region A the KER peaks at higher values, and the trend again confirms the presence of early Auger decay and fragmentation after relaxation. The excess energy in region A amounts to about 10 eV after dissociation to NH2+. However, the maximum KER is observed at lower values (∼5.7 eV). This can be explained as the “leak” of the available energy into different degrees of freedom in the molecular NH2+ fragment.24
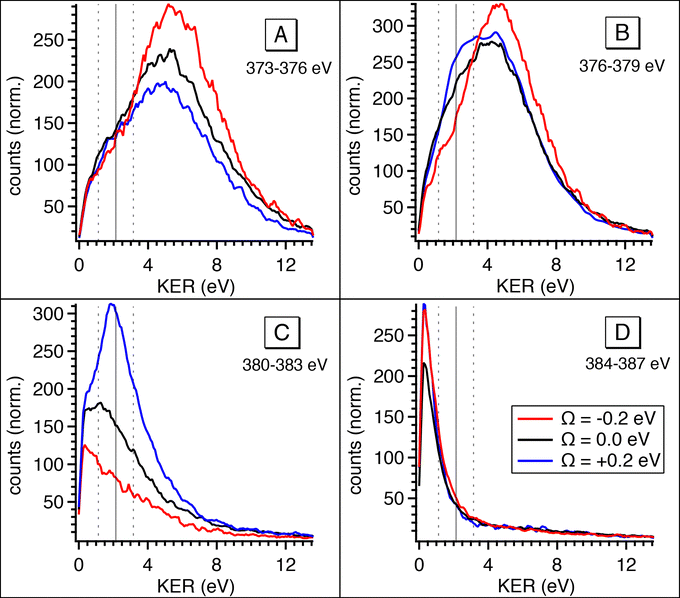 | ||
| Fig. 7 Integrated kinetic energy release distributions extracted from the 2D maps (Fig. 6) for electron kinetic energy regions A, B, C, D. The colours of the curves correspond to different photon energies at which the coincidence data was recorded: Ω = −200 meV (red), on top of the resonance (black), Ω = +200 meV (blue). | ||
The situation is more complex for region B, where we can identify two main contributions: in the KER interval corresponding to UFD, i.e. around 2 eV, we see a shoulder, which increases with photon energy. This trend is analogous to the one in region C and a sign for ultrafast dissociation. At higher KER the trend is similar to region A and suggests fragmentation after early Auger decay. From these findings we can confirm that in region B two dissociation pathways coexist, i.e. fragmentation before and after Auger decay.
From the coincidence data we can obtain a rough estimate of the contributions of the late Auger decays occurring in the UFD fragment, which appear in regions B and C. Areas in the 2D electron–ion energy correlation maps in Fig. 6 (top) for KER of 2.2 ± 1 eV, which corresponds to KER of ions produced via the UFD process, and Auger electron energies between 376–383 eV (B and C regions) amount to 10(1)%, 14(1)% and 20(1)% from all coincidence events producing NH2+ ion for −200, 0 and +200 meV detunings, respectively. And NH2+ ion yields 54% of all the ions, as extracted from the total TOF in Fig. 4b. However, this estimate does not represent UFD efficiency as our AEPICO measurements cover only a part of resonant Auger final states and, markedly, UFD efficiency is photon energy dependent.
4. Conclusion
We report here a detailed study on fragmentation dynamics of core-excited ammonia molecules. We have used two complementary methods, and namely high-resolution resonant Auger spectroscopy and electron-energy-selected Auger electron–photoion coincidence (AEPICO) spectroscopy. By exploiting such complementarity, a complete overview of all possible dissociation patterns is achieved. In particular, we are able to disentangle different dissociation patterns with different timescales, i.e. fragmentation before relaxation (UFD) and fragmentation after relaxation. The resonant Auger results are interpreted on the ground of the core-hole-clock method and allow investigating ultrafast dissociation on the few-fs timescale. A fit analysis of the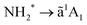 transition also provides detailed information on the potential energy surfaces of the states involved in the decay process. In turn, the coincidence measurements provide additional information on all final states which are dissociative, and which ionic fragments can be produced in timescales either corresponding to the core-hole lifetime or longer. In particular, we show that for the NH2+ ionic fragment we are able to disentangle dissociation patterns occurring either before or after Auger decay. Furthermore, while the ã1A1 electronic state of NH2+ was already described in the literature, we are able to identify two additional cationic states, the
transition also provides detailed information on the potential energy surfaces of the states involved in the decay process. In turn, the coincidence measurements provide additional information on all final states which are dissociative, and which ionic fragments can be produced in timescales either corresponding to the core-hole lifetime or longer. In particular, we show that for the NH2+ ionic fragment we are able to disentangle dissociation patterns occurring either before or after Auger decay. Furthermore, while the ã1A1 electronic state of NH2+ was already described in the literature, we are able to identify two additional cationic states, the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 and the
1B1 and the ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 ones, of the NH2+ fragment reached by late Auger decays in the already dissociated core-excited NH3 molecule. Therefore, the combined use of the two techniques gives a detailed picture of all dissociation events and their interplay with electronic relaxation subsequent to core excitation.
1A1 ones, of the NH2+ fragment reached by late Auger decays in the already dissociated core-excited NH3 molecule. Therefore, the combined use of the two techniques gives a detailed picture of all dissociation events and their interplay with electronic relaxation subsequent to core excitation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge SOLEIL Synchrotron in France for time on the PLEIADES beamline under Proposals No. 20171496 and 20201704. We are grateful to SOLEIL staff, in particular to C. Nicolas, for smoothly running the facility. O. T. acknowledges financial support from the French Agence Nationale de la Recherche (ANR) through the MUSTACHE project (ANR-18-CE30-0015).References
- M. Simon, L. Journel, R. Guillemin, W. C. Stolte, I. Minkov, F. Gel’mukhanov, P. Sałek, H. Ågren, S. Carniato, R. Taïeb, A. C. Hudson and D. W. Lindle, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 020706(R) CrossRef.
- T. Marchenko, L. Journel, T. Marin, R. Guillemin, S. Carniato, M. Žitnik, M. Kavčič, K. Bučar, A. Mihelič, J. Hoszowska, W. Cao and M. Simon, J. Chem. Phys., 2011, 134, 144308 CrossRef CAS PubMed.
- P. Morin and I. Nenner, Phys. Rev. Lett., 1986, 56, 1913 CrossRef CAS.
- O. Björneholm, S. Sundin, S. Svensson, R. R. T. Marinho, A. Naves de Brito, F. Gel’mukhanov and H. Ågren, Phys. Rev. Lett., 1997, 79, 3150 CrossRef.
- O. Björneholm, et al. , Phys. Rev. Lett., 2000, 84, 2826 CrossRef.
- I. Hjelte, M. N. Piancastelli, R. F. Fink, O. Björneholm, M. Bässler, R. Feifel, A. Giertz, H. Wang, K. Wiesner, A. Ausmees, C. Miron, S. L. Sorensen and S. Svensson, Chem. Phys. Lett., 2001, 334, 151 CrossRef CAS.
- I. Hjelte, M. N. Piancastelli, C. M. Jansson, K. Wiesner, O. Björneholm, M. Bässler, S. L. Sorensen and S. Svensson, Chem. Phys. Lett., 2003, 370, 781 CrossRef CAS.
- O. Travnikova, V. Kimberg, R. Flammini, X.-J. Liu, M. Patanen, C. Nicolas, S. Svensson and C. Miron, J. Phys. Chem. Lett., 2013, 4, 2361 CrossRef CAS.
- O. Björneholm, A. Nilsson, A. Sandell, B. Hernnäs and N. Mårtensson, Phys. Rev. Lett., 1992, 68, 1892 CrossRef.
- O. Björneholm, S. Sundin, S. Svensson, R. R. T. Marinho, A. Naves de Brito, F. Gel’mukhanov and H. Ågren, Phys. Rev. Lett., 1997, 79, 3150 CrossRef.
- P. A. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703 CrossRef.
- R. Feifel, F. Burmeister, P. Sałek, M. N. Piancastelli, M. Bässler, S. L. Sorensen, C. Miron, H. Wang, I. Hjelte, O. Björneholm, A. Naves de Brito, F. Gel’mukhanov, H. Ågren and S. Svensson, Phys. Rev. Lett., 2000, 85, 3133 CrossRef CAS PubMed.
- L. Rosenqvist, K. Wiesner, A. Naves de Brito, M. Bässler, A. Ausmees, R. Feifel, I. Hjelte, S. L. Sorensen, C. Miron, H. Wang, M. N. Piancastelli, S. Svensson and O. Björneholm, J. Chem. Phys., 2001, 115, 3614 CrossRef CAS.
- E. Kukk, G. Prümper, R. Sankari, M. Hoshino, C. Makochekanwa, M. Kitajima, H. Tanaka, H. Yoshida, Y. Tamenori, E. Rachlew and K. Ueda, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, 3677 CrossRef CAS , and references therein.
- K. Le Guen, C. Miron, D. Céolin, R. Guillemin, N. Leclercq, M. Simon, P. Morin, A. Mocellin, O. Björneholm, A. Naves de Brito and S. L. Sorensen, J. Chem. Phys., 2007, 127, 114315 CrossRef CAS.
- H. Sann, T. Havermeier, C. Müller, H.-K. Kim, F. Trinter, M. Waitz, J. Voigtsberger, F. Sturm, T. Bauer, R. Wallauer, D. Schneider, M. Weller, C. Goihl, J. Tross, K. Cole, J. Wu, M. S. Schöffler, H. Schmidt-Böcking, T. Jahnke, M. Simon and R. Dörner, Phys. Rev. Lett., 2016, 117, 243002 CrossRef CAS PubMed.
- N. Walsh, A. Sankari, J. Laksman, T. Andersson, S. Oghbaie, F. Afaneh, E. P. Månsson, M. Gisselbrecht and S. L. Sorensen, Phys. Chem. Chem. Phys., 2015, 17, 18944 RSC.
- A. Lindgren, M. Gisselbrecht, F. Burmeister, A. Naves de Brito, A. Kivimäki and S. L. Sorensen, J. Chem. Phys., 2005, 122, 114306 CrossRef.
- M. Nagasono, K. Mase, S. Tanaka and T. Urisu, Surf. Sci., 1997, 390, 102 CrossRef CAS.
- F. Qi, L. Sheng, Y. Zhang, S. Yu and W.-K. Li, Chem. Phys. Lett., 1995, 234, 450 CrossRef CAS.
- R. Locht, Ch Servais, M. Ligot, M. Davister and J. Momigny, Chem. Phys., 1988, 125, 425 CrossRef CAS.
- R. I. Reed and W. Snedden, J. Chem. Soc. (Resumed), 1959, 4132 CAS.
- L. Journel, R. Guillemin, A. Haouas, P. Lablanquie, F. Penent, J. Palaudoux, L. Andric, M. Simon, D. Céolin, T. Kaneyasu, J. Viefhaus, M. Braune, W. B. Li, C. Elkharrat, F. Catoire, J.-C. Houver and D. Dowek, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 042710 CrossRef.
- O. Travnikova, E. Kukk, F. Hosseini, S. Granroth, E. Itälä, T. Marchenko, R. Guillemin, I. Ismail, R. Moussaoui, L. Journel, J. D. Bozek, R. Püttner, P. Krasnov, V. Kimberg, F. Gel’mukhanov, M. N. Piancastelli and M. Simon, Phys. Chem. Chem. Phys., 2022, 24, 5842 RSC.
- O. Travnikova, et al., to be published.
- https://www.synchrotron-soleil.fr/Recherche/LignesLumiere/PLEIADES .
- D. Céolin, C. Miron, M. Simon and P. Morin, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 171 CrossRef.
- C. Miron, M. Simon, N. Leclercq and P. Morin, Rev. Sci. Instrum., 1997, 68, 3728 CrossRef CAS.
- D. Edvardsson, P. Baltzer, L. Karlsson, B. Wannberg, D. M. P. Holland, D. A. Shaw and E. E. Rennie, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2583 CrossRef CAS.
- J. Schirmer, A. B. Trofimov, K. J. Randall, J. Feldhaus, A. M. Bradshaw, Y. Ma, C. T. Chen and F. Sette, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1136 CrossRef CAS.
- H. Iwayama, T. Kaneyasu, Y. Hikosaka and E. Shigemasa, J. Chem. Phys., 2016, 145, 7 CrossRef PubMed.
- S. D. Peyerimhoff and R. J. Buenker, Chem. Phys., 1979, 42, 167 CrossRef CAS; S. Y. Chu, A. K. Q. Siu and E. F. Hayes, J. Am. Chem. Soc., 1972, 94, 2969 CrossRef.
- O. Travnikova, C. Miron, M. Bässler, R. Feifel, M. Piancastelli, S. Sorensen and S. Svensson, J. Electron Spectrosc. Relat. Phenom., 2009, 174, 100 CrossRef CAS.
- J. C. Stephens, Y. Yamaguchi, C. D. Sherrill and H. F. Schaefer III, J. Phys. Chem. A, 1998, 102, 3999 CrossRef CAS.
- S. Willitsch, J. M. Dyke and F. Merkt, Mol. Phys., 2004, 102, 1543 CrossRef CAS.
- R. Püttner, I. Dominguez, T. J. Morgan, C. Cisneros, R. F. Fink, E. Rotenberg, T. Warwick, M. Domke, G. Kaindl and A. S. Schlachter, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 3415 CrossRef.
- A. R. Hoy and P. R. Bunker, J. Mol. Spectrosc., 1979, 74, 1 CrossRef CAS.
- D. F. Smith Jr. and J. Overend, Spectrochim. Acta, Part A, 1972, 28, 471 CrossRef.
- G. Osmann, P. R. Bunker, P. Jensen and W. P. Kraemer, J. Mol. Spectrosc., 1997, 186, 319 CrossRef CAS PubMed.
- S. J. Dunlavey, J. M. Dyke, N. Jonathan and A. Morris, Mol. Phys., 1980, 39, 1121 CrossRef CAS.
- C. R. Claydon, G. A. Segal and H. S. Taylor, J. Chem. Phys., 1971, 54, 3799 CrossRef CAS.
- B. P. Stoicheff, Can. J. Phys., 2001, 79, 165 CrossRef CAS.
| This journal is © the Owner Societies 2023 |