Open Access Article
Open Access ArticleHow fast do defects migrate in halide perovskites: insights from on-the-fly machine-learned force fields†
Mike
Pols
 ,
Victor
Brouwers
,
Sofía
Calero
,
Victor
Brouwers
,
Sofía
Calero
 and
Shuxia
Tao
and
Shuxia
Tao
 *
*
Materials Simulation & Modelling, Department of Applied Physics, Eindhoven University of Technology, Eindhoven 5600 MB, The Netherlands. E-mail: s.x.tao@tue.nl
First published on 22nd March 2023
Abstract
The migration of defects plays an important role in the stability of halide perovskites. It is challenging to study defect migration with experiments or conventional computer simulations. The former lacks an atomic-scale resolution and the latter suffers from short simulation times or a lack of accuracy. Here, we demonstrate that machine-learned force fields, trained with an on-the-fly active learning scheme against accurate density functional theory calculations, allow us to probe the differences in the dynamical behaviour of halide interstitials and halide vacancies in two closely related compositions CsPbI3 and CsPbBr3. We find that interstitials migrate faster than vacancies, due to the shorter migration paths of interstitials. Both types of defects migrate faster in CsPbI3 than in CsPbBr3. We attribute this to the less compact packing of the ions in CsPbI3, which results in a larger motion of the ions and thus more frequent defect migration jumps.
Despite the rapid developments of halide perovskite optoelectronic devices,1,2 the poor stability of the material remains a major obstacle for large scale applications. These stability problems include material decomposition,3 halide segregation4 and ion accumulation at interfaces,5 all of which involve the migration of point defects. In experiments, the motion of ions and defects can be probed directly through impedance spectroscopy6 or indirectly through changes in optoelectronic properties, i.e. the band gap.7 Although experiments provide valuable information on the macroscopic behaviour, the identification of their microscopic properties is challenging. Various computational studies have provided microscopic insights into the defects, such as the type and concentration of defects in halide perovskites,8 defect migration9 and defect-induced degradation at perovskite grain boundaries.10 However, the too high computational cost of ab initio methods and the limited accuracy of empirical force fields has prevented conventional computational methods from studying the subtle effects of the defect type and changes in composition on the defect migration rates, which remain an unclear and debated subject.11–15
Machine-learned force fields (MLFFs) have emerged as an attractive computational method to investigate the dynamics of complex materials at an accuracy that is close to ab initio methods.16,17 MLFFs typically require an extensive amount of reference data in the training set, making their construction non-trivial and laborious. As a result of this, on-the-fly learning schemes, that generate training sets with minimal human intervention have become popular.18–20 During an on-the-fly training, high-error atomic configurations, identified by Bayesian uncertainty predictions, are continuously added to the training set during a molecular dynamics (MD) run with the current best model. This scheme has proven to be robust and accurate for studying the lattice dynamics of halide perovskites, including phase transitions and cation rotations,21,22 but their application to complex defect processes in perovskites has not yet been explored.
In this work, we employ on-the-fly trained MLFFs to investigate defect migration in halide perovskites. From extensive testing, we conclude that the transferability of MLFFs can not be assumed, and a high accuracy can only be achieved if it is explicitly trained against the exact defect type and chemical composition of interest. Using CsPbX3 (X = I/Br) as model systems, we demonstrate that MLFFs can probe the effects of the defect type (interstitial or vacancy) and perovskite composition (CsPbI3 or CsPbBr3) on the dynamical behaviour of these defects. From an analysis of the MD simulations, we connect the differences in the diffusion rates to the typical motion of the ions in the lattice.
We use the FLARE++ package19,20 to train sparse Gaussian process (SGP) models using the multielement atomic cluster expansion23 to map the local atomic environments. Whenever the Bayesian error estimate of the model exceeds a threshold, a density functional theory (DFT) calculation at the generalized gradient approximation (GGA) level is performed in VASP24–26 and its energies, forces and stresses are added to the training set and the model is retrained. To increase the efficiency with which the models can be evaluated, the MLFF predictions are mapped onto low-dimensional polynomial models after training according to the procedure outlined by Xie et al.27 The accuracy of the resulting models is then assessed by comparing their atomic force and total energy predictions with those from DFT calculations. Subsequently, the mapped models are used in large-scale MD simulations with LAMMPS.28 A description of the theory of SGP models and computational settings of the DFT calculations and large-scale MD simulations can be found in Note 1 (ESI†).
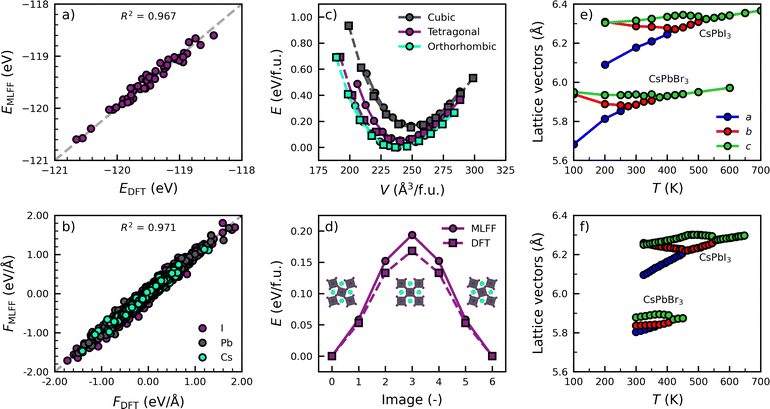
We start by training two models for both perovskite compositions, i.e. CsPbI3 and CsPbBr3, to describe the characteristic phase transitions between the various photoactive phases (cubic, tetragonal and orthorhombic).29,30 To efficiently sample configurations in each phase, we train from a high to low temperatures, resulting in the inclusion of 163, 62, 472 local environments in the training set for Cs, Pb and I, respectively. The full details of the model training and validation can be found in Note 2 (ESI†). To check the accuracy of the models, we compare the energies and force components of the CsPbI3 model with those from DFT calculations in Fig. 1a and b. We evaluate 50 equally spaced frames from a simulation of at 700 K and atmospheric pressure. The high values of the coefficient of determination, R2 = 0.967 and R2 = 0.971, for the parity of the energies and forces, respectively, illustrate the high accuracy of the models. This is further confirmed by the low mean absolute errors (MAEs) in the energies (1.8 meV per atom) and forces (0.044 eV Å−1), comparable to those for various materials in literature.18,20,21
In addition, our models accurately replicate two important properties relevant to its phase behaviour in Fig. 1c and d. Specifically, the model accurately predicts the relative energies of the different perovskite phases, the orthorhombic phase as the most stable, followed by the tetragonal and cubic phase. Furthermore, a good agreement is found between the model and DFT calculations in tetragonal CsPbI3 for the bulk modulus (B0,MLFF = 18.3 GPa; B0,DFT = 14.2 GPa) and the inversion barrier of PbI6 octahedra (ΔEMLFF = 0.19 eV; ΔEDFT = 0.17 eV), of which more details are found in Note 2 (ESI†). Finally, we use the models to simulate the phase transitions of CsPbI3 and CsPbBr3. In Fig. 1e and f, we monitor the evolution of the lattice parameters as a function of the temperature and compare them with experiments.29,30 The details of the simulations are found in Note 3 (ESI†). The comparison shows an excellent qualitative agreement. Not only do the models correctly predict the order in which the phases occur, they also correctly describe that CsPbBr3 has phase transitions at lower temperatures than CsPbI3.29,30 We note that the models slightly underpredict the experimental phase transition temperatures (<100 K), which we attribute to a slight overprediction of the lattice volume by our models of about 3% for CsPbI3 and 4% for CsPbBr3 compared to experiments.
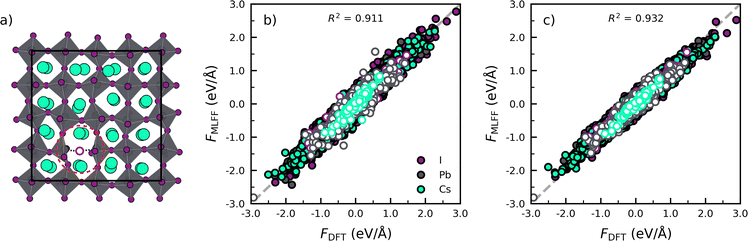
Next we assess the transferability of the models trained for the phase transitions in pristine perovskites to defective lattices, i.e. CsPbI3 with an iodide vacancy as shown in Fig. 2a. To do so, we compare the forces predicted by the MLFF against results obtained from DFT calculations in Fig. 2b. Subsequently, we make a similar comparison for a model explicitly trained against CsPbI3 with an iodide vacancy in Fig. 2c. The full details of the simulations and analysis, defect model training and defect environment recognition can be found in Note 4 (ESI†).
Focusing on the model trained against the phase transitions of bulk CsPbI3 first (Fig. 2b), we find that the MLFF captures the overall dynamical behaviour of the bulk perovskites, as evidenced by the high value of R2 = 0.911 for the force predictions. However, by distinguishing the force components for atoms close to and far away from the defect (rdefcut = 4.5 Å; Note 4 in ESI†), we find a considerable decrease in R2 when going from a bulk environment (Rbulk2 = 0.914) to the defect environment (Rdefect2 = 0.843). This indicates that the phase transition model lacks accuracy for the description of environment near the defects. A further analysis of the R2 individual atomic species, shows that near the vacancy defect, Pb (RPb2 = 0.822) and I (RI2 = 0.857) force components are poorly described due to the breaking of a Pb–I bond. Noticeably, an explicit training of the MLFF on CsPbI3 with a halide vacancy can decrease the errors and lead to improved R2 values for Pb (RPb2 = 0.888) and I (RI2 = 0.915) and an overall higher value of R2 = 0.932 for the full system. Altogether, the analysis confirms that the retraining incorporates atomic configurations that represent the defects, thus improving the accuracy of the description of the defects.
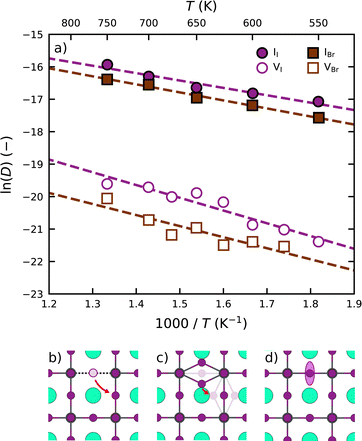
Following the above analysis, we now train four new MLFFs, each tailored to studying a specific type of halide defects (vacancies and interstitials) in CsPbI3 and CsPbBr3. With these models, the defect dynamics in model systems with two point defects per 256 formula units are investigated, resulting in a defect concentration of 3–4 × 1019 cm−3. We focus on the migration of defects at relatively high temperatures ranging from 550 K to 750 K. This is to ensure that defect migration can occur during our 2.5 ns simulations and to exclude the effects of phase transitions. The training procedure and production simulations are detailed in Note 5 (ESI†). The temperature dependence of the diffusion coefficients is shown in Fig. 3a. We analyze the temperature evolution of the diffusion coefficients D with an Arrhenius relation.31
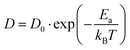 | (1) |
| Perovskite | Defect | D 0 (×10−6 s) | E a (eV) |
|---|---|---|---|
| CsPbI3 | VI | 0.7 ± 0.5 | 0.34 ± 0.04 |
| CsPbI3 | II | 2.2 ± 1.0 | 0.20 ± 0.02 |
| CsPbBr3 | VBr | 0.1 ± 0.2 | 0.29 ± 0.06 |
| CsPbBr3 | IBr | 2.0 ± 0.5 | 0.21 ± 0.01 |
We observe that interstitials generally migrate faster than vacancies. This follows from a combined higher diffusion attempt frequency (D0) and lower diffusion migration barrier (Ea). We explain this observation using the differences in the migration pathways of the two types of defects, schematic overviews of which are found in Fig. 3b and c for CsPbI3. Although both defects require the rotation of a halide ion around a Pb ion, the migration pathway for interstitials (2.2 Å) is substantially shorter than that for vacancies (4.5 Å). This difference stems from the fact that vacancies occupy a single lattice site (Fig. 3b), whereas the interstitial geometry is an iodide bridge geometry (Fig. 3c) in which two iodide ions occupy a single lattice site that results in an approximate halving of the distance to be covered by the point defect upon migration. As a result of their slower migration, the self-diffusion coefficients of halide vacancies in Fig. 3a exhibit a larger spread than those of the halide interstitials.
Moreover, we find that defects are more prone to migration in CsPbI3 than in CsPbBr3. We explain this observation by the more compact crystal packing in CsPbBr3 than in CsPbI3, also reflected by the higher Goldschmidt tolerance factor for CsPbBr3 (0.82) when compared to CsPbI3 (0.81).32 The more compact crystal packing results in a smaller amount of freedom for the ions to move (Fig. 3d). As such, the halide ions exhibit an overall lower mobility in the perovskite lattice, which is further supported by analyses of the scaled root mean squared displacement (RMSD) of the halide ions (Note 3 in ESI†) confirming that Br ions in CsPbBr3 show considerably less motion (0.165) than I ions in CsPbI3 (0.185). We note that the degree of motion of the halide ions depends closely on the phase of the perovskite, in line with experimental reports,33 where the diffusion dynamics of defects can vary between the different phases.
In summary, we demonstrate that on-the-fly trained MLFFs can accurately model defect migration in inorganic halide perovskites. The high accuracy and efficiency of these models allow us to identify the qualitative trends in migration rates of different defect types in different chemical compositions. We find that interstitials are more mobile than vacancies and that both types of defects migrate faster in CsPbI3 than in CsPbBr3. Moreover, we highlight that the transferability of the models can not be assumed and a high accuracy can only be achieved once explicitly trained against processes in the chemical environment of interest.
We acknowledge SURF for providing computational resources (Project No. EINF-2160). S. T. acknowledges funding from START-UP (Project No. 740.018.024) and Vidi (Project No. VI.Vidi.213.091) from the Dutch Research Council (NWO).
Conflicts of interest
There are no conflicts to declare.References
- M. Kim, J. Jeong, H. Lu, T. K. Lee, F. T. Eickemeyer, Y. Liu, I. W. Choi, S. J. Choi, Y. Jo, H.-B. Kim, S.-I. Mo, Y.-K. Kim, H. Lee, N. G. An, S. Cho, W. R. Tress, S. M. Zakeeruddin, A. Hagfeldt, J. Y. Kim, M. Grätzel and D. S. Kim, Science, 2022, 375, 302–306 CrossRef CAS PubMed.
- A. Fakharuddin, M. K. Gangishetty, M. Abdi-Jalebi, S.-H. Chin, A. R. bin Mohd Yusoff, D. N. Congreve, W. Tress, F. Deschler, M. Vasilopoulou and H. J. Bolink, Nat. Electron., 2022, 5, 203–216 CrossRef CAS.
- Z. Ni, H. Jiao, C. Fei, H. Gu, S. Xu, Z. Yu, G. Yang, Y. Deng, Q. Jiang, Y. Liu, Y. Yan and J. Huang, Nat. Energy, 2022, 7, 65–73 CrossRef CAS.
- A. J. Knight and L. M. Herz, Energy Environ. Sci., 2020, 13, 2024–2046 RSC.
- J. Li, Q. Dong, N. Li and L. Wang, Adv. Energy Mater., 2017, 7, 1602922 CrossRef.
- A. Guerrero, J. Bisquert and G. Garcia-Belmonte, Chem. Rev., 2021, 121, 14430–14484 CrossRef CAS PubMed.
- K. Datta, B. T. van Gorkom, Z. Chen, M. J. Dyson, T. P. A. van der Pol, S. C. J. Meskers, S. Tao, P. A. Bobbert, M. M. Wienk and R. A. J. Janssen, ACS Appl. Energy Mater., 2021, 4, 6650–6658 CrossRef CAS PubMed.
- H. Xue, G. Brocks and S. Tao, Phys. Rev. Mater., 2022, 6, 055402 CrossRef CAS.
- N. Phung, A. Al-Ashouri, S. Meloni, A. Mattoni, S. Albrecht, E. L. Unger, A. Merdasa and A. Abate, Adv. Energy Mater., 2020, 10, 1903735 CrossRef CAS.
- M. Pols, T. Hilpert, I. A. Filot, A. C. T. van Duin, S. Calero and S. Tao, ACS Appl. Mater. Interfaces, 2022, 14, 40841–40850 CrossRef CAS PubMed.
- C. Lin, S. Li, W. Zhang, C. Shao and Z. Yang, ACS Appl. Energy Mater., 2018, 1, 1374–1380 CrossRef CAS.
- S. R. G. Balestra, J. M. Vicent-Luna, S. Calero, S. Tao and J. A. Anta, J. Mater. Chem. A, 2020, 8, 11824–11836 RSC.
- J. M. Azpiroz, E. Mosconi, J. Bisquert and F. D. Angelis, Energy Environ. Sci., 2015, 8, 2118–2127 RSC.
- M. Pols, J. M. Vicent-Luna, I. Filot, A. C. T. van Duin and S. Tao, J. Phys. Chem. Lett., 2021, 12, 5519–5525 CrossRef CAS PubMed.
- P. Delugas, C. Caddeo, A. Filippetti and A. Mattoni, J. Phys. Chem. Lett., 2016, 7, 2356–2361 CrossRef CAS PubMed.
- N. Artrith and A. M. Kolpak, Comput. Mater. Sci., 2015, 110, 20–28 CrossRef CAS.
- M. F. C. Andrade, H.-Y. Ko, L. Zhang, R. Car and A. Selloni, Chem. Sci., 2020, 11, 2335–2341 RSC.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, npj Comput. Mater., 2020, 6, 1–11 CrossRef.
- J. Vandermause, Y. Xie, J. S. Lim, C. J. Owen and B. Kozinsky, Nat. Commun., 2022, 13, 5183 CrossRef CAS PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- H. Grüninger, M. Bokdam, N. Leupold, P. Tinnemans, R. Moos, G. A. De Wijs, F. Panzer and A. P. M. Kentgens, J. Phys. Chem. C, 2021, 125, 1742–1753 CrossRef PubMed.
- R. Drautz, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- Y. Xie, J. Vandermause, L. Sun, A. Cepellotti and B. Kozinsky, npj Comput. Mater., 2021, 7, 1–10 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Cryst. Growth Des., 2013, 13, 2722–2727 CrossRef CAS.
- A. Marronnier, G. Roma, S. Boyer-Richard, L. Pedesseau, J.-M. Jancu, Y. Bonnassieux, C. Katan, C. C. Stoumpos, M. G. Kanatzidis and J. Even, ACS Nano, 2018, 12, 3477–3486 CrossRef CAS PubMed.
- S. Arrhenius, Z. Phys. Chem., 1889, 4U, 96–116 CrossRef.
- S. Tao, I. Schmidt, G. Brocks, J. Jiang, I. Tranca, K. Meerholz and S. Olthof, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed.
- M. N. F. Hoque, N. Islam, Z. Li, G. Ren, K. Zhu and Z. Fan, ChemSusChem, 2016, 9, 2692–2698 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational methods, on-the-fly training procedures, model validations and production simulations. See DOI: https://doi.org/10.1039/d3cc00953j |
| This journal is © The Royal Society of Chemistry 2023 |