Role of structural dimensionality in the magneto-chiral dichroism of chiral molecular ferrimagnets†
Matteo
Atzori
 *,
Ivan
Breslavetz
*,
Ivan
Breslavetz
 ,
Kevin
Paillot
,
Kevin
Paillot
 ,
Geert L. J. A.
Rikken
,
Geert L. J. A.
Rikken
 and
Cyrille
Train
and
Cyrille
Train

Laboratoire National des Champs Magnétiques Intenses (LNCMI) – CNRS, Univ. Grenoble Alpes, INSA Toulouse, Univ. Toulouse Paul Sabatier, EMFL, F-38042 Grenoble, France. E-mail: matteo.atzori@lncmi.cnrs.fr
First published on 28th June 2022
Abstract
Here we report on magneto-chiral dichroism (MChD) detected with visible light on the chiral molecular ferrimagnet [{CrIII(CN)6}(MnIINH2ala)3]·3H2O (X = S, R; NH2ala = 2-aminoalanine). Single crystals suitable for magneto-chiral optical measurements were grown starting from enantiopure precursors. X-ray diffraction and magnetic measurements confirmed the 3D-helical structure of the material, its absolute configuration, and its ferrimagnetic ordering below 35 K. Absorption and MChD spectra were measured between 520 and 900 nm from room temperature down to 4 K. At 4 K the electronic spectrum features spin-allowed and spin-forbidden transitions of CrIII centers and metal-to-metal charge transfer bands. The MChD spectra below the magnetic ordering temperature exhibit absolute configuration-dependent MChD signals, whose shape and intensity closely resamble that of a recently investigated 2D-layered chiral ferrimagnet featuring the same building blocks but different chiral ligands and a lower structural dimensionality. By comparing the temperature and magnetic field dependence of the MChD signals in these two chiral molecular ferrimagnets, we unravel the effect of structural dimensionality in MChD and provide chemical design criteria towards highly responsive magneto-chiral optical materials.
Introduction
Magneto-chiral dichroism (MChD) represents the ability of chiral molecules and materials to enantioselectively and non-reciprocally absorb unpolarized light when placed in a magnetic field.1,2 This phenomenon is particularly fascinating because it allows chiral systems to interact with an unpolarized light source thanks to the magnetic field, which is, as unpolarized light, a non-chiral physical entity.3,4 However, as elegantly demonstrated by Laurence Barron in 1986, achiral physical entities can be combined into chiral ones to permit chiral interactions with chemical systems,5–7 and MChD represents one of these phenomena. To be more specific, when two enantiomers of a chiral systems are placed in a magnetic field, a given enantiomer can potentially absorb more light than in zero field, generating a positive MChD signal. If this occurs, the other enantiomer will absorb less light than in zero field, providing a negative MChD signal.3 The intensity of this enantioselective differential absorption of light is equal in magnitude for the two enantiomers and provide mirrored MChD spectra, as for natural circular dichroism (NCD).8 At the same time, the intensity of the MChD signals is proportional to the magnetization of the sample,9 similarly to what observed in magnetic circular dichroism (MCD),10,11 as a consequence of the intrinsic magnetization-related nature of both MChD and MCD.It has been proposed, but not yet demonstrated that this light-matter interaction can be potentially used for the optical read-out of magnetic data in magneto-optical disks.12–14 Compare to what is technologically established using circularly polarized light, the use of chiral materials can permit the replacement of polarized light by a simpler unpolarized light source. While the microscopic parameters that are at the basis of MCD spectral responses of magnetic materials are investigated since several decades,10,11 those at the origin of MChD are not yet fully understood. This is principally related to two aspects. First, MChD has been experimentally demonstrated 25 years ago1 but an intense research activity to understand which physico-chemical microscopic parameters are at the basis of this phenomenon started only recently.14–23 The aim of these studies is to provide a fundamental understanding of MChD and to propose design principles to prepare highly MChD responsive chiral magnetic materials. Second, MChD is a cross effect between natural optical activity (NOA) and magnetic optical activity (MOA).2,8 The respective contributions of these two complex phenomena are energy and chromophore dependent, making prediction and rationalization of MChD rather difficult.
We have recently reported the magnetic, optical and MChD investigation of a chiral molecular ferrimagnet formulated as [MnII(X-pnH)(H2O)][CrIII(CN)6]·H2O (X = S, R; pn = 1,2-propanediamine) (1), where the paramagnetic MnII and CrIII ions are antiferromagnetically coupled at low temperatures through cyanide-bridging ligands.15 This interaction provides a long range ferrimagnetic ordering within the bidimensional layers that composes the crystal structure below a critical temperature Tc of 38 K.24,25 Temperature and magnetic field dependent MChD signals were clearly observed in the visible range of the electromagnetic spectrum, and the most intense signals were associated to the spin-forbidden transitions of MnII, which was the only metal chromophore directly coordinated by a chiral ligand.15 Weaker signals were also evidenced for the spin-allowed transitions of CrIII but their broadness and weak intensity do not permit to clearly assign them.
Interestingly, the authors that first reported the synthesis, magnetic and structural characterization of this 2D chiral ferrimagnet, also reported another chiral magnetic material formulated as [{CrIII(CN)6}(MnIINH2ala)3]·3H2O (X = S, R; NH2ala = 2-aminoalanine) (2).26 This system was obtained using the same building blocks as for 1 with the only exception that the chiral 1,2-propanediamine ligand was substituted with chiral 2-aminoalanine. Despite the ligand change, the coordination environment around the MnII and CrIII centres remains essentially similar, but the overall dimensionality of the crystal structure increases, going from a 2D-layered to a 3D-helical arrangement whose helicity is dictated by the absolute configuration of the chiral ligand.26 Astonishingly, despites the increased dimensionality, 2 shows a very similar magnetic response with respect to 1, with a critical ordering temperature Tc of ca. 35 K.
These two systems constitute therefore an ideal case study to explore the role of structural dimensionality on the MChD response. Indeed, since the coordination environment remains very similar, as well as the magnitude of the magnetic interactions, by performing a temperature and magnetic field dependent MChD investigation one can understand the role of structural dimensionality on the overall MChD response.
Here we recall the main structural features and magnetic properties for the two compounds and we report a full optical and magneto-chiral optical investigation of 2 on oriented single crystals. Finally, we analyse and discuss the obtained results by comparing them to those previously obtained on 1 under the same conditions.
Results and discussion
Material preparation
Compound 2 was prepared according to what was already reported in the literature by reacting enantiopure 2-aminoalanine with MnCl2·4H2O and K3[CrIII(CN)6].26 Powder X-ray diffraction analysis performed on microcrystalline samples of 2-(S) and 2-(R) show a very good agreement with respect to the pattern calculated on the basis of the single crystal X-ray data (Fig. S1, ESI†). Slow diffusion (several weeks) of a slightly basic aqueous solution containing (S)- or (R)-2-aminoalanine and MnCl2·4H2O in a H2O:isopropanol solution of K3[CrIII(CN)6] provides orange-brown hexagonal-shape single crystals of 2-(S) or 2-(R) with a good optical quality, a key feature for quantitative measurements of MChD (Fig. S2, ESI†).Molecular and crystal structure
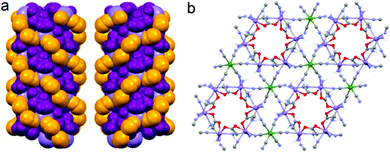
Although the crystal structure of compound 2 was already described,26 here we recall the main features needed to follow the discussion on the magnetic and magneto-chiral optical properties, as well as for the comparison with the crystal structure of 1.2 crystallizes in the hexagonal chiral space group P63 with triple-strand helical chains that develop along the c crystallographic axis. Left- and right-handed helical chirality is observed depending on the absolute configuration of the chiral ligand (R = left-handed, S = right-handed) (Fig. 1(a)). These helical chains are interconnected by hexacyanidochromate(III) building blocks (Fig. 1(b)).
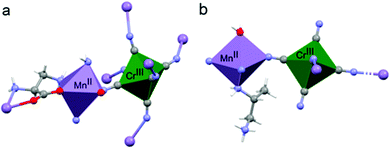
The coordination geometry around the CrIII center slightly deviates from a pure octahedral Oh symmetry due to the coordination. Each of the six cyanide ligands of the [CrIII(CN)6]3− moiety indeed bridges one MnII ion, inducing a slight radial distortion around the C3 symmetry axis (Fig. 2(a)). The MnII ions are instead hexacoordinated by two cyanide ligand of two different [CrIII(CN)6]3− moieties, and by two 2-aminoalanine ligands. Each 2-aminoalanine ligand bridges two MnII ions in a bidentate mode using its three different functional groups (Fig. 2(a)).
One MnII ion is chelated through one oxygen of the carboxylate and the amino group in 2 position, forming a 5-membered chelate ring, and another MnII ion through one oxygen of the carboxylate and the amino group in 3 position forming a 6-membered chelate ring. Overall, four nitrogens and two oxygens surround each MnII ion. The resulting octahedron is distorted due to the bidentate coordination mode of the chiral ligand. This is further enhanced by the fact that two different chelate-ring are present. Indeed, both axial and radial distortion of the idealized octahedral geometry are observed (Fig. 2(a)).
As a brief reminder, 1 crystallizes in the orthorhombic chiral space group P212121 with 2D layers of [MnII(X-pnH)(H2O)][CrIII(CN)6] (X = S, R) units that develop in a squared fashion parallel to the ab plane (Fig. 3).15
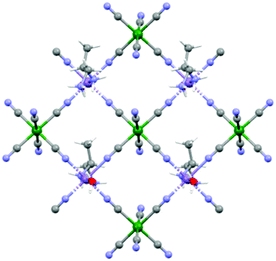 | ||
| Fig. 3 View of the squared 2D-layers of 1 that develops along the ab crystallographic plane. Color codes: violet, MnII; green, CrIII; red, O; light-blue, N; gray, C; white, H. | ||
Similarly to 2, the coordination geometry of the CrIII center only slightly deviates from an octahedral symmetry due to the coordination (Fig. 2(b)). In this case, only four out of six cyanide ligands act as bridging ligands towards MnII centers. The MnII centers are hexacoordinated, with four cyanide ligands of four different [CrIII(CN)6]3− moieties on the plane, one axial water molecule, and the amino group in 2 position of the chiral 1,2-propanediamine ligand that completes the coordination polyhedron. Also in this case, the MnII octahedron is both radially and axially distorted (Fig. 2(b)).
Overall, in both materials the coordination of the chiral ligands around the MnII ions induces the highest distortion of metal polyhedron while that of the CrIII is only slightly affected. It is instructive to remember here that d–d transitions are formally forbidden and should not exhibit optical activity.27,28 However, the coupling between the d-orbitals of the metal and the molecular orbitals of the ligand allows observation of optical activity. The rotary strength has been correlated to the degree of radial and axial distortion in mononuclear tris-chelated complexes by theoretical calculations.27,28
Magnetic properties
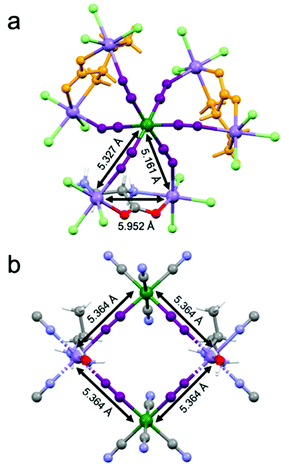
Magnetic measurements as a function of the temperature and the magnetic field have been performed on a microcrystalline sample of 2-(R). They confirm the magnetic behavior previously observed, in particular the ferrimagnetic ordering below 35 K (Fig. S3 and S4, ESI†).26 It is important to recall here that 1 similarly shows ferrimagnetic ordering below 38 K. While 1 shows a square arrangement of paramagnetic ions with a well-defined super-exchange pathway for the magnetic interaction between MnII and CrIII ions mediated by the cyanide ligands whose distance is 5.364 Å (Fig. 4(a)), the situation for 2 is more complex. Indeed, the paramagnetic ions are arranged in a heptanuclear unit where a central CrIII ions interacts with six MnII ions (Fig. 4(b)). The super-exchange pathways between CrIII and MnII are mediated by cyanide ligands and the distances are of 5.327 Å and 5.161 Å as two crystallographic independent MnII centers are present. At the same time, a super-exchange interaction between two MnII ions is ensured by the bridging chiral ligand. The intermetallic MnII⋯MnII distance is 5.952 Å, thus comparable to that of the CrIII⋯MnII interaction.On the basis of the super-exchange theory, passing from four- to six-connected CrIII centers while increasing the dimensionality from a 2D to a 3D structure, one could expect an increase of the ordering temperature.291 and 2 shows instead very similar magnetic ordering temperatures, thus suggesting that the more complex arrangement of the metal ions and competitive interactions between MnII⋯MnII and CrIII⋯MnII in 2 compensate the potential gain in the ordering temperature value.30,31
Optical properties
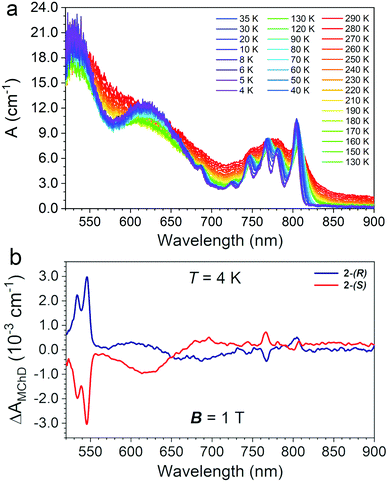
Single-crystals of 2 of ca. 1 mm × 0.8 mm × 0.8 mm (Fig. S2, ESI†) were used to record absorption spectra in transmission mode perpendicularly to the c crystallographic axis as a function of the temperature (290–4 K) in the 520–900 nm spectral range. The temperature variation of the absorption coefficient (A, cm−1) is reported in Fig. 5(a).The electronic spectrum at room temperature shows three broad absorption bands centred at ca. λ = 520, 640 and 780 nm, the latter more structured than the others (Fig. 5(a)). By lowering the temperature down to 4 K, the spectrum became better defined and distinct peaks appear. The two intense and broad absorption bands at ca. λ = 520 and 640 nm are assigned to the two low-energy spin-allowed d–d transitions of the octahedral CrIII centres, 4T1 ← 4A2, and 4T2 ← 4A2, respectively, and the weak intensity peak at ca. 685 nm to the spin-forbidden transition, 2T2 ← 4A2. At low temperature the absorption at ca. λ = 780 nm appears as a series of narrow peaks that are assigned to a set of metal-to-metal charge transfer (MMCT) transitions.24,25,32,33 The number and the nature of the observed transitions of 2 are similar to those observed for 1.15 However, some differences can be highlighted: (i) all bands are broader for 2 with respect to that of 1; (ii) 2 shows a high energy spin-allowed 4T1 ← 4A2 absorption that is red-shifted and more intense with respect that of 1; (iii) the spin-forbidden transitions of the high-spin MnII centres that were observed for 1 between 520 and 550 nm are masked in 2 by the red-shifted spin-allowed transition of the CrIII centres. On the basis of the Tanabe-Sugano diagram for octahedral CrIII complexes,34 the energy of the lowest energy spin-allowed transition for CrIII can be used to extract the value of the crystal field parameter ΔO, 16100 cm−1. The spin-forbidden 2T2 ← 4A2 transition is rather insensitive to the coordination environment, and indeed, its energy is not changed with respect to that of 1. However, the intensity of the high energy spin-allowed band, which is close to the saturation limit of the detector, do not allow an accurate determination of the λmax, hence of the B Racah parameter for 2. For 1, the value of ΔO/B was 37.15 Finally, the broadening of the MMCT bands in 2 compared to 1 is ascribed the presence of two different MnII sites bridged to the CrIII center.
Magneto-chiral dichroism
MChD measurements on 2-(S) and 2-(R) were performed in transmission mode perpendicularly to the c crystallographic axis using the same single crystals used for absorption measurements. Measurements were performed in the temperature range 4.0–80 K with an alternating magnetic field B (Ω = 0.4 Hz) of ±1.0 T applied along the light propagation vector k. Fig. 5(b) shows a spectrum in the entire investigated range for the two enantiomers at T = 4.0 K, featuring multiple MChD signals. Measurements performed under the same conditions for 2-(S) and 2-(R) provide signals of opposite signs, resulting in mirror image spectra. The most intense and sharp MChD signals are observed in the λ = 520–550 nm range, followed by sharp signals of lower intensity at λ = 770 and 800 nm. A broad and derivative type MChD signal centred at λ = 650 nm of weak intensity is also observed. At first sight, following the band assignments of the absorption spectrum, the most intense MChD signals might be attributed to the 4T1 ← 4A2 spin-allowed transition of CrIII. To confirm this, it is instructive to compare the low temperature MChD spectrum with that of 1.15 The MChD spectra of the two compounds show very similar features. Indeed, MChD signals are observed in the same spectral ranges, and show similar ΔAMChD values. For both systems, the highest intensity signal is found at ca. λ = 545 nm, and provides values of ΔAMChD of the order of 2.5–3.0 × 10−3 cm−1, that of 2 only slightly higher than 1. Accordingly, such comparison contradicts the initial assignment of the most intense MChD signals to the 4T1 ← 4A2 spin-allowed transition of CrIII, because the energy, shape and intensity of these MChD signals closely resemble those related to spin-forbidden transitions of the MnII chromophore in 1, suggesting the same assignment in 2. The signals of lower intensity at lower energy are associated to the MMCT bands, with a broadening of the signals clearly related to that of the originating absorption bands. Finally, though broader and weaker than the others, the MChD signal associated to the spin-allowed 4T2 ← 4A2 CrIII transition in 2 has sufficiently high intensity to be clearly observed, while for 1 it was at the limit of the spectrometer capabilities.Overall, this clearly suggests that the key factors that drive the MChD response in chiral magnetic materials are associated to (i) the nature of the chromophores, (ii) the nature of their electronic transitions, and (iii) the distortion of the coordination geometry of the chromophores induced by the chiral ligands, whereas the overall structural dimensionality, that is the relative position of the chromophores in the crystal structure and their connectivity, plays a minor role.
The temperature dependence of ΔAMChD was investigated for the most intense MChD signals (520–560 nm) for both 2-(S) and 2-(R), and the results are reported in Fig. 6.
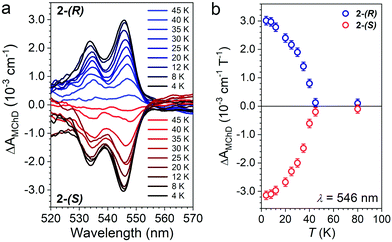 | ||
| Fig. 6 ΔAMChD at different temperatures (see legend) for both 2-(R) and 2-(S) in the 520–570 nm range (a). Temperature dependence of ΔAMChD at λ = 546 nm for both enantiomers (b). | ||
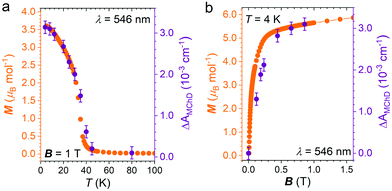
The strongest signal at λ = 546 nm is clearly observed up to 40 K, slightly above the ordering temperature of the material (Tc = 35 K), and then loses intensity. This behavior is in agreement with the proportionality of MChD with the magnetization of the sample.9,15–17 Unfortunately, given the superposition of the MnII and CrIII absorption bands in this energy region, a quantitative determination of the gMChD cannot be performed. However, given the relative low intensity of ΔAMChD with respect to what observed for other highly-responsive systems, the gMChD should not exceed a few percent per Tesla.
To confirm that the enhancement of the MChD signal is driven by the spontaneous magnetization of the material, ΔAMChD data were compared to magnetization data collected in the same conditions (Fig. 7).
Similarly to what observed for 1,15 magnetic and magneto-optical data for 2 shows the same temperature and magnetic field dependence, demonstrating the close correlation between the magneto-chiral optical response and the magnetization of the material.
Conclusions
In conclusion, we have investigated the optical and magneto-chiral optical properties of a chiral 3D ferrimagnet based on MnII and CrIII ions. This chiral material provides MChD signals associated with the spin-forbidden transitions of MnII, MMCT bands and spin-allowed transition of CrIII, the highest in intensity being the formers. The optical and MChD response as a function of energy, temperature and the magnetic field are very similar to that observed in a chiral 2D ferrimagnet based on the same chromophores and featuring similar coordinating building blocks. This clearly indicates that the immediate environment around the chromophores is a key factor in driving MChD in the visible region of the electromagnetic spectrum, while the dimensionality of the overall structural arrangement, that is the relative position of the chromophores in the crystal structure and their connectivity, does not play a crucial role. This provides a new clue for the design of efficient MChD responsive magneto-chiral optical materials. Chemists can indeed optimize the local chiral environment and the nature of the chromophores to enhance the intensity of the MChD and increase the magnetic ordering temperature by playing with the connectivity and nature of the magnetic centres and the nature of the bridging ligand. Synthetic efforts into these directions are currently underway in our laboratory.Experimental
Synthesis
Compounds 2-(S) and 2-(R) were prepared following the procedure reported in the literature26 starting from commercially available enantiopure ligands (S)- and (R)-2-aminoalanine (Tokyo Chemical Industry, >97%).Powder X-ray diffractometry
Wide-Angle Powder X-Ray Diffraction (PXRD) patterns on polycrystalline samples of 2-(S) and 2-(R) were recorded with a Bruker Endevor D8 Advance DAVINCI diffractometer in a theta-theta configuration equipped with a linear detector. The scans were collected within the range 5–40° (2θ) using Cu-Kα radiation (λ = 1.540 Å). Simulated patterns were generated from the atomic coordinates of the single-crystal structure solutions using the Mercury CSD 3.5 software (copyright CCDC, https://www.ccdc.cam.ac.uk/mercury/)35 using a FWHM (full width at half maximum) of 0.10 and a 2θ step of 0.025.Magnetic measurements
Magnetization and susceptibility measurements were performed in the 4.0–300 K temperature range with an applied magnetic field of 1.0 T on polycrystalline samples of compound 2-(R) with mass of 13.10 mg by using a Quantum Design VSM-SQUID magnetometer. Hysteresis measurements were performed at T = 4 K on the same sample with applied external magnetic field between ±7 T. Susceptibility data were corrected for the sample holders previously measured using the same conditions and for the diamagnetic contributions as deduced by using Pascal's constant tables.36Magneto-chiral dichroism spectroscopy
MChD spectra were recorded with a home-made multichannel MChD spectrometer operating in the visible and near infrared spectral window (420–1600 nm) between 4.0 and 300 K with an alternating magnetic field B up to ±2 T. A detailed description of the measurement apparatus has been reported elsewhere.37 MChD spectra were acquired on enantiopure single crystals of 2-(R) and 2-(S). The samples were mounted on a titanium sample holder over a 0.8 mm hole diameter centered with respect to a 1.0 mm diameter collimated beam. Measurements were performed in the 4.0–80 K range with an alternating magnetic field B = ±1.0 T and frequency Ω = 0.04 Hz. MChD spectra as a function of the magnetic field were recorded at T = 4.0 K for alternating magnetic fields of different amplitudes (0.0–1.0 T). The MChD signals were obtained at each temperature/field by recording, on average, 30.000 spectra with an integration time, tint of 5 ms, every 10 ms. Unpolarized light was provided by Thorlabs broadband Tungsten–Halogen (Thorlabs SLS201L) for wide-range Vis-NIR measurements. The data were collected with a OPTOSKY detector equipped with a thermoelectric cooled sensor operating in the 420–1000 nm spectral region with a resolution of 16 bits. Each spectrum was correlated to a specific magnetic field value by a dual channel digitizer (Picoscope 5000B) acquiring simultaneously triggers from the spectrometer and the magnetic field from a Hall effect sensor placed in proximity of the sample. Data are then post-processed as a synchronous detection with a MatLab routine to obtain a MChD spectrum.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the French National Research Agency (ANR) through MONAFER (ANR-18-CE09-0032), and MaChiNaCo (ANR-19-CE09-0018) projects.Notes and references
- G. L. J. A. Rikken and E. Raupach, Nature, 1997, 390, 493–494 CrossRef CAS
.
- L. D. Barron and J. Vrbancich, Mol. Phys., 1984, 51, 715–730 CrossRef CAS
.
- M. Atzori, G. L. J. A. Rikken and C. Train, Chem. – Eur. J., 2020, 26, 9784–9791 CrossRef CAS PubMed
.
- M. Atzori, C. Train, E. A. Hillard, N. Avarvari and G. L. J. A. Rikken, Chirality, 2021, 33, 844–857 CrossRef CAS PubMed
.
- L. D. Barron, J. Am. Chem. Soc., 1986, 108, 5539–5542 CrossRef CAS
.
- L. D. Barron, Chem. Rev., 1986, 15, 189 CAS
.
- L. D. Barron, Chem. Phys. Lett., 1986, 123, 423–427 CrossRef CAS
.
- G. L. J. A. Rikken and E. Raupach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 5081–5084 CrossRef CAS
.
- C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729–734 CrossRef CAS PubMed
.
- P. J. Stephens, J. Chem. Phys., 1970, 52, 3489 CrossRef CAS
.
-
W. R. Mason, A Practical Guide to Magnetic Circular Dichroism Spectroscopy, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2007 Search PubMed
.
- L. D. Barron, Nat. Mater., 2008, 7, 691–692 CrossRef CAS PubMed
.
- J. R. Galán-Mascarós, Nat. Phys., 2015, 11, 7–8 Search PubMed
.
- M. Ceolín, S. Goberna-Ferrón and J. R. Galán-Mascarós, Adv. Mater., 2012, 24, 3120–3123 CrossRef PubMed
.
- M. Atzori, I. Breslavetz, K. Paillot, K. Inoue, G. L. J. A. Rikken and C. Train, J. Am. Chem. Soc., 2019, 141, 20022–20025 CrossRef CAS PubMed
.
- M. Atzori, K. Dhbaibi, H. Douib, M. Grasser, V. Dorcet, I. Breslavetz, K. Paillot, O. Cador, G. L. J. A. Rikken, B. le Guennic, J. Crassous, F. Pointillart and C. Train, J. Am. Chem. Soc., 2021, 143, 2671–2675 CrossRef CAS PubMed
.
- M. Atzori, F. Santanni, I. Breslavetz, K. Paillot, A. Caneschi, G. L. J. A. Rikken, R. Sessoli and C. Train, J. Am. Chem. Soc., 2020, 142, 13908–13916 CrossRef CAS PubMed
.
- M. Atzori, H. Ludowieg, M. Cortijo, I. Breslavetz, K. Paillot, P. Rosa, C. Train, J. Autschbach, E. A. Hillard and G. L. J. A. Rikken, Sci. Adv., 2021, 7, eabg2859 CrossRef CAS PubMed
.
- K. Taniguchi, S. Kishiue, S. Kimura and H. Miyasaka, J. Phys. Soc. Jpn., 2019, 88, 93708 CrossRef
.
- K. Taniguchi, M. Nishio, S. Kishiue, P.-J. Huang, S. Kimura and H. Miyasaka, Phys. Rev. Mater., 2019, 3, 45202 CrossRef CAS
.
- R. Sessoli, M.-E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69–74 Search PubMed
.
- J. Goulon, A. Rogalev, F. Wilhelm, C. Goulon-Ginet, P. Carra, D. Cabaret and C. Brouder, Phys. Rev. Lett., 2002, 88, 237401 CrossRef CAS PubMed
.
- D. Mitcov, M. Platunov, C. D. Buch, A. Reinholdt, A. R. Døssing, F. Wilhelm, A. Rogalev and S. Piligkos, Chem. Sci., 2020, 11, 8306–8311 RSC
.
- K. Inoue, K. Kikuchi, M. Ohba and H. Ōkawa, Angew. Chem., Int. Ed., 2003, 42, 4810–4813 CrossRef CAS PubMed
.
- Y. Yoshida, K. Inoue, K. Kikuchi and M. Kurmoo, Chem. Mater., 2016, 28, 7029–7038 CrossRef CAS
.
- H. Imai, K. Inoue, K. Kikuchi, Y. Yoshida, M. Ito, T. Sunahara and S. Onaka, Angew. Chem., Int. Ed., 2004, 43, 5618–5621 CrossRef CAS PubMed
.
- F. E. Jorge, J. Autschbach and T. Ziegler, J. Am. Chem. Soc., 2005, 127, 975–985 CrossRef CAS PubMed
.
- F. E. Jorge, J. Autschbach and T. Ziegler, Inorg. Chem., 2003, 42, 8902–8910 CrossRef CAS PubMed
.
-
M. Atzori and F. Artizzu, Functional Molecular Materials, Pan Stanford Publishing, 2018 Search PubMed
.
-
D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed
.
-
J.-P. Launay and M. Verdaguer, Electrons in Molecules, Oxford University Press, 2013 Search PubMed
.
- A. B. P. Lever and S. A. Rice, Phys. Today, 1969, 22, 77 CrossRef
.
- Y.-S. Meng, O. Sato and T. Liu, Angew. Chem., Int. Ed., 2018, 57, 12216–12226 CrossRef CAS PubMed
.
- Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS
.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457 CrossRef CAS
.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS
.
- G. Kopnov and G. L. J. A. Rikken, Rev. Sci. Instrum., 2014, 85, 53106 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures. See DOI: https://doi.org/10.1039/d2tc01777f |
| This journal is © The Royal Society of Chemistry 2022 |