Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anharmonic lattice dynamics of superionic lithium nitride†
Gabriel
Krenzer
 a,
Chang-Eun
Kim
a,
Chang-Eun
Kim
 b,
Kasper
Tolborg
b,
Kasper
Tolborg
 a,
Benjamin J.
Morgan
a,
Benjamin J.
Morgan
 *c and
Aron
Walsh
*c and
Aron
Walsh
 *ad
*ad
aDepartment of Materials, Imperial College London, Exhibition Road, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bLawrence Livermore National Laboratory, Livermore, CA 94550, USA
cDepartment of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: b.j.morgan@bath.ac.uk
dDepartment of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea
First published on 19th October 2021
Abstract
Superionic crystals reach an ionic conductivity comparable to liquid electrolytes following a superionic transition at high temperature. The physical mechanisms that lead to this behaviour remain poorly understood. It has been proposed that superionic transitions are accompanied by the breakdown of specific phonon modes linked to characteristic diffusion processes. Any changes in vibrational properties across the superionic transition may therefore provide insights into the underlying physics of this phenomenon. Here, we apply a combination of lattice dynamics and ab initio molecular dynamics to probe the vibrational properties of the archetypal superionic conductor Li3N. We assess harmonic, quasi-harmonic, and anharmonic descriptions of the phonons. The harmonic and quasi-harmonic models show no change in features across the superionic transition. The anharmonic model, however, exhibits a breakdown for all modes. The implications for developing lattice-dynamics-based descriptors for superionic conductors are discussed.
1 Introduction
Superionic conductors are solids that reach a liquid-like ionic conductivity at a temperature Ts before reaching their melting point.1,2 This makes superionic conductors promising candidate solid electrolytes for applications such as fuel cells and all-solid-state batteries.3–5 The fundamental physics of superionic phase-transitions, and the mechanistic details of ion transport in the superionic regime, remain poorly understood, which limits the scope for the rational design and optimisation of superionic solid electrolytes for specific applications. A better understanding of the physical basis of superionic phase-transition behaviour and of the factors that cause some materials to exhibit superionic phases is therefore desirable both as an intellectual endeavour and as the basis for developing improved solid electrolytes for practical applications.6Superionic conductors that exhibit a superionic transition can be classified type-I or type-II according to the nature of the transition.1,7 Type-I superionic conductors, such as AgI, exhibit a discontinuous superionic transition, accompanied by a first-order structural phase transition at Ts from a poorly-conducting phase to the superionic phase.1 In contrast, type-II superionic conductors, such as β-PbF2, exhibit a continuous superionic transition, accompanied by a second-order phase transition associated with a constant-pressure heat capacity peak at Ts.1,8 For both type-I and type-II superionic conductors, the superionic transition is associated with a marked increase in ionic conductivity as well as a decrease in ionic conductivity activation energy, which is often interpreted as evidence of a qualitative change in diffusion mechanism of the mobile ionic species across the superionic transition.
Ionic transport in conventional (non-superionic) solids is usually considered as being effected by a sequence of discrete “hops”, where individual mobile ions undergo stochastic moves between available crystallographic sites.9,10 While this model is usually appropriate for ionic solids with low-to-medium ionic conductivities, fast ionic conduction is often associated with highly-concerted ionic motion, in which groups of ions undergo cooperative near-simultaneous motion.8,11–15 This observational correlation between fast-ion conduction and cooperative ion-transport mechanisms suggests that ionic motion in superionic conductors might be better described in terms of appropriate collective degrees of freedom, rather than independent single-atom coordinates.16 One appealing choice of basis for describing collective dynamics in a crystal is the set of normal modes of vibration, which correspond to phonon eigenvectors. Because phonons can be directly probed using established experimental methods, theoretical descriptions of superionic conduction in terms of phonon behaviour can, in principle, also be compared directly to experimental data for real materials.
Previous experimental studies have shown dramatic changes in phonon behaviour for particular solid electrolytes when heated above their superionic transition temperatures. In CuCrSe2, AgCrSe2, and γ-LiAlO2 the superionic transition is accompanied by a breakdown of specific phonon modes,17–19 characterised by marked softening and extreme broadening of one or more phonon modes. Above the superionic phase-transition temperature, specific features of discrete phonon modes are no longer able to be accurately identified on spectra. This suggests that the associated vibrational degrees of freedom are lost, and that the phonon picture breaks down for these modes in the superionic regime. One proposed interpretation of this behaviour is that the corresponding vibrational degrees of freedom are transferred to translational degrees of freedom,17 with the phonon breakdown suggested as the physical mechanism driving the superionic transition from conventional hopping-mediated diffusion to liquid-like “stochastic” diffusion,17 or correlated ionic motion.18
Phonon or vibrational density-of-states data have also been used to construct a range of cheap-to-compute descriptors for various properties of fast-ion conductors, including for ionic conductivity, activation energy, and electrochemical stability window.20,21 Computationally cheap descriptors of specific properties are increasingly used in high-throughput materials discovery, where data from electronic-structure methods are combined with data-mining techniques to screen large numbers of materials to identify candidates with, hopefully, desirable properties.22–25 The Debye frequency, obtained by speed-of-sound measurements, and the mobile-ion phonon band-centre, ωav, calculated from density functional theory (DFT) or from inelastic neutron scattering data, have previously been proposed as descriptors for ionic conductivity and activation energy, respectively, within individual solid electrolyte families.20,26,27 The host-framework phonon band-centre, meanwhile, has been used as a descriptor for the electrochemical stability window of Li-ion conductors.20 The utility of cheap-to-compute descriptors within high-throughput computational workflows is illustrated by a study by Muy et al. in which screening against a set of descriptors that included the lithium-ion phonon band-centre was used to predict 18 promising lithium-ion conductors, with one, Li3ErCl6, then shown to display a high room-temperature ionic conductivity of 0.3 mS cm−1.28
The phonon band-centre for a given solid electrolyte is defined as the “centre-of-mass” when integrating over the full vibrational density-of-states (DOS), and can be computed for the full set of phonon modes, or for a subset using the atom-projected phonon DOS.20 While this descriptor is much cheaper to compute than directly calculating ionic conductivities; for example, from molecular dynamics simulations; it neglects the effect of temperature on ion dynamics because the phonon DOS is computed within the harmonic approximation at 0 K.29 The conventional phonon band-centre is therefore not expected to be able to fully describe a superionic transition—in particular for a type-II transition where the host-framework structure does not change. At non-zero temperatures phonon modes are not equally populated, but instead are populated according to Bose–Einstein statistics. A Bose–Einstein-weighted phonon band-centre, for example, therefore might better describe the effects of changing temperature on ionic conductivity than a conventional unweighted phonon band-centre, and may therefore be able to describe the changes in ionic conductivity that occur across a superionic transition.
Here, we consider the question of how the phonons of a superionic solid electrolyte change across the superionic transition, and what implications this has for various descriptors of ionic conductivity in the context of superionic materials. We consider the archetypal superionic conductor Li3N, and compare the phonon behaviour calculated at harmonic, quasi-harmonic, and anharmonic levels of theory.
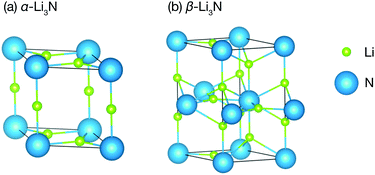
Li3N is a structurally and compositionally-simple long-studied superionic conductor.30–45 It has three phases: the α- and the β-phase (Fig. 1), which we consider here, and the γ-phase, which is only stable under high pressure at about 35 GPa,46 and which we therefore will not discuss further. The α-phase consists of alternating Li2N layers and pure Li layers. The α-phase conducts ions in its Li2N plane at a rate of 1.2 × 10−3 S cm−1 at 300 K.35 For several decades, it remained the highest Li ionic conductivity measured in a crystal around room temperature. Commercial applications, however, have been hindered by a low electrochemical stability, 0.45 V versus Li+/Li.47 The β-phase has a similar structure but exhibits another pure Li layer in between each Li2N plane. It conducts ions in its pure Li layer at a rate of 2.085 × 10−4 S cm−1.48 It is clear from the structures of the two phases that they are related by a first order structural phase transition.
Previous X-ray data for α-Li3N indicate that this phase exhibits a superionic transition at Ts ≈ 678 K.41 Below this temperature, the thermal mean-squared-displacements of the Li ions41 and the ionic conductivity36 increase both linearly, suggesting Li3N exhibits a type-II superionic transition involving only the α-phase. Based on analysis of X-ray diffraction data, Schulz and Thiemann have proposed that the superionic transition is driven by the increasing amplitude of strongly-directional anharmonic vibrations between Li sites in the Li2N plane, and that these same anharmonic vibrations promote diffusion in the superionic phase.41
In this work, we first compute harmonic phonon spectra using finite difference methods for both α-Li3N and β-Li3N. Within the harmonic approximation we find that α-Li3N is the thermodynamically preferred phase above 300 K, and we therefore discount β-Li3N as playing a role in the superionic transition at Ts ≈ 678 K. We then show that simple descriptors derived from this harmonic model, such as the phonon band-centre, are not able to describe the superionic transition, even when including a temperature-weighting. We then consider thermal expansion effects within the quasi-harmonic approximation (QHA). We again find that simple descriptors derived from the QHA are unable to describe the superionic transition of Li3N and conclude that thermal expansion is not sufficient to explain the superionic transition behaviour of Li3N. In contrast, within an anharmonic model, we observe a phonon breakdown above 678 K, which we interpret as a signature of the superionic transition, following previous experimental studies showing phonon breakdown at superionic transitions in CuCrSe2, AgCrSe2, and γ-LiAlO2.17–19 We propose that the origin of this phonon breakdown within our computational model is due to a dramatically decreased residence time for the mobile lithium within individual sites, with this becoming comparable to their characteristic vibrational time period, which prevents the calculation of a well-defined harmonic restoring force for these ions.
2 Method
2.1 Harmonic lattice dynamics
First-principles calculations using Density Functional Theory (DFT) were carried out to analyse the vibrational and ionic transport properties of Li3N. The crystal potential energy, Φ, can be expressed in terms of the displacement ujl of the jth atom in the lth unit cell. Φ can be expanded as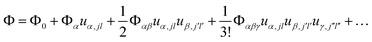 | (1) |
| F(V, T) = Uel(V) + Fph(V, T), | (2) |
Fph(T) = −kBTln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z(T), Z(T), | (3) |
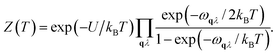 | (4) |
All of the DFT calculations were performed within the VASP code,50 using the PBEsol generalized gradient approximation exchange–correlation functional.51 Projector augmented-wave pseudopotentials were used to model the ion cores,52,53 while treating the N 2s and 2p, and the Li 1s and 2s electrons as valence electrons. The electronic wave functions were expanded in a plane-wave basis with a kinetic-energy cutoff of 950 eV. We used 4 × 4 × 4 and 8 × 8 × 4 Monkhorst–Pack k-point meshes to sample the Brillouin zone for the α- and the β-phases, respectively.54k-Point mesh sizes were reduced for relevant supercell calculations to preserve net k-point density. Geometry optimisations were performed using a quasi-Newton algorithm with a convergence setting of 0.005 eV Å−1 for the atomic forces. The resulting optimised structures of α-Li3N and β-Li3N are shown in Fig. 1. The calculated lattice parameters for these DFT-optimised structures compare well with previous computational and experimental data (full details are given in Table S1 of the ESI†).
The potential energy surface (PES) for a given vibrational mode at a particular wave vector can be obtained by calculating the internal energies of a set of structures along the corresponding normal-mode coordinate. We have used the program MODEMAP,55 which computes the displacement of atoms along a given eigenvector eqλj using
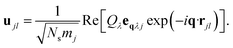 | (5) |
2.2 Phonon band-centre
The phonon band-centre, or average vibrational frequency, is a DOS-weighted average frequency defined as20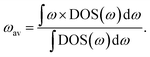 | (6) |
This quantity can be calculated for specific species, such as the mobile ions, by using the projected DOS of that species instead of the total DOS. We also define a temperature-dependent Bose–Einstein-weighted phonon band-centre obtained by weighting each DOS(ω) term by the mean phonon occupation number, n(ω):
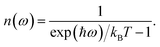 | (7) |
2.3 Quasi-harmonic approximation
Within the harmonic approximation, the vibrational DOS is temperature independent, and any temperature dependence arises only through considering phonon occupation numbers. The quasi-harmonic approximation (QHA) goes beyond this harmonic model, by considering how phonon frequencies vary in response to thermal changes in equilibrium volume. Within the QHA, phonon frequencies at a given volume are treated within the harmonic approximation. The equilibrium volume at a given temperature can then be found by minimising eqn (2) with respect to volume at each temperature. The mode Grüneisen parameter, γqλ provides a measure of anharmonicity with respect to changes in volume, and can be obtained from the gradient ∂ωqλ/∂V via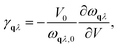 | (8) |
2.4 Ab initio molecular dynamics
While the quasi-harmonic approximation does include some temperature dependence, by allowing for thermal expansion, it does not give a complete description of the non-zero temperature phonon behaviour. In particular, phonon modes within the QHA are assumed to be non-interacting and have infinite phonon lifetimes. To go beyond the QHA and to consider a fully anharmonic phonon model, we have performed a series of “ab initio” molecular dynamics simulations (AIMD). We have then used the post-processing software DYNAPHOPY56 to extract the phonon frequencies and phonon lifetimes as a function of temperature. DYNAPHOPY uses atom velocities, vjl(t), which can be directly derived from AIMD trajectories, to compute the velocity auto-correlation function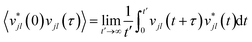 | (9) |
Taking the Fourier transform of the velocity auto-correlation function gives the power spectrum,
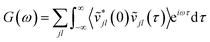 | (10) |
To characterise the degree of lithium-ion diffusion in our AIMD simulations, we compute mean-squared displacements (MSDs) for the lithium ions as57 as
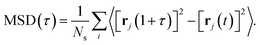 | (11) |
All MSD analysis was performed using the post-processing software KINISI. We also compute the time-averaged probability density of the lithium ions, P(rj), by projecting the AIMD trajectory onto a uniform 3D grid and calculating the time-average number of atoms at each grid point.58
Our DFT-AIMD simulations were performed in a canonical (N, V, T) ensemble. A canonical ensemble was preferred to an isobaric-isothermic (N, p, T) ensemble. Parinello–Rahman dynamics59,60 requires complete convergence with respect to the plane wave basis set, which makes it more expensive than simulations performed within a canonical ensemble. Volume effects were also found to be marginal for the properties investigated (Fig. 6). Molecular dynamics simulations with variable cell volume are therefore not necessary. The temperature in the AIMD simulations is kept fluctuating around a given value by using the Nose–Hoover thermostat. A 4 × 4 × 4 supercell was chosen with the Brillouin zone sampled only at the Γ-point. For these AIMD simulations, the plane-wave energy cutoff was reduced to 300 eV to lower the computational cost. We performed simulations at 300 K, 400 K, 500 K, 600 K and 678 K. At each temperature, we performed 10 independent AIMD simulations with different random seeds. Each simulation was run for 8000 steps with a timestep δt = 2 fs. We exclude the first 300 steps of each simulation to allow equilibration, giving a total of 154 ps of independent trajectory data at each temperature. Mean-squared displacements were calculated over a time scale of 15.4 ps, averaged over each set of 10 independent runs to improve our statistics.
3 Results
3.1 Polymorphism of Li3N
We first consider the α-Li3N and β-Li3N polymorphs within the harmonic approximation, to evaluate their relative thermodynamic stability as a function of temperature. Within the harmonic approximation, we calculate the free energy as a function of temperature of both α- and β-Li3N using eqn (2) and (3). This analysis predicts that the β-phase is more stable than the α-phase in the range 0 K to 300 K, with α-Li3N becoming the more stable polymorph above 300 K (Fig. 2). This phase-transition temperature is broadly consistent with previous neutron powder diffraction data,61 which showed a steady increase in proportion of α-Li3N with respect to β-Li3N in a α/β mixed phase sample with increasing temperature above 473 K, with only a small fraction, 2.5 wt%, of the β-phase detected at 673 K. Because β-Li3N is predicted to be thermodynamically favoured only below 300 K, which is well below the superionic transition temperature Ts ≈ 678 K, we conclude that β-Li3N is not involved in the superionic transition behaviour of Li3N. We therefore solely focus on α-Li3N in the remainder of this study.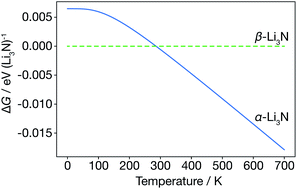 | ||
| Fig. 2 Free energy of α-Li3N relative to β-Li3N, calculated from the harmonic Helmholtz free energy. | ||
3.2 Superionic transition of α-Li3N
Fig. 3 presents calculated Li-ion mean-squared displacements (MSDs) after a simulation time of t = 15.4 ps as a function of temperature and time-averaged Li-ion probability densities in a single ab Li2N plane at 600 K and 678 K. The MSD data show the onset of Li-ion diffusion (on our simulation timescale) at 600 K, which can also be seen in a log–log plot of the MSD data (Fig. S1 (ESI†)). These MSD data also show a dramatic increase in lithium-ion displacements over the AIMD simulation timescale between 600 K and 678 K. At 678 K the average Li-ion displacement after 15.4 ps is larger than the Li-site nearest-neighbour distance. The time-averaged lithium-ion probability densities (Fig. 3(b)) also show a distinct change in Li-ion behaviour between 600 K and at 678 K. At 600 K, the Li-ion density is localised around the formal lithium-ion sites, which is consistent with a conventional “hopping” ion-diffusion process. At 678 K the Li-ion density is more diffuse with clear “interstitial” contributions, indicative of significantly more mobile lithium ions. These data are consistent with the experimental observations of Schulz and Thiemann41 who reported a decrease in Li-ion site occupation probabilities and a more diffuse Li-ion density from 600 K to 678 K, which was attributed to the onset of superionic conduction in α-Li3N.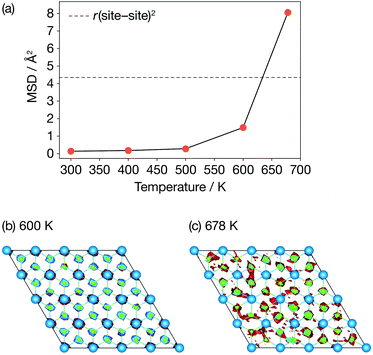 | ||
| Fig. 3 Diffusive properties of α-Li3N from AIMD. (a) Mean squared displacements of Li ions as a function of temperature; (b) & (c) time-averaged probability densities of Li ions in the ab Li2N plane. | ||
3.3 Harmonic lattice dynamics
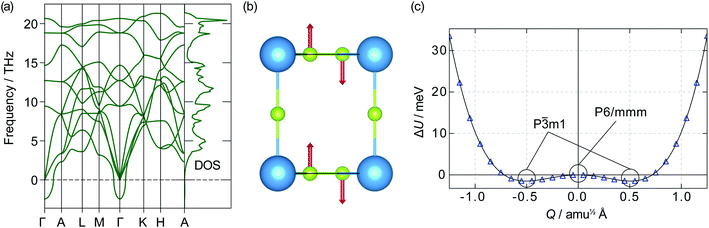
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 symmetry. If a displacive phase transition were to happen around Ts, this could be the mechanism behind the superionic transition. Out-of-plane motion of lithium ions has previously been identified as an essential part of the diffusion mechanism in α-Li3N.63 Our data, however, show the energy barrier between the two wells is only 1.20 meV, which corresponds to a thermal energy of 14 K. At temperatures above 14 K, therefore, atomic vibrations will behave as for a single harmonic (quadratic) potential.62 Even below 14 K, the P
m1 symmetry. If a displacive phase transition were to happen around Ts, this could be the mechanism behind the superionic transition. Out-of-plane motion of lithium ions has previously been identified as an essential part of the diffusion mechanism in α-Li3N.63 Our data, however, show the energy barrier between the two wells is only 1.20 meV, which corresponds to a thermal energy of 14 K. At temperatures above 14 K, therefore, atomic vibrations will behave as for a single harmonic (quadratic) potential.62 Even below 14 K, the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase may not be stable due to zero-point motion and quantum tunnelling; such behaviour has been observed in the quantum paraelectric SrTiO3.64,65 The effects of the double-well PES are therefore expected to be largely negligible within the stability range of α-Li3N (>300 K cf.Fig. 2), and to have little effect at the superionic transition temperature Ts ≈ 678 K. We conclude from this analysis that the displacive phase transition predicted for α-Li3N does not contribute towards the mechanism of the superionic transition observed in Li3N.‡
m1 phase may not be stable due to zero-point motion and quantum tunnelling; such behaviour has been observed in the quantum paraelectric SrTiO3.64,65 The effects of the double-well PES are therefore expected to be largely negligible within the stability range of α-Li3N (>300 K cf.Fig. 2), and to have little effect at the superionic transition temperature Ts ≈ 678 K. We conclude from this analysis that the displacive phase transition predicted for α-Li3N does not contribute towards the mechanism of the superionic transition observed in Li3N.‡
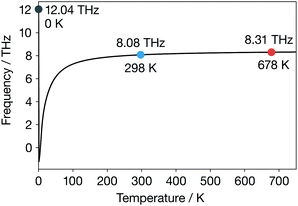
For α-Li3N above 300 K, the temperature-dependent phonon band-centre has a nearly constant value. Notably, we do not predict any change in behaviour at 678 K, as might be expected if this descriptor were describing something fundamental about the ionic conduction across the superionic transition. We further expect that using a temperature-dependent fully-anharmonic phonon DOS will not change the overall value of the phonon band-centre across the superionic transition either.29 This result is perhaps not unexpected because the phonon band-centre is an average quantity, and it has been suggested that a superionic transition is associated with the breakdown of a single phonon mode.17–19 Our finding that the phonon band-centre fails to capture any signature of the superionic transition in α-Li3N, even when temperature-dependent phonon occupations are incorporated, shows that this metric may not be reliable as a descriptor of ionic conductivities in solid electrolytes that exhibit a superionic phase transition. More generally, this result challenges the idea that the phonon band centre provides a useful conceptual framework for thinking about the microscopic dynamics of fast-ion conductors and how these relate to macroscopic ion-transport.
3.4 Quasi-harmonic approximation
Fig. 6 presents the constant-pressure heat capacity (panel (a)) and the temperature dependent phonon dispersion of α-Li3N (panel (b)) calculated within the QHA from 0 K to 690 K, and the resulting properties are shown in Fig. 6. The constant pressure heat capacity, CP, shown in Fig. 6(a) is extrapolated from the free energies, while the thermal dependence of the phonon dispersion, shown in Fig. 6(b) is calculated using the mode Grüneisen parameters defined in eqn (8). CP is linear around Ts ≈ 678 K. There is no peak or discontinuity in the CP close to Ts, which reflects the inability of the QHA to capture the α-Li3N superionic transition. The calculated values of the weighted average of the mode Grüneisen parameters range from −1.6 to 0.9, which results in mild softening of the phonon dispersion, as shown in Fig. 6(b), but, again, gives no distinct mode softening at 678 K that might correspond to the superionic transition. In contrast, a QHA treatment of cubic CeO2 does predict the emergence of imaginary modes at high temperature.66 For the case of Li3N, thermal expansion effects alone cannot be the physical mechanism driving the superionic transition observed at 678 K. This conclusion stresses that Grüneisen parameters, a common measure of anharmonicity, are not a general descriptor for superionic transitions.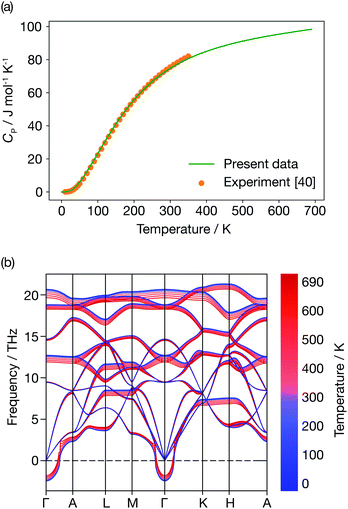 | ||
| Fig. 6 Quasi-harmonic properties of α-Li3N. (a) Constant pressure heat capacity profile. (b) Temperature dependence of the phonon dispersion. | ||
3.5 Anharmonic phonon breakdown
To go beyond the QHA lattice dynamics description, we consider a higher-order anharmonic model by mapping from the AIMD simulations onto a basis of phonon modes. We calculate velocity auto-correlation functions from phonon mode velocities, vqλ(t), using eqn (9), and power spectra, Gqλ, using eqn (10). In contrast to the harmonic and quasi-anharmonic models discussed above, where we found no signature of the superionic transition, here a phonon breakdown occurs at 678 K (Fig. 7). Above 600 K there is a drastic increase in the average phonon linewidth (inversely proportional to the mode lifetime), which is correlated with the large MSD of Li ions in the supercell. Such a discontinuous increase in average phonon linewidth cannot solely arise from three-phonon scattering contributions. Only a smooth increase in linewidth would then be observed.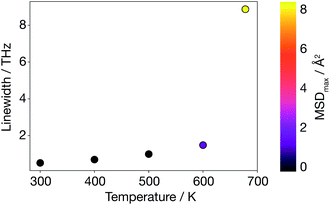 | ||
| Fig. 7 Average anharmonic phonon linewidth calculated as a function of temperature using AIMD data; the MSD colour map shows that a phonon breakdown is observed when diffusion is large. | ||
This behaviour is consistent with previous experimental studies in other solid electrolytes where the superionic transition has been found to be accompanied by an increase in phonon linewidth.17–19 In contrast to these experimental studies, where the phonon breakdown at the superionic transition was associated with the breakdown of a particular mode, we are not able to assign a single-phonon breakdown at this stage. Instead, as shown in Fig. S4 (ESI†), our model predicts a general phonon breakdown that involves almost all phonon modes at all q. Only acoustic phonon modes near the Γ-point remain coherent, which is expected since the centre of mass is not allowed to drift over the course of an AIMD simulation run with the VASP code. In short, the lattice dynamics description has broken down in α-Li3N at the superionic transition.
We interpret the results as a sign that the normal-mode-decomposition-technique applied to moderately sized supercells fails in the diffusive regime. It represents an inability to project the velocity auto-correlation functions obtained from the high-temperature AIMD back onto the wave vectors, q, or the eigenvectors, eqλ that represent small harmonic displacements.
Once in the superionic regime, Li ions are not restricted to their regular lattice sites and diffuse, Fig. 3(c). The mobile Li ions only vibrate for a short time at each individual lattice site before undergoing a diffusion event; this picture is supported by the large calculated average linewidth at 678 K. In a conventional “hopping” regime, where the average residence time for the mobile ions at individual sites is expected to be significantly greater than the average vibrational period,10 long-range vibrational order is preserved and the average motion of ions can still be described by a set of normal-modes. We also note that ions occupying interstitial positions may disrupt the long-ranged coherence of any lattice vibrations in a supercell model, which will further contribute to the reduction in mode lifetimes.
Nevertheless, in another study using the normal-mode-decomposition-technique to probe the vibrational behaviour of AgCrSe2 across its superionic transition, Wang and Chen67 replicated experimental results18 and observed the breakdown of Ag-dominated transverse acoustic modes. Other phonon modes with little or no contribution to Ag remained coherent throughout the transition. From a computational point of view, the velocity auto-correlation functions could not be projected back onto the vibrational eigenvectors of the phonon modes where Ag ions were involved because they were diffusing and occupying interstitial positions.18 On the other hand, where Ag-contributions were absent, the small harmonic displacements remained well-defined and the corresponding phonon modes stayed coherent throughout the superionic transition. Such a selective phonon breakdown is possible because the Ag-projected vibrational DOS is localised at low frequencies.18 Both CuCrSe2 and γ-LiAlO2 also show localised site-projected vibrational DOS, with distinct regions where the mobile species dominates and others where it contributes little or not all to the total vibrational DOS.17,19
In Li3N, however, the site-projected vibrational DOS for the diffusing Li ions is flat (Fig. 8). Diffusing Li ions are involved in all phonon modes. In the superionic regime, we calculate a large broadening for all the phonon modes except acoustic modes near the Γ-point because they are all altered to some degree by the diffusion of Li ions. In addition, when Li ions in the Li2N plane are diffusing, the structure (Fig. 1) may resemble a series of LiN strings. Their vibrations will be different than regular Li3N. On the other hand, materials like ternary triangular chalcogenides such as AgCrSe2 and CuCrSe2 maintain their well-defined layered structures even in the disordered superionic state.68
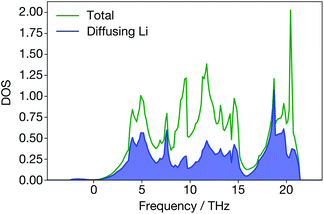 | ||
| Fig. 8 Total and site-projected vibrational density-of-states from DFT; diffusing Li ions contribute to all the peaks in the total vibrational density-of-states. | ||
These results suggest an explanation for why the (quasi)harmonic models fail to show any signature of the superionic transition in α-Li3N. A quadratic potential, even when it is allowed to soften, or harden, in response to temperature effects misses the physics involved. The superionic state can only be described by including changes in the potential energy surface sampled by the mobile Li ions and thus requires higher-order anharmonic terms from eqn (2) to be included.
Looking beyond lithium nitride, a consequence of this analysis is that descriptors which seek to capture superionic phase transitions must include some features of higher-order anharmonicity. It is doubtful that data from harmonic or QHA models alone will be sufficient for this purpose. Our results do demonstrate that phonon linewidths may be suitable, but that more effort is needed to understand the fundamental physics from a computational lattice dynamics perspective. For example, can the transition be understood in terms of a specific anharmonic term in the standard expansion of the potential energy (eqn (2))? Or can the transition be attributed to specific self-phonon or phonon–phonon interactions? Experimentally, our results also raise the question of whether a general phonon breakdown can be measured in systems where the mobile species is involved in most, or all, phonon modes. We anticipate that the general conclusions drawn here, and these associated open questions, are likely to be relevant for other superionic conductors.
4 Conclusions
We have computed the lattice dynamics properties of the archetypal superionic conductor Li3N using different levels of phonon theory. We show that the physics of superionic conductors is complex, even in a system as compositionally and structurally simple as Li3N. Our results confirm that β-Li3N is not involved in the superionic transition of Li3N, but that the superionic transition is specific to α-Li3N. We have demonstrated that both the harmonic and quasi-harmonic approximations fail to provide a signature of the superionic transition at 678 K. By using AIMD simulations to capture the high-order anharmonicity of the system, we identify a breakdown in the computed phonons in the superionic regime as quantified through the computed vibrational linewidths. This observation mirrors previous experimental observations of phonon breakdown at superionic transitions in other systems.17–19 We suggest that the breakdown comes from a combination of short occupation times of the diffusing ions at their formal lattice sites and an increase in the occupation of interstitial positions, with both effects potentially contributing to a radical change in the way the diffusing ions are vibrating, preventing their ion dynamics from being directly mapped onto a set of normal-modes. In particular, diffusing Li ions are involved in all normal-modes, which gives rise to a general phonon breakdown instead of a mode-specific one. We anticipate these conclusions to hold for other superionic conductors, and highlight a number of questions that emerge from our findings regarding the nature of the relationship between anharmonic contributions to ion dynamics and superionic phase transitions.Author contributions
G. K. contributed to data curation, formal analysis, investigation, validation, visualisation, writing the original draft, as well as reviewing and editing the manuscript. C. E. K. contributed to formal analysis, as well as reviewing and editing the manuscript. K. T. contributed to validation, as well as reviewing and editing the present manuscript. B. J. M. contributed to supervision, visualisation, as well as reviewing and editing the manuscript. A. W. contributed to conceptualisation, funding acquisition, project administration, resources, supervision, as well as reviewing and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. K. thanks Abel Carreras for support using DYNAPHOPY, Andrew McCluskey for support using KINISI, and Samantha Hood for assistance with finite difference methods. G. K. and A. W. acknowledge the Faraday Institution for funding a PhD studentship (faraday.ac.uk; EP/S003053/1), grant number FIRG025. C. E. K. acknowledges the Lawrence Livermore National Laboratory U.S. Department of Energy, for funding through the Postdoctorate Career Development Program, contract DE-AC52-07NA27344. K.T. acknowledges the Independent Research Fund Denmark for funding through the International Postdoctoral grant (0164-00015B). B.J.M. acknowledges support from the Royal Society (Grants UF130329 and URF/R/191006). We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1).References
- J. B. Boyce and B. A. Huberman, Superionic conductors: Transitions, structures, dynamics, Phys. Rep., 1979, 51, 189–265 CrossRef CAS.
- S. Hull, Superionics: crystal structures and conduction processes, Rep. Prog. Phys., 2004, 67, 1233 CrossRef CAS.
- J. B. Goodenough and P. Singh, Review—solid electrolytes in rechargeable electrochemical cells, J. Electrochem. Soc., 2015, 162, A2387–A2392, DOI:10.1149/2.0021514jes.
- E. Jay, M. Rushton, A. Chroneos, R. Grimes and J. Kilner, Genetics of superionic conductivity in lithium lanthanum titanates, Phys. Chem. Chem. Phys., 2015, 17, 178–183 RSC.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed.
- B. J. Morgan, Understanding fast-ion conduction in solid electrolytes, Philos. Trans. R. Soc., A, 2021, 379, 20190451 CrossRef CAS.
- D. A. Keen, Disordering phenomena in superionic conductors, J. Phys.: Condens. Matter, 2002, 14, R819–R857 CrossRef CAS.
- H. Zhang, X. Wang, A. Chremos and J. F. Douglas, Superionic UO2: A model anharmonic crystalline material, J. Chem. Phys.s, 2019, 150, 174506 CrossRef.
- G. H. Vineyard, Frequency factors and isotope effects in solid state rate processes, J. Phys. Chem. Solids, 1957, 3, 121–127 CrossRef CAS.
- C. R. A. Catlow, Static lattice simulation of structure and transport in superionic conductors, Solid State Ionics, 1983, 8, 89–107 CrossRef CAS.
- C. R. A. Catlow, Atomistic mechanisms of ionic transport in fast-ion conductors, J. Chem. Soc., Faraday Trans., 1990, 86, 1167 RSC.
- M. Xu, J. Ding and E. Ma, One-dimensional stringlike cooperative migration of lithium ions in an ultrafast ionic conductor, Appl. Phys. Lett., 2012, 101, 031901 CrossRef.
- M. Burbano, D. Carlier, F. Boucher, B. J. Morgan and M. Salanne, Sparse cyclic excitations explain the low ionic conductivity of stoichiometric Li7La3Zr2O12, Phys. Rev. Lett., 2016, 116, 135901 CrossRef PubMed.
- B. J. Morgan, Mechanistic origin of superionic lithium diffusion in anion-disordered Li6PS5X argyrodites, Chem. Mater., 2021, 33, 2004–2018 CrossRef CAS PubMed.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- N. Molinari, et al., Spectral denoising for accelerated analysis of correlated ionic transport, Phys. Rev. Lett., 2021, 127, 025901 CrossRef CAS PubMed.
- J. L. Niedziela, et al., Selective breakdown of phonon quasiparticles across superionic transition in CuCrSe2, Nat. Phys., 2019, 15, 73–78 Search PubMed.
- J. Ding, et al., Anharmonic lattice dynamics and superionic transition in AgCrSe2, Proc. Natl. Acad. Sci., 2020, 117, 3930–3937 CrossRef CAS PubMed.
- Q. Hu, et al., Observation of specific optical phonon modes dominating Li ion diffusion in γ-LiAlO2 ceramic, Ceram. Int., 2021, 47, 17980–17985 CrossRef CAS.
- S. Muy, et al., Tuning mobility and stability of lithium ion conductors based on lattice dynamics, Energy Environ. Sci., 2018, 11, 850–859 RSC.
- S. Muy, R. Schlem, Y. Shao-Horn and W. G. Zeier, Phonon–ion interactions: Designing ion mobility based on lattice dynamics, Adv. Energy Mater., 2021, 11, 2002787 CrossRef CAS.
- S. Curtarolo, et al., The high-throughput highway to computational materials design, Nat. Mater., 2013, 12, 191–201 CrossRef CAS.
- D. W. Davies, et al., Computational screening of all stoichiometric inorganic materials, Chem, 2016, 1, 617–627 CAS.
- D. W. Davies, et al., Descriptors for electron and hole charge carriers in metal oxides, J. Phys. Chem. Lett., 2019, 11, 438–444, DOI:10.1021/acs.jpclett.9b03398.
- B. He, et al., High-throughput screening platform for solid electrolytes combining hierarchical ion-transport prediction algorithms, Sci. Data, 2020, 7, 151 CrossRef.
- M. A. Kraft, et al., Influence of lattice polarizability on the ionic conductivity in the lithium superionic argyrodites Li6PS5X (X= Cl, Br, I), J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed.
- T. Krauskopf, et al., Comparing the descriptors for investigating the influence of lattice dynamics on ionic transport using the superionic conductor Na3PS4–xSex, J. Am. Chem. Soc., 2018, 140, 14464–14473 CrossRef CAS PubMed.
- S. Muy, et al., High-throughput screening of solid-state Li-ion conductors using lattice-dynamics descriptors, iScience, 2019, 16, 270–282 CrossRef CAS PubMed.
- A. K. Sagotra, D. Chu and C. Cazorla, Influence of lattice dynamics on lithium-ion conductivity: A first-principles study, Phys. Rev. Mater., 2019, 3, 035405 CrossRef CAS.
- E. Zintl and G. Brauer, Konstitution des lithiumnitrids, Zeitschrift für Elektrochemie und Angewandte Physikalische Chemie, 1935, 41, 102–107 CAS.
- E. Masdupuy, Contribution à l'étude des nitrures, des acétylures et des siliciures: mise en évidence de l’ion N3−, PhD thesis, Université de Toulouse, 1957.
- S. Bishop, P. Ring and P. Bray, NMR studies of 7Li in polycrystalline lithium nitride, J. Chem. Phys., 1966, 45, 1525–1531 CrossRef CAS.
- A. Rabenau and H. Schulz, Re-evaluation of the lithium nitride structure, J. Less-Common Met., 1976, 50, 155–159 CrossRef CAS.
- B. Boukamp and R. Huggins, Lithium ion conductivity in lithium nitride, Phys. Lett. A, 1976, 58, 231–233 CrossRef.
- U. v. Alpen, A. Rabenau and G. Talat, Ionic conductivity in Li3N single crystals, Appl. Phys. Lett., 1977, 30, 621–623 CrossRef.
- B. Boukamp and R. Huggins, Fast ionic conductivity in lithium nitride, Mater. Res. Bull., 1978, 13, 23–32 CrossRef CAS.
- J. Wahl and U. Holland, Local ionic motion in the superionic conductor Li3N, Solid State Commun., 1978, 27, 237–241 CrossRef CAS.
- H. Schulz and K. Schwarz, Is there an N3− ion in the crystal structure of the ionic conductor lithium nitride (Li3N)?, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 999–1005 CrossRef.
- H. Chandrasekhar, G. Bhattacharya, R. Migoni and H. Bilz, Infrared and Raman spectra and lattice dynamics of the superionic conductor Li3N, Phys. Rev. B: Solid State, 1978, 17, 884 CrossRef CAS.
- D. W. Osborne and H. E. Flotow, Lithium nitride (Li3N): heat capacity from 5 to 350 K and thermochemical properties to 1086 K, J. Chem. Thermodyn., 1978, 10, 675–682 CrossRef CAS.
- H. Schulz and K. Thiemann, Defect structure of the ionic conductor lithium nitride (Li3N), Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 309–314 CrossRef.
- T. Lapp, S. Skaarup and A. Hooper, Ionic conductivity of pure and doped Li3N, Solid State Ionics, 1983, 11, 97–103 CrossRef CAS.
- M. Wolf, J. Walker and C. Catlow, A molecular dynamics simulation study of the superionic conductor lithium nitride. I, J. Phys. C: Solid State Phys., 1984, 17, 6623 CrossRef CAS.
- M. Wolf and C. Catlow, A molecular dynamics simulation study of the superionic conductor lithium nitride. II, J. Phys. C: Solid State Phys., 1984, 17, 6635 CrossRef CAS.
- H. J. Beister, S. Haag, R. Kniep, K. Strössner and K. Syassen, Phase transformations of lithium nitride under pressure, Angew. Chem., Int. Ed. Engl., 1988, 27, 1101–1103 CrossRef.
- D. H. Gregory, Lithium nitrides as sustainable energy materials, Chem. Rec., 2008, 8, 229–239 CrossRef CAS.
- N. Tapia-Ruiz, et al., Low dimensional nanostructures of fast ion conducting lithium nitride, Nat. Commun., 2020, 11, 1–8 Search PubMed.
- W. Li, et al., Li+ ion conductivity and diffusion mechanism in α-Li3N and β-Li3N, Energy Environ. Sci., 2010, 3, 1524–1530 RSC.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, et al., Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. M. Skelton, et al., Anharmonicity in the high-temperature Cmcm phase of SnSe: Soft modes and three-phonon interactions, Phys. Rev. Lett., 2016, 117, 075502 CrossRef PubMed.
- A. Carreras, A. Togo and I. D. Tanaka, A code for extracting phonon quasiparticles from molecular dynamics simulations, Comput. Phys. Commun., 2017, 221, 221–234 CrossRef CAS.
- A. McCluskey and B. J. Morgan, Kinisi: Uncertainty Quantification in Diffusion, 2021, https://kinisi.readthedocs.io/en/latest/index.html Search PubMed.
- Z. Zhu, I.-H. Chu, Z. Deng and S. P. Ong, Role of Na+ interstitials and dopants in enhancing the Na+ conductivity of the cubic Na3PS4 superionic conductor, Chem. Mater., 2015, 27, 8318–8325 CrossRef CAS.
- M. Parrinello and A. Rahman, Crystal structure and pair potentials: A molecular-dynamics study, Phys. Rev. Lett., 1980, 45, 1196 CrossRef CAS.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- A. Huq, J. W. Richardson, E. R. Maxey, D. Chandra and W.-M. Chien, Structural studies of Li3N using neutron powder diffraction, J. Alloys Compd., 2007, 436, 256–260 CrossRef CAS.
- M. T. Dove, Theory of displacive phase transitions in minerals, Am. Mineral., 1997, 82, 213–244 CAS.
- A. D. Mulliner, P. D. Battle, W. I. David and K. Refson, Dimer-mediated cation diffusion in the stoichiometric ionic conductor Li3N, Phys. Chem. Chem. Phys., 2016, 18, 5605–5613 RSC.
- K. A. Müller, W. Berlinger and E. Tosatti, Indication for a novel phase in the quantum paraelectric regime of SrTiO3, Z. Phys. B: Condens. Matter, 1991, 84, 277–283 CrossRef.
- O. Kvyatkovskii, Quantum effects in incipient and low-temperature ferroelectrics (a review), Phys. Solid State, 2001, 43, 1401–1419 CrossRef CAS.
- J. Buckeridge, D. Scanlon, A. Walsh, C. Catlow and A. Sokol, Dynamical response and instability in ceria under lattice expansion, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214304 CrossRef.
- C. Wang and Y. Chen, Highly selective phonon diffusive scattering in superionic layered agcrse 2, npj Comput. Mater., 2020, 6, 1–6 CrossRef CAS.
- J. Wang, J. Ding, O. Delaire and G. Arya, Atomistic mechanisms underlying non-arrhenius ion transport in superionic conductor AgCrSe2, ACS Appl. Energy Mater., 2021, 4, 7157–7167 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta07631k |
| ‡ An imaginary mode was also observed in the phonon dispersion of β-Li3N at the K-point and is shown in Fig. S2(a) (ESI†). In this case, however, the energy barrier between the two wells of the PES shown in Fig. S2(b) (ESI†) is 40.95 meV. This corresponds to a thermal energy of 475.2 K, which is beyond the stability range of the β-phase according to the calculated phase diagram and neutron powder diffraction data.61 It is therefore possible that β-Li3N takes its lower energy-lower symmetry structure with P63cm symmetry, instead of the accepted P63/mmc symmetry. This point is discussed further in the ESI.† |
| This journal is © The Royal Society of Chemistry 2022 |