Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Yield precursor in primary creep of colloidal gels†
Jae Hyung
Cho‡
 * and
Irmgard
Bischofberger
* and
Irmgard
Bischofberger
 *
*
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jaehcho@mit.edu; irmgard@mit.edu
First published on 22nd September 2022
Abstract
Colloidal gels under constant moderate stress flow only after a prolonged solid-like deformation. Predicting the time-dependent yielding of the gels would facilitate control of their mechanical stability and transport, but early detectable signs of such delayed solid-to-fluid transition remain unknown. We show that the shear rate of colloidal gels under constant stress can forecast an eventual yielding during the earliest stage of deformation known as primary creep. The shear rate before failure exhibits a characteristic power-law decrease as a function of time, distinct from the linear viscoelastic response. We model this early-stage behavior as a series of uncorrelated local plastic events that are thermally activated, which illuminates the exponential dependence of the yield time on the applied stress. By revealing underlying viscoplasticity, this precursor to yield in the macroscopic shear rate provides a convenient tool to predict the yielding of a gel well in advance of its actual occurrence.
1 Introduction
Gels formed by networks of aggregated particles serve as pharmaceuticals, cosmetics, foods, and functionalized materials in novel biomedical and energy storage applications.1–3 The usefulness of particulate gels can be largely attributed to their mechanical versatility. They resist deformations like solids under small stresses, but flow like liquids under stresses above a certain threshold, termed the yield stress.4,5 A transition from solid-like deformation to fluid-like flow occurs immediately upon the application of a sufficiently large stress. When the applied stress is just above the yield stress, however, solid-like deformation can continue for a long time, until the system eventually fluidizes.6–18 Given how general such delayed solid-to-fluid transition is, capturing early signs of approaching yield would improve our ability to control stability19,20 and transport21,22 of these ubiquitous soft materials.To date, most known precursors of yield are found during later phases of the solid-like deformation. Delayed yielding of particulate gels under constant stress, similar to that of numerous other systems including colloidal glasses,23 microgel suspensions,24–26 polymer gels27,28 and harder materials,29,30 is preceded by three stages of creep.10,12,13,16–18 In the first stage, known as primary creep, that begins after a nearly instantaneous elastic response upon the application of the stress, the deformation continuously slows down as if the system were about to stop deforming and statically support the load without yield. Under stresses larger than the yield stress, however, secondary creep ensues during which the strain rate stays approximately constant at a finite value. The strain rate then rapidly increases during tertiary creep, which results in the fracture of the gel network. Yielding, therefore, becomes predictable only after the onset of secondary creep by the rebound of the strain rate. This macroscopic signature of imminent failure concurs with microscopic bursts of irreversible structural rearrangements detected via dynamic light scattering.16,31
In this work, we demonstrate that delayed yielding of particulate gels can be predicted by the temporal change in the rate of deformation already during primary creep. Using rotational rheometry, we show that gels composed of attractive colloidal particles exhibit a characteristic power-law decrease in the macroscopic shear rate with time prior to yielding. Distinct from the linear viscoelastic response, the power-law decay of the shear rate is observed when the strain falls within a range that is independent of the applied stress. The presence of this yield precursor mirrors permanent, plastic deformations during primary creep. We hence model the macroscopic behavior as a series of mesoscopic plastic events that are thermally activated and uncorrelated in space and time. Despite its simplicity, the model reproduces the rate of change in the shear rate occurring in a stress-independent strain range. Furthermore, the model enables us to infer the exponential dependence of the yielding time on the applied stress, consistent with experimental findings. We show that this exponential dependence implies that the mesoscopic plastic events in our gels involve particle-scale rearrangements. Our results indicate that the accumulation of local plastic deformations in colloidal gels gives rise to an early yield precursor readily measurable on a macroscopic scale.
2 Experimental methods
2.1 Particle synthesis and characterization
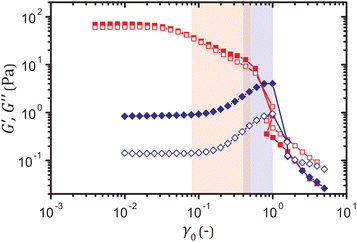
To show the generality of the precursor to yield in primary creep, we use two types of gels that exhibit markedly different yielding mechanisms under oscillatory strains, yet a nearly identical power-law decay of the shear rate under constant stresses. One system is characterized by the storage and the loss moduli, G′ and G′′ respectively, that gradually decrease with the strain amplitude γ0 after the linear regime. For the other system, by contrast, G′ and G′′ increase with γ0, which can be ascribed to stretching of force-bearing strands of particles,32–34 until the moduli sharply drop upon fracture, as shown in Fig. 1.Both the strain-softening and the strain-hardening gels are composed of polystyrene-poly(N-isopropylacrylamide) (PS-PNIPAM) core–shell particles, synthesized by an emulsion polymerization protocol.35,36 For the synthesis of the particles of the strain-softening gel, we follow the protocol described in ref. 15, which is slightly modified from that of ref. 37. In a 1 L flask equipped with a stirrer, a reflex condenser, and a gas inlet, 25.02 g of N-isopropylacrylamide (NIPAM, Acros Organics) and 0.2008 g of the stabilizer sodium dodecyl sulfate (SDS, Sigma-Aldrich) are dissolved in 525.14 g of DI water. After the solution is bubbled with nitrogen for 30 min, 142.75 g of styrene (Sigma-Aldrich) is added, and the mixture is heated to 80 °C in nitrogen atmosphere. Then 0.3521 g of the initiator potassium persulfate (KPS, Acros Organics) dissolved in 15.00 g of DI water is added to the mixture. After 6 h, the dispersion is cooled to room temperature and cleaned through repeated centrifugation and supernatant exchange. For the synthesis of the particles of the strain-hardening gel, we follow an additional step of the seeded emulsion polymerization in ref. 37 that increases the thickness of the PNIPAM shell, with slight modification of the ratio of the materials. For each 100 g of the particles obtained from the first part, 12.58 g of NIPAM and 0.8994 g of the crosslinker N,N′-methylenebis(acrylamide) (BIS, Sigma-Aldrich) are added, and the mixture is heated to 80 °C. After the addition of 0.1264 g of KPS dissolved in 9.43 g of DI water, the mixture is stirred for 4 h. The suspension is then cooled to room temperature, and cleaned by dialysis against DI water for approximately four weeks. When preparing samples at desired volume fractions, we density-match all samples using a H2O/D2O mixture of 52/48 v/v to prevent sedimentation. To minimize the effect of electrostatic interactions, we add 0.5 M of sodium thiocyanate (NaSCN) to screen the charges of the particles.
At temperatures T lower than the gelation temperatures Tg, the thermosensitive PNIPAM shells induce sufficiently long-ranged steric repulsions stabilizing the particles. Both types of shells, however, are negligibly thin compared to the PS cores, such that when the shells shrink with increasing T, the particles aggregate by van der Waals attraction. We estimate the gelation temperatures Tg by measuring the temperature at which the storage modulus G′ becomes larger than the loss modulus G′′ at a frequency ω = 6.3 rad s−1 during a temperature ramp experiment at a ramp rate of 0.2 °C min−1, sufficiently slow to ensure uniform sample temperature.15 For the strain-softening gel and the strain-hardening gel particles, Tg = 27.3 °C and 25.5 °C, respectively. Since both types of particles are made of dense PS cores covered in much thinner PNIPAM shells,15,37 we measure the volume fraction of our samples from the changes in their mass after drying in an oven, and assuming that the particle density is equal to the density of polystyrene ρ = 1.05 g cm−3.
We perform all our experiments at T = 30 °C at which both types of particles aggregate by van der Waals attraction to form kinetically arrested networks of uniformly sized clusters with a fractal dimension df = 1.8 ± 0.1,35,36 a signature of gels formed by diffusion-limited cluster aggregation.38–41 The hydrodynamic radii a measured via dynamic light scattering (BI-200SM, Brookhaven Instruments) at T = 30 °C, are 90.3 ± 1.6 nm and 116.3 ± 1.8 nm for the strain-softening and the strain-hardening gel particles, respectively. Since all the measurements are taken at T = 30 °C, the temperature dependence of the attraction strength between the particles does not play a role in our findings.
2.2 Rheometry
We use a stress-controlled rheometer (DHR-3, TA Instruments) with a cone-plate geometry of diameter 40 mm. Sandpaper (grit size 600: average diameter 16 μm) is attached to the geometry to minimize wall slip, and the edge of the loaded sample is sealed with light mineral oil (Sigma-Aldrich) to prevent evaporation. Sample loading on the rheometer is done at a lower temperature T = 20 °C < Tg at which both types of particles are stable. Before each experiment, the sample is rejuvenated at T = 20 °C while being presheared at a shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 for 180 s. Gelation is then initiated by rapidly increasing the temperature to T = 30 °C > Tg at a sample time ts = 0 s. This protocol allows us to prepare the sample without shear history. We let the gel evolve until ts = 2200 s before applying a constant stress σ0, to ensure aging is slower than the deformation due to σ0, as described in the ESI† (Fig. S1).42
= 500 s−1 for 180 s. Gelation is then initiated by rapidly increasing the temperature to T = 30 °C > Tg at a sample time ts = 0 s. This protocol allows us to prepare the sample without shear history. We let the gel evolve until ts = 2200 s before applying a constant stress σ0, to ensure aging is slower than the deformation due to σ0, as described in the ESI† (Fig. S1).42
3 Results
3.1 Experiments: characteristic power-law decay of the shear rate before yield
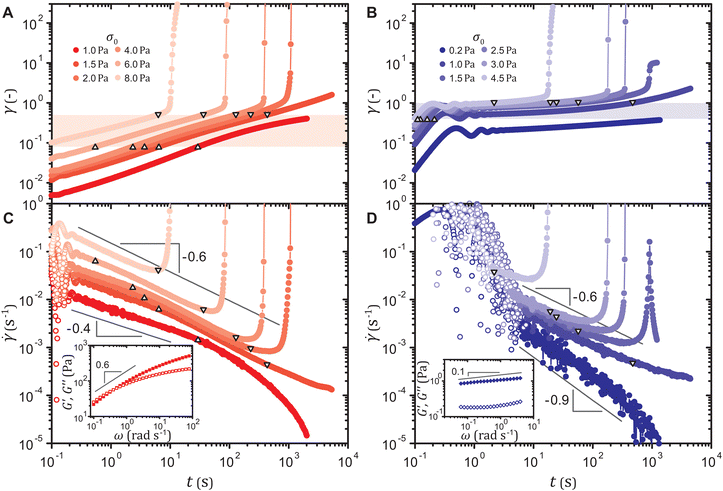
Both types of gels yield after delays when subject to stresses slightly higher than their yield thresholds. Upon the application of a stress σ0 at time t = 0 s, the strain γ(t) initially exhibits an oscillatory response induced by the coupling between the instrument inertia and the sample elasticity. The amplitude of oscillation decays more rapidly for the strain-softening gel due to its larger viscoelastic moduli,43,44 but for either system, the true material response soon ensues in which γ(t) gradually increases, as shown in Fig. 2(A) and (B) for a particle volume fraction ϕ = 5.0%. For a stress σ0 lower than the yield threshold, the strain γ(t) plateaus at late times. For σ0 higher than the threshold, γ(t) rapidly increases marking macroscopic and catastrophic yield, once it reaches a critical value that weakly decreases with σ0. The yield leads to fluidization of the system after which the strain γ increases linearly with time t (Fig. S2(A)–(D), ESI†), except for the strain-hardening gels that yield after delays longer than approximately 700 s; these systems can recover their stiffness such that γ saturates to a constant, as reported for denser colloidal gels that resolidify after yield.17,45 For either type of gel under a stress very close to the yield stress, yielding does not occur for the duration of the experiment even when the strain increases beyond the critical range. In such an extended deformation, aging becomes no longer negligible, as described in the ESI.† This may suggest that as particles within the network slowly migrate to form more energetically stable configurations, the toughness of the slowly deforming network is enhanced.15 Effects of gel aging during creep warrant more focused investigations and are outside the scope of this work.The shape of the strain curves γ(t) on log–log scales depends on the magnitude of the initial strain. The curve for the time derivative of the strain, the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t), displays the temporal change in the deformation rate unaffected by the initial strain. We find that delayed yielding, given sufficiently long primary creep, is preceded by a power-law decrease in the shear rate
(t), displays the temporal change in the deformation rate unaffected by the initial strain. We find that delayed yielding, given sufficiently long primary creep, is preceded by a power-law decrease in the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) with an exponent −0.6, as shown in Fig. 2(C) and (D). For the strain-softening gels that do not yield, the shear rate obeys a power law
(t) with an exponent −0.6, as shown in Fig. 2(C) and (D). For the strain-softening gels that do not yield, the shear rate obeys a power law ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ t−0.4 until it rapidly approaches zero, which reflects the viscoelastic spectrum in the inset of Fig. 2(C). Linear viscoelastic behaviors in creep and in small-amplitude oscillatory shear are equivalent in that G*(ω) = 1/[iωĴ(ω)], where G*(ω) ≡ G′(ω) + iG′′(ω) denotes the frequency ω dependent complex modulus and Ĵ(ω) the Fourier transform of the creep compliance J(t) ≡ γ(t)/σ0.46 Substituting J(t) = tαH(t), where α is a constant and H(t) the unit step function, into the relation results in G*(ω) = (iω)α/Γf(α + 1) ∼ ωα, where Γf denotes the Gamma function. Hence, G*(ω) ∼ ω0.6 dictates that
∼ t−0.4 until it rapidly approaches zero, which reflects the viscoelastic spectrum in the inset of Fig. 2(C). Linear viscoelastic behaviors in creep and in small-amplitude oscillatory shear are equivalent in that G*(ω) = 1/[iωĴ(ω)], where G*(ω) ≡ G′(ω) + iG′′(ω) denotes the frequency ω dependent complex modulus and Ĵ(ω) the Fourier transform of the creep compliance J(t) ≡ γ(t)/σ0.46 Substituting J(t) = tαH(t), where α is a constant and H(t) the unit step function, into the relation results in G*(ω) = (iω)α/Γf(α + 1) ∼ ωα, where Γf denotes the Gamma function. Hence, G*(ω) ∼ ω0.6 dictates that ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t0.6−1 ∼ t−0.4. For the gels that do yield, the linear viscoelastic response lasts until the strain γ(t) enters a range γ = 0.08–0.5 highlighted in Fig. 2(A), where a distinct power-law behavior
(t) ∼ t0.6−1 ∼ t−0.4. For the gels that do yield, the linear viscoelastic response lasts until the strain γ(t) enters a range γ = 0.08–0.5 highlighted in Fig. 2(A), where a distinct power-law behavior ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ t−0.6 appears, irrespective of the applied stress σ0. This range of strain γ agrees with the range of strain amplitude γ0 in which the gel strain-softens under oscillatory strains, as shown in Fig. 1, which suggests that
∼ t−0.6 appears, irrespective of the applied stress σ0. This range of strain γ agrees with the range of strain amplitude γ0 in which the gel strain-softens under oscillatory strains, as shown in Fig. 1, which suggests that ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ t−0.6 is associated with plastic deformation. The strain-hardening gels exhibit a similar behavior, as displayed in Fig. 2(D). For those that do not yield, the shear rate rapidly decreases after the linear viscoelastic response
∼ t−0.6 is associated with plastic deformation. The strain-hardening gels exhibit a similar behavior, as displayed in Fig. 2(D). For those that do not yield, the shear rate rapidly decreases after the linear viscoelastic response ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t0.1−1 ∼ t−0.9, while for those that do yield, the characteristic power law
(t) ∼ t0.1−1 ∼ t−0.9, while for those that do yield, the characteristic power law ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 appears in the strain range γ = 0.4–1.0 corresponding to the range of γ0 in which the gel strain-hardens. For the yielding strain-hardening gels, the strain γ enters this range from the outset, and hence the transition from the linear viscoelastic response to
(t) ∼ t−0.6 appears in the strain range γ = 0.4–1.0 corresponding to the range of γ0 in which the gel strain-hardens. For the yielding strain-hardening gels, the strain γ enters this range from the outset, and hence the transition from the linear viscoelastic response to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 is not observed. Least-squares fitting to the shear rate
(t) ∼ t−0.6 is not observed. Least-squares fitting to the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) in these strain ranges results in power-law exponents of −0.60 ± 0.05 for the strain-softening gel and −0.57 ± 0.01 for the strain-hardening gel.
(t) in these strain ranges results in power-law exponents of −0.60 ± 0.05 for the strain-softening gel and −0.57 ± 0.01 for the strain-hardening gel.
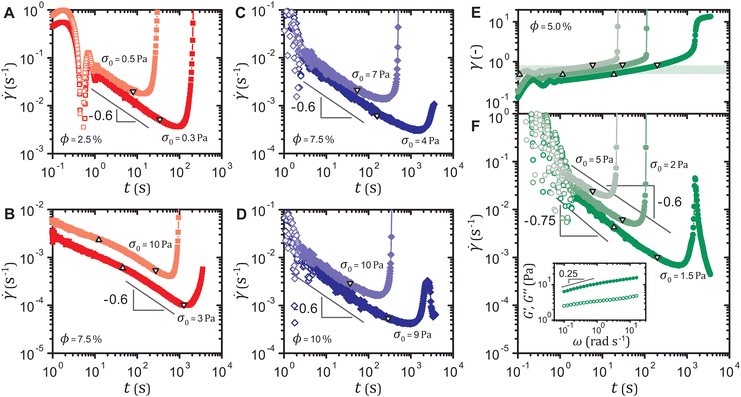
This power-law decrease in the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 consistently emerges prior to delayed yielding in all our samples, when the total strain exceeds the linear viscoelastic regime and viscoplasticity dominates primary creep. Both the strain-softening and the strain-hardening gels for volume fractions other than ϕ = 5.0% exhibit
(t) ∼ t−0.6 consistently emerges prior to delayed yielding in all our samples, when the total strain exceeds the linear viscoelastic regime and viscoplasticity dominates primary creep. Both the strain-softening and the strain-hardening gels for volume fractions other than ϕ = 5.0% exhibit ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 before yielding, as shown in Fig. 3(A)–(D). Altering the linear viscoelasticity by mixing the two types of particles to form a binary gel network36 also does not affect the exponent −0.6, as displayed in Fig. 3(E) and (F). The frequency dependence of the moduli G′,G′′ ∼ ω0.25 shown in the inset of Fig. 3(F) leads to
(t) ∼ t−0.6 before yielding, as shown in Fig. 3(A)–(D). Altering the linear viscoelasticity by mixing the two types of particles to form a binary gel network36 also does not affect the exponent −0.6, as displayed in Fig. 3(E) and (F). The frequency dependence of the moduli G′,G′′ ∼ ω0.25 shown in the inset of Fig. 3(F) leads to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t0.25−1 = t−0.75 in the linear viscoelastic regime, followed by the characteristic decay
(t) ∼ t0.25−1 = t−0.75 in the linear viscoelastic regime, followed by the characteristic decay ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 as the strain γ falls within the range 0.5–0.8 independent of the applied stress σ0. We therefore identify
(t) ∼ t−0.6 as the strain γ falls within the range 0.5–0.8 independent of the applied stress σ0. We therefore identify ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) ∼ t−0.6 as a common yield precursor in our gels during primary creep.
(t) ∼ t−0.6 as a common yield precursor in our gels during primary creep.
3.2 Model: macroscopic manifestation of accumulating local plastic events
The shear rate exhibits the characteristic power-law decay in our experiments when the total strain enters a range where plastic deformations can occur. Most yield stress fluids indeed undergo plastic deformations prior to macroscopic yielding.4,5 The yield precursor thus likely stems from incipient viscoplastic deformations in the gels under constant stresses. Inspired by the development of elastoplastic models,47–54 we build a minimal model that reproduces the temporal evolution of the shear rate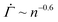 , where
, where 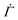 and n denote the dimensionless shear rate and time respectively, in a stress-independent range of strain Γ through a series of local plastic events. In elastoplastic models, amorphous solids are described as networks of uniformly sized mesoscopic blocks that can locally yield.49 The gel microstructure composed of networks of uniformly sized fractal clusters, illustrated in Fig. 4(A), entails a mesoscopic characteristic length, the size of the clusters. Given such structural hierarchy, we coarse-grain the structure of the gel network to parallel arrays of serially connected units, as shown in Fig. 4(B). Each unit, representing a cluster or its subset, bears the uniform dimensionless applied stress Σ0. For simplicity, we reduce the dimension of the coarse-grained system to one by considering a single array of mesoscopic units connected in series, as displayed in Fig. 4(C). Although the arrays are depicted as perfectly vertical structures between two horizontal rigid plates in Fig. 4(B) and (C), our model assumes no specific geometry of the arrays as long as the mesoscopic units are serially connected from one boundary to the other.
and n denote the dimensionless shear rate and time respectively, in a stress-independent range of strain Γ through a series of local plastic events. In elastoplastic models, amorphous solids are described as networks of uniformly sized mesoscopic blocks that can locally yield.49 The gel microstructure composed of networks of uniformly sized fractal clusters, illustrated in Fig. 4(A), entails a mesoscopic characteristic length, the size of the clusters. Given such structural hierarchy, we coarse-grain the structure of the gel network to parallel arrays of serially connected units, as shown in Fig. 4(B). Each unit, representing a cluster or its subset, bears the uniform dimensionless applied stress Σ0. For simplicity, we reduce the dimension of the coarse-grained system to one by considering a single array of mesoscopic units connected in series, as displayed in Fig. 4(C). Although the arrays are depicted as perfectly vertical structures between two horizontal rigid plates in Fig. 4(B) and (C), our model assumes no specific geometry of the arrays as long as the mesoscopic units are serially connected from one boundary to the other.
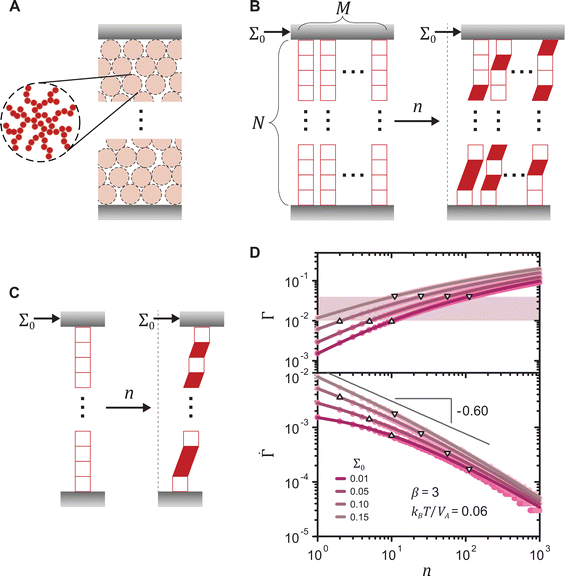 | ||
Fig. 4 (A) Schematic of the mesoscopic structure of a colloidal gel that comprises a network of uniformly sized fractal clusters between two rigid plates. (B) Coarse-graining of the gel structure to a set of M parallel arrays, each of which is formed by N serially connected mesoscopic units (open squares). Upon the application of a constant stress Σ0 at time n = 0, the number of plastically deformed units (filled parallelograms) gradually increases with n. (C) One-dimensional representation of the model. (D) Strain Γ and shear rate 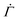 of the 1D model (lines) and the 2D model (circles) under different stresses for a shape parameter β = 3 of the local yield stress distribution and a thermal energy density kBT/Va = 0.06. Triangles and inverted triangles represent data points corresponding to the lower and the upper bounds, respectively, of the highlighted strain range Γ = 0.01–0.04. For the 1D model, the results are exact averaged quantities numerically evaluated by eqn (2). For the 2D model, the results are obtained from simulations for N = 105 and M = 102. of the 1D model (lines) and the 2D model (circles) under different stresses for a shape parameter β = 3 of the local yield stress distribution and a thermal energy density kBT/Va = 0.06. Triangles and inverted triangles represent data points corresponding to the lower and the upper bounds, respectively, of the highlighted strain range Γ = 0.01–0.04. For the 1D model, the results are exact averaged quantities numerically evaluated by eqn (2). For the 2D model, the results are obtained from simulations for N = 105 and M = 102. | ||
To define the local yield criteria, we adopt several details of the model presented in ref. 53 and 54. The local yield threshold Σy of each unit is sampled from a Weibull distribution of the shape parameter β and the scale parameter 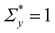 (Fig. S3, ESI†). The Weibull distribution, a common extreme value distribution, can arise if the local threshold is set by the strength of the weakest link within each unit.55,56 At time n = 0, each unit with a local threshold Σy lower than the applied stress Σ0 yields, resulting in the local strain Γl = 1. We then assume thermal activation of plastic events with the same local strain by letting each unyielded mesoscopic unit yield with probability
(Fig. S3, ESI†). The Weibull distribution, a common extreme value distribution, can arise if the local threshold is set by the strength of the weakest link within each unit.55,56 At time n = 0, each unit with a local threshold Σy lower than the applied stress Σ0 yields, resulting in the local strain Γl = 1. We then assume thermal activation of plastic events with the same local strain by letting each unyielded mesoscopic unit yield with probability
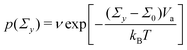 | (1) |
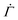 at time n ≥ 1 as
at time n ≥ 1 as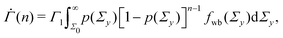 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Σyβ) denotes the probability density function for the Weibull distribution of the local yield stress Σy (see the ESI† for the derivation). The average total strain at time n ≥ 1 is
exp(−Σyβ) denotes the probability density function for the Weibull distribution of the local yield stress Σy (see the ESI† for the derivation). The average total strain at time n ≥ 1 is 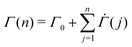 , where Γ0 = 1 − exp(−Σ0β) denotes the initial strain equal to the cumulative distribution function of the Weibull distribution evaluated at Σy = Σ0.
, where Γ0 = 1 − exp(−Σ0β) denotes the initial strain equal to the cumulative distribution function of the Weibull distribution evaluated at Σy = Σ0.
The resulting shear rate shows a near power-law decay with a stress-independent exponent within a strain range, as experimentally found in primary creep. For a shape parameter β = 3 and a thermal energy density kBT/Va = 0.06, for instance, we observe that the shear rate follows 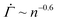 within a strain range Γ = 0.01–0.04 for stresses from Σ0 = 0.01–0.15, as shown in Fig. 4(D). We note that the power-law exponent of
within a strain range Γ = 0.01–0.04 for stresses from Σ0 = 0.01–0.15, as shown in Fig. 4(D). We note that the power-law exponent of 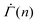 varies as β and kBT/Va are altered. The stress independence of the exponent within a strain range, however, does not depend on the specifics of the parameters (Fig. S4(A) and (B), ESI†). The monotonic decrease in
varies as β and kBT/Va are altered. The stress independence of the exponent within a strain range, however, does not depend on the specifics of the parameters (Fig. S4(A) and (B), ESI†). The monotonic decrease in 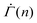 is a consequence of the gradual depletion of unyielded mesoscopic units with lower yield thresholds, and hence reflects a statistical hardening effect.48,54 This effect provides an explanation for why macroscopic plastic deformation slows down under constant stress and why the power-law exponent of the shear rate depends on the corresponding total strain in the experiments. Under the assumption that each unit yields once at most, the total strain at any given time represents the level of the exhaustion of unyielded units, which dictates the likely number of plastic events during the next unit time increment.
is a consequence of the gradual depletion of unyielded mesoscopic units with lower yield thresholds, and hence reflects a statistical hardening effect.48,54 This effect provides an explanation for why macroscopic plastic deformation slows down under constant stress and why the power-law exponent of the shear rate depends on the corresponding total strain in the experiments. Under the assumption that each unit yields once at most, the total strain at any given time represents the level of the exhaustion of unyielded units, which dictates the likely number of plastic events during the next unit time increment.
We confirm that the stress independence of the power-law exponent of the shear rate 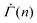 in a fixed strain range holds true for other local yield stress distributions than the Weibull distribution commonly used in elastoplastic models.52 Evaluation of eqn (2) using the normal distribution instead of the Weibull distribution gives rise to a power-law creep in a fixed strain range, as shown in the ESI.† The corresponding exponent depends on the choice of the mean and the standard deviation, but is largely independent of the applied stress Σ0 (Fig. S5(A), ESI†). Using the exponential or the uniform distribution leads to a logarithmic creep Γ ∼ ln(n), or
in a fixed strain range holds true for other local yield stress distributions than the Weibull distribution commonly used in elastoplastic models.52 Evaluation of eqn (2) using the normal distribution instead of the Weibull distribution gives rise to a power-law creep in a fixed strain range, as shown in the ESI.† The corresponding exponent depends on the choice of the mean and the standard deviation, but is largely independent of the applied stress Σ0 (Fig. S5(A), ESI†). Using the exponential or the uniform distribution leads to a logarithmic creep Γ ∼ ln(n), or 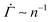 , for all strain Γ, as shown both numerically and analytically in the ESI† including Fig. S5(B) and (C) (ESI†). Containing only one free parameter, neither an exponential nor a uniform distribution can be used to describe a yield threshold distribution with a peak around a finite value and a power-law exponent that changes with the strain. Despite their limitations, the one-parameter distributions successfully capture the stress independence of the exponent.
, for all strain Γ, as shown both numerically and analytically in the ESI† including Fig. S5(B) and (C) (ESI†). Containing only one free parameter, neither an exponential nor a uniform distribution can be used to describe a yield threshold distribution with a peak around a finite value and a power-law exponent that changes with the strain. Despite their limitations, the one-parameter distributions successfully capture the stress independence of the exponent.
To validate the reduction of the model dimension to 1D, we simulate the creep deformation of the two-dimensional (2D) model illustrated in Fig. 4(B). In the 2D model, a uniform strain is imposed to individual arrays of serially connected mesoscopic units at every time step to reflect the uniform macroscopic strain of a sample in the cone-plate geometry in the experiment. For each time increment, after letting each unyielded unit deform with a probability determined by eqn (1), we equate the resulting mean of the total strains of individual arrays to the uniform macroscopic strain for the entire system. For the arrays whose total strains are larger than the mean, yielded units with the largest yield thresholds are then restored, while for the arrays whose total strains are smaller than the mean, unyielded units with the smallest yield thresholds are deformed to ensure that every array has the same total strain at any given time n. Though this correlation among multiple parallel arrays slightly lowers the resultant shear rate 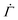 by skewing the distribution of the local yield thresholds of unyielded units towards larger values, the overall dependence of
by skewing the distribution of the local yield thresholds of unyielded units towards larger values, the overall dependence of 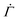 on time n closely agrees with the results from the 1D model, as shown in Fig. 4(D) and Fig. S4(A and B) in the ESI.†
on time n closely agrees with the results from the 1D model, as shown in Fig. 4(D) and Fig. S4(A and B) in the ESI.†
The initial slow changes in the shear rate 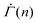 before the characteristic power law
before the characteristic power law 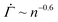 , displayed in Fig. 4(D), cannot be observed in the experiments, in which the viscoelasticity, absent in the model, dominates the system response at low strains. Once the strain in the experiments reaches a level that requires permanent deformations, the viscoelastic response is subdued, rendering the viscoplastic response dominant as captured by the model. After the power law
, displayed in Fig. 4(D), cannot be observed in the experiments, in which the viscoelasticity, absent in the model, dominates the system response at low strains. Once the strain in the experiments reaches a level that requires permanent deformations, the viscoelastic response is subdued, rendering the viscoplastic response dominant as captured by the model. After the power law 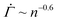 , the accumulation of yielded units in real systems should eventually induce stronger correlations among different local plastic events leading to a proliferation of irreversible deformations throughout the gel network prior to the macroscopic yield.16 Our model, which explicitly represents the onset of plasticity by excluding such correlations, continues to display a decreasing shear rate
, the accumulation of yielded units in real systems should eventually induce stronger correlations among different local plastic events leading to a proliferation of irreversible deformations throughout the gel network prior to the macroscopic yield.16 Our model, which explicitly represents the onset of plasticity by excluding such correlations, continues to display a decreasing shear rate 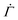 at late times without secondary or tertiary creep.
at late times without secondary or tertiary creep.
3.3 Exponential dependence of yield time on applied stress
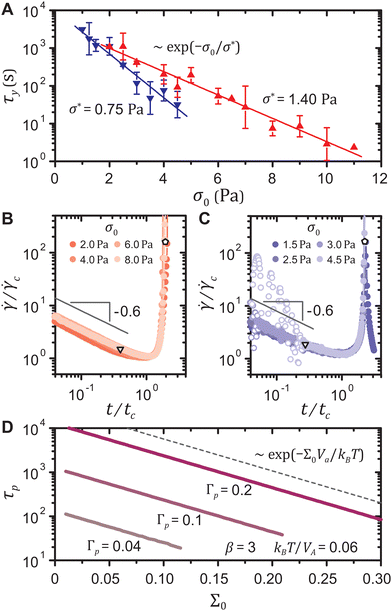
In the experiments, we find that both the strain-softening and the strain-hardening gels exhibit a yield time τy, measured at the inflection point of the shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) for the fluidizing samples or at the local peak of
(t) for the fluidizing samples or at the local peak of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) for the re-solidifying ones, that decreases with the stress σ0 as τy ∼ exp(−σ0/σ*), where σ* denotes a characteristic stress, as shown in Fig. 5(A). Such exponential dependence of τy on σ0, reported for various other colloidal gels, has been mainly attributed to the thermal activation of interparticle bond rupture.7,8,10–13,18
(t) for the re-solidifying ones, that decreases with the stress σ0 as τy ∼ exp(−σ0/σ*), where σ* denotes a characteristic stress, as shown in Fig. 5(A). Such exponential dependence of τy on σ0, reported for various other colloidal gels, has been mainly attributed to the thermal activation of interparticle bond rupture.7,8,10–13,18
Our model predicts the exponential stress dependence of the yield time without accounting for bond rupture, and in addition implies that the local plastic deformations during primary creep are accompanied by network rearrangements triggered at the particle level. The experimental shear rate curves ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) from the end of the primary creep to yield for different σ0 can be collapsed onto a master curve on log–log scales for either type of gel, as displayed in Fig. 5(B) and (C). Thus, τy ∼ exp(−σ0/σ*) requires that the time at which the yield precursor ends also exponentially decreases with σ0. The model indeed shows that the time elapsed τp to reach an arbitrary total strain Γp scales as exp(−Σ0Va/kBT), as shown in Fig. 5(D). This scaling is robust for different thermal energy densities kBT/Va, different shape parameters β of the Weibull distribution of the local yield thresholds, and even for the three other types of distributions (normal, exponential, and uniform), as delineated in the ESI† including Fig. S6(A to C). Comparing the scaling parameters between the experiments and the model, σ* = kBT/Va, we estimate the activation radii ra ≡ (3Va/4π)1/3 to be 89.3 ± 1.8 nm and 110.1 ± 3.8 nm for the strain-softening and the strain-hardening gel, respectively, surprisingly close to the particle hydrodynamic radii a = 90.3 ± 1.6 nm and 116.3 ± 1.8 nm. This agreement hints towards particle-scale rearrangements triggering the local plastic events, reminiscent of the particle-scale plasticity observed in gels under cyclic loadings.58
(t) from the end of the primary creep to yield for different σ0 can be collapsed onto a master curve on log–log scales for either type of gel, as displayed in Fig. 5(B) and (C). Thus, τy ∼ exp(−σ0/σ*) requires that the time at which the yield precursor ends also exponentially decreases with σ0. The model indeed shows that the time elapsed τp to reach an arbitrary total strain Γp scales as exp(−Σ0Va/kBT), as shown in Fig. 5(D). This scaling is robust for different thermal energy densities kBT/Va, different shape parameters β of the Weibull distribution of the local yield thresholds, and even for the three other types of distributions (normal, exponential, and uniform), as delineated in the ESI† including Fig. S6(A to C). Comparing the scaling parameters between the experiments and the model, σ* = kBT/Va, we estimate the activation radii ra ≡ (3Va/4π)1/3 to be 89.3 ± 1.8 nm and 110.1 ± 3.8 nm for the strain-softening and the strain-hardening gel, respectively, surprisingly close to the particle hydrodynamic radii a = 90.3 ± 1.6 nm and 116.3 ± 1.8 nm. This agreement hints towards particle-scale rearrangements triggering the local plastic events, reminiscent of the particle-scale plasticity observed in gels under cyclic loadings.58
4 Discussion and conclusions
We demonstrate that during the first stage of deformation, primary creep, a characteristic power-law decay of the shear rate![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) forecasts delayed yielding of colloidal gels under constant stress. The power-law decrease in the shear rate, different from the linear viscoelastic behavior, occurs in a stress-independent strain range, which corresponds to the range of input strains that cause nonlinear stress responses in strain-controlled experiments. We interpret this yield precursor as a consequence of a series of thermally activated and spatiotemporally uncorrelated plastic deformations of mesoscopic units by building a coarse-grained model that assumes a distribution of local yield stresses and a uniformly applied external stress. Although designed to account for the early-stage viscoplastic deformation only, the model furthermore illuminates how the thermal activation of plastic events even during the first stage of creep deformation manifests itself in the exponential dependence of the yield time τy on the stress σ0. These results clarify the existence of plasticity in gels during primary creep, which has been inferred from the increase in the electrical conductivity of carbon black gels under constant stresses.59
(t) forecasts delayed yielding of colloidal gels under constant stress. The power-law decrease in the shear rate, different from the linear viscoelastic behavior, occurs in a stress-independent strain range, which corresponds to the range of input strains that cause nonlinear stress responses in strain-controlled experiments. We interpret this yield precursor as a consequence of a series of thermally activated and spatiotemporally uncorrelated plastic deformations of mesoscopic units by building a coarse-grained model that assumes a distribution of local yield stresses and a uniformly applied external stress. Although designed to account for the early-stage viscoplastic deformation only, the model furthermore illuminates how the thermal activation of plastic events even during the first stage of creep deformation manifests itself in the exponential dependence of the yield time τy on the stress σ0. These results clarify the existence of plasticity in gels during primary creep, which has been inferred from the increase in the electrical conductivity of carbon black gels under constant stresses.59
For all our experiments, a common yield precursor appears: a power-law exponent −0.6 of the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t), which can be reproduced by our model with a set of the Weibull shape parameter β = 3 of the local yield stress distribution and the thermal energy density kBT/Va = 0.06 within a strain range Γ = 0.01–0.04. We emphasize, however, that these results do not imply that the exponent of −0.6 is universal for colloidal gels. The primary creep deformations of other types of colloidal gels prior to yielding may be better described by different exponents, which can still be captured through our model by tuning β, kBT/Va, or even the strain range of interest. What our findings consistently indicate is that the macroscopic sign of early-stage plastic deformation arises when the level of depletion of readily deformable local units reaches a certain range. Regardless of the choice of the model parameters and even the type of yield stress distribution, the temporal decrease in the shear rate can be approximated with a power-law exponent independent of the applied stress, as long as the total strain falls within a fixed range.
(t), which can be reproduced by our model with a set of the Weibull shape parameter β = 3 of the local yield stress distribution and the thermal energy density kBT/Va = 0.06 within a strain range Γ = 0.01–0.04. We emphasize, however, that these results do not imply that the exponent of −0.6 is universal for colloidal gels. The primary creep deformations of other types of colloidal gels prior to yielding may be better described by different exponents, which can still be captured through our model by tuning β, kBT/Va, or even the strain range of interest. What our findings consistently indicate is that the macroscopic sign of early-stage plastic deformation arises when the level of depletion of readily deformable local units reaches a certain range. Regardless of the choice of the model parameters and even the type of yield stress distribution, the temporal decrease in the shear rate can be approximated with a power-law exponent independent of the applied stress, as long as the total strain falls within a fixed range.
The coexistence of viscoelastic and viscoplastic responses in primary creep of our colloidal gels raises the question as to why viscoelasticity alone seems to successfully account for the primary creep dynamics in other colloidal gels.14,16 The apparent absence of viscoplasticity may be caused by coincidental similarity between viscoelastic and viscoplastic power-law exponents. For instance, the similarity of the two exponents −0.75 and −0.6 of the binary gel in Fig. 3(F) renders the distinction slightly less obvious than it is for the strain-softening gel in Fig. 3(B), where exponents −0.4 and −0.6 represent viscoelastic and viscoplastic responses, respectively. Also, the strain range in which viscoplasticity dominates may be narrow for systems that exhibit brittleness, in which the upper end of the linear strain regime is immediately followed by the strain at macroscopic yield. Both the strain-softening and the strain-hardening gels in this work are characterized by sufficiently broad strain ranges between the linear regime and the strain at the crossover between G′ and G′′, as shown in Fig. 1, thus enabling us to observe the coexistent viscoelasticity and viscoplasticity with ease.
We note that neither the experimental nor the modeling results display the double exponential dependence of the yield time on the stress, reported for some other colloidal gels.10,11 The presence of the two exponential regimes in these systems is ascribed to simultaneous dissociation of multiple interparticle bonds in thick force-bearing strands, which leads to rupture of the entire strands. In fractal colloidal gels like ours, the gel network is primarily composed of thin force-bearing strands, in which rearrangements on single-particle scales alone can trigger mesoscopic and macroscopic deformations. The single-particle-scale rearrangement inferred by the agreement between the activation radii and the hydrodynamic radii of the individual particles corroborates this hypothesis.
Developing a more comprehensive description of the gels in creep prior to yielding requires the model be expanded with further details. The expression for the shear rate in eqn (2) assumes that the number of serially connected mesoscopic units N within the 1D array is sufficiently large, such that 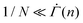 at any given time n, for the averaging to be physically meaningful. The experimental analog of N can be found by identifying the characteristic length scale of each mesoscopic unit and the total length of an array, which likely necessitates a direct microscopic imaging of the deforming gel. Such an investigation would provide insight into how the mesoscopic units are associated with the DLCA clusters, how the particle-scale activation triggers a mesoscale plastic event, and the topology of a deformation-governing array of mesoscopic units within the 3D system. Defining realistic correlations among distinct plastic events could elucidate how this incipient plastic behavior evolves into macroscale network rearrangements and shear localizations that may even introduce cracks during secondary and tertiary creep.52 The difference in the duration of these later stages of creep between the strain-softening and the strain-hardening gels, exhibited by the scaled shear rate curves in Fig. 5(B) and (C), should be accounted for in modeling the spatiotemporal correlations. It is, however, the minimal nature of our model in this work that clarifies how a slowdown of viscoplastic deformation serves as a precursor to failure. Capturing this early mechanical, macroscopic signature of yield will allow for convenient prediction of solid-to-fluid transitions, and hence enable more deft manipulation of colloidal gels in diverse settings.
at any given time n, for the averaging to be physically meaningful. The experimental analog of N can be found by identifying the characteristic length scale of each mesoscopic unit and the total length of an array, which likely necessitates a direct microscopic imaging of the deforming gel. Such an investigation would provide insight into how the mesoscopic units are associated with the DLCA clusters, how the particle-scale activation triggers a mesoscale plastic event, and the topology of a deformation-governing array of mesoscopic units within the 3D system. Defining realistic correlations among distinct plastic events could elucidate how this incipient plastic behavior evolves into macroscale network rearrangements and shear localizations that may even introduce cracks during secondary and tertiary creep.52 The difference in the duration of these later stages of creep between the strain-softening and the strain-hardening gels, exhibited by the scaled shear rate curves in Fig. 5(B) and (C), should be accounted for in modeling the spatiotemporal correlations. It is, however, the minimal nature of our model in this work that clarifies how a slowdown of viscoplastic deformation serves as a precursor to failure. Capturing this early mechanical, macroscopic signature of yield will allow for convenient prediction of solid-to-fluid transitions, and hence enable more deft manipulation of colloidal gels in diverse settings.
Author contributions
J. H. C. and I. B. designed the research. J. H. C. performed the research and analyzed the data. J. H. C. and I. B. wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Thibaut Divoux and Gareth H. McKinley for helpful discussions. We acknowledge support from the MIT Research Support Committee and Kwanjeong Educational Foundation, Awards No. 16AmB02M and No. 18AmB59D.References
- J. K. Sahoo, M. A. VandenBerg and M. J. Webber, Adv. Drug Delivery Rev., 2018, 127, 185–207 CrossRef CAS PubMed.
- A. Z. Nelson, K. S. Schweizer, B. M. Rauzan, R. G. Nuzzo, J. Vermant and R. H. Ewoldt, Curr. Opin. Solid State Mater. Sci., 2019, 23, 100758 CrossRef CAS.
- S. Tagliaferri, A. Panagiotopoulos and C. Mattevi, Mater. Adv., 2021, 2, 540–563 RSC.
- N. J. Balmforth, I. A. Frigaard and G. Ovarlez, Annu. Rev. Fluid Mech., 2014, 46, 121–146 CrossRef.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- C. J. Rueb and C. F. Zukoski, J. Rheol., 1997, 41, 197–218 CrossRef CAS.
- V. Gopalakrishnan and C. F. Zukoski, J. Rheol., 2007, 51, 623–644 CrossRef CAS.
- T. Gibaud, D. Frelat and S. Manneville, Soft Matter, 2010, 6, 3482–3488 RSC.
- M. Laurati, S. U. Egelhaaf and G. Petekidis, J. Rheol., 2011, 55, 673–706 CrossRef CAS.
- J. Sprakel, S. B. Lindström, T. E. Kodger and D. A. Weitz, Phys. Rev. Lett., 2011, 106, 248303 CrossRef.
- S. B. Lindström, T. E. Kodger, J. Sprakel and D. A. Weitz, Soft Matter, 2012, 8, 3657–3664 RSC.
- T. Brenner, S. Matsukawa, K. Nishinari and R. Johannsson, J. Non-Newtonian Fluid Mech., 2013, 196, 1–7 CrossRef CAS.
- V. Grenard, T. Divoux, N. Taberlet and S. Manneville, Soft Matter, 2014, 10, 1555–1571 RSC.
- M. Leocmach, C. Perge, T. Divoux and S. Manneville, Phys. Rev. Lett., 2014, 113, 038303 CrossRef CAS PubMed.
- D. C. E. Calzolari, I. Bischofberger, F. Nazzani and V. Trappe, J. Rheol., 2017, 61, 817–831 CrossRef CAS.
- S. Aime, L. Ramos and L. Cipelletti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3587–3592 CrossRef CAS PubMed.
- E. Moghimi, A. B. Schofield and G. Petekidis, J. Phys.: Condens. Matter, 2021, 33, 284002 CrossRef CAS.
- T. E. Kusuma, P. J. Scales, R. Buscall, D. R. Lester and A. D. Stickland, J. Rheol., 2021, 65, 355–370 CrossRef CAS.
- T. B. J. Blijdenstein, E. van der Linden, T. van Vliet and G. A. van Aken, Langmuir, 2004, 20, 11321–11328 CrossRef CAS.
- Y. Liang, G. Gillies, H. Patel, L. Matia-Merino, A. Ye and M. Golding, Food Hydrocolloids, 2014, 36, 245–255 CrossRef CAS.
- C. Chang, Q. D. Nguyen and H. P. Rønningsen, J. Non-Newtonian Fluid Mech., 1999, 87, 127–154 CrossRef CAS.
- G. T. Chala, S. A. Sulaiman and A. Japper-Jaafar, J. Non-Newtonian Fluid Mech., 2018, 251, 69–87 CrossRef CAS.
- M. Siebenbürger, M. Ballauff and T. Voigtmann, Phys. Rev. Lett., 2012, 108, 255701 CrossRef.
- P. H. T. Uhlherr, J. Guo, C. Tiu, X. M. Zhang, J. Z. Q. Zhou and T. N. Fang, J. Non-Newtonian Fluid Mech., 2005, 125, 101–119 CrossRef CAS.
- F. Caton and C. Baravian, Rheol. Acta, 2008, 47, 601–607 CrossRef CAS.
- T. Divoux, C. Barentin and S. Manneville, Soft Matter, 2011, 7, 8409–8418 RSC.
- S. N. Karobi, T. L. Sun, T. Kurokawa, F. Luo, T. Nakajima, T. Nonoyama and J. P. Gong, Macromolecules, 2016, 49, 5630–5636 CrossRef CAS.
- A. Pommella, L. Cipelletti and L. Ramos, Phys. Rev. Lett., 2020, 125, 268006 CrossRef CAS.
- M. C. Miguel, A. Vespignani, M. Zaiser and S. Zapperi, Phys. Rev. Lett., 2002, 89, 165501 CrossRef PubMed.
- H. Nechad, A. Helmstetter, R. El Guerjouma and D. Sornette, Phys. Rev. Lett., 2005, 94, 045501 CrossRef CAS.
- L. Cipelletti, K. Martens and L. Ramos, Soft Matter, 2019, 16, 82–93 RSC.
- T. Gisler, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 1999, 82, 1064–1067 CrossRef CAS.
- J. Colombo and E. Del Gado, J. Rheol., 2014, 58, 1089–1116 CrossRef CAS.
- M. Bouzid and E. Del Gado, Langmuir, 2018, 34, 773–781 CrossRef CAS.
- J. H. Cho, R. Cerbino and I. Bischofberger, Phys. Rev. Lett., 2020, 124, 088005 CrossRef CAS PubMed.
- J. H. Cho and I. Bischofberger, Phys. Rev. E, 2021, 103, 032609 CrossRef CAS PubMed.
- N. Dingenouts, C. Norhausen and M. Ballauff, Macromolecules, 1998, 31, 8912–8917 CrossRef CAS.
- P. Meakin, Phys. Rev. Lett., 1983, 51, 1119–1122 CrossRef.
- D. A. Weitz and M. Oliveria, Phys. Rev. Lett., 1984, 52, 1433–1436 CrossRef CAS.
- D. A. Weitz, J. S. Huang, M. Y. Lin and J. Sung, Phys. Rev. Lett., 1984, 53, 1657–1660 CrossRef CAS.
- P. van Dongen and M. H. Ernst, Phys. Rev. Lett., 1985, 54, 1396 CrossRef CAS PubMed.
- M. Mours and H. H. Winter, Rheol. Acta, 1994, 33, 385–397 CrossRef CAS.
- R. H. Ewoldt and G. H. McKinley, Rheol. Bull., 2007, 76, 4–6 Search PubMed.
- C. Baravian and D. Quemada, Rheol. Acta, 1998, 37, 223–233 CrossRef CAS.
- B. J. Landrum, W. B. Russel and R. N. Zia, J. Rheol., 2016, 60, 783–807 CrossRef CAS.
- J. D. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 3rd edn, 1980 Search PubMed.
- V. V. Bulatov and A. S. Argon, Modell. Simul. Mater. Sci. Eng., 1994, 2, 167–184 CrossRef.
- J. C. Baret, D. Vandembroucq and S. Roux, Phys. Rev. Lett., 2002, 89, 195506 CrossRef.
- D. Rodney, A. Tanguy and D. Vandembroucq, Modell. Simul. Mater. Sci. Eng., 2011, 19, 083001 CrossRef.
- D. Bouttes and D. Vandembroucq, AIP Conf. Proc., 2013, 1518, 481–486 CrossRef CAS.
- S. Merabia and F. Detcheverry, Europhys. Lett., 2016, 116, 46003 CrossRef.
- A. Nicolas, E. E. Ferrero, K. Martens and J. L. Barrat, Rev. Mod. Phys., 2018, 90, 45006 CrossRef CAS.
- D. F. Castellanos and M. Zaiser, Phys. Rev. Lett., 2018, 121, 125501 CrossRef CAS PubMed.
- D. F. Castellanos and M. Zaiser, Eur. Phys. J. B, 2019, 92, 139 CrossRef.
- M. J. Alava, P. K. Nukala and S. Zapperi, Adv. Phys., 2006, 55, 349–476 CrossRef.
- Z. P. Bažant, Proc. R. Soc. A, 2019, 475, 20180617 CrossRef.
- H. K. Chan and A. Mohraz, Phys. Rev. E, 2012, 85, 041403 CrossRef PubMed.
- J. M. van Doorn, J. E. Verweij, J. Sprakel and J. van der Gucht, Phys. Rev. Lett., 2018, 120, 208005 CrossRef CAS PubMed.
- A. Helal, T. Divoux and G. H. McKinley, Phys. Rev. Appl., 2016, 6, 064004 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00884j |
| ‡ Present address: Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA. |
| This journal is © The Royal Society of Chemistry 2022 |