Metal–organic frameworks as O₂-selective adsorbents for air separations

Abstract

Oxygen is a critical gas in numerous industries and is produced globally on a gigatonne scale, primarily through energy-intensive cryogenic distillation of air. The realization of large-scale adsorption-based air separations could enable a significant reduction in associated worldwide energy consumption and would constitute an important component of broader efforts to combat climate change. Certain small-scale air separations are carried out using N₂-selective adsorbents, although the low capacities, poor selectivities, and high regeneration energies associated with these materials limit the extent of their usage. In contrast, the realization of O₂-selective adsorbents may facilitate more widespread adoption of adsorptive air separations, which could enable the decentralization of O₂ production and utilization and advance new uses for O₂. Here, we present a detailed evaluation of the potential of metal–organic frameworks (MOFs) to serve as O₂-selective adsorbents for air separations. Drawing insights from biological and molecular systems that selectively bind O₂, we survey the field of O₂-selective MOFs, highlighting progress and identifying promising areas for future exploration. As a guide for further research, the importance of moving beyond the traditional evaluation of O₂ adsorption enthalpy, ΔH, is emphasized, and the free energy of O₂ adsorption, ΔG, is discussed as the key metric for understanding and predicting MOF performance under practical conditions. Based on a proof-of-concept assessment of O₂ binding carried out for eight different MOFs using experimentally derived capacities and thermodynamic parameters, we identify two existing materials and one proposed framework with nearly optimal ΔG values for operation under user-defined conditions. While enhancements are still needed in other material properties, the insights from the assessments herein serve as a guide for future materials design and evaluation. Computational approaches based on density functional theory with periodic boundary conditions are also discussed as complementary to experimental efforts, and new predictions enable identification of additional promising MOF systems for investigation.

---

David E. Jaramillo

David Jaramillo completed his PhD at UC Berkeley with Professor Jeffrey Long as an NSF Graduate Research Fellow. In the Long group, David worked on developing new metal–organic frameworks that engage in strong orbital interactions for gas storage and gas separations. Before graduate school, David studied Chemistry and Philosophy at Harvard. He is currently Co-Founder and CTO of Verne, a Bay Area startup developing hydrogen solutions for the heavy-duty transportation sector.

Adam Jaffe

Adam Jaffe is an Assistant Professor of Chemistry at the University of Notre Dame. He received his A.B. in Chemistry from Princeton University (2012) and his PhD in Inorganic Chemistry working with Prof. Hemamala I. Karunadasa at Stanford University (2017). He joined the lab of Prof. Jeffrey R. Long at the University of California, Berkeley (2017–2021) as an NIH postdoctoral fellow evaluating the separation of O2 from air in redox-active porous materials. He arrived at Notre Dame in 2021 where the Jaffe group now develops hybrid material platforms and studies their structure-property relationships, including at high pressure.

Benjamin E. R. Snyder

Dr Benjamin Snyder is currently an Arnold O. Beckman Postdoctoral Fellow working with Professor Jeffrey Long at UC Berkeley to design metal–organic frameworks as solid adsorbents for gas separations. Previously, he was an NSF Graduate Research Fellow and Stanford Graduate Fellow with Professor Edward Solomon at Stanford University, where he developed new site-selective spectroscopic probes of transition metal active sites in heterogeneous catalysts. Dr Snyder is broadly interested in the Physical Inorganic Chemistry of porous materials.

Alex Smith

Alex Smith received his B.A. in 2018 from the University of Chicago, where he studied Physics and Computer Science while researching ligated gold nanoparticles with molecular dynamics. In his PhD work with Professor Jeffrey B. Neaton he studies small molecule binding in metal–organic frameworks with density functional theory.

Jeffrey B. Neaton

Jeffrey B. Neaton is a Professor in the Department of Physics at the University of California, Berkeley, a Senior Faculty Scientist in the Materials Sciences Division at Lawrence Berkeley National Laboratory, and a Member of the Kavli Energy NanoSciences Institute at Berkeley. He has been the Associate Laboratory Director for Energy Sciences at Berkeley Lab since 2017. He received his PhD in physics from Cornell University in 2000, and was a postdoc at Rutgers University until 2003. Neaton was awarded the Presidential Early Career Award for Scientists and Engineers, and he is a fellow of the American Physical Society.

Jeffrey R. Long

Jeffrey R. Long is the C. Judson King Distinguished Professor of Chemistry and Chemical & Biomolecular Engineering at the University of California, Berkeley and a Faculty Senior Scientist in the Materials Sciences Division at Lawrence Berkeley National Laboratory. His research involves the synthesis and physical characterization of new materials with potential applications in sustainable energy and environmental remediation, and his 375 publications have received more than 85 000 citations. He co-founded and directed the start-up company Mosaic Materials, which was recently acquired by Baker Hughes and is developing metal–organic frameworks for low-energy carbon dioxide capture.

---

1. Introduction

1.1 Current air separation technologies and their limitations

Oxygen is one of the foundational gases of the industrial sector.¹ Today, fossil fuel combustion alone consumes O₂ directly from air on a massive scale of ∼25 gigatonnes per year, about 8 gigatonnes more than the annual natural production of O₂.² Moreover, enriched (>21%) or high-purity oxygen (>95%) is essential for numerous applications, including within the medical and aerospace industries,^1,3 as well as in a variety of chemical processes, such as the production of phthalic anhydride, acetaldehyde synthesis via the Wacker Process, and ethylene oxide production.^1,4 The COVID-19 pandemic has also highlighted the importance of medical-grade oxygen and its existing supply chain issues.⁵ These and many other processes depend on the separation of oxygen from air. As a result, this process is performed on a scale of hundreds of millions of tonnes per year.⁶

Importantly, high-purity O₂ is also critical for next-generation carbon capture processes poised to play a critical role in reducing emissions from large-scale combustion plants. For example, oxy-fuel power plants, which are currently in the pilot stage, use O₂ (∼95%) instead of air to produce a concentrated CO₂ flue gas stream.^7–9 This process renders post-combustion CO₂ capture more viable by reducing the energy needed for regeneration while also decreasing NO_x emissions. Likewise, high-purity O₂ is necessary for carrying out pre-combustion CO₂ capture in fossil fuel gasification plants.^10,11

Approximately 70% of O₂ generated in industry is obtained via cryogenic distillation of air,¹² which is predominantly a centralized process that takes place in large air separation plants. First pioneered by Linde in the late 19^th century, this process exploits the small difference in the boiling points of O₂ and N₂ (Table 1).^1,13 In brief, low-temperature air is fed into large distillation columns that feature pressure and temperature gradients and numerous trays where liquid and vapor phases equilibrate. Within these columns, nitrogen vapor rises and increases in purity, while liquid oxygen descends the columns and increases in purity. Cryogenic distillation plants can generate O₂ with 95% purity or higher at 1000 to 5000 tonnes per day. This method is a remarkable feat of engineering, considering the small difference in vapor pressure between the two gases. Nevertheless, cryogenic separation units are very capital-intensive projects that require operation at relatively high capacities.¹⁴ As a result, the energy required to separate one tonne of O₂ from air is approximately 245 kW h (Table 2),^6,14 more than four times greater than the minimum separation work of 58 kW h per tonne at 25 °C (see ESI Section S1†).¹⁴ Further, owing primarily to the similar vapor pressures of argon and O₂,¹³ achieving O₂ purities greater than 95% requires additional expensive refrigeration that increases the overall energy demand per tonne of O₂.⁶

Table 1 Relevant properties of the key components of air

	N2	O2	Ar
Molar fraction	0.78	0.21	00.93
Normal boiling point (K)	77.3	90.2	87.3
Kinetic diameter (Å)	3.64	3.47	3.54
Polarizability × 10^25 (cm^3)	17.703	15.812	16.411
Quadrupole moment × 10^26 (esu cm^2)	1.52	0.39	0
Electron affinity (eV)	<0	0.450	<0

---

Table 2 Overview of current air separation processes

	Cryogenic distillation^a	Adsorptive separations^b	Membrane separations^c
a Values obtained from ref. 6, 14, and 19. b Values obtained from ref. 6, 14, and 19. c Values obtained from ref. 6 and 20. The largest reported capacity per day is an estimate from ref. 6.
Operating pressures	1–6 bar	0.2–6 bar	1–6 bar
Operating temperatures	77–298 K	298–318 K	298–318 K
O2 purity achieved	>95%	<95%	<50%
O2 production scale per day	1000 tonnes	100 tonnes	10 tonnes
Largest reported capacity per day	5000 tonnes (Air Liquide)	340 tonnes (Linde)	25 tonnes
Energy demand per tonne	220–270 kW h at 95% purity	500 kW h at 95% purity	300 kW h at 40% purity

---

Adsorptive air separation represents the second most common process for oxygen production, accounting for ∼20% of O₂ produced in industry.¹⁴ This approach currently exploits differences in the polarizability and quadrupole moment of O₂ and N₂ (Table 1). Briefly, pressurized air is fed through beds containing an adsorbent that selectively binds N₂. The most commonly used adsorbent is a low-silica zeolite exchanged with lithium ions, known as Li-LSX,^12,15 which features exposed Li⁺ sites that preferentially interact with N₂. Once the adsorbent is saturated with the gas, the bed is depressurized to near ambient pressure, resulting in elution of an O₂-enriched stream, followed by N₂. A process operating under such conditions is referred to as pressure swing adsorption (PSA). Air can also be fed into the adsorbent bed at near ambient pressure, and in this case vacuum or heat can then be applied to regenerate the adsorbent, in so-called vacuum swing adsorption (VSA) or temperature swing adsorption (TSA) processes.^12,14,16,17 Further, the above separation methods can be combined to engender pressure-temperature or vacuum-temperature swing adsorption processes. Importantly, adsorptive air separations can serve a complementary role to cryogenic distillation, as they can operate under a more variable load (for instance, by changing the number of adsorbent beds in use), are substantially less capital-intensive for small-scale applications, and entail minimal startup time. Adsorptive air separation plants typically consume 500 kW h per tonne of O₂ produced at 90–95% purity,^14,18 although a much lower value of 270 kW h per tonne of O₂ has been reported (Table 2).¹² This energy demand is nearly double that of cryogenic distillation, and the resulting oxygen purity is generally lower. This higher energy cost arises due to the need to regenerate the adsorbent, as discussed above. Additionally, zeolites typically exhibit low N₂ uptake, and therefore substantial quantities of adsorbent material are required—roughly 1 tonne of zeolite is needed for producing 1 tonne of O₂ per day. In all, these shortcomings preclude the more wide-spread application of Li-LSX adsorbents for air separations.

Polymeric membrane-based air separations are the youngest commercial technology for extracting O₂ from air, and operate by passing an air stream through a series of membrane units.^18–20 These processes function under a solution-diffusion mechanism and discriminate oxygen and nitrogen based on their permeabilities. Industrially relevant membranes are permselective with respect to oxygen, and so the resulting permeate is O₂-enriched air. As a result of their mechanism of operation, membrane separations can be carried out continuously under ambient conditions, without the need for regeneration. As such, polymer membranes have the potential to offer considerable reductions in capital costs and operating expenses relative to adsorption and cryogenic distillation. However, for the majority of membranes studied to date, permeate O₂ concentrations are limited by the minor solubilization difference between O₂ and N₂.²¹ This shortcoming, combined with similarities in the kinetic diameters of N₂ and O₂, manifests as a permeability-selectivity tradeoff that limits permeate purities to below 40–50% O₂.^18,21 Note that ceramic membranes, which function through a different mechanism, may find use in industrial applications. However, these membranes typically require very high temperatures to operate, in the range of 800−900 °C.^19,22

1.2 The potential impact of O₂-selective adsorbents in air separations

In general, established air separation technologies operate by distinguishing O₂ and N₂ based on relatively small differences in their boiling points, polarizabilities, and quadrupole moments. However, the property that most distinguishes O₂ from N₂ (and Ar) is its electron affinity (Table 1). Oxygen can readily accept one or two electrons from a single metal center, whereas nitrogen is generally redox-inactive.²³ Biological systems exploit this difference to selectively and reversibly bind O₂ using iron(II)- and copper(I)-containing proteins. In particular, hemoglobin and myoglobin,^24,25 hemerythrin,²⁶ and hemocyanin²⁷ are representative examples of proteins containing metal sites that bind O₂via electron transfer.

The realization of adsorbents that are capable of similar strong yet reversible chemisorption of O₂ could transform the air separation industry. Indeed, because the partial pressure of O₂ in air is approximately four times less than that of N₂, the amount of O₂-selective adsorbent needed to process a given quantity of air will be one quarter of the quantity needed for an analogous N₂-selective adsorbent. As a result, even in a scenario where the enthalpy of O₂ binding in an O₂-selective adsorbent is comparable to the N₂ binding enthalpy in Li-LSX, the overall regeneration energy needed for the O₂-selective material would be substantially lower, perhaps even 50% lower, assuming the material exhibits a high selectivity for O₂ (ESI Section S2†).²⁸ In principle, energy-efficient O₂-selective adsorbents could be implemented in all air separation applications that currently utilize N₂-selective adsorbents. Additionally, O₂-selective adsorbents could promote the adoption of new separation processes based on adsorption, including small-scale, variable-load oxygen production, mixed-matrix membrane air separations, and hybrid processes with cryogenic distillation. Overall, a commercially viable O₂-selective adsorbent could support the decentralization of oxygen production and utilization. Furthermore, O₂-selective adsorbents with high volumetric capacities might be less costly than cryogenic distillation for mid- and even large-scale air separations, enabling the use of smaller contactors and thereby incurring lower capital expenses.²⁹

1.3 Metal–organic frameworks as O₂-selective adsorbents

Research focused on the development of O₂-selective adsorbents has been ongoing since the 1970s,^30–34 although few materials have been discovered that show thermodynamic selectivity for oxygen over nitrogen, and no O₂-selective adsorbent is commercially viable at present. Extensive early work focused on the development of molecular compounds that bind O₂ in solution and in the solid-state, most notably featuring cobalt(II).^30–34 However, many of these complexes exhibit poor stabilities, low capacities, and/or irreversible O₂ binding, making them unsuitable for implementation in practical air separation processes. Immobilization of cobalt complexes on porous solid substrates, such as silicates and polymers,^35–37 has been shown to improve cycling performance, but these materials typically exhibit low O₂ capacities. Considering these shortcomings, an ideal adsorbent would incorporate a high density of redox-active open metal sites immobilized in a robust, rigid porous framework.

Metal–organic frameworks (MOFs) can satisfy both criteria. These crystalline, porous materials are assembled from metal nodes and multitopic organic linkers, and they have emerged as promising candidates to replace traditional adsorbents in numerous industrial applications.^38,39 Structure types of MOFs span a vast library, and in some cases, the as-synthesized material features metal ions with coordination spheres that are completed with solvent molecules introduced during synthesis. Removal of this solvent with heating under reduced pressure (desolvation) generates coordinatively-unsaturated (or “open”) metal centers that can directly interact with adsorbate molecules. The appropriate choice of metal and linker can give rise to a material featuring open metal sites that preferentially bind certain guests based on specific selectivity handles, including gas polarizability,⁴⁰ π-acidity,⁴¹ and electron affinity.⁴²

In 2010, the metal–organic framework Cr₃(btc)₂ (btc³⁻ = 1,3,5-benzenetricarboxylate) was reported to strongly bind O₂via electron transfer to form a Cr^III–O₂⁻ adduct.⁴² The pristine material features a high-density of exposed chromium(II) sites and accordingly displays a high O₂ uptake of 11 wt% at 298 K and an O₂/N₂ selectivity of ∼22 based on single-component adsorption data, notably five times higher than that achieved with cobalt(II) molecules immobilized on silica.³⁶ This discovery represented a significant advance in the design of O₂-selective adsorbents and validated the strategy of using redox-active open metal sites in MOFs to target guests based on differences in electron affinity. However, because of the highly exothermic O₂ binding in Cr₃(btc)₂, the material capacity decreases with repeated cycling, likely owing to incomplete regeneration of the open metal sites and/or sample degradation. This result therefore also underscores the importance of designing a material exhibiting selective and reversible O₂ binding. Since this seminal work, several studies have focused on the design of MOFs featuring open metal sites that are capable of selective oxygen capture via electron transfer chemistry.^43–45 This effort has focused on the chemical space containing monovalent, divalent, and trivalent redox-active metal sites in diverse coordination environments, ranging from anionic oxygen donors in a square pyramidal geometry to nitrogen heterocycles in a trigonal pyramidal geometry.^42–48 Although no MOF has been discovered to date that can be considered a commercially viable O₂-selective adsorbent, a number of promising systems and materials design strategies have emerged in recent years.

In this Perspective, we provide a comprehensive survey of the field of O₂-selective MOFs with the goal of motivating continued progress and new directions in this emerging area of research. A summary of key molecular and biological systems that reversibly bind O₂ is presented in Section 2 to introduce the various species known to form upon binding and reduction of O₂ at open metal sites, as well as relevant design considerations for tuning O₂ binding in MOFs. In Section 3, these concepts are applied in a survey of key framework materials studied to date, which highlights progress and promising areas for future exploration. A critical contribution in the latter section is an in-depth examination of the relevant thermodynamic parameters and working conditions for adsorptive air separation processes. Traditionally, only O₂ binding enthalpies have been presented in the literature along with O₂/N₂ selectivities at a range of temperatures, precluding meaningful comparisons across materials. We discuss the free energy of O₂ binding as the most important metric to consider when evaluating and designing new MOFs for practical air separations and calculate ΔG values for preliminary comparison and benchmarking of existing materials. In Section 4, density functional theory (DFT) approaches for materials evaluation are discussed that can support experimental efforts, and promising MOF targets based on the aforementioned thermodynamic considerations are identified. A brief summary and conclusions are presented in Section 5.

2. Design inspiration from molecular and biological examples of reversible O₂ binding

2.1 Fundamental considerations

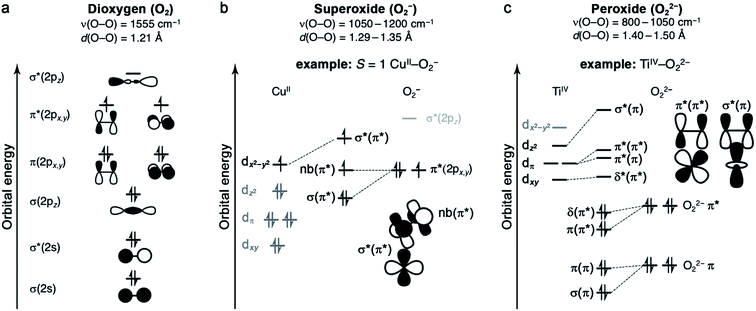
Oxygen binding at a redox-active metal center is an exothermic reaction, facilitated by a strong charge-transfer component. The resulting enthalpic driving force is offset to varying degrees by an entropic penalty.^49,50 The entropy of O₂ binding is made up of translational, rotational, vibrational, and electronic components (ESI Section S3†), and ultimately cannot exceed the entropy of free O₂.⁵¹ Typically, the greater the degree of charge transfer, the stronger the metal–oxygen bonding, and the fewer degrees of freedom for the bound O₂. As such, enthalpy and entropy tend to correlate broadly.⁴⁹ Nevertheless, as discussed below, it is important to quantify ΔS in addition to ΔH, because small entropic changes can meaningfully impact ΔG under practical conditions for O₂ separations.

The properties of O₂ as a ligand are determined by its frontier molecular orbitals (Fig. 1a).^49,52 As a result of its filled and stable π and σ bonding orbitals, oxygen features a strong O=O double bond and is a poor π donor. Each π* orbital contains an unpaired electron, giving rise to the S = 1 ground state of dioxygen. Finally, O₂ features a high-energy vacant σ*(2p_z) orbital. One- or two-electron reduction results in partial or complete filling of the π* orbitals and the formation of superoxide (O₂⁻) or peroxide (O₂²⁻) ligands, respectively. Successive reductions weaken and break the O–O π bond, simultaneously stabilizing the σ*(2p_z) orbital such that it can participate in back-bonding interactions.⁵³ While it is generally useful to classify oxygen as a ligand according to the level of reduction, from neutral dioxygen to peroxide, transition metal–O₂ complexes can be highly covalent, which can complicate the assignment of formal oxidation states.

Fig. 1 (a) Qualitative molecular orbital diagram of dioxygen. (b) Qualitative electronic structure of an S = 1 end-on Cu^II–O₂⁻ complex, with key orbital interactions highlighted. (c) Qualitative electronic structure of a side-on Ti^IV–O₂²⁻ complex, showing two molecular orbital interactions. For the resulting molecular orbitals, the bond type is indicated by the nature of the M–O₂ interaction, and the contributing O–O bond type is indicated in parentheses.

2.2 Dioxygen complexes

Stable metal–O₂ molecular complexes are rare because neutral O₂ is generally a poor ligand. Nonetheless, there are cases where O₂ binding induces a perturbation of the metal electronic structure that imparts stability in the absence of appreciable net electron transfer. For example, the Pauling and Coryell model of hemoglobin involves O₂ binding to an initially high-spin (S = 2) heme iron(II) center, resulting in singlet O₂ bound to a low-spin (S = 0) iron(II).⁵⁴ This model is qualitatively correct for the picket fence iron porphyrin, Fe^II(TpivPP)(1-MeIm) (TpivPP = meso-tetra(α,α,α,α-o-pivalamidophenyl)porphyrin; 1-MeIm = 1-methylimidazole),^51,55,56 a hemoglobin model complex, but is not fully descriptive of hemoglobin (see Section 2.6).⁵⁷ While there is no discrete electron transfer from iron to O₂ in this complex, the binding is nonetheless very exothermic in the solid state (ΔH = −65.3 kJ mol⁻¹, Table 3), and importantly reversible.⁵¹ Indeed, no degradation of the complex was observed over the course of more than 200 O₂ binding/vacuum cycles. This strong yet reversible binding stems in part from strong backbonding from the metal into the O₂ π* orbital, enabled by the high degree of porphyrin-iron covalency.⁵⁶ Additionally there is σ-donation from O₂ to the d_z² orbital of iron. These interactions collectively weaken the O–O bond, resulting in a redshifted O–O stretch of 1159 cm⁻¹, which is within the diagnostic range for superoxide.⁵⁸ This example illustrates the limitations of formal assignments in highly covalent metal–O₂ interactions and demonstrates that the O–O stretching frequency is not always sufficient to assign the degree of O₂ reduction definitively.⁵⁹ Furthermore, this result suggests targeting iron-based frameworks with highly covalent bonding between metal and linker as a strategy to achieve strong, reversible O₂ binding.

Table 3 O₂ binding properties of notable biological and synthetic examples

Compound	−ΔH (kJ mol^−1)	−ΔS (J mol^−1 K^−1)	ΔG298 (kJ mol^−1)	M–O2 assignment	Ref.
a Collected in the solid state. 1-MeIm = N-methylimidazole. b Binding of the O2 to the first site in human hemoglobin in a buffer solution with pH = 7.6. c Binding of O2 to the fourth site human hemoglobin in a buffer solution with pH = 7.6. d N4 = N^1N^1N^4N^4-Tetrakis(2-(pyridin-4-yl)ethyl)butane-1,4-diamine. e Binding of O2 to P interruptus hemocyanin in buffer solution with pH = 9.6.
Fe(TpivPP)(1-MeIm)O2^a	65.3	183.0	−10.8	Fe^II–O2	55
Co(TpivPP)(1-MeIm)O2^a	55.6 ± 3.8	192.5 ± 12	1.70	Co^III–O2^−	62
(Hemoglobin)O2^b	43.1 ± 4.6	74.1 ± 15.5	−21.0	Fe^II–O2/Fe^III–O2^−	91
(Hemoglobin)(O2)4^c	85.0 ± 18.0	190.6 ± 60.2	−28.1	Fe^II–O2/Fe^III–O2^−	91
[Cu2(N4PY2)(O2)]^2+^d	58 ± 2	165 ± 8	−9.0	Cu2O2^2−	64
(Hemocyanin)O2^e	46	67	−26	Cu2O2^2−	50

---

2.3 Superoxide (O₂⁻) complexes

Metal–O₂⁻ complexes form upon transfer of a single electron from a reducing metal center (e.g., Cr^II, Mn^I, Fe^II, Ni^I, and Cu^I) into the half-filled π* orbital of O₂.⁵² Population of this antibonding orbital weakens the π bond of O₂, resulting in a modest elongation of the O–O distance from 1.21 to 1.29–1.35 Å, as well as a redshift of the O–O stretching mode from 1555 cm⁻¹ to 1050–1200 cm⁻¹ (Fig. 1b).^23,60 Superoxide may bind in either a side-on or an end-on mode. The end-on binding mode involves localization of negative charge on the proximal oxygen and a bent M–O–O angle. Side-on binding, while potentially more sterically demanding, can improve metal–superoxide orbital overlap. For both binding modes, the unpaired electron on superoxide resides in a π* orbital, and magnetic coupling between the superoxide and metal center is determined by overlap of this orbital with half-filled metal d orbitals. For example, in an end-on d⁹ copper(II) superoxide complex (Fig. 1b), the singly occupied d_x²−y² orbital is orthogonal to the superoxide π* non-bonding orbital, affording an S = 1 ground state that arises from ferromagnetic coupling between the metal and O₂⁻.⁶¹

The formation of end-on superoxide upon O₂ binding is also well-documented for five-coordinate cobalt(II) Schiff base complexes. Oxygen binding in solution results in the formation of a superoxide ion bound to cobalt(III), with enthalpies ranging from −33 to −77 kJ mol⁻¹, and a corresponding high entropic penalty of >150 J mol⁻¹ K⁻¹.²⁴ The oxygenation of cobalt(II) Schiff base complexes in solution is often reversible, although it is very dependent on solvent and temperature. Particularly at high temperature and in non-polar solvents, the formation of a Co^III₂(μ²-O₂²⁻) species can occur, which is usually an irreversible process.²⁴ Another well-known Co^III–O₂⁻ complex is Co(TpivPP)(1-MeIm)(O₂), a model for cobalt-substituted hemoglobin that reversibly binds O₂ (Table 3).^58,62,63

2.4 Peroxide (O₂²⁻) complexes

In general, peroxide complexes form upon transfer of two electrons from one or more metal centers to fill the formerly half-occupied π* orbitals of O₂. In compounds featuring a metal prone to two-electron chemistry, such as titanium(II), manganese(II), or a second- or third-row transition metal, both electrons may derive from the same metal center.⁵² Reduction of O₂ to peroxide is associated with significant lengthening of the O–O bond, from 1.21 to 1.40–1.50 Å, as well as a pronounced redshift in the O–O stretching mode to approximately 800–1050 cm⁻¹ (Fig. 1c).⁶⁰ In mononuclear complexes, peroxide tends to bind in a side-on fashion, as there is no efficient mechanism for polarizing the O₂²⁻ charge on a single oxygen atom (Fig. 1c). One notable peroxide complex is oxy-hemocyanin, which features a binuclear copper(II) core with a side-on bridging O₂²⁻.²⁷ This oxygen-binding protein has inspired the development of a diverse class of molecular mimics,⁵⁰ including [Cu₂(N4PY2)(O₂)]²⁺ (N4 = N¹,N¹,N⁴,N⁴-tetrakis(2-(pyridin-4-yl)ethyl)butane-1,4-diamine), which binds O₂ reversibly in solution.⁶⁴ Interestingly, increasing temperature and decreasing O₂ pressure in the headspace of the reaction vessel enables repeated cycling between oxygenated and deoxygenated forms. This molecule binds O₂via single-electron transfer from each copper(I), and this event is associated with an enthalpy of −58 kJ mol⁻¹ and an entropy of −165 J mol⁻¹ K⁻¹, such that the reaction is exergonic at 298 K (Table 3).

2.5 Metal and ligand selection and secondary-sphere effects

As discussed above, reversible O₂ binding at open metal sites can generate a spectrum of O₂ species and binding modes. Further fine-tuning of O₂ binding affinity can be accomplished by changing the metal identity in an isostructural series of compounds, perturbing the electronic structure of the metal via ligand modifications,^61–63 or by altering the steric and noncovalent interactions in the secondary coordination sphere (Fig. 2).^33,49,65 The first effect is well-illustrated by the series of complexes (TPP)M(O₂)(py) (TPP = tetraphenylporphyrin; M = Cr^II, Fe^II, or Co^II; py = pyridine), wherein the equilibrium constant for oxygenation increases from Co to Cr (Fig. 2a).^66–69 Indeed, O₂ binding in Cr(TPP)(py) is irreversible, even at low temperatures.⁶⁸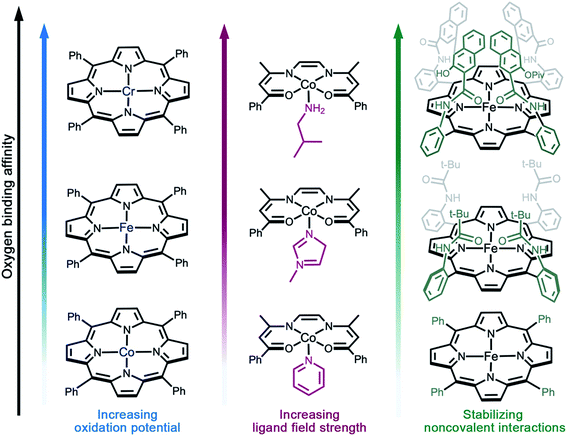

Fig. 2 Illustration of design strategies from molecular chemistry to enhance O₂ binding affinity. (a) Utilizing early- to mid-transition metals,^67–69 (b) increasing the ligand field strength,⁷¹ and (c) using bulky side groups that engage in stabilizing non-covalent interactions with the reduced O₂ species.^55,67,82 Axial solvent ligands are omitted for clarity; in the single coronet iron porphyrin (top right), the distal two naphthalene molecules have been modified for simplicity.

Examples of electronic structure perturbation by ligand modification abound for divalent first-row metal complexes.^{49,65,69–71} In numerous cobalt(II) five-coordinate Schiff base and five-coordinate porphyrin complexes, cobalt adopts a low-spin, d⁷ configuration (S = 1/2), with the unpaired electron residing in the d_z² orbital.^72–75 Oxygen binds end-on to the metal site, mediated by a d_z²–π* orbital interaction that enables electron transfer.⁷⁶ It is possible to destabilize the d_z² energy by changing the axial ligand, which lowers the potential for metal-centered oxidation, thereby increasing O₂ affinity (Fig. 2b).^49,65,76,77 In addition, derivatization of the axial ligand can modify the σ and π bonding contributions to oxygen binding. Analogously, subtle modifications to the linker in cobalt(II) frameworks have been shown to give rise to substantial differences in O₂ binding enthalpies (see Section 3.5).

Noncovalent interactions can also stabilize bound O₂ or promote reversible O₂ binding, as exemplified in several biomimetic systems,^55,78–85 and hydrogen bonding is known to stabilize the reduced O₂ species bound in myoglobin and hemoglobin.^70,86 Additionally, incorporating steric bulk around the metal–O₂ adduct can stabilize reactive O₂ intermediates. For example, iron(II)–porphyrin compounds undergo irreversible oxidation to form oxo-bridged dinuclear species in solution.⁸⁷ In contrast, the picket fence iron(II) porphyrin Fe^II(TpivPP)(1-MeIm)₂ features substantial steric bulk around the metal center, which prevents bridge formation and enables reversible O₂ binding at 25 °C (Fig. 2c).⁵⁵ More recent strategies combining steric protection with favorable non-covalent interactions have also proven fruitful. For example, single-coronet and twin-coronet iron(II) porphyrins featuring hydroxyl-functionalized dinaphthalene moieties have been designed to replicate the hydrophobic environment of the active sites in hemoglobin and myoglobin and to promote biomimetic hydrogen bonding interactions with bound O₂.^82,83 Despite their ubiquity in biology and small molecule chemistry, secondary sphere interactions remain underutilized in MOF chemistry and represent a worthwhile target for future research in the design of O₂-selective materials.⁸⁸

2.6 Lessons from biology: cooperative O₂ binding

Hemoglobin is the prototypical iron-containing O₂ transport protein and features four subunits, with each containing a heme active site.^89,90 The heme iron(II) center is a five-coordinate species with the fifth site occupied by an axial histidine ligand, resulting in a high spin (S = 2) ground state. Dioxygen binds the first heme site with an enthalpy of −43.1 kJ mol⁻¹, yielding a diamagnetic species with an end-on bound O₂.⁹¹ A recent study of oxyhemoglobin using X-ray spectroscopy and a valence bond configuration interaction multiplet model revealed mixed low spin Fe^II/Fe^III character with at least 50% iron(III), reflecting a highly covalent Fe–O₂ interaction.⁵⁷ The change in the iron(II) spin state upon O₂ binding is associated with the depopulation of iron-based orbitals with σ* character, resulting in a contraction of the iron–nitrogen bonds. This local structural change is propagated to the global protein structure via the axial histidine, effecting a transition from the so-called ‘tense’ state (low O₂ affinity) to the ‘relaxed’ state (high O₂ affinity).⁸⁹ This change facilitates subsequent O₂ binding events at the other heme sites. For example, O₂ binding to the fourth heme is associated with an enthalpy of −85.0 kJ mol⁻¹ (Table 3).⁹¹ This cooperativity is key to the function of hemoglobin, enabling the capture and release of relatively large quantities of O₂ in response to a small change in oxygen partial pressure, and is associated with a sigmoidal O₂ binding curve. An unrealized goal in the design of O₂-selective MOFs is to harness cooperativity to enhance material working capacities for O₂ separations, an approach that has proven to be effective for other gaseous adsorbents, including CO₂ and CO.^92,93 As discussed below (see Section 3.4), a triazolate-based framework featuring high-spin iron(II) has been shown to react with O₂ to form low-spin iron(III) bound to superoxide, reminiscent of the mechanism of O₂ binding in hemoglobin.⁴⁵ As such, further exploration of the reduction of O₂ to superoxide by iron-containing MOFs of different topologies may be a fruitful direction in pursuit of cooperative O₂ binding in MOFs.

3. Oxygen-selective metal–organic frameworks

3.1 Enthalpy and entropy considerations for O₂ adsorbents

The enthalpy of O₂ binding at an open metal site is a critical parameter for evaluating the adsorption performance of a material. Indeed, the energy consumption of an adsorption process depends heavily on the enthalpy of adsorption, and in some cases, the enthalpy can represent half of the total energy required for adsorbent regeneration.⁹⁴ As such, the O₂ binding enthalpy is a critical metric to optimize in the design of a commercially relevant O₂-selective MOF, and one that can be judiciously tuned using synthetic chemistry. Perhaps unsurprisingly, there has been a historical focus on this particular parameter. In general, the lower the O₂ binding enthalpy of a material, the lower the corresponding energy demand for adsorbent regeneration. However, if the enthalpy of O₂ binding is too low, the material may not exhibit sufficient selectivity for O₂ over N₂.

The enthalpy of N₂ binding at open metal sites has been experimentally determined for a number of frameworks^44,45,95,96 with corresponding values typically ranging from −10 to −25 kJ mol⁻¹ (vs. ΔH = −22.5 kJ mol⁻¹ for Li-LSX⁹⁷). Accordingly, candidate MOFs for O₂-selective air separations should ideally exhibit O₂ binding enthalpies well above this range. However, materials that exhibit O₂ binding enthalpies that surpass −80 kJ mol⁻¹ may not afford any energy savings over the current industrial benchmark, N₂-selective Li-LSX, due to the energy required to regenerate the O₂ adsorbent (see ESI Section S2†). Thus, to provide a baseline for analysis, we propose −45 kJ mol⁻¹ as a reasonable target O₂ binding enthalpy, which would correspond to a material regeneration energy that is ∼50% less than that required for Li-LSX.^28,97 While an even higher enthalpy of adsorption is likely to be associated with greater O₂/N₂ selectivity, it would come at the cost of greater energy demand for regeneration.

While the enthalpy of O₂ binding is a key factor that will impact the overall energy of adsorbent-based air separations, this parameter must be considered together with the entropy of adsorption. Indeed, it is ΔG, and not ΔH alone, that determines the adsorption properties of a material. In particular, ΔG for the primary O₂ binding site will determine the working capacity under a given set of conditions.⁹⁸ This information is necessary to establish the potential performance of the material in an adsorptive process (see Section 3.5). As such, a binding enthalpy of −45 kJ mol⁻¹ is desirable as long as the corresponding entropy of binding results in an appropriate ΔG for the adsorption process. Relative to binding enthalpy, it is much more difficult to tune the entropy of O₂ binding via metal and/or linker modifications. Entropies of adsorption are not typically reported in the literature, and currently there is no consistent method for reporting both ΔH and ΔS for O₂-selective adsorbents.⁹⁹ As such, to enable a more rigorous comparison of materials in this Perspective, we calculated enthalpy and entropy values for several key O₂-selective frameworks using published Langmuir–Freundlich fits or O₂ adsorption data (see ESI Sections S4 and S5 for details and Tables S1–S9†).^44–47,88 More generally, we suggest that routine determination of binding enthalpies and entropies is a critical facet of materials characterization, requiring minimal additional work, that will enable more rigorous development and benchmarking of MOFs for practical application.

3.2 Key framework structure types

Despite the effectively limitless structural variability possible for metal–organic frameworks, a relatively limited number of frameworks have been studied for selective O₂ adsorption. Here, we briefly describe six key framework structure types that have been studied for selective O₂ capture (Fig. 3).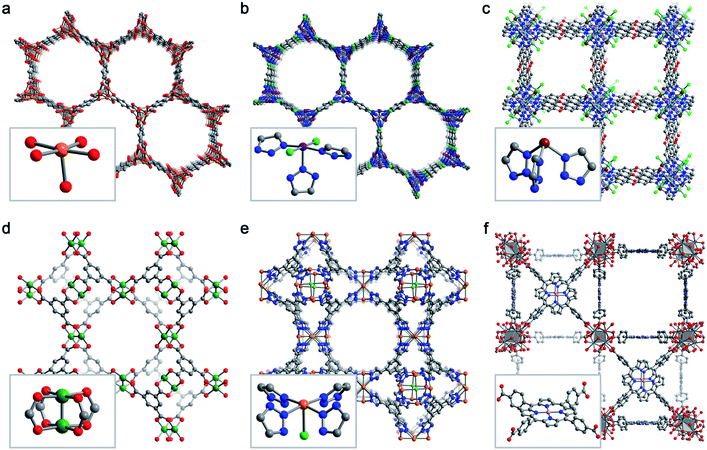

Fig. 3 Representative structures obtained from powder X-ray diffraction (a, b, e), powder neutron diffraction (c, d), or single-crystal X-ray diffraction (f) depicting the six MOF structure types discussed in Section 3.2. Insets show the first coordination sphere of each open metal site. (a) Fe₂(dobdc),⁴³ (b) Co₂Cl₂(bbta),⁸⁸ (c) Cu^I-MFU-4l,¹¹⁰ (d) Cu₃(btc)₂,¹¹⁵ (e) Fe-BTTri,¹²⁴ and (f) Mn-PCN-224.⁴⁷ Orange, purple, green, pink, grey, red, and blue spheres represent Fe, Co, Cu, Mn, C, O, and N atoms, respectively; H atoms are omitted for clarity.

3.2.1 M₂(dobdc). The M₂(dobdc) (M = Mg^II, Mn^II, Fe^II, Co^II, Ni^II, Cu^II, Zn^II; dobdc⁴⁻ = 2,5-dioxido-1,4-benzenedicarboxylate; MOF-74, CPO-27)^95,100–103 family of frameworks features one-dimensional hexagonal pores with vertices lined by helical chains of coordinatively unsaturated divalent metal centers (Fig. 3a). The metals exhibit a square pyramidal coordination geometry, with open coordination sites facing into the pore interior, and are ligated by weak-field carboxylate and aryloxide ligands. These frameworks are particularly attractive, owing to their facile syntheses, tunability, and high density of open metal sites (6.54 mmol g⁻¹ in the case of Fe₂(dobdc), Table 4). Oxygen adsorption has been studied in the Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺ and Cu²⁺ variants of M₂(dobdc).^43,95,96

Table 4 Theoretical and experimental O₂ capacities, IAST O₂/N₂ selectivities, reported binding enthalpies, and reported O–O infrared stretching frequencies for selected metal–organic frameworks, organized from highest to lowest binding enthalpy

MOF	Theoretical O2 capacity^a		Experimental uptake at 1 bar^b			IAST/T (K)	−ΔHO2 (kJ mol^−1)	O–O^c (cm^−1)	Ref.
	mmol g^−1	wt (%)	mmol g^−1	wt%	T (K)
a Calculated based on gravimetric density of open metal sites. b For Cr-BTT, Cr3(btc)2, and Fe2(dobdc), reported uptakes in wt% were converted to mmol g^−1; all other framework capacities were reported in mmol g^−1 and converted to wt%. c Stretching frequencies reported at temperatures associated with reversible O2 binding.
Cr-BTT	3.94	11.2	2.57	7.59	298	2570/298	65	1193	123
Cr3(btc)2	6.43	17.1	3.9	11	298			1129	42
Cu^I-MFU-4l	1.69	5.13	2.33	6.94	233		53		46
Fe-BTTri	3.91	11.1	5.90	15.9	195	27/195	51	1199	45
Mn-PCN-224	0.73	2.3	0.86	2.7	298		49.6(8)	984	47
Co2(OH)2(bbta)	6.45	17.1	7.57	19.5	195	42/195	49(2)	1151	88
Co-BDTriP	3.87	11.0	4.8	13	195	105/195	47(1)		44
Fe2(dobdc)	6.54	17.3	8.16	20.7	211	8/214	41	1129	43
Co-BTTri	3.86	11.0	4.8	13	195	41/195	34(1)		44
Fe-PCN-224	0.73	2.3	0.26	0.83	298		34(4)		129
Co-PCN-224	0.73	2.3	2.00	6.02	195		15.2(6)		130

---

3.2.2 M₂X₂(bbta). Analogous to M₂(dobdc), the M₂X₂(bbta) (M = Mn^II, Fe^II, Co^II, Ni^II; X = Cl⁻, Br⁻, F⁻, OH⁻; H₂bbta = 1H,5H-benzo(1,2-d:4,5-d′)bistriazole) structure type^{88,93,104–107} also features one-dimensional hexagonal channels with pore vertices lined by coordinatively-unsaturated, square pyramidal M^II sites. However, the primary metal coordination sphere is occupied by two basal and one apical triazolate ligands and two μ²-halide or hydroxide ligands (Fig. 3b). Several expanded-pore analogues of this family have also been developed—including the recently reported vanadium variant⁴¹—of the type M₂Cl₂(btdd) (H₂btdd = bis(1H-1,2,3-triazolo[4,5-b],[4′,5′-i])dibenzo[1,4]dioxin).^105,108 While only Co₂X₂(bbta) (X = Cl⁻ and OH⁻) has been studied for O₂ separations,⁸⁸ the tunability and metal site density of this material class render it a promising target for further exploration. As an example, the metal site density of Co₂(OH)₂(bbta) is 6.45 mmol g⁻¹, comparable to the M₂(dobdc) series (Table 4).

3.2.3 M-MFU-4l. The framework MFU-4l, or Zn₅Cl₄(btdd)₃, features pentanuclear zinc nodes, each bridged by btdd²⁻ linkers to six other nodes, resulting in three-dimensional pore system with square pore openings.¹⁰⁹ An octahedral zinc(II) ion sits at the center of each pentanuclear node, and four tetrahedral zinc(II) sites capped by terminal chloride ligands occupy the periphery. Approximately two of these four tetrahedral zinc sites can be post-synthetically exchanged with other divalent metals to yield M^II-MUF-4l (M = Mn, Fe, Co, Ni, and Cu).¹¹⁰ Reduction of Cu^II-MFU-4l yields Cu^I-MFU-4l, which features trigonal pyramidal copper(I) sites (Fig. 3c).⁴⁶ Although their density is low (1.69 mmol g⁻¹), these open copper(I) sites interact strongly (ΔH = −52.6(6) kJ mol⁻¹) and reversibly with O₂. Interestingly, a recent investigation of O₂ binding in Cu^I-MFU-4l using near-edge X-ray absorption fine structure spectroscopy and DFT revealed that the interaction between copper(I) and O₂ is highly covalent, and that O₂ most likely binds side on at the metal site in its triplet configuration.¹¹¹ Given the high tunability^110,112,113 of this structure type, it could serve as an excellent platform to optimize O₂ binding through ligand modification, as an example. We note that the isoreticular framework MFU-4, or Zn₅Cl₄(bbta)₃, is known,¹¹⁴ and although it has not been demonstrated, if the peripheral Zn^II–Cl units in the structure can be replaced with Cu^I, then the corresponding material could exhibit a significantly greater O₂ capacity than Cu^I-MFU-4l.

3.2.4 M₃(btc)₂. As discussed above, the first MOF investigated for O₂ adsorption was Cr₃(btc)₂,⁴² which belongs to a larger family of M₃(btc)₂ materials (also known as M-HKUST-1; M = Cr^II, Fe^II, Ni^II, Cu^II, Zn^II, Mo^II, Ru^II).^115–122 This cubic framework structure features dinuclear paddlewheel-type nodes, each coordinated by four carboxylate groups provided by the triangular trimesate linkers. Each exposed metal site from each paddlewheel node points into a cavity and is accessible to guest molecules (Fig. 3d). This structure class also features a high density of open metal sites (6.43 mmol g⁻¹ for Cr₃(btc)₂, Table 4). To date, Cr₃(btc)₂ is the only material studied for selective O₂ uptake in this family. However, solvated Fe₃(btc)₂ has been isolated and structurally characterized,¹²² and the permanently porous and fully desolvated framework represents an interesting candidate for further study.

3.2.5 M–Benzenetrisazolates. The frameworks Cr₃[(Cr₄Cl)₃(BTT)₈]₂ (Cr-BTT; H₃BTT = 1,3,5-tri(1H-tetrazol-5-yl)benzene),¹²³ M₃[(M₄Cl)₃(BTTri)₈]₂ (M-BTTri; M = Fe^II, Co^II; H₃BTTri = 1,3,5-tri(1H-1,2,3-triazol-5-yl)benzene),^44,45,124 and Co₃[(Co₄Cl)₃(BDTriP)₈]₂ (Co-BDTriP; H₃BDTriP = 5,5′-(5-(1H-pyrazol-4-yl)-1,3-phenylene)bis(1H-1,2,3-triazole))⁴⁴ are O₂ adsorbents belonging to a large family of cubic M–benzenetrisazolate MOFs (Fig. 3e) with open metal site densities close to 4 mmol g⁻¹ (Table 4).^125–127 These sodalite-type structures are built up of truncated octahedra with square nodes formed by four M²⁺ centers bridged by a central μ⁴-Cl and triangular faces formed by benzenetrisazolate linkers. These frameworks are anionic and are charge-balanced by three extra-framework M^II ions per formula unit. Each square pyramidal metal center is coordinated by four basal azolate nitrogen atoms and one apical chloride. The material Co-BDTriP is unique in that it features a distribution of cobalt(II) sites bound by a combination of pyrazolates and triazolates.⁴⁴ Notably, Cr-BTT exhibits one of the highest O₂ capacities of any framework studied to date, 7.6 wt% at 298 K and 1 bar.¹²³

3.2.6 M-PCN-224. The M-PCN-224 frameworks (M = Mn^II, Fe^II, Co^II, Ni^II, Cu^II) consist of zirconium cluster nodes connected by tetratopic porphyrin linkers in a cubic architecture.^47,128–132 The composition of these frameworks is highly variable depending on the synthetic conditions used, and as such it is not straightforward to specify one representative chemical formula. However, a recent study demonstrated that different post-synthetic treatments of the as-synthesized precursor PCN-224 (ref. 133) yield well-defined structures (H₂tcpp)₃[Zr₆O₄(OH)₄(CH₃CO₂)₆]₂ or (H₂tcpp)₃[Zr₆O₄(μ-OH)₄(OH)₆]₂ (H₂tcpp = 5,10,15,20-tetrakis(4-carboxyphenyl)porphyrin). For simplicity, in the subsequent discussion and calculations, we assume a formula of M₃(tcpp)₃[Zr₆O₄(μ-OH)₄(OH)₆]₂ for the M-PCN-224 frameworks. Of the frameworks studied to date, the Mn^II, Fe^II, and Co^II variants have been shown to selectively adsorb O₂. The isolated four-coordinate square planar metal centers in M-PCN-224 (Fig. 3f) mimic metalloporphyrin active sites in proteins, including hemoglobin and myoglobin. As the framework structural rigidity precludes binuclear decomposition pathways encountered with molecular compounds, these frameworks serve as important model systems for O₂ binding in biological systems. However, these MOFs exhibit the lowest metal site densities among the materials considered here (approximately 0.73 mmol g⁻¹).

3.3 Tuning O₂ binding through ligand modification

Typically, MOFs that feature open metal sites are constructed using weak-field linkers, such as 2,5-dioxido-1,4-benzenedicarboxylate.^100,133 As such, the metal nodes are best described as Lewis acidic¹³⁴ and generally interact weakly with oxygen.⁹⁵ A telling example is Co₂(dobdc), which remains high-spin when bound to CO, and exhibits an O₂ binding enthalpy of just −18.56(3) kJ mol⁻¹.⁹⁶ As discussed in Section 2, strong oxygen binding in molecular cobalt complexes is well documented,⁴⁹ but it was only in 2016 that a cobalt(II)-based framework with a stronger ligand field than Co₂(dobdc) was reported. The material Co-BTTri exhibits a modest O₂ adsorption enthalpy of −34(1) kJ mol⁻¹ (Table 4) for loadings up to ∼2 mmol g⁻¹ (6 wt%).⁴⁴ Vibrational modes corresponding to the O₂ adduct could not be observed at room temperature, but calculations suggest there is only partial electron transfer from cobalt(II) to O₂ (0.31 electron equivalents). The theoretical uptake of the material, assuming one bound O₂ at each low-spin cobalt(II) site, is 3.86 mmol g⁻¹ (11.0 wt%); however, the experimental uptake at the cobalt sites was approximately 2.8 mmol g⁻¹ (8.2 wt%), as determined from the inflection point in the plot of the isosteric heat of adsorption as a function of loading. This lower than expected capacity is common in frameworks with open metal sites and may be due to the presence of residual coordinated synthesis solvent or blocked pore access¹³⁵ or potentially even metal site vacancies.^136,137 Interestingly, the N₂ enthalpy of adsorption in Co-BTTri is only −12(1) kJ mol⁻¹,⁴⁴ and this relatively weak affinity for N₂ suggests that the low-spin cobalt(II) sites are neither strongly Lewis acidic or π-basic.

Replacement of the triangular BTTri³⁻ linker with the more basic BDTriP³⁻, which features one pyrazolate and two triazolate donors, yields the framework Co-BDTriP.⁴⁴ Characterization of this material via single-crystal X-ray diffraction supports the presence of a statistical distribution of five unique cobalt centers coordinated by a combination of triazolates and pyrazolates. Notably, at very low loadings, the isosteric heat of O₂ adsorption in Co-BDTriP is −47(1) kJ mol⁻¹, corresponding to O₂ bound at approximately 12% of the cobalt(II) sites in the material. This enthalpy is much larger than the highest binding enthalpy characterized for Co-BTTri (and within the range observed for cobalt(II) Schiff complexes, see Section 2.3), and was ascribed to O₂ binding at cobalt sites ligated by three or more pyrazolates. Relative to the enthalpy of O₂ binding in Co-BTTri at low-loading, this larger value can be rationalized as arising from a greater degree of charge transfer from cobalt(II) to O₂, resulting from the more basic (electron-donating) pyrazolate groups. With increasing gas loading, the enthalpy of O₂ binding in Co-BDTriP decreases, and at a loading of approximately 1 mmol g⁻¹, Co-BDTriP and Co-BTTri exhibit similar binding enthalpies. Interestingly, increasing the linker basicity from Co-BTTri to Co-BDTriP has little effect on the enthalpy of N₂ adsorption. The more basic linker environment in Co-BDTriP may destabilize the d_z² orbital of cobalt(II) relative to that in Co-BTTri, yielding a less Lewis-acidic metal center and thereby diminishing the σ interaction between the HOMO of N₂ and cobalt, compensating for any enhanced π-backbonding. Considering the enhancement in O₂ binding enthalpy at low loadings upon moving from Co-BTTri to Co-BDTriP, a promising target may be the material Co₃[(Co₄X)₃(BTP)₈]₂ (hereafter, Co-BTP, H₃BTP = 1,3,5-tri(1H-pyrazol-4-yl)benzene), featuring all pyrazolate donors. Such a material isostructural to Co-BTTri and Co-BDTriP has not yet been isolated, although the framework Co₃(BTP)₂ has previously been synthesized,¹³⁸ suggesting that appropriate synthetic conditions may yield Co-BTP. In general, the results for Co-BTTri and Co-BDTriP indicate that further investigation of suitable frameworks featuring basic azolate-based linkers and cobalt(II) centers is a worthwhile pursuit.

The open metal sites in Co₂Cl₂(bbta) exhibit a square pyramidal metal coordination geometry, similar to that in Co-BTTri and Co-BDTriP. However, the metal sites are ligated by two trans basal chloride ions and three triazolates (Fig. 3b).¹⁰⁵ The O₂ binding enthalpy of −15 kJ mol⁻¹ in Co₂Cl₂(bbta)⁸⁸ is significantly lower than in Co-BTTri and Co-BDTriP, and perhaps surprisingly, even lower than in Co₂(dobdc). Here, the replacement of a strong σ-donating nitrogen ligand with a weakly σ-donating chloride likely attenuates metal-to-oxygen charge transfer, and thus the cobalt(II) sites in Co₂Cl₂(bbta) are both insufficiently reducing and poor Lewis acids.

Replacing the bridging chlorides in Co₂Cl₂(bbta) with more basic hydroxides yields the material Co₂(OH)₂(bbta).¹⁰⁶ This framework exhibits an O₂ binding enthalpy of −49(2) kJ mol⁻¹ at low loadings, the highest value reported to date for a cobalt framework.⁸⁸In situ variable-temperature diffuse reflectance Fourier transform spectroscopy (DRIFTS) was used to characterize the O₂ binding and revealed an O–O stretch at 1151 cm⁻¹, consistent with a superoxide moiety bound end-on to cobalt(III). DRIFTS data also indicate that the superoxide is stabilized by hydrogen bonding interactions with the bridging hydroxo groups of the framework, reminiscent of the stabilization of superoxide in oxygen binding proteins. Calculations suggest that this secondary coordination lowers the binding energy of O₂ by 20 kJ mol⁻¹, highlighting the significant impact of subtle coordination sphere changes in isostructural MOFs. This additional interaction also contributes to a very large entropy of adsorption of −186(7) J mol⁻¹ K⁻¹.

Interestingly, the calculated saturation capacity of the strong O₂ binding site in Co₂(OH)₂(bbta)—determined from fits using a dual-site Langmuir model—was found to be 2.46 mmol g⁻¹, only 38% of the theoretical capacity based on open metal site density. However, data from powder X-ray diffraction analysis revealed that the actual occupancy is much higher (approximately 75%), indicating that the chosen adsorption model was not adequate for describing the O₂ uptake in this material. Together with in situ DRIFTS data obtained at different O₂ loadings, these results revealed that O₂ binding weakens as a function of loading, a rare example of example of negatively cooperative gas binding in a metal–organic framework.¹³⁹ Notably, the same extended lattice interactions that promote initial strong O₂ binding contribute to this unusual effect. Indeed, with increasing O₂ loading, the proportion of cobalt(III)–O₂⁻ moieties also increases, rendering neighboring cobalt(II) sites less electron-donating and therefore less likely to bind O₂via electron transfer. This unexpected result highlights that the nature of electronic communication between metal sites in MOFs must be tuned carefully to achieve desired O₂ binding properties. Here, the appropriate choice of a secondary metal could potentially give rise to an ordered mixed-metal framework of the type CoM(OH)₂(bbta) that exhibits a high enthalpy of O₂ binding in the absence of negative cooperativity. In this case, it may be possible to achieve an O₂ uptake as high as 3 mmol g⁻¹. However, due to the presence of hydrogen bonding interactions, even in this case, O₂ binding is still likely to be associated with a high entropic penalty. As an alternative, replacing the hydroxide moieties with bridging methoxide or methylthiolate anions would remove such interactions and potentially still provide sufficient reducing power at the metal center to ensure a high binding enthalpy.

3.4 Tuning O₂ binding through metal selection

One of the most well-studied isostructural framework series is M₂(dobdc) (M = Mn^II, Fe^II, Co^II, Ni^II, Cu^II, Zn^II).¹³³ Excluding the iron variant, the open metal sites in this family behave like Lewis acids, and generally, they preferentially bind N₂ over O₂,^43,95,96 given the greater polarizability and quadrupole moment of N₂ (Table 1).⁹⁷ Characterization of O₂ binding in the Mn, Co, Ni, and Cu variants revealed that the metal–O₂ interactions are also predominately electrostatic in nature.^95,96

The case of O₂ binding in Fe₂(dobdc) is unique and can be partly rationalized by the fact that iron(II) exhibits a lower ionization energy than Mn^II, Co^II, Ni^II, and Cu^II. Uptake of O₂ in Fe₂(dobdc) results in very steep adsorption isotherm and occurs via superoxide or peroxide formation, depending on the temperature.⁴³ At 211 K, ∼90% of the iron sites reversibly bind O₂, with a total uptake for the material of 6.54 mmol g⁻¹ (17.3 wt%) at 1 bar. Notably, the material is stable to repeated cycling and exhibits no loss in capacity at 211 K over the course of at least 13 adsorption/desorption cycles. The enthalpy of O₂ adsorption in this material was calculated to be −41 kJ mol⁻¹. Although this value is lower than the binding enthalpy determined for Co₂(OH)₂(bbta), the associated O₂ moiety in Fe₂(dobdc) is more reduced than that bound in Co₂(OH)₂(bbta), as judged from their respective O–O stretches of 1129 and 1151 cm⁻¹ (Table 4). The enhanced stabilization of bound O₂ in Co₂(OH)₂(bbta) relative to Fe₂(dobdc) can again be ascribed to the substantial enthalpic contribution from hydrogen bonding (as discussed above). At room temperature, O₂ binding in Fe₂(dobdc) results in irreversible formation of iron(III)–peroxide species at half of the iron sites, with the second reducing equivalent provided by the remaining iron sites. As expected, the O–O bond of the reduced moiety is substantially weakened, and a very low O–O stretch of 790 cm⁻¹ was characterized via IR spectroscopy. The ordered substitution of 50% or more of the iron(II) sites in Fe₂(dobdc) with another divalent metal could potentially suppress the electron transfer between metal sites that leads to irreversible peroxide formation and enable access to a material exhibiting high, reversible O₂ uptake. Of note, while metal⋯metal communication in Fe₂(dobdc) has a deleterious effect on O₂ uptake, it is interesting to consider how the participation of two adjacent metal sites in one reduction and binding event, as observed here, could be manipulated via linker and secondary-sphere interactions to achieve positive cooperativity in O₂ binding.

The framework Fe-BTTri was recently reported, enabling preliminary evaluation of the influence of metal identity on O₂ binding in M-BTTri. Interestingly, the local iron coordination environment in this material bears some resemblance to the heme site of hemoglobin.⁴⁵ At 195 K, 64% of the exposed high-spin iron(II) framework sites bind O₂via superoxide formation with an enthalpy of −51 kJ mol⁻¹, which is 1.5 times that of the binding enthalpy in Co-BTTri. The material reversibly adsorbs 3.3 mmol g⁻¹ (9.6 wt%) of O₂ at 195 K and 210 mbar over the course of 5 cycles. In situ DRIFTS data obtained at 195 K revealed an O–O stretch at 1199 cm⁻¹, which, together with Mössbauer data, confirms the presence of superoxide bound to low-spin iron(III), reminiscent of the mechanism of O₂ binding in hemoglobin (Section 2.6). This complete electron transfer from iron(II) to O₂ contrasts with the partial electron transfer upon O₂ binding in Co-BTTri. Above 258 K, O₂ binding is irreversible.

The M-PCN-224 (M = Mn^II, Fe^II, Co^II) framework class is another instructive example to evaluate the importance of metal identity for O₂ binding in MOFs.^47,129,130 In contrast to what is observed for M₂(dobdc), the enthalpy of O₂ binding in M-PCN-224 increases from cobalt to iron to manganese, consistent with the general trend observed for metalloporphyrin complexes (Section 2). Note, however, that O₂ binding to Mn-PCN-224 (ref. 47) is a two-electron process, whereas one-electron reduction occurs upon O₂ uptake in the other two frameworks. In Mn-PCN-224, 85% of the manganese(II) sites bind O₂ with an enthalpy of −49.6(8) kJ mol⁻¹. The resulting adduct is an η²-peroxomanganese(IV), and the reaction is reversible upon purging with argon.

The framework Fe-PCN-224 (ref. 129) provides a rare example of a base-free heme model. In this material, the high-spin ferrous centers bind O₂ at 195 K to form low-spin iron(III)–superoxo moieties, as characterized using single-crystal X-ray diffraction and Mössbauer spectroscopy data collected at 100 K. Oxygen binding is only appreciable at 195 K and below, and from low-temperature (141, 156, and 195 K) isotherm data the O₂ binding enthalpy was determined to be −34(4) kJ mol⁻¹, consistent with the formation of a superoxo moiety. Notably, this value is substantially lower than that associated with O₂ binding in hemoglobin as well as in biomimetic compounds that feature a bound axial imidazole.^51,91 Using reported isotherm data obtained at higher temperatures (226, 273, and 298 K), we calculated an even lower binding enthalpy of −19(2) kJ mol⁻¹. The large difference in the enthalpy values for the given temperature regimes suggests that binding of O₂ at and near room temperature is associated with the formation of an iron–O₂ adduct distinct from that observed at lower temperatures. In all, these data suggest that electron transfer from iron to O₂ in this system is temperature-dependent, and further studies are warranted to investigate this possibility.

Dioxygen binding in Co-PCN-224 (ref. 130) results in the formation of a low-spin Co^III–superoxide complex, as characterized via single-crystal X-ray diffraction and EPR spectroscopy performed at 85 K. Oxygen adsorption data collected at higher temperatures (113, 141, 156, and 195 K) were used to calculate an enthalpy of O₂ binding of −15.2(6) kJ mol⁻¹, which is much lower than that associated with superoxide formation in Co(TpivPP)(1-MeIm) (Table 3). It is possible that at the higher temperatures associated with isotherm data collection, O₂ binding results in a Co^II–O₂ species. Indeed, an enthalpy of −15.2(6) kJ mol⁻¹ is more consistent with reported enthalpies of −15 and −18.56(3) kJ mol⁻¹ associated with the formation of Co^II–O₂ adducts in Co₂Cl₂(bbta)⁸⁸ and Co₂(dobdc),⁹⁶ respectively. In all, the above results suggest that the detailed investigation of O₂ binding modes in Fe-PCN-224 and Co-PCN-224 as a function of temperature, including the determination of enthalpies and entropies, represents a worthwhile fundamental study.

3.5 Evaluating optimal ΔG for O₂-selective adsorptive processes

As discussed above, values of ΔH are traditionally reported for O₂-selective adsorbents, but the ΔG of O₂ binding is a more meaningful metric for evaluating the performance of a material under practical working conditions. In particular, the ΔG of O₂ binding is a key parameter for determining the useable surface coverage, Δθ, defined as the difference between the surface coverage under adsorption (θ_ads) and desorption (θ_des) conditions (see ESI Section S6†).⁹⁸ The maximal value of Δθ under a given set of working conditions is 1, corresponding to complete coverage of the primary O₂ binding sites upon adsorption (θ_ads = 1) and zero coverage upon desorption (θ_des = 0). Thus, for a given set of target conditions, it is possible to calculate an optimal ΔG value that will maximize theoretical useable capacity. Note that this analysis is intended as a useful starting point, and a comprehensive evaluation of a candidate material will necessarily consider other factors such as O₂/N₂ selectivity (see Section 3.6) and adsorption kinetics.

The specific working conditions for an adsorptive air separation process depend on a multitude of factors, including capital and operating costs, production scale, location, and load variability.^{12,18,94,140,141} For the purposes of the present assessment, we considered a VSA process under two sets of working conditions, namely adsorption of air at 1 bar and 298 K and desorption at 10 or 1 mbar, which are common minimum pressures for dry reciprocating pumps. Based on progress achieved thus far in the development of O₂-selective MOFs and the inherent tunability of these materials, we propose that these conditions represent reasonable targets and additionally would afford considerable costs and energy savings relative to current technologies.

Optimal surface coverage under these two sets of conditions is achieved for ΔG₂₉₈ values of −10.49 and −7.64 kJ mol⁻¹, for desorption at 1 and 10 mbar, respectively. These values are shown as blue and purple lines, respectively, in the plot of ΔS vs. ΔH given in Fig. 4a. The points plotted in Fig. 4a represent the calculated values of ΔG at 298 K associated with O₂ binding at the open metal sites in eight reported frameworks and the hypothetical material Co-BTP, based on calculated ΔS and ΔH values (see the ESI Section S5 for details and Table S11†). An implicit assumption in comparing these data is that the ΔH and ΔS values for each framework are temperature-independent, given the range of temperatures (typically well below 298 K) used to collect adsorption data. While this assumption is not always valid, as discussed previously for Fe- and Co-PCN-224, these results are intended to serve as a proof-of-concept demonstration of using ΔG as a key parameter for more comprehensive benchmarking than has been accessible based on ΔH alone. Overall, the data in Fig. 4a highlight that O₂ binding in most of the MOFs analyzed is not sufficiently exergonic for achieving optimal useable surface coverage under the considered conditions. The one outlier is Cu^I-MFU-4l, for which the ΔG of O₂ binding at the open copper(I) sites is calculated to be −6(1) kJ mol⁻¹. The hypothetical material Co-BTP is also predicted to have a near-optimal ΔG of −11 kJ mol⁻¹. Interestingly, recall the ΔG₂₉₈ of O₂ binding in the molecule Fe(TpivPP)(1-MeIm)₂ is −10.8 kJ mol⁻¹ (Table 3), which suggests that the pursuit of new framework types featuring analogous iron–porphyrin units may be a promising design strategy. Ultimately, using these values as a guideline for evaluating materials must be done with caution, considering that an optimal ΔG₂₉₈ value must be associated with a sufficiently high enthalpy of adsorption to ensure selectivity over N₂ while minimizing regeneration energy.

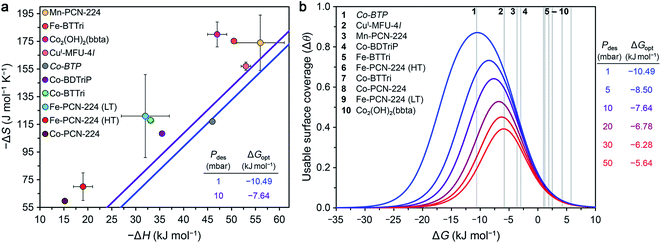Fig. 4 (a) Calculated enthalpy and entropy values of O₂ binding in nine selected frameworks as discussed in the text (colored circles). The optimal Gibbs free energies (ΔG_opt) that maximize O₂ useable surface coverage (Δθ) at 298 K for a VSA process with adsorption at 0.21 bar and desorption 1 and 10 mbar are plotted as blue and purple lines, respectively (see Section S6 of the ESI†). (b) O₂ useable surface coverage at 298 K plotted as a function of ΔG for a range of desorption pressures, following adsorption at 0.21 bar. The optimal Gibbs free energy (ΔG_opt) associated with the maximum useable capacity at each pressure is also given. The Gibbs free energies of O₂ binding for the same frameworks in (a) are shown in the plot as grey bars. As a result of the non-linear relationship between Δθ and ΔG, minor deviations from ΔG_opt have a significant impact on the value of Δθ. See Tables S13 and S14† for the calculated working capacity of each framework under the considered VSA process conditions.

We also determined Δθ as a function of ΔG for several desorption pressures ranging from 1 to 50 mbar, as shown in Fig. 4b, where the same frameworks from Fig. 4a are indicated as numbered grey lines. As a result of the non-linear dependence of Δθ on ΔG and the desorption pressure (see ESI Section S6†), minor deviations in ΔG and P_des can dramatically impact Δθ. For example, the lowest desorption pressures are associated with the largest gains in surface coverage. Only Cu^I-MFU-4l and Co-BTP exhibit ΔG values that give rise to optimal useable surface coverage. Targeting materials that exhibit similar open metal sites and associated enthalpy and entropy values is a worthwhile pursuit.

The combined use of high temperature and vacuum to regenerate an adsorbent, in a so-called vacuum temperature swing adsorption (VTSA) process, can give rise to higher useable surface coverages than accessible with the use of VSA or TSA alone.¹⁴ Additionally, incorporating a temperature swing for desorption enables the recovery of waste heat, albeit generally at the expense of slower cycle times. We assessed the performance of the same MOFs considered above in a VTSA process involving adsorption of air at 298 K and 1 bar (0.21 mbar O₂) and desorption at 338 K and 10 mbar (Table 5). Under these conditions, Co-BTP and Cu^I-MFU-4l again exhibit the highest useable surface coverages of all the frameworks, with Δθ = 0.86 and 0.71, respectively. These values are comparable to that achieved using a VSA process and desorption at 1 mbar and 298 K. In other words, the Δ40 K temperature swing compensates for the 10-fold weaker vacuum in this process. Finally, we emphasize that the foregoing analysis is helpful only to compare the ΔG of adsorption across different frameworks and relative to a defined process condition, and this parameter alone is not sufficient to qualify benchmark adsorbents. It is also critical to consider other factors, such as the density of binding sites in an adsorbent, as well as its O₂/N₂ selectivity (as discussed below).

Table 5 Calculated useable surface coverages (Δθ) and gravimetric and volumetric O₂ working capacities for nine frameworks discussed in the text as implemented in VTSA process with P_ads = 0.21 bar O₂ at 298 K and P_des = 0.01 bar at 338 K. Gravimetric working capacities (mmol g⁻¹) were obtained by multiplying Δθ by estimated gravimetric O₂ capacities for each MOF, determined in most cases from the inflection point of the experimental isosteric heat of adsorption as a function of loading (see Section S5 of the ESI for details).^a Volumetric working capacities (g L⁻¹) were calculated by multiplying Δθ by the estimated volumetric O₂ capacity for each framework (see Table S12 for details)

MOF	Surface coverage, Δθ	Working capacity (mmol g^−1)	Working capacity (g L^−1)
a The inflection point was approximated from the second derivative of the enthalpy versus loading, estimated using the finite difference method.
Co-BTP	0.86	2.4	78.0
Cu^I-MFU-4l	0.71	1.1	20.3
Co-BDTriP	0.43	0.90	29.2
Mn-PCN-224	0.52	0.29	4.3
Co-BTTri	0.083	0.23	6.8
Fe-BTTri	0.095	0.22	6.2
Fe-PCN-224 HT	0.088	0.048	0.77
Co-PCN-224	0.068	0.048	0.75
Co2(OH)2(bbta)	0.014	0.035	1.2
Fe-PCN-224 LT	0.039	0.021	0.34

---

3.6 O₂ working capacities and selectivities

3.6.1 Working capacities. The theoretical O₂ capacity of an adsorbent, as determined from the density of open metal sites in the MOFs discussed here, is a property inherent to the material. In contrast, the actual working capacity of the framework will also depend on the process conditions. In general, the greater the working capacity of the material, the lower the operating and capital costs of the adsorptive process. Specifically, increasing gravimetric working capacity (units of mmol g⁻¹, for example) can increase the product throughput, defined as kg of O₂ separated per kg adsorbent per hour, whereas increasing volumetric working capacity (units of g L⁻¹, for example) can decrease the necessary contactor size—or the size of the system that contains the adsorbent bed—and therefore capital costs.¹²

To estimate the working capacities of the nine investigated frameworks under the aforementioned VTSA process conditions—O₂ adsorption at 298 K and 0.21 bar/desorption at 10 mbar and 338 K—we first determined an estimated gravimetric O₂ capacity in each case (in units of mmol g⁻¹), based on the inflection point in the plot of enthalpy of adsorption as a function of loading (see the ESI Section S5 for details and Table S12†). The gravimetric working capacity in each case was then calculated as the product of this estimated capacity and the process-specific Δθ value for each MOF. Separately, volumetric working capacities (in units of g L⁻¹) were calculated as the analogous product of Δθ and the estimated volumetric capacity in each case. Each estimated volumetric capacity was obtained as the product of the theoretical volumetric capacity (calculated from the single-crystal density) and the multiplicative factor [estimated capacity (mmol g⁻¹)]/[theoretical capacity (mmol g⁻¹)] (see Table S12† for details; note that the volumetric density of a pellet might differ substantially from the single-crystal value). Table 5 summarizes the resulting gravimetric and volumetric working capacities for each framework in the VTSA process. The materials Cu^I-MFU-4l and Co-BDTriP exhibit the highest working capacities of the eight reported frameworks considered, although these capacities are relatively low (∼1 mmol g⁻¹). Interestingly, the gravimetric working capacity of Co-BTP is predicted to be 2.4 mmol g⁻¹. Under the VSA process conditions described earlier, Cu^I-MFU-4l and Co-BDTriP again exhibit the highest volumetric and gravimetric working capacities of the reported materials (see Fig. S2 and Tables S13, S14†). It is noteworthy that the useable surface coverage and gravimetric and volumetric working capacities of those two frameworks are largest even though their associated enthalpies of O₂ binding are not the highest of the materials considered. Ultimately, these data emphasize the importance of considering both ΔH and ΔS when evaluating potential material targets.

We selected Cu^I-MFU-4l, Co-BDTriP, and Co-BTP to further investigate the effects of desorption temperature on volumetric working capacities and useable surface coverages in a VTSA process involving adsorption of air at 298 K and 1 bar (0.21 bar O₂) and desorption at 0.2 bar (see Fig. S3 and S4,† respectively). The working capacities of Cu^I-MFU-4l and Co-BDTriP increase with increasing desorption temperature until they begin to plateau above 370 K, reaching values of ∼21 and 29 g L⁻¹, respectively, at 418 K. In the case of Co-BTP, the working capacity is projected to increase with temperature up to at least 418 K, the highest temperature considered. As might be expected, the useable surface coverage of each material also generally increases with increasing desorption temperature (Fig. S4†). Interestingly, at the lowest desorption temperatures, Cu^I-MFU-4l and Co-BDTriP exhibit slightly higher working capacities and useable surface coverages than Co-BTP, whereas Co-BTP outperforms both frameworks at the highest desorption temperatures.

3.6.2 O₂/N₂ selectivities. The rigorous determination of adsorbent selectivity for one component of a complex mixture, such as O₂ from air, requires the collection of multi-component adsorption data. One approach is to conduct breakthrough experiments, which require a large amount of sample and dedicated instrumentation. However, reasonable selectivity estimates can be obtained using single-component adsorption data and Ideal Adsorbed Solution Theory (IAST).¹⁴² This theory extends Raoult's Law to the adsorbed-gaseous equilibrium and assumes that the adsorbed phase will behave like an ideal solution; IAST has been shown to be accurate across a wide range of adsorbents and gas mixtures.^143,144 However, it is important to note that a redox-mediated adsorption mechanism may result in a non-negligible thermodynamic change in the adsorbent, in which case the assumptions of IAST may not fully hold. In these cases, more accurate assessments of adsorption selectivity can be gained from Monte Carlo simulations.^145–147 Experimentally, adsorption selectivities can also be measured using in situ Fourier transform IR¹⁴⁸ and NMR¹⁴⁹ spectroscopies, mass spectrometry coupled with volumetric assays,¹⁵⁰ and multi-component equilibrium adsorption measurements.¹⁵¹

Table 4 includes the reported O₂/N₂ IAST selectivities for several frameworks for a 21 : 79 O₂/N₂ mixture at 1 bar. Because these values are reported at different temperatures, it is difficult to draw precise comparisons. Nonetheless, we note some key takeaways. For instance, the selectivity of Co-BDTriP is more than double that of Co-BTTri at 195 K, highlighting the power of ligand modifications to tune adsorption properties. However, the most practical materials will be those that are highly selective for O₂ at ambient temperature or above.^14,152 Cr-BTT displays the highest 298 K IAST selectivity of all the materials examined, although it is not entirely stable to repeated cycling.¹²³ Calculated 298 K IAST values for Cu^I-MFU-4l and Co-BDTriP, which exhibit the highest calculated capacities at 298 K, are 6.5 and 14, respectively, for a 21 : 79 O₂/N₂ mixture at 1 bar (Fig. S5 and S6†). Note that these values are based on isotherm data collected at lower temperatures (203 to 233 K), and it will be important to validate these estimates experimentally. Even still, based on all the metrics evaluated above, these two MOFs clearly stand apart from the rest as the most promising O₂-selective adsorbents, and it may be worthwhile to pursue synthetic variants that exhibit further optimized O₂ adsorption properties suitable for practical applications.

3.7 O₂ adsorption without metal coordination

We conclude Section 3 with a brief overview of some additional frameworks that have been shown to selectively bind O₂via mechanisms that do not involve redox-active open metal sites. As only a small fraction of frameworks studied to date feature such sites, it is of interest to explore alternative strategies for achieving selective O₂ uptake in metal–organic frameworks.

3.7.1 Outer-sphere electron transfer. Recently it was shown that reduced frameworks of the type A_xFe₂(bdp)₃ (A = Na⁺, K⁺; bdp²⁻ = 1,4-benzenedipyrazolate; 0 < x ≤ 2)¹⁵³ are capable of selectively binding O₂ over N₂ at ambient (25 °C) or even elevated (200 °C) temperatures.¹⁵² These mixed-valence materials are prepared via chemical reduction of the parent Fe₂(bdp)₃ with alkali naphthalenides and feature one-dimensional pyrazolate-bridged chains of coordinatively-saturated iron centers. Notably, O₂ uptake in these materials occurs due to outer-sphere electron transfer, in contrast to the MOFs discussed above, and the resulting superoxide moieties are stabilized by alkali cations residing within the pores. A suite of structural and spectroscopic data indicate that superoxide formation is associated with significant rearrangement of the alkali cation positions. This phenomenon is kinetically limiting at ambient temperature, precluding the use of these materials for practical applications. However, the use of larger, templating cations that would promote O₂ reduction may be a means of enhancing cyclability. Ultimately, these results represent an important proof-of-concept of the utility of outer-sphere electron transfer for promoting strong, selective O₂ binding and motivate further pursuit of chemically or electrochemically reduced frameworks for selective O₂ binding.

3.7.2 O₂ binding at redox-active linkers. Metal–organic frameworks can also be synthesized with redox-active organic linkers. If these linkers are sufficiently reducing and not sterically encumbered, they may also serve as O₂ binding sites. Few examples of reversible O₂ binding to organic molecules exist,^154,155 and to our knowledge only one example exists in a framework. In particular, the flexible, porous coordination solid comprised of Zn-4,4′-bipyridyl chains bridged by TCNQ (7,7,8,8-tetracyano-p-quinodimethane) dimers was shown to bind O₂ at 77 K.¹⁵⁶ Although the adsorption data were obtained below the boiling point of O₂ and are therefore not directly relevant to the separation of O₂ from air, these results are nonetheless intriguing. Indeed, in situ IR and Raman spectroscopy data suggest partial charge transfer from the TCNQ dimers to O₂. It may be possible to access more reduced O₂ species in MOFs, and at higher temperatures, through the use of more reducing linkers. For example, electrochemically reduced trinitroarene molecules have been shown to reversibly bind O₂ as μ-O₂²⁻ species.^154,155

3.7.3 Additional binding modalities. A small number of materials have been reported to selectively bind O₂ over N₂ through other diverse mechanisms. We highlight a few examples here, although in most cases the selectivity for O₂ is not fully explained. The framework Sc₃(btc)₂ exhibits slight selectivity for O₂ over N₂ at 298 K, which was attributed to framework flexibility and a purported favorable binding pocket for O₂.¹⁵⁷ The microporous metal formate Mn(HCOO)₂ has also been shown to selectively adsorb O₂ over Ar and N₂ below 140 K, although the mechanism is not well-understood.¹⁵⁸ Finally, a family of multicomponent frameworks featuring triangular Cu^I₃(HPyC)₃ (HPyC⁻ = 4-pyrazolecarboxylate) units have been shown to undergo facile oxidation in the presence of water.¹⁵⁹ Upon oxidation, the linear copper(I) centers are converted to square planar copper(II) with coordination spheres completed by a terminal hydroxide and μ³-OH. This reaction is reversible with heating under vacuum or treatment with a mildly reducing solvent. This mechanism is clearly distinct from the other modes of O₂ binding at transition metal sites discussed above, and it is interesting to consider, as a more general strategy, the use of water or other small molecules to facilitate reversible O₂ adsorption in MOFs.

4. Density functional theory calculations of O₂ binding in MOFs

4.1 DFT-based methods for predicting O₂ binding energies in MOFs

Density functional theory-based computational studies of O₂ binding in MOFs can play an important role in supporting experimental design and characterization efforts, and in advancing understanding of binding mechanisms. In general, it can be a challenge to predict the nature of small molecule binding at coordinatively-unsaturated, open-shell transition metals in MOFs using contemporary DFT methods, given that unit cells may contain hundreds of atoms, and because standard functionals can fail to adequately treat exchange and correlation effects associated with van der Waals dispersion and states having open-shell spin and localized d orbital character. Previous studies that have predicted energies associated with O₂ binding to open metal sites in MOFs have used DFT calculations that either treat the full crystalline system with periodic boundary conditions^160–162 or focus on the local O₂ binding environment using cluster models.^44,163,164

MOFs are highly ordered, crystalline materials that can be modeled using periodic boundary conditions, and periodic DFT calculations, typically carried out using an entire unit cell, can enable a realistic description of the framework structure. Important onsite correlation effects—associated with redox-active transition metal centers with open d shells—can be addressed with periodic DFT calculations using hybrid functions or semi-empirical Hubbard U corrections (so-called “DFT + U calculations”),¹⁶¹ which act on the d-states localized on the metal centers. Although empirical in nature and approximate, Hubbard U corrections can lead to improved treatments of electron–electron interactions and are less computationally expensive than using hybrid functionals on a MOF with a large unit cell. It should be noted that prior calculations of energies associated with O₂ (ref. 160 and 161) and CO₂ (ref. 40 and 165) binding in MOFs using DFT + U have shown that the energies can increase or decrease monotonically with increasing U, depending on the nature of binding. While it is possible to obtain Hubbard U values with a first-principles approach, such values do not always improve agreement with experiment.^158,162

Cluster calculations, where only a small number of atoms near the binding site are treated explicitly, can reduce computational complexity while allowing for a more accurate treatment of open-shell systems, through more efficient use of hybrid functionals or more rigorous treatment of local interactions, for example through the use of so-called higher-rung density functionals or even beyond-DFT wave-function based quantum chemistry approaches. However, care must be taken when choosing this approach, as cluster calculations do not consider long-range interactions, which may be important in influencing experimental O₂ binding properties. Relatedly, cluster calculations typically “lock in” the positions of certain atoms, fixing them to their periodic bulk positions, to prevent atomic displacements that would be unfeasible or unrealistic in the extended MOF system. If the initial constrained bond lengths are unfeasibly large (or small) based on the experimentally known spin state for an O₂-bound metal site, it can be difficult to converge the calculation to the correct spin state. Knowledge of the metal–ligand bond lengths alone leaves some ambiguity for how one ought to fix the atomic positions in the cluster. This ambiguity is less of an issue when performing calculations with periodic boundary conditions, where the atomic positions and lattice parameters can relax with greater freedom. For scenarios where calculations on truncated MOF clusters are desirable due to the aforementioned advantages, a periodic DFT calculation at a lower level of theory can first be performed to establish reasonable bounds for variations in bond lengths.⁴⁴

4.2 DFT calculations of O₂ binding in M–benzenetrisazolates

In this section, we describe the results of DFT calculations performed using clusters and periodic boundary conditions to determine predicted O₂ binding energies in the M-BTT, M-BTTri, and hypothetical M-BTP frameworks (M = Cr^II, Mn^II, Fe^II, Co^II). The M–benzenetrisazolates were chosen for this purpose as they represent the largest and most thoroughly investigated family of materials studied to date for O₂ capture and exhibit promising capacities, adsorption enthalpies, and metal site densities.

For DFT cluster calculations, we used the four-metal cluster [M₄Cl(azolate)₈]⁻ to represent the local binding site and the TPSSh hybrid functional (see Fig. S7 and ESI Section S7.2† for details). As shown in Fig. 5a, our DFT calculations predict an increase in the O₂ binding strength with increasing basicity of the azolate linker for all four metals considered, consistent with available experimental data. The calculated O₂ binding energies for the model clusters for Fe-BTTri, and Co-BTTri are larger than the experimentally determined enthalpies for the frameworks, but we note that the degree of over- or under-estimation is heavily influenced by the choice of exchange-correlation functional (see Table S18†). Overall, our calculations suggest that Mn-BTP, Fe-BTT,¹²⁵ and Co-BTP may be promising materials for O₂ separations, given that their predicted binding energies are near the proposed optimal binding enthalpy of −45 kJ mol⁻¹ (refer to Section 3.1). We note that while the synthesis of Co-BTT has been reported,¹²⁷ its O₂ adsorption properties have not been investigated. Based on these calculations and the experimental enthalpies of O₂ adsorption in the congeners with more basic ligands (Co-BTTri and Co-BTTriP), Co-BTT is not likely of interest for further study related to air separations.

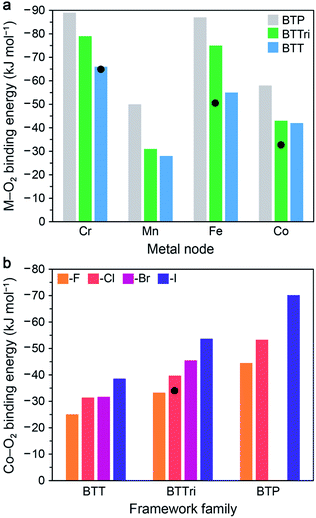Fig. 5 (a) Results of DFT cluster calculations for O₂ binding energies in a series of model four-metal clusters [M₄Cl(azolate)₈]⁻ (M = Cr^II, Mn^II, Fe^II, and Co^II; azolate = pyrazolate, triazolate, or tetrazolate to represent BTP³⁻, BTTri³⁻, or BTT³⁻ linkers). The TPSSh functional was used for M = Mn^II, Fe^II, and Co^II, and M06 was used for Cr^II (see Section S7.2 of the ESI† for details). Experimental enthalpy values are shown as black circles for Cr-BTT, Fe-BTTri, and Co-BTTri. As can be seen, TPSSh tends to overestimate experimental binding energies. Binding energies trend with the basicity of the azolate across all metals. (b) DFT calculations with periodic boundary conditions (PBE-D3 + U, U = 3.3 eV) for O₂ binding energies for the series of [(Co₄X)₃(benzenetrisazolate)₈] (X = F⁻, Cl⁻, Br⁻, and I⁻; benezentrisazolate = BTT³⁻, BTTri³⁻, and BTP³⁻). The experimental O₂ binding enthalpy for Co-BTTri is shown as a black circle. Notably, binding energies trend with the electropositivity of the halide.

Our calculations of O₂ binding to open metal sites in the M–benzenetrisazolate frameworks were carried out using periodic boundary conditions with an eye toward identifying other isostructural materials that may display O₂ binding enthalpies near the proposed optimal value of −45 kJ mol⁻¹. We started with the experimentally determined structure for Co-BTTri and replaced the linker or halide to obtain the various structures considered. Calculations were performed on unit cells of the type [(Co₄X)₃(benzenetrisazolate)₈] (X = F⁻, Cl⁻, Br⁻, and I⁻; benezentrisazolate = BTT³⁻, BTTri³⁻, and BTP³⁻) without charge balancing cations. As such, to represent the anionic framework accurately with an overall neutral unit cell, we added three extra electrons and a positive neutralizing background charge (see ESI Section S7.1† for details). All of the atoms and the lattice vectors were then relaxed. We performed all DFT calculations with PBE + U, and we also employed a pairwise correction term, Grimme D3, to capture van der Waals dispersion corrections. These periodic DFT + D3 + U calculations ultimately enabled us to perform full geometry optimizations without constraining the positions of the atoms, as is necessary in the cluster calculations.

As shown in Fig. 5b, these calculations predict that the O₂ binding energy increases upon moving from X = F⁻ to I⁻. This result may be explained by considering that the electron density around the cobalt sites will increase with the electropositivity of the μ⁴-halide, and therefore charge transfer to O₂ would be increasingly favored. The results further suggest that Co₃[(Co₄Br)₃(BTTri)₈]_2, Co₃[(Co₄I)₃(BTTri)₈]₂, Co₃[(Co₄F)₃(BTP)₈]₂, and Co₃[(Co₄Cl)₃(BTP)₈]₂ may be promising target materials. While the absolute binding energies will be dependent upon the choice of exchange–correlation functional, including the choice of the method used to treat dispersion interactions and the Hubbard U value chosen, it is expected that trends found with a given functional should hold for other choices of functional. Thus, since Co₃[(Co₄Cl)₃(BTTri)₈]₂ has an experimental binding energy below the target value of −45 kJ mol⁻¹, based on our calculated trends, we would expect that Co₃[(Co₄X)₃(BTTri)₈]₂ with X = Br or I would have binding enthalpies close to −45 kJ mol⁻¹. Since no members of the Co₃[(Co₄X)₃(BTP)₈]₂ series have yet been synthesized, whether any of its variants would have a binding enthalpy near −45 kJ mol⁻¹ is unclear, although we would expect from our trends that Co₃[(Co₄Cl)₃(BTP)₈]₂ would bind O₂ more strongly than Co₃[(Co₄Cl)₃(BTTri)₈]₂ and that substituting chloride with larger halides would increase the binding enthalpy.

4.3 Benchmarking entropic contributions to O₂ binding in MOFs

While the calculation of O₂ binding enthalpies is important for evaluating candidate adsorbents, the free energy of adsorption enables a more holistic evaluation of material performance, as discussed in detail above. Obtaining vibrational properties from calculations allows one to additionally calculate ΔS and estimate the ΔG of adsorption. With the calculated free energy in hand, one can also estimate the adsorption isotherm from an ab initio calculation. In addition, vibrational calculations provide the O–O stretching frequency, an important observable for determining the degree of charge transfer to dioxygen.

Given the predominant focus in the experimental literature on the enthalpy of O₂ binding in candidate MOFs, computational efforts have also often focused on this thermodynamic variable. To support future computational and experimental efforts in this area, we investigated how accurately cluster calculations can estimate the ΔS of O₂ binding for the systems of interest here. We chose the M-PCN-224 (M = Mn^II, Fe^II, Co^II) family as a model system because (i) their experimental O₂ binding entropies span a wide range of values (see Fig. 4a) and (ii) the cubic pore shape, face-centered location of the porphyrins (see Fig. 3f), and pore size (approximately 19 Å) are such that one may less ambiguously select the relevant cluster—in this case the metal–porphyrin molecule—when compared to the M-BTTri series.

We first examined various functionals for their accuracy in predicting binding energy. In the case of Mn-porphyrin, many commonly used functionals, even ones benchmarked to transition metal datasets (e.g., MN15, ωB97X-D, M06, PBE0),^166–169 failed to predict the peroxide species bound to Mn(II) (see ESI Section S7.3 for details and Table S20†). Both TPSSh and B97M-rV yielded good estimates of binding energies, but B97M-rV requires far more expensive frequency calculations. Ultimately, TPSSh correctly identified the peroxide and superoxide species that form upon O₂ binding in Mn- and Fe-porphyrin, respectively. The calculated entropy of O₂ binding in Mn-porphyrin is very close to the value calculated for Mn-PCN-224 using the Clausius–Clapeyron relationship (−179 vs. −174 ± 20 J mol⁻¹ K⁻¹, respectively, see Tables S20 and S11†). Similarly, the calculated entropy of O-₂ binding in Fe-porphyrin is −143 J mol⁻¹ K⁻¹, consistent with the value of −121 ± 30 J mol⁻¹ K⁻¹ determined for Fe-PCN-224 at low temperature (Tables S21 and S11†). In contrast, TPSSh did not identify the superoxide species bound in Co-porphyrin, and the calculated O₂ binding entropy is much larger than that determined for Co-PCN-224 (−139 vs. −59.6 ± 0.7 J mol⁻¹ K⁻¹, respectively).

5. Conclusions and outlook

As a result of their high surface areas and atom-level tunability, metal–organic frameworks have emerged as promising candidates for O₂-selective adsorptive air separations. In particular, a number of MOFs featuring coordinatively-unsaturated redox-active metal sites have been discovered to date that are capable of selectively binding O₂ over N₂. Additional strategies for selective O₂ adsorption have also begun to emerge, such as outer-sphere electron transfer from redox-active frameworks and non-redox-mediated chemisorption of O₂. Overall, the continued investigation of new MOFs and O₂ adsorption mechanisms is a key fundamental driver of this important, nascent area of research.

With an eye toward practical applications, frameworks with open metal sites are the most promising materials studied to date. Design strategies have focused on tuning the linker and local coordination environment to generate open metal sites that are sufficiently reducing for selective O₂ binding and can be regenerated using relatively mild swings in temperature or pressure. However, significant improvements are still needed to render MOFs competitive with the incumbent adsorptive air separation technology based on nitrogen-selective zeolites.

Drawing on inspiration from molecular and biological systems that strongly and reversibly bind O₂, we have identified design considerations for further enhancing selective, reversible O₂ uptake in MOFs (Section 2), surveyed key frameworks studied to date for selective O₂ uptake (Sections 3.2–3.4), and evaluated relevant performance metrics (Sections 3.5 and 3.6). While the enthalpy of O₂ binding has traditionally been used to judge material performance, it is the free energy of adsorption, ΔG, that is most important in evaluating suitability for a practical separation process. Thus, going forward, it will be critical for researchers to adopt a more holistic approach, considering both the enthalpy and entropy of O₂ binding in the evaluation of any new MOF for air separations. Other important parameters to consider are gravimetric and volumetric O₂ capacities, based on exposed metal site density, which can readily be estimated from experimental data.

For new frameworks, it will be critical to characterize these properties under working conditions relevant for practical separations, and ambient temperature data should be reported when possible. More rigorous characterization will in turn enable a greater fundamental understanding of O₂ binding at open metal sites. Never has it been so facile to determine thermodynamic parameters for O₂ binding across isostructural series, as exemplified in the case of the M-PCN-224 (M = Mn^II, Fe^II, Co^II) frameworks. Importantly, this understanding will also carry over to other fields working on O₂ activation and reactivity.¹⁷⁰

The free energy of O₂ binding can ultimately be used to determine optimal working conditions for a given adsorbent, or alternatively, to identify an optimal adsorbent for a given set of working conditions. Using available experimental data, we put the latter concept into practice and evaluated the performance of nine MOFs in representative vacuum swing and vacuum/temperature swing adsorption processes. Two known MOFs, Cu^I-MFU-4l and Co-BDTriP, and the hypothetical material Co-BTP, stood out from this analysis as top performers. Beyond this practical insight, these results also suggest that design iterations based on the former two frameworks (and pursuit of Co-BTP) are promising research directions.

Finally, it is important to note that the guidelines established here encompass only material-level factors that can be tuned to accelerate the development of O₂-selective MOFs. Beyond initial design, characterization, and identification of promising candidates, numerous system level factors will also be key to consider in prioritizing materials, such as pellet density, thermal conductivity, cost of synthesis, and impurity resilience. In all, there is a wealth of chemistry yet to be explored in the development of MOFs for selective O₂ capture.

Author contributions

D. E. J, T. D. H., and J. R. L. conceived the manuscript. D. E. J., A. J., B. E. R. S., A. S., E. T., R. R., M. N. D., W. D., J. B. N., T. D. H., and J. R. L. prepared and contributed to portions of the manuscript. K. R. M. provided a critical review and contributed to revisions.

Data availability

The datasets supporting this article have been uploaded as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Department of Energy Office of Science, Office of Basic Energy Sciences, under Award DESC0019992. Work by T. D. H. was supported by the U.S. Army Research Office (W911NF-14-1-0168/P00005). A. J. gratefully acknowledges the National Institute of General Medical Sciences of the National Institutes of Health for support through a postdoctoral fellowship under award number F32GM131587. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. B. E. R. S is grateful for support through an Arnold O. Beckman Postdoctoral Fellowship in Chemical Sciences.

References

1. M. J. Kirschner, A. Alekseev, S. Dowy, M. Grahl, L. Jansson, P. Keil, G. Lauermann, M. Meilinger, W. Schmehl, H. Weckler and C. Windmeier, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2017, pp. 1–32.
2. J. Huang, J. Huang, X. Liu, C. Li, L. Ding and H. Yu, Sci. Bull., 2018, 63, 1180–1186.
3. D. Cecere, E. Giacomazzi and A. Ingenito, Int. J. Hydrogen Energy, 2014, 39, 10731–10747.
4. C. Baukal, Oxygen-Enhanced Combustion, CRC Press, 2nd edn, 2013.
5. M. Behnam, J. Bernstein, T. Gambell and S. Karunakaran, McKinsey Article, COVID-19 exposes a critical shortage of oxygen in developing countries, 2020.
6. S. S. Hashim, A. R. Mohamed and S. Bhatia, Renew. Sustain. Energy Rev., 2011, 15, 1284–1293.
7. I. Saanum and M. Ditaranto, Energy Fuel., 2017, 31, 4445–4451.
8. M. B. Toftegaard, J. Brix, P. A. Jensen, P. Glarborg and A. D. Jensen, Prog. Energy Combust. Sci., 2010, 36, 581–625.
9. R. J. Allam, Energy Proc., 2009, 1, 461–470.
10. D. Jansen, M. Gazzani, G. Manzolini, E. Van Dijk and M. Carbo, Int. J. Greenh. Gas Control, 2015, 40, 167–187.
11. N. Perrin, C. Paufique and M. Leclerc, Energy Proc., 2014, 63, 524–531.
12. R. T. Yang, in Adsorbents: Fundamentals and Applications, John Wiley & Sons, Inc., 2003, pp. 280–381.
13. F. G. Kerry, Industrial gas handbook: Gas separation and purification, Taylor and Franciss Group, LLC, Boca Raton, Florida, 2007.
14. T. Banaszkiewicz, M. Chorowski and W. Gizicki, AIP Conf. Proc., 2014, 1573, 1373–1378.
15. C.C. Chaod, US Pat., 4859217, 1989.
16. R. Kumar, Sep. Sci. Technol., 1996, 31, 877–893.
17. S. Basu and A. K. Debnath, Advanced Ultrasupercritical Thermal Power Plant and Associated Auxiliaries, 2019.
18. A. R. Smith and J. Klosek, Fuel Process. Technol., 2001, 70, 115–134.
19. B. Belaissaoui, Y. Le Moullec, H. Hagi and E. Favre, Sep. Purif. Technol., 2014, 125, 142–150.
20. K. C. Chong, S. O. Lai, H. S. Thiam, H. C. Teoh and S. L. Heng, J. Eng. Sci. Technol., 2016, 11, 1016–1030.
21. L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185.
22. S. M. Hashim, A. R. Mohamed and S. Bhatia, Adv. Colloid Interface Sci., 2010, 160, 88–100.
23. P. L. Holland, Dalton Trans., 2010, 39, 5415–5425.
24. F. Basolo, B. M. Hoffman and J. A. Ibers, Acc. Chem. Res., 1975, 8, 384–392.
25. J. P. Collman, Acc. Chem. Res., 1977, 10, 265–272.
26. R. E. Stenkamp, Chem. Rev., 1994, 94, 715–726.
27. E. I. Solomon, P. Chen, M. Metz, S. K. Lee and A. E. Palmer, Angew. Chem., Int. Ed., 2001, 40, 4570–4590.
28. A. Jayaraman and R. T. Yang, Chem. Eng. Sci., 2005, 60, 625–634.
29. M. Xu, H. C. Wu, Y. S. Lin and S. Deng, Chem. Eng. J., 2018, 354, 62–74.
30. M. Calvin and R. H. Bailes, J. Am. Chem. Soc., 1947, 69, 1886–1893.
31. D. Chen, A. E. Martell and Y. Sun, Inorg. Chem., 1989, 28, 2647–2652.
32. D. Chen and A. E. Martell, Inorg. Chem., 1987, 26, 1026–1030.
33. G. Q. Li and R. Govind, Ind. Eng. Chem. Res., 1994, 33, 755–783.
34. D. Ramprasad, G. P. Pez, B. H. Toby, T. J. Markley and R. M. Pearlstein, J. Am. Chem. Soc., 1995, 117, 10694–10701.
35. R. J. P. Corriu, E. Lancelle-Beltran, A. Mehdi, C. Reyé, S. Brandès and R. Guilard, J. Mater. Chem., 2002, 12, 1355–1362.
36. G. Dubois, R. Tripier, S. Brandès, F. Denat and R. Guilard, J. Mater. Chem., 2002, 12, 2255–2261.
37. N. D. Hutson and R. T. Yang, Ind. Eng. Chem. Res., 2000, 39, 2252–2259.
38. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
39. J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
40. K. Lee, J. D. Howe, L. C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678.
41. D. E. Jaramillo, D. A. Reed, H. Z. H. Jiang, J. Oktawiec, M. W. Mara, A. C. Forse, D. J. Lussier, R. A. Murphy, M. Cunningham, V. Colombo, D. K. Shuh, J. A. Reimer and J. R. Long, Nat. Mater., 2020, 19, 517–521.
42. L. J. Murray, M. Dinca, J. Yano, S. Chavan, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7856–7857.
43. E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822.
44. D. J. Xiao, M. I. Gonzalez, L. E. Darago, K. D. Vogiatzis, E. Haldoupis, L. Gagliardi and J. R. Long, J. Am. Chem. Soc., 2016, 138, 7161–7170.
45. D. A. Reed, D. J. Xiao, H. Z. H. Jiang, K. Chakarawet, J. Oktawiec and J. R. Long, Chem. Sci., 2020, 11, 1698–1702.
46. D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832–5836.
47. A. T. Gallagher, J. Y. Lee, V. Kathiresan, J. S. Anderson, B. M. Hoffman and T. D. Harris, Chem. Sci., 2018, 9, 1596–1603.
48. J. A. Mason, L. E. Darago, W. W. Lukens and J. R. Long, Inorg. Chem., 2015, 54, 10096–10104.
49. E. C. Niederhoffer, J. H. Timmons and A. E. Martell, Chem. Rev., 1984, 84, 137–203.
50. K. D. Karlin, S. Kaderli and A. D. Zuberbühler, Acc. Chem. Res., 1997, 30, 139–147.
51. J. P. Collman, J. I. Brauman and K. S. Suslick, J. Am. Chem. Soc., 1975, 97, 7185–7186.
52. M. H. Gubelmann and A. F. Williams, in Transition Metal Complexes Structures and Spectra, Springer, 1983, pp. 1–65.
53. M. J. Baldwin, D. E. Roo, J. E. Pate, K. Fujisawa, N. Kitajima and E. I. Solomon, J. Am. Chem. Soc., 1992, 114, 10421–10431.
54. L. Pauling and C. Coryell, Proc. Natl. Acad. Sci. USA, 1936, 210–216.
55. J. P. Collman, R. R. Gagne, C. Reed, T. R. Halbert, G. Lang and W. T. Robinson, J. Am. Chem. Soc., 1975, 97, 1427–1439.
56. S. A. Wilson, T. Kroll, R. A. Decreau, R. K. Hocking, M. Lundberg, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 1124–1136.
57. J. J. Yan, T. Kroll, M. L. Baker, S. A. Wilson, R. Decréau, M. Lundberg, D. Sokaras, P. Glatzel, B. Hedman and K. O. Hodgson, Proc. Natl. Acad. Sci. USA, 2019, 116, 2854–2859.
58. J. P. Collman, J. I. Brauman, T. R. Halbert and K. S. Suslick, Proc. Natl. Acad. Sci. USA, 1976, 73, 3333–3337.
59. J. M. Praetorius, D. P. Allen, R. Wang, J. D. Webb, F. Grein, P. Kennepohl and C. M. Crudden, J. Am. Chem. Soc., 2008, 130, 3724–3725.
60. C. J. Cramer, W. B. Tolman, K. H. Theopold and A. L. Rheingold, Proc. Natl. Acad. Sci. USA, 2003, 100, 3635–3640.
61. J. W. Ginsbach, R. L. Peterson, R. E. Cowley, K. D. Karlin and E. I. Solomon, Inorg. Chem., 2013, 52, 12872–12874.
62. J. P. Collman, R. R. Gagne, J. Kouba and H. Ljusberg-Wahren, J. Am. Chem. Soc., 1974, 96, 6800–6802.
63. J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert, S. E. Hayes and K. S. Suslick, J. Am. Chem. Soc., 1978, 100, 2761–2766.
64. K. D. Karlin, M. S. Haka, R. W. Cruse and Y. Gultneh, J. Am. Chem. Soc., 1985, 107, 5828–5829.
65. R. D. Jones, D. A. Summerville and F. Basolo, Chem. Rev., 1979, 79, 139–179.
66. F. A. Walker, D. Beroiz and K. M. Kadish, J. Am. Chem. Soc., 1976, 98, 3484–3489.
67. C. J. Weschler, D. L. Anderson and F. Basolo, J. Am. Chem. Soc., 1975, 97, 6707–6713.
68. C. A. Cheung, S. K. Grimes, C. J. Wong and J. Reed, J. Am. Chem. Soc., 1976, 98, 5028–5030.
69. F. A. Walker, J. Am. Chem. Soc., 1972, 95, 1154–1159.
70. L. S. Chen, M. E. Koehler, B. C. Pestel and S. C. Cummings, J. Am. Chem. Soc., 1978, 100, 7243–7248.
71. M. J. Carter, D. P. Rillema and F. Basolo, J. Am. Chem. Soc., 1974, 96, 392–400.
72. B. M. Hoffman, D. L. Diemente and F. Basolo, J. Am. Chem. Soc., 1970, 92, 61–65.
73. B. M. Hoffman, F. Basolo and D. L. Diemente, J. Am. Chem. Soc., 1973, 95, 6497–6498.
74. B. B. Wayland, J. V Minkiewicz and M. E. Abd-Elmageed, J. Am. Chem. Soc., 1974, 96, 2795–2801.
75. L. M. Engelhardt and M. Green, J. Chem. Soc., Dalton Trans., 1972, 6, 724–728.
76. A. Dedieu, M. M. Rohmer and A. Veilard, J. Am. Chem. Soc., 1976, 98, 5789–5800.
77. A. E. Martell, Acc. Chem. Res., 1982, 15, 155–162.
78. T. Nishiura, Y. Chiba, J. Nakazawa and S. Hikichi, Inorg. Chem., 2018, 57, 14218–14229.
79. G. D. Armstrong and A. G. Sykes, Inorg. Chem., 1986, 25, 3135–3139.
80. P. E. Ellis, J. E. Linard, T. Szymanski, R. D. Joanes, J. R. Budge and F. Basolo, J. Am. Chem. Soc., 1980, 102, 1889–1896.
81. J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert, E. Bunnenberg, R. E. Linder, G. N. LaMar, J. Del Gaudio, G. Lang and K. Spartalian, J. Am. Chem. Soc., 1980, 102, 4182–4192.
82. A. Kossanyi, F. Tani, N. Nakamura and Y. Naruta, Chem.–Eur. J., 2001, 7, 2862–2872.
83. F. Tani, M. Matsura, K. Ariyama, T. Setoyama, T. Shimada, S. Kobayashi, T. Hayashi, T. Matsuo, Y. Hisaeda and Y. Naruta, Chem.–Eur. J., 2003, 9, 862–870.
84. J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert and K. S. Suslick, Proc. Natl. Acad. Sci. USA, 1978, 75, 564–568.
85. B. Ward, C.-B. Wang and C. K. Chang, J. Am. Chem. Soc., 1981, 103, 5236–5238.
86. S. E. V. Phillips and B. P. Schoenborn, Nature, 1981, 292, 81–82.
87. D. H. Chin, G. N. La Mar and A. L. Balch, J. Am. Chem. Soc., 1980, 102, 4344–4350.
88. J. Oktawiec, H. Z. H. Jiang, J. G. Vitillo, D. A. Reed, L. E. Darago, B. A. Trump, V. Bernales, H. Li, K. A. Colwell, H. Furukawa, C. M. Brown, L. Gagliardi and J. R. Long, Nat. Commun., 2020, 11, 1–11.
89. W. A. Eaton, E. R. Henry, J. Hofrichter and A. Mozzarelli, Nat. Struct. Biol., 1999, 6, 351–358.
90. K. L. Bren, R. Eisenberg and H. B. Gray, Proc. Natl. Acad. Sci. USA, 2015, 112, 13123–13127.
91. C. R. Johnson, D. W. Ownby, S. J. Gill and K. S. Peters, Biochemistry, 1992, 31, 10074–10082.
92. T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocella, F. Giordanino, S. O. Odoh and W. S. Drisdell, Nature, 2015, 519, 303–308.
93. D. A. Reed, B. K. Keitz, J. Oktawiec, J. A. Mason, T. Runčevski, D. J. Xiao, L. E. Darago, V. Crocellà, S. Bordiga and J. R. Long, Nature, 2017, 550, 96–100.
94. B. A. Mersmann, B. Fill, R. Hartmann and S. Maurer, Chem. Eng. Technol., 2000, 23, 937–944.
95. M. H. Rosnes, D. Sheptyakov, A. Franz, M. Frontzek, P. D. C. Dietzel and P. A. Georgiev, Phys. Chem. Chem. Phys., 2017, 19, 26346–26357.
96. M. I. Gonzalez, J. A. Mason, E. D. Bloch, S. J. Teat, K. J. Gagnon, G. Y. Morrison, W. L. Queen and J. R. Long, Chem. Sci., 2017, 8, 4387–4398.
97. D. Y. Koh, B. R. Pimentel, V. P. Babu, N. Stephenson, S. W. Chai, A. Rosinski and R. P. Lively, Microporous Mesoporous Mateer., 2018, 256, 140–146.
98. H. Swenson and N. P. Stadie, Langmuir, 2019, 35, 5409–5426.
99. A. Nuhnen and C. Janiak, Dalton Trans., 2020, 49, 10295–10307.
100. N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518.
101. P. D. C. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., Int. Ed., 2005, 44, 6354–6358.
102. P. D. C. Dietzel, B. Panella, M. Hirscher, R. Blom and H. Fjellvåg, Chem. Commun., 2006, 1, 959–961.
103. S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870–10871.
104. P. Q. Liao, X. Y. Li, J. Bai, C. T. He, D. D. Zhou, W. X. Zhang, J. P. Zhang and X. M. Chen, Chem.–Eur. J., 2014, 20, 11303–11307.
105. A. J. Rieth, Y. Tulchinsky and M. Dincã, J. Am. Chem. Soc., 2016, 138, 9401–9404.
106. X. F. Lu, P. Q. Liao, J. W. Wang, J. X. Wu, X. W. Chen, C. T. He, J. P. Zhang, G. R. Li and X. M. Chen, J. Am. Chem. Soc., 2016, 138, 8336–8339.
107. A. J. Rieth, A. M. Wright, G. Skorupskii, J. L. Mancuso, C. H. Hendon and M. Dinca, J. Am. Chem. Soc., 2019, 141, 13858–13866.
108. S. S. Park, Y. Tulchinsky and M. Dinca, J. Am. Chem. Soc., 2017, 139, 13260–13263.
109. D. Denysenko, M. Grzywa, M. Tonigold, B. Streppel, I. Krkljus, M. Hirscher, E. Mugnaioli, U. Kolb, J. Hanss and D. Volkmer, Chem.–Eur. J., 2011, 17, 1837–1848.
110. D. Denysenko, J. Jelic, K. Reuter and D. Volkmer, Chem.–Eur. J., 2015, 21, 8188–8199.
111. G. M. Su, H. Wang, B. R. Barnett, J. R. Long, D. Prendergast and W. S. Drisdell, Chem. Sci., 2021, 12, 2156–2164.
112. R. Röβ-Ohlenroth, B. Bredenkötter and D. Volkmer, Organometallics, 2019, 38, 3444–3452.
113. P. Schmieder, M. Grzywa, D. Denysenko, M. Hambach and D. Volkmer, Dalton Trans., 2015, 44, 13060–13070.
114. S. Biswas, M. Grzywa, H. P. Nayek, S. Dehnen, I. Senkovska, S. Kaskelc and D. Volkmer, Dalton Trans., 2009, 33, 6487–6495.
115. S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150.
116. L. Xie, S. Liu, C. Gao, R. Cao, J. Cao, C. Sun and Z. Su, Inorg. Chem., 2007, 46, 7782–7788.
117. J. I. Feldblyum, M. Liu, D. W. Gidley and A. J. Matzger, J. Am. Chem. Soc., 2011, 133, 18257–18263.
118. P. Maniam and N. Stock, Inorg. Chem., 2011, 50, 5085–5097.
119. M. Kramer, U. Schwarz and S. Kaskel, J. Mater. Chem., 2006, 16, 2245–2248.
120. O. Kozachuk, K. Yusenko, H. Noei, Y. Wang, S. Walleck, T. Glaser and R. A. Fischer, Chem. Commun., 2011, 47, 8509–8511.
121. C. R. Wade and M. Dinca, Dalton Trans., 2012, 41, 7931–7938.
122. Y. Yue, H. Arman, Z. J. Tonzetich and B. Chen, Z. Anorg. Allg. Chem., 2019, 645, 797–800.
123. E. D. Bloch, W. L. Queen, M. R. Hudson, J. A. Mason, D. J. Xiao, L. J. Murray, R. Flacau, C. M. Brown and J. R. Long, Angew. Chem., Int. Ed., 2016, 55, 8605–8609.
124. D. A. Reed, D. J. Xiao, M. I. Gonzalez, L. E. Darago, Z. R. Herm, F. Grandjean and J. R. Long, J. Am. Chem. Soc., 2016, 138, 5594–5602.
125. K. Sumida, S. Horike, S. S. Kaye, Z. R. Herm, W. L. Queen, C. M. Brown, F. Grandjean, G. J. Long, A. Dailly and J. R. Long, Chem. Sci., 2010, 1, 184–191.
126. M. Dinča, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876–16883.
127. S. Biswas, M. Maes, A. Dhakshinamoorthy, M. Feyand, D. E. De Vos, H. Garcia and N. Stock, J. Mater. Chem., 2012, 22, 10200–10209.
128. D. Feng, W. C. Chung, Z. Wei, Z. Y. Gu, H. L. Jiang, Y. P. Chen, D. J. Darensbourg and H. C. Zhou, J. Am. Chem. Soc., 2013, 135, 17105–17110.
129. J. S. Anderson, A. T. Gallagher, J. A. Mason and T. D. Harris, J. Am. Chem. Soc., 2014, 136, 16489–16492.
130. A. T. Gallagher, M. L. Kelty, J. G. Park, J. S. Anderson, J. A. Mason, J. P. S. Walsh, S. L. Collins and T. D. Harris, Inorg. Chem. Front., 2016, 3, 536–540.
131. C. J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708.
132. D. Z. Zee and T. D. Harris, Chem. Sci., 2020, 11, 5447–5452.
133. E. D. Bloch, M. R. Hudson, J. A. Mason, S. Chavan, V. Crocellà, J. D. Howe, K. Lee, A. L. Dzubak, W. L. Queen, J. M. Zadrozny, S. J. Geier, L. C. Lin, L. Gagliardi, B. Smit, J. B. Neaton, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 10752–10761.
134. R. Poloni, K. Lee, R. F. Berger, B. Smit and J. B. Neaton, J. Phys. Chem. Lett., 2014, 5, 861–865.
135. W. L. Queen, M. R. Hudson, E. D. Bloch, J. A. Mason, M. I. Gonzalez, J. S. Lee, D. Gygi, J. D. Howe, K. Lee, T. A. Darwish, M. James, V. K. Peterson, S. J. Teat, B. Smit, J. B. Neaton, J. R. Long and C. M. Brown, Chem. Sci., 2014, 5, 4569–4581.
136. M. Asgari, S. Jawahery, E. D. Bloch, M. R. Hudson, R. Flacau, B. Vlaisavljevich, J. R. Long, C. M. Brown and W. L. Queen, Chem. Sci., 2018, 9, 4579–4588.
137. S. J. Geier, J. A. Mason, E. D. Bloch, W. L. Queen, M. R. Hudson, C. M. Brown and J. R. Long, Chem. Sci., 2013, 4, 2054–2061.
138. V. Colombo, S. Galli, H. J. Choi, G. D. Han, A. Maspero, G. Palmisano, N. Masciocchi and J. R. Long, Chem. Sci., 2011, 2, 1311–1319.
139. A. M. Wright, Z. Wu, G. Zhang, J. L. Manusco, R. J Comito, R. W. Day, C. H. Hendon, J. T. Miller and M. Dincă, Chem, 2018, 4, 2894–2901.
140. D. M. Ruthven and S. Farooq, Gas Sep. Purif., 1990, 4, 141–148.
141. T. R. Gaffney, Curr. Opin. Solid State Mater. Sci., 1996, 1, 69–75.
142. K. S. Walton and D. S. Sholl, AIChE J., 2015, 61, 2757–2762.
143. R. Krishna and J. M. Van Baten, Phys. Chem. Chem. Phys., 2011, 13, 10593–10616.
144. P. Billemont, N. Heymans, P. Normand and G. De Weireld, Adsorption, 2017, 23, 225–237.
145. R. Krishna and J. M. Van Baten, ACS Omega, 2020, 5, 20535–20542.
146. E. D. Akten, R. Siriwardane and D. S. Sholl, Energy Fuel., 2003, 17, 977–983.
147. J. Liu, S. Keskin, D. S. Sholl and J. K. Johnson, J. Phys. Chem. C, 2011, 115, 12560–12566.
148. L. Ohlin and M. Grahn, J. Phys. Chem. C, 2014, 118, 6207–6213.
149. M. Sin, N. Kavoosi, M. Rauche, J. Pallmann, S. Paasch, I. Senkovska, S. Kaskel and E. Brunner, Langmuir, 2019, 35, 3162–3170.
150. J. A. Mason, T. M. McDonald, T. H. Bae, J. E. Bachman, K. Sumida, J. J. Dutton, S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2015, 137, 4787–4803.
151. M. K. Taylor, T. Runčevski, J. Oktawiec, J. E. Bachman, R. L. Siegelman, H. Jiang, J. A. Mason, J. D. Tarver and J. R. Long, J. Am. Chem. Soc., 2018, 140, 10324–10331.
152. A. Jaffe, M. E. Ziebel, D. M. Halat, N. Biggins, R. A. Murphy, K. Chakarawet, J. A. Reimer and J. R. Long, J. Am. Chem. Soc., 2020, 142, 14627–14637.
153. M. L. Aubrey, B. M. Wiers, S. C. Andrews, T. Sakurai, S. E. Reyes-Lillo, S. M. Hamed, C. J. Yu, L. E. Darago, J. A. Mason, J. O. Baeg, F. Grandjean, G. J. Long, S. Seki, J. B. Neaton, P. Yang and J. R. Long, Nat. Mater., 2018, 17, 625–632.
154. I. Gallardo and G. Guirado, Phys. Chem. Chem. Phys., 2008, 10, 4456–4462.
155. J. M. Aubry, C. Pierlot, J. Rigaudy and R. Schmidt, Acc. Chem. Res., 2003, 36, 668–675.
156. S. Shimomura, M. Higuchi, R. Matsuda, K. Yoneda, Y. Hijikata, Y. Kubota, Y. Mita, J. Kim, M. Takata and S. Kitagawa, Nat. Chem., 2010, 2, 633–637.
157. D. F. Sava Gallis, K. W. Chapman, M. A. Rodriguez, J. A. Greathouse, M. V. Parkes and T. M. Nenoff, Chem. Mater., 2016, 28, 3327–3336.
158. H. Kim, D. G. Samsonenko, M. Yoon, J. W. Yoon, Y. K. Hwang, J. S. Chang and K. Kim, Chem. Commun., 2008, 4697–4699.
159. B. Tu, Q. Pang, H. Xu, X. Li, Y. Wang, Z. Ma, L. Weng and Q. Li, J. Am. Chem. Soc., 2017, 139, 7998–8007.
160. A. S. Rosen, M. R. Mian, T. Islamoglu, H. Chen, O. K. Farha, J. M. Notestein and R. Q. Snurr, J. Am. Chem. Soc., 2020, 142, 4317–4328.
161. A. S. Rosen, J. M. Notestein and R. Q. Snurr, J. Chem. Phys., 2020, 152, 224101.
162. S. N. Maximoff and B. Smit, Nat. Commun., 2014, 5, 1–9.
163. Y. Wang, J. Yang, Z. Li, Z. Zhang, J. Li, Q. Yang and C. Zhong, RSC Adv., 2015, 5, 33432–33437.
164. B. Supronowicz, A. Mavrandonakis and T. Heine, J. Phys. Chem. C, 2013, 117, 14570–14578.
165. G. W. Mann, K. Lee, M. Cococcioni, B. Smit and J. B. Neaton, J. Chem. Phys., 2016, 144, 174104.
166. S. P. de Visser and M. J. Stillman, Int. J. Mol. Sci., 2016, 17, 1–25.
167. P. Rydberg and L. Olsen, J. Phys. Chem. A, 2009, 113, 11949–11953.
168. N. S. Venkataramanan, A. Suvitha, H. Nejo, H. Mizuseki and Y. Kawazoe, Int. J. Quantum Chem., 2011, 110, 2340–2351.
169. T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103.
170. X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491–2553.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03577d

‡ Current address: Department of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, Indiana 46556, USA.

§ Current address: Department of Chemistry, University of California Davis, Davis, California 95616, USA.

---