Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Autonomous polymer synthesis delivered by multi-objective closed-loop optimisation†
Stephen T.
Knox‡
 ,
Sam J.
Parkinson‡§
,
Clarissa Y. P.
Wilding
,
Richard A.
Bourne
,
Sam J.
Parkinson‡§
,
Clarissa Y. P.
Wilding
,
Richard A.
Bourne
 and
Nicholas J.
Warren
and
Nicholas J.
Warren
 *
*
School of Chemical and Process Engineering, University of Leeds, Woodhouse Lane, Leeds, LS2 9JT, West Yorkshire, UK. E-mail: n.warren@leeds.ac.uk
First published on 18th February 2022
Abstract
Application of artificial intelligence and machine learning for polymer discovery offers an opportunity to meet the drastic need for the next generation high performing and sustainable polymer materials. Here, these technologies were employed within a computationally controlled flow reactor which enabled self-optimisation of a range of RAFT polymerisation formulations. This allowed for autonomous identification of optimum reaction conditions to afford targeted polymer properties – the first demonstration of closed loop (i.e. user-free) optimisation for multiple objectives in polymer synthesis. The synthesis platform comprised a computer-controlled flow reactor, online benchtop NMR and inline gel permeation chromatography (GPC). The RAFT polymerisation of tert-butyl acrylamide (tBuAm), n-butyl acrylate (BuA) and methyl methacrylate (MMA) were optimised using the Thompson sampling efficient multi-objective optimisation (TSEMO) algorithm which explored the trade-off between molar mass dispersity (Đ) and monomer conversion without user interaction. The pressurised computer-controlled flow reactor allowed for polymerisation in normally “forbidden” conditions – without degassing and at temperatures higher than the normal boiling point of the solvent. Autonomous experimentation included comparison of five different RAFT agents for the polymerisation of tBuAm, an investigation into the effects of polymerisation inhibition using BuA and intensification of the otherwise slow MMA polymerisation.
Introduction
Chemical exploration is undergoing significant diversification from the traditional model of manually performed make-then-test experiments.1–4 A range of technologies have equipped the synthetic chemist for enhanced productivity and effectiveness – from in situ analyses to the increasing digitisation and automation of labwork, including computer-controlled reactors and experiments.5,6 With this automation, comes the ability to integrate machine learning algorithms into synthetic chemistry applications – providing an opportunity for a step-change in innovation. These algorithms can be used to optimise chemical processes and vary in complexity and use.Optimisation of chemical processes has traditionally involved a significant (and often arduous) workload and commitment of research time. Furthermore, optimisations are also often performed using the “one variable at a time” (OVAT) approach – which can lead to the identification of false optima.7 One of the simpler, more appropriate, alternatives to OVAT is structured investigation of the reaction space using the statistical design of experiments (DoE) approach – whereby conditions are screened with a set of multivariate experiments.8 For example, an effective optimisation workflow for RAFT polymerisation has been illustrated by Abetz and co-workers,9 who demonstrate accurate prediction and targeting of polymer properties from a DoE screen.
The use of more dynamic, machine learning based approaches offer the opportunity for optimisation with further reduced user input; indeed, so-called blackbox algorithms do not require any prior knowledge,10 such as the Nelder–Mead simplex11,12 and Stable Noisy Optimisation by Branch and Fit (SNOBFIT)13,14 algorithms, which allow for single objective optimisations – i.e. finding the most desirable result for an objective such as yield15 or purity.16
Chemical process optimisation is seldom achieved through a single variable approach since there are usually multiple conflicting objectives. Some initial multi-objective work in the field of polymer synthesis includes the in silico and subsequent manual optimisation of the emulsion copolymerisation of styrene and butyl acrylate, optimising for conversion and particle size with 14 input variables by Lapkin and co-workers.17 Machine learning methods have also recently been applied to RAFT polymerisations by Chen and co-workers to optimise conditions for molecular weight properties.18
Another powerful demonstration of the effectiveness of machine learning guided multi-objective optimisation in polymer synthesis is given by Reis et al., in their work optimising 19F MRI agents – where the identified agents were found to outperform conventional materials.19 Automated flow chemistry forms the basis for the synthetic element of this work – and has shown great promise in the field of polymer science.20,21
However, it is where the entire optimisation process can be automated – combining reactors, online analyses, and algorithms into a closed-loop that the opportunity presented can be fully realised – that is, a thorough exploration of the complexities of a chemical system with a much-reduced user workload. Indeed this has been demonstrated using the Bayesian optimisation method, Thompson sampling efficient multi-objective optimisation (TSEMO), for small molecule examples – to optimise for several conflicting variable pairs – space–time yield (STY) optimised with E-factor, impurity content and starting material conversion.22–24
Bayesian optimisations, such as TSEMO, are well-suited to the non-linear, noisy and expensive to evaluate data associated with chemical systems.10,25,26 The output from these optimisations is the Pareto front – a set of obtainable non-dominated solutions, where a “non-dominated solution is one which cannot be improved upon without a detrimental effect on the other”10 – this front then illustrates the trade-off between the objectives of the experiment.
Synthetic polymer chemistry suffers inherent trade-offs in process efficiency and product quality. To obtain greater control over the polymerisation process, for example, where controlled molecular weight and molar mass dispersity (Đ) are required, reversible de-activation radical polymerisation can be used. Reversible addition fragmentation chain transfer (RAFT) polymerisation27 is one of the most versatile examples of this technology, where the addition of a chain transfer agent (CTA) mediates the radical polymerisation process. However, judicious control over the ratio of initiator to CTA is required: a high concentration of initiator relative to CTA results in a fast, but less controlled polymerisation, where side reactions cause an unwanted increase in Đ. This trade-off means these processes are time consuming if a low Đ is required. Efficient exploration of the trade-off between conversion and Đ presents an enormous opportunity to identify the optimum control that can be achieved under certain condition limits.
Perhaps the reason for the reluctance of the polymer community to embrace these technologies is that polymerisation systems are in their nature complex, where the desired initiation and propagation, co-exist with side reactions such as unwanted termination and chain transfer. The complex reaction network would require substantial mechanistic measurements and modelling to enable accurate a priori prediction of appropriate reaction conditions for a targeted polymer. However, this should be considered an opportunity to instead apply and develop new machine learning with orthogonal analysis to optimise these complex systems.
Recently, real-time tools for monitoring conversion and Đ have been integrated into a range of automated synthetic platforms including online low-field NMR and GPC.21,28–31 This has laid the foundations for autonomous, “intelligent” platforms capable of using machine learning algorithms to optimise the polymerisation process. Indeed, Junkers and co-workers have applied single objective optimisation algorithms to polymerisations, using either GPC32 or NMR spectroscopy,33 allowing for targeting of one of molecular weight and conversion respectively. These technologies represent the first experimental forays of polymer chemists into the field of “intelligent” polymer synthesis. However, in synthesising a polymer, both conversion and molecular weight information (in particular, dispersity) are simultaneously important. Developing the capability to autonomously explore how these features interact will therefore offer great opportunities for developing the next generation of advanced materials.
Herein, we present an automated polymer synthesis platform, combining orthogonal online NMR spectroscopy and GPC which enables closed-loop multi-objective optimisation of RAFT polymerisations. The effectiveness of such an approach is demonstrated using both screening and in conjunction with the TSEMO multi-objective algorithm – which enable user-free experiments to give a comprehensive picture of the chemical system of interest. For the first time, multiple objectives are simultaneously considered in the closed-loop optimisation problem. The power of the holistic nature of this approach is not to be underestimated – it lays the foundation for a step change in productivity and discovery with a heavy reduction in lab workload and effectively opening the polymer lab to 24/7 productivity. Furthermore, pressurised flow chemistry enables experimentation above the normal boiling point of the selected solvents (methanol/dioxane) – illustrating the vast potential of this approach to discover new opportunities in polymer science.
Results and discussion
The versatile, fully autonomous synthetic platform comprised a stainless steel tubular flow reactor (pressurised to 7 bar);34–36 which then feeds into at-line GPC and online benchtop NMR (Fig. 1); all controlled using a custom-built MATLAB interface37 (more details can be found in the ESI†).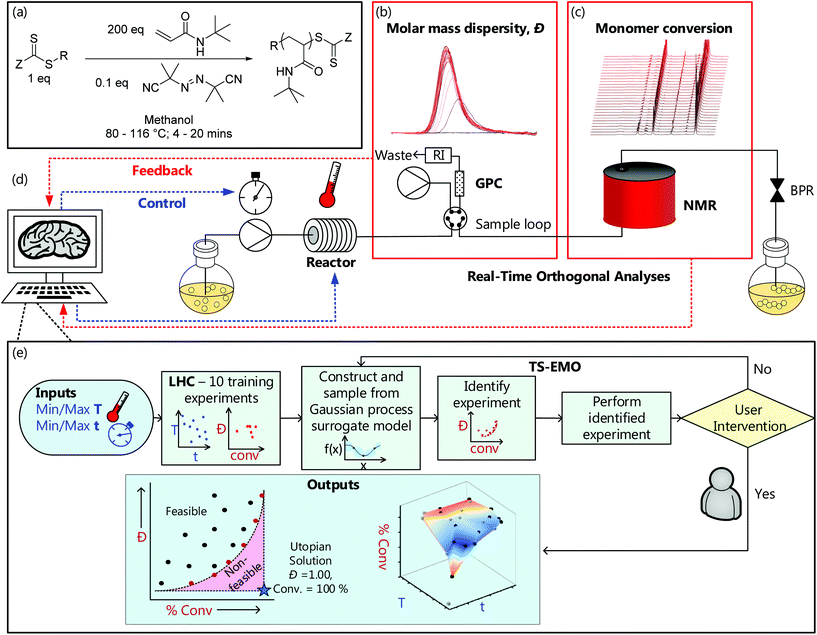 | ||
| Fig. 1 (a) Generalised scheme for the RAFT synthesis of P(tBuAm)200. Example (b) gel permeation chromatography (GPC) chromatograms and (c) 1H nuclear magnetic resonance (NMR) spectra from the automated continuous flow platform used in this work (see ESI† for full platform details and all analytical data). (d) Schematic of that automated platform and (e) an overview of the structure of the machine learning directed (Thompson-sampling efficient multi-objective optimisation (TSEMO) algorithm) experiments used in this work. | ||
Programmed RAFT polymerisation of tert-butylacrylamide (tBuAm) in methanol (Fig. 1a) was performed in the presence of TTC-1 and AIBN ([monomer]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA]
[CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [initiator] 200
[initiator] 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1), at pre-defined reaction temperatures between 80 °C and 116 °C and reaction times between 4 and 20 minutes. NMR spectra (Fig. 1c/see ESI†) were obtained on demand at steady state and processed using an automated script which conducted phase and baseline correction. Subsequently, automated integration of peaks relating to the (monomer) vinyl region (6.4–5.8 ppm) and the (monomer + polymer) aliphatic region (2.3–0.0 ppm) enabled calculation of conversion. A programmable switching valve was used for extraction of gel permeation chromatography (GPC) samples (approx. 3 μl), and molecular weight information obtained by use of a rapid-GPC column and RI detector. This data (Fig. 1b/see ESI†) was also automatically processed, outputting number average molecular weight (Mn), weight average molecular weight (Mw) and molar mass dispersity (Đ) based on calibration with a series of near-monodisperse poly(methyl methacrylate) standards. It is worth noting that since the reactor used is a tubular flow reactor, that any Đ values are not only contingent on the chemistry at the given conditions, but also the residence time distribution of that reactor. This is shown by Reis et al.,38 who demonstrate a narrower RTD and subsequent Đ for narrower tubing, longer residence times and lower viscosity systems.
0.1), at pre-defined reaction temperatures between 80 °C and 116 °C and reaction times between 4 and 20 minutes. NMR spectra (Fig. 1c/see ESI†) were obtained on demand at steady state and processed using an automated script which conducted phase and baseline correction. Subsequently, automated integration of peaks relating to the (monomer) vinyl region (6.4–5.8 ppm) and the (monomer + polymer) aliphatic region (2.3–0.0 ppm) enabled calculation of conversion. A programmable switching valve was used for extraction of gel permeation chromatography (GPC) samples (approx. 3 μl), and molecular weight information obtained by use of a rapid-GPC column and RI detector. This data (Fig. 1b/see ESI†) was also automatically processed, outputting number average molecular weight (Mn), weight average molecular weight (Mw) and molar mass dispersity (Đ) based on calibration with a series of near-monodisperse poly(methyl methacrylate) standards. It is worth noting that since the reactor used is a tubular flow reactor, that any Đ values are not only contingent on the chemistry at the given conditions, but also the residence time distribution of that reactor. This is shown by Reis et al.,38 who demonstrate a narrower RTD and subsequent Đ for narrower tubing, longer residence times and lower viscosity systems.
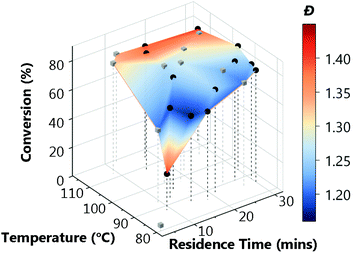
The rich dataset (Fig. 2a), generated with no human interaction comprises conversion and Đ data over several reaction times, across a broad temperature range. A colour-mapped surface (Fig. 2a) visualises the search space of this automated screen enabling identification of trends in conversion (y-axis) and Đ (colour). For example, the highest conversion (83%) is obtained at 107 °C, with a reaction time of 20 min, with Đ = 1.34. Alternatively, the lowest Đ (1.19) with a reasonable conversion (74%) can be achieved by reacting at 98 °C for a reaction time of 16 min. Although a longer reaction time at this temperature allows an increase in conversion to 80%, it has the caveat of an increase in Đ to 1.24. The data obtained here clearly illustrate the expected trade-off in conversion and Đ, where it is difficult to accelerate to enable high conversions over a specified timescale (by increasing temperature) without causing an unwanted increase in Đ. It is also noted that at 116 °C, reduced conversions were observed alongside much higher Đ polymers. This results from the premature consumption of initiator, which precludes the ability to achieve high conversions (see ESI† for relative consumption of initiator). The associated increase in Đ could derive from the resultant higher radical flux at shorter reaction times and competing undesired side-reactions such as chain transfer to polymer or solvent. To obtain such detailed polymerisation kinetic information by traditional methods (batch sampling, offline NMR/GPC, manual data processing) would require extensive user input.
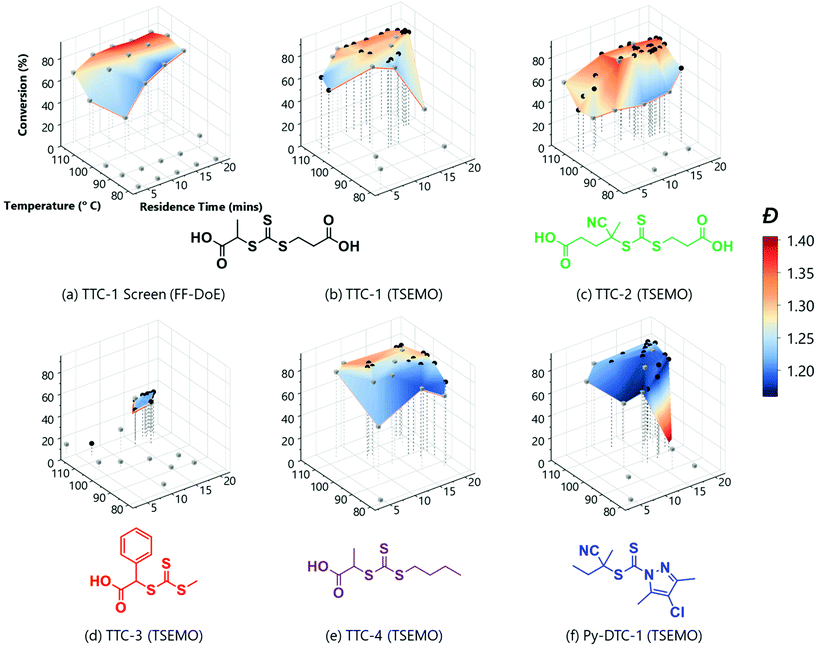 | ||
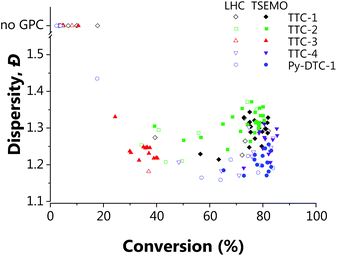
| Fig. 2 Conditions and subsequent monomer conversion and molar mass dispersity, Đ for the automated polymerisation of tert-butyl acrylamide using AIBN as the initiator and a range of RAFT agents – either trithiocarbonate based (TTC-x), or a pyrazole based dithiocarbonate (Py-DTC-1). (a) Shows the results from the full factorial design of experiments screen with TTC-1 and (b)–(f) show the TSEMO based optimisations for the five different RAFT agents, as labelled. The structure colours relate to the data shown in Fig. 3. [Condition limits: 4–20 min, 80–120 °C.] | ||
A disadvantage of the automated screen is unwanted data density in a non-relevant region of the reaction space (i.e. 11 experiments with low conversions). Ideally, a greater data density in a region of interest would enhance the exploration of the parameter space.
An alternative approach, which aims to achieve this targeted investigation, is possible using the aforementioned (Bayesian) TSEMO algorithm to optimise for more than one variable (Fig. 2b – all analysis data available in ESI†). TSEMO uses some initial training data to build a probabilistic model using Gaussian process modelling and selects future experiments using Thompson spectral sampling and the non-dominated sorting genetic algorithm II (NSGA-II),39 balancing exploration of that which is unknown and exploitation of that which is currently optimal. The algorithm is designed to target the theoretical utopian solution as provided by the user – in this case, that is to maximise conversion (to 100%) and minimise dispersity (to 1.0) and, in doing so, explore the trade-off between these two objectives. The result is a dataset which contains a set of non-dominated optimum points, the Pareto front.
The same RAFT system was explored using this approach whereby the only user interaction was to initially define limits for the conditions (4–20 min, 80–116 °C). The system used Latin hypercube (LHC) sampling to generate ten experimental conditions distributed throughout the reaction parameter space. The reactor executed these experiments autonomously, and the online NMR and GPC data was generated and processed in the same manner as the automated screen (see grey cubes on Fig. 2b). This formed the training data used to build the initial surrogate model upon which the TSEMO algorithm based four new experiments (black circles on Fig. 2b) with conditions chosen to experimentally identify the Pareto front (trade-off curve) of the objective. This process proceeded iteratively, focussing experiments within a smaller reaction space between 12–20 minutes and 100–116 °C. Unlike previous work, there is no user intervention required for manual characterisation and/or data processing while the multi-objective optimisation is performed.17–19 The user ended the optimisation where sequential experiments repeatedly gave no real benefit to product quality. In principle, this intervention can occur at any point where the user is satisfied with the product or can be continued to yield a more thorough exploration of parameter space. The surface obtained using the algorithm (Fig. 2b) is directly comparable to that obtained from the automated screen (Fig. 2a). However, the optimisation conducts more ‘useful’ experiments within the highest data density in the region of most interest.
With the successful mapping of parameter space in the above system, we chose to use this algorithm for evaluation of several different RAFT polymerisation systems. In these systems, the only a priori knowledge is the boundary limits of the time and temperature ranges. A key component of RAFT polymerisations is the RAFT agent itself – and the selection of an appropriate agent is essential for a successful polymerisation.40,41 On the whole, an appropriate RAFT agent to use for a particular monomer can be found using the extensive literature.27,41–43 However, it is well-known that subtler changes to the structure will also influence the polymerisation, though the extent of this influence is not always obvious. Using the automated platform presented here, in conjunction with the TSEMO algorithm, we were able to probe the reaction space for four different trithiocarbonate based RAFT agents (TTC-1, TTC-2, TTC-4 & TTC-3 – see Fig. 2b–e), which all have differences in molecular structure that may cause subtle differences in the polymerisation kinetics and resultant polymer properties. These results were then compared to a pyrazole based dithiocarbonate RAFT agent (Py-DTC-1, Fig. 2f) which have been found by Gardiner et al. to outperform these trithiocarbonates in polymerising acrylamide monomers.44
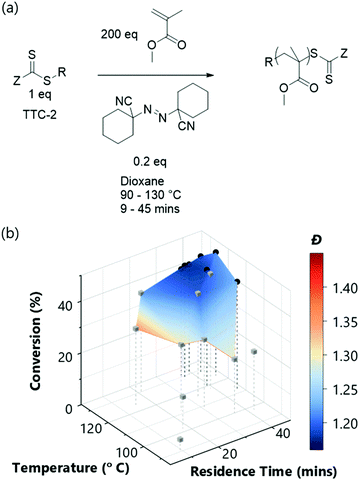
Initial observations indicate clear differences between the candidates. Furthermore, the results here again show the algorithm to be significantly more efficient in terms of inconsequential experiments – for TTC-1, TTC-2 and Py-DTC-1, there are only three unsuccessful experiments (i.e. negligible conversion) compared to eleven in the screen. For TTC-4, this reduces to just one. These were conducted in the initialisation portion of the optimisation experiment, from the Latin hypercube sampling of the reaction conditions. Following this, the TSEMO algorithm found only conditions which result in conversions sufficient to give valid GPC data for these systems. The much slower polymerisation with TTC-3 displays the effectiveness of the algorithm even more obviously – after eight of the ten Latin hypercube experiments gave a conversion <20%, only one of the fourteen TSEMO experiments did so. The “successful” experiments were clustered around the only viable region within the reaction conditions explored – with temperatures ≥108 °C and reaction times >15 min. It is important to note that the algorithm identifies these regions of interest with no prior knowledge of the chemistry/kinetics and hence this represents a powerful tool not only for experts, but also for non-polymer chemists who simply require a polymer with defined characteristics. It is also worth noting that were the screen performed for TTC-3, at least 18 experiments would be required to find conditions producing monomer conversion of any consequence.
The most notable difference between the reaction spaces of the studied systems is the markedly reduced conversions for TTC-3, with all experiments yielding conversions <40%. Any differences in properties derive from the changes to the Z- and R-groups – which are critical in determining the RAFT equilibria behaviour.40,41 These results do not discount the possibility to obtain greater conversions using TTC-3 as the RAFT agent, but instead explore that which is achievable within the conditions explored (4–20 minutes residence time, 80–120 °C). A possible explanation for the reduced conversions obtained using this RAFT agent may be inhibition in the RAFT pre-equilibrium. The increased stability of benzyl radicals (the R group for TTC-3) has been shown to inhibit reinitiation of RAFT polymerisations.45 This effect would show itself more readily with the short timeframes used in this work. The subtler decreases in dispersity from TTC-2 to TTC-1, TTC-4 and Py-DTC-1 in turn are apparent from the surface colourmaps in Fig. 2.
These subtler changes are better visualised using Fig. 3 – where the reaction space is presented in terms of the objectives, conversion and dispersity. From this plot, the series of “optimum” points can be elucidated where conversion cannot be improved without an adverse effect upon dispersity (or vice versa).24 In the context of these two objectives, the optimum points represent the Pareto front, which separates the achievable properties from the ‘utopian solution’, at the far bottom right of the plot, corresponding to a conversion of 100% and a dispersity of 1.0. The combination of the 3D surface and Pareto front enables a thorough description of the system and their relative usefulness will vary from application to application. The overall performance of each RAFT agent used here is immediately obvious, with small movements towards the bottom right of Fig. 3 indicating an improvement in attainable properties. As was also evident in the screen, there is a trade-off between the two objectives – lower dispersities are obtained where the polymerisation is not forced to high conversions with harsher conditions. The results obtained confirmed that which has been observed previously regarding the superior performance of Py-DTC-1 relative to the trithiocarbonate candidates.44 There are three datapoints using Py-DTC-1 which dominate all of the results obtained for TTC-1 and TTC-2, with conversions >82.1% and dispersities <1.2. TTC-4 was shown to be the optimum trithiocarbonate, with both improved conversions and a significant drop in dispersity (1.25 to 1.20) at conversions around 80%.
The application of this data for end-users could differ substantially: sometimes a narrow molecular weight is of great importance, but a lower conversion is an acceptable cost (for example, in this case that applies to the results for TTC-1, TTC-4 and Py-DTC at 60–75% conversion). In others, efficiency of the process may be of a far greater importance, where an increase in dispersity is tolerable should function be maintained. Critically, the platform enables data-rich evaluation and determination of viable options, such as screening which of the available RAFT agents provide suitable conversions (in this case TTC-1, TTC-2, TTC-4 and Py-DTC). With that said, it was noted that there were some limitations to the approach used. There was some degree of clustering of the experiments selected in batches by the TSEMO algorithm (where a batch size of four was used to prevent waiting for GPC analysis to complete) and a possibility of improved results in a wider search area, and so for the most promising trithiocarbonate RAFT agent, TTC-4, a second self-optimisation was performed with adjusted parameters. The batch size predicted by the TSEMO algorithm was reduced to one and the residence time limit increased to 30 minutes. The temperature range explored was not changed as a clear optimum was present in the middle of the range studied. Fig. 4 shows more evenly distributed experiments – while the algorithm clearly succeeds in targeting favourable properties, the same degree of clustering is eliminated.
The surfaces/plots reveal the relative ease with which acrylamides can be polymerised, though polymerisation control is not always guaranteed. There were a range of acceptable conditions for the polymerisation of acrylamides, even though these polymerisations are conducted without degassing. Four of the five candidates show a plateau-like region with respect to conversion, and dispersities <1.3 were also obtained. Furthermore, no dispersities >1.42 were obtained in even the harshest conditions. It is recognised that conversions >90% were not obtained, but this was attributed to the monomer system employed – similar upper limits in conversion were obtained for hydrophobic acrylamide derivatives, including tBuAm, by Pichot and co-workers.46
An acrylate-based RAFT polymerisation represents a more challenging system for the platform to optimise – as deviations from ideal radical polymerisation mechanisms exist.47 Work by Junkers and co-workers explore the diverse products that can be formed using this chemical system even for low target molecular weights, using flow methods in conjunction with online mass-spectrometry.47 Presenting the polymerisation of n-butyl acrylate (BuA – see Fig. 5a for scheme) to our platform for optimisation offered a greater challenge – with a greater propensity to form higher dispersity products – as shown by Fig. 5b. The presence of inhibitor (4-methoxyphenol (MEHQ)) within this monomer also enabled demonstration of how the algorithm can be used to accommodate batch-to-batch variability: an initial autonomous exploration of the polymerisation reaction space was performed using the monomer as supplied (inhibited), and then again with the inhibitor removed (uninhibited). Autonomous exploration of the polymerisation parameter space was successfully executed involving 42 experiments requiring just a few hours of user input. Again, to perform such experiments manually would be a significant undertaking (generally prohibitively so, for such a nuanced investigation), with an associated (non-negligible) workup time in running and processing the NMR/GPC analyses. This workload would generally render thorough investigation of such a subtle change (inhibitor removal) inviable, but the platform enables this comparison.
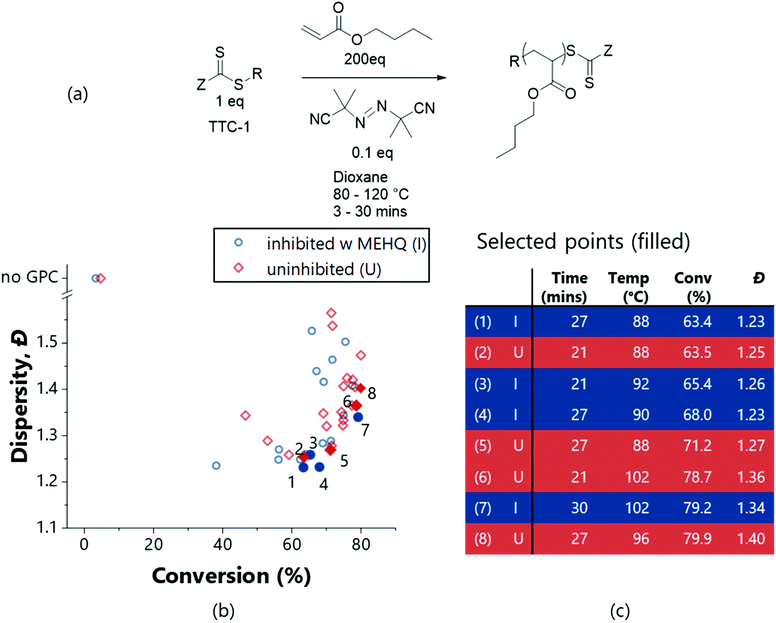 | ||
Fig. 5 Multi-objective optimisations (TSEMO algorithm) for the RAFT polymerisation of n-butyl acrylate (scheme in (a)) inhibited (I – blue circles) and uninhibited (U – red squares), using TTC-1 as the RAFT agent and AIBN as the initiator, in dioxane ([monomer]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA] [CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [initiator] 200 [initiator] 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, 30% w/w). [Condition limits: 3–30 min, 80–120 °C.] The full data for selected points (filled and numbered in (b)) are given in (c). For surfaces and all experimental data see ESI.† 0.1, 30% w/w). [Condition limits: 3–30 min, 80–120 °C.] The full data for selected points (filled and numbered in (b)) are given in (c). For surfaces and all experimental data see ESI.† | ||
Broadly the use of inhibitor (Fig. 5 – blue) reduces the conversion in conjunction with an enhancement in dispersity; with the optimal dispersity (i.e., minimum, point 4) being for an experiment containing inhibitor. However, the optimal conversion is achieved without inhibitor (i.e., maximum, point 8). While both the inhibited and uninhibited reactions show different outcomes for the same conditions, the self-optimised optimal polymer properties are similar. The inhibitor indeed inhibits reaction – to achieve a polymer of comparable conversion and dispersity, harsher conditions are required. As can be seen in Fig. 5b, to obtain a conversion of around 63% at 88 °C, a residence time of 21 min is required for the uninhibited system (point 2), compared to 27 min for the inhibited (point 1). Alternatively, an increase in temperature to 92 °C for the inhibited system will give a similar uplift in conversion (point 3). A balanced increase of both temperature and time gives point 4, the optimum in terms of dispersity. Nearing the optimum in terms of conversion (points 6, 7 and 8); higher conversions are obtained at the cost of increased dispersity, as is illustrated by comparing (4) to (7). The inhibited system again yielded less converted and lower dispersity polymers ((7) vs. (6) and (8)) despite harsher conditions. Fundamentally, this illustrates the advantage of the self-optimisation approach – that by performing optimisations, product quality can be maintained (or even improved) despite batch variation. Furthermore, a subtle improvement in product quality was obtained using the reactant as supplied (inhibited) which is of benefit to the user due to the reduced workload (i.e. purification)-taking entries (1) and (2) of Fig. 5b, a lower dispersity is obtained for the same conversion.
The RAFT polymerisation of BuA was also optimised using the higher temperature initiator, 1,1-azobis(cyclohexanecarbo-nitrile) (ACHN) to investigate the effect of decoupling radical flux from the remainder of the polymerisation kinetics. The results (see ESI†) indicate that the loss of control observed as temperature increases is down to non-ideal polymerisation kinetics at higher temperatures, independent of radical flux, as dispersities are seen to rise across the reaction space. This supports the conclusion of Asua and co-workers48 who found a low [initiator]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [CTA] did not guarantee polymerisation control. Further study using additional techniques (e.g. high-field NMR/MALDI) may provide more clarity, but from a pragmatic point of view, this system was rejected due to inferior performance.
[CTA] did not guarantee polymerisation control. Further study using additional techniques (e.g. high-field NMR/MALDI) may provide more clarity, but from a pragmatic point of view, this system was rejected due to inferior performance.
The final system optimised was the RAFT polymerisation of a methacrylate monomer to assess whether flow chemistry could intensify an otherwise slow process. Typically, methyl methacrylate requires hours to achieve even modest conversions49 but the pressurised flow reactor provides access to higher temperatures than would conventionally be used.50 This affords the potential for an accelerated polymerisation (albeit with an increased likelihood for termination events). In this case, ACHN was again selected as the initiator to maintain radical flux at higher temperatures and was used at a higher concentration (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 [CTA]
0.2 [CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ACHN]) to increase the rate of the slower reaction (for scheme see Fig. 6a). Furthermore, the lower temperature limit of the experiment was increased to 90 °C (since all reactions under this temperature had resulted in negligible conversion when using ACHN for the polymerisation of n-butyl acrylate). This experiment illustrates the value provided by the diagnostic reactor conditions (see ESI†); as the reactor failed following experiment 17 – all later experiments were discarded, ensuring unreliable data was not used.
[ACHN]) to increase the rate of the slower reaction (for scheme see Fig. 6a). Furthermore, the lower temperature limit of the experiment was increased to 90 °C (since all reactions under this temperature had resulted in negligible conversion when using ACHN for the polymerisation of n-butyl acrylate). This experiment illustrates the value provided by the diagnostic reactor conditions (see ESI†); as the reactor failed following experiment 17 – all later experiments were discarded, ensuring unreliable data was not used.
The effectiveness of the TSEMO algorithm in selecting appropriate conditions for successful experiments based upon inferior data generated from the initial LHC is again demonstrated here (Fig. 6). All but one of the LHC experiments gave a conversion of <40%, whereas each of the seven TSEMO experiments gave conversions >40% (achieved using temperatures ≥112 °C and reaction times ≥36 min). While this is of course lower than the other conversions obtained, in the timeframe given it is impressive – a literature value for a similar RAFT polymerisation (trithiocarbonate RAFT agent at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 [CTA]
0.2 [CTA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [initiator]) gives 61.5% conversion after 8 hours of reaction at 75 °C.49
[initiator]) gives 61.5% conversion after 8 hours of reaction at 75 °C.49
Conclusions
In conclusion, we have successfully developed a polymer synthesis and analysis platform capable of conducting automated RAFT polymerisation under conditions not feasible using typical batch techniques. A programmable screen of conditions for the polymerisation of tert-butyl acrylamide with no human interaction was successfully achieved but resulted in several redundant experiments. It was clear from the obtained data that there existed optimum conditions for maximising conversion and minimising molar mass dispersity. To combat the inefficiency, a Bayesian machine learning algorithm, TSEMO, was integrated into the control software which enabled identification of this optimum parameter space in fewer experiments. This algorithm was subsequently used to map out the reaction space for several other RAFT polymerisation reactions where the CTA, initiator and monomers were changed. The experiments produced rich datasets regarding the reaction. These optimisation experiments required minimal prior knowledge of the chemical system, and the only human interaction required was to prepare reagent solutions and set parameter limits. In this context, they represent the first example of closed-loop multi-objective optimisation and present enormous opportunities for the future of polymer science. Further studies clarifying the properties of polymers produced at the extreme conditions used here will be of great value, especially to confirm the presence of RAFT agent as polymer end-groups. The wider application of these technologies, both across different polymerisation techniques, and incorporating further input variables and objectives offers a whole host of exciting future opportunities.Data availability
The datasets supporting this article have been uploaded as part of the ESI.† The code for the TSEMO algorithm used in this work can be found at https://github.com/Eric-Bradford/TS-EMO.Author contributions
STK – data curation, investigation, methodology, software, writing – original draft, writing – review & editing; SJP – data curation, investigation, methodology, software, writing – review & editing; CYPW – investigation, software, visualization, writing – review & editing; RAB – funding acquisition, software, supervision, writing – review & editing; NJW – conceptualization, funding acquisition, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Anna Gerdova and Jurgen Kolz from Magritek for helpful discussions regarding NMR spectroscopy. We would also like to thank Adam Clayton for discussions regarding the TSEMO algorithm. We would like to thank the EPSRC for funding for STK & NJW (EP/S000380/1) and RAB (EP/R032807/1).Notes and references
- S. V. Ley, D. E. Fitzpatrick, R. J. Ingham and R. M. Myers, Angew. Chem., Int. Ed., 2015, 54, 3449–3464 CrossRef CAS PubMed.
- D. E. Fitzpatrick and S. V. Ley, Tetrahedron, 2018, 74, 3087–3100 CrossRef CAS.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 22858–22893 CrossRef CAS PubMed.
- C. Houben and A. A. Lapkin, Curr. Opin. Chem. Eng., 2015, 9, 1–7 CrossRef.
- S. Chatterjee, M. Guidi, P. H. Seeberger and K. Gilmore, Nature, 2020, 579, 379–384 CrossRef CAS PubMed.
- V. Sans and L. Cronin, Chem. Soc. Rev., 2016, 45, 2032–2043 RSC.
- R. Leardi, Anal. Chim. Acta, 2009, 652, 161–172 CrossRef CAS PubMed.
- S. A. Weissman and N. G. Anderson, Org. Process Res. Dev., 2015, 19, 1605–1633 CrossRef CAS.
- T. Eckert, F. C. Klein, P. Frieler, O. Thunich and V. Abetz, Polymers (Basel), 2021, 13, 3147 CrossRef CAS PubMed.
- A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, React. Chem. Eng., 2019, 4, 1545–1554 RSC.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264 RSC.
- W. Huyer and A. Neumaier, ACM Trans. Math. Softw., 2008, 35, 1–25 CrossRef.
- N. Holmes, G. R. Akien, A. J. Blacker, R. L. Woodward, R. E. Meadows and R. A. Bourne, React. Chem. Eng., 2016, 1, 366–371 RSC.
- J. P. McMullen, M. T. Stone, S. L. Buchwald and K. F. Jensen, Angew. Chem., Int. Ed., 2010, 49, 7076–7080 CrossRef CAS PubMed.
- A. D. Clayton, L. A. Power, W. R. Reynolds, C. Ainsworth, D. R. J. Hose, M. F. Jones, T. W. Chamberlain, A. J. Blacker and R. A. Bourne, J. Flow Chem., 2020, 10, 199–206 CrossRef.
- C. Houben, N. Peremezhney, A. Zubov, J. Kosek and A. A. Lapkin, Org. Process Res. Dev., 2015, 19, 1049–1053 CrossRef CAS PubMed.
- Y. Gu, P. Lin, C. Zhou and M. Chen, Sci. China: Chem., 2021, 64, 1039–1046 CrossRef CAS.
- M. Reis, F. Gusev, N. G. Taylor, S. H. Chung, M. D. Verber, Y. Z. Lee, O. Isayev and F. A. Leibfarth, J. Am. Chem. Soc., 2021, 143, 17677–17689 CrossRef CAS PubMed.
- M. H. Reis, F. A. Leibfarth and L. M. Pitet, ACS Macro Lett., 2020, 9, 123–133 CrossRef CAS.
- N. Zaquen, M. Rubens, N. Corrigan, J. Xu, P. B. Zetterlund, C. Boyer and T. Junkers, Prog. Polym. Sci., 2020, 101256 CrossRef CAS.
- A. D. Clayton, A. M. Schweidtmann, G. Clemens, J. A. Manson, C. J. Taylor, C. G. Niño, T. W. Chamberlain, N. Kapur, A. J. Blacker, A. A. Lapkin and R. A. Bourne, Chem. Eng. J., 2020, 384, 123340 CrossRef CAS.
- J. A. Manson, A. D. Clayton, C. G. Niño, R. Labes, T. W. Chamberlain, A. J. Blacker, N. Kapur and R. A. Bourne, Chimia, 2019, 73, 817–822 CrossRef PubMed.
- A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282 CrossRef CAS.
- B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96 CrossRef CAS PubMed.
- K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem. Methods, 2021, 1, 116–122 CrossRef.
- G. Moad, E. Rizzardo and S. H. Thang, Polymer, 2008, 49, 1079–1131 CrossRef CAS.
- S. T. Knox and N. J. Warren, React. Chem. Eng., 2020, 5, 405–423 RSC.
- Z. Wang, Y. Zhou and M. Chen, Chin. J. Chem., 2022, 40, 285–296 CrossRef.
- J. J. Haven, J. Vandenbergh and T. Junkers, Chem. Commun., 2015, 51, 4611–4614 RSC.
- J. J. Haven and T. Junkers, Eur. J. Org. Chem., 2017, 6474–6482 CrossRef CAS.
- M. Rubens, J. H. Vrijsen, J. Laun and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 3183–3187 CrossRef CAS PubMed.
- M. Rubens, J. Van Herck and T. Junkers, ACS Macro Lett., 2019, 8, 1437–1441 CrossRef CAS.
- S. Parkinson, N. S. Hondow, J. S. Conteh, R. A. Bourne and N. J. Warren, React. Chem. Eng., 2019, 4, 852–861 RSC.
- S. T. Knox, S. Parkinson, R. Stone and N. J. Warren, Polym. Chem., 2019, 10, 4774–4778 RSC.
- S. Parkinson, S. T. Knox, R. A. Bourne and N. J. Warren, Polym. Chem., 2020, 11, 3465–3474 RSC.
- E. Bradford, A. M. Schweidtmann and A. Lapkin, TS-EMO, https://github.com/Eric-Bradford/TS-EMO Search PubMed.
- M. H. Reis, T. P. Varner and F. A. Leibfarth, Macromolecules, 2019, 52, 3551–3557 CrossRef CAS.
- E. Bradford, A. M. Schweidtmann and A. Lapkin, J. Glob. Optim., 2018, 71, 407–438 CrossRef.
- D. J. Keddie, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 2012, 45, 5321–5342 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2012, 65, 985 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2005, 58, 379 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2006, 59, 669 CrossRef CAS.
- J. Gardiner, I. Martinez-Botella, J. Tsanaktsidis and G. Moad, Polym. Chem., 2016, 7, 481–492 RSC.
- Y. K. Chong, J. Krstina, T. P. T. Le, G. Moad, A. Postma, E. Rizzardo and S. H. Thang, Macromolecules, 2003, 36, 2256–2272 CrossRef CAS.
- B. de Lambert, M.-T. Charreyre, C. Chaix and C. Pichot, Polymer, 2005, 46, 623–637 CrossRef CAS.
- J. J. Haven, N. Zaquen, M. Rubens and T. Junkers, Macromol. React. Eng., 2017, 11, 1700016 CrossRef.
- A. Veloso, W. García, A. Agirre, N. Ballard, F. Ruipérez, J. C. de la Cal and J. M. Asua, Polym. Chem., 2015, 6, 5437–5450 RSC.
- J. Ma and H. Zhang, Macromol. Res., 2015, 23, 67–73 CrossRef CAS.
- V. Hessel, D. Kralisch and N. Kockmann, Nov. Process Wind. Innov. Gates to Intensified Sustain. Chem. Process, 2015, pp. 1–314 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. Description of synthetic platform and experimental procedures, methods for automated GPC and NMR, and additional data including full datasets for each optimisation. See DOI: 10.1039/d2py00040g |
| ‡ These authors contributed equally. |
| § Current address: School of Chemistry, University of Birmingham, Birmingham B15 2TT, UK. |
| This journal is © The Royal Society of Chemistry 2022 |