Application of transfer learning to predict diffusion properties in metal–organic frameworks†
Yunsung
Lim
 and
Jihan
Kim
*
and
Jihan
Kim
*
Department of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291, Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: jihankim@kaist.ac.kr
First published on 21st June 2022
Abstract
Transfer learning (TL) facilitates the way in which a model can learn well with small amounts of data by sharing the knowledge from a pre-trained model with relatively large data. In this work, we applied TL to demonstrate whether the knowledge gained from methane adsorption properties can improve a model that predicts the methane diffusion properties within metal–organic frameworks (MOFs). Because there is a large discrepancy in computational costs between the Monte Carlo (MC) and molecular dynamics (MD) simulations for gas molecules in MOFs, relatively cheap MC simulations were leveraged in helping to predict the diffusion properties and we demonstrate performance improvement with this method. Furthermore, we conducted a feature importance analysis to identify how the knowledge from the source task can enhance the model for the target task, which can elucidate the process and help choose the optimal source target to be used in the TL process.
Design, System, ApplicationMetal–organic frameworks (MOFs) are promising materials for various applications and due to their highly tunable nature, there is a potentially infinite number of MOFs that can be synthesized by combining metal nodes and organic linkers. Recently with the advent of various deep learning methods, the process to select and design the best candidate materials for a given application has been explored by many different research groups. However, most of these deep learning methods require large amounts of data which limits their scope to those studies where the time it takes to obtain said data is short. Transfer learning (TL) is a way to overcome these limitations, where one can in principle utilize the knowledge gained from one problem where obtaining data is cheap to solve a different but related problem where obtaining data is expensive. For the test case, we used methane gas uptakes of over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 hypothetical MOFs and used this dataset to improve the prediction of methane diffusion coefficients of MOFs, in which the latter requires long computational times. In our opinion, this approach can be expanded to accelerate the discovery or design of new MOF candidates with various applications where data are sparse or difficult to obtain. 000 hypothetical MOFs and used this dataset to improve the prediction of methane diffusion coefficients of MOFs, in which the latter requires long computational times. In our opinion, this approach can be expanded to accelerate the discovery or design of new MOF candidates with various applications where data are sparse or difficult to obtain.
|
Introduction
Metal–organic frameworks (MOFs) are comprised of tunable building blocks (i.e. metal nodes and organic linkers)1 and are seen as promising materials for various energy and environmental related applications.2–6 In particular, with facile synthesis, the number of MOFs that have been synthesized is near 0.1 million,7 and as such, the accumulated data for all the experimentally synthesized MOFs can be an excellent source for materials informatics. In particular, experimentally synthesized MOFs have been added to the Cambridge Crystallographic Data Centre (CCDC) database8 and hypothetical MOFs (hMOFs) have been created in silico to provide a wealth of datasets for various machine learning studies.9–11In this context, various deep learning methods have been recently developed and applied as principle methods to analyze these MOF databases.12–19 Burner et al. predicted adsorption properties related to CO2 using a deep neural network that uses combinations of geometric and chemical descriptors.20 Rosen et al. did quantum chemical calculations within MOFs to construct a database (QMOF database) and applied machine learning (ML) with the database to prove the effectiveness of the ML approach to discover MOFs with exceptional electronic properties.21 Lee et al. utilized a deep neural network as an efficient tool to explore a vast MOF space to design novel MOFs as an adsorbent for methane adsorption.11 However, these conventional deep learning methods all require a sufficiently large amount of datasets to train a model with an acceptable level of accuracy. For computational simulations such as grand canonical Monte Carlo (GCMC) simulations that require a relatively short wall time, this is not too much of a concern. However, certain simulations such as molecular dynamics (MD) and quantum chemical calculations take significantly large computational resources and as such can be the major bottleneck that hinders the progress for machine learning studies.22 Within this line of reasoning, it would be useful if one can use the dataset from simulations that require a low computational cost and transfer this knowledge to build machine learning models that facilitate the prediction of properties that require large computational resources.
This kind of procedure to exploit knowledge from a large data set to enable a model trained properly for a smaller data set is called transfer learning (TL).23 Recently, Yamada et al. developed the Python library for TL tasks in various types of materials (e.g. small organic molecules, polymers, and inorganic crystalline materials), XenonPy.MDL. More than 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 models that are pre-trained with various property data exist in the library. Then, they used the pre-trained model from their library to improve prediction performance with small data by leveraging the knowledge of the big data.24 Jha et al. applied TL to develop a model that can accurately predict experimental formation energy values.25 For MOFs, Ma et al. tested the transfer of knowledge from the same physical properties (adsorption properties) within hypothetical MOFs using a deep neural network. They observed that TL can work between two different guest molecules, H2 and CH4.26
000 models that are pre-trained with various property data exist in the library. Then, they used the pre-trained model from their library to improve prediction performance with small data by leveraging the knowledge of the big data.24 Jha et al. applied TL to develop a model that can accurately predict experimental formation energy values.25 For MOFs, Ma et al. tested the transfer of knowledge from the same physical properties (adsorption properties) within hypothetical MOFs using a deep neural network. They observed that TL can work between two different guest molecules, H2 and CH4.26
In this work, we seek to develop a model that predicts diffusion properties in MOFs by transferring the knowledge learned from adsorption properties. As mentioned previously, diffusion properties require running long MD simulations and as such, compared to adsorption property simulations (via GCMC), the computational cost it takes to prepare a dataset for machine learning purposes is very large. As a case study, the methane (CH4) molecule was used as a test gas molecule to demonstrate the capabilities of our workflow. Methane is one of the most widely used target molecules for chemical separations (e.g. H2/CH4, N2/CH4, CO2/CH4, CH4/other hydrocarbons)27–30 and as such, it is important to compute the diffusion coefficients of these small molecules. Moreover, given that many of the porous materials have large diffusion barriers that separate the pores of the materials, many of the self-diffusion coefficients are very small which require running very long MD simulations.31 In this computational work, we discover that the prediction of the self-diffusion coefficients (diffusion property) with a small size dataset (<500) can be improved by up to 25% using knowledge from the gas uptakes (adsorption property) of a relatively large size dataset (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). Moreover, feature importance analysis is conducted to elucidate why the transfer learning is effective between diffusion and adsorption properties. This transferability can open up a new opportunity to build machine learning models that entail computing properties with a high computational cost such as results from the ab initio quantum chemistry methods or experimental results.
000). Moreover, feature importance analysis is conducted to elucidate why the transfer learning is effective between diffusion and adsorption properties. This transferability can open up a new opportunity to build machine learning models that entail computing properties with a high computational cost such as results from the ab initio quantum chemistry methods or experimental results.
Results and discussion
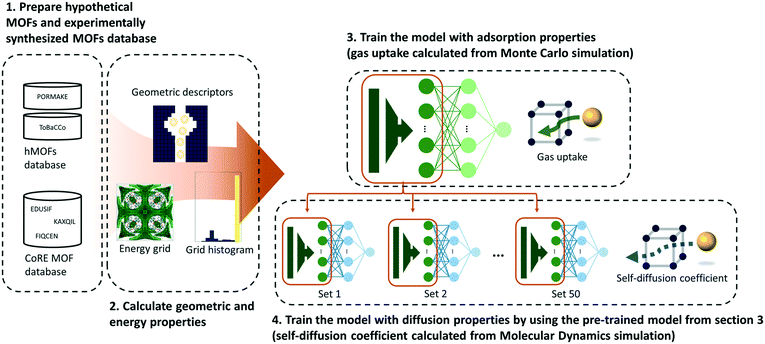
As shown in Fig. 1, a multilayer perceptron (MLP) model was designed with geometric and energy descriptors used as features for the model. Given that this work is the first attempt to apply TL between different properties within the MOF field, a simple model and descriptors were used in this work. For the test case system, the methane gas uptake that can be computed via GCMC simulation was selected as the source property, while the methane self-diffusion coefficient under a dilute condition (D∞S) that can be computed via MD simulation was selected as the target property. Since GCMC simulations require much less computational resources compared to the MD simulations, large data of gas uptake can be easily prepared and be used effectively to train the diffusive predictive machine learning models. Considering that the various flexible motions within MOFs (linker vibration/rotation and breathing nature) can change the adsorption and diffusion properties,32,33 more realistic values can be obtained when the flexibility of the MOFs was simulated. However, in this work, we assumed the MOFs as rigid to obtain static adsorption and diffusion properties for the machine learning model.Pre-training
Based on general intuition, high affinity binding sites in the MOF structures can hinder the penetration of gas molecules via structures, so the gas uptake and self-diffusion coefficient may show an inversely proportional relationship. And if there was a straightforward meaningful relationship between two properties, the utility of TL would be put into question. To ensure that this is not the case, the relationship between the methane gas uptake and self-diffusion coefficient was visualized (Fig. 2). As shown in Fig. 2, although few structures follow the inverse relationship, the relationship is less clear-cut than our general intuition. From this result, we could see that the TL in this task (gas uptake to self-diffusion coefficient) might be worthwhile.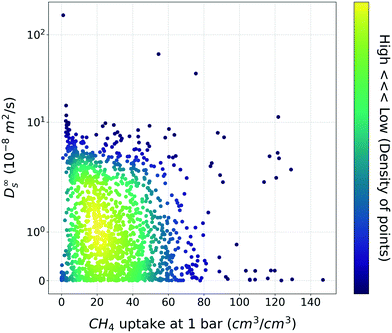 | ||
| Fig. 2 Scatter plot between the methane uptake and self-diffusion coefficient under the dilute condition. The color bar denotes the density of MOFs within the vicinity of the points. | ||
To leverage the knowledge in predicting the target property (self-diffusion coefficient), a model pre-trained with the source property (gas uptake) should be prepared. As such, the methane gas uptakes of hMOFs at 12 different pressures from 0.25 bar to 100 bar were obtained. 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 hMOFs from the PORMAKE and ToBaCCo database were used and the data set was divided into training, validation, and test set with the ratio of 72
845 hMOFs from the PORMAKE and ToBaCCo database were used and the data set was divided into training, validation, and test set with the ratio of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
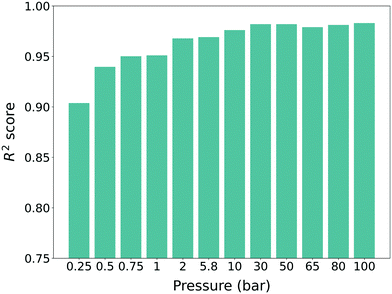
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 for cross-validation. The uptake results were normalized to a value between 0 and 1 during the training process. For each pressure, different machine learning models were trained and all of the models showed high performance (R2 score >0.9) (see Fig. 3). One can also see a slight increasing trend of the R2 score for higher pressure, which follows the results from previous work.34,35 As such, we can conclude that our pre-trained models were trained properly with the source domain (hMOFs and methane gas uptake) and as such, they were ready to be used for training with the target domain (experimentally synthesized MOFs and self-diffusion coefficient).
20 for cross-validation. The uptake results were normalized to a value between 0 and 1 during the training process. For each pressure, different machine learning models were trained and all of the models showed high performance (R2 score >0.9) (see Fig. 3). One can also see a slight increasing trend of the R2 score for higher pressure, which follows the results from previous work.34,35 As such, we can conclude that our pre-trained models were trained properly with the source domain (hMOFs and methane gas uptake) and as such, they were ready to be used for training with the target domain (experimentally synthesized MOFs and self-diffusion coefficient).
Transfer learning
Next, TL tasks with 3 different data sizes (100, 300, and 500) were performed using the 12 pre-trained models from the gas uptakes (where the data size refers to the number of self-diffusion coefficient data). For convenience, these models were labelled i-TL-p (where i is the data size from 100 to 500 and p is the pressure from 0.25 bar to 100 bar). Given that there can be high variance in the performance of the models due to the small data size, 50 random draws were conducted from the raw data set that consists of self-diffusion coefficients of 1563 experimentally synthesized MOFs to preserve generality. To measure the performance, holdout cross-validation was performed with every random draw. The drawn data set was divided into training, validation, and test set with the ratio of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8
8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20. Since the self-diffusion coefficient values vary greatly from 10−5 to 102 (10−8 m2 s−1), the logarithmic value of
20. Since the self-diffusion coefficient values vary greatly from 10−5 to 102 (10−8 m2 s−1), the logarithmic value of 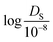 was used for model evaluation to prevent bias towards extreme values (see ESI† Fig. S1).
was used for model evaluation to prevent bias towards extreme values (see ESI† Fig. S1).
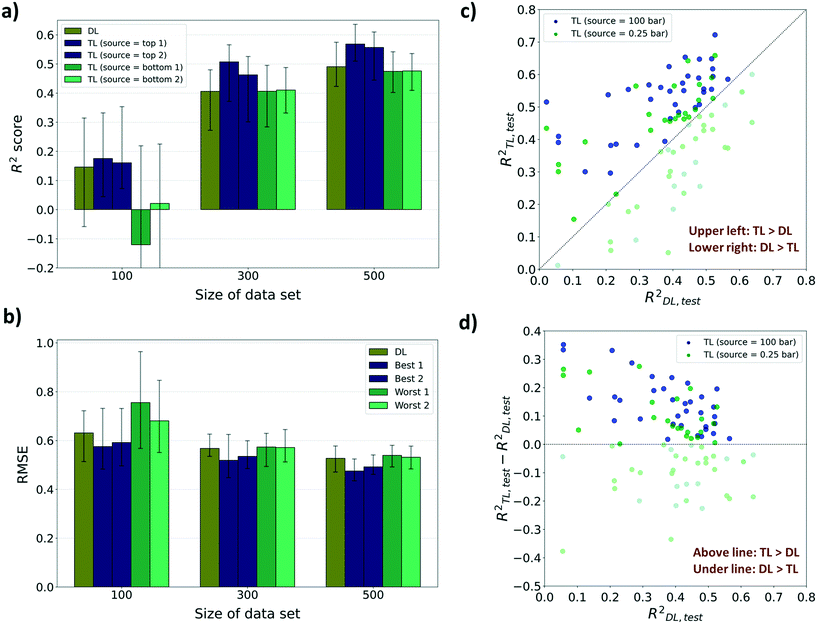
For performance evaluation criteria for both TL and direct learning (DL, training without a pre-training model) models, the R2 score was mainly used. There were enhancements in the performance to predict diffusion properties when leveraging knowledge from adsorption properties at several pressures for sizes 300 and 500. However, in the case of size 100, no significant improvements were found in the performance despite using the pre-trained model, and at certain pressures, the performance deteriorated compared to DL. As shown in Fig. 4a, the highest R2 score of the TL model among 12 pressures for size 100 is 0.175 which is a 19.8% improvement from the R2 score of the DL model (R2DL,size100 = 0.146). Although there are improvements in R2 scores for certain pressures amongst size 100 models, R2 scores of the worst cases were negative which means that there was no significant relationship between the true value and the predicted value. Meanwhile, the highest R2 score among the TL models at sizes 300 and 500, respectively, improved to 24.8% and 15.7%, respectively, from the R2 score of the DL models (R2DL,size300 = 0.406, R2TL(100bar),size300 = 0.507, R2DL,size500 = 0.491, R2TL(2bar),size500 = 0.568) and the lowest R2 score still showed a positive value. This type of improvement was retained when the performance metric was changed to root mean squared error (RMSE) and mean absolute error (MAE). There were decreases in RMSE and MAE for the top 2 TL models among 12 pressures compared to the DL model (Fig. 4b and ESI† Fig. S2). Considering that a small RMSE denotes high performance, the highest RMSE among the TL models at sizes 300 and 500 shows, respectively, only 1.05% and 2.32% higher than the RMSE of the DL model (RMSEDL,size300 = 0.568, RMSEDL,size500 = 0.527). However, there was a 19.7% increase in RMSE at size 100 compared to the RMSE of the DL model (RMSEDL,size100 = 0.631, see Fig. 4b). Likewise, in the case of MAE as the evaluation metric, the highest MAE among the TL models at size 100 is 16.0% higher than the MAE of the DL model (MAEDL,size100 = 0.463), while those at sizes 300 and 500 show no increase (MAEDL,size300 = 0.416, MAEDL,size500 = 0.377, see ESI† Fig. S2). The phenomenon that the pre-trained model cannot work properly with a small data size was ascribed to the difference between the gas uptake and self-diffusion coefficient. Considering that the first layer of the pre-trained model was frozen during the TL task, the model cannot find a meaningful relationship between MOF representation from the first layer and self-diffusion coefficients with a small size of dataset. However, the model can learn unique patterns between MOF representation and self-diffusion coefficients as the size of the data becomes larger.
For further analysis, we compared the R2 scores of the TL model and the DL model for every 50 random draws with the best and the worst TL cases (see Fig. 4c and d). The pre-trained models with gas uptakes at 100 bar and 0.25 bar are respectively shown to be the best and the worst source datasets to lead to accurate self-diffusion coefficient prediction. The pre-trained model at 100 bar was found to have ranked at least 2nd place in all nine cases while the pre-trained model at 0.25 bar was ranked last place or just above the bottom in eight out of nine cases (nine cases: R2 score, RMSE, and MAE results for sizes 100, 300, and 500). Out of these results, the data from size 300 were further analyzed because there was the largest improvement in prediction performance by applying the pre-trained model compared to DL. As shown in Fig. 4c, 300-TL-100 (navy) showed a higher R2 score than 300-TL-0.25 (green) in 39 out of 50 randomly drawn sets. The R2TL,test of 300-TL-100 ranged up to 0.722 which is much higher than the R2TL,test of 300-TL-0.25, up to 0.658. The trend was maintained even when the evaluation metric was changed to RMSE and MAE. 300-TL-100 (navy) showed lower value than 300-TL-0.25 (green) in 39 out of 50 randomly drawn sets with respect to RMSE and 43 with respect to MAE (see ESI† Fig. S3). To identify how often the TL models outperform the DL models, R2TL–R2DL was calculated (see Fig. 4d) where R2TL–R2DL > 0 means that the TL model shows better prediction performance than the DL model. The knowledge from the gas uptake at 100 bar helps the model surpass the model without any knowledge for 37 out of 50 randomly drawn sets. However, 300-TL-0.25 surpassed the DL models in only 25 sets, and as such, we can expect that no significant difference occurred by borrowing knowledge from the gas uptake at 0.25 bar, but rather the knowledge disturbed the prediction of the self-diffusion coefficient.
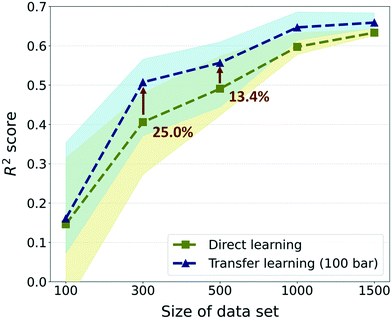
Furthermore, to investigate the effectiveness of the TL as the data size increases, we compared the previous results with much larger data sizes of 1000 and 1500. For these sizes, only 5 random draws were conducted considering that the raw data set only contains self-diffusion coefficients of 1563 frameworks and many of them should be overlapping in randomly drawn sets. Overall, although there were enhancements in prediction performance in data sizes larger than 300, the gap in performance between TL and DL is reduced as the size of the data increases (see Fig. 5). The best TL model (300-TL-100) showed an improvement of 25.0% in the R2 score compared to the DL model for size 300, but the improvement is reduced to 13.4% for size 500 and the degree of performance improvement approximately converged in size 1500. Nevertheless, just as the R2 score of the TL model in size 300 is higher than that of the DL model in size 500, it is still valid in a small data size where TL can reduce the process of collecting data, which is a bottleneck of deep learning. Moreover, considering that the standard for moderate prediction accuracy is R2 score >0.5,36 it was an unacceptable model to predict the self-diffusion coefficient with only 300 data size, but with the help of the pre-trained model, the model can be equipped with a moderate predictive power for self-diffusion coefficients. Even if different evaluation metrics (RMSE and MAE) are applied, the TL model in size 300 still performs better than the DL model in size 500 (see ESI† Fig. S4). Considering that the simulation time for the self-diffusion coefficient is >1800 times larger than that for gas uptake, better performance can be achieved with 62.62% of computational costs when 200 self-diffusion coefficient calculations are substituted with the 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 gas uptake calculations (more details are shown in Section S3 of the ESI†).
845 gas uptake calculations (more details are shown in Section S3 of the ESI†).
Model interpretation
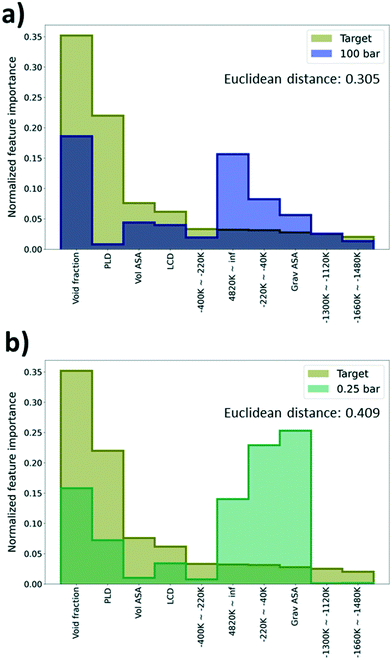
As deep learning models generally work as a black box, it is difficult to identify what is learned via the models during the training process. To overcome this limitation, feature importance was measured to identify the important features that help in the predictions. Specifically, permutation feature importance (PFI)37 was measured using the Python package, eli5.38 PFI is calculated based on an intuition that there is a coherent relationship between the feature importance and the model performance. Here, feature importance for every 55 features (geometric descriptors and energy descriptors) used for learning was estimated. Given that feature importance from PFI calculation only shows the relative importance between features in a single model, the PFI results were normalized as a discrete probability distribution with the sum of instances equal to one.Using the PFI results, we tried to explain why there is a performance difference among the TL models even if they shared the same type of physical properties from the GCMC simulation (albeit with different pressures). As such, the PFI result from the DL model trained with just the self-diffusion coefficient data was set as a reference and compared with the PFI results from the pre-trained models that were regarded as the best (100 bar) and the worst models (0.25 bar) in the previous section. The model that shows the highest R2 score among 5 models with size 1500 was selected as a reference model to construct a robust PFI result. Comparing the importance of the top 10 features based on PFI values of the reference model, both the reference and the best model share the “void fraction” as the most important feature, and other features were rather important for the worst model. Likewise, when the tendencies of the PFI values are similar, better performance improvement can be expected in TL. Interestingly, the “gravimetric surface area” (Grav ASA in Fig. 6a and b) and “energy range at −220k–40k”, which were not regarded as impactful features in the prediction of the self-diffusion coefficient, show a high importance (see Fig. 6a and b).
In addition, the Euclidean distance between two vectors, which consists of PFI values of the previously selected 10 features from the reference and the pre-trained model, was calculated to quantify the similarity of the PFI results. A small distance can imply a high similarity between two vectors. The distance of the best model is 0.305 which is much lower than the distance of the worst model, 0.409. From the results, we can say that the best model possessed a higher similarity with the reference model than the worst model in terms of the feature importance. Thus, we can expect that the PFI can be one method to identify whether the pre-trained model can provide meaningful knowledge for the TL task or not (see Section S4, ESI†).
Conclusion
In summary, we conducted a transfer learning study on MOFs to predict the methane self-diffusion coefficients with MOF descriptors as inputs as well as the knowledge gained from the training process with the methane gas uptakes. Although self-diffusion coefficients and gas uptakes are obtained using different simulation methods, the extracted MOF representations from the source domain (MOFs to gas uptakes) provide meaningful information to predict the self-diffusion coefficient of experimentally synthesized MOFs. As such, we can improve the prediction performance with a relatively small size of diffusion data. From our results, we demonstrate that instead of collecting data that requires a high computational cost in a brute-force manner, performance can be improved via collecting easily obtained data that is related to the target property. Although our study was focused on using methane uptake to facilitate the prediction of methane diffusion data, we surmise that this type of study can be extended to other systems and other applications, which can help accelerate discovery related to MOFs and deep learning.Materials and methods
Materials database
Two MOF databases were used in this work: (1) a hypothetical MOF database (hMOFs) and (2) experimentally synthesized MOF database (CoRE MOF database).39 Given that it is relatively convenient to obtain large amounts of hMOFs, the hMOF database was used as the source data set and the experimentally synthesized MOF database was used as the target data set for our TL task.The hMOFs were generated using two top-down based MOF construction packages: PORMAKE11 and ToBaCCo.10 PORMAKE has an advantage in the generation of structures with a high degree of diversity due to its large elements database which contains 719 node building blocks, 234 edge building blocks, and 1775 topologies. So, it can properly reflect the high tunability of MOFs. On the other hand, ToBaCCo can generate more synthesizable structures because it limits the elements database to only 41 highly symmetric topologies and building blocks that were already used in synthesized MOFs.10,40 Altogether, a total of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 845 hMOFs were obtained from the two MOF construction tools (12
845 hMOFs were obtained from the two MOF construction tools (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 from PORMAKE and 11
605 from PORMAKE and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 from ToBaCCo). Since the hMOFs generated from PORMAKE and ToBaCCo contain no solvents within the structures, all solvents removed CoRE MOF 2019 dataset were selected to endow the same conditions for both databases.
240 from ToBaCCo). Since the hMOFs generated from PORMAKE and ToBaCCo contain no solvents within the structures, all solvents removed CoRE MOF 2019 dataset were selected to endow the same conditions for both databases.
Properties and descriptors
The gas uptake was calculated via GCMC simulation using an in-house GPU code.41 As the GPU code can calculate the gas uptake at various pressures at once, we calculated the gas uptakes at 12 pressures from a very low pressure (0.25 bar) to a high pressure (100 bar). 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte Carlo iterations were conducted with a pore-blocking algorithm. By the way, the GPU code uses fugacity instead of pressure to reflect the practical phenomenon, especially in high pressure. So, pressure was converted into fugacity using the Peng–Robinson equation of state.42 The temperature and force field for the guest molecule and MOFs were fixed as 298 K and the universal force field (UFF)43 to control the condition except for pressure during the transfer of knowledge.
000 Monte Carlo iterations were conducted with a pore-blocking algorithm. By the way, the GPU code uses fugacity instead of pressure to reflect the practical phenomenon, especially in high pressure. So, pressure was converted into fugacity using the Peng–Robinson equation of state.42 The temperature and force field for the guest molecule and MOFs were fixed as 298 K and the universal force field (UFF)43 to control the condition except for pressure during the transfer of knowledge.
The self-diffusion coefficient was obtained from MD simulation using the LAMMPS software package.44 To calculate the self-diffusion coefficient, mean squared displacement (MSD) of methane molecules was recorded and the Einstein relation was used (eqn (1)).
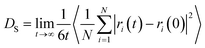 | (1) |
Five geometric descriptors (the largest cavity diameter, pore limiting diameter, volumetric surface area, gravimetric surface area, and void fraction) were obtained from the Zeo++ software.51 Surface areas were calculated with a nitrogen probe and void fractions were calculated with a helium probe. Moreover, energy descriptors were used to apply chemical factors during prediction.52 Energy descriptors were created with two steps (see Section S5 of the ESI† for details). First, energy grids (energy values are calculated in a grid at specified regular intervals) were generated as a spacing of 1 angstrom using the GRIDAY algorithm.53 Then, every value within energy grids was converted into a histogram with 50 bins. The normalized counts for bins were used as features for the deep neural network.
Details on transfer learning
In this work, a multilayer perceptron (MLP) was used as a transferable deep neural network (DNN) to predict adsorption and diffusion properties with geometric and energy descriptors. The MLP model consists of an input layer, 1st hidden layer, 2nd hidden layer, and output layer. The number of neurons was respectively 55, 512, 128, and 1 for the four dense layers. Both the hidden layers used the ReLU54 function as an activation function. The dropout layer was inserted between the 2nd hidden layer and output layer to alleviate overfitting.55 The dropout rate was fixed at 0.5 for both source and target tasks. For stable and efficient learning, the learning rate is fixed at 0.00001 and the Adam56 optimizer was used. The learning lasted for 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps (1 mini-batch per 1 step) to guarantee the convergence of the model's performance and the models that have the highest performance in the validation set were saved to prevent overfitting. The batch size was selected as 1000 for the source task and the size of the training data set for the target task.
000 steps (1 mini-batch per 1 step) to guarantee the convergence of the model's performance and the models that have the highest performance in the validation set were saved to prevent overfitting. The batch size was selected as 1000 for the source task and the size of the training data set for the target task.
To achieve transfer of knowledge, first of all, the model was trained with the hypothetical MOF databases (PORMAKE and ToBaCCo databases) as inputs and gas uptakes at certain pressures as outputs. Then, the pre-trained model was fine-tuned with experimentally synthesized MOFs (CoRE MOF database) as inputs and self-diffusion coefficients as outputs. During training in progress, the weights between the input layer and the first hidden layer are frozen and the other weights are finely tuned to find the optimal value to predict the self-diffusion coefficient. The data and associated scripts for the TL models in this work are available at https://github.com/YunsungLim/TL-from-adsorption-to-diffusion-in-MOFs.
Author contributions
Y. L. and J. K. wrote the manuscript. Y. L. conducted the overall computational studies such as molecular simulation, construction of the deep learning model, and training the model. J. K. formulated the project. All the authors contributed to exchanging ideas and discussed on this work.Conflicts of interest
The authors declare no competing interests.Acknowledgements
Y. L. and J. K. acknowledge funding from the National Research Foundation of Korea (NRF) under Project Number 2021M3A7C208974512.References
- O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714 CrossRef CAS PubMed.
- J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450–1459 RSC.
- L. S. Xie, G. Skorupskii and M. Dincă, Chem. Rev., 2020, 120, 8536–8580 CrossRef CAS PubMed.
- H. B. Wu and X. W. Lou, Sci. Adv., 2017, 3, eaap9252 CrossRef PubMed.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Chem. Rev., 2012, 112, 1105–1125 CrossRef CAS PubMed.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068 CrossRef CAS PubMed.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, ACS Appl. Mater. Interfaces, 2021, 13, 23647–23654 CrossRef CAS PubMed.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- S. Chong, S. Lee, B. Kim and J. Kim, Coord. Chem. Rev., 2020, 423, 213487 CrossRef CAS.
- C. Altintas, O. F. Altundal, S. Keskin and R. Yildirim, J. Chem. Inf. Model., 2021, 61, 2131–2146 CrossRef CAS PubMed.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- Y. Lim, J. Park, S. Lee and J. Kim, J. Mater. Chem. A, 2021, 9, 21175–21183 RSC.
- A. Nandy, C. Duan and H. J. Kulik, J. Am. Chem. Soc., 2021, 143, 17535–17547 CrossRef CAS PubMed.
- H. Park, Y. Kang, W. Choe and J. Kim, J. Chem. Inf. Model., 2022, 62, 1190–1198 CrossRef CAS PubMed.
- X. Zhang, K. Zhang, H. Yoo and Y. Lee, ACS Sustainable Chem. Eng., 2021, 9, 2872–2879 CrossRef CAS.
- J. Burner, L. Schwiedrzik, M. Krykunov, J. Luo, P. G. Boyd and T. K. Woo, J. Phys. Chem. C, 2020, 124, 27996–28005 CrossRef CAS.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- J. P. Ulmschneider, M. B. Ulmschneider and A. Di Nola, J. Phys. Chem. B, 2006, 110, 16733–16742 CrossRef CAS PubMed.
- K. Weiss, T. M. Khoshgoftaar and D. Wang, J. Big Data, 2016, 3, 9 CrossRef.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, ACS Cent. Sci., 2019, 5, 1717–1730 CrossRef CAS PubMed.
- D. Jha, K. Choudhary, F. Tavazza, W.-k. Liao, A. Choudhary, C. Campbell and A. Agrawal, Nat. Commun., 2019, 10, 5316 CrossRef CAS PubMed.
- R. Ma, Y. J. Colón and T. Luo, ACS Appl. Mater. Interfaces, 2020, 12, 34041–34048 CrossRef CAS PubMed.
- T.-H. Weng, H.-H. Tseng and M.-Y. Wey, Int. J. Hydrogen Energy, 2009, 34, 8707–8715 CrossRef CAS.
- S. Li, Z. Zong, S. J. Zhou, Y. Huang, Z. Song, X. Feng, R. Zhou, H. S. Meyer, M. Yu and M. A. Carreon, J. Membr. Sci., 2015, 487, 141–151 CrossRef CAS.
- Y. Zhang, J. Sunarso, S. Liu and R. Wang, Int. J. Greenhouse Gas Control, 2013, 12, 84–107 CrossRef CAS.
- R. Ma, F. Wang, J. Lin, H. Guo, T. Zhou, S. Liu, Z. Guo and X. Guo, Microporous Mesoporous Mater., 2020, 305, 110306 CrossRef CAS.
- J. Kim, M. Abouelnasr, L.-C. Lin and B. Smit, J. Am. Chem. Soc., 2013, 135, 7545–7552 CrossRef CAS PubMed.
- M. Witman, S. Ling, S. Jawahery, P. G. Boyd, M. Haranczyk, B. Slater and B. Smit, J. Am. Chem. Soc., 2017, 139, 5547–5557 CrossRef CAS PubMed.
- E. Haldoupis, T. Watanabe, S. Nair and D. S. Sholl, ChemPhysChem, 2012, 13, 3449–3452 CrossRef CAS PubMed.
- M. Pardakhti, P. Nanda and R. Srivastava, J. Phys. Chem. C, 2020, 124, 4534–4544 CrossRef CAS.
- G. S. Fanourgakis, K. Gkagkas, E. Tylianakis and G. Froudakis, J. Phys. Chem. C, 2020, 124, 7117–7126 CrossRef CAS.
- D. S. Moore and S. Kirkland, The basic practice of statistics, WH Freeman New York, 2007 Search PubMed.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef.
- https://eli5.readthedocs.io/en/latest/ .
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Energy Environ. Sci., 2016, 9, 3279–3289 RSC.
- J. Kim, R. L. Martin, O. Rübel, M. Haranczyk and B. Smit, J. Chem. Theory Comput., 2012, 8, 1684–1693 CrossRef CAS PubMed.
- https://github.com/CorySimon/PREOS .
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. Kim, S. Lee and J. Kim, Langmuir, 2019, 35, 3917–3924 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- C. Altintas, I. Erucar and S. Keskin, ACS Appl. Mater. Interfaces, 2018, 10, 3668–3679 CrossRef CAS PubMed.
- M. Z. Aghaji, M. Fernandez, P. G. Boyd, T. D. Daff and T. K. Woo, Eur. J. Inorg. Chem., 2016, 2016, 4505–4511 CrossRef CAS.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174 RSC.
- https://github.com/Sangwon91/GRIDAY .
- A. F. Agarap, 2018, arXiv:1803.08375.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- J. B. Diederik and P. Kingma, 2014, arXiv:1412.6980.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2me00082b |
| This journal is © The Royal Society of Chemistry 2022 |