Open Access Article
Open Access ArticleHigh resolution off resonant spectroscopy as a probe of the oxidation state†
Michal
Nowakowski
 *a,
Aleksandr
Kalinko
*a,
Aleksandr
Kalinko
 b,
Jakub
Szlachetko
b,
Jakub
Szlachetko
 c,
Rafał
Fanselow
c,
Rafał
Fanselow
 d and
Matthias
Bauer
d and
Matthias
Bauer
 a
a
aDepartment Chemie, Universität Paderborn, Warburger Str. 100, 33098 Paderborn, Germany. E-mail: michal.nowakowski@upb.de
bDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany
cSOLARIS National Synchrotron Radiation Centre, Jagiellonian University, Krakow 30-392, Poland
dInstitute of Nuclear Physics Polish Academy of Sciences, Kraków, 31-342, Poland
First published on 29th September 2022
Abstract
Currently, chemistry and physics are strongly dependent on the concept of the oxidation state. While the formal oxidation state is easily evaluated, the real physical oxidation state value is often difficult to determine and significantly varies from the formal values. Determination of the ionization threshold in X-ray absorption spectroscopy (XANES) relies on the absorption edge position and sometimes poses limitations, mainly due to the edge resonances. Moreover, the lower energy states can be probed only within x-soft or XUV photons providing only surface state information of probed materials. Here, we employ high energy resolution off-resonant spectroscopy to determine both 1s and 3p binding energies of Fe-based materials and therefore correlate to their physical oxidation state. The results are compared to the ones obtained with classical X-ray absorption, X-ray emission, and photoelectron spectroscopies. The observed differences in binding energies are discussed in a frame of initial and final state interactions with the atom's electronic configurations. The presented methodology is discussed towards potential use to single-shot experiments and application at X-ray free-electron lasers. Alternatively, core level X-ray emission spectroscopy can be used, but the emission line positions are strongly affected by spin-orbit interaction. However, due to the energy transfer from the photon to the excited core electron, the same information as in XANES is probed in high energy resolution off-resonant spectroscopy (HEROS). Based on the Kramers–Heisenberg theory, we propose a new approach for ionization threshold determination which is free of the limitations encountered in XANES-based determination of the core state energy. Namely, the value of core state energy can be determined analytically using a few HEROS spectra recorded with significantly higher spectral resolution. This approach provides a basis for the universal physical oxidation state determination method.
Introduction
Electronic structure determination of chemical complexes employing hard X-ray spectroscopy is an ongoing challenge. While most of the definitions and conventions are unambiguous, the definition of fundamental oxidation states is based on textbook formalism. Numerous attempts to assign physical oxidation states based on spectroscopic approaches exist.1–3 While covalent compounds with synergistic donor and acceptor bonds remain a significant challenge,4 ionic compounds are intrinsically more suited to establish experimental methods for oxidation state determination.A canonical way to assign an oxidation state is to use X-ray absorption spectroscopy (XAS). The method is based on photoexcitation of core-level electrons above the Fermi level of a compound, and in simple understanding, the absorption coefficient is proportional to the density of unoccupied states (unoccupied DOS). XAS theory, instrumentation, and applications are well described in the literature and textbooks.5–11 In K-edge spectroscopy of 3d metal compounds, the electron is excited from a 1s2 state resulting in a 1s1εp final state (superscript represents the number of electrons). In simple electrostatic terms, the absorption edge sensitivity to the oxidation state can be explained as the difference in electrostatic potential between the non-ionized N electron and the N-1 electron system. The energy required for photoexcitation of the 1s electron will be lower for the N-electron system since the total core potential is less negative than in the N-1 electron system. Thus, the edge position for the N-electron system will be observed at smaller energies compared to that for the N-1 electron system.12,13 Alternatively, the 1s → 4p transition (to continuum, with a limited lifetime) energy is used to correlate the metal-ligand bond distance (R) to the oxidation state. In simple compounds the distance gets shorter for a higher oxidation state, and the energy of the 4p acceptor state rises by a factor of R−2 relative to the ionization threshold.14 The edge position is higher in energy for a higher oxidation state in both cases. K-edge X-ray absorption near edge structure (XANES) of transition metals (TM) is based on 1s → np transition (n = 3,4,5), and the position of the inflection point of the rising edge is used as a measure for the ionization threshold.15 The edge position can be determined experimentally from the maximum of the Ist or zero value of the IInd derivative. Unfortunately, XANES or high energy resolution fluorescence detected (HERFD) XANES16 are often heavily affected by ligand contributions in the rising edge.17,18 The presence of additional transitions (1s → 3d, 1s → 2pLignad, and 1s → 4p) in the edge region that have intrinsic lifetimes and experimental broadening leads to ambiguities.19 Although carefully selected references can sometimes account for these, more often than not, they hinder precise oxidation state determination. In many cases, for example for Mn contamination in air, a linear combination fitting (LCF) analysis of XANES spectra allowed the determination of the oxidation state of compounds in the pollution mixture.20 The fingerprinting property of near-edge was also demonstrated for Cu in determination of the oxidation state of reagents in catalytic reactions via LCF.21 However, the method is limited for the cases where feasible references with similar electronic structure are available. In such cases, uncertainties are mostly arising from spectral intensities, precision of energy calibration curves, energy resolution and experimental stability. The final error bar for the oxidation state obtained by the LCF procedure is amplified by the aforementioned factors and fitting procedure giving rise to values between 10 and 20%. In some geologic and analytic studies, the problem of the edge position was circumvented by using the intrinsic sensitivity of the pre-edge feature to determine the oxidation state solely or in cross-reference with Mössbauer spectroscopy.22–26
Complementary to XAS, X-ray emission spectroscopy (XES) can be used to get more insight into the electronic structure of an atom. While the physical principles are the same as in XAS, the method is focused on occupied densities of states from which a created core hole is filled, resulting in a fluorescence decay channel. For 3d transition metals, the analysis of the core-to-core (CtC) Kβ XES mainline, described by a 1s13p63dn → 1s23p53dn+1 transition is the method of choice for the oxidation state determination in the limit of K edge excitation. The resulting spectrum is broadened by the initial and final lifetimes. The presence of unpaired 3d electrons induces additional 3p–3d exchange interaction that lifts the 3d state degeneration and leads to an additional split in the mainline accompanied by the appearance of a satellite Kβ′ peak.27–29 The energy difference between Kβ and Kβ′ lines which describes the energy distinction between high- and low-spin states and is denoted in spin-orbit coupling theory, changes with the number of unpaired 3d electrons (spin multiplicity) and the oxidation state.30 The position of the Kβ mainline is affected by spin-orbit coupling and the valence shell angular momentum, causing an entangled nature of all interactions.19 Moreover, the Kβ mainline position is influenced by the ligand field, and the corresponding charge transfer to a metal center frequently referred to as covalency.29 A localized nature of CtC-XES is considered allowing an oxidation state determination in simple compounds31–33 and more complex systems34,35 similar to XANES spectroscopy; the mentioned influences also cause some uncertainties here.
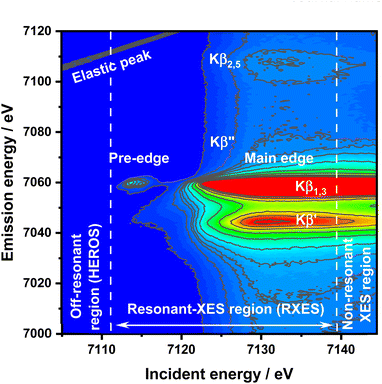
Despite these difficulties and disadvantages of XANES and CtC-XES, a precise oxidation state determination is of the utmost importance in numerous disciplines, like understanding chemical reactivity and electronic structures. Here, the formal oxidation state is defined as the charge of an atom if all of its bonds were fully ionic, while the physical oxidation state represents the ‘real’ charge on the atom, which is affected by the nature of the chemical bonding. Hard X-ray K-edge spectroscopy offers unique properties to understand chemical systems under realistic conditions, like high pressures and temperatures; thus, a more precise oxidation state determination is highly desired. Resonant X-ray emission spectroscopy (RXES), frequently referred to as RIXS (resonant inelastic X-ray scattering),36–39 offers new approaches here. RXES is a coherent process in which an electron is excited to a localized state above the Fermi level with near-simultaneous emission of a fluorescence photon.19,40 The fluorescence emission from a narrow bandwidth (i.e. 1 eV) is recorded with varied incident beam energy efficiently discriminated by energy dispersive analyzing crystals. The two-dimensional information on incidence and emission energies allows for spectral analysis with lifetime broadening being reduced significantly.19 RXES therefore provides highly resolved, complete information on the electronic structure of compounds in the form of a 2D matrix of internally calibrated XAS and XES spectra.41 Information about unoccupied and occupied electronic states can be derived by performing integration along the vertical and horizontal axes over selected regions of interest, respectively. The RXES plane can be divided into three regions dominated by different physical processes:42 Off-resonant-, resonant-, and non-resonant XES (high resolution off-resonant spectroscopy XES or HEROS-XES, RXES, and nXES). The main difference between nXES and RXES is that in nXES the emission is retarded which results in lost coherence of the process. In such a case, a 1s core electron is photoexcited to the continuum (1s > εp), while in RXES it is photoexcited to the lowest unoccupied levels. On the other hand, in HEROS the excited electron is directly involved in the decay process.41 In the case of Kβ RXES of 3d metals, the lowest final state will be 1s23p53dn+1. Recently, RXES was proposed as a tool for oxidation state analysis, and there were certain improvements of significant value34 however, not beyond the already established know-how of the method.19,37 The excitations in the resonant regime are an impeccable tool for identifying the electronic states and interactions contributing to the physical oxidation state, yet they do not provide a way to quantify this value. This paper aims to demonstrate off-resonant spectroscopy application to determine the ionization threshold value for an atom experimentally. The absorption threshold is understood here in accordance with the International Union of Crystallography definition, as an energy of the first allowed transition in the absorption spectrum.43 Thus, similar to the XAS-based experiment, we want to establish HEROS as a tool for precise and sample environment-independent physical oxidation state measurement.
Materials and methods
Experimental details
HEROS and RXES measurements were conducted at the P64 undulator beamline at PETRA III, DESY.44 A Si(111) double crystal monochromator (DCM) was used for energy selection while beam focusing and harmonic rejection were achieved using cylindrical Si mirrors. The estimated flux on a sample was 1013 ph per s. The signal acquisition in wavelength-dispersive mode was made using a von Hamos emission spectrometer45 equipped with eight Si(440) analyzer crystals. A Pilatus 100 k position-sensitive detector under normal conditions was used for signal detection. The incident energy resolution ΔE/E was 2 × 10−4, and the beam spot size on the sample was 100 × 300 μm2 (V × H). The DCM calibration was performed using the first inflection point in the Fe foil XAS spectrum set to 7112 eV. The total experimental resolution, including beam, sample, and spectrometer contributions, was determined by using the FWHM value of the elastic peak fitted by using a Gaussian function independently for each sample. The commercial FeS, α-Fe2O3 nanopowder, and FeCl3 samples (all purchased from Sigma-Aldrich and used without further purification) were measured as powders enclosed in two layers of Kapton. First, the Kβ RXES planes were recorded (Fig. 1 for FeCl3). Afterward, off-resonant spectra were collected with longer accumulation times for the selected incident energies.Off-resonant spectroscopy
For an incident X-ray beam energy tuned significantly below the ionization threshold of an atom, a different physical effect compared to excitations in a resonant regime will occur, leading to the new spectroscopic method, high resolution off resonant spectroscopy (HEROS).46–50 Like RXES, HEROS is a coherent scattering process with additional instant energy transfer from the emitted photon to the excited electron. It is possible due to energy conservation for the scattering process at a given energy loss E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eem(E) = Einc – Ef – E, where Eem is the emission energy, Einc is the incident energy, and Ef is the final state energy. In a simple understanding of the K-edge example, the excitation occurs on the Lorentzian tail of the 1s state. During excitation of the electron above the Fermi level by the incoming energy Einc < EK, the remaining energy is transferred from the emitted fluorescence photon (Eem) to the excited electron in the quasi-simultaneous process. Therefore, the energy of the emitted photon is reduced by the value of energy transferred to the electron excited above the Fermi level. The following points make HEROS an attractive alternative to conventional XAS or HERFD: (1) the incoming beam energy defines the emission energy; (2) both incoming beam and emitted radiations are below the ionization threshold; (3) fluorescence can be measured with fixed optical geometry and with one incident energy. Due to the mentioned properties, a HEROS spectrum is proportional to the unoccupied density of states, and is free of self-absorption effects.49 Moreover, the fixed setup for HEROS accumulation makes it a good candidate for time-resolved, shot-to-shot studies, of which proof-of-concept measurements were already demonstrated for Pt(acac)2 thermal decomposition.51 The limitation of HEROS applications to 3d metal compounds is a low cross-section for the process resulting in two-three orders of magnitude smaller signals than for RXES.42 This limitation can be circumvented by sufficiently long signal acquisition, increased concentration of the absorber or by performing experiments at brighter sources. With decreasing radiation decay channel yield for elements with Z < 20 at the expense of non-radiative decay channels, the relatively low cross-sections of the off-resonant scattering will make the measurements impossible. On the other hand, 5d elements exhibit significantly stronger HEROS signals regarding the emission mainline than 3d elements.52 Moreover, the HEROS-like scattering signal is visible for incident energies above the absorption edge, and in the case of 3d elements, this scattering is covered by the intense emission mainline. The scattering signal above the resonance is visible, especially in the constant energy transfer RXES plane at the pre-edge resonance. The RXES planes for Fe2O3, and FeS are available in the ESI,† while the RXES plane for FeCl3 is shown in Fig. 1. With a proper intensity scale adjustment one could see that HEROS signal features originate from the constant energy transfer contributions that shift continuously with the incident energy.
Eem(E) = Einc – Ef – E, where Eem is the emission energy, Einc is the incident energy, and Ef is the final state energy. In a simple understanding of the K-edge example, the excitation occurs on the Lorentzian tail of the 1s state. During excitation of the electron above the Fermi level by the incoming energy Einc < EK, the remaining energy is transferred from the emitted fluorescence photon (Eem) to the excited electron in the quasi-simultaneous process. Therefore, the energy of the emitted photon is reduced by the value of energy transferred to the electron excited above the Fermi level. The following points make HEROS an attractive alternative to conventional XAS or HERFD: (1) the incoming beam energy defines the emission energy; (2) both incoming beam and emitted radiations are below the ionization threshold; (3) fluorescence can be measured with fixed optical geometry and with one incident energy. Due to the mentioned properties, a HEROS spectrum is proportional to the unoccupied density of states, and is free of self-absorption effects.49 Moreover, the fixed setup for HEROS accumulation makes it a good candidate for time-resolved, shot-to-shot studies, of which proof-of-concept measurements were already demonstrated for Pt(acac)2 thermal decomposition.51 The limitation of HEROS applications to 3d metal compounds is a low cross-section for the process resulting in two-three orders of magnitude smaller signals than for RXES.42 This limitation can be circumvented by sufficiently long signal acquisition, increased concentration of the absorber or by performing experiments at brighter sources. With decreasing radiation decay channel yield for elements with Z < 20 at the expense of non-radiative decay channels, the relatively low cross-sections of the off-resonant scattering will make the measurements impossible. On the other hand, 5d elements exhibit significantly stronger HEROS signals regarding the emission mainline than 3d elements.52 Moreover, the HEROS-like scattering signal is visible for incident energies above the absorption edge, and in the case of 3d elements, this scattering is covered by the intense emission mainline. The scattering signal above the resonance is visible, especially in the constant energy transfer RXES plane at the pre-edge resonance. The RXES planes for Fe2O3, and FeS are available in the ESI,† while the RXES plane for FeCl3 is shown in Fig. 1. With a proper intensity scale adjustment one could see that HEROS signal features originate from the constant energy transfer contributions that shift continuously with the incident energy.
The principles of HEROS can be explained based on the generalized Kramers–Heisenberg equation derived by Tulkki and Årberg describing the double differential cross-section for the resonant inelastic X-ray scattering.37,53–55 The equation describes scattering as a two-stage mechanism: absorption of a photon by the initial atomic state leading to an intermediate state and deexcitation to the final state within the atomic lifetime. The interference between the initial and final configurations can be neglected for hard X-ray energies in a coherent process.42,53,54 The assumption that the oscillator strength describing the excitation above the Fermi level is proportional to the unoccupied DOS functions and intensity of the emitted fluorescence to the cross-section will allow to simplify the equation and rewrite it for given photoelectron energy49 in the case of the Kβ emission line region for 3d metals. The lifetime of the final state is neglected and replaced by a Dirac delta function to maintain energy conservation.49–51,56 The integral can be calculated analytically, using the relation Eem = Einc − |EM3| − E for the integral solution, and the result will be as follows:50
 | (1) |
 | ||
| Fig. 2 HEROS-XES to HEROS-XAS transition according to eqn (1) for all studied references performed on spectra recorded at an incident energy of 7100 eV. | ||
Results and discussion
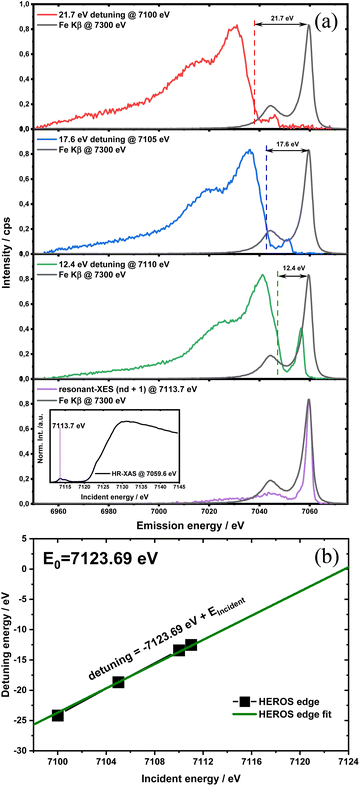
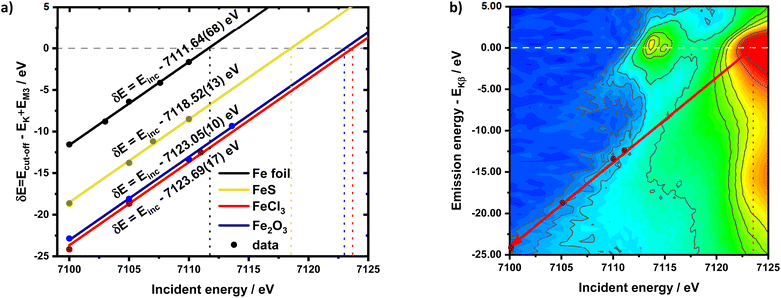
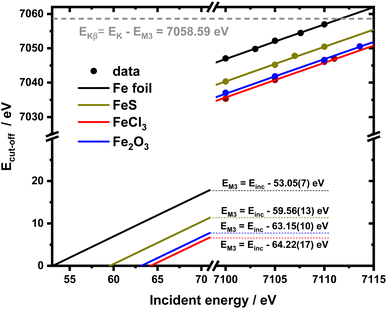
HEROS-XES probes a convoluted final state distribution with an unoccupied density of states, and the high energy cut-off relates to EK in XAS via energy conservation for the scattering process. The HEROS-XES edge (high energy cut-off) can be defined as Ecut-off = EK – δE – EM3, where δE is the detuning energy of the incoming X-rays with respect to the 1s threshold energy. Since δE equals Einc – EK, the HEROS-XES cut-off can simply be defined as Einc–EM3. The energy conservation of the scattering process under off-resonant conditions can be used to determine the position of E1s from the condition of δE = 0. In the case of δE → 0, HEROS-XES is transferred to RXES, and the condition: Einc = EK is fulfilled. Therefore, the HEROS-XES spectra can be measured at several incidence energies far from resonances, and the thus obtained dataset is used to extrapolate towards EK with high precision. Eqn (1) provides the linear relation between EK–EM3–E and incident beam energy for such excitation conditions. This behavior is shown in Fig. 3 for FeCl3. The detuning parameter δE for XES is defined as the energy gap between the FeCl3 Kβ mainline position and the determined HEROS-XES high energy cut-off Ecut-off; thus, δE = Ecut-off – EK + EM3. The HEROS-XES spectra are compared to the nXES spectrum recorded at an incident energy of 7300 eV. For an incident energy of 7113.7 eV that corresponds to resonant excitation into the 3d state, HEROS-XES is entirely substituted by the RXES spectrum of the 1s23p53d4 state (Fig. 3a, bottom). The nXES maximum is 7059.47 eV, while the RXES maximum arises at 7059.87 eV. A different final state and multielectron interaction can account for this variance.28,34,59 We recognize the RXES Kβ1,3 mainline position at the incidence of 7113.7 eV as the correct ionization threshold for the 3p 1s transition since it represents the first state populated by the photoionization event for the lowest incident energy, without additional energy transfer from the emitted photon.HEROS is well described in terms of inelastic X-ray scattering. The energy conservation rule for the scattering process in the off-resonant region provides EK = EM3 + Ecut-off – δE. To extrapolate absorption edge position the EK, high quality RXES plane or sets of HEROS-XES spectra for different Einc values are required to determine the Ecut-off from their derivatives. Additionally, an RXES spectrum corresponding to the first unoccupied state is necessary. This state can be precisely determined based on the RXES plane measurement and extracted HERFD-XANES spectrum as shown in Fig. 4a, bottom. In this way, a first accessible unoccupied state defined by the relation EK – EM3 and not affected by energy transfer from the emitted photon will be characterized. The advantage of this approach is that the evolution of derivatives can be tracked with changing Einc (see the ESI† for derivatives) in a fixed arrangement, and emission spectra are collected in an energy-dispersive mode, which offers superior resolution. The proposed solution will be highly advantageous, especially for the FEL experiments with a fixed setup: single-shot measurements, single-shot pump-probe experiments, and single-shot X-ray pump – X-ray probe experiments. While the X-ray spectrometers are operating at a relatively high diffraction order of the crystal, the energy resolution is superior to typical resolution for incidence beam monochromators working with Si(111) crystals. Additionally, the core-hole lifetime broadening due to the final state 3pn−14p1 is present.
The calibration scheme proposed in Fig. 3 can be expanded further to form a 2D calibration plane based on different compounds. Fig. 4a presents a 2D calibration plane for Fe0–FeIII compounds. For each HEROS-XES spectrum, a δE was computed and plotted as a function of the incident energy in the same way as shown in Fig. 3b. Linear relations were extrapolated to δE = 0 corresponding to the incident energy equal to E0 in XAS. The universal relation for the E1 value corresponding to any point on the calibration plane can be derived from simple geometry as:
| δE = Einc + δE1 − Einc1 | (2) |
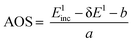 | (3) |
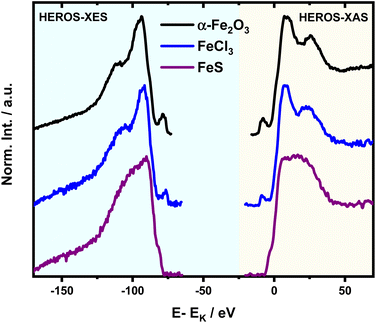
It is interesting to evaluate from KH formalism and eqn (1) the low energy limit for the scattering process, i.e., the lowest incidence energy required to induce the off-resonant scattering process. The lowest incidence energy has to be equal to the energy of the final state (EM3) from energy conservation. Thanks to this property, the obtained calibration curves for oxidation state determination can be employed to determine the energy of the final state by extrapolating the calibration curves to Ecutoff = 0. In Fig. 5, we show the obtained result used to extract the 3p final state (M3 edge) energies for the measured samples. The M3 energy values are shown in Table 1 and compared to the XPS data and the results extracted from high-resolution XAS measurements. For the latter, we used Kβ emission energy (3p → 1s) and subtracted the K energy that has been obtained from the inflection point of the absorption curves. There is clear evidence of the difference between X-ray and XPS data. This effect can be assigned to the penetration depths that can be achieved in both measurements. The measured signal in the XPS experiment contains a significant contribution of surface states mixed with bulk state information. In the case of X-rays, the penetration depth is in the range of a few microns, and the bulk properties of the material are probed. In this context, we should emphasize that only the X-ray spectroscopy methods can give insights into the high electronic orbitals with bulk sensitivity. The HEROS and XANES data comparison indicate small change in the eV range for FeS and FeCl3, while the obtained values for α-Fe2O3 and Fe are essentially the same. The difference may result from the interaction between the initial and final states with remaining electronic states, particularly 3p-3d exchange interaction.29 Also, the E1s edge position extracted from the XAS curve may not be precise enough as the near edge spectra are overlapped with resonant features. Furthermore, we should note the difference in the scheme of the scattering process. In non-resonant XES, the 1s core hole is filled within a 0.55 fs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57 lifetime, and this scattering time is constant, independent of the incidence energy. In the case of the off-resonant scattering process, the time of scattering equals:64
57 lifetime, and this scattering time is constant, independent of the incidence energy. In the case of the off-resonant scattering process, the time of scattering equals:64
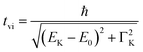 | (4) |
 | ||
| Fig. 5 2D calibration plane from figure recalculated for the absolute Ecut-off values and extended till 0 to extrapolate EM3 values. | ||
Finally, we would like to point out that the absorption edge position or absorption threshold is not well defined.43 According to the most popular experimental approach the absorption edge is composed of an atomic background, modelled by atan or erf functions convoluted with specific electronic transitions modelled by using Lorentzian or Voight functions.15,43 By definition, the absorption edge starts when the incident energy is enough to promote transition of the core electron to a continuum.43 However, absorption cross section can be derived directly from Fermi’s golden rule written for X-ray absorption with wavefunctions for all electronic states used; thus, XANES involves bound states and a continuum. One can argue that the absorption threshold, especially in the context of the physical oxidation state, should be considered, where the first unoccupied states emerge, including pre-edge transitions. Such an understanding was already proven to be correct in the analysis of the composition of glasses65,66 and minerals.22,26 Here, we do not contest the definition of the absorption threshold or its relation to the physical oxidation state. Furthermore, since relation (2) is linear, the presented approach can be extended to any edge feature, including the pre-edge.
Conclusions
These results offer new physical oxidation state determination opportunities, which could be problematic based only on the XANES edge position. An ambiguity of this approach is recognized in the literature, for example, for Cr species.7 The minimal requirement for a correct calibration curve is three different oxidation states, and the most suitable reference would be a single, neutral Me atom and separate Me2+ and Me3+ ions. With an apparent lack of perfect references, the most plausible references for the oxidation state analysis should be a metal foil as the Me0 reference, MeF2 for Me2+, and MeF3 for Me3+ since F is the most electronegative element in the periodic table. Alternatively, a proposed calibration scheme based on the relative positions of the HEROS cutoff and Kβ mainline maximum can establish a correct energy grid. The presented method allows for environment-independent E0 determination at a given energy grid. As a consequence of the equivalence of HEROS and HERFD, with respect to the challenges in determining the edge position, the methods are the same. While the HEROS-based approach benefits from enhanced resolution of XES spectrometers, the Ecut-off determination still is affected by noise in the derivatives of the spectra and restricted to elements with Z > 20. However, the same approach can be utilized to calibrate the energy scale at charge integrating detectors at FEL sources, where much more intense signals can be achieved. Although the proposed method would also test a linear dependence between the formal oxidation state and E0, it is beyond the scope of the current communication.The definition of the physical oxidation state remains ambiguous due to the problems with its precise determination, and this uncertainty raises several problems in physics and chemistry. We have demonstrated that using off-resonant XES spectroscopy, information about XAS EK can be derived. HEROS-XES contains information about unoccupied DOS functions of an atom, and the spectra can be transformed into HEROS-XAS. The XAS-related detuning parameter δE does not affect the position of the HEROS-XAS edge (E0) while the HEROS-XES edge (E0(Einc – EM3 – Eem)) shifts linearly with the incident energy. This property can be used to derive a relation between the XES-related detuning parameter δE and E0 to determine the absorption edge energy. The precise and unbiased absorption edge shape value of E0 can help render the exact value of the oxidation state, which is a significant step closer to obtaining a well-defined oxidation state of an atom in a molecule. We should emphasize that the proposed methodology can be very relevant for studies of 3d-based metals (e.g. Ti, Cr, or Cu), metal-centered molecules important for biological research or nanomaterials as well as hybrid-systems important for renewable energy technologies. Importantly, application of X-rays allows for in situ research and for determination of electronic structure changes and the energy distribution of charges as a function of time with time-resolved pump-probe experiments at synchrotrons and X-ray free electron lasers. When using dispersive type spectrometers, the HEROS spectra may be recorded with single-shot and shot-to-shot modes without the need for scanning of any optical components of the beamline and end station. Moreover, the use of a stochastic self-amplified spontaneous emission process that delivers broadband X-ray spectra may be considered for application. High energy resolution for the latter may be maintained with recently developed reconstruction methods applied with SASE XFEL beams.67
Author contributions
Conceptualization: MN, JS, MB; data curation: MN, AK; formal analysis: MN; funding acquisition: MB; investigation: MN, AK, JS, RF, MB; methodology: MN; project administration: MN; resources: MN, MB; software: AK; supervision: MB; validation: MN, AK, JS, RF, MB; visualization: MN; writing – original draft: MN, AK; writing – review & editing: MN, AK, JS, RF, MB.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PETRA III at DESY and beamline P64 are acknowledged for the provision of beamtime. MN and MB acknowledge the German BMBF for funding in frame of project Syn-XAS (FKZ 05K18PPA) and FocusPP64 (FKZ05K19PP1). JS and RF acknowledge partial support from the National Science Centre (Poland) and their grant no. 2020/37/B/ST3/0055. The authors would like to thank dr. Wolfgang Caliebe (Petra III, DESY) for assistance.Notes and references
- S. Pehkonen, Analyst, 1995, 120, 2655–2663 RSC.
- J. J. Leani, H. J. Sánchez, M. Valentinuzzi and C. Pérez, J. Anal. At. Spectrom., 2011, 26, 378–382 RSC.
- P. H. L. Sit, R. Car, M. H. Cohen and A. Selloni, Inorg. Chem., 2011, 50, 10259–10267 CrossRef CAS PubMed.
- L. Burkhardt, Y. Vukadinovic, M. Nowakowski, A. Kalinko, J. Rudolph, P. A. Carlsson, C. R. Jacob and M. Bauer, Inorg. Chem., 2020, 59, 3551–3561 CrossRef CAS PubMed.
- W. M. Kwiatek, M. Galka, a. L. Hanson, C. Paluszkiewicz and T. Cichocki, J. Alloys Compd., 2001, 328, 276–282 CrossRef CAS.
- K. K. Gunter, L. M. Miller, M. Aschner, R. Eliseev, D. Depuis, C. E. Gavin and T. E. Gunter, Neurotoxicology, 2002, 23, 127–146 CrossRef CAS PubMed.
- M. Tromp, J. Moulin, G. Reid and J. Evans, AIP Conf. Proc., 2007, 882, 699–701 CrossRef CAS.
- F. de Groot, G. Vankó and P. Glatzel, J. Phys. Condens. Matter, 2009, 21, 104207 CrossRef PubMed.
- J. J. Rehr, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- J. J. Ã. Rehr, Radiat. Phys. Chem., 2006, 75, 1547–1558 CrossRef CAS.
- M. Bauer and H. Bertagnolli, Methods Phys. Chem., 2012, 1, 231–269 CAS.
- R. G. Shulman, Y. Yafet, P. Eisenberger and W. E. Blumberg, Proc. Natl. Acad. Sci., 1976, 73, 1384–1388 CrossRef CAS PubMed.
- J. A. Kirby, D. B. Goodin, T. Wydrzynski, A. S. Robertson and M. P. Klein, J. Am. Chem. Soc., 1981, 103, 5537–5542 CrossRef CAS.
- C. R. Natoli, Springer Proc. Phys., 1984, 13, 38–42 Search PubMed.
- J. Stöhr, in NEXAFS Spectroscopy, ed. H. K. V. Lotsch, G. Ertl, R. Gomer and D. L. Mills, Springer-Verlag Berlin Heidenberg, Berlin, 2nd edn, 1996, pp. 211–238 Search PubMed.
- M. Bauer, Phys. Chem. Chem. Phys., 2014, 16, 13827–13837 RSC.
- J. Rabeah, M. Bauer, W. Baumann, A. E. C. McConnell, W. F. Gabrielli, P. B. Webb, D. Selent and A. Brückner, ACS Catal., 2013, 3, 95–102 CrossRef CAS.
- R. Grauke, R. Schepper, J. Rabeah, R. Schoch, U. Bentrup, M. Bauer and A. Brückner, ChemCatChem, 2019, 1025–1035 Search PubMed.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- S. Datta, A. M. Rule, J. N. Mihalic, S. N. Chillrud, B. C. Bostick, J. P. Ramos-Bonilla, I. Han, L. M. Polyak, A. S. Geyh and P. N. Breysse, Environ. Sci. Technol., 2012, 46, 3101–3109 CrossRef CAS PubMed.
- S. H. Lee, I. Sullivan, D. M. Larson, G. Liu, F. M. Toma, C. Xiang and W. S. Drisdell, ACS Catal., 2020, 10, 8000–8011 CrossRef CAS.
- A. J. Berry, G. M. Yaxley, A. B. Woodland and G. J. Foran, Chem. Geol., 2010, 278, 31–37 CrossRef CAS.
- M. Wilke, O. Hahn, A. B. Woodland and K. Rickers, J. Anal. At. Spectrom., 2009, 24, 1364 RSC.
- A. Boubnov, H. Lichtenberg, S. Mangold and J. D. Grunwaldt, J. Synchrotron Radiat., 2015, 22, 410–426 CrossRef CAS PubMed.
- E. Cottrell, K. a. Kelley, A. Lanzirotti and R. a. Fischer, Chem. Geol., 2009, 268, 167–179 CrossRef CAS.
- M. Wilke, F. Farges, P. E. Petit, G. E. Brown and F. Martin, Am. Mineral., 2001, 86, 714–730 CrossRef CAS.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. Debeer, J. Am. Chem. Soc., 2010, 132, 9715–9727 CrossRef CAS PubMed.
- G. Vankó, T. Neisius, G. Molnár, F. Renz, S. Kárpáti, A. Shukla and F. M. F. De Groot, J. Phys. Chem. B, 2006, 110, 11647–11653 CrossRef PubMed.
- M. Pollock, U. Delgado-Jaime, M. Atanasov, F. Neese and S. Debeer, J. Am. Chem. Soc., 2014, 136, 9453–9463 CrossRef PubMed.
- G. Peng, X. Wang, C. R. Randall, J. A. Moore and S. P. Cramer, Appl. Phys. Lett., 1994, 65, 2527–2529 CrossRef CAS.
- J. A. Rees, A. Wandzilak, D. Maganas, N. I. C. Wurster, S. Hugenbruch, J. K. Kowalska, C. J. Pollock, F. A. Lima, K. D. Finkelstein and S. DeBeer, J. Biol. Inorg Chem., 2016, 21, 793–805 CrossRef CAS PubMed.
- H. Visser, E. Anxolabéhère-Mallart, U. Bergmann, P. Glatzel, J. H. Robblee, S. P. Cramer, J.-J. Girerd, K. Sauer, M. P. Klein and V. K. Yachandra, J. Am. Chem. Soc., 2001, 123, 7031–7039 CrossRef CAS PubMed.
- G. Tirao, S. Ceppi, A. L. Cappelletti and E. V. Pannunzio Miner, J. Phys. Chem. Solids, 2010, 71, 199–205 CrossRef CAS.
- R. G. Castillo, A. W. Hahn, B. E. Van Kuiken, J. T. Henthorn, J. McGale and S. DeBeer, Angew. Chem., 2021, 133, 10200–10209 CrossRef.
- J. Kowalska and S. DeBeer, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 1406–1415 CrossRef CAS PubMed.
- F. M. F. De Groot, P. Glatzel, U. Bergmann, P. A. Van Aken, R. A. Barrea, S. Klemme, M. Hävecker, A. Knop-Gericke, W. M. Heijboer and B. M. Weckhuysen, J. Phys. Chem. B, 2005, 109, 20751–20762 CrossRef CAS PubMed.
- A. Kotani and S. Shin, Rev. Mod. Phys., 2001, 73, 203–246 CrossRef CAS.
- P. Glatzel, M. Sikora, G. Smolentsev and M. Fernández-García, Catal. Today, 2009, 145, 294–299 CrossRef CAS.
- L. J. P. Ament, M. Van Veenendaal, T. P. Devereaux, J. P. Hill and J. Van Den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- M. Nowakowski, J. Czapla-Masztafiak, J. Szlachetko and W. M. Kwiatek, Chem. Phys., 2017, 493, 49–55 CrossRef CAS.
- J. P. Rueff and A. Shukla, Rev. Mod. Phys., 2010, 82, 847–896 CrossRef CAS.
- C. J. Milne, T. J. Penfold and M. Chergui, Coord. Chem. Rev., 2014, 277–278, 44–68 CrossRef CAS.
- C. T. Chantler, Int. Tables Crystallogr., 2021, 1–9 Search PubMed.
- W. A. Caliebe, V. Murzin, A. Kalinko and M. Görlitz, AIP Conf. Proc., 2019, 2054, 060031 CrossRef.
- A. Kalinko, W. A. Caliebe, R. Schoch and M. Bauer, J. Synchrotron Radiat., 2020, 27, 31–36 CrossRef CAS PubMed.
- H. Hayashi, R. Takeda, Y. Udagawa, T. Nakamura, H. Miyagawa, H. Shoji, S. Nanao and N. Kawamura, Phys. Scr., T, 2005, 115, 1094–1096 CrossRef.
- H. Hayashi, R. Takeda, Y. Udagawa, T. Nakamura, H. Miyagawa, H. Shoji, S. Nanao and N. Kawamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–9 CrossRef.
- J. Szlachetko, J. C. Dousse, M. Berset, K. Fennane, M. Szlachetko, J. Hoszowska, R. Barrett, M. Pajek and A. Kubala-Kukus, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 1–11 CrossRef.
- W. Błachucki, J. Szlachetko, J. Hoszowska, J. C. Dousse, Y. Kayser, M. Nachtegaal and J. Sá, Phys. Rev. Lett., 2014, 112, 1–5 CrossRef PubMed.
- W. Błachucki, J. Hoszowska, J. C. Dousse, Y. Kayser, R. Stachura, K. Tyrała, K. Wojtaszek, J. Sá and J. Szlachetko, Spectrochim. Acta, Part B, 2017, 136, 23–33 CrossRef.
- J. Szlachetko, M. Nachtegaal, J. Sá, J. Dousse, J. Hoszowska, E. Kleymenov, M. Janousch, O. Safonova, C. König and J. van Bokhoven, Chem. Commun., 2012, 48, 10898–10900 RSC.
- I. Pudza, A. Kalinko, A. Cintins and A. Kuzmin, Acta Mater., 2021, 205, 116581 CrossRef CAS.
- J. Tulkki and T. Aberg, J. Phys. B At. Mol., 1982, 15, L435–L440 CrossRef CAS.
- T. Åberg and J. Tulkki, in Atomic Inner-Shell Physics, ed. B. Crasemann, Plenum, New York, Springer, Boston, MA, Boston, 1985, pp. 419–463 Search PubMed.
- P. Eisenberger, P. M. Platzman and H. Winick, Phys. Rev. Lett., 1976, 36, 623–626 CrossRef CAS.
- J. Szlachetko and Y. Kayser, in High-Resolution XAS/XES: Analyzing Electronic Structures of Catalysts, ed. J. Sá, CRC Press, Boca Raton, 2014, pp. 59–116 Search PubMed.
- J. L. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56 CrossRef CAS.
- M. L. Berger, J. Hubbell, S. Seltzer, J. Chang, J. Coursey, R. Sukumar, D. Zucker, K. Olsen, NIST Standard Reference Database 8 (XGAM), 2010 Search PubMed.
- G. Vanko, A. Bordage, P. Glatzel, E. Gallo, M. Rovezzi, W. Gawelda, A. Galler, C. Bressler, G. Doumy, A. M. March, E. P. Kanter, L. Young, S. H. Southworth, S. E. Canton, J. Uhlig, G. Smolentsev, V. Sundstrom, K. Haldrup, T. B. Van Driel, M. M. Nielsen, K. S. Kjaer and H. T. Lemke, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 166–171 CrossRef CAS.
- J. Wang, B. Mao, M. G. White, C. Burda and J. L. Gole, RSC Adv., 2012, 2, 10209–10216 RSC.
- T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441–2449 CrossRef CAS.
- K. Shimada, T. Mizokawa, K. Mamiya, T. Saitoh, A. Fujimori and T. Kamimura, Surf. Sci. Spectra, 1999, 6, 321–336 CrossRef CAS.
- P. Mills and J. L. Sullivan, J. Phys. D. Appl. Phys., 1983, 16, 723–732 CrossRef CAS.
- F. Gelmukhanov, P. Sałek, T. Privalov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 380–389 CrossRef CAS.
- F. Farges, Y. Lefrère, S. Rossano, A. Berthereau, G. Calas and G. E. Brown, J. Non. Cryst. Solids, 2004, 344, 176–188 CrossRef CAS.
- F. Farges, S. Rossano, Y. Lefrre, M. Wilke and G. E. Brown Jr, Phys. Scr., 2005, T115, 957–959 CrossRef CAS.
- Y. Kayser, C. Milne, P. Juranić, L. Sala, J. Czapla-Masztafiak, R. Follath, M. Kavčič, G. Knopp, J. Rehanek, W. Błachucki, M. G. Delcey, M. Lundberg, K. Tyrała, D. Zhu, R. Alonso-Mori, R. Abela, J. Sá and J. Szlachetko, Nat. Commun., 2019, 10, 1–10 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ja00232a |
| This journal is © The Royal Society of Chemistry 2022 |