Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantification routines for full 3D elemental distributions of homogeneous and layered samples obtained with laboratory confocal micro XRF spectrometers†
Frank
Förste
 *a,
Leona
Bauer
*a,
Leona
Bauer
 a,
Korbinian
Heimler
b,
Bastian
Hansel
b,
Carla
Vogt
b,
Birgit
Kanngießer
a and
Ioanna
Mantouvalou
c
a,
Korbinian
Heimler
b,
Bastian
Hansel
b,
Carla
Vogt
b,
Birgit
Kanngießer
a and
Ioanna
Mantouvalou
c
aTechnische Universität Berlin, 10623 Berlin, Germany. E-mail: ffoerste@physik.tu-berlin.de
bTechnische Universität Bergakademie Freiberg, 09599 Freiberg, Germany
cHelmholtz-Zentrum Berlin, 12489 Berlin, Germany
First published on 4th July 2022
Abstract
Confocal micro-X-ray fluorescence spectroscopy can be performed with laboratory spectrometers for elemental imaging with 3D resolution. Due to self-absorption inside a specimen and energy effects induced by the used polycapillary optics, interpretation of data can be challenging. Thus, quantification techniques to reconstruct sample composition and geometry are mandatory to widen the applicability of the technique to further fields of analytical chemistry. We present an analytical routine which facilitates the quantitative investigation of 3D data sets obtained with laboratory spectrometers. By fully calibrating the spectrometer parameters the procedure is generalized to be suitable for all spectrometers with known excitation spectra and polycapillary optics. Calibration and validation measurements on homogeneous and stratified samples are presented with a discussion on uncertainties and challenges. Finally, the localization of a goethite needle in a quartz matrix is presented as an example of a possible routine application.
Introduction
In various fields of analytical chemistry, the knowledge of the local elemental composition of samples in the micrometre regime is of significant importance. Micro X-ray fluorescence analysis (MXRF) is a well-established and reliable tool that allows 2D lateral qualitative elemental imaging1,2 as well as the quantification of the mass depositions or concentrations.3,4In 2003|2004 5,6 MXRF was extended by performing MXRF in a confocal setup. Here, the foci of two X-ray optics form a probing volume in the micrometre range from which the fluorescence is in first approximation detected. By moving the sample trough the probing volume and collecting the intensities of the fluorescing radiation as a function of position, point spectra (0D), line profiles (1D), 2D maps or full 3D volumes can be obtained.7 Confocal MXRF (CMXRF) spectroscopy thus allows a flexible non-destructive three-dimensional elemental analysis of a sample or specific parts therein and was broadly applied to various fields e.g. archaeology, biology and cultural heritage 8–12 and is especially beneficial for biological samples where due to low absorption inside the specimen deep regions can be examined.
Concerning quantification, routines for the investigation of homogeneous bulk13,14,15 and layered samples16,17 have been developed using monochromatic excitation for experiments performed with synchrotron radiation. Recently, full 3D reconstruction for CMXRF data measured with monochromatic excitation was shown.18
Regarding polychromatic excitation from X-ray tube spectrometers, we developed a quantification routine for stratified samples which is discussed in detail in a previous work.16 Briefly, the approach is based on a modified fundamental parameter equation (FP), where a separation of the characteristic parameters of the excitation and detection lenses is possible due to the assumption that the radiation from the characteristic lines of the excitation spectrum is mainly responsible for photoionization. While this separation holds for many systems, it is not valid for laboratory spectrometers with anodes such as rhodium (Rh), where the transmission of the polycapillary full lens in the excitation channel dampens the intensity of the K fluorescence lines.
Based on the formalism in Mantouvalou et al.,16 we show in this work a more generalized calibration procedure which widens the applicability of the algorithm. For this purpose, software tools for fast deconvolution of large data cuboids, as well as calibration and quantification routines are presented. Through the measurement of homogeneous and stratified reference samples, the uncertainties of the quantification approach are assessed. Finally, to demonstrate the versatility of the methodology, the measurement and quantification of a geological sample using a different spectrometer is presented. The introduced routine, thus, facilitates the quantitative analysis of 3D elemental distributions of heterogeneous objects. And due to the use of laboratory equipment, repeated measurements on a high number of samples are rendered feasible, further establishing the CMXRF technique as an analytical tool for application fields such as biology, biomedicine, environmental sciences, mineralogy or forensics.
Theory
The quantification for CMXRF data aims at the full reconstruction of composition and structure of a sample through the analysis of net peak fluorescence intensities as a function of position in 3D space. The self-absorption of excitation and fluorescence radiation inside the sample is the critical entity, which complicates the analytical description of 3D data sets.We have shown in previous works the analytical description for fluorescence data from 1D line scans into the depth, the so-called depth profiles, for stratified samples and validated the approach for monochromatic19 and polychromatic excitation.16
For homogeneous bulk samples, the net peak intensity Φi of a fluorescence line i at the measurement position xn is given as
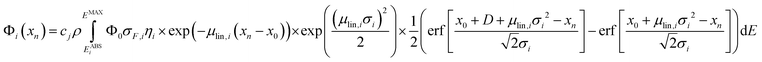 | (1) |
Both, the integral sensitivity ηi and the probing volume size σi are functions of the excitation E0 and fluorescence energy Ei:
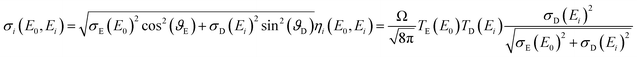 | (2) |
| σE|D = σMAXE|Dexp(σEXPE|DE0|i) + σOFFE|D | (3) |
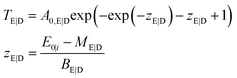 | (4) |
In our previous work,17 a separation of the spot sizes and transmission functions of the two lenses was performed: the assumption was made that the probing volume size does not depend significantly on the excitation energy, because the characteristic lines were dominating the excitation spectrum. Through this assumption, the spot sizes and the transmission functions could be separated.
Here, we propose to fully characterize the 2D σi and ηi functions. With the definition of the combined transmission
| TC (E0, Ei) = A0 exp(−exp(zE) − exp(zD) − zE − zD + 2) | (5) |
Two possibilities will be presented in the following. When the experimental setup allows for the separated characterization of the excitation lens in MXRF geometry, the parameters of σE and TE can be derived beforehand. Then, the remaining parameters are accessible through a direct fitting approach when measuring reference samples with known composition and density. If the experimental separation is not possible, all parameters can be fitted directly at the cost of increased uncertainty in the fitting procedure.
After the calibration is performed, eqn (1) can be used when analysing homogeneous samples. For stratified samples with k layers, eqn (1) can be extended with the net peak intensity Φi at measurement position xn given as
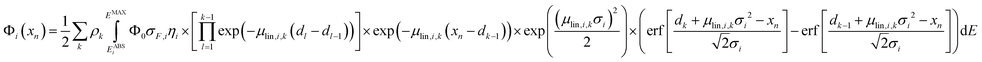 | (6) |
The full methodology for the quantification of a lateral homogenous unknown sample, thus, entails the following steps. First, the used spectrometer must be calibrated with the depth profile measurement of known reference samples. Via fitting the calculated data (with eqn (1)) to the experimental data by adjusting the setup parameters, both the spot sizes and transmission of the lenses are characterized and through these, the 3D functions of integral sensitivity and probing volume size are derived. Second, the CMXRF experiment is performed on the unknown sample either as depth profile, virtual slice or full 3D mapping. For the reconstruction of this measurement, a sample model including sample geometry, density and composition is required as initial assumption. With this model and the calibrated setup parameters, the quantification is performed by fitting the sample parameters to best match the experimental data using eqn (1) or (6).
Material and methods
Spectrometer
In this work a modified commercial spectrometer (M4 Tornado, Bruker Nano GmbH) adapted for CMXRF21 was utilized. It has been equipped with a 50 W Rh-microfocus tube, two polycapillary lenses and two silicon drift detectors (SDD). The polycapillary lenses are mounted with 50° in respect to the sample plane. The setup allows to perform both MXRF and CMXRF sequentially. The tube parameters for all measurements were 50 kV and 1000 μA and measurements were performed in ambient pressure.In addition, measurements were performed with a similar M4 Tornado located at TU Bergakademie Freiberg, equipped with a 30 W Rh-microfocus tube (50 kV, 600 μA) under 20 mbar vacuum atmosphere. The two spectrometers will be referred to as the BLiX setup and the Freiberg setup, respectively.
Samples
For the calibration of the setups, sets of reference samples were available. A collection of pure element reference samples (Bruker Nano calibration palette), a set of thick glass multi-element samples (A4, B2, C3, D3, E3, F3 of Breitländer GmbH22) as well as commercially available razor blades and thin metal foils were used for the BLiX setup. For the Freiberg setup, the same pure element palette was available. For the 3D calibration two multi-element glass reference materials (NIST 610 and BAM S005c) were used.For validation purposes, 7 pulverized standard reference materials (SRMs): NIST 697 Bauxite,23 NIST 1577 Bovine Liver,24 NIST 1646 Estuarine Sediment,25 BCR 129 Hay Powder,26 BCR 176R Fly Ash,27 BCR 667 Estuarine Sediment and CC 144 Sewage Sludge28 were homogenized by shaking and approximately 300 mg were pressed into 12 mm diametrical pellets using a hydraulic press. The density of the samples was calculated based on their size and measured weight.
For validation on stratified samples, 3 different stratified polymer samples, further labelled as multilayer, were measured. The multilayer specimen consists of 5 layers of ethylene propylene diene monomer rubber (EPDM) with varying amounts of zinc oxide as additive. These samples were already analysed in previous work.29
As an application example a goethite needle included in smoky quartz was selected from the mineralogical collection of the Geoscientific Collections of the TU Bergakademie Freiberg and examined with the Freiberg setup. Details for all samples can be found in the Table S1 of the (ESI).†
Experimental
For the calibration of the probing volume in CMXRF mode, depth scans with 5 μm step size and 15 s measurement time per voxel were performed on all six Breitländer glass samples.
First, depth profiling scans with 5 μm, 10 μm and 20 μm step size were performed on one multilayer (ZnO L) with 20 s measurement time per point. Then, 3D measurements were performed on the two other multilayer samples (ZnO B and K) with a step size of 10 μm in depth and 25 μm lateral. The number of steps were 10 times 10 laterally and, depending on the thickness of the sample, between 35 and 63 in depth resulting in 3500 to 6300 voxels. A measurement time of 20 s per voxel was used leading to an overall measurement time of 20 h to 36 h including the stage movement delays.
Software
Measurements performed with CMXRF quickly result in large datasets consisting of thousands of spectra. There are different software solutions to deconvolve large amounts of spectra and retrieve the net peak intensities of fluorescence lines such as PyMCA30 or the software of the instruments (Esprit by Bruker)31 but they are not specifically adapted to handle 3D datasets. For this reason, a deconvolution software called SpecFit was developed which reaches a deconvolution speed of 1250 spectra per minute or approximately 20.8 per second.To calibrate the parameters of the excitation lens, a software called Polytrans was used, see detailed description in Bauer et al.20 Briefly, the Sherman equation, with a calculated X-ray tube spectrum based on an formalism developed by Ebel32 in the used geometry and the transmission function of the excitation lens approximated by a Gumbel distribution, is used to simulate the measured MXRF data on thick one element standards. The parameters of the Gumbel distribution are the fitting parameters which are optimized for a best match between calculation and measurement. The spot size σE(E0) is determined by the analysis of knife edge scans. A Gaussian normal distribution fit on the derivative of the intensity profile directly yields the spot size σE(Ei) for the specific fluorescence energy. An exponential decaying fit on all evaluated spot sizes delivers an energy dependent spot size σE(E0).
For calibration and quantification purposes for CMXRF data, a software called AbsCor was developed. This software can handle 1D to 3D data sets and can also perform besides the here presented calibration and quantification routines absorption correction on the data sets. For this correction 3 different approaches are implemented which have been published already elsewhere 33,34. The functionalities both of SpecFit and AbsCor are described in detail in the SI.
For all the presented data, individual XRF spectra were deconvolved using SpecFit and the resulting net peak intensities were used either for further evaluation with AbsCor or were visualized using Origin 2015 and ImageJ 1.53f51.
Results
Calibration
For the calibration 31 depth profiles were used, leading to an over-determination of the 9 fitting parameters and, thus, ensuring convergence of the optimization.
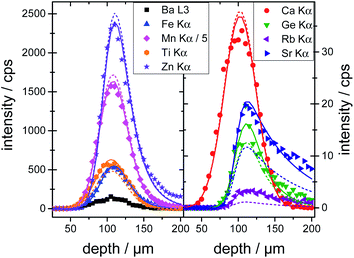
The calibrated depth profiles for the glasses A4 are plotted in Fig. 1. The measured depth profiles are displayed as symbols and the corresponding calculated depth profiles with dashed solid lines. The graphs for the other two glasses can be seen in Fig. S4 and S5 in the ESI.†
Visually the measured and calculated depth profiles show an overall good agreement with deviations especially for the high energy profiles, see the Rb Kα and Sr Kα depth profiles in Fig. 1. As already shown in previous work,21,19 the glasses introduce an uncertainty of approximately 5–10% in the absolute quantification of concentrations. Additionally, the formalism for the calibration spans a multi-dimensional space, where the solution might not be the global minimum. The fluorescence energy of the used elements spans from 3.3 keV for potassium K radiation to 14.9 keV for yttrium K radiation which is the energy range where the sensitivity of the setup is highest. Quantification performed on fluorescence lines with energies outside this range are based solely on extrapolations and will meet higher uncertainties and deviations.
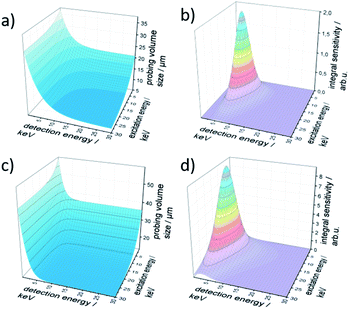
The resulting probing volume size σ is plotted in Fig. 2a in the energy range of 0 keV to 30 keV for both excitation and detection energy. The characteristic exponential decay of polycapillary spot size is clearly visible. Likewise, the trend to smaller probing volume sizes with increasing fluorescence energy is reflected.
The integral sensitivity η is plotted in Fig. 2b. As the integral sensitivity is mainly dependent on the transmission of the lenses it follows closely the Gumbel distributions of the excitation and detection lens. The sensitivity of the setup is mirrored directly by the amplitude of the integral sensitivity.
Validation with thick homogeneous samples (BLiX setup)
To validate the calibration of the BLiX setup, depth profiling measurements on the glasses and the SRM's are quantified. In this case, the surface position x0 and the concentration cj of the element j were the fitting parameters.All six glasses including the three glasses used in the calibration as well as the SRMs were quantified. For glass A4, the quantified depth profiles are shown as solid lines in Fig. 1. Due to the fact, that the concentrations are free fitting parameters, the agreement between measurement and quantification is higher than the one between measurement and calibration.
The quality of both the calibration and the quantification can be assessed by comparing the certified concentration values for all measured glasses and SRM's. In Fig. 3 the deviation of the quantified values from the certified values is plotted as a function of certified concentration values for all samples.
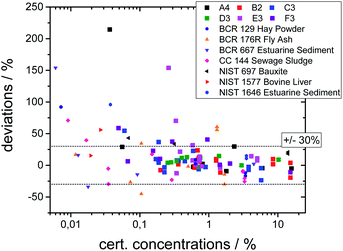 | ||
| Fig. 3 Deviations of the quantified concentration values to the certified values as a function of certified values. | ||
The deviations are below 30% for most elements, but significantly higher deviations occur. This can be explained by the following reasons. First, the statistical uncertainty for trace elements leads to higher uncertainties as visible in Fig. 3. Second, an overlap between fluorescence lines with a high difference in concentration leads to uncertainties in the deconvolution process. Third, especially for the SRM's, inhomogeneities inside the samples or surface contaminations may lead to incorrect values. And last, the calibration procedure introduces energy-dependent uncertainties, because due to a reduced sensitivity the values below 3 keV and above 15 keV have higher uncertainties. Thus, the quantification works best for elements with concentrations above 0.1% and with K-fluorescence lines in this range, i.e. Ca to Sr.
Quantification of layered samples (BLiX setup)
For an estimation of the optimal step size, depth profiles on one multilayer sample were measured with the BLiX setup with varying step sizes and the quantification was performed with the surface position x0, the layer boundaries dl and the mean concentrations cj of element j in every layer as fitting variables. Well-defined starting parameters and bounds are necessary to avoid not reasonable fit results. Usually, a fit takes about 20 seconds per depth profile. With incorrect starting parameters a fit may take significantly longer or may fail to converge to the measured profile.Table S3 and Fig. S6 in the ESI† show the measurements and quantification results, which agree within 10% to the certified values irrespective of the step size. Therefore, for the following measurements a depth step width of 10 μm was selected.
The implemented 3D quantification routine for stratified samples was tested on the other two multilayer specimen ZnO B and K and is discussed in the following.
For quantification, the surface positions x0, the layer boundaries dl and the mean concentrations cj of element j in every layer were fitted for every measured depth profile, neglecting lateral variations of absorption due to heterogeneities of the structure. Here, the overall fitting time on the measured data cubes was 2000 s or approximately half an hour.
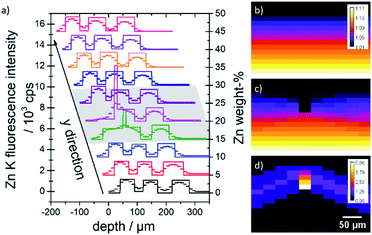
A quantification was performed on both samples. In Fig. 4 measurement data and quantified concentration value distributions are displayed for ZnO B (a) and ZnO K (b). The measured Zn K fluorescence intensities are displayed as grey values in counts per s on the left and the quantified weight percent Zn concentration values are displayed as false colour in cyan on the right. The samples are oriented with the surface on top.
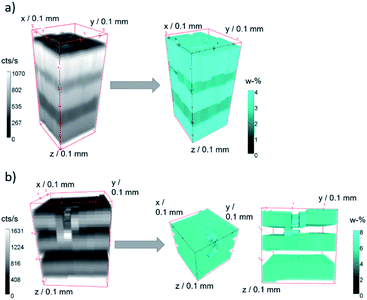 | ||
| Fig. 4 Raw 3D measurement Zn K fluorescence data (grey, left) in counts per second and quantified Zn concentration values (cyan, right) in weight percent for sample ZnO B (a) and ZnO K (b). | ||
For both measurements, the five layers of the specimen are clearly separated, and the fluorescence intensities decrease slightly into the depth. Both samples show lateral heterogeneities. In the case of sample ZnO B, variations in the surface position and the thickness of the layers can be discerned in the measurement data. The difference in surface position to the plane of measurement amounts to about 35 μm over a distance of 250 μm (10 pixel). With the assumption of a maximal probing volume size of 34 μm FWHM for Zn K fluorescence radiation, this slowly varying surface has negligible effect on the absorption of neighbouring depth profiles. The quantified intensity distribution thus can be utilized for absolute thickness and concentration evaluations.
In the case of sample ZnO K, a dent in the surface at the approximate position x = 0 mm, y = 1 mm, z = 0 mm is present. Here, the 3D data can be interpreted, that the first Zn-containing layer together with the second layer were mechanically pushed together, resulting in a thin layer with the same Zn content. This thinner layer is therefore seen as brighter voxels in the quantified reconstruction in Fig. 4b, right.
Fig. 5a exemplifies this with the help of the corresponding depth profiles at x = 0 μm. The reconstructions of the ZnO concentrations (straight lines) and the measured Zn K fluorescence (scatter) are displayed with x- and y-axis offsets. The influence of the changed absorption in the area of the dent (grey shaded area) can be calculated using a simple Lambert–Beer estimation, see Fig. 5(b) and (d). The maximal error amounts to roughly 5%, which is negligible compared to the uncertainties of the calibration.
Table 1 displays the average ZnO concentrations and layer thicknesses for the two samples in comparison to previous work.35 For ZnO B the average concentrations are in good agreement within the uncertainties with a deviation of below 10%. Multilayer ZnO K on the other hand displays significantly lower values for layer 2 and 4 and higher values for 1 and 3. Since the layer thicknesses of this sample are in the range of the probing volume size for Zn K fluorescence radiation (∼34 μm FWHM) a clear separation between the layers is challenging. This does not affect the first layer but can lead to errors in the optimization routine for the following layers which directly leads to erroneous concentrations as observed.
| This work | Previous work | Certified ZnO/% | Deviation/% | |||
|---|---|---|---|---|---|---|
| Calculated ZnO/% | Thickness/μm | Calculated ZnO/% | Thickness/μm | |||
| ZnO B | ||||||
| Layer 0 | 4.16 ± 0.09 | 123 ± 3 | 4.15 ± 0.09 | 125 ± 5 | 4.07 | 2.2 |
| Layer 1 | 2.83 ± 0.11 | 54 ± 5 | 2.68 ± 0.09 | 100 ± 4 | 2.64 | 7.4 |
| Layer 2 | 4.11 ± 0.08 | 106 ± 4 | 4.23 ± 0.18 | 97 ± 4 | 4.07 | 1.0 |
| Layer 3 | 2.79 ± 0.06 | 95 ± 4 | 2.72 ± 0.07 | 89 ± 8 | 2.64 | 5.6 |
| Layer 4 | 4.20 ± 0.07 | 129 ± 2 | 4.12 ± 0.12 | 100 ± 5 | 4.07 | 3.2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| ZnO K | ||||||
| Layer 0 | 5.08 ± 0.23 | 49 ± 2 | 5.16 ± 0.12 | 46 ± 3 | 5.24 | −3.0 |
| Layer 1 | 0.46 ± 0.20 | 35 ± 4 | 0.12 ± 0.07 | 39 ± 3 | 0.00 | — |
| Layer 2 | 4.70 ± 0.09 | 55 ± 3 | 5.29 ± 0.19 | 49 ± 3 | 5.24 | −10.4 |
| Layer 3 | 0.03 ± 0.04 | 43 ± 2 | 0.03 ± 0.01 | 63 ± 4 | 0.00 | — |
| Layer 4 | 4.76 ± 0.10 | 59 ± 2 | 5.17 ± 0.19 | 54 ± 3 | 5.24 | −9.2 |
Additionally, since the samples are about 15 years old, it can be assumed that degradation occurred. This could lead to a variation of the density or the elemental composition, which are sensitive parameters for quantification. This effect could be bigger for thinner samples, as observed, as they are more affected by outside influences. Also, the different measurements were not performed at the same location, possibly causing differences in the measured values due to the already mentioned inhomogeneities. The layer thicknesses slightly differ from the values obtained in the work of Mantouvalou et al.35 This can again be explained by the inhomogeneity of the multilayer.
Quantification of a goethite needle in smoky quartz (Freiberg setup)
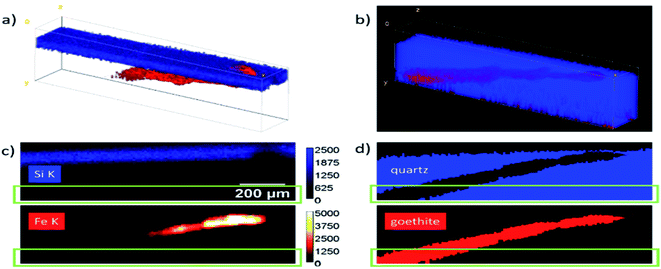
A geological sample from Geoscientific Collections of the TU Bergakademie Freiberg consisting of a goethite needle included in smoky quartz was measured with the Freiberg setup. For reconstruction, a data cube of 20 × 120 × 35 voxels was selected. The sample was modelled as a multilayer system. The first and third layer were assumed to be quartz with a density of 2.65 g cm−3 and the second layer as goethite with a density of 4.28 g cm−3.The surface of the quartz was determined using a scattering peak at 9.9 keV. The thicknesses of all layers were fitted for all xz positions as defined in Fig. 6. Fig. 6a shows the net peak intensities for Fe K in red and Si K in blue in a 3D volume representation. The absorption of the Si K fluorescence can clearly be seen. In panel (b) the reconstructed sample is shown as 3D projection data. Here, only the layer boundaries are the fitting results with blue voxels representing quartz and red voxels the goethite needle. A full rotation of the data cubes as movie can be found in the Video S1 in the ESI.†
For a better comparison, one virtual yx slice of the data cubes is presented in panels (c) and (d). The reconstructed data give additional information on the position and size of the goethite needle. Absorption effects as well as effects which arise due to the different size of the probing volume for the Fe and Si K radiation are corrected in this representation. For deeper parts in the data cube, the fluorescence intensities are reduced so much, that the uncertainty increases significantly. The green rectangles mark the region, where the Fe K intensity is reduced to <1% of the maximum value, resulting in a photon noise of > 10%.
Conclusions
This work introduces a quantification procedure based on the analytical approach for a primary fluorescence calculation in homogeneous bulk and stratified samples measured with laboratory CMXRF setups. Based on a formalism for depth profiling measurements 16,19, the procedure works optimally for samples with slowly varying matrix or density changes such as polymer samples or biological specimen.Software solutions to extract the fluorescence intensities of large data cuboids, to calibrate the utilized setup and to quantify measurements were developed and introduced. A novel feature of the presented calibration is, that it does not use the assumption, that the characteristic lines of the X-ray tube are predominant in the excitation process. Especially when using Rh X-ray tubes, this assumption cannot be readily made, as the characteristic lines are not efficiently transported by the first polycapillary optic. Thereby, the procedure widens the applicability of quantification procedures to essentially all confocal spectrometers using X-ray tube excitation and polycapillary optics.
Additionally, the presented quantification routine and software can handle laboratory full 3D CMXRF datasets for the first time published. It was tested on homogeneous bulk samples yielding good agreements with certified values. Reliable fits and quantitative results for bulk samples can be achieved even for low signal-to-noise ratios. This is true if no significant contamination is distorting the measured depth profile and an overall homogeneity of the sample is assured.
Beyond bulk samples, quantification on 3D datasets of 3 multilayer systems was performed yielding good agreements with certified and prior determined values. Even for samples with layer thicknesses comparable to the size of the probing volume, deviations below 10% were achieved. Additionally, it was shown, that for materials with low mass attenuation like polymers or biological samples, lateral micro-heterogeneities result in uncertainties in the range of 5%.
Finally, the position of a goethite needle included in smoky quartz could be visualized in 3D. Here, although the different phases of the sample have distinctly different matrices and densities, the reconstruction of the surface and position in space of the included needle was successful and resulted in an absorption corrected 3D image. On the one hand, this enables non-destructive mineral inclusion analysis to expand specialized examinations of geo-analytical matter in the future. On the other hand, due to the use of laboratory spectrometers, routine investigations of a statistically relevant number of samples can be envisioned.
The presented quantification routine provides valuable improvements in terms of accessibility, stability and reliability and is therefore a significant step towards broad acceptance of laboratory CMXRF as a fully quantitative method. Yet there is still room for further improvements. The quantification relies on the assumption that the samples are relatively flat and laterally homogeneous. Under this premise the quantification is reliable and fast. If samples with edges or high-density differences are examined, the routine quickly reaches its boundaries. Additionally, implementation of scattered information can further improve the quantification routine. For some special classes of specimen where secondary fluorescence and other higher order effects play a significant role 36,37(higher density samples or samples with distinct absorption edges), these effects could also be included in the quantification methodology. Finally, the implementation of different geometrical structures, e.g., edges and local inclusions is planned for the near future.
Author contributions
Frank Förste: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. Leona Bauer: investigation, writing – review & editing. Korbinian Heimler: investigation, writing – review & editing. Bastian Hansel: investigation, writing – review & editing. Carla Vogt: resources, writing – review & editing. Birgit Kanngieβer: funding acquisition, resources, writing – review & editing. Ioanna Mantouvalou: conceptualization, methodology, supervision, visualization, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We grateful acknowledge support from the Mineralogical collection of the Geoscientific Collections of the TU Bergakademie Freiberg providing the smoky quartz-goethite sample for this investigation.References
- S. Majumdar, J. R. Peralta-Videa, H. Castillo-Michel, J. Hong, C. M. Rico and J. L. Gardea-Torresdey, Anal. Chim. Acta, 2012, 755, 1–16 CrossRef CAS.
- E. S. Rodrigues, M. H. F. Gomes, N. M. Duran, J. G. B. Cassanji, T. N. M. Da Cruz, A. Sant'Anna Neto, S. M. Savassa, E. de Almeida and H. W. P. Carvalho, Front. Recent Dev. Plant Sci., 2018, 9, 1588 CrossRef.
- S. Flude, M. Haschke and M. Storey, Mineral. Mag., 2017, 81, 923–948 CrossRef CAS.
- P. Kump and K. Vogel-Mikuš, J. Instrum., 2018, 13, C05014 CrossRef.
- B. Kanngießer, Spectrochim. Acta, Part B, 2003, 58, 609–614 CrossRef.
- K. Janssens, K. Proost and G. Falkenberg, Spectrochim. Acta, Part B, 2004, 59, 1637–1645 CrossRef.
- T. Wolff, I. Mantouvalou, W. Malzer, J. Nissen, D. Berger, I. Zizak, D. Sokaras, A. Karydas, N. Grlj and P. Pelicon, J. Anal. At. Spectrom., 2009, 24, 669–675 RSC.
- B. Kanngießer, W. Malzer, A. F. Rodriguez and I. Reiche, Spectrochim. Acta, Part B, 2005, 60, 41–47 CrossRef.
- R. D. Perez, H. J. Sánchez, C. A. Perez and M. Rubio, Radiat. Phys. Chem., 2010, 79, 195–200 CrossRef CAS.
- S. Choudhury, T. Swanston, T. L. Varney, D. M. L. Cooper, G. N. George, I. J. Pickering, V. Grimes, B. Bewer and I. Coulthard, Archaeometry, 2016, 58, 207–217 CrossRef CAS.
- F. Förste, I. Mantouvalou, B. Kanngießer, H. Stosnach, L. A.-M. Lachner, K. Fischer and K. Krause, Physiol. Plant., 2020, 168, 934–947 CrossRef.
- U. E. A. Fittschen and G. Falkenberg, Anal. Bioanal. Chem., 2011, 400, 1743–1750 CrossRef CAS PubMed.
- I. Mantouvalou, W. Malzer and B. Kanngießer, Spectrochim. Acta, Part B, 2012, 77, 9–18 CrossRef CAS.
- I. Szalóki, A. Gerényi, G. Radócz, A. Lovas, B. de Samber and L. Vincze, J. Anal. At. Spectrom., 2017, 32, 334–344 RSC.
- I. Szalóki, A. Gerényi, F. Fodor, G. Radócz, V. Czech and L. Vincze, Anal. Chem., 2021, 93, 11660–11668 CrossRef.
- I. Mantouvalou, T. Wolff, C. Seim, V. Stoytschew, W. Malzer and B. Kanngießer, Anal. Chem., 2014, 86, 9774–9780 CrossRef CAS.
- M. Czyzycki, D. Wegrzynek, P. Wrobel and M. Lankosz, X-Ray Spectrom., 2011, 40, 88–95 CrossRef CAS.
- X.-S. Lin, L.-L. Zhang, J.-H. Xu, Y. He, Y. Zheng, S. Yan, D.-X. Liang and A.-G. Li, J. Anal. At. Spectrom., 2021, 36, 2353–2361 RSC.
- I. Mantouvalou, W. Malzer, I. Schaumann, L. Lühl, R. Dargel, C. Vogt and B. Kanngiesser, Anal. Chem., 2008, 80, 819–826 CrossRef CAS PubMed.
- L. J. Bauer, R. Gnewkow, F. Förste, D. Grötzsch, S. Bjeoumikhova, B. Kanngießer and I. Mantouvalou, J. Anal. At. Spectrom., 2021, 36, 2519–2527 RSC.
- T. Lachmann, G. van der Snickt, M. Haschke and I. Mantouvalou, J. Anal. At. Spectrom., 2016, 31, 1989–1997 RSC.
- B. GmbH and B. Eichproben, Glasses (XRF-Monitor Samples), 2010 Search PubMed.
- P. R. William, SRM 697 Bauxite, National Institute of Standards and Technology Search PubMed.
- P. R. William, SRM 1577b Bovine Liver Search PubMed.
- E. Willie, SRM 1646 Estuarine Sediment, May Search PubMed.
- D. Florian, BCR 129 Hay Powder Search PubMed.
- H. Emons, BCR 176R Fly Ash Search PubMed.
- C. C. Doris Florian 144 Sewage Sludge Search PubMed.
- I. Schaumann, W. Malzer, I. Mantouvalou, L. Lühl, B. Kanngießer, R. Dargel, U. Giese and C. Vogt, Spectrochim. Acta, Part B, 2009, 64, 334–340 CrossRef.
- V. A. Solé, E. Papillon, M. Cotte, P. Walter and J. A. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68 CrossRef.
- Bruker, Esprit, Bruker Search PubMed.
- H. Ebel, X-Ray Spectrometry, 1999, 28, 255–266 CrossRef CAS.
- M. Pagels, Diplomarbeit, Technische Universität Berlin, 2007 Search PubMed.
- I. Mantouvalou, T. Lachmann, S. P. Singh, K. Vogel-Mikuš and B. Kanngießer, Anal. Chem., 2017, 89, 5453–5460 CrossRef CAS.
- I. Mantouvalou, Quantitative 3D Micro X-ray fluorescence spectroscopy, Techn. Univ., Berlin, Diss., 2009 Search PubMed.
- D. Sokaras and A.-G. Karydas, Anal. Chem., 2009, 81, 4946–4954 CrossRef CAS.
- K. Tsuji, A. Tabe, P. Wobrauscheck and C. Streli, Powder Diffr., 2015, 30, 109–112 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ja00119e |
| This journal is © The Royal Society of Chemistry 2022 |