Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Concurrent determination of U, Np, Pu, Am, and Cm in clay systems at ultra-trace levels with accelerator mass spectrometry†
Daniel
Glückman
 *a,
Francesca
Quinto
*a,
Francesca
Quinto
 a,
Karin
Hain
b,
Claudia
Joseph
a,
Karin
Hain
b,
Claudia
Joseph
 a,
Vanessa
Montoya
a,
Vanessa
Montoya
 ac,
Peter
Steier
b and
Horst
Geckeis
a
ac,
Peter
Steier
b and
Horst
Geckeis
a
aKarlsruhe Institute of Technology (KIT), Institute for Nuclear Waste Disposal (INE), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: daniel.glueckman@kit.edu
bFaculty of Physics, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria
cEngineered and Geosystems Analysis, Expert Group Waste & Disposal, Institute for Environment, Health and Safety, Belgian Nuclear Research Centre - SCK CEN, 2400 Mol, Belgium
First published on 24th June 2022
Abstract
The geochemistry of actinides under reducing conditions in a deep geological nuclear waste repository is characterized by low solubility and strong sorption to mineral surfaces. The quantification of actinide migration (i.e. diffusion) at resulting concentration levels requires an analytical method able to determine actinide concentrations down to ultra-trace levels (≈fg g−1). In the actual study, such an analytical procedure was tested by using accelerator mass spectrometry (AMS), one of the very few analytical techniques that can presently meet those requirements. Specimens simulating the sample matrix representative for a diffusion experiment in natural clay rock were produced by spiking clay rock powders (Opalinus Clay or Callovo-Oxfordian Clay) and aliquots of corresponding pore waters with the actinide nuclides 233U, 237Np, 244Pu, and 248Cm in amounts ranging from approximately 3 × 10−19 to 5 × 10−15 mol per sample (≈0.07–1000 fg per sample). The actinide nuclides were separated as group via Fe(OH)3 co-precipitation and then analyzed sequentially with AMS. During such analysis a decrease in count rates by up to a factor of 6 was observed in high-matrix clay rock samples compared to low-matrix standard solutions. Since the chemical yield of the actinides in the Fe(OH)3 co-precipitation step prior to analysis turned out to be quantitative, this observation must originate from a reduction of the sputter rate of the actinide nuclides in the AMS ion source, which can be described partly as a dilution effect. By determining chemical-ionization-yield factors, suitable non-isotopic tracers were identified for 237Np and 243Am. This allowed for the concurrent determination of all actinide nuclides at levels down to 3 × 10−19 mol per sample. Different actinides in a deep geological formation may be present in concentration ranges differing by orders of magnitude depending on their chemical form and solubility. Such concentration spreads were simulated by preparing clay rock/pore water samples where each individual sample contained 233U, 237Np, 244Pu, 243Am, and 248Cm at quantities ranging from approximately 3 × 10−19 to 4 × 10−15 mol per sample. The presented sample preparation procedure, in combination with the extraordinary detection sensitivity of AMS allows for the simultaneous determination of diffusion profiles of several actinides at ultra-trace levels within one experiment.
1 Introduction
Clay rock is a potential host rock for the final disposal of high-level nuclear waste (HLW) in deep geological formations. It is expected that under reducing conditions of the clay rock/pore water system actinides potentially released from radioactive waste forms exhibit low solubility and undergo strong sorption. Consequently, actinide species in their reduced oxidation state are expected to be rather immobile, and diffusion as the main transport mechanism in clay rock will be very slow. An analytical method able to determine actinides down to ultra-trace levels (≈fg g−1) is needed to experimentally examine such anticipated diffusion profiles. One of the most sensitive analytical techniques for the determination of rare, long-lived actinides in natural samples is accelerator mass spectrometry (AMS). At the Vienna Environmental Research Accelerator (VERA), the overall detection efficiency, measured as unambiguous 236U events in the detector per atom of 236U in the sample, is equal to approximately 2.2 × 10−4 counts in environmental samples.1 Such sensitivity allows for the determination of actinide nuclides down to quantities of ag per sample or 10−19 mol per sample without previous chemical separation from each other, and in the presence of naturally occurring uranium.2,3The present study aimed at the testing of a highly sensitive method for the analysis of actinides in clay systems by applying AMS and for the simultaneous determination of different actinides in the same clay sample. There are various issues to be tackled for such multi-actinide analyses. Particularly challenging is the choice of yield tracers with a sufficient degree of isotopic purity, as well as the non-availability of isotopic tracers for 237Np and 243Am.2 The use of carefully chosen isotopic and non-isotopic tracers has already been reported to allow for the concurrent AMS measurement of several actinides in one sample and was applied to granitic groundwater samples from the Grimsel Test Site in Switzerland.2,3 In these studies, a group separation of the actinides from the sample matrix via Fe(OH)3 co-precipitation was performed with the use of 239Pu and 248Cm as non-isotopic tracers for the determination of 237Np and 243Am, respectively. These groundwater samples featured a low ionic strength (≈10−3 mol L−1) and therefore had a low matrix content. However, clay rock samples present a significantly more complex matrix that can have an impact on the performance of the chemical procedure, as well as on the analysis with AMS.
In the actual work, the multi-actinide analysis with AMS was tested with clay rock and clay pore water matrices of Opalinus Clay (OPA) and Callovo-Oxfordian Clay (COx). Both clay rock formations are investigated as reference host rocks for the disposal of highly radioactive waste in Switzerland and France, respectively. Before testing the analytical method for different relevant concentration levels of U, Np, Pu, Am, and Cm, solubility and speciation calculations for the five studied actinides under reducing conditions were performed with the software PHREEQC v.3.4
In detail, the following steps were performed: (i) testing of the sensitivity of the analytical method for the determination of U, Np, Pu, and Cm in OPA and COx, (ii) the concurrent determination of U, Np, Pu, Am, and Cm with concentrations ranging from 3 × 10−19 to 4 × 10−15 mol per sample, reflecting their expected relative concentrations, in OPA and COx, and the corresponding pore waters within diffusion experiments, (iii) determination of the suitability of 244Pu and 248Cm as non-isotopic tracers for 237Np and 243Am, respectively, in clay matrix samples, and (iv) investigation of the influence of the sample matrix on the efficiency of the analytical procedure.
2 Experimental
2.1 Materials
Standard solutions of 233U (IRM-040/1), 237Np (Eckert & Ziegler P.O. No P701765), 244Pu (IRM-042a), and 243Am (Eckert & Ziegler P.O. No P624735), and an in-house solution of 248Cm were gravimetrically diluted down to approximately 3.3 × 10−12 mol L−1 to be used as actinide tracers. All dilutions and solutions used in the sample preparation, as well as in the cleaning of the vessels were prepared with ultra-pure water from a Milli-Q® Advantage A10 water purification system (18.2 MΩ cm (22 ± 1) °C; Merck Millipore, Darmstadt, Germany). Nitric acid (65%, ultrapure grade, Roth, Karlsruhe, Germany), hydrochloric acid (34%, ultrapure grade, Roth, Karlsruhe, Germany), ammonia solution (25%, Suprapur®, Merck, Darmstadt, Germany), and iron powder (99.99%, metals basis, Alfa Aesar™, Puratronic™, Fisher Scientific, Schwerte, Germany) were employed as reagents during sample preparation.OPA (borehole BLT-14) was obtained from the underground research laboratory (URL) in Mont Terri located in St. Ursanne, Switzerland,5 while COx (borehole EST 104) originated from the URL in Meuse/Haute-Marne in Bure, France.6 The clay rock samples were ground to fine powders by using a metal blade (Hoffmann SE, München, Germany).
Synthetic OPA and COx pore waters were prepared as described by Pearson et al. (1998),7 with a pH of 7.6 and an ionic strength of 0.36 mol L−1 and by Savoye et al. (2015),8 with a pH of 7.4 and an ionic strength of 0.33 mol L−1, respectively.
2.2 Solubility and speciation calculations
In order to estimate the solubility limit of the investigated actinides in OPA and COx pore water under repository conditions, solubility and speciation calculations were carried out with PHREEQC v.3,4 using the ThermoChimie v.10 database,9 including ionic strength corrections using the specific ion interaction theory (SIT) approach.The geochemical parameters of OPA and COx pore waters used for the calculations, such as elemental composition, pH, and Eh were based on the characterization of natural pore waters and are shown in ESI Table S1.† For OPA pore water, the elemental composition was obtained from Gautschi (2017),10 with a pH of 7.5, an ionic strength of 0.23 mol L−1, and an Eh of –185 mV. The elemental composition of COx pore water is described by Vinsot et al. (2008),11 with a pH of 7.2, an ionic strength of 0.32 mol L−1, and an Eh of –200 mV.
The relative concentrations of the actinides (Table 2) obtained from these speciation calculations served for the preparation of the samples in the actual experiment and for the identification of the most relevant chemical parameters affecting the studied system. The calculated solid phases of the five actinides and their corresponding dominant aquatic species in the two pore waters are shown in ESI Table S2.†
2.3 Sample description
In order to simulate specimens obtained from a clay rock diffusion experiment,12 three types of sample series were prepared containing the actinide nuclides and one of the following matrices: (a) 100 mg of OPA or COx powder (hereafter referred to as matrix type A); (b) 20 mL of OPA or COx synthetic pore water (hereafter referred to as matrix type B); furthermore, (c) spiked standard solutions, containing 5 mL of 1 mol L−1 HNO3, in the absence of clay rock/pore water matrices (hereafter referred to as matrix type C).These three types of sample series were further grouped into four different sample sets: (i) sensitivity test samples, (ii) concentration test samples, (iii) matrix test samples, and (iv) blank samples. In this way, a total of 20 spiked samples and 10 procedural blank samples were obtained, whose compositions are listed in Table 1 and described in more detail in the following paragraphs.
| Sample set | Clay rock/mg | Pore water/mL | Actinide nuclides/(mol per sample) |
|---|---|---|---|
| a Resembling relative solubility concentrations (Table 2). | |||
| (i) Sensitivity test samples | ≈3 × 10−19, 4 × 10−18, 3 × 10−17, 4 × 10−16, or 5 × 10−15 | ||
| Matrix type A | 100 | — | |
| (ii) Concentration test samples | ≈3 × 10−19 to 4 × 10−15a | ||
| Matrix type A | 100 | — | |
| Matrix type B | — | 20 | |
| (iii) Matrix test samples | ≈5 × 10−16 | ||
| Matrix type A | 100 | — | |
| Matrix type B | — | 20 | |
| Matrix type C | — | — | |
| (iv) Blank samples | — | ||
| Matrix type A | 100 | — | |
This sample set aimed at simulating specimens obtained from a real actinide diffusion experiment in clay rock where the actinides – due to their different solubilities in clay pore waters (Table 2) – are present at quantities differing by up to four orders of magnitude from each other. The goal was to show that the concurrent ultra-trace determination of the five actinide nuclides, present at such differing quantities, within the same sample target would be possible.
| Actinide | Actinide concentration in OPA/(mol L−1) | Actinide concentration in COx/(mol L−1) | Actinide amounts added to OPA; COx concentration test samples/(mol per sample) |
|---|---|---|---|
| Utotal | 1.2 × 10−6 | 4.0 × 10−7 | ≈3.7 × 10−15; 2.4 × 10−17 |
| U(IV) | 3.2 × 10−9 | 3.2 × 10−9 | |
| U(VI) | 1.1 × 10−6 | 4.0 × 10−7 | |
| Nptotal | 1.1 × 10−9 | 1.2 × 10−9 | ≈2.1 × 10−18; 4.6 × 10−19 |
| Np(IV) | 1.1 × 10−9 | 1.2 × 10−9 | |
| Np(V) | 9.7 × 10−15 | 5.7 × 10−15 | |
| Putotal | 5.3 × 10−10 | 1.4 × 10−8 | ≈2.8 × 10−19; 2.7 × 10−18 |
| Pu(III) | 5.2 × 10−10 | 1.4 × 10−8 | |
| Pu(IV) | 1.6 × 10−11 | 2.1 × 10−11 | |
| Am(III) | 2.0 × 10−6 | 3.0 × 10−6 | ≈2.9 × 10−15; 2.4 × 10−16 |
| Cm(III) | 1.9 × 10−6 | 3.0 × 10−6 | ≈2.8 × 10−16; 1.8 × 10−17 |
2.4 Sample preparation and analysis
For the determination of diffusion profiles in clay rock, the clay rock sample has to be abraded in thin layers.14 The actinides are then extracted from the obtained clay powder samples with HNO3. As a consequence of the desorption procedure, a variety of clay matrix elements also dissolve. To simulate such a matrix, to each matrix type A sample actinide tracers were added gravimetrically and mixed with 5 mL of 1 mol L−1 HNO3. All samples were prepared at room temperature and under aerobic conditions. The suspensions were left in centrifuge tubes (Sarstedt AG & Co. KG, Nümbrecht, Germany) for 7 d and were occasionally shaken. Subsequently, the samples were centrifuged at 4000 rpm for 10 min (Megafuge 8, Heraeus, Thermo Scientific, Dreieich, Germany) and the supernatants were then processed for the AMS analysis. The samples of matrix type B were acidified with 5 mL of 1 mol L−1 HNO3 and the actinide tracer solutions were added. The as-obtained sample solutions from matrix type A, as well as the samples with type B and C matrices, undergo the same steps of chemical preparation for the AMS analysis, as described in the text below.1 mL of a 3.2 mg mL−1 FeCl3 solution (prepared from iron powder, mentioned in the “Materials” section), was added to each sample of matrix types A, B, and C. This resulted in an Fe concentration of 290 mg L−1. Afterwards, a solution of 25% NH3 was added dropwise, while gently shaking the centrifuge tube in order to obtain a brownish precipitate of Fe(OH)3 with which the actinides were co-precipitated. After 1 day, the suspensions were centrifuged for 10 min at 4000 rpm. Afterwards, the supernatants were discarded and the Fe(OH)3 precipitates were washed twice with 5 mL of a 0.05% NH3 solution. Finally, a few drops of 0.05% NH3 solution were added and the wet precipitates were transferred to Eppendorf tubes (Eppendorf Safe-Lock, 0.5 mL, Eppendorf GmbH, Germany). The samples were centrifuged for 5 min at 4000 rpm and the remaining supernatants were discarded. The Fe(OH)3 precipitates were dried at 80 °C for 4 h, transferred into quartz crucibles and converted to Fe2O3 in a furnace (Nabertherm P330, Nabertherm, Lilienthal, Germany) at 800 °C for 3 h. The obtained Fe2O3 pins, each with a total mass of a few mg and a diameter of approximately 1 mm, were pressed into sample holders suited for the AMS 3 MV tandem accelerator VERA (Vienna Environmental Research Accelerator, Vienna, Austria).1
The actinide nuclides were measured by setting the terminal voltage at 1.65 MV and choosing the 3+ charge state after stripping with helium, following the procedure described by Winkler et al. (2015).15 The count rates of the five actinide nuclides, 233U, 237Np, 244Pu, 243Am, and 248Cm, were sequentially measured from the same sample according to the multi-actinide analysis method.3 In the present study, since the total amount of any actinide nuclide in a sample was known, the measuring time dedicated to each nuclide was accordingly defined a priori and further adjusted during the measurement as approximately inversely proportional to the square root of its count rate. This allowed for optimizing the duration of the measurement of all nuclides in a sample and reducing the difference in the relative uncertainty due to counting statistics between the count rate of nuclides whose concentration differs by orders of magnitude.2 Tuning samples containing the in-house reference material for uranium, Vienna-KkU,16 with a 236U/238U isotopic ratio of (6.98 ± 0.32) × 10−11 were measured in regular intervals in order to correct for variations in the efficiency of detection. Particular care was taken in determining the background levels of the actinides and their origin. To this purpose, the samples were periodically alternated in the measurement sequence with four procedural blanks. Furthermore, the investigated masses, 233 u, 237 u, 244 u, 243 u, and 248 u were scanned in a sample containing an iron–graphite mixture which can be considered as an instrumental blank, which was provided by VERA. In that way, the contribution of a possible background from the ion source can be identified separately from the background of the procedural blanks.
The aforementioned additional 6 procedural blank samples (three samples per clay type) were analysed for the elemental compositions of (a) the supernatants resulting after the simulated desorption, (b) the supernatants resulting after Fe(OH)3 co-precipitation, and (c) the respective washing solutions. In this way, the co-precipitation efficiencies of natural analogues for the studied actinide tracers were investigated, i.e., 238U(VI) for 233U(VI), 232Th(IV) for 237Np(IV) and 244Pu(IV), and La(III), Ce(III), and Eu(III) for 243Am(III) and 248Cm(III). The overall matrix contents of the AMS targets were estimated by determining the co-precipitation efficiencies of the matrix elements, too, such as Na, Ca, and Al, as well as by weighing of the Fe2O3 pins.
The above-mentioned supernatant and washing solutions were analysed with a quadrupole ICP-MS (XSERIES 2 Quadrupole ICP-MS, Thermo Fisher Scientific, Schwerte, Germany). For calibration, we used the certified reference standard SPS-SW2 (Spectrapure Standards as, P.O. Box 190 Manglerud, Oslo, Norway) containing 45 metal elements with concentrations ranging from 2.5 ng mL−1 to 10 μg mL−1.
2.5 Chemical-ionization-yield (CIY) factor
The determined count rates of the five actinide nuclides in the matrix test samples were compared with their added amounts in order to estimate the chemical-ionization-yield (CIY) factors. The ionization yield indicates the fraction of an element in the AMS target that is sputtered as negative ions in the ion source. It was observed in previous studies3,17,18 that different actinides do not exhibit the same ionization yield during an AMS measurement. Generally, these studies show that the ionization yield increases with the atomic number of the actinide element. The chemical yield indicates which fraction of an element is recovered after the several steps of sample preparation, such as an Fe(OH)3 co-precipitation. Since in the frame of an AMS analysis it is not possible to discriminate between the ionization yield and chemical yield, the CIY is used, representing a combination of both phenomena. However, as already mentioned in the previous section, the chemical yields of the actinides were estimated by determining the yields of natural analogues (e.g. Th and U) in the Fe(OH)3 precipitates.In order to evaluate the relative efficiency of the analysis of an actinide nuclide with respect to another one, the CIY can be estimated with the formula in eqn (1), shown as an example for 237Np and 244Pu:
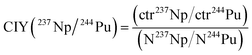 | (1) |
3 Results and discussion
3.1 Solubility and speciation of U, Np, Pu, Am, and Cm
As mentioned in “Experimental”, Section 2, before the preparation of the concentration test samples, solubility and speciation calculations were carried out. In the following, the results of these calculations will be commented in terms of the speciation of the actinides in the chosen clay systems, in order to elucidate the expected concentration ranges of the several actinide species. The most influencing parameters of the solubility of the actinides, and consequently, their aqueous speciation, are pH, redox potential and the carbonate concentration of the clay pore water. The dominating aquatic species of the actinides in both OPA and COx pore water were calculated to be their hydroxo and carbonato complexes (ESI Table S2†), with contributions of sulphate and silicate complexes in the cases of Pu and Am, respectively. The as-calculated solubility concentrations ranged from approximately 10−11 mol L−1 to 10−6 mol L−1 (Table 2).For Am and Cm, the only relevant oxidation state was +III with solubility concentrations of approximately 10−6 mol L−1, while for Np, the dominant oxidation state was +IV with a solubility concentration of approximately 10−9 mol L−1 in both pore waters. For U and Pu, the maximum concentrations were very sensitive to small changes of pH and carbonate concentration of the two pore water systems which stabilize the redox state +VI and +III in U and Pu, respectively. In the case of Pu, a solubility concentration of ≈5 × 10−10 mol L−1 was calculated for OPA pore water, which was lower by a factor of 25 as compared to COx pore water (≈10−8 mol L−1).
This is due to the fact that COx pore water is more reducing, and has a lower pH and higher carbonate concentration, consequently increasing the concentration of Pu(III), which forms soluble carbonato complexes. Pu(IV) is present as Pu(OH)4(aq) to a lesser extent in both clay systems. In the case of U, the +VI oxidation state is by far the most abundant in aqueous solution. U shows a 3 times higher solubility concentration (≈10−6 mol L−1) in OPA pore water as in COx pore water (≈4 × 10−7 mol L−1), since OPA has higher pH and the pore water contains more calcium. Hence, the formation of U(VI) carbonato complexes with stoichiometries Ca2–xUO2(CO3)3−2x (with 0 ≤ x ≤ 2) is favored, increasing the solubility of U.19 A smaller fraction of the soluble U species is due to U(IV) forming U(OH)4 (aq).
3.2 Determination of the background
For the determination of the background levels of the actinide nuclides four procedural blank samples were analysed. In Table 3, the measurement times and numbers of counts in each procedural blank are reported for the investigated nuclides 233U, 237Np, 244Pu, and 248Cm. The masses were analysed for a total measurement time ranging from 1431 s for 237Np in COx Blank II to 3691 s for 244Pu, as well as 248Cm in OPA Blank II. The four investigated procedural blanks showed very low count rates (ctrs) for all actinide nuclides. In some cases, no counts were detected.| OPA Blank I | OPA Blank II | COx Blank I | COx Blank II | Sum | |
|---|---|---|---|---|---|
| Measurement time for 233U/s | 3690 | 3647 | 1477 | 1476 | 10290 |
| Number of counts for 233U | 0 | 0 | 1 | 0 | 1 |
| Measurement time for 237Np/s | 3688 | 3641 | 1474 | 1431 | 10233 |
| Number of counts for 237Np | 2 | 1 | 2 | 0 | 5 |
| Measurement time for 244Pu/s | 3689 | 3691 | 1476 | 1451 | 10307 |
| Number of counts for 244Pu | 1 | 4 | 0 | 0 | 5 |
| Measurement time for 248Cm/s | 3683 | 3691 | 1476 | 1476 | 10328 |
| Number of counts for 248Cm | 2 | 4 | 4 | 6 | 16 |
The quantification of the background of each individual actinide nuclide was performed as follows: the numbers of counts (cts [–]) and the respective measurement times [s] in all four blank samples were summed up. Such combination of the numbers of counts of the four blank samples was possible, since OPA and COx clay rock have similar elemental compositions. Then, the uncertainty of the numbers of counts of each nuclide was determined. Given that the counting of signals obeys the Poisson distribution, the Poisson uncertainty (σP [–]) of the numbers of counts was estimated according to eqn (2):
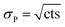 | (2) |
Subsequently, the sum counts and the sum measurement times for each of the four nuclides were divided by each other and multiplied by 3600 s, giving the background as average ctr [h−1] (Table 4).
| 233U | 237Np | 244Pu | 248Cm | |
|---|---|---|---|---|
| Background/(h−1) | 0.34 | 1.76 | 1.75 | 5.58 |
| σ ctr/(h−1) | 0.35 | 0.79 | 0.78 | 1.39 |
In order to determine the statistical uncertainty (σctr [h−1]) of such average ctr, the uncertainty of the number of counts (σP) was divided by the sum measurement time (tsum [s]), as shown in eqn (3):
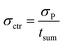 | (3) |
The determined background levels and their respective uncertainties are presented in Table 4.
As can be seen, the background ctr of 248Cm is equal to (5.58 ± 1.39) h−1 and about 16 times higher than that observed for 233U and about 3 times higher than that of 237Np and 244Pu. Such increased background may be explained by the existence of molecular interference during the low energy AMS measurement of mass 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u in the 3+ charge state, as previously investigated by Christl et al. (2014).17 These authors demonstrated how this background might be actually caused by the not complete destruction of the quite stable diatomic cation (232Th16O)3+ during the He stripping process in the tandem accelerator. This phenomenon can be considered a likely explanation for the observed background at mass 248 u also in the actual study, given the presence of naturally occurring 232Th in the samples with matrix type A (determined with ICP-MS and equal to around 0.36 and 0.16 μg per sample in OPA and COx, respectively) and considering the high efficiency of co-precipitation of Th with Fe(OH)3 as will be described in Section 7 (“Efficiency of the Fe(OH)3 co-precipitation”). It is important to note that the observed level of background does not significantly impair the sensitivity in the analysis of 248Cm, since it is consistent with a concentration of 248Cm of about 4 × 10−19 mol per sample, as will be discussed in the following section (“Sensitivity and performance of AMS in clay systems”).
u in the 3+ charge state, as previously investigated by Christl et al. (2014).17 These authors demonstrated how this background might be actually caused by the not complete destruction of the quite stable diatomic cation (232Th16O)3+ during the He stripping process in the tandem accelerator. This phenomenon can be considered a likely explanation for the observed background at mass 248 u also in the actual study, given the presence of naturally occurring 232Th in the samples with matrix type A (determined with ICP-MS and equal to around 0.36 and 0.16 μg per sample in OPA and COx, respectively) and considering the high efficiency of co-precipitation of Th with Fe(OH)3 as will be described in Section 7 (“Efficiency of the Fe(OH)3 co-precipitation”). It is important to note that the observed level of background does not significantly impair the sensitivity in the analysis of 248Cm, since it is consistent with a concentration of 248Cm of about 4 × 10−19 mol per sample, as will be discussed in the following section (“Sensitivity and performance of AMS in clay systems”).
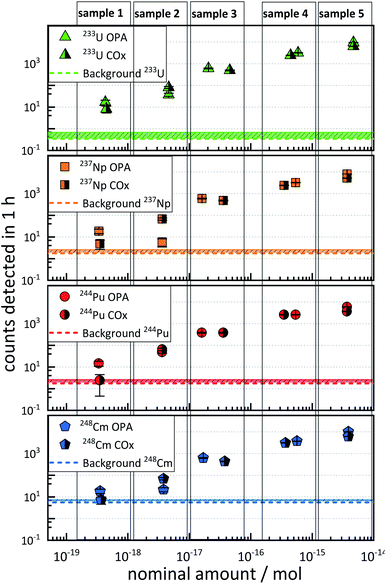
3.3 Sensitivity and performance of AMS in clay systems
The results of the sensitivity test samples are depicted in Fig. 1. Each plot represents the ctr as a function of the nominal amount of 233U, 237Np, 244Pu, and 248Cm in the five different AMS targets (denoted as “sample 1” to “sample 5”), and each of which contains approximately the same amounts of the four actinide nuclides. The ctr of each actinide nuclide increased with increasing nominal amount of nuclides in both OPA and COx samples.It was observed that this increase in ctr was not linear with respect to the relative nominal amount of an actinide nuclide.
Such non-linearity can arise from the fact that different AMS targets may exhibit up to 50% variability in the ctr for a given amount of nuclide.20
The ctrs ranged from a minimum of 2.4 ± 1.6 h−1 (nominal 3 × 10−19 mol 244Pu in COx) to a maximum of (1.02 ± 0.03) × 104 h−1 (nominal 4 × 10−15 mol 248Cm in OPA). The ctrs of 237Np, 244Pu, and 248Cm in COx with a nominal amount of ≈4 × 10−19 mol per nuclide were consistent with the background, indicated as dashed horizontal lines in Fig. 1. The ctrs in samples with nominal nuclide amounts of ≈4 × 10−18 mol or more were significantly higher than the background, except for 4 × 10−18 mol 237Np in OPA. In this case, the ctr was even lower than for a nominal amount of 3 × 10−19 mol. This observation might be explained by an exceptionally low chemical yield of 237Np.
It can be stated that an accurate determination of 233U, 237Np, 244Pu, and 248Cm was possible in matrix type A down to levels of approximately 4 × 10−18 mol, since the determination of nominal amounts of approximately 4 × 10−19 mol per nuclide was, in some cases, hampered by a similarly high ctr in the blank samples.
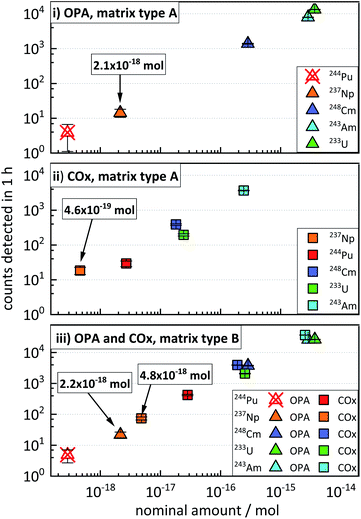
3.4 Concurrent determination of actinides in clay systems over several orders of magnitude
This section illustrates the results from the concentration test samples (described in “Experimental”, Section 3.2), aiming at the simulation of clay and pore water samples from experiments possibly involving the concurrent diffusion of 233U, 237Np, 244Pu, 243Am, and 248Cm. The data presented in Fig. 2 show an increase in the average ctr of each actinide nuclide with increasing nominal amount of nuclides in the four concentration test samples. The ctrs ranged from a minimum of 3.9 ± 2.1 h−1 for 244Pu in OPA (matrix type A) (Fig. 2i) to a maximum of (3.68 ± 0.04) × 104 h−1 for 243Am in COx (matrix type B) (Fig. 2iii). The ctrs of 244Pu in OPA matrix type A and matrix type B were consistent with the background (Fig. 2i and iii). The ctr for a certain nominal amount of nuclides in samples of matrix type B was significantly higher, than in samples of matrix type A. For instance, for a nominal amount of ≈4 × 10−15 mol of 233U in OPA matrix type A, a ctr of (1.33 ± 0.02) × 104 cts h−1 was determined, while for matrix type B, a ctr (2.66 ± 0.03) × 104 h−1 was obtained. This behaviour can be explained by a dilution effect during the sputtering of the AMS target in the AMS ion source, as will be discussed in the following Section 5 (“Influence of the sample matrix on the efficiency of the analytical method”). The determination of actinide nuclides in matrix type A samples was possible down to (2.1 ± 0.6) × 10−18 mol in OPA and (4.6 ± 1.1) × 10−19 mol in COx, respectively. In matrix type B samples actinide nuclides were determined down to (2.2 ± 0.5) × 10−18 mol in OPA and (4.8 ± 0.6) × 10−18 mol in COx, respectively.These results show that multi-actinide analysis can be successfully applied to the concurrent determination of ultra-trace amounts of the five actinide nuclides in the same sample, with relative nuclide quantities covering more than three orders of magnitude.
3.5 Influence of the sample matrix on the efficiency of the analytical method
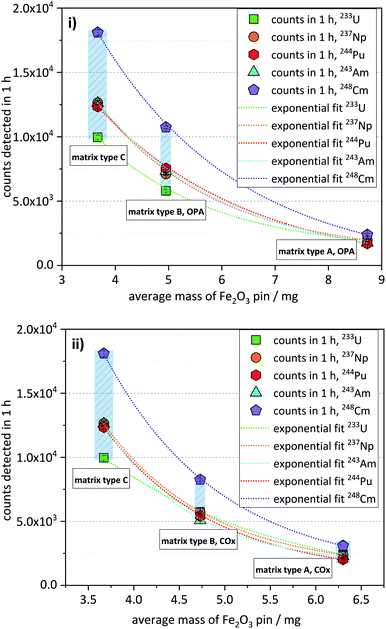
The matrix test samples contained the nuclides 233U, 237Np, 244Pu, 243Am, and 248Cm, each with a nominal concentration of about 5 × 10−16 mol per sample.As already described in the previous section, matrix type A samples, having the highest matrix content, exhibited the lowest ctrs, while samples of matrix type B showed approximately three times higher ctrs. Samples of matrix type C, having the lowest matrix content, showed the highest ctrs, being up to 6 times higher compared with matrix type A (Fig. 3). This trend is shown for both OPA (Fig. 3i) and COx matrices (Fig. 3ii). As can also be seen in Fig. 3, there is a non-linear, but rather a somewhat exponential correlation between the ctr of a nuclide and the average mass of the corresponding Fe2O3 pin (listed in Table 5).
| Matrix type A: OPA | Matrix type A: COx | Matrix type B: OPA | Matrix type B: COx | Matrix type C | |
|---|---|---|---|---|---|
| Mass/(mg) | 8.73 ±0.05 | 6.30 ±0.22 | 4.95 ±0.11 | 4.73 ±0.12 | 3.67 ±0.17 |
As will be described in Section 7 (“Efficiency of the Fe(OH)3 co-precipitation”), the co-precipitation of some matrix elements, like Al and Ca, may be significant and increase the mass of the Fe2O3 pin. In this way, the observed trend of decreasing ctrs with increasing mass of the Fe2O3 pin can be attributed to the corresponding matrix content of the AMS target.
The phenomenon depicted in Fig. 3 can be interpreted as an increase of overall detection efficiency, with decreasing matrix content. The overall detection efficiency is expressed here as an unambiguous number of events counted in the detector per atom of a certain actinide nuclide in the sample during one-hour measurement. The observed trend can be explained considering that in the ion source of the high-intensity Multi-Cathode Source for Negative Ions by Cesium Sputtering type (MC-SNICS),21 used at VERA, a similar sputter rate typically of several mono-layers per second22 can be assumed for all the samples that are analyzed during the same measurement run. The sputtering rate of the actinide nuclides during this process would be lower in the AMS targets with a higher matrix compared to those with a lower matrix but with the same content of actinide nuclides, in a process that could be described as a dilution effect on the observed ctr of the actinides.
A further influence of certain matrix elements on the ionization efficiency of the actinide nuclides cannot be explained by the actual experiment and a more extensive study should be carried out in order to identify such phenomena. Finally, the authors can exclude a dependency of the chemical yield of the Fe(OH)3 co-precipitation of the actinide nuclides on the matrix of the sample, since this has been proven to be quantitative for matrix type A samples, as will be described in Section 7.
3.6 Investigation of non-isotopic tracers
The suitability of non-isotopic tracers was investigated by comparing the CIY factors of several pairs of actinide nuclides and their variation in different matrices (Table 6). The CIY factors were estimated based on the ctrs of the matrix test samples (Section 5) and eqn (1). The average CIY factors ranged from 1.1 ± 0.1 (for 237Np/244Pu) to 1.7 ± 0.4 (for 248Cm/233U). The variation was more pronounced for nuclides with strongly different chemical characteristics, for instance, 248Cm/233U (CIY = 1.3 ± 0.02 to 2.24 ± 0.09), while it was less distinct for nuclides, which are chemically more similar, for instance 237Np/244Pu (CIY = 0.94 ± 0.04 to 1.22 ± 0.1) and 248Cm/243Am (CIY = 1.3 ± 0.1 to 1.49 ± 0.05). It can be assumed that the relative behaviours of two nuclides to each other—both during AMS sample preparation and during sputtering in the AMS ion source—are less affected by the sample matrix if the two nuclides share similar chemical properties. These results show that in clay matrices 244Pu can be used for 237Np as a non-isotopic tracer as well as 248Cm for 243Am, respectively, with relative standard deviations from 8 to 10% in their CIY factors, as observed in the actual study.| 237Np/244Pu | 248Cm/243Am | 248Cm/233U | |
|---|---|---|---|
| Matrix type A, OPA | 1.2 ± 0.1 | 1.3 ± 0.1 | 1.3 ± 0.2 |
| Matrix type A, COx | 1.2 ± 0.1 | 1.3 ± 0.2 | 1.6 ± 0.2 |
| Matrix type B, OPA | 0.94 ± 0.04 | 1.34 ± 0.05 | 2.24 ± 0.09 |
| Matrix type B, COx | 1.04 ± 0.04 | 1.49 ± 0.05 | 1.74 ± 0.06 |
| Matrix type C | 1.04 ± 0.03 | 1.33 ± 0.04 | 2.02 ± 0.07 |
| Average CIY | 1.1 ± 0.1 | 1.32 ± 0.08 | 1.7 ± 0.4 |
3.7 Efficiency of the Fe(OH)3 co-precipitation
Element concentrations and the derived co-precipitation efficiencies described in this section are expressed as average values obtained from the analysis of three separate samples per clay type. In the procedural blank samples of both clay types, more than 99% of Fe (desorbed from clay rock + added as FeCl3), initially dissolved in the acidic extract, was recovered in the Fe(OH)3 precipitate, as shown in Table 7. Hence, the Fe(OH)3 precipitation was quantitative. Furthermore, the two washing steps of the precipitate did not significantly affect the stability of the Fe(OH)3 precipitate, since the concentration of re-dissolved Fe in the washing solution was negligible. In fact, the fraction of Fe present in the Fe(OH)3 precipitate after each washing step was less than 1% lower compared to the initial precipitate.| Element | Fraction co-precipitated with Fe(OH)3/% | Fraction present in the Fe(OH)3 precipitate, after the 1st washing step/% | Fraction present in the Fe(OH)3 precipitate, after the 2nd washing step/% | |||
|---|---|---|---|---|---|---|
| OPA | COx | OPA | COx | OPA | COx | |
| Na(I) | 11.1 ± 0.5 | 1.7 ± 0.1 | 9.7 ± 0.6 | 0.8 ± 0.2 | 8.8 ± 0.7 | 0.8 ± 0.2 |
| K(I) | 16.5 ± 0.5 | 9.6 ± 0.1 | 10.6 ± 1.1 | 9.6 ± 0.1 | 4.8 ± 1.7 | 9.6 ± 0.1 |
| Mg(II) | 20.1 ± 0.9 | 15.6 ± 0.5 | 16.3 ± 1.7 | 11.4 ± 1.4 | 15.2 ± 2.0 | 11.2 ± 1.4 |
| Ca(II) | 19.7 ± 0.8 | 14.1 ± 0.2 | 16.2 ± 1.5 | 10.2 ± 1.0 | 15.1 ± 1.8 | 10.0 ± 1.7 |
| Sr(II) | 25.3 ± 1.7 | 20.4 ± 0.7 | 22.4 ± 2.3 | 16.7 ± 1.5 | 21.5 ± 2.5 | 16.5 ± 1.6 |
| Al(III) | 99.8 ± 4.2 | 98.2 ± 2.5 | 97.8 ± 4.9 | 97.1 ± 3.1 | 96.1 ± 5.3 | 94.7 ± 3.8 |
| Fe(III) | 99.9 ± 1.9 | 99.8 ± 1.3 | 99.5 ± 2.0 | 99.5 ± 1.4 | 99.4 ± 2.1 | 99.4 ± 1.5 |
| La(III) | 99.0 ± 3.7 | 99.7 ± 2.2 | 98.5 ± 3.8 | 99.4 ± 2.4 | 98.3 ± 4.0 | 99.2 ± 2.5 |
| Ce(III) | 99.5 ± 3.4 | 99.8 ± 3.4 | 99.2 ± 3.6 | 99.6 ± 3.5 | 99.1 ± 3.7 | 99.5 ± 3.6 |
| Eu(III) | 98.3 ± 3.9 | 96.8 ± 3.2 | 97.1 ± 4.0 | 94.6 ± 3.4 | 95.8 ± 4.1 | 92.5 ± 3.6 |
| 232Th(IV) | 99.8 ± 2.8 | 99.5 ± 3.2 | 99.4 ± 3.1 | 99.2 ± 3.4 | 99.3 ± 3.1 | 98.9 ± 3.4 |
| 238U(VI) | 96.6 ± 3.4 | 95.2 ± 4.1 | 94.1 ± 3.7 | 91.8 ± 4.4 | 91.6 ± 3.9 | 88.5 ± 4.7 |
Elements listed in Table 7 with oxidation states +III and higher were quantitatively co-precipitated with Fe(OH)3. In particular, the naturally occurring lanthanides, such as La(III) and Ce(III) which serve as chemical analogues of 243Am(III) and 248Cm(III), and Th(IV) as an analogue of 244Pu(IV), show a co-precipitation efficiency of about 99% and also negligible re-dissolution during the two washing steps. Eu(III) shows a somewhat lower efficiency for its co-precipitation with Fe(OH)3 with a value of (96.8 ± 3.2)% for, e.g., the blanks containing the COx clay matrix and a higher degree of re-dissolution in the two washing steps, down to (92.5 ± 3.6)%, for the same blanks, accounting for around 4.3% of the amount of Eu(III) initially co-precipitated. Such a value is, however, consistent with the statistical uncertainty of the aforementioned efficiencies. A similar trend was observed for the naturally occurring 238U(VI) with an initial co-precipitation efficiency of (96.6 ± 3.4)% and (95.2 ± 4.1)%, for the blanks containing OPA and COx clay, respectively, and a subsequent re-dissolution after the two washing steps of 5% and 5.6%, respectively. Also in this case, the fraction of re-dissolved U(VI) is consistent within the statistical uncertainties. The very high efficiency (≥95%) for the final co-precipitation of Al(III) with Fe(OH)3 implies that an amount of Al equal to approximately 436 and 132 μg, for the OPA and COx blanks respectively, is to be found in the Fe2O3 pin of the AMS target. As shown in Table 7, the mono and divalent matrix elements (i.e. Na, K, Mg, Ca, and Sr) were not quantitatively co-precipitated. In fact, after the second washing step, a fraction ≤22% of these elements was recovered in the precipitates. However, even such low co-precipitation efficiencies can significantly contribute to the matrix of the final AMS target. This is particularly relevant for Ca, whose concentration in the acidic extract of the clay samples is at the level of several hundred mg L−1 (Table 8) and, in this way, contributed 509 μg (OPA) and 496 μg (COx) to the Fe2O3 pin of the final AMS target.
| Element | Initial concentration in desorption solution/(mg L−1) | |
|---|---|---|
| OPA | COx | |
| a Fe concentrations also include Fe originating from the FeCl3 solution (290 mg L−1) added prior to the Fe(OH)3 precipitation step. | ||
| Na(I) | (2.02 ± 0.08) × 101 | (9.68 ± 0.02) × 100 |
| K(I) | (1.65 ± 0.04) × 101 | (1.19 ± 0.02) × 101 |
| Mg(II) | (6.5 ± 0.2) × 101 | (3.08 ± 0.02) × 101 |
| Ca(II) | (4.8 ± 0.2) × 102 | (7.10 ± 0.03) × 102 |
| Sr(II) | (2.1 ± 0.1) × 100 | (4.15 ± 0.09) × 100 |
| Al(III) | (6.5 ± 0.2) × 101 | (2.00 ± 0.03) × 101 |
| Fe(III)a | (5.83 ± 0.01) × 102 | (4.68 ± 0.06) × 102 |
| La(III) | (4.8 ± 0.2) × 10−2 | (6.1 ± 0.1) × 10−2 |
| Ce(III) | (1.78 ± 0.06) × 10−1 | (1.19 ± 0.04) × 10−1 |
| Eu(III) | (5.8 ± 0.2) × 10−3 | (3.3 ± 0.1) × 10−3 |
| 232Th(IV) | (5.2 ± 0.1) × 10−2 | (2.29 ± 0.07) × 10−2 |
| 238U(VI) | (2.85 ± 0.09) × 10−3 | (2.15 ± 0.08) × 10−3 |
This experiment indicates that, while a high efficiency of the Fe(OH)3 co-precipitation for the group separation of the tracer actinide nuclides 233U(VI), 237Np(V), 244Pu(IV), 243Am(III), and 248Cm(III) similar to their natural analogues can be assumed, their separation from the matrix elements is only partial and has to be accounted responsible for the significantly higher mass of the AMS targets of samples of matrix type A compared with those of matrix types B and C, as listed in Table 5.
4 Conclusions
The present study demonstrated the analytical capability of AMS in OPA and COx clay matrices by an accurate and sensitive determination of the actinide nuclides 233U, 237Np, 244Pu, and 248Cm down to 3 × 10−19 mol per sample. Even though an up to 6-fold decrease in the ctr of the actinide nuclides was observed in the clay matrix samples compared to the standard ones, that can be attributed to the undesired co-precipitation of some matrix elements with Fe(OH)3, the employed sample preparation procedure presents the advantage of a quantitative co-precipitation of the actinides. This allows for the use of non-isotopic tracers, such as 244Pu for 237Np and 248Cm for 243Am, as demonstrated in this work and, in this way, for the concurrent determination of the investigated actinide nuclides.It was shown that such concurrent determination of 233U, 237Np, 244Pu, 243Am, and 248Cm, from the same AMS target is also possible in samples in which the investigated nuclides are present at quantities covering more than three orders of magnitude, down to 5× 10−19 mol per sample, resembling their relative solubility in clay pore water.
The presented experimental results demonstrate that samples from laboratory diffusion experiments for actinides can be analysed down to concentration levels up to eight orders of magnitude lower as compared to those obtained in the study of Joseph et al. (2013)12 for 233U diffusion through OPA. Furthermore, this study offers the analytical capability of studying the simultaneous diffusion of U, Np, Pu, Am, and Cm through the same clay sample, down to ultra-trace levels. The outcomes of this study pave the way to the still unexplored experimental observation of the diffusion behaviour of actinides at ultra-trace levels through clay rock.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank F. Geyer for carrying out the ICP-MS measurements and M. Plaschke for his scientific advice.References
- P. Steier, K. Hain, U. Klötzli, J. Lachner, A. Priller, S. Winkler and R. Golser, Nucl. Instrum. Methods Phys. Res., Sect. B, 2019, 458, 82–89 CrossRef CAS.
- F. Quinto, R. Golser, M. Lagos, M. Plaschke, T. Schäfer, P. Steier and H. Geckeis, Anal. Chem., 2015, 87, 5766–5773 CrossRef CAS PubMed.
- F. Quinto, I. Blechschmidt, C. Garcia Perez, H. Geckeis, F. Geyer, R. Golser, F. Huber, M. Lagos, B. Lanyon, M. Plaschke, P. Steier and T. Schäfer, Anal. Chem., 2017, 89, 7182–7189 CrossRef CAS PubMed.
- PHREEQC v.3, https://wwwbrr.cr.usgs.gov/projects/GWC_cou-pled/phreeqc/ Search PubMed.
- P. Bossart and M. Thury, Mont Terri Rock Laboratory – Project, Programme 1996 to 2007 and Results, 2008 Search PubMed.
- ANDRA, Evaluation of the Feasibility of a Geological Repository in an Argillaceous Formation, 2005 Search PubMed.
- F. J. Pearson, OPALINUS CLAY EXPERIMENTAL WATER: A1Type, Version 980318, 1998 Search PubMed.
- S. Savoye, C. Beaucaire, B. Grenut and A. Fayette, Appl. Geochem., 2015, 61, 41–52 CrossRef CAS.
- Thermochimie v.10 Database, https://www.thermochimie-tdb.com/ Search PubMed.
- A. Gautschi, Grundwasser, 2017, 22, 221–233 CrossRef CAS.
- A. Vinsot, S. Mettler and S. Wechner, Phys. Chem. Earth, 2008, 33, S75–S86 CrossRef.
- C. Joseph, L. R. Van Loon, A. Jakob, R. Steudtner, K. Schmeide, S. Sachs and G. Bernhard, Geochim. Cosmochim. Acta, 2013, 109, 74–89 CrossRef CAS.
- P. Steier, F. Dellinger, O. Forstner, R. Golser, K. Knie, W. Kutschera, A. Priller, F. Quinto, M. Srncik, F. Terrasi, C. Vockenhuber, A. Wallner, G. Wallner and E. M. Wild, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 268, 1045–1049 CrossRef.
- L. R. Van Loon and W. Müller, Appl. Radiat. Isot., 2014, 90, 197–202 CrossRef CAS PubMed.
- S. R. Winkler, P. Steier, J. Buchriegler, J. Lachner, J. Pitters, A. Priller and R. Golser, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 361, 458–464 CrossRef CAS.
- P. Steier, M. Bichler, L. Keith Fifield, R. Golser, W. Kutschera, A. Priller, F. Quinto, S. Richter, M. Srncik, P. Terrasi, L. Wacker, A. Wallner, G. Wallner, K. M. Wilcken and E. Maria Wild, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266, 2246–2250 CrossRef CAS.
- M. Christl, X. Dai, J. Lachner, S. Kramer-Tremblay and H. A. Synal, Nucl. Instrum. Methods Phys. Res., Sect. B, 2014, 331, 225–232 CrossRef CAS.
- M. López-Lora and E. Chamizo, Nucl. Instrum. Methods Phys. Res., Sect. B, 2019, 455, 39–51 CrossRef.
- J. Y. Lee, S. Amayri, V. Montoya, D. Fellhauer, X. Gaona and M. Altmaier, Appl. Geochem., 2019, 111, 104374 CrossRef CAS.
- F. Quinto, E. Hrnecek, M. Krachler, W. Shotyk, P. Steier and S. R. Winkler, Environ. Sci. Process. Impacts, 2013, 15, 839–847 RSC.
- C. Vockenhuber, I. Ahmad, R. Golser, W. Kutschera, V. Liechtenstein, A. Priller, P. Steier and S. Winkler, Int. J. Mass Spectrom., 2003, 223–224, 713–732 CrossRef CAS.
- R. Middleton, D. Juenemann and J. Klein, Nucl. Instrum. Methods Phys. Res., Sect. B, 1994, 93, 39–51 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ja00107a |
| This journal is © The Royal Society of Chemistry 2022 |